| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
40. Распространение излучения
Яркость элементарной излучающей площадки в общем случае зависит как от ее расположения, так и от направления излучения [см. формулу (172)]. Однако яркости многих излучателей (например, раскаленных тел, светорассеивающих поверхностей) можно принять независимыми от направления. Тогда, как это следует из формулы (172),

где  сила света площадки
сила света площадки  по направлению нормали при постоянной яркости.
по направлению нормали при постоянной яркости.
Такое излучение называется излучением, подчиняющимся закону Ламберта.
Площадка  (рис. 87) имеет одинаковую во всех направлениях яркость
(рис. 87) имеет одинаковую во всех направлениях яркость 
Элементарный телесный угол, охватывающий пространство между двумя круговыми конусами с общей вершиной в центре

Рис. 87. Излучение с площадки 

Рис. 88. Поток излучения между параллельными и соосными круглымиплощадками
площадки  и плоскими углами между образующими и нормалью
и плоскими углами между образующими и нормалью  [см. формулу (162)],
[см. формулу (162)], 
Учитывая формулы (162) и (173), получаем, что поток от элемента поверхности  в пределах телесного угла
в пределах телесного угла  будет равен
будет равен

Полный поток излучения от площадки  в полусферу
в полусферу

Разделив обе части формулы (188) на площадь  источника, получим, что для плоской поверхности, излучающей по закону Ламберта, энергетическая светимость
источника, получим, что для плоской поверхности, излучающей по закону Ламберта, энергетическая светимость

Следовательно, если на светорассеивающей поверхности получена энергетическая освещенность Ее, а она равна энергетической светимости, то энергетическая яркость этой поверхности согласно выражению (189)

Найдем поток излучения  в телесном угле
в телесном угле  ограниченном внутренней полостью прямого кругового конуса с плоским углом при вершине, равным 2а, от излучающей малой площадки
ограниченном внутренней полостью прямого кругового конуса с плоским углом при вершине, равным 2а, от излучающей малой площадки  нормаль к которой совпадает с осью конуса (рис. 88). Примем, что излучающая площадка является идеально рассеивающей, т. е. подчиняется закону Ламберта.
нормаль к которой совпадает с осью конуса (рис. 88). Примем, что излучающая площадка является идеально рассеивающей, т. е. подчиняется закону Ламберта.
Интегрируя равенство (187) при  в пределах от
в пределах от  до а, получаем искомый поток излучения от элементарной площадки
до а, получаем искомый поток излучения от элементарной площадки 


Рис. 89. Поток излучения между произвольно расположенными площадками

Рис. 90. Схема для определения освещенности площадки  параллельной излучающей площадке
параллельной излучающей площадке 
Этот поток упадет на площадку 
Найдем поток излучения с круговой площадки  на параллельную ей площадку
на параллельную ей площадку  в пределах телесного угла
в пределах телесного угла  ограниченного боковой поверхностью прямого кругового конуса с вершиной центра площадки
ограниченного боковой поверхностью прямого кругового конуса с вершиной центра площадки 
Обозначим плоский угол при вершине конуса  Примем, что энергетическая яркость площадки
Примем, что энергетическая яркость площадки  одинакова по всем направлениям.
одинакова по всем направлениям.
При отсутствии потерь поток излучения, падающий на площадки  т. е. в прямом и обратном направлении, одинаков. Поэтому его значение можно определить по формуле (191) с внесением следующих изменений:
т. е. в прямом и обратном направлении, одинаков. Поэтому его значение можно определить по формуле (191) с внесением следующих изменений:  заменим на
заменим на  угол
угол  на угол
на угол  Таким образом, поток излучения, поступающий с площадки
Таким образом, поток излучения, поступающий с площадки  на площадку
на площадку 

Заметим, что яркости излучающей и облучаемой площадок одинаковы.
Энергетическая освещенность площадки 
Найдем поток излучения  поступающий с элементарного излучателя (площадки
поступающий с элементарного излучателя (площадки  на малую площадку
на малую площадку  (рис. 89), при произвольной ориентации их друг относительно друга. Центры площадок лежат на оси образованной световой трубки и находятся на расстоянии I друг от друга, а нормали к площадкам с осью трубки образуют соответственно углы
(рис. 89), при произвольной ориентации их друг относительно друга. Центры площадок лежат на оси образованной световой трубки и находятся на расстоянии I друг от друга, а нормали к площадкам с осью трубки образуют соответственно углы 
Поток излучения, поступающий на площадку  определим по формуле, получаемой из равенства (187):
определим по формуле, получаемой из равенства (187):

Из рис. 89 следует, что  поэтому
поэтому

Формула (194) справедлива при соблюдении закона Ламберта.
На основании закона сохранения энергии, т. е. при сохранении потока излучения, можно также написать:

где 
Рассмотрим частный случай, когда площадки  параллельны, но их нормали не совпадают (рис. 90). Из рис. 90 следует, что
параллельны, но их нормали не совпадают (рис. 90). Из рис. 90 следует, что 
Подставив эти данные в формулу (195), получим

Если 

Энергетические освещенности соответственно равны:

Следовательно,

Энергетическая освещенность убывает к краю площадки пропорционально косинусу четвертой степени угла направления излучения относительно нормали к освещаемой площадке.
Из формул (193) и (195) следует, что

т. e. произведение площади нормального сечения световой трубки  и элементарного телесного угла
и элементарного телесного угла  с вершиной в плоскости этого сечения сохраняется инвариантным для любого сечения световой трубки.
с вершиной в плоскости этого сечения сохраняется инвариантным для любого сечения световой трубки.
Инвариант по формуле (197) называют геометрическим фактором и обозначают  Заметим, что геометрический фактор в виде знаменателя входит в формулу (173), которая в этом случае в энергетических величинах получает следующий вид:
Заметим, что геометрический фактор в виде знаменателя входит в формулу (173), которая в этом случае в энергетических величинах получает следующий вид: 
Рассмотрим более общий случай, когда световая трубка преломляется поверхностью раздела двух сред с показателями преломления  (рис. 91). Пусть площадь элемента преломляющей
(рис. 91). Пусть площадь элемента преломляющей

Рис. 91. Преломленная световая трубка

Рис. 92. Схема для вывода инварианта Штраубеля
поверхности  а телесные углы, имеющие вершины в центре этого элемента и опирающиеся на торцы
а телесные углы, имеющие вершины в центре этого элемента и опирающиеся на торцы  световой трубки,
световой трубки,  Если углы между нормалями к площадкам
Если углы между нормалями к площадкам  и преломленной осью световой трубки обозначить через
и преломленной осью световой трубки обозначить через  соответственно, то получим:
соответственно, то получим:

где  и
и  расстояния между центрами площадки
расстояния между центрами площадки  и площадок
и площадок  соответственно.
соответственно.
Если вершины телесных углов поместить в центры площадок  а контур площадки
а контур площадки  принять за направляющую, то значения этих телесных углов будут соответственно равны:
принять за направляющую, то значения этих телесных углов будут соответственно равны: 

где  углы падения и преломления в центре площадки
углы падения и преломления в центре площадки 
Рассмотрим световую трубку с торцами  состоящую из двух частей, границей которых является площадка
состоящую из двух частей, границей которых является площадка  На основании инварианта (197) получим следующие два равенства:
На основании инварианта (197) получим следующие два равенства:

и

из которых следует, что

Обратимся к рис. 92, на котором показаны элементарные площадки  расстояние между центрами которых
расстояние между центрами которых  Телесный угол, соответствующий площадке
Телесный угол, соответствующий площадке  с вершиной в центре площадки
с вершиной в центре площадки  обозначим через
обозначим через  Этот телесный угол высекает на сфере радиуса
Этот телесный угол высекает на сфере радиуса  площадку
площадку  (угол — угол между нормалями к площадкам). Угол
(угол — угол между нормалями к площадкам). Угол  сохраняет свое значение и для преломленной части световой трубки (на рисунке не показана), так как лучи при преломлении не выходят из плоскости падения.
сохраняет свое значение и для преломленной части световой трубки (на рисунке не показана), так как лучи при преломлении не выходят из плоскости падения.
По определению телесного угла 
Площадь высекаемого этим телесным  элементарного участка сферы, который можно считать прямоугольником,
элементарного участка сферы, который можно считать прямоугольником, 
Следовательно,

По аналогии для преломленной части световой трубки

При дифференцировании уравнения закона преломления  получим
получим 
Перемножая левые и правые части двух последних равенств и умножая их на  находим:
находим:

Последовательная подстановка равенств  в формулу (201) дает следующий инвариант:
в формулу (201) дает следующий инвариант:

Этот инвариант — инвариант Штраубеля — имеет место для световой трубки с любым числом преломлений, т. е.

где  число преломляющих поверхностей.
число преломляющих поверхностей.
Для случая действия зеркальной отражающей поверхности при  из равенств (199) и (200) следует, что
из равенств (199) и (200) следует, что  т. е. при отражении элементарной световой трубки значения телесных углов, опирающихся на отражающую площадку, в пространствах изображений и предметов сохраняются, а инвариант Штраубеля для одной отражающей поверхности имеет вид:
т. е. при отражении элементарной световой трубки значения телесных углов, опирающихся на отражающую площадку, в пространствах изображений и предметов сохраняются, а инвариант Штраубеля для одной отражающей поверхности имеет вид:

Инвариант Штраубеля, представленный формулами  имеет место при постоянстве потока излучения как при преломлении, так и при отражении.
имеет место при постоянстве потока излучения как при преломлении, так и при отражении.
Используя понятие геометрического фактора  получим, что
получим, что 
Если световая трубка заполнена оптически однородной средой, то яркость светового пучка не изменяется  в формулах (191)-(194)].
в формулах (191)-(194)].
При преломлении световой трубки в условиях постоянства потока излучения  и при разных показателях преломления
и при разных показателях преломления  в пространствах предмета и изображения имеем: для пространства предметов
в пространствах предмета и изображения имеем: для пространства предметов  для пространства изображений
для пространства изображений  Приравнивая правые части этих равенств и используя инвариант Штраубеля (202), получаем для одной преломляющей поверхности
Приравнивая правые части этих равенств и используя инвариант Штраубеля (202), получаем для одной преломляющей поверхности

Для последовательных преломлений через  поверхностей энергетическая яркость на выходе системы
поверхностей энергетическая яркость на выходе системы

Из формулы (205) следует, что отношение энергетической яркости к квадрату показателя преломления инвариантно на всем протяжении элементарного пучка, не имеющего потерь за счет поглощения и отражения.
Все зависимости, приведенные в этом параграфе, относятся и к световым величинам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
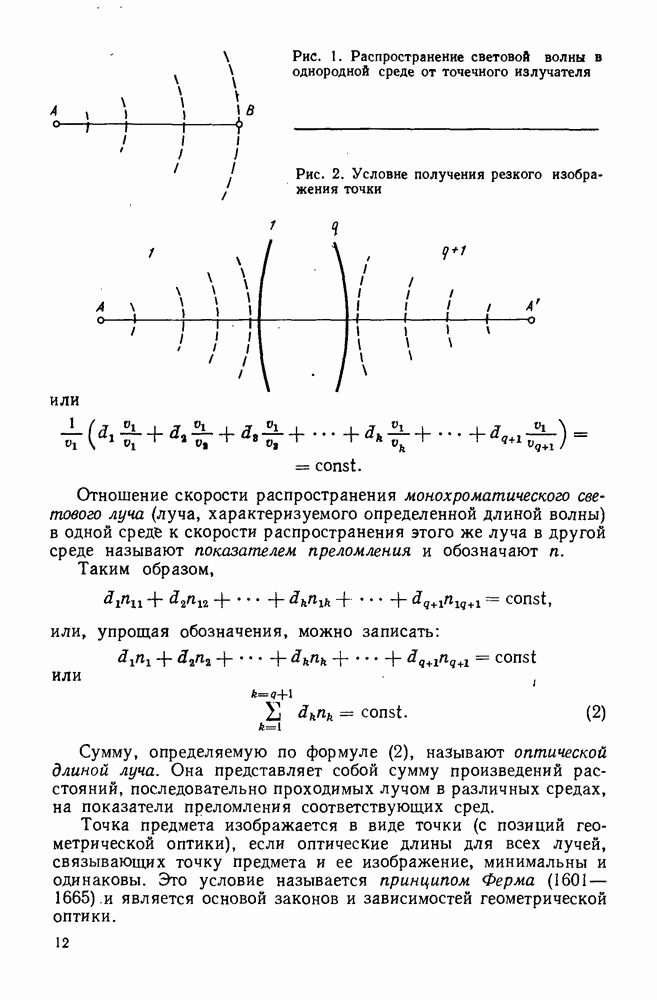
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
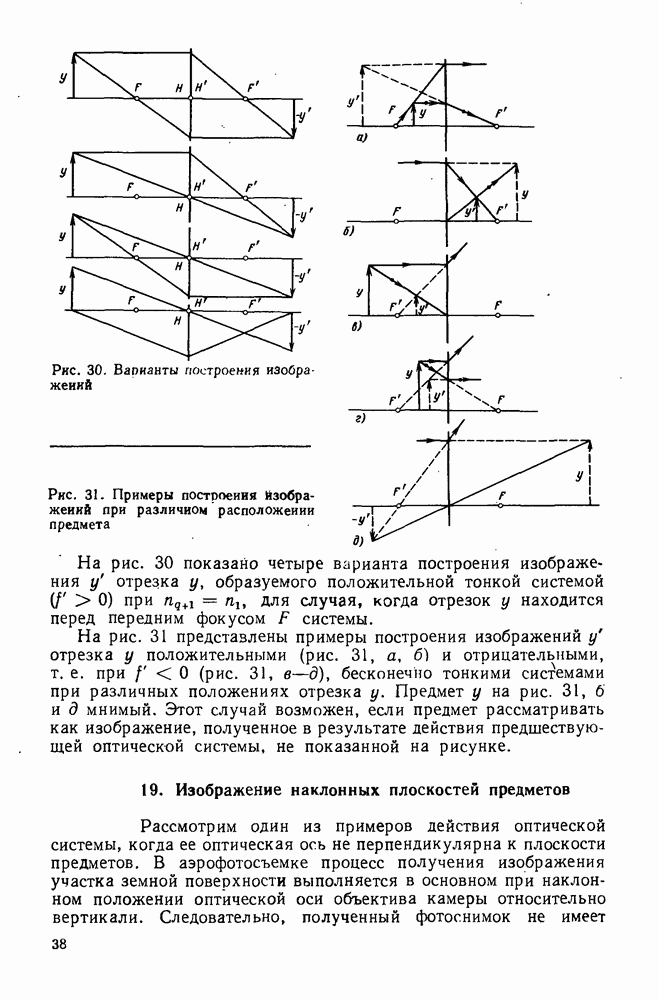
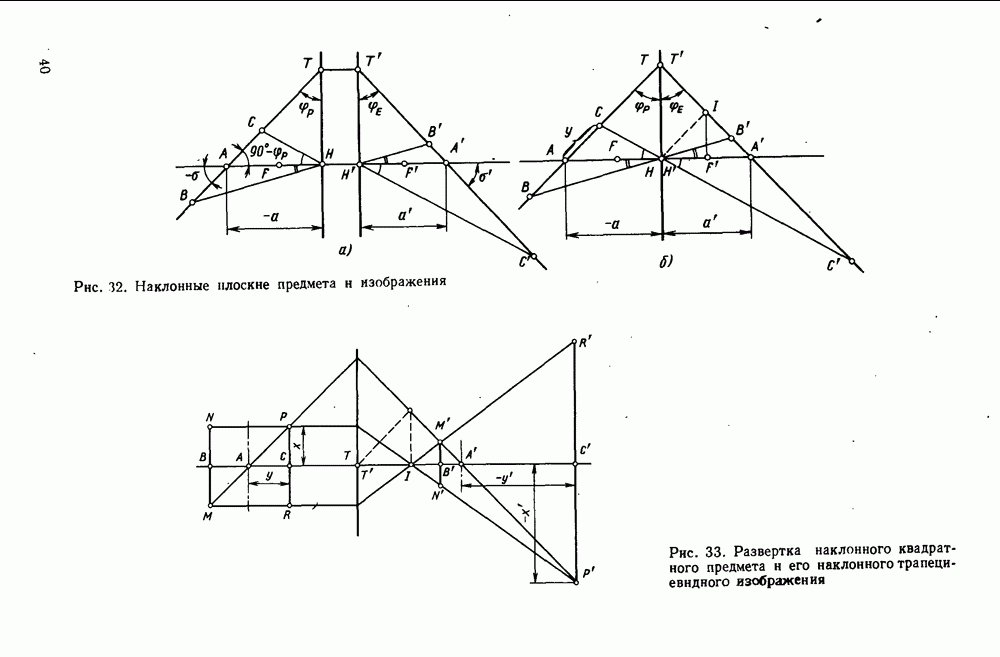
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
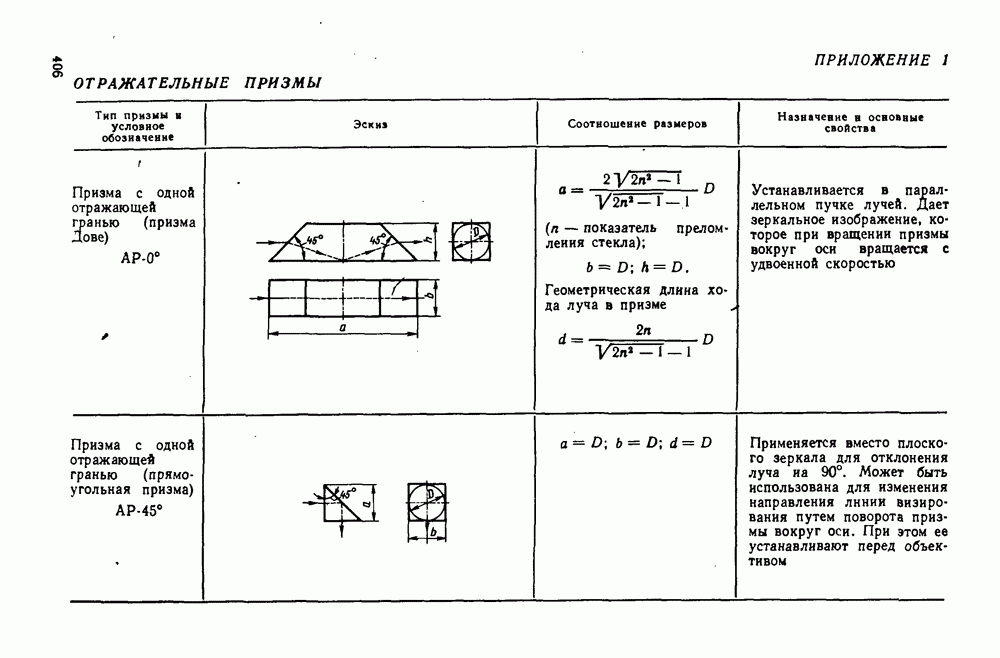
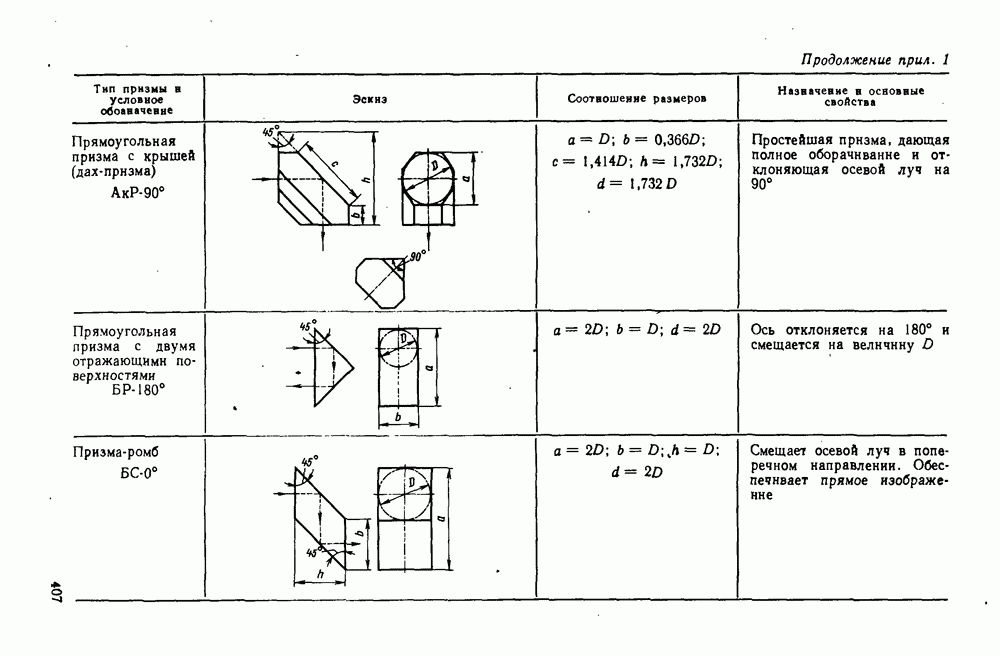
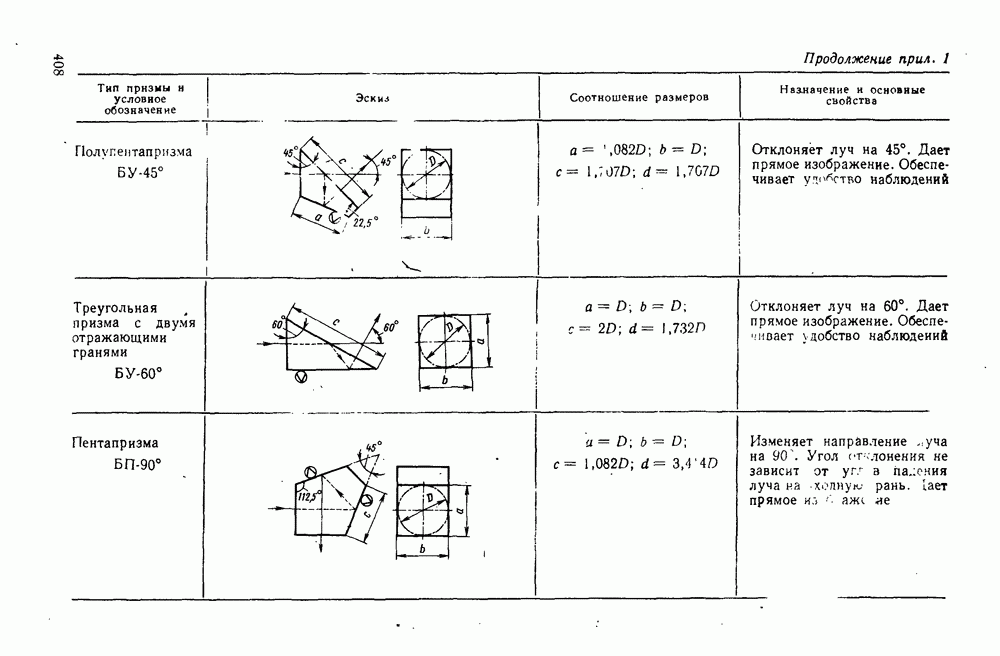
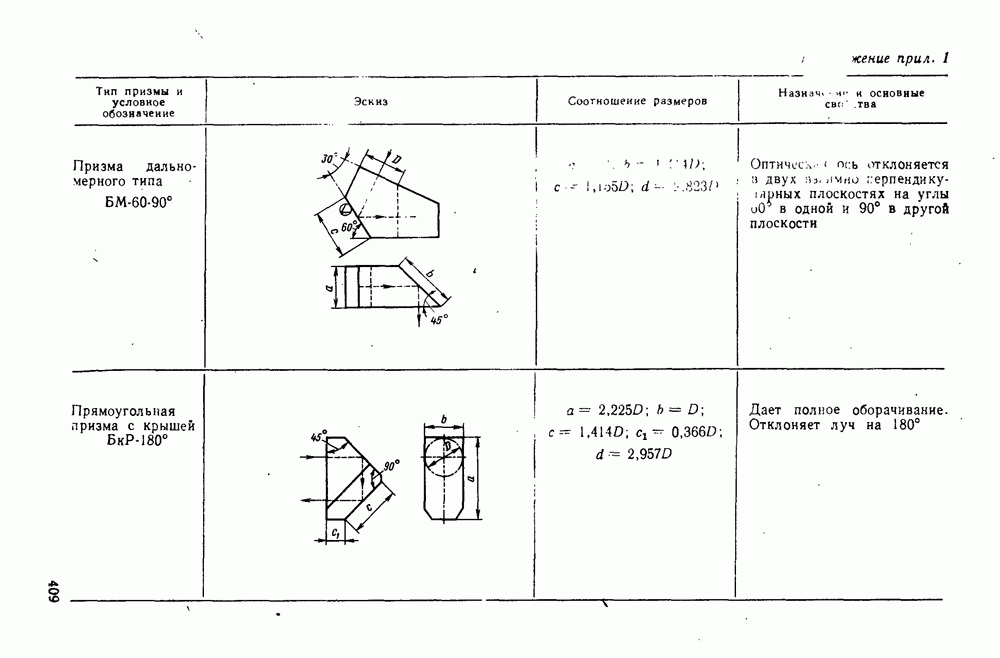
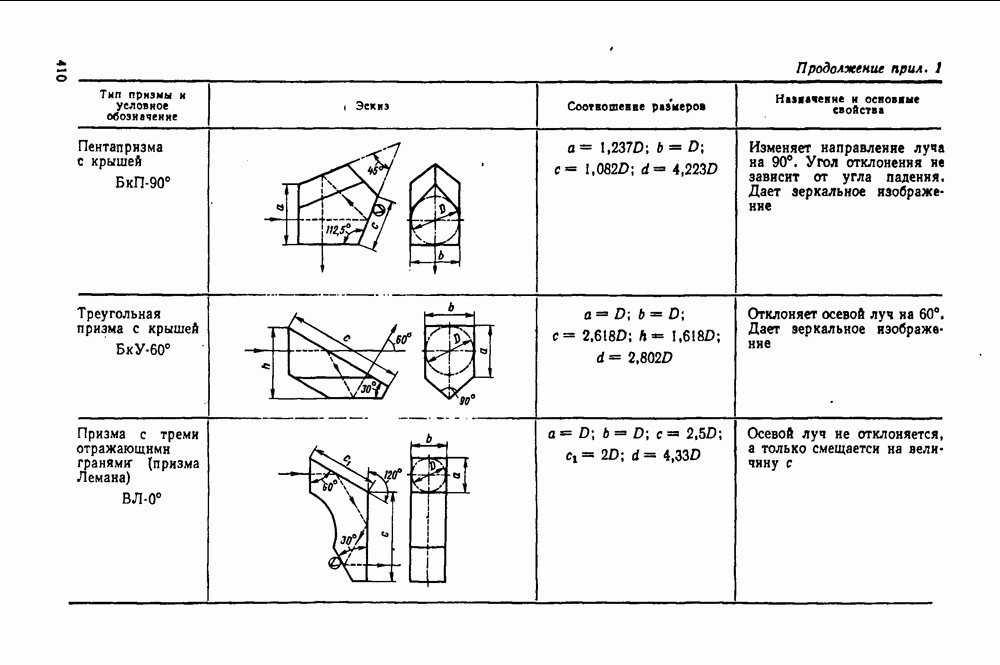
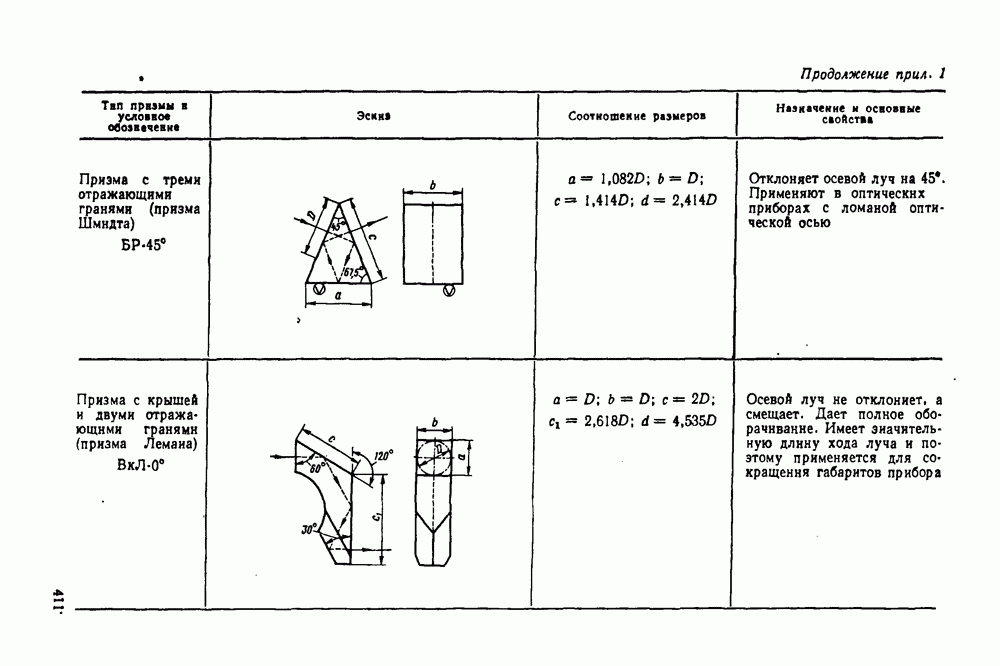
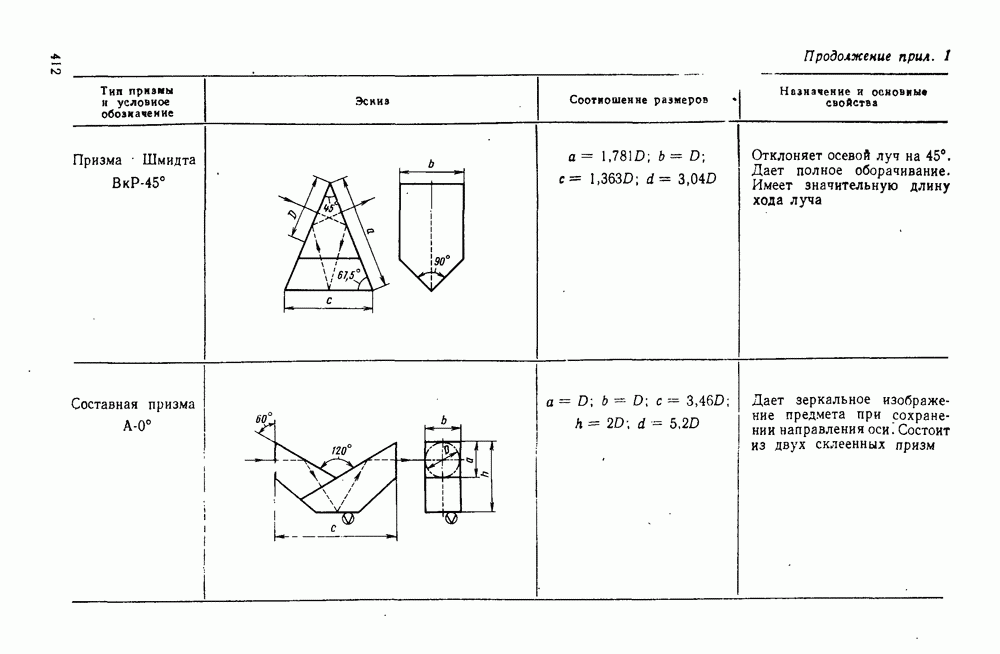
- 29. Отражательные призмы
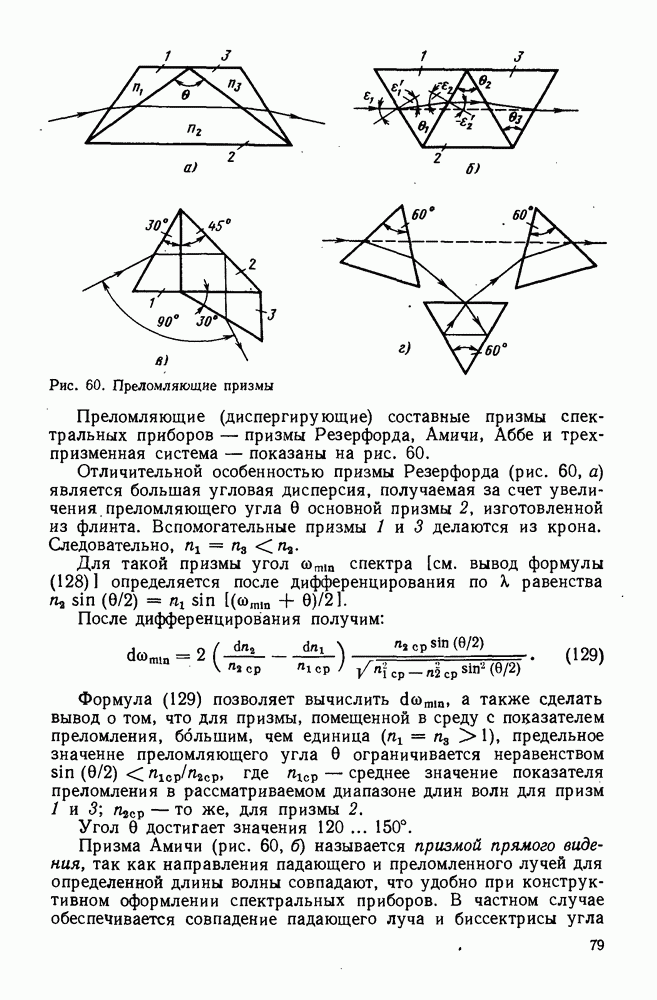
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
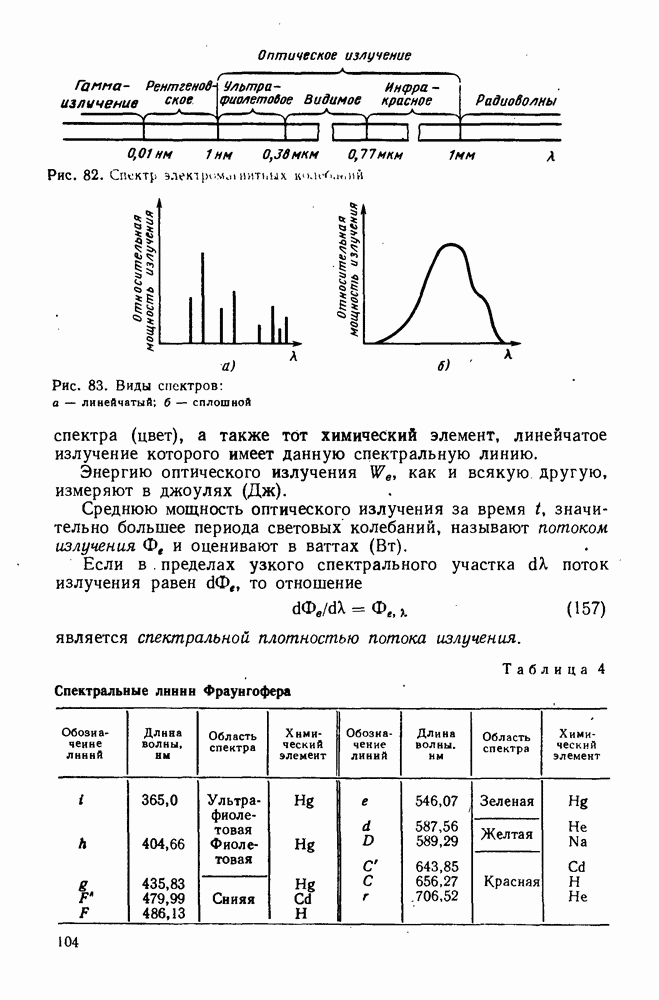
- 37. Оптическое излучение. Поток излучения
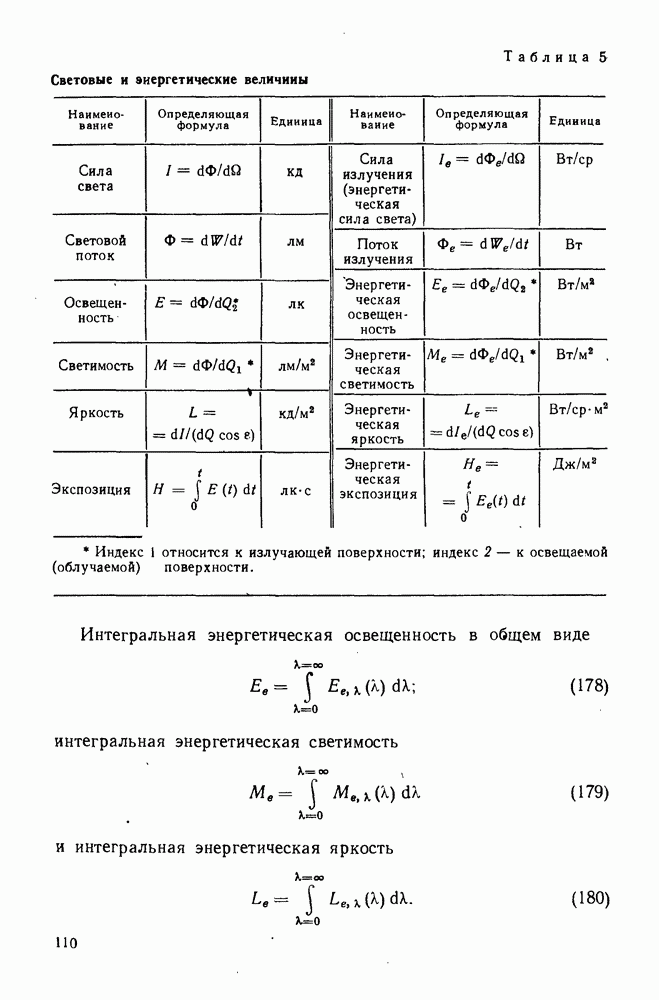
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
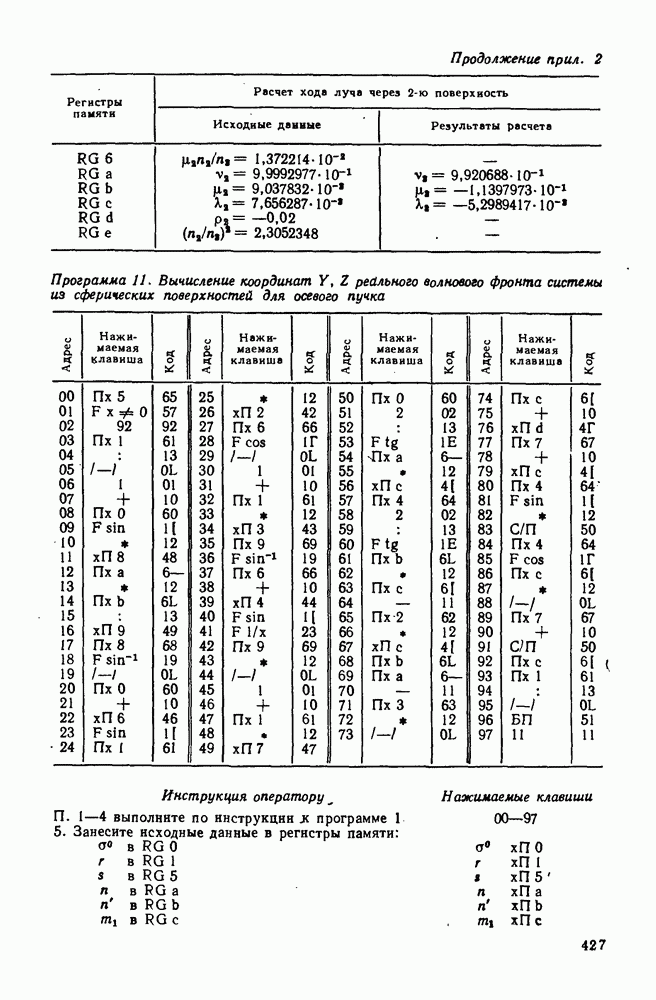
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
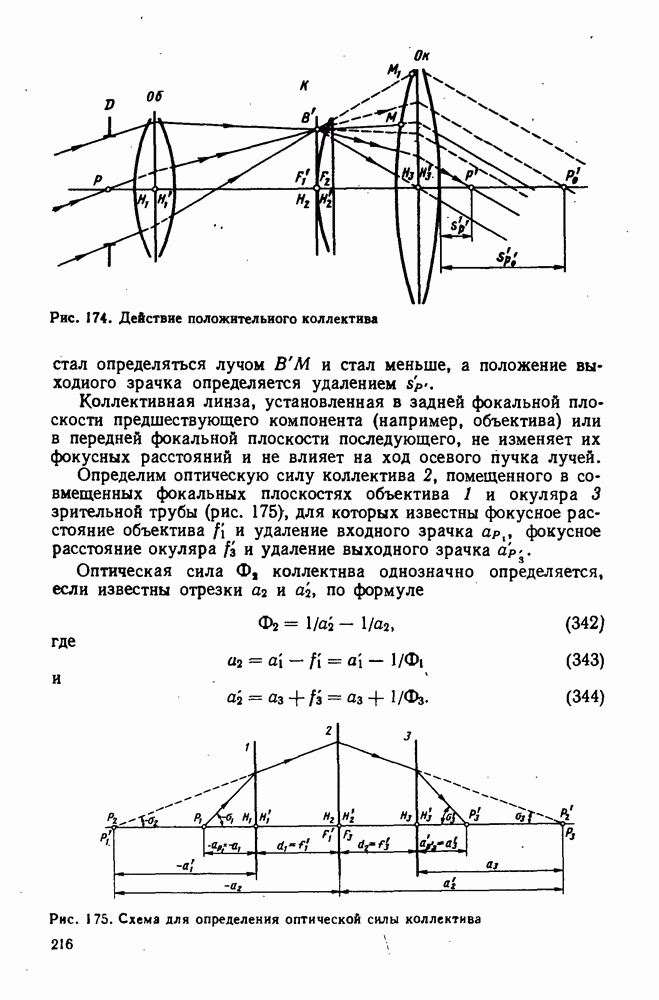
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
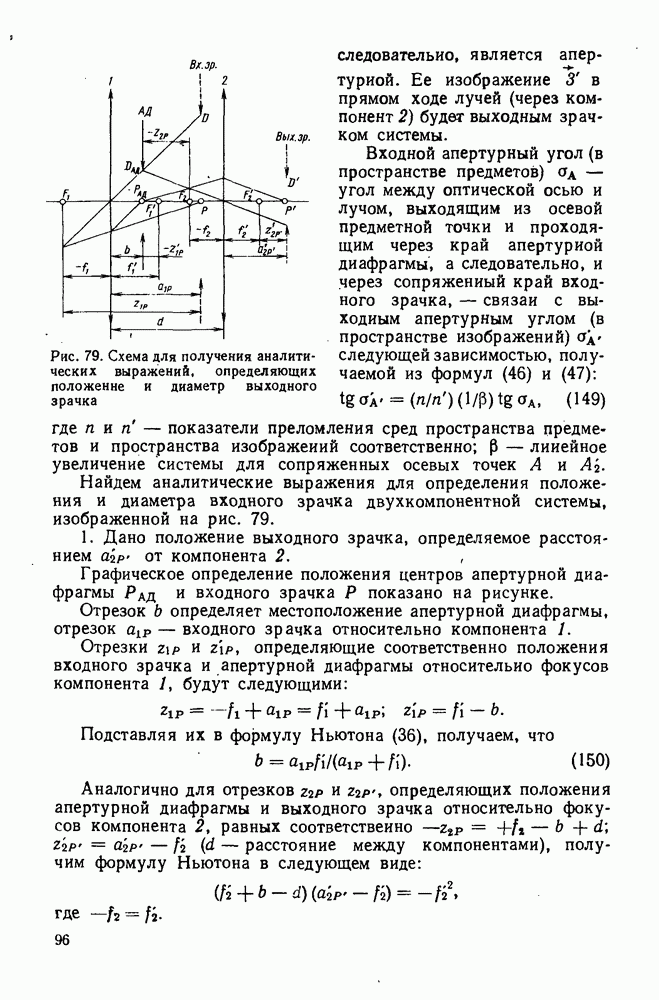
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
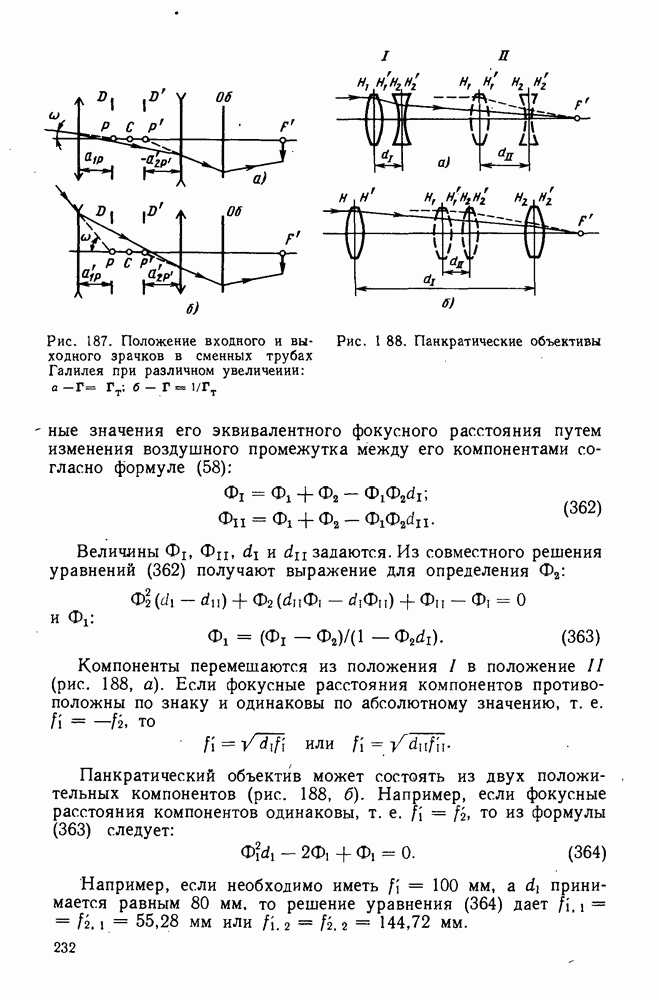
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
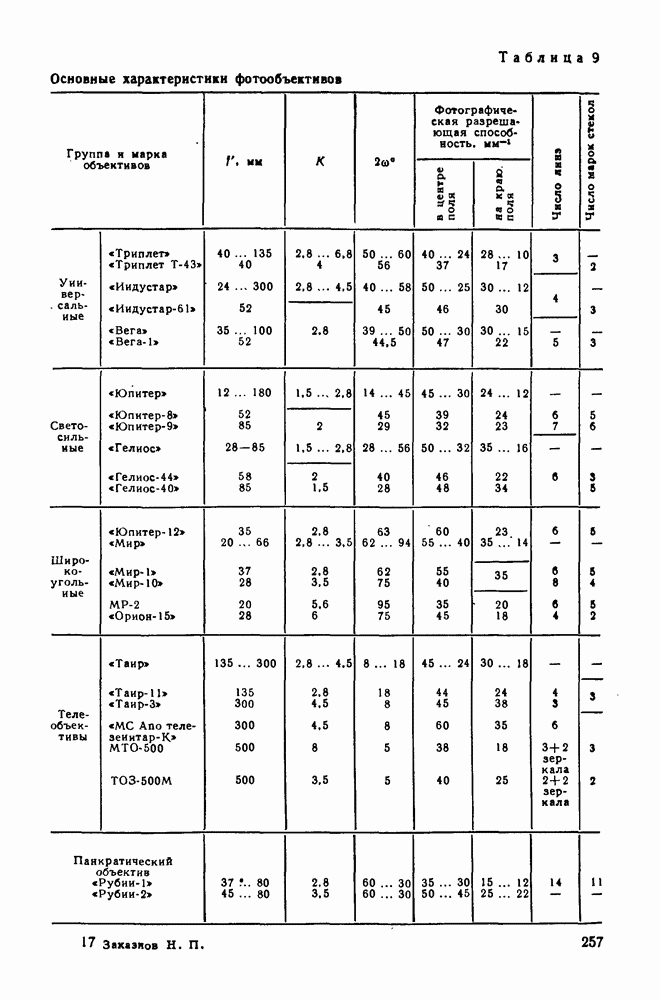
- 83. Основные характеристики фотообъектива
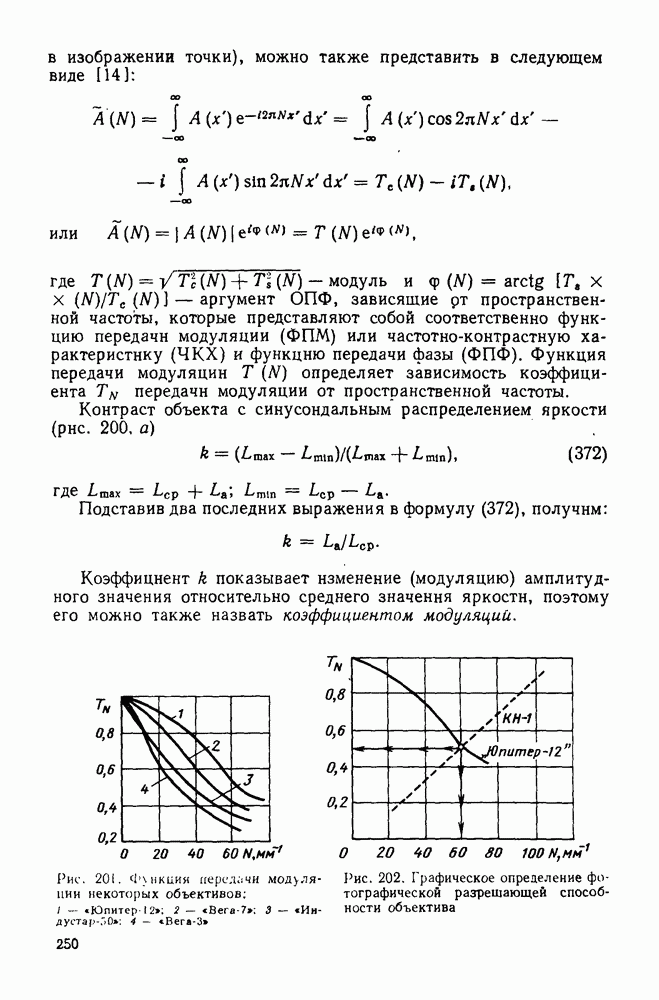
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
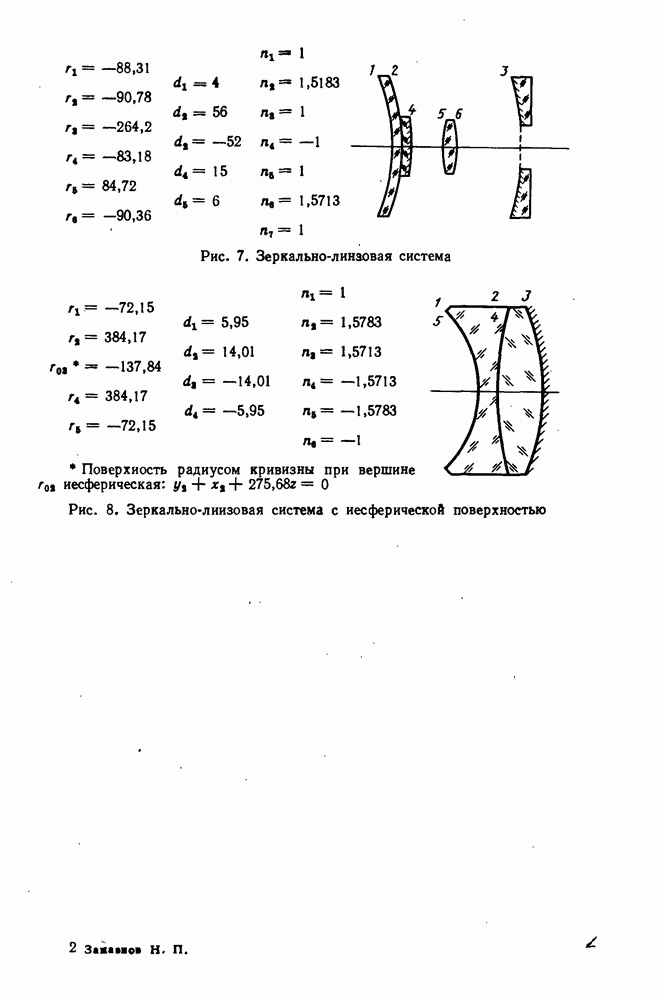
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы