| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
55. Хроматизм положения
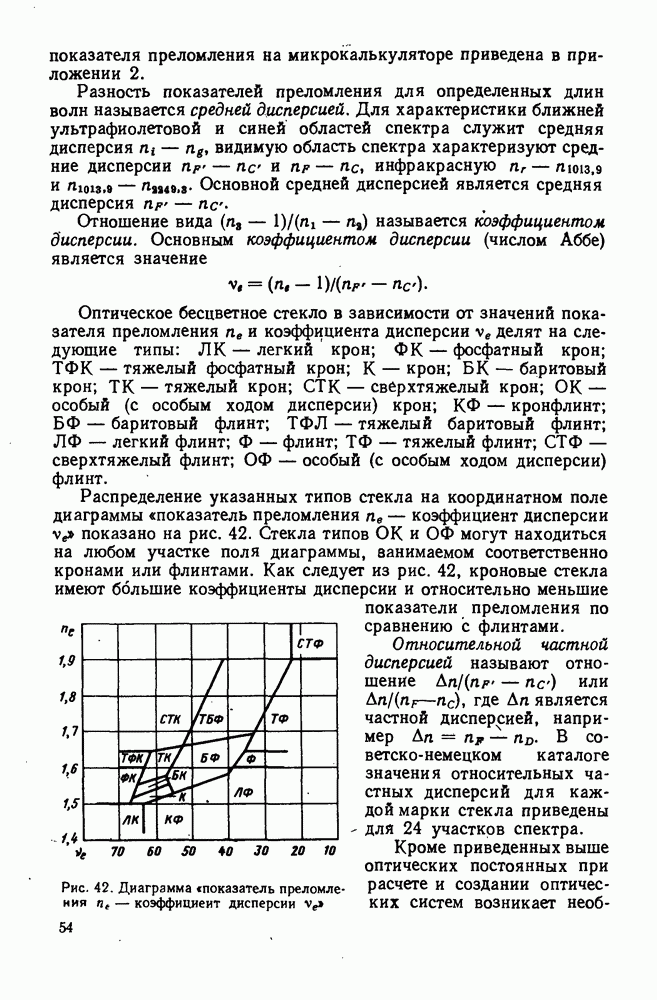
Хроматические аберрации появляются в оптических системах в результате некомпенсированной дисперсии, т. е. разложения на монохроматические составляющие излучения сложного спектрального состава при прохождении лучей через преломляющие поверхности.
Явление разложения на монохроматические составляющие сложного по спектральному составу излучения при его прохождении через линзовые оптические системы обнаруживается уже в параксиальной области. При этом параксиальные изображения предмета, образованные оптической системой в лучах с различными длинами волн, будут различаться как по положению, так и по размеру в зависимости от оптических характеристик материалов (см. гл. V, п. 25), из которых изготовлены линзы.
Аберрация оптической системы, при наличии которой изображения предметной точки, образуемые в лучах различных длин волн, получаются в разных местах вдоль оптической оси, называется хроматической аберрацией положения, или хроматизмом положения.
Пусть (рис. 128) на оптическую систему от осевой точки А приходит излучение сложного спектрального состава. Выделим параксиальные лучи, соответствующие коротковолновой, основной и длинноволновой частям спектра излучения на длинах волн 
Вследствие хроматизма положения изображения  точки А образованы в разных местах на расстояниях
точки А образованы в разных местах на расстояниях  причем
причем 
Хроматизм положения  измеряется разностью расстояний для двух длин волн
измеряется разностью расстояний для двух длин волн 

При наличии этой аберрации в плоскости параксиального изображения для  изображение точки будет иметь нежелательную цветную окраску и будет размытым.
изображение точки будет иметь нежелательную цветную окраску и будет размытым.
Точное значение хроматизма положения определяют по результатам расчета хода двух параксиальных осевых лучей для 

Рис. 128. Хроматизм положения
Приближенно  можно вычислить по формуле
можно вычислить по формуле 

где  первая хроматическая сумма (см. прил. 3);
первая хроматическая сумма (см. прил. 3);  высота первого вспомогательного луча;
высота первого вспомогательного луча;

— хроматический параметр;  коэффициент дисперсии (см. п. 25);
коэффициент дисперсии (см. п. 25);  для воздуха
для воздуха 
Найдем хроматизм положения одиночной тонкой линзы, расположенной в воздухе (рис. 129). По формуле отрезков (38) при  а имеем
а имеем  Для различных лучей спектра
Для различных лучей спектра  Дифференцированием формулы (38) найдем, что при
Дифференцированием формулы (38) найдем, что при  справедливо равенство
справедливо равенство  откуда
откуда

Для определения величины  продифференцируем формулу (96) тонкой линзы. При
продифференцируем формулу (96) тонкой линзы. При  получим
получим  и далее
и далее

где  .
.
Из формул (281) и (282) следует, что

Если предмет расположен в бесконечности  то для тонкой линзы
то для тонкой линзы  следовательно, хроматизм положения
следовательно, хроматизм положения

Как следует из формулы (284), положительные линзы имеют хроматизм положения отрицательный, а отрицательные линзы — положительный.
Пример. Вычислить хроматизм Положения одиночной тонкой лиизы, имеющей фокусное расстояние  показатель преломление
показатель преломление 
коэффициент дисперсии  для 1) бесконечно удаленной предметной точкк и 2) предметной точки, удаленной на расстояние
для 1) бесконечно удаленной предметной точкк и 2) предметной точки, удаленной на расстояние 
Решение. 1. По формуле (284) получим  т. е. если бы лннза имела относительное отверстие
т. е. если бы лннза имела относительное отверстие  то только иследствие хроматизма положения вместо точки получилось бы пятно диаметром
то только иследствие хроматизма положения вместо точки получилось бы пятно диаметром 
2. Изображение получится также на двойном фокусном расстоянии 
По формуле (283) имеем  хроматизм положения в 4 раза больше, чем в первом случае.
хроматизм положения в 4 раза больше, чем в первом случае.
Этот пример показывает, что при приближении предмета к оптической системе хроматизм положения возрастает..
Хроматизм положения одиночных линз положительной (кривая 1) и отрицательной (кривая 2) иллюстрируют характеристические графики зависимости  показанные на рис. 130. Соответствующим подбором материалов и фокусных расстояний положительной и отрицательной линз можно исправить хроматизм положения
показанные на рис. 130. Соответствующим подбором материалов и фокусных расстояний положительной и отрицательной линз можно исправить хроматизм положения  т. е. достигнуть ахроматизма (рис. 130, кривая 3).
т. е. достигнуть ахроматизма (рис. 130, кривая 3).
Рассмотрим условие ахроматизации двухлинзового тонкого склеенного объектива, расположенного в воздухе, для бесконечно удаленного предмета. Оптическая сила такого объектива согласно (63) будет равна:

тогда  Дифференцируя формулу простой линзы, получаем
Дифференцируя формулу простой линзы, получаем

Условием исправления хроматизма является равенство  Подставляя величины и
Подставляя величины и  в формулу (285), определим условие ахроматизации:
в формулу (285), определим условие ахроматизации:

Решая совместно (285) и (287), получаем формулы для вычисления оптических сил линз, составляющих ахроматическую пару:

Из полученных формул можно сделать следующие выводы.

Рис. 129. Схема для определения хроматизма положеиня одиночной тонкой линзы

Рис. 130. Графики хроматической аберрации положения
1. Для исправления хроматизма положения необходима комбинация из линз, имеющих фокусные расстояния разных знаков [см. формулу (287)].
2. Положительная линза должна быть изготовлена: для положительного объектива из материала, имеющего больший коэффициент дисперсии, и для отрицательного объектива из материала, имеющего меньший коэффициент дисперсии. Таким образом, из стекла, имеющего больший коэффициент дисперсии (как правило, это кроновое стекло), изготовляют линзу, знак фокусного расстояния которой определяет знак фокусного расстояния всего объектива.
3. Условие ахроматизации  может быть удовлетворено для отрицательной линзы в форме мениска. Эту возможность впервые показал
может быть удовлетворено для отрицательной линзы в форме мениска. Эту возможность впервые показал  Максутов в 1941 г. Действительно, если продифференцировать формулу линзы и приравнять
Максутов в 1941 г. Действительно, если продифференцировать формулу линзы и приравнять  то условие ахроматизации мениска Максутова имеет следующий вид:
то условие ахроматизации мениска Максутова имеет следующий вид:

При ахроматизации двухлинзового объектива удается совместить цветные параксиальные изображения осевых точек только для лучей с длинами волн  (см. рис. 130, кривая 5), изображение в основном «цвете» оказывается на расстоянии
(см. рис. 130, кривая 5), изображение в основном «цвете» оказывается на расстоянии  не равном расстояниям
не равном расстояниям  Таким образом, при ахроматизации в объективе имеется остаточный хроматизм, который называют вторичным спектром и который можно оценить разностью
Таким образом, при ахроматизации в объективе имеется остаточный хроматизм, который называют вторичным спектром и который можно оценить разностью

Вторичный спектр  в области аберраций первого порядка можно вычислить для двухлинзового склеенного объектива по следующей формуле (при условии, что
в области аберраций первого порядка можно вычислить для двухлинзового склеенного объектива по следующей формуле (при условии, что 

где  коэффициенты дисперсии;
коэффициенты дисперсии;  относительные частные дисперсии соответственно для материалов первой и второй линз объектива.
относительные частные дисперсии соответственно для материалов первой и второй линз объектива.
Для уменьшения вторичного спектра следует выбирать такие пары стекол, у которых относительные частные дисперсии у одинаковы, а коэффициенты дисперсии сильно различаются.
Пример. Определим по формуле  в видимой области
в видимой области  значения вторичного спектра для ряда стекл:
значения вторичного спектра для ряда стекл:
1. Обычные стекла:

2. Сильно различающиеся по коэффициенту дисперсии стекла

(см. скан)
Как следует из примера, в  и во
и во  случаях вторичный спектр составляет
случаях вторичный спектр составляет  и его необходимо исправлять в длиннофокусных объективах, аэрофотообъективах, объективах большого увеличения и объективах для цветной фотографии или при проецировании цветных изображений. При малой разности между
и его необходимо исправлять в длиннофокусных объективах, аэрофотообъективах, объективах большого увеличения и объективах для цветной фотографии или при проецировании цветных изображений. При малой разности между  оказывается также малой разность между и
оказывается также малой разность между и  и 4-й случаи), что обусловливает крутой радиус склейки и невозможность исправления сферической аберрации.
и 4-й случаи), что обусловливает крутой радиус склейки и невозможность исправления сферической аберрации.
При исправлении вторичного спектра удается совместить цветные изображения осевых точек для трех длин волн, т. е. получить  Такая степень коррекции (кривая 4 на рис. 130) называется апохроматической.
Такая степень коррекции (кривая 4 на рис. 130) называется апохроматической.
В советско-немецком каталоге оптического стекла имеются таблицы, позволяющие выбирать пары стекол с уменьшенным вторичным спектром.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
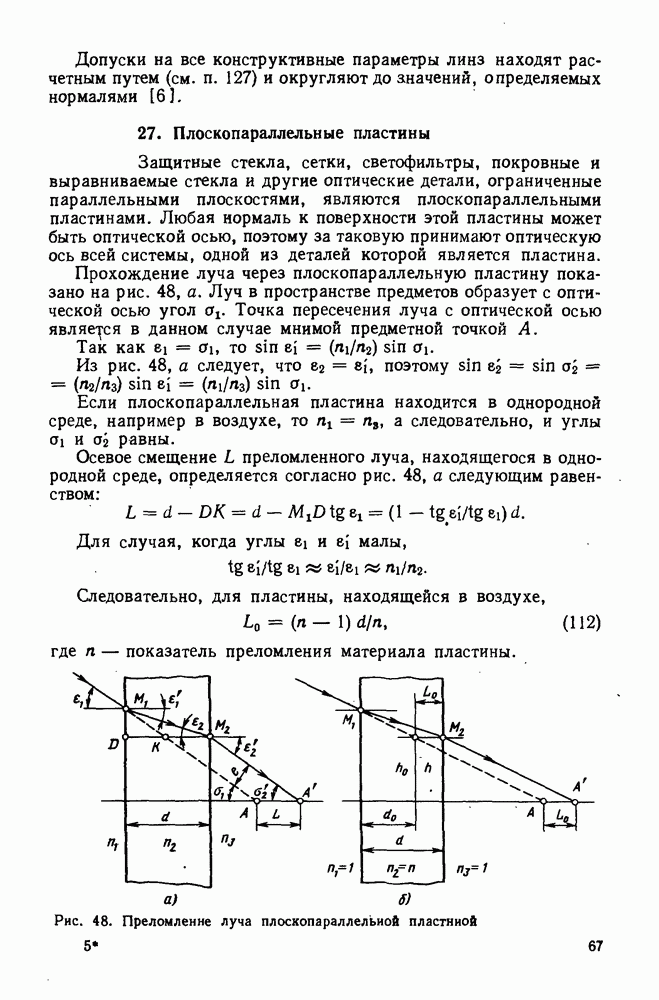
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
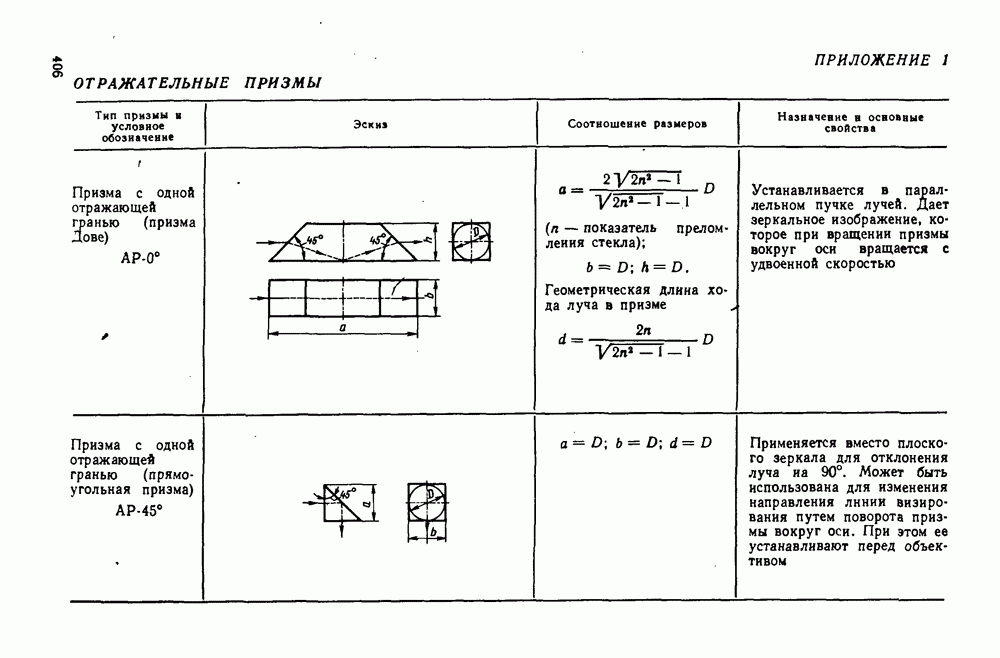
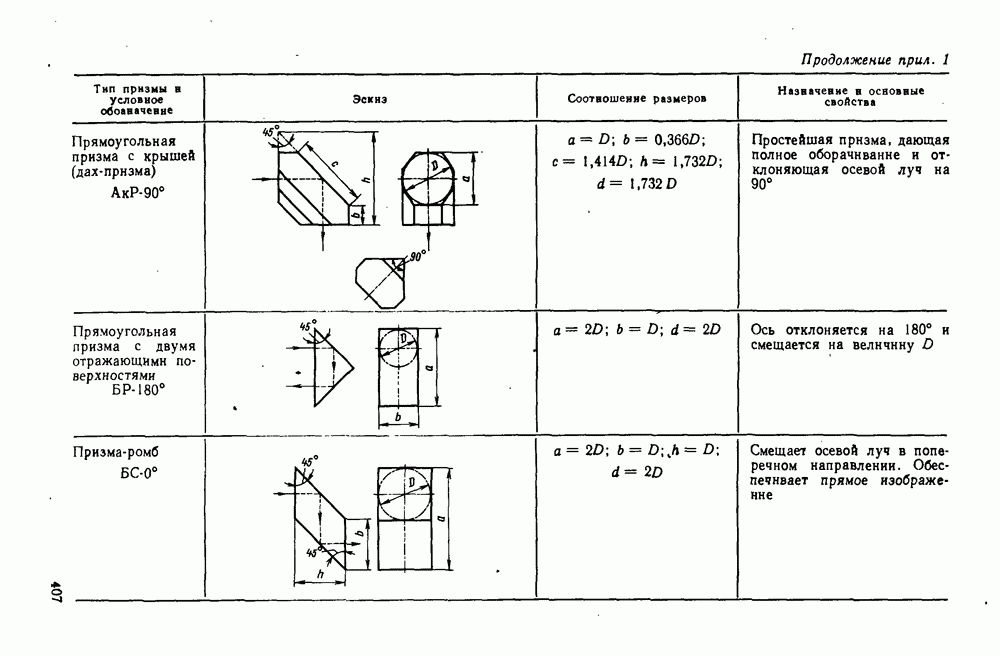
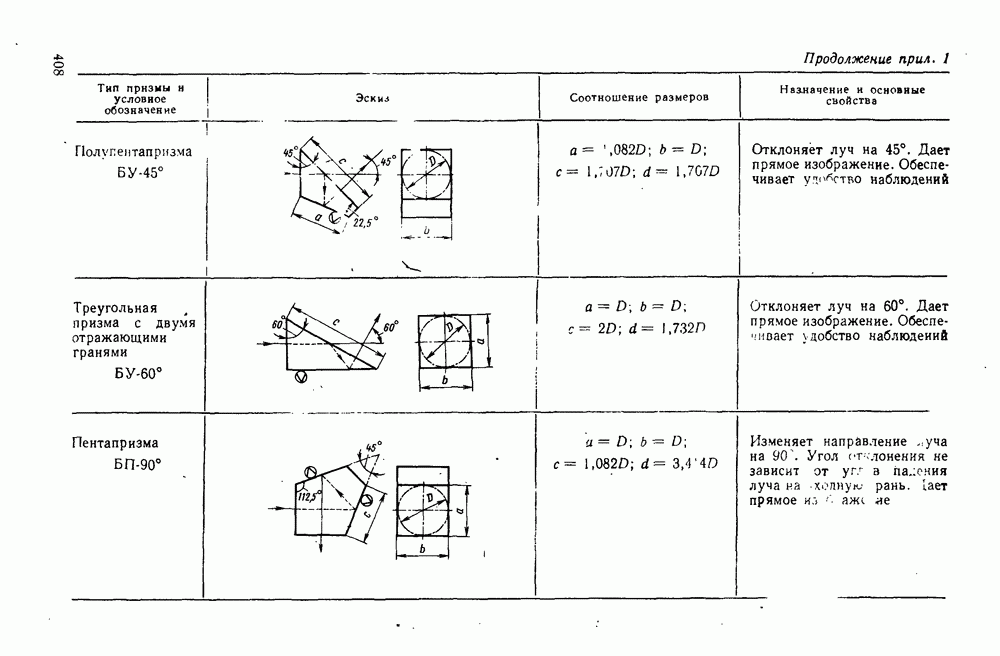
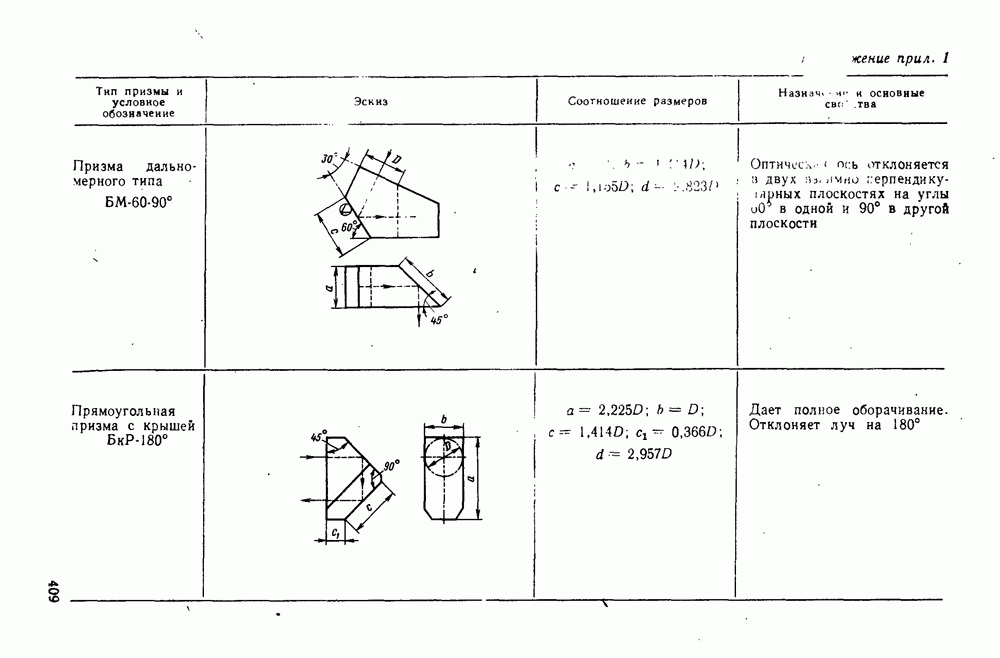
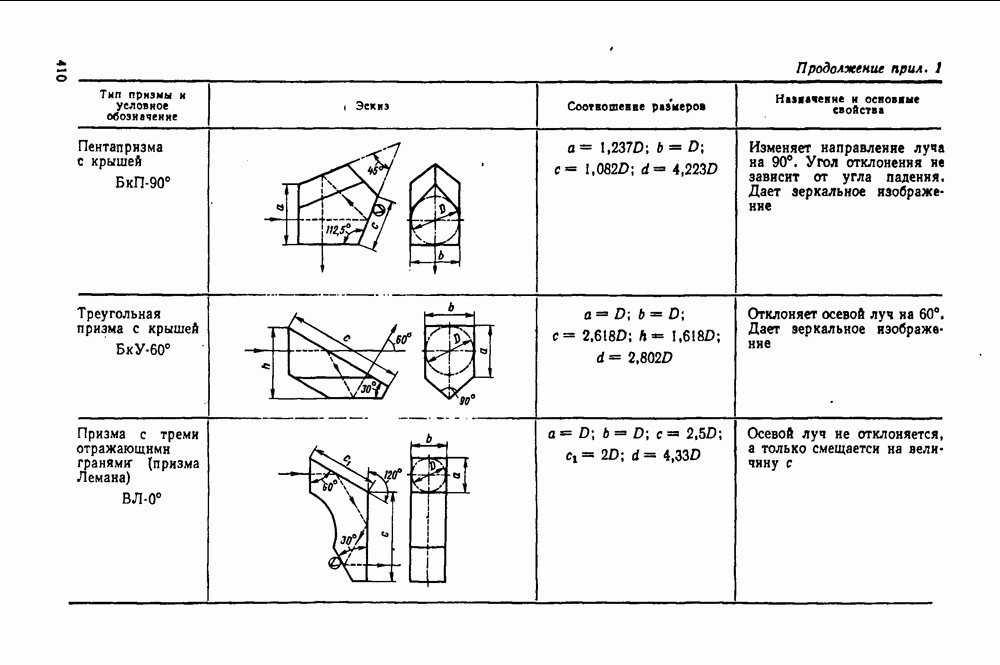
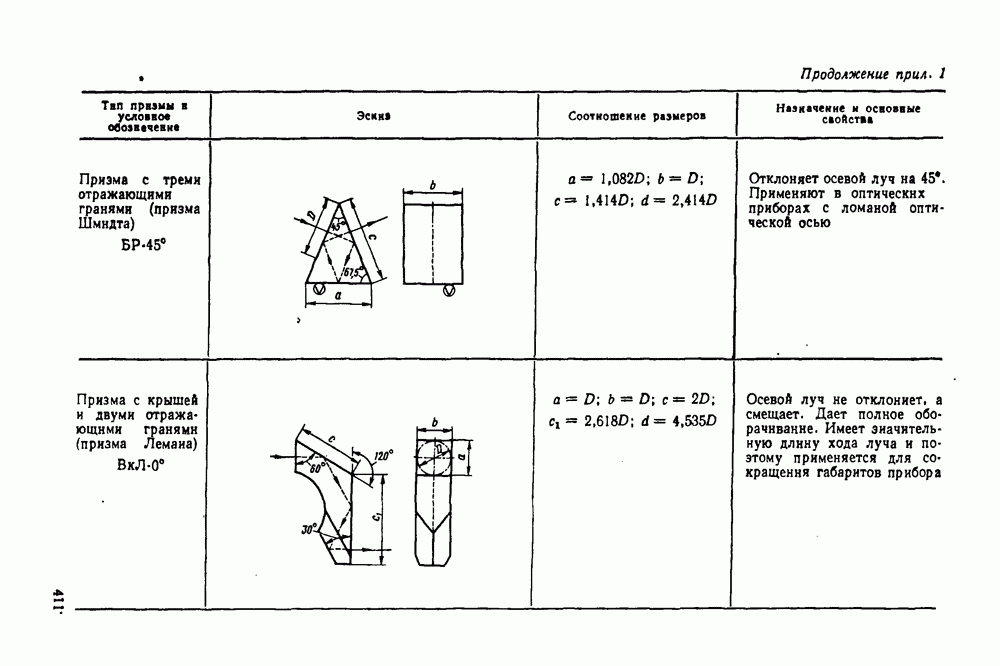
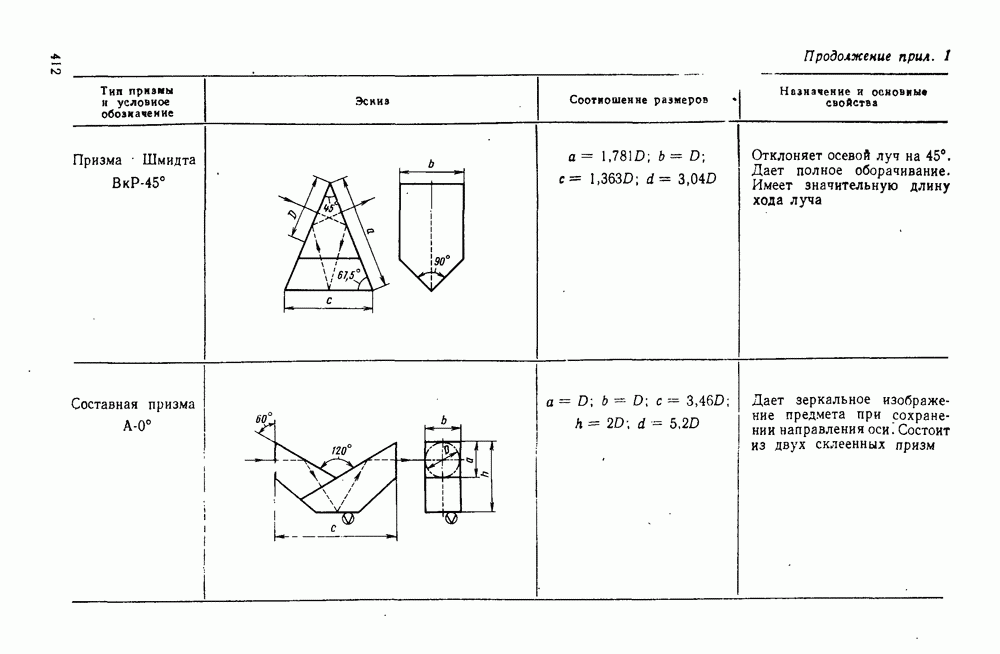
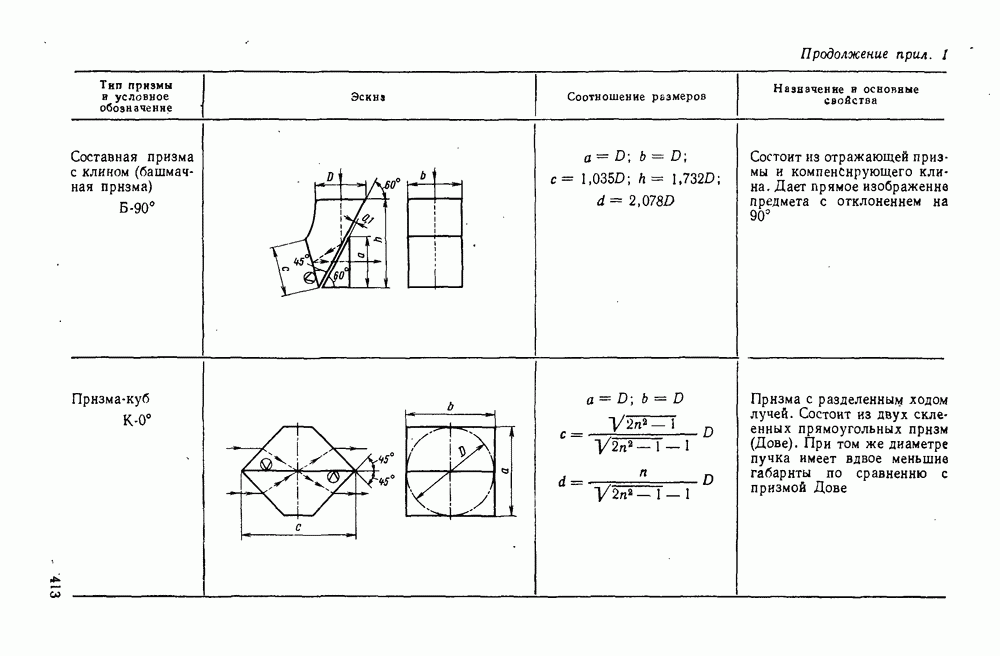
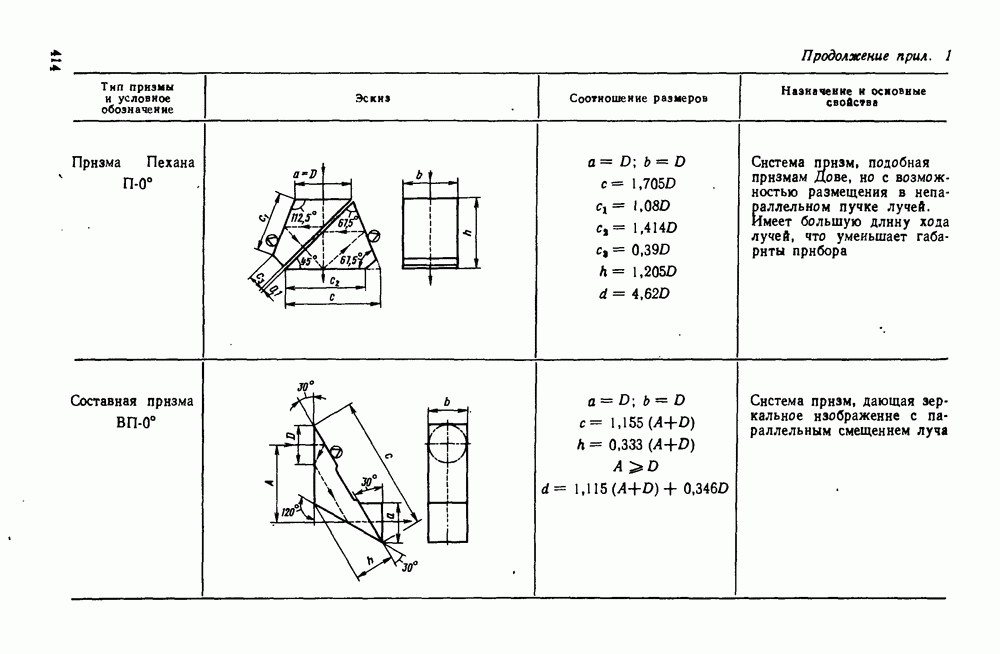
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы