| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
109. Характеристика трансформированного изображения и его получение
Оптические системы, сформированные из оптических деталей с круговой симметрией, когда плоскость предмета, а следовательно, и плоскость изображения перпендикулярны к оптической оси, дают изображения, подобные плоскому предмету, т. е. с постоянным масштабом по всему полю. Любое осевое сечение этих систем равнозначно.
В некоторых случаях требуются системы, образующие изображения с различным масштабом в двух взаимно перпендикулярных направлениях. Такие системы необходимы, например, в регистрирующих приборах (световой поток от нити накаливания электролампы заполняет протяженную щель прибора) и в широкоэкранном кинематографе, когда съемки и показ широкоэкранных фильмов обеспечиваются с помощью обычной 35-миллиметровой кинопленки, и т. п.
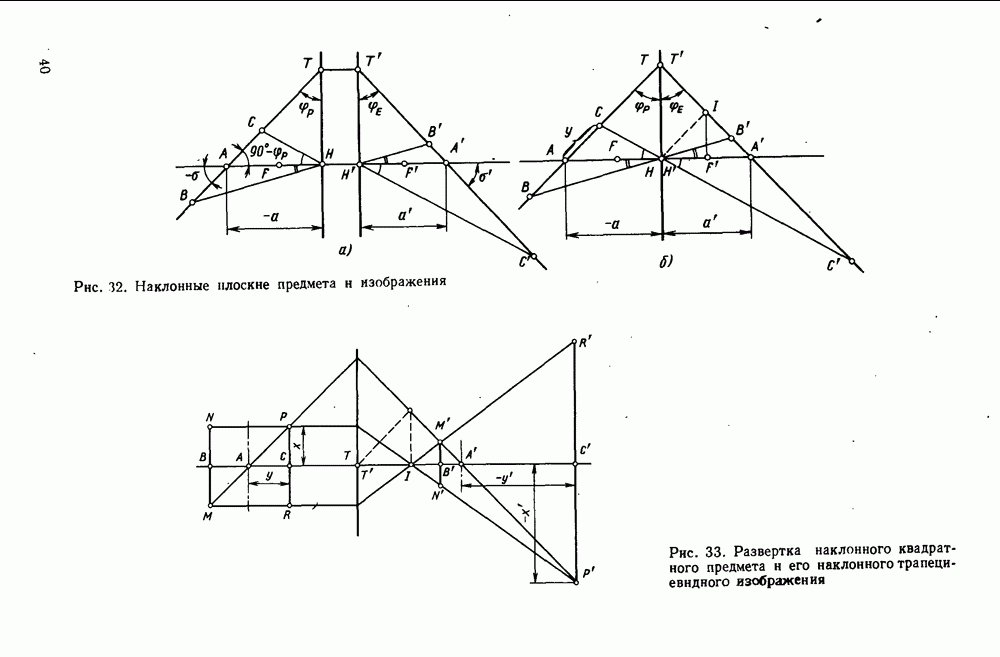
Процесс получения изображений с переменным масштабом называется трансформированием. В результате трансформирования прямоугольник с одним соотношением сторон преобразуется в прямоугольник с другим соотношением сторон или вместо прямоугольника получают фигуры в виде параллелограмма, трапеции или другого четырехугольника. Примером трансформирования с привлечением оптической системы круговой симметрии является получение изображения предмета, находящегося на наклонной плоскости по отношению к оптической оси (см. рис. 32 и 33).
Как правило, системы двоякой симметрии формируют из цилиндрических линз или из их комбинаций с осесимметричными линзами. В этих системах различают два сечения. Одно из них (сечение 1), в котором действуют направляющие цилиндрических поверхностей (обычно дуги окружностей), называется главным (первым), а сечение  ему перпендикулярное, в котором находятся образующие цилиндрических поверхностей, — вторым. В некоторых случаях в обоих сечениях имеются и направляющие и образующие цилиндрических поверхностей, тогда выбор одного из этих сечений произволен. Оптические системы этого вида называют анаморфозными
ему перпендикулярное, в котором находятся образующие цилиндрических поверхностей, — вторым. В некоторых случаях в обоих сечениях имеются и направляющие и образующие цилиндрических поверхностей, тогда выбор одного из этих сечений произволен. Оптические системы этого вида называют анаморфозными  (греч.) — искажение формы.
(греч.) — искажение формы.
При действии анаморфозных систем изображения принимают расширенный, суженный или наклонный вид по сравнению с первоначальным видом предмета (см. рис. 254). Расширение

Рис. 254. Виды трансформированных изображений
изображения может происходить как за счет увеличения ширины а, так и за счет уменьшения высоты  а сужение — при увеличении высоты и уменьшении ширины.
а сужение — при увеличении высоты и уменьшении ширины.
За основу геометрических представлений о расширенном и суженном изображениях принимают отношение ширины изображения к ширине предмета — коэффициент ширины  и отношение высоты изображения к высоте предмета — коэффициент высоты
и отношение высоты изображения к высоте предмета — коэффициент высоты 
Отношение коэффициентов ширины и высоты  представляет собой коэффиииент анаморфозы.
представляет собой коэффиииент анаморфозы.
Образование наклонного изображения основано на расширении или сужении условного прямоугольника, в котором исходный предмет повернут на некоторый угол. Параметрами трансформированного изображения в этом случае являются угол наклона  коэффициент ширины
коэффициент ширины  и коэффициент высоты
и коэффициент высоты 
Трансформированные изображения могут быть получены с помощью различных оптических систем двоякой симметрии, в которых в основном применяются цилиндрические линзы. Однако существуют системы с использованием цилиндрических отражающих поверхностей и преломляющих призм [3].
Рассмотрим действие цилиндрической линзы.
На положительную (плосковыпуклую) цилиндрическую линзу (рис. 255) направим пучок параллельных лучей, который образует изображение в виде отрезка прямой, перпендикулярного к оптической оси и проходящего через задний фокус  сечения
сечения  длинаэтого отрезка
длинаэтого отрезка  (в сечении
(в сечении  равна длине
равна длине  цилиндрической линзы. Если точечный источник света А (рис. 256) по отношению к этой же линзе расположен на конечном расстоянии — а, то его изображение имеет вид отрезка прямой, перпендикулярного к оптической оси (рис. 256). Расстояние
цилиндрической линзы. Если точечный источник света А (рис. 256) по отношению к этой же линзе расположен на конечном расстоянии — а, то его изображение имеет вид отрезка прямой, перпендикулярного к оптической оси (рис. 256). Расстояние  этого изображения
этого изображения

Рис. 255. Действие цилиндрической линзыдля случая, когда точечный предмет находится в бесконечности

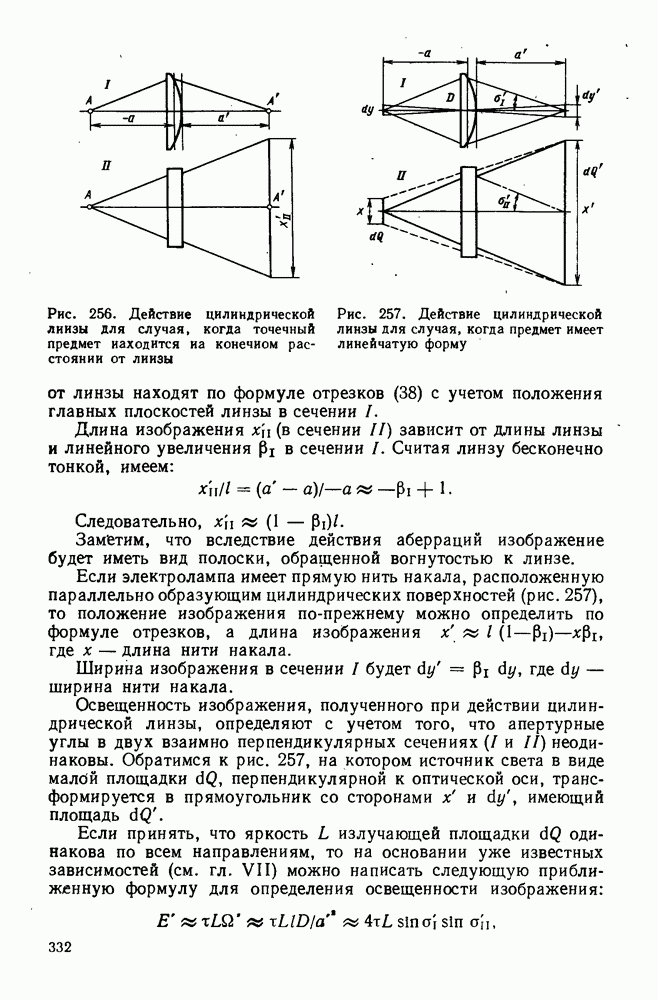
Рис. 256. Действие цилиндрической лиизы для случая, когда точечный предмет находится на конечном расстоянии от лиизы

Рис. 257. Действие цилиндрической линзы для случая, когда предмет имеет линейчатую форму
от линзы находят по формуле отрезков (38) с учетом положения главных плоскостей линзы в сечении 
Длина изображения  (в сечении II) зависит от длины линзы и линейного увеличения
(в сечении II) зависит от длины линзы и линейного увеличения  в сечении
в сечении  Считая линзу бесконечно тонкой, имеем:
Считая линзу бесконечно тонкой, имеем:

Следовательно, 
Заметим, что вследствие действия аберраций изображение будет иметь вид полоски, обращенной вогнутостью к линзе.
Если электролампа имеет прямую нить накала, расположенную параллельно образующим цилиндрических поверхностей (рис. 257), то положение изображения по-прежнему можно определить по формуле отрезков, а длина изображения  где
где  длина нити накала.
длина нити накала.
Ширина изображения в сечении  будет
будет  где
где  ширина нити накала.
ширина нити накала.
Освещенность изображения, полученного при действии цилиндрической линзы, определяют с учетом того, что апертурные углы в двух взаимно перпендикулярных сечениях  и II) неодинаковы. Обратимся к рис. 257, на котором источник света в виде малбй площадки
и II) неодинаковы. Обратимся к рис. 257, на котором источник света в виде малбй площадки  перпендикулярной к оптической оси, трансформируется в прямоугольник со сторонами
перпендикулярной к оптической оси, трансформируется в прямоугольник со сторонами  имеющий площадь
имеющий площадь 
Если принять, что яркость  излучающей площадки
излучающей площадки  одинакова по всем направлениям, то на основании уже известных зависимостей (см. гл. VII) можно написать следующую приближенную формулу для определения освещенности изображения:
одинакова по всем направлениям, то на основании уже известных зависимостей (см. гл. VII) можно написать следующую приближенную формулу для определения освещенности изображения:

где  коэффициент пропускания системы;
коэффициент пропускания системы;  апертурные углы в пространстве изображений в сечениях I и II соответственно.
апертурные углы в пространстве изображений в сечениях I и II соответственно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
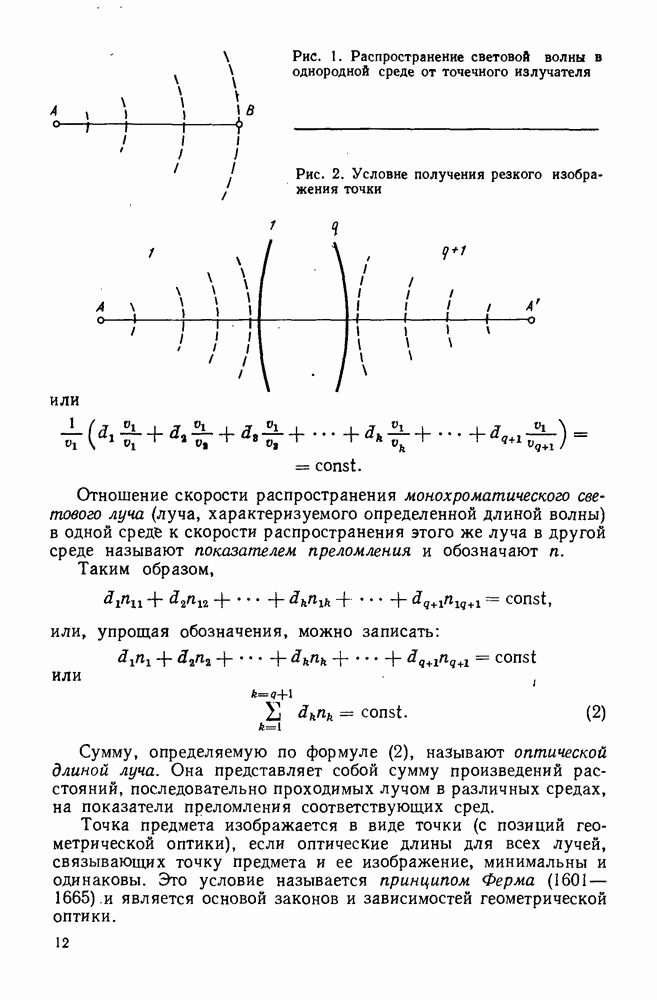
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
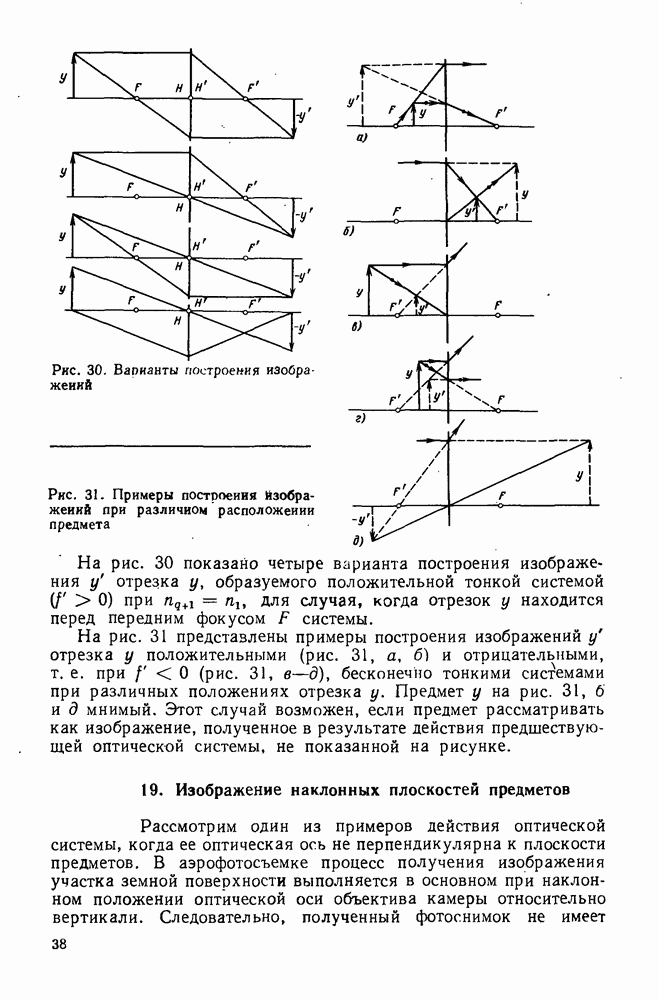
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
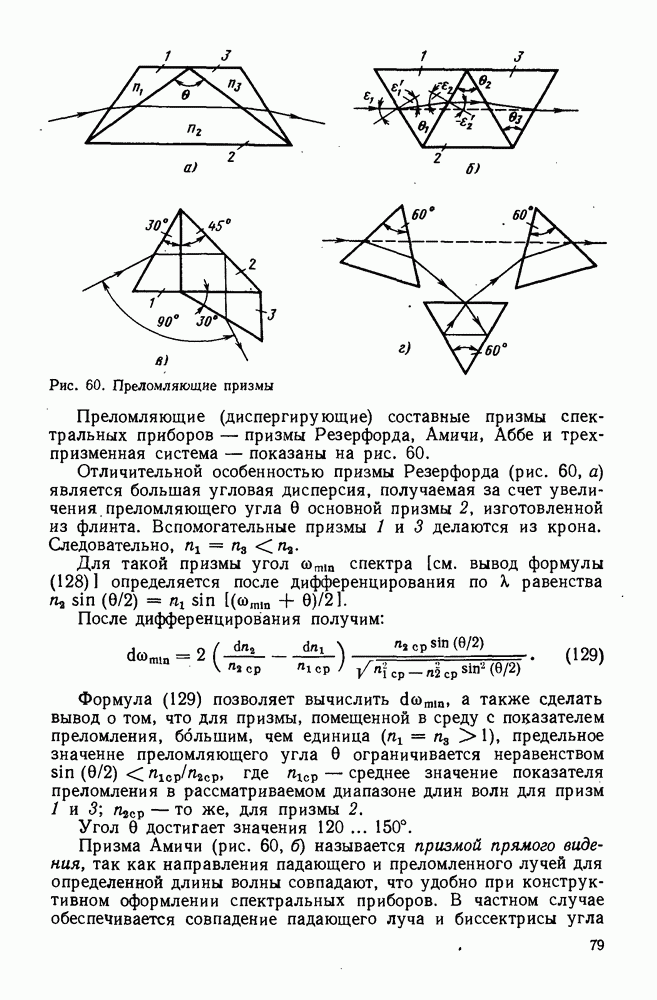
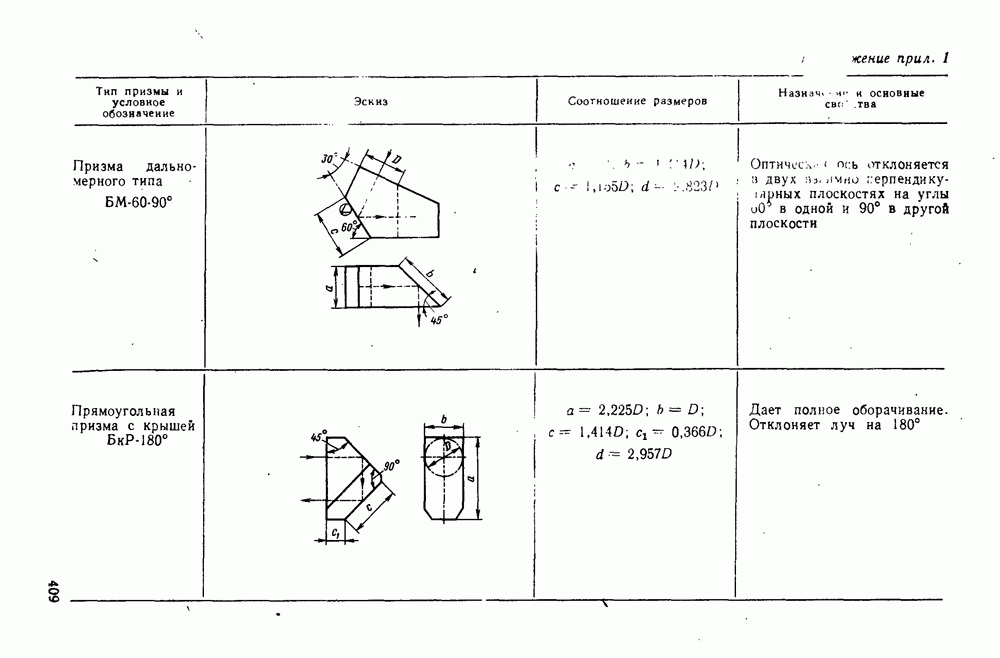
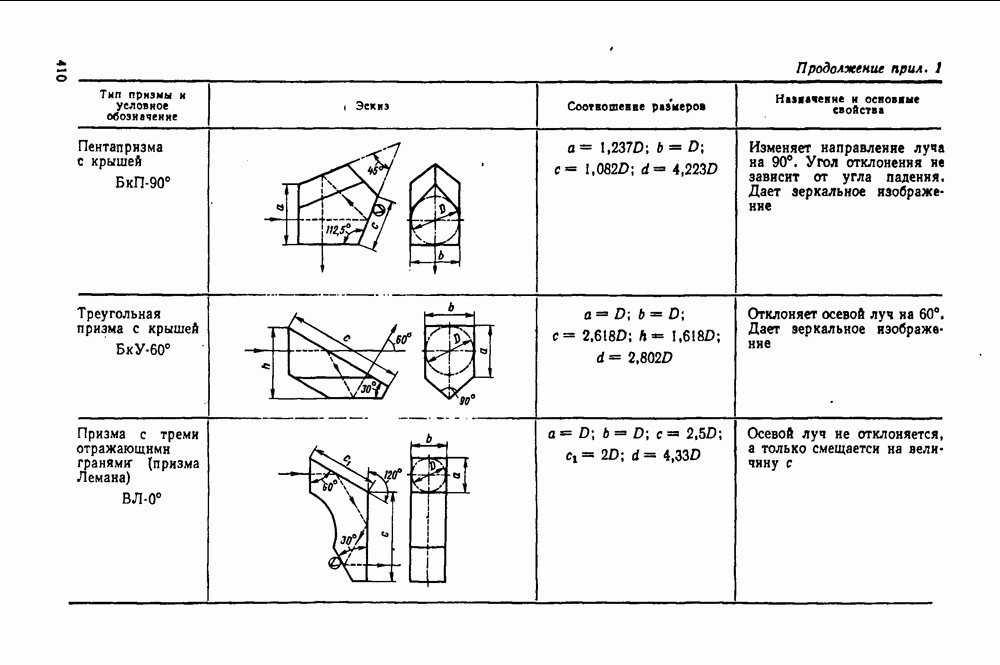
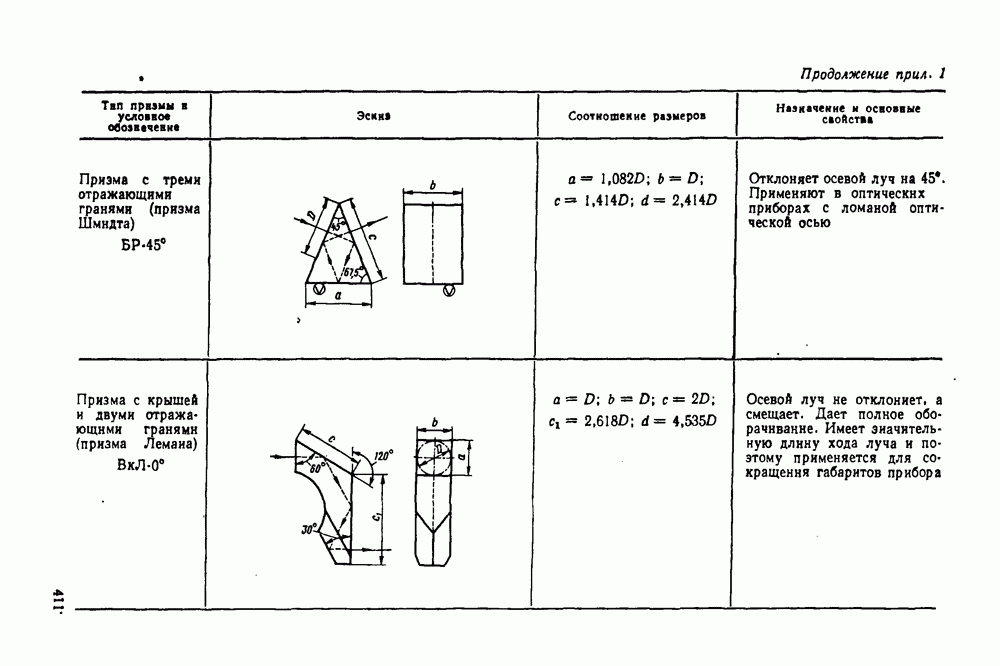
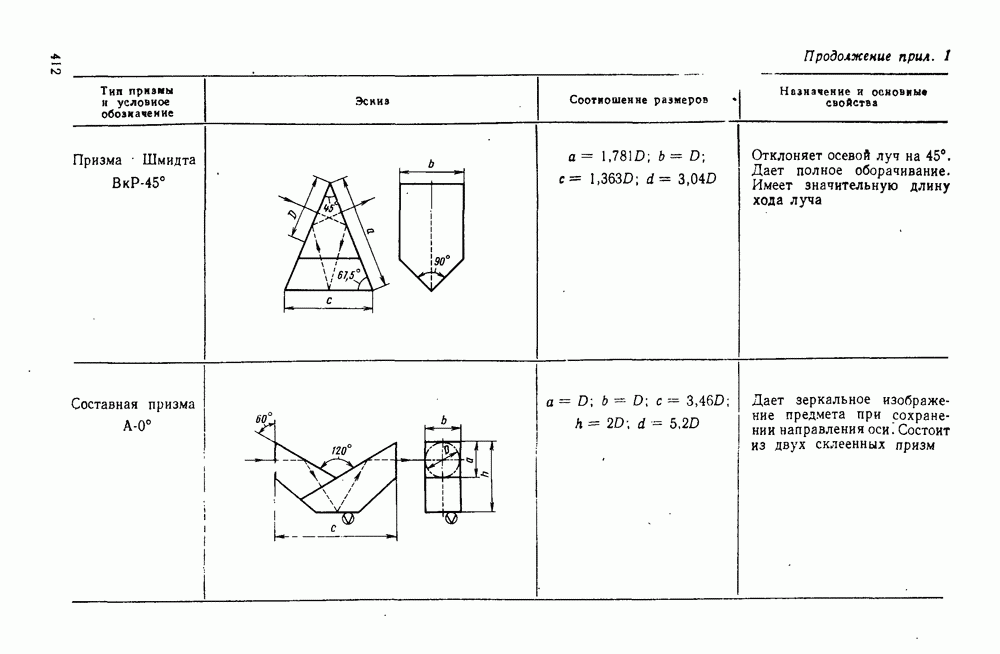
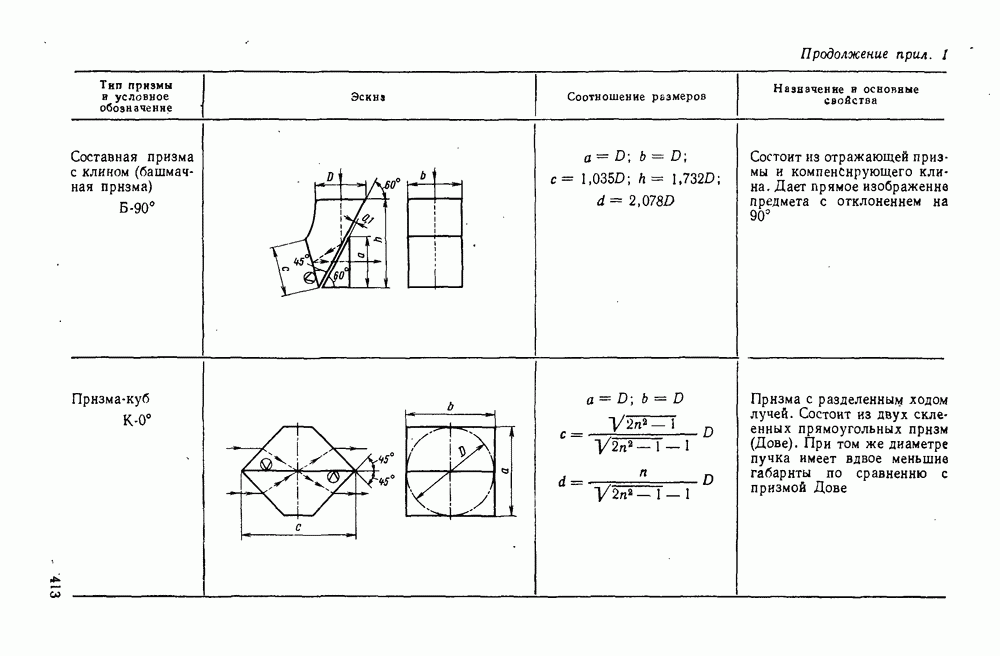
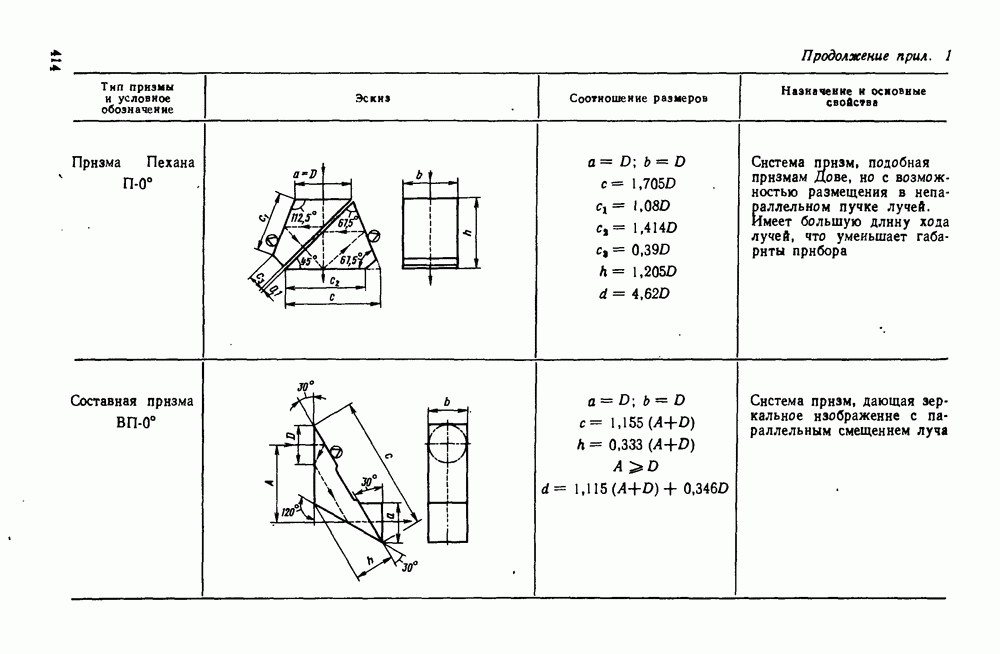
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
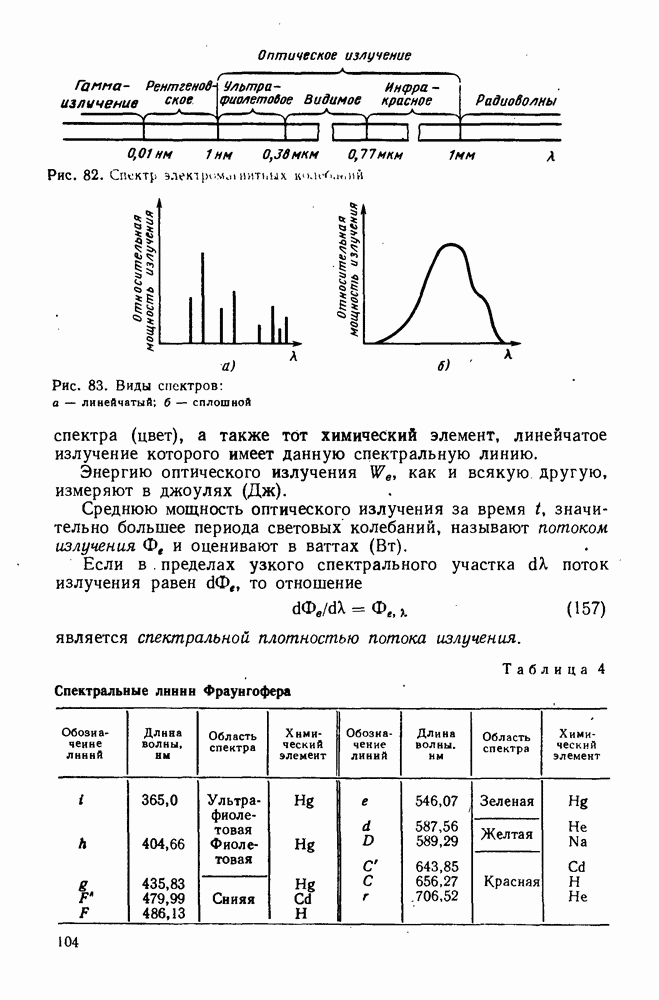
- 37. Оптическое излучение. Поток излучения
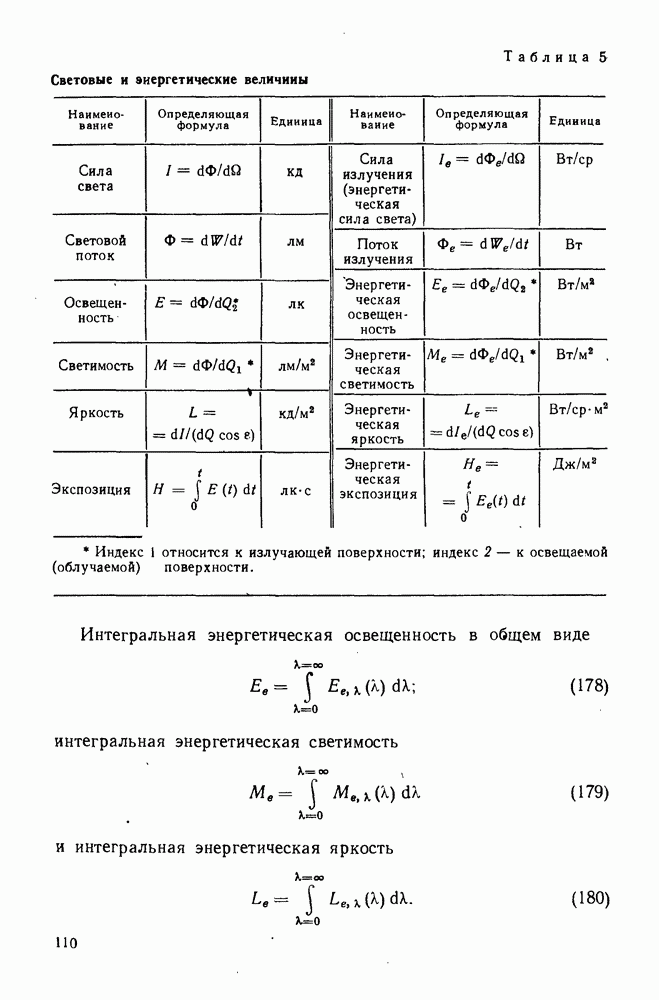
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
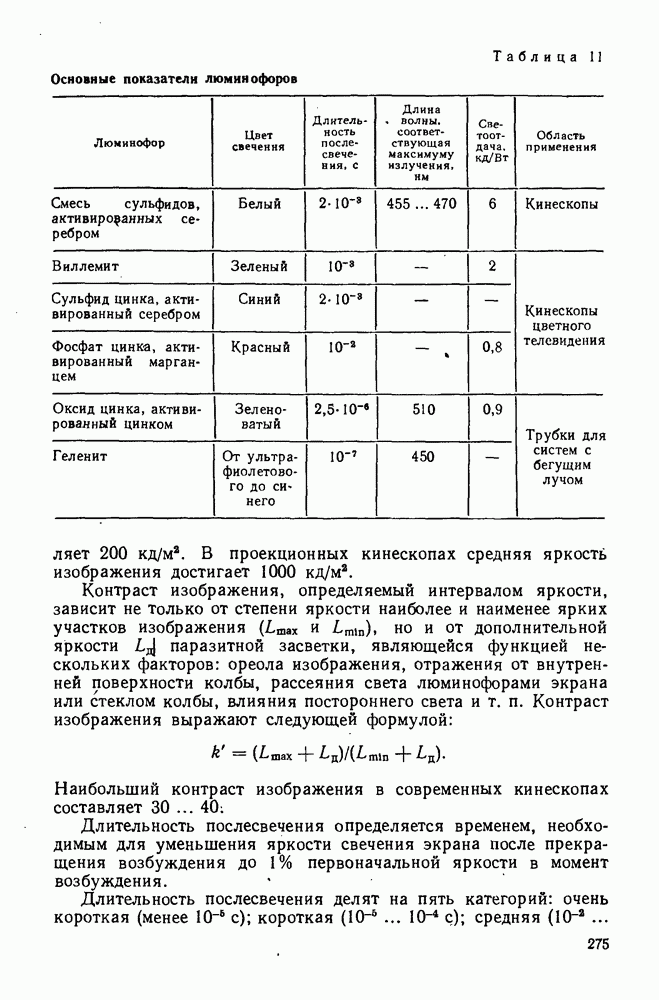
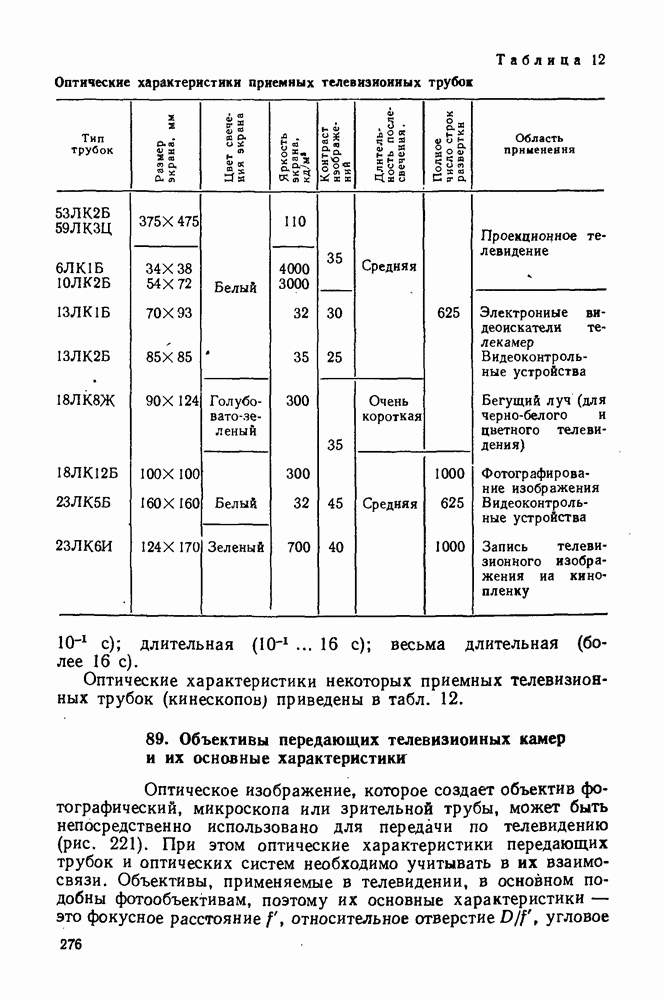
- 88. Оптические характеристики передающих и приемных телевизионных трубок
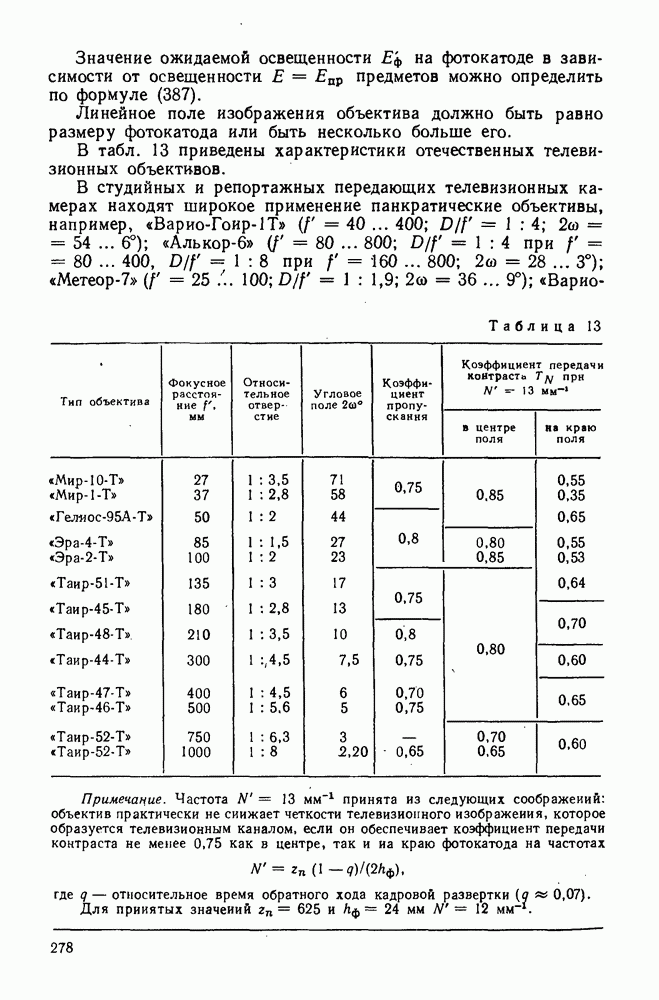
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы