| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
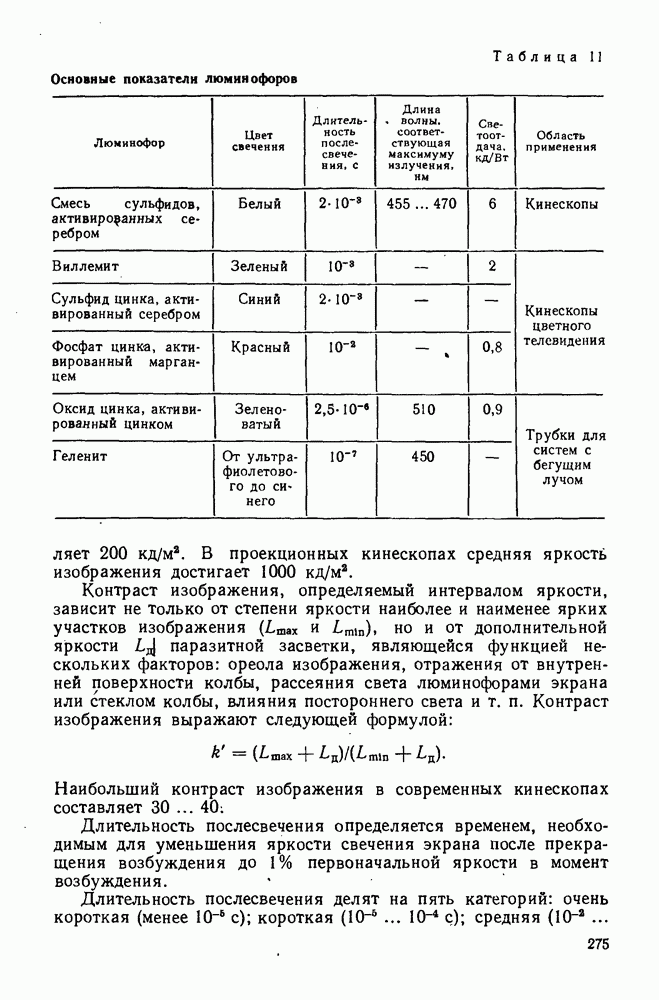
43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
Поток излучения, прошедший через оптическую систему, ослабляется. На вход оптической системы (во входной зрачок) поступает поток [см. формулу (191)].

где  энергетическая яркость излучающего участка
энергетическая яркость излучающего участка  поверхности, расположенного перпендикулярно к оптической оси и пересекаемого ею;
поверхности, расположенного перпендикулярно к оптической оси и пересекаемого ею;  апертурный угол в пространстве предметов.
апертурный угол в пространстве предметов.
Поток излучения, прошедший оптическую систему и падающий на площадку  [см. формулу (192)], с учетом коэффициента пропускания
[см. формулу (192)], с учетом коэффициента пропускания  оптической системы, а также изменения яркости по формуле (205) будет следующим:
оптической системы, а также изменения яркости по формуле (205) будет следующим:

где  показатели преломления среды пространства изображений и пространства предметов соответственно;
показатели преломления среды пространства изображений и пространства предметов соответственно;  апертурный угол в пространстве изображений.
апертурный угол в пространстве изображений.
Кроме того, поток излучения, выходящий из оптической системы, на основании формулы (191) с учетом коэффициента пропускания

Приравнивая правые части формул (216) и (217), получаем:

или

Заменяя отношение сопряженных площадок  на отношение квадратов сопряженных отрезков у и у, приходим к условию синусов:
на отношение квадратов сопряженных отрезков у и у, приходим к условию синусов:

где  линейное увеличение оптической системы.
линейное увеличение оптической системы.
Этому условию должна удовлетворять оптическая с истема, изображающая элементарную площадку, расположенную перпендикулярно к оптической оси и пересекаемую ею, при любых конечных апертурных углах 
Освещенность изображения  может быть вычислена по одной из двух формул:
может быть вычислена по одной из двух формул:

Заметим, что большая часть оптических систем находится в воздухе, поэтому  Следовательно, в этих случаях освещенность изображения элементарной площадки, перпендикулярной к оптической оси и пересекаемой последней,
Следовательно, в этих случаях освещенность изображения элементарной площадки, перпендикулярной к оптической оси и пересекаемой последней,

Представим  в виде, удобном для выполнения вычислений. Так, для оптической системы, показанной на рис. 96, можно записать:
в виде, удобном для выполнения вычислений. Так, для оптической системы, показанной на рис. 96, можно записать:

где  диаметр выходного зрачка;
диаметр выходного зрачка;  отрезки, определяющие положения выходного зрачка и плоскости изображения.
отрезки, определяющие положения выходного зрачка и плоскости изображения.
Если линейное увеличение системы  а линейное увеличение в зрачках
а линейное увеличение в зрачках  диаметр входного зрачка), то
диаметр входного зрачка), то  где
где  заднее фокусное расстояние оптической системы.
заднее фокусное расстояние оптической системы.
Таким образом,

Внесем значение  по равенству (221) в формулу (218):
по равенству (221) в формулу (218):

Если, как это часто бывает, линейное увеличение в зрачках  то
то

а для оптической системы, находящейся в воздухе,


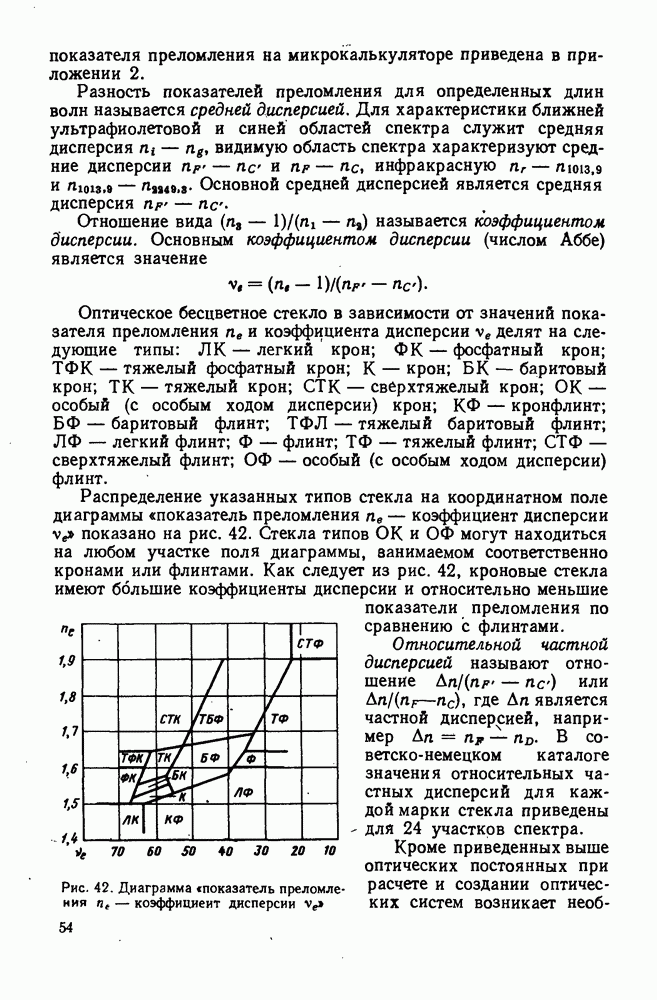
Рис. 96. Схема для определения выходного апертурного угла
В случае, когда предмет находится в бесконечности  освещенность определяется по формулам
освещенность определяется по формулам

или (при  )
)

Отметим, что в формулах  на основании равенства (190) и с учетом коэффициента отражения
на основании равенства (190) и с учетом коэффициента отражения  диффузно рассеивающей поверхности, светящейся отраженным светом, можно принять, что
диффузно рассеивающей поверхности, светящейся отраженным светом, можно принять, что

где  — энергетическая освещенность излучающей поверхности.
— энергетическая освещенность излучающей поверхности.
Если излучающий элемент поверхности  располагается вне оптической оси (см. рис. 96), то для определения освещенности его изображения
располагается вне оптической оси (см. рис. 96), то для определения освещенности его изображения  следует учесть, во-первых, изменение освещенности от угла
следует учесть, во-первых, изменение освещенности от угла  между оптической осью и осью пучка лучей в пространстве изображений, который образует изображение центра площади
между оптической осью и осью пучка лучей в пространстве изображений, который образует изображение центра площади  (главного луча) [см. формулу (196)] и, во-вторых, явление виньетирования, характеризуемое коэффициентом виньетирования
(главного луча) [см. формулу (196)] и, во-вторых, явление виньетирования, характеризуемое коэффициентом виньетирования  (см. п. 36). Поэтому освещенность такой элементарной внеосевой площадки
(см. п. 36). Поэтому освещенность такой элементарной внеосевой площадки

где  — освещенность осевой площадки, вычисленная по одной из формул
— освещенность осевой площадки, вычисленная по одной из формул 
Из анализа формул  вытекает важный вывод о том, что освещенность пропорциональна квадрату отношения диаметра входного зрачка оптической системы к ее фокусному расстоянию.
вытекает важный вывод о том, что освещенность пропорциональна квадрату отношения диаметра входного зрачка оптической системы к ее фокусному расстоянию.
Это отношение называется относительным отверстием, а величина, ему обратная, — диафрагменным числом К. Следовательно, чем меньше диафрагменное число, тем больше освещенность изображения.

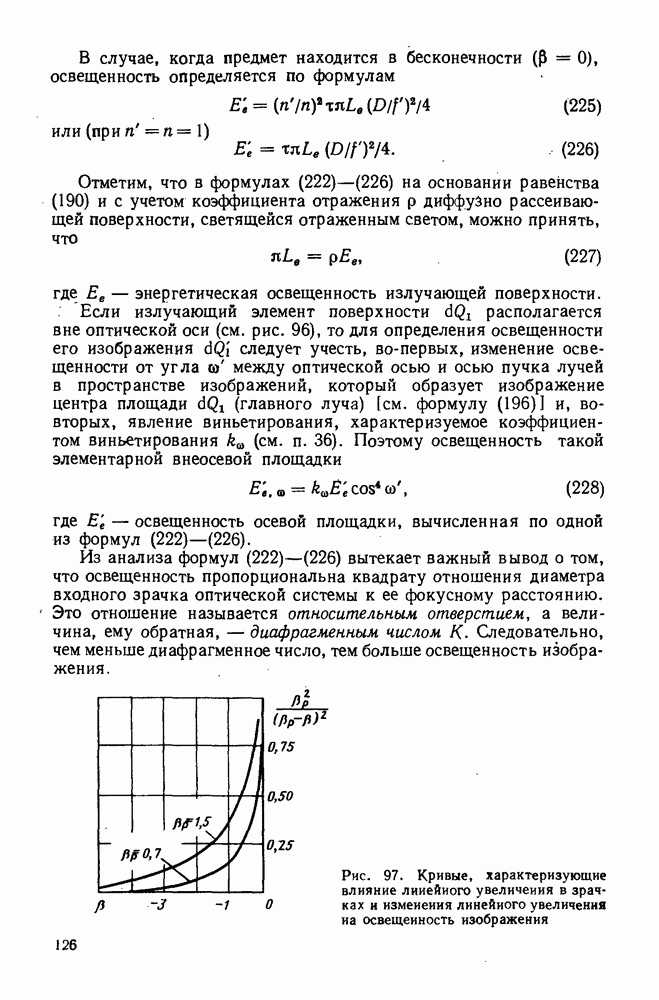
Рис. 97. Кривые, характеризующие влияние линейного увеличения в зрачках и изменения линейного увеличения на освещенность изображения
Квадрат относительного отверстия называется геометрической светосилой, а его произведение на коэффициент пропускания оптической системы,  физической светосилой.
физической светосилой.
Влияние линейного увеличения в зрачках  на освещенность изображения можно оценить с помощью рис. 97, где показаны кривые, характеризующие изменение значений
на освещенность изображения можно оценить с помощью рис. 97, где показаны кривые, характеризующие изменение значений  пропорциональных освещенности изображения, при изменении линейного увеличения
пропорциональных освещенности изображения, при изменении линейного увеличения  для
для  при прочих одинаковых условиях. Например, для
при прочих одинаковых условиях. Например, для  при изменении линейного увеличения в зрачках с 0,7 до 1,5 освещенность возрастает в 2,2 раза. Определим освещенность изображения, получаемого на оси оптической системы, для входного зрачка, имеющего форму кольца. Этот случай имеет место в зеркальных и зеркально-линзовых системах, когда центральная часть зрачка экранируется (см. рис. 6).
при изменении линейного увеличения в зрачках с 0,7 до 1,5 освещенность возрастает в 2,2 раза. Определим освещенность изображения, получаемого на оси оптической системы, для входного зрачка, имеющего форму кольца. Этот случай имеет место в зеркальных и зеркально-линзовых системах, когда центральная часть зрачка экранируется (см. рис. 6).
Освещенность изображения вычисляют по формуле

получаемой для кольцевой формы зрачка в соответствии с формулой (217).
В формуле (229) угол одех — выходной апертурный угол, образованный лучом, идущим через внешний край выходного зрачка; угол  угол, образованный лучом, идущим через внутренний край выходного зрачка с оптической осью.
угол, образованный лучом, идущим через внутренний край выходного зрачка с оптической осью.
Из формулы (220) следует, что

где  диаметры внешнего и внутреннего контуров выходного зрачка;
диаметры внешнего и внутреннего контуров выходного зрачка;  отрезки, определяющие положение выходного зрачка и плоскости изображения относительно заднего фокуса системы.
отрезки, определяющие положение выходного зрачка и плоскости изображения относительно заднего фокуса системы.
Для энергетически эквивалентной системы диаметр выходного зрачка круглой формы без экранирования получается из условия равенства площадей обоих зрачков

и соответственно выходной апертурный угол — из формулы

Все соотношения, приведенные в этом параграфе, сохраняются при замене энергетических величин световыми.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
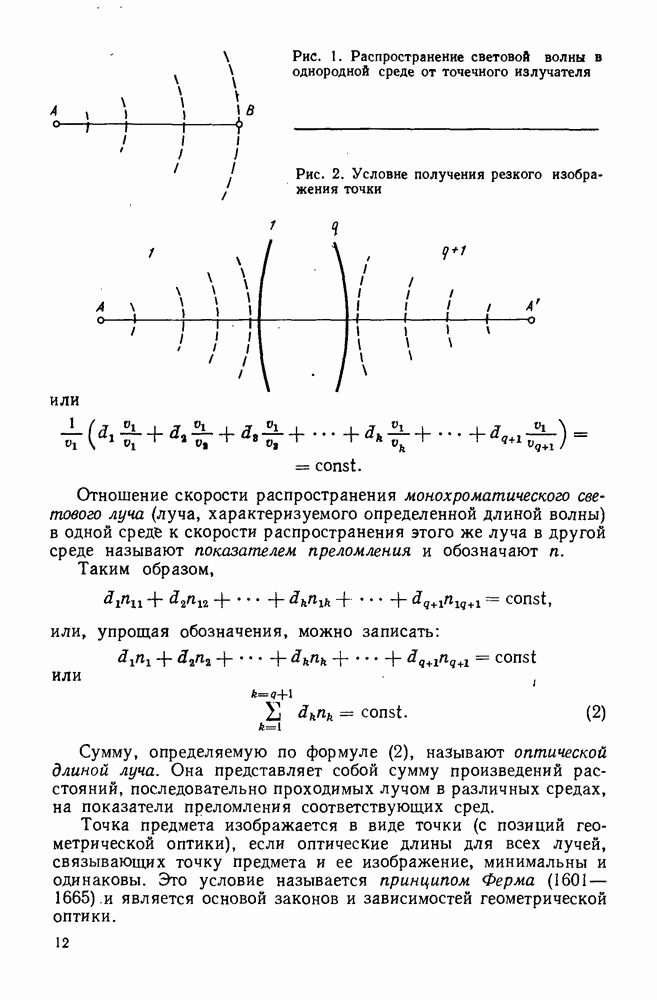
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
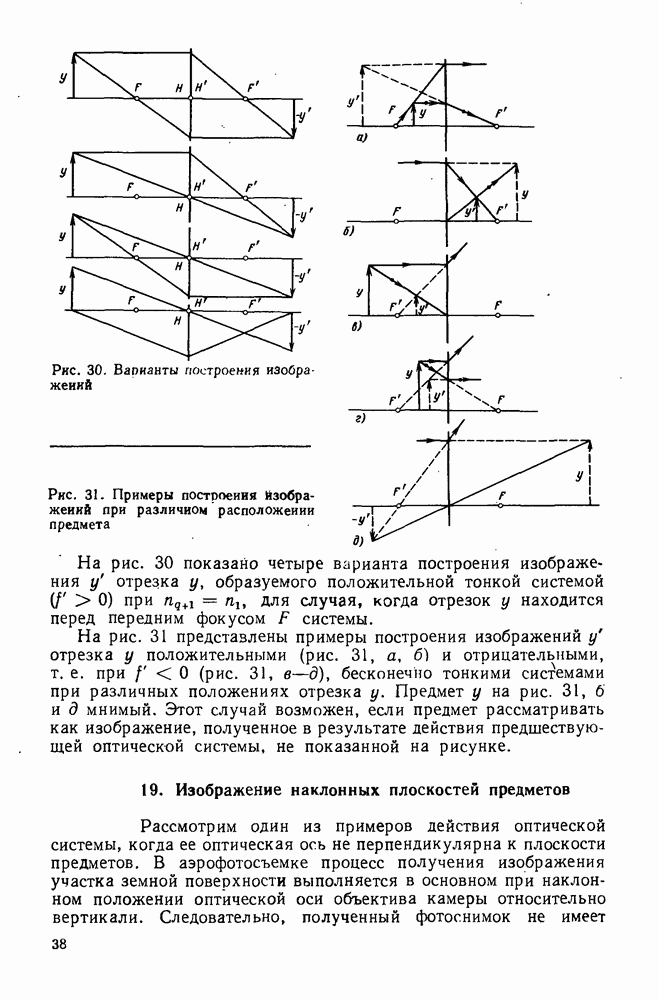
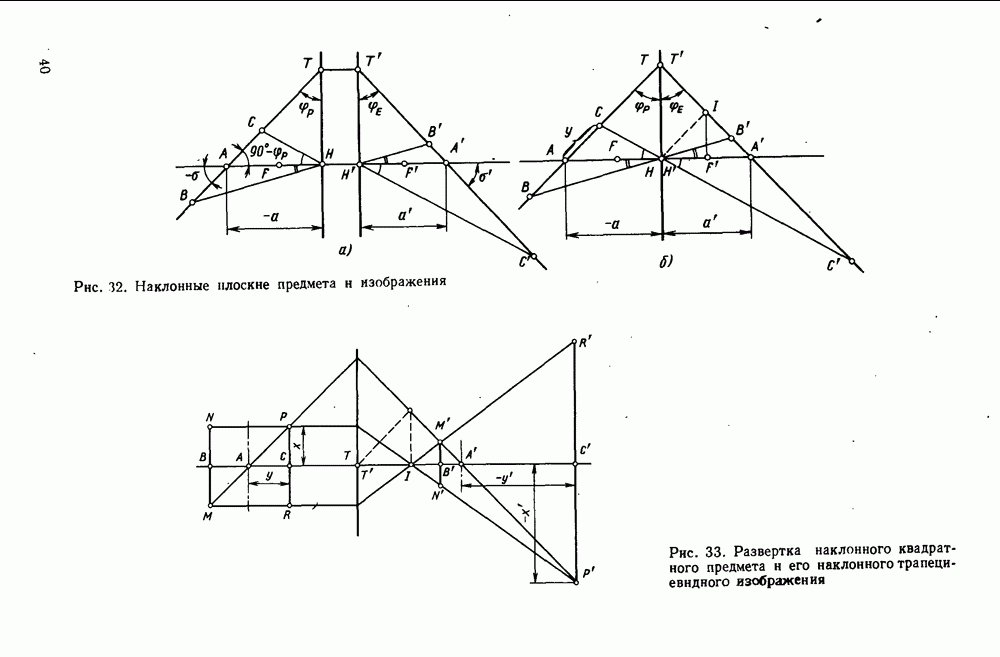
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
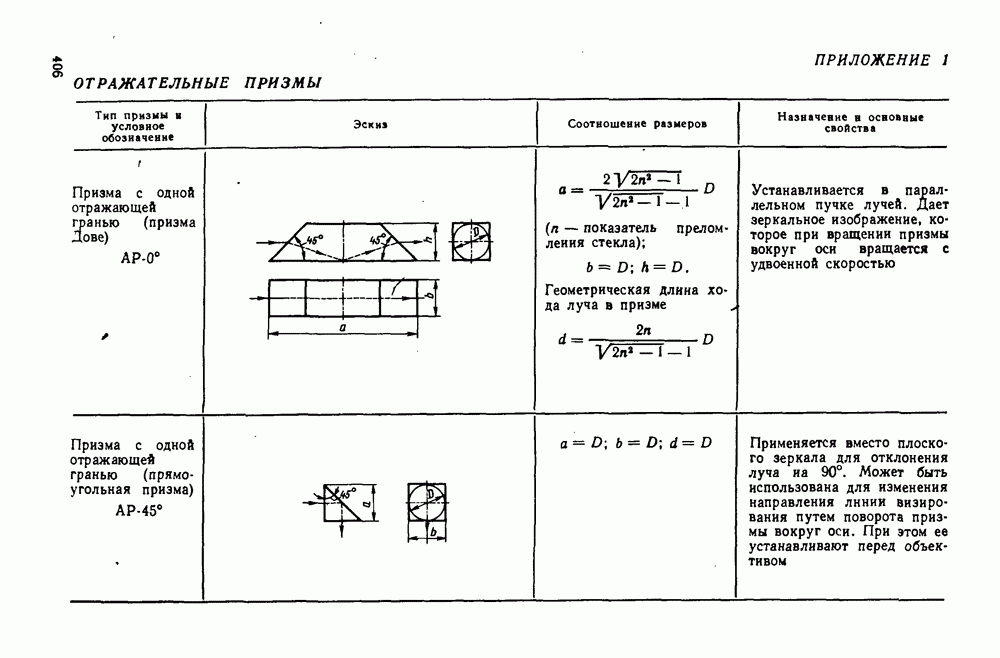
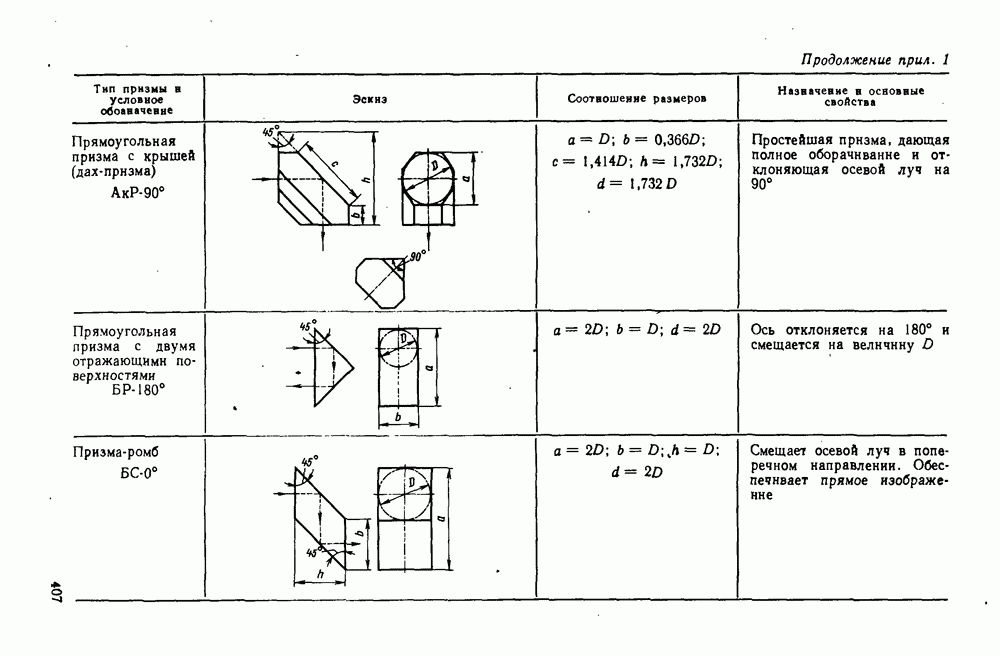
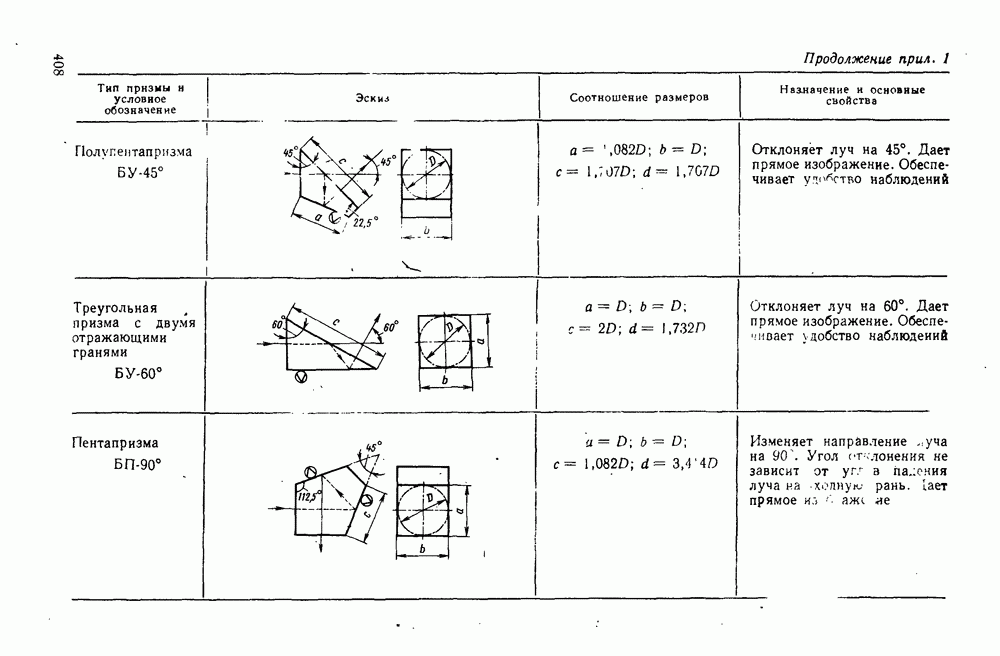
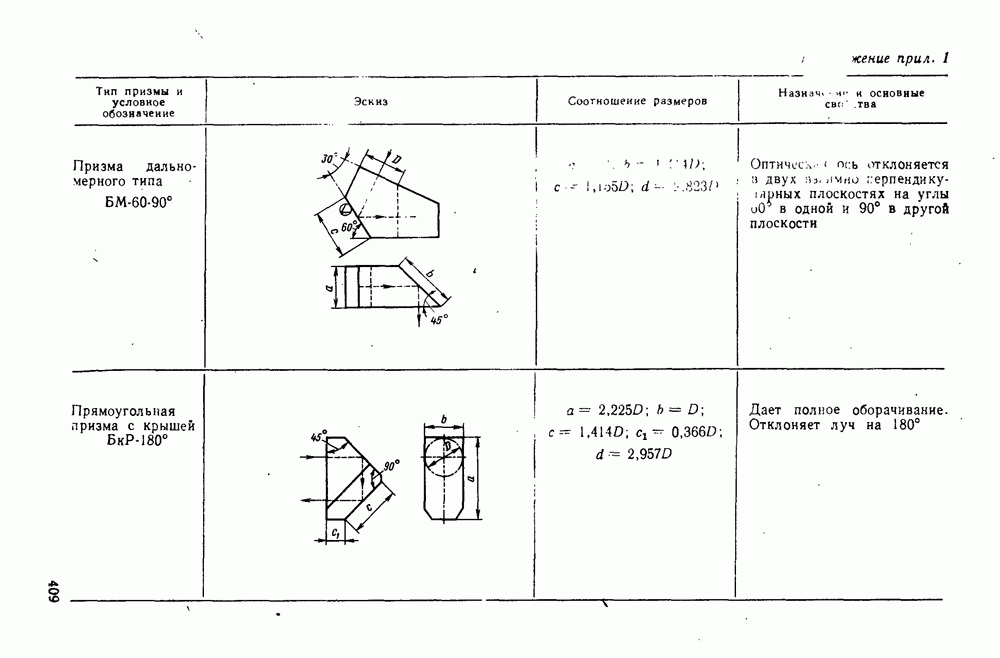
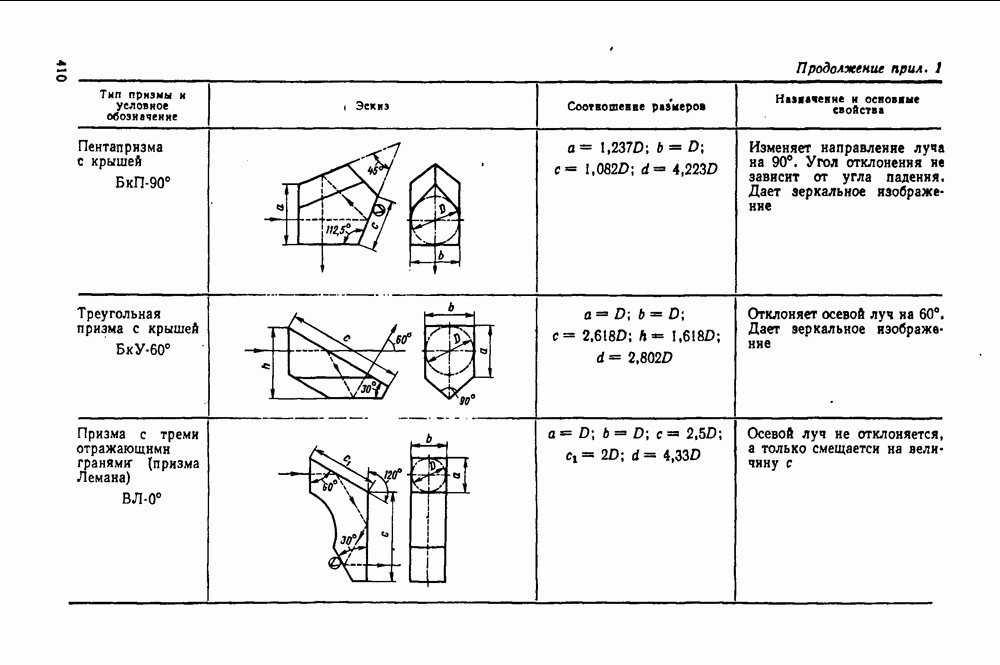
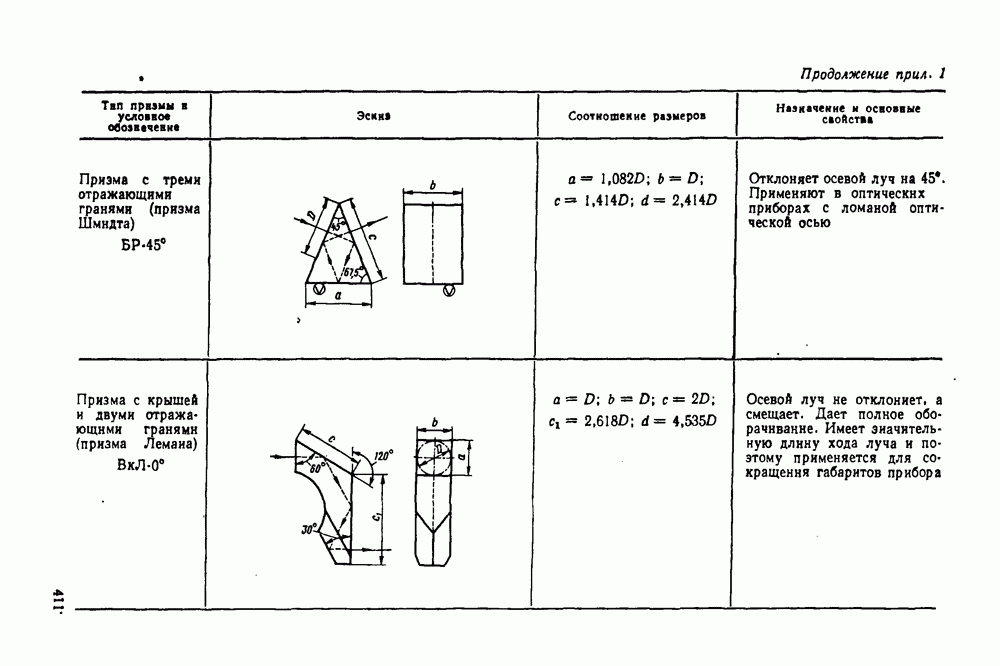
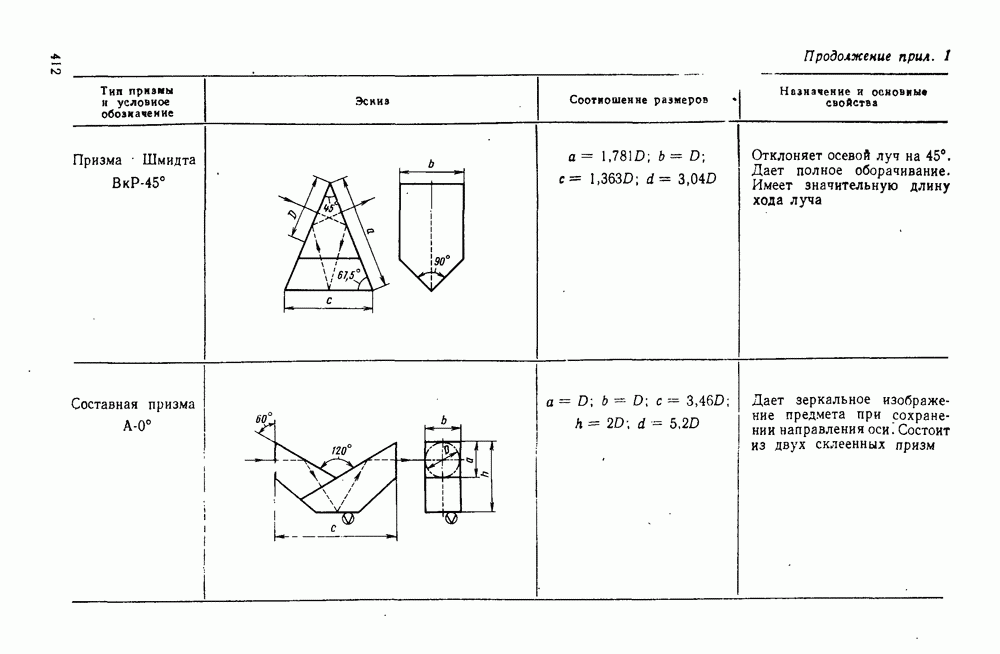
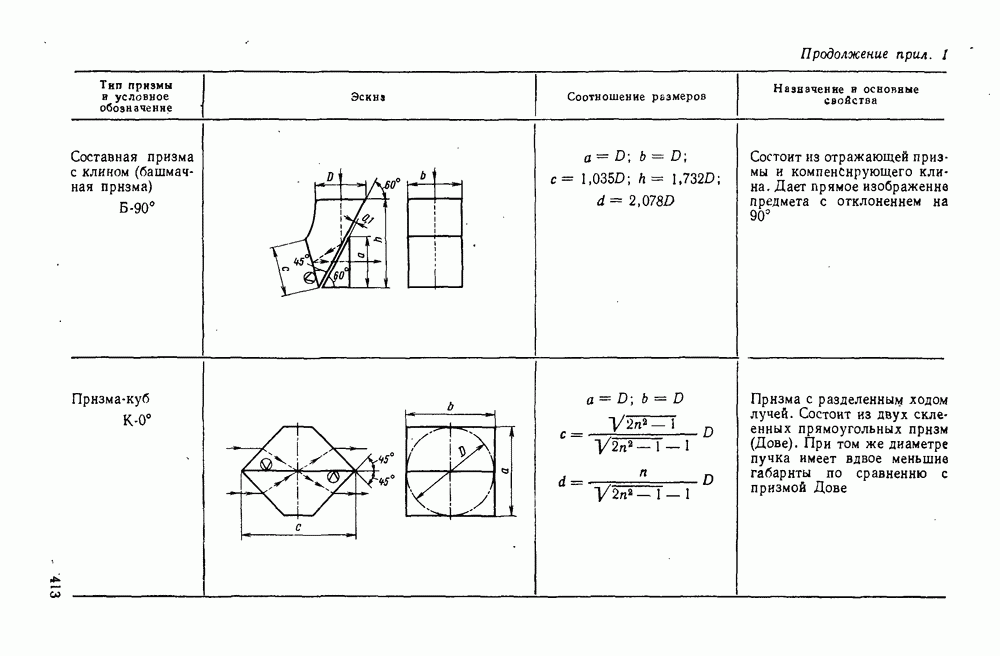
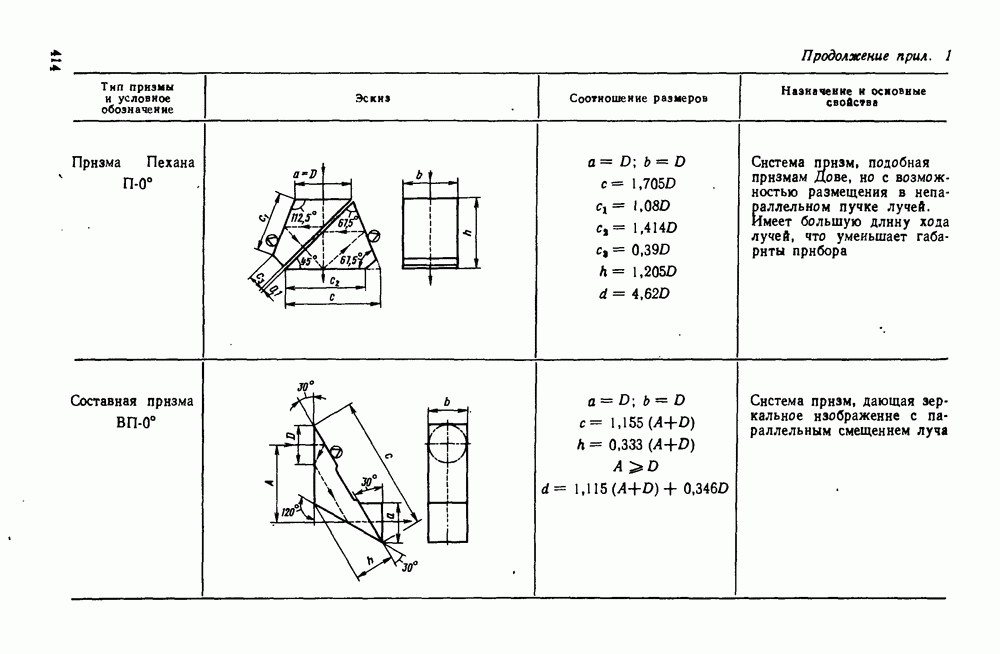
- 29. Отражательные призмы
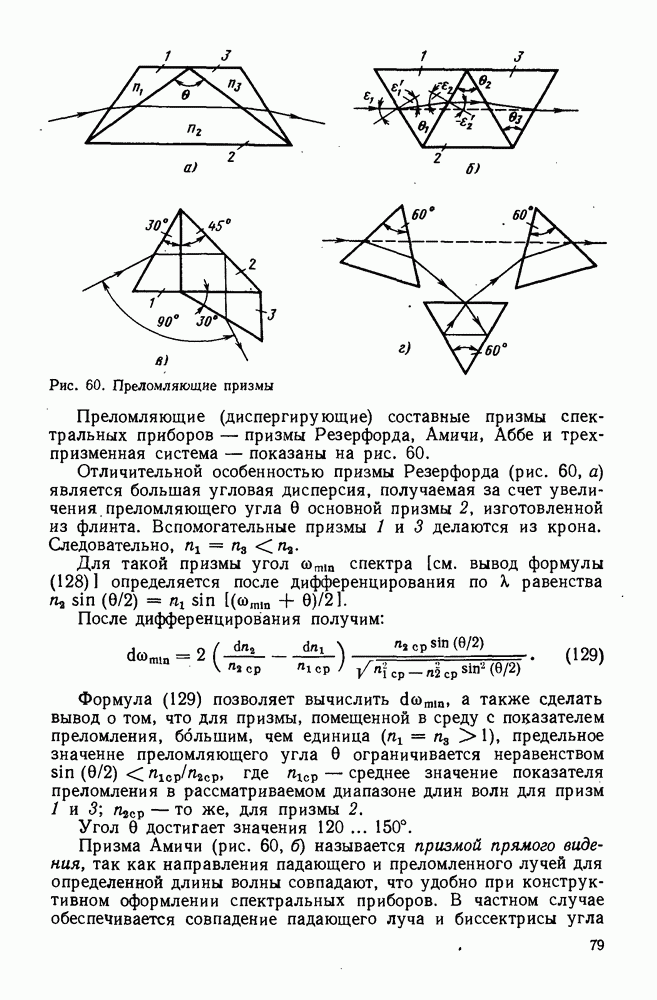
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
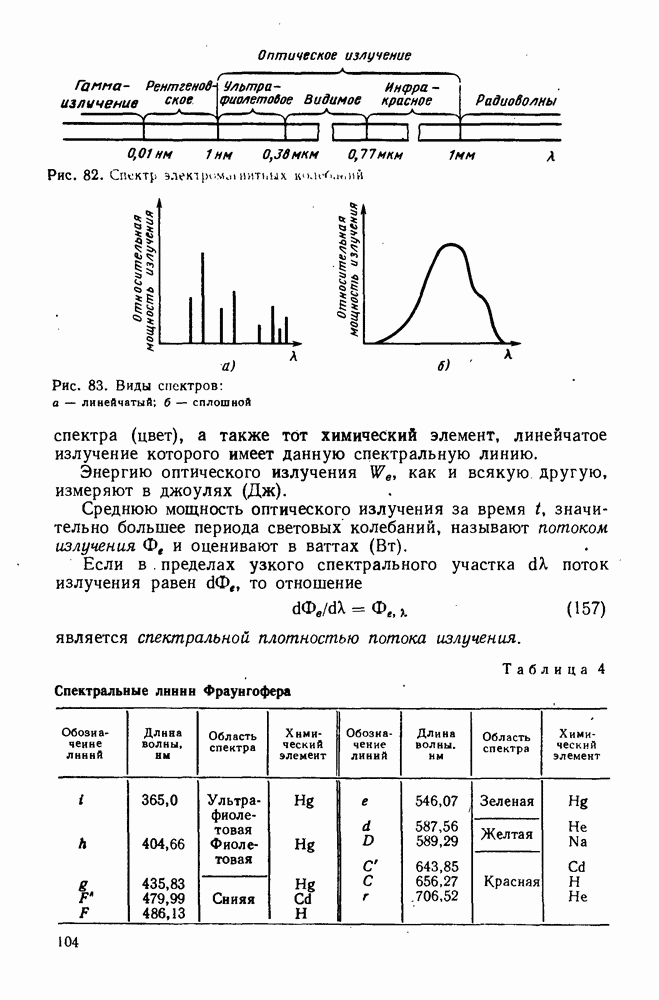
- 37. Оптическое излучение. Поток излучения
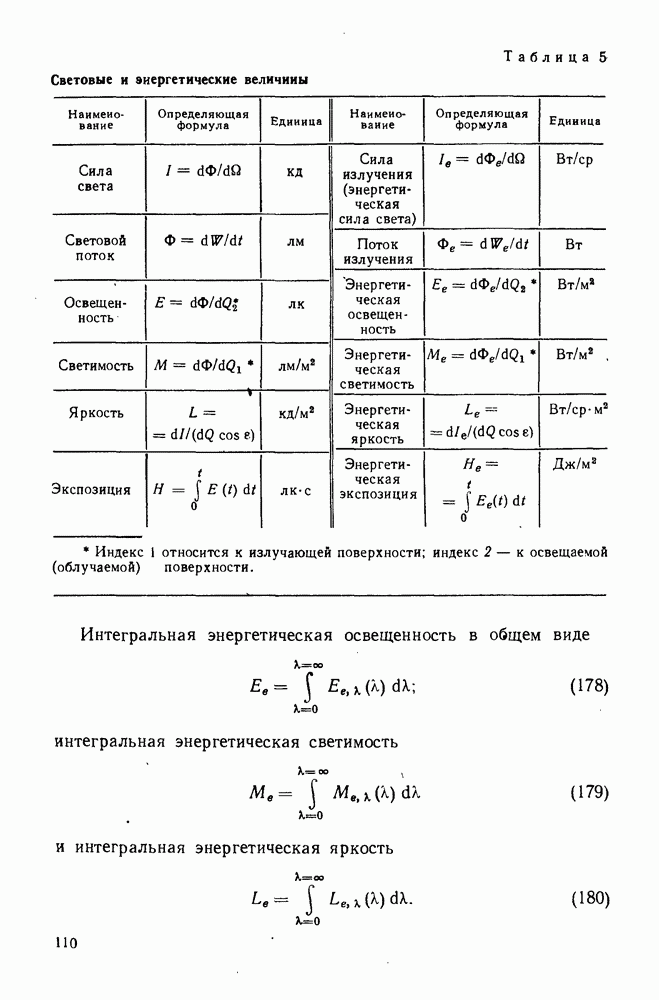
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
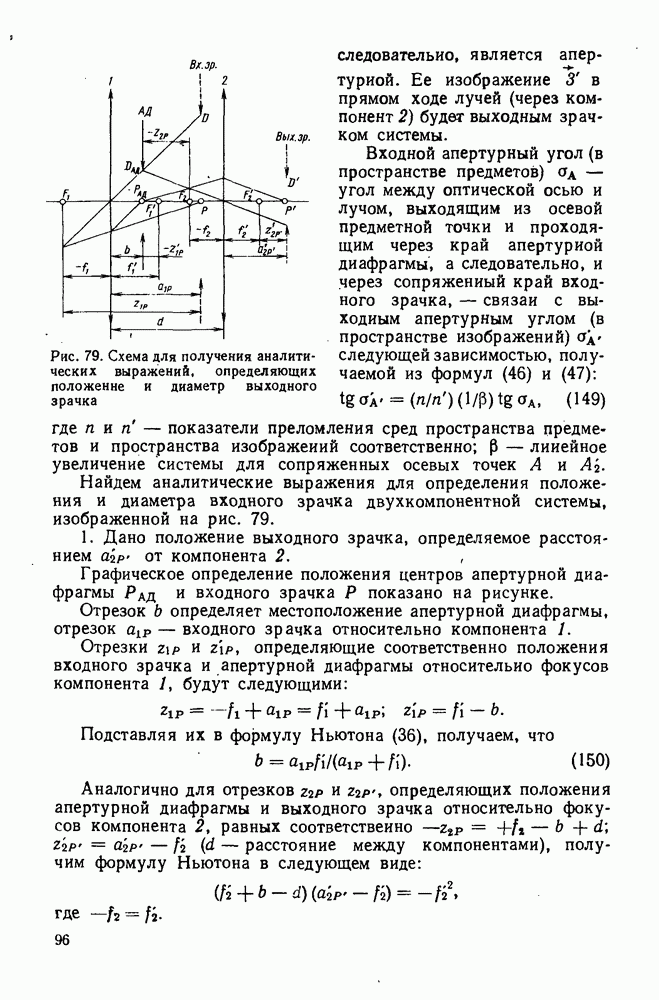
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
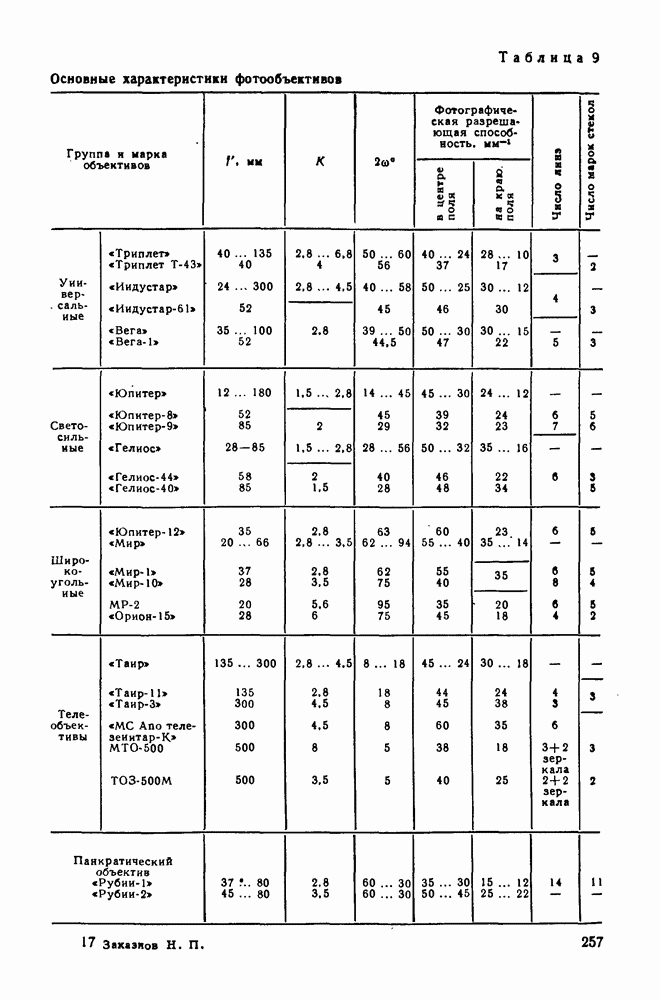
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы