| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
30. Преломляющие призмы и клинья
Оптическая деталь с плоскими преломляющими поверхностями 1 и 2, образующими двугранный угол  называется преломляющей призмой. Сечение призмы плоскостью, перпендикулярной к ребру двугранного угла, будет главным сечением призмы (рис. 59).
называется преломляющей призмой. Сечение призмы плоскостью, перпендикулярной к ребру двугранного угла, будет главным сечением призмы (рис. 59).
Угол  между направлениями входящего и выходящего лучей называется углом отклонения, а угол
между направлениями входящего и выходящего лучей называется углом отклонения, а угол  между преломляющими плоскими гранями — преломляющим углом призмы.
между преломляющими плоскими гранями — преломляющим углом призмы.
Рассмотрим ход луча в главном сечении призмы. Угол преломления на первой грани определяется из формулы

(призма находится в воздухе).

Рис. 59. Ход луча в преломляющей призме
Из рис. 59 следует

тогда

Угол отклонения луча призмой

Представляет интерес отыскание значения угла падения на первую грань призмы, при котором угол отклонения  преломленного луча будет наименьшим.
преломленного луча будет наименьшим.
Для этой цели, пользуясь формулой (121), запишем:

или

Кроме того, из равенства (119) имеем:

Продифференцировав формулы (118) и (120), получим следующие равенства:

из которых, учитывая равенства (122) и (123), найдем выражение

Кроме того, перемножая правые и левые части формул (118) и (120), получим равенство

Одновременное существование равенств (124) и (125) возможно только при условии, когда

Так как вторая производная  то равенства (126) определяют условие получения сйщщ при данном преломляющем угле
то равенства (126) определяют условие получения сйщщ при данном преломляющем угле  призмы. Из этих же равенств следует, что получается при таком расположении преломленного луча внутри призмы, при котором этот луч перпендикулярен к биссектрисе преломляющего угла
призмы. Из этих же равенств следует, что получается при таком расположении преломленного луча внутри призмы, при котором этот луч перпендикулярен к биссектрисе преломляющего угла 
Для определения  служит формула (120), из которой с учетом равенств (126) и (119) получаем выражение
служит формула (120), из которой с учетом равенств (126) и (119) получаем выражение

используемое при выборе показателя преломления материала призмы  измеряются, например, на гониометре).
измеряются, например, на гониометре).
Рассмотрим влияние изменения показателя преломления материала призмы на угол отклонения преломленного луча. Показатель преломления зависит от длины волны монохроматического излучения. Поэтому, если луч, поступающий в призму, монохроматический, то при преломлении отдельные монохроматические составляющие этого луча будут отклоняться на разные углы (дисперсия призмы).
Угловой дисперсией призмы называется зависимость угла отклонения луча от длины световой волны, равная производной этого угла по длине волны, т. е. 
Найдем угловую дисперсию призмы для случая, описываемого формулой (127). В результате ее дифференцирования получим выражение

где  дисперсия материала призмы;
дисперсия материала призмы;  среднее значение показателя преломления в данном интервале
среднее значение показателя преломления в данном интервале  длин волн.
длин волн.
Угловое значение  дисперсии вычисляют по формуле
дисперсии вычисляют по формуле

 разность показателей преломления на краях данного интервала длин волн
разность показателей преломления на краях данного интервала длин волн 
Если  (стекло K8), то
(стекло K8), то  рад
рад  .
.
Угловая дисперсия призмы  и угловое значение дисперсии
и угловое значение дисперсии  будут большими, если угол отклонения
будут большими, если угол отклонения 
Преломляющие призмы в основном применяют в виде диспергирующих элементов в спектральных приборах.
Из формулы (128), которая определяет угловое значение дисперсии, следует, что эта величина тем больше, чем больше преломляющий угол  призмы. Ограничение на угол
призмы. Ограничение на угол  накладывается той же формулой, а именно:
накладывается той же формулой, а именно:  где
где  среднее значение показателя преломления материала призмы в заданном диапазоне длин волн.
среднее значение показателя преломления материала призмы в заданном диапазоне длин волн.
При невыполнении этого неравенства наблюдается полное внутреннее отражение на второй преломляющей грани призмы. Следует отметить, что формула (128) определяет угловое значение дисперсии при наименьшем угле отклонения. Если угол отклонения  то соответственно увеличивается и угловая дисперсия. Однако при этом уменьшается разрешающая сила спектрального прибора, что и определяет использование преломляющих призм в положении наименьшего отклонения.
то соответственно увеличивается и угловая дисперсия. Однако при этом уменьшается разрешающая сила спектрального прибора, что и определяет использование преломляющих призм в положении наименьшего отклонения.
Наиболее часто преломляющий угол призмы выбирают равным 60°.

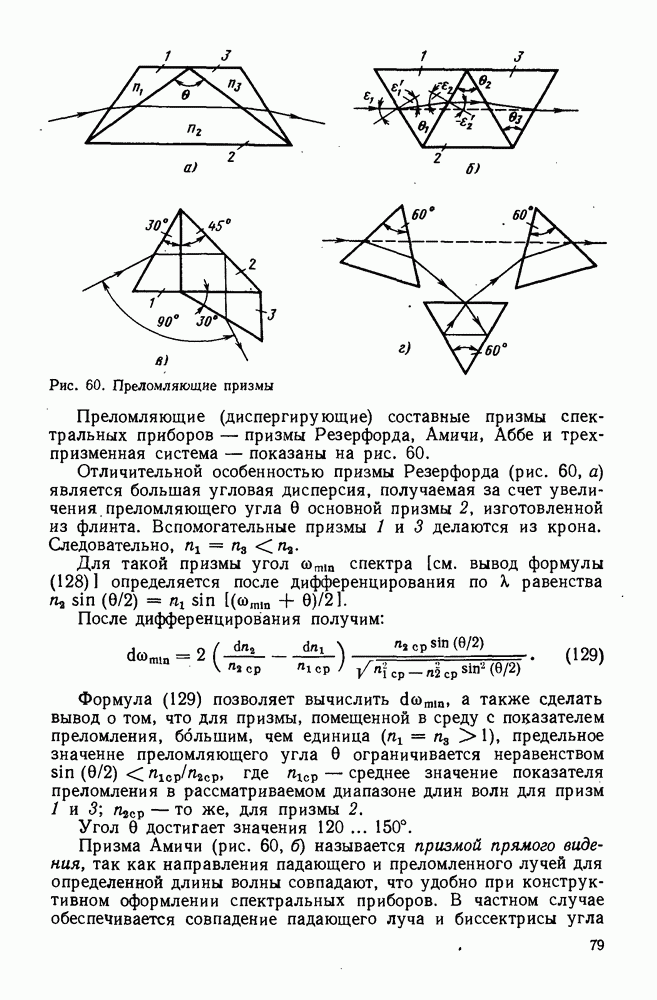
Рис. 60. Преломляющие призмы
Преломляющие (диспергирующие) составные призмы спектральных приборов — призмы Резерфорда, Амичи, Аббе и трехпризменная система — показаны на рис. 60.
Отличительной особенностью призмы Резерфорда (рис. 60, а) является большая угловая дисперсия, получаемая за счет увеличения преломляющего угла  основной призмы 2, изготовленной из флинта. Вспомогательные призмы 1 и 3 делаются из крона. Следовательно,
основной призмы 2, изготовленной из флинта. Вспомогательные призмы 1 и 3 делаются из крона. Следовательно, 
Для такой призмы угол  спектра [см. вывод формулы (128)] определяется после дифференцирования по
спектра [см. вывод формулы (128)] определяется после дифференцирования по  равенства гц
равенства гц 
После дифференцирования получим:

Формула (129) позволяет вычислить  а также сделать вывод о том, что для призмы, помещенной в среду с показателем преломления, большим, чем единица
а также сделать вывод о том, что для призмы, помещенной в среду с показателем преломления, большим, чем единица  предельное значение преломляющего угла
предельное значение преломляющего угла  ограничивается неравенством
ограничивается неравенством  где
где  среднее значение показателя преломления в рассматриваемом диапазоне длин волн для призм
среднее значение показателя преломления в рассматриваемом диапазоне длин волн для призм  то же, для призмы 2.
то же, для призмы 2.
Угол  достигает значения
достигает значения 
Призма Амичи (рис. 60, б) называется призмой прямого видения, так как направления падающего и преломленного лучей для определенной длины волны совпадают, что удобно при конструктивном оформлении спектральных приборов. В частном случае обеспечивается совпадение падающего луча и биссектрисы угла
дисперсии. Призмы 1 и 3 изготовляют из крона, призму 2 — из флинта 
Из рис. 60, б при использовании условия прямого видения получается следующая зависимость между преломляющими углами и показателями преломления (призма 2 равнобедренная):

Для призмы прямого видения значение угловой дисперсии не достигает максимума.
Призма Аббе (рис. 60, в) относится к призмам постоянного отклонения с углом  Для уменьшения поглощения призму с полным внутренним отражением выполняют из крона. На рис.
Для уменьшения поглощения призму с полным внутренним отражением выполняют из крона. На рис.  показана система прямого видения из трех преломляющих призм.
показана система прямого видения из трех преломляющих призм.
Если преломляющий угол  призмы мал
призмы мал  , то такую призму называют клином. Формула (120) при этом принимает следующий вид:
, то такую призму называют клином. Формула (120) при этом принимает следующий вид: 
Используя равенство (121), получим 
Из последних двух формул и формулы (118) получим значение угла отклонения луча клином  .
.
Если принять условие, что угол падения  мал, откуда следует и малость угла преломления
мал, откуда следует и малость угла преломления  то
то

Клин, как и призма, имеет дисперсию и соответствующее ей угловое значение дисперсии.
Из формулы (130) следует, что угловое значение дисперсии клина 
Например, для диапазона длин волн, границы которого соответствуют синему  и красному
и красному  цветам,
цветам,  где
где  средняя дисперсия материала клина
средняя дисперсия материала клина 
Оптические клинья в оптических системах используют в качестве компенсаторов при юстировке и измерениях. Однако более часто клиновидность проявляется как ошибка, допущенная при изготовлении плоскопараллельных пластин, предварительная оценка влияния которой обеспечивает задание ее допустимого значения.
Рассмотрим использование клина в качестве компенсатора. При вращении клина (рис. 61) изображение осевой точки описывает окружность радиусом у, который зависит от значения угла отклонения  и от расстояния
и от расстояния  между клином и плоскостью изображения:
между клином и плоскостью изображения:

К сожалению, движение изображения по окружности в целях измерения и компенсации использовать нельзя. Прямолинейное
движение изображения с достаточной степенью точности может быть обеспечено двумя одинаковыми клиньями, вращаемыми в противоположных направлениях на равные углы  (рис. 62).
(рис. 62).
Наибольший суммарный угол отклонения будет, очевидно, тогда, когда главные сечения клиньев лежат в одной плоскости, а преломляющие углы направлены в одну сторону:

При вращении клиньев угол отклонения в рассматриваемой меридиональной плоскости будет следующим:

С помощью, например, сферической тригонометрии доказывается, что горизонтальной (боковой) составляющей угла отклонения луча можно пренебречь.
Прямолинейное движение изображения может быть получено также при поступательном перемещении клина по направлению падающего луча. В этом случае (рис. 63) перемещение клина из положения 1 в положение 2 на расстояние  вызывает смещение изображения:
вызывает смещение изображения:

Из формулы (131) следует, что перемещение  клина и смещение
клина и смещение  изображения прямо пропорциональны.
изображения прямо пропорциональны.
Поступательно перемещающийся клин в отличие от вращающихся клиньев можно использовать в сходящихся пучках лучей. Для компенсации или измерения малых угловых или линейных величин пользуются парой вращающихся клиньев. Большому углу поворота  соответствует малое изменение в положении преломленного луча. Поступательно перемещающийся клин, используемый для компенсации и измерения малых линейных величин, является менее точным.
соответствует малое изменение в положении преломленного луча. Поступательно перемещающийся клин, используемый для компенсации и измерения малых линейных величин, является менее точным.

Рис. 61. Вращение клииа

Рис. 62. Вращение двух клиньев

Рис. 63. Поступательное перемещение клина

Рис. 64. Клин с переменным преломляющим углом
Клин с переменным преломляющим углом  может быть выполнен из двух линз: плосковыпуклой и вогнуто-плоской, составляющих плоскопараллельную пластину и подвижно соединенных так, как показано на рис. 64.
может быть выполнен из двух линз: плосковыпуклой и вогнуто-плоской, составляющих плоскопараллельную пластину и подвижно соединенных так, как показано на рис. 64.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
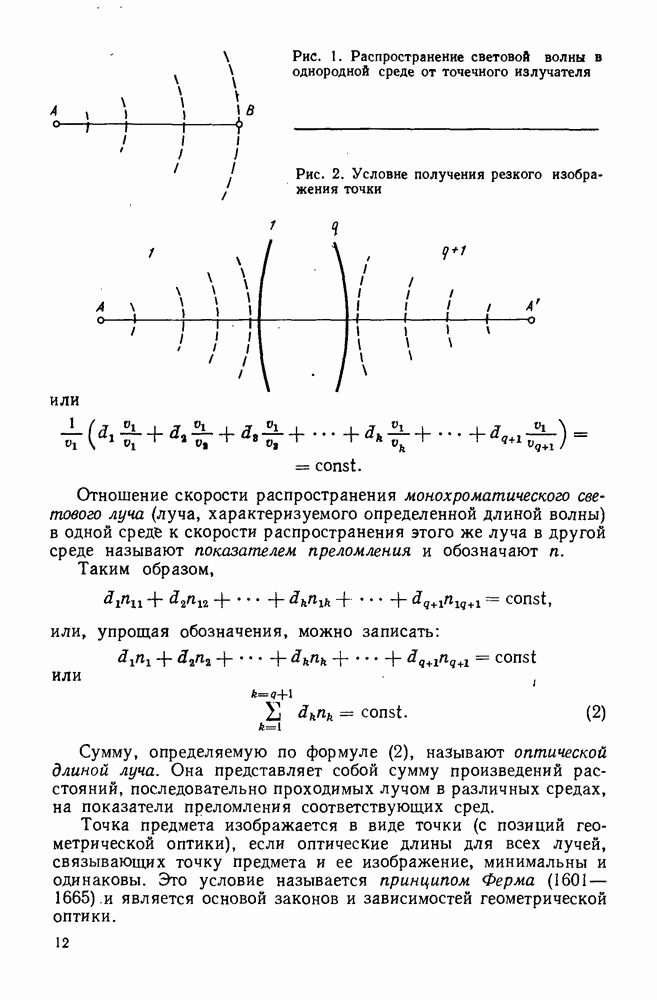
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
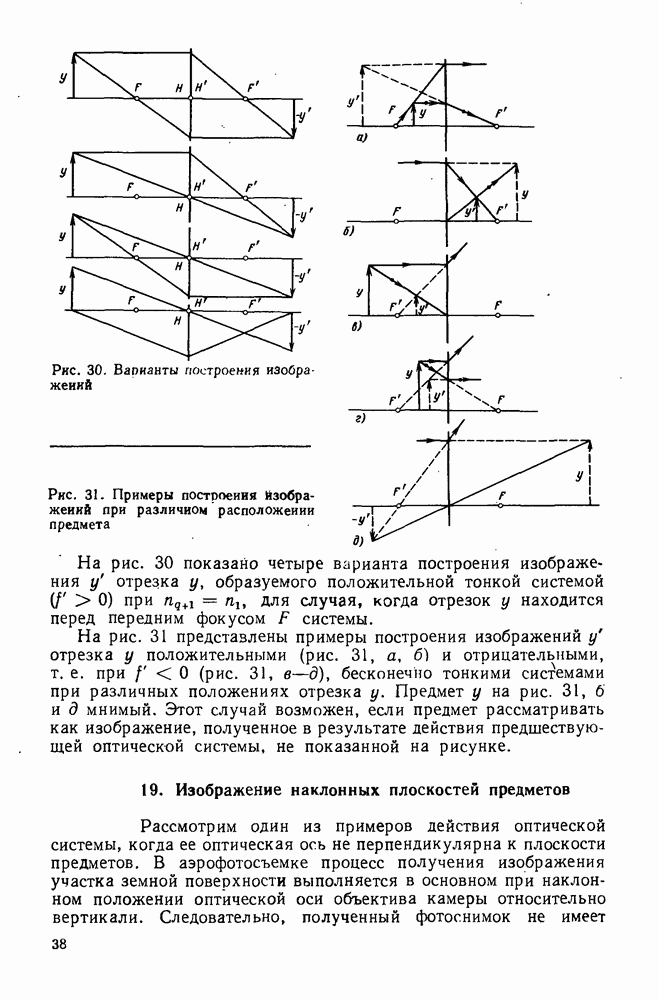
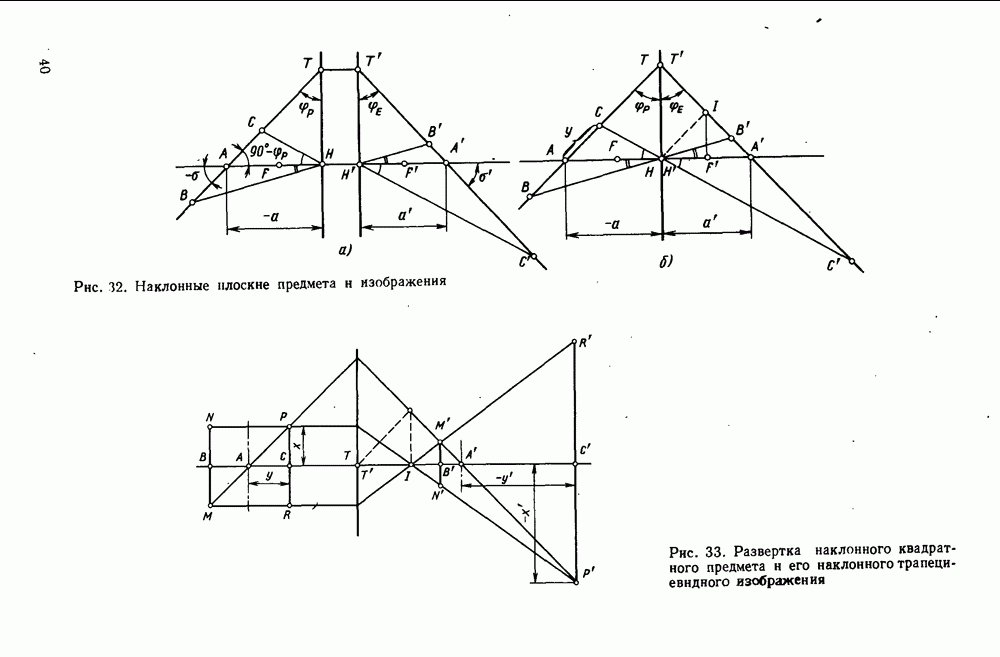
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
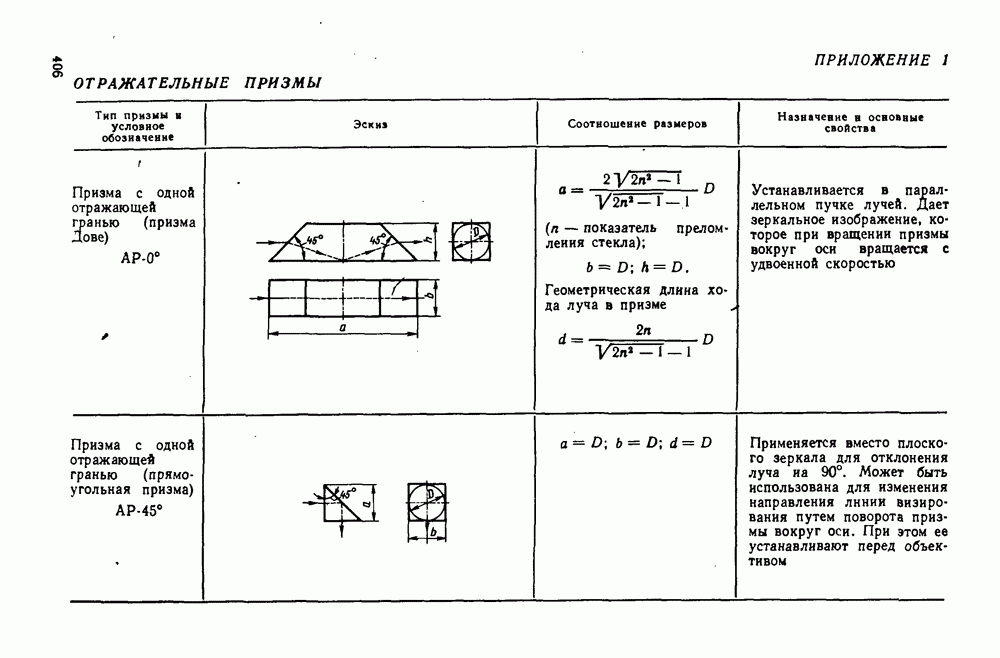
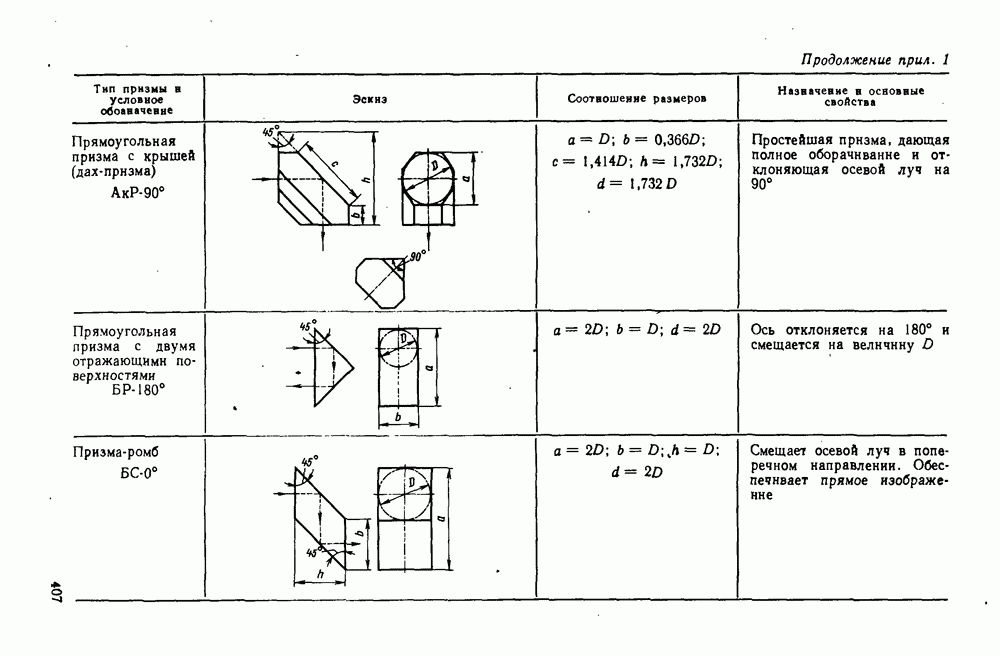
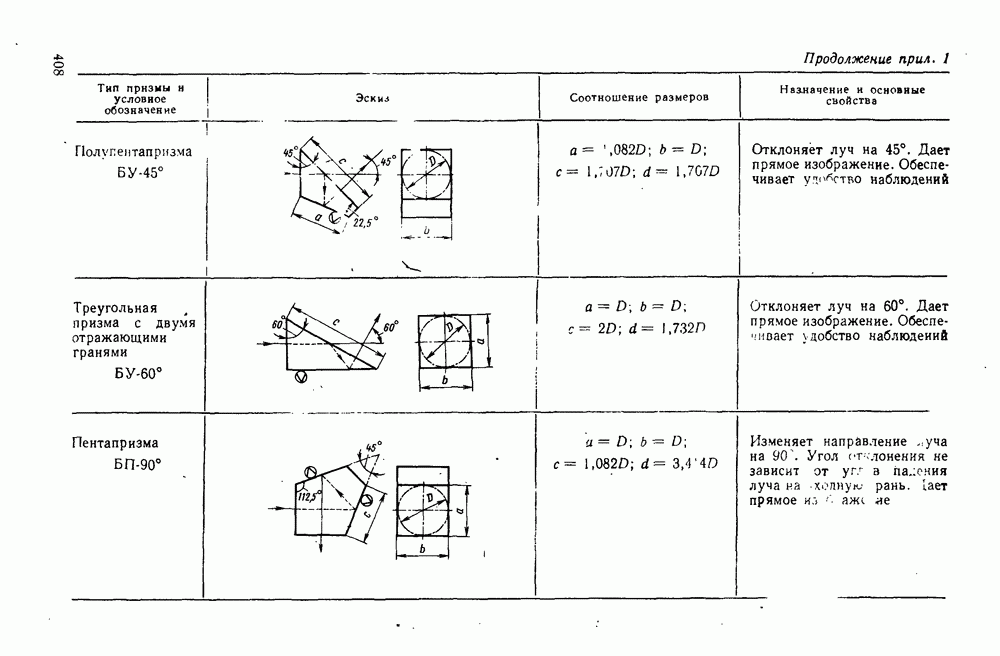
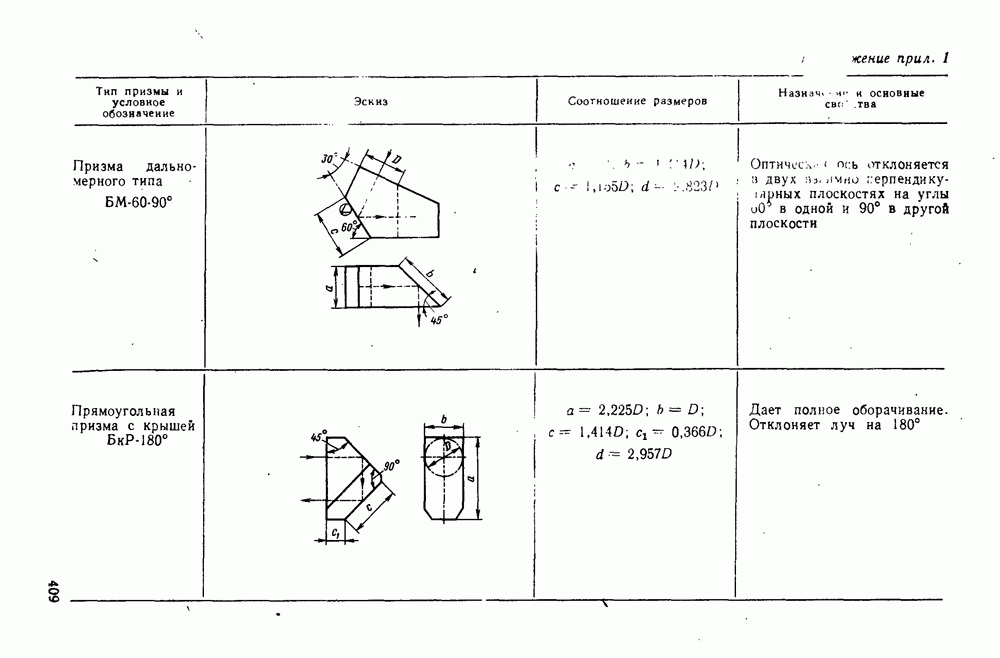
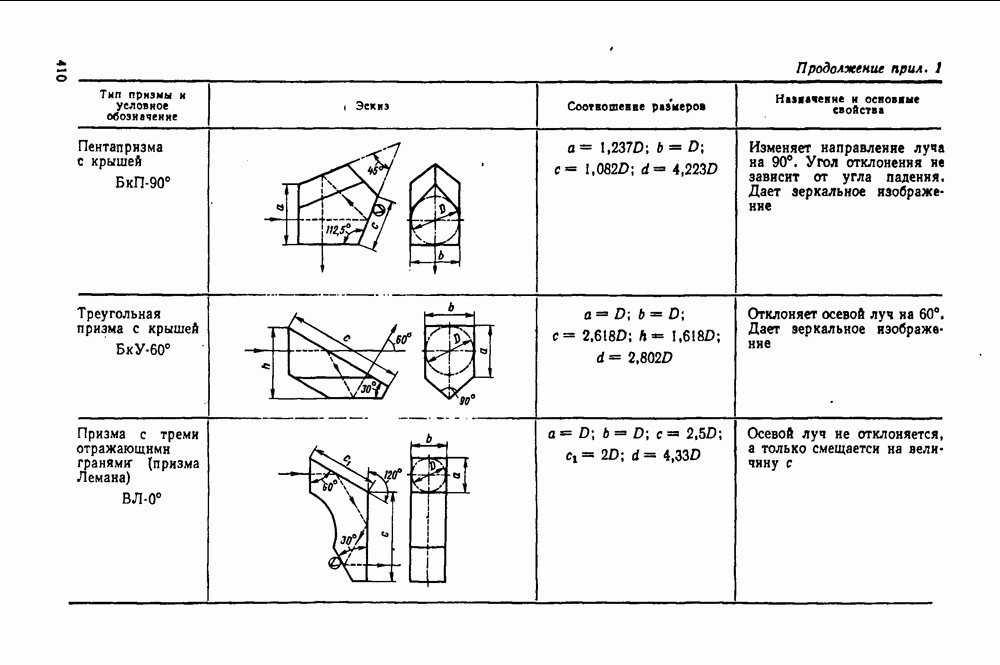
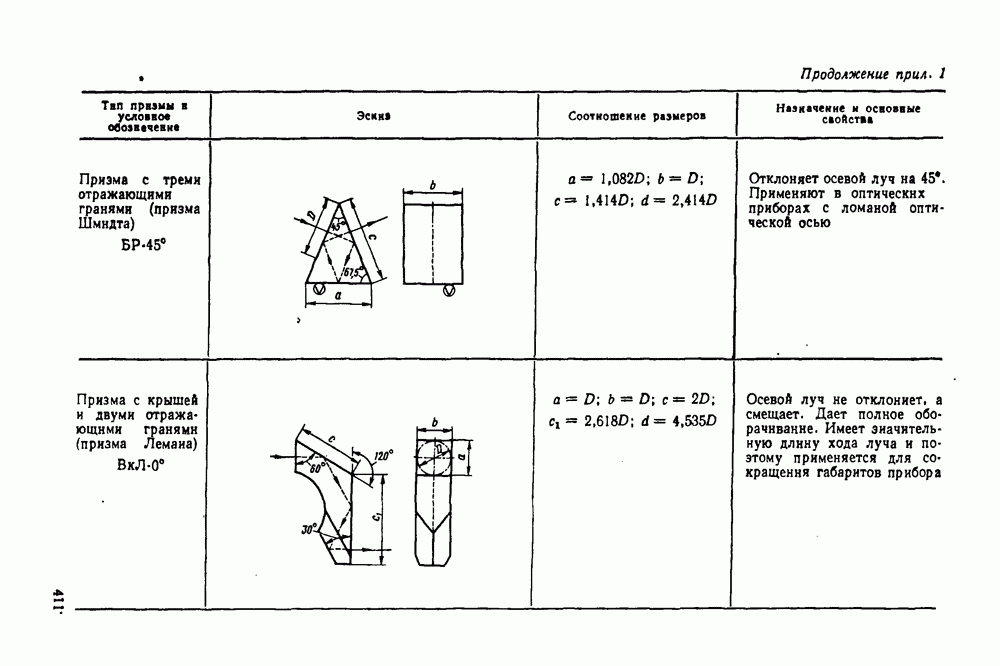
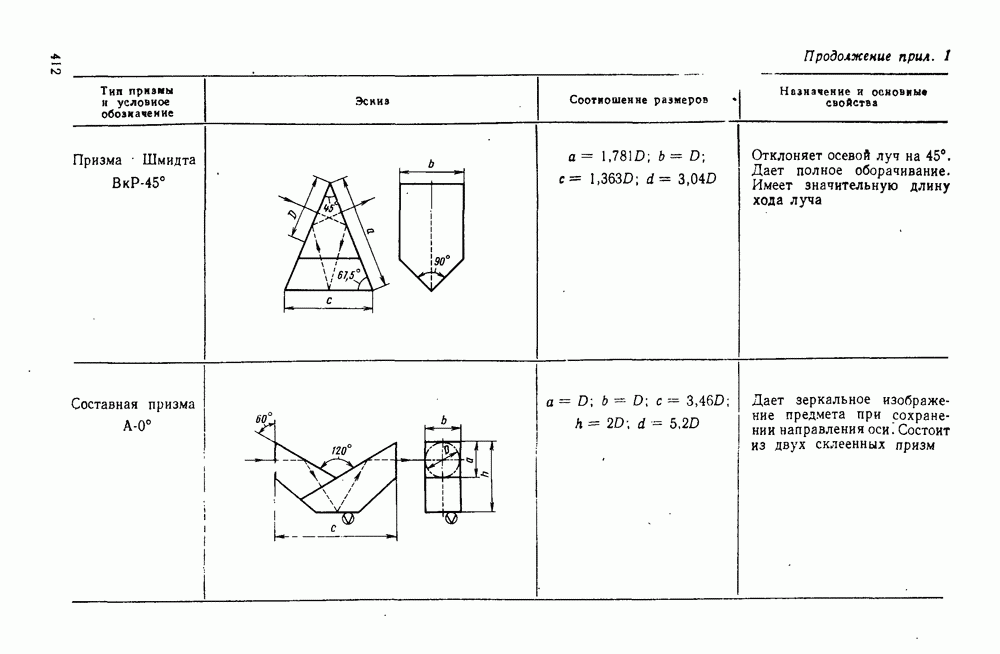
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы