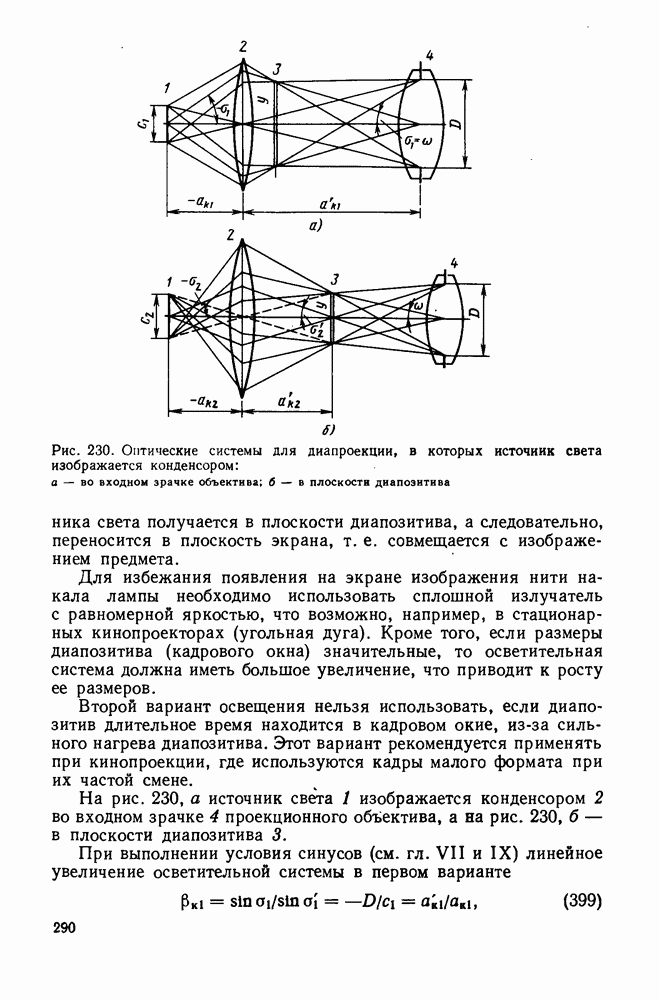
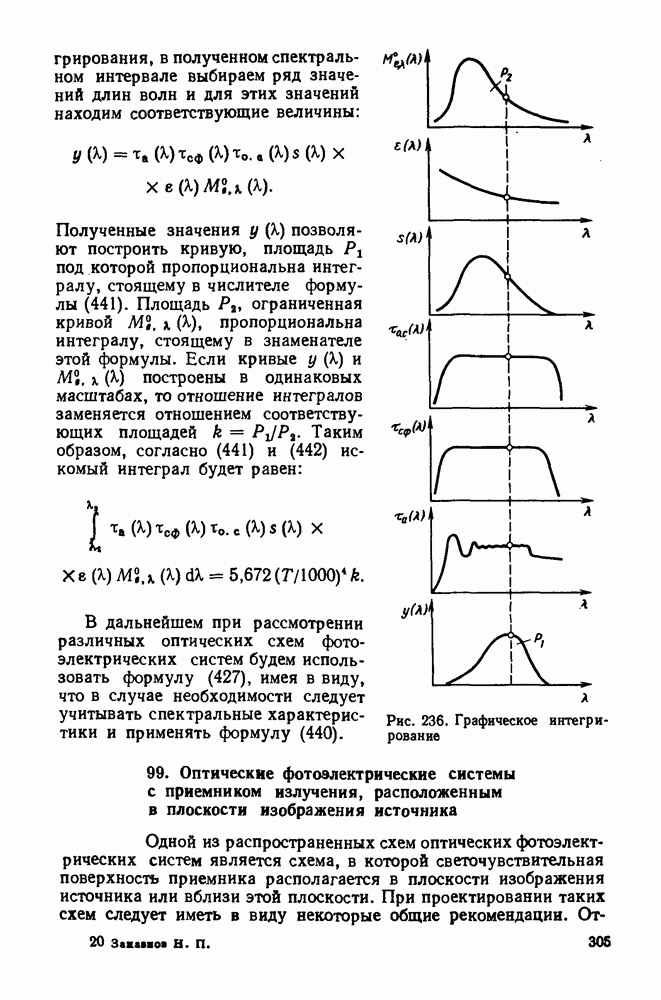
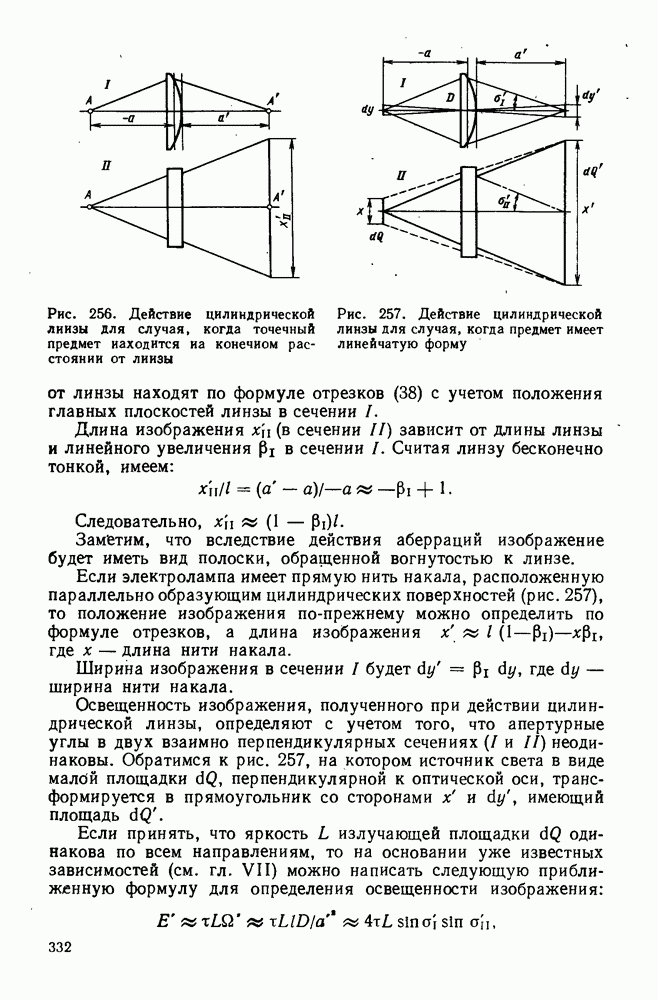
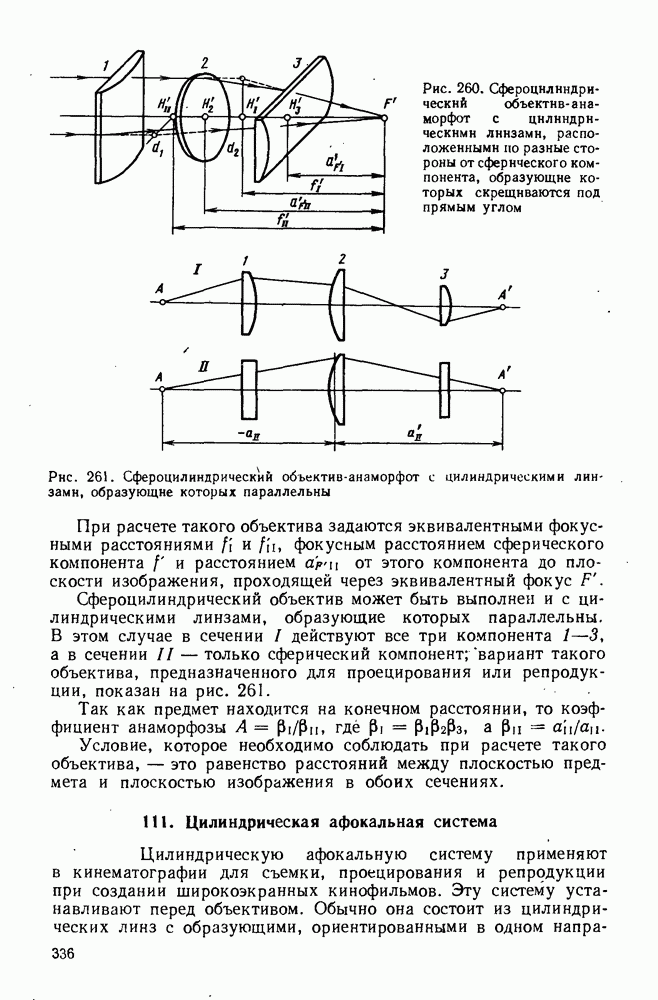
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
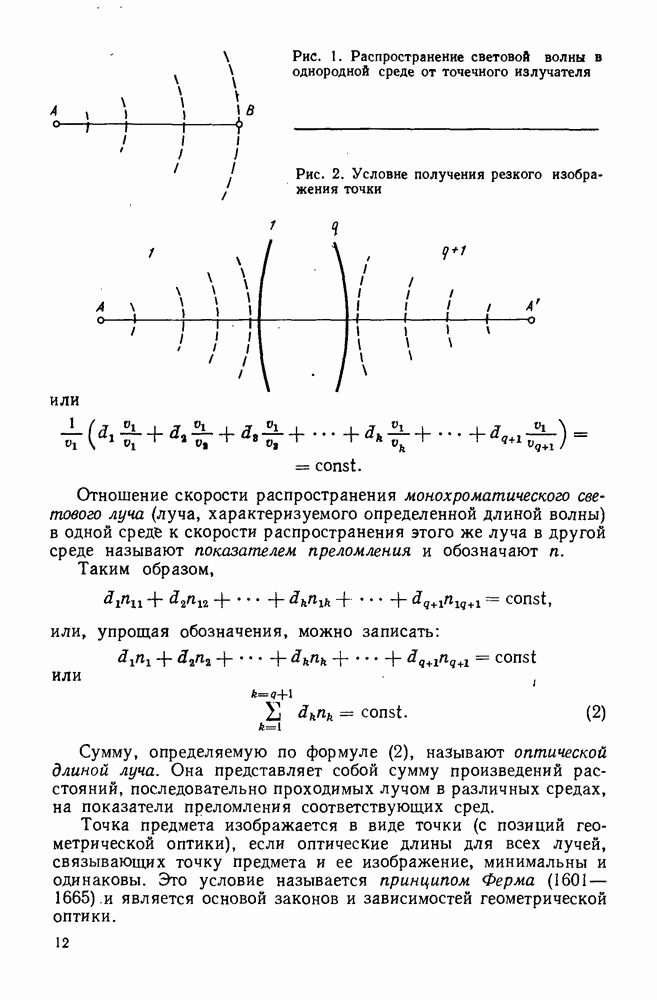
14. Кардинальные элементы идеальной оптической системы
Среди множества точек пространства предметов имеются бесконечно удаленные точки. Каждая бесконечно удаленная точка принадлежит пучку параллельных прямых (пучок

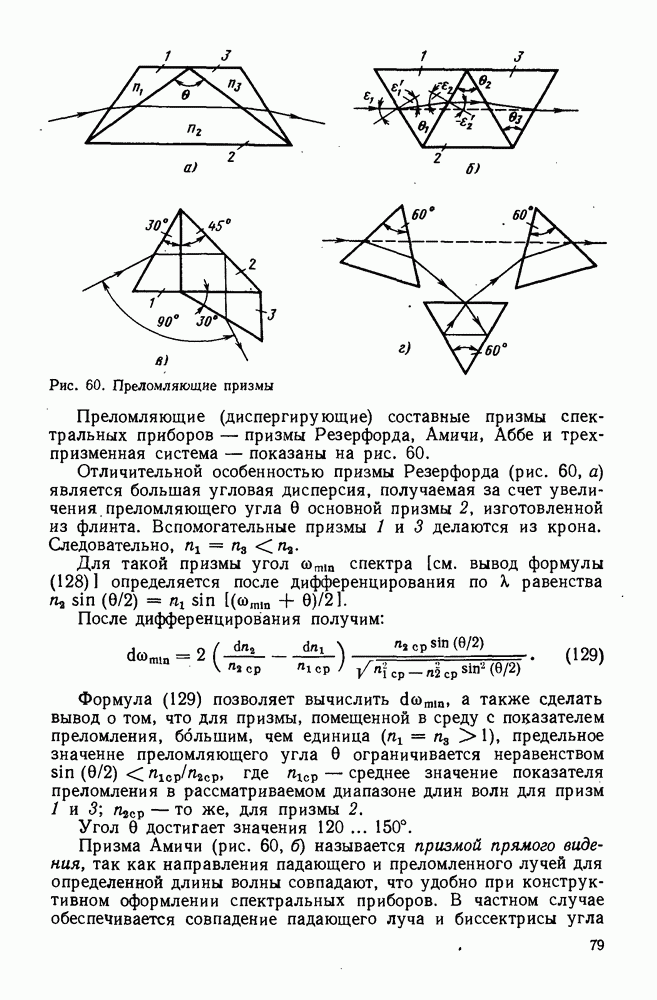
Рис. 20. Кардинальные элементы оптической системы
параллельных прямых пересекается в бесконечно удаленной точке).
Множеством бесконечно удаленных точек является бесконечно удаленная плоскость. Возьмем в этой плоскости точку  принадлежащую оптической оси (рис. 20). Из точки
принадлежащую оптической оси (рис. 20). Из точки  исходит пучок параллельных лучей, каждый из которых параллелен оптической оси, падающих, например, на преломляющукэ поверхность 1 осесимметричной оптической системы. Эта система, если она идеальна, в пространстве изображений обеспечит получение осевой точки
исходит пучок параллельных лучей, каждый из которых параллелен оптической оси, падающих, например, на преломляющукэ поверхность 1 осесимметричной оптической системы. Эта система, если она идеальна, в пространстве изображений обеспечит получение осевой точки  сопряженной с бесконечно удаленной осевой точкой. Точку
сопряженной с бесконечно удаленной осевой точкой. Точку  называют задним фокусом оптической системы.
называют задним фокусом оптической системы.
Плоскость, проходящую через задний фокус перпендикулярно к оптической оси, называют задней фокальной плоскостью оптической системы.
Действие оптической системы из  преломляющих и отражающих поверхностей можно рассматривать как действие некоторой пары условных сопряженных плоскостей, перпендикулярных к оптической оси, линейное увеличение в которых
преломляющих и отражающих поверхностей можно рассматривать как действие некоторой пары условных сопряженных плоскостей, перпендикулярных к оптической оси, линейное увеличение в которых  (рис. 20). Одну из этих плоскостей называют задней главной плоскостью оптической системы, а точку
(рис. 20). Одну из этих плоскостей называют задней главной плоскостью оптической системы, а точку  ее пересечения с оптической осью — задней главной точкой оптической системы.
ее пересечения с оптической осью — задней главной точкой оптической системы.
Положение задней главной плоскости определяется точкой  пересечения продолжения луча или самого луча, идущего параллельно оптической оси в пространстве предметов, с Продолжением этого же луча или самого луча, прошедшего оптическую систему и образующего в пересечении с оптической осью задний фокус
пересечения продолжения луча или самого луча, идущего параллельно оптической оси в пространстве предметов, с Продолжением этого же луча или самого луча, прошедшего оптическую систему и образующего в пересечении с оптической осью задний фокус 
Расстояние  между задней главной точкой
между задней главной точкой  и задним фокусом
и задним фокусом  называют задним фокусным расстоянием оптической системы.
называют задним фокусным расстоянием оптической системы.
Приведенные определения можно отнести и к случаю обратного хода луча через оптическую систему, т. е. лучей, идущих справа налево. В этом случае другую плоскость, сопряженную с задней главной плоскостью (в обратном ходе лучей), называют передней главной плоскостью, а точку  ее пересечения с оптической осью — передней главной точкой. Положение передней главной плоскости определяется точкой пересечения продолжения
ее пересечения с оптической осью — передней главной точкой. Положение передней главной плоскости определяется точкой пересечения продолжения
луча или самого луча в обратном ходе (справа налево), идущего параллельно оптической оси, с продолжением этого же луча или самого луча, прошедшего оптическую систему и образующего в пересечении с оптической осью передний фокус  в пространстве предметов. С фокусом
в пространстве предметов. С фокусом  сопряжена бесконечно удаленная точка
сопряжена бесконечно удаленная точка  оптической оси в пространстве изображений.
оптической оси в пространстве изображений.
Плоскость, проходящую через передний фокус перпендикулярно к оптической оси, называют передней фокальной плоскостью. Расстояние  от передней главной точки до переднего фокуса является передним фокусным расстоянием оптической системы.
от передней главной точки до переднего фокуса является передним фокусным расстоянием оптической системы.
Фокусы, фокальные плоскости, главные плоскости, главные точки и фокусные расстояния называют кардинальными элементами оптической системы.
На рис. 20 показаны две пары сопряженных лучей и их продолжений:  и
и  Следовательно, точки
Следовательно, точки  находящиеся на главных плоскостях и расположенные на одном и том же расстоянии
находящиеся на главных плоскостях и расположенные на одном и том же расстоянии  от оптической оси, полученные как пересечения пары лучей, сопряженных с другой парой, также являются сопряженными. Отсюда следует подтверждение того, что линейное увеличение в главных плоскостях
от оптической оси, полученные как пересечения пары лучей, сопряженных с другой парой, также являются сопряженными. Отсюда следует подтверждение того, что линейное увеличение в главных плоскостях  следовательно, задняя главная точка
следовательно, задняя главная точка  является изображением передней главной, точки
является изображением передней главной, точки 
Таким образом, главные плоскости можно определить как плоскости, в которых 
При высоте  падения лучей в прямом и обратном ходе (рис. 20) получаем следующие формулы для определения фокусных расстояний:
падения лучей в прямом и обратном ходе (рис. 20) получаем следующие формулы для определения фокусных расстояний:

где  угол между лучом, прошедшим оптическую систему, и оптической осью в пространстве изображений (прямой ход луча); а — угол между лучом, прошедшим оптическую систему, и оптической осью в пространстве предметов (обратный ход луча).
угол между лучом, прошедшим оптическую систему, и оптической осью в пространстве изображений (прямой ход луча); а — угол между лучом, прошедшим оптическую систему, и оптической осью в пространстве предметов (обратный ход луча).
При малой высоте А падения лучей при прямом и обратном ходе формулы для расчета фокусных расстояний принимают вид:

Идеальную оптическую систему можно представить бесконечно тонкой. В этом случае передняя и задняя главные плоскости совпадают, что отвечает условию равенства 4-1 линейного увеличения в главных плоскостях. На вход такой идеальной оптической системы, заданной совмещенными главными плоскостями, передним  и задним
и задним  фокусными расстояниями и разделяющей среды с показателями преломления
фокусными расстояниями и разделяющей среды с показателями преломления  поступает пучок параллельных лучей под малым углом а к оптической оси (рис.
поступает пучок параллельных лучей под малым углом а к оптической оси (рис.  Этот пучок выходит из одной бесконечно удаленной точки В пространства предметов. Луч
Этот пучок выходит из одной бесконечно удаленной точки В пространства предметов. Луч  пучка проходит через передний фокус
пучка проходит через передний фокус  После действия оптической системы он пойдет
После действия оптической системы он пойдет
параллельно оптической оси и пересечет заднюю фокальную плоскость в точке В, являющейся изображением бесконечно удаленной точки В.
Луч 2 проходит через совмещенные главные точки (точку  ), образуя с оптической осью угол падения
), образуя с оптической осью угол падения  равный углу а. Отметим, что оптическая ось является нормалью ко всем поверхностям центрированной оптической системы, вершины которых в случае бесконечно тонкой системы совпадают с точкой
равный углу а. Отметим, что оптическая ось является нормалью ко всем поверхностям центрированной оптической системы, вершины которых в случае бесконечно тонкой системы совпадают с точкой  После действия оптической системы луч 2 пройдет через точку В, образуя с оптической осью угол преломления
После действия оптической системы луч 2 пройдет через точку В, образуя с оптической осью угол преломления 

Рис. 21. Ход параллельного пучка лучей через идеальную оптическую систему
Из построений, выполненных на рис. 21, находим, что  следовательно, —
следовательно, — 
При  угол
угол  и поэтому при малых углах
и поэтому при малых углах  Так как по закону преломления
Так как по закону преломления  то
то

Полученное равенство позволяет сделать следующий вывод: отношение фокусных расстояний идеальной оптической системы с преломляющими поверхностями равно отношению показателей преломления соответствующих сред, находящихся по обе стороны от оптической системы, взятому со знаком «минус», который указывает на расположение фокусов  по разные стороны от совмещенного положения главных плоскостей этой системы.
по разные стороны от совмещенного положения главных плоскостей этой системы. 
В тех случаях, когда оптическая система находится в однородной среде, например в воздухе  т. е. заднее и переднее фокусные расстояния равны по абсолютному значению.
т. е. заднее и переднее фокусные расстояния равны по абсолютному значению.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
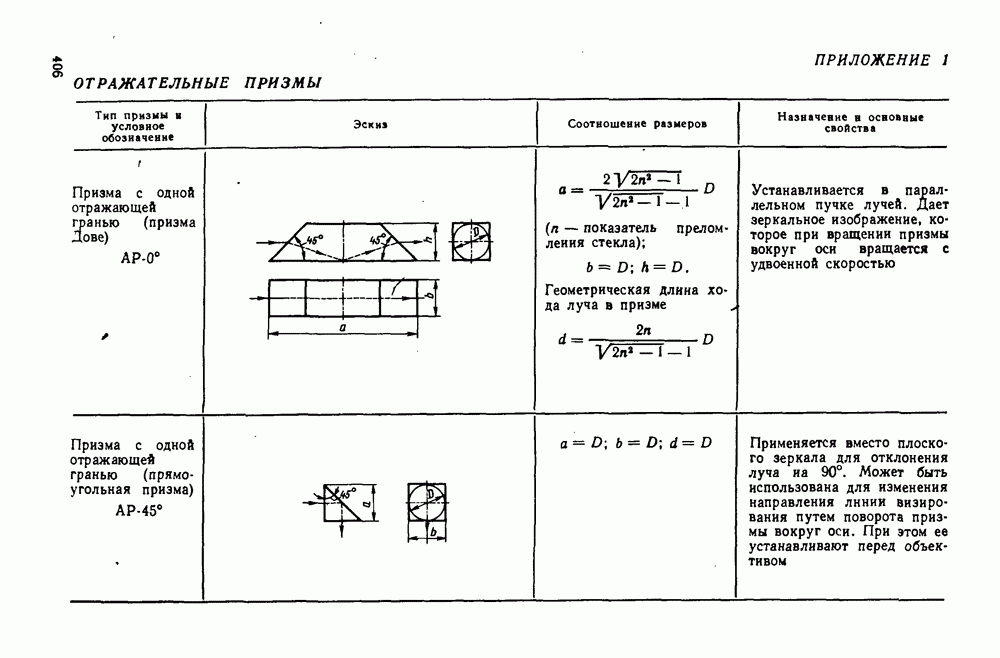
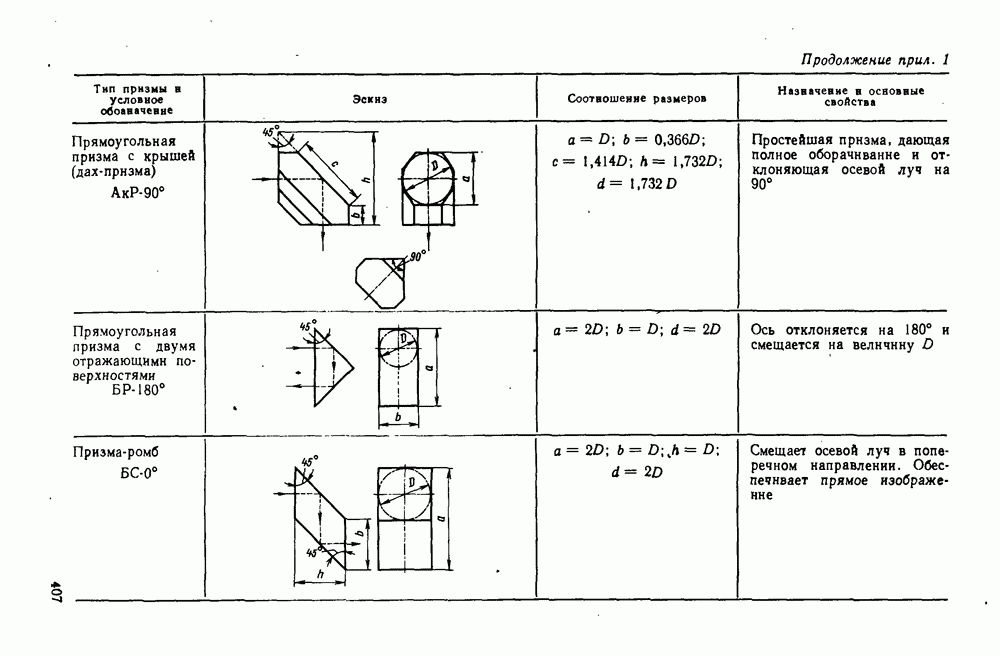
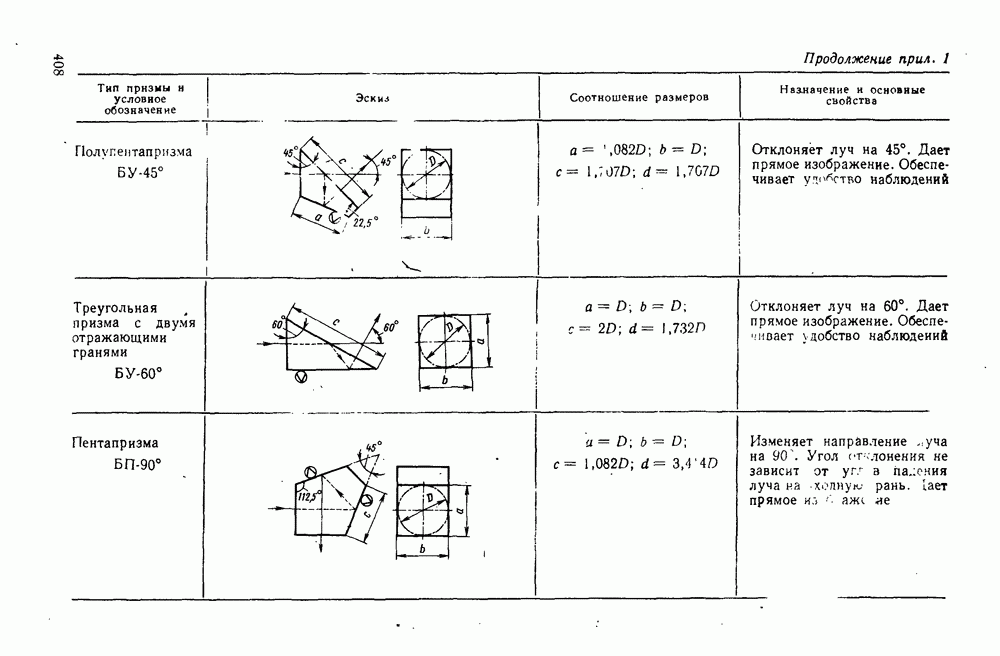
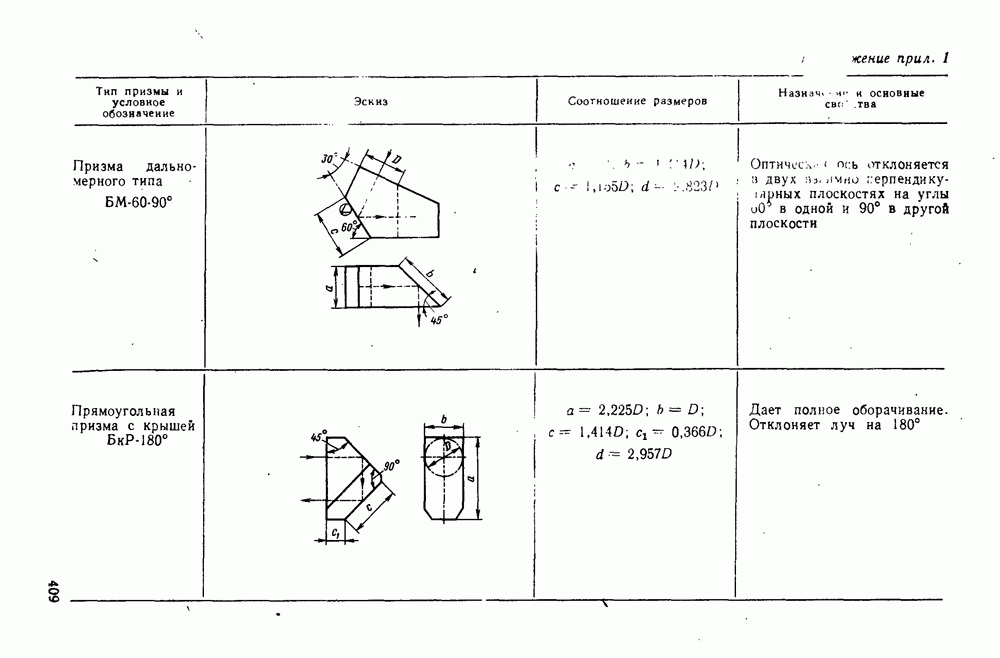
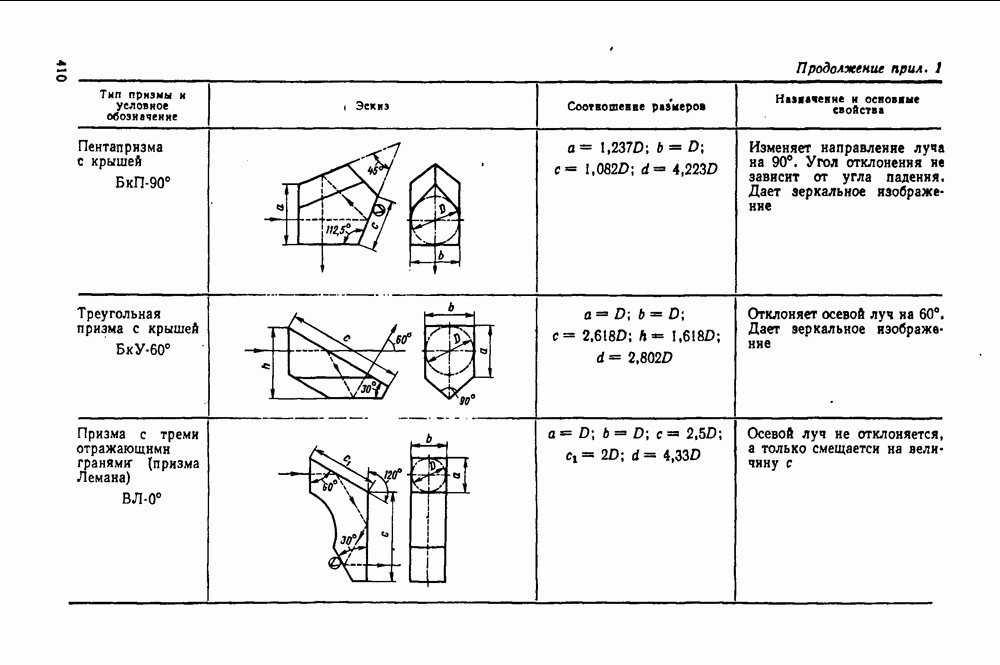
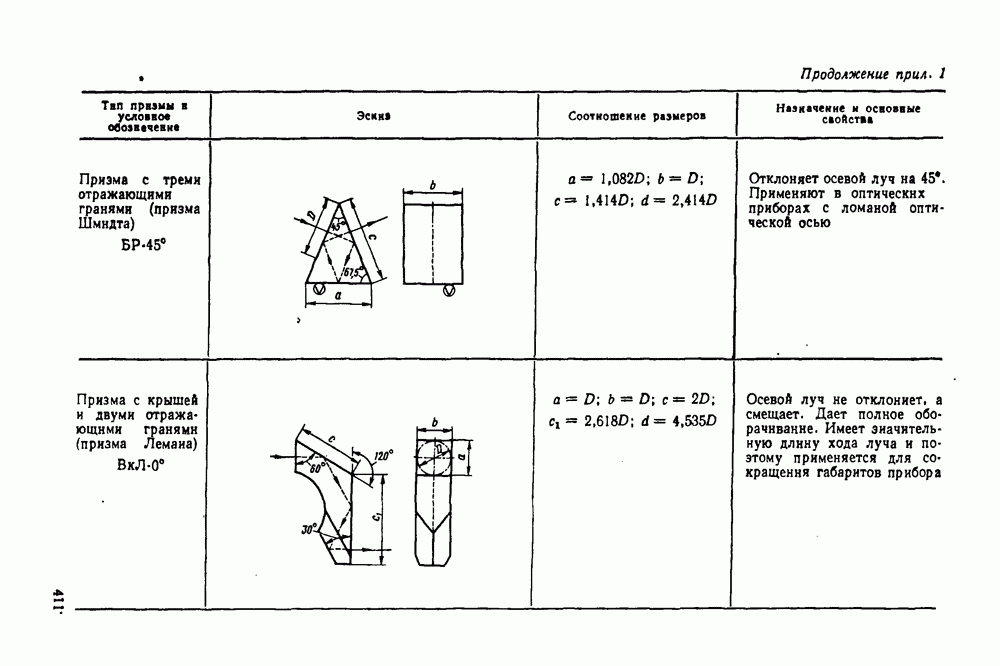
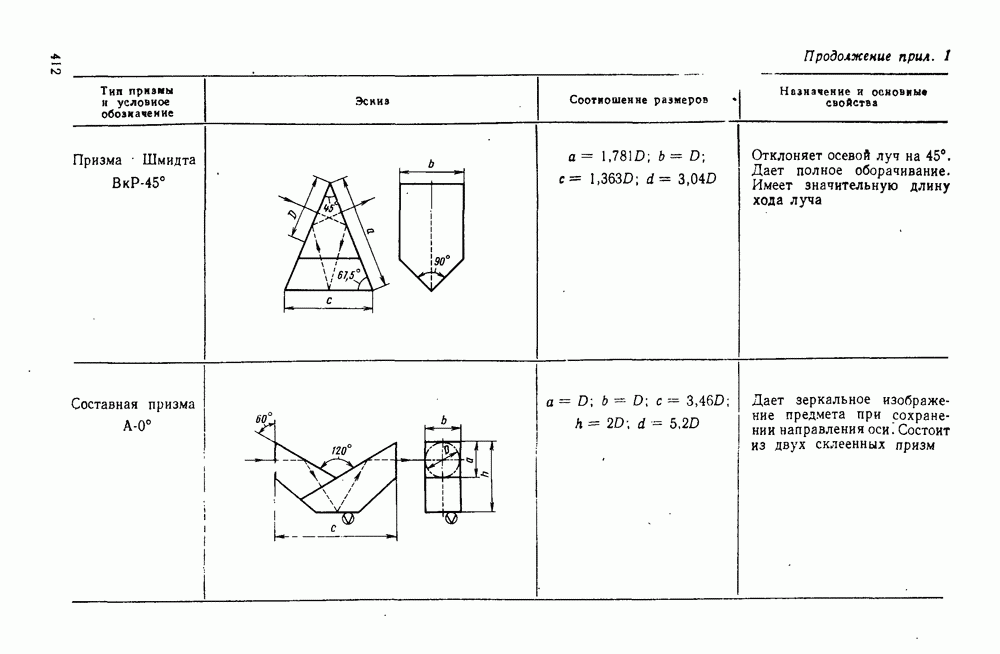
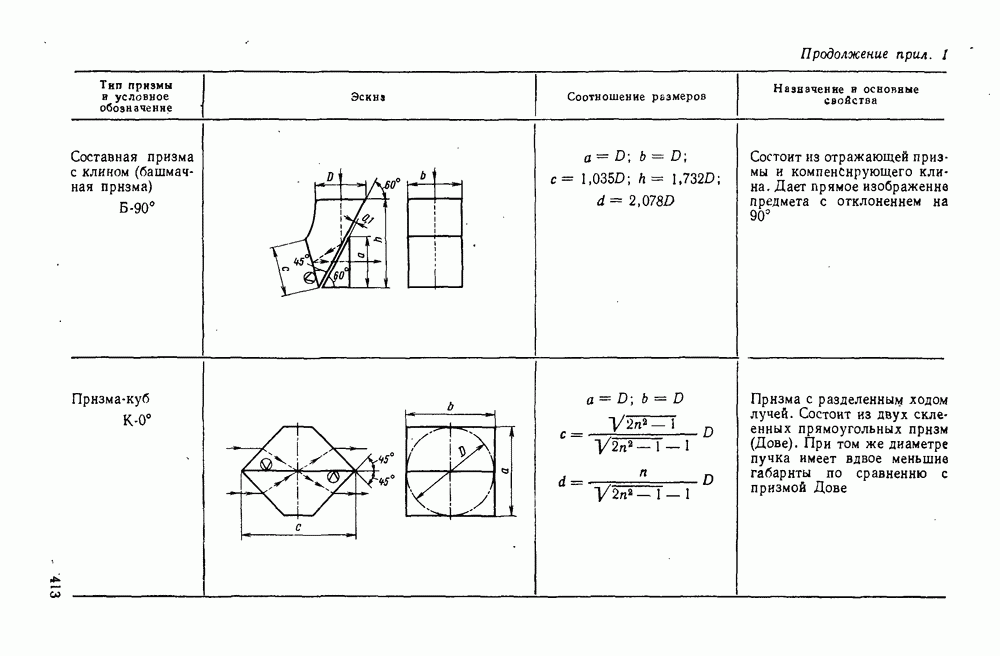
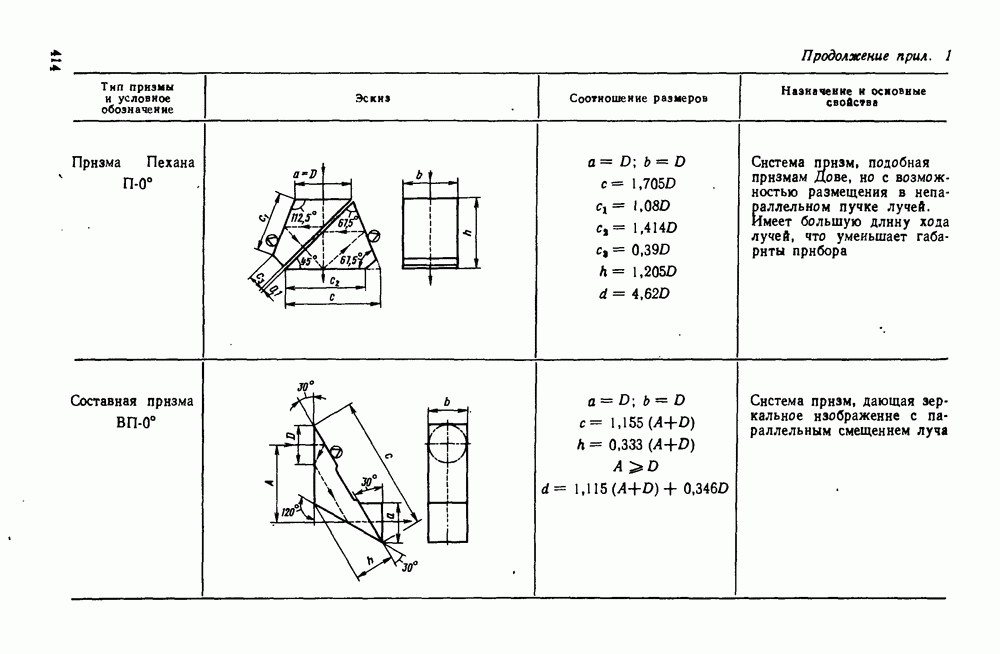
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
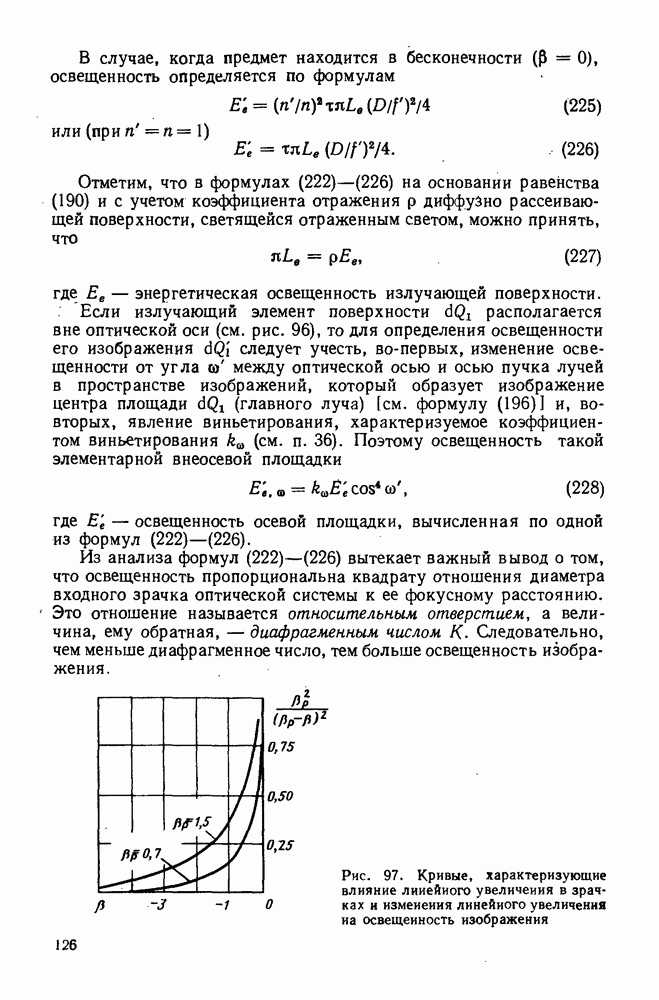
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
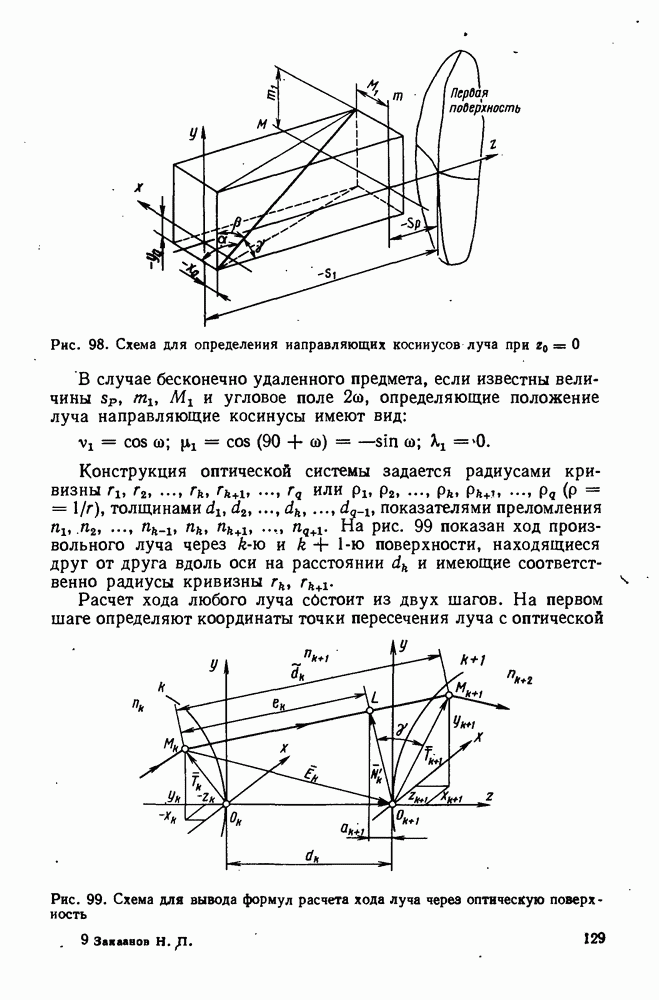
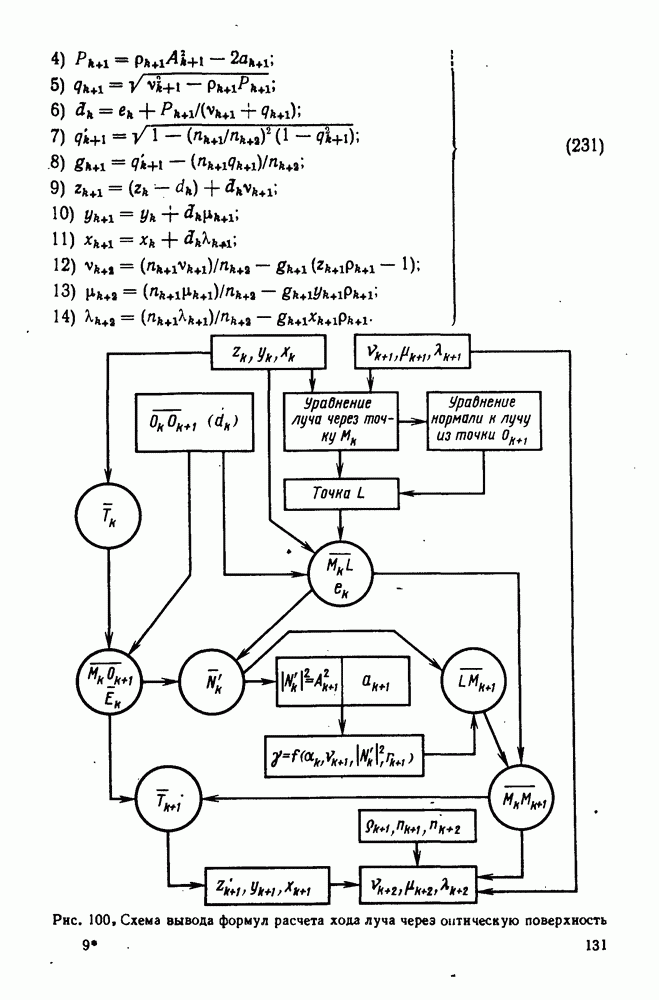
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
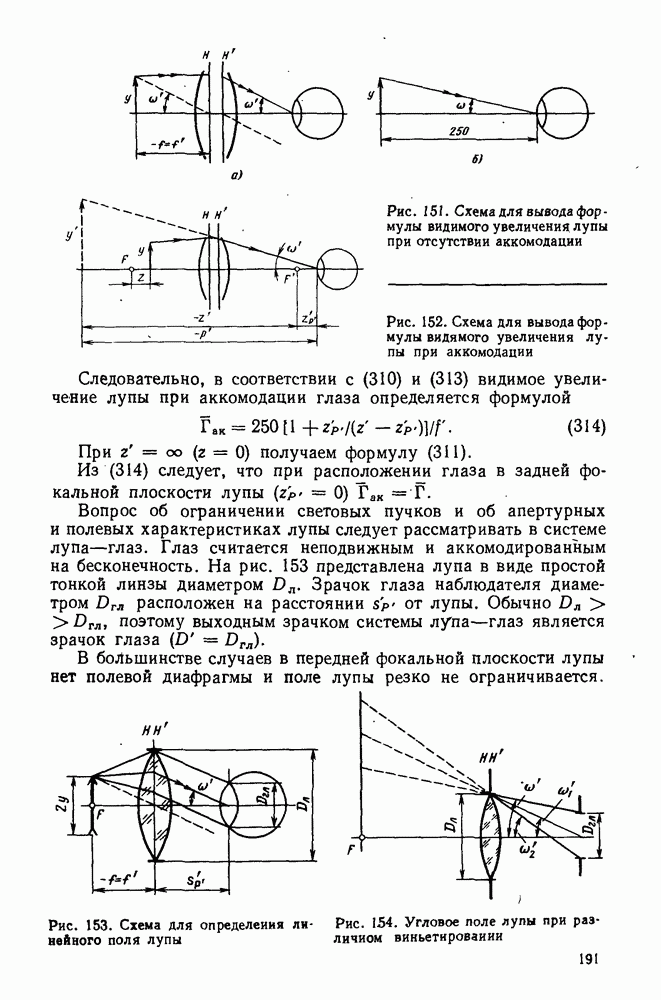
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
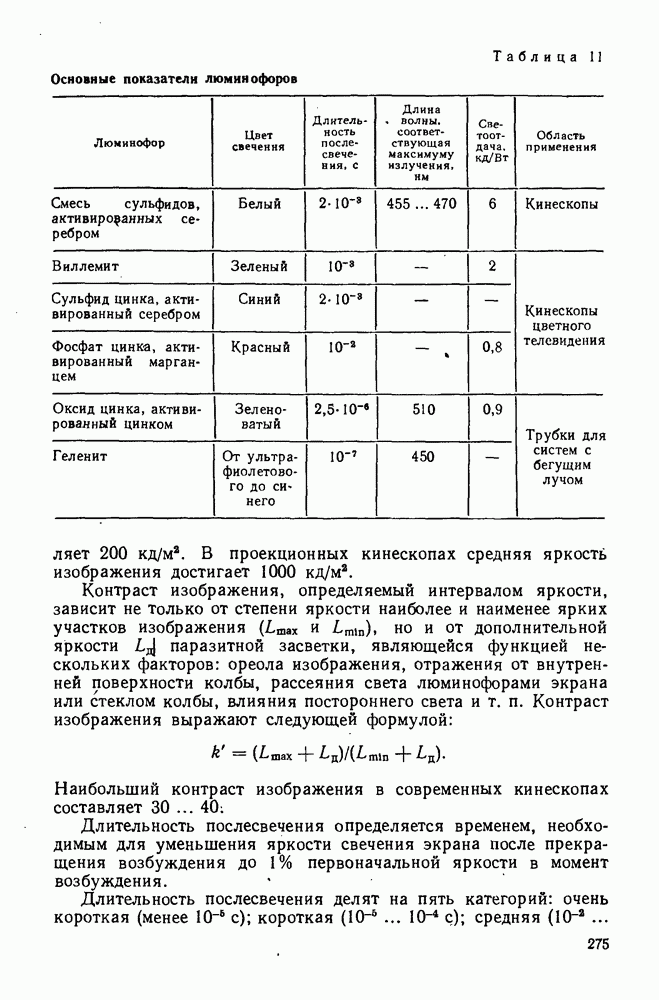
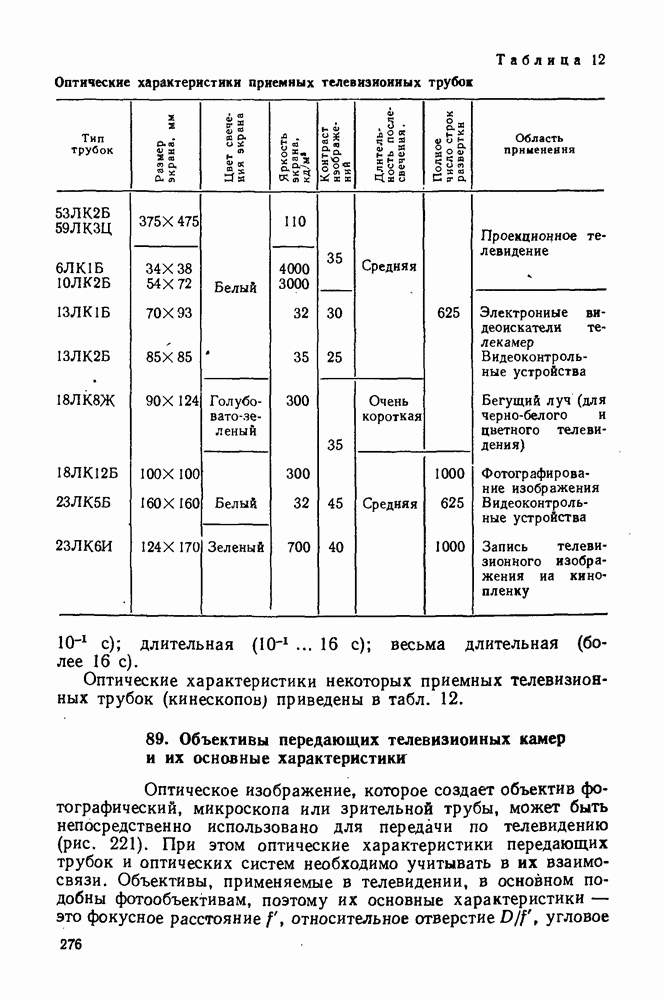
- 88. Оптические характеристики передающих и приемных телевизионных трубок
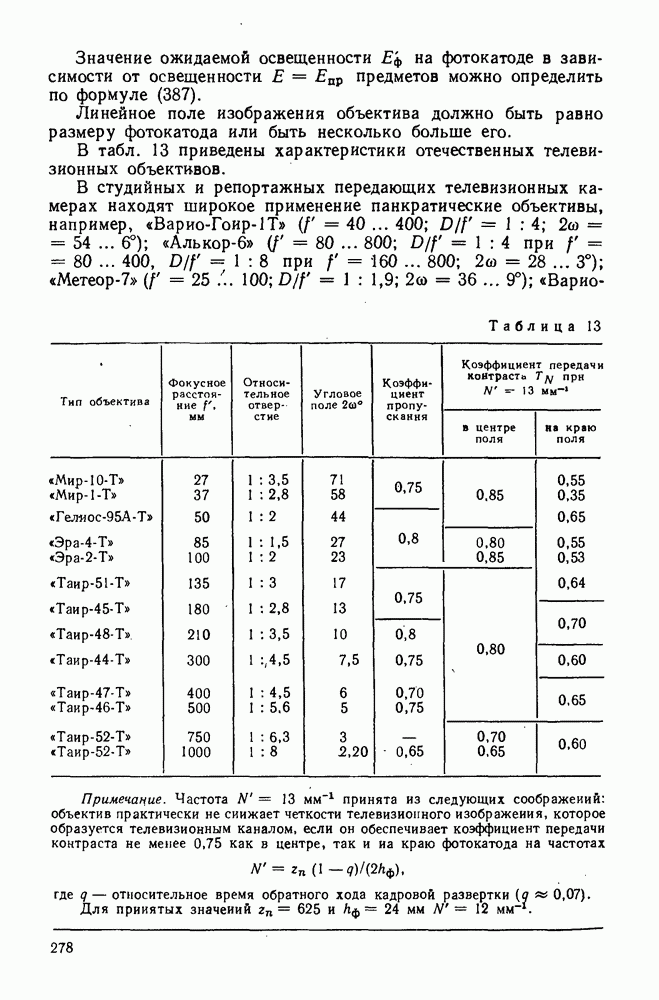
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
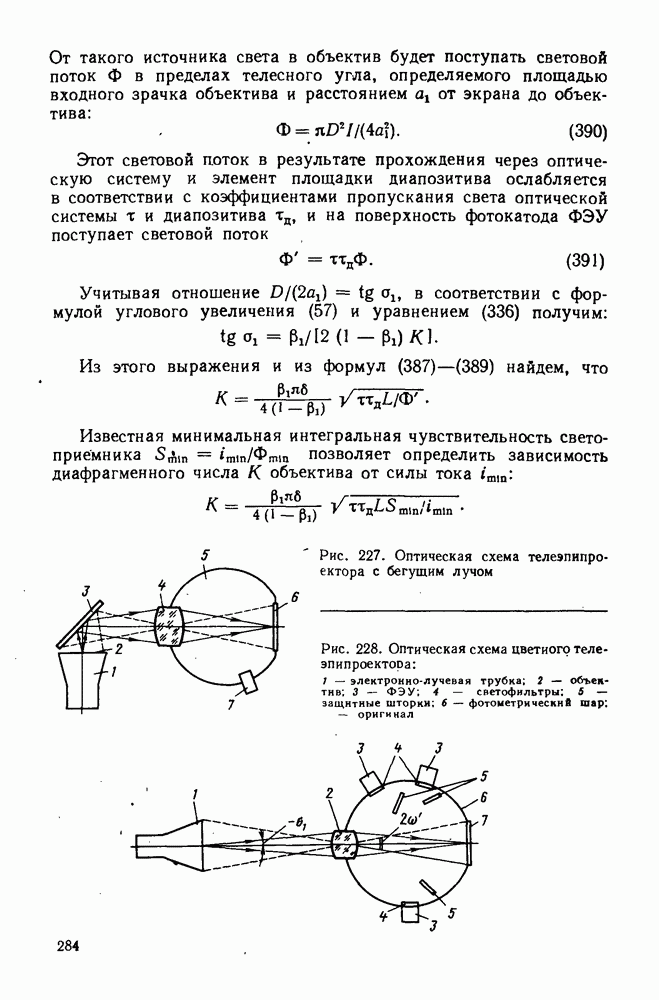
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы