| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
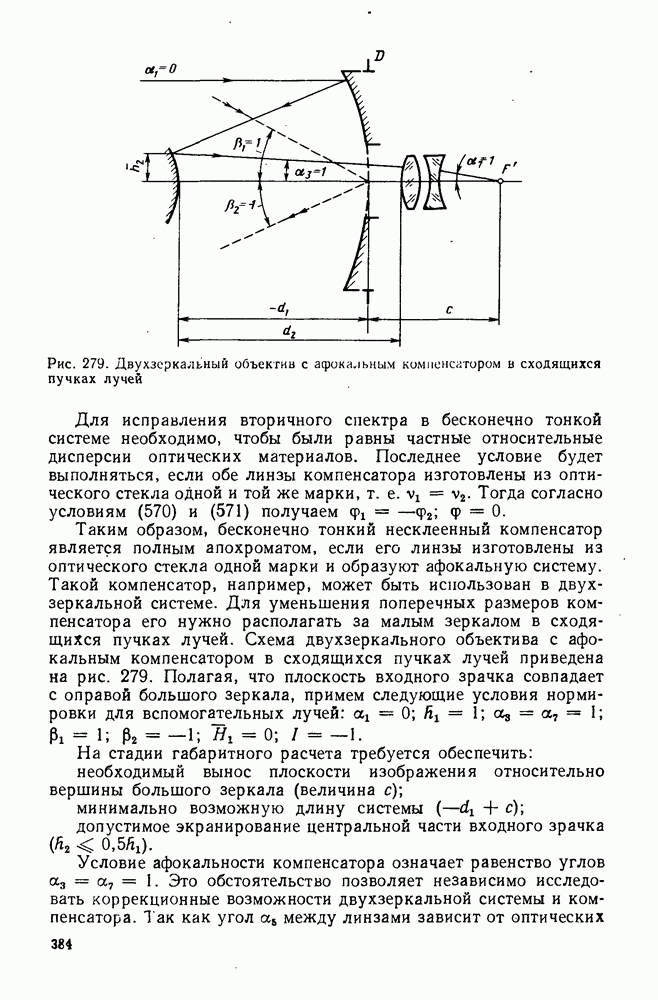
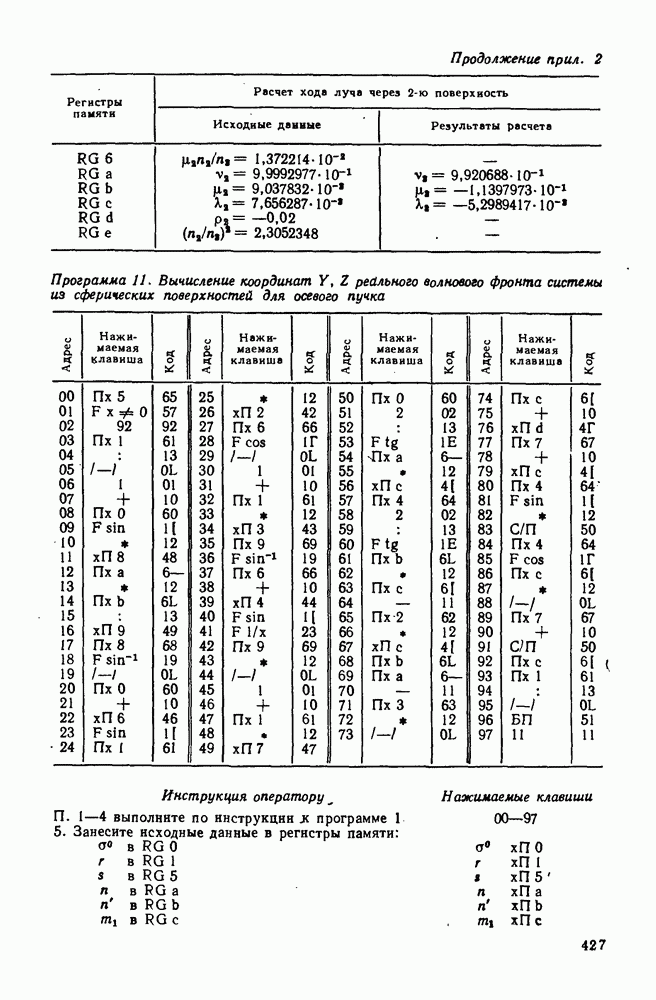
120. Расчет двухливэового несклеенного объектива
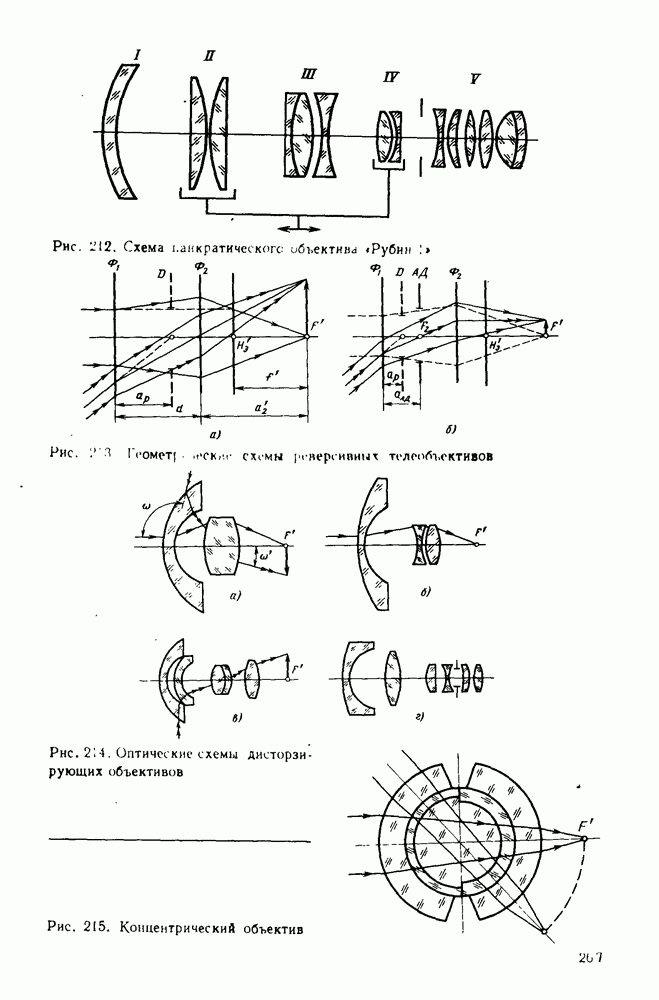
По сравнению с двухлинзовым склеенным объективом двухлинзовый несклеенный тонкий объектив имеет один дополнительный параметр: четвертый радиус кривизны. Поэтому с учетом условий масштаба в двухлинзовом несклеенном объективе можно исправить три аберрации.
Принципиальная схема двухлинзового несклеенного объектива показана на рис. 273. Считая объектив бесконечно тонким, примем следующие условия нормировки вспомогательных лучей: 
По техническим условиям на расчет объектива будем считать известными его основные характеристики  и значения остаточных аберраций: продольную сферическую для края зрачка, хроматизм положения и кому для края поля с учетом виньетирования.
и значения остаточных аберраций: продольную сферическую для края зрачка, хроматизм положения и кому для края поля с учетом виньетирования.
В соответствии с указанными техническими условиями по (265), (270) и (280) вычисляем значения сумм Зейделя:

Вторая сумма Зейделя для случая тонкой системы согласно (498) выражается через параметры  Тогда, определив по (537)
Тогда, определив по (537)  и по
и по  при заданном положении входного зрачка
при заданном положении входного зрачка  находим необходимое значение параметра
находим необходимое значение параметра 
Таким образом, с точки зрения коррекции монохроматических аберраций задача по расчету двухлинзового несклеенного объектива сводится к определению его конструктивных параметров, удовлетворяющих наперед заданным значениям величин  Одним из возможных способов решения указанной задачи может быть способ, основанный на использовании основных параметров тонких компонентов [37].
Одним из возможных способов решения указанной задачи может быть способ, основанный на использовании основных параметров тонких компонентов [37].

Рис. 273. Двухлянзовый несклеенный объектив
Учитывая принятые условия нормировки, по формуле углов получим  Тогда условие исправления хроматизма в объективе обеспечивается согласно формуле (532):
Тогда условие исправления хроматизма в объективе обеспечивается согласно формуле (532):

Параметры  всего объектива зависят от соответствующих параметров каждой линзы. Так как объектив является бесконечно тонким, то
всего объектива зависят от соответствующих параметров каждой линзы. Так как объектив является бесконечно тонким, то

Величины  первой линзы и
первой линзы и  второй выразим через их основные параметры. При этом следует иметь в виду, что для первой линзы
второй выразим через их основные параметры. При этом следует иметь в виду, что для первой линзы  для второй —
для второй — 
Используя формулы (506), получим:

где  основные параметры тонкой линзы; параметр
основные параметры тонкой линзы; параметр  .
.
Основные параметры тонкой линзы связаны между собой приближенной формулой (536):

Величина  каждой линзы определяется по формуле [37]:
каждой линзы определяется по формуле [37]:

Так как марки оптического стекла двухлинзового объектива вы. браны, то по формулам (543) можно вычислить величину  каждой линзы. Подставляя выражения (541) в формулы (540) и учитывая зависимости (542), получаем два уравнения: квадратное и первой степени. В этих уравнениях неизвестными являются основные параметры
каждой линзы. Подставляя выражения (541) в формулы (540) и учитывая зависимости (542), получаем два уравнения: квадратное и первой степени. В этих уравнениях неизвестными являются основные параметры  тонких линз объектива. Если квадратное уравнение будет иметь вещественные корни, то из
тонких линз объектива. Если квадратное уравнение будет иметь вещественные корни, то из  лученных решений целесообразно взять такие, которые соответствуют меньшим абсолютным значениям параметров
лученных решений целесообразно взять такие, которые соответствуют меньшим абсолютным значениям параметров 
Определив величины  каждой линзы, можно найти соответствующие значения параметров
каждой линзы, можно найти соответствующие значения параметров 

От параметров а каждой линзы необходимо перейти к параметрам  двухлинзового несклеенного объектива. Этот переход выполняется согласно формуле (502). Для первой линзы:
двухлинзового несклеенного объектива. Этот переход выполняется согласно формуле (502). Для первой линзы:  Для второй линзы:
Для второй линзы: 
Таким образом, определив все значения параметров а бесконечно тонкого объектива и установив толщины линз и расстояние между ними, вычисляем конструктивные параметры исходного варианта, объектива по формуле (249). После этого выполняем контрольное вычисление остаточных аберраций на ЭВМ. На основании результатов этого расчета осуществляется последующая аберрационная коррекция объектива.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
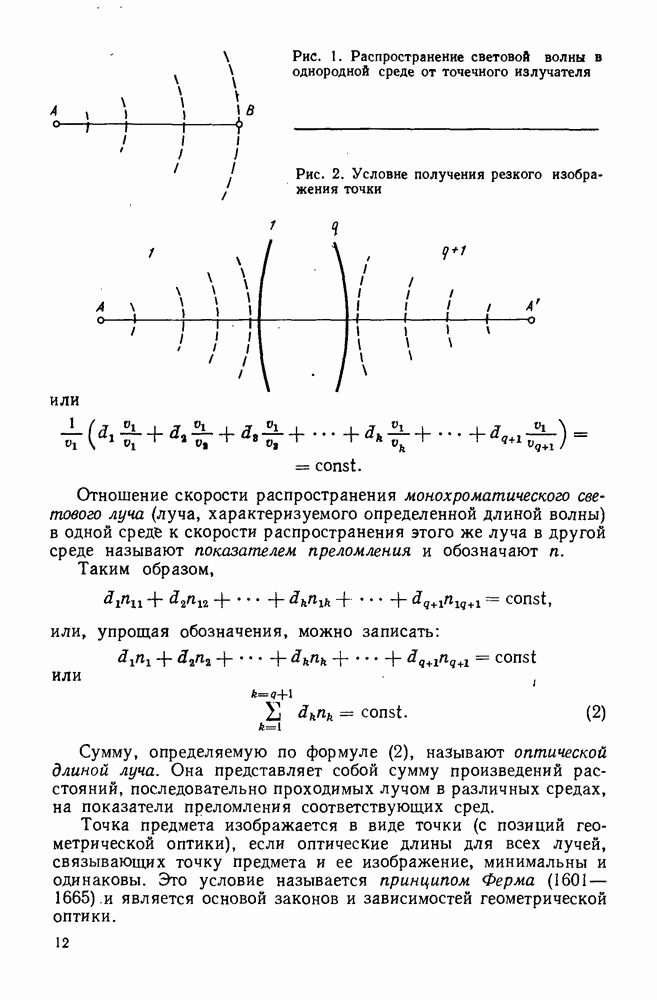
- 1. Принцип Ферма
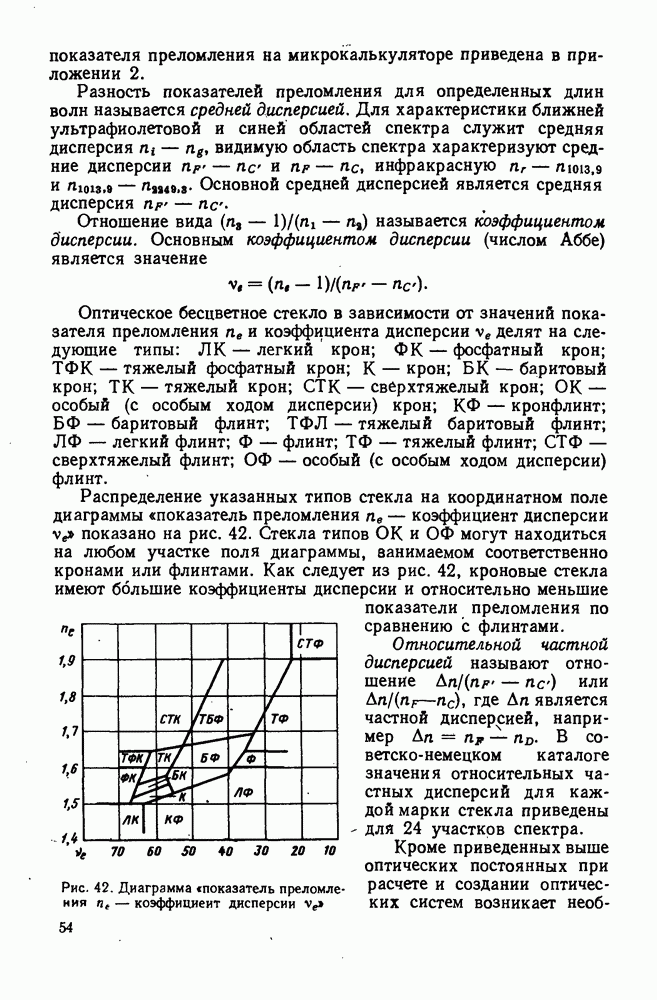
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
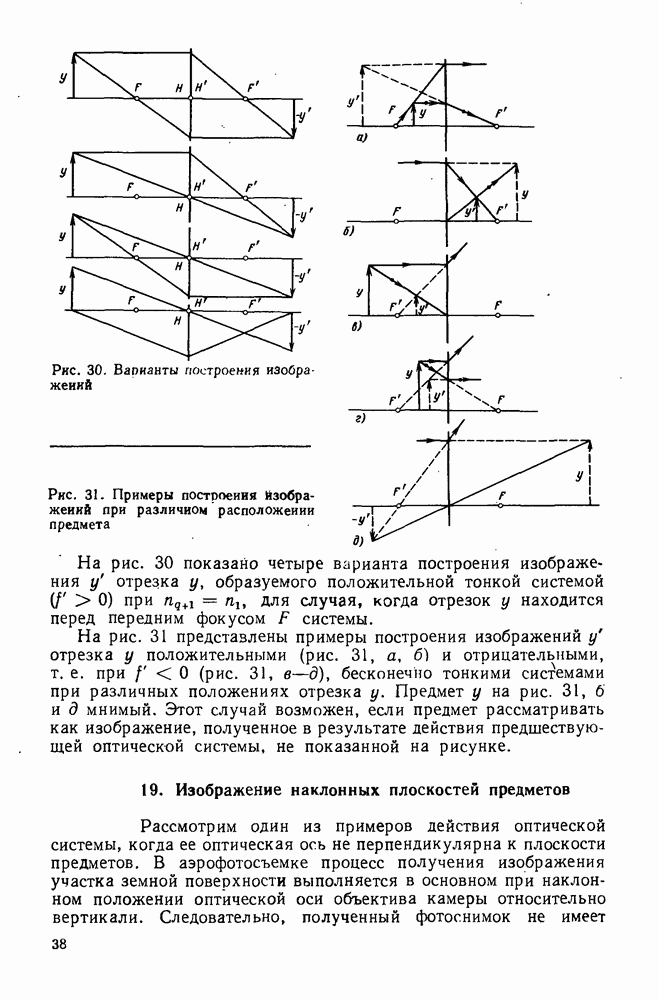
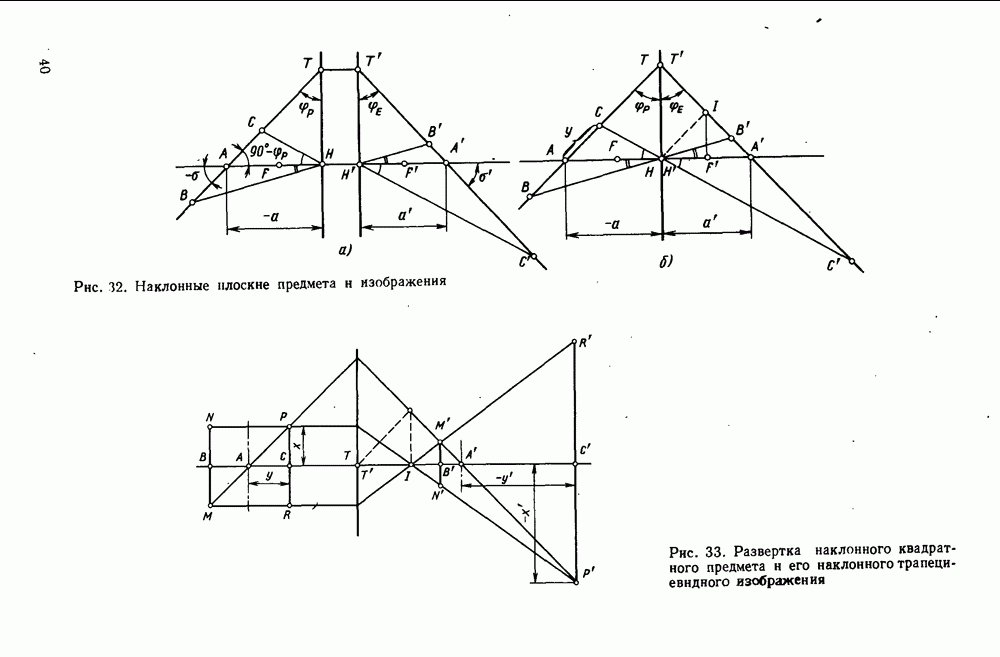
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
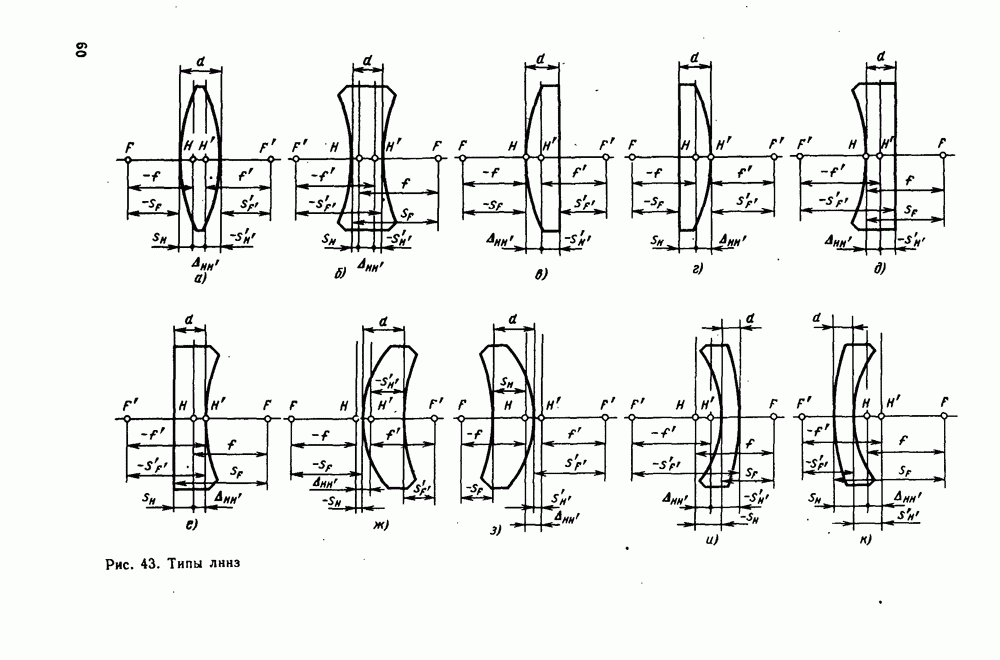
- 26. Линзы
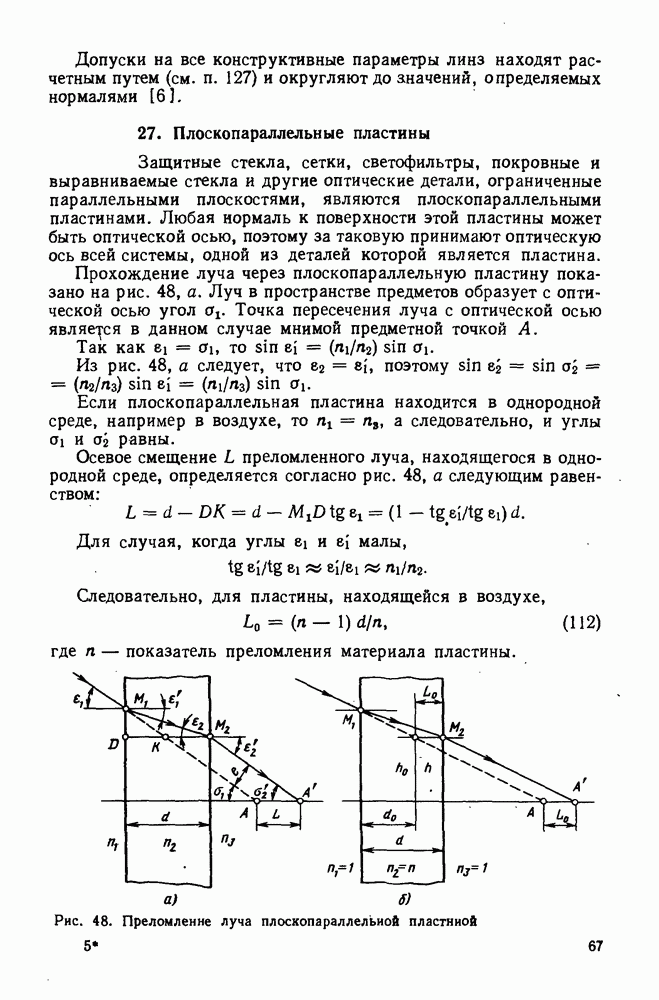
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
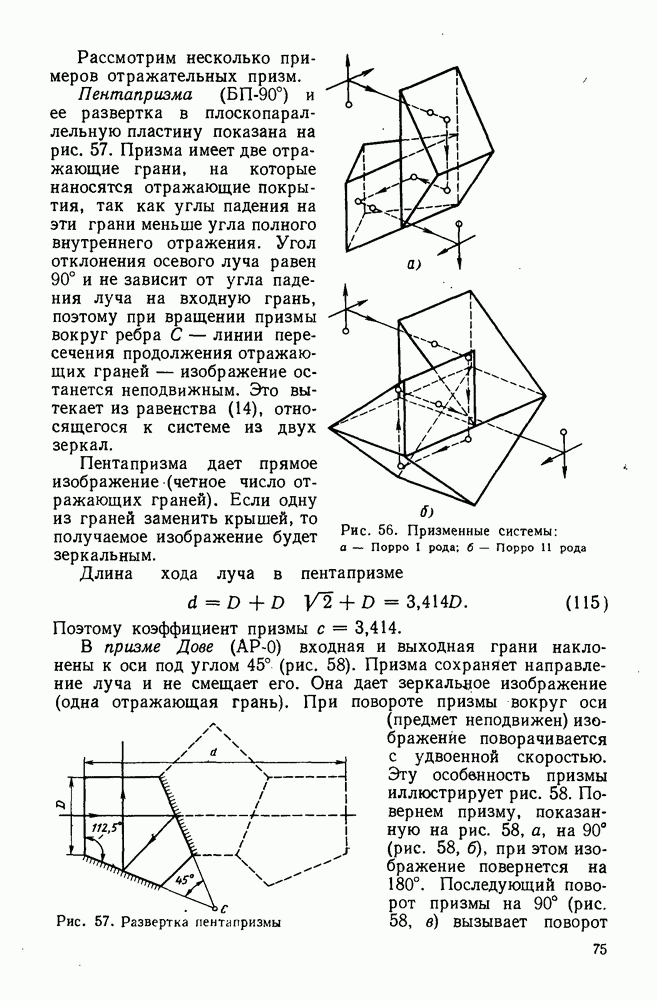
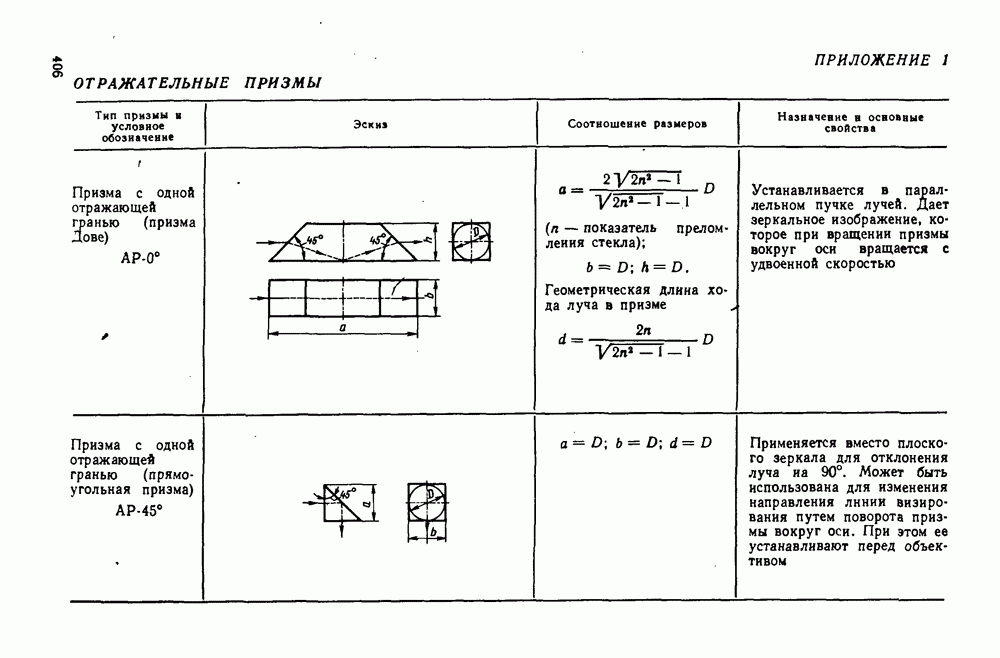
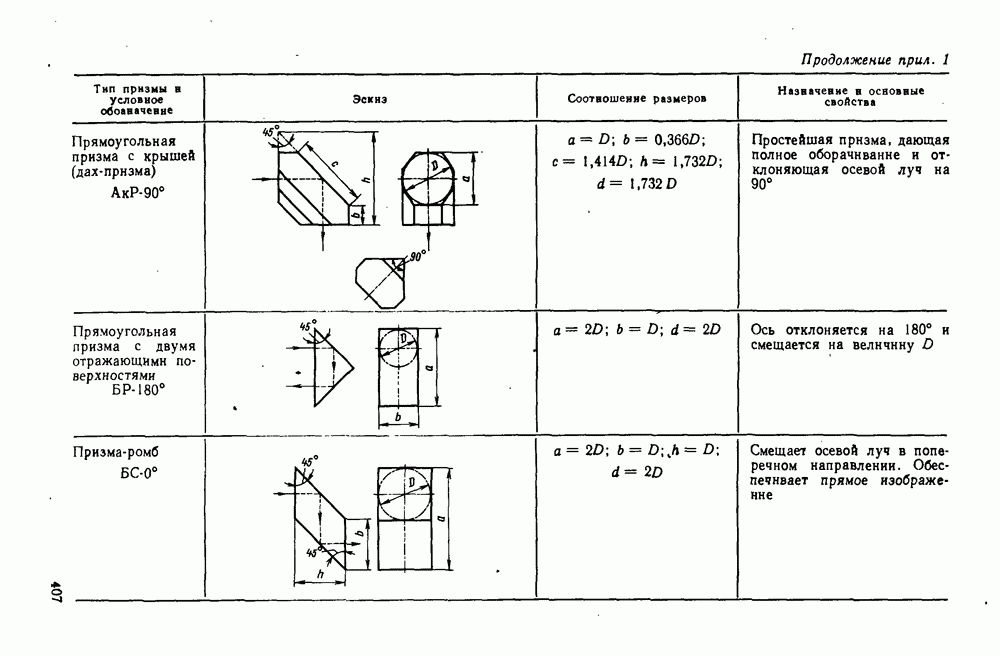
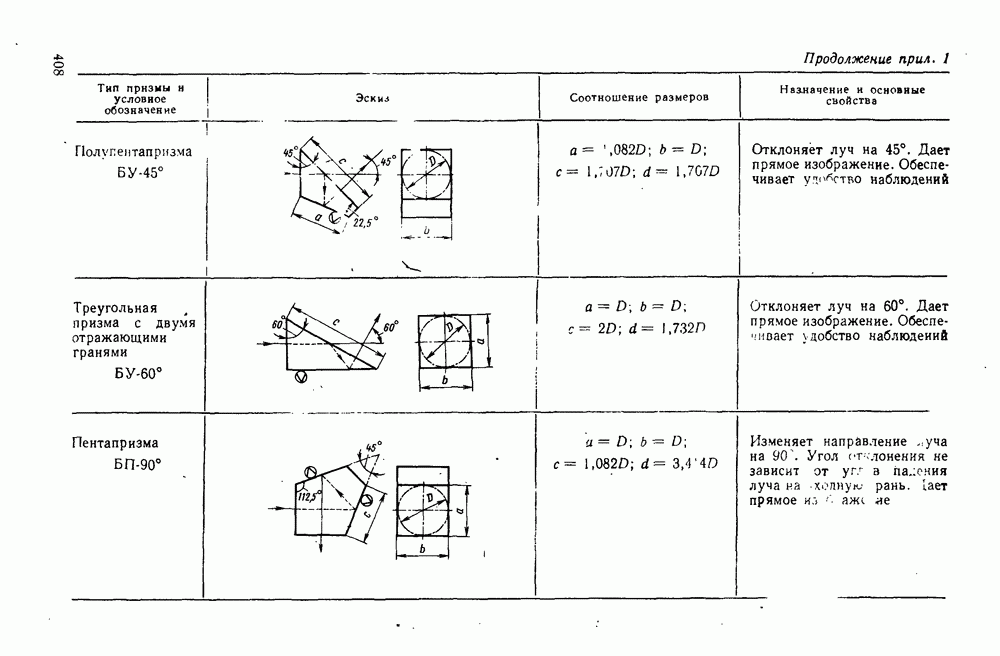
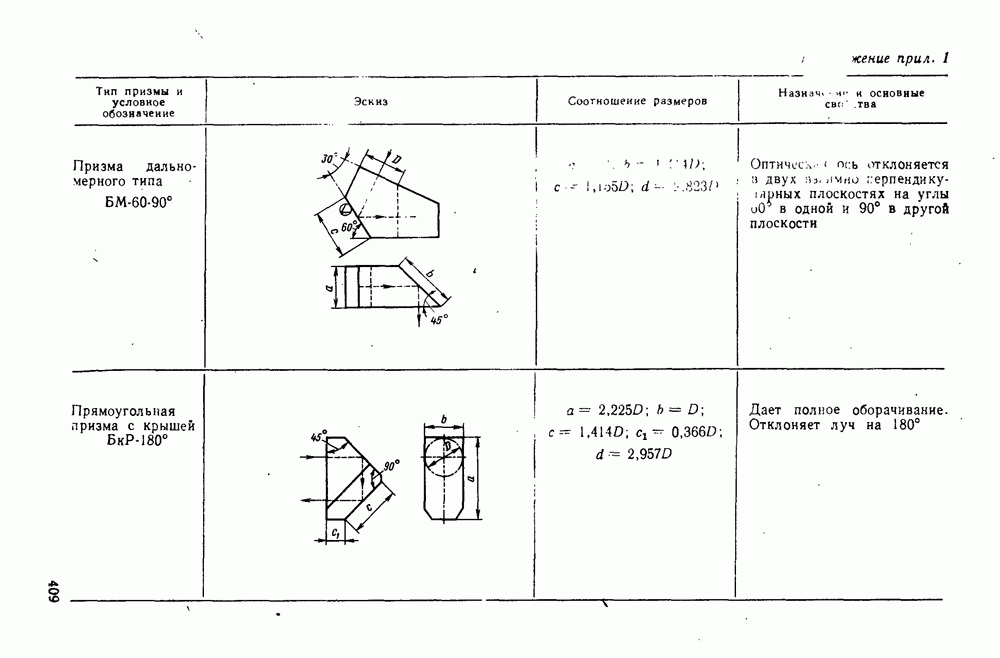
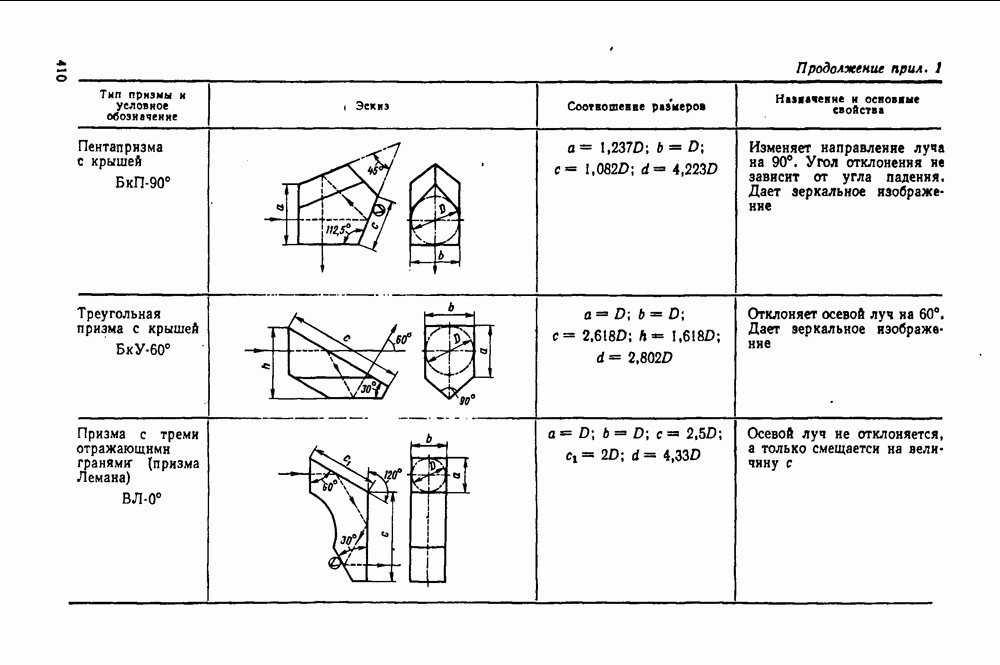
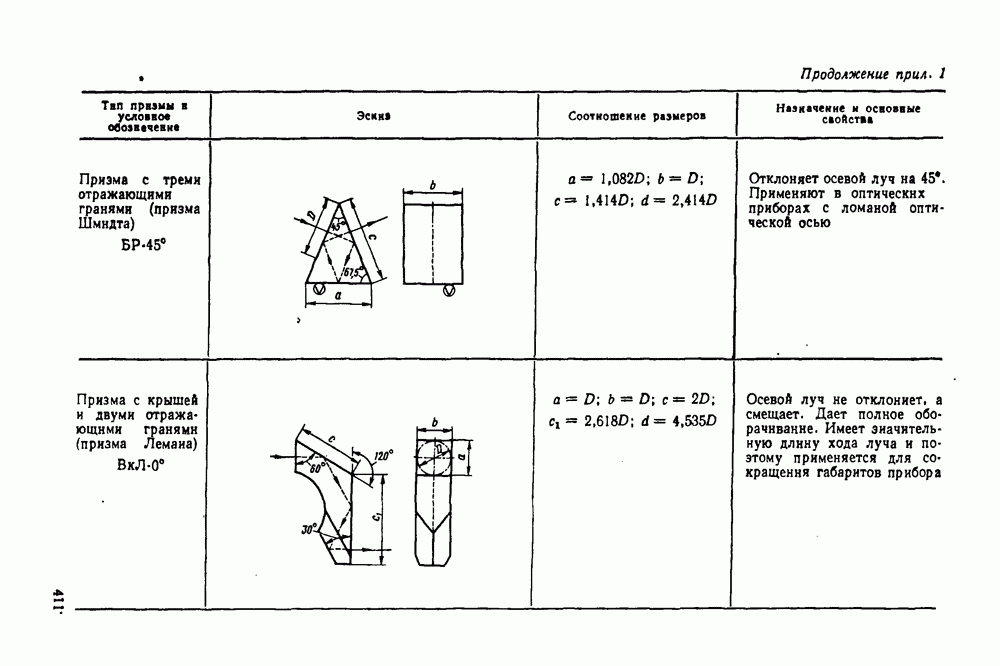
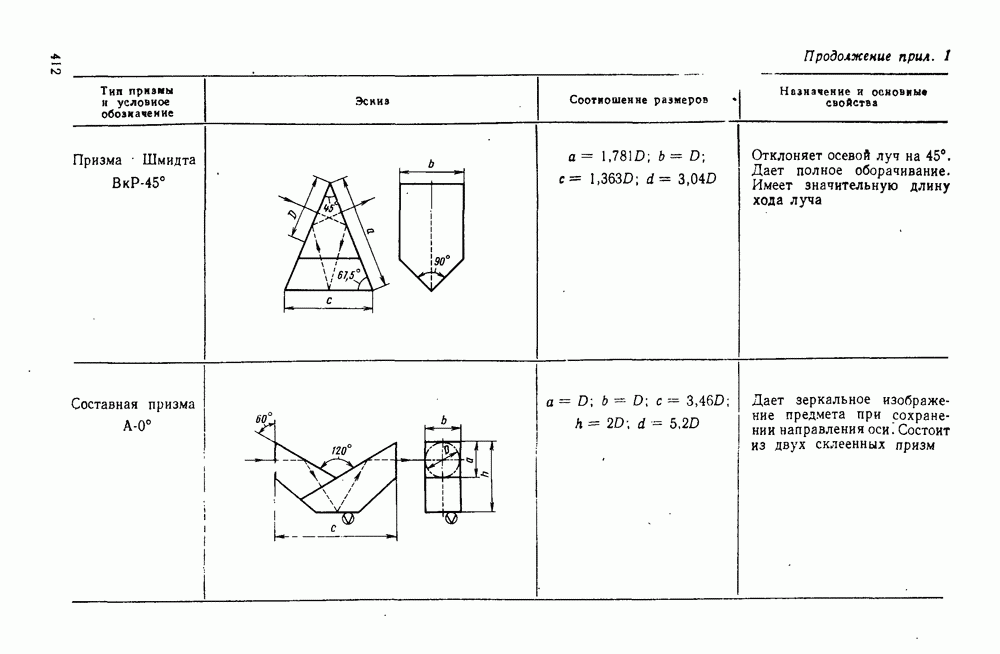
- 29. Отражательные призмы
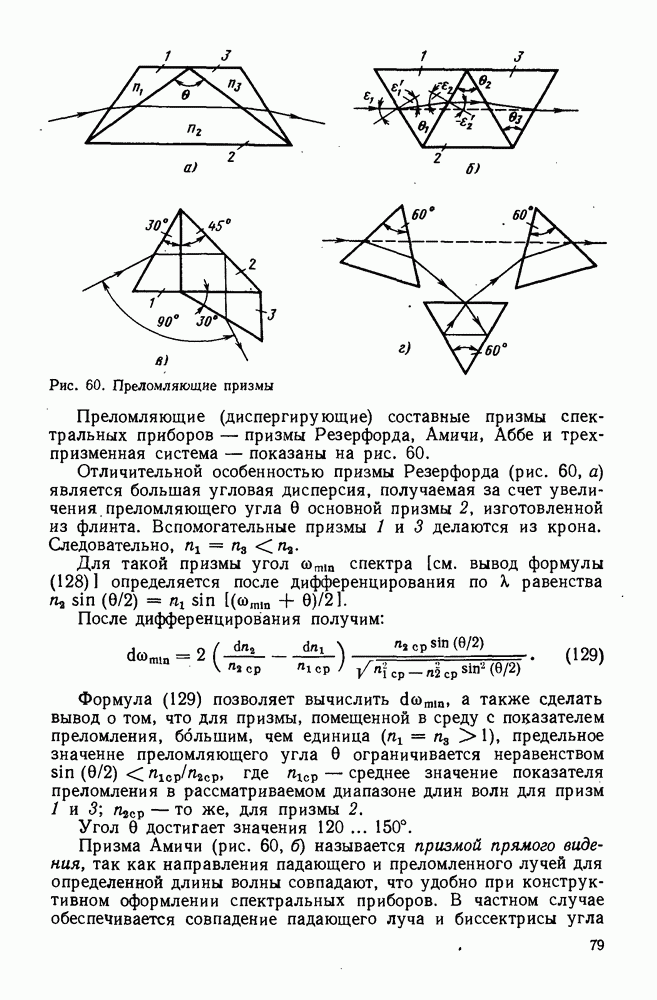
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
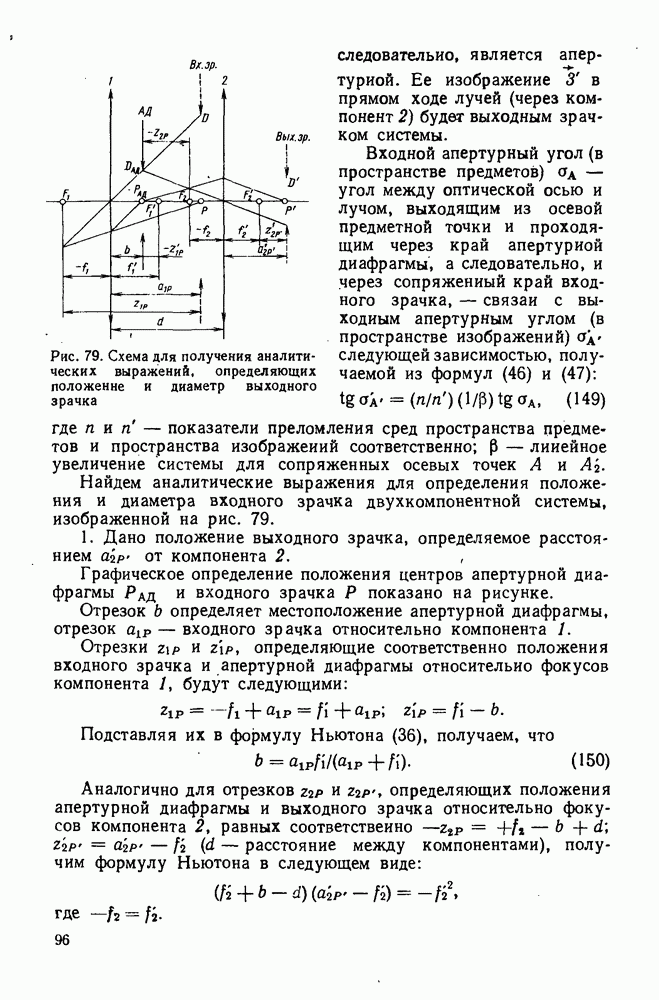
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
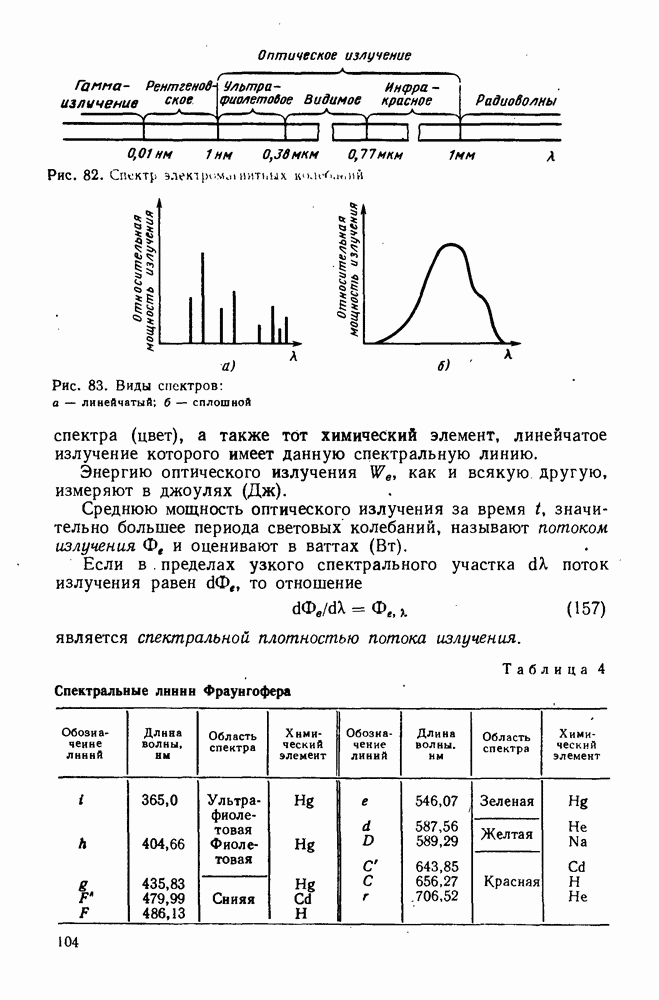
- 37. Оптическое излучение. Поток излучения
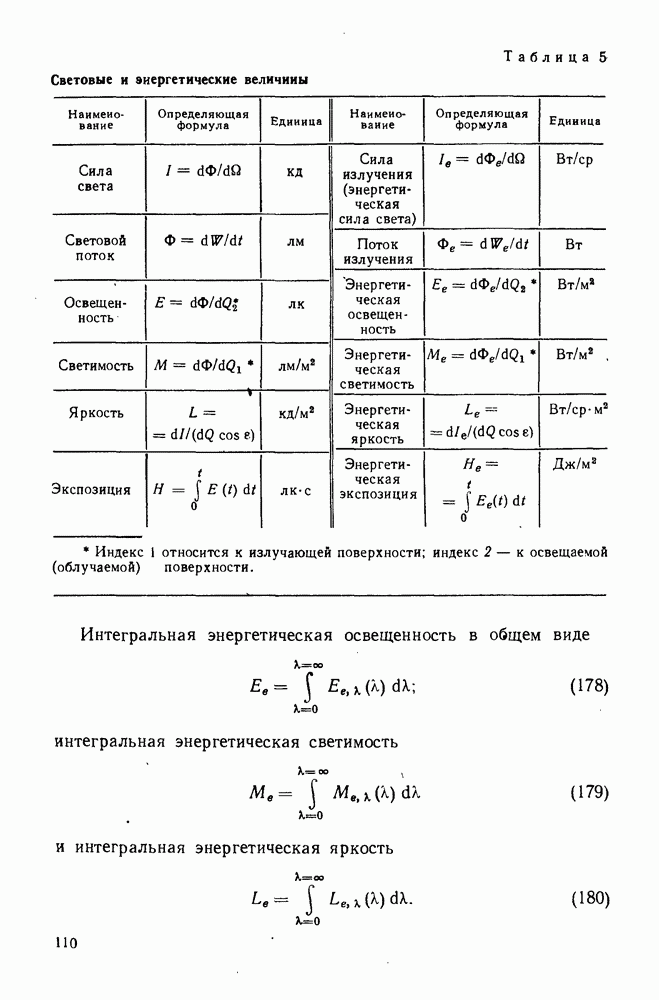
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы