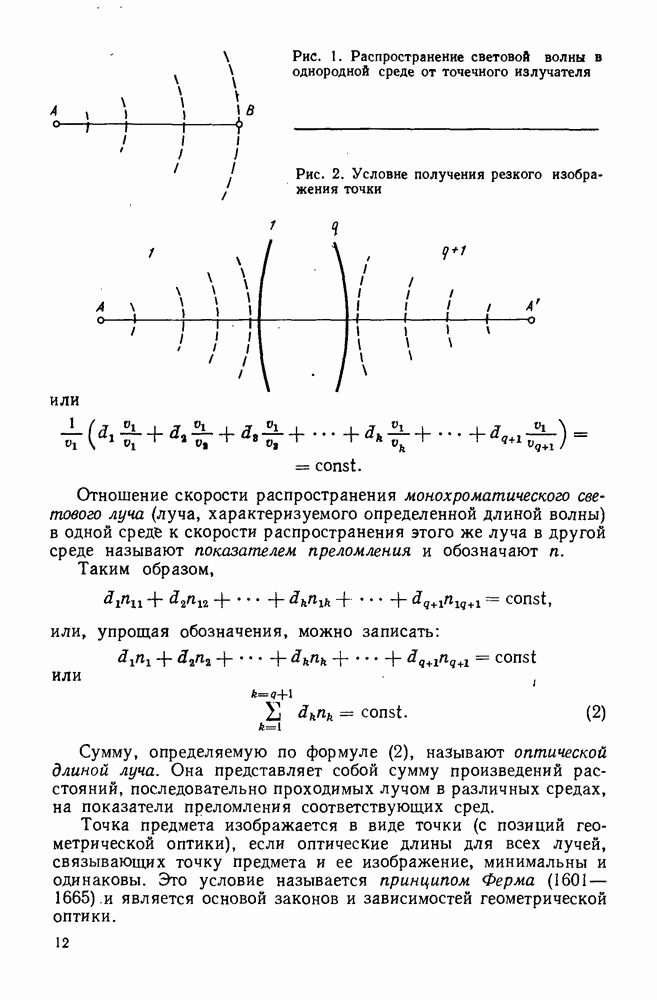
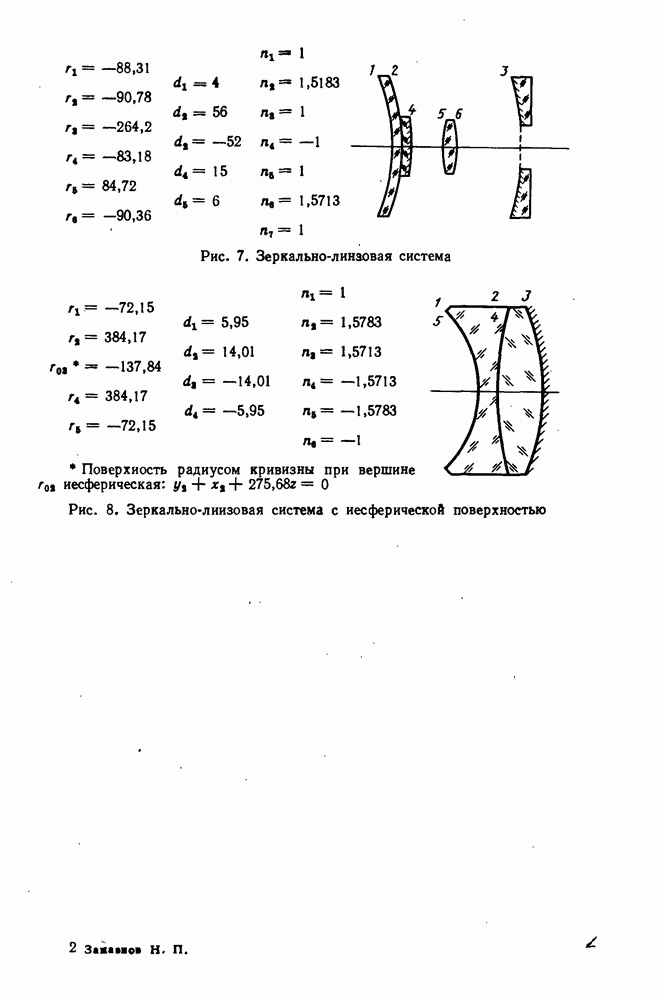
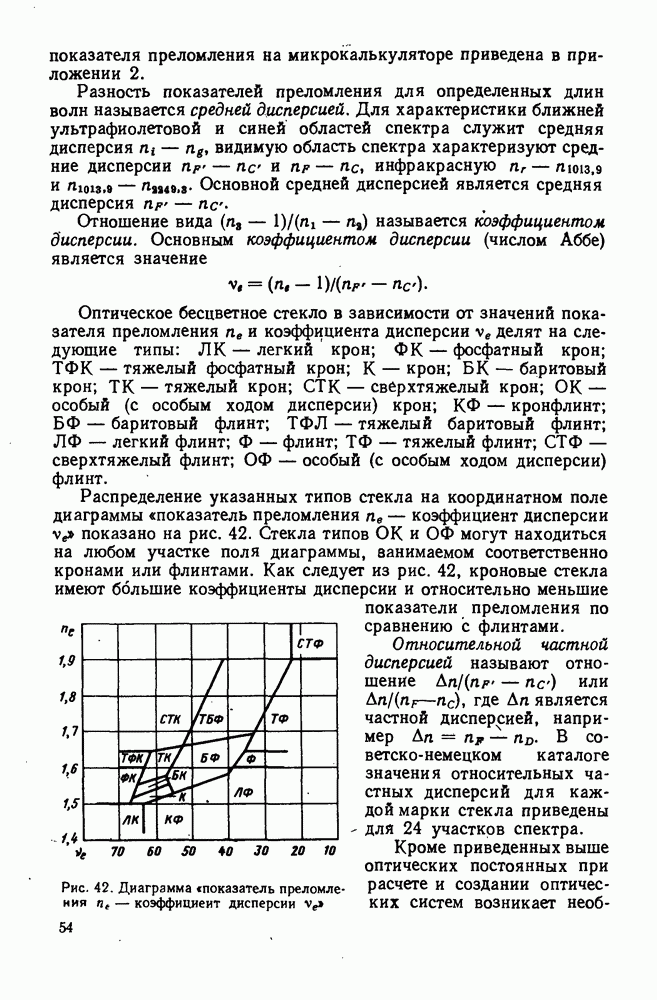
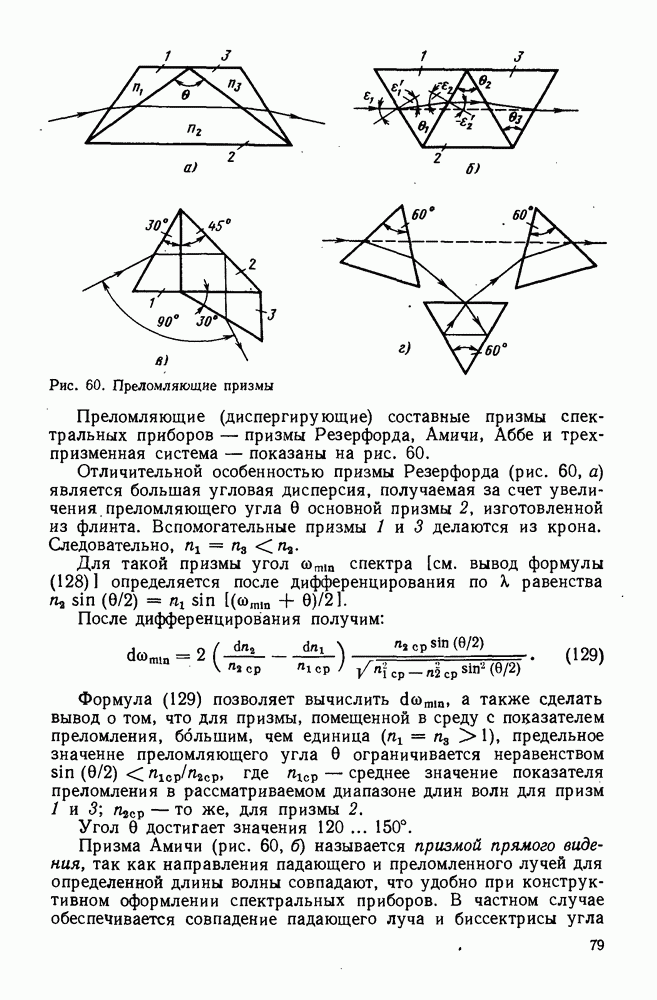
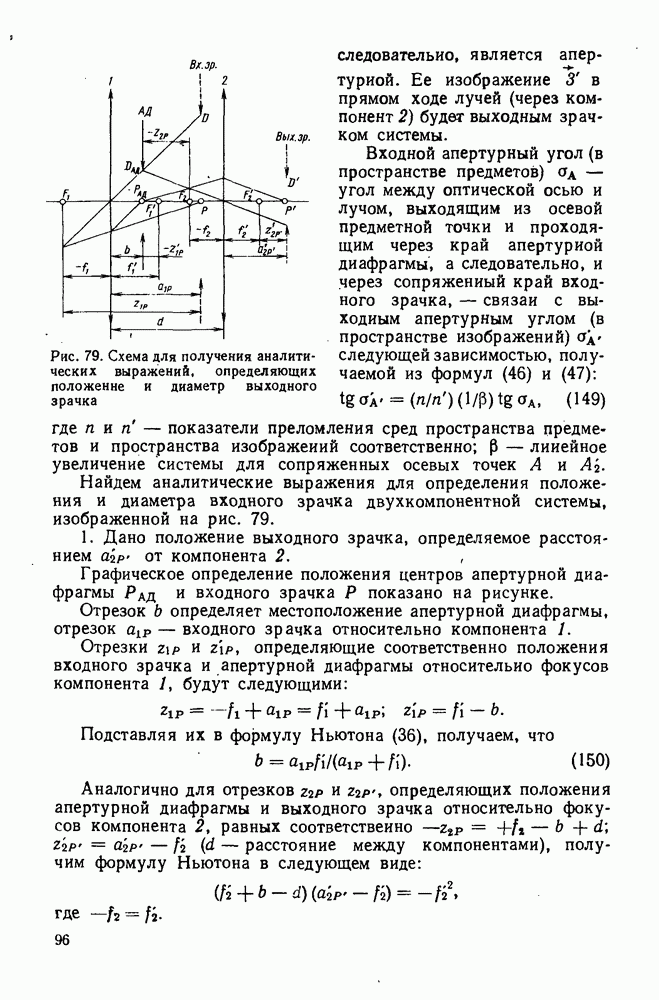
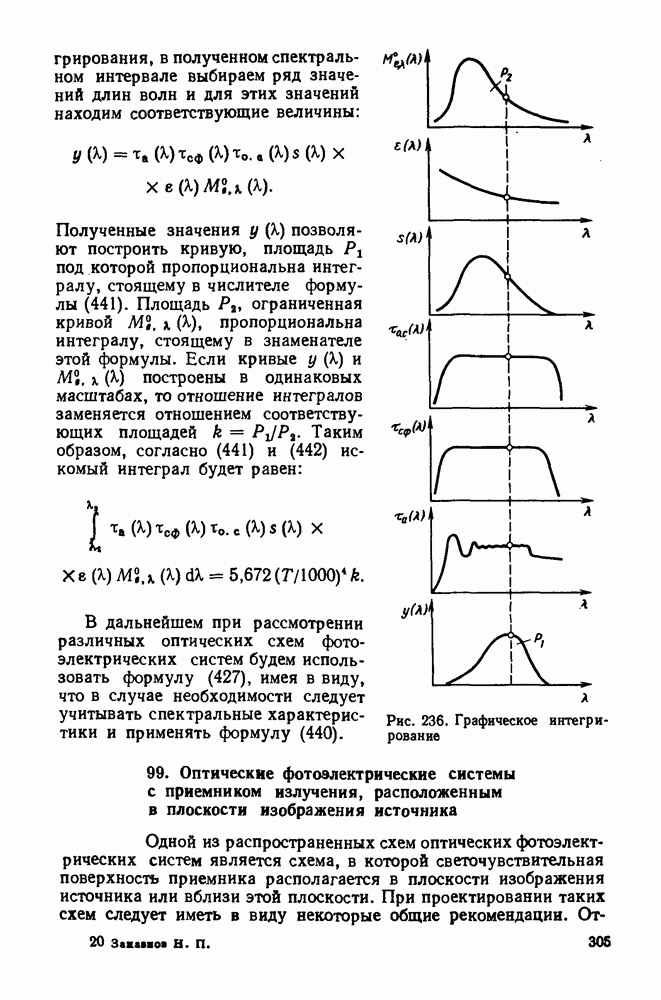
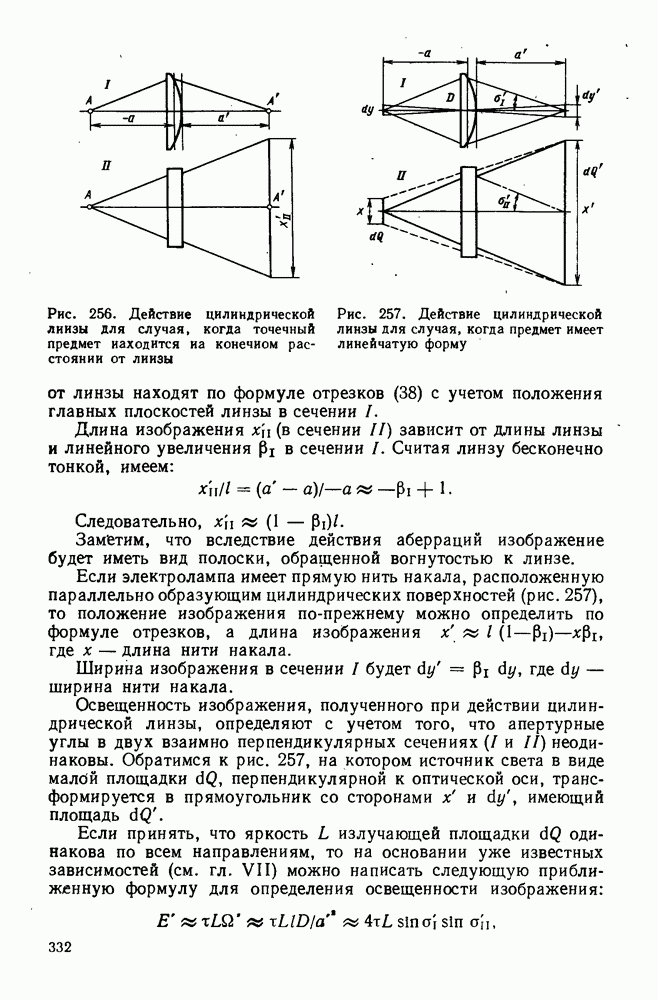
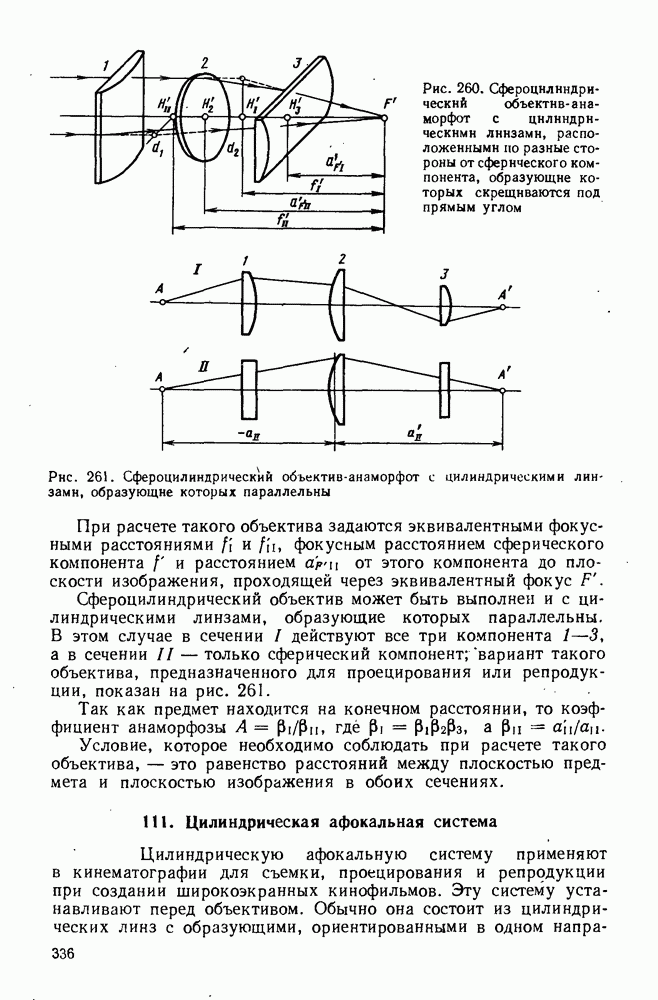
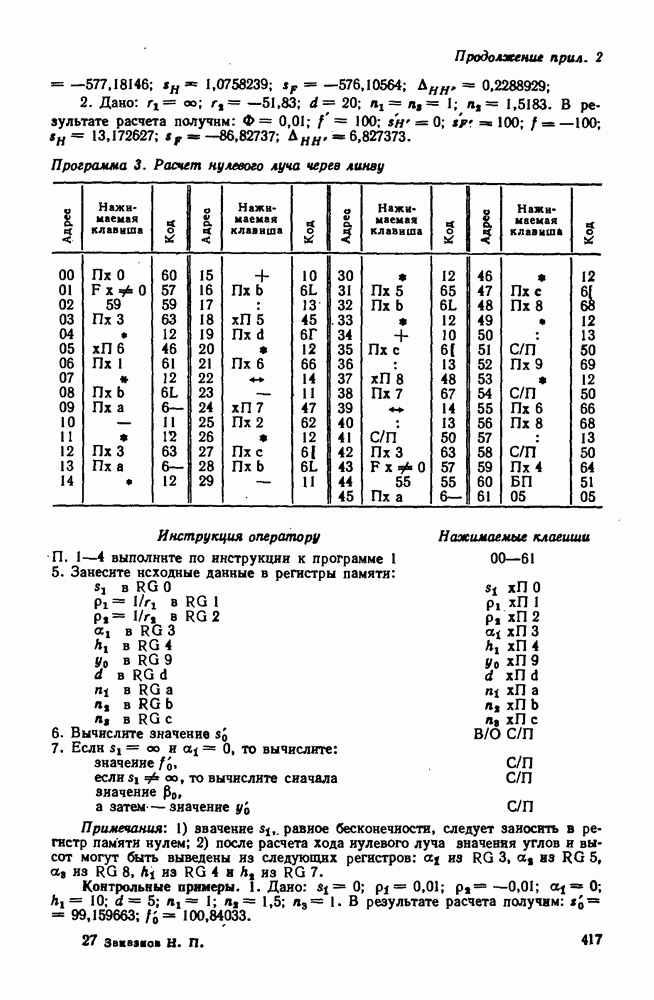
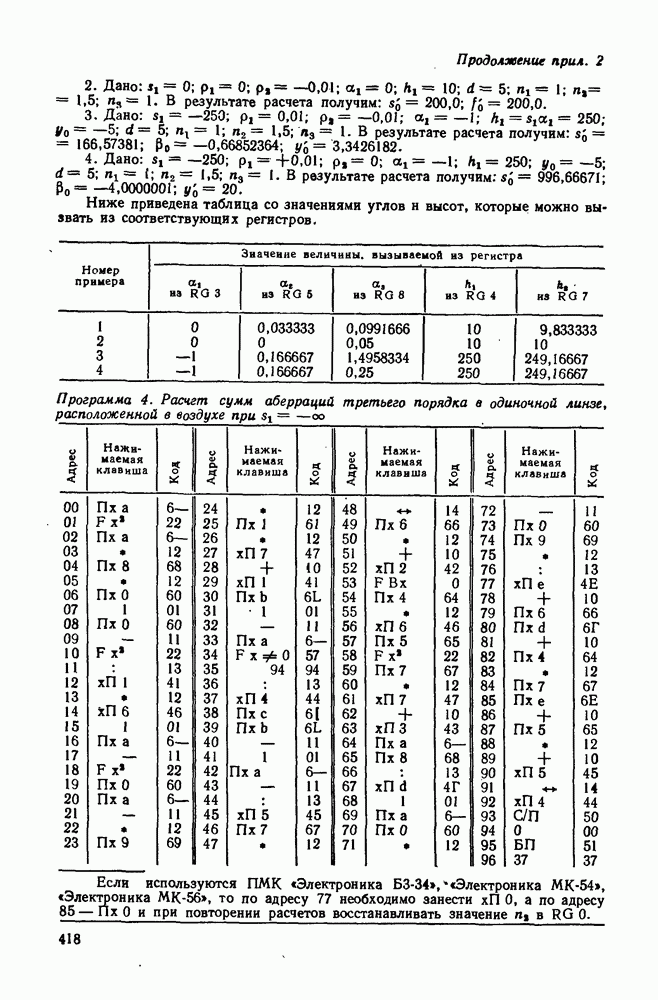
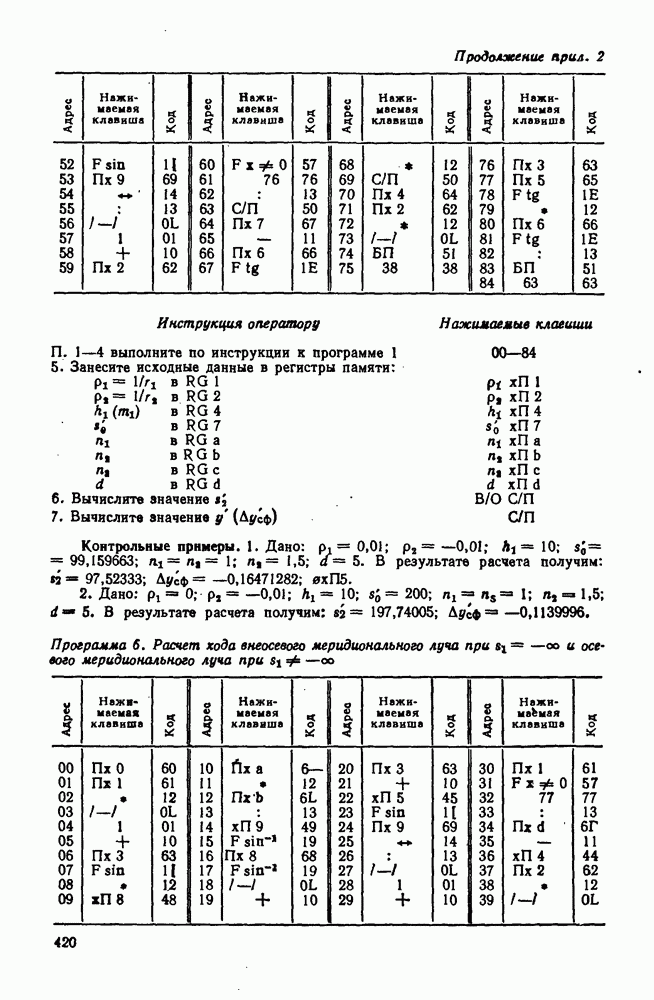
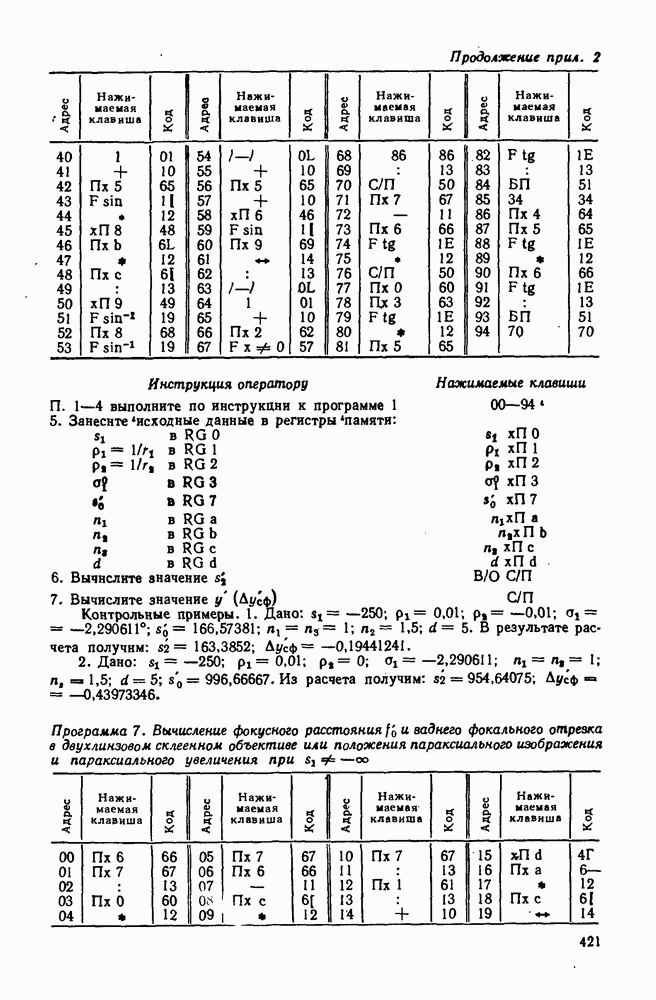
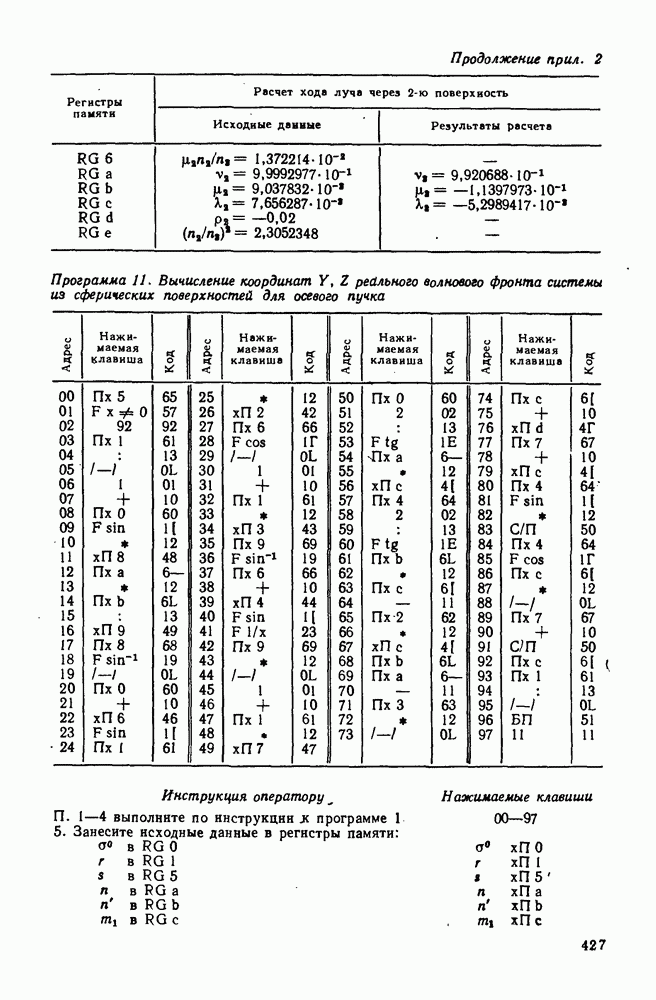
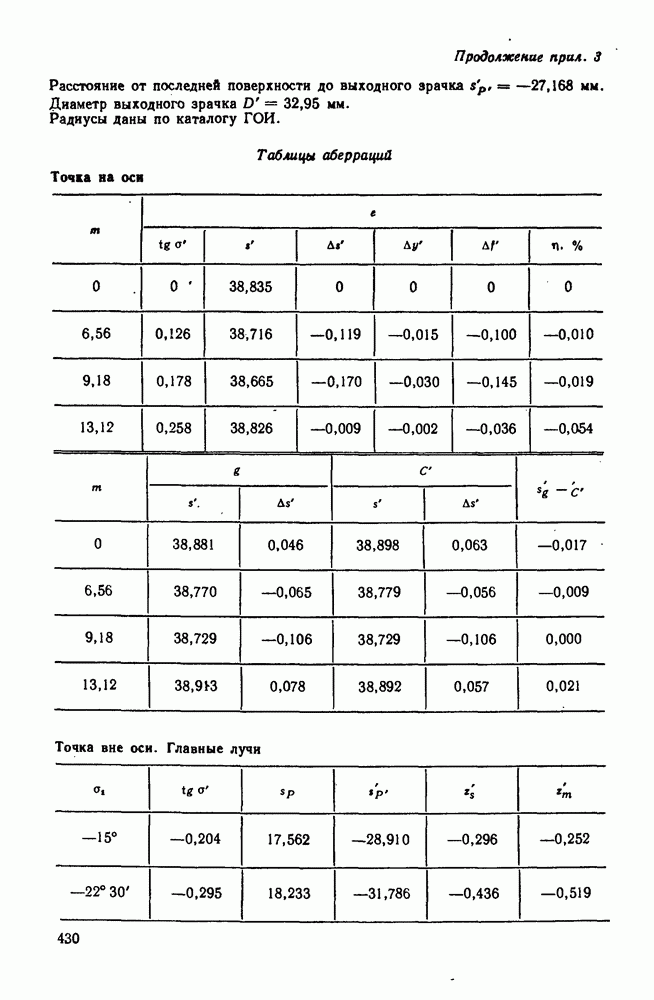
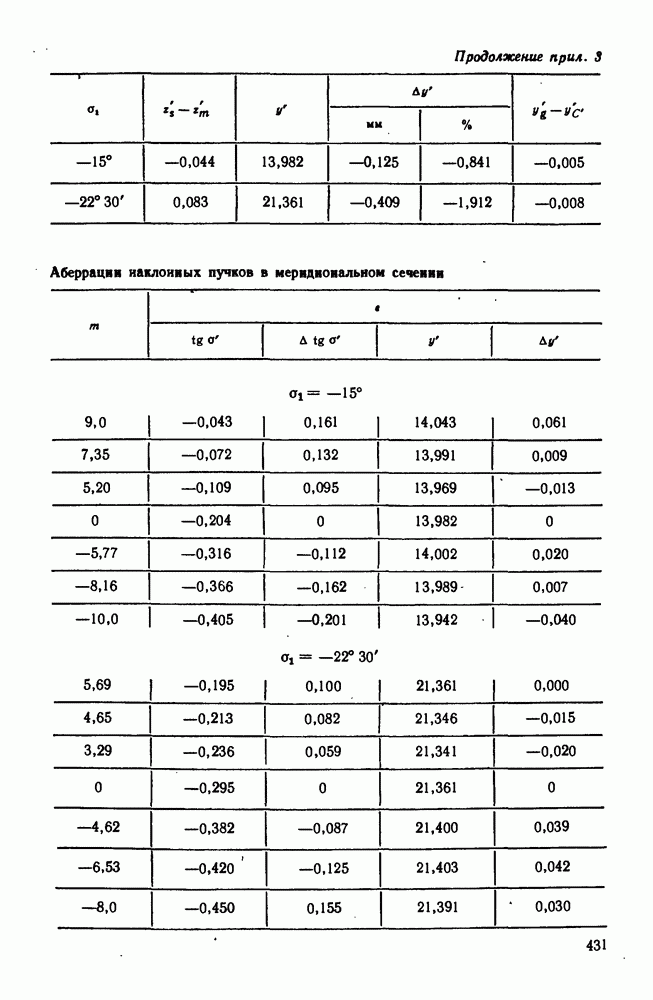
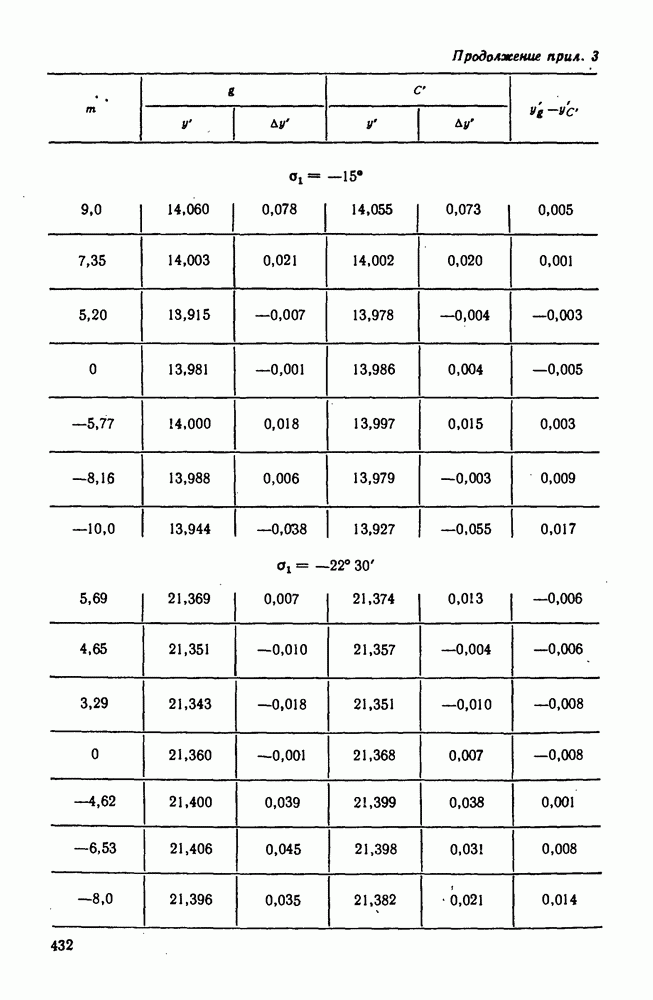
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
Одной из распространенных схем оптических фотоэлектрических систем является схема, в которой светочувствительная поверхность приемника располагается в плоскости изображения источника или вблизи этой плоскости. При проектировании таких схем следует иметь в виду некоторые общие рекомендации.

Рис. 237. Схема оптической фотоэлектрической системы; источник на конечном расстоянии
Отдельные участки светочувствительной поверхности приемника излучения могут иметь неодинаковую чувствительность. Поэтому для обеспечения устойчивой работы всей системы желательно, чтобы изображение источника занимало как можно большую часть светочувствительной поверхности приемника. Однако для полного использования потока излучения, входящего во входной зрачок оптической системы, необходимо, чтобы оптическая система не имела виньетирования и изображение источника излучения вписывалось в светочувствительную поверхность приемника. Указанные условия будут оптимально выполняться в том случае, если форма источника излучения подобна светочувствительной поверхности приемника.
Рассмотрим различные схемы фотоэлектрических систем с приемником излучения, расположенным в плоскости изображения источника.
Однокомпонентная система; источник излучения на конечном расстоянии. Принципиальная схема такой системы показана на рис. 237. При расчете оптической системы будем исходить из условия, что выбран источник излучения, имеющий энергетическую яркость  и площадь
и площадь  и приемник, имеющий интегральную чувствительность
и приемник, имеющий интегральную чувствительность  и площадь
и площадь  Приемник должен иметь минимальную реакцию
Приемник должен иметь минимальную реакцию  Задавшись коэффициентом пропускания оптической системы
Задавшись коэффициентом пропускания оптической системы  определим апертурный угол в пространстве предметов по формуле (427):
определим апертурный угол в пространстве предметов по формуле (427):

При малом расстоянии между источником и оптической системой  Светофильтр в системе не используется. Формула (443) справедлива при условии, что оптическая система свободна от виньетирования, а изображение источника вписывается в светочувствительную поверхность приемника. Последнее обеспечивается соответствующим выбором линейного увеличения. Если, например, источник имеет форму прямоугольника размером
Светофильтр в системе не используется. Формула (443) справедлива при условии, что оптическая система свободна от виньетирования, а изображение источника вписывается в светочувствительную поверхность приемника. Последнее обеспечивается соответствующим выбором линейного увеличения. Если, например, источник имеет форму прямоугольника размером  а светочувствительная поверхность приемника круглая, то оптическая система должна иметь линейное увеличение
а светочувствительная поверхность приемника круглая, то оптическая система должна иметь линейное увеличение


Рис. 238. Схема оптической фотоэлектрической системы; источник в бесконечности
где  диаметр светочувствительной поверхности приемника. Знак минус в формуле (444) означает, что изображение источника обратное.
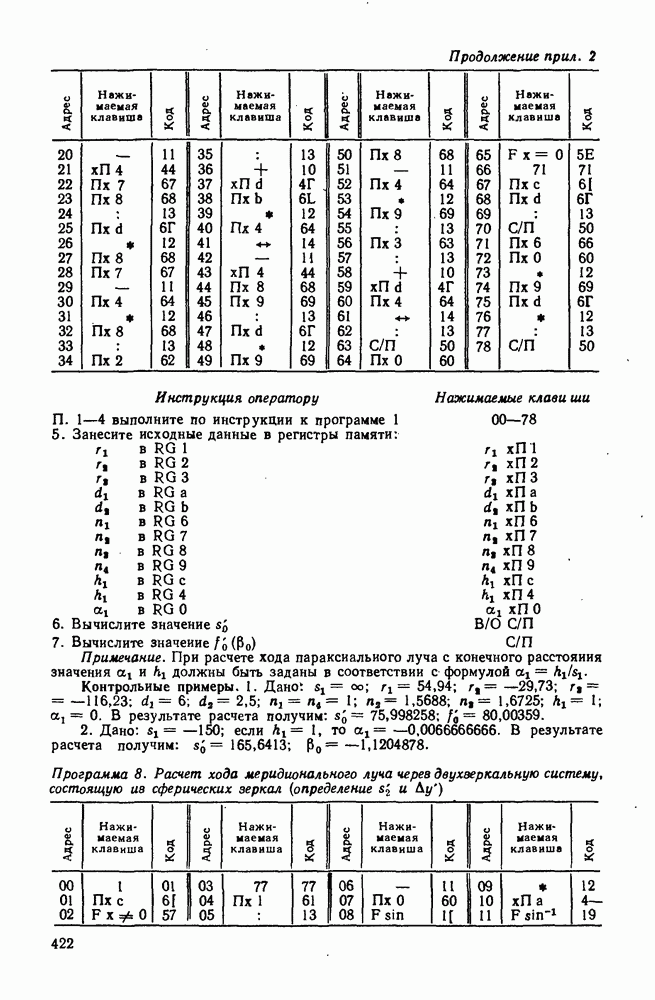
диаметр светочувствительной поверхности приемника. Знак минус в формуле (444) означает, что изображение источника обратное.
Если задано расстояние между источником и приемником  то согласно
то согласно  получим значения а и а. В первоначальном варианте расчета можно считать оптическую систему бесконечно тонкой, т. е.
получим значения а и а. В первоначальном варианте расчета можно считать оптическую систему бесконечно тонкой, т. е. 
Обычно входной зрачок оптической системы совпадает с первой поверхностью. Тогда для бесконечно тонкой системы  следовательно, диаметр входного зрачка определяется по формуле (428):
следовательно, диаметр входного зрачка определяется по формуле (428): 
Конструкция оптической системы зависит от угла  Если
Если  то можно использовать однолинзовую
то можно использовать однолинзовую  для
для  применяют двухлинзовую, а для
применяют двухлинзовую, а для  трехлинзовую систему. Выбрав конструкцию системы, уточн. от ее коэффициент пропускания
трехлинзовую систему. Выбрав конструкцию системы, уточн. от ее коэффициент пропускания  а также длину отрезкой а и а.
а также длину отрезкой а и а.
Однокомпонентная система; источник излучения расположен в бесконечности. В этом случае светочувствительная поверхность приемника устанавливается в задней фокальной плоскости оптической системы (рис. 238). Если максимальный угловой размер источника относительно передней главной точки равен  то размер его изображения в задней фокальной плоскости
то размер его изображения в задней фокальной плоскости  и это изображение должно вписываться в светочувствительную поверхность приемника, т. е.
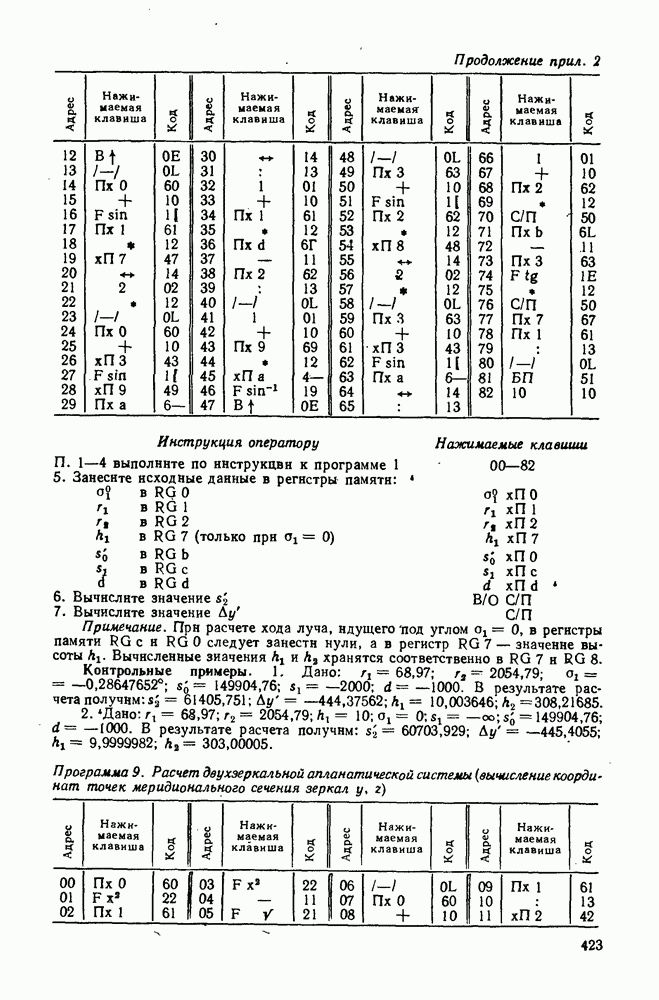
и это изображение должно вписываться в светочувствительную поверхность приемника, т. е.  где пр — диаметр светочувствительной поверхности приемника. Следовательно, фокусное расстояние системы должно быть
где пр — диаметр светочувствительной поверхности приемника. Следовательно, фокусное расстояние системы должно быть 
Если изображение источника значительно меньше светочувствительной поверхности приемника, то приемник следует сместить относительно фокальной плоскости.
Выбрав источник и приемник излучения, по формуле (427) можно вычислить синус апертурного угла в пространстве предметов, а по формуле (428) — диаметр входного зрачка оптической системы. Учитывая, что  (источник излучения расположен в бесконечности), можно принять
(источник излучения расположен в бесконечности), можно принять  Поэтому
Поэтому

Размеры бесконечно удаленного источника характеризуют его угловой величиной  Если считать, что источник имеет круглую форму, а
Если считать, что источник имеет круглую форму, а  его размер в радианах, то площадь этого источника
его размер в радианах, то площадь этого источника  Подставив значение
Подставив значение  в формулу (445),
в формулу (445),
получим выражение для вычисления диаметра входного зрачка оптической системы:

Оптическая фотоэлектрическая система для регистрации излучения звезд. Широкое развитие космических исследований за последние десятилетия привело к созданию различных фотоэлектрических систем, предназначенных для регистрации излучения звезд. При расчете таких систем необходимо учитывать специфику фотометрических единиц, принятых в астрономии и астрофизике и основанных на понятии звездной величины 
По отношению к поверхности Земли звезда является идеально точечным источником, который можно характеризовать освещенностью, создаваемой звездой на поверхности Земли или у границы земной атмосферы. Звездная величина  является мерой, определяющей блеск звезды, т. е. создаваемую ею освещенность на плоскости, перпендикулярной к падающим лучам. Шкала звездных величин устанавливается формулой
является мерой, определяющей блеск звезды, т. е. создаваемую ею освещенность на плоскости, перпендикулярной к падающим лучам. Шкала звездных величин устанавливается формулой

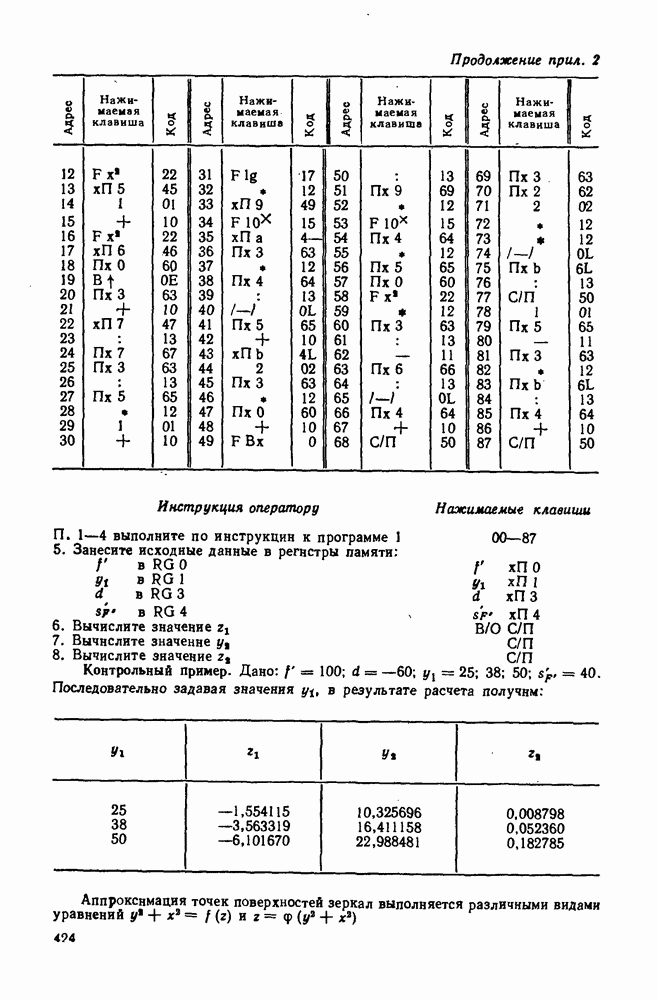
где  освещенность от звезды у границы земной атмосферы,
освещенность от звезды у границы земной атмосферы, 
Согласно формуле (447) звезда первой величины создает освещенность  второй
второй  и т.д.
и т.д.
Формулой (447) можно пользоваться и для характеристики излучения источников конечных размеров, например Луны, Солнца и других земных источников. Так, во рремя полнолуния Луна создает на поверхности Земли освещенность около  что соответствует звездной величине
что соответствует звездной величине 
При расчете фотоэлектрических систем для регистрации излучения звезд возникает необходимость перехода от световых величин, устанавливаемых формулой (447), к энергетическим. Звезды излучают, как черное тело, но температура их различна. Все они разбиты на спектральные классы, обозначенные прописными буквами латинского алфавита. Переход от блеска звезды (освещенности, измеренной в люксах) к энергетической освещенности, измеряемой в ваттах на квадратный метр, выполняется через световую эффективность, измеряемую в люменах на ватт 

Звезда спектрального класса А с температурой поверхности  имеет световую эффективность
имеет световую эффективность  Очевидно, максимальное значение световой эффективности будет у звезды спектрального класса
Очевидно, максимальное значение световой эффективности будет у звезды спектрального класса  с температурой поверхности 6000 К, как у Солнца, световая эффективность которого
с температурой поверхности 6000 К, как у Солнца, световая эффективность которого 
Принципиальная схема оптической фотоэлектрической системы для регистрации излучения звезд показана на рис. 239. Если

Рис. 239. Схема оптической фотоэлектрической системы для регистрации излучения звезд
известна звездная величина  то по формуле (447) можно найти освещенность
то по формуле (447) можно найти освещенность  создаваемую звездой у границы земной атмосферы.
создаваемую звездой у границы земной атмосферы.
Зная спектральный класс звезды, по формуле (448) определяем энергетическую освещенность у границы земной атмосферы: 
Пусть оптическая фотоэлектрическая система с диаметром входного зрачка  расположена на поверхности Земли. Тогда с учетом коэффициента пропускания атмосферы та определим поток излучения, поступающий от звезды во входной зрачок системы:
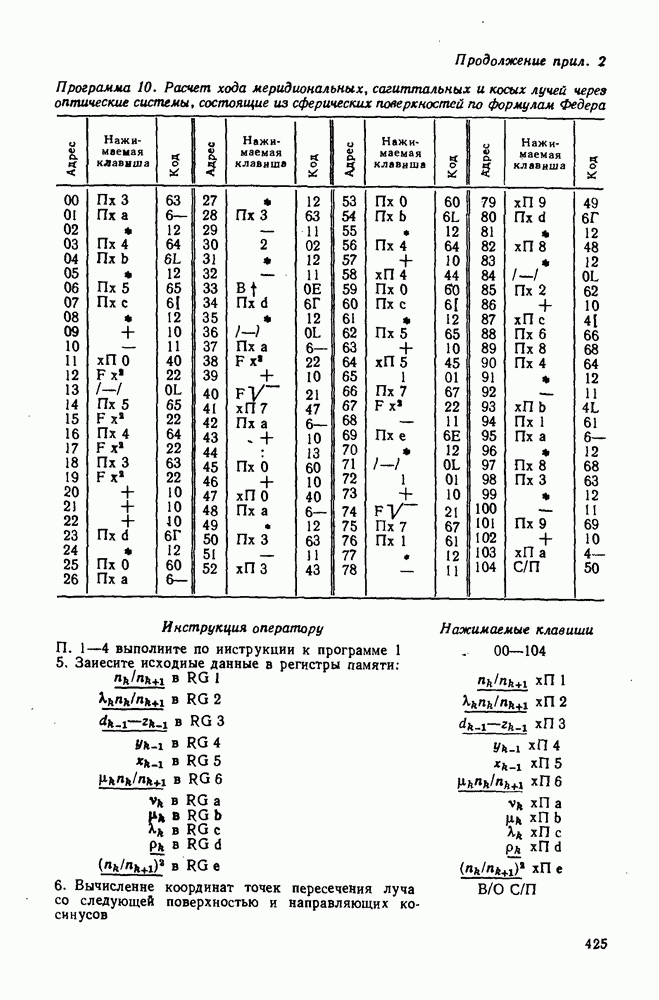
расположена на поверхности Земли. Тогда с учетом коэффициента пропускания атмосферы та определим поток излучения, поступающий от звезды во входной зрачок системы: 
Изображение звезды будет получаться в задней фокальной плоскости оптической системы, и в случае хорошо корригированной системы оно будет представлять собой дифракциошюе изображение точки. Поэтому для использования большей части светочувствительной поверхности приемника его располагают на некотором расстоянии за задней фокальной плоскостью. Получаемое при этом световое пятно должно быть не больше светочувствительной поверхности приемника. В некоторых случаях смещение приемника относительно заднего фокуса обусловлено необходимостью установки в задней фокальной плоскости анализирующего устройства.
Если  — коэффициент пропускания оптической системы, включая анализатор, то на светочувствительную поверхность приемника будет поступать поток излучения
— коэффициент пропускания оптической системы, включая анализатор, то на светочувствительную поверхность приемника будет поступать поток излучения

Если интегральная чувствительность приемника  то реакция приемника
то реакция приемника

Таким образом, для регистрации излучения звезды заданной звездной величины  при выбранном приемнике необходимо иметь оптическую систему с диаметром входного зрачка
при выбранном приемнике необходимо иметь оптическую систему с диаметром входного зрачка

Фокусное расстояние оптической системы не влияет на размер изображения звезды, поэтому при его выборе следует иметь в виду значение относительного отверстия 
Двухкомпонентная система. Принципиальная схема такой системы, состоящей из тонких компонентов, показана на рис. 240. Одним из возможных вариантов системы является установка источника излучения в передней фокальной плоскости первого компонента, а светочувствительной поверхности приемника — в задней фокальной плоскости второго компонента.

Рис. 240. Схема двухкомпонентной оптической фотоэлектрической системы
В этом случае линейное увеличение системы, определяемое по формуле

выбирают так, чтобы изображение источника вписывалось в светочувствительную поверхность приемника. Поэтому, если выбраны источник и приемник излучения, то можно определить линейное увеличение двухкомпонентной системы, например по формуле (444). Тогда, задавшись значением фокусного расстояния первого компонента, по формуле (451) вычисляют фокусное расстояние второго компонента.
Синус апертурного угла в пространстве предметов находят по формуле (443):

где  коэффициент пропускания двухкомпонентной оптической системы.
коэффициент пропускания двухкомпонентной оптической системы.
Диаметр первого компонента  Диаметр второго компонента определяют из условия отсутствия виньетирования для точки источника, наиболее удаленной от оптической оси. Если, например, источник излучения имеет форму прямоугольника размером
Диаметр второго компонента определяют из условия отсутствия виньетирования для точки источника, наиболее удаленной от оптической оси. Если, например, источник излучения имеет форму прямоугольника размером  то максимальный угол наклона пучка параллельных лучей, вышедших из первого компонента, рассчитывают по формуле
то максимальный угол наклона пучка параллельных лучей, вышедших из первого компонента, рассчитывают по формуле

Тогда при выбранном расстоянии  между компонентами вычисляют необходимый диаметр второго компонента:
между компонентами вычисляют необходимый диаметр второго компонента:

При значительных расстояниях между компонентами диаметр второго компонента, найденный по формуле (452), может иметь настолько большое значение, что его реализация принципиально невозможна. В этом случае приходится допускать виньетирование.

Рис. 241. Схема двухкомпонентной оптической фотоэлектрической системы при значительном расстоянии между компонентами
Двухкомпонентную систему, имеющую виньетирование, можно рассчитать в следующей последовательности (рис. 241).
Источник излучения и первый компонент оптической системы можно рассматривать как прожектор дальнего действия, имеющий силу излучения

где  — коэффициент пропускания первого компонента оптической системы;
— коэффициент пропускания первого компонента оптической системы;  сила излучения источника;
сила излучения источника;  диаметр выходного зрачка первого компонента;
диаметр выходного зрачка первого компонента;  диаметр источника.
диаметр источника.
Если расстояние  между компонентами больше дистанции оформления светового пучка, то на входном зрачке второго компонента оптической системы будет создана энергетическая освещенность
между компонентами больше дистанции оформления светового пучка, то на входном зрачке второго компонента оптической системы будет создана энергетическая освещенность  где
где  — коэффициент пропускания атмосферы на расстоянии
— коэффициент пропускания атмосферы на расстоянии 
Полагая диаметр входного зрачка второго компонента равным  определим поток излучения, поступающий во второй компонент
определим поток излучения, поступающий во второй компонент  а затем — поток излучения, падающий на светочувствительную поверхность приемника
а затем — поток излучения, падающий на светочувствительную поверхность приемника  где
где  коэффициент пропускания второго компонента оптической системы.
коэффициент пропускания второго компонента оптической системы.
Реакция приемника излучения, установленного в задней фокальной плоскости второго компонента, 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
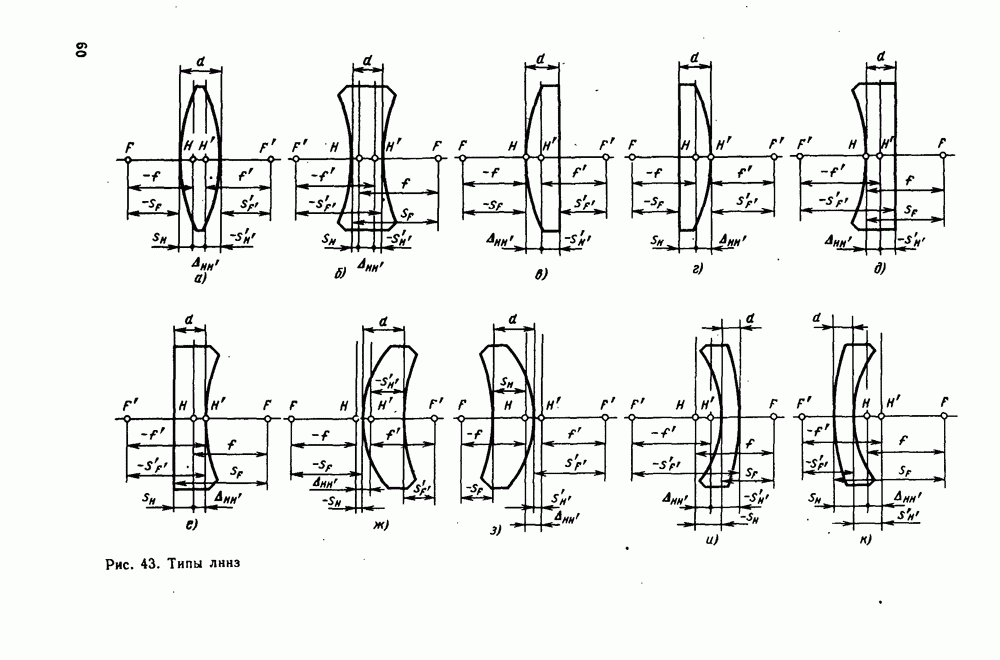
- 26. Линзы
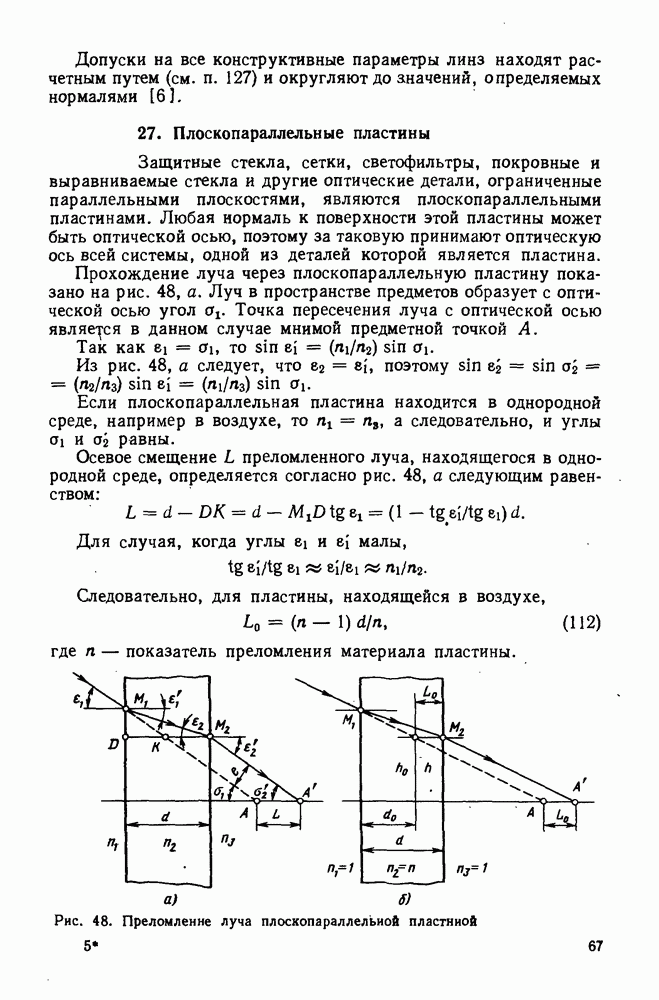
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
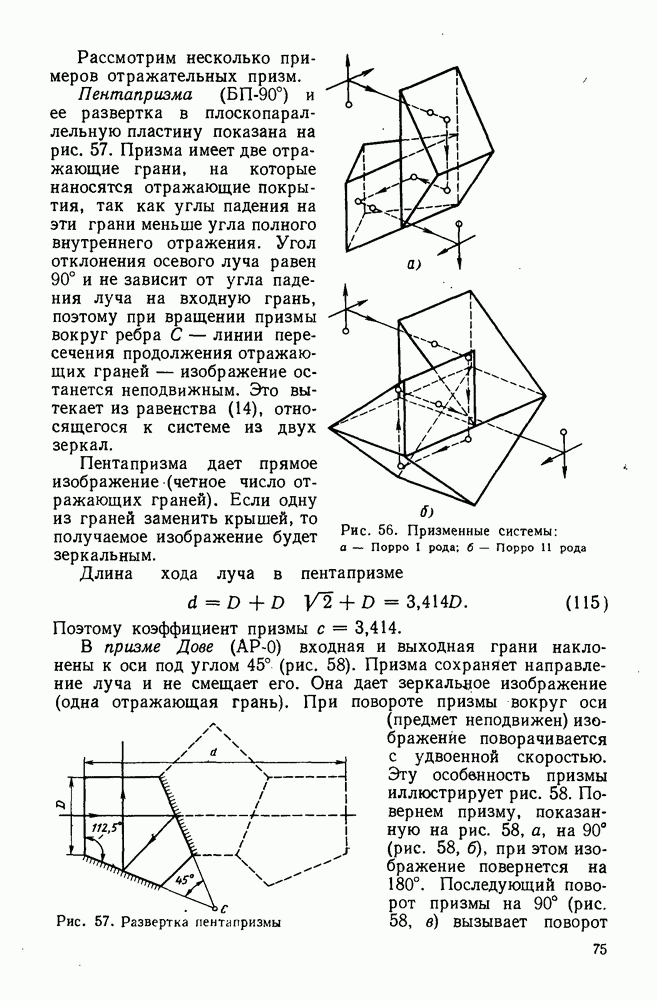
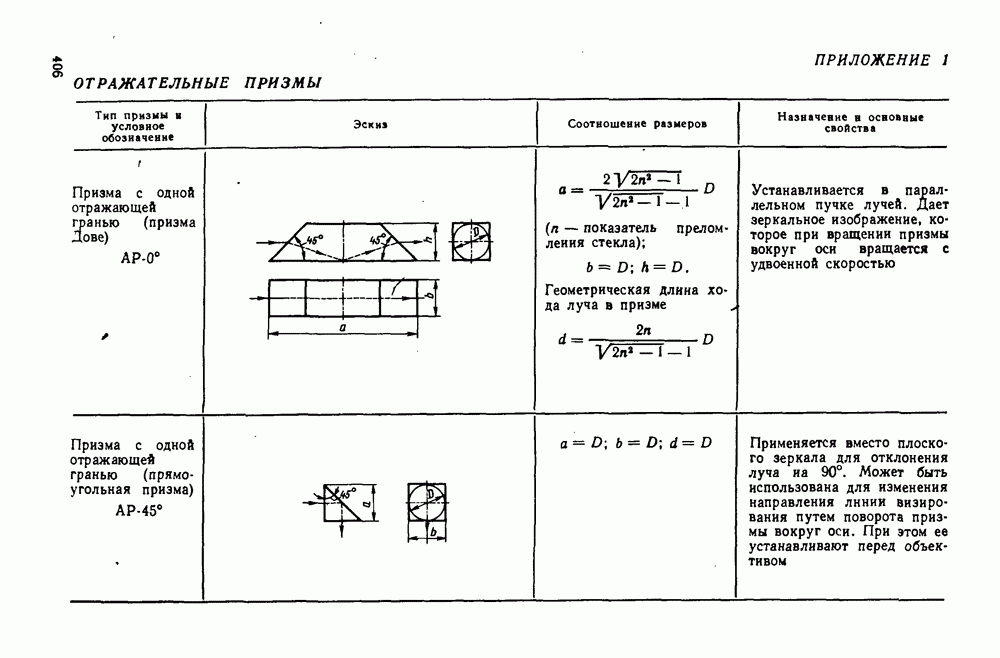
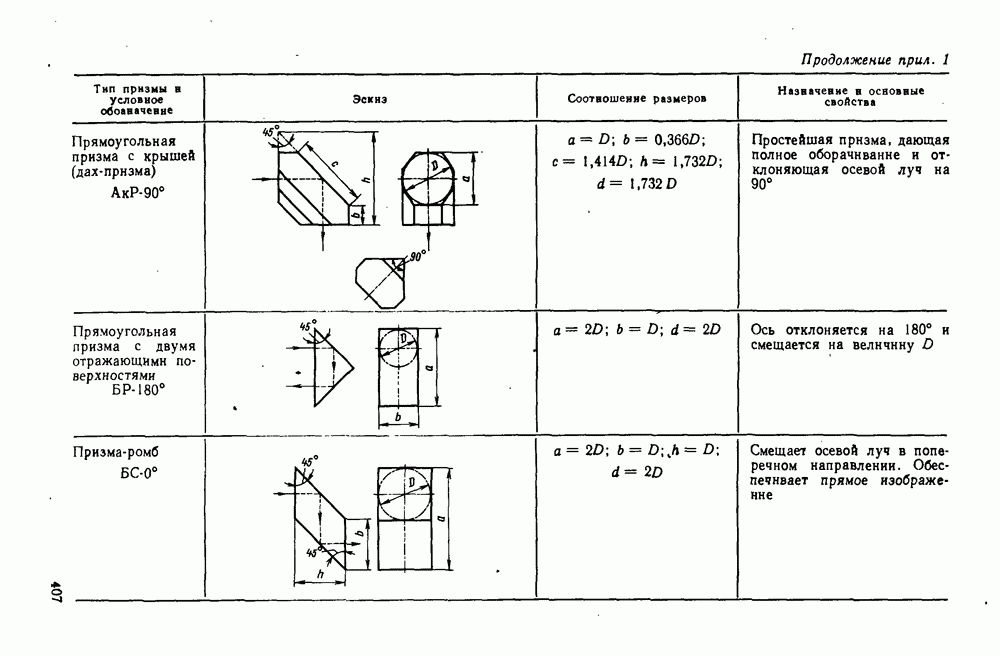
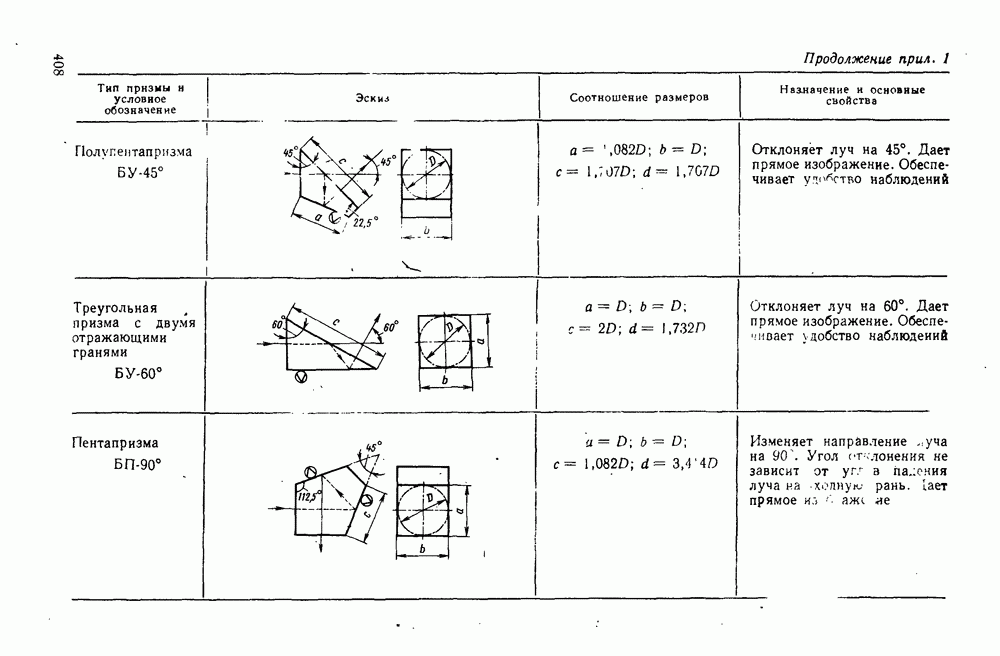
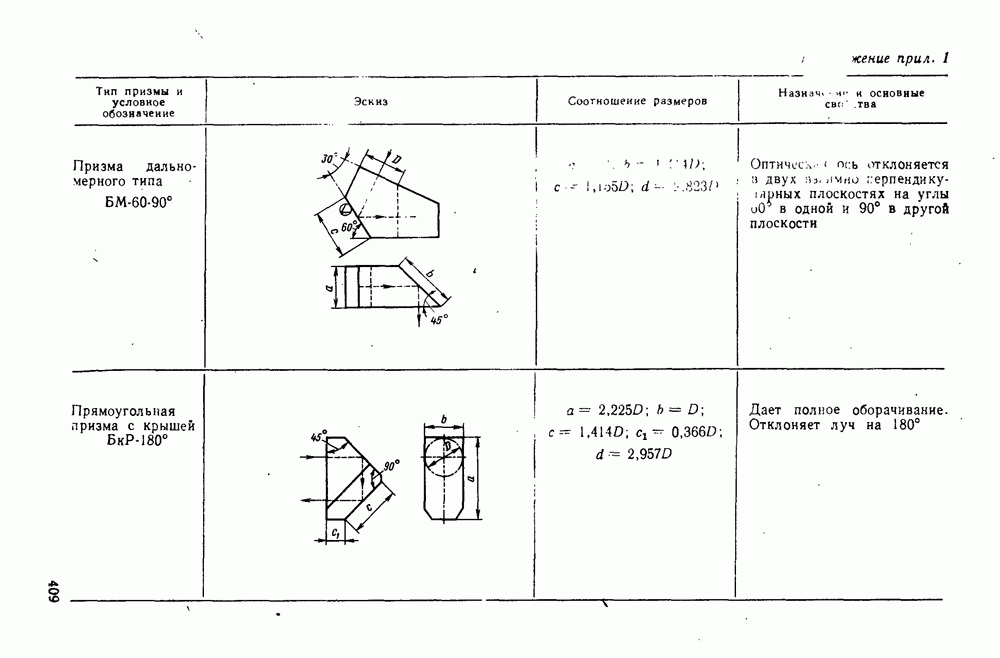
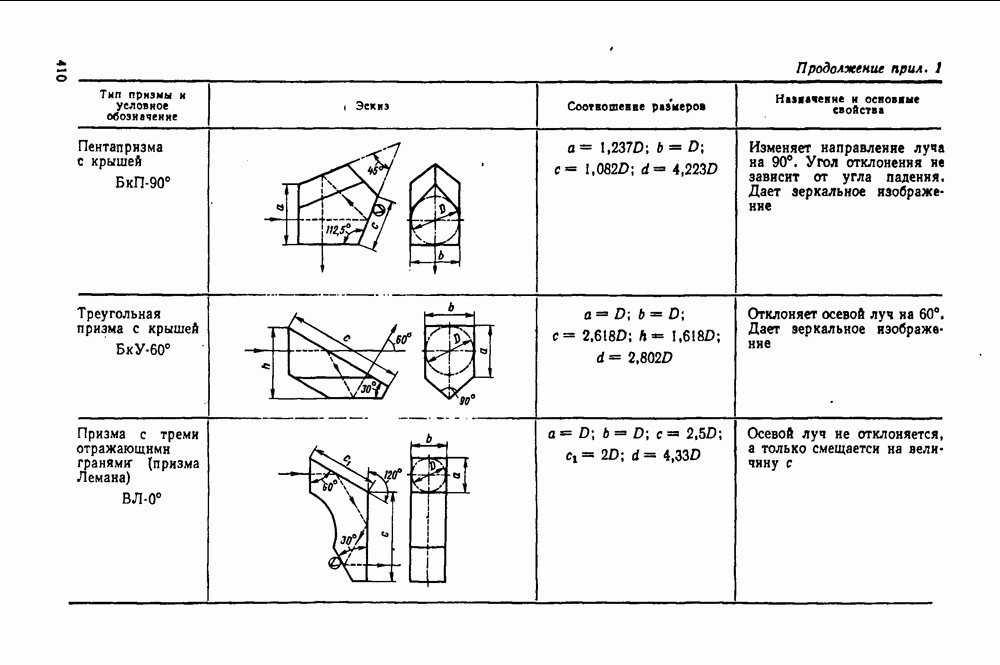
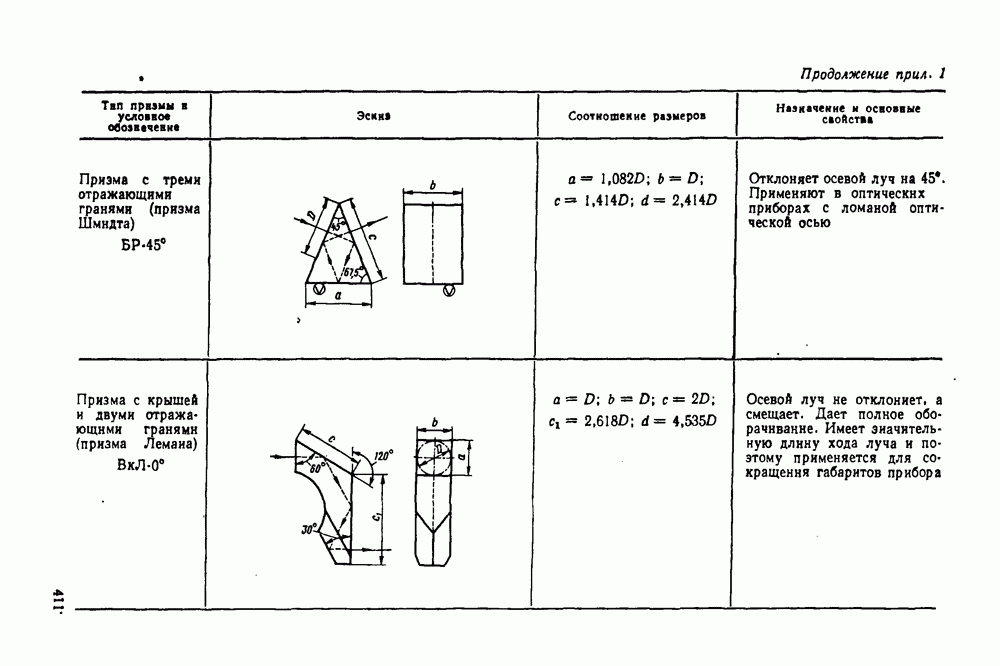
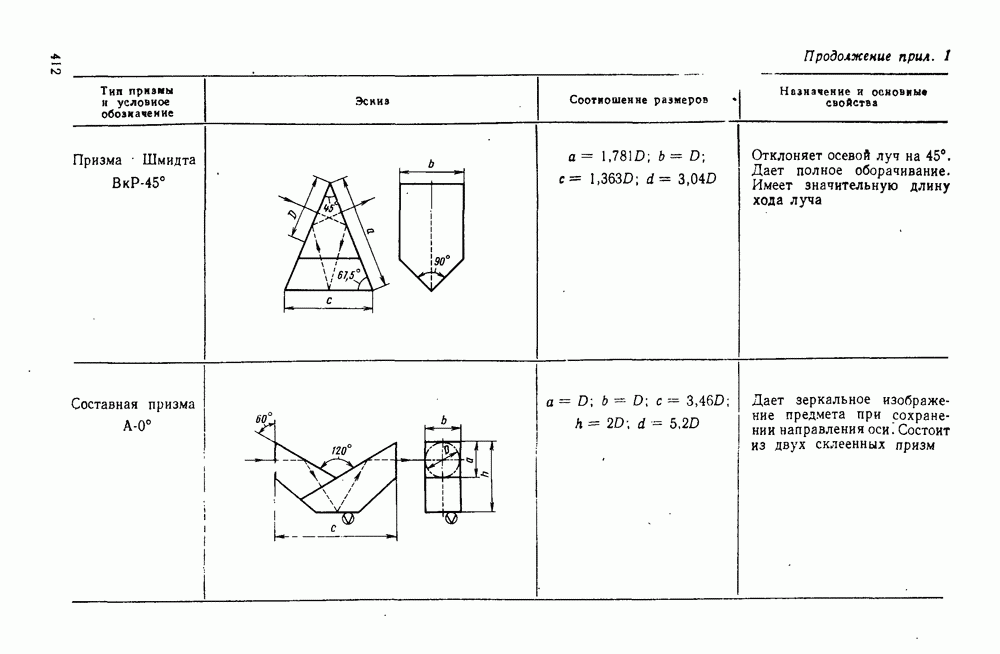
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
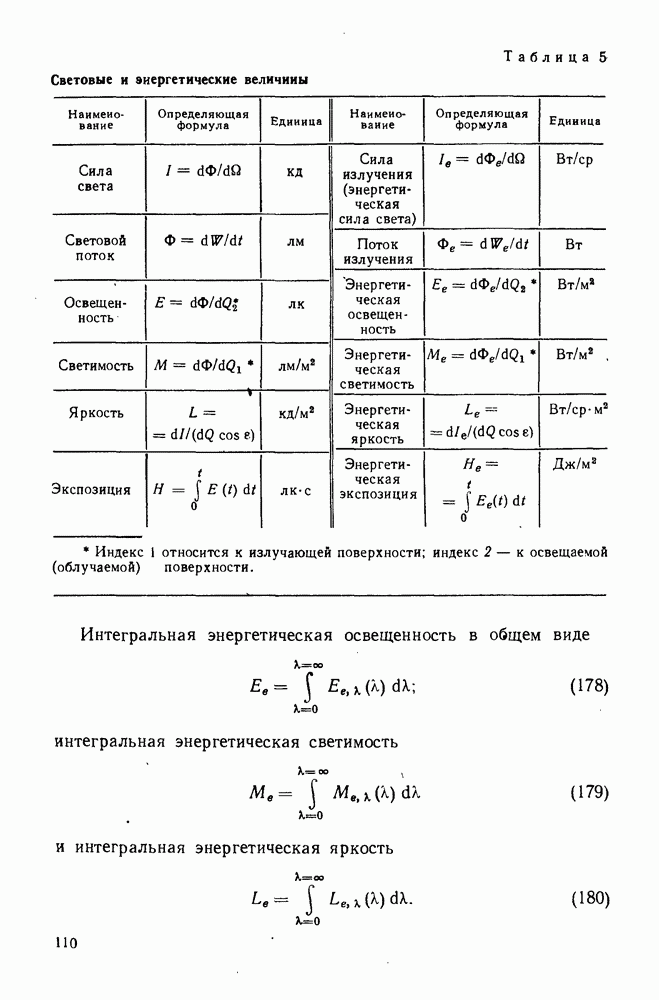
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
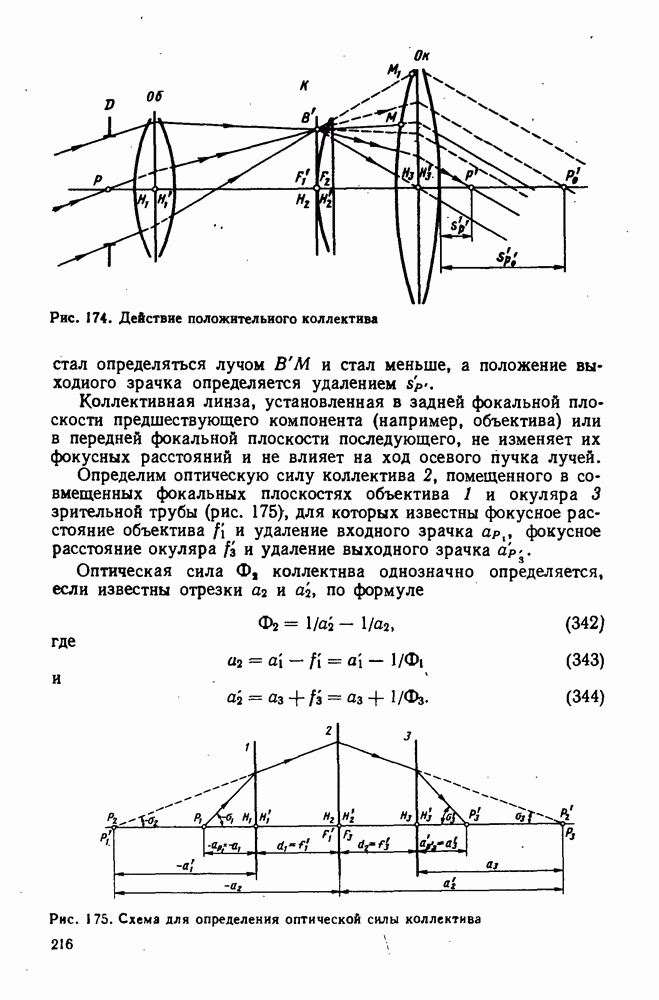
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
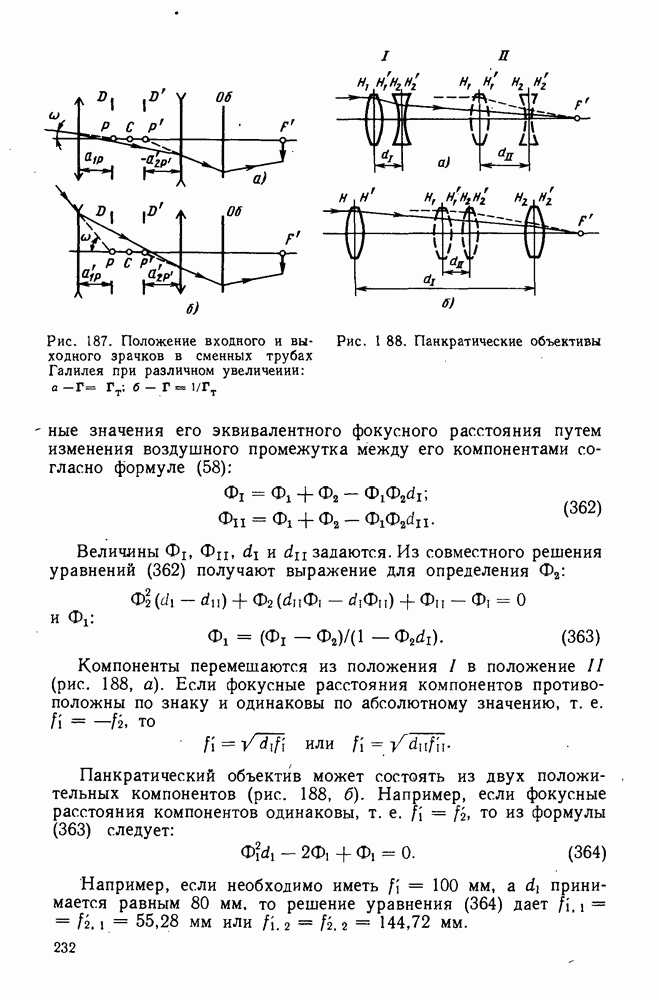
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
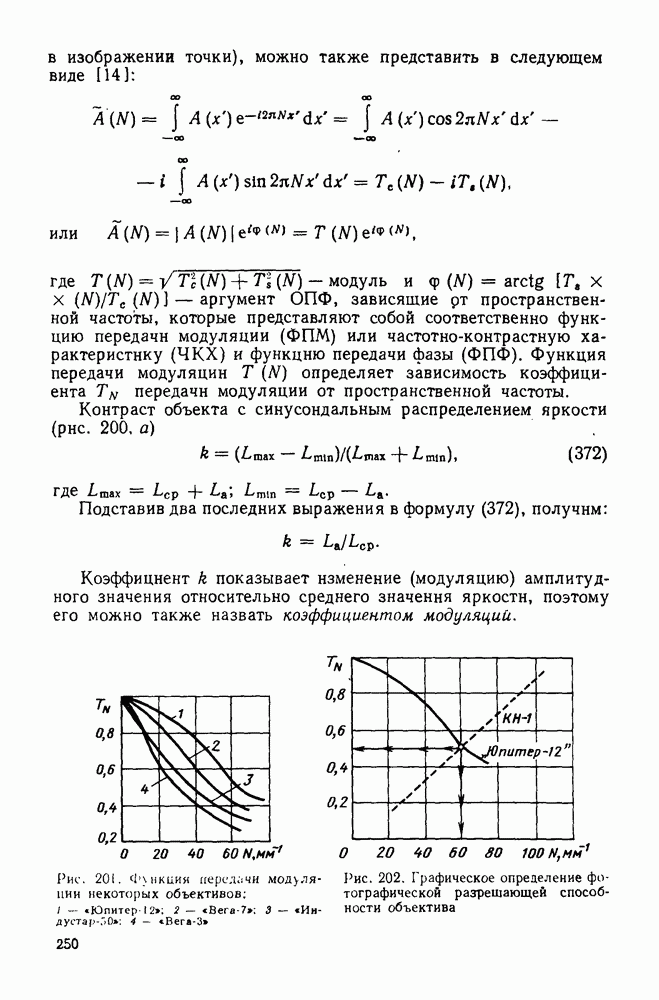
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
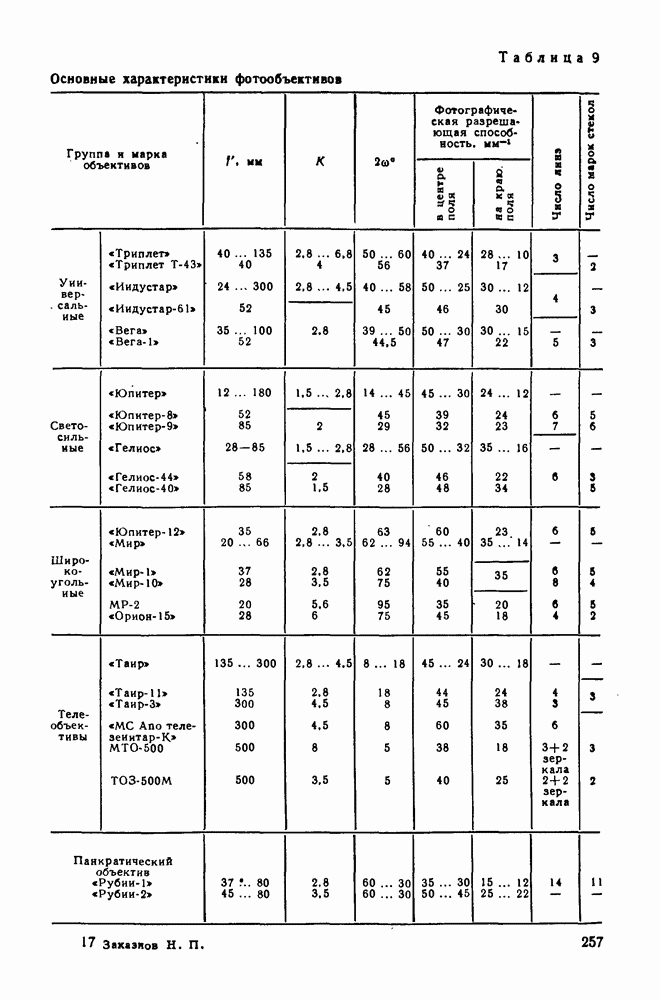
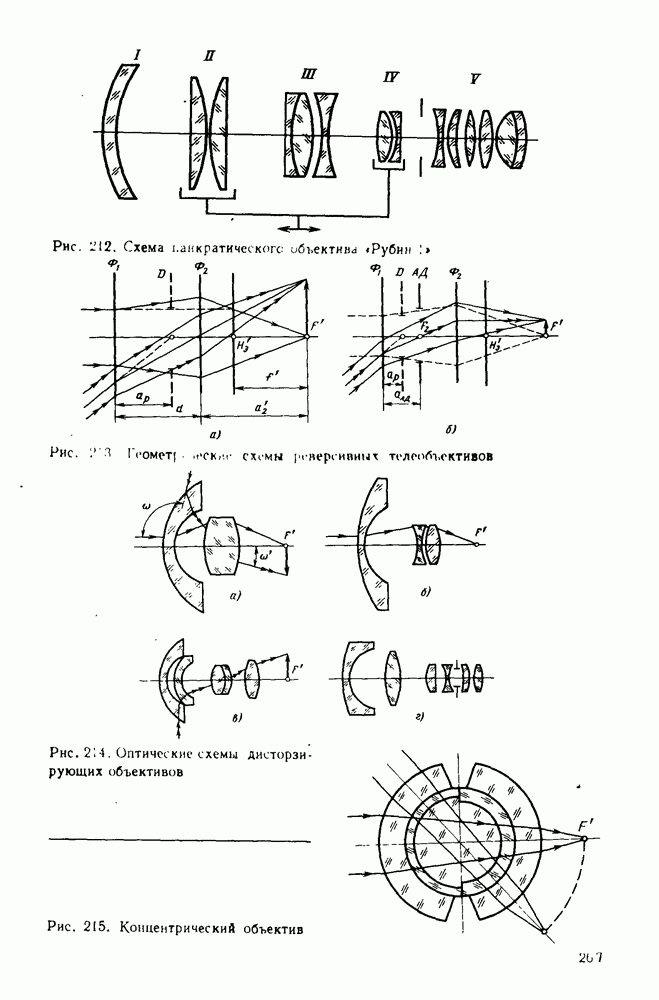
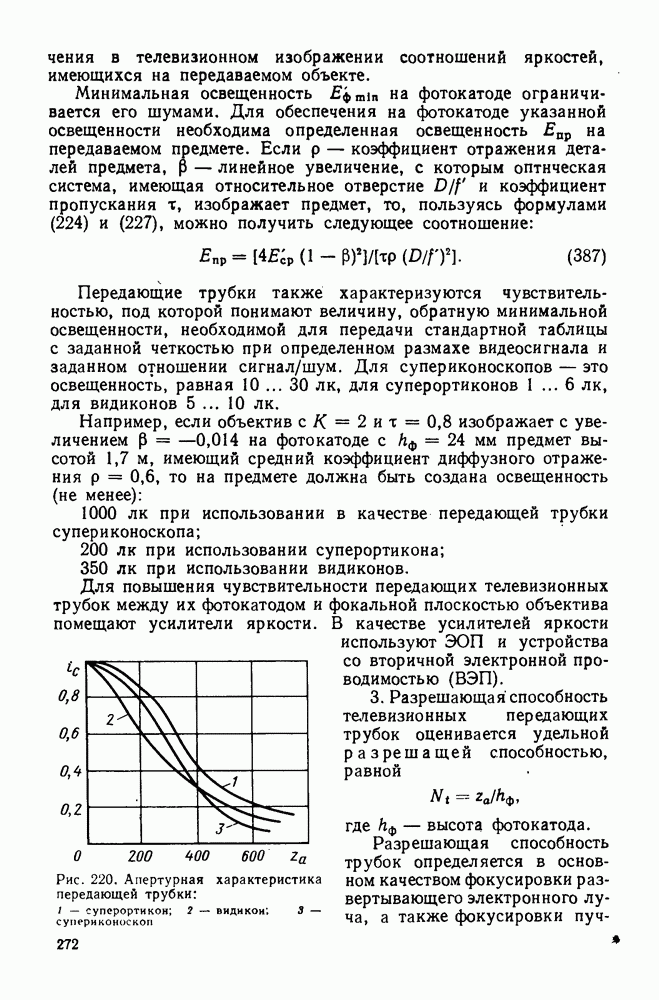
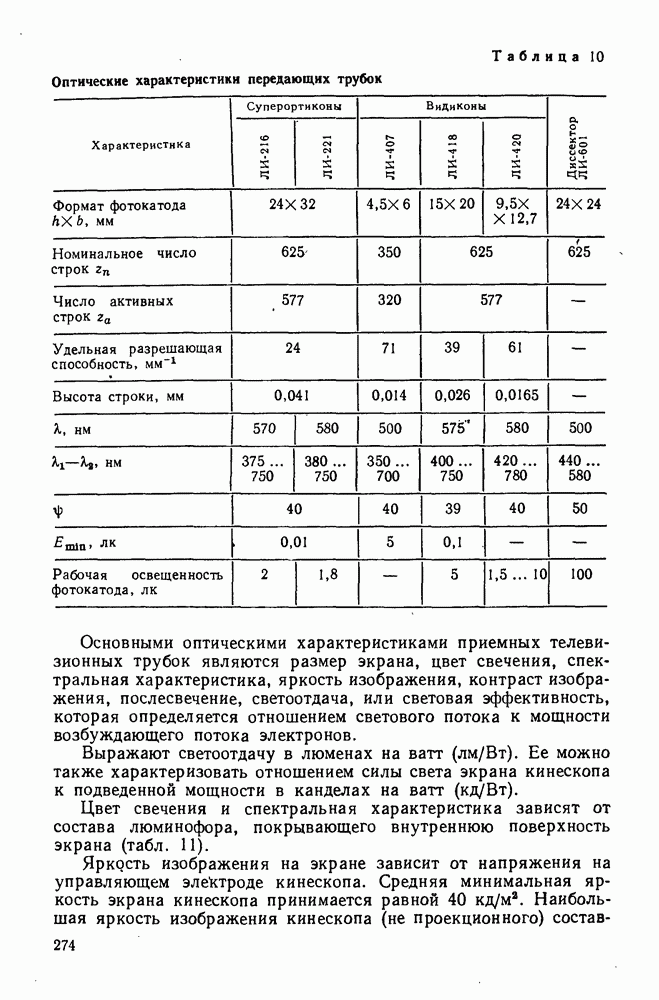
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
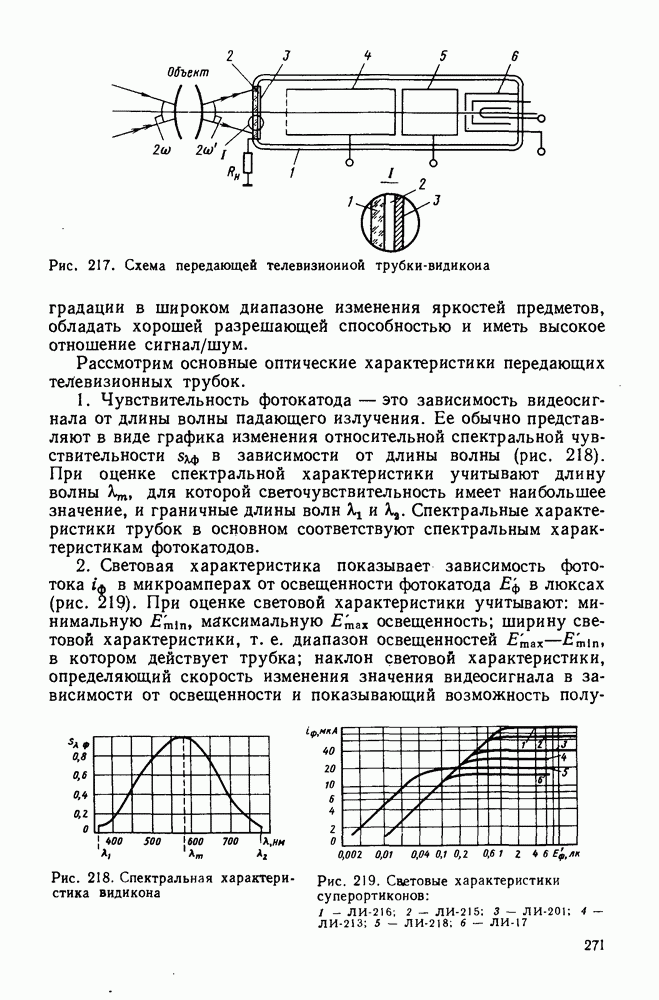
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
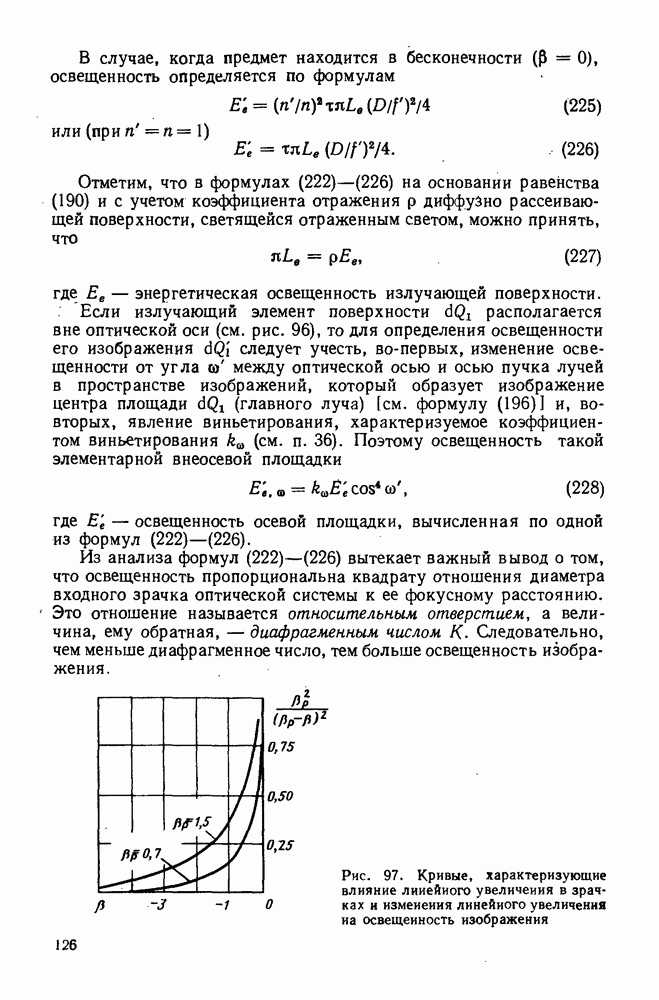
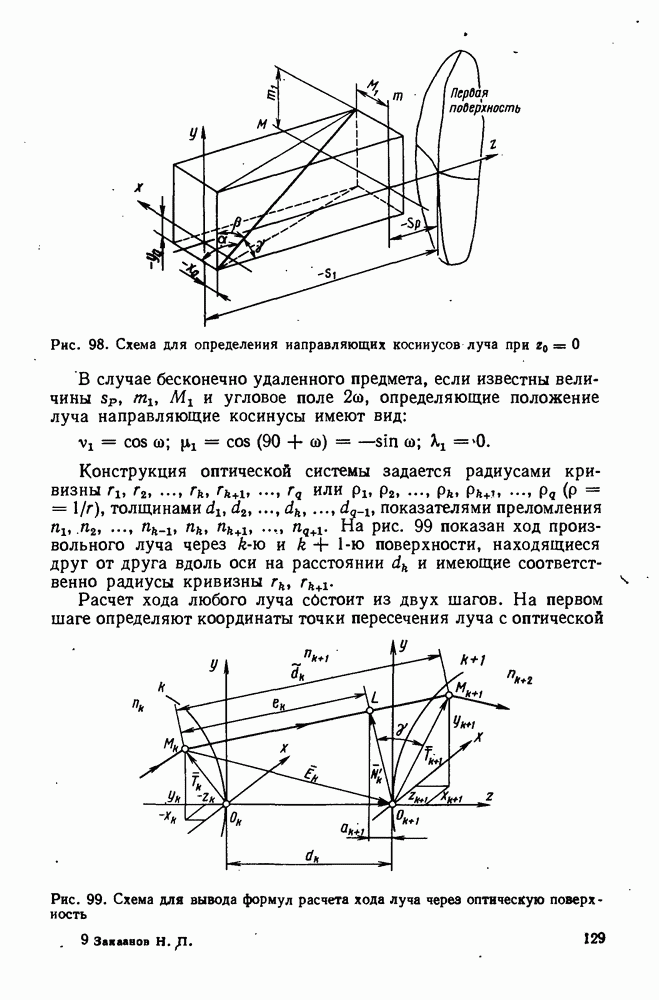
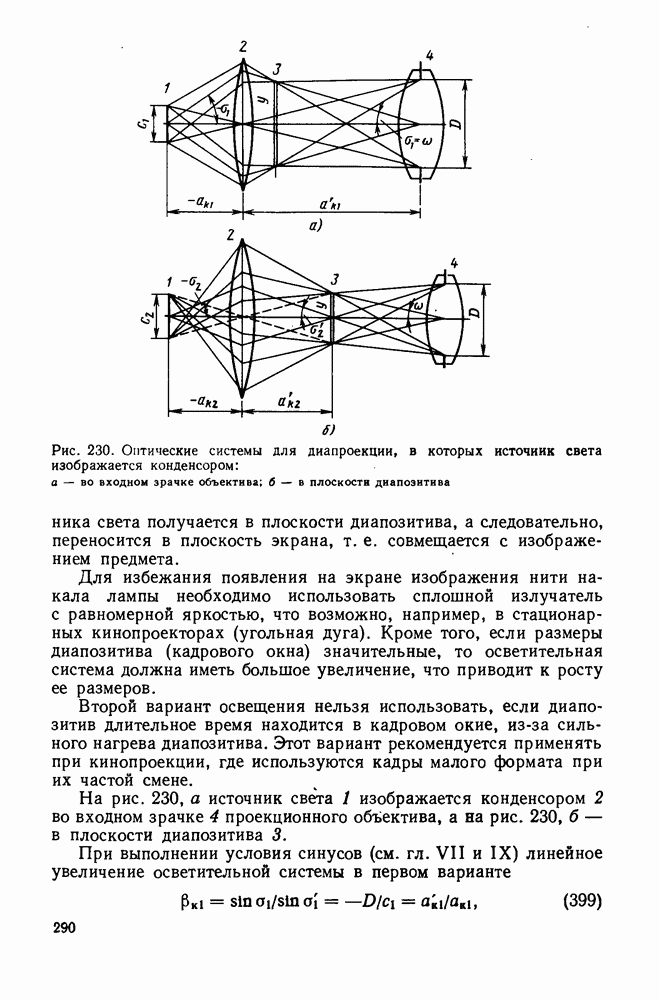
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
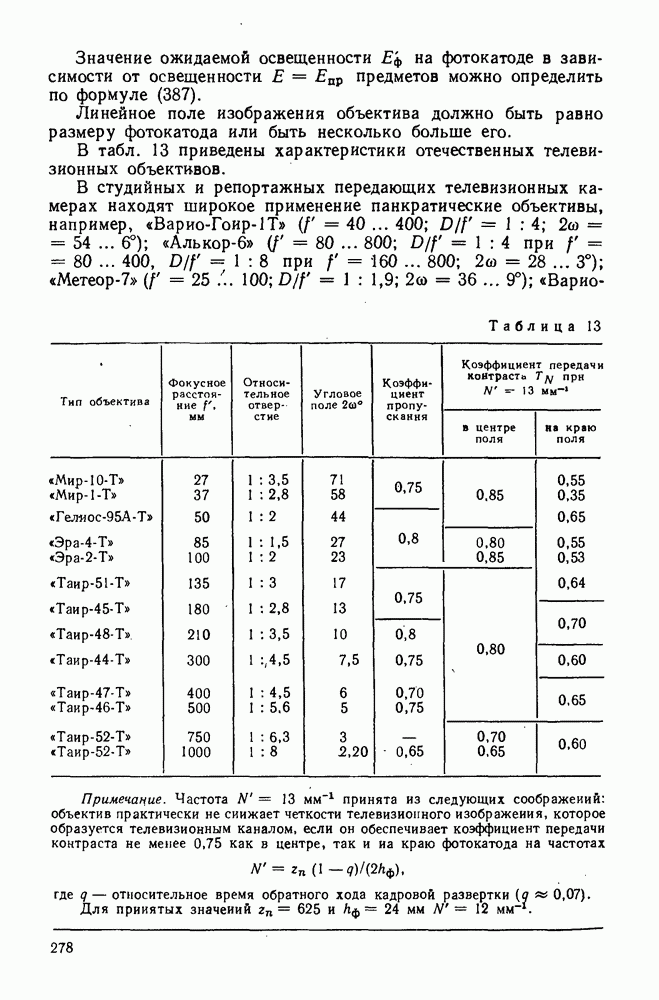
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы