| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
124. Расчет зеркально-линзовых систем
Для компенсации осевых и полевых аберраций зеркальных систем используются различные линзовые компенсаторы. Эти компенсаторы могут быть установлены как перед зеркальной частью системы, т. е. в параллельных пучках лучей, если предмет расположен в бесконечности, так и внутри системы, т. е. в сходящихся пучках лучей. Конструкция компенсатора должна быть такой, чтобы он имел минимальные хроматические аберрации. Рассмотрим некоторые схемы таких компенсаторов.
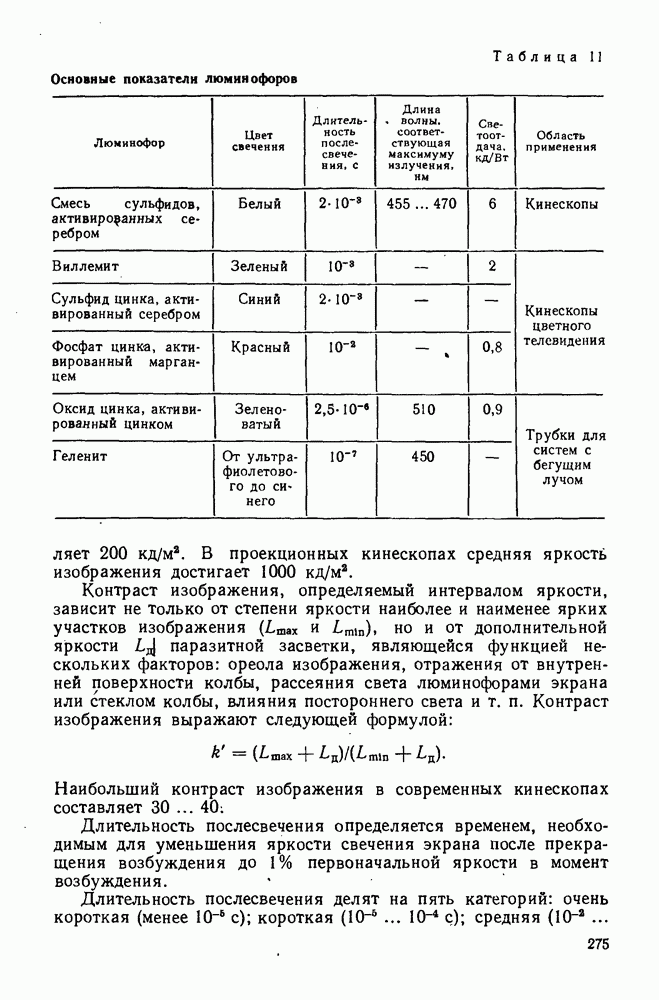
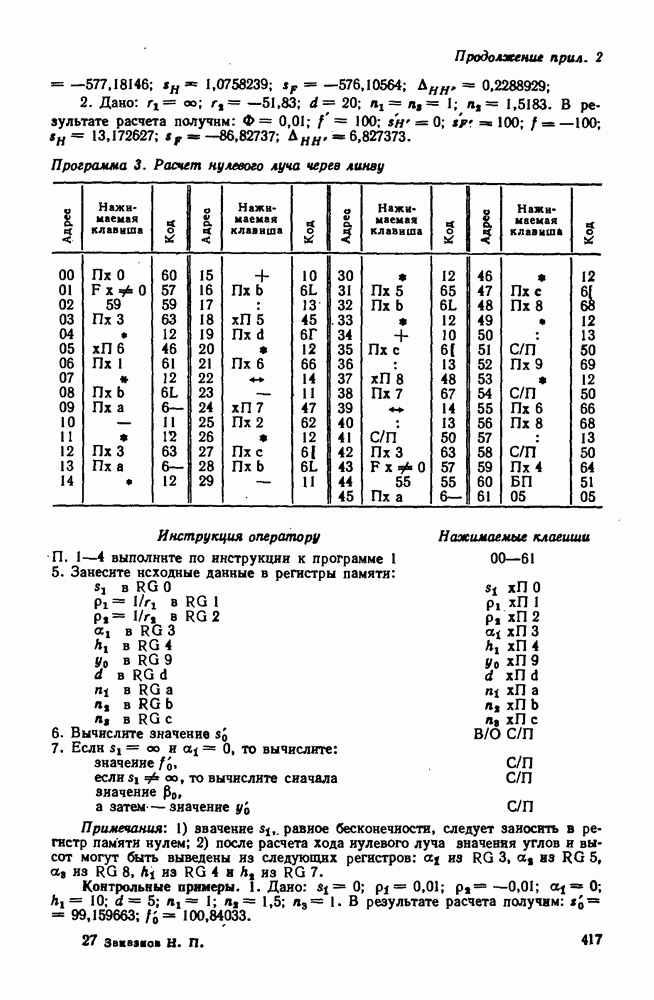
Менисковый компенсатор в параллельных пучках лучей. Одной из простейших схем зеркально-линзовой системы является схема, состоящая из линзового компенсатора и сферического зеркала (рис. 278). Для бесконечно удаленного предмета примем следующие условия нормировки: 

Рис. 278. Сферическое зеркало с менисковым компенсатором
Для устранения хроматизма положения в компенсаторе конечной толщины согласно формуле (280) необходимо выполнить условие

Из последнего соотношения с учетом принятых условий нормировки получим:

Так как по формуле высот  то последнее выражение для
то последнее выражение для  будет иметь вид:
будет иметь вид:

Решение полученного квадратного уравнения устанавливает связь между углами 

Так как  то окончательно имеем:
то окончательно имеем:

где  фокусное расстояние компенсатора.
фокусное расстояние компенсатора.
Следует отметить, что в условие (567) не входит коэффициент дисперсии  стекла линзы. Это означает, что хроматизм положения компенсатора исправлен для любой длины волны, т. е. компенсатор является полным апохроматом при любой марке оптического стекла.
стекла линзы. Это означает, что хроматизм положения компенсатора исправлен для любой длины волны, т. е. компенсатор является полным апохроматом при любой марке оптического стекла.
Для получения вещественных корней в формуле (567) должно выполняться условие  Очевидно, что при положительном компенсаторе
Очевидно, что при положительном компенсаторе  это условие приводит к практически неприемлемой конструкции линзы.
это условие приводит к практически неприемлемой конструкции линзы.
Условие (567) всегда выполняется, если компенсатор является отрицательным  отрицательная менисковая линза. Этот компенсатор был предложен в 1941 г. проф. Д. Д. Максутовым и известен под названием «Мениск Максутова».
отрицательная менисковая линза. Этот компенсатор был предложен в 1941 г. проф. Д. Д. Максутовым и известен под названием «Мениск Максутова».
В зависимости от знака перед квадратным корнем в формуле (566) возможны два варианта конструкции компенсатора: мениск, обращенный к зеркалу вогнутой стороной, или мениск, обращенный к зеркалу выпуклой стороной (рис. 278). Выбор варианта конструкции компенсатора определяется возможностью коррекции других аберраций.
Основное назначение мениска Максутова состоит в том, чтобы компенсировать сферическую аберрацию сферического зеркала
или зеркальной системы, не имеющей несферических поверхностей. Для рассматриваемой системы выражения первой суммы Зейделя будут иметь вид:

где

Согласно формулам (568) и (569) можно рекомендовать следующую методику исследований коррекционных возможностей системы. При заданном фокусном расстоянии системы  выбираем толщину мениска
выбираем толщину мениска  диаметр мениска. Задавшись величиной
диаметр мениска. Задавшись величиной  по формуле (566) находим соответствующее значение
по формуле (566) находим соответствующее значение  а по формулам (569) — поверхностные коэффициенты
а по формулам (569) — поверхностные коэффициенты  и высоту
и высоту  Тогда согласно (568) при условии, что
Тогда согласно (568) при условии, что  рассчитываем
рассчитываем  а затем — расстояние между мениском и зеркалом
а затем — расстояние между мениском и зеркалом 
Указанные вычисления выполняются для ряда сочетаний  Для оценки полевых аберраций необходимо вычислить параметры
Для оценки полевых аберраций необходимо вычислить параметры  с помощью которых по формулам (498) можно определить
с помощью которых по формулам (498) можно определить 
На основании проведенных исследований выбирают наиболее рациональный вариант системы.
Менисковый компенсатор рекомендуется применять в зеркальных системах с относительным отверстием до  так как при больших относительных отверстиях качество изображения заметно ухудшается вследствие сильного увеличения сферохроматической аберрации.
так как при больших относительных отверстиях качество изображения заметно ухудшается вследствие сильного увеличения сферохроматической аберрации.
Афокальный компенсатор в сходящихся пучках лучей. Для расширения коррекционных возможностей компенсатора необходимо усложнить его оптическую схему. Рассмотрим схему компенсатора, состоящего из двух бесконечно тонких линз, расположенных в сходящихся пучках лучей. Конструкция компенсатора должна быть такой, чтобы он не вносил хроматических аберраций. Для бесконечно тонкой системы последнее требование сводится к выполнению условия

где  и
и  оптические силы линз компенсатора.
оптические силы линз компенсатора.
Оптическая сила всего компенсатора


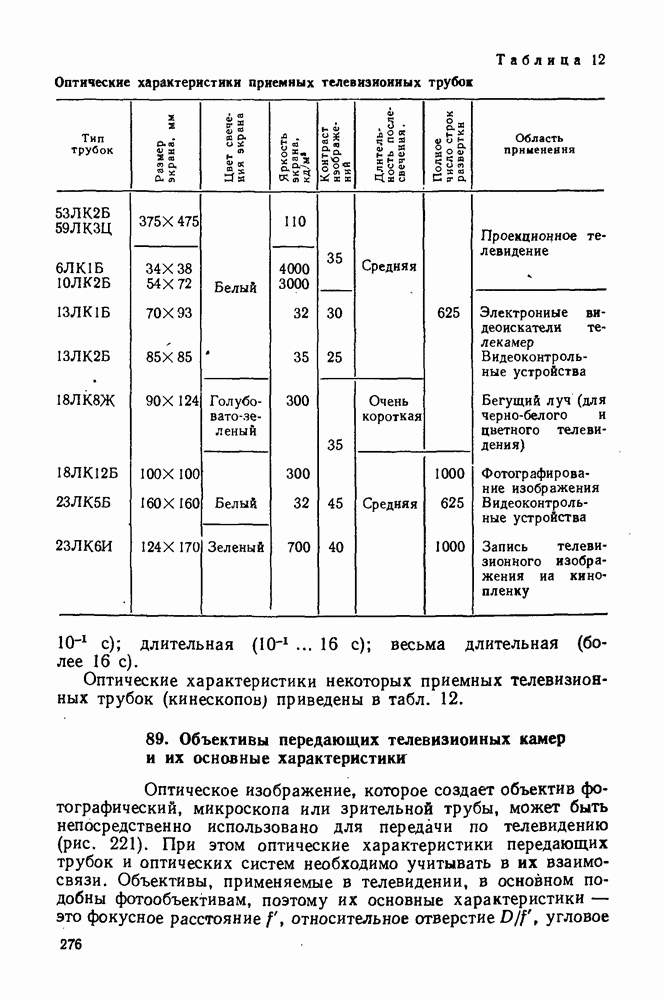
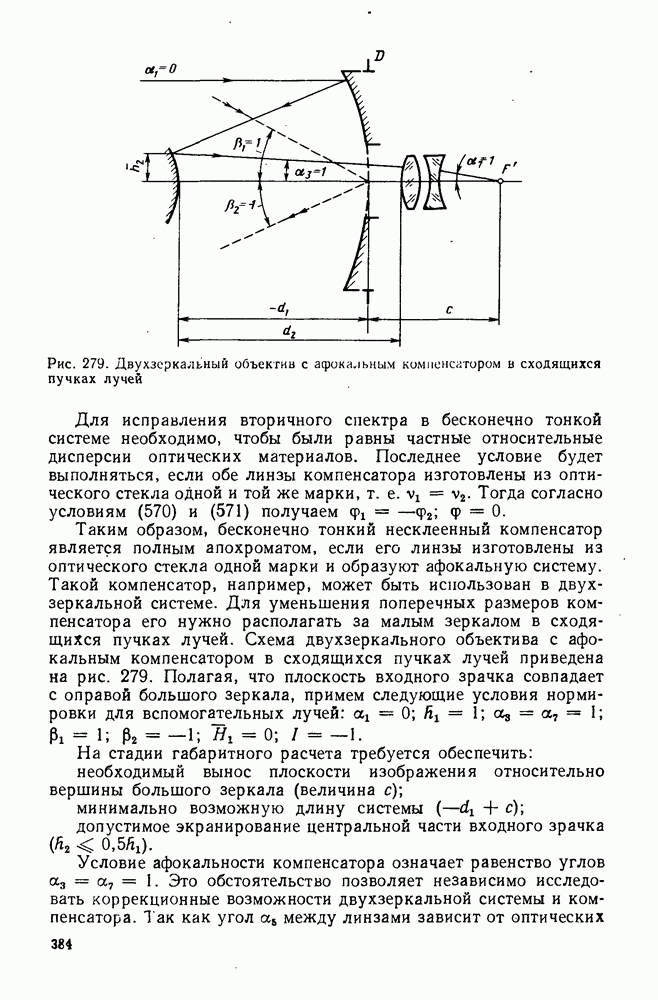
Рис. 279. Двухзеркальный объектна с афокальным компенсатором в сходящихся пучках лучей
Для исправления вторичного спектра в бесконечно тонкой системе необходимо, чтобы были равны частные относительные дисперсии оптических материалов. Последнее условие будет выполняться, если обе линзы компенсатора изготовлены из оптического стекла одной и той же марки, т. е.  Тогда согласно условиям (570) и (571) получаем
Тогда согласно условиям (570) и (571) получаем 
Таким образом, бесконечно тонкий несклеенный компенсатор является полным апохроматом, если его линзы изготовлены из оптического стекла одной марки и образуют афокальную систему. Такой компенсатор, например, может быть иснользован в двухзеркальной системе. Для уменьшения поперечных размеров компенсатора его нужно располагать за малым зеркалом в сходящихся пучках лучей. Схема двухзеркального объектива с афокальным компенсатором в сходящихся пучках лучей приведена на рис. 279. Полагая, что плоскость входного зрачка совпадает с оправой большого зеркала, примем следующие условия нормировки для вспомогательных лучей: 
На стадии габаритного расчета требуется обеспечить: необходимый вынос плоскости изображения относительно вершины большого зеркала (величина с);
минимально возможную длину системы  ; допустимое экранирование центральной части входного зрачка
; допустимое экранирование центральной части входного зрачка 
Условие афокальности компенсатора означает равенство углов  Это обстоятельство позволяет независимо исследовать коррекционные возможности двухзеркальной системы и компенсатора. Так как угол
Это обстоятельство позволяет независимо исследовать коррекционные возможности двухзеркальной системы и компенсатора. Так как угол  между линзами зависит от оптических
между линзами зависит от оптических
сил линз компенсатора, то компенсатор имеет два свободных параметра  рациональный выбор которых дает возможность исправить две аберрации: сферическую и кому. При определении конструктивных параметров компенсатора следует иметь в виду, что его коррекционные возможности зависят от положения компенсатора относительно вершины малого зеркала. Если компенсатор располагать ближе к малому зеркалу, то он сильнее будет влиять на сферическую аберрацию системы, если компенсатор приближать к задней фокальной плоскости, то возрастает его влияние на полевые аберрации.
рациональный выбор которых дает возможность исправить две аберрации: сферическую и кому. При определении конструктивных параметров компенсатора следует иметь в виду, что его коррекционные возможности зависят от положения компенсатора относительно вершины малого зеркала. Если компенсатор располагать ближе к малому зеркалу, то он сильнее будет влиять на сферическую аберрацию системы, если компенсатор приближать к задней фокальной плоскости, то возрастает его влияние на полевые аберрации.
Рассмотренный компенсатор был предложен в 1934 г. проф. В. Н. Чуриловским. Применение компенсатора целесообразно при относительных отверстиях до 
Афокальный компенсатор в параллельных пучках лучей. В светосильных зеркально-линзовых объективах с относительным отверстием до  для получения высокого качества изображения необходимо применять афокальный компенсатор, устанавливаемый в параллельных пучках лучей, т. е. перед большим зеркалом. Этот компенсатор был предложен в 1942 г. Д. С. Волосовым, Д. Ю. Гальперном и Ш. Я· Печатниковой. Диаметр такого компенсатора соизмерим с диаметром большого зеркала.
для получения высокого качества изображения необходимо применять афокальный компенсатор, устанавливаемый в параллельных пучках лучей, т. е. перед большим зеркалом. Этот компенсатор был предложен в 1942 г. Д. С. Волосовым, Д. Ю. Гальперном и Ш. Я· Печатниковой. Диаметр такого компенсатора соизмерим с диаметром большого зеркала.
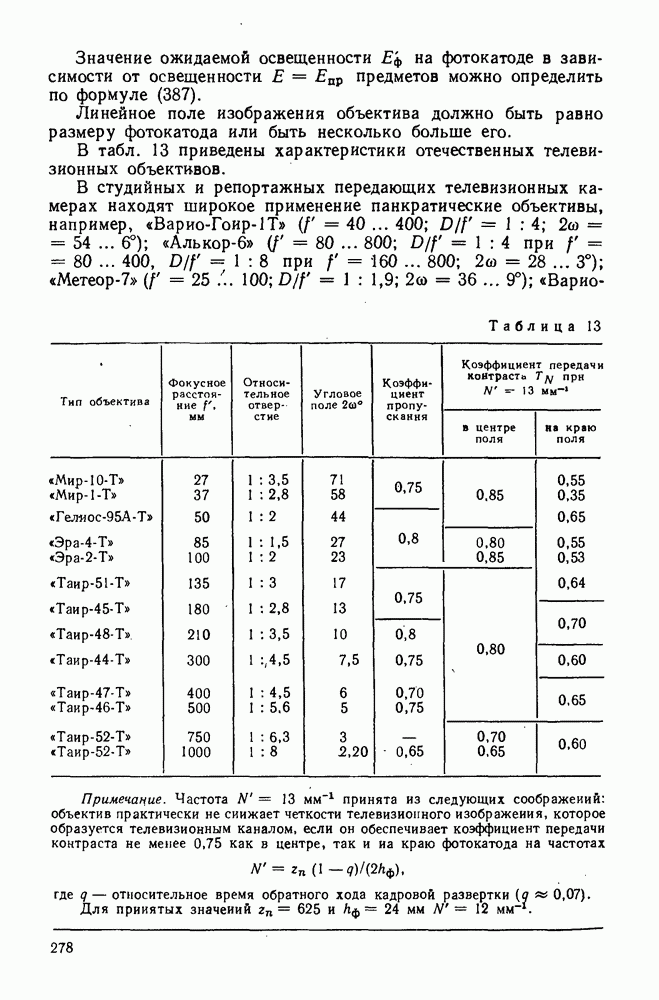
Схема зеркально-линзового объектива с афокальным компенсатором в параллельных пучках лучей приведена на рис. 280. Полагая, что плоскость входного зрачка совпадает с бесконечно тонким компенсатором, будем иметь следующие условия нормировки для вспомогательных лучей:  Обычно конструктивные параметры зеркальной части объектива определяют из условия обеспечения требуемых длины всей системы, выноса плоскости изображения, экранирования центральной части зрачка и др. Зная аберрации зеркальной части системы, необходимо определить конструктивные параметры компенсатора, при которых обеспечивается наилучшее состояние коррекции. Так как компенсатор является афокальным
Обычно конструктивные параметры зеркальной части объектива определяют из условия обеспечения требуемых длины всей системы, выноса плоскости изображения, экранирования центральной части зрачка и др. Зная аберрации зеркальной части системы, необходимо определить конструктивные параметры компенсатора, при которых обеспечивается наилучшее состояние коррекции. Так как компенсатор является афокальным  а параметр а определяется оптической силой линз, то имеем два свободных параметра:
а параметр а определяется оптической силой линз, то имеем два свободных параметра:  . С конструктивной точки
. С конструктивной точки

Рис. 280. Двухзеркальный объектив с афокальным компенсатором в параллельных пучках лучей
зрения иногда может оказаться рациональным в качестве малого зеркала использовать последнюю поверхность комненсатора. Так как радиус малого зеркала находят при расчете зеркальной части системы, то в этом случае параметр  определяется выбором радиуса
определяется выбором радиуса  малого зеркала:
малого зеркала:

где  показатель преломления стекла линз компенсатора.
показатель преломления стекла линз компенсатора.
В заключение отметим, что в зеркально-линзовых объективах используют как афокальные, так и неафокальные компенсаторы, устанавливаемые в параллельных и сходящихся пучках лучей. Эффективным средством расширения коррекционных возможностей таких систем является применение в них несферических поверхностей. Более подробные сведения об аберрационном расчете зеркальных и зеркально-линзовых систем можно найти в работе Г. Г. Слюсарева [33].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
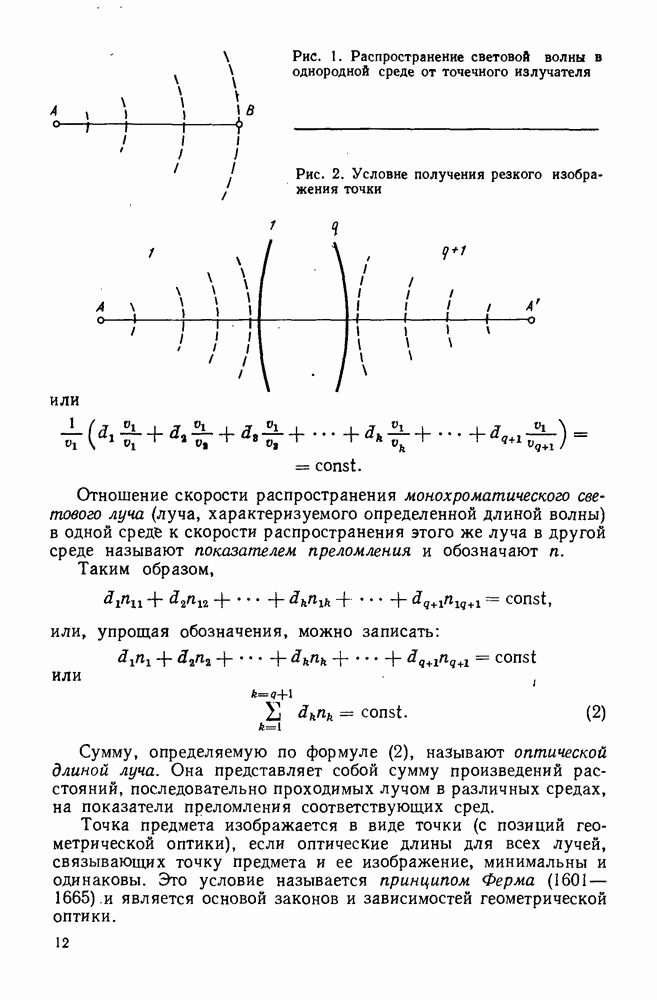
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
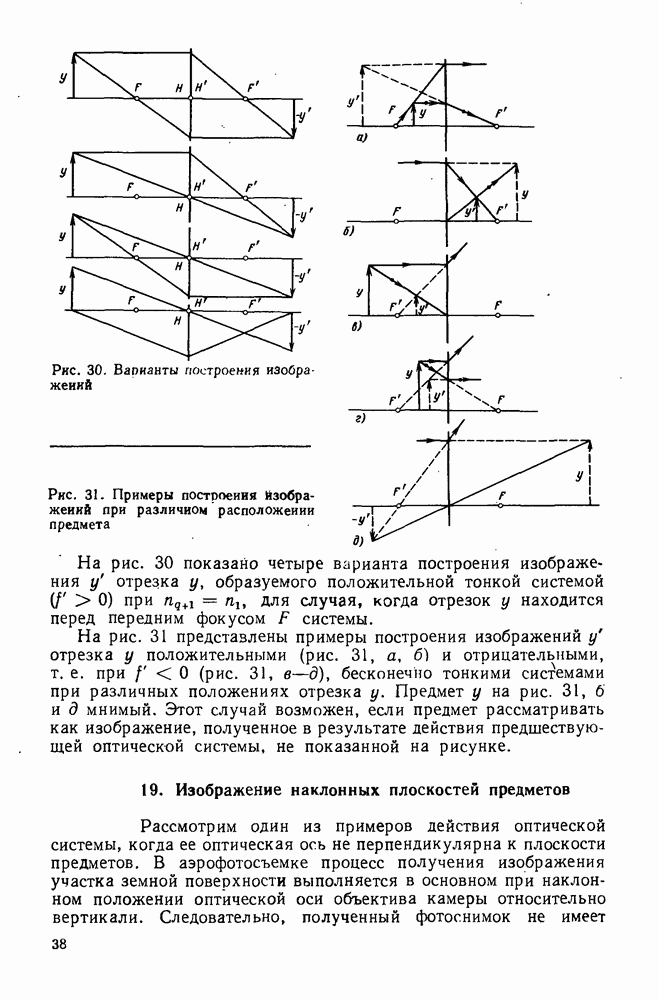
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
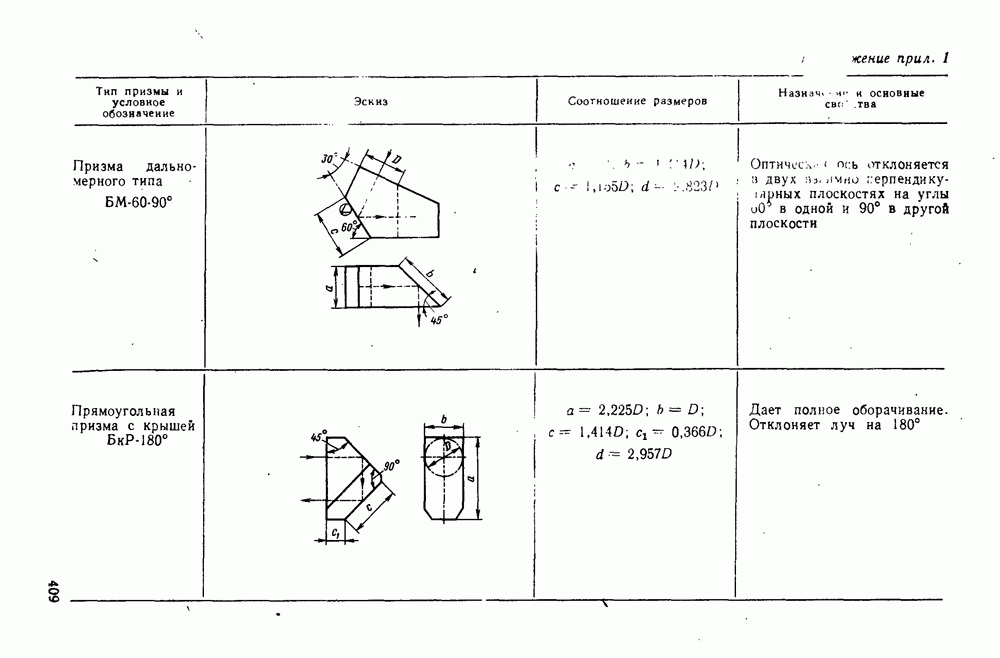
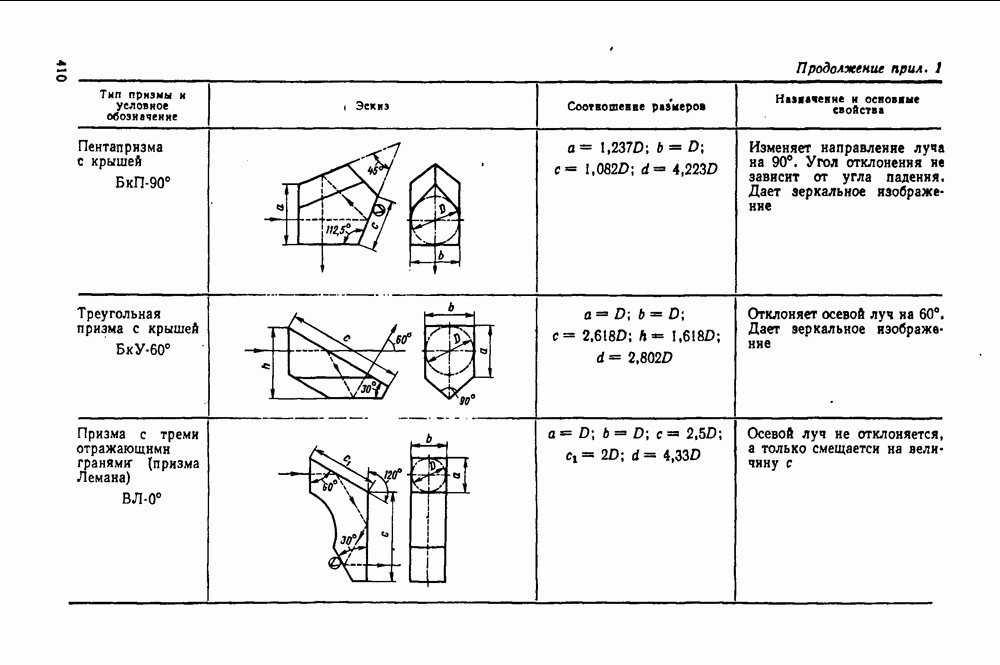
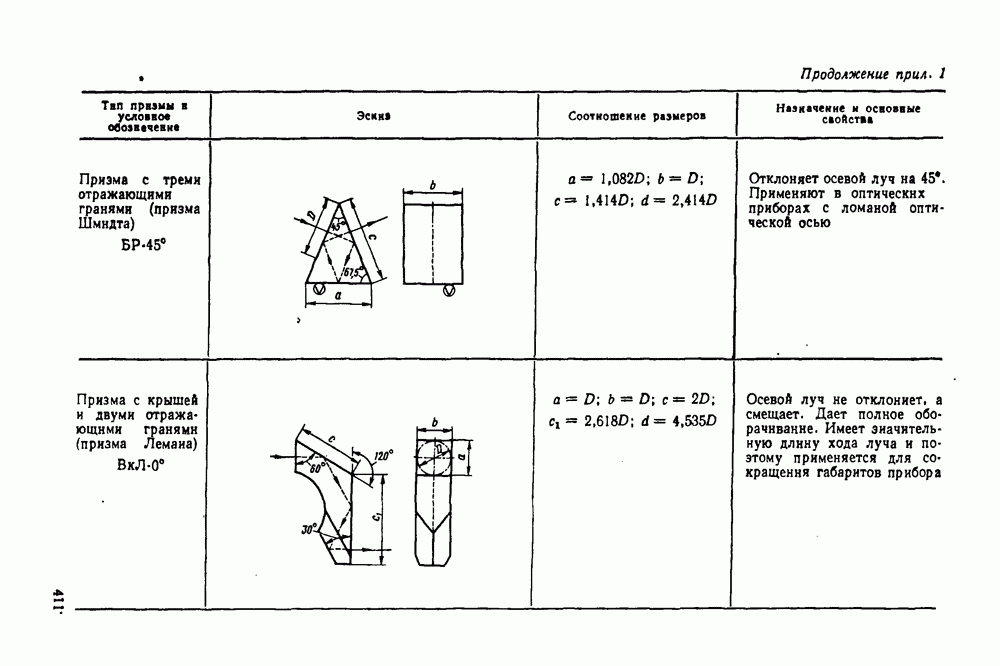
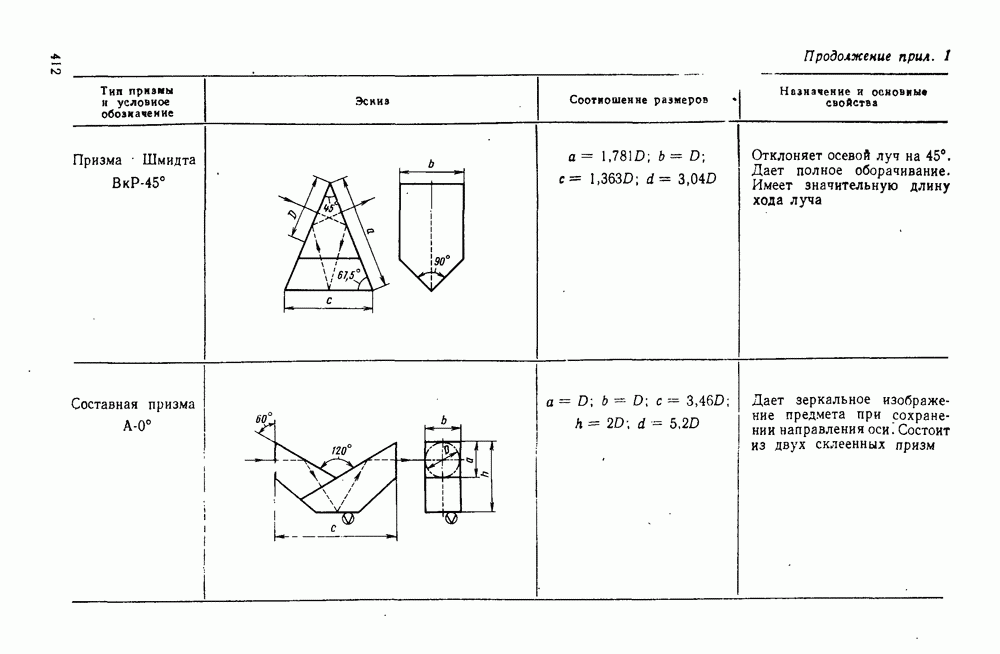
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы