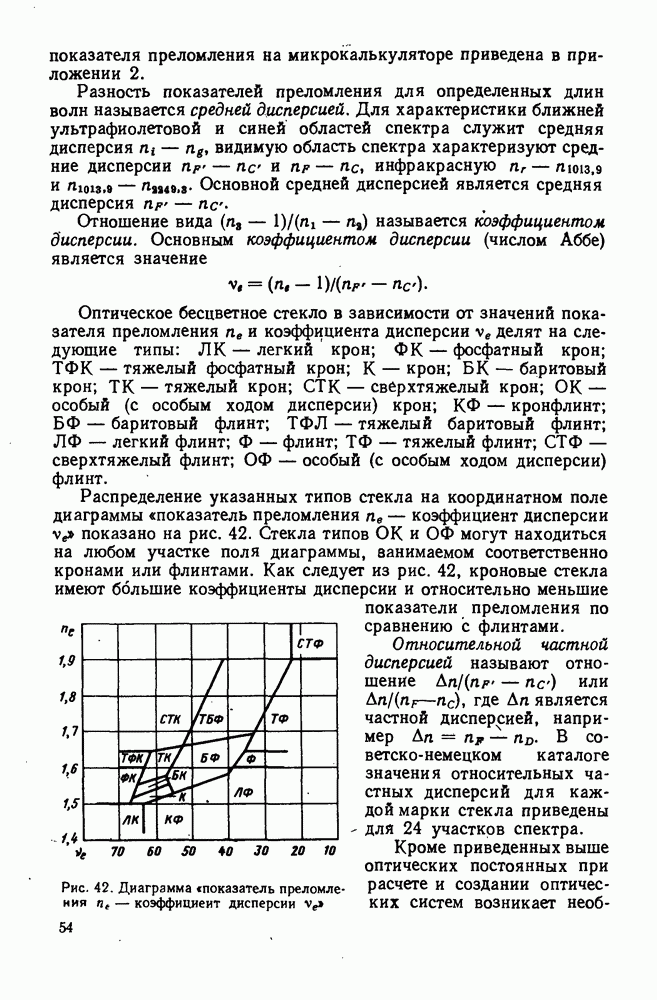
26. Линзы

Линзой называют оптическую деталь, ограниченную двумя преломляющими обычно осесимметричными и центрированными поверхностями. Наиболее часто встречающиеся линзы ограничены двумя сферическими поверхностями. Если одна из поверхностей — плоскость, то она должна быть перпендикулярна к оптической оси.

Линзы с осесимметричными и центрированными поверхностями обеспечивают в параксиальной области сохранение гомоцентричности пучка лучей в пространстве изображений.

При отсутствии круговой симметрии хотя бы одной из поверхностей (например, одна из поверхностей линзы цилиндрическая, а вторая плоская) гомоцентричность (в параксиальной области) будет обеспечиваться только в одной из секущих плоскостей, включающих оптическую ось.

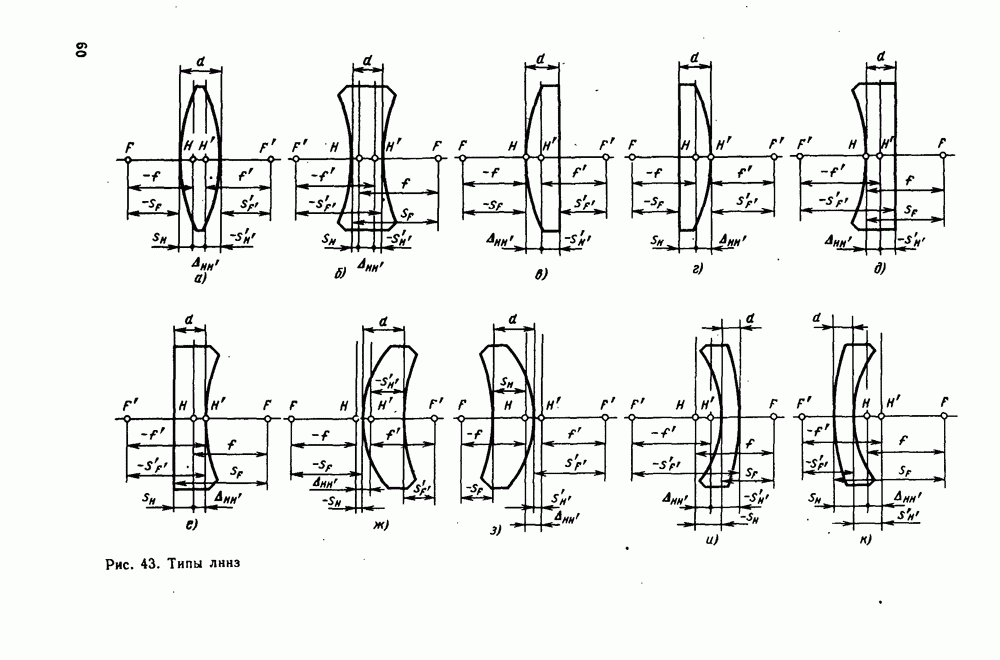
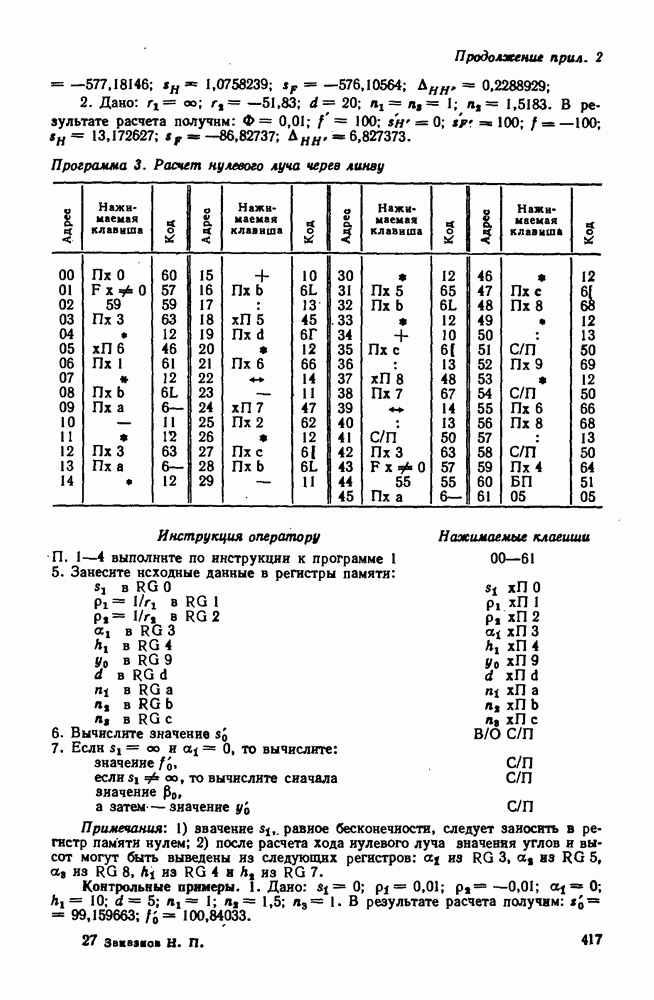
Рассмотрим преломляющее действие отдельной лиизы со сферическими поверхностями (рис. 43, а), пользуясь для этой цели нулевыми лучами.

Конструктивными параметрами линзы со сферическими поверхностями (одна из них может быть плоской) будут радиусы сфер толщина по оптической оси и показатель преломления материала линзы показатели преломления сред соответственно перед и после линзы). Воспользуемся ими для определения фокусных расстояний линзы, ее фокальных отрезков положения главных плоскостей относительно вершин сферических поверхностей (отрезки и расстояния между главными плоскостями (главными точками).

Заметим, что последующее изложение в равной мере может быть распространено и на несферические осесимметричные линзы, так как они в параксиальной области действуют как сферические с радиусами, равными радиусам кривизны при вершине несферических поверхностей.

Согласно формулам (85), (82) и (83) имеем:

Последовательная подстановка этих выражений дает следующую формулу для определения заднего фокусного расстояния линзы:

Переднее фокусное расстояние определяют по формуле

Сравнивая формулы (88) и (89), получим для линзы справедливо такое же соотношение между задним и передним фокусными расстояниями, как и для идеальной оптической системы [формула (34)].

Оптическая сила линзы является одной из ее основных характеристик. Она является также мерой оптического действия системы, состоящей из комбинации линз.

Чем больше (по абсолютному значению) оптическая сила, тем ближе к линзе располагается изображение и тем меньше размер этого изображения [см. формулу (41)].

(кликните для просмотра скана)

Если линза находится в воздухе то

Единицей оптической силы является диоптрия (дптр), которая равна оптической силе линзы, находящейся в воздухе, с фокусным расстоянием, равным

Поэтому оптическая сила линзы в диоптриях где в миллиметрах.

Оценка оптической силы линз в диоптриях принята в офтальмологии.

Заднее и переднее фокусные расстояния каждой из преломляющих поверхностей линзы в соответствии с формулой (76) равны

После подстановки правых частей этих равенств в формулы (88) и (89) получим, что оптическая сила линзы

и окончательно

где оптическая сила первой преломляющей поверхности линзы; оптическая сила второй преломляющей поверхности линзы.

Формулу (90) полезно сравнить с формулой (56), определяющей оптическую силу двухкомпонентной оптической системы, находящейся в воздухе, между компонентами которой — среда с показателем преломления Из сравнения следует, что линзу можно представить как двухкомпонентную систему, в которой — оптическая сила 1-й преломляющей поверхности, -й преломляющей поверхности линзы.

Задний фокальный отрезок линзы получаем по формуле (86):

При обратном ходе луча находим передний фокальный отрезок

На рис. 43, а показана линза толщиной с отмеченными значениями фокусных расстояний и фокальных отрезков Найдем отрезки определяющие положение главных плоскостей относительно вершин преломляющих поверхностей. Из рисунка следует, что Тогда согласно формулам (91) и (92)

Расстояние между главными плоскостями определяется равенством

Пример. Рассчитать двояковыпуклую линзу, с одной стороны которой находится воздух с другой — вода Лннза имеет следующие конструктивные параметры:

При вычислении по формулам (88) и (89) получаем Фокальные отрезки [формулы (91) и (92)]: Расстояние между главными плоскостями [формула (95)]

Для расчета линзы, находящейся в воздухе на основании формул (88)-(95) получим:

Все линзы можно разделить на три группы:

линзы, поверхности которых имеют разные по знаку радиусы кривизны: двояковыпуклые и двояковогнутые (рис. 43, а и б);

линзы, одна из поверхностей которых плоская: выпуклоплоские и плосковыпуклые, вогнуто-плоские и плосковогиутые (рис. 43, в-е);

линзы, имеющие одинаковые по знаку радиусы кривизны: выпукло-вогнутые и вогнуто-выпуклые толщиной по оси, большей толщины по краю (рис. 43, ж и з), вогнуто-выпуклые и выпукло-вогнутые толщиной по оси, меиьшей толщины по краю (рис. 43, и, к). Такие линзы называются менисками.

Линзы обычно являются осесимметричными деталями. Однако в некоторых случаях используются и цилиндрические линзы (см. гл. XX).

Рассмотрим особенности находящихся в воздухе лииз различных типов со сферическими и плоскими поверхностями.

Двояковогнутая линза (рис. 43, б) имеет Заднее фокусное расстояние отрицательно при любой толщине линзы, что определяет ее рассеивающее действие. Эта лииза является отрицательной.

Выпукло-плоская линза (рис. 43, в) имеет Значения фокусных расстояний фокальных отрезков отрезков а также расстояние между главными плоскостями определяются по формулам, получаемым из (96)- (104):

Из формул (105) следует, что, во-первых, фокусные расстояния не зависят от толщины линзы, во-вторых, передняя главная плоскость касается выпуклой преломляющей поверхности.

Плосковыпуклая линза (рис. 43, г) имеет Расчетные формулы аналогичны предыдущим:

Линзы с одной преломляющей поверхностью плоской и другой — выпуклой являются собирательными (положительными).

Вогнуто-плоская линза (см. рис. 43, д) имеет Формулы для этой линзы следующие:

Из сопоставления полученных формул с формулами (105), относящимися к выпукло-плоской линзе, вытекает их полное соответствие друг с другом.

Плосковогнутая линза (рис. 43, е) с описывается следующими формулами:

Эти формулы полностью совпадают с формулами (106), относящимися к плосковыпуклой линзе.

Выпукло-вогнутый мениск (рис. 43, ж) с при Это линза является собирательной (положительной), так как Отрезки отрицательны, следовательно, передняя главная плоскость находится перед линзой.

Вогнуто-выпуклый мениск (рис. 43, з) при также относится к положительным линзам. Задняя главная плоскость всегда располагается за линзой.

Вогнуто-выпуклый мениск (рис. 43, и) с при относится к отрицательным линзам Передняя главная плоскость этого мениска находится перед линзой.

Выпукло-вогнутый мениск (рис. 43, к) с при также относится к отрицательным линзам Задняя главная плоскость этого мениска находится за линзой.

Рис. 44. Телескопические линзы: а — двояковыпуклая; б - выпукло-вогнутая

В случаях, когда между конструктивными параметрами линзы, входящими в формулу (96), имеет место соотношение вогнуто-выпуклые и выпукло-вогнутые линзы будут положительными, т. е. Иными словами, увеличивая толщину отрицательный мениск можно превратить в положительный.

Телескопическая линза — линза, преобразующая параллельные лучи, падающие на нее, также в параллельные при их выходе из линзы. Конструктивные параметры этой линзы определяются из соотношения (96) при В этом случае

Из формулы (76) следует, что заднее фокусное расстояние первой сферической поверхности линзы

а переднее фокусное расстояние второй поверхности линзы

Используя формулы (107)-(109), получаем, что

Два варианта телескопических линз, соответствующие формуле (110), — двояковыпуклая и выпукло-вогнутая линзы показаны на рис. 44.

Линзы с концентрическими сферическими поверхностями (рис. 45) имеют совмещенные главные плоскости, т. е. расстояние

Рис. 45. Лнизы с концентрическими сферическими поверхностями

между этими плоскостями равно нулю, что следует из формулы (104). При этом

В равенстве (111) заменим по формуле (96). Тогда после преобразований получим что и определяет конструктивные параметры линзы.

Фокусные расстояния концентрической линзы определяют по следующей формуле:

Линзы со сферическими поверхностями равных радиусов имеют фокусное расстояние, определяемое по формуле (96) с учетом равенства радиусов

Если при этом толщина линзы то получим линзу-шар, для которой

Линзы с обращенными главными плоскостями показаны на рис. 46. В этих линзах расстояние между главными плоскостями отрицательно, т. е. по ходу луча первой будет задняя главная плоскость, а второй — передняя. Из формулы (104) следует, что рассматриваемый случай имеет место, когда

Подставим в это неравенство значение найденное по формуле (96), и после преобразований получим, что для линзы с обращенными главными плоскостями должно выполняться следующее условие:

При этом расстояние вычисленное по формуле (104), будет отрицательным.

Линзы с несферическими преломляющими поверхностями [11, 27], используемые в качестве оптических деталей приборов, обеспечивают повышение качества оптического изображения, увеличение поля оптической системы и ее относительного отверстия, упрощение оптической системы (уменьшение числа компонентов, а следовательно, габаритных размеров и массы).

Рис. 46. Лннзы с обращенными главными плоскостями

Рис. 47. Сфероэллиптическая линза

Преломляющие поверхности в виде поверхностей второго и высшего порядков используются в линзах осветительных систем, в объективах и окулярах. Например, в осветительной системе микроскопа применяется двояковыпуклая линза, одна из поверхностей которой является параболоидом вращения, в гидрообъективах М. М. Русинова и П. Д. Иванова применяется плосковогнутая линза с параболоидной или эллипсоидной поверхностью. Примером линзы с несферической поверхностью также является сфероэллиптическая линза, обеспечивающая гомоцентрический пучок лучей в пространстве изображений. Эта линза выпуклой эллипсоидной поверхностью обращена к предмету. Вогнутая сферическая поверхность линзы имеет центр в заднем ее фокусе (рис. 47).

Уравнение эллипса, являющегося меридиональным сечением эллипсоида, в этом случае имеет следующий

где — координаты меридионального сечения эллипсоида (начало координат в вершине эллипса); задний фокальный отрезок, равный т. е. радиусу сферической поверхности.

Конструктивные параметры линзы, определяющие их оптическое действие, находят при расчете оптических систем. К этим параметрам относятся оптические постоянные материала линз (обычно оптического стекла), радиусы сферических поверхностей или уравнения для несферических поверхностей, толщина вдоль оптической оси и световые диаметры.

К линзам предъявляются специальные требования в отношении шероховатости поверхности, качества материала (например, категории стекла), просветляющих покрытий и допусков на конструктивные параметры согласно ГОСТам и нормалям оптической промышленности.

Расчетные радиусы сферических поверхностей должны быть, как правило, согласованы с ГОСТ 1807-75.

Для облегчения изготовления и обеспечения надежного крепления между диаметром линзы толщиной по оси и толщиной по краю должны выдерживаться следующие соотношения:

1) для положительных линз при этом толщина по краю

2) для отрицательных линз при этом толщина по оси

Диаметр линзы при вычисленном световом диаметре зависит от способа крепления линзы.

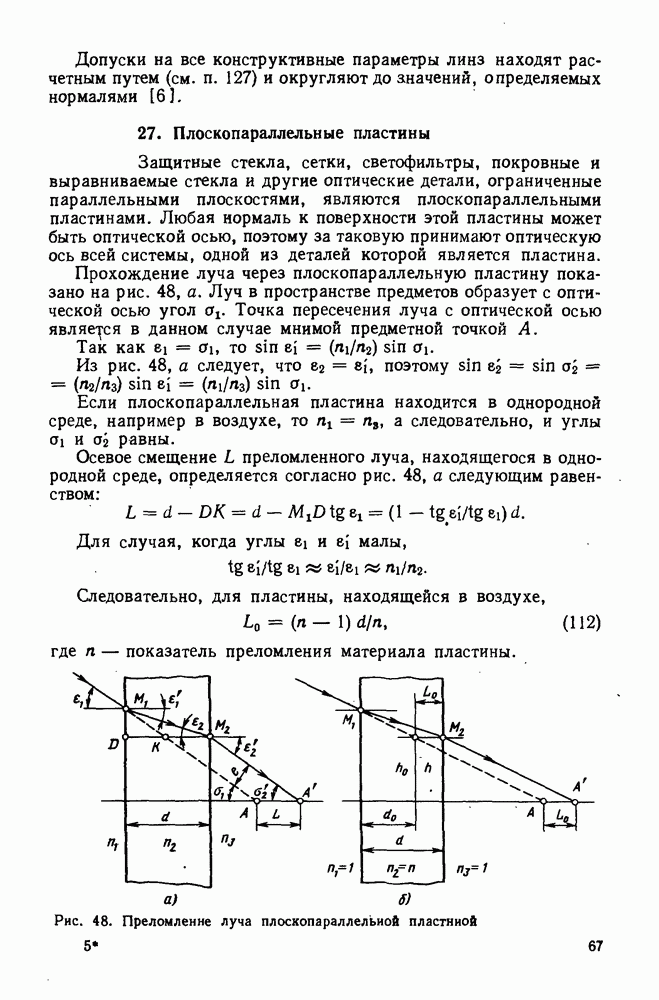
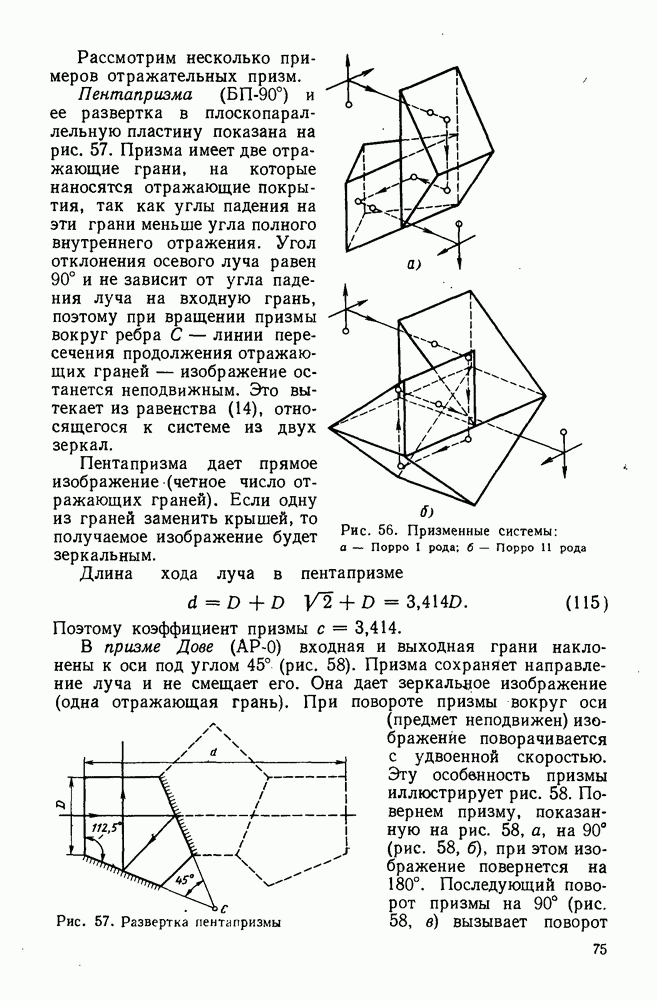
Допуски на все конструктивные параметры линз находят расчетным путем (см. п. 127) и округляют до значений, определяемых нормалями [6].