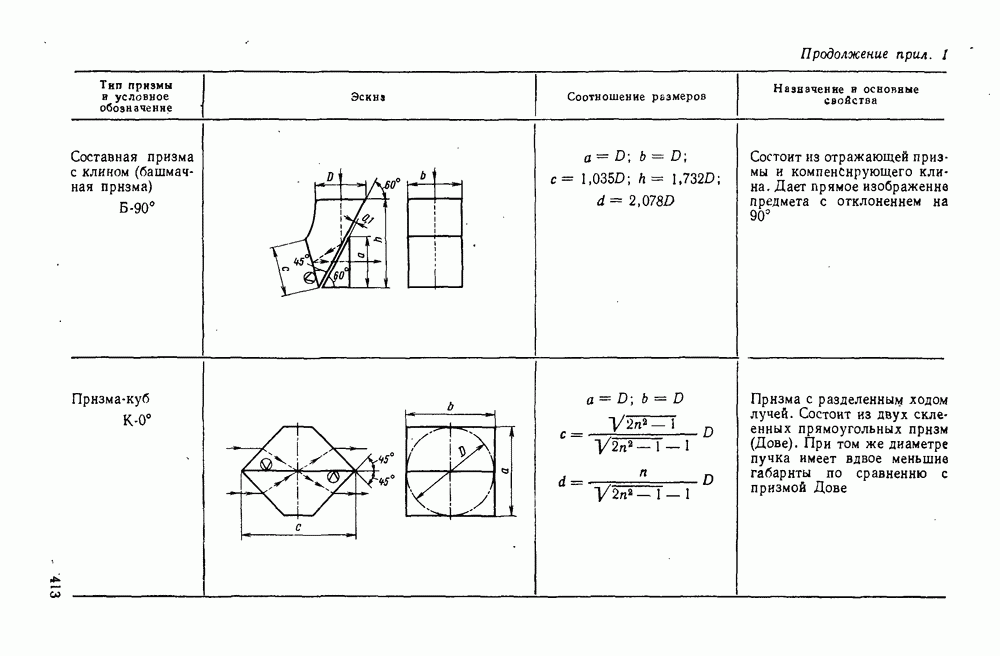
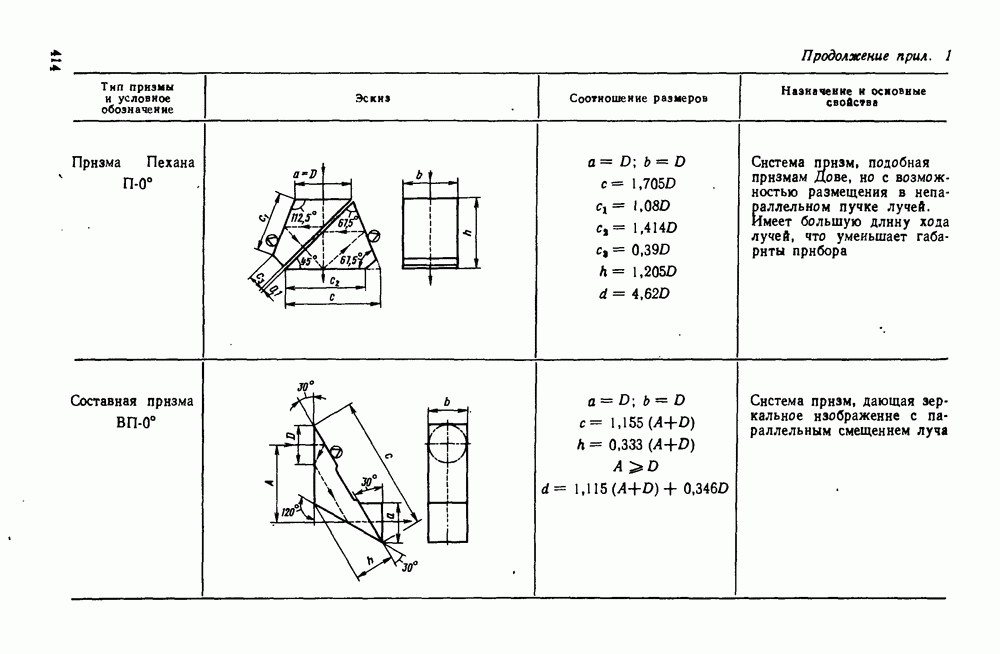
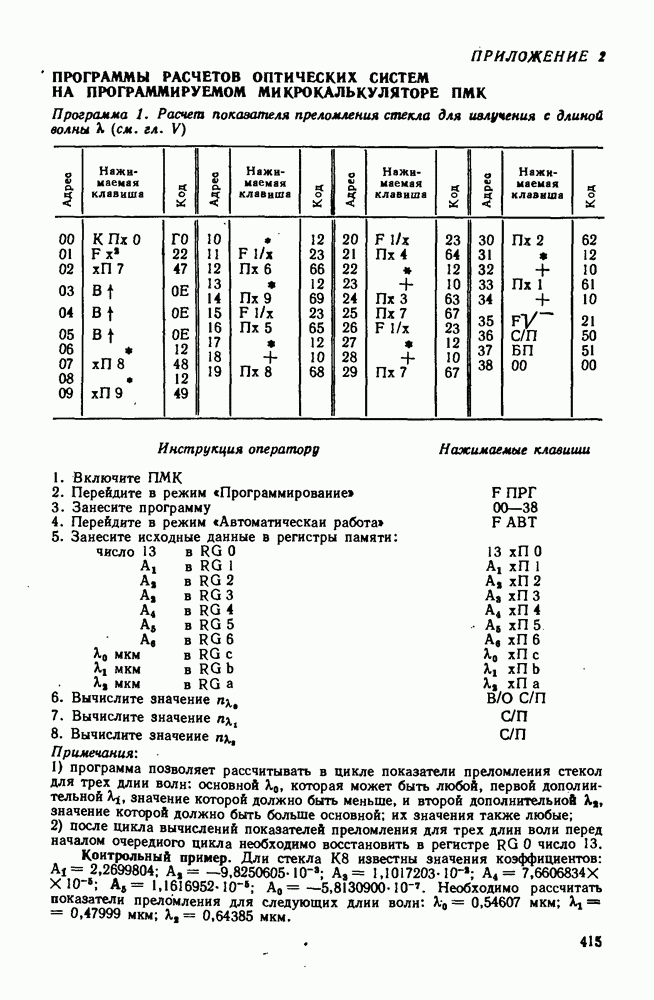
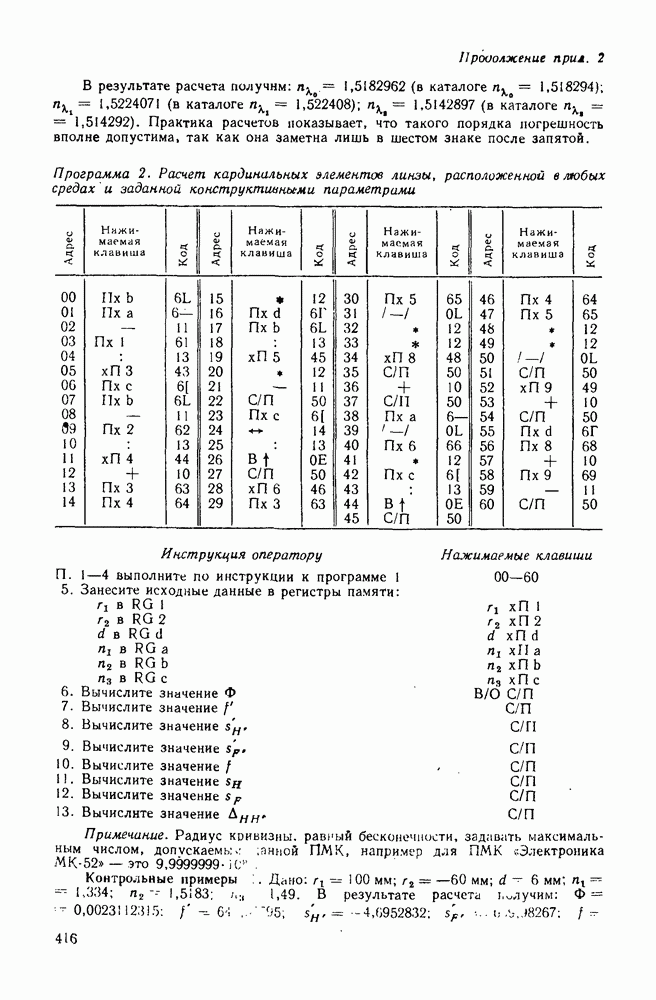
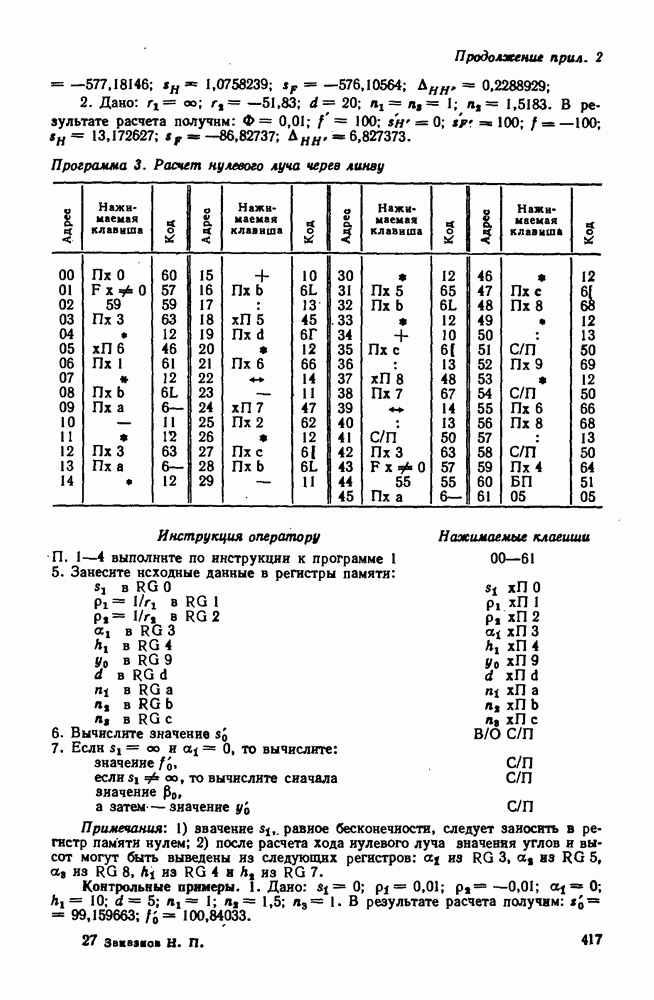
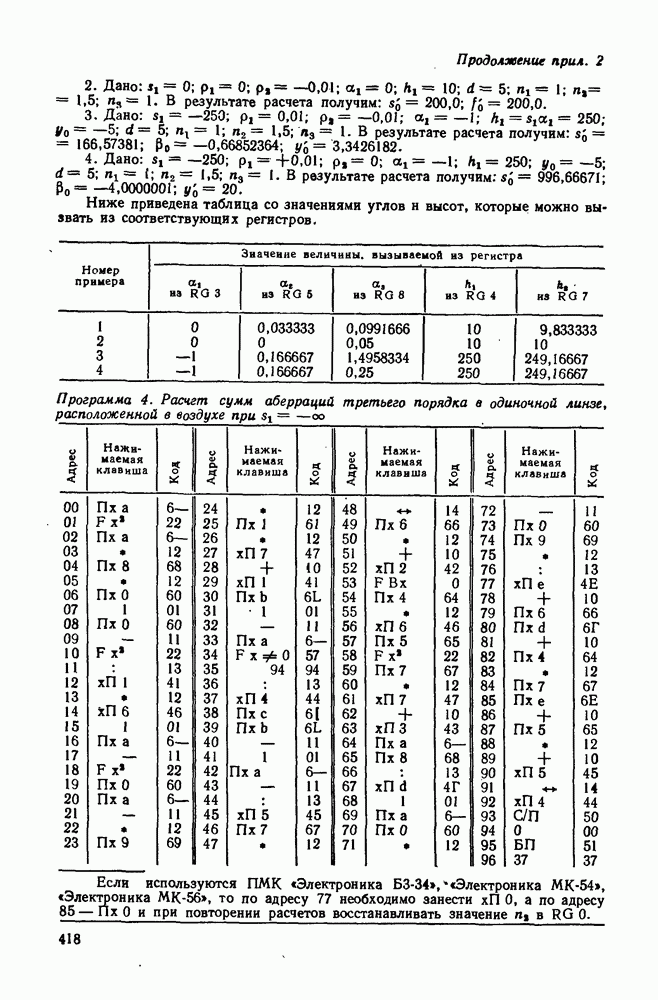
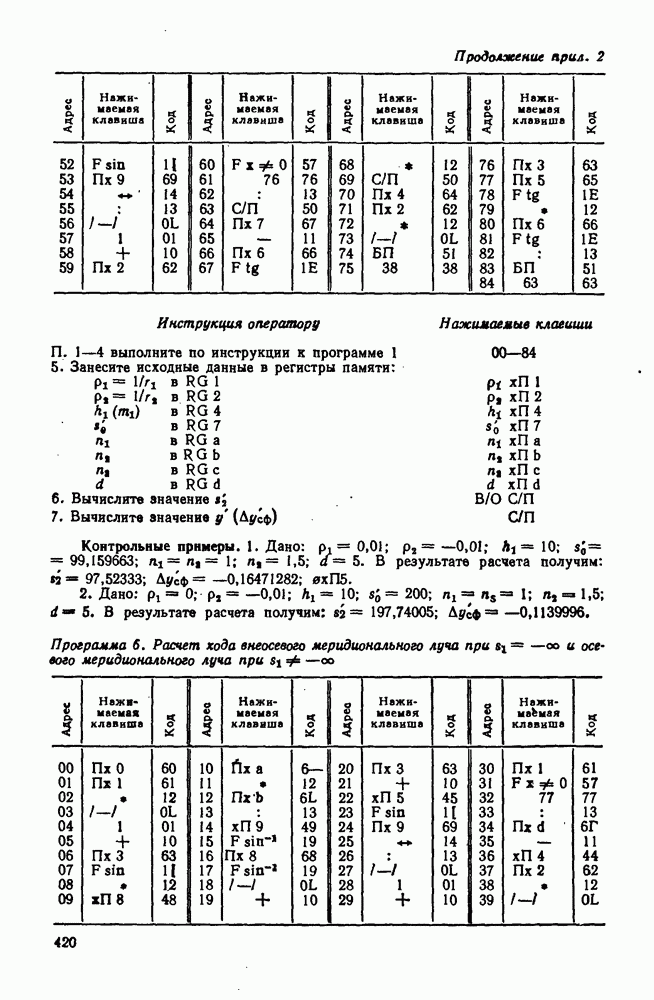
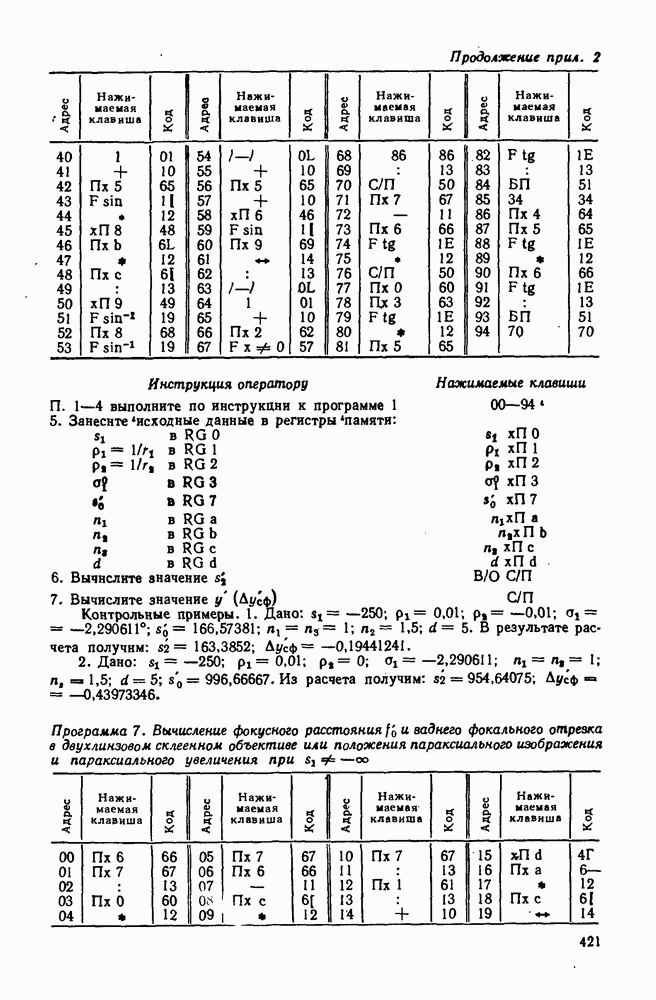
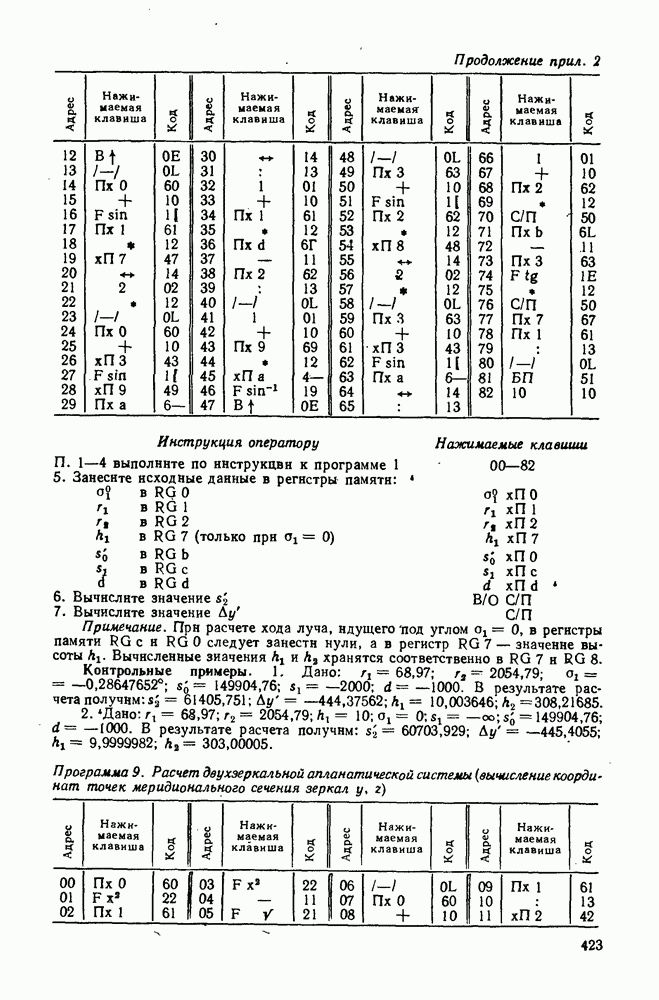
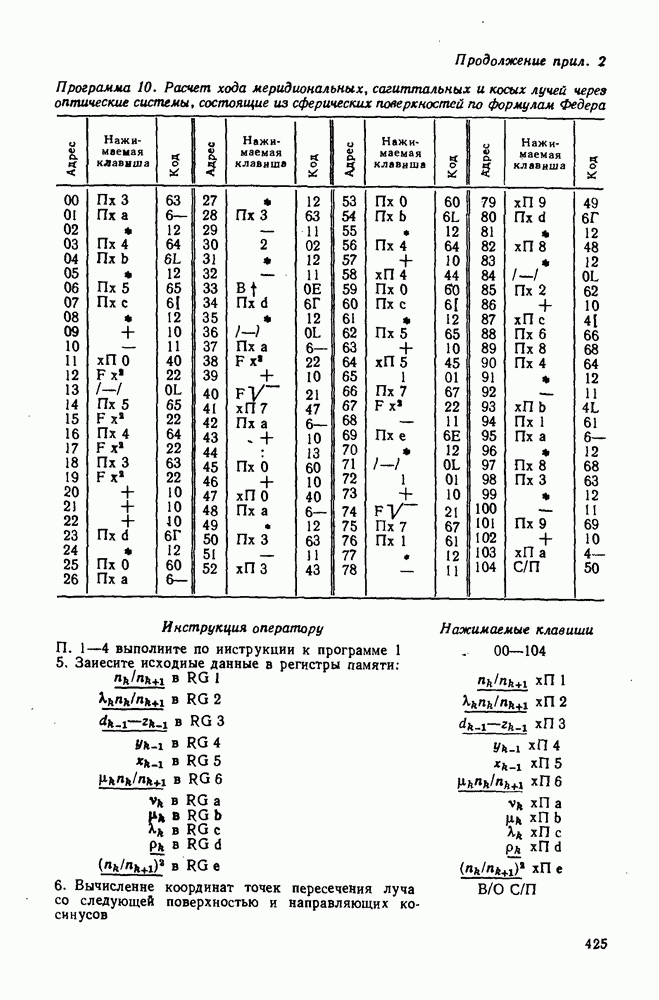
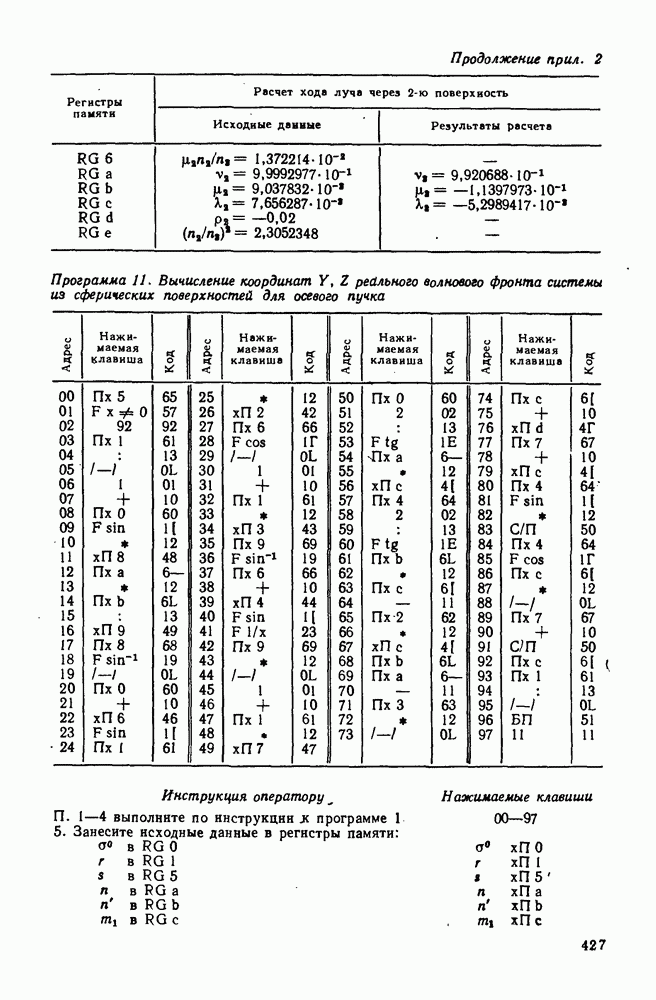
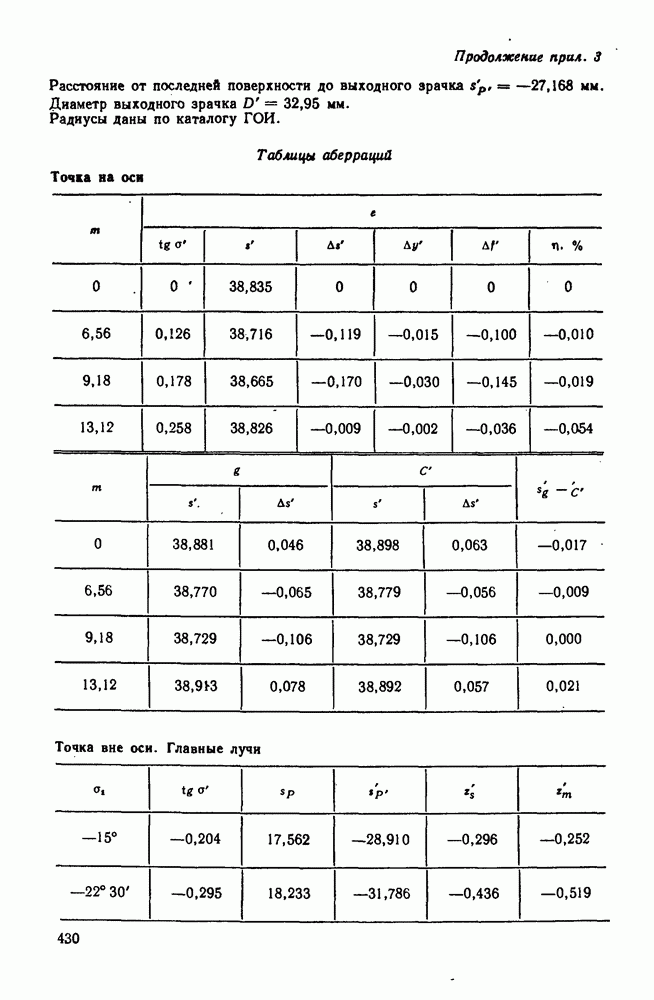
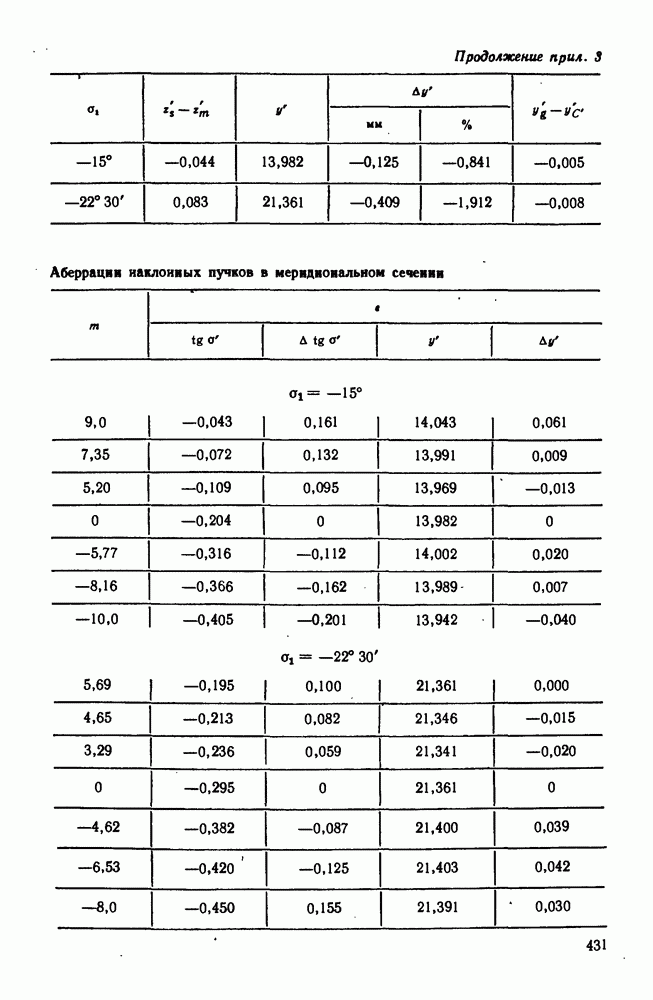
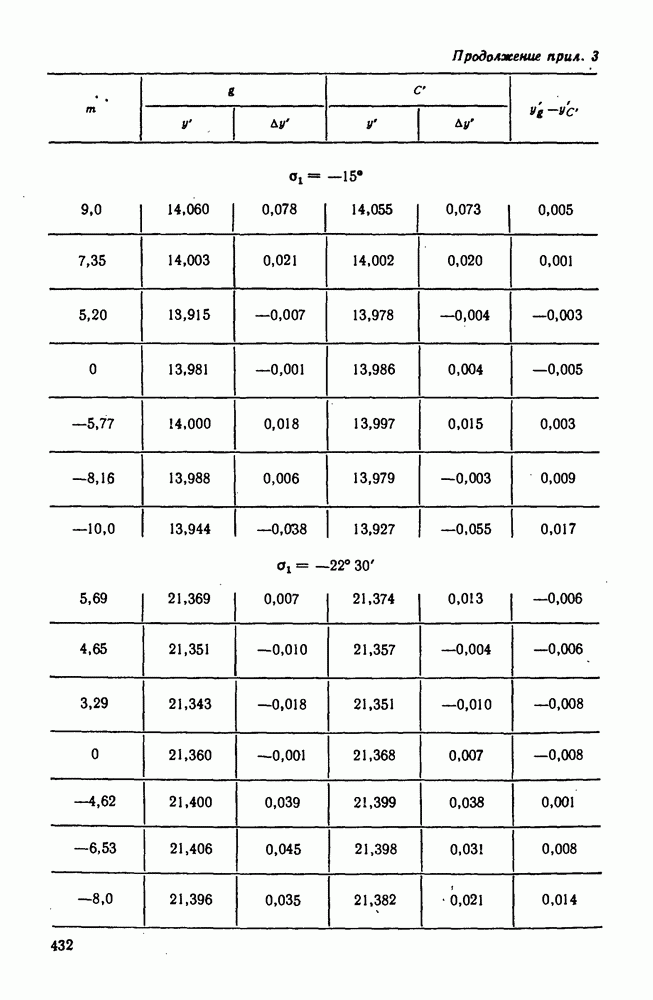
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
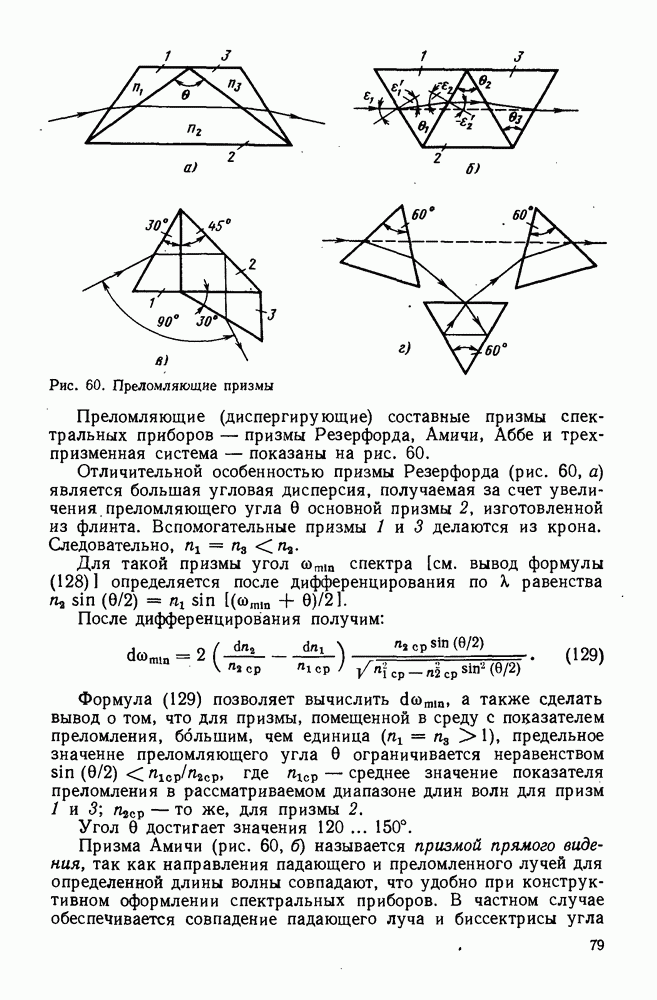
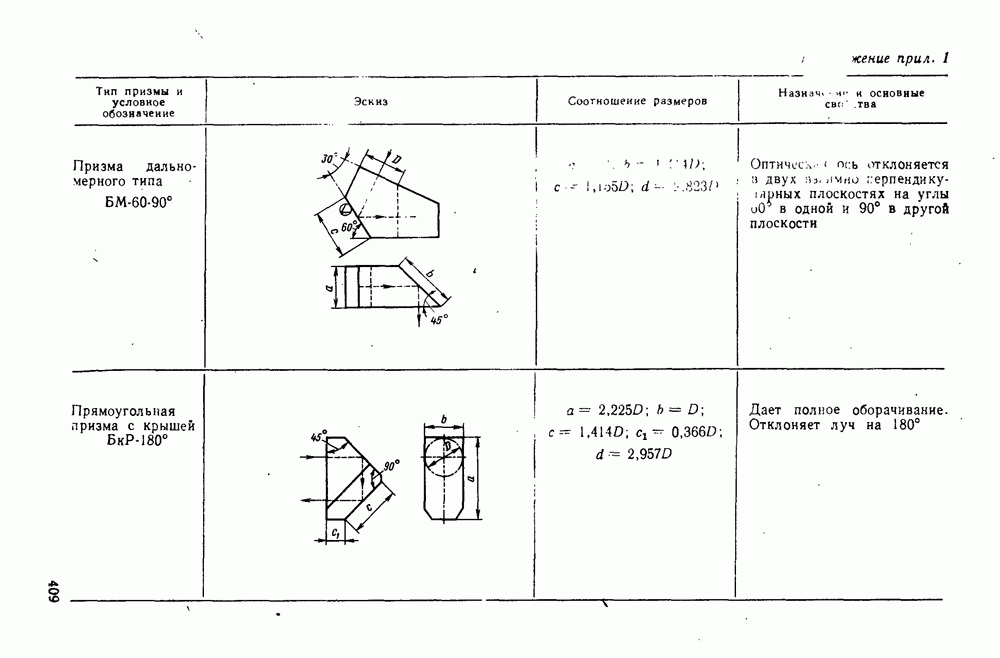
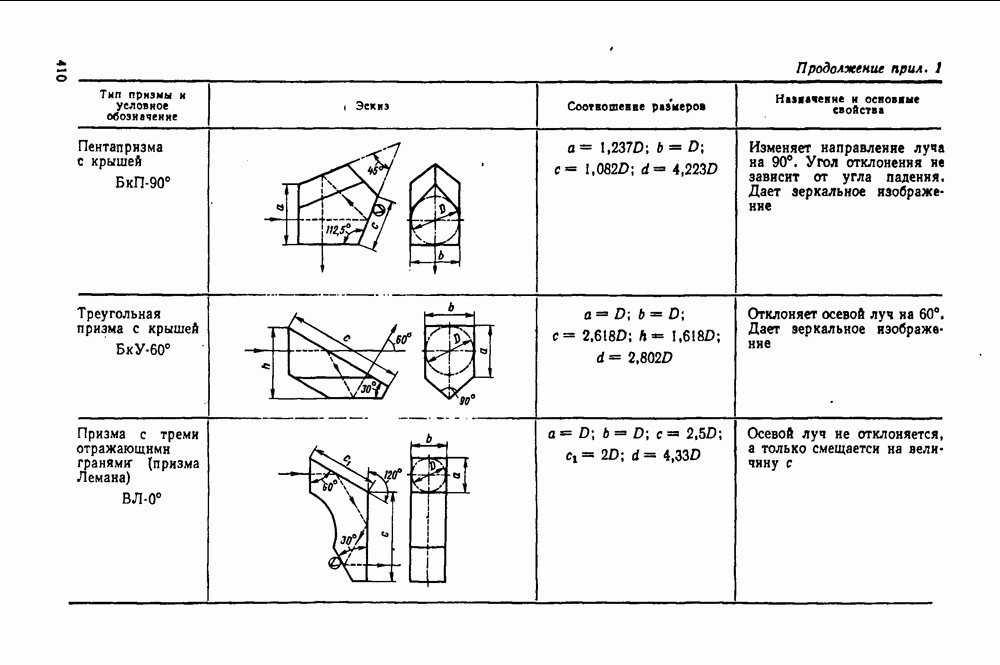
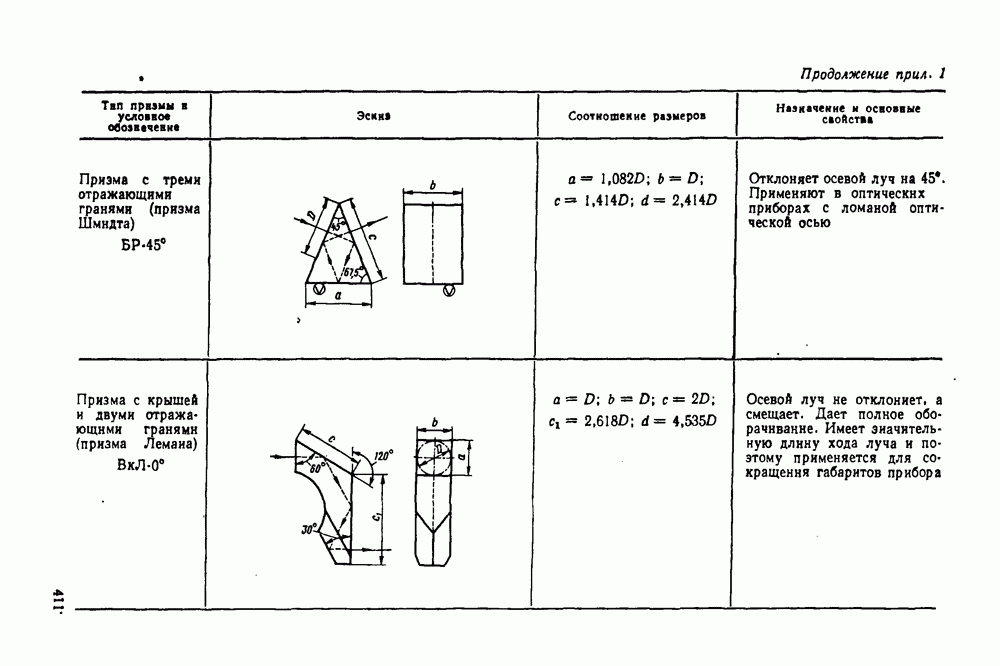
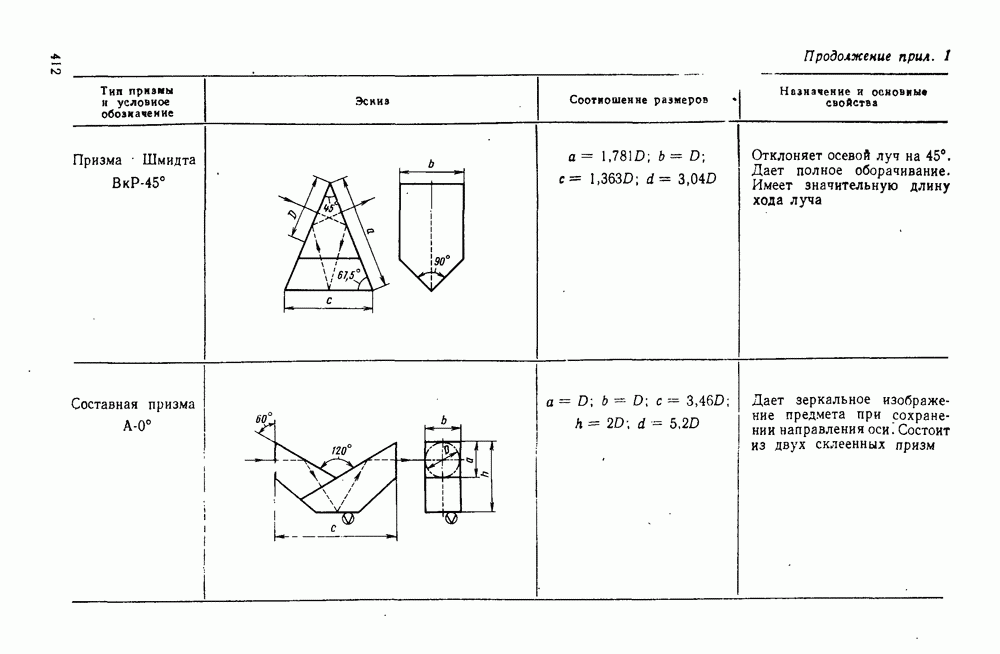
53. Астигматизм и кривизна поверхности изображения
Рассмотрим изображение точки, расположенной вне оси, пучками лучей, проходящих в двух взаимно перпендикулярных сечениях — меридиональном и сагиттальном (рис. 120). При этом будем считать, что оба пучка, выходящие из внеосевой точки В, бесконечно близки к главному лучу, т. е. опираются на

Рис. 120. Структура астигматического пучка
отверстие малого диаметра в плоскости входного зрачка. Так как кривизны сферических поверхностей для этих взаимно перпендикулярных пучков оказываются неодинаковыми, то точки схода меридионального и сагиттального пучков по выходе из оптической системы получаются в разных местах. Расстояние по оптической оси от плоскости идеального изображения (точка  ) до точек схода меридионального и сагиттального пучков соответственно обозначают
) до точек схода меридионального и сагиттального пучков соответственно обозначают  Эти расстояния рассчитывают по формулам (241).
Эти расстояния рассчитывают по формулам (241).
Аберрация для точки вне оси, когда ее, изображения, образуемые меридиональными и сагиттальными пучками, лежат в разных местах, называется астигматизмом. Эту аберрацию характеризуют разностью отрезков  и называют астигматической разностью.
и называют астигматической разностью.
Из рис. 120 следует, что при наличии астигматизма в месте схода  меридионального пучка получается горизонтальный отрезок, в месте схода
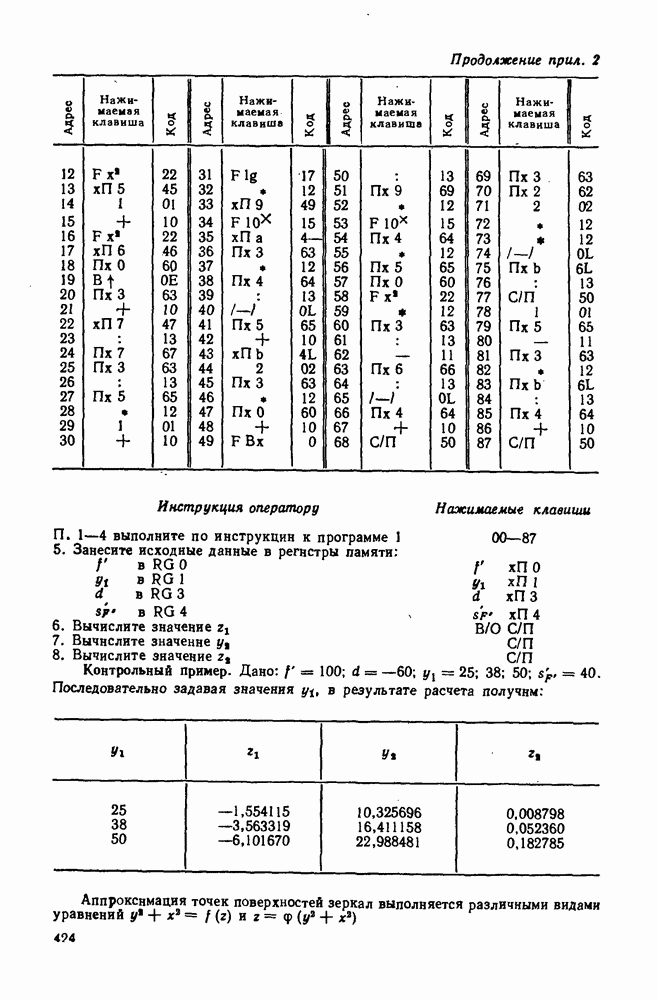
меридионального пучка получается горизонтальный отрезок, в месте схода  сагиттального пучка — вертикальный отрезок. В плоскости Гаусса изображение точки в данном случае представляет собой эллипс, большая ось которого вертикальна. Если плоскость изображения перемещать от точки
сагиттального пучка — вертикальный отрезок. В плоскости Гаусса изображение точки в данном случае представляет собой эллипс, большая ось которого вертикальна. Если плоскость изображения перемещать от точки  к точке
к точке  то при разных ее положениях изображение точки будет представлять собой горизонтальную линию, эллипс, большая ось которого горизонтальна, — кружок правильной формы, эллипс, большая ось которого вертикальна, — вертикальную линию. Пучки лучей, дающие такого вида изображение, называются астигматическими.
то при разных ее положениях изображение точки будет представлять собой горизонтальную линию, эллипс, большая ось которого горизонтальна, — кружок правильной формы, эллипс, большая ось которого вертикальна, — вертикальную линию. Пучки лучей, дающие такого вида изображение, называются астигматическими.
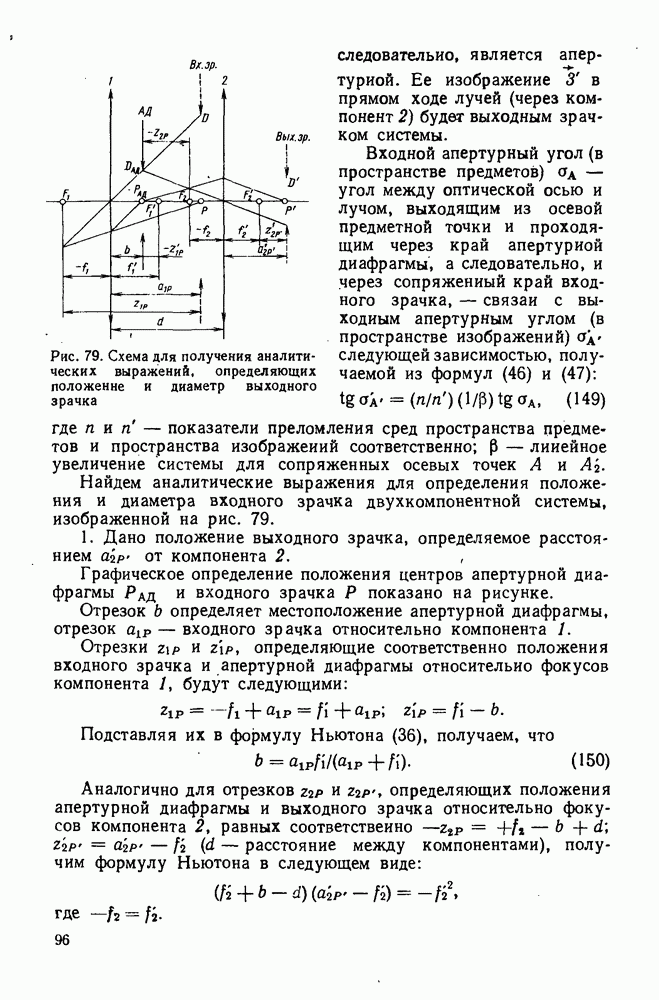
Для случая протяженного объекта,  например, участка плоскости, нужно рассматривать совокупность точек этого объекта, каждая из которых изображается астигматическими пучками лучей. Если объектом является отрезок прямой А В длиной у, расположенный в меридиональной плоскости (рис. 121), то каждой точке этого отрезка будут соответствовать меридиональное
например, участка плоскости, нужно рассматривать совокупность точек этого объекта, каждая из которых изображается астигматическими пучками лучей. Если объектом является отрезок прямой А В длиной у, расположенный в меридиональной плоскости (рис. 121), то каждой точке этого отрезка будут соответствовать меридиональное  и сагиттальное
и сагиттальное  изображения. Соединяя полученцые точки, получим кривые
изображения. Соединяя полученцые точки, получим кривые  являющиеся соответственно меридиональным и сагиттальным изображением предмета у. Если кривые
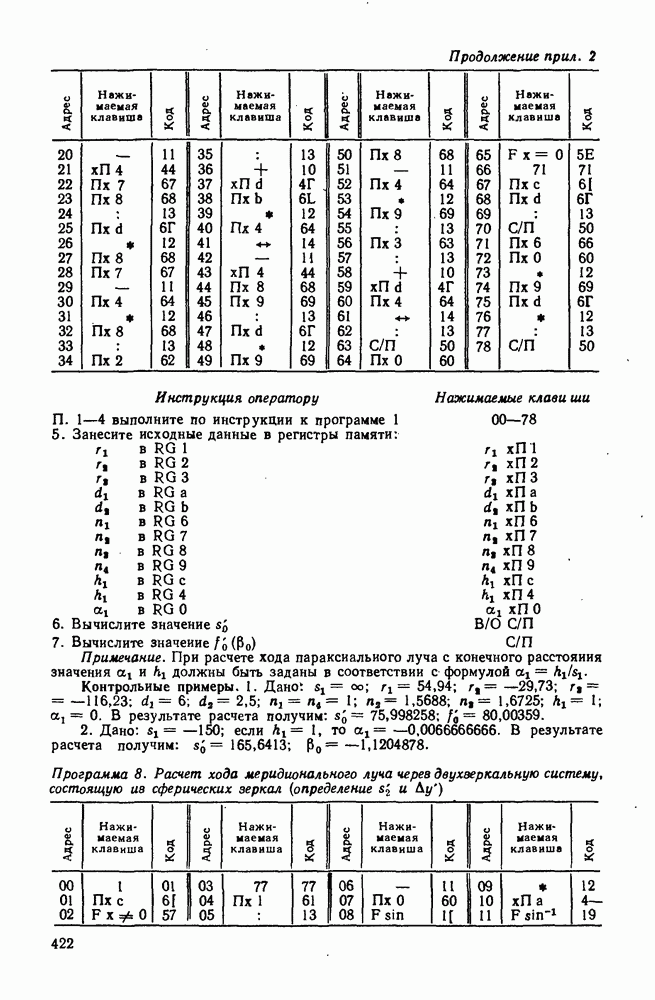
являющиеся соответственно меридиональным и сагиттальным изображением предмета у. Если кривые  вращать вокруг оптической оси, то получим
вращать вокруг оптической оси, то получим

Рис. 121. Изображения отрезков, образуемых астигматическими пучками
астигматические поверхности вращения, касательные к плоскости Гаусса в точке А на оси.
Между кривыми изображений  проходит средняя кривая изображения у. На поверхности изображения, которая получается при вращении вокруг оптической оси кривой у, каждая точка предмета у изображается в виде кружка правильной формы.
проходит средняя кривая изображения у. На поверхности изображения, которая получается при вращении вокруг оптической оси кривой у, каждая точка предмета у изображается в виде кружка правильной формы.
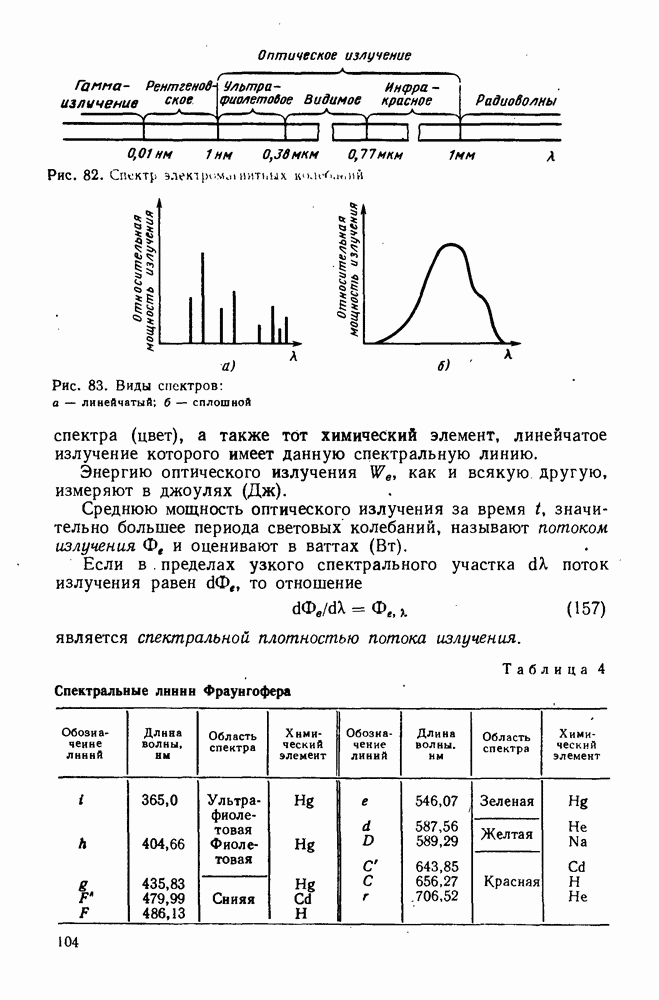
Таким образом, наличие в оптической системе аберраций астигматизма и кривизны поверхности изображения при условии, что изображение проецируется на плоскость, приводит к нерезкому изображению точек. Эта нерезкость увеличивается по мере удаления точки от оптической оси. Отметим характерные особенности изображения, создаваемого системой, имеющей астигматизм, для случая, когда объектом является двумерная фигура (рис. 122, а). Элементарные меридиональные пучки, изображающие каждую точку в виде линий (рис. 122, б), перпендикулярных к различно ориентированным меридиональным плоскостям, дадут резкое изображение окружности, так как элементарные отрезки меридиональных изображений, налагаясь друг на друга, не нарушат резкости изображения; изображения точек, принадлежащих радиусам, будут получаться в виде элементарных линий, перпендикулярных к радиусам, причем длина этих линий будет возрастать по мере удаления от оптической оси. Элементарные сагиттальные пучки будут изображать каждую точку объекта в виде линий, перпендикулярных к различно ориентированным

Рис. 122. Изображение плоской фигуры астигматическими пучками

Рис. 123. Графическое представление астигматизма и кривизны поверхности изображений
сагиттальным плоскостям, т. е. не исказят изображений радиусов, а изображения окружностей будут представлять собой элементарные радиальные отрезки, длина которых увеличивается по мере их удаления от оптической оси (рис. 122, б).
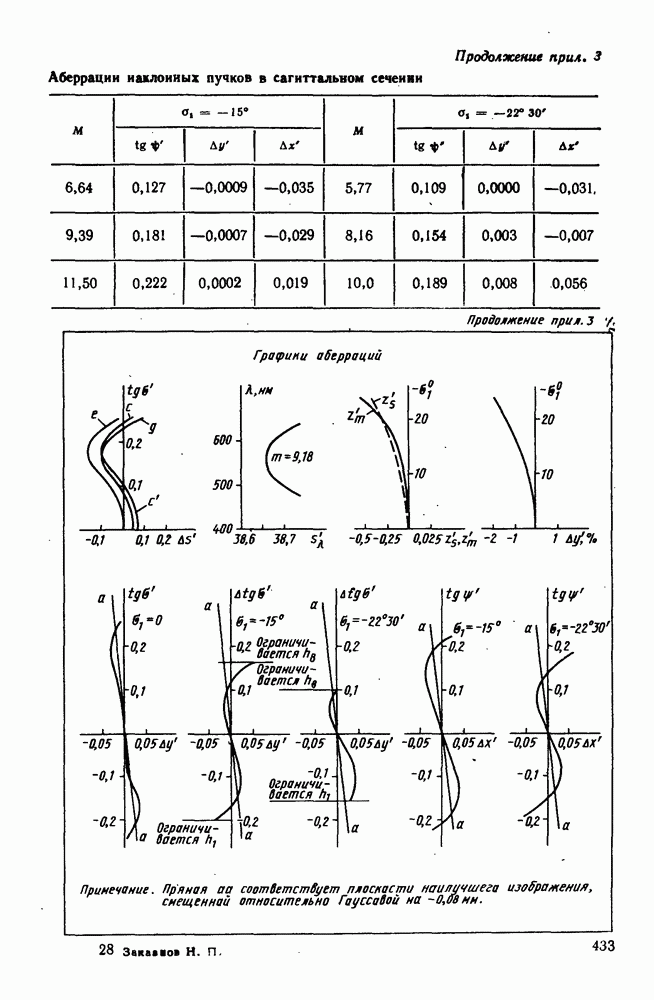
Астигматизм и кривизну поверхности изображения оптической системы обычно характеризуют величинами  которые сводятся в таблицы и иллюстрируются графиками. По оси ординат откладывают углы
которые сводятся в таблицы и иллюстрируются графиками. По оси ординат откладывают углы  для главных лучей, выходящих из различных точек предмета, или линейный размер предмета у, а по оси абсцисс — отрезки
для главных лучей, выходящих из различных точек предмета, или линейный размер предмета у, а по оси абсцисс — отрезки 
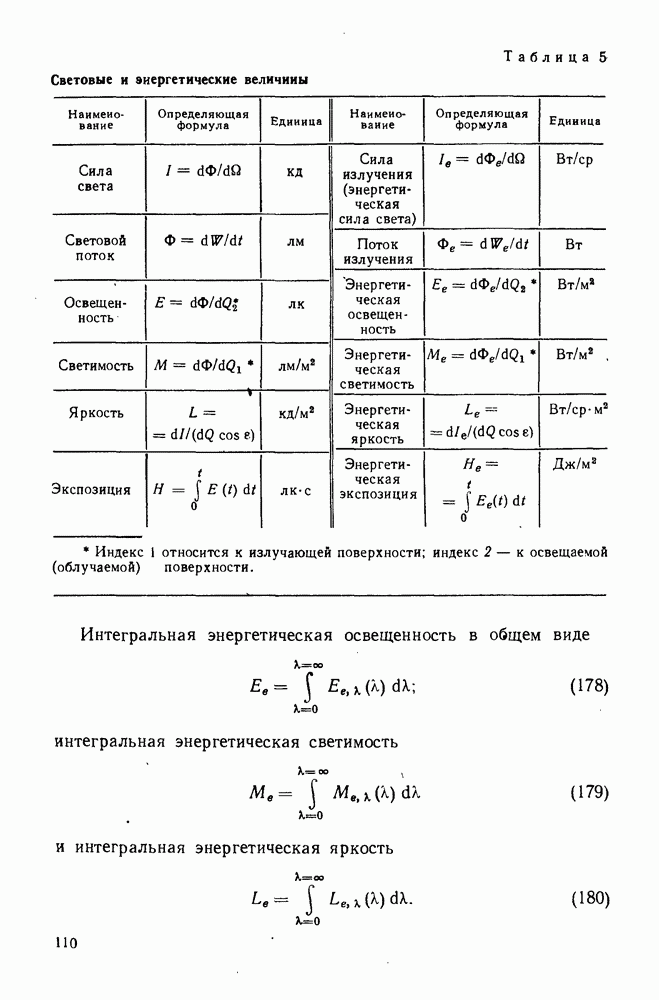
Различные случаи коррекции астигматизма и кривизны поверхности изображения иллюстрирует рис. 123. При наличии в системе астигматизма и кривизны поверхности изображения (под последней понимается средняя кривая  расположенная между кривыми
расположенная между кривыми  даже при отсутствии астигматизма
даже при отсутствии астигматизма  изображение по полю плоской поверхности получается нерезким (рис. 123, а). На рис. 123, б показан случай исправления кривизны поверхности изображения
изображение по полю плоской поверхности получается нерезким (рис. 123, а). На рис. 123, б показан случай исправления кривизны поверхности изображения  при неисправленном астигматизме.
при неисправленном астигматизме.
Для получения резкого изображения в пределах всего поля необходимо исправить и астигматизм и кривизну поверхности изображения. В таких системах, называемых анастигматами, астигматизм и кривизна поверхности изображения, практически полностью исправляются для некоторого угла поля и имеют допустимые значения в пределах всего поля оптической системы. График остаточных аберраций астигматизма и кривизны поверхности изображений объектива-анастигмата «Индустар», у которого обе аберрации практически полностью исправлены для угла поля до  и сравнительно невелики на самом краю поля, показан на рис. 123, в.
и сравнительно невелики на самом краю поля, показан на рис. 123, в.
Приближенные значения аберраций астигматизма и кривизны поверхности изображения можно вычислить по формулам
аберраций третьего порядка. Эти аберрации определяются через суммы Зейделя 

Рис. 124. Схема для вывода формул астигматизма и кривизны поверхности изображений
Рассмотрим соотношения для плоского меридионального пучка, выходящего из внеосевой предметной точки В, расположенной в бесконечности (рис. 124). Меридиональная составляющая поперечной аберрации третьего порядка для бесконечно удаленного предмета при условиях нормировки (258) и неравенстве нулю  и
и  определяется согласно (259):
определяется согласно (259):

если предмет и изображение в воздухе, т. е. 
Из рассмотрения подобных треугольников в пространстве изображений согласно рис. 124 имеем:

Учитывая, что  и подставляя в последнюю формулу
и подставляя в последнюю формулу  из (275), получаем
из (275), получаем

Аналогичные рассуждения позволяют, пользуясь выражением для сагиттальной составляющей поперечной аберрации третьего порядка, получить из (259)

Тогда астигматическая разность 
Таким образом, астигматизм пропорционален квадрату углового поля оптической системы. Для его исправления в области аберраций третьего порядка необходимо выполнить условие  В этом случае обе астигматические поверхности сливаются и согласно (276) и (277)
В этом случае обе астигматические поверхности сливаются и согласно (276) и (277)

т. е. коэффициент  определяет аберрацию кривизны поверхности изображений при исправленном астигматизме.
определяет аберрацию кривизны поверхности изображений при исправленном астигматизме.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
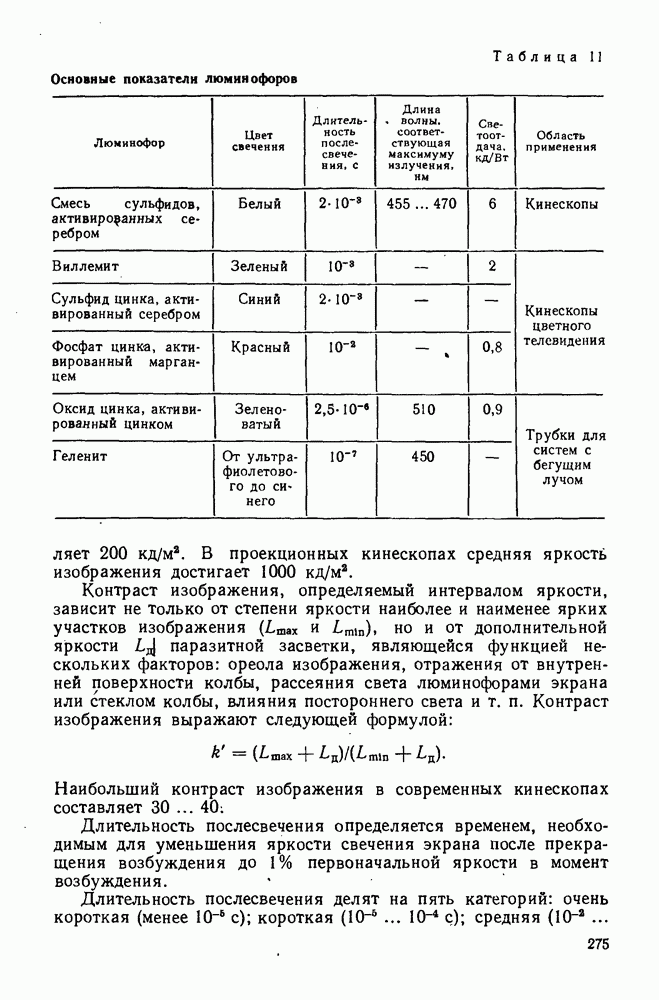
- 25. Материалы, применяемые для изготовления оптических деталей
- 26. Линзы
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
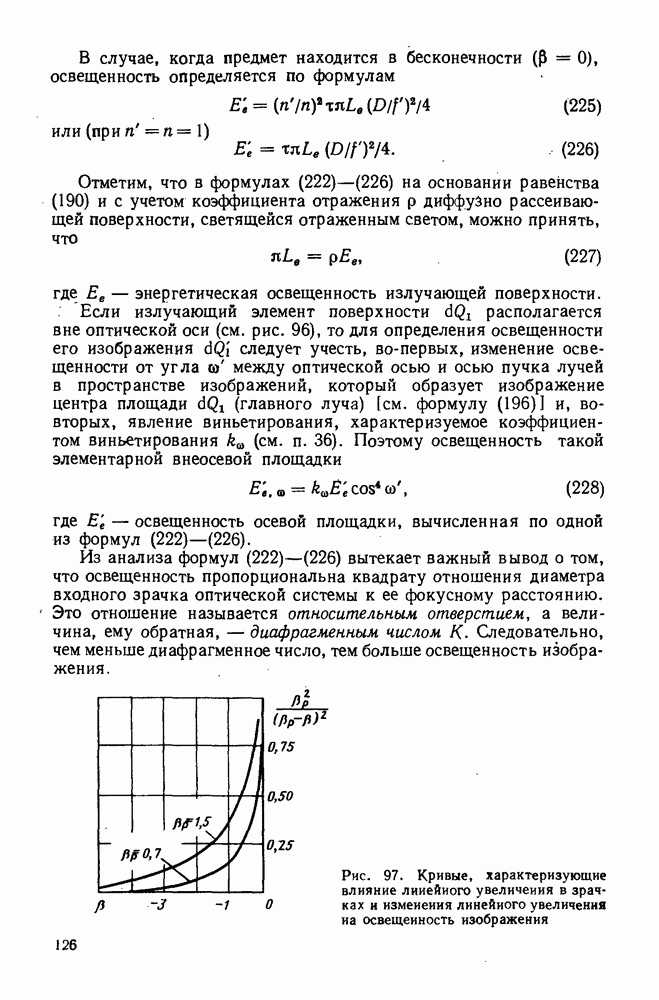
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
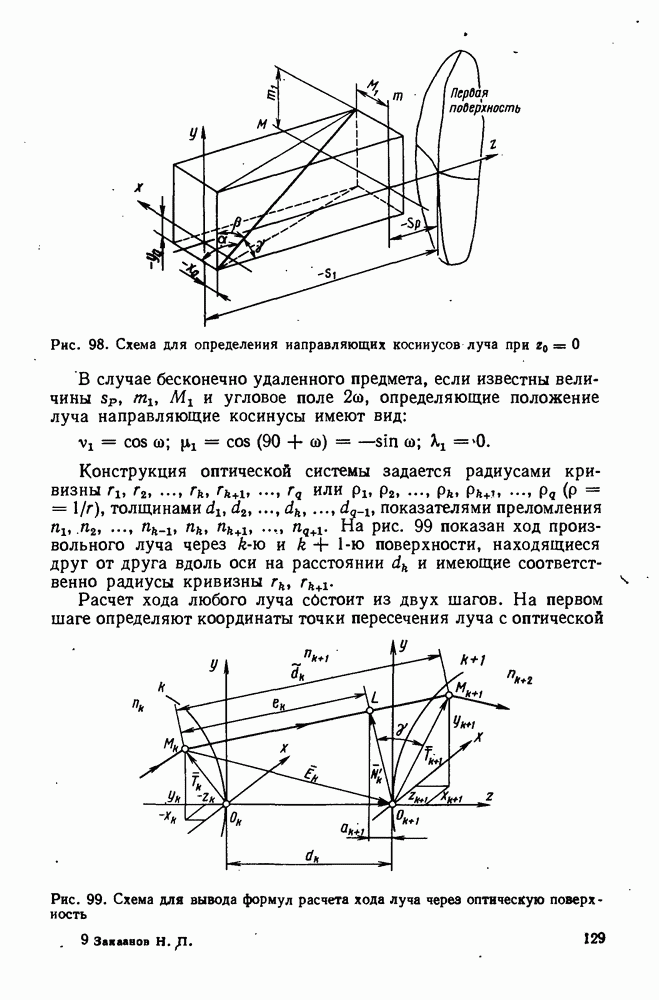
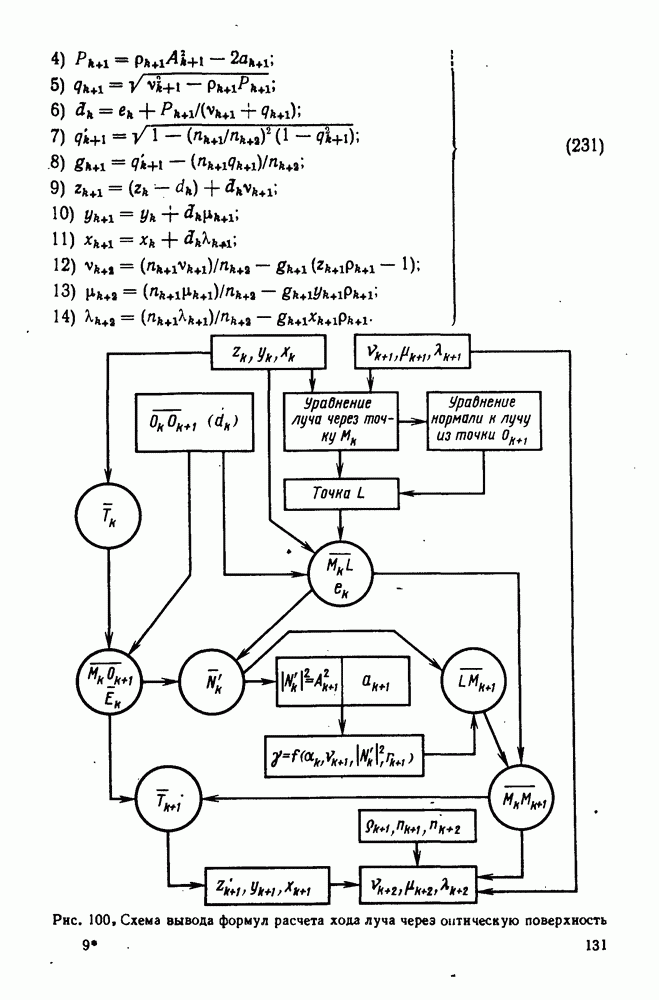
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
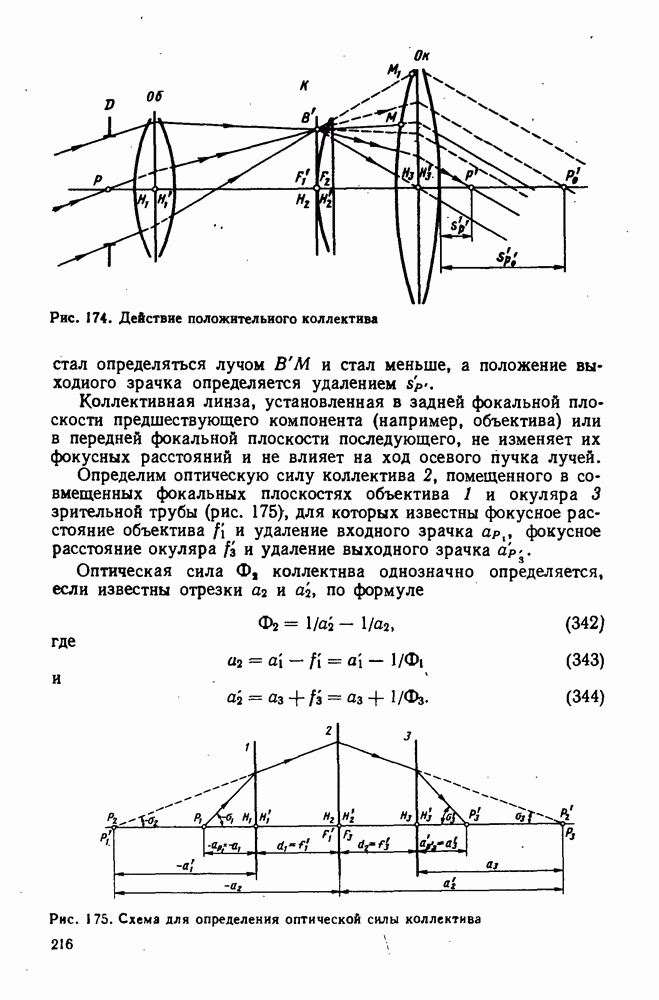
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
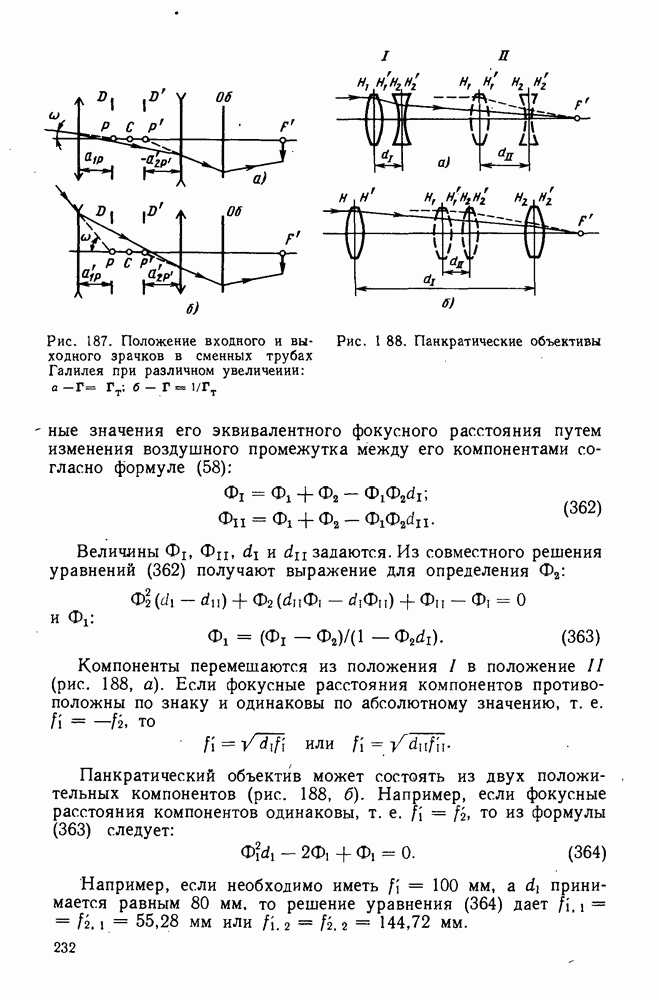
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
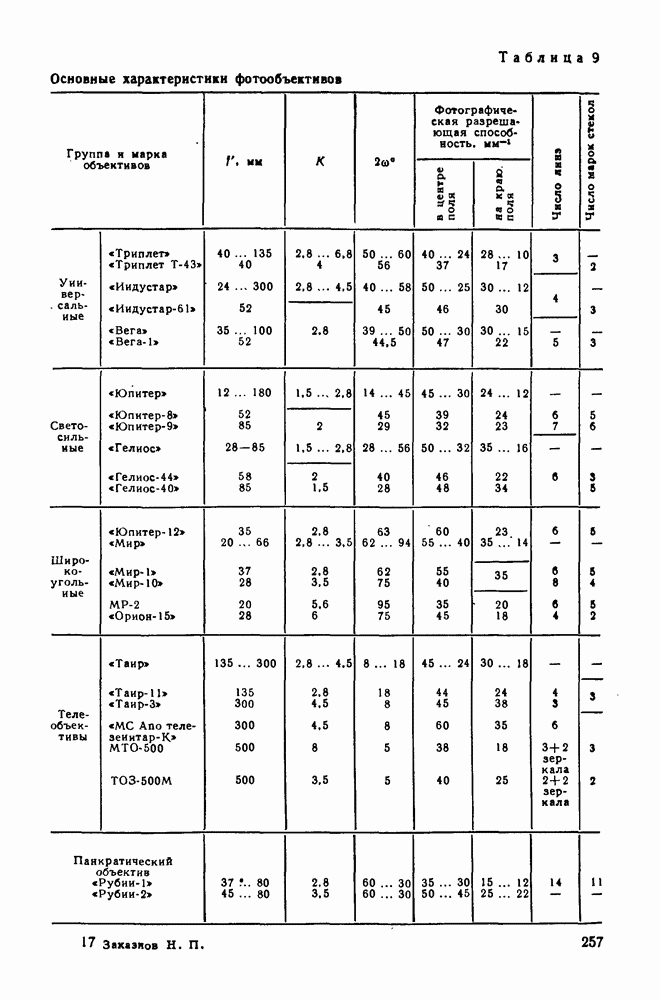
- 83. Основные характеристики фотообъектива
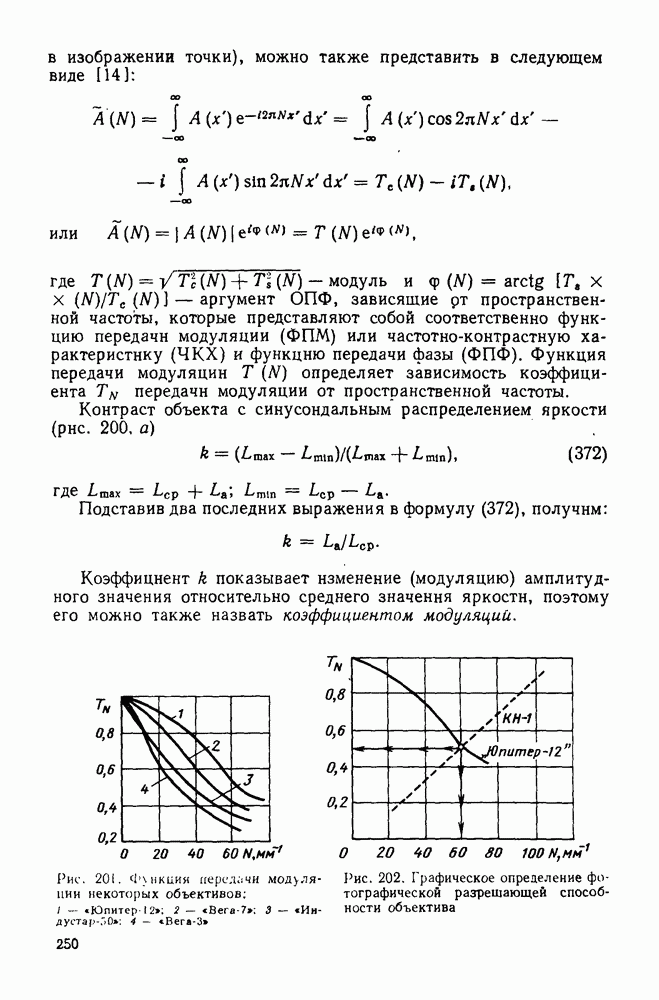
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
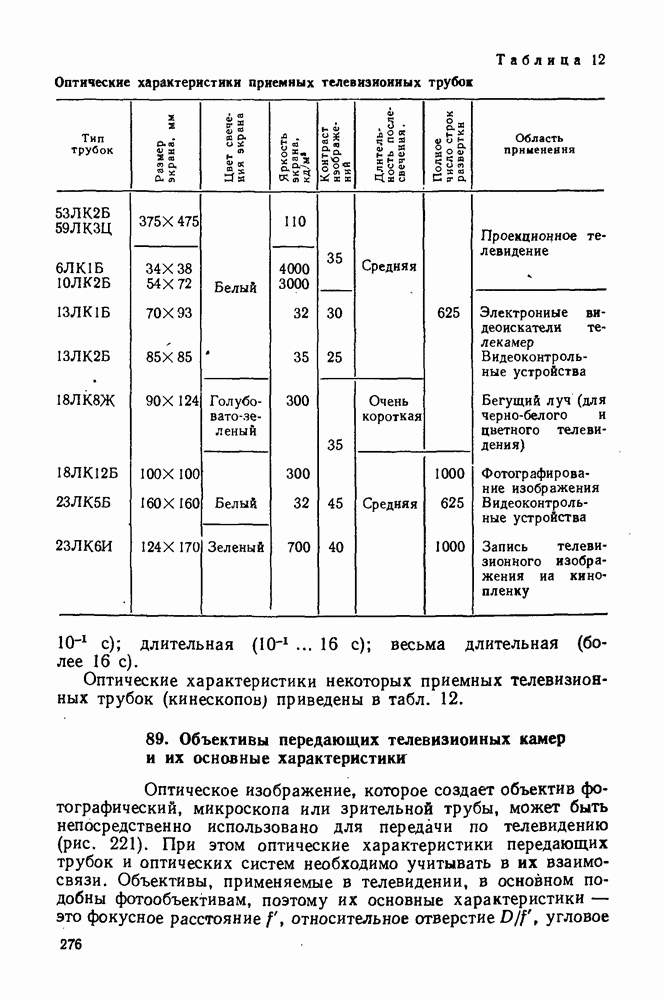
- 88. Оптические характеристики передающих и приемных телевизионных трубок
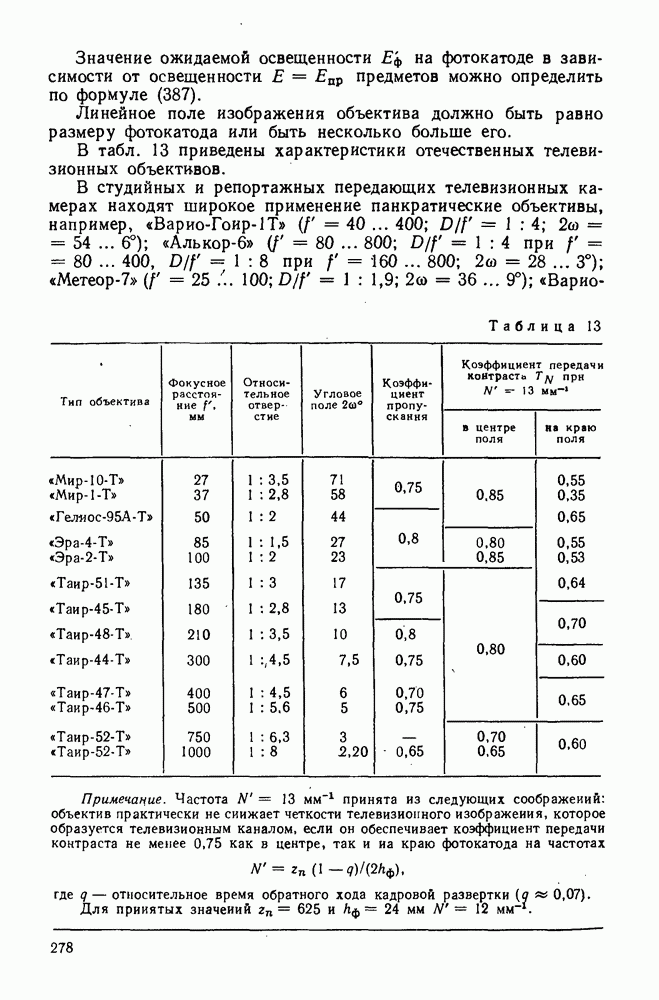
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
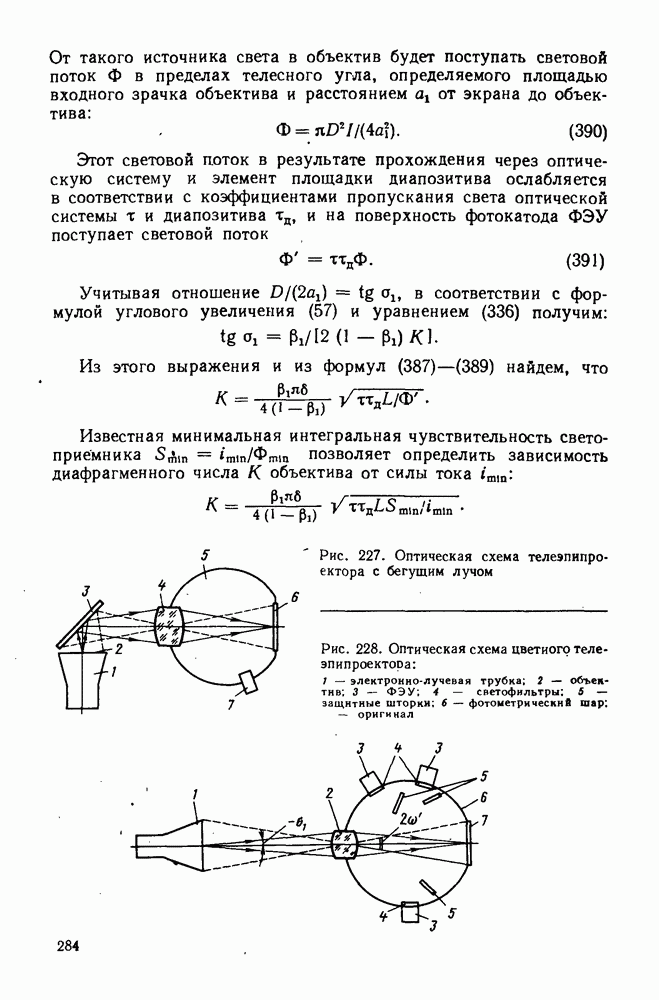
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы