| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
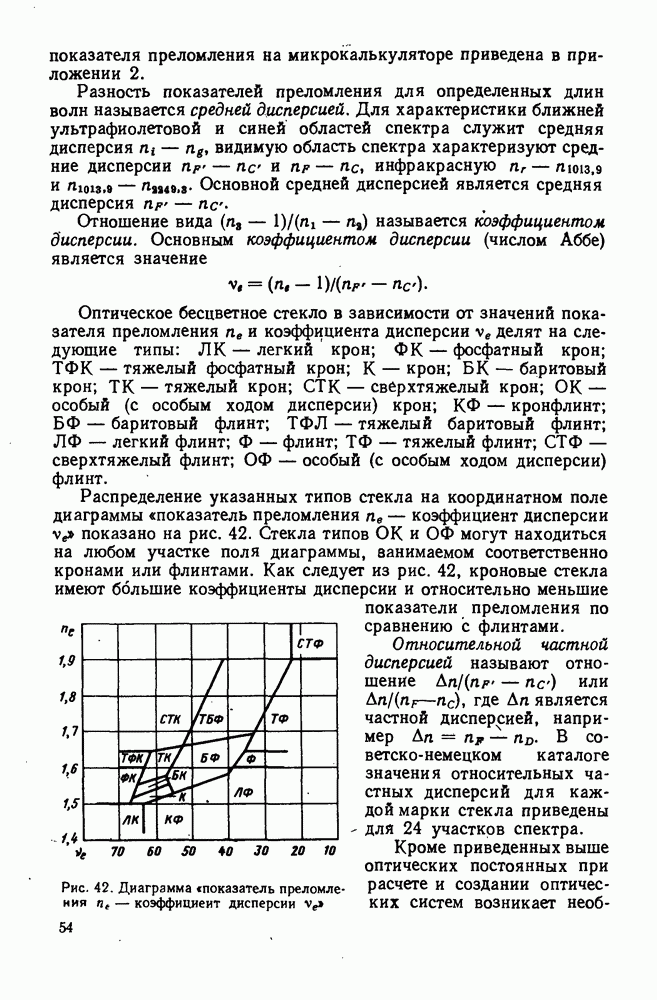
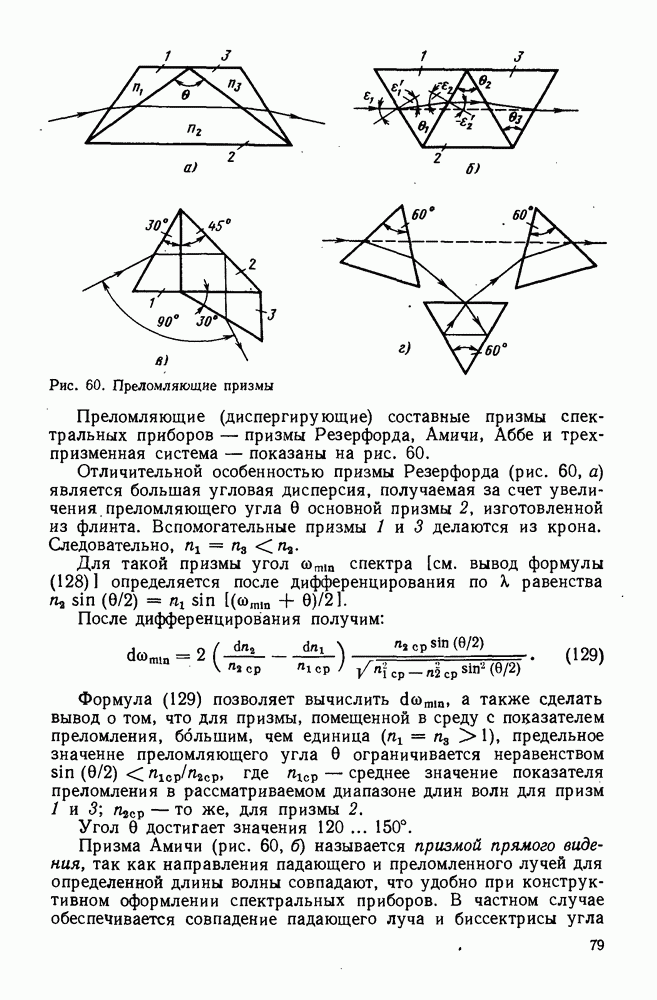
32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
Линзы Френеля представляют собой оптические детали со ступенчатой поверхностью (рис. 67).
Чем меньше расстояние между соседними ступеньками, тем точнее выполняется условие уменьшения остаточных аберраций при малой толщине линзы. Наименьшее достигнутое расстояние между ступеньками равно  Ступеньки могут быть разграничены концентрическими, спиральными или параллельными канавками и представляют собой в первых двух случаях участки конических или сферических поверхностей, а в третьем случае — участки плоскостей или цилиндрических поверхностей.
Ступеньки могут быть разграничены концентрическими, спиральными или параллельными канавками и представляют собой в первых двух случаях участки конических или сферических поверхностей, а в третьем случае — участки плоскостей или цилиндрических поверхностей.
Такие поверхности с малым шагом технологически возможно выполнить путем прессования из пластмасс.
Материалом для линз Френеля может быть полиметилметакрилат, имеющий следующие характеристики:  ; температурный коэффициент показателя преломления
; температурный коэффициент показателя преломления  температурный коэффициент линейного расширения
температурный коэффициент линейного расширения  температура размягчения
температура размягчения  Этот материал обладает хорошим пропусканием в ультрафиолетовой области спектра.
Этот материал обладает хорошим пропусканием в ультрафиолетовой области спектра.
Пластмассовые линзы Френеля находят применение в качестве луп, конденсоров, призм, зеркал и других оптических деталей, обеспечивая малые габаритные размеры системы.
Элемент эффективного профиля ступенчатой осесимметричной поверхности, разделяющей среды с показателями преломления  показан на рис. 68.
показан на рис. 68.

Рис. 67. Линза Френеля

Рис. 68. Элемент эффективного профиля линзы Френеля
Рассмотрим возможность получения с помощью этой поверхности гомоцентрического пучка лучей, образующих изображение осевой  принимая, что каждая ступенька является бесконечно узкой.
принимая, что каждая ступенька является бесконечно узкой.
Луч  встречающий бесконечно узкий эффективный профиль в точке
встречающий бесконечно узкий эффективный профиль в точке  на расстоянии
на расстоянии  от оптической оси, после преломления в пересечении с оптической осью даст точку А. Нормаль к рассматриваемому участку профиля пересечет оптическую ось в точке С под углом
от оптической оси, после преломления в пересечении с оптической осью даст точку А. Нормаль к рассматриваемому участку профиля пересечет оптическую ось в точке С под углом  который определяет положение образующей взятого участка профиля.
который определяет положение образующей взятого участка профиля.
Найдем значения углов  для разных высот
для разных высот  падения лучей при заданных положениях точки А и ее изображения А (отрезки —а и а).
падения лучей при заданных положениях точки А и ее изображения А (отрезки —а и а).
Из рис. 68 следует:  По закону преломления
По закону преломления  получим:
получим:

После преобразований из формулы (134) находим следующую зависимость для вычисления углов  определяющих, например, наклон профилей конических кольцевых участков ступенчатой преломляющей поверхности:
определяющих, например, наклон профилей конических кольцевых участков ступенчатой преломляющей поверхности:

где углы  предварительно вычисляют по заданным отрезкам
предварительно вычисляют по заданным отрезкам  для различных
для различных 
Формулу (135) можно использовать для расчета тонкой линзы Френеля с плоской второй поверхностью, аберрациями которой можно пренебречь.
Заднее фокусное расстояние линзы Френеля определим по значению  при
при  При этом условии из формулы (135) имеем:
При этом условии из формулы (135) имеем:  Следовательно,
Следовательно,

Таким образом, при малой высоте

где  находят по формуле (135) при малом значении
находят по формуле (135) при малом значении 
Световой диаметр  линзы получается при угле падения луча
линзы получается при угле падения луча  . Из рис. 69 имеем:
. Из рис. 69 имеем:

где  предельное значение угла преломления;
предельное значение угла преломления;  — апертурный угол линзы Френеля в пространстве изображений, т. е. угол между оптической осью и крайним лучом, прошедшим линзу
— апертурный угол линзы Френеля в пространстве изображений, т. е. угол между оптической осью и крайним лучом, прошедшим линзу  апертурный угол в пространстве предметов, сопряженный
апертурный угол в пространстве предметов, сопряженный
С УГЛОМ 
Из формулы (136) следует, что

Учитывая, что  получаем:
получаем:

где  определяется согласно закону преломления
определяется согласно закону преломления 
Решив квадратное уравнение (137), находим световой диаметр линзы Френеля:

Аксиконом называется оптическая деталь или оптическая система, вызывающая значительное нарушение гомоцентричности пучка лучей, выходящих из предметной точки. Изображение осевой точки получается в виде отрезка прямой, являющейся частью оптической оси в пространстве изображений, а в выбранной плоскости изображения — в виде круга достаточно большого диаметра. Это обстоятельство используют при создании оптических систем, не нуждающихся в фокусировке при изменении положения предмета относительно оптической системы, для обеспечения заданного распределения освещенности в плоскости изображения, компенсации нарушения гомоцентричности за счет действия других компонентов схемы.
На рис. 70 показана оптическая осесимметричная деталь типа линзы. Ее первая поверхность плоская, вторая — коническая.
В меридиональном сечении эту коническую линзу можно представить как преломляющую равнобедренную призму с преломляющим углом  размер
размер  которой по оптической оси известен. Найдем изображение А осевой точки А, расположенной на оптической
которой по оптической оси известен. Найдем изображение А осевой точки А, расположенной на оптической

Рис. 69. Схема для определения светового диаметра линзы Френеля

Рис. 70. Действие конического аксикома
оси на расстоянии  от «входной грани». Положение А зависит от угла
от «входной грани». Положение А зависит от угла 
Для высоты  падения луча имеем:
падения луча имеем:

По закону преломления

Из рис. 70 следует:

Повторное использование закона преломления позволяет найти угол преломления на второй «грани»:

И, наконец, угол между преломленным лучом и оптической осью

Отрезок  определяющий положение точки А, отсчитывается от вершины преломляющей поверхности (в данном случае от вершины конуса).
определяющий положение точки А, отсчитывается от вершины преломляющей поверхности (в данном случае от вершины конуса).
Из рис. 70 следует:

где  высота падения луча на коническую поверхность.
высота падения луча на коническую поверхность.
Обозначим длину луча в пределах конической линзы через  Тогда
Тогда

где

 заданное расстояние от оптической оси до острого края сечения конической линзы (точка
заданное расстояние от оптической оси до острого края сечения конической линзы (точка 
Из формулы (143), учитывая формулы (144), (145) и (139), получим, что

Рассмотрим формулу (146) при  т. е. для случая, когда осевая предметная точка находится в бесконечности. При этом
т. е. для случая, когда осевая предметная точка находится в бесконечности. При этом  тогда
тогда

Для параксиального луча  а для луча, падающего на край конической линзы
а для луча, падающего на край конической линзы 

Следовательно, наибольшая продольная протяженность в изображении точки (сферическая аберрация) в рассматриваемом случае 

Оценим ее значение для конкретных конструктивных параметров конической линзы. Пусть 
Используя формулы (140), (142), (147), находим, что 
Согласно определению рассмотренная деталь (линза) и будет аксиконом.
Обычно конические аксиконы применяются с углом  Если при этом угол является малым
Если при этом угол является малым  то и
то и  Учитывая, что при этом
Учитывая, что при этом  из формулы (146) получим:
из формулы (146) получим:

а при 

Но так как  формулу (130), относящуюся к клину], то
формулу (130), относящуюся к клину], то

Найдем наименьшее расстояние  от аксикона до предметной осевой точки, при котором полное внутреннее отражение от конической поверхности отсутствует.
от аксикона до предметной осевой точки, при котором полное внутреннее отражение от конической поверхности отсутствует.
Из формулы (141) при  имеем:
имеем:  где
где  угол полного внутреннего отражения.
угол полного внутреннего отражения.
Так как каждый в отдельности углы  меньше 90°, то, учитывая формулу (140), будем иметь
меньше 90°, то, учитывая формулу (140), будем иметь 
Из формул (139) и (140) следует, что


Рис. 71. Типы аксиконов: а — конондная лннэа; б - положительный меннск; в — коническое зеркало
Примеры аксиконов показаны на рис. 71. При выборе аксикона стремятся получить наибольшую освещенность изображения в заданном интервале на оптической оси пространства изображений.
Оптическим растром называется совокупность из линзовых или зеркальных элементов (ячеек), имеющих оптическую силу. Расстояние между осями двух смежных элементов, измеренное по нормали к их осям симметрии, называют периодом, или шагом, растра.
Каждый элемент оптического растра формирует изображение предмета. Таким образом, число полученных изображений предмета равно числу элементов растра.
Если оптические силы всех элементов одинаковы (рис. 72), то изображения  предмета
предмета  получаются в одной плоскости (когда оптические элементы безаберрационны).
получаются в одной плоскости (когда оптические элементы безаберрационны).
При обратном ходе лучей из отдельных «предметов», полученных в виде закрепленных изображений (например, на фотопластинке), восстанавливается пространственное положение предмета.
Действие растровой осветительной системы показано на рис. 73. Наклонный пучок лучей, идущий от источника света С, заполняет входной зрачок последующей оптической системы. Элементом растра 1 обеспечивается получение изображения  центра источника света С. Элемент растра 2 направляет пучок во входной зрачок.
центра источника света С. Элемент растра 2 направляет пучок во входной зрачок.
Период  растра 1 является заданным. Тогда согласно рис. 73 период растра 2
растра 1 является заданным. Тогда согласно рис. 73 период растра 2

где  расстояние между растрами;
расстояние между растрами;  удаление источника света С от растра 1.
удаление источника света С от растра 1.

Рис. 72. Оптический растр

Рис. 73. Растровая осветительная система
Число элементов растра 2 должно быть равно числу элементов растра 1.
Фокусные расстояния осевых ячеек растров  и 2 определяются по формуле (38):
и 2 определяются по формуле (38):

где  удаление изображения 3 от растра 2.
удаление изображения 3 от растра 2.
Другим примером применения оптического растра являются экраны направленного отражения. Зеркальные элементы растрового экрана могут быть сферическими и цилиндрическими.
На рис. 74 показано сечение элемента растрового экрана. В этом сечении отраженный поток рассеивается в пределах заданного угла  Из рис. 74 следует:
Из рис. 74 следует:

где  размер сечения элементов;
размер сечения элементов;  радиус сферической или цилиндрической поверхности элемента.
радиус сферической или цилиндрической поверхности элемента.
Из равенства (148) следует, что, во-первых, растровый экран эквивалентен диффузному экрану  при
при  во-вторых, для увеличения кажущейся яркости изображения уменьшение угла 2? обеспечивается увеличением радиуса вогнутой цилиндрической поверхности, т. е. увеличением фокусного расстояния элемента растра.
во-вторых, для увеличения кажущейся яркости изображения уменьшение угла 2? обеспечивается увеличением радиуса вогнутой цилиндрической поверхности, т. е. увеличением фокусного расстояния элемента растра.
Разнообразные примеры устройства и применения оптических растров приведены в работе [6].
Перспективной элементной базой для оптических систем является градиентная оптика [6]. В градиентных элементах (гринах) используются

Рис. 74. Элемент растрового экрана
прозрачные изотропные среды, в которых показатель преломления есть функция координат точки среды. По виду функции  различают три типа гринов:
различают три типа гринов:
1) с осевым распределением показателя преломления: 
2) с радиальным (цилиндрическим) распределением: 
3) со сфероконцентрическим распределением: 
Примером гринов первого типа является сверхпроводящее волокно для систем связи, второго — силовые оптические элементы. В последнем случае традиционные конструктивные параметры дополняются осесимметричным градиентом показателя преломления. Проектирование и исследование оптических систем с градиентными линзами показало, что конструкция систем упрощается (за счет уменьшения числа компонентов).
Другим перспективным элементом, используемым как компонент оптической системы, является дифракционная линза (пластина).
Дифракционная линза (киноформ) представляет собой периодическую кольцевую структуру, изготовляемую, например, способом фотолитографии. Киноформ рассматривается как бесконечно тонкий транспарант с заданным амплитудным коэффициентом пропускания. Изменение кривизны волнового фронта после действия дифракционного элемента в практически приемлемом приближении рассматривается в рамках геометрической оптики [4].
Так как при прохождении пучков лучей через киноформы силовое действие сопровождается изменением в спектральном составе излучения, то эти элементы используют для коррекции не только сферической, но и хроматических аберраций.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 1. Принцип Ферма
- 2. Показатель преломления
- 3. Правила знаков
- 4. Законы преломления и отражения
- 5. Полное внутреннее отражение
- 6. Преломляющие и отражающие поверхности
- Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ
- 7. Преломление лучей плоской поверхностью
- 8. Преломление лучей сферической поверхностью
- 9. Отражение лучей плоской поверхиостью
- 10. Отражение лучей сферической поверхностью
- 11. Преломление лучей несферической поверхностью
- 12. Отражение от несферических поверхностей
- Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА
- 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение
- 14. Кардинальные элементы идеальной оптической системы
- 15. Зависимости между положениями и размерами предмета и изображения
- 16. Угловое увеличение. Узловые точки
- 17. Продольное увеличение
- 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами
- 19. Изображение наклонных плоскостей предметов
- 20. Расчет хода луча через идеальную систему
- 21. Оптические системы из нескольких компонентов
- Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ
- 23. Инвариант Гюйгенса-Гельмгольца
- 24. Расчет хода нулевых лучей
- Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ
- 25. Материалы, применяемые для изготовления оптических деталей
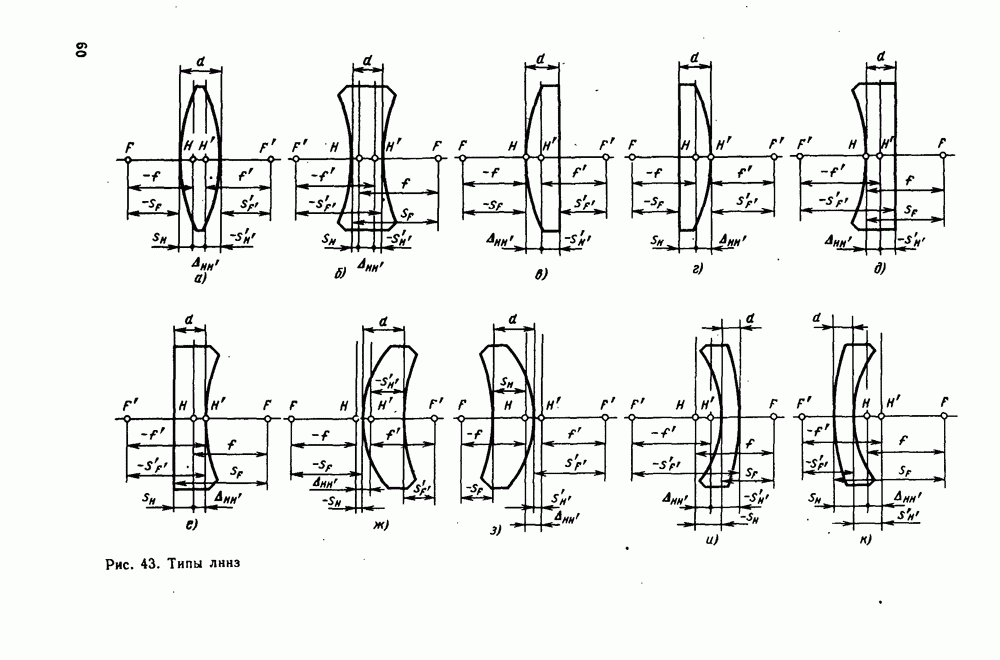
- 26. Линзы
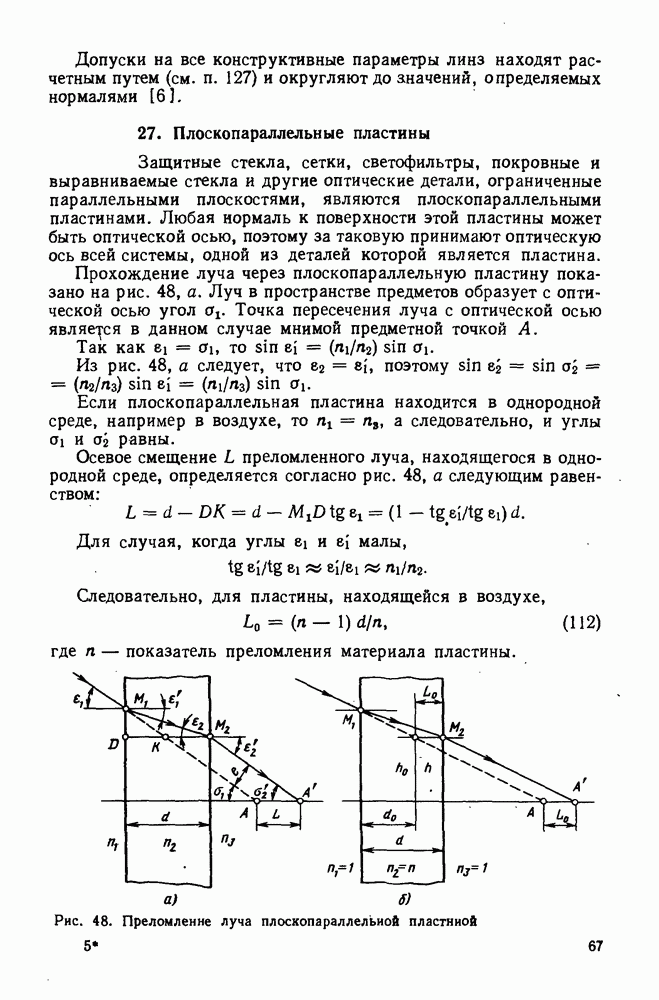
- 27. Плоскопараллельные пластины
- 28. Плоские, сферические и несферические зеркала
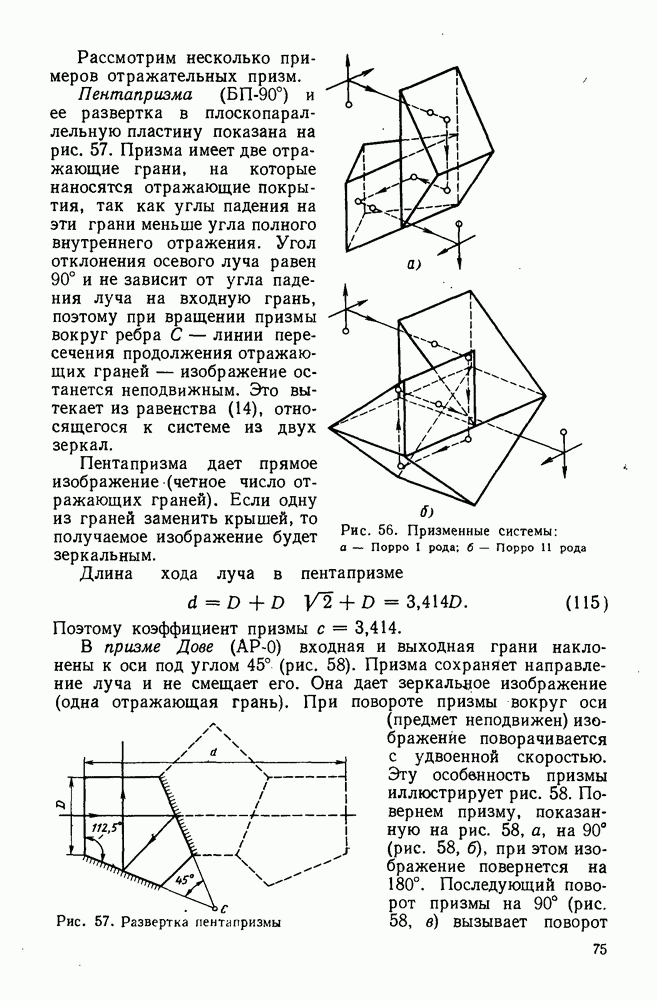
- 29. Отражательные призмы
- 30. Преломляющие призмы и клинья
- 31. Световоды и волоконная оптика
- 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы
- Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ
- 34. Входной и выходной зрачки
- 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна
- 36. Действующее отверстие входного зрачка
- Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ
- 37. Оптическое излучение. Поток излучения
- 38. Энергетические и световые величины и их единицы
- 39. Связь между световыми и энергетическими величинами
- 40. Распространение излучения
- 41. Коэффициент пропускания оптической системы
- 42. Прохождение потока излучения через светофильтр
- 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы
- Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ
- 44. Формулы для расчета хода лучей на ЭВМ
- 45. Формулы для расчета хода бесконечно тонких астигматических пучков
- 46. Выбор начальных данных для расчета хода лучей
- Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 47. Общие положения о вычислении аберраций оптической системы
- 48. Аберрации третьего порядка
- 49. Условия нормировки вспомогательных лучей
- 50. Сферическая аберрация
- 51. Меридиональная кома
- 52. Условие синусов и условие изопланатизма
- 53. Астигматизм и кривизна поверхности изображения
- 54. Дисторсия
- Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ
- 56. Хроматизм увеличения
- 57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков
- Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА
- 58. Устройство глаза
- 59. Основные характеристики глаза
- 60. Недостатки глаза и их коррекция
- Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ
- 61. Назначение и виды осветительных систем
- 62. Оптическая схема прожектора дальнего действия
- 63. Зеркальные осветительные системы
- 64. Линзовые конденсоры
- Глава XIII. ЛУПА И МИКРОСКОП
- 65. Лупа и ее характеристики
- 66. Оптическая схема микроскопа и его основные характеристики
- 67. Разрешающая способность микроскопа
- 68. Глубина изображаемого пространства для микроскопа
- 69. Объективы и окуляры микроскопа
- 70. Осветительные системы микроскопов
- Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА
- 71. Схема телескопической системы и ее основные характеристики
- 72. Разрешающая способность телескопической системы
- 73. Основные сведения об объективах и окулярах телескопических систем
- 74. Фокусировка окуляра телескопической системы
- 75. Применение коллектива в зрительной трубе
- 76. Расчет зрительной трубы Кеплера
- 77. Схема зрительной трубы Галилея и ее расчет
- 78. Расчет призменного монокуляра
- 79. Расчет зрительной трубы с линзовой оборачивакщей системой
- 80. Основные сведения о зрительных трубах переменного увеличения
- 81. Стереоскопические телескопические системы
- 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет
- Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ
- 83. Основные характеристики фотообъектива
- 84. Разрешающая способность и функция передачи модуляции фотографической системы
- 85. Глубина изображаемого пространства и глубина резкости
- 86. Определение выдержки при фотографировании
- 87. Основные типы фотографических объективов
- Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ
- 88. Оптические характеристики передающих и приемных телевизионных трубок
- 89. Объективы передающих телевизионных камер и их основные характеристики
- 90. Разрешающая способность и ФПМ телевизионной системы
- 91. Телевизионная система с «бегущим лучом»
- Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ
- 92. Виды и особенности проекционных систем
- 93. Эпископическая проекционная система
- 94. Диаскопическая проекционная система
- 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой
- Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
- 96. Некоторые характеристики и параметры приемников излучения
- 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам
- 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам
- 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника
- 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника
- 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке
- 102. Некоторые принципиальные схемы оптических фотоэлектрических систем
- Глава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ
- 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой
- 105. Оптические системы для концентрации излучения лазера
- 106. Оптические системы для уменьшения расходимости лазерного пучка
- 107. Оптическая фотоэлектрическая система с лазером
- 108. Оптические системы, применяемые в голографии
- Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ
- 109. Характеристика трансформированного изображения и его получение
- 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты
- 111. Цилиндрическая афокальная система
- Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ
- 112. Общие сведения о методах аберрационного расчета оптических систем
- 113. Допустимые остаточные аберрации в различных оптических системах
- 114. Связь между параметрами 1-го и 2-го вспомогательных лучей
- 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов
- 116. Основные параметры тонких компонентов
- 117. Аберрации оптических систем с иесферическими поверхностями
- 118. Расчет оптической системы на минимум сферической аберрации
- 119. Расчет двухлинзового склеенного объектива
- 120. Расчет двухливэового несклеенного объектива
- 121. Расчет светосильного двухкомпоиентного объектива
- 122. Расчет объектива типа триплета
- 123. Расчет зеркальных систем
- 124. Расчет зеркально-линзовых систем
- 125. Об автоматизированной коррекции оптических систем на ЭВМ
- 126. Суммирование аберраций
- 127. О допусках в оптических системах
- 128. Оценка качества изображения по результатам аберрационного расчета
- 129. Волновая аберрация оптической системы