| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
17.3. ПЛАЗМА В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
Сравнивая (17.2.12) с выражением, характеризующим кеплеровское движение по круговой орбите радиуса 

можно сформулировать общую теорему: если в диполъном магнитном поле вращающегося центрального тела находится элемент плазмы в состоянии частичной коротации, его кинетическая энергия равна двум третям кинетической энергии кеплеровского движения по круговой орбите с тем же радиусом.
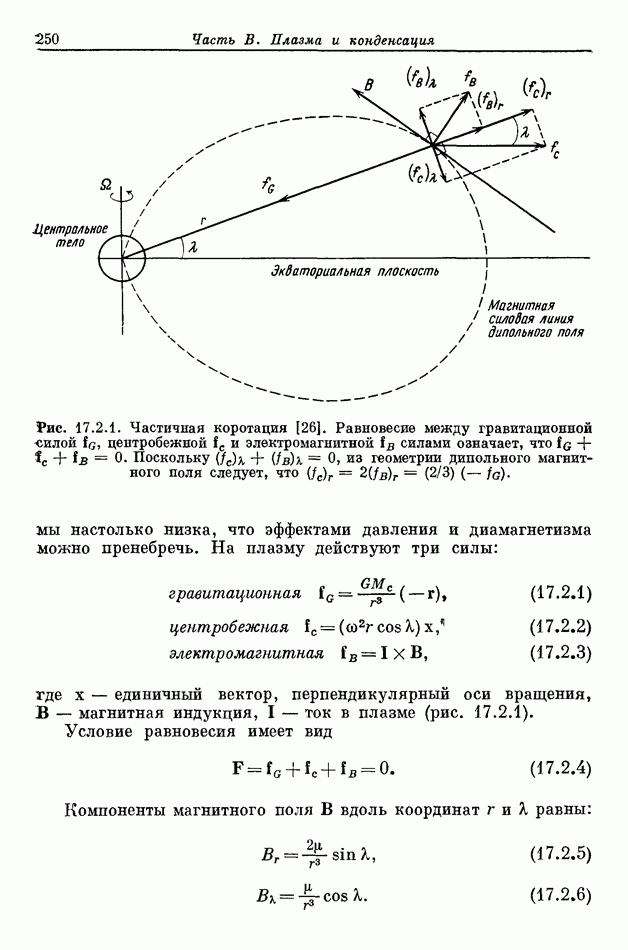
Коэффициент 2/3 получается из геометрии дипольного поля и вводится потому, что направление центробежной силы образует меньший угол с магнитной силовой линией, чем направление гравитационной силы. Элемент плазмы удерживается против действия гравитационной силы частично центробежной силой и частично силой, возникающей при взаимодействии тока  с магнитным полем. Проведенный выше анализ, строго говоря, применим только к плазме, находящейся на ненулевых широтах. Экваториальная плоскость с точки зрения математики представляет собой особенность. Однако поскольку эта плоскость будет занята диском из зерен и газа толщиной в несколько градусов, то математическая особенность не представляет интереса для физики.
с магнитным полем. Проведенный выше анализ, строго говоря, применим только к плазме, находящейся на ненулевых широтах. Экваториальная плоскость с точки зрения математики представляет собой особенность. Однако поскольку эта плоскость будет занята диском из зерен и газа толщиной в несколько градусов, то математическая особенность не представляет интереса для физики.
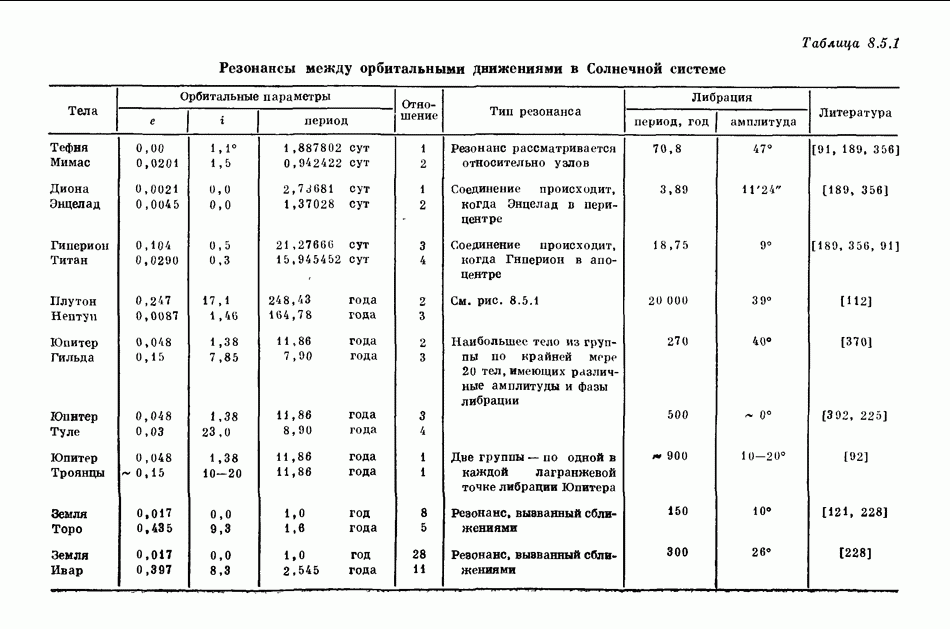
В табл. 17.3.1 проведено сравнение энергии и момента количества движения кеплеровского движения по круговой орбите с круговым движением замагниченной плазмы.
Таблица 17.3.1 (см. скан) Сравнение кеплеровского движения и частичной коротации
Если плазма обладает значительной тепловой энергией, диамагнитное отталкивание от дипольного поля создает направленную наружу силу, имеющую компоненту, которая прибавляется к центробежной силе. При этом коэффициент в уравнении (17.2.12) становится меньше 2/3. Можно показать, что этот эффект значителен, если тепловая энергия  степень ионизации,
степень ионизации,  — постоянная Больцмана, а Те и
— постоянная Больцмана, а Те и  электронная и ионная температуры) сравнима с кинетической энергией частицы плазмы
электронная и ионная температуры) сравнима с кинетической энергией частицы плазмы  Возьмем для примера среду в окрестности Сатурна и положим, что
Возьмем для примера среду в окрестности Сатурна и положим, что  (равно орбитальной скорости Мимаса) и
(равно орбитальной скорости Мимаса) и  Отсюда найдем, что если
Отсюда найдем, что если  то
то  следовательно, в рассмотренном нами случае роль температуры, вероятно, не очень важна.
следовательно, в рассмотренном нами случае роль температуры, вероятно, не очень важна.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- От редактора перевода
- Предисловие
- I. Введение
- 1.1. ФУНДАМЕНТАЛЬНЫЙ ПОДХОД К ПРОБЛЕМЕ
- 1.2. СИСТЕМА ПЛАНЕТ — СИСТЕМЫ СПУТНИКОВ
- 1.3. ПЯТЬ ЭТАПОВ ЭВОЛЮЦИИ
- 1.4. НАПРАВЛЯЮЩИЕ ПРОЦЕССЫ ОТДЕЛЬНЫХ ЭТАПОВ ЭВОЛЮЦИИ
- 1.5. ТРЕБОВАНИЯ К МОДЕЛЯМ И ОГРАНИЧЕНИЯ
- Часть А. Современное состояние и основные законы
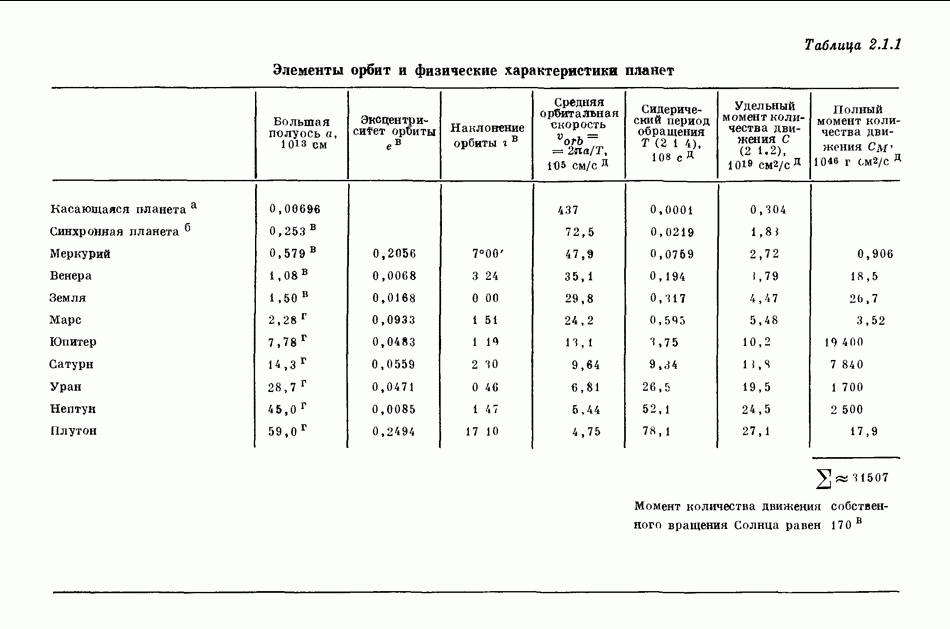
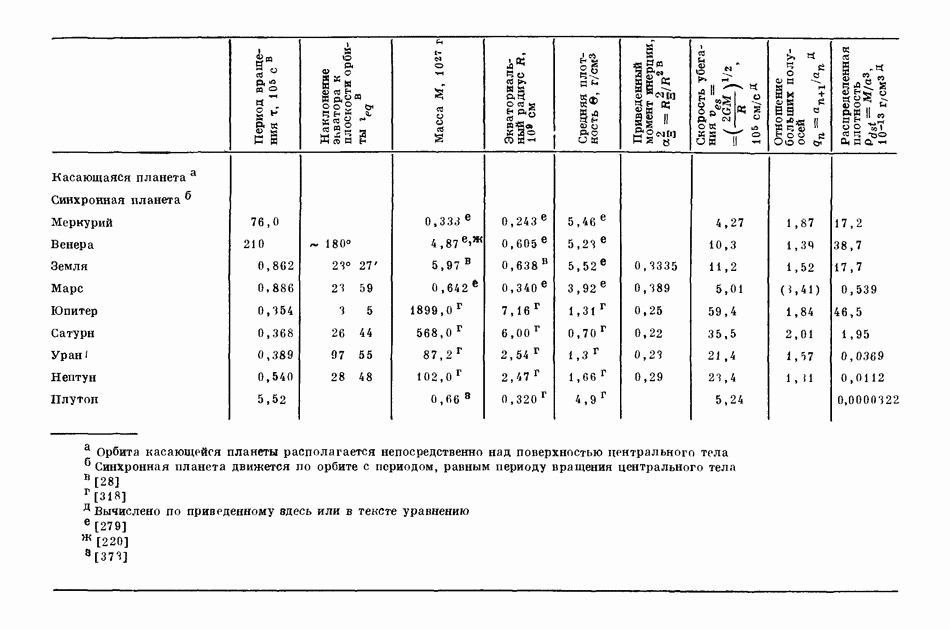
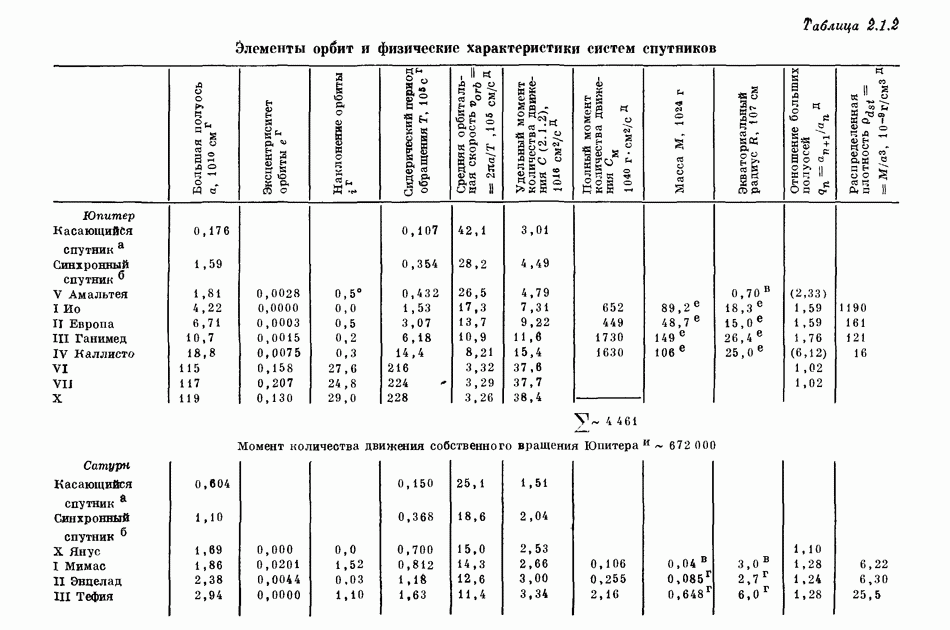
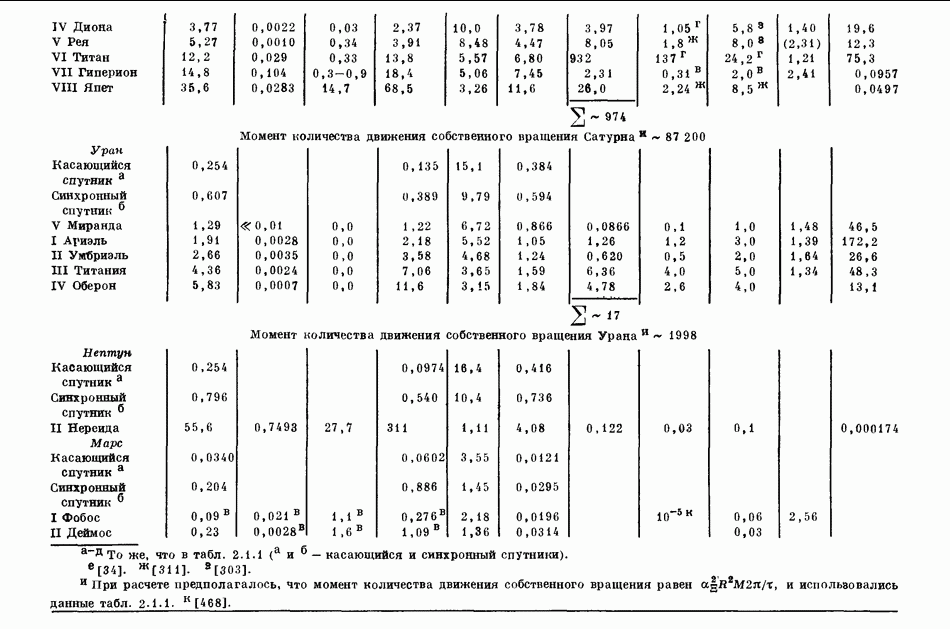
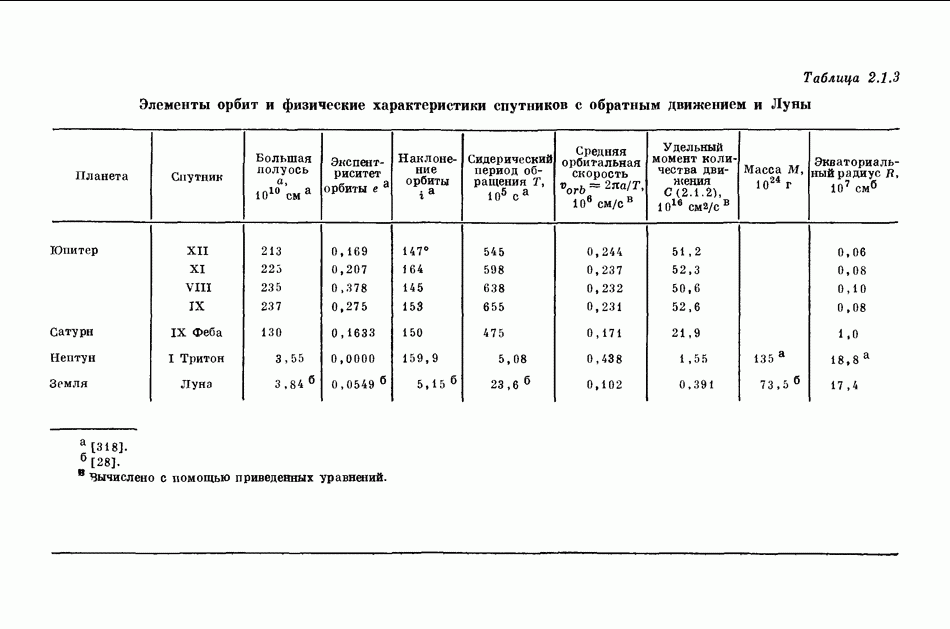
- 2.1. ХАРАКТЕРИСТИКИ ОРБИТ ПЛАНЕТ И СПУТНИКОВ
- 2.2. ФИЗИЧЕСКИЕ СВОЙСТВА ПЛАНЕТ И СПУТНИКОВ
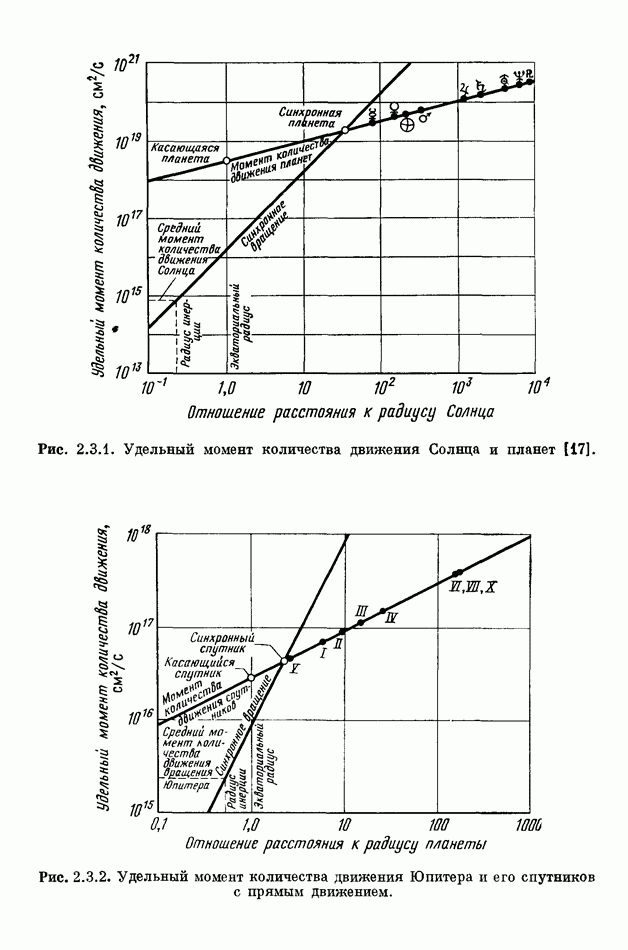
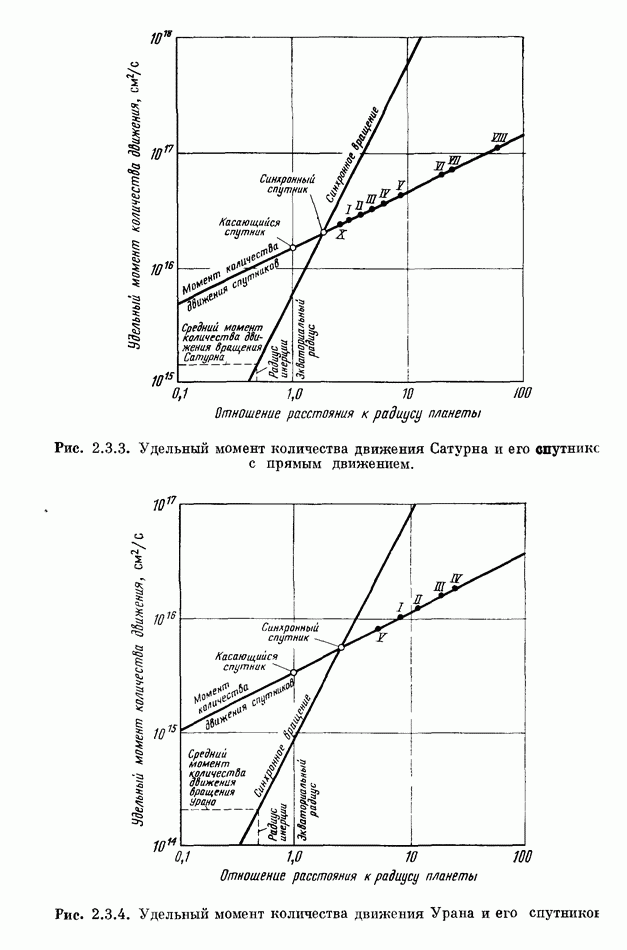
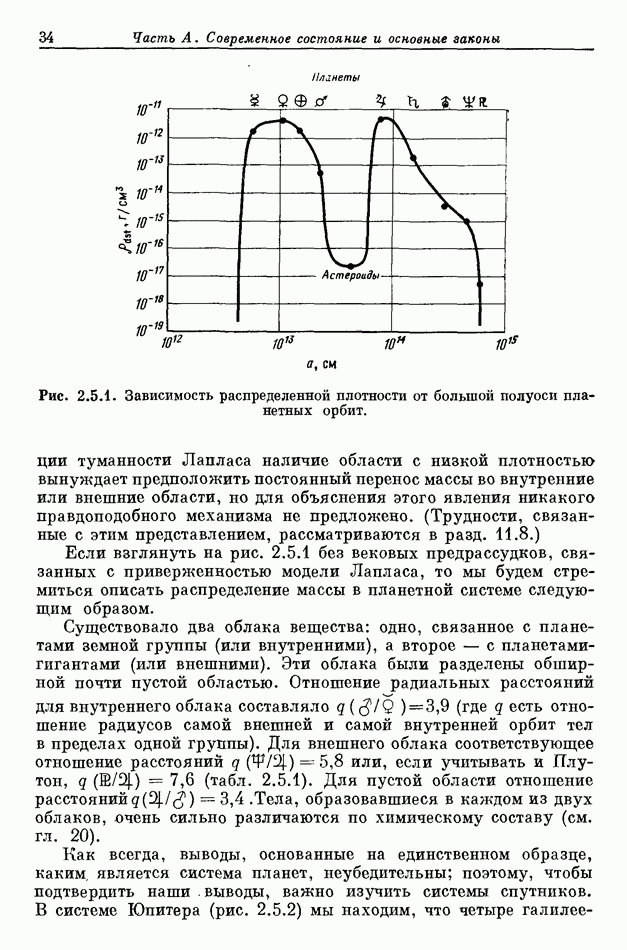
- 2.3. СПУТНИКИ С ПРЯМЫМ И ОБРАТНЫМ ДВИЖЕНИЕМ
- 2.4. МОДЕЛЬ ЛАПЛАСА И ФУНКЦИЯ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
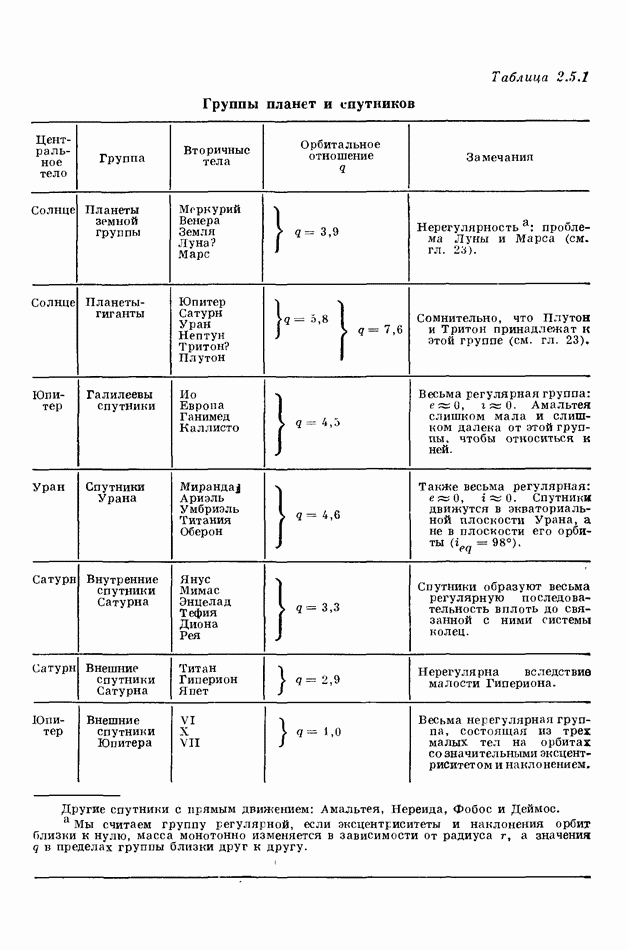
- 2.5. ОБСУЖДЕНИЕ ГРАФИКОВ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
- 2.6. «ЗАКОН» ТИЦИУСА — БОДЕ
- 3. Движение планет и спутников
- 3.1. МЕТОД ВЕДУЩЕГО ЦЕНТРА В ЗАДАЧАХ НЕБЕСНОЙ МЕХАНИКИ
- 3.2. КРУГОВЫЕ ОРБИТЫ
- 3.3. КОЛЕБАНИЯ, ВИДОИЗМЕНЯЮЩИЕ КРУГОВУЮ ОРБИТУ
- 3.4. ДВИЖЕНИЕ В ГРАВИТАЦИОННОМ ПОЛЕ, ОБРАТНО ПРОПОРЦИОНАЛЬНОМ КВАДРАТУ РАССТОЯНИЯ
- 3.5. НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И БОЛЬШИЕ ЭКСЦЕНТРИСИТЕТЫ
- 3.6. ДВИЖЕНИЕ В ПОЛЕ ВРАЩАЮЩЕГОСЯ ЦЕНТРАЛЬНОГО ТЕЛА
- 3.7. ДВИЖЕНИЕ ПЛАНЕТ, ВОЗМУЩАЕМОЕ ДРУГИМИ ПЛАНЕТАМИ
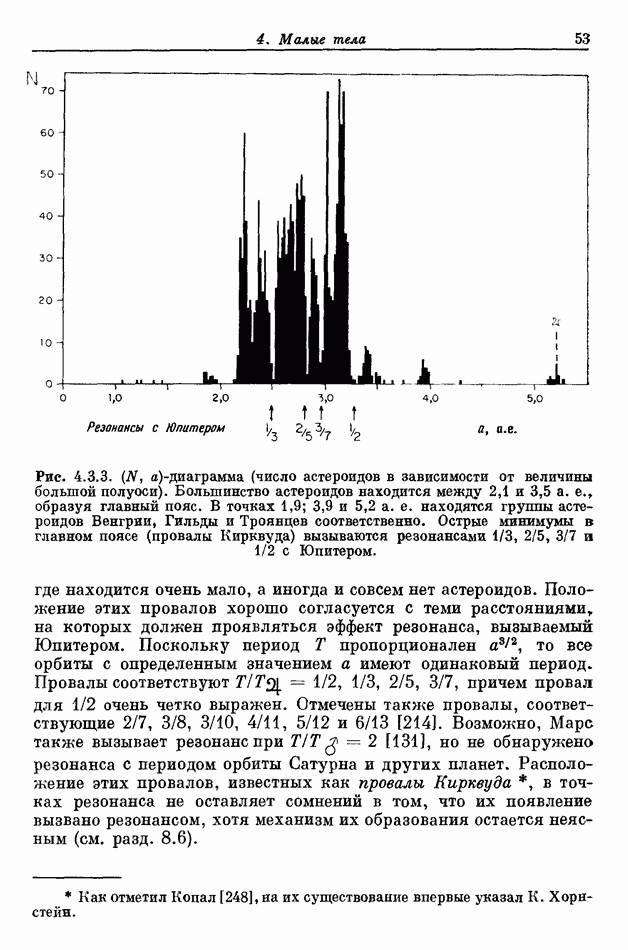
- 4. Малые тела
- 4.2. РАЗЛИЧИЕ В ЭВОЛЮЦИИ БОЛЬШИХ И МАЛЫХ ТЕЛ
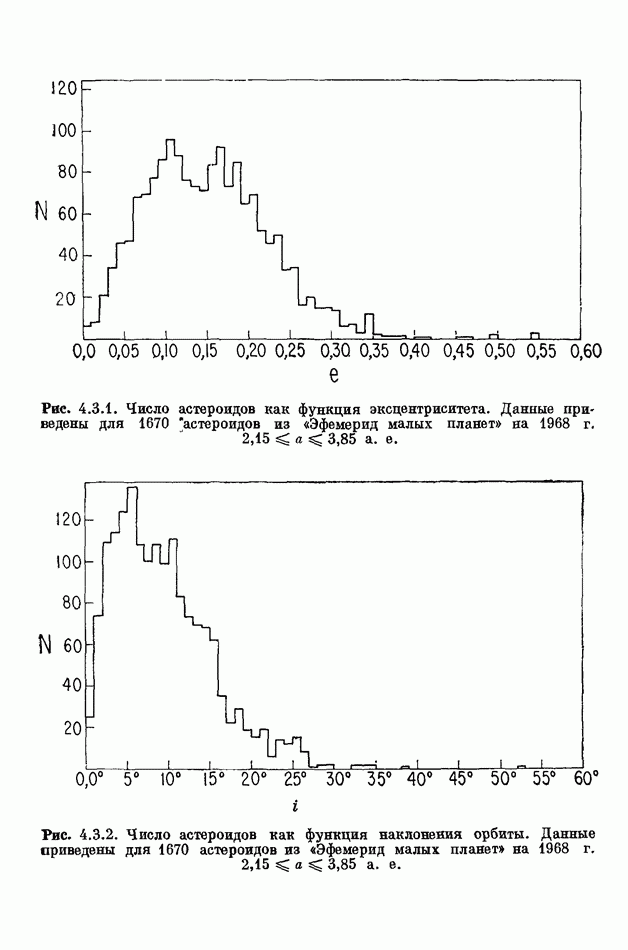
- 4.3. ГЛАВНЫЙ ПОЯС АСТЕРОИДОВ
- 4.3.1. НЕНАБЛЮДАЕМЫЕ АСТЕРОИДЫ
- 4.3.2. СЕМЕЙСТВА ХИРАЯМЫ
- 4.3.3. СТРУЙНЫЕ ПОТОКИ АСТЕРОИДОВ
- 4.3.4. ЭВОЛЮЦИЯ ГЛАВНОГО ПОЯСА
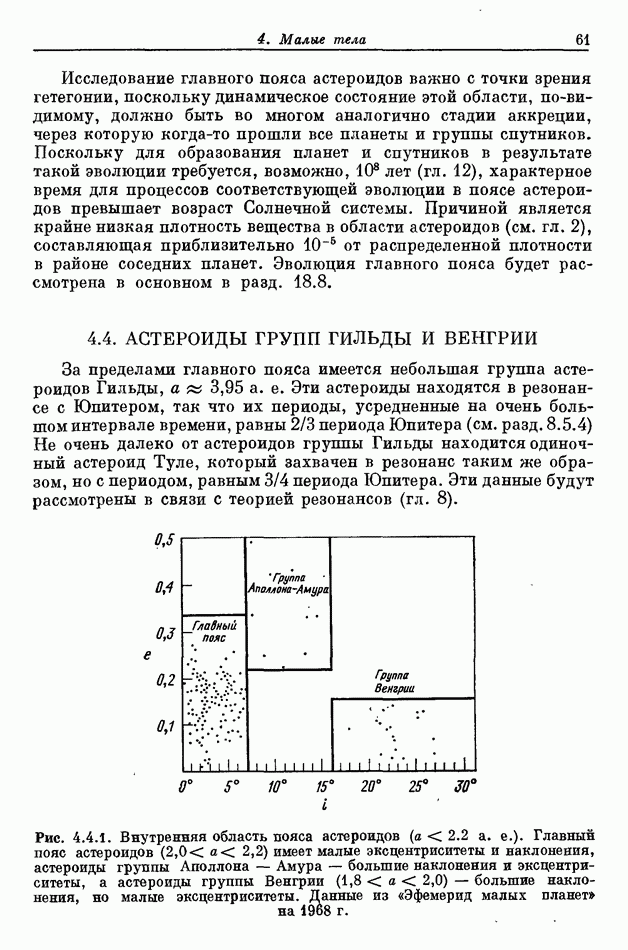
- 4.4. АСТЕРОИДЫ ГРУПП ГИЛЬДЫ И ВЕНГРИИ
- 4.5. ТРОЯНЦЫ
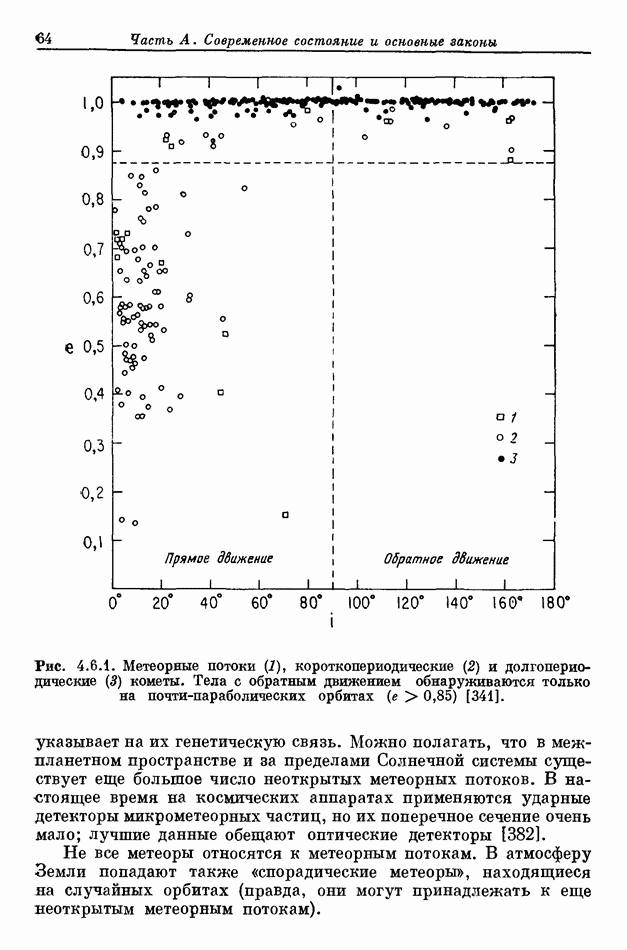
- 4.6. СЕМЕЙСТВО КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 4.6.2. МЕТЕОРНЫЕ ПОТОКИ
- 4.6.3. ДОЛГОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 4.6.4. КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 5. Силы, действующие на малые тела
- 5.2. ГРАВИТАЦИОННЫЕ ВОЗДЕЙСТВИЯ
- 5.2.1. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ
- 5.2.2. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ, ВОЗМУЩАЕМОЕ СТОЛКНОВЕНИЯМИ
- 5.3. ЭЛЕКТРОМАГНИТНЫЕ ЭФФЕКТЫ
- 5.4. ГРАНИЦА МЕЖДУ ДВИЖЕНИЯМИ, ОБУСЛОВЛЕННЫМИ ГРАВИТАЦИОННЫМИ И ЭЛЕКТРОМАГНИТНЫМИ СИЛАМИ
- 5.5. РАДИАЦИОННЫЕ ЭФФЕКТЫ
- 5.5.1. РАДИАЦИОННОЕ ДАВЛЕНИЕ
- 5.5.2. ЭФФЕКТ ПОЙНТИНГА — РОБЕРТСОНА
- 5.6. ВЫВОДЫ
- 6. Кеплеровское движение взаимодействующих тел: струйные потоки
- 6.2. МЕЖПЛАНЕТНАЯ СРЕДА
- 6.3. ЭФФЕКТЫ СТОЛКНОВЕНИЙ
- 6.4. ПРОСТАЯ МОДЕЛЬ СТРУЙНОГО ПОТОКА
- 6.4.1. ДВИЖЕНИЕ ЧАСТИЦ, ИСПУСКАЕМЫХ СО СПУТНИКА
- 6.4.2. СРАВНЕНИЕ С ТОРОМ ИО
- 6.4.3. ЭФФЕКТ СТОЛКНОВЕНИЙ
- 6.5. ВЫВОДЫ ИЗ МОДЕЛИ СТРУЙНОГО ПОТОКА
- 6.6. СТРУЙНЫЙ ПОТОК И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ
- 6.7. ПРОСТАЯ МОДЕЛЬ ОТРИЦАТЕЛЬНОЙ ДИФФУЗИИ
- 6.8. ПРОДОЛЖИТЕЛЬНОСТЬ СЖАТИЯ СТРУЙНОГО ПОТОКА
- 6.9. СТОЛКНОВЕНИЯ ЧАСТИЦ СО СТРУЙНЫМ ПОТОКОМ
- 6.10. СТРУЙНЫЕ ПОТОКИ КАК НЕБЕСНЫЕ ОБЪЕКТЫ
- 7. Столкновения: фрагментация и аккреция
- 7.1. ОБРАЗОВАНИЕ МАЛЫХ ТЕЛ: ФРАГМЕНТАЦИЯ И АККРЕЦИЯ
- 7.2. РАСПРЕДЕЛЕНИЕ ПО РАЗМЕРАМ
- 7.3. ТРИ ПРОСТЫЕ МОДЕЛИ
- 7.3.2. ФРАГМЕНТАЦИЯ
- 7.3.3. ДАННЫЕ НАБЛЮДЕНИЙ, ИМЕЮЩИЕ ОТНОШЕНИЕ К МОДЕЛЯМ
- 7.4. ПЕРЕХОД ОТ ФРАГМЕНТАЦИИ К АККРЕЦИИ
- 8. Резонансные структуры в Солнечной системе
- 8.1. РЕЗОНАНСЫ В СОЛНЕЧНОЙ СИСТЕМЕ
- 8.2. РЕЗОНАНС И КОЛЕБАНИЯ МАЯТНИКА
- 8.3. ПРОСТАЯ МОДЕЛЬ РЕЗОНАНСА
- 8.4. ОТКЛОНЕНИЯ ОТ ТОЧНОГО РЕЗОНАНСА
- 8.5. РЕЗОНАНС МЕЖДУ ОРБИТАЛЬНЫМИ ДВИЖЕНИЯМИ
- 8.5.2. РЕЗОНАНС ЗЕМЛЯ — ТОРО И ДРУГИЕ РЕЗОНАНСЫ ЗЕМЛИ И АСТЕРОИДОВ
- 8.5.3. ТРОЯНЦЫ
- 8.5.4. АСТЕРОИДЫ ГРУППЫ ГИЛЬДЫ
- 8.5.5. ТИТАН — ГИПЕРИОН
- 8.5.6. ДИОНА — ЭНЦЕЛАД
- 8.5.7. ТЕФИЯ — МИМАС
- 8.5.8 ИО — ЕВРОПА — ГАНИМЕД
- 8.6. ПРОВАЛЫ КИРКВУДА
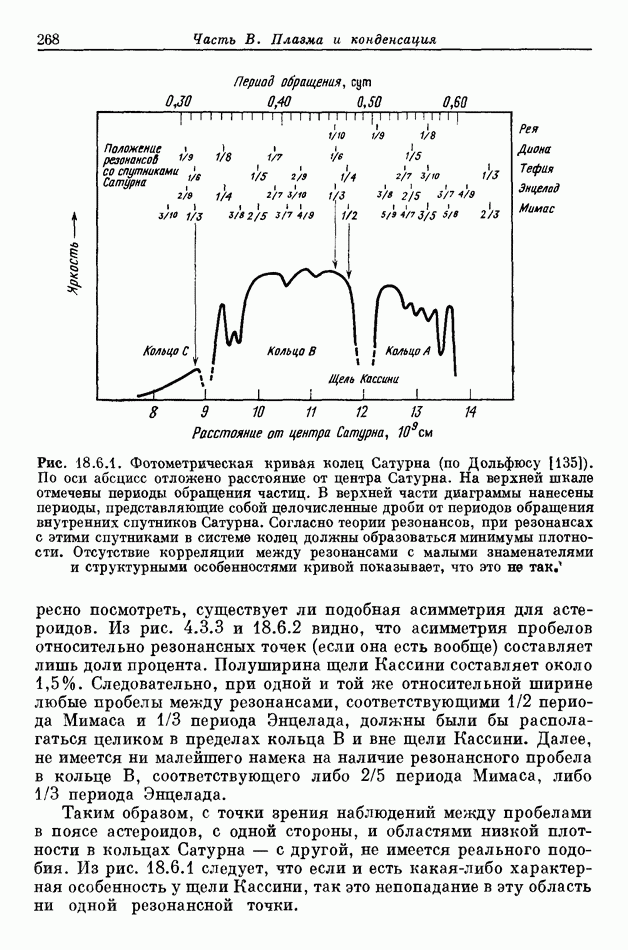
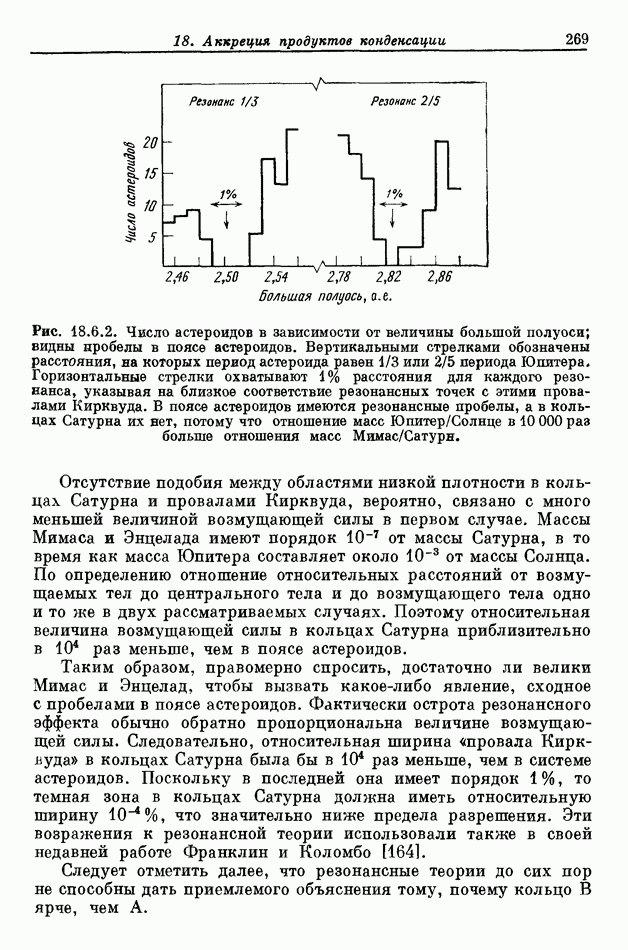
- 8.7. ОБ ОТСУТСТВИИ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В СИСТЕМЕ КОЛЕЦ САТУРНА
- 8.8. РЕЗОНАНСЫ МЕЖДУ ВРАЩЕНИЕМ И ОРБИТАЛЬНЫМ ДВИЖЕНИЕМ
- 8.9. ПОЧТИ-СОИЗМЕРИМОСТИ
- 9. Вращение и приливы
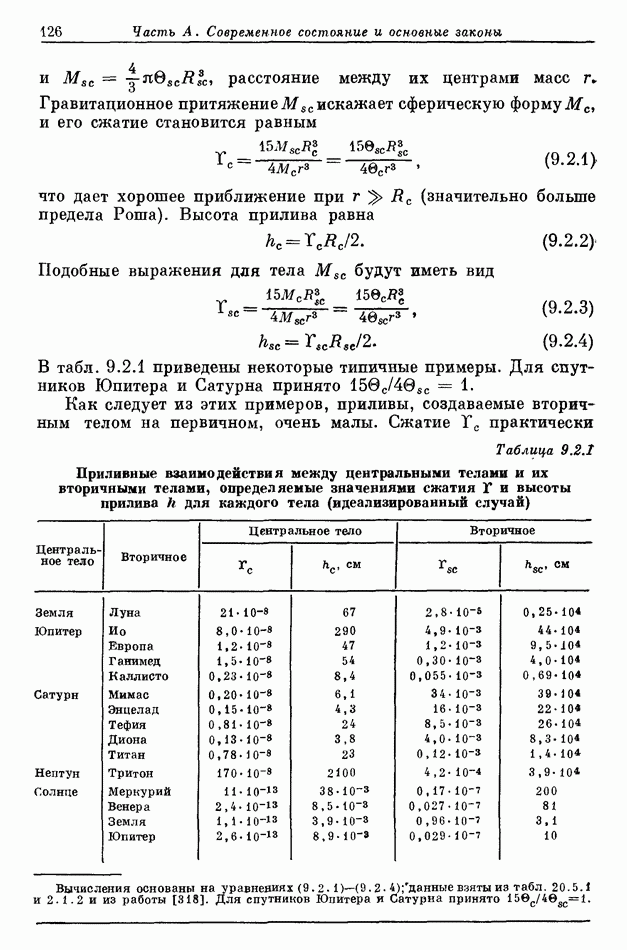
- 9.2. АМПЛИТУДА ПРИЛИВОВ
- 9.3. ПРИЛИВНОЕ ТОРМОЖЕНИЕ ВРАЩЕНИЯ ЦЕНТРАЛЬНОГО ТЕЛА
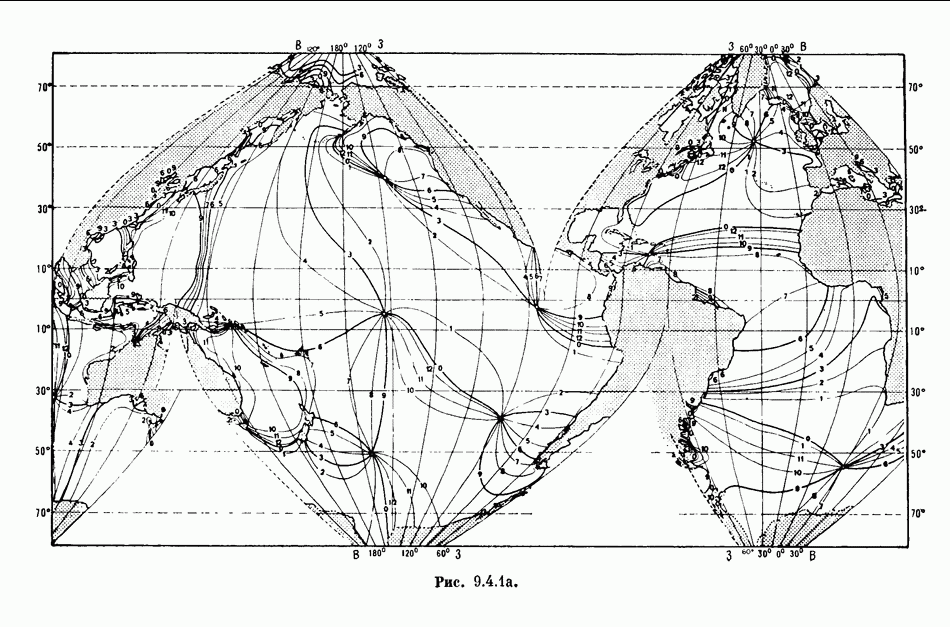
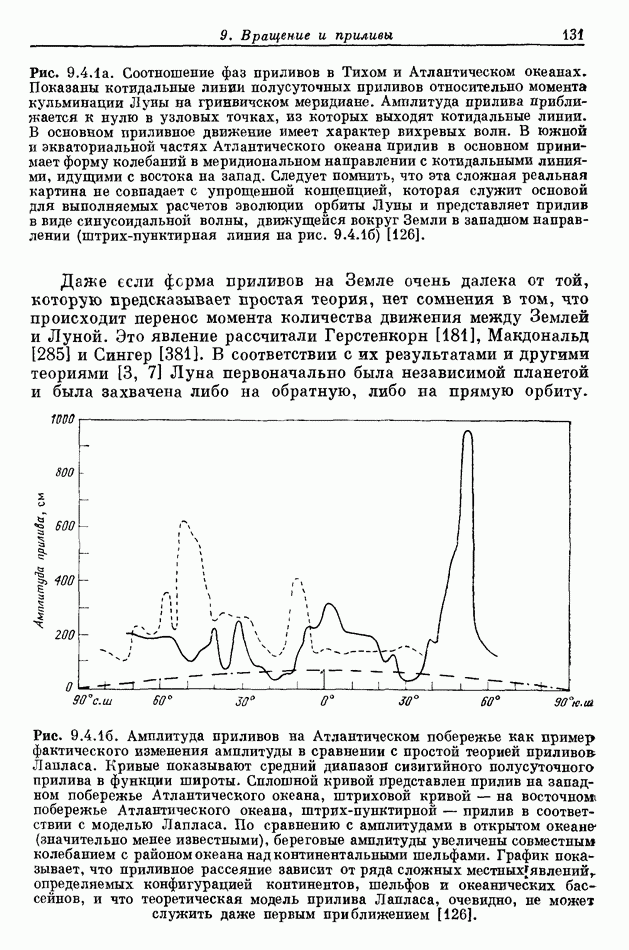
- 9.4. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ ПРИЛИВАМИ, ВЫЗЫВАЕМЫМИ СПУТНИКАМИ
- 9.5. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ СОЛНЕЧНЫМИ ПРИЛИВАМИ
- 9.6. ЭВОЛЮЦИЯ СПУТНИКОВ ПЛАНЕТ ПОД ДЕЙСТВИЕМ ПРИЛИВОВ
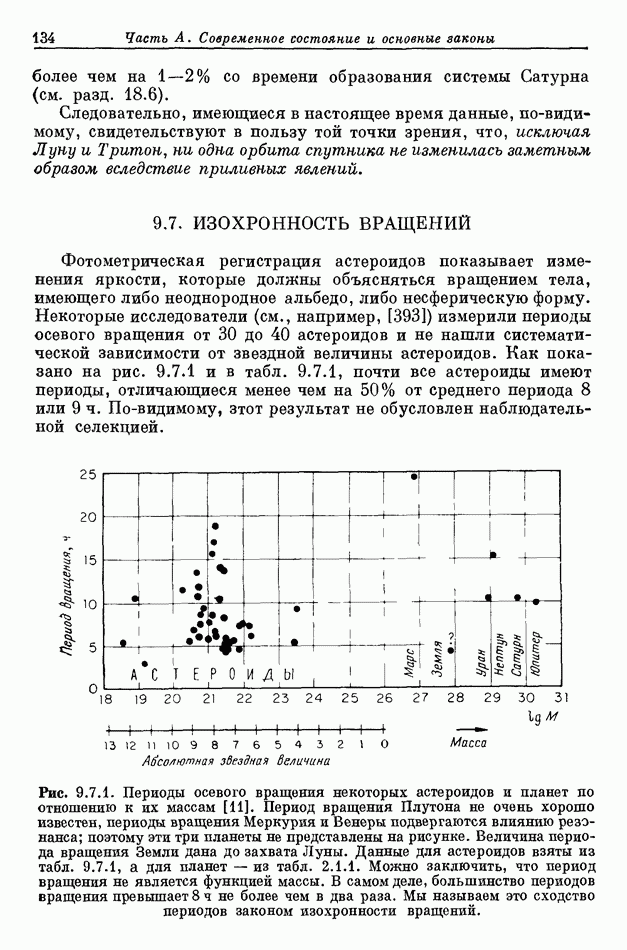
- 9.7. ИЗОХРОННОСТЬ ВРАЩЕНИЙ
- 9.8. ВЫВОДЫ ИЗ ИЗОХРОННОСТИ ВРАЩЕНИЙ
- 10. Постаккреционные изменения в Солнечной системе
- 10.1. УСТОЙЧИВОСТЬ ОРБИТ
- 10.2. РЕЗОНАНС И УСТОЙЧИВОСТЬ
- 10.3. УСТОЙЧИВОСТЬ КОЛЕЦ САТУРНА И ПОЯСА АСТЕРОИДОВ
- 10.4. ПОСТОЯНСТВО ВРАЩЕНИЙ
- 10.5. О ВОЗМОЖНОСТИ. РЕКОНСТРУКЦИИ ГЕТЕГОННЫХ ПРОЦЕССОВ
- Часть Б. Аккреция небесных тел
- 11.2. ГРАВИТАЦИОННЫЙ КОЛЛАПС ГАЗОВОГО ОБЛАКА
- 11.2.1. ВОЗРАЖЕНИЯ ПРОТИВ ГРАВИТАЦИОННОГО КОЛЛАПСА КАК МЕХАНИЗМА ОБРАЗОВАНИЯ ПЛАНЕТ И СПУТНИКОВ
- 11.3. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ: АККРЕЦИЯ ПУТЕМ ЗАХВАТА ЧАСТИЦ ИЛИ ГАЗА
- 11.4. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5. НЕГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5.1. ВОЗРАЖЕНИЯ ПРОТИВ ПРОЦЕССА НЕГРАВИТАЦИОННОЙ АККРЕЦИИ
- 11.5.2. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ
- 11.5.3. ЭЛЕКТРОСТАТИЧЕСКИ ПОЛЯРИЗОВАННЫЕ ЗЕРНА
- 11.5.4. РЫХЛЫЕ СКОПЛЕНИЯ
- 11.6. АККРЕЦИЯ РЕЗОНАНСНО ЗАХВАЧЕННЫХ ЗЕРЕН
- 11.7. НЕОБХОДИМЫЕ СВОЙСТВА ПРОЦЕССА АККРЕЦИИ
- 11.8. СОВРЕМЕННОЕ СОСТОЯНИЕ АСТЕРОИДОВ, МЕТЕОРНЫХ ТЕЛ И КОМЕТ И ГИПОТЕЗА ВЗОРВАВШЕЙСЯ ПЛАНЕТЫ
- 12. Об аккреции планет и спутников
- 12.1. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ
- 12.2. СТРУЙНЫЙ ПОТОК КАК ПРОМЕЖУТОЧНАЯ СТАДИЯ В ОБРАЗОВАНИИ ПЛАНЕТ И СПУТНИКОВ
- 12.3. АККРЕЦИЯ ЗАРОДЫША
- 12.4. БАЛАНС МАССЫ СТРУЙНОГО ПОТОКА
- 12.5. ЭНЕРГЕТИЧЕСКИЙ БАЛАНС В СТРУЙНОМ ПОТОКЕ
- 12.6. АККРЕЦИЯ ПРИ ПОСТОЯННОЙ СКОРОСТИ ПОСТУПЛЕНИЯ ВЕЩЕСТВА В СТРУЙНЫЙ ПОТОК
- 12.7. ЗАМЕЧАНИЕ
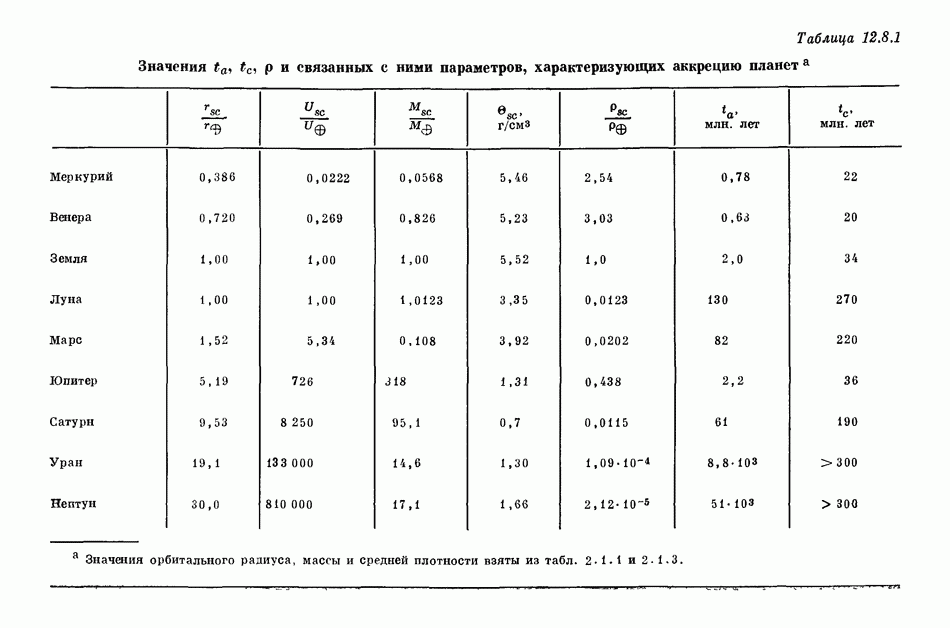
- 12.8. ЧИСЛЕННЫЕ ЗНАЧЕНИЯ
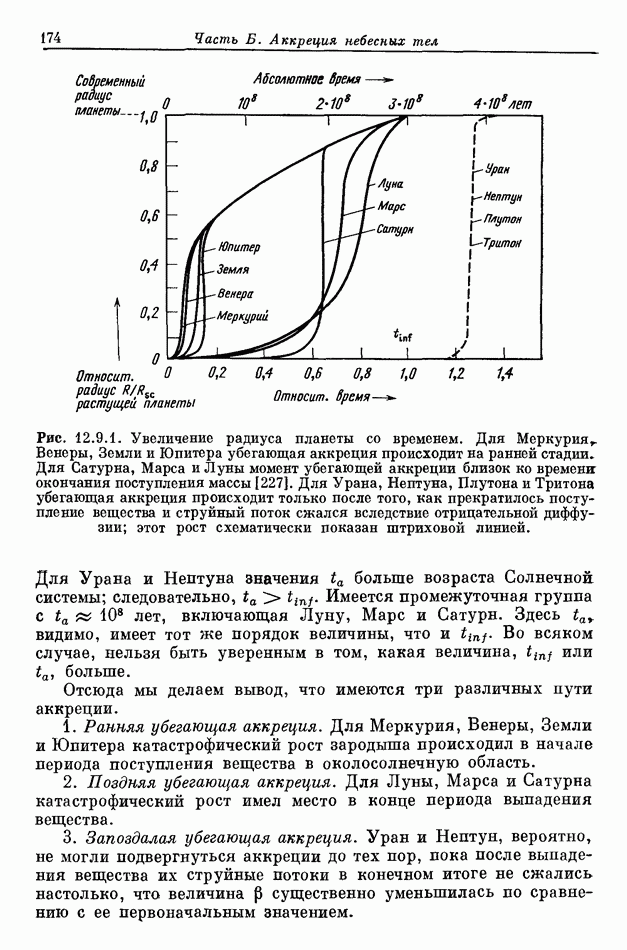
- 12.9. ВЫВОДЫ ОТНОСИТЕЛЬНО РАЗЛИЧНЫХ ТИПОВ АККРЕЦИИ
- 12.10. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ТЕЛА НА РАННЕЙ СТАДИИ ЕГО СУЩЕСТВОВАНИЯ
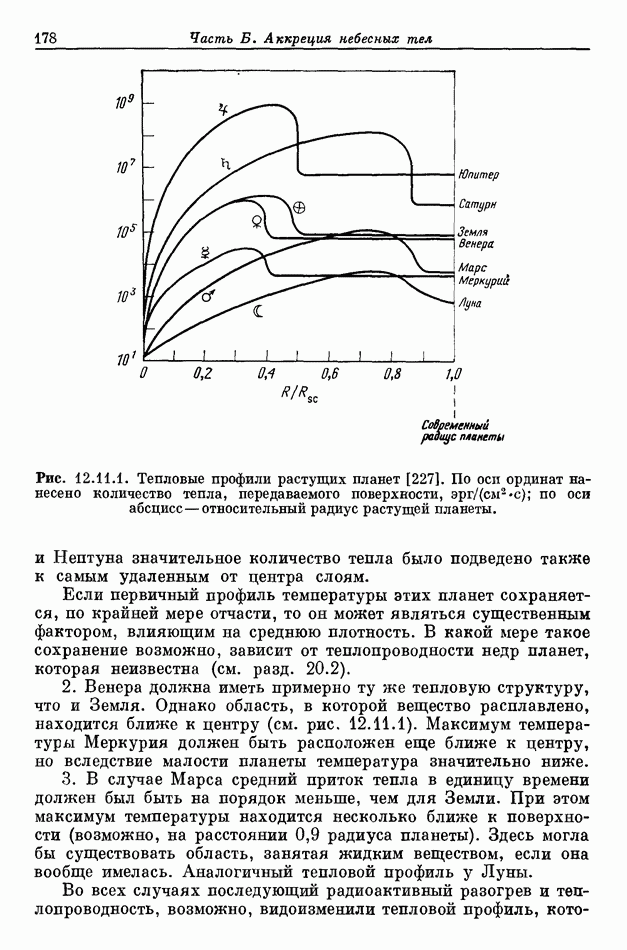
- 12.11. ВЫВОДЫ О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ ПЛАНЕТ
- 12.12. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ
- 12.13. ДИФФЕРЕНЦИАЦИЯ ВЕЩЕСТВА, ОБУСЛОВЛЕННАЯ ТЕПЛОВЫМ ФРОНТОМ АККРЕЦИИ
- 13. Вращение и аккреция
- 13.1. СОУДАРЕНИЯ ЗЕРЕН И СОБСТВЕННОЕ ВРАЩЕНИЕ ЗАРОДЫША
- 13.2. АККРЕЦИЯ С КРУГОВЫХ ОРБИТ НА НЕГРАВИТИРУЮЩИЙ ЗАРОДЫШ
- 13.3. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
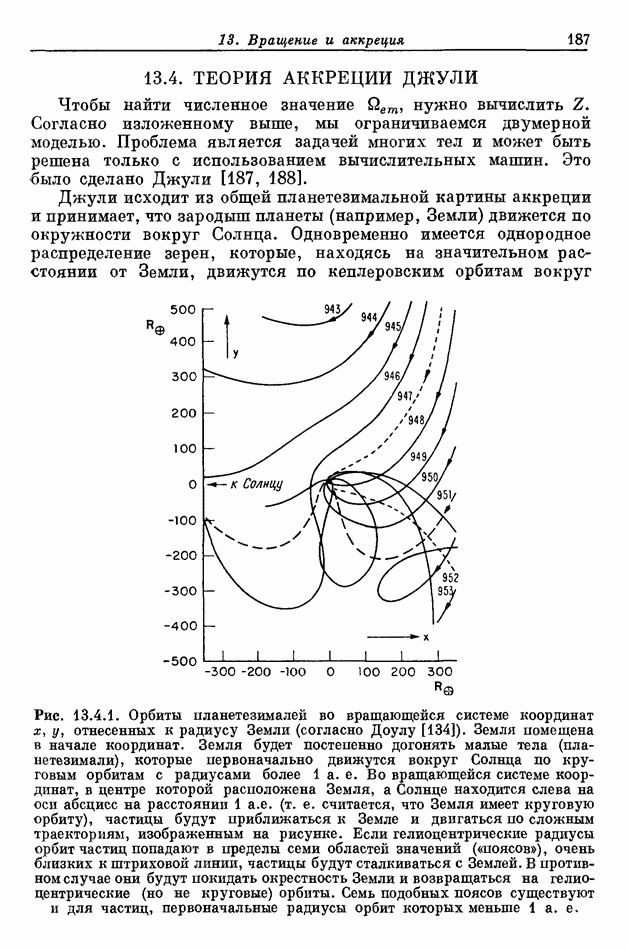
- 13.4. ТЕОРИЯ АККРЕЦИИ ДЖУЛИ
- 13.5. СТАТИСТИЧЕСКАЯ ТЕОРИЯ АККРЕЦИИ
- 13.5.1. АККРЕЦИЯ НА СТАДИИ, ПРЕДШЕСТВУЮЩЕЙ УБЕГАЮЩЕЙ АККРЕЦИИ
- 13.6. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ И СОБСТВЕННОЕ ВРАЩЕНИЕ ПЛАНЕТ
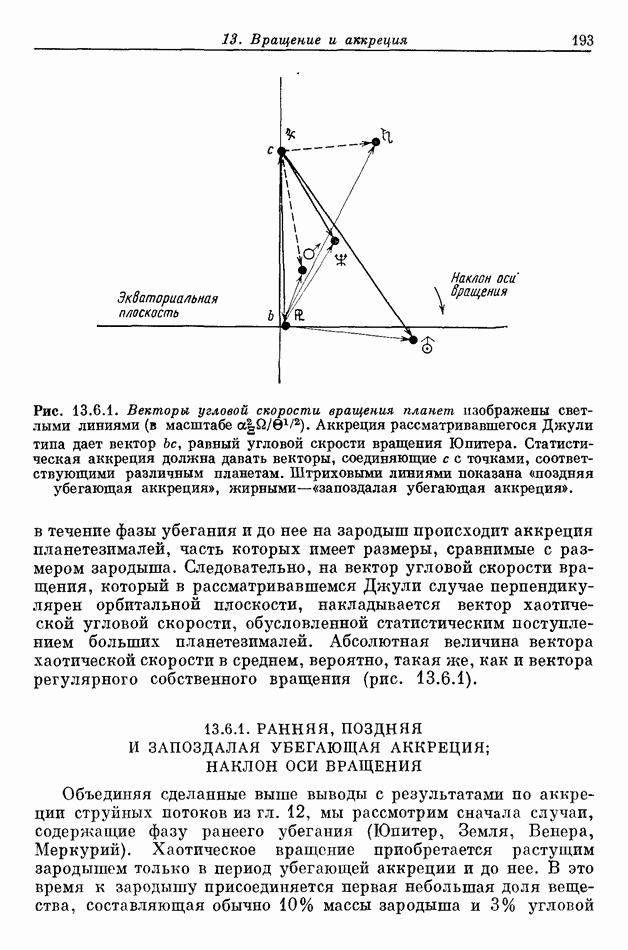
- 13.6.1. РАННЯЯ, ПОЗДНЯЯ И ЗАПОЗДАЛАЯ УБЕГАЮЩАЯ АККРЕЦИЯ; НАКЛОН ОСИ ВРАЩЕНИЯ
- 13.6.2. ПЕРИОД ВРАЩЕНИЯ
- 13.6.3. ОБРАТНОЕ ВРАЩЕНИЕ ВЕНЕРЫ
- 14. Взаимосвязи между кометами и метеорными телами
- 14.2. ПОЛОЖИТЕЛЬНАЯ И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ; МЕТЕОРНЫЕ ПОТОКИ КАК СТРУЙНЫЕ ПОТОКИ
- 14.3. МЕХАНИЗМ АККРЕЦИИ В МЕТЕОРНЫХ ПОТОКАХ
- 14.4. НАБЛЮДЕНИЯ ОБРАЗОВАНИЯ КОМЕТ В МЕТЕОРНЫХ ПОТОКАХ
- 14.5. ДОЛГО- И КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 14.6 ВЫВОДЫ О ПРИРОДЕ КОМЕТ, ОСНОВАННЫЕ НА ЭМИССИОННЫХ ХАРАКТЕРИСТИКАХ
- 14.7. АНАЛОГИИ МЕЖДУ ПОТОКАМИ КОМЕТ И АСТЕРОИДОВ
- 14.8. СРАВНЕНИЕ С АККРЕЦИЕЙ ПЛАНЕТ И СПУТНИКОВ
- Часть В. Плазма и конденсация
- 15. Физика плазмы и гетегония
- 15.2 СВЯЗЬ МЕЖДУ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКОЙ ПЛАЗМЫ
- 15.3. ПЕРВОЕ И ВТОРОЕ ПРИБЛИЖЕНИЯ В ФИЗИКЕ КОСМИЧЕСКОЙ ПЛАЗМЫ
- 15.3.3. НЕКОТОРЫЕ ЛАБОРАТОРНЫЕ ЭКСПЕРИМЕНТЫ, ОТНОСЯЩИЕСЯ К КОСМИЧЕСКОЙ ФИЗИКЕ
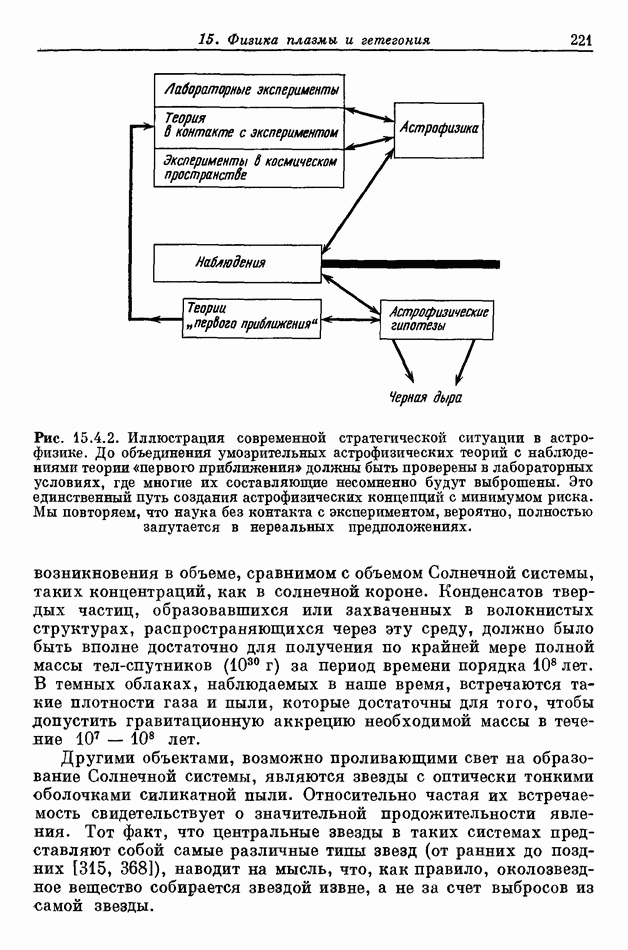
- 15.4. СТРАТЕГИЯ АНАЛИЗА ГЕТЕГОННОЙ ПЛАЗМЫ
- 15.5. ТРЕБУЕМЫЕ СВОЙСТВА МОДЕЛИ
- 15.6. НЕКОТОРЫЕ СУЩЕСТВУЮЩИЕ ТЕОРИИ
- 16. Модель гетегонной плазмы
- 16.1. НАМАГНИЧЕННОЕ ЦЕНТРАЛЬНОЕ ТЕЛО
- 16.2. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
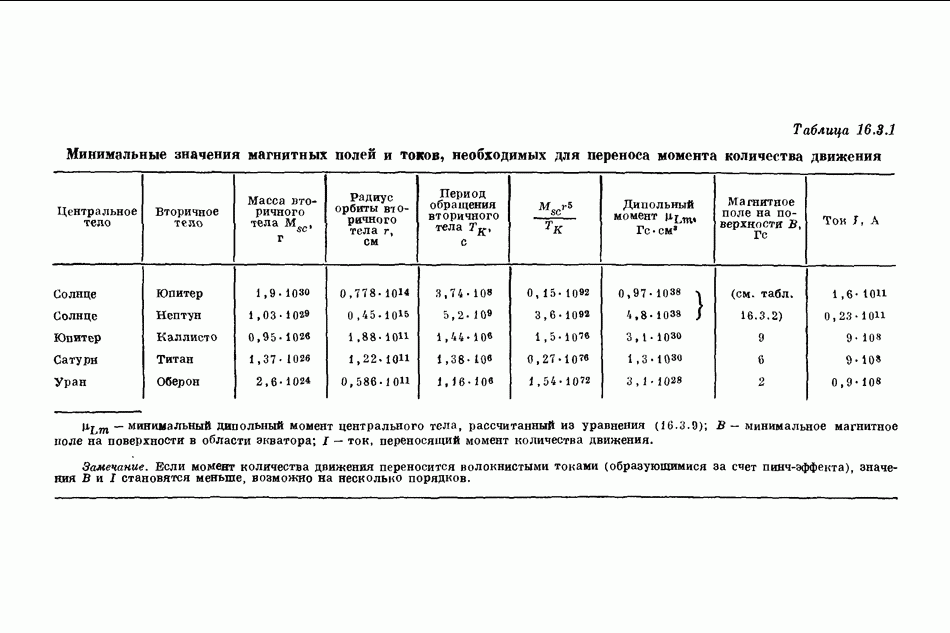
- 16.3. ПЕРЕНОС МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 16.4. УДЕРЖАНИЕ ПЕРВИЧНОГО ОБЛАКА
- 16.5. ПЛАЗМА КАК ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 16.6. ВЫВОДЫ ОТНОСИТЕЛЬНО МОДЕЛИ
- 16.7. ГЕТЕГОННЫЕ ТУМАННОСТИ
- 16.8. ЭФФЕКТЫ ОБЛУЧЕНИЯ
- 16.9. МОДЕЛЬ И ПРИНЦИП ГЕТЕГОНИИ
- 17. Перенос момента количества движения и конденсация зерен
- 17.1. ИЗОРОТАЦИЯ ФЕРРАРО И ЧАСТИЧНАЯ КОРОТАЦИЯ
- 17.2. ЧАСТИЧНАЯ КОРОТАЦИЯ ПЛАЗМЫ В МАГНИТНОМ И ГРАВИТАЦИОННОМ ПОЛЯХ
- 17.2.1. СВЯЗЬ МЕЖДУ ИЗОРОТАЦИЕЙ ФЕРРАРО И ЧАСТИЧНОЙ КОРОТАЦИЕЙ
- 17.3. ПЛАЗМА В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 17.4. ЗАМЕЧАНИЕ
- 17.5. КОНДЕНСАЦИЯ ПЛАЗМЫ: ЗАКОНА ДВУХ ТРЕТЕЙ
- 17.6. ВЫДЕЛЕНИЕ ЭНЕРГИИ ПРИ ПЕРЕНОСЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 18. Аккреция продуктов конденсации
- 18.2. ЭВОЛЮЦИЯ ОРБИТ ВСЛЕДСТВИЕ СТОЛКНОВЕНИЙ
- 18.3. ПРЕДЕЛ РОША
- 18.4. МОДЕЛЬ ЭВОЛЮЦИИ ОРБИТ
- 18.5. АККРЕЦИЯ В ПРЕДЕЛАХ …
- 18.6. СТРУКТУРА КОЛЕЦ САТУРНА
- 18.6.2. МОЖЕТ ЛИ СТРУКТУРА КОЛЕЦ САТУРНА ИМЕТЬ ГЕТЕГОННОЕ ПРОИСХОЖДЕНИЕ?
- 18.6.3. ГЕТЕГОННАЯ ТЕОРИЯ КОЛЕЦ САТУРНА
- 18.6.4. ТЕОРИЯ ЩЕЛИ КАССИНИ
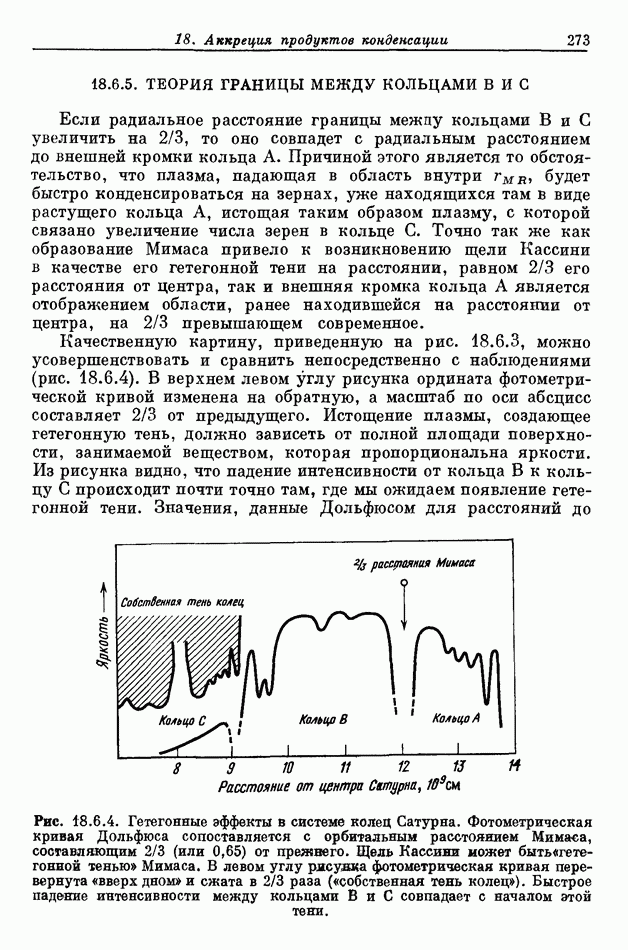
- 18.6.5. ТЕОРИЯ ГРАНИЦЫ МЕЖДУ КОЛЬЦАМИ В И С
- 18.6.6. АНАЛИЗ РЕЗУЛЬТАТОВ
- 18.7. АККРЕЦИЯ ЗА ПРЕДЕЛОМ …
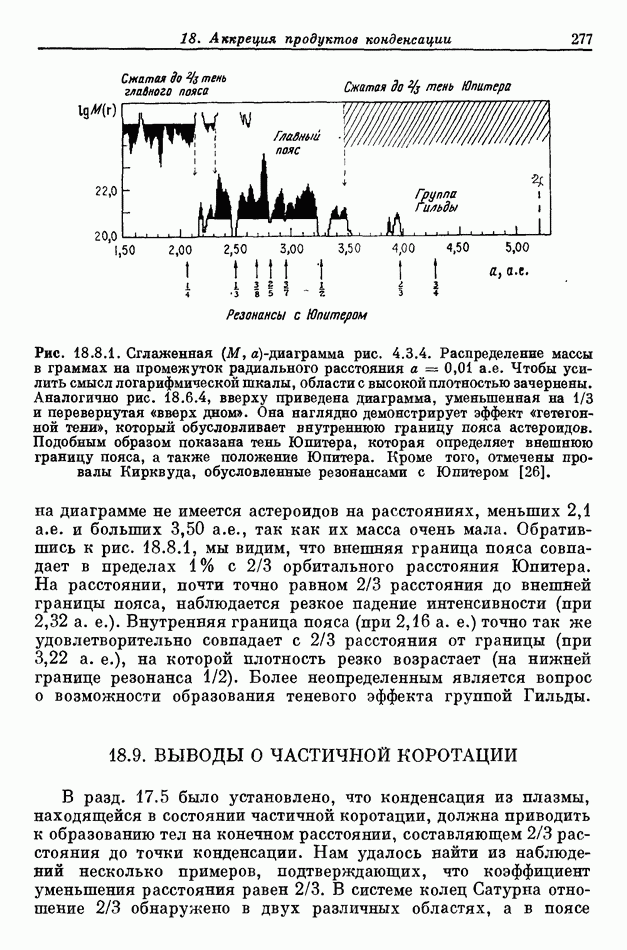
- 18.8. ОБРАЗОВАНИЕ ПОЯСА АСТЕРОИДОВ
- 18.9. ВЫВОДЫ О ЧАСТИЧНОЙ КОРОТАЦИИ
- 18.10. ОБРАЗОВАНИЕ СПУТНИКОВ И ПЛАНЕТ
- 18.11. АККРЕЦИЯ ЛЕТУЧИХ ВЕЩЕСТВ
- 19. Транспланетная конденсация
- 19.1. МЕЖПЛАНЕТНАЯ И ТРАНСПЛАНЕТНАЯ КОНДЕНСАЦИЯ
- 19.2. ГРАНИЦА МЕЖДУ МЕЖПЛАНЕТНЫМ И ТРАНСПЛАНЕТНЫМ ПРОСТРАНСТВОМ
- 19.3. КОНДЕНСАЦИЯ ТЕЛ НА ПОЧТИ-ПАРАБОЛИЧЕСКИХ ОРБИТАХ
- 19.4. ТЕЛА С ДОЛГОПЕРИОДИЧЕСКИМИ ОРБИТАМИ
- 19.5. ДИФФУЗИЯ ПОЧТИ ПАРАБОЛИЧЕСКИХ ОРБИТ: СБЛИЖЕНИЯ С ПЛАНЕТАМИ
- 19.6. ГЕНЕТИЧЕСКИЕ СВЯЗИ КОМПЛЕКСА КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 19.7. ВЫВОДЫ О СЕМЕЙСТВАХ МЕТЕОРНЫХ ТЕЛ
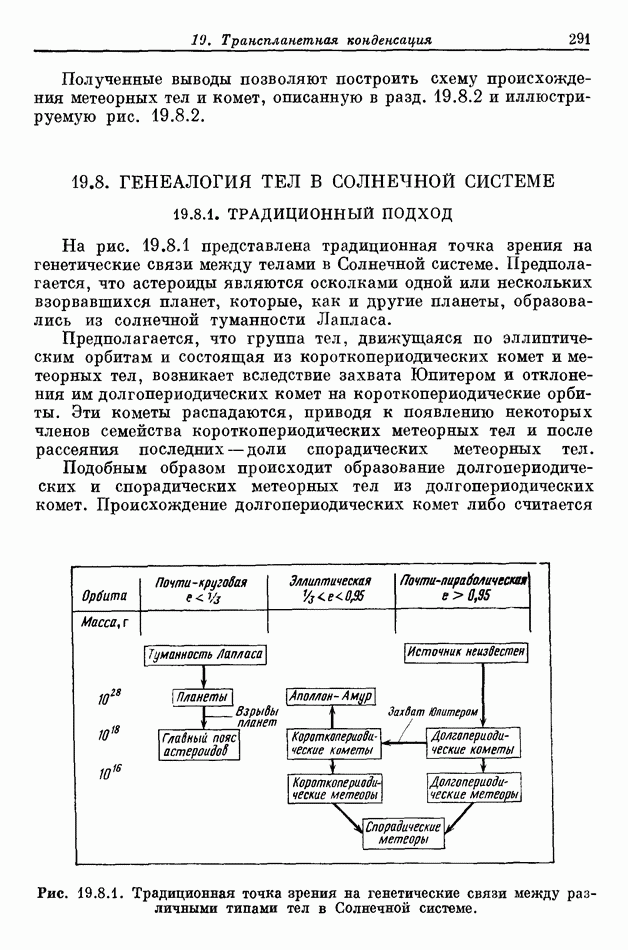
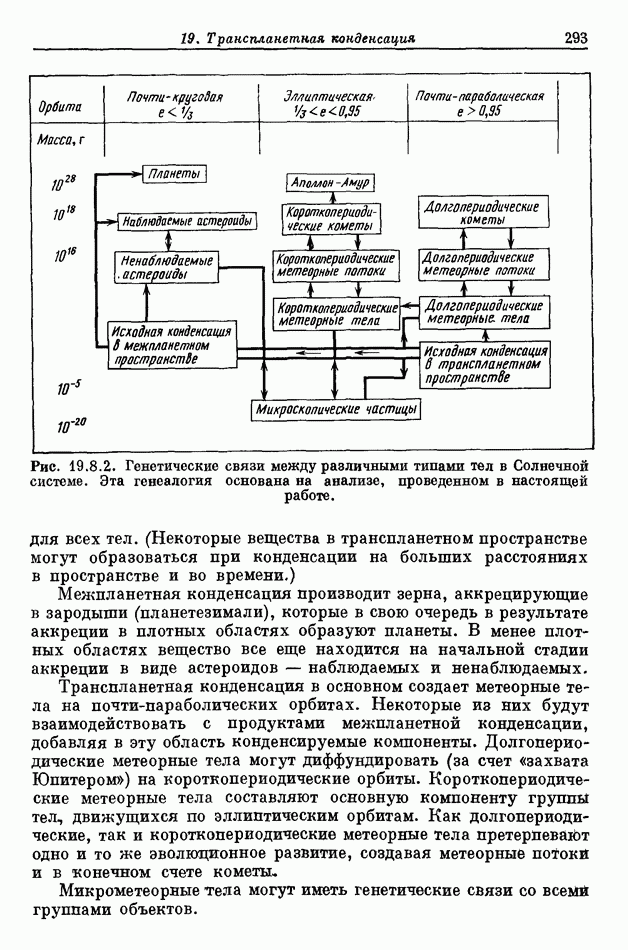
- 19.8. ГЕНЕАЛОГИЯ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- Часть Г. Физическая и химическая структура Солнечной системы
- 20. Химическая структура Солнечной системы
- 20.2. ИСТОЧНИКИ ИНФОРМАЦИИ О ХИМИЧЕСКОМ СОСТАВЕ
- 20.3. ДИФФЕРЕНЦИАЦИЯ ХИМИЧЕСКОГО СОСТАВА ДО И ПОСЛЕ АККРЕЦИИ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
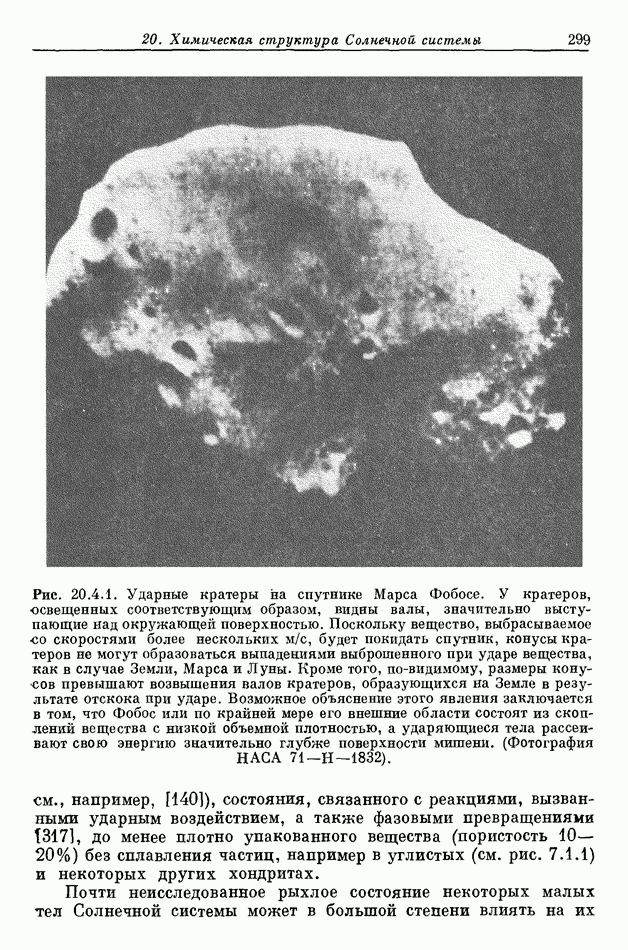
- 20.4. НЕИЗВЕСТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА
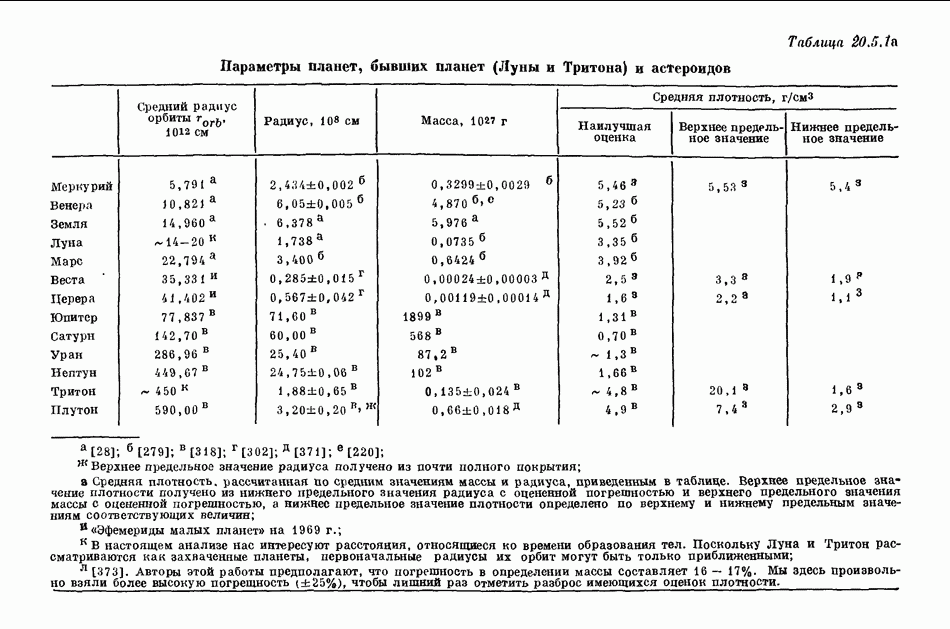
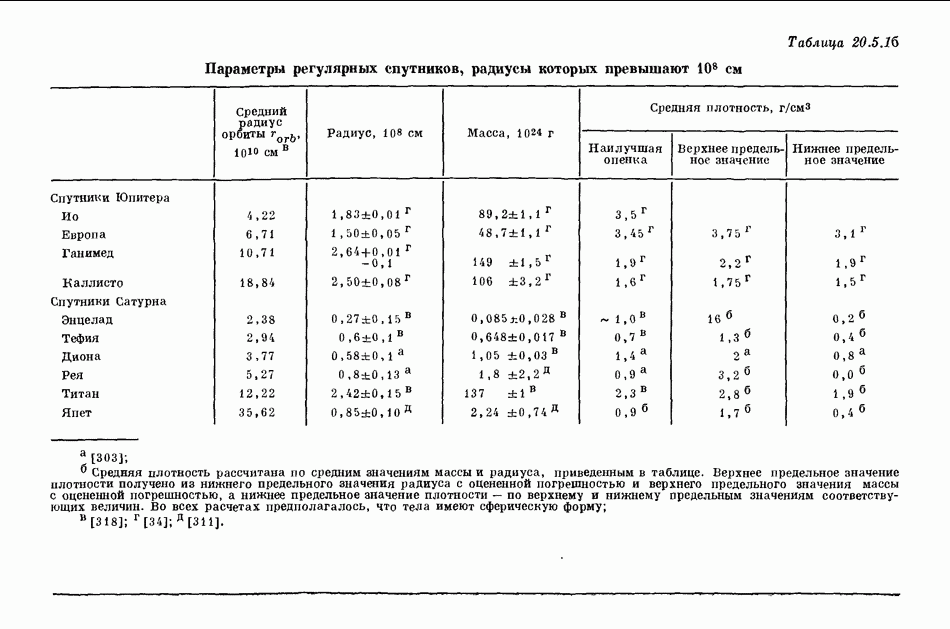
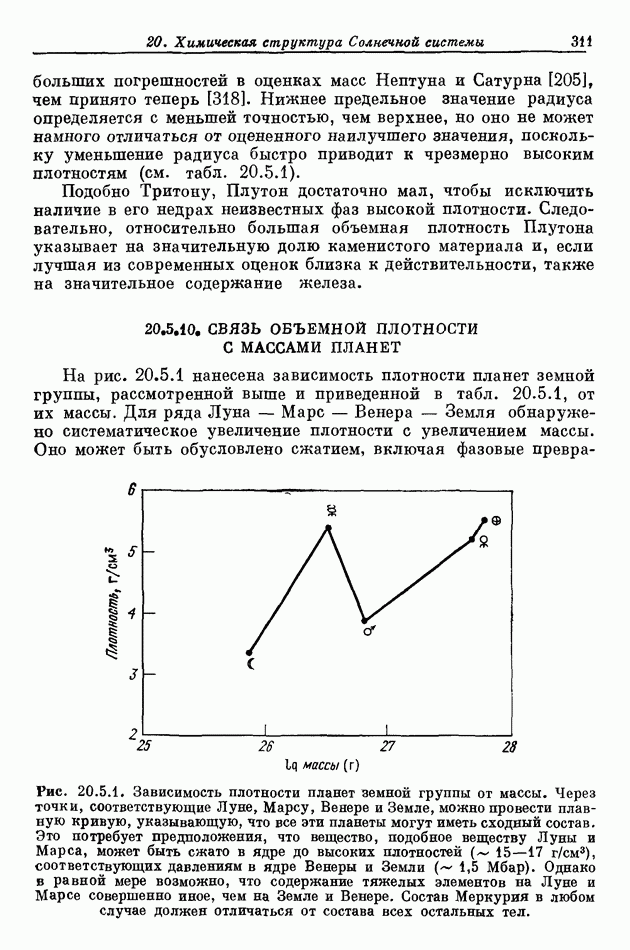
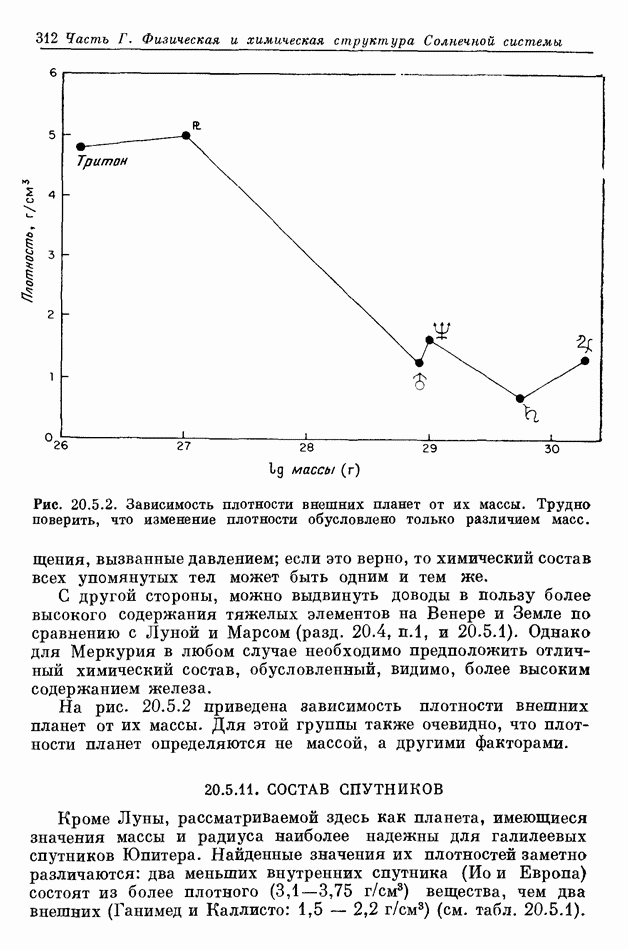
- 20.5. СОСТАВ ПЛАНЕТ И СПУТНИКОВ
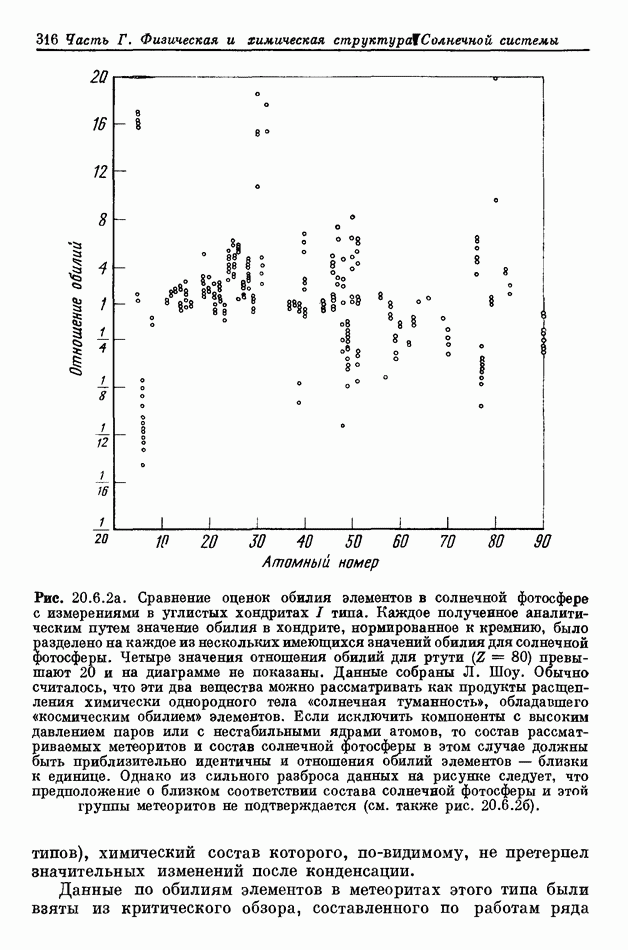
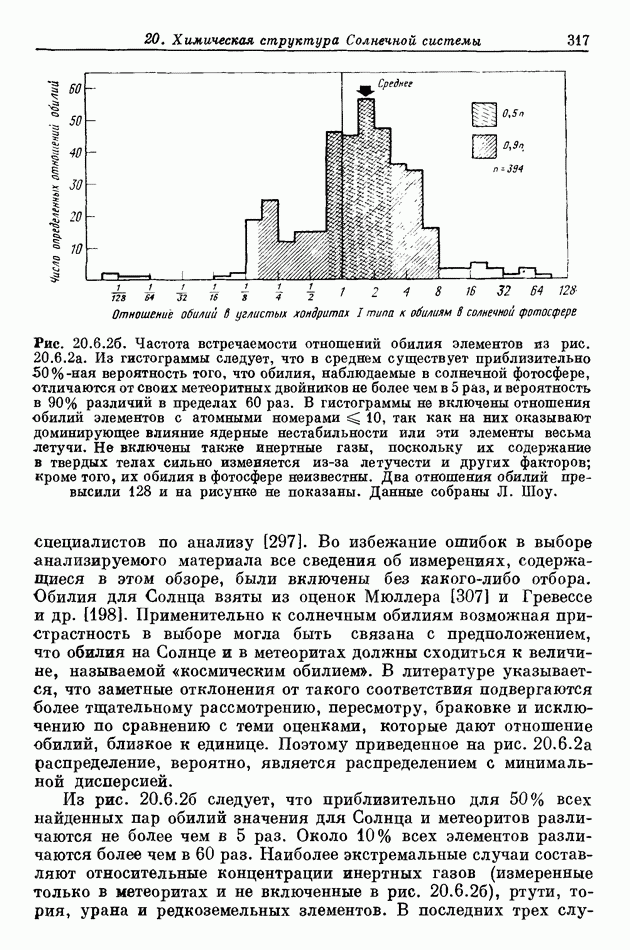
- 20.6. СОСТАВ СОЛНЦА
- 20.6.2. АНАЛИЗ КОРПУСКУЛЯРНОГО ИЗЛУЧЕНИЯ СОЛНЦА
- 20.6.3. ЗНАЧЕНИЕ ДАННЫХ ПО ОБИЛИЯМ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ ФОТОСФЕРЕ
- 20.7. РЕГУЛЯРНОСТЬ ОБЪЕМНЫХ ПЛОТНОСТЕЙ В СОЛНЕЧНОЙ СИСТЕМЕ
- 21. Распределение массы и критическая скорость
- 21.1. РАСПРЕДЕЛЕНИЕ МАССЫ В СОЛНЕЧНОЙ СИСТЕМЕ
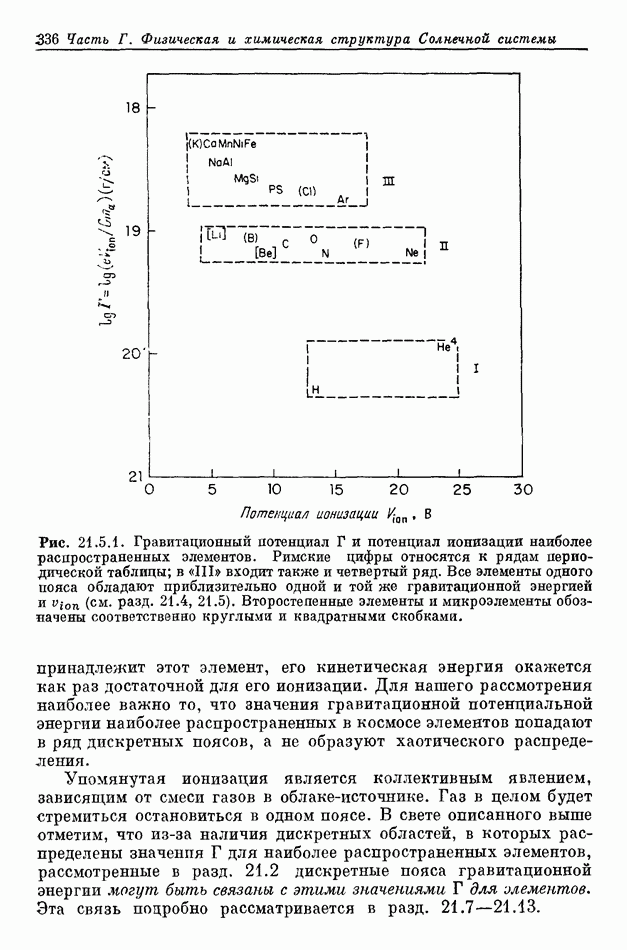
- 21.2. ПОЯСА ВТОРИЧНЫХ ТЕЛ В ЗАВИСИМОСТИ ОТ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 21.3. СРАВНИТЕЛЬНОЕ ИЗУЧЕНИЕ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 21.4. ЦТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ ДЛЯ ОБРАЗОВАНИЯ ПОЯСОВ
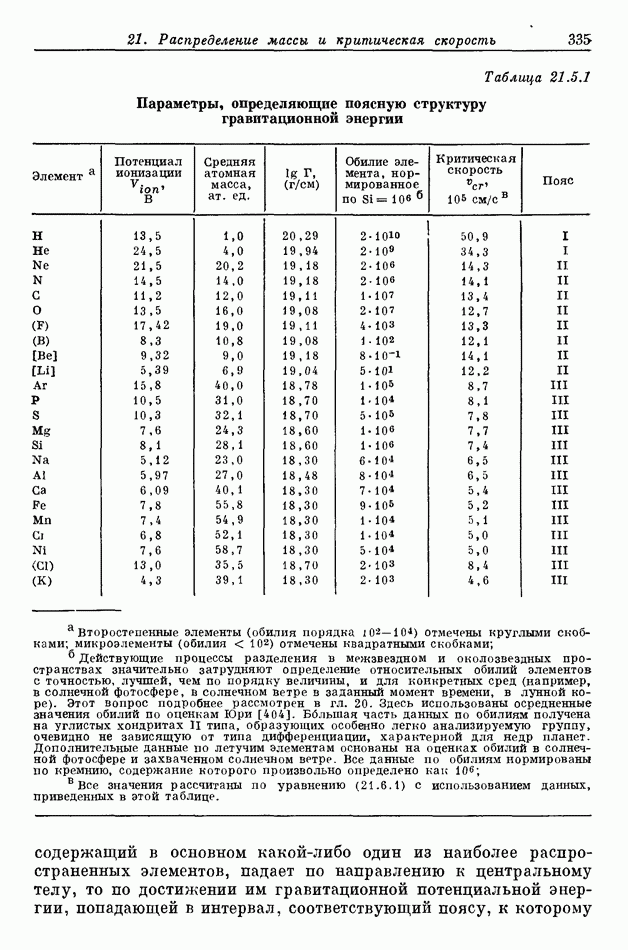
- 21.5. ПОПЫТКИ ИНТЕРПРЕТАЦИИ ПОЯСНОЙ СТРУКТУРЫ
- 21.6. ТРИ ВОЗРАЖЕНИЯ
- 21.7. ПОИСКИ «КРИТИЧЕСКОЙ СКОРОСТИ»
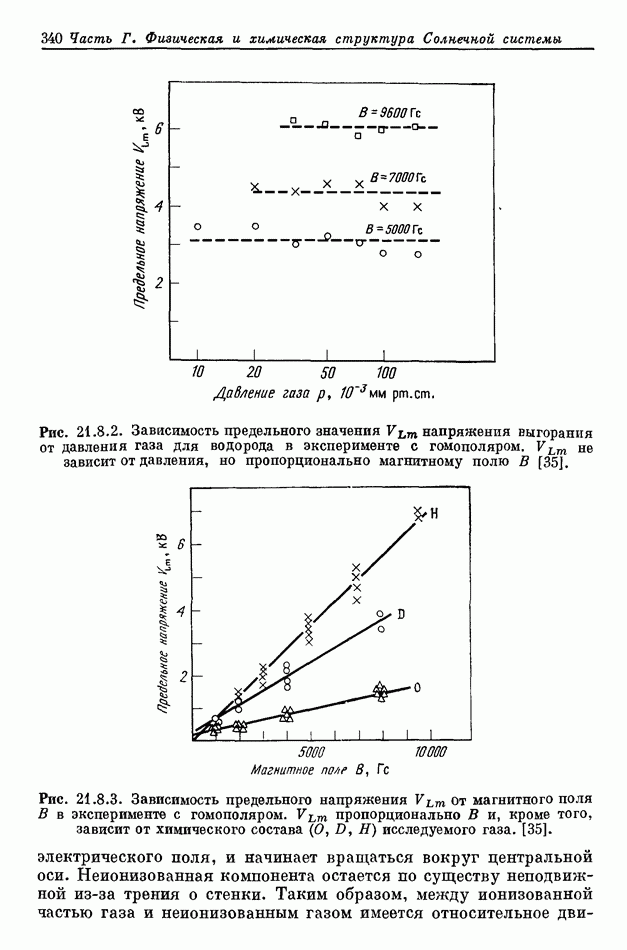
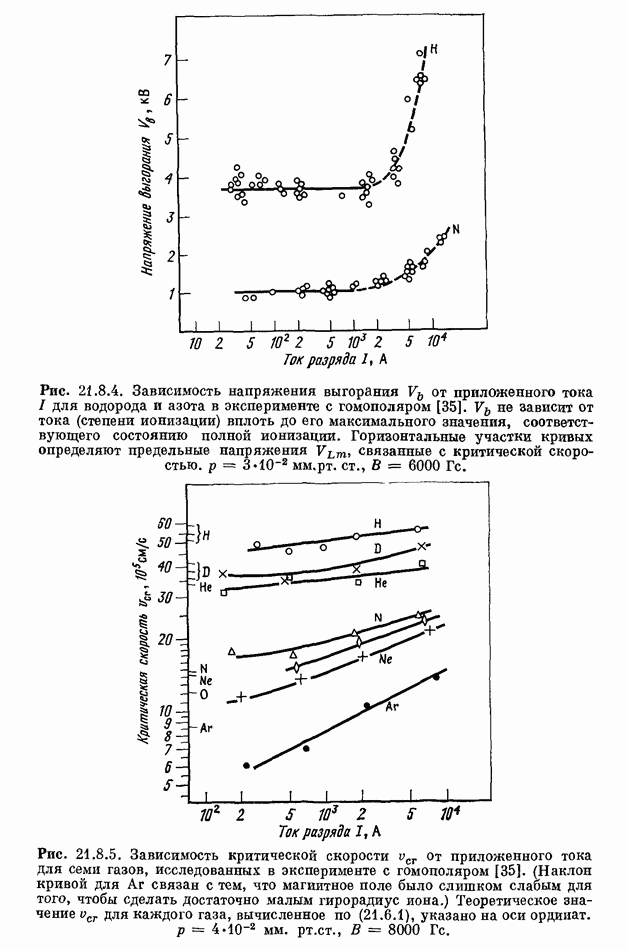
- 21.8. ЭКСПЕРИМЕНТЫ ПО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.8.2. ПЛАЗМЕННЫЙ ПУЧОК, СТАЛКИВАЮЩИЙСЯ С ОБЛАКОМ НЕЙТРАЛЬНОГО ГАЗА
- 21.8.3. ДРУГИЕ ЭКСПЕРИМЕНТЫ
- 21.9. ТЕОРИЯ КРИТИЧЕСКОЙ СКОРОСТИ
- 21.10. ВЫВОДЫ ОТНОСИТЕЛЬНО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.11. ХИМИЧЕСКИЙ СОСТАВ ВЫПАДАЮЩЕГО ГАЗА
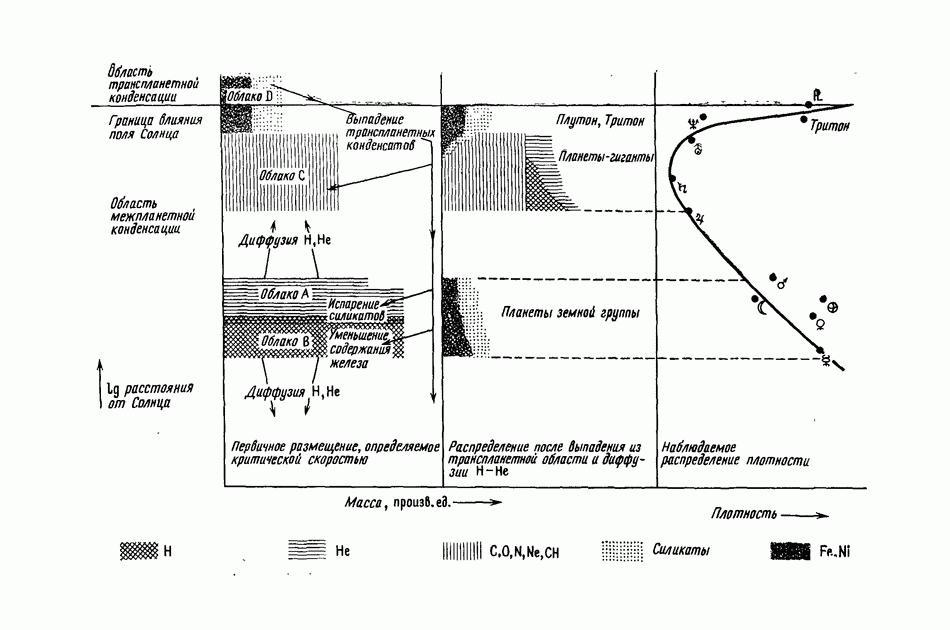
- 21.11.2. ОБЛАКА A, B, C и D В СОЛНЕЧНОЙ СИСТЕМЕ
- 21.11.3. СОВЕРШЕНСТВОВАНИЕ ОСНОВНОЙ МОДЕЛИ
- 21.11.4. ВЛИЯНИЕ МЕЖЗВЕЗДНЫХ МОЛЕКУЛ
- 21.12. ХИМИЧЕСКИЙ СОСТАВ СОЛНЕЧНОЙ СИСТЕМЫ И РАЗМЕЩЕНИЕ НЕОДНОРОДНОЙ ПЛАЗМЫ
- 21.12.2. ВЛИЯНИЕ ТРАНСПЛАНЕТНОЙ КОНДЕНСАЦИИ НА СОСТАВ ПЛАНЕТ И СПУТНИКОВ
- 21.12.3. ФРАКЦИОНИРОВАНИЕ, СВЯЗАННОЕ С КОНДЕНСАЦИЕЙ ИЛИ СЛЕДУЮЩЕЕ ЗА НЕЙ
- 21.12.4. ВЫВОДЫ О ХИМИЧЕСКОМ СОСТАВЕ НЕБЕСНЫХ ТЕЛ
- 21.13. ИЗМЕНЕНИЕ РАССТОЯНИЯ ИОНИЗАЦИИ ДЛЯ КРИТИЧЕСКОЙ СКОРОСТИ ИЗ-ЗА ВЗАИМОДЕЙСТВИЯ С ПЛАЗМОЙ В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 22. Метеориты и предшествующие им состояния
- 22.1. ИНТЕРПРЕТАЦИЯ ЭВОЛЮЦИОННЫХ ДАННЫХ, ЗАПЕЧАТЛЕННЫХ В МЕТЕОРИТАХ
- 22.2. ИСТОЧНИКИ МЕТЕОРИТОВ
- 22.3. ЭФФЕКТЫ СЕЛЕКЦИИ
- 22.4. ВЕРХНИЕ ПРЕДЕЛЫ РАЗМЕРОВ ТЕЛ, ПРЕДШЕСТВУЮЩИХ МЕТЕОРИТАМ
- 22.5. ПРЕДШЕСТВУЮЩИЕ СОСТОЯНИЯ РОДИТЕЛЬСКИХ ТЕЛ МЕТЕОРИТОВ
- 22.6. ЭВОЛЮЦИЯ СТРУЙНОГО ПОТОКА И СВОЙСТВА МЕТЕОРИТОВ
- 22.7. СИЛЫ СЦЕПЛЕНИЯ В МЕТЕОРИТНОМ ВЕЩЕСТВЕ
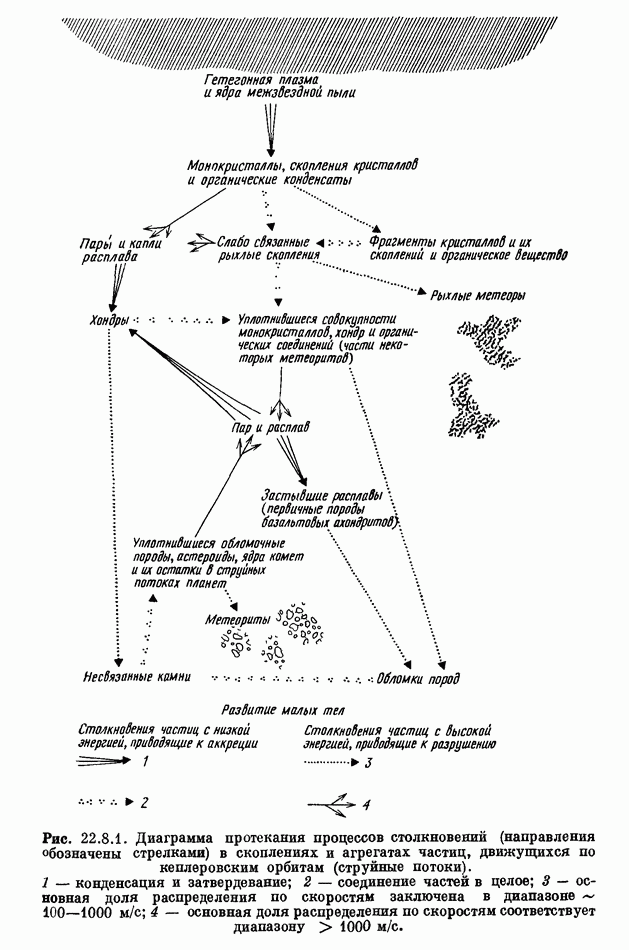
- 22.8. ЭВОЛЮЦИОННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ПРЕДШЕСТВУЮЩИХ СОСТОЯНИЙ МЕТЕОРИТОВ
- 22.9. ВОЗРАСТНЫЕ СООТНОШЕНИЯ В ЭВОЛЮЦИИ РОДИТЕЛЬСКИХ СТРУЙНЫХ ПОТОКОВ МЕТЕОРИТОВ
- 22.9.1. ЗАМЫКАНИЕ РЕЗЕРВУАРОВ ТУГОПЛАВКИХ КОМПОНЕНТ
- 22.9.2. ВОЗРАСТЫ КРИСТАЛЛИЗАЦИИ
- 22.9.3. ВОЗРАСТЫ УДЕРЖАНИЯ ГАЗА
- 22.9.4. ВОЗРАСТЫ ДЕГАЗАЦИИ
- 22.9.5. ТРЕКИ ЧАСТИЦ И ВНЕДРЕНИЕ ПЛАЗМЫ В МЕТЕОРИТАХ
- 22.9.6. ВОЗРАСТЫ ОБЛУЧЕНИЯ КОСМИЧЕСКИМИ ЛУЧАМИ ВЫСОКИХ ЭНЕРГИЙ
- 22.10. ОБЩИЕ ЗАМЕЧАНИЯ О ДАННЫХ, ЗАФИКСИРОВАННЫХ В МЕТЕОРИТАХ
- 23. Строение групп вторичных тел
- 23.1. ИОНИЗАЦИЯ В ПРОЦЕССЕ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- 23.2. ПОЛНАЯ ИОНИЗАЦИЯ
- 23.3. ЧАСТИЧНАЯ ИОНИЗАЦИЯ
- 23.4. ИЗМЕНЕНИЕ ВРАЩЕНИЯ ВО ВРЕМЯ ОБРАЗОВАНИЯ ВТОРИЧНЫХ ТЕЛ
- 23.5. НАБЛЮДАЕМЫЕ ЗНАЧЕНИЯ …
- 23.6. РАСПРЕДЕЛЕНИЕ МАССЫ В ЗАВИСИМОСТИ ОТ …
- 23.7. АНАЛИЗ СТРОЕНИЯ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 23.8. ПОЛНЫЙ ПЕРЕЧЕНЬ ЗНАЧЕНИЙ … ДЛЯ ВСЕХ ТЕЛ
- 23.9. ЗАВЕРШЕННОСТЬ
- 23.9.1. ЗАМЕЧАНИЕ О ВНУТРЕННЕЙ ГРАНИЦЕ СИСТЕМЫ СПУТНИКОВ
- 23.9.2. НАКЛОН ПОЯСОВ НА ДИАГРАММЕ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЩЭНЕРГИИ
- 23.9.3. ДРУГИЕ ЗАКОНОМЕРНОСТИ В СТРОЕНИИ ГРУПП
- 23.10. ВЫВОДЫ О МОДЕЛИ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- Часть Д. Частные проблемы
- 24. Происхождение и эволюция системы Земля-Луна
- 24.2. СРАВНЕНИЕ С ДРУГИМИ СИСТЕМАМИ СПУТНИКОВ
- 24.3. СТРУКТУРА НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ ЗЕМЛИ
- 24.4 ТЕОРИЯ ЗАХВАТА
- 24.5 ПРИЛИВНАЯ ЭВОЛЮЦИЯ ЛУННОЙ ОРБИТЫ
- 24.6. РАЗРУШЕНИЕ НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ
- 24.7. АККРЕЦИЯ И ТЕПЛОВАЯ СТРУКТУРА ЛУНЫ
- 24.8. СОСТАВ ЛУНЫ
- 24.9. ВЫВОДЫ
- 25. Свойства Солнца на ранней стадии его существования
- 25.2 МАССА СОЛНЦА
- 25.3. МАГНИТНОЕ ПОЛЕ СОЛНЦА
- 25.4. ПЕРИОД СОБСТВЕННОГО ВРАЩЕНИЯ СОЛНЦА
- 25.5. ИЗЛУЧЕНИЕ СОЛНЦА, СОЛНЕЧНЫЙ ВЕТЕР
- 25.6. ЭФФЕКТЫ ВЫГОРАНИЯ ДЕЙТЕРИЯ НА СОЛНЦЕ
- 25.7. ЗАМЕЧАНИЯ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 26. Происхождение океана и атмосферы Земли
- 26.1. ЗЕМНОЙ ОКЕАН И ОБРАЗОВАНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
- 26.2. СТАДИИ ОТДАЛЕННЫХ ПРЕДШЕСТВЕННИКОВ
- 26.2.2. ПЕРВИЧНЫЕ ЗЕРНА КАК НОСИТЕЛИ КОМПОНЕНТ АТМОСФЕРЫ И ОКЕАНА
- 26.2.3. ВНЕЗЕМНЫЕ ИСТОЧНИКИ ВОДЫ
- 26.2.4. ЗАПАСЫ ИНЕРТНЫХ И ХИМИЧЕСКИ АКТИВНЫХ ЛЕТУЧИХ
- 26.3. СТАДИИ БЛИЖАЙШИХ ПРЕДШЕСТВЕННИКОВ
- 26.3.1. ЭВОЛЮЦИЯ ПРЕДШЕСТВОВАВШИХ ЗЕМЛЕ ПЛАНЕТЕЗИМАЛЕЙ
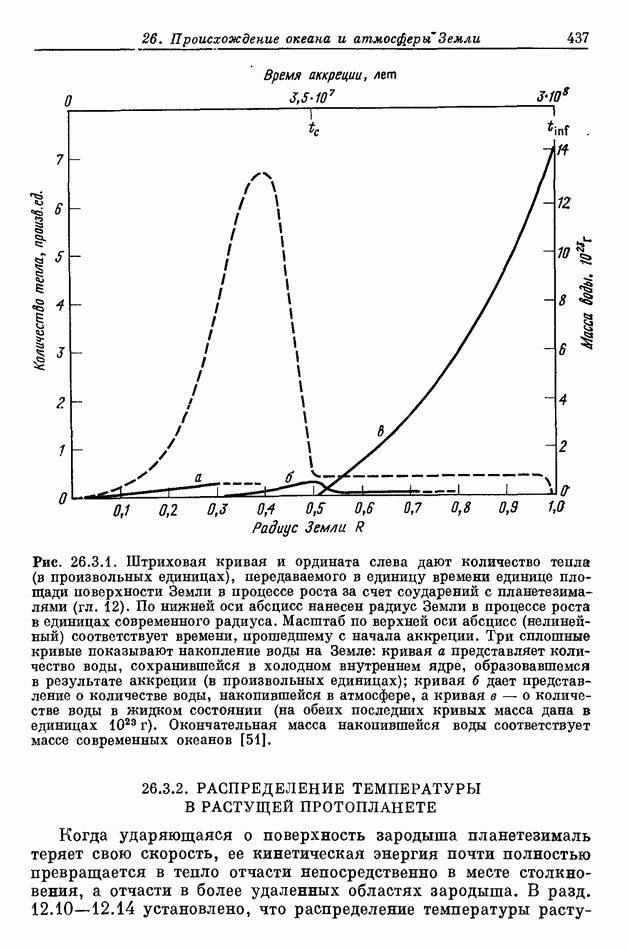
- 26.3.2. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В РАСТУЩЕЙ ПРОТОПЛАНЕТЕ
- 26.3.3. ЯДРО ЗЕМЛИ
- 26.3.4. ВЫСВОБОЖДЕНИЕ ТЕПЛА И УЛЕТУЧИВАНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ
- 26.4. НАКОПЛЕНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ ЗЕМЛИ
- 26.4.2. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ И СОСТОЯНИЕ ВОДЫ
- 26.4.3. ДЕТАЛИЗАЦИЯ МОДЕЛИ
- 26.5. ПОСТУПЛЕНИЕ ВОДЫ В ЛИТОСФЕРУ
- 26.5.2. СТАЦИОНАРНОЕ СОСТОЯНИЕ ПРОПИТЫВАНИЯ И ВЫСВОБОЖДЕНИЯ
- 26.5.3. ВОЗМОЖНЫЕ ОСТАТКИ ЛЕТУЧИХ ВЕЩЕСТВ ПЛАНЕТЕЗИМАЛЕЙ В ЗЕМНОЙ КОРЕ И МАНТИИ
- 26.6. ОКЕАН И СИСТЕМА ЗЕМЛЯ — ЛУНА
- 26.7. ИТОГИ И ВЫВОДЫ
- 27. Межзвездные облака и образование звезд
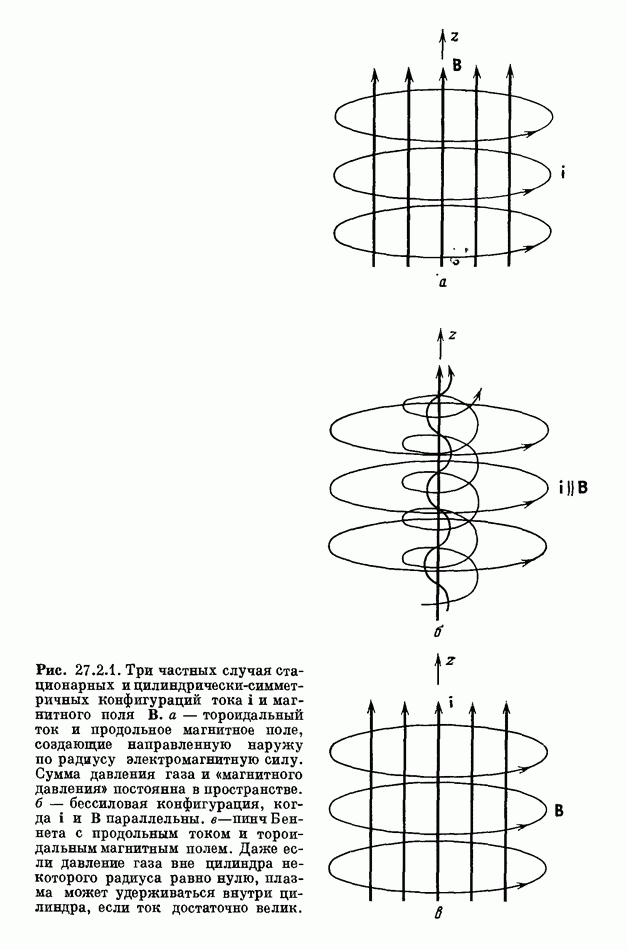
- 27.2. МАГНИТНАЯ ГИДРОДИНАМИКА ОБЛАКОВ КОСМИЧЕСКОЙ ПЛАЗМЫ
- 27.2.3. БЕССИЛОВЫЕ МАГНИТНЫЕ ПОЛЯ И СОЗДАНИЕ ВОЛОКОН
- 27.2.4. СПОСОБСТВУЮТ ИЛИ ПРОТИВОДЕЙСТВУЮТ СЖАТИЮ МАГНИТНЫЕ ПОЛЯ?
- 27.2.5. ПИНЧ-СЖАТИЕ ТЕМНЫХ МЕЖЗВЕЗДНЫХ ОБЛАКОВ
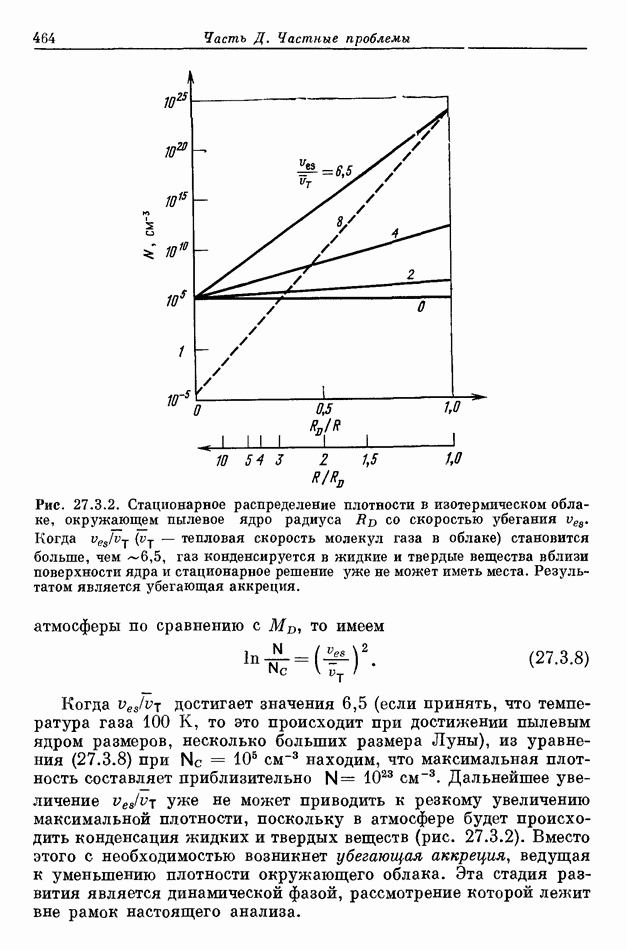
- 27.3. ОБРАЗОВАНИЕ ЗВЕЗД В ОБЛАКЕ ПЫЛЕВОЙ ПЛАЗМЫ
- 27.3.2. ДВИЖЕНИЕ ПЫЛИ В ОБЛАКЕ ПЛАЗМЫ
- 27.3.3. ОСЕДАНИЕ ПЫЛИ В ГРАВИТАЦИОННОМ ПОЛЕ
- 27.3.4. ОБРАЗОВАНИЕ СТЕЛЛЕЗИМАЛЕЙ
- 27.3.5. ДВУХСТУПЕНЧАТАЯ АККРЕЦИЯ
- 27.3.6. СВОЙСТВА ПРОТО-СОЛНЦА И ОКРУЖАЮЩЕЙ ЕГО СРЕДЫ
- 27.3.7. ВЫВОДЫ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 28. Заключительные замечания