| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.8. ПРОДОЛЖИТЕЛЬНОСТЬ СЖАТИЯ СТРУЙНОГО ПОТОКА
Предположим, что тело движется со скоростью  по кемеровской орбите с большой полуосью
по кемеровской орбите с большой полуосью  и орбита достаточно близка к круговой, так что можно применить метод ведущего центра. Предположим далее, что возмущения в поле отсутствуют и сила обратно пропорциональна квадрату расстояния. Следовательно, орбита тела остается эллипсом, который не будет прецессировать.
и орбита достаточно близка к круговой, так что можно применить метод ведущего центра. Предположим далее, что возмущения в поле отсутствуют и сила обратно пропорциональна квадрату расстояния. Следовательно, орбита тела остается эллипсом, который не будет прецессировать.
Предположим, что это тело испускает частицу со скоростью  (относительно тела) в радиальном направлении. Эта частица будет колебаться с амплитудой
(относительно тела) в радиальном направлении. Эта частица будет колебаться с амплитудой

Аналогично этому частицы, испускаемые в осевом направлении, будут колебаться с той же амплитудой. Далее, частицы выброшенные в тангенциальном направлении (вперед), будут иметь удельный момент количества движения  который, будучи равным
который, будучи равным  при
при  является таким же, как для частицы на круговой орбите радиуса
является таким же, как для частицы на круговой орбите радиуса

Следовательно, они будут колебаться с амплитудой  и их наибольшее расстояние от орбиты тела будет равно
и их наибольшее расстояние от орбиты тела будет равно 
Частицы, испускаемые со скоростью  будут оставаться внутри тора, меньший радиус которого равен
будут оставаться внутри тора, меньший радиус которого равен  где
где  определяется уравнением (6.8.1), а а лежит в интервале от 1 до 4 в зависимости от угла испускания. Этот результат справедлив и в том случае, когда тело движется по орбите, которая не является точно круговой.
определяется уравнением (6.8.1), а а лежит в интервале от 1 до 4 в зависимости от угла испускания. Этот результат справедлив и в том случае, когда тело движется по орбите, которая не является точно круговой.
Если тело (или несколько тел на одной и той же орбите) испускает молекулы газа со среднеквадратичной тепловой скоростью  то газ будет ограничен поверхностью тора со средней толщиной
то газ будет ограничен поверхностью тора со средней толщиной

Мы используем х как меру меньшего радиуса струйного потока, даже если некоторые частицы колеблются с большей амплитудой, В качестве типичного примера можно упомянуть, что тепловая
скорость молекулы водорода при  порядка
порядка  см/с. Если положить
см/с. Если положить  см/с (орбитальная скорость Земли), то при
см/с (орбитальная скорость Земли), то при  имеем
имеем 
Струйные потоки отличаются от колец в теории Лапласа тем, что средняя длина свободного пробега частиц в струйном потоке велика по сравнению с его размерами. Далее, такие потоки не обязательно должны быть круговыми. Фактически явления, которые мы рассматриваем, будут происходить даже в потоках с большим эксцентриситетом.
Поскольку подробная теория струйных потоков еще не разработана, мы ограничимся приблизительным рассмотрением, которое позволяет сделать по крайней мере качественный обзор некоторых важных явлений. Предположим, что имеется струйный поток, состоящий из большого числа  частиц, движение которых ограничено поверхностью тора с меньшим радиусом
частиц, движение которых ограничено поверхностью тора с меньшим радиусом  Средняя относительная скорость частиц равна и. Если все частицы имеют одинаковые массы та и сечения соударения а, то каждая частица в торе будет испытывать столкновения с частотой порядка
Средняя относительная скорость частиц равна и. Если все частицы имеют одинаковые массы та и сечения соударения а, то каждая частица в торе будет испытывать столкновения с частотой порядка

где  среднее время между двумя столкновениями,
среднее время между двумя столкновениями,  концентрация частиц, равная
концентрация частиц, равная

Если каждая частица представляет собой сферу с радиусом  и средней плотностью
и средней плотностью  то ее масса
то ее масса  Форма частиц может значительно отличаться от сферической (в крайнем случае они могут быть игловидными), но для оценки порядка величин мы принимаем сферическую форму. Если подставим в (6.8.4) объемную плотность
Форма частиц может значительно отличаться от сферической (в крайнем случае они могут быть игловидными), но для оценки порядка величин мы принимаем сферическую форму. Если подставим в (6.8.4) объемную плотность  то получим
то получим

Если в качестве типичной относительной скорости принять  см/с, то можно найти соответствующие значения радиуса частицы
см/с, то можно найти соответствующие значения радиуса частицы  и величины
и величины  которые приведены в табл. 6.8.1.
которые приведены в табл. 6.8.1.
Таблица 6.8.1 (см. скан) Характеристики плотности в струйных потоках
Чтобы струйный поток сохранялся, интервал между столкновениями для данной частицы  должен быть меньше, чем постоянная времени процессов рассеяния. Наиболее важными из этих процессов являются несовпадение прецессий различных орбит в струйном потоке и эффект Пойнтинга — Робертсона. С точностью до порядка величины мы можем положить
должен быть меньше, чем постоянная времени процессов рассеяния. Наиболее важными из этих процессов являются несовпадение прецессий различных орбит в струйном потоке и эффект Пойнтинга — Робертсона. С точностью до порядка величины мы можем положить  лет
лет  с [428]. Исходя из этого определяются значения
с [428]. Исходя из этого определяются значения  а с помощью уравнения (6.8.4) — значения
а с помощью уравнения (6.8.4) — значения  приведенные в табл. 6.8.1.
приведенные в табл. 6.8.1.
Сжатие струйного потока вызывается неупругими столкновениями между частицами. Постоянная времени сжатия должна быть порядка нескольких  Это также означает, что струйный поток может сформироваться только при отсутствии разрушительного воздействия с постоянной времени меньше Например, различие прецессий перицентров и узлов эллиптической орбиты будет разрушать струйный поток, если только
Это также означает, что струйный поток может сформироваться только при отсутствии разрушительного воздействия с постоянной времени меньше Например, различие прецессий перицентров и узлов эллиптической орбиты будет разрушать струйный поток, если только  не будет меньше периода разности прецессий.
не будет меньше периода разности прецессий.
В более строгой модели струйного потока должно учитываться распределение частиц по размерам. Поскольку наименьшие частицы обычно наиболее многочисленны, их взаимные столкновения будут наиболее важны для сохранения струйного потока.
Поскольку относительные скорости во внутренней части струйного потока уменьшаются, то аккреция частиц, приводящая к образованию более крупных тел, будет становиться все более эффективной. Следовательно, продолжительность сжатия струйного потока является величиной примерно такого же порядка, что и  Однако с образованием более крупных тел
Однако с образованием более крупных тел  будет увеличиваться, а сжимающая сила — уменьшаться. В конечном счете струйный поток не сможет больше сохраняться.
будет увеличиваться, а сжимающая сила — уменьшаться. В конечном счете струйный поток не сможет больше сохраняться.
Следует помнить, что струйный поток образуется, если только имеется достаточное взаимодействие между частицами. В кольцах Сатурна взаимодействия между частицами очень малы. Частицы не образуют струйных потоков и движутся по орбитам с периодами, пропорциональными 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- От редактора перевода
- Предисловие
- I. Введение
- 1.1. ФУНДАМЕНТАЛЬНЫЙ ПОДХОД К ПРОБЛЕМЕ
- 1.2. СИСТЕМА ПЛАНЕТ — СИСТЕМЫ СПУТНИКОВ
- 1.3. ПЯТЬ ЭТАПОВ ЭВОЛЮЦИИ
- 1.4. НАПРАВЛЯЮЩИЕ ПРОЦЕССЫ ОТДЕЛЬНЫХ ЭТАПОВ ЭВОЛЮЦИИ
- 1.5. ТРЕБОВАНИЯ К МОДЕЛЯМ И ОГРАНИЧЕНИЯ
- Часть А. Современное состояние и основные законы
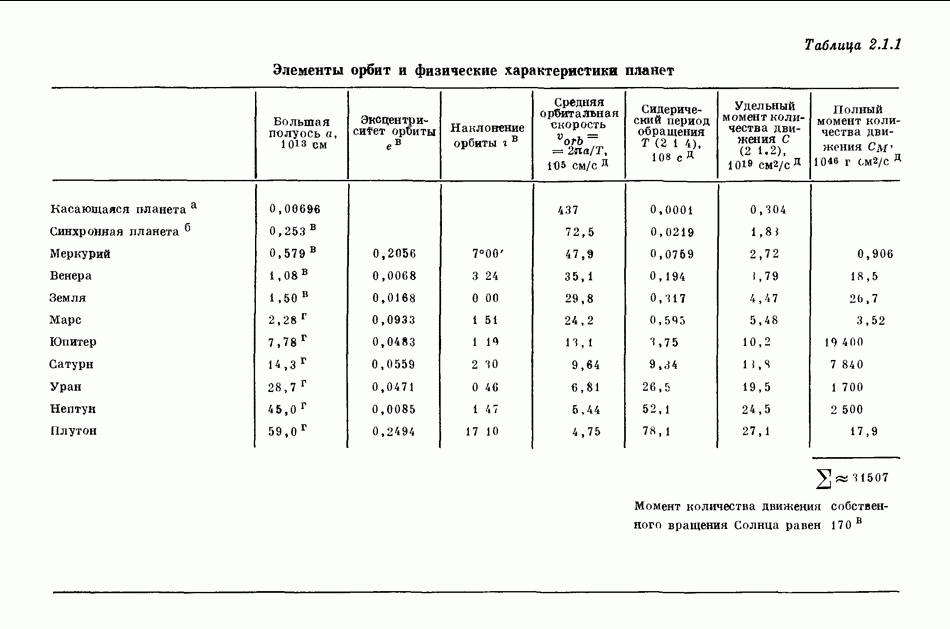
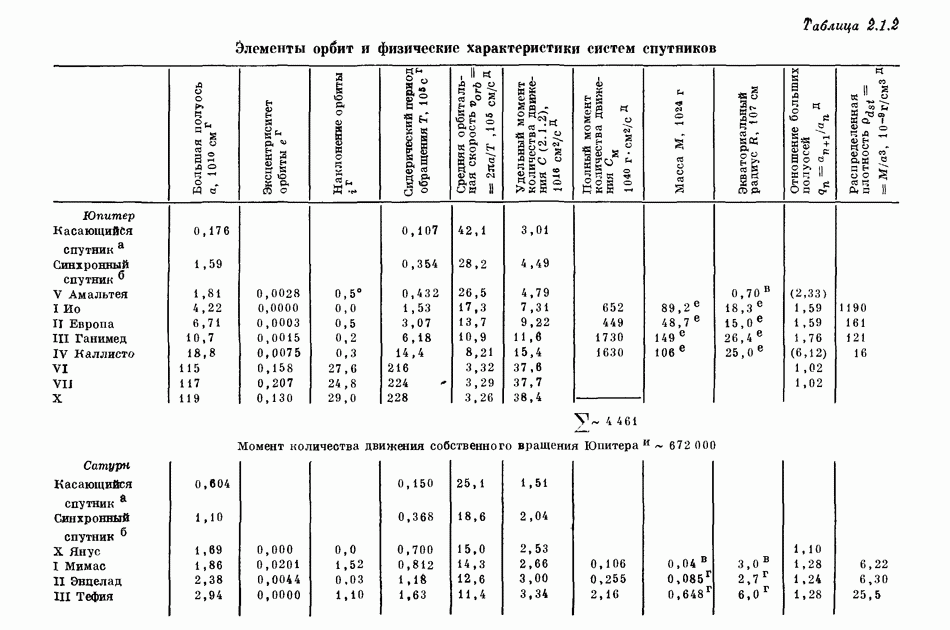
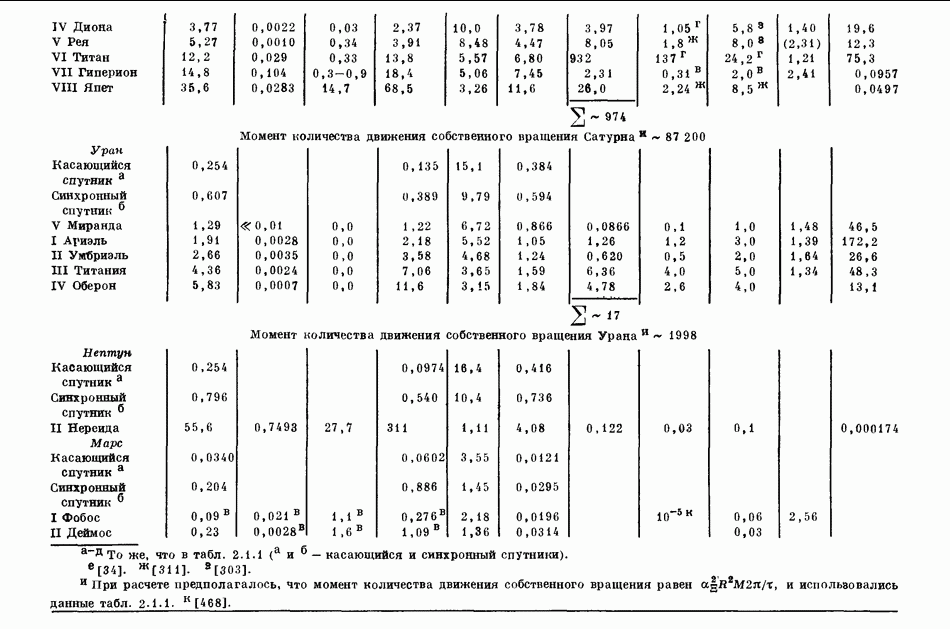
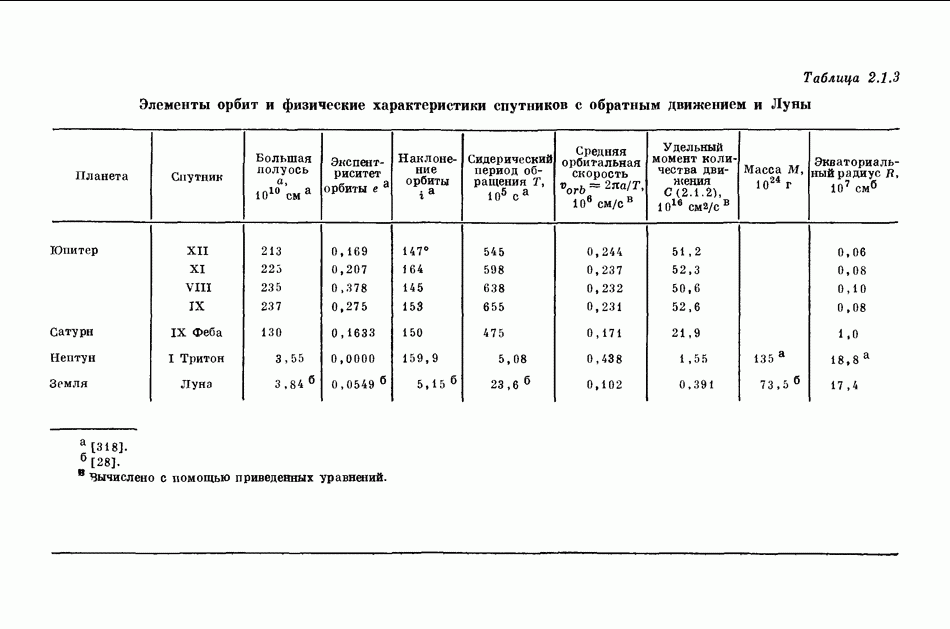
- 2.1. ХАРАКТЕРИСТИКИ ОРБИТ ПЛАНЕТ И СПУТНИКОВ
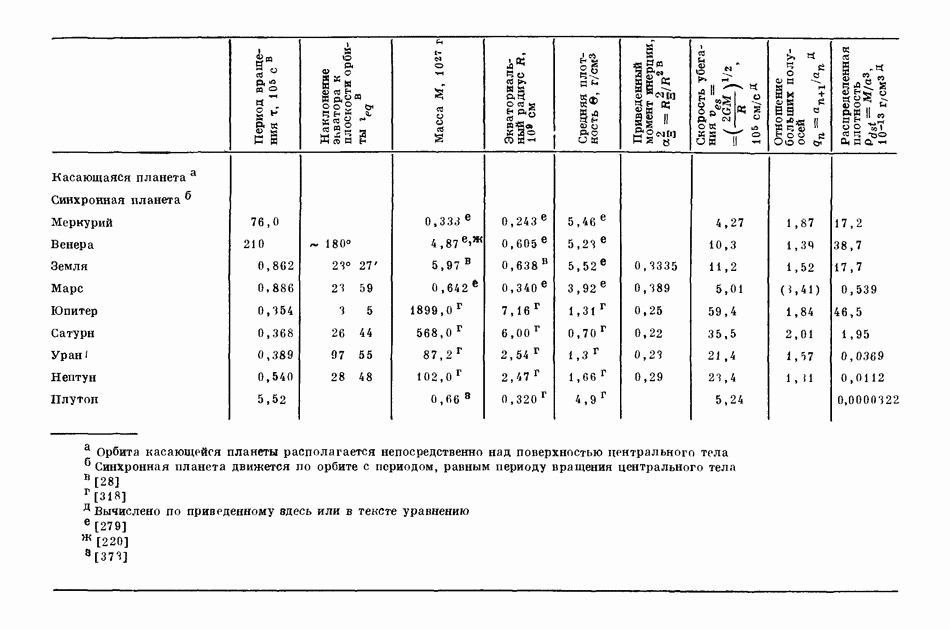
- 2.2. ФИЗИЧЕСКИЕ СВОЙСТВА ПЛАНЕТ И СПУТНИКОВ
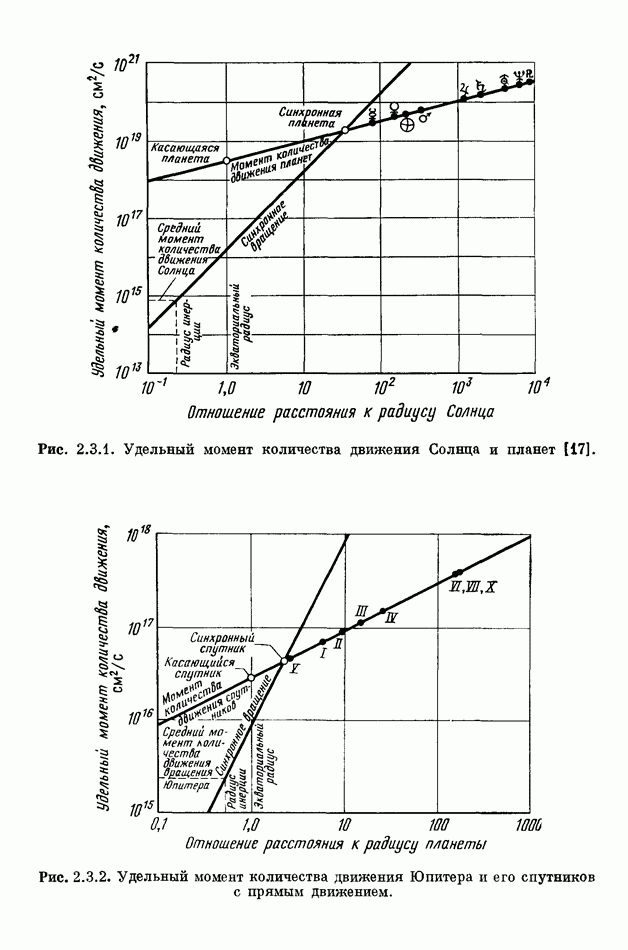
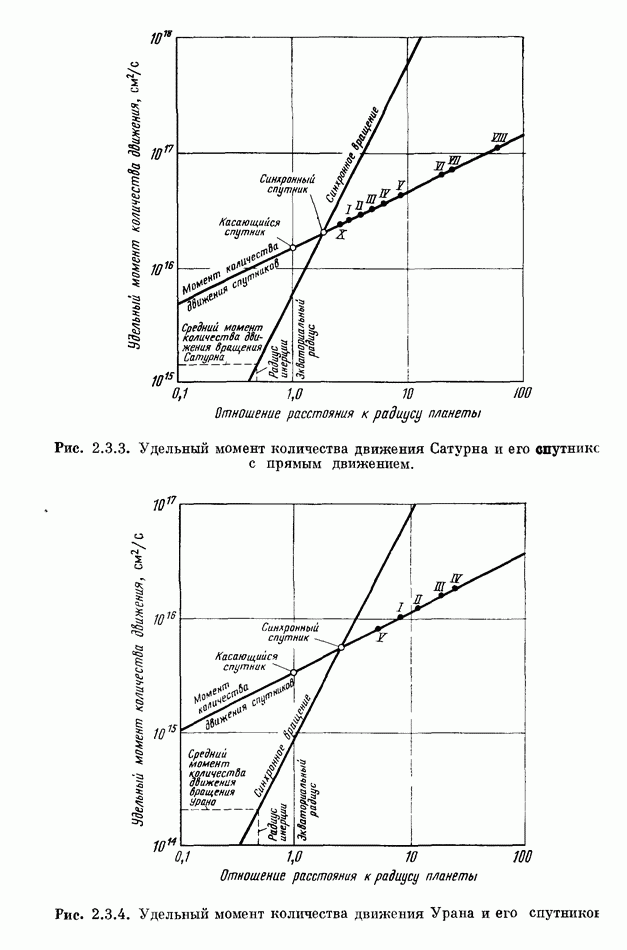
- 2.3. СПУТНИКИ С ПРЯМЫМ И ОБРАТНЫМ ДВИЖЕНИЕМ
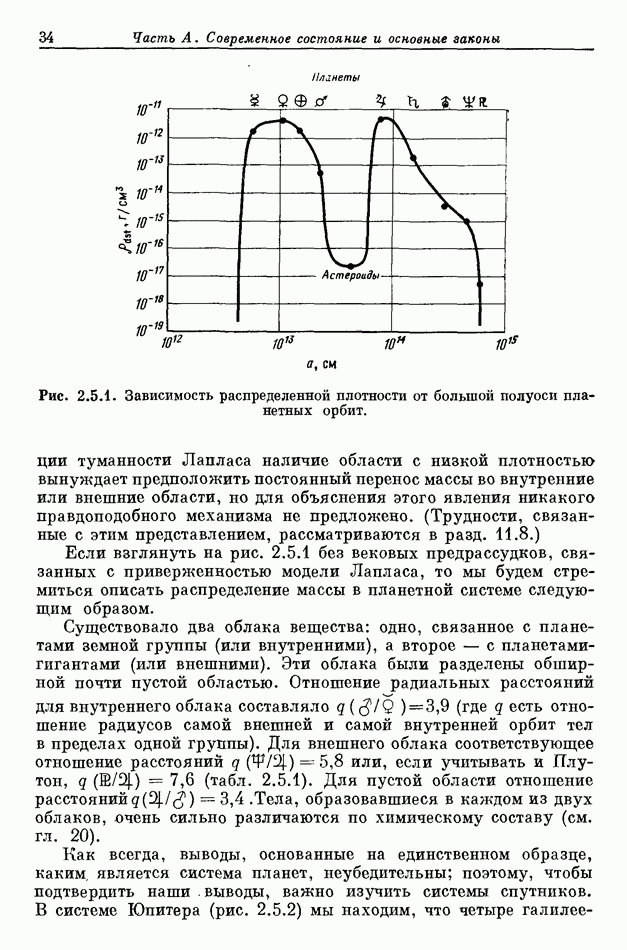
- 2.4. МОДЕЛЬ ЛАПЛАСА И ФУНКЦИЯ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
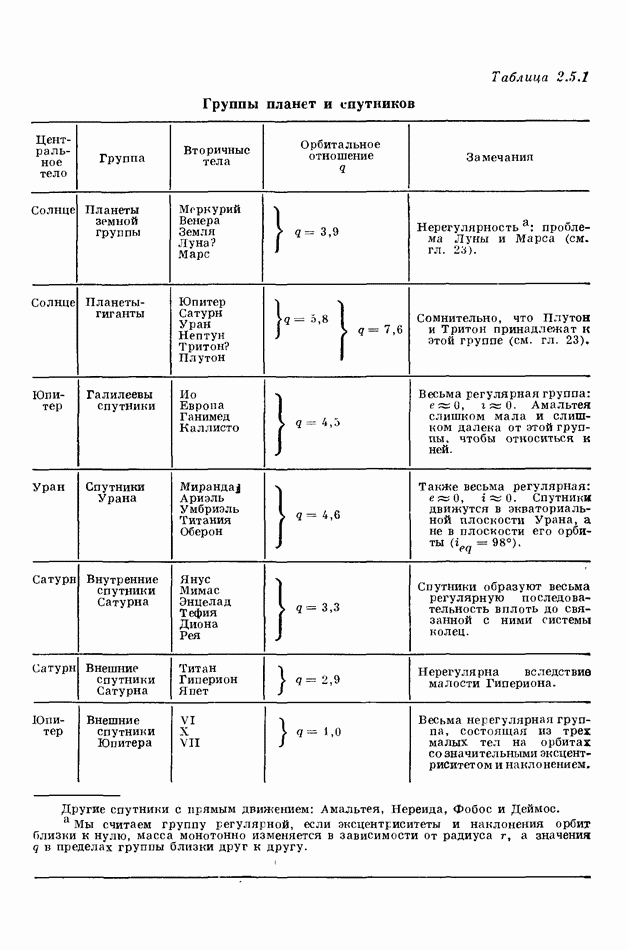
- 2.5. ОБСУЖДЕНИЕ ГРАФИКОВ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
- 2.6. «ЗАКОН» ТИЦИУСА — БОДЕ
- 3. Движение планет и спутников
- 3.1. МЕТОД ВЕДУЩЕГО ЦЕНТРА В ЗАДАЧАХ НЕБЕСНОЙ МЕХАНИКИ
- 3.2. КРУГОВЫЕ ОРБИТЫ
- 3.3. КОЛЕБАНИЯ, ВИДОИЗМЕНЯЮЩИЕ КРУГОВУЮ ОРБИТУ
- 3.4. ДВИЖЕНИЕ В ГРАВИТАЦИОННОМ ПОЛЕ, ОБРАТНО ПРОПОРЦИОНАЛЬНОМ КВАДРАТУ РАССТОЯНИЯ
- 3.5. НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И БОЛЬШИЕ ЭКСЦЕНТРИСИТЕТЫ
- 3.6. ДВИЖЕНИЕ В ПОЛЕ ВРАЩАЮЩЕГОСЯ ЦЕНТРАЛЬНОГО ТЕЛА
- 3.7. ДВИЖЕНИЕ ПЛАНЕТ, ВОЗМУЩАЕМОЕ ДРУГИМИ ПЛАНЕТАМИ
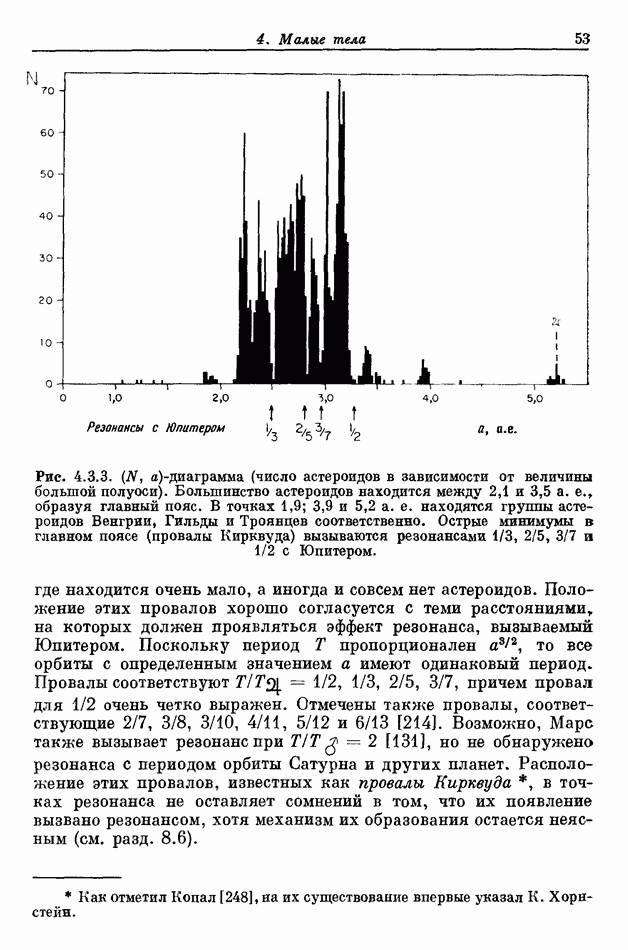
- 4. Малые тела
- 4.2. РАЗЛИЧИЕ В ЭВОЛЮЦИИ БОЛЬШИХ И МАЛЫХ ТЕЛ
- 4.3. ГЛАВНЫЙ ПОЯС АСТЕРОИДОВ
- 4.3.1. НЕНАБЛЮДАЕМЫЕ АСТЕРОИДЫ
- 4.3.2. СЕМЕЙСТВА ХИРАЯМЫ
- 4.3.3. СТРУЙНЫЕ ПОТОКИ АСТЕРОИДОВ
- 4.3.4. ЭВОЛЮЦИЯ ГЛАВНОГО ПОЯСА
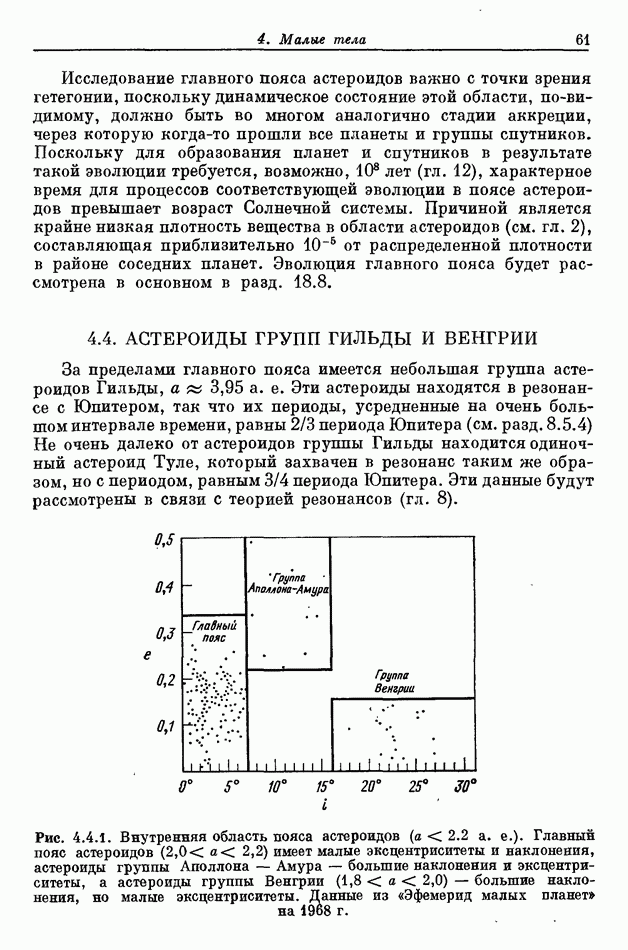
- 4.4. АСТЕРОИДЫ ГРУПП ГИЛЬДЫ И ВЕНГРИИ
- 4.5. ТРОЯНЦЫ
- 4.6. СЕМЕЙСТВО КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 4.6.2. МЕТЕОРНЫЕ ПОТОКИ
- 4.6.3. ДОЛГОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 4.6.4. КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 5. Силы, действующие на малые тела
- 5.2. ГРАВИТАЦИОННЫЕ ВОЗДЕЙСТВИЯ
- 5.2.1. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ
- 5.2.2. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ, ВОЗМУЩАЕМОЕ СТОЛКНОВЕНИЯМИ
- 5.3. ЭЛЕКТРОМАГНИТНЫЕ ЭФФЕКТЫ
- 5.4. ГРАНИЦА МЕЖДУ ДВИЖЕНИЯМИ, ОБУСЛОВЛЕННЫМИ ГРАВИТАЦИОННЫМИ И ЭЛЕКТРОМАГНИТНЫМИ СИЛАМИ
- 5.5. РАДИАЦИОННЫЕ ЭФФЕКТЫ
- 5.5.1. РАДИАЦИОННОЕ ДАВЛЕНИЕ
- 5.5.2. ЭФФЕКТ ПОЙНТИНГА — РОБЕРТСОНА
- 5.6. ВЫВОДЫ
- 6. Кеплеровское движение взаимодействующих тел: струйные потоки
- 6.2. МЕЖПЛАНЕТНАЯ СРЕДА
- 6.3. ЭФФЕКТЫ СТОЛКНОВЕНИЙ
- 6.4. ПРОСТАЯ МОДЕЛЬ СТРУЙНОГО ПОТОКА
- 6.4.1. ДВИЖЕНИЕ ЧАСТИЦ, ИСПУСКАЕМЫХ СО СПУТНИКА
- 6.4.2. СРАВНЕНИЕ С ТОРОМ ИО
- 6.4.3. ЭФФЕКТ СТОЛКНОВЕНИЙ
- 6.5. ВЫВОДЫ ИЗ МОДЕЛИ СТРУЙНОГО ПОТОКА
- 6.6. СТРУЙНЫЙ ПОТОК И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ
- 6.7. ПРОСТАЯ МОДЕЛЬ ОТРИЦАТЕЛЬНОЙ ДИФФУЗИИ
- 6.8. ПРОДОЛЖИТЕЛЬНОСТЬ СЖАТИЯ СТРУЙНОГО ПОТОКА
- 6.9. СТОЛКНОВЕНИЯ ЧАСТИЦ СО СТРУЙНЫМ ПОТОКОМ
- 6.10. СТРУЙНЫЕ ПОТОКИ КАК НЕБЕСНЫЕ ОБЪЕКТЫ
- 7. Столкновения: фрагментация и аккреция
- 7.1. ОБРАЗОВАНИЕ МАЛЫХ ТЕЛ: ФРАГМЕНТАЦИЯ И АККРЕЦИЯ
- 7.2. РАСПРЕДЕЛЕНИЕ ПО РАЗМЕРАМ
- 7.3. ТРИ ПРОСТЫЕ МОДЕЛИ
- 7.3.2. ФРАГМЕНТАЦИЯ
- 7.3.3. ДАННЫЕ НАБЛЮДЕНИЙ, ИМЕЮЩИЕ ОТНОШЕНИЕ К МОДЕЛЯМ
- 7.4. ПЕРЕХОД ОТ ФРАГМЕНТАЦИИ К АККРЕЦИИ
- 8. Резонансные структуры в Солнечной системе
- 8.1. РЕЗОНАНСЫ В СОЛНЕЧНОЙ СИСТЕМЕ
- 8.2. РЕЗОНАНС И КОЛЕБАНИЯ МАЯТНИКА
- 8.3. ПРОСТАЯ МОДЕЛЬ РЕЗОНАНСА
- 8.4. ОТКЛОНЕНИЯ ОТ ТОЧНОГО РЕЗОНАНСА
- 8.5. РЕЗОНАНС МЕЖДУ ОРБИТАЛЬНЫМИ ДВИЖЕНИЯМИ
- 8.5.2. РЕЗОНАНС ЗЕМЛЯ — ТОРО И ДРУГИЕ РЕЗОНАНСЫ ЗЕМЛИ И АСТЕРОИДОВ
- 8.5.3. ТРОЯНЦЫ
- 8.5.4. АСТЕРОИДЫ ГРУППЫ ГИЛЬДЫ
- 8.5.5. ТИТАН — ГИПЕРИОН
- 8.5.6. ДИОНА — ЭНЦЕЛАД
- 8.5.7. ТЕФИЯ — МИМАС
- 8.5.8 ИО — ЕВРОПА — ГАНИМЕД
- 8.6. ПРОВАЛЫ КИРКВУДА
- 8.7. ОБ ОТСУТСТВИИ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В СИСТЕМЕ КОЛЕЦ САТУРНА
- 8.8. РЕЗОНАНСЫ МЕЖДУ ВРАЩЕНИЕМ И ОРБИТАЛЬНЫМ ДВИЖЕНИЕМ
- 8.9. ПОЧТИ-СОИЗМЕРИМОСТИ
- 9. Вращение и приливы
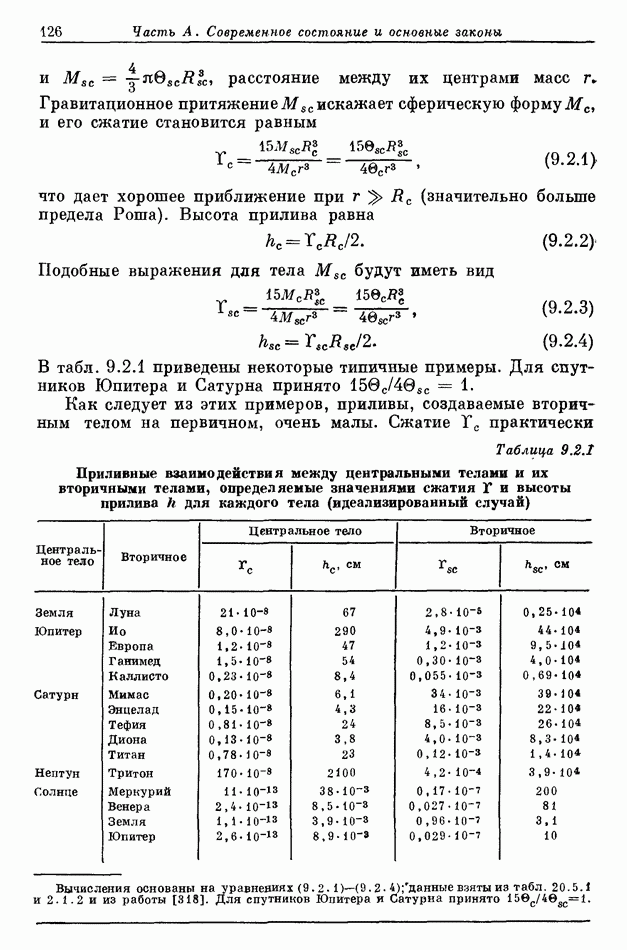
- 9.2. АМПЛИТУДА ПРИЛИВОВ
- 9.3. ПРИЛИВНОЕ ТОРМОЖЕНИЕ ВРАЩЕНИЯ ЦЕНТРАЛЬНОГО ТЕЛА
- 9.4. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ ПРИЛИВАМИ, ВЫЗЫВАЕМЫМИ СПУТНИКАМИ
- 9.5. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ СОЛНЕЧНЫМИ ПРИЛИВАМИ
- 9.6. ЭВОЛЮЦИЯ СПУТНИКОВ ПЛАНЕТ ПОД ДЕЙСТВИЕМ ПРИЛИВОВ
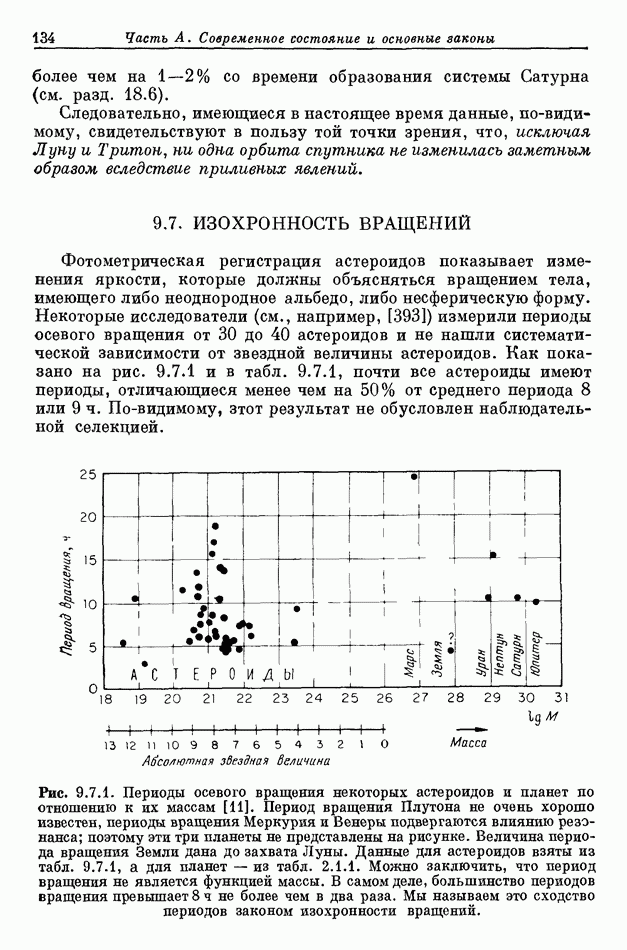
- 9.7. ИЗОХРОННОСТЬ ВРАЩЕНИЙ
- 9.8. ВЫВОДЫ ИЗ ИЗОХРОННОСТИ ВРАЩЕНИЙ
- 10. Постаккреционные изменения в Солнечной системе
- 10.1. УСТОЙЧИВОСТЬ ОРБИТ
- 10.2. РЕЗОНАНС И УСТОЙЧИВОСТЬ
- 10.3. УСТОЙЧИВОСТЬ КОЛЕЦ САТУРНА И ПОЯСА АСТЕРОИДОВ
- 10.4. ПОСТОЯНСТВО ВРАЩЕНИЙ
- 10.5. О ВОЗМОЖНОСТИ. РЕКОНСТРУКЦИИ ГЕТЕГОННЫХ ПРОЦЕССОВ
- Часть Б. Аккреция небесных тел
- 11.2. ГРАВИТАЦИОННЫЙ КОЛЛАПС ГАЗОВОГО ОБЛАКА
- 11.2.1. ВОЗРАЖЕНИЯ ПРОТИВ ГРАВИТАЦИОННОГО КОЛЛАПСА КАК МЕХАНИЗМА ОБРАЗОВАНИЯ ПЛАНЕТ И СПУТНИКОВ
- 11.3. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ: АККРЕЦИЯ ПУТЕМ ЗАХВАТА ЧАСТИЦ ИЛИ ГАЗА
- 11.4. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5. НЕГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5.1. ВОЗРАЖЕНИЯ ПРОТИВ ПРОЦЕССА НЕГРАВИТАЦИОННОЙ АККРЕЦИИ
- 11.5.2. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ
- 11.5.3. ЭЛЕКТРОСТАТИЧЕСКИ ПОЛЯРИЗОВАННЫЕ ЗЕРНА
- 11.5.4. РЫХЛЫЕ СКОПЛЕНИЯ
- 11.6. АККРЕЦИЯ РЕЗОНАНСНО ЗАХВАЧЕННЫХ ЗЕРЕН
- 11.7. НЕОБХОДИМЫЕ СВОЙСТВА ПРОЦЕССА АККРЕЦИИ
- 11.8. СОВРЕМЕННОЕ СОСТОЯНИЕ АСТЕРОИДОВ, МЕТЕОРНЫХ ТЕЛ И КОМЕТ И ГИПОТЕЗА ВЗОРВАВШЕЙСЯ ПЛАНЕТЫ
- 12. Об аккреции планет и спутников
- 12.1. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ
- 12.2. СТРУЙНЫЙ ПОТОК КАК ПРОМЕЖУТОЧНАЯ СТАДИЯ В ОБРАЗОВАНИИ ПЛАНЕТ И СПУТНИКОВ
- 12.3. АККРЕЦИЯ ЗАРОДЫША
- 12.4. БАЛАНС МАССЫ СТРУЙНОГО ПОТОКА
- 12.5. ЭНЕРГЕТИЧЕСКИЙ БАЛАНС В СТРУЙНОМ ПОТОКЕ
- 12.6. АККРЕЦИЯ ПРИ ПОСТОЯННОЙ СКОРОСТИ ПОСТУПЛЕНИЯ ВЕЩЕСТВА В СТРУЙНЫЙ ПОТОК
- 12.7. ЗАМЕЧАНИЕ
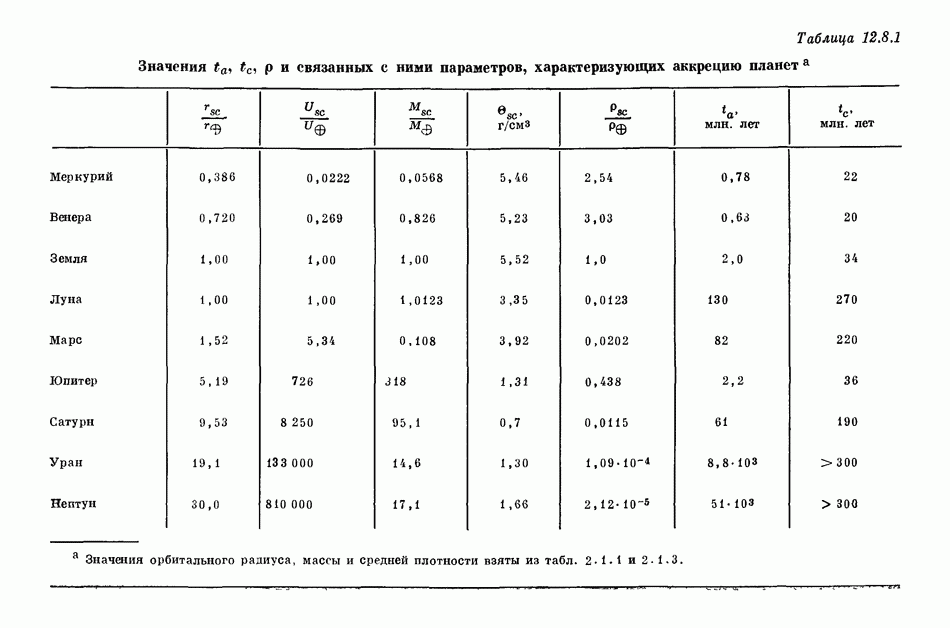
- 12.8. ЧИСЛЕННЫЕ ЗНАЧЕНИЯ
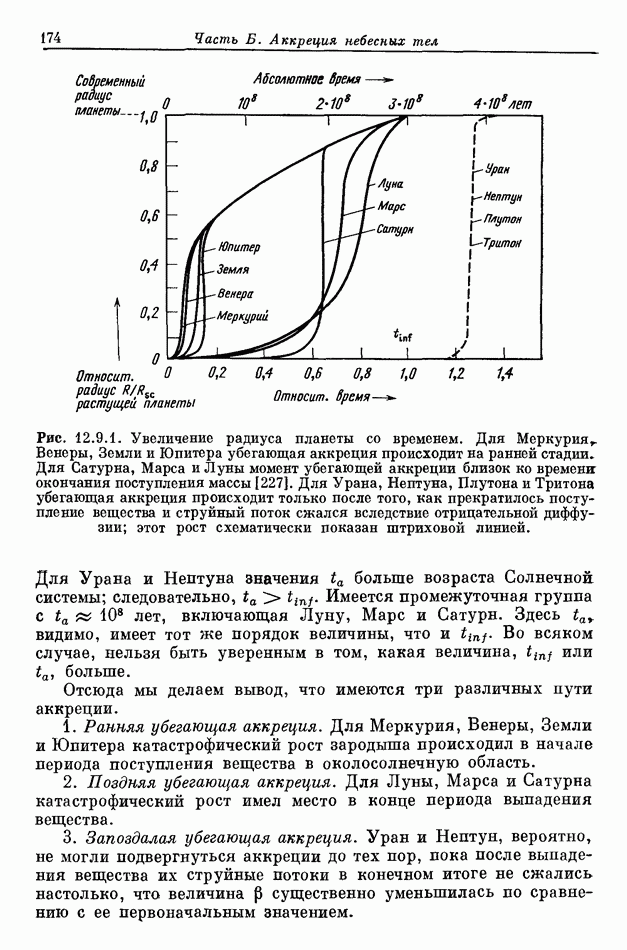
- 12.9. ВЫВОДЫ ОТНОСИТЕЛЬНО РАЗЛИЧНЫХ ТИПОВ АККРЕЦИИ
- 12.10. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ТЕЛА НА РАННЕЙ СТАДИИ ЕГО СУЩЕСТВОВАНИЯ
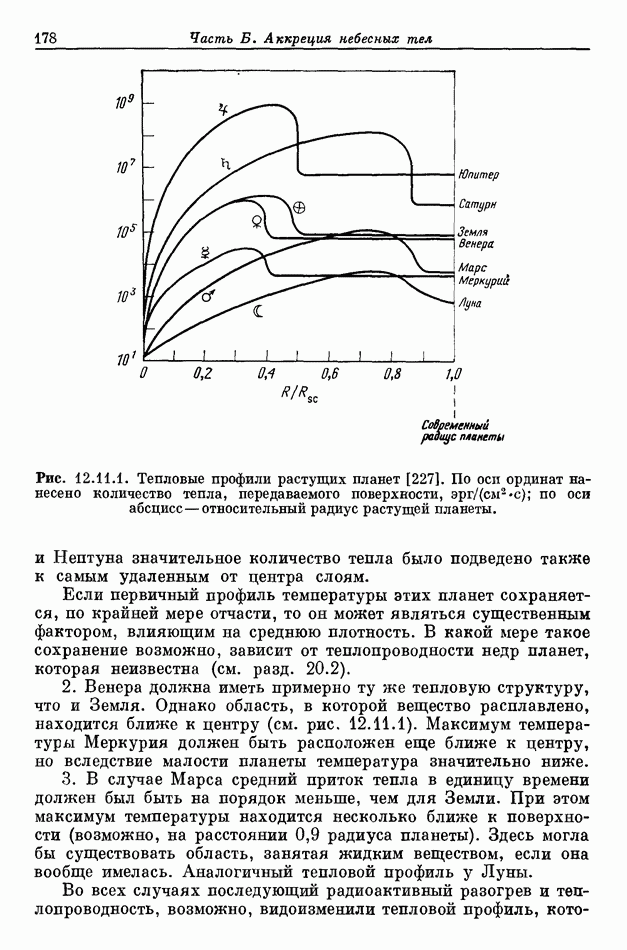
- 12.11. ВЫВОДЫ О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ ПЛАНЕТ
- 12.12. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ
- 12.13. ДИФФЕРЕНЦИАЦИЯ ВЕЩЕСТВА, ОБУСЛОВЛЕННАЯ ТЕПЛОВЫМ ФРОНТОМ АККРЕЦИИ
- 13. Вращение и аккреция
- 13.1. СОУДАРЕНИЯ ЗЕРЕН И СОБСТВЕННОЕ ВРАЩЕНИЕ ЗАРОДЫША
- 13.2. АККРЕЦИЯ С КРУГОВЫХ ОРБИТ НА НЕГРАВИТИРУЮЩИЙ ЗАРОДЫШ
- 13.3. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
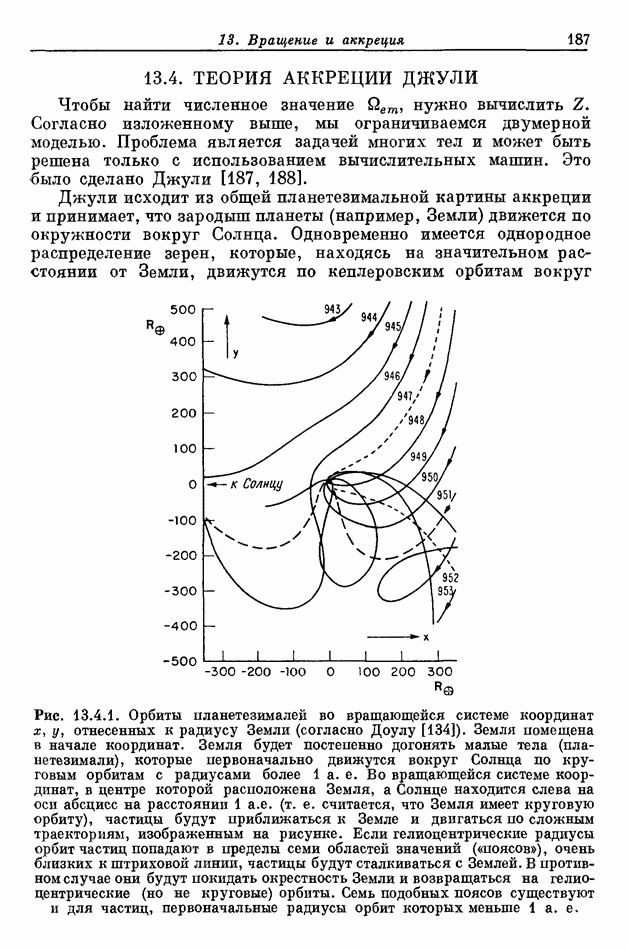
- 13.4. ТЕОРИЯ АККРЕЦИИ ДЖУЛИ
- 13.5. СТАТИСТИЧЕСКАЯ ТЕОРИЯ АККРЕЦИИ
- 13.5.1. АККРЕЦИЯ НА СТАДИИ, ПРЕДШЕСТВУЮЩЕЙ УБЕГАЮЩЕЙ АККРЕЦИИ
- 13.6. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ И СОБСТВЕННОЕ ВРАЩЕНИЕ ПЛАНЕТ
- 13.6.1. РАННЯЯ, ПОЗДНЯЯ И ЗАПОЗДАЛАЯ УБЕГАЮЩАЯ АККРЕЦИЯ; НАКЛОН ОСИ ВРАЩЕНИЯ
- 13.6.2. ПЕРИОД ВРАЩЕНИЯ
- 13.6.3. ОБРАТНОЕ ВРАЩЕНИЕ ВЕНЕРЫ
- 14. Взаимосвязи между кометами и метеорными телами
- 14.2. ПОЛОЖИТЕЛЬНАЯ И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ; МЕТЕОРНЫЕ ПОТОКИ КАК СТРУЙНЫЕ ПОТОКИ
- 14.3. МЕХАНИЗМ АККРЕЦИИ В МЕТЕОРНЫХ ПОТОКАХ
- 14.4. НАБЛЮДЕНИЯ ОБРАЗОВАНИЯ КОМЕТ В МЕТЕОРНЫХ ПОТОКАХ
- 14.5. ДОЛГО- И КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 14.6 ВЫВОДЫ О ПРИРОДЕ КОМЕТ, ОСНОВАННЫЕ НА ЭМИССИОННЫХ ХАРАКТЕРИСТИКАХ
- 14.7. АНАЛОГИИ МЕЖДУ ПОТОКАМИ КОМЕТ И АСТЕРОИДОВ
- 14.8. СРАВНЕНИЕ С АККРЕЦИЕЙ ПЛАНЕТ И СПУТНИКОВ
- Часть В. Плазма и конденсация
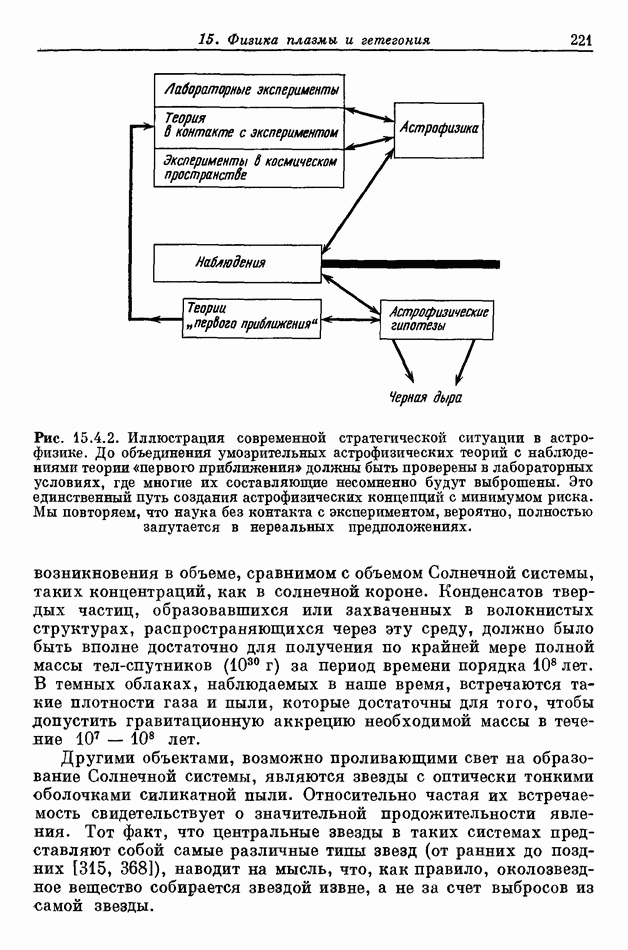
- 15. Физика плазмы и гетегония
- 15.2 СВЯЗЬ МЕЖДУ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКОЙ ПЛАЗМЫ
- 15.3. ПЕРВОЕ И ВТОРОЕ ПРИБЛИЖЕНИЯ В ФИЗИКЕ КОСМИЧЕСКОЙ ПЛАЗМЫ
- 15.3.3. НЕКОТОРЫЕ ЛАБОРАТОРНЫЕ ЭКСПЕРИМЕНТЫ, ОТНОСЯЩИЕСЯ К КОСМИЧЕСКОЙ ФИЗИКЕ
- 15.4. СТРАТЕГИЯ АНАЛИЗА ГЕТЕГОННОЙ ПЛАЗМЫ
- 15.5. ТРЕБУЕМЫЕ СВОЙСТВА МОДЕЛИ
- 15.6. НЕКОТОРЫЕ СУЩЕСТВУЮЩИЕ ТЕОРИИ
- 16. Модель гетегонной плазмы
- 16.1. НАМАГНИЧЕННОЕ ЦЕНТРАЛЬНОЕ ТЕЛО
- 16.2. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
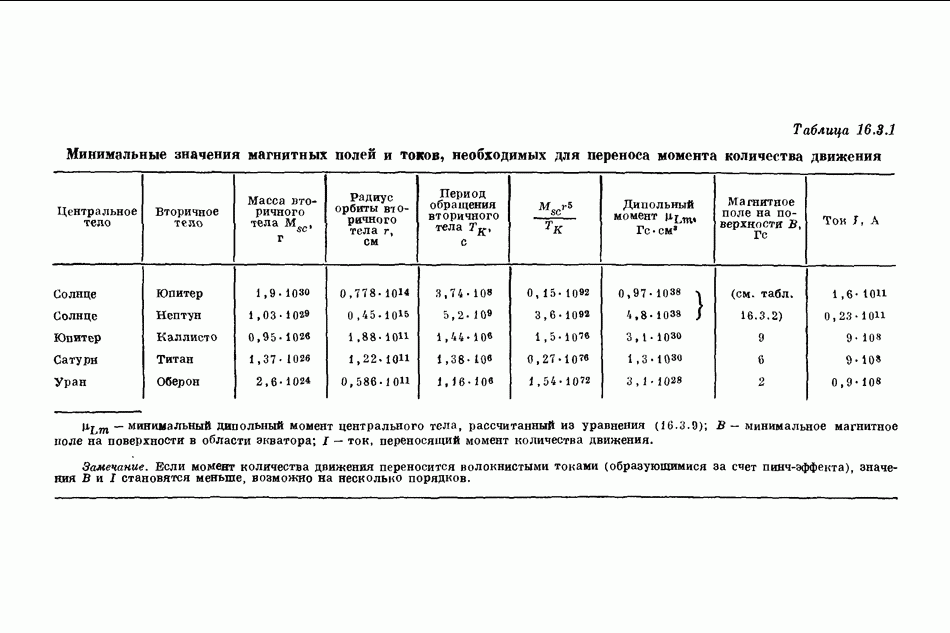
- 16.3. ПЕРЕНОС МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 16.4. УДЕРЖАНИЕ ПЕРВИЧНОГО ОБЛАКА
- 16.5. ПЛАЗМА КАК ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 16.6. ВЫВОДЫ ОТНОСИТЕЛЬНО МОДЕЛИ
- 16.7. ГЕТЕГОННЫЕ ТУМАННОСТИ
- 16.8. ЭФФЕКТЫ ОБЛУЧЕНИЯ
- 16.9. МОДЕЛЬ И ПРИНЦИП ГЕТЕГОНИИ
- 17. Перенос момента количества движения и конденсация зерен
- 17.1. ИЗОРОТАЦИЯ ФЕРРАРО И ЧАСТИЧНАЯ КОРОТАЦИЯ
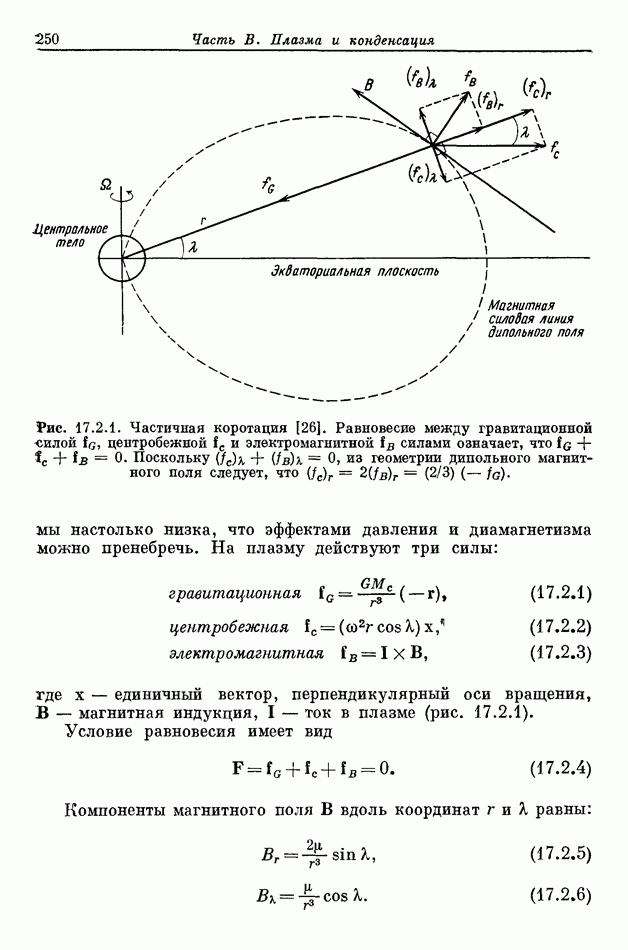
- 17.2. ЧАСТИЧНАЯ КОРОТАЦИЯ ПЛАЗМЫ В МАГНИТНОМ И ГРАВИТАЦИОННОМ ПОЛЯХ
- 17.2.1. СВЯЗЬ МЕЖДУ ИЗОРОТАЦИЕЙ ФЕРРАРО И ЧАСТИЧНОЙ КОРОТАЦИЕЙ
- 17.3. ПЛАЗМА В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 17.4. ЗАМЕЧАНИЕ
- 17.5. КОНДЕНСАЦИЯ ПЛАЗМЫ: ЗАКОНА ДВУХ ТРЕТЕЙ
- 17.6. ВЫДЕЛЕНИЕ ЭНЕРГИИ ПРИ ПЕРЕНОСЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 18. Аккреция продуктов конденсации
- 18.2. ЭВОЛЮЦИЯ ОРБИТ ВСЛЕДСТВИЕ СТОЛКНОВЕНИЙ
- 18.3. ПРЕДЕЛ РОША
- 18.4. МОДЕЛЬ ЭВОЛЮЦИИ ОРБИТ
- 18.5. АККРЕЦИЯ В ПРЕДЕЛАХ …
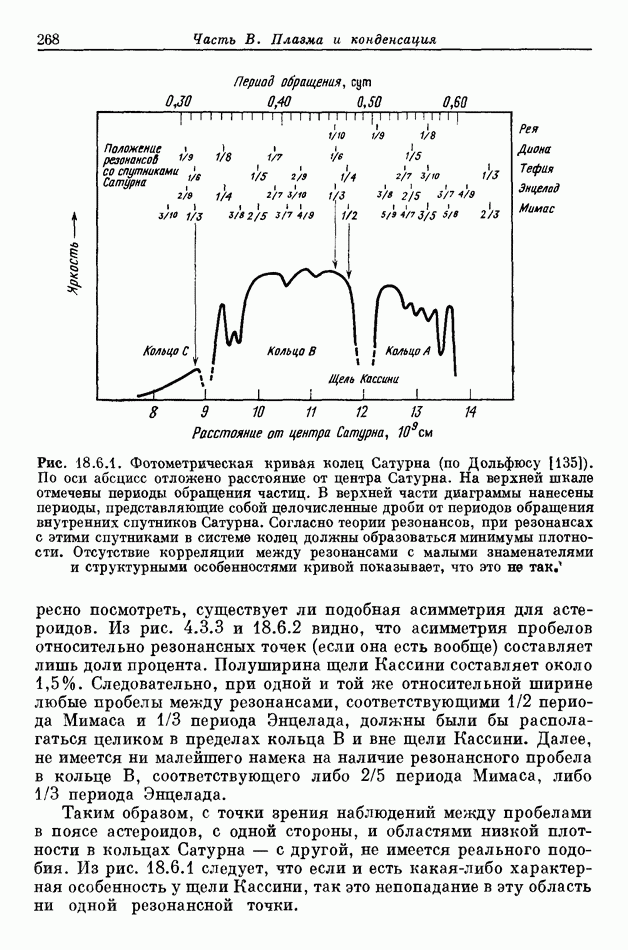
- 18.6. СТРУКТУРА КОЛЕЦ САТУРНА
- 18.6.2. МОЖЕТ ЛИ СТРУКТУРА КОЛЕЦ САТУРНА ИМЕТЬ ГЕТЕГОННОЕ ПРОИСХОЖДЕНИЕ?
- 18.6.3. ГЕТЕГОННАЯ ТЕОРИЯ КОЛЕЦ САТУРНА
- 18.6.4. ТЕОРИЯ ЩЕЛИ КАССИНИ
- 18.6.5. ТЕОРИЯ ГРАНИЦЫ МЕЖДУ КОЛЬЦАМИ В И С
- 18.6.6. АНАЛИЗ РЕЗУЛЬТАТОВ
- 18.7. АККРЕЦИЯ ЗА ПРЕДЕЛОМ …
- 18.8. ОБРАЗОВАНИЕ ПОЯСА АСТЕРОИДОВ
- 18.9. ВЫВОДЫ О ЧАСТИЧНОЙ КОРОТАЦИИ
- 18.10. ОБРАЗОВАНИЕ СПУТНИКОВ И ПЛАНЕТ
- 18.11. АККРЕЦИЯ ЛЕТУЧИХ ВЕЩЕСТВ
- 19. Транспланетная конденсация
- 19.1. МЕЖПЛАНЕТНАЯ И ТРАНСПЛАНЕТНАЯ КОНДЕНСАЦИЯ
- 19.2. ГРАНИЦА МЕЖДУ МЕЖПЛАНЕТНЫМ И ТРАНСПЛАНЕТНЫМ ПРОСТРАНСТВОМ
- 19.3. КОНДЕНСАЦИЯ ТЕЛ НА ПОЧТИ-ПАРАБОЛИЧЕСКИХ ОРБИТАХ
- 19.4. ТЕЛА С ДОЛГОПЕРИОДИЧЕСКИМИ ОРБИТАМИ
- 19.5. ДИФФУЗИЯ ПОЧТИ ПАРАБОЛИЧЕСКИХ ОРБИТ: СБЛИЖЕНИЯ С ПЛАНЕТАМИ
- 19.6. ГЕНЕТИЧЕСКИЕ СВЯЗИ КОМПЛЕКСА КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 19.7. ВЫВОДЫ О СЕМЕЙСТВАХ МЕТЕОРНЫХ ТЕЛ
- 19.8. ГЕНЕАЛОГИЯ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- Часть Г. Физическая и химическая структура Солнечной системы
- 20. Химическая структура Солнечной системы
- 20.2. ИСТОЧНИКИ ИНФОРМАЦИИ О ХИМИЧЕСКОМ СОСТАВЕ
- 20.3. ДИФФЕРЕНЦИАЦИЯ ХИМИЧЕСКОГО СОСТАВА ДО И ПОСЛЕ АККРЕЦИИ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- 20.4. НЕИЗВЕСТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА
- 20.5. СОСТАВ ПЛАНЕТ И СПУТНИКОВ
- 20.6. СОСТАВ СОЛНЦА
- 20.6.2. АНАЛИЗ КОРПУСКУЛЯРНОГО ИЗЛУЧЕНИЯ СОЛНЦА
- 20.6.3. ЗНАЧЕНИЕ ДАННЫХ ПО ОБИЛИЯМ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ ФОТОСФЕРЕ
- 20.7. РЕГУЛЯРНОСТЬ ОБЪЕМНЫХ ПЛОТНОСТЕЙ В СОЛНЕЧНОЙ СИСТЕМЕ
- 21. Распределение массы и критическая скорость
- 21.1. РАСПРЕДЕЛЕНИЕ МАССЫ В СОЛНЕЧНОЙ СИСТЕМЕ
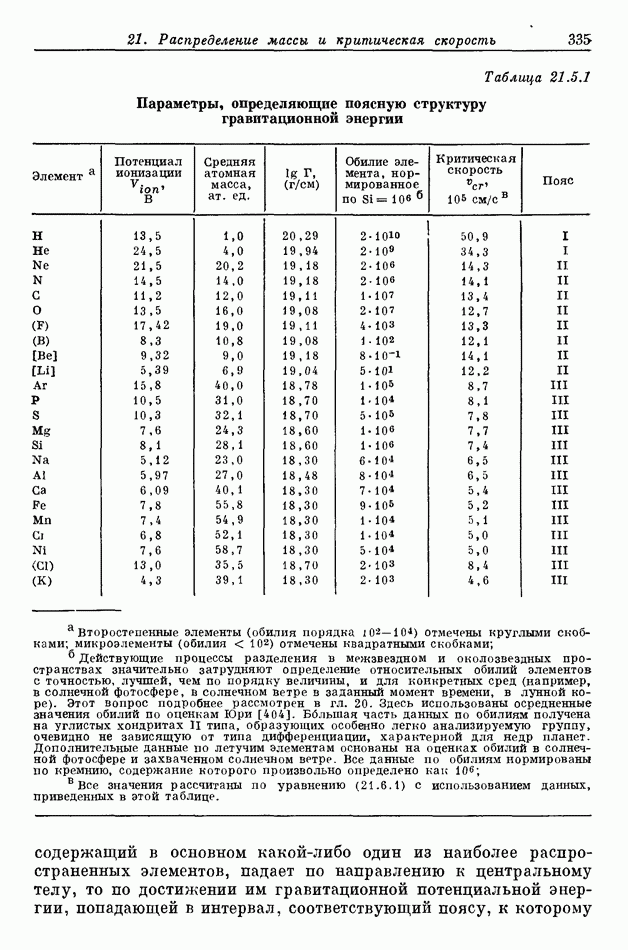
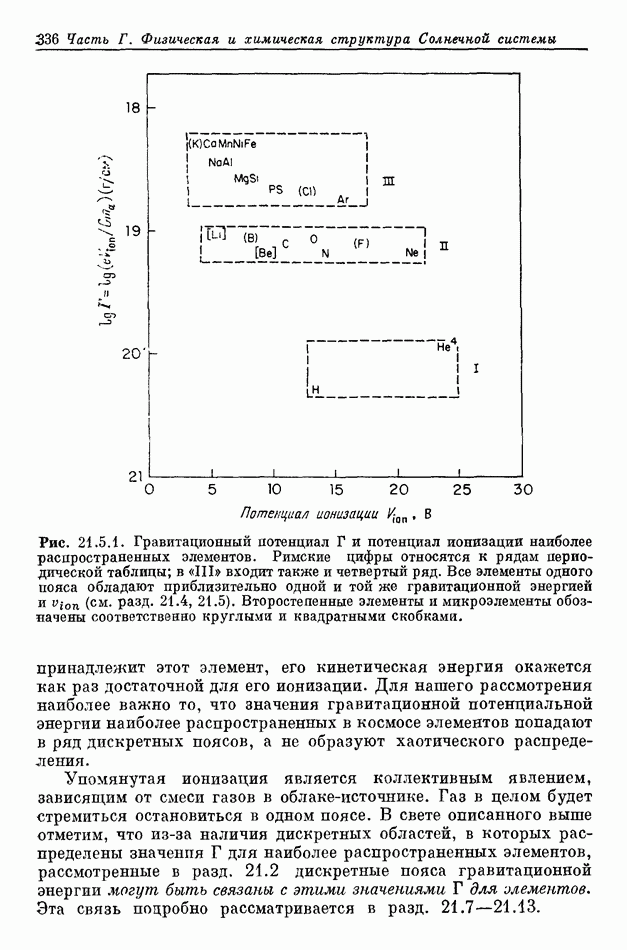
- 21.2. ПОЯСА ВТОРИЧНЫХ ТЕЛ В ЗАВИСИМОСТИ ОТ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 21.3. СРАВНИТЕЛЬНОЕ ИЗУЧЕНИЕ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 21.4. ЦТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ ДЛЯ ОБРАЗОВАНИЯ ПОЯСОВ
- 21.5. ПОПЫТКИ ИНТЕРПРЕТАЦИИ ПОЯСНОЙ СТРУКТУРЫ
- 21.6. ТРИ ВОЗРАЖЕНИЯ
- 21.7. ПОИСКИ «КРИТИЧЕСКОЙ СКОРОСТИ»
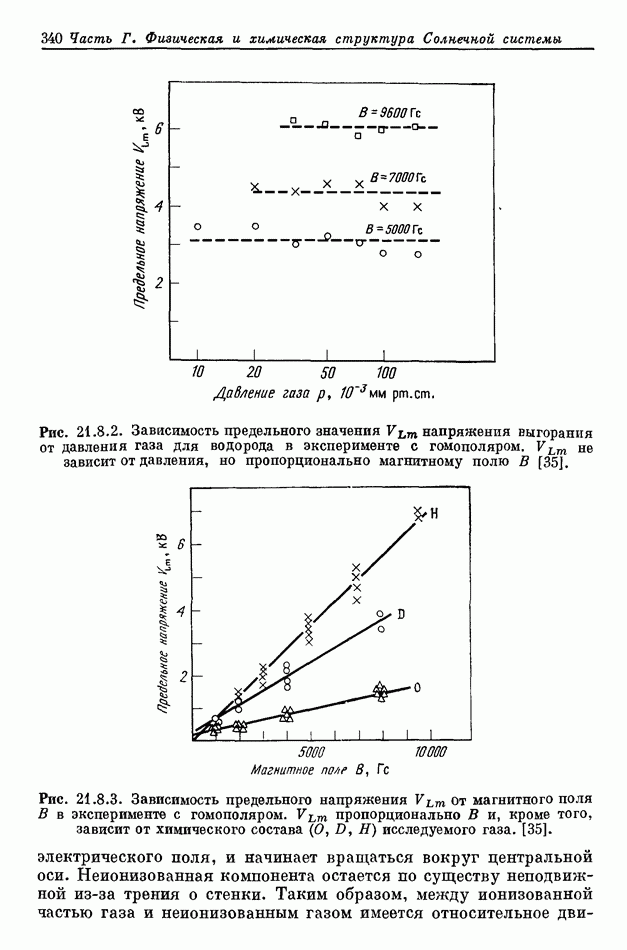
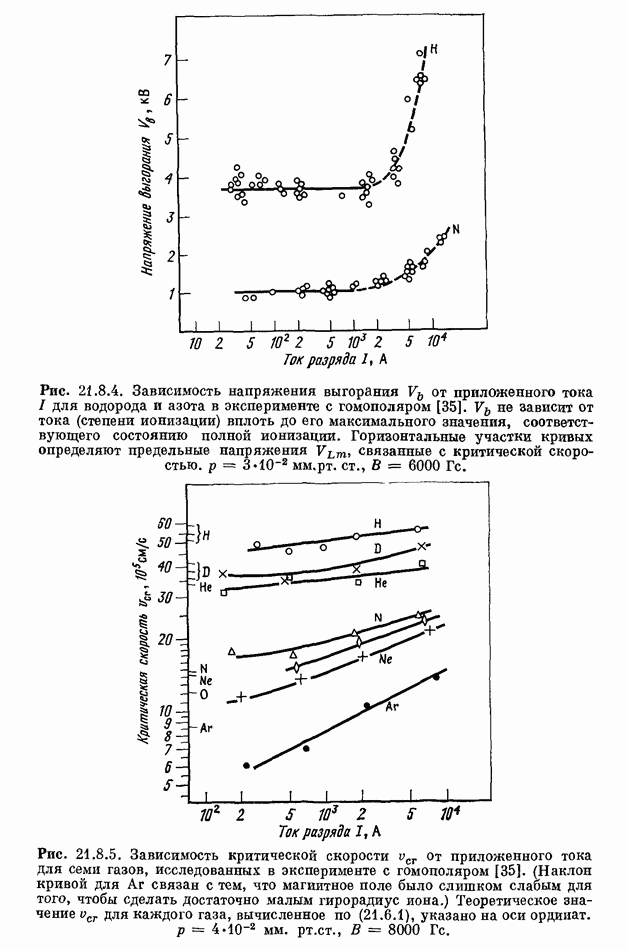
- 21.8. ЭКСПЕРИМЕНТЫ ПО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.8.2. ПЛАЗМЕННЫЙ ПУЧОК, СТАЛКИВАЮЩИЙСЯ С ОБЛАКОМ НЕЙТРАЛЬНОГО ГАЗА
- 21.8.3. ДРУГИЕ ЭКСПЕРИМЕНТЫ
- 21.9. ТЕОРИЯ КРИТИЧЕСКОЙ СКОРОСТИ
- 21.10. ВЫВОДЫ ОТНОСИТЕЛЬНО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.11. ХИМИЧЕСКИЙ СОСТАВ ВЫПАДАЮЩЕГО ГАЗА
- 21.11.2. ОБЛАКА A, B, C и D В СОЛНЕЧНОЙ СИСТЕМЕ
- 21.11.3. СОВЕРШЕНСТВОВАНИЕ ОСНОВНОЙ МОДЕЛИ
- 21.11.4. ВЛИЯНИЕ МЕЖЗВЕЗДНЫХ МОЛЕКУЛ
- 21.12. ХИМИЧЕСКИЙ СОСТАВ СОЛНЕЧНОЙ СИСТЕМЫ И РАЗМЕЩЕНИЕ НЕОДНОРОДНОЙ ПЛАЗМЫ
- 21.12.2. ВЛИЯНИЕ ТРАНСПЛАНЕТНОЙ КОНДЕНСАЦИИ НА СОСТАВ ПЛАНЕТ И СПУТНИКОВ
- 21.12.3. ФРАКЦИОНИРОВАНИЕ, СВЯЗАННОЕ С КОНДЕНСАЦИЕЙ ИЛИ СЛЕДУЮЩЕЕ ЗА НЕЙ
- 21.12.4. ВЫВОДЫ О ХИМИЧЕСКОМ СОСТАВЕ НЕБЕСНЫХ ТЕЛ
- 21.13. ИЗМЕНЕНИЕ РАССТОЯНИЯ ИОНИЗАЦИИ ДЛЯ КРИТИЧЕСКОЙ СКОРОСТИ ИЗ-ЗА ВЗАИМОДЕЙСТВИЯ С ПЛАЗМОЙ В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 22. Метеориты и предшествующие им состояния
- 22.1. ИНТЕРПРЕТАЦИЯ ЭВОЛЮЦИОННЫХ ДАННЫХ, ЗАПЕЧАТЛЕННЫХ В МЕТЕОРИТАХ
- 22.2. ИСТОЧНИКИ МЕТЕОРИТОВ
- 22.3. ЭФФЕКТЫ СЕЛЕКЦИИ
- 22.4. ВЕРХНИЕ ПРЕДЕЛЫ РАЗМЕРОВ ТЕЛ, ПРЕДШЕСТВУЮЩИХ МЕТЕОРИТАМ
- 22.5. ПРЕДШЕСТВУЮЩИЕ СОСТОЯНИЯ РОДИТЕЛЬСКИХ ТЕЛ МЕТЕОРИТОВ
- 22.6. ЭВОЛЮЦИЯ СТРУЙНОГО ПОТОКА И СВОЙСТВА МЕТЕОРИТОВ
- 22.7. СИЛЫ СЦЕПЛЕНИЯ В МЕТЕОРИТНОМ ВЕЩЕСТВЕ
- 22.8. ЭВОЛЮЦИОННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ПРЕДШЕСТВУЮЩИХ СОСТОЯНИЙ МЕТЕОРИТОВ
- 22.9. ВОЗРАСТНЫЕ СООТНОШЕНИЯ В ЭВОЛЮЦИИ РОДИТЕЛЬСКИХ СТРУЙНЫХ ПОТОКОВ МЕТЕОРИТОВ
- 22.9.1. ЗАМЫКАНИЕ РЕЗЕРВУАРОВ ТУГОПЛАВКИХ КОМПОНЕНТ
- 22.9.2. ВОЗРАСТЫ КРИСТАЛЛИЗАЦИИ
- 22.9.3. ВОЗРАСТЫ УДЕРЖАНИЯ ГАЗА
- 22.9.4. ВОЗРАСТЫ ДЕГАЗАЦИИ
- 22.9.5. ТРЕКИ ЧАСТИЦ И ВНЕДРЕНИЕ ПЛАЗМЫ В МЕТЕОРИТАХ
- 22.9.6. ВОЗРАСТЫ ОБЛУЧЕНИЯ КОСМИЧЕСКИМИ ЛУЧАМИ ВЫСОКИХ ЭНЕРГИЙ
- 22.10. ОБЩИЕ ЗАМЕЧАНИЯ О ДАННЫХ, ЗАФИКСИРОВАННЫХ В МЕТЕОРИТАХ
- 23. Строение групп вторичных тел
- 23.1. ИОНИЗАЦИЯ В ПРОЦЕССЕ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- 23.2. ПОЛНАЯ ИОНИЗАЦИЯ
- 23.3. ЧАСТИЧНАЯ ИОНИЗАЦИЯ
- 23.4. ИЗМЕНЕНИЕ ВРАЩЕНИЯ ВО ВРЕМЯ ОБРАЗОВАНИЯ ВТОРИЧНЫХ ТЕЛ
- 23.5. НАБЛЮДАЕМЫЕ ЗНАЧЕНИЯ …
- 23.6. РАСПРЕДЕЛЕНИЕ МАССЫ В ЗАВИСИМОСТИ ОТ …
- 23.7. АНАЛИЗ СТРОЕНИЯ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 23.8. ПОЛНЫЙ ПЕРЕЧЕНЬ ЗНАЧЕНИЙ … ДЛЯ ВСЕХ ТЕЛ
- 23.9. ЗАВЕРШЕННОСТЬ
- 23.9.1. ЗАМЕЧАНИЕ О ВНУТРЕННЕЙ ГРАНИЦЕ СИСТЕМЫ СПУТНИКОВ
- 23.9.2. НАКЛОН ПОЯСОВ НА ДИАГРАММЕ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЩЭНЕРГИИ
- 23.9.3. ДРУГИЕ ЗАКОНОМЕРНОСТИ В СТРОЕНИИ ГРУПП
- 23.10. ВЫВОДЫ О МОДЕЛИ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- Часть Д. Частные проблемы
- 24. Происхождение и эволюция системы Земля-Луна
- 24.2. СРАВНЕНИЕ С ДРУГИМИ СИСТЕМАМИ СПУТНИКОВ
- 24.3. СТРУКТУРА НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ ЗЕМЛИ
- 24.4 ТЕОРИЯ ЗАХВАТА
- 24.5 ПРИЛИВНАЯ ЭВОЛЮЦИЯ ЛУННОЙ ОРБИТЫ
- 24.6. РАЗРУШЕНИЕ НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ
- 24.7. АККРЕЦИЯ И ТЕПЛОВАЯ СТРУКТУРА ЛУНЫ
- 24.8. СОСТАВ ЛУНЫ
- 24.9. ВЫВОДЫ
- 25. Свойства Солнца на ранней стадии его существования
- 25.2 МАССА СОЛНЦА
- 25.3. МАГНИТНОЕ ПОЛЕ СОЛНЦА
- 25.4. ПЕРИОД СОБСТВЕННОГО ВРАЩЕНИЯ СОЛНЦА
- 25.5. ИЗЛУЧЕНИЕ СОЛНЦА, СОЛНЕЧНЫЙ ВЕТЕР
- 25.6. ЭФФЕКТЫ ВЫГОРАНИЯ ДЕЙТЕРИЯ НА СОЛНЦЕ
- 25.7. ЗАМЕЧАНИЯ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 26. Происхождение океана и атмосферы Земли
- 26.1. ЗЕМНОЙ ОКЕАН И ОБРАЗОВАНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
- 26.2. СТАДИИ ОТДАЛЕННЫХ ПРЕДШЕСТВЕННИКОВ
- 26.2.2. ПЕРВИЧНЫЕ ЗЕРНА КАК НОСИТЕЛИ КОМПОНЕНТ АТМОСФЕРЫ И ОКЕАНА
- 26.2.3. ВНЕЗЕМНЫЕ ИСТОЧНИКИ ВОДЫ
- 26.2.4. ЗАПАСЫ ИНЕРТНЫХ И ХИМИЧЕСКИ АКТИВНЫХ ЛЕТУЧИХ
- 26.3. СТАДИИ БЛИЖАЙШИХ ПРЕДШЕСТВЕННИКОВ
- 26.3.1. ЭВОЛЮЦИЯ ПРЕДШЕСТВОВАВШИХ ЗЕМЛЕ ПЛАНЕТЕЗИМАЛЕЙ
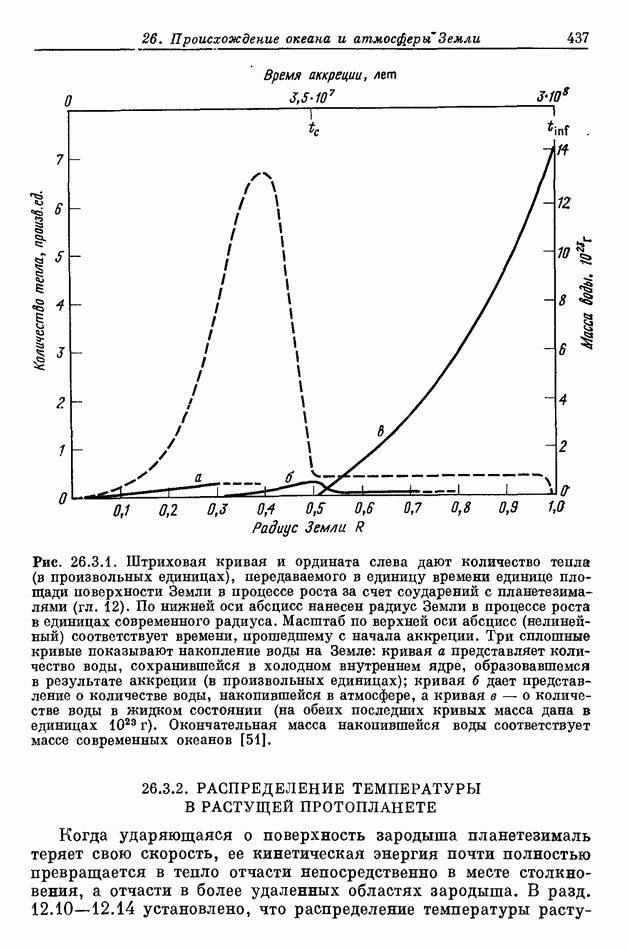
- 26.3.2. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В РАСТУЩЕЙ ПРОТОПЛАНЕТЕ
- 26.3.3. ЯДРО ЗЕМЛИ
- 26.3.4. ВЫСВОБОЖДЕНИЕ ТЕПЛА И УЛЕТУЧИВАНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ
- 26.4. НАКОПЛЕНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ ЗЕМЛИ
- 26.4.2. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ И СОСТОЯНИЕ ВОДЫ
- 26.4.3. ДЕТАЛИЗАЦИЯ МОДЕЛИ
- 26.5. ПОСТУПЛЕНИЕ ВОДЫ В ЛИТОСФЕРУ
- 26.5.2. СТАЦИОНАРНОЕ СОСТОЯНИЕ ПРОПИТЫВАНИЯ И ВЫСВОБОЖДЕНИЯ
- 26.5.3. ВОЗМОЖНЫЕ ОСТАТКИ ЛЕТУЧИХ ВЕЩЕСТВ ПЛАНЕТЕЗИМАЛЕЙ В ЗЕМНОЙ КОРЕ И МАНТИИ
- 26.6. ОКЕАН И СИСТЕМА ЗЕМЛЯ — ЛУНА
- 26.7. ИТОГИ И ВЫВОДЫ
- 27. Межзвездные облака и образование звезд
- 27.2. МАГНИТНАЯ ГИДРОДИНАМИКА ОБЛАКОВ КОСМИЧЕСКОЙ ПЛАЗМЫ
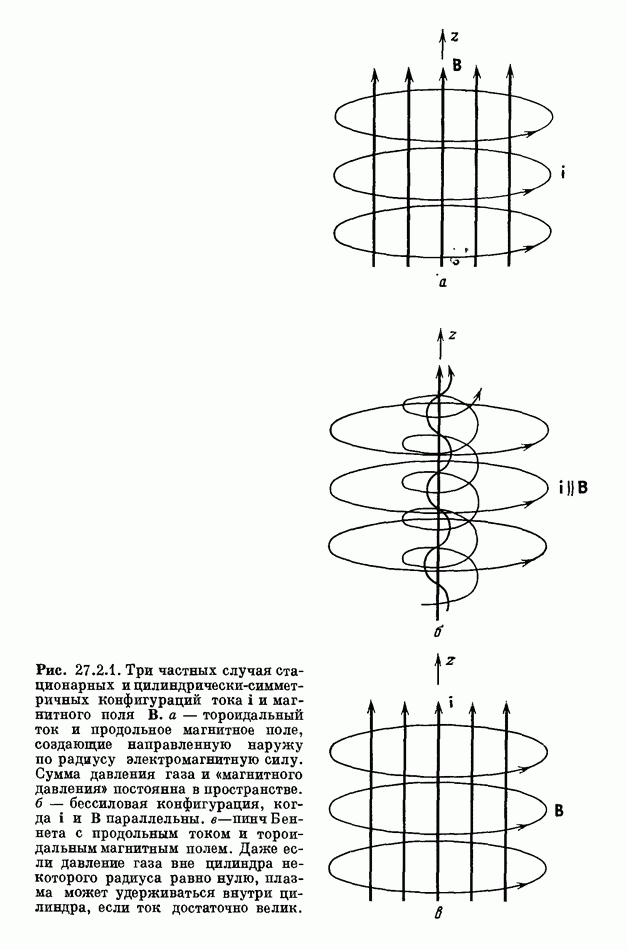
- 27.2.3. БЕССИЛОВЫЕ МАГНИТНЫЕ ПОЛЯ И СОЗДАНИЕ ВОЛОКОН
- 27.2.4. СПОСОБСТВУЮТ ИЛИ ПРОТИВОДЕЙСТВУЮТ СЖАТИЮ МАГНИТНЫЕ ПОЛЯ?
- 27.2.5. ПИНЧ-СЖАТИЕ ТЕМНЫХ МЕЖЗВЕЗДНЫХ ОБЛАКОВ
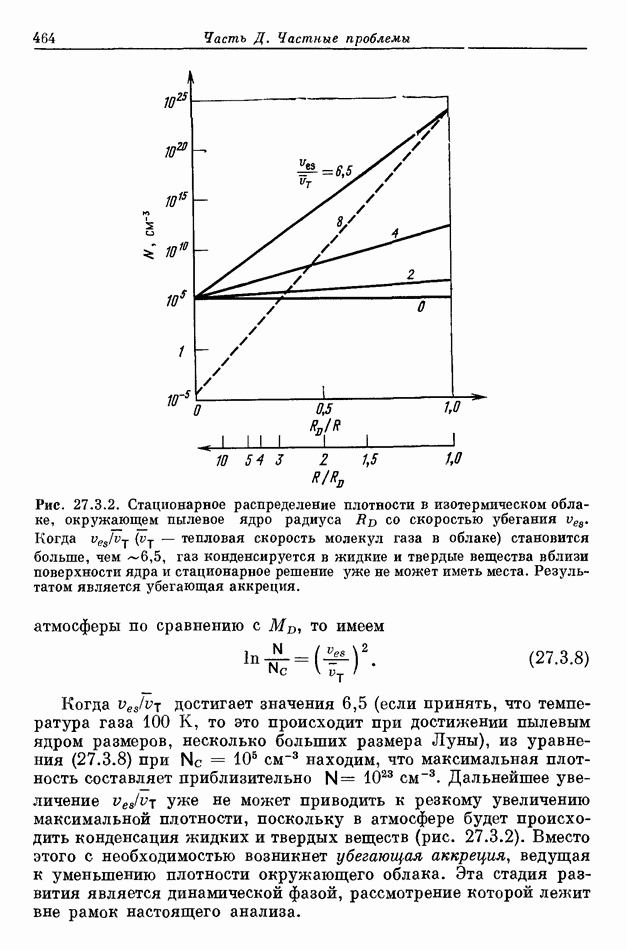
- 27.3. ОБРАЗОВАНИЕ ЗВЕЗД В ОБЛАКЕ ПЫЛЕВОЙ ПЛАЗМЫ
- 27.3.2. ДВИЖЕНИЕ ПЫЛИ В ОБЛАКЕ ПЛАЗМЫ
- 27.3.3. ОСЕДАНИЕ ПЫЛИ В ГРАВИТАЦИОННОМ ПОЛЕ
- 27.3.4. ОБРАЗОВАНИЕ СТЕЛЛЕЗИМАЛЕЙ
- 27.3.5. ДВУХСТУПЕНЧАТАЯ АККРЕЦИЯ
- 27.3.6. СВОЙСТВА ПРОТО-СОЛНЦА И ОКРУЖАЮЩЕЙ ЕГО СРЕДЫ
- 27.3.7. ВЫВОДЫ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 28. Заключительные замечания