| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
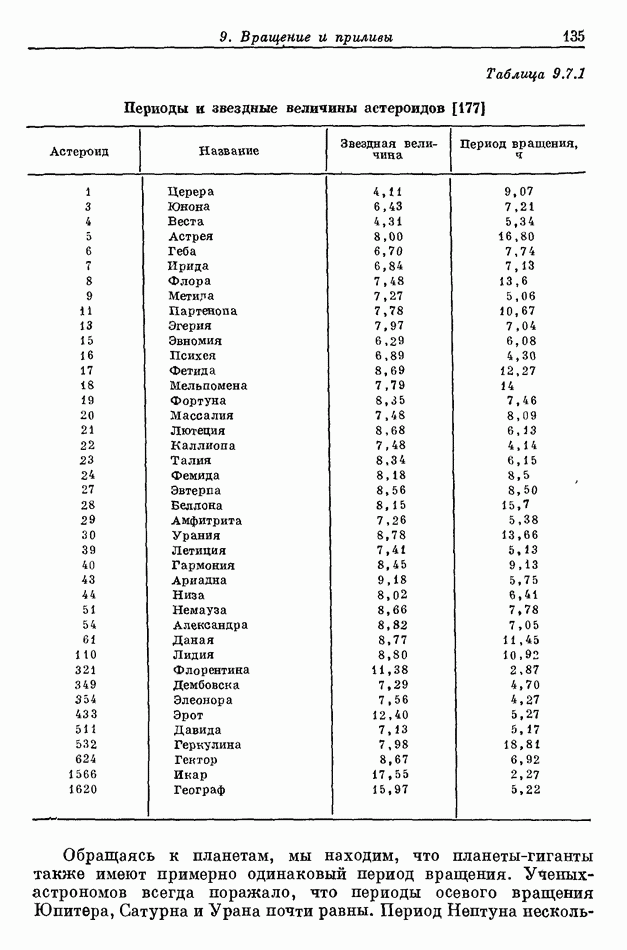
17.5. КОНДЕНСАЦИЯ ПЛАЗМЫ: ЗАКОНА ДВУХ ТРЕТЕЙ
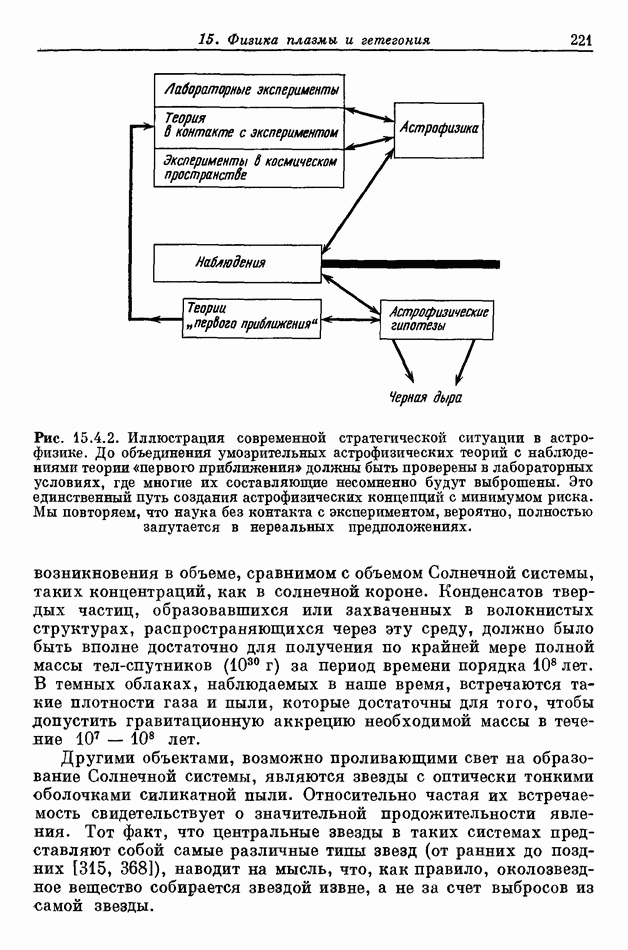
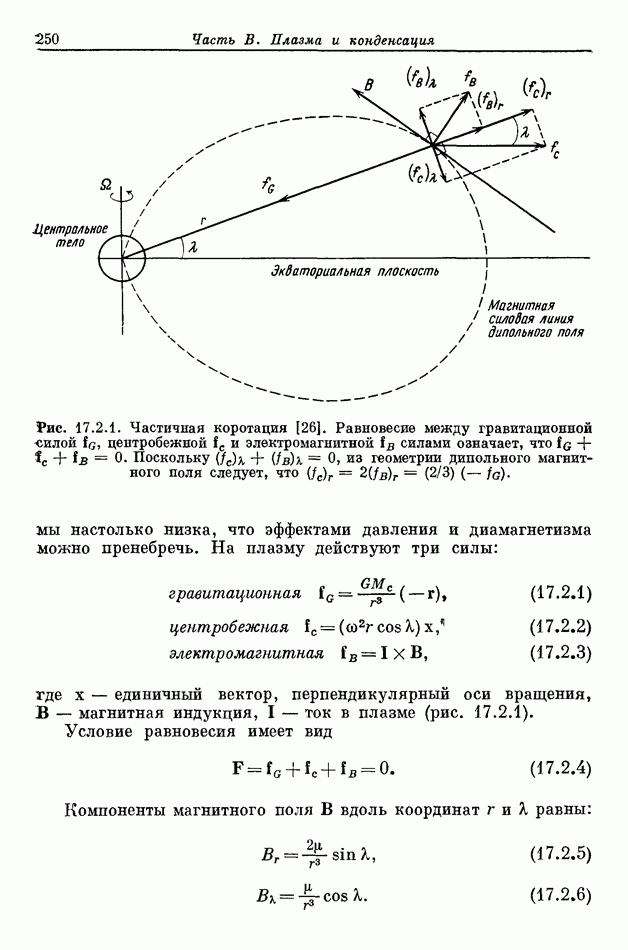
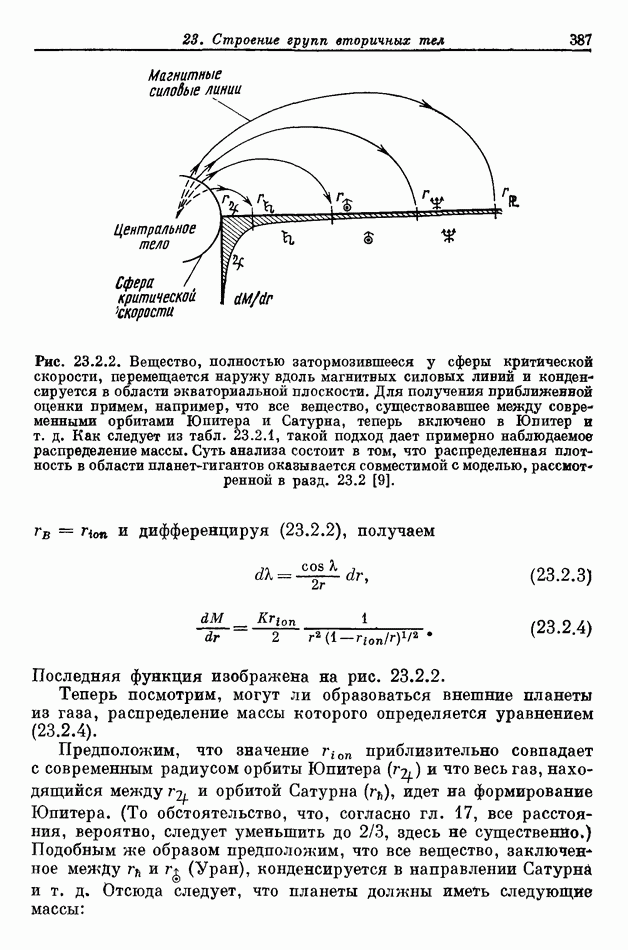
Если масса зерна в плазме переходит через предельное значение  (см. разд. 5.4), характер его движения изменяется и при определенных условиях его траекторией будет кеплеровский эллипс. Ограничимся простым случаем, когда зерна выросли до достаточно больших размеров или их электрический заряд уменьшился настолько, что на них не влияют ни электромагнитные силы, ни вязкость, обусловленная плазмой. Более того, предположим, что переход через указанное предельное значение происходит мгновенно, так что начальная скорость зерна равняется скорости элемента плазмы, из которого оно образуется.
(см. разд. 5.4), характер его движения изменяется и при определенных условиях его траекторией будет кеплеровский эллипс. Ограничимся простым случаем, когда зерна выросли до достаточно больших размеров или их электрический заряд уменьшился настолько, что на них не влияют ни электромагнитные силы, ни вязкость, обусловленная плазмой. Более того, предположим, что переход через указанное предельное значение происходит мгновенно, так что начальная скорость зерна равняется скорости элемента плазмы, из которого оно образуется.
Поскольку начальная скорость зерна составляет (2/3) от кеплеровской скорости движения по круговой орбите в месте его расположения, зерно, находящееся первоначально в положении  будет двигаться по эллипсу с эксцентриситетом
будет двигаться по эллипсу с эксцентриситетом  (рис. 17.5.1). Его апоцентр А расположен в точке с координатами
(рис. 17.5.1). Его апоцентр А расположен в точке с координатами  а перицентр
а перицентр  в точке
в точке 

Эллипс пересекает экваториальную плоскость  в узловых точках
в узловых точках  где
где

При достижении зерном точки лежащей на окружности радиуса  угловая скорость становится равной угловой скорости тела, движущегося по кеплеровской окружности радиуса
угловая скорость становится равной угловой скорости тела, движущегося по кеплеровской окружности радиуса  в плоскости орбиты зерна.
в плоскости орбиты зерна.
Если предположить, что зерна выделяются только из кольцевого элемента плазмы  то все они будут пересекать экваториальную плоскость по окружности радиуса
то все они будут пересекать экваториальную плоскость по окружности радиуса  Предположим, что по круговой кеплеровской орбите радиуса
Предположим, что по круговой кеплеровской орбите радиуса  в экваториальной плоскости движется малое тело (зародыш), которое будет сталкиваться с зернами. Предположим теперь, что все зерна, сталкивающиеся с зародышем, будут им удерживаться. Каждое зерно имеет такой же момент количества движения на единицу массы, как и зародыш. Однако вектор момента количества движения зародыша параллелен оси вращения, в то время как у зерна он составляет с осью угол
в экваториальной плоскости движется малое тело (зародыш), которое будет сталкиваться с зернами. Предположим теперь, что все зерна, сталкивающиеся с зародышем, будут им удерживаться. Каждое зерно имеет такой же момент количества движения на единицу массы, как и зародыш. Однако вектор момента количества движения зародыша параллелен оси вращения, в то время как у зерна он составляет с осью угол  В случае когда
В случае когда  настолько мало, что можно считать
настолько мало, что можно считать  зародыш будет увеличиваться в размерах, но его орбита не будет изменяться. (Если
зародыш будет увеличиваться в размерах, но его орбита не будет изменяться. (Если 
зародыш будет медленно по спирали двигаться внутрь, увеличиваясь в размерах.)
Если смотреть из системы координат, связанной с зародышем, то векторы скорости прибывающих зерен будут расположены в меридиональной плоскости зародыша. Эти скорости имеют составляющую, параллельную оси вращения центрального тела и равную  и составляющую в экваториальной плоскости центрального тела, направленную к нему и равную
и составляющую в экваториальной плоскости центрального тела, направленную к нему и равную 
Выше существование зародыша предполагалось исключительно для того, чтобы проиллюстрировать важную роль круговой орбиты с радиусом  в экваториальной плоскости. Все зерна, которые выделяются на расстоянии
в экваториальной плоскости. Все зерна, которые выделяются на расстоянии  от центра, будут пересекать экваториальную плоскость на периферии этого круга независимо от величины (при условии, что можно положить
от центра, будут пересекать экваториальную плоскость на периферии этого круга независимо от величины (при условии, что можно положить  Эти зерна будут сталкиваться друг с другом и срастаться, образуя все большие зародыши, до тех пор пока они не станут достаточно большими для аккреции меньших зерен. Полученные таким образом крупные тела будут двигаться в экваториальной плоскости
Эти зерна будут сталкиваться друг с другом и срастаться, образуя все большие зародыши, до тех пор пока они не станут достаточно большими для аккреции меньших зерен. Полученные таким образом крупные тела будут двигаться в экваториальной плоскости  круговой орбите с радиусом
круговой орбите с радиусом 
17.5.1. ВЫВОДЫ
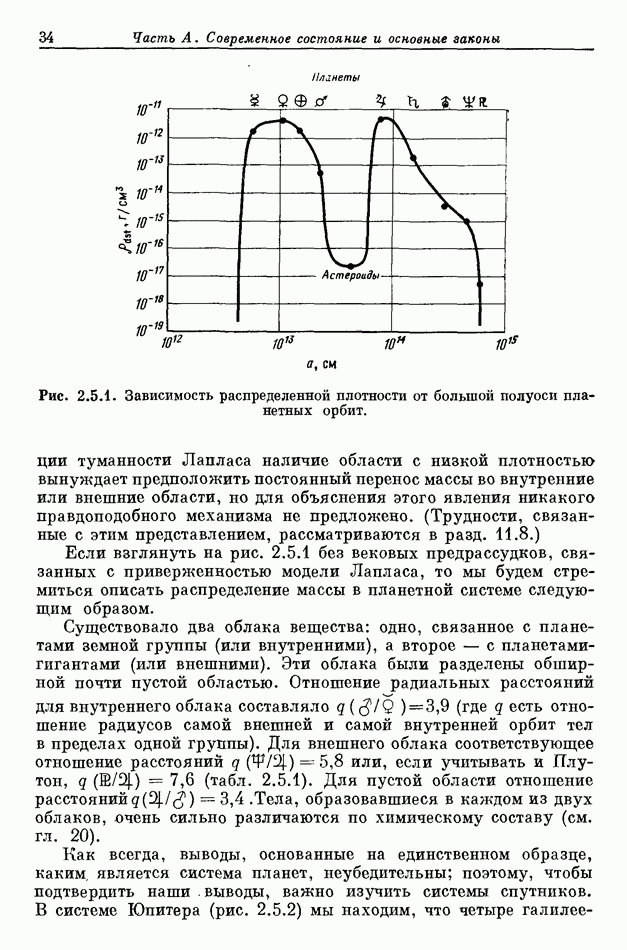
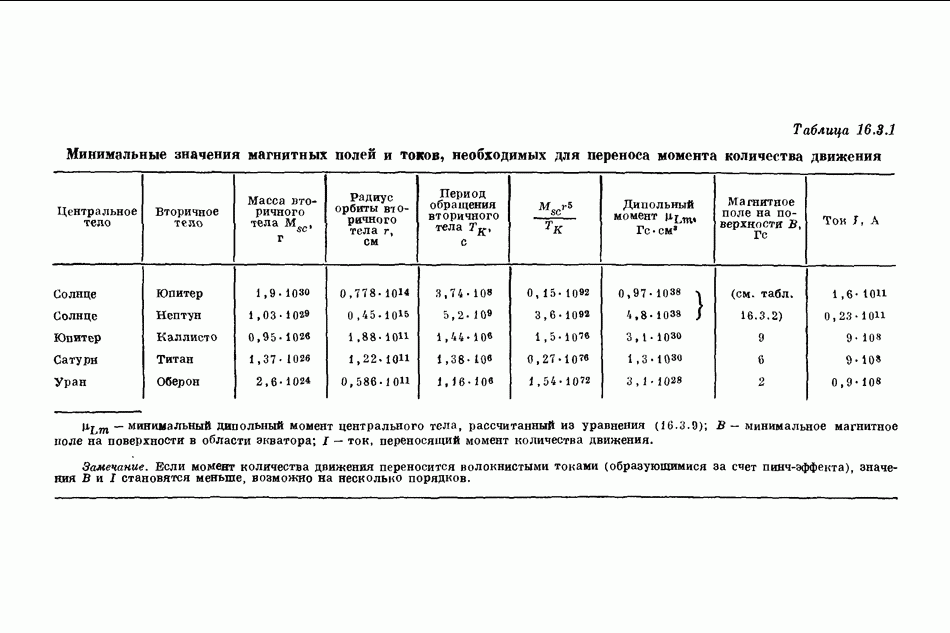
Суммируя наши результаты, мы находим что облако плазмы  дипольном поле вращающегося центрального тела не обязательно должно приобрести угловую скорость, равную скорости центрального тела. Если в области между облаком плазмы и центральным телом плотность настолько низка, что параллельное электрическое поле может отличаться от нуля, то возможно стационарное состояние, характеризуемое частичной коротацией (см. табл. 17.3.1). Если на расстоянии от центра
дипольном поле вращающегося центрального тела не обязательно должно приобрести угловую скорость, равную скорости центрального тела. Если в области между облаком плазмы и центральным телом плотность настолько низка, что параллельное электрическое поле может отличаться от нуля, то возможно стационарное состояние, характеризуемое частичной коротацией (см. табл. 17.3.1). Если на расстоянии от центра  происходит конденсация зерен из такой плазмы, то зерна будут двигаться по эллипсам с большой полуосью
происходит конденсация зерен из такой плазмы, то зерна будут двигаться по эллипсам с большой полуосью  и эксцентриситетом
и эксцентриситетом  . Взаимные столкновения между совокупностями таких зерен в конце концов будут приводить к движению сконденсированного вещества по окружности радиуса
. Взаимные столкновения между совокупностями таких зерен в конце концов будут приводить к движению сконденсированного вещества по окружности радиуса  расположенной в экваториальной плоскости (см. рис. 17.5.1).
расположенной в экваториальной плоскости (см. рис. 17.5.1).
В более общем случае, когда конденсация имеет место в протяженной области в широком диапазоне широт и расстояний от центра, вероятно, каждое сконденсированное зерно будет в конечном счете двигаться по окружности на расстоянии, составляющем 2/3 от того расстояния, на котором произошла конденсация. Это может случиться при определенных условиях, но в общем случае это несправедливо, так как столкновения между зернами уже не ограничиваются экваториальной плоскостью. Должны существовать конкурирующие процессы, посредством которых
происходит аккреция зерен, приводящая к увеличению зародышей, движущихся по эксцентрическим орбитам. Однако большие полуоси этих орбит равны 2/3 от средневзвешенных радиусов-векторов точек конденсации (см. гл. 18).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- От редактора перевода
- Предисловие
- I. Введение
- 1.1. ФУНДАМЕНТАЛЬНЫЙ ПОДХОД К ПРОБЛЕМЕ
- 1.2. СИСТЕМА ПЛАНЕТ — СИСТЕМЫ СПУТНИКОВ
- 1.3. ПЯТЬ ЭТАПОВ ЭВОЛЮЦИИ
- 1.4. НАПРАВЛЯЮЩИЕ ПРОЦЕССЫ ОТДЕЛЬНЫХ ЭТАПОВ ЭВОЛЮЦИИ
- 1.5. ТРЕБОВАНИЯ К МОДЕЛЯМ И ОГРАНИЧЕНИЯ
- Часть А. Современное состояние и основные законы
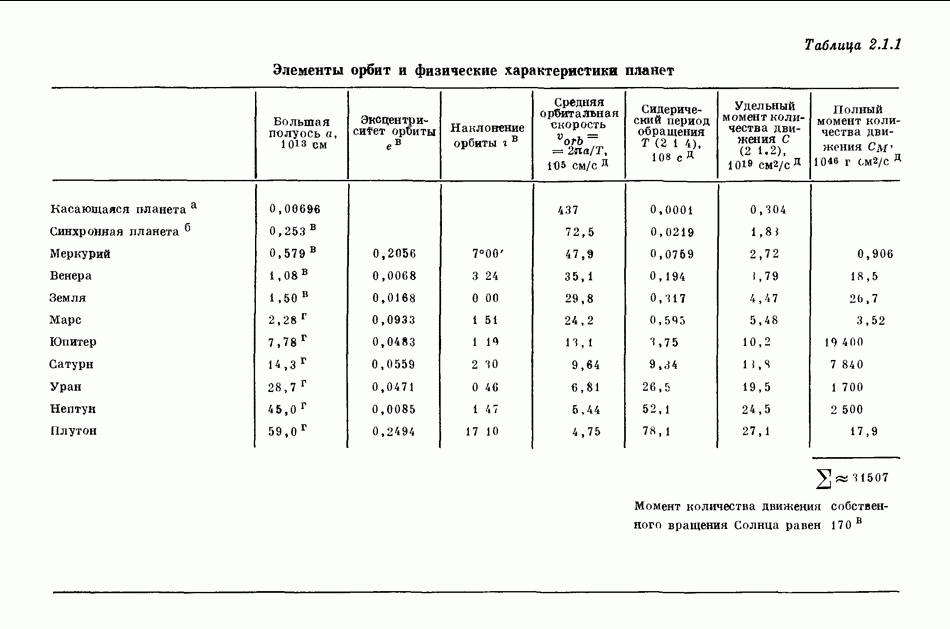
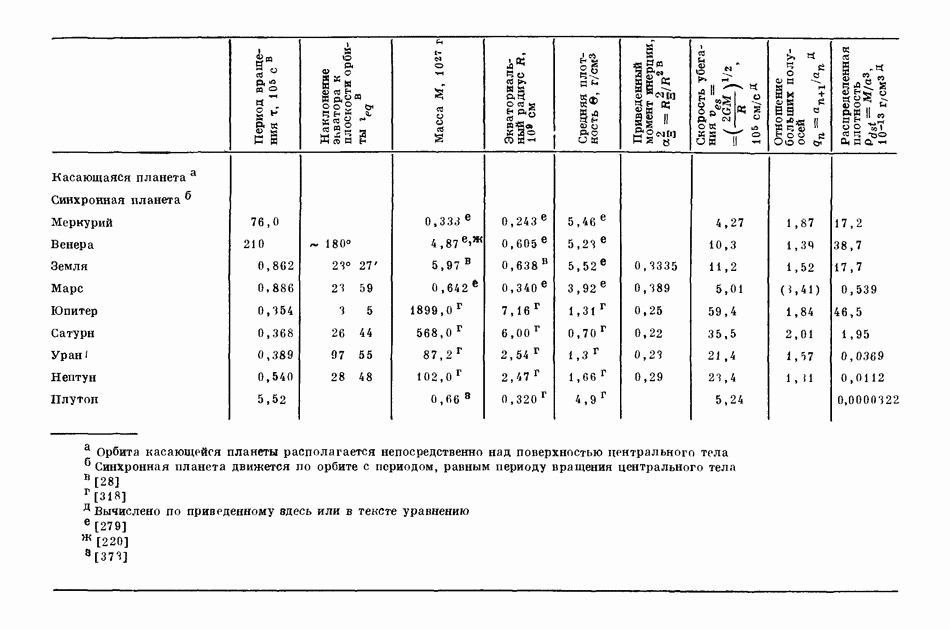
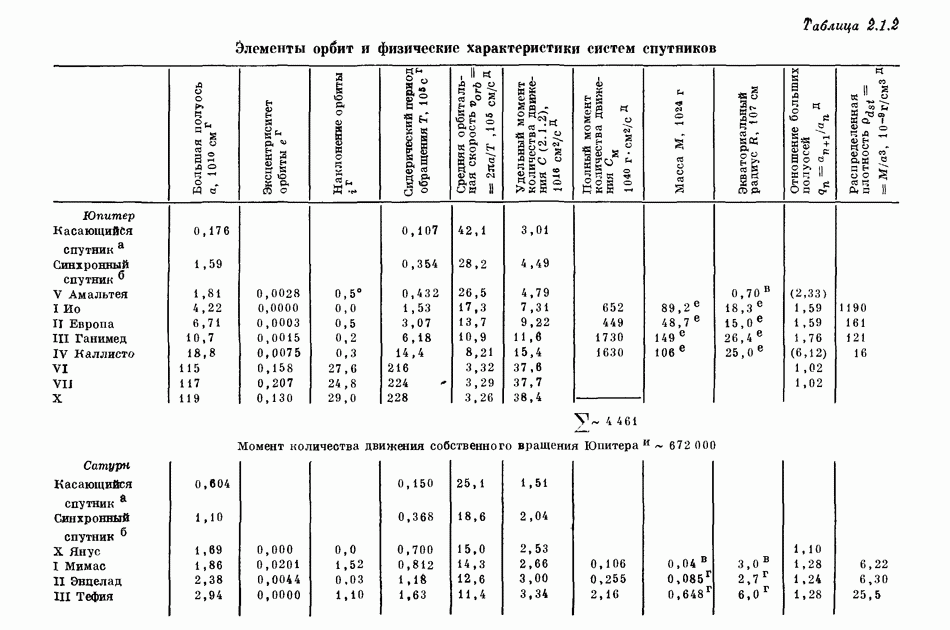
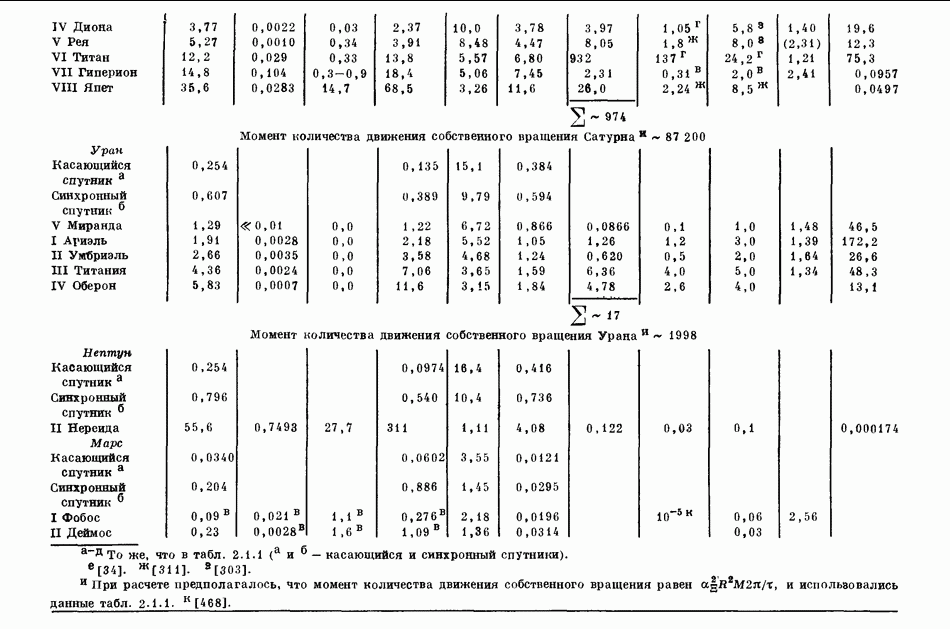
- 2.1. ХАРАКТЕРИСТИКИ ОРБИТ ПЛАНЕТ И СПУТНИКОВ
- 2.2. ФИЗИЧЕСКИЕ СВОЙСТВА ПЛАНЕТ И СПУТНИКОВ
- 2.3. СПУТНИКИ С ПРЯМЫМ И ОБРАТНЫМ ДВИЖЕНИЕМ
- 2.4. МОДЕЛЬ ЛАПЛАСА И ФУНКЦИЯ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
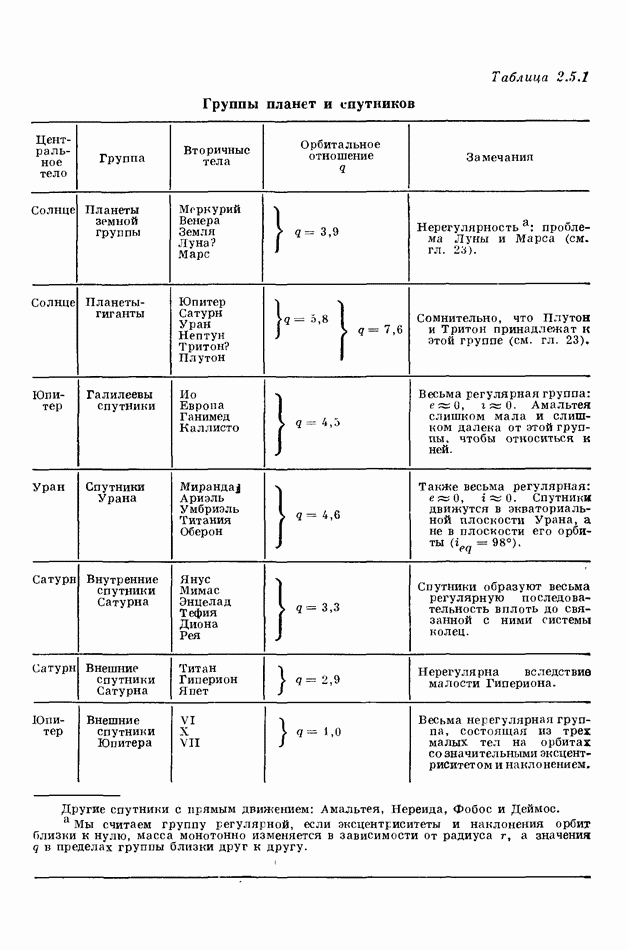
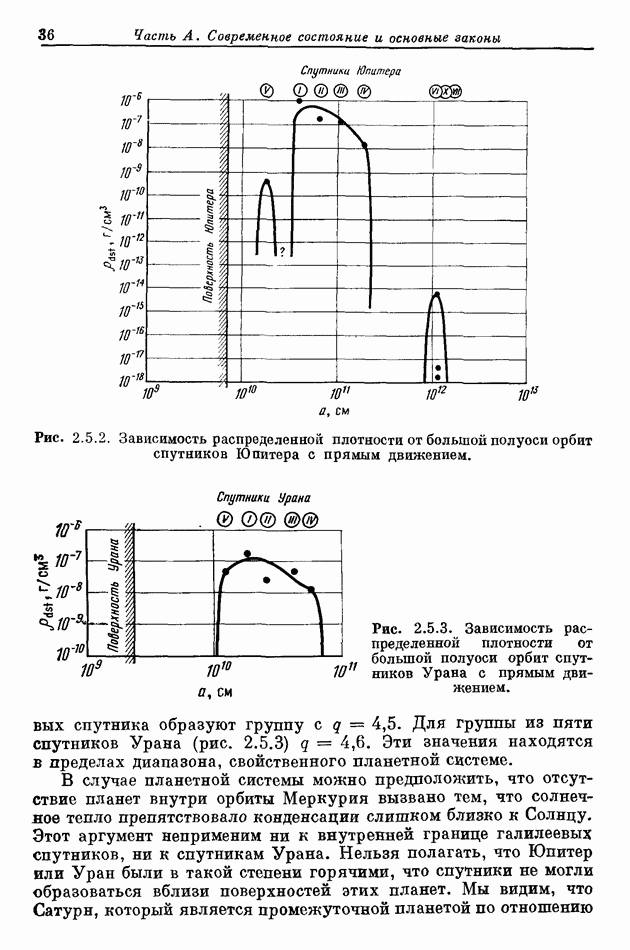
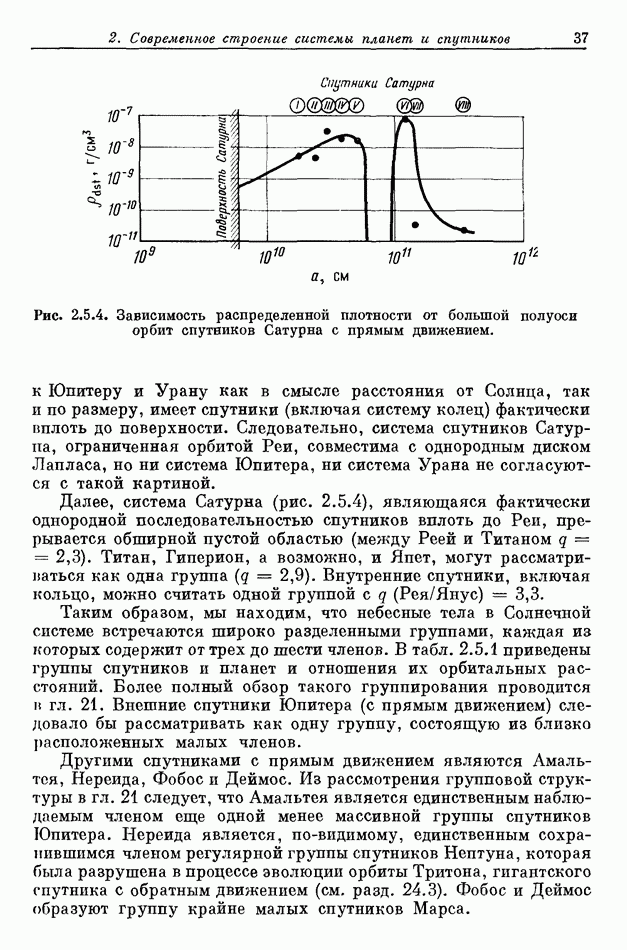
- 2.5. ОБСУЖДЕНИЕ ГРАФИКОВ РАСПРЕДЕЛЕННОЙ ПЛОТНОСТИ
- 2.6. «ЗАКОН» ТИЦИУСА — БОДЕ
- 3. Движение планет и спутников
- 3.1. МЕТОД ВЕДУЩЕГО ЦЕНТРА В ЗАДАЧАХ НЕБЕСНОЙ МЕХАНИКИ
- 3.2. КРУГОВЫЕ ОРБИТЫ
- 3.3. КОЛЕБАНИЯ, ВИДОИЗМЕНЯЮЩИЕ КРУГОВУЮ ОРБИТУ
- 3.4. ДВИЖЕНИЕ В ГРАВИТАЦИОННОМ ПОЛЕ, ОБРАТНО ПРОПОРЦИОНАЛЬНОМ КВАДРАТУ РАССТОЯНИЯ
- 3.5. НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И БОЛЬШИЕ ЭКСЦЕНТРИСИТЕТЫ
- 3.6. ДВИЖЕНИЕ В ПОЛЕ ВРАЩАЮЩЕГОСЯ ЦЕНТРАЛЬНОГО ТЕЛА
- 3.7. ДВИЖЕНИЕ ПЛАНЕТ, ВОЗМУЩАЕМОЕ ДРУГИМИ ПЛАНЕТАМИ
- 4. Малые тела
- 4.2. РАЗЛИЧИЕ В ЭВОЛЮЦИИ БОЛЬШИХ И МАЛЫХ ТЕЛ
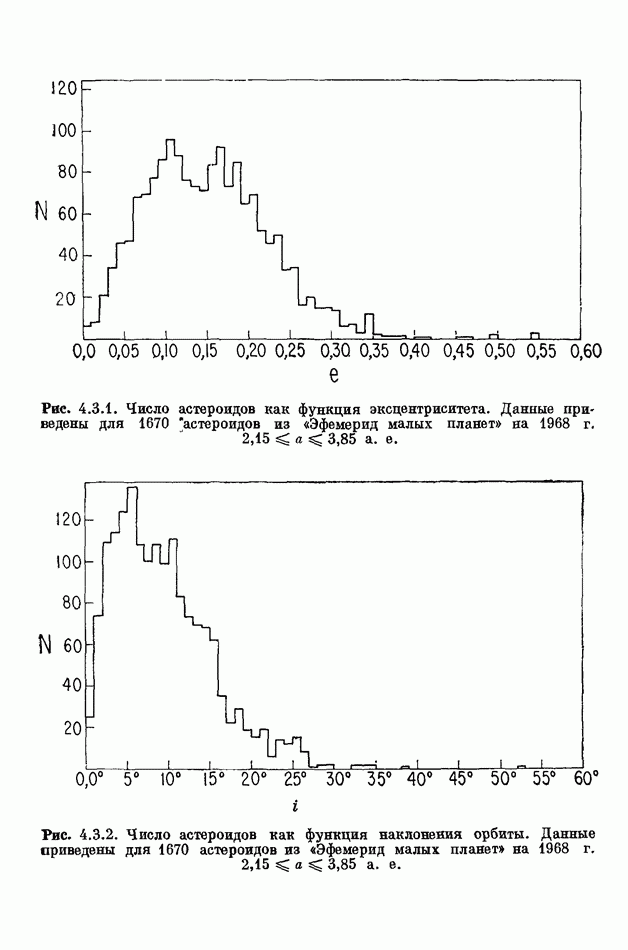
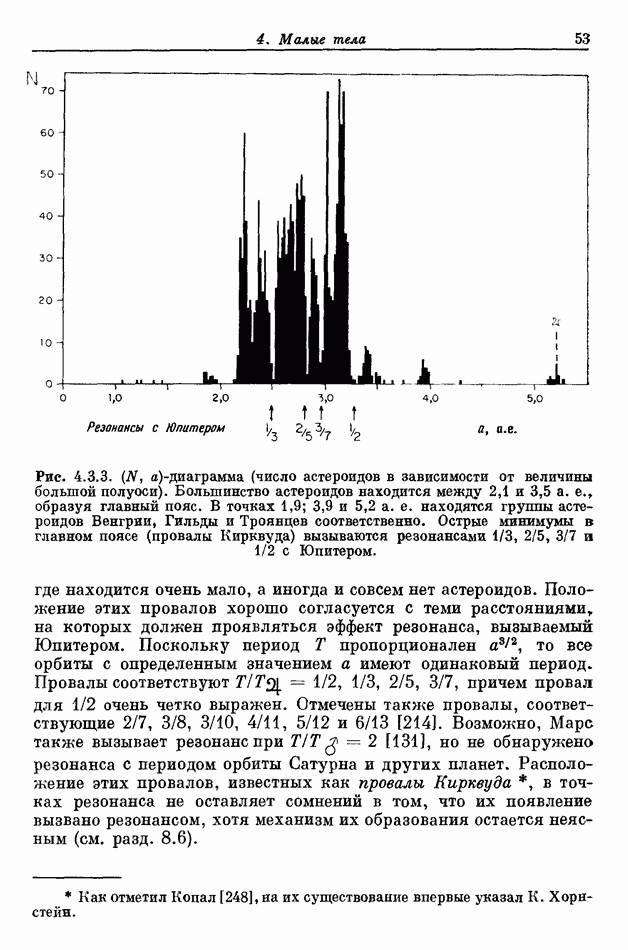
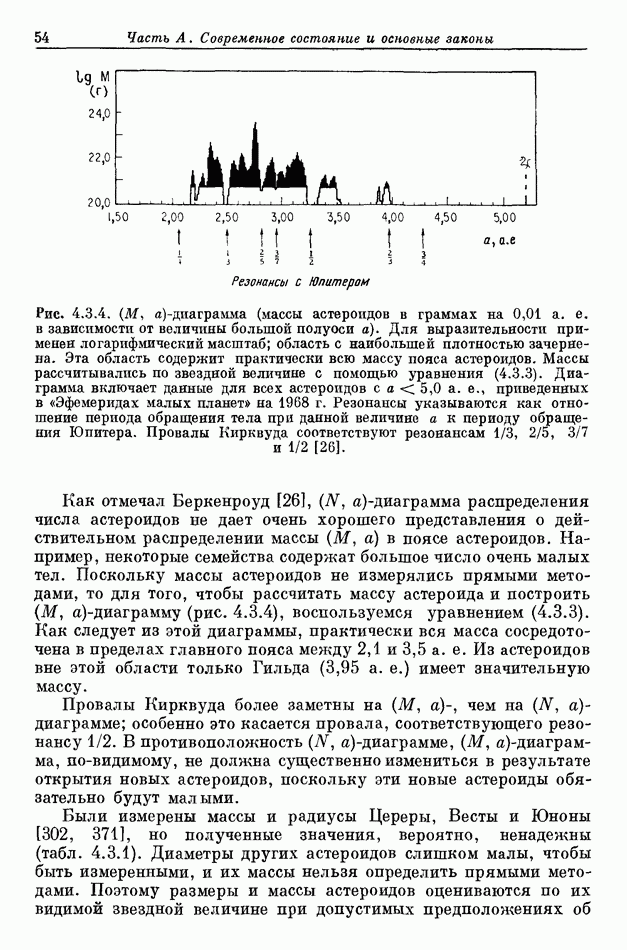
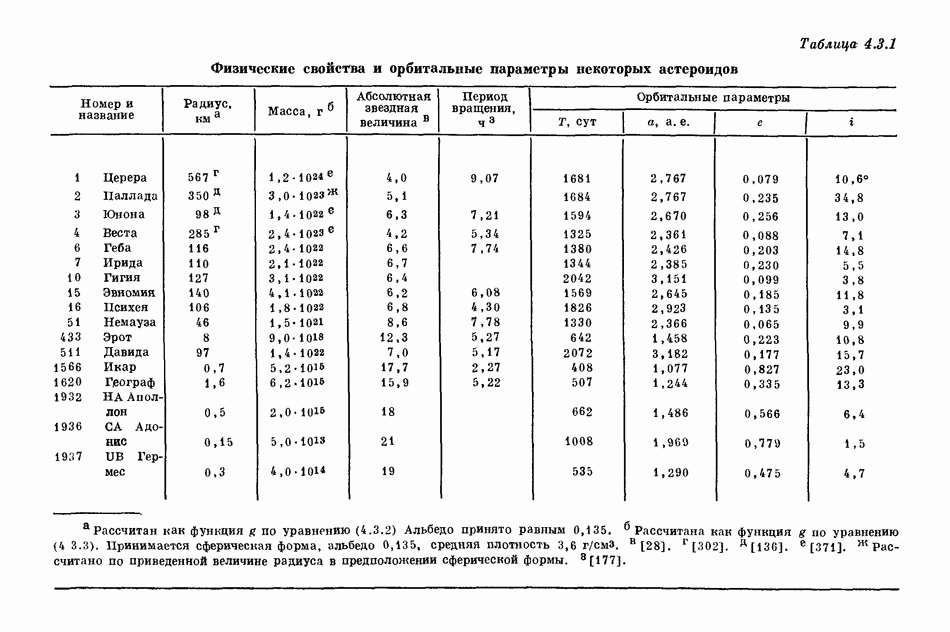
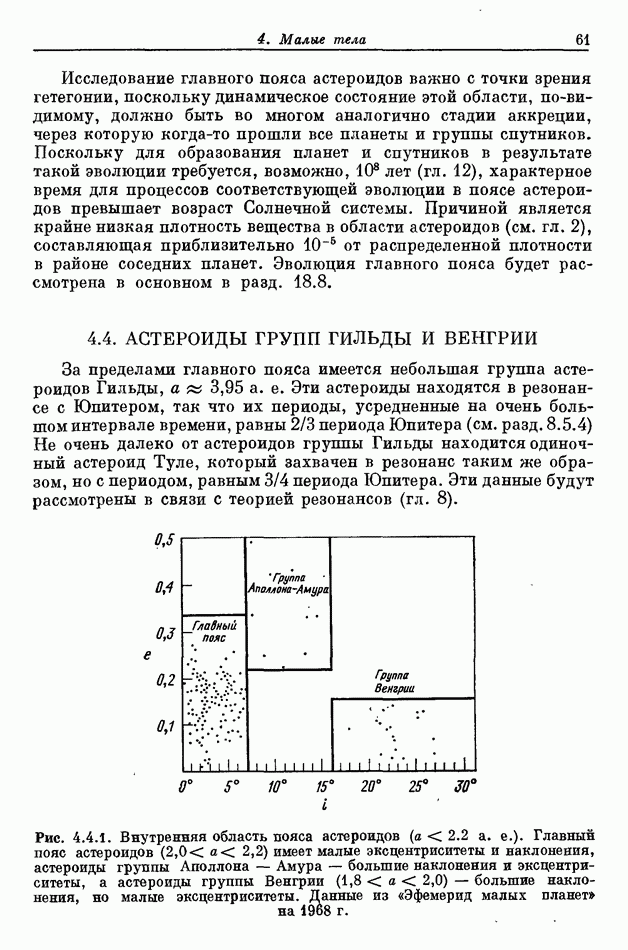
- 4.3. ГЛАВНЫЙ ПОЯС АСТЕРОИДОВ
- 4.3.1. НЕНАБЛЮДАЕМЫЕ АСТЕРОИДЫ
- 4.3.2. СЕМЕЙСТВА ХИРАЯМЫ
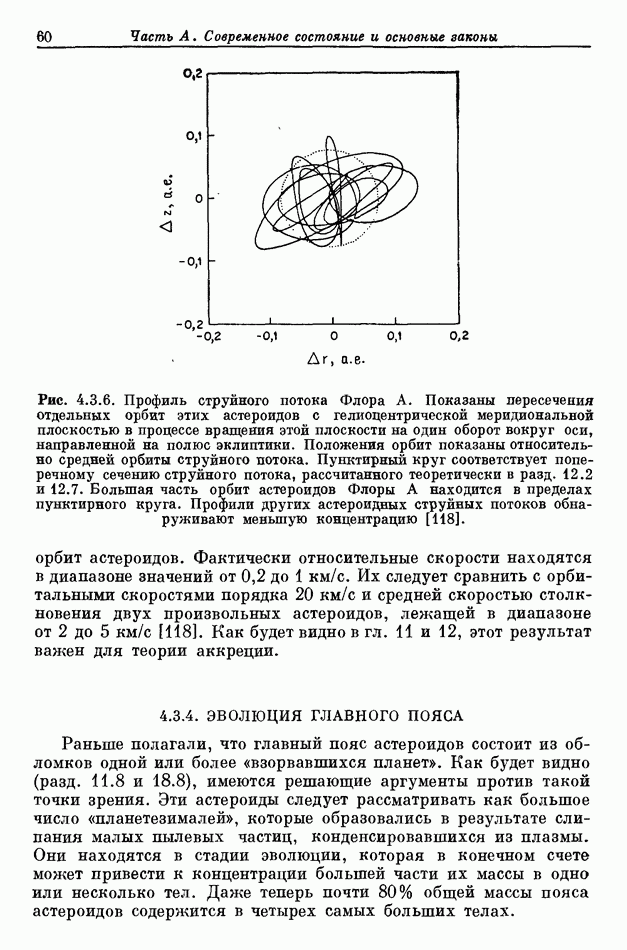
- 4.3.3. СТРУЙНЫЕ ПОТОКИ АСТЕРОИДОВ
- 4.3.4. ЭВОЛЮЦИЯ ГЛАВНОГО ПОЯСА
- 4.4. АСТЕРОИДЫ ГРУПП ГИЛЬДЫ И ВЕНГРИИ
- 4.5. ТРОЯНЦЫ
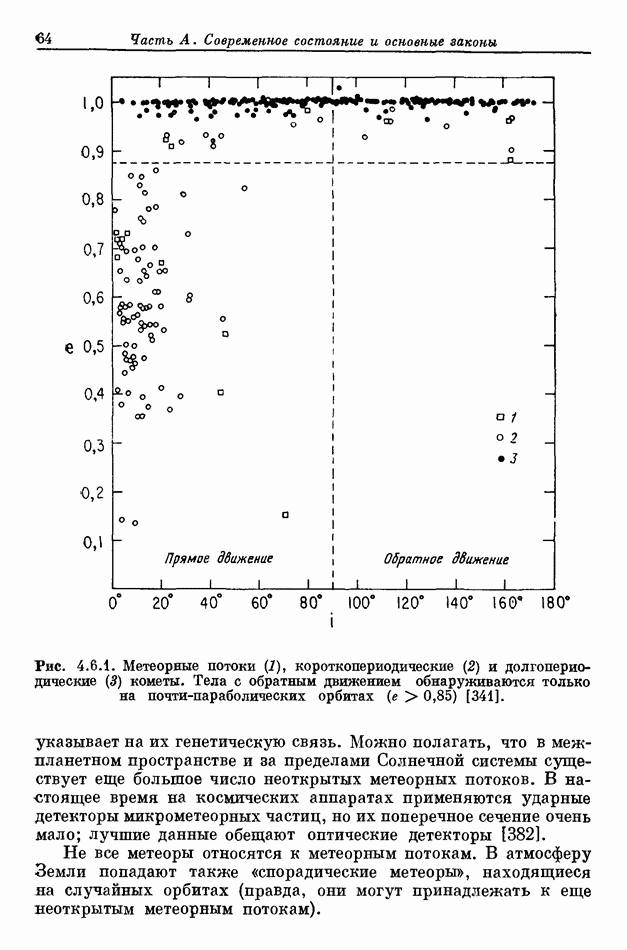
- 4.6. СЕМЕЙСТВО КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 4.6.2. МЕТЕОРНЫЕ ПОТОКИ
- 4.6.3. ДОЛГОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 4.6.4. КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 5. Силы, действующие на малые тела
- 5.2. ГРАВИТАЦИОННЫЕ ВОЗДЕЙСТВИЯ
- 5.2.1. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ
- 5.2.2. КЕПЛЕРОВСКОЕ ДВИЖЕНИЕ, ВОЗМУЩАЕМОЕ СТОЛКНОВЕНИЯМИ
- 5.3. ЭЛЕКТРОМАГНИТНЫЕ ЭФФЕКТЫ
- 5.4. ГРАНИЦА МЕЖДУ ДВИЖЕНИЯМИ, ОБУСЛОВЛЕННЫМИ ГРАВИТАЦИОННЫМИ И ЭЛЕКТРОМАГНИТНЫМИ СИЛАМИ
- 5.5. РАДИАЦИОННЫЕ ЭФФЕКТЫ
- 5.5.1. РАДИАЦИОННОЕ ДАВЛЕНИЕ
- 5.5.2. ЭФФЕКТ ПОЙНТИНГА — РОБЕРТСОНА
- 5.6. ВЫВОДЫ
- 6. Кеплеровское движение взаимодействующих тел: струйные потоки
- 6.2. МЕЖПЛАНЕТНАЯ СРЕДА
- 6.3. ЭФФЕКТЫ СТОЛКНОВЕНИЙ
- 6.4. ПРОСТАЯ МОДЕЛЬ СТРУЙНОГО ПОТОКА
- 6.4.1. ДВИЖЕНИЕ ЧАСТИЦ, ИСПУСКАЕМЫХ СО СПУТНИКА
- 6.4.2. СРАВНЕНИЕ С ТОРОМ ИО
- 6.4.3. ЭФФЕКТ СТОЛКНОВЕНИЙ
- 6.5. ВЫВОДЫ ИЗ МОДЕЛИ СТРУЙНОГО ПОТОКА
- 6.6. СТРУЙНЫЙ ПОТОК И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ
- 6.7. ПРОСТАЯ МОДЕЛЬ ОТРИЦАТЕЛЬНОЙ ДИФФУЗИИ
- 6.8. ПРОДОЛЖИТЕЛЬНОСТЬ СЖАТИЯ СТРУЙНОГО ПОТОКА
- 6.9. СТОЛКНОВЕНИЯ ЧАСТИЦ СО СТРУЙНЫМ ПОТОКОМ
- 6.10. СТРУЙНЫЕ ПОТОКИ КАК НЕБЕСНЫЕ ОБЪЕКТЫ
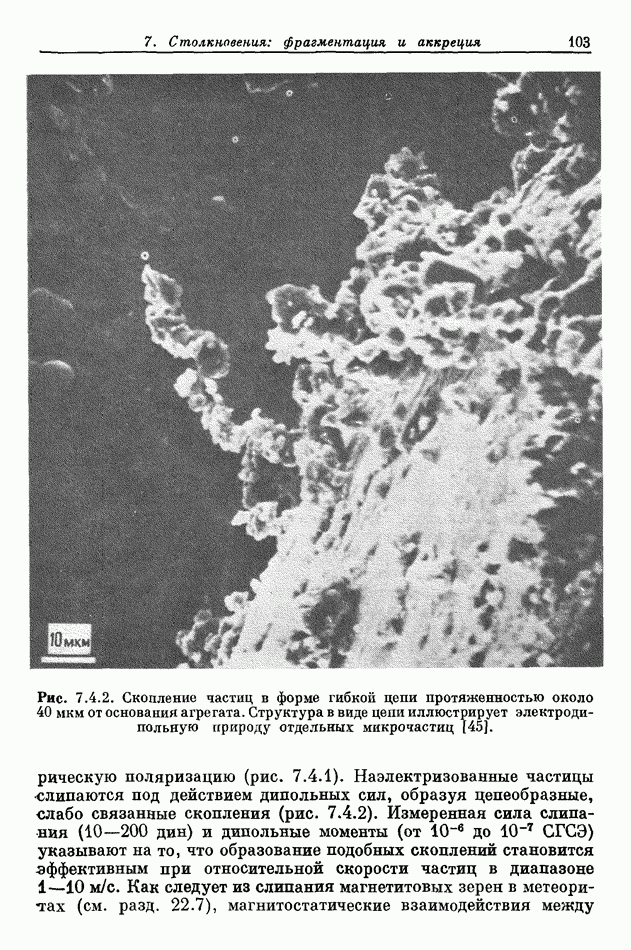
- 7. Столкновения: фрагментация и аккреция
- 7.1. ОБРАЗОВАНИЕ МАЛЫХ ТЕЛ: ФРАГМЕНТАЦИЯ И АККРЕЦИЯ
- 7.2. РАСПРЕДЕЛЕНИЕ ПО РАЗМЕРАМ
- 7.3. ТРИ ПРОСТЫЕ МОДЕЛИ
- 7.3.2. ФРАГМЕНТАЦИЯ
- 7.3.3. ДАННЫЕ НАБЛЮДЕНИЙ, ИМЕЮЩИЕ ОТНОШЕНИЕ К МОДЕЛЯМ
- 7.4. ПЕРЕХОД ОТ ФРАГМЕНТАЦИИ К АККРЕЦИИ
- 8. Резонансные структуры в Солнечной системе
- 8.1. РЕЗОНАНСЫ В СОЛНЕЧНОЙ СИСТЕМЕ
- 8.2. РЕЗОНАНС И КОЛЕБАНИЯ МАЯТНИКА
- 8.3. ПРОСТАЯ МОДЕЛЬ РЕЗОНАНСА
- 8.4. ОТКЛОНЕНИЯ ОТ ТОЧНОГО РЕЗОНАНСА
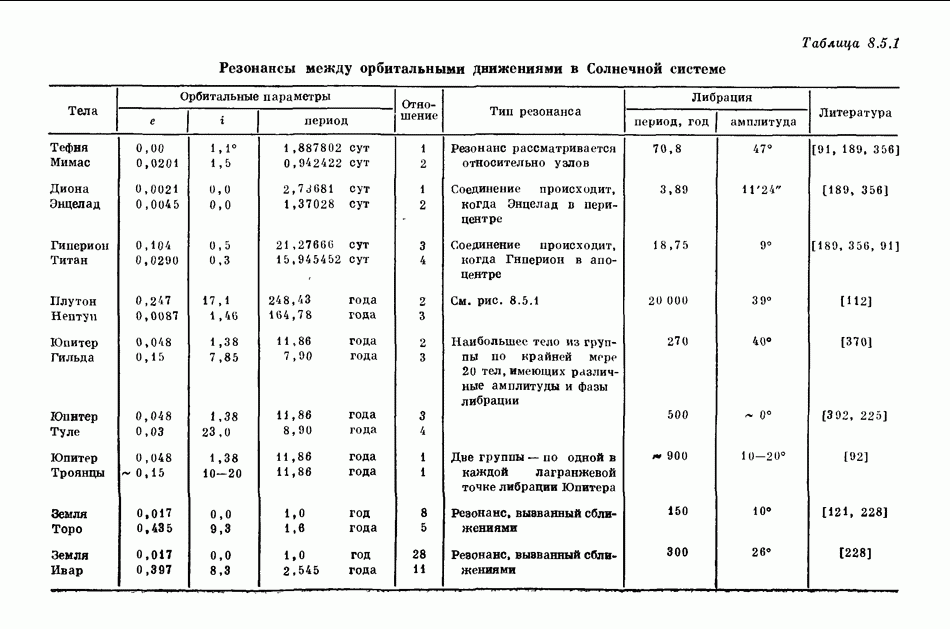
- 8.5. РЕЗОНАНС МЕЖДУ ОРБИТАЛЬНЫМИ ДВИЖЕНИЯМИ
- 8.5.2. РЕЗОНАНС ЗЕМЛЯ — ТОРО И ДРУГИЕ РЕЗОНАНСЫ ЗЕМЛИ И АСТЕРОИДОВ
- 8.5.3. ТРОЯНЦЫ
- 8.5.4. АСТЕРОИДЫ ГРУППЫ ГИЛЬДЫ
- 8.5.5. ТИТАН — ГИПЕРИОН
- 8.5.6. ДИОНА — ЭНЦЕЛАД
- 8.5.7. ТЕФИЯ — МИМАС
- 8.5.8 ИО — ЕВРОПА — ГАНИМЕД
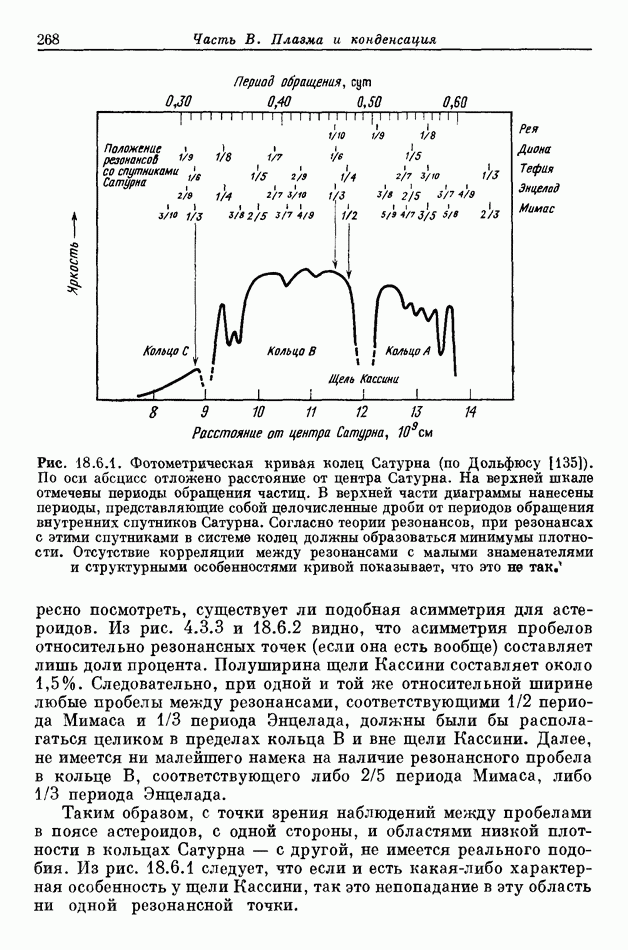
- 8.6. ПРОВАЛЫ КИРКВУДА
- 8.7. ОБ ОТСУТСТВИИ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В СИСТЕМЕ КОЛЕЦ САТУРНА
- 8.8. РЕЗОНАНСЫ МЕЖДУ ВРАЩЕНИЕМ И ОРБИТАЛЬНЫМ ДВИЖЕНИЕМ
- 8.9. ПОЧТИ-СОИЗМЕРИМОСТИ
- 9. Вращение и приливы
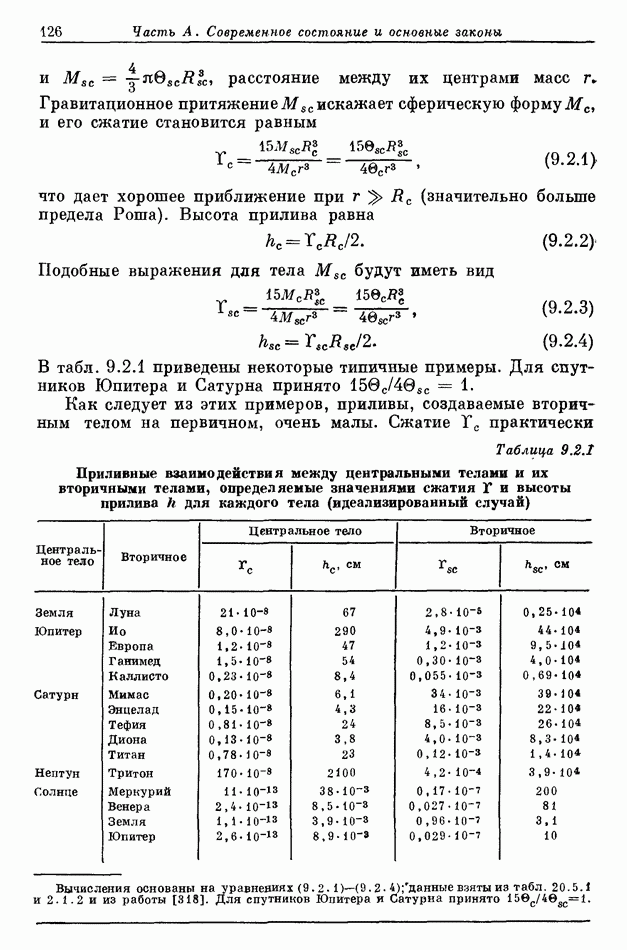
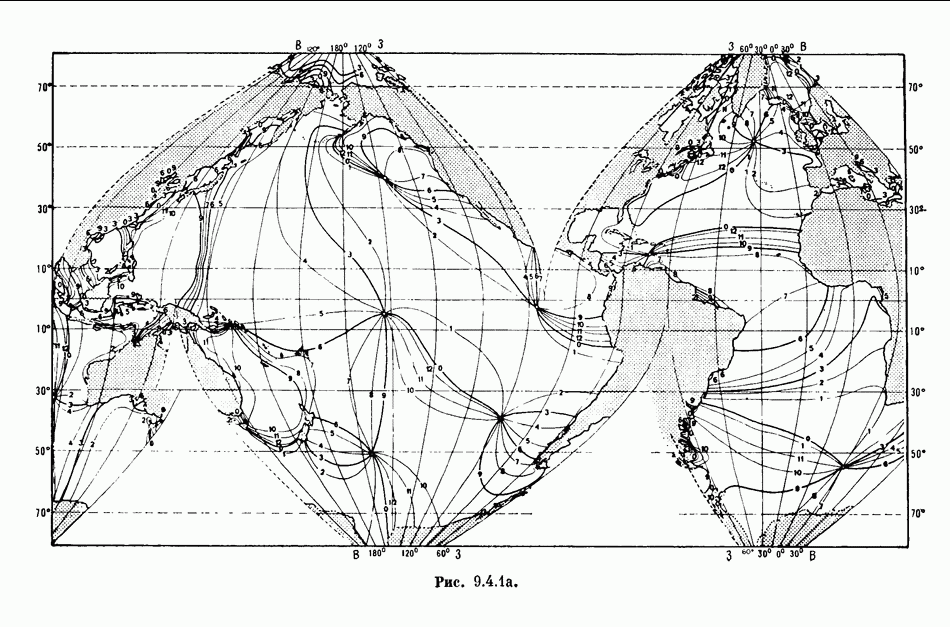
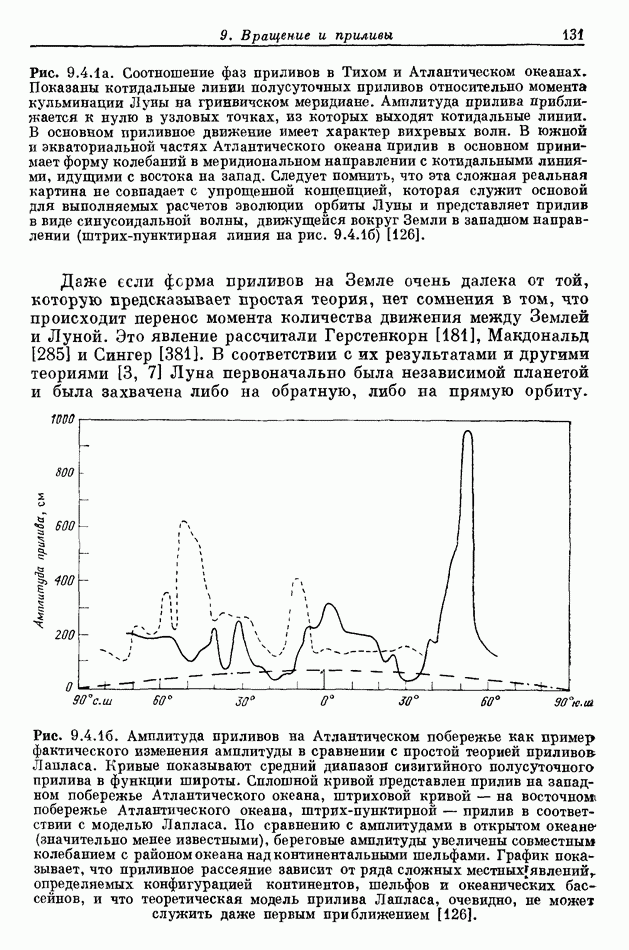
- 9.2. АМПЛИТУДА ПРИЛИВОВ
- 9.3. ПРИЛИВНОЕ ТОРМОЖЕНИЕ ВРАЩЕНИЯ ЦЕНТРАЛЬНОГО ТЕЛА
- 9.4. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ ПРИЛИВАМИ, ВЫЗЫВАЕМЫМИ СПУТНИКАМИ
- 9.5. ТОРМОЖЕНИЕ ВРАЩЕНИЯ ПЛАНЕТ СОЛНЕЧНЫМИ ПРИЛИВАМИ
- 9.6. ЭВОЛЮЦИЯ СПУТНИКОВ ПЛАНЕТ ПОД ДЕЙСТВИЕМ ПРИЛИВОВ
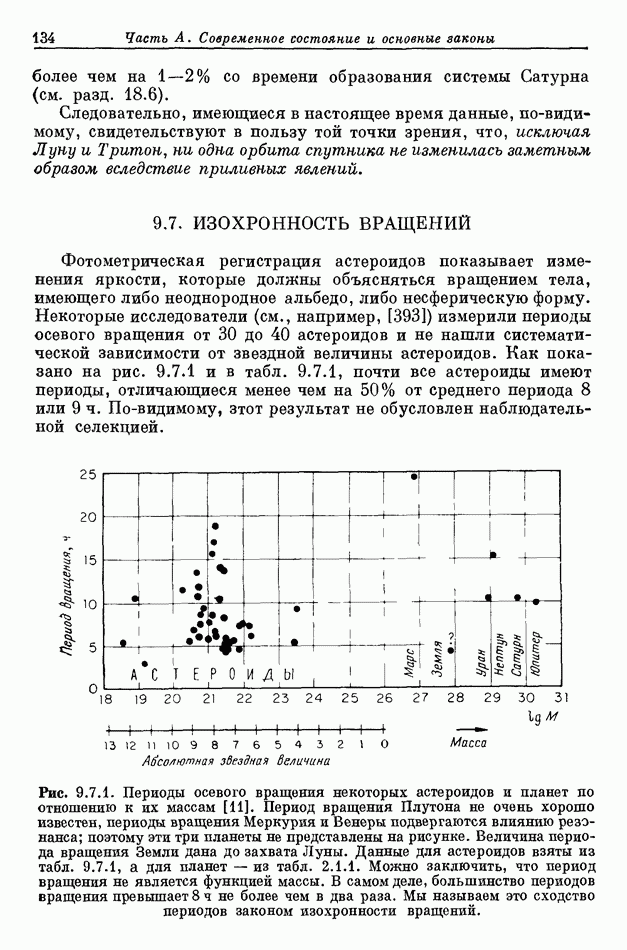
- 9.7. ИЗОХРОННОСТЬ ВРАЩЕНИЙ
- 9.8. ВЫВОДЫ ИЗ ИЗОХРОННОСТИ ВРАЩЕНИЙ
- 10. Постаккреционные изменения в Солнечной системе
- 10.1. УСТОЙЧИВОСТЬ ОРБИТ
- 10.2. РЕЗОНАНС И УСТОЙЧИВОСТЬ
- 10.3. УСТОЙЧИВОСТЬ КОЛЕЦ САТУРНА И ПОЯСА АСТЕРОИДОВ
- 10.4. ПОСТОЯНСТВО ВРАЩЕНИЙ
- 10.5. О ВОЗМОЖНОСТИ. РЕКОНСТРУКЦИИ ГЕТЕГОННЫХ ПРОЦЕССОВ
- Часть Б. Аккреция небесных тел
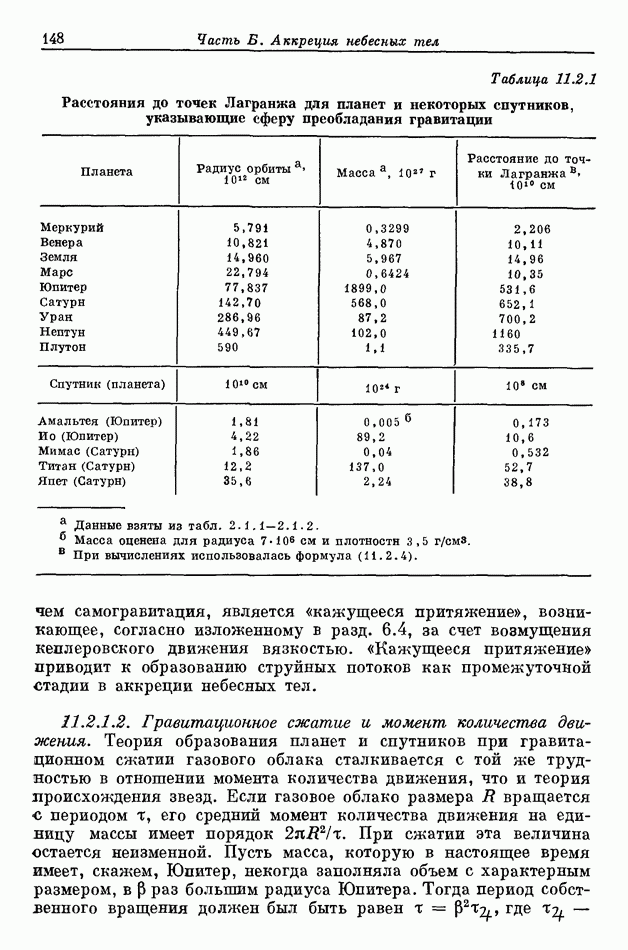
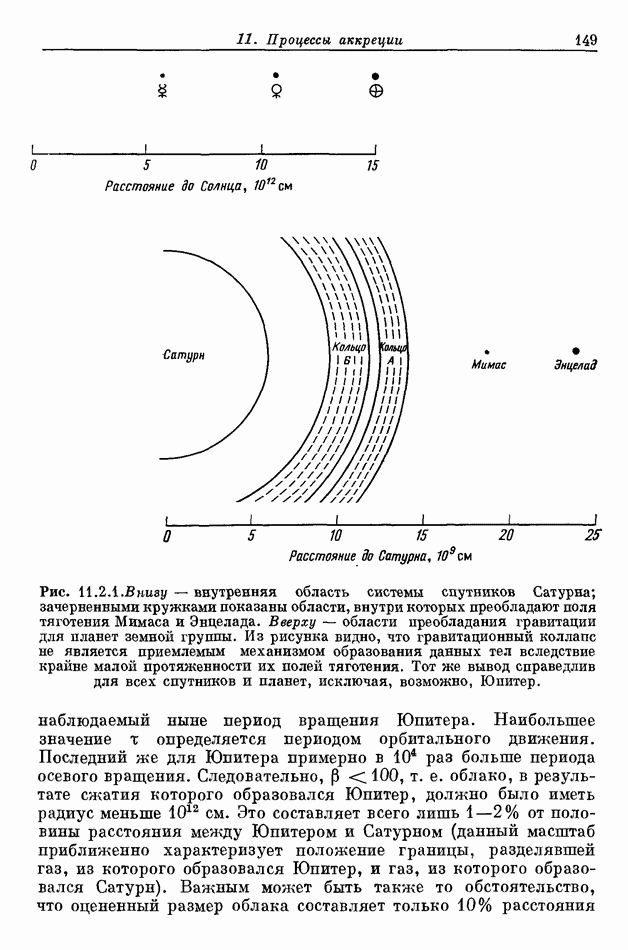
- 11.2. ГРАВИТАЦИОННЫЙ КОЛЛАПС ГАЗОВОГО ОБЛАКА
- 11.2.1. ВОЗРАЖЕНИЯ ПРОТИВ ГРАВИТАЦИОННОГО КОЛЛАПСА КАК МЕХАНИЗМА ОБРАЗОВАНИЯ ПЛАНЕТ И СПУТНИКОВ
- 11.3. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ: АККРЕЦИЯ ПУТЕМ ЗАХВАТА ЧАСТИЦ ИЛИ ГАЗА
- 11.4. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5. НЕГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 11.5.1. ВОЗРАЖЕНИЯ ПРОТИВ ПРОЦЕССА НЕГРАВИТАЦИОННОЙ АККРЕЦИИ
- 11.5.2. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ
- 11.5.3. ЭЛЕКТРОСТАТИЧЕСКИ ПОЛЯРИЗОВАННЫЕ ЗЕРНА
- 11.5.4. РЫХЛЫЕ СКОПЛЕНИЯ
- 11.6. АККРЕЦИЯ РЕЗОНАНСНО ЗАХВАЧЕННЫХ ЗЕРЕН
- 11.7. НЕОБХОДИМЫЕ СВОЙСТВА ПРОЦЕССА АККРЕЦИИ
- 11.8. СОВРЕМЕННОЕ СОСТОЯНИЕ АСТЕРОИДОВ, МЕТЕОРНЫХ ТЕЛ И КОМЕТ И ГИПОТЕЗА ВЗОРВАВШЕЙСЯ ПЛАНЕТЫ
- 12. Об аккреции планет и спутников
- 12.1. ПЛАНЕТЕЗИМАЛЬНАЯ АККРЕЦИЯ
- 12.2. СТРУЙНЫЙ ПОТОК КАК ПРОМЕЖУТОЧНАЯ СТАДИЯ В ОБРАЗОВАНИИ ПЛАНЕТ И СПУТНИКОВ
- 12.3. АККРЕЦИЯ ЗАРОДЫША
- 12.4. БАЛАНС МАССЫ СТРУЙНОГО ПОТОКА
- 12.5. ЭНЕРГЕТИЧЕСКИЙ БАЛАНС В СТРУЙНОМ ПОТОКЕ
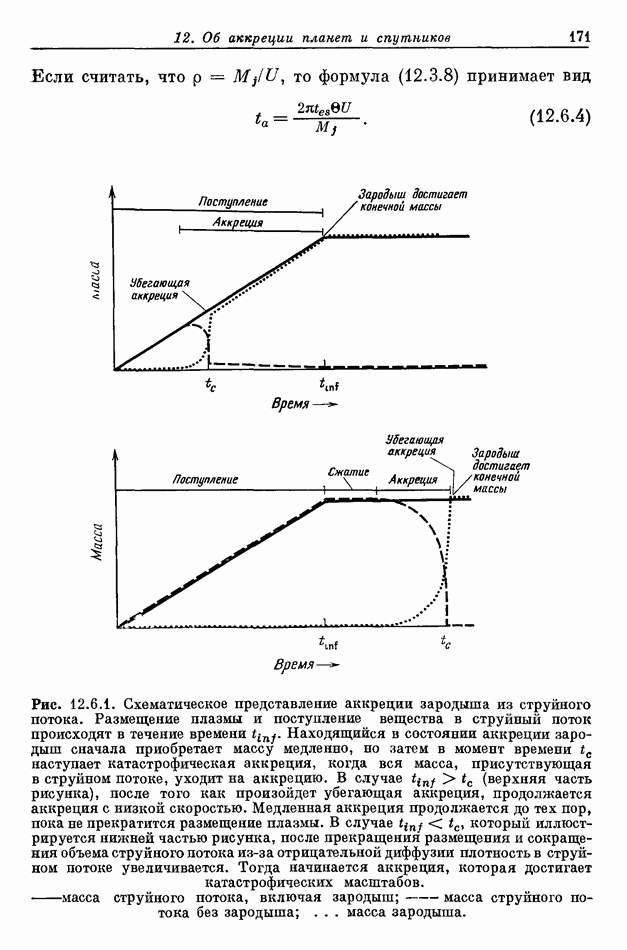
- 12.6. АККРЕЦИЯ ПРИ ПОСТОЯННОЙ СКОРОСТИ ПОСТУПЛЕНИЯ ВЕЩЕСТВА В СТРУЙНЫЙ ПОТОК
- 12.7. ЗАМЕЧАНИЕ
- 12.8. ЧИСЛЕННЫЕ ЗНАЧЕНИЯ
- 12.9. ВЫВОДЫ ОТНОСИТЕЛЬНО РАЗЛИЧНЫХ ТИПОВ АККРЕЦИИ
- 12.10. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ТЕЛА НА РАННЕЙ СТАДИИ ЕГО СУЩЕСТВОВАНИЯ
- 12.11. ВЫВОДЫ О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ ПЛАНЕТ
- 12.12. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ
- 12.13. ДИФФЕРЕНЦИАЦИЯ ВЕЩЕСТВА, ОБУСЛОВЛЕННАЯ ТЕПЛОВЫМ ФРОНТОМ АККРЕЦИИ
- 13. Вращение и аккреция
- 13.1. СОУДАРЕНИЯ ЗЕРЕН И СОБСТВЕННОЕ ВРАЩЕНИЕ ЗАРОДЫША
- 13.2. АККРЕЦИЯ С КРУГОВЫХ ОРБИТ НА НЕГРАВИТИРУЮЩИЙ ЗАРОДЫШ
- 13.3. ГРАВИТАЦИОННАЯ АККРЕЦИЯ
- 13.4. ТЕОРИЯ АККРЕЦИИ ДЖУЛИ
- 13.5. СТАТИСТИЧЕСКАЯ ТЕОРИЯ АККРЕЦИИ
- 13.5.1. АККРЕЦИЯ НА СТАДИИ, ПРЕДШЕСТВУЮЩЕЙ УБЕГАЮЩЕЙ АККРЕЦИИ
- 13.6. АККРЕЦИЯ В СТРУЙНЫХ ПОТОКАХ И СОБСТВЕННОЕ ВРАЩЕНИЕ ПЛАНЕТ
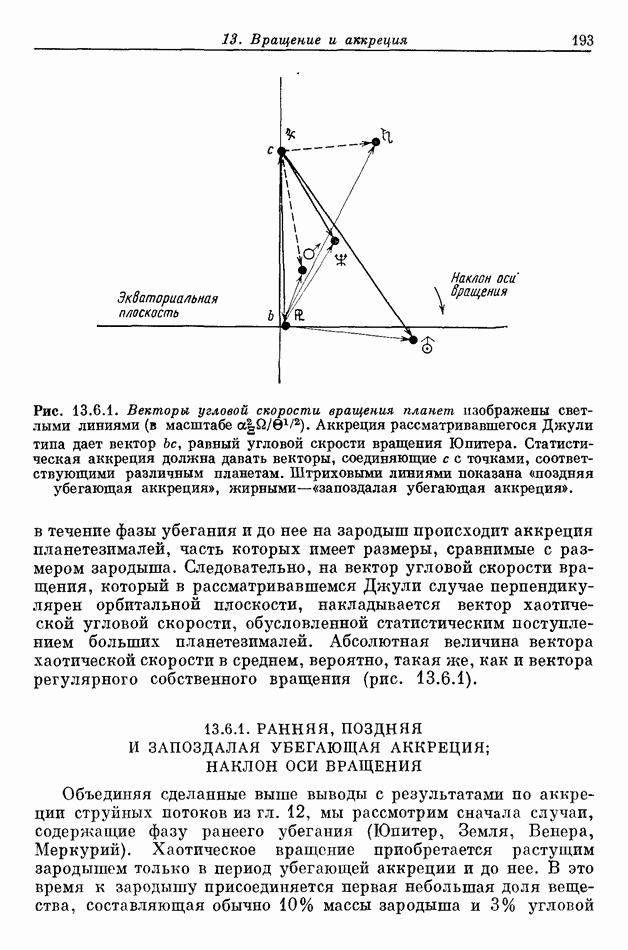
- 13.6.1. РАННЯЯ, ПОЗДНЯЯ И ЗАПОЗДАЛАЯ УБЕГАЮЩАЯ АККРЕЦИЯ; НАКЛОН ОСИ ВРАЩЕНИЯ
- 13.6.2. ПЕРИОД ВРАЩЕНИЯ
- 13.6.3. ОБРАТНОЕ ВРАЩЕНИЕ ВЕНЕРЫ
- 14. Взаимосвязи между кометами и метеорными телами
- 14.2. ПОЛОЖИТЕЛЬНАЯ И ОТРИЦАТЕЛЬНАЯ ДИФФУЗИЯ; МЕТЕОРНЫЕ ПОТОКИ КАК СТРУЙНЫЕ ПОТОКИ
- 14.3. МЕХАНИЗМ АККРЕЦИИ В МЕТЕОРНЫХ ПОТОКАХ
- 14.4. НАБЛЮДЕНИЯ ОБРАЗОВАНИЯ КОМЕТ В МЕТЕОРНЫХ ПОТОКАХ
- 14.5. ДОЛГО- И КОРОТКОПЕРИОДИЧЕСКИЕ КОМЕТЫ
- 14.6 ВЫВОДЫ О ПРИРОДЕ КОМЕТ, ОСНОВАННЫЕ НА ЭМИССИОННЫХ ХАРАКТЕРИСТИКАХ
- 14.7. АНАЛОГИИ МЕЖДУ ПОТОКАМИ КОМЕТ И АСТЕРОИДОВ
- 14.8. СРАВНЕНИЕ С АККРЕЦИЕЙ ПЛАНЕТ И СПУТНИКОВ
- Часть В. Плазма и конденсация
- 15. Физика плазмы и гетегония
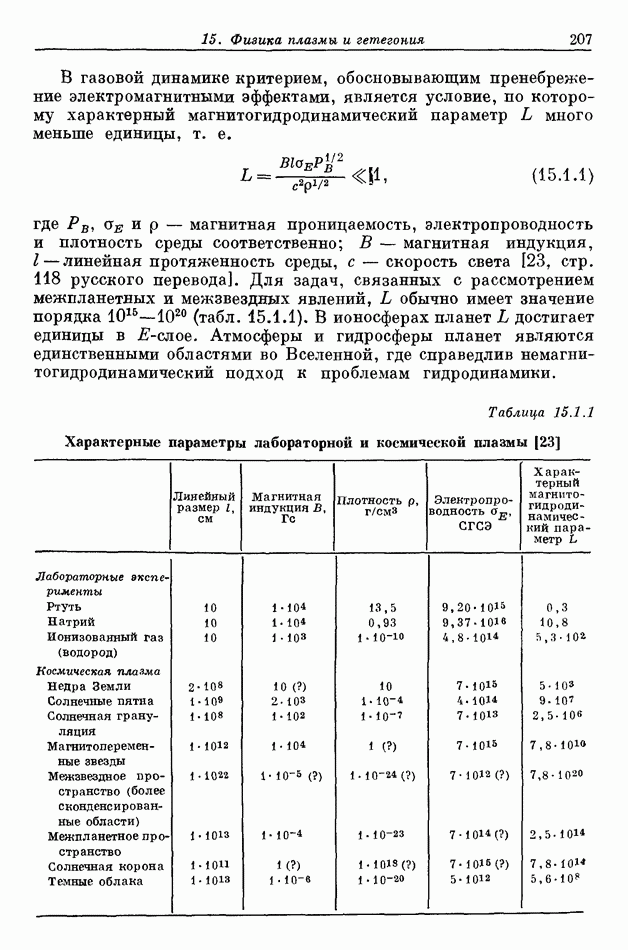
- 15.2 СВЯЗЬ МЕЖДУ ЭКСПЕРИМЕНТАЛЬНОЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКОЙ ПЛАЗМЫ
- 15.3. ПЕРВОЕ И ВТОРОЕ ПРИБЛИЖЕНИЯ В ФИЗИКЕ КОСМИЧЕСКОЙ ПЛАЗМЫ
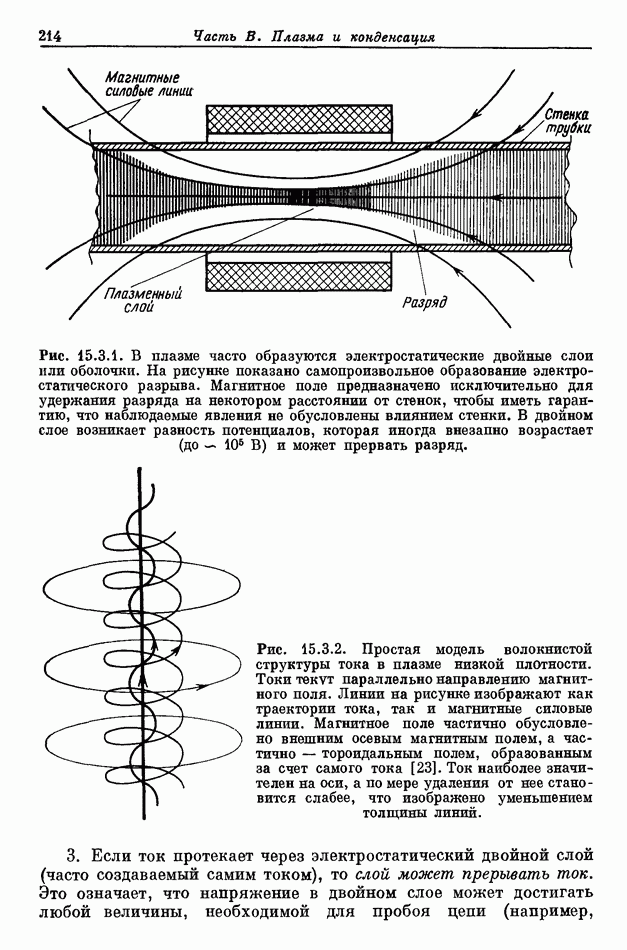
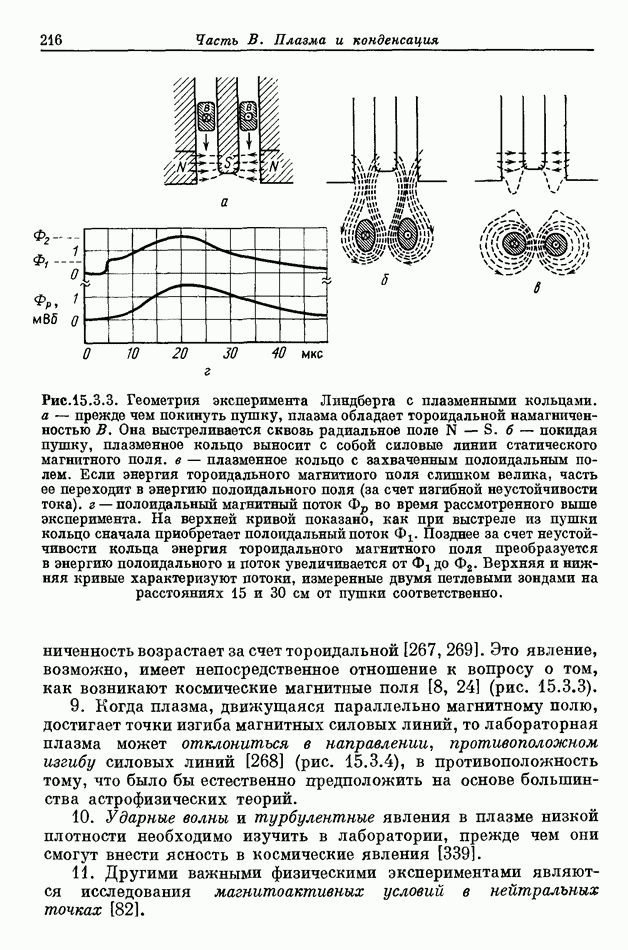
- 15.3.3. НЕКОТОРЫЕ ЛАБОРАТОРНЫЕ ЭКСПЕРИМЕНТЫ, ОТНОСЯЩИЕСЯ К КОСМИЧЕСКОЙ ФИЗИКЕ
- 15.4. СТРАТЕГИЯ АНАЛИЗА ГЕТЕГОННОЙ ПЛАЗМЫ
- 15.5. ТРЕБУЕМЫЕ СВОЙСТВА МОДЕЛИ
- 15.6. НЕКОТОРЫЕ СУЩЕСТВУЮЩИЕ ТЕОРИИ
- 16. Модель гетегонной плазмы
- 16.1. НАМАГНИЧЕННОЕ ЦЕНТРАЛЬНОЕ ТЕЛО
- 16.2. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- 16.3. ПЕРЕНОС МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 16.4. УДЕРЖАНИЕ ПЕРВИЧНОГО ОБЛАКА
- 16.5. ПЛАЗМА КАК ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 16.6. ВЫВОДЫ ОТНОСИТЕЛЬНО МОДЕЛИ
- 16.7. ГЕТЕГОННЫЕ ТУМАННОСТИ
- 16.8. ЭФФЕКТЫ ОБЛУЧЕНИЯ
- 16.9. МОДЕЛЬ И ПРИНЦИП ГЕТЕГОНИИ
- 17. Перенос момента количества движения и конденсация зерен
- 17.1. ИЗОРОТАЦИЯ ФЕРРАРО И ЧАСТИЧНАЯ КОРОТАЦИЯ
- 17.2. ЧАСТИЧНАЯ КОРОТАЦИЯ ПЛАЗМЫ В МАГНИТНОМ И ГРАВИТАЦИОННОМ ПОЛЯХ
- 17.2.1. СВЯЗЬ МЕЖДУ ИЗОРОТАЦИЕЙ ФЕРРАРО И ЧАСТИЧНОЙ КОРОТАЦИЕЙ
- 17.3. ПЛАЗМА В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 17.4. ЗАМЕЧАНИЕ
- 17.5. КОНДЕНСАЦИЯ ПЛАЗМЫ: ЗАКОНА ДВУХ ТРЕТЕЙ
- 17.6. ВЫДЕЛЕНИЕ ЭНЕРГИИ ПРИ ПЕРЕНОСЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
- 18. Аккреция продуктов конденсации
- 18.2. ЭВОЛЮЦИЯ ОРБИТ ВСЛЕДСТВИЕ СТОЛКНОВЕНИЙ
- 18.3. ПРЕДЕЛ РОША
- 18.4. МОДЕЛЬ ЭВОЛЮЦИИ ОРБИТ
- 18.5. АККРЕЦИЯ В ПРЕДЕЛАХ …
- 18.6. СТРУКТУРА КОЛЕЦ САТУРНА
- 18.6.2. МОЖЕТ ЛИ СТРУКТУРА КОЛЕЦ САТУРНА ИМЕТЬ ГЕТЕГОННОЕ ПРОИСХОЖДЕНИЕ?
- 18.6.3. ГЕТЕГОННАЯ ТЕОРИЯ КОЛЕЦ САТУРНА
- 18.6.4. ТЕОРИЯ ЩЕЛИ КАССИНИ
- 18.6.5. ТЕОРИЯ ГРАНИЦЫ МЕЖДУ КОЛЬЦАМИ В И С
- 18.6.6. АНАЛИЗ РЕЗУЛЬТАТОВ
- 18.7. АККРЕЦИЯ ЗА ПРЕДЕЛОМ …
- 18.8. ОБРАЗОВАНИЕ ПОЯСА АСТЕРОИДОВ
- 18.9. ВЫВОДЫ О ЧАСТИЧНОЙ КОРОТАЦИИ
- 18.10. ОБРАЗОВАНИЕ СПУТНИКОВ И ПЛАНЕТ
- 18.11. АККРЕЦИЯ ЛЕТУЧИХ ВЕЩЕСТВ
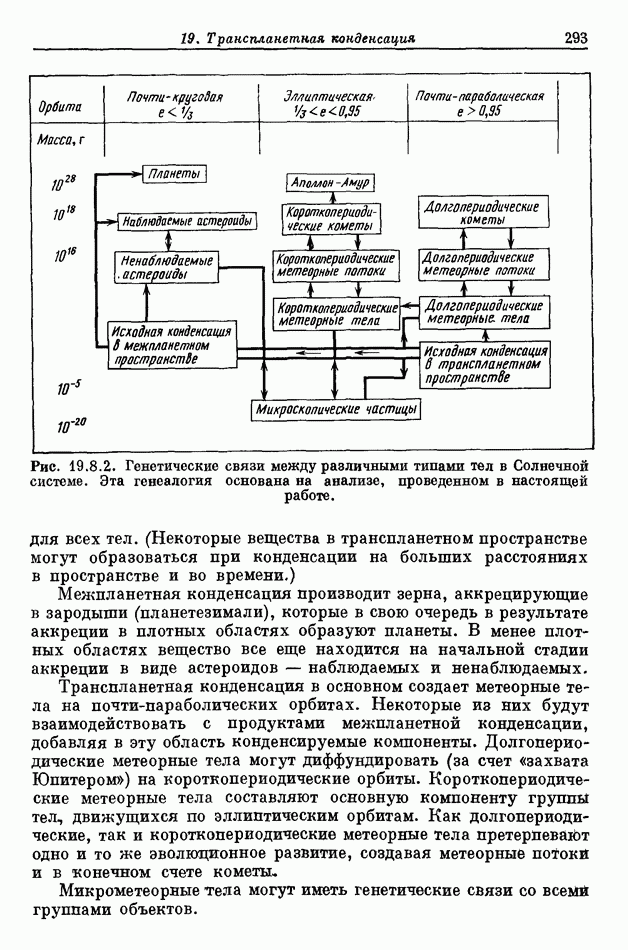
- 19. Транспланетная конденсация
- 19.1. МЕЖПЛАНЕТНАЯ И ТРАНСПЛАНЕТНАЯ КОНДЕНСАЦИЯ
- 19.2. ГРАНИЦА МЕЖДУ МЕЖПЛАНЕТНЫМ И ТРАНСПЛАНЕТНЫМ ПРОСТРАНСТВОМ
- 19.3. КОНДЕНСАЦИЯ ТЕЛ НА ПОЧТИ-ПАРАБОЛИЧЕСКИХ ОРБИТАХ
- 19.4. ТЕЛА С ДОЛГОПЕРИОДИЧЕСКИМИ ОРБИТАМИ
- 19.5. ДИФФУЗИЯ ПОЧТИ ПАРАБОЛИЧЕСКИХ ОРБИТ: СБЛИЖЕНИЯ С ПЛАНЕТАМИ
- 19.6. ГЕНЕТИЧЕСКИЕ СВЯЗИ КОМПЛЕКСА КОМЕТ — МЕТЕОРНЫХ ТЕЛ
- 19.7. ВЫВОДЫ О СЕМЕЙСТВАХ МЕТЕОРНЫХ ТЕЛ
- 19.8. ГЕНЕАЛОГИЯ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- Часть Г. Физическая и химическая структура Солнечной системы
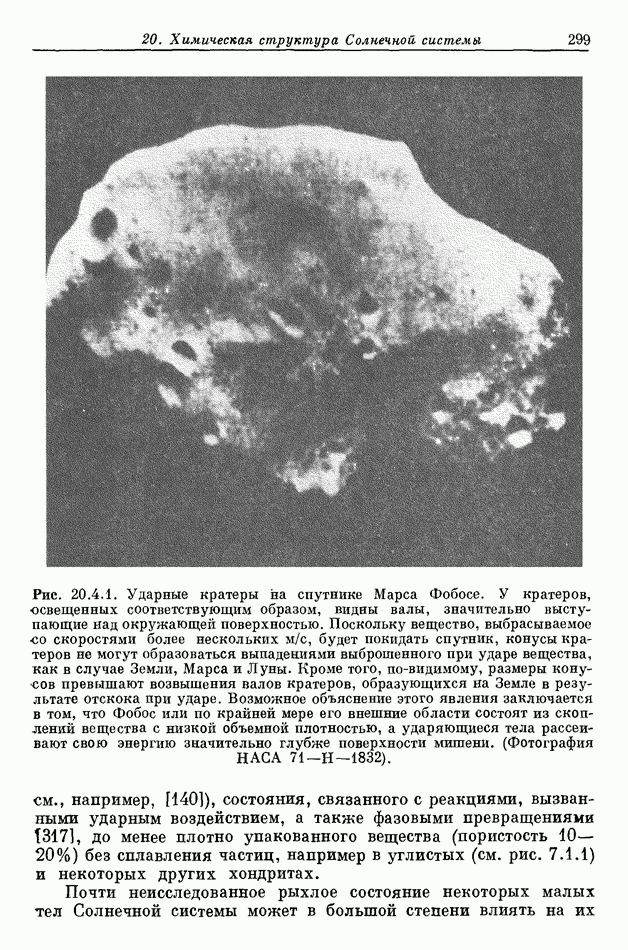
- 20. Химическая структура Солнечной системы
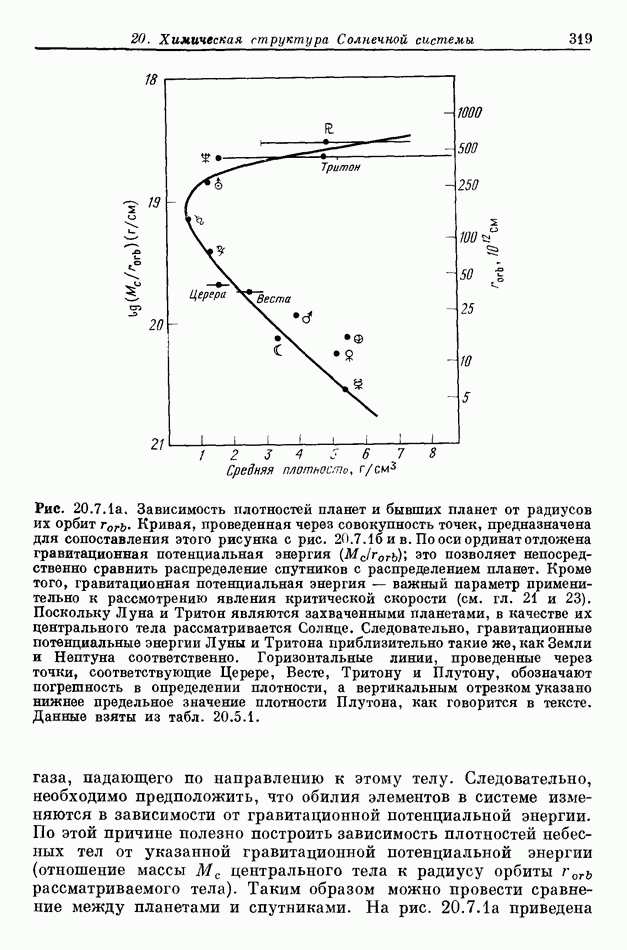
- 20.2. ИСТОЧНИКИ ИНФОРМАЦИИ О ХИМИЧЕСКОМ СОСТАВЕ
- 20.3. ДИФФЕРЕНЦИАЦИЯ ХИМИЧЕСКОГО СОСТАВА ДО И ПОСЛЕ АККРЕЦИИ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- 20.4. НЕИЗВЕСТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА
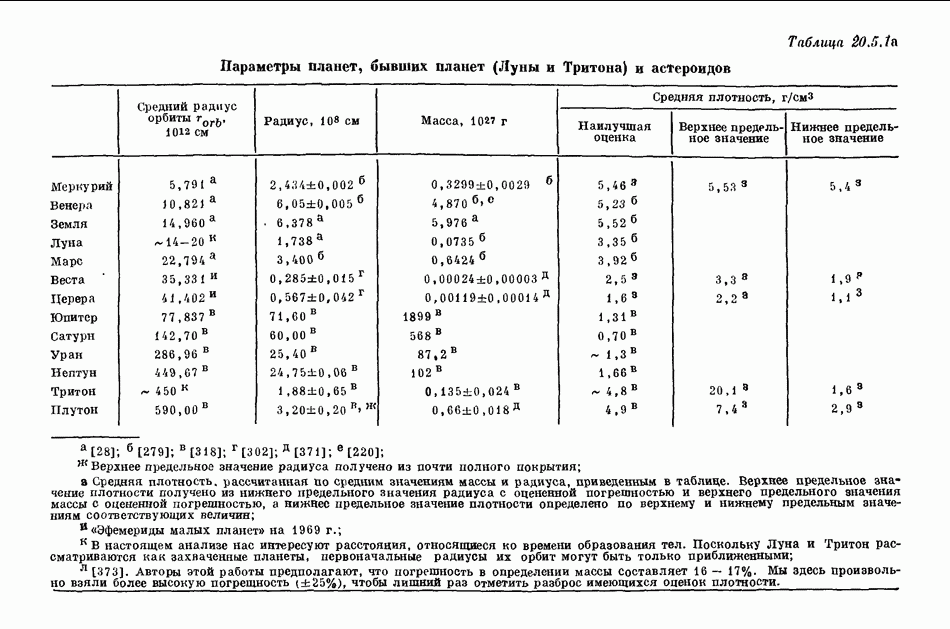
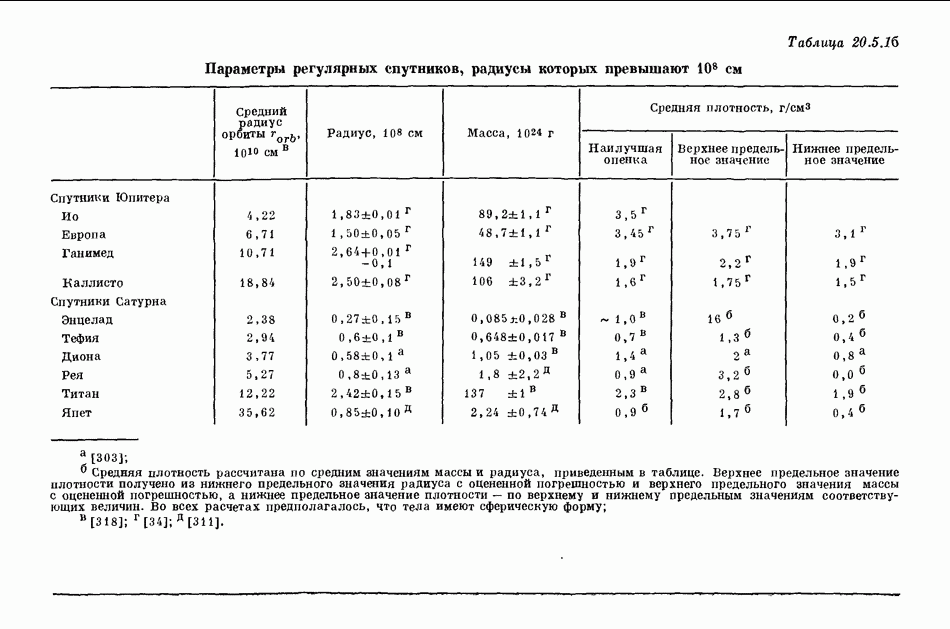
- 20.5. СОСТАВ ПЛАНЕТ И СПУТНИКОВ
- 20.6. СОСТАВ СОЛНЦА
- 20.6.2. АНАЛИЗ КОРПУСКУЛЯРНОГО ИЗЛУЧЕНИЯ СОЛНЦА
- 20.6.3. ЗНАЧЕНИЕ ДАННЫХ ПО ОБИЛИЯМ ЭЛЕМЕНТОВ В СОЛНЕЧНОЙ ФОТОСФЕРЕ
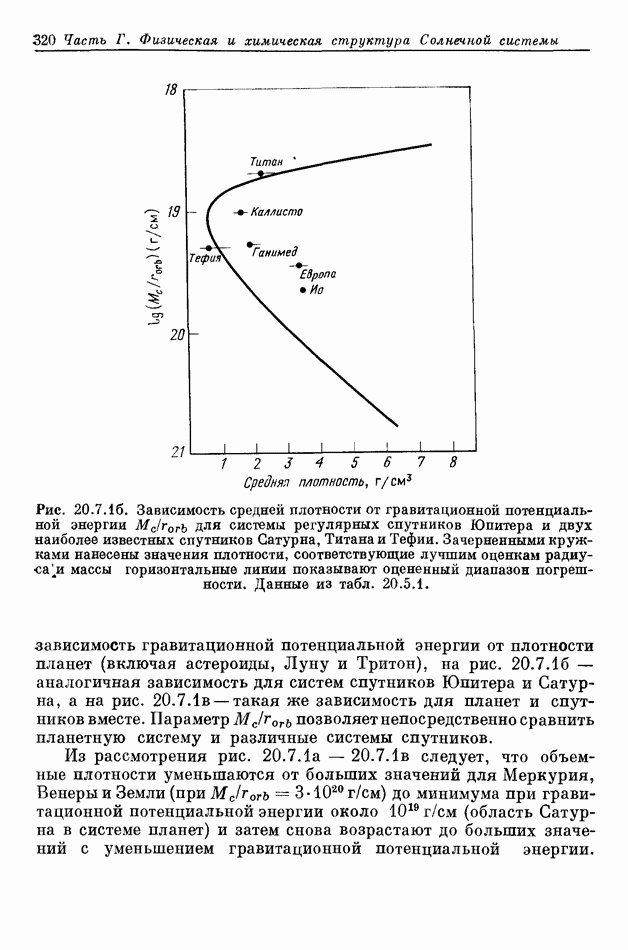
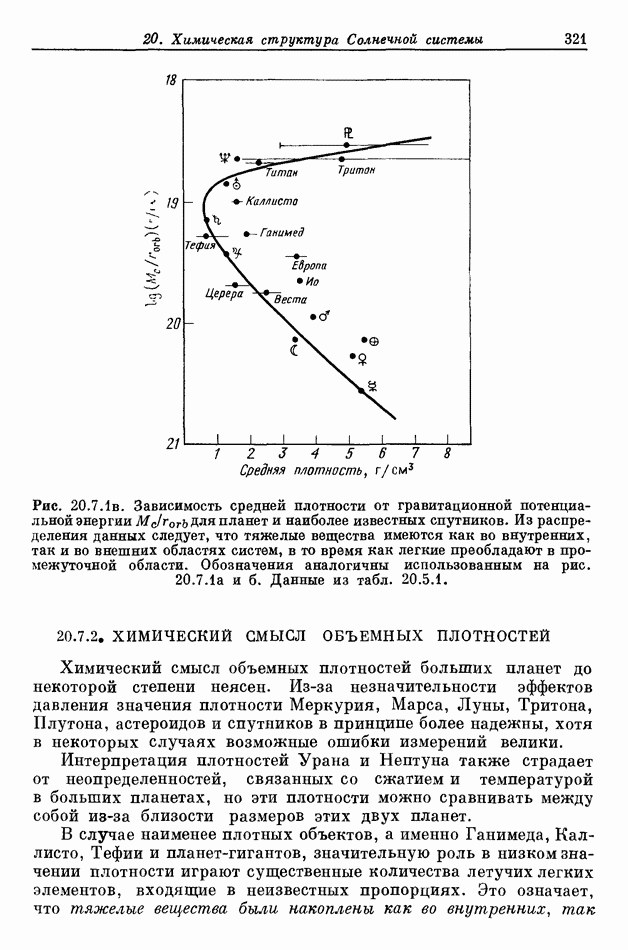
- 20.7. РЕГУЛЯРНОСТЬ ОБЪЕМНЫХ ПЛОТНОСТЕЙ В СОЛНЕЧНОЙ СИСТЕМЕ
- 21. Распределение массы и критическая скорость
- 21.1. РАСПРЕДЕЛЕНИЕ МАССЫ В СОЛНЕЧНОЙ СИСТЕМЕ
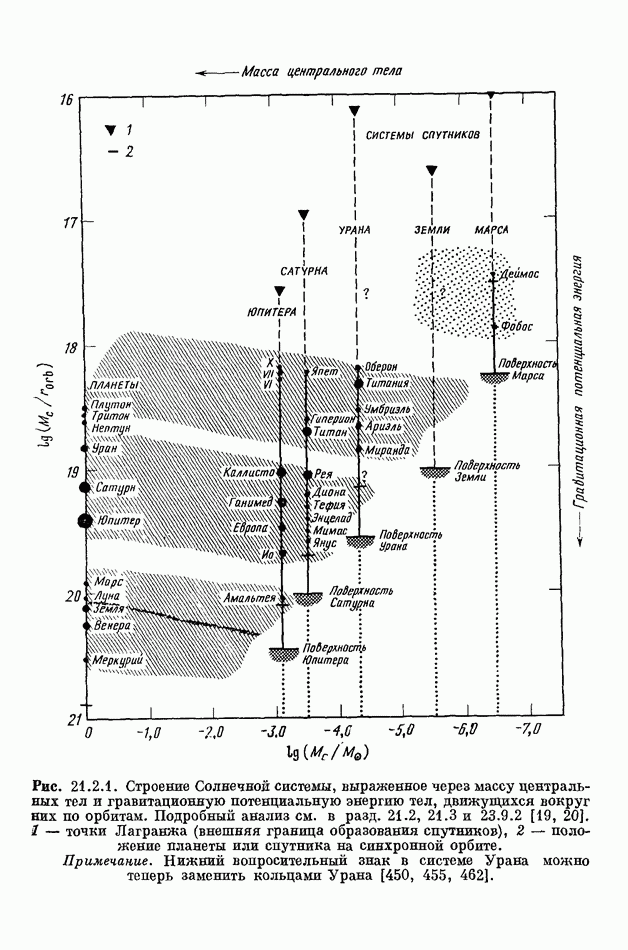
- 21.2. ПОЯСА ВТОРИЧНЫХ ТЕЛ В ЗАВИСИМОСТИ ОТ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 21.3. СРАВНИТЕЛЬНОЕ ИЗУЧЕНИЕ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 21.4. ЦТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ ДЛЯ ОБРАЗОВАНИЯ ПОЯСОВ
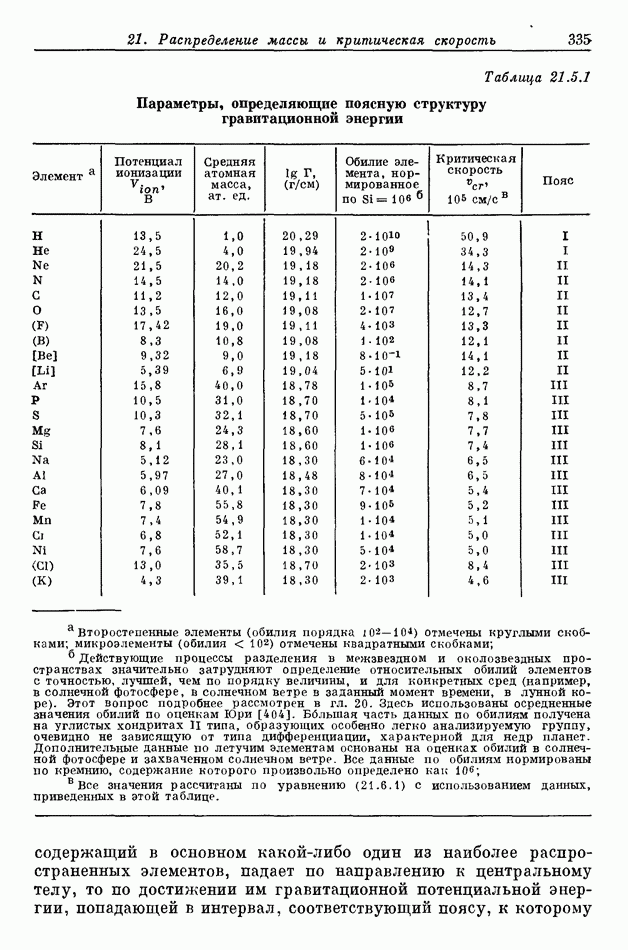
- 21.5. ПОПЫТКИ ИНТЕРПРЕТАЦИИ ПОЯСНОЙ СТРУКТУРЫ
- 21.6. ТРИ ВОЗРАЖЕНИЯ
- 21.7. ПОИСКИ «КРИТИЧЕСКОЙ СКОРОСТИ»
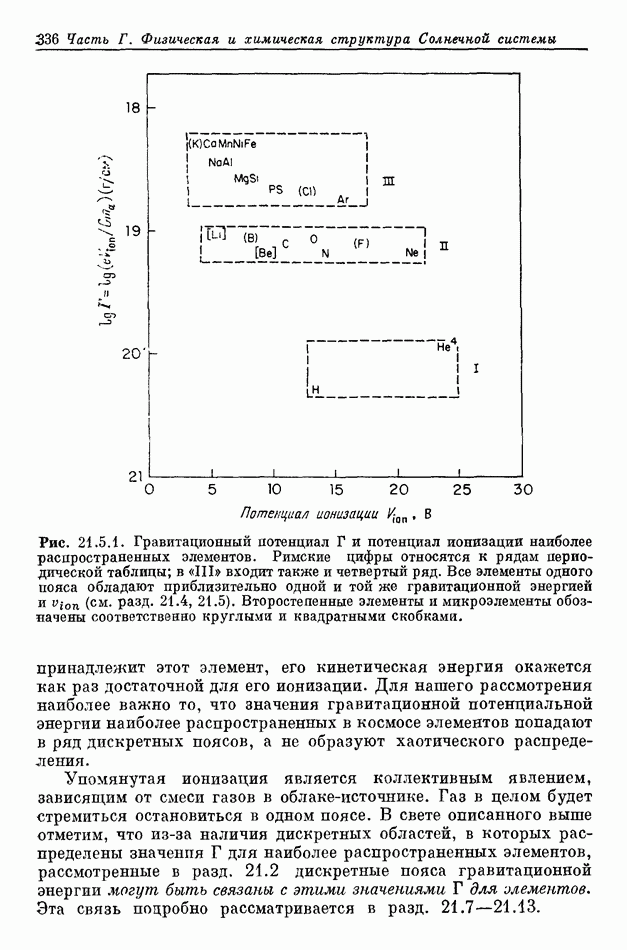
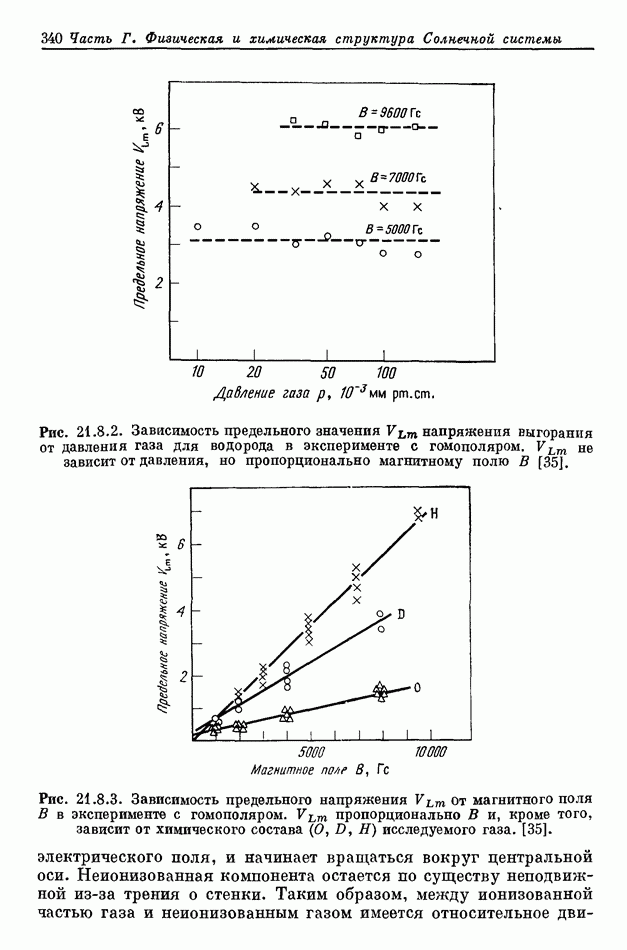
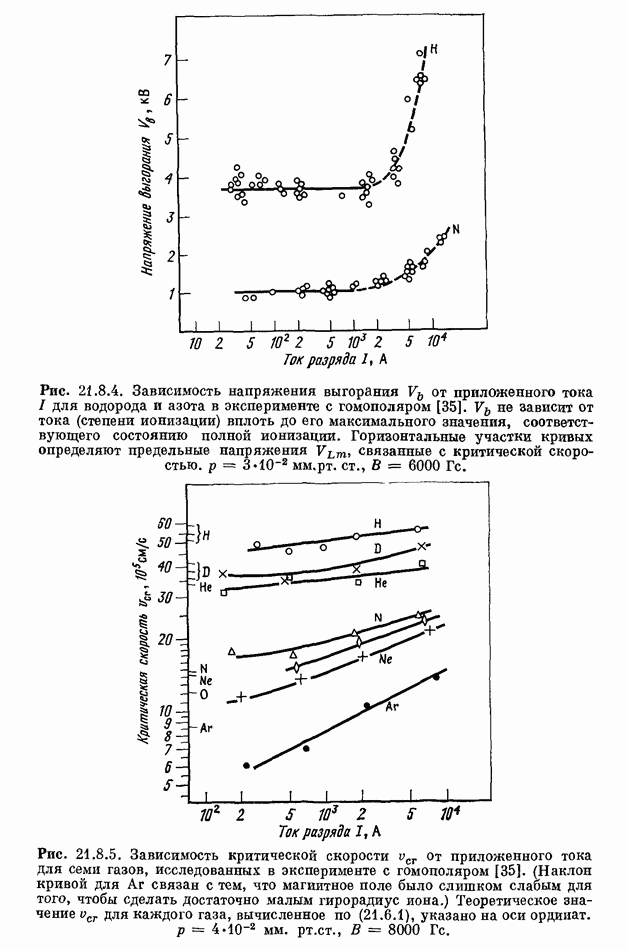
- 21.8. ЭКСПЕРИМЕНТЫ ПО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.8.2. ПЛАЗМЕННЫЙ ПУЧОК, СТАЛКИВАЮЩИЙСЯ С ОБЛАКОМ НЕЙТРАЛЬНОГО ГАЗА
- 21.8.3. ДРУГИЕ ЭКСПЕРИМЕНТЫ
- 21.9. ТЕОРИЯ КРИТИЧЕСКОЙ СКОРОСТИ
- 21.10. ВЫВОДЫ ОТНОСИТЕЛЬНО КРИТИЧЕСКОЙ СКОРОСТИ
- 21.11. ХИМИЧЕСКИЙ СОСТАВ ВЫПАДАЮЩЕГО ГАЗА
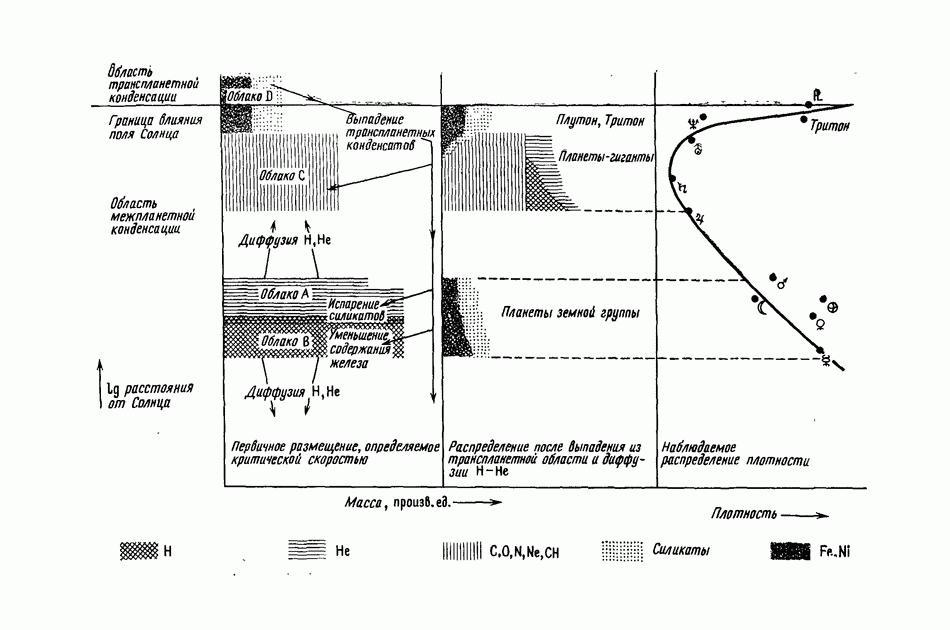
- 21.11.2. ОБЛАКА A, B, C и D В СОЛНЕЧНОЙ СИСТЕМЕ
- 21.11.3. СОВЕРШЕНСТВОВАНИЕ ОСНОВНОЙ МОДЕЛИ
- 21.11.4. ВЛИЯНИЕ МЕЖЗВЕЗДНЫХ МОЛЕКУЛ
- 21.12. ХИМИЧЕСКИЙ СОСТАВ СОЛНЕЧНОЙ СИСТЕМЫ И РАЗМЕЩЕНИЕ НЕОДНОРОДНОЙ ПЛАЗМЫ
- 21.12.2. ВЛИЯНИЕ ТРАНСПЛАНЕТНОЙ КОНДЕНСАЦИИ НА СОСТАВ ПЛАНЕТ И СПУТНИКОВ
- 21.12.3. ФРАКЦИОНИРОВАНИЕ, СВЯЗАННОЕ С КОНДЕНСАЦИЕЙ ИЛИ СЛЕДУЮЩЕЕ ЗА НЕЙ
- 21.12.4. ВЫВОДЫ О ХИМИЧЕСКОМ СОСТАВЕ НЕБЕСНЫХ ТЕЛ
- 21.13. ИЗМЕНЕНИЕ РАССТОЯНИЯ ИОНИЗАЦИИ ДЛЯ КРИТИЧЕСКОЙ СКОРОСТИ ИЗ-ЗА ВЗАИМОДЕЙСТВИЯ С ПЛАЗМОЙ В СОСТОЯНИИ ЧАСТИЧНОЙ КОРОТАЦИИ
- 22. Метеориты и предшествующие им состояния
- 22.1. ИНТЕРПРЕТАЦИЯ ЭВОЛЮЦИОННЫХ ДАННЫХ, ЗАПЕЧАТЛЕННЫХ В МЕТЕОРИТАХ
- 22.2. ИСТОЧНИКИ МЕТЕОРИТОВ
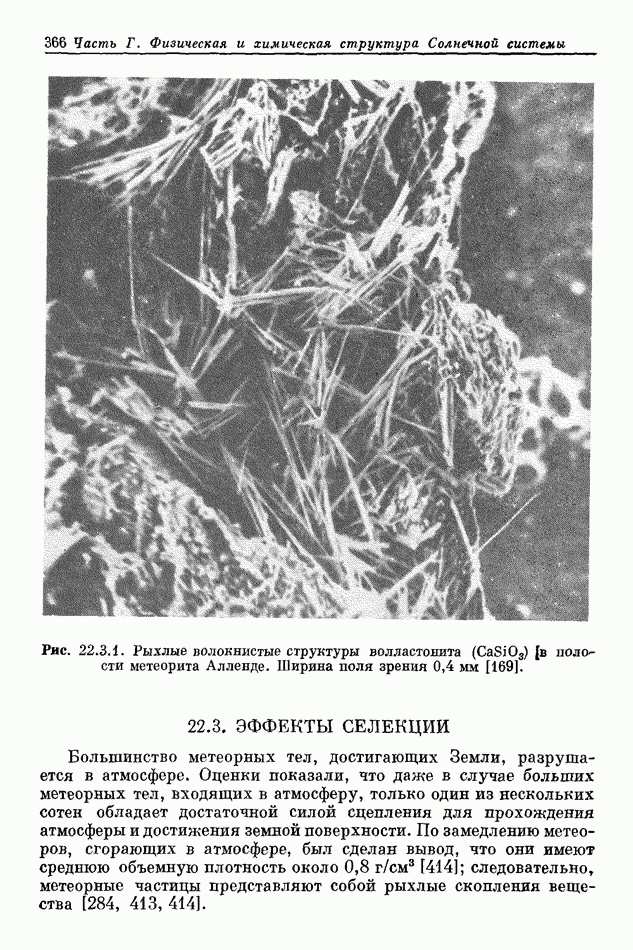
- 22.3. ЭФФЕКТЫ СЕЛЕКЦИИ
- 22.4. ВЕРХНИЕ ПРЕДЕЛЫ РАЗМЕРОВ ТЕЛ, ПРЕДШЕСТВУЮЩИХ МЕТЕОРИТАМ
- 22.5. ПРЕДШЕСТВУЮЩИЕ СОСТОЯНИЯ РОДИТЕЛЬСКИХ ТЕЛ МЕТЕОРИТОВ
- 22.6. ЭВОЛЮЦИЯ СТРУЙНОГО ПОТОКА И СВОЙСТВА МЕТЕОРИТОВ
- 22.7. СИЛЫ СЦЕПЛЕНИЯ В МЕТЕОРИТНОМ ВЕЩЕСТВЕ
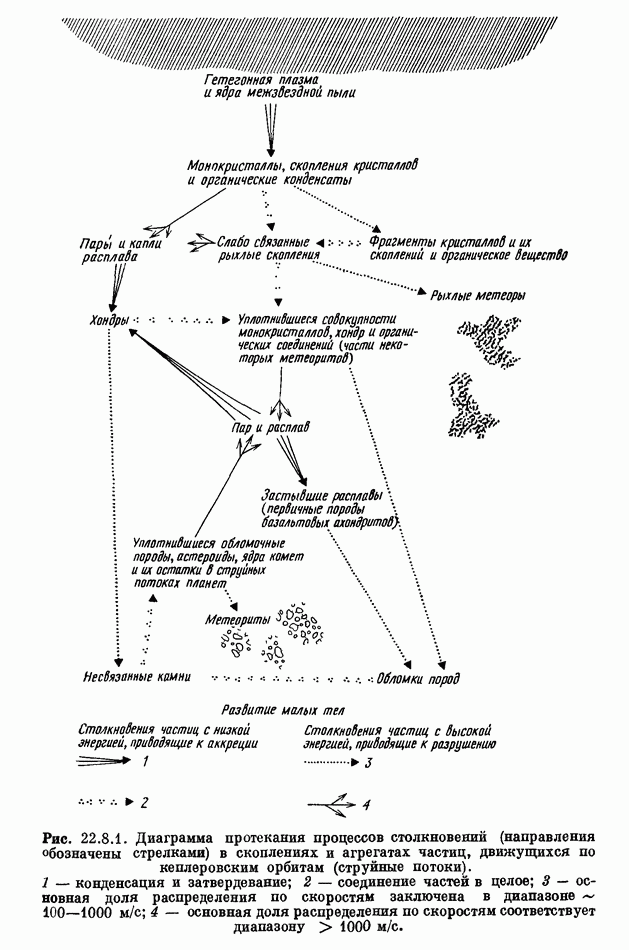
- 22.8. ЭВОЛЮЦИОННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ПРЕДШЕСТВУЮЩИХ СОСТОЯНИЙ МЕТЕОРИТОВ
- 22.9. ВОЗРАСТНЫЕ СООТНОШЕНИЯ В ЭВОЛЮЦИИ РОДИТЕЛЬСКИХ СТРУЙНЫХ ПОТОКОВ МЕТЕОРИТОВ
- 22.9.1. ЗАМЫКАНИЕ РЕЗЕРВУАРОВ ТУГОПЛАВКИХ КОМПОНЕНТ
- 22.9.2. ВОЗРАСТЫ КРИСТАЛЛИЗАЦИИ
- 22.9.3. ВОЗРАСТЫ УДЕРЖАНИЯ ГАЗА
- 22.9.4. ВОЗРАСТЫ ДЕГАЗАЦИИ
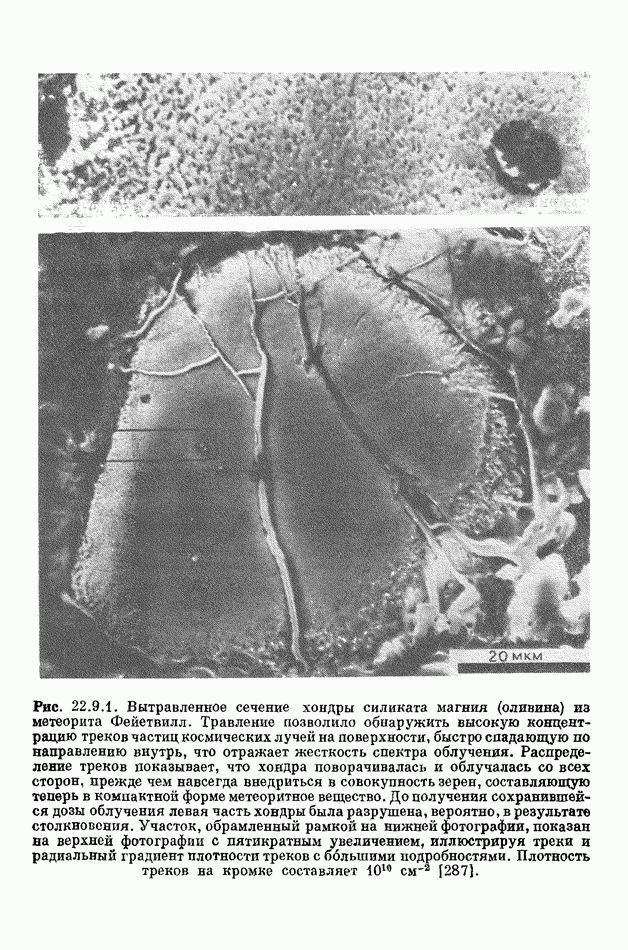
- 22.9.5. ТРЕКИ ЧАСТИЦ И ВНЕДРЕНИЕ ПЛАЗМЫ В МЕТЕОРИТАХ
- 22.9.6. ВОЗРАСТЫ ОБЛУЧЕНИЯ КОСМИЧЕСКИМИ ЛУЧАМИ ВЫСОКИХ ЭНЕРГИЙ
- 22.10. ОБЩИЕ ЗАМЕЧАНИЯ О ДАННЫХ, ЗАФИКСИРОВАННЫХ В МЕТЕОРИТАХ
- 23. Строение групп вторичных тел
- 23.1. ИОНИЗАЦИЯ В ПРОЦЕССЕ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- 23.2. ПОЛНАЯ ИОНИЗАЦИЯ
- 23.3. ЧАСТИЧНАЯ ИОНИЗАЦИЯ
- 23.4. ИЗМЕНЕНИЕ ВРАЩЕНИЯ ВО ВРЕМЯ ОБРАЗОВАНИЯ ВТОРИЧНЫХ ТЕЛ
- 23.5. НАБЛЮДАЕМЫЕ ЗНАЧЕНИЯ …
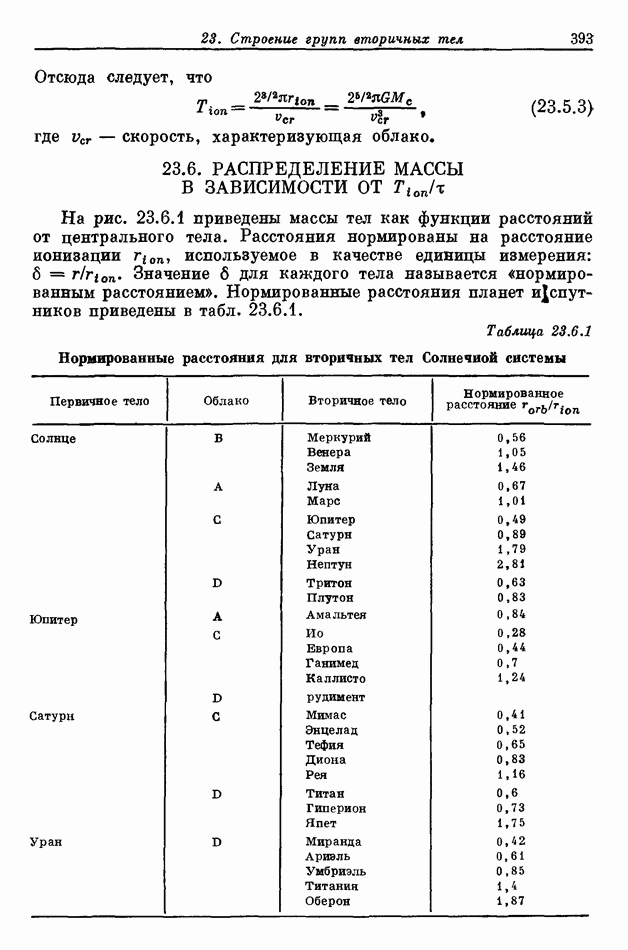
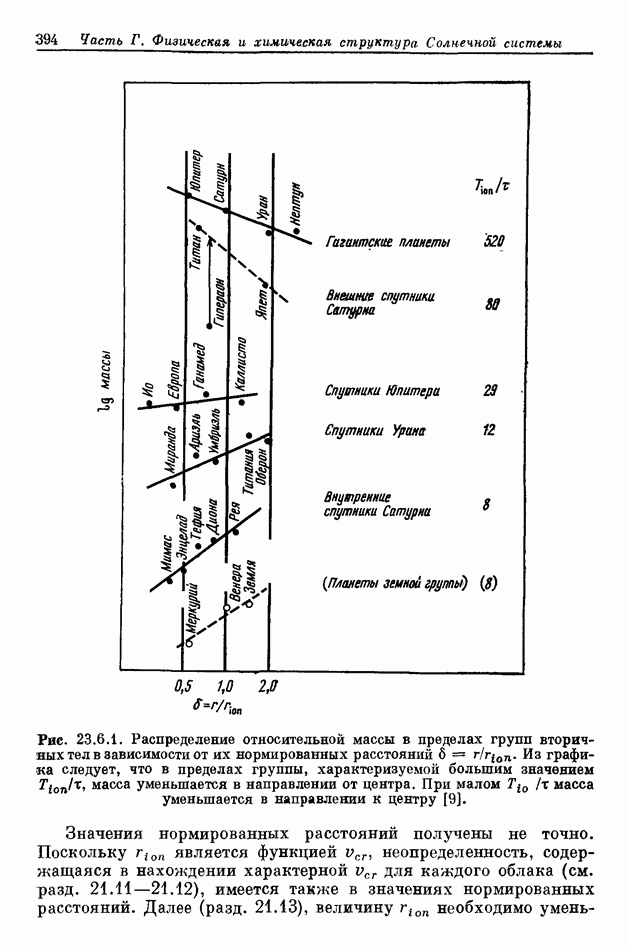
- 23.6. РАСПРЕДЕЛЕНИЕ МАССЫ В ЗАВИСИМОСТИ ОТ …
- 23.7. АНАЛИЗ СТРОЕНИЯ ГРУПП ВТОРИЧНЫХ ТЕЛ
- 23.8. ПОЛНЫЙ ПЕРЕЧЕНЬ ЗНАЧЕНИЙ … ДЛЯ ВСЕХ ТЕЛ
- 23.9. ЗАВЕРШЕННОСТЬ
- 23.9.1. ЗАМЕЧАНИЕ О ВНУТРЕННЕЙ ГРАНИЦЕ СИСТЕМЫ СПУТНИКОВ
- 23.9.2. НАКЛОН ПОЯСОВ НА ДИАГРАММЕ ГРАВИТАЦИОННОЙ ПОТЕНЦИАЛЬНОЩЭНЕРГИИ
- 23.9.3. ДРУГИЕ ЗАКОНОМЕРНОСТИ В СТРОЕНИИ ГРУПП
- 23.10. ВЫВОДЫ О МОДЕЛИ РАЗМЕЩЕНИЯ ПЛАЗМЫ
- Часть Д. Частные проблемы
- 24. Происхождение и эволюция системы Земля-Луна
- 24.2. СРАВНЕНИЕ С ДРУГИМИ СИСТЕМАМИ СПУТНИКОВ
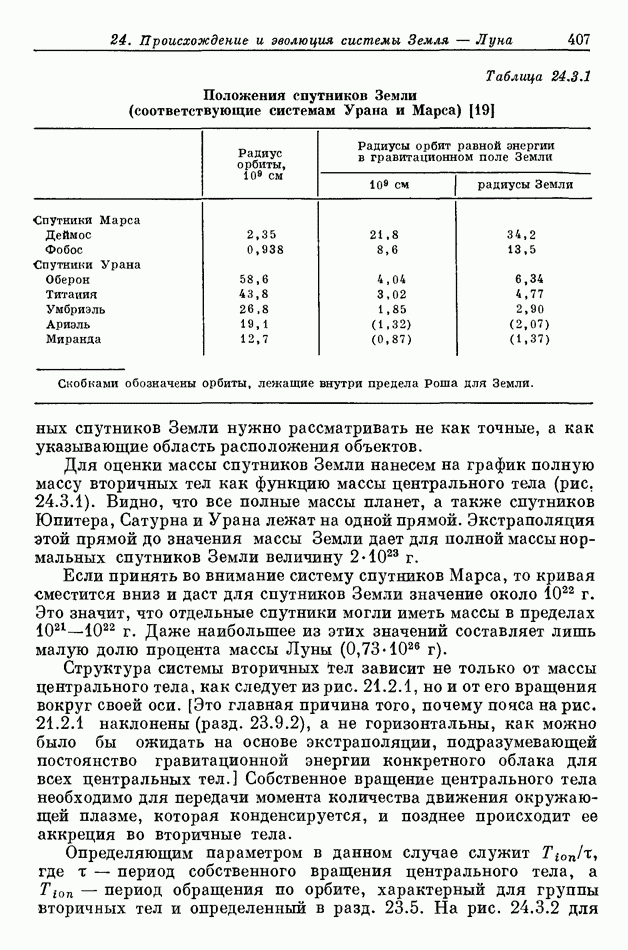
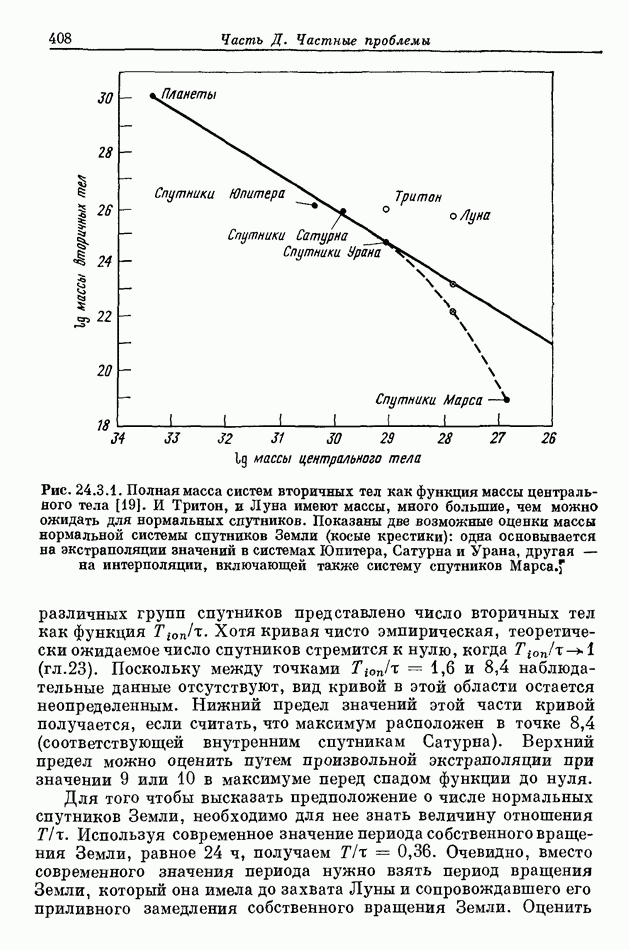
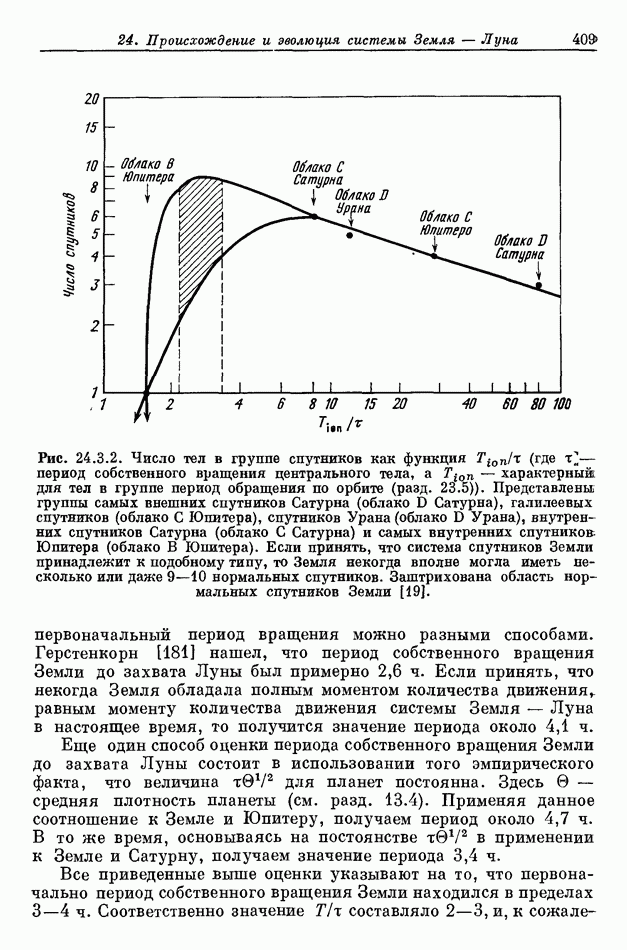
- 24.3. СТРУКТУРА НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ ЗЕМЛИ
- 24.4 ТЕОРИЯ ЗАХВАТА
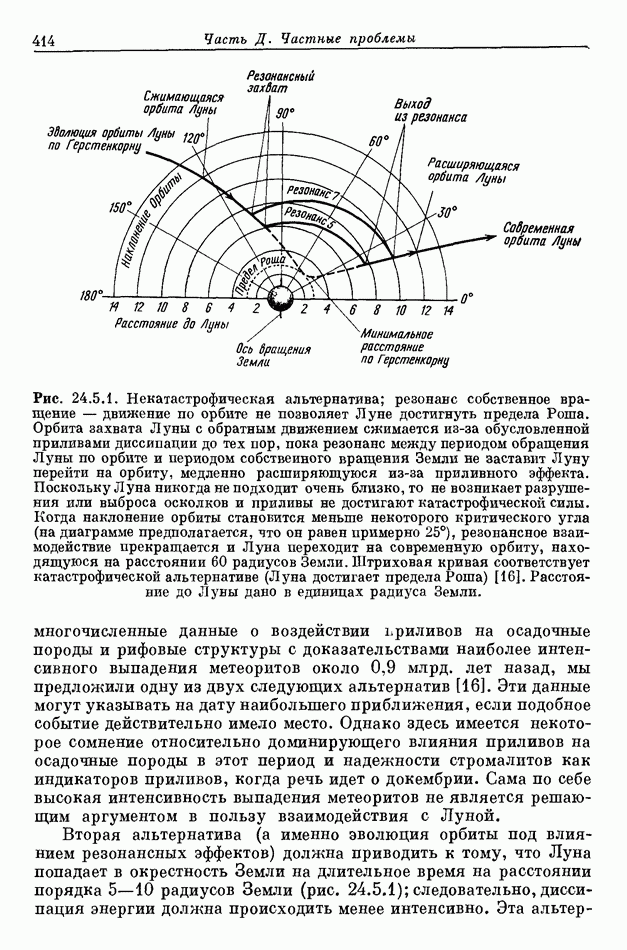
- 24.5 ПРИЛИВНАЯ ЭВОЛЮЦИЯ ЛУННОЙ ОРБИТЫ
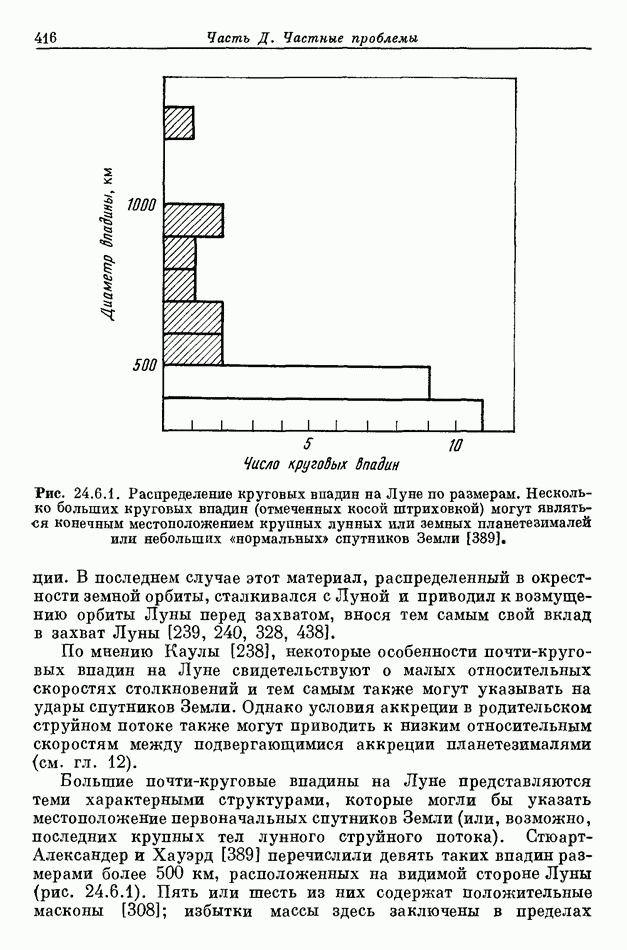
- 24.6. РАЗРУШЕНИЕ НОРМАЛЬНОЙ СИСТЕМЫ СПУТНИКОВ
- 24.7. АККРЕЦИЯ И ТЕПЛОВАЯ СТРУКТУРА ЛУНЫ
- 24.8. СОСТАВ ЛУНЫ
- 24.9. ВЫВОДЫ
- 25. Свойства Солнца на ранней стадии его существования
- 25.2 МАССА СОЛНЦА
- 25.3. МАГНИТНОЕ ПОЛЕ СОЛНЦА
- 25.4. ПЕРИОД СОБСТВЕННОГО ВРАЩЕНИЯ СОЛНЦА
- 25.5. ИЗЛУЧЕНИЕ СОЛНЦА, СОЛНЕЧНЫЙ ВЕТЕР
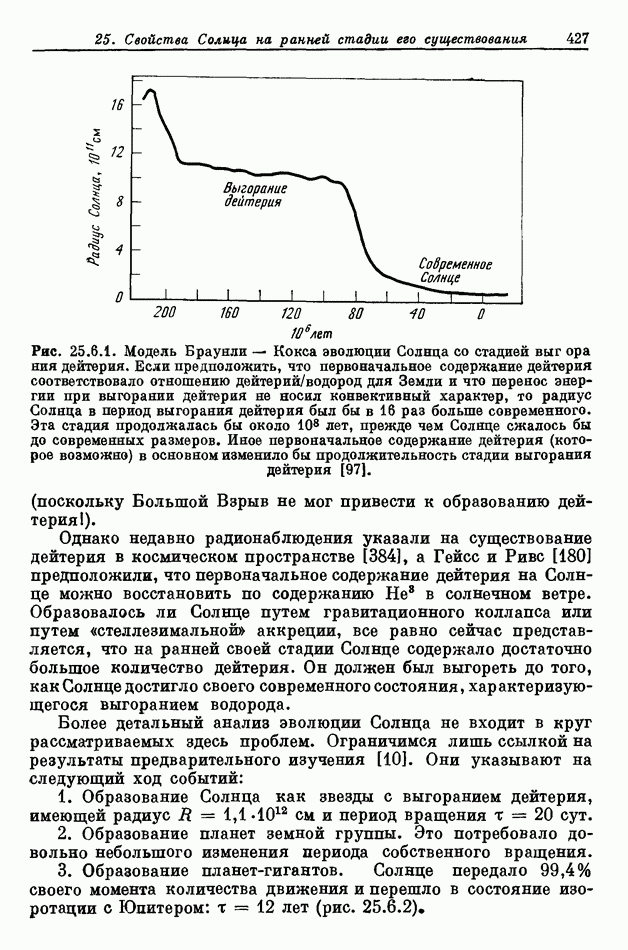
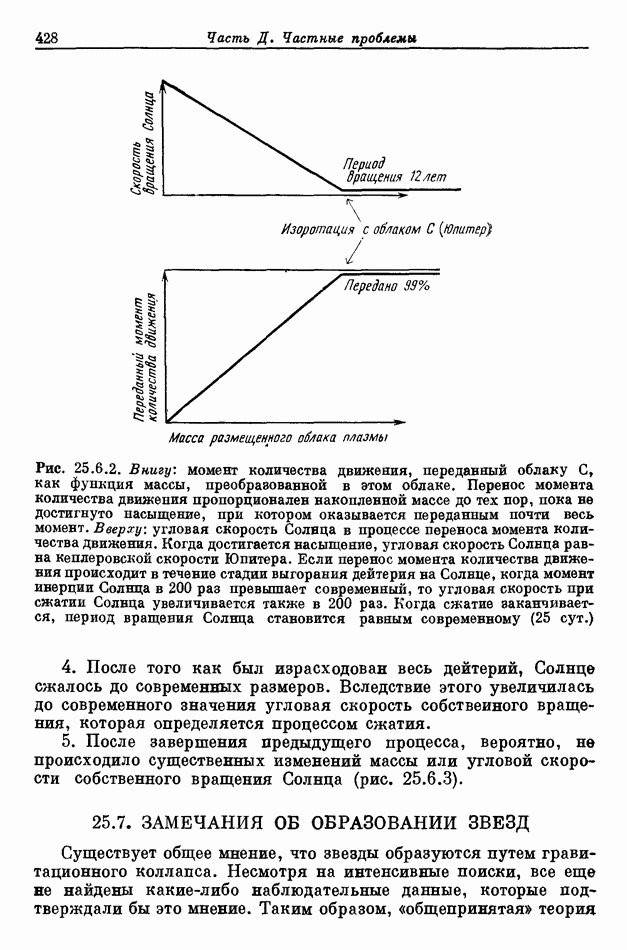
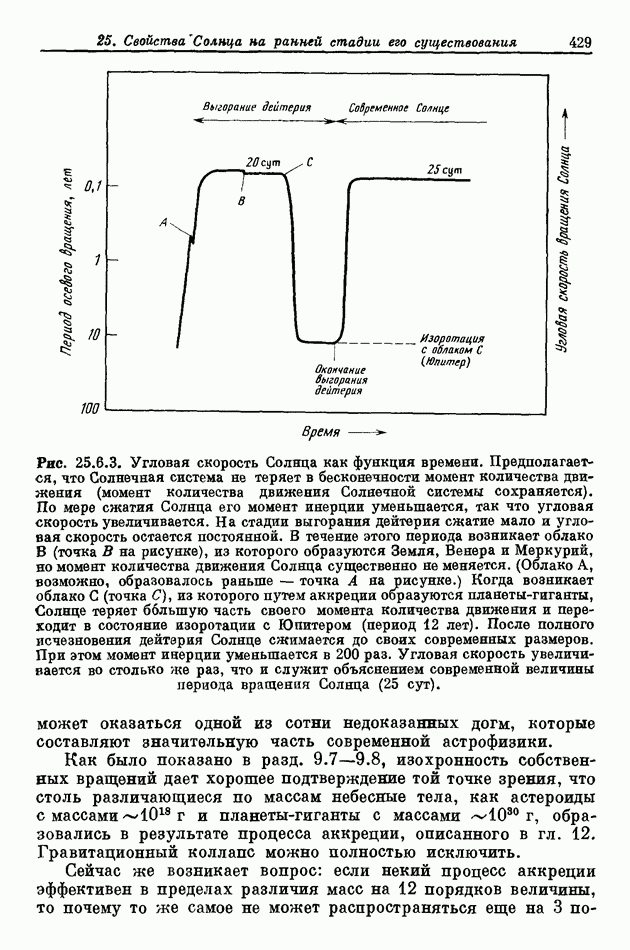
- 25.6. ЭФФЕКТЫ ВЫГОРАНИЯ ДЕЙТЕРИЯ НА СОЛНЦЕ
- 25.7. ЗАМЕЧАНИЯ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 26. Происхождение океана и атмосферы Земли
- 26.1. ЗЕМНОЙ ОКЕАН И ОБРАЗОВАНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
- 26.2. СТАДИИ ОТДАЛЕННЫХ ПРЕДШЕСТВЕННИКОВ
- 26.2.2. ПЕРВИЧНЫЕ ЗЕРНА КАК НОСИТЕЛИ КОМПОНЕНТ АТМОСФЕРЫ И ОКЕАНА
- 26.2.3. ВНЕЗЕМНЫЕ ИСТОЧНИКИ ВОДЫ
- 26.2.4. ЗАПАСЫ ИНЕРТНЫХ И ХИМИЧЕСКИ АКТИВНЫХ ЛЕТУЧИХ
- 26.3. СТАДИИ БЛИЖАЙШИХ ПРЕДШЕСТВЕННИКОВ
- 26.3.1. ЭВОЛЮЦИЯ ПРЕДШЕСТВОВАВШИХ ЗЕМЛЕ ПЛАНЕТЕЗИМАЛЕЙ
- 26.3.2. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В РАСТУЩЕЙ ПРОТОПЛАНЕТЕ
- 26.3.3. ЯДРО ЗЕМЛИ
- 26.3.4. ВЫСВОБОЖДЕНИЕ ТЕПЛА И УЛЕТУЧИВАНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ
- 26.4. НАКОПЛЕНИЕ ВОДЫ В ПРОЦЕССЕ АККРЕЦИИ ЗЕМЛИ
- 26.4.2. ФРОНТ ТЕПЛОВЫХ ПЯТЕН АККРЕЦИИ И СОСТОЯНИЕ ВОДЫ
- 26.4.3. ДЕТАЛИЗАЦИЯ МОДЕЛИ
- 26.5. ПОСТУПЛЕНИЕ ВОДЫ В ЛИТОСФЕРУ
- 26.5.2. СТАЦИОНАРНОЕ СОСТОЯНИЕ ПРОПИТЫВАНИЯ И ВЫСВОБОЖДЕНИЯ
- 26.5.3. ВОЗМОЖНЫЕ ОСТАТКИ ЛЕТУЧИХ ВЕЩЕСТВ ПЛАНЕТЕЗИМАЛЕЙ В ЗЕМНОЙ КОРЕ И МАНТИИ
- 26.6. ОКЕАН И СИСТЕМА ЗЕМЛЯ — ЛУНА
- 26.7. ИТОГИ И ВЫВОДЫ
- 27. Межзвездные облака и образование звезд
- 27.2. МАГНИТНАЯ ГИДРОДИНАМИКА ОБЛАКОВ КОСМИЧЕСКОЙ ПЛАЗМЫ
- 27.2.3. БЕССИЛОВЫЕ МАГНИТНЫЕ ПОЛЯ И СОЗДАНИЕ ВОЛОКОН
- 27.2.4. СПОСОБСТВУЮТ ИЛИ ПРОТИВОДЕЙСТВУЮТ СЖАТИЮ МАГНИТНЫЕ ПОЛЯ?
- 27.2.5. ПИНЧ-СЖАТИЕ ТЕМНЫХ МЕЖЗВЕЗДНЫХ ОБЛАКОВ
- 27.3. ОБРАЗОВАНИЕ ЗВЕЗД В ОБЛАКЕ ПЫЛЕВОЙ ПЛАЗМЫ
- 27.3.2. ДВИЖЕНИЕ ПЫЛИ В ОБЛАКЕ ПЛАЗМЫ
- 27.3.3. ОСЕДАНИЕ ПЫЛИ В ГРАВИТАЦИОННОМ ПОЛЕ
- 27.3.4. ОБРАЗОВАНИЕ СТЕЛЛЕЗИМАЛЕЙ
- 27.3.5. ДВУХСТУПЕНЧАТАЯ АККРЕЦИЯ
- 27.3.6. СВОЙСТВА ПРОТО-СОЛНЦА И ОКРУЖАЮЩЕЙ ЕГО СРЕДЫ
- 27.3.7. ВЫВОДЫ ОБ ОБРАЗОВАНИИ ЗВЕЗД
- 28. Заключительные замечания