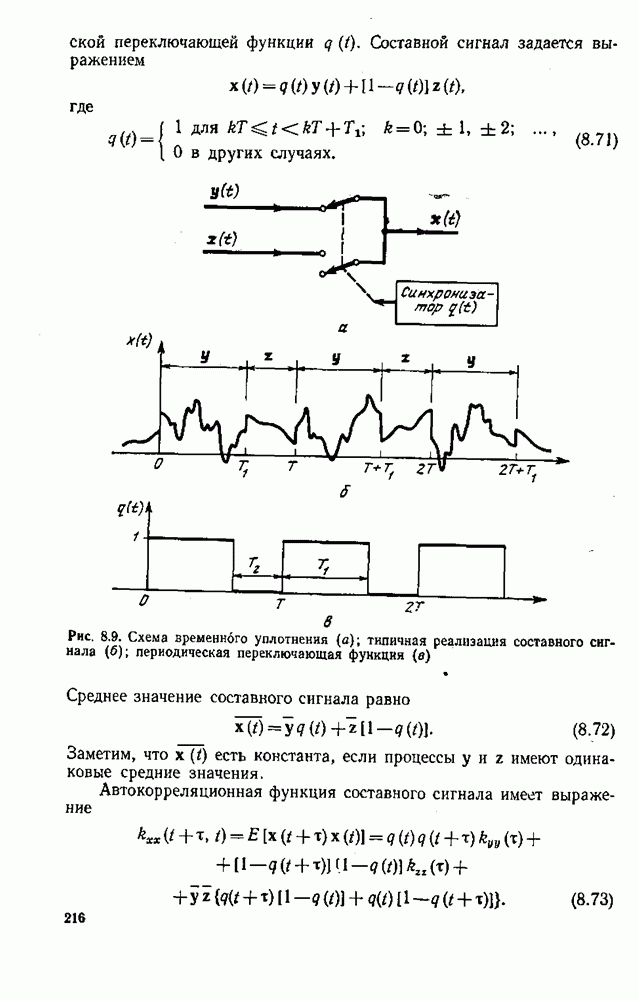
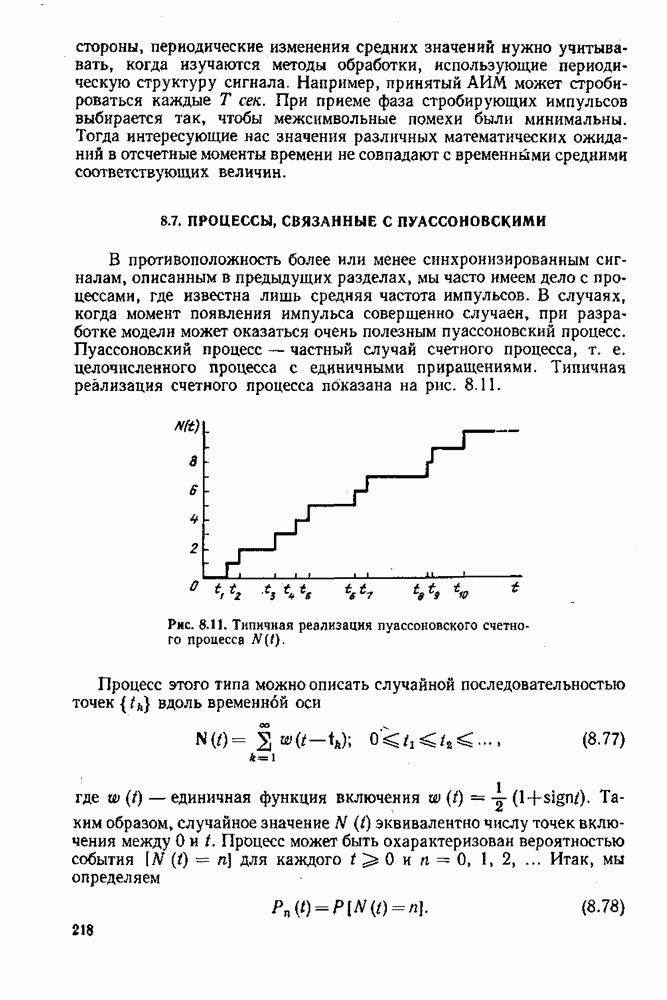
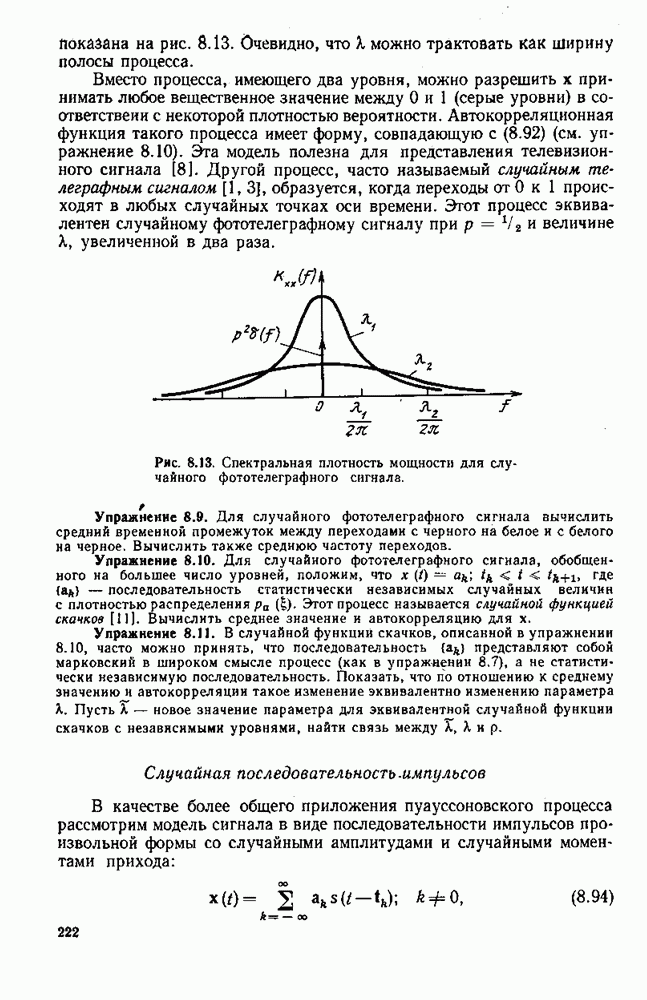
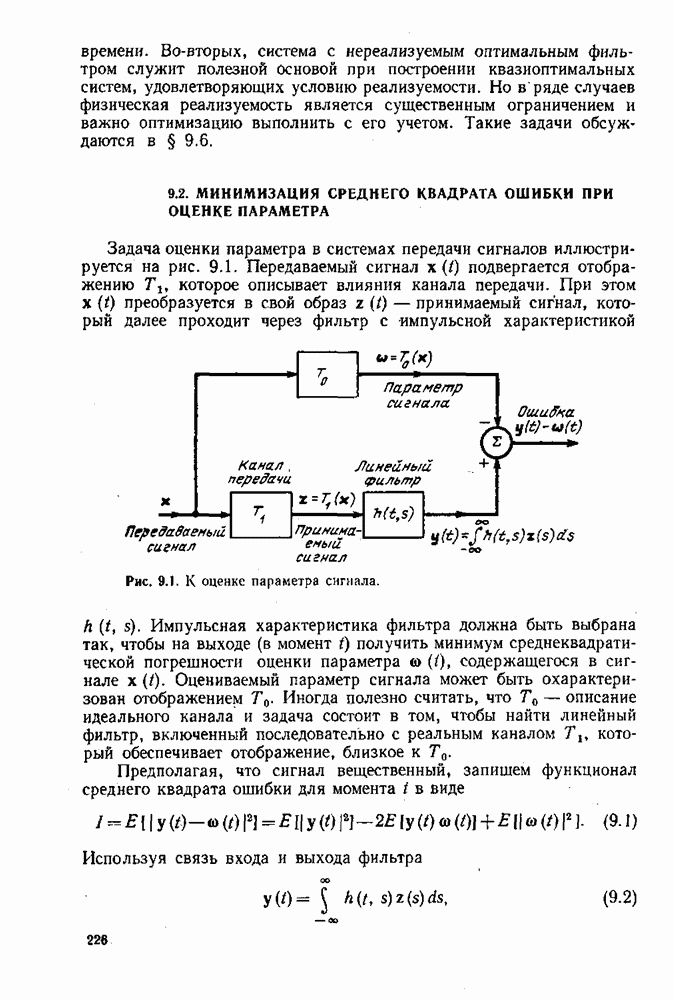
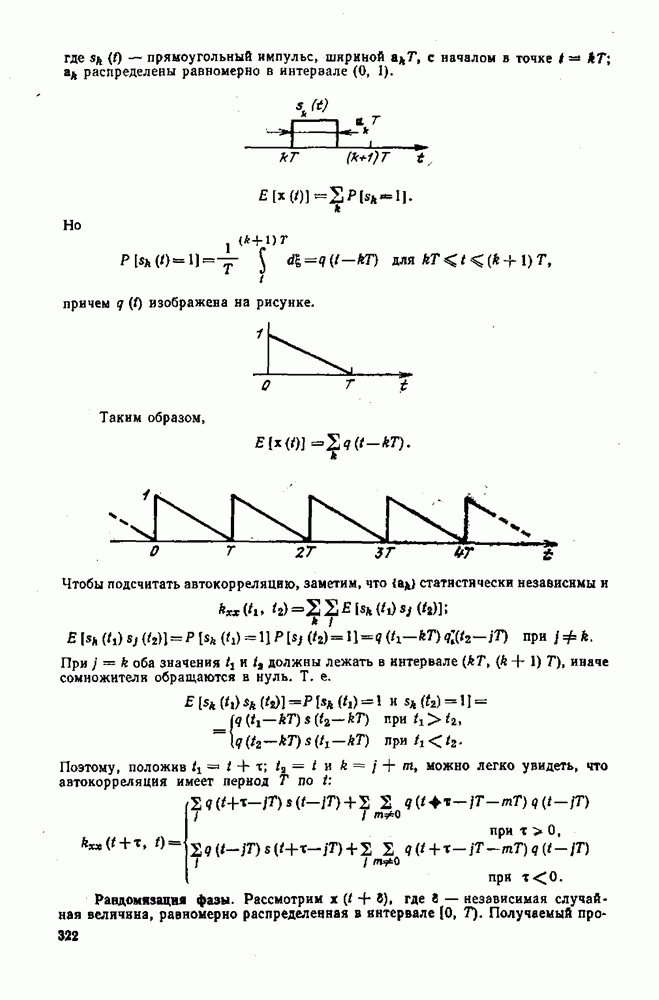
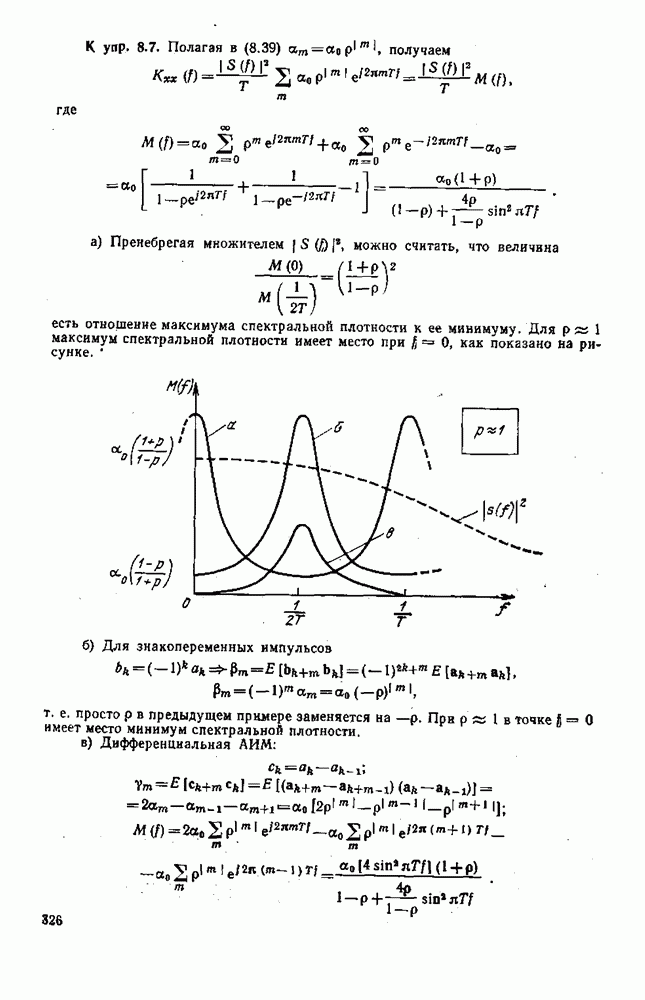
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4. ВАРИАЦИОННАЯ ЗАДАЧА БЕЗ ОГРАНИЧЕНИЙ
В строгой формулировке задача оптимизации сигнала состоит в нахождении сигнала  максимизирующего или минимизирующего функционал
максимизирующего или минимизирующего функционал  Это вариационная задача без дополнительных ограничений. Мы рассмотрим такую задачу, чтобы выявить вариационные методы отыскания необходимых условий, которым должно удовлетворять решение. Если х — вещественная переменная, а не функция, мы просто должны найти точки, в которых
Это вариационная задача без дополнительных ограничений. Мы рассмотрим такую задачу, чтобы выявить вариационные методы отыскания необходимых условий, которым должно удовлетворять решение. Если х — вещественная переменная, а не функция, мы просто должны найти точки, в которых  и вычислить значения
и вычислить значения  во всех этих точках, чтобы установить, где достигается максимум, а где минимум. Если х — вектор, то произвольное приращение х — также вектор, и величина приращения I неодкозначна, она зависит от направления. Иными словами, мы не можем однозначно определить производную от
во всех этих точках, чтобы установить, где достигается максимум, а где минимум. Если х — вектор, то произвольное приращение х — также вектор, и величина приращения I неодкозначна, она зависит от направления. Иными словами, мы не можем однозначно определить производную от  в точке х. Единственное, что можно сделать, это вычислить приращение 1 при изменении х вдоль определенного направления. Пусть х и
в точке х. Единственное, что можно сделать, это вычислить приращение 1 при изменении х вдоль определенного направления. Пусть х и  — элементы нормированного линейного пространства, и
— элементы нормированного линейного пространства, и  тогда для действительного
тогда для действительного  производная по направлению от I по х вдоль и определяется следующим образом:
производная по направлению от I по х вдоль и определяется следующим образом:

причем предполагается, что этот предел существует, если  непрерывный функционал.
непрерывный функционал.
Теперь потребуем, чтобы в стационарной точке функционала  (например, в
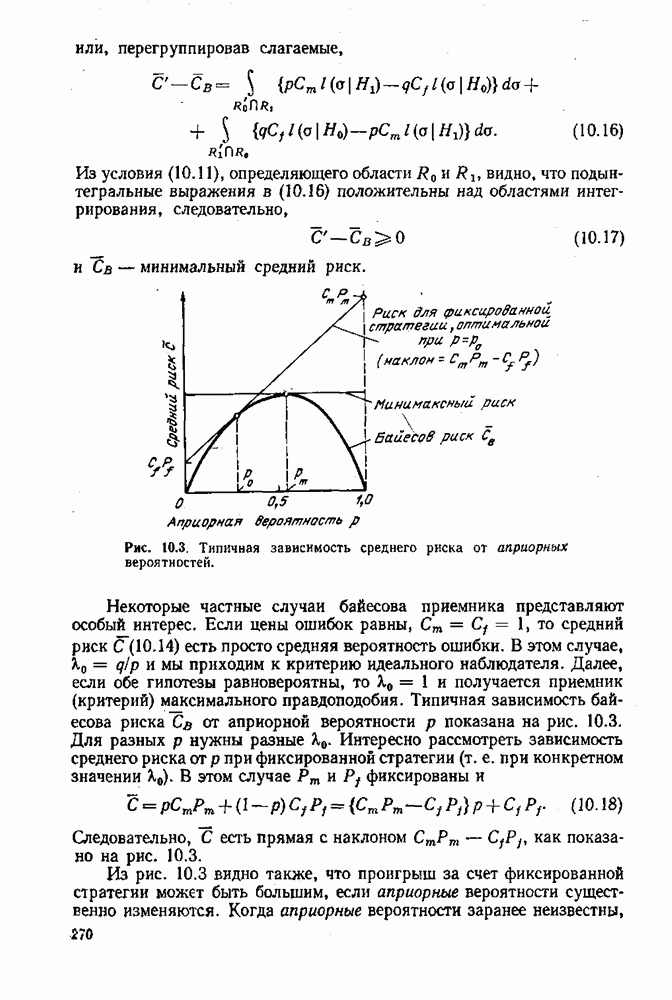
(например, в  производная по направлению
производная по направлению  обращалась в нуль для всевозможных и.
обращалась в нуль для всевозможных и.
В противном случае, если  , то при достаточно малом
, то при достаточно малом  величина
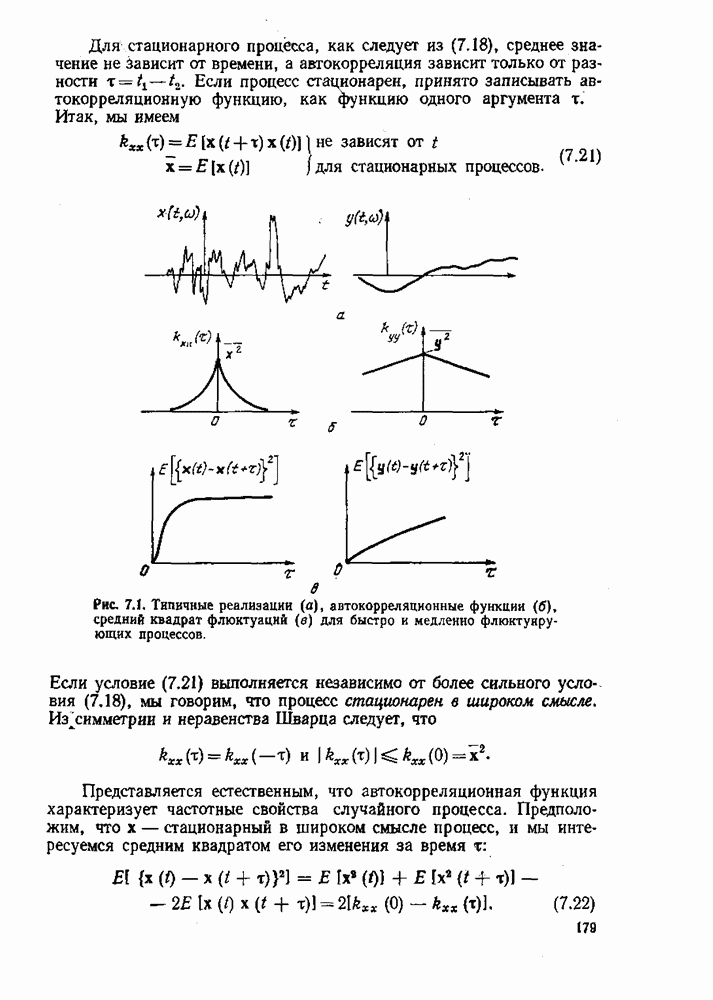
величина  может быть как больше, так и меньше, чем
может быть как больше, так и меньше, чем  Поскольку для характеристики сигналов мы будем использовать линейные и квадратичные функционалы, заметим, что
Поскольку для характеристики сигналов мы будем использовать линейные и квадратичные функционалы, заметим, что

Из (6.32) видно, что производная по направлению линейного функционала не зависит от х, чего и следовало ожидать по аналогии с функциями действительного переменного. Продолжая аналогию, мы могли бы ожидать, что производная по направлению квадартичного функционала должна быть линейным функционалом от  однако из (6.33) видно, что это не совсем верно. Сказанное верно для вещественных линейных пространств, когда
однако из (6.33) видно, что это не совсем верно. Сказанное верно для вещественных линейных пространств, когда  . В этой связи было бы желательно ограничиться вещественными пространствами. Хотя рассмотрение только вещественных функционалов от вещественных сигналов не вносит ограничения с практической точки зрения, важно, чтобы мы могли рассматривать и функционалы, аргументами которых являются комплексные функции. Например,
. В этой связи было бы желательно ограничиться вещественными пространствами. Хотя рассмотрение только вещественных функционалов от вещественных сигналов не вносит ограничения с практической точки зрения, важно, чтобы мы могли рассматривать и функционалы, аргументами которых являются комплексные функции. Например,  может быть комплексным для вещественного сигнала. Заметим, однако, что вещественное пространство может иметь комплексные базисные функции при условии, что все скаляры (скалярные произведения) вещественны. Если мы ограничим область допустимых функций частоты, такими, что
может быть комплексным для вещественного сигнала. Заметим, однако, что вещественное пространство может иметь комплексные базисные функции при условии, что все скаляры (скалярные произведения) вещественны. Если мы ограничим область допустимых функций частоты, такими, что  , то все линейные функционалы и все квадратичные функционалы, соответствующие операторам во временной области, будут вещественными и, кроме того,
, то все линейные функционалы и все квадратичные функционалы, соответствующие операторам во временной области, будут вещественными и, кроме того,  для всех допустимых X и Y. Главное преимущество подобного рассмотрения, ограниченного вещественными пространствами, состоит в том, что в этом случае все производные по направлению от функционалов можно выразить через вектор градиента.
для всех допустимых X и Y. Главное преимущество подобного рассмотрения, ограниченного вещественными пространствами, состоит в том, что в этом случае все производные по направлению от функционалов можно выразить через вектор градиента.
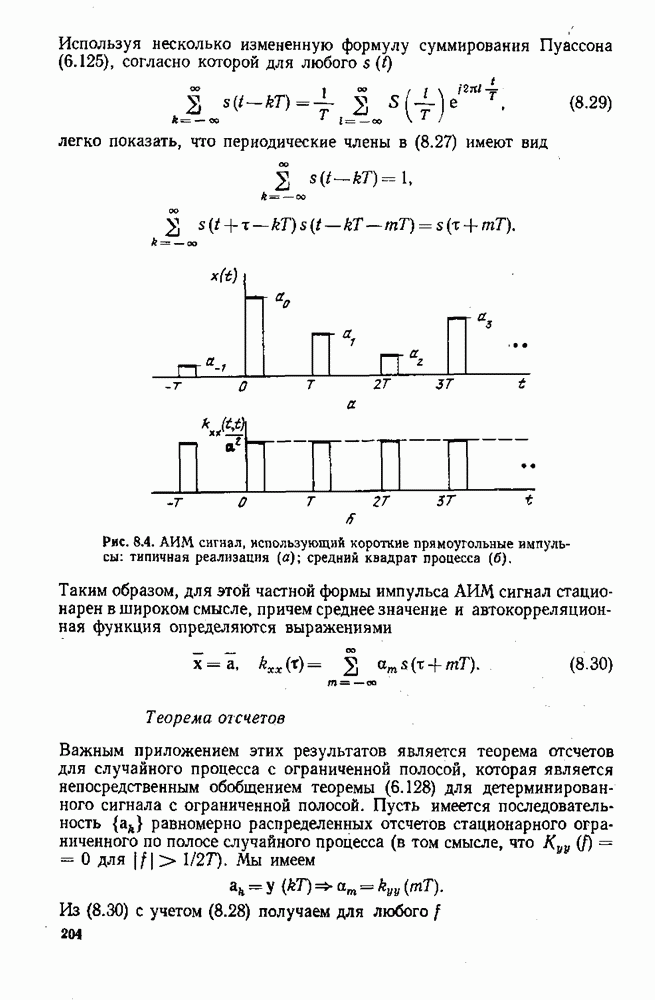
Градиент линейного и квадратичного функционалов
Пусть  — полная ортонормальная система в вещественном пространстве и пусть
— полная ортонормальная система в вещественном пространстве и пусть  — вещественный функционал. Положим
— вещественный функционал. Положим

Теперь, предполагая, что  есть непрерывная функция от х при любом и, мы можем написать
есть непрерывная функция от х при любом и, мы можем написать

где вектор  может зависеть от х, но не от
может зависеть от х, но не от  :
:

где 
В любой точке производную по направлению и всегда можно выразить как скалярное произведение векторов  . Вектор
. Вектор  называется грйдиентом
называется грйдиентом 
Из неравенства Шварца мы имеем

где равенство достигается только в случае, когда и пропорционально  при этом величина производной по направлению максимальна и равна норме вектора градиента. Некоторые численные методы отыскания стационарных точек функционала используют последовательные приближения и состоят в вычислении значений функционала в последовательных точках, причем перемещение от точки к точке каждый раз происходит вдоль вектора градиента. При этом предполагается, что мы быстрее всего достигнем экстремума, если будем двигаться на каждом шаге по направлению максимального изменения функционала. Эти методы называются методами наискорейшего спуска (или подъема).
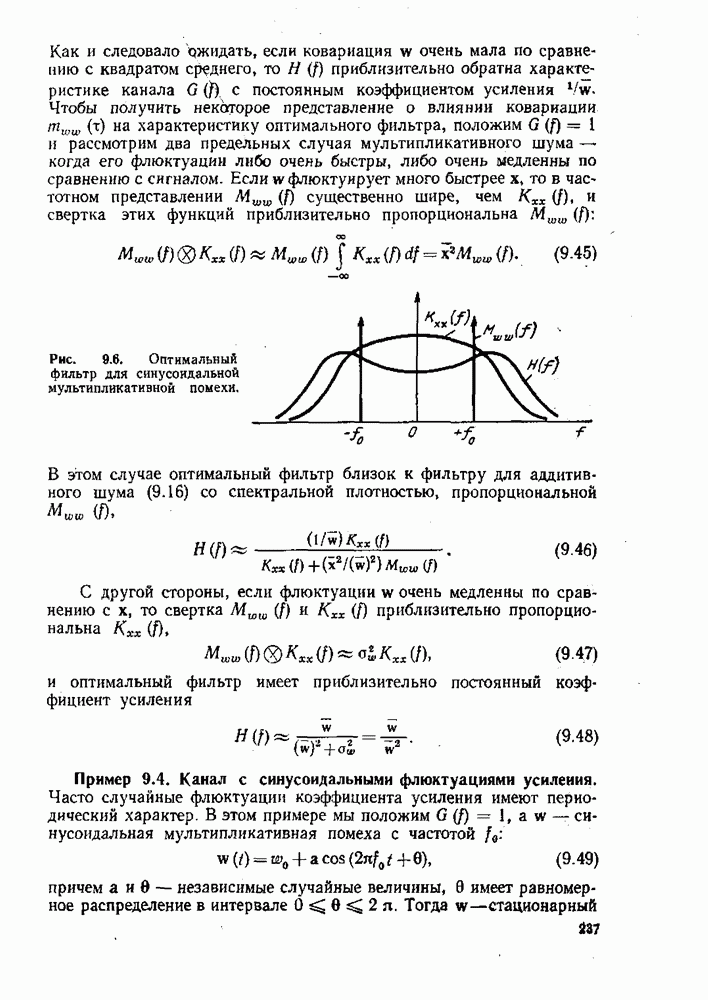
при этом величина производной по направлению максимальна и равна норме вектора градиента. Некоторые численные методы отыскания стационарных точек функционала используют последовательные приближения и состоят в вычислении значений функционала в последовательных точках, причем перемещение от точки к точке каждый раз происходит вдоль вектора градиента. При этом предполагается, что мы быстрее всего достигнем экстремума, если будем двигаться на каждом шаге по направлению максимального изменения функционала. Эти методы называются методами наискорейшего спуска (или подъема).
Сравнивая (6.32) и (6.34), мы видим, что в случае вещественного линейного функционала градиент имеет вид

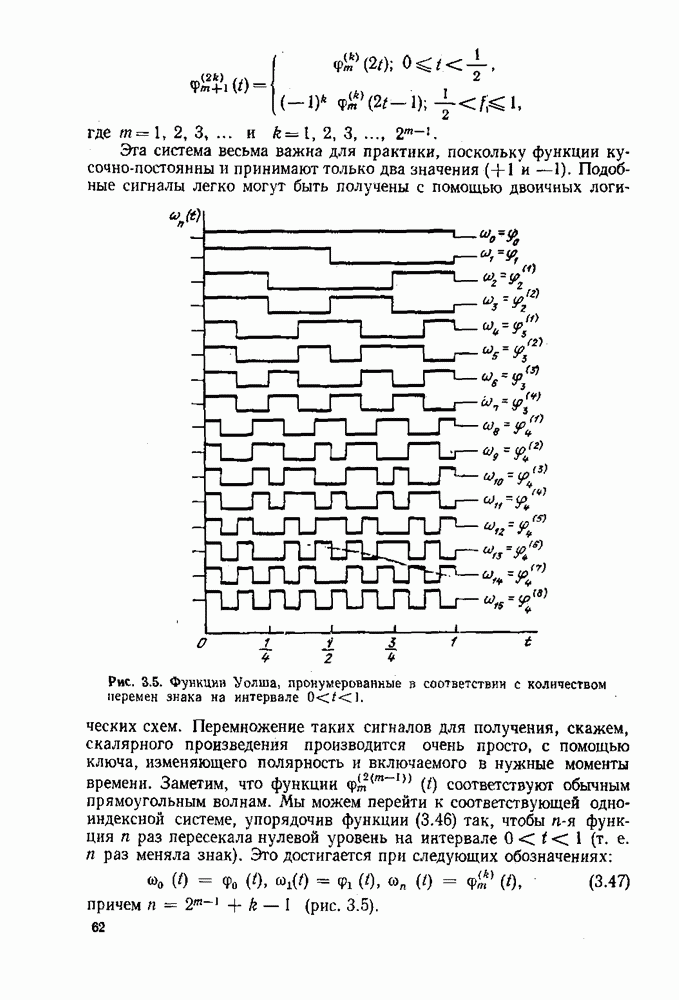
а из (6,33) находим градиент для вещественного квадратичного функционала

Предположим, что задача оптимизации состоит в отыскании экстремума функционала, представляющего собой линейную комбинацию квадратичного и линейного функционалов. Тогда

где

Необходимым условием экстремума является существование стационарной точки функционала  т. е. точки, в которой
т. е. точки, в которой  обращается в нуль. Дейстаител
обращается в нуль. Дейстаител  при всех и тогда и только тогда, когда
при всех и тогда и только тогда, когда  Следовательно, необходимое условие экстремума есть
Следовательно, необходимое условие экстремума есть

или, в частотной форме,

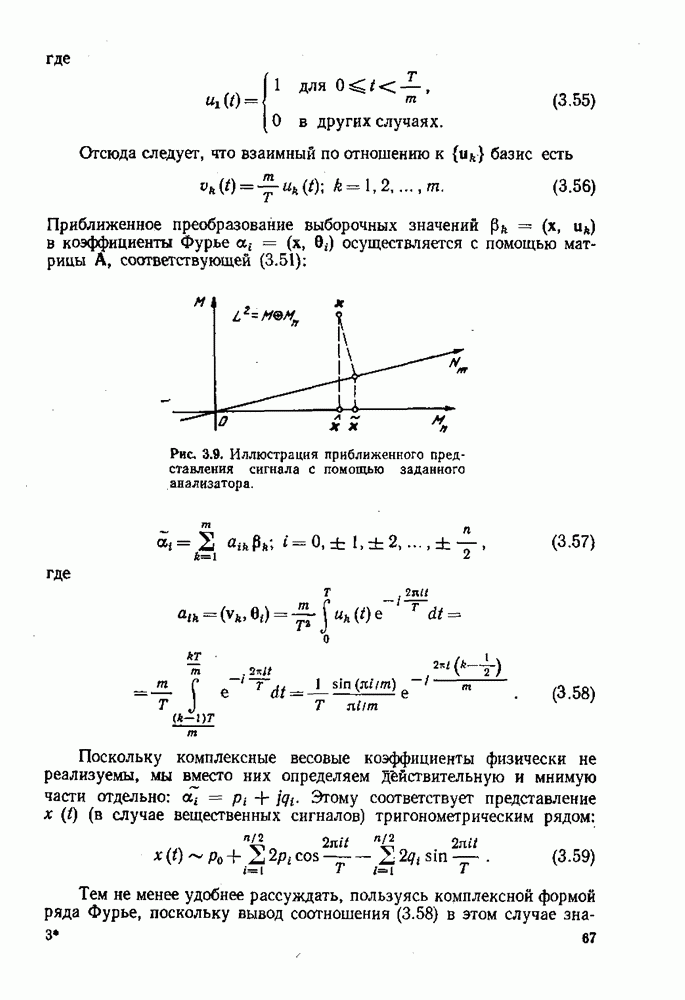
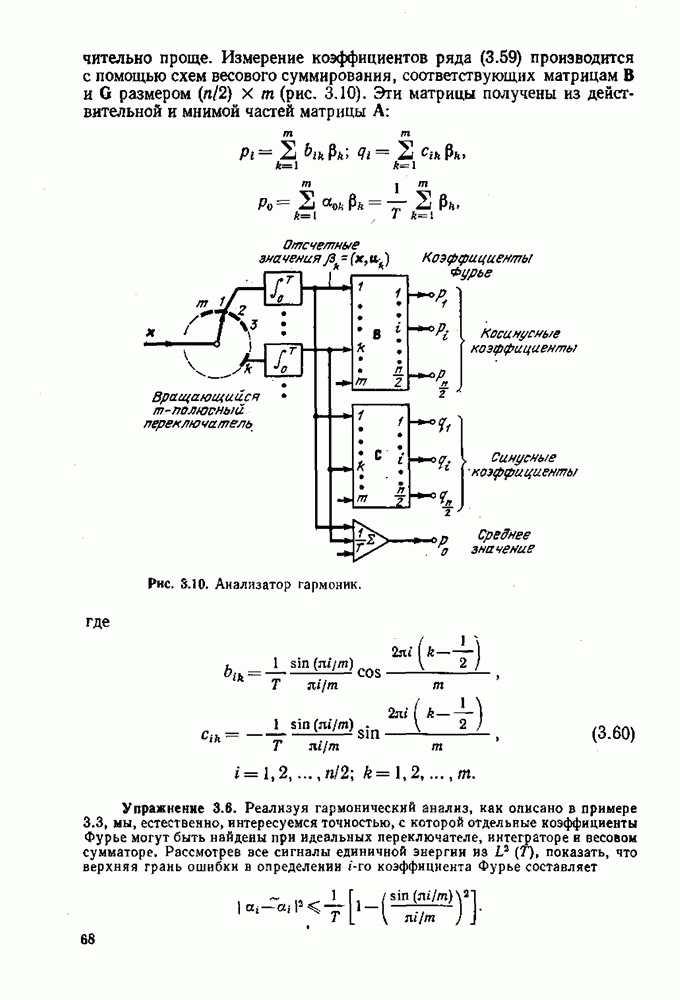
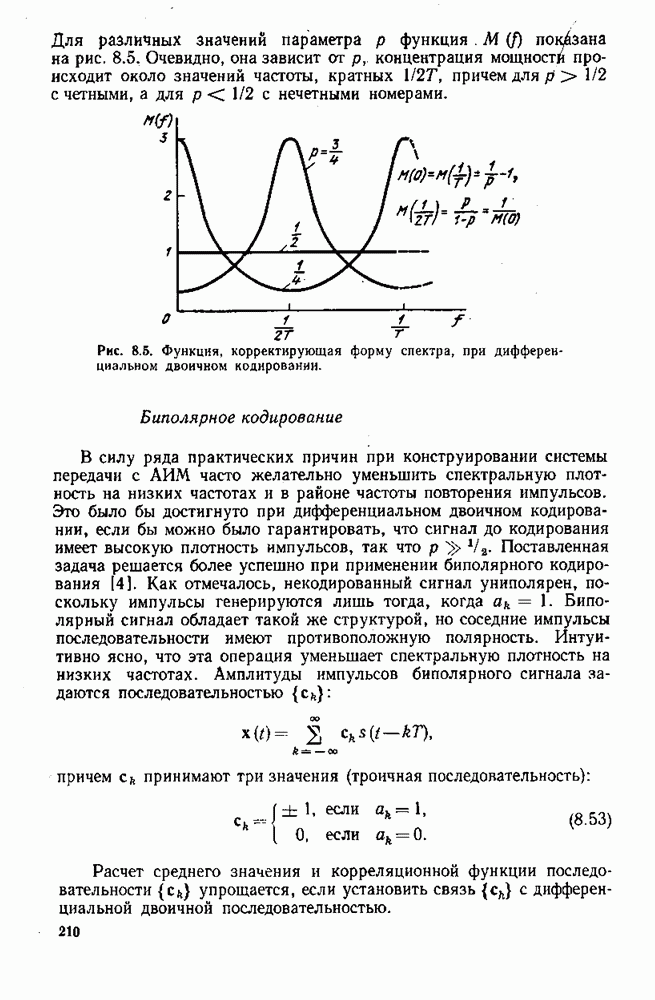
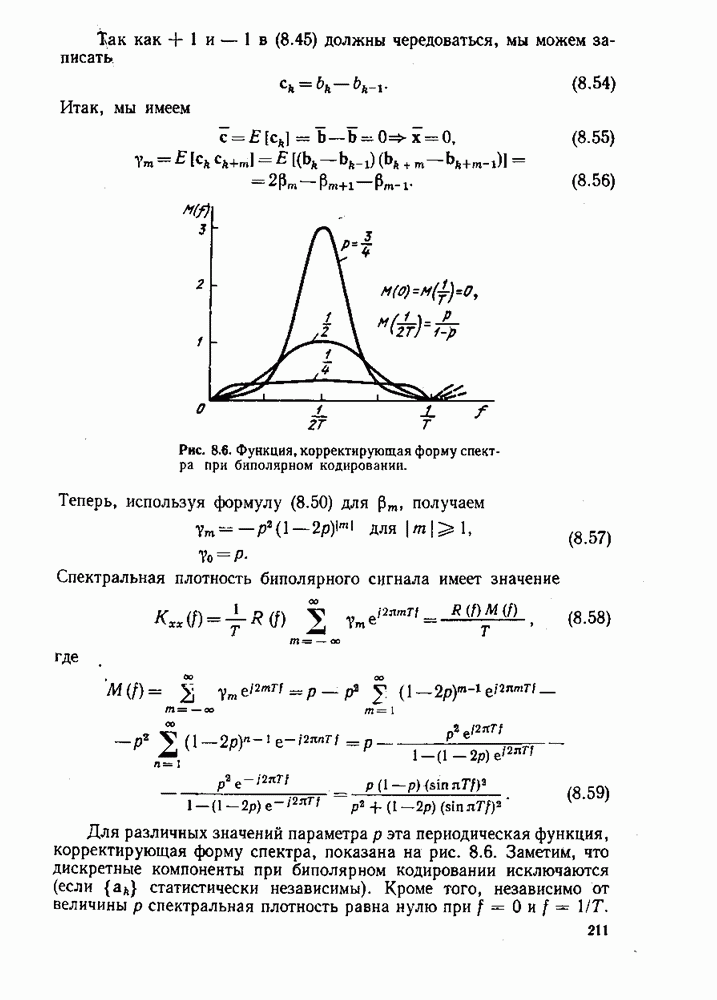
На основании этих условий можно сделать несколько общих замечаний о задаче поиска экстремума. Если ограничиться функционалами, состоящими из линейных и квадратичных функционалов, то необходимые условия экстремума выражаются линейными уравнениями (в общем случае интегральными уравнениями Фредгольма), для решения которых известен ряд методов [2], Заметим, что ядро интегрального уравнения всегда самосопряженное. Если функционал не включает линейной части, получается однородное уравнение, и нетривн альное решение существует только в случае, если оператор  сингулярный. Кроме того, если А — самосопряженный оператор, то для однородного случая
сингулярный. Кроме того, если А — самосопряженный оператор, то для однородного случая  в стационарной точке.
в стационарной точке.
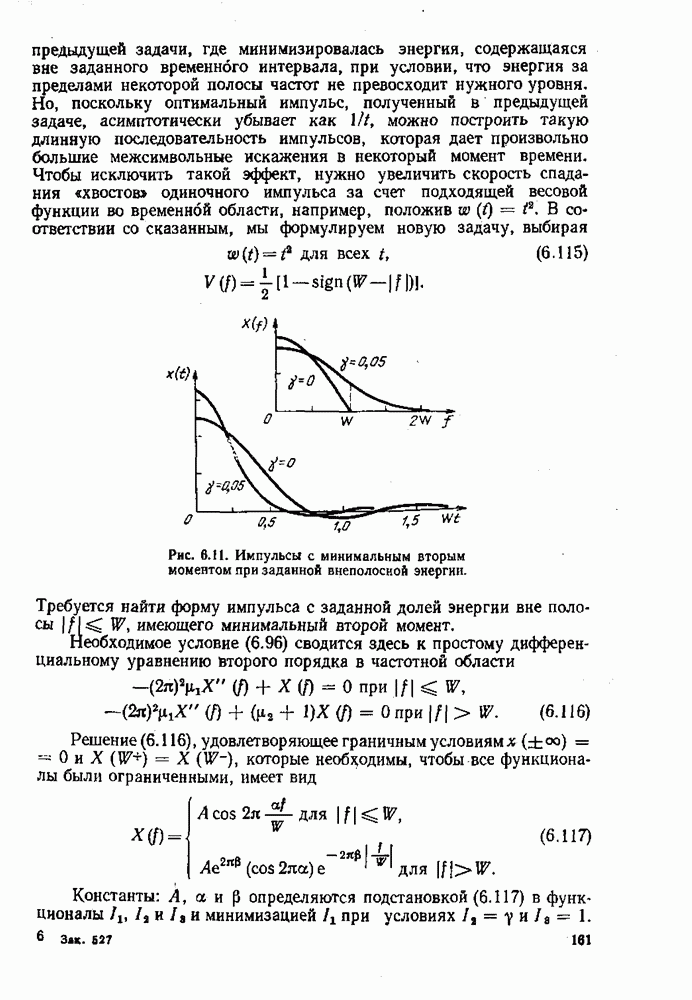
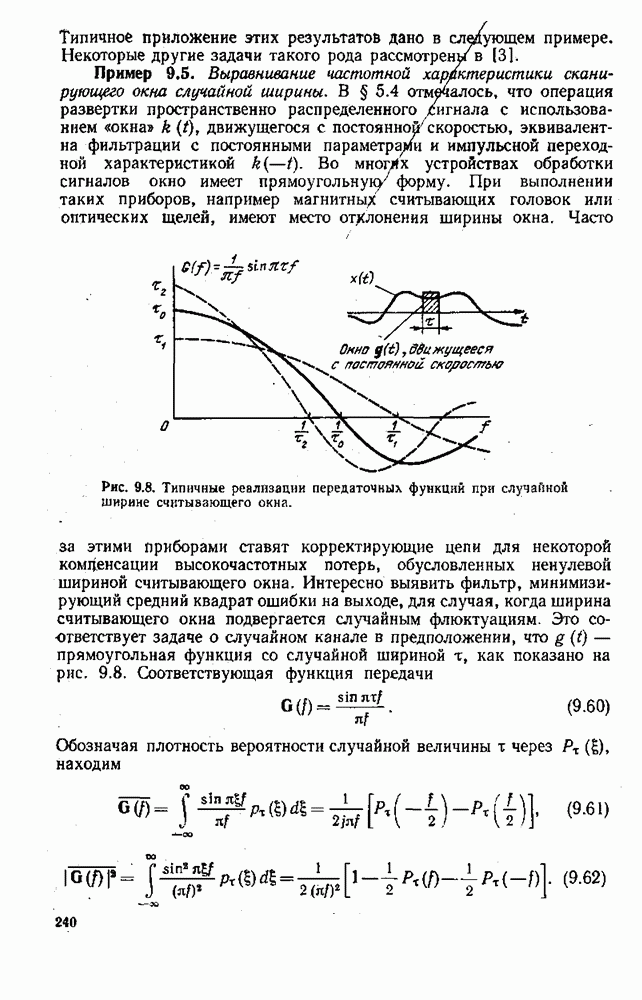
Практически задача редко ставится в сформулированном виде, без ограничений на допустимые функции. Такие практические условия, как, например, конечная величина энергии сигнала, обычно ограничивают область допустимых решений. Иными словами, функции, максимизирующие (минимизирующие) функционал, должны одновременно удовлетворять некоторым дополнительным условиям, К счастью, с помощью метода множителей Лагранжа необходимые условия в задаче с ограничениями получаются в основном таким же путем, как в задаче без ограничений. Этот метод рассмотрен в следующем параграфе.
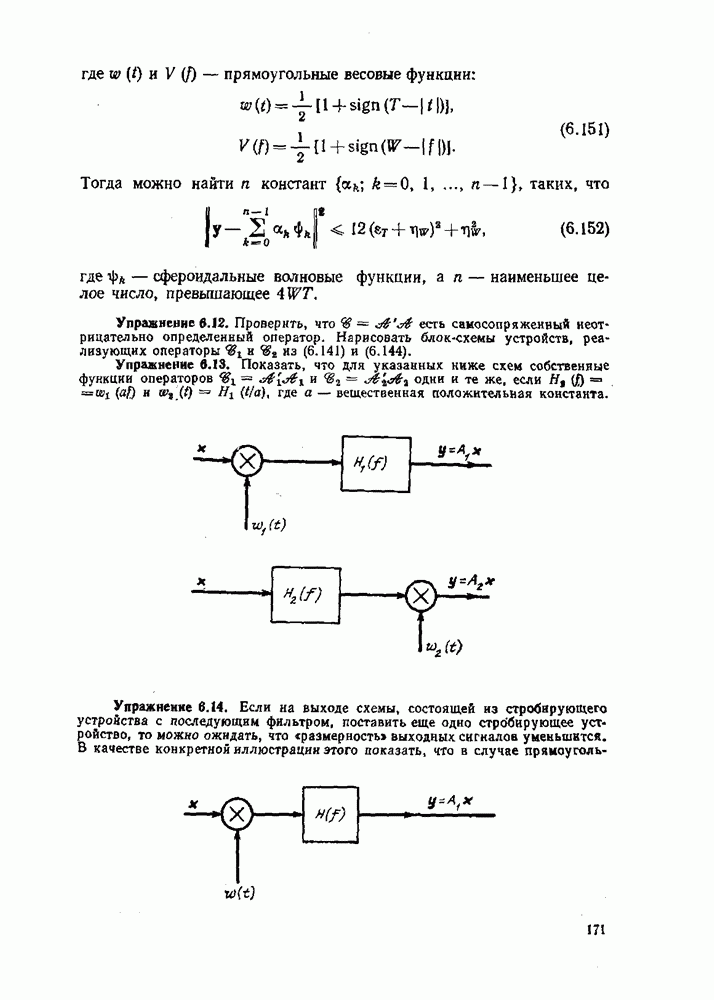
Упражнение 6.1. Показать, что для непрерывного комплексного функционала  определенного на пространстве со скалярным произведением, производная по направлению (комплексная) имеет вид
определенного на пространстве со скалярным произведением, производная по направлению (комплексная) имеет вид

где  и
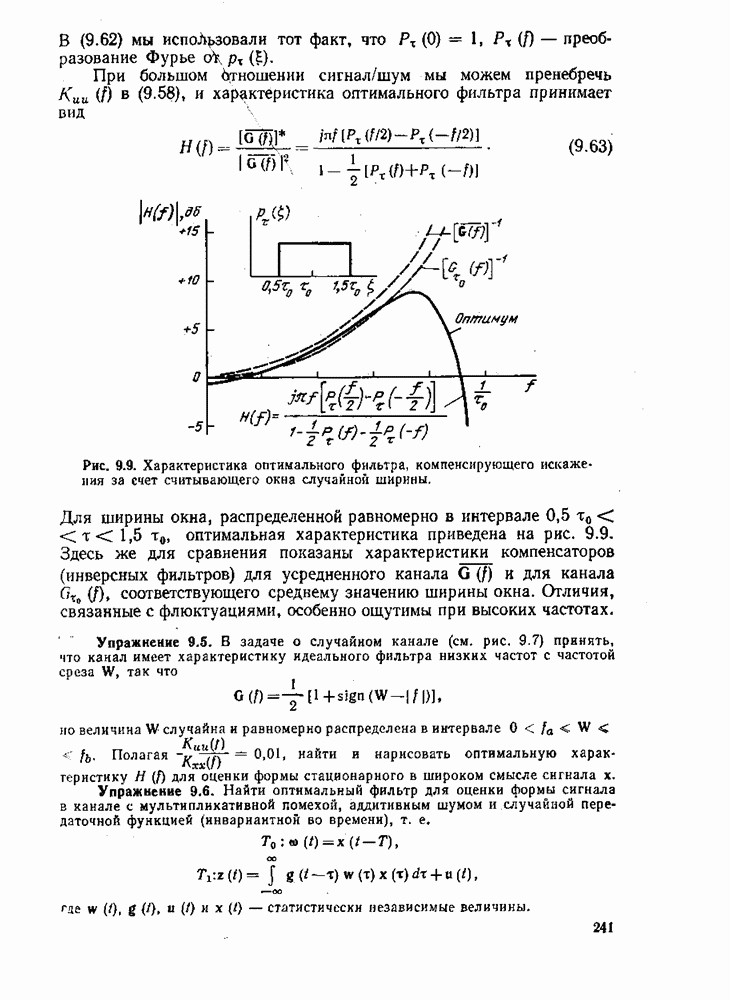
и  могут зависеть от х, но не от
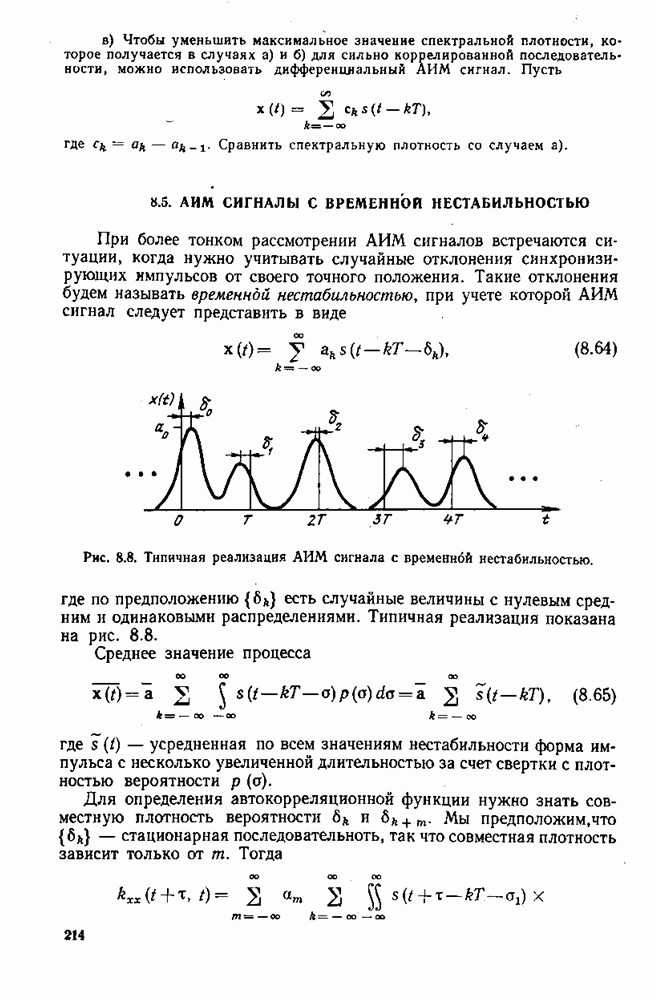
могут зависеть от х, но не от  .
.
Упражнение 6.2. Показать, что, если — ограниченный оператор, то производная  направлению от функционала
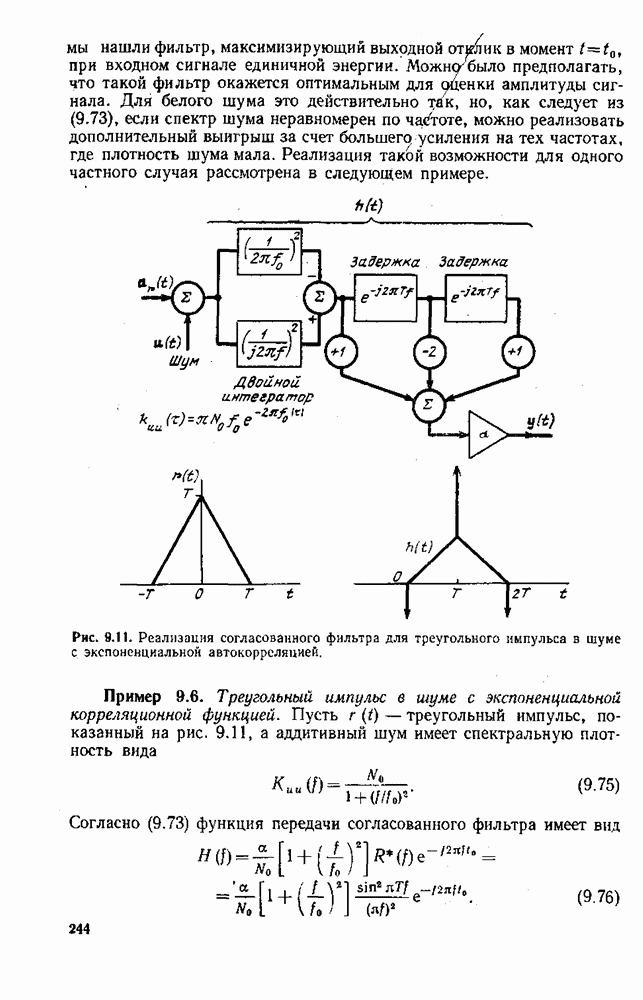
направлению от функционала  в (6.33) есть непрерывный функционал от х при любом и,
в (6.33) есть непрерывный функционал от х при любом и,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- 1. ВВЕДЕНИЕ
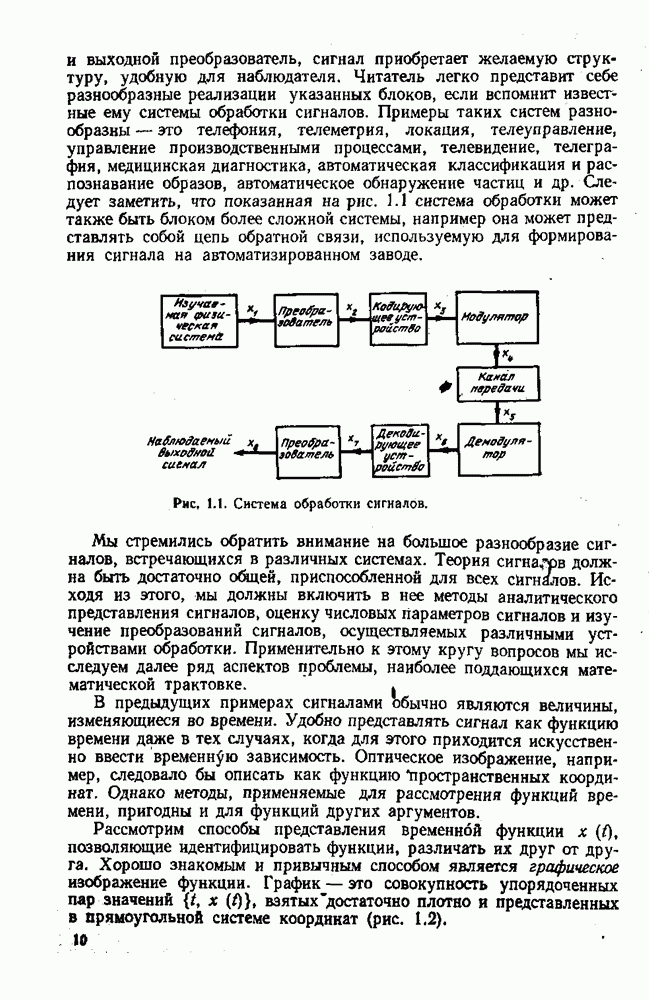
- 1.1. СИСТЕМЫ ОБРАБОТКИ СИГНАЛОВ
- 1.2. МНОЖЕСТВА СИГНАЛОВ
- 1.3. ОТОБРАЖЕНИЯ И ФУНКЦИОНАЛЫ
- 2 ПРОСТРАНСТВА СИГНАЛОВ
- 2.1. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
- 2.2. СХОДИМОСТЬ И НЕПРЕРЫВНОСТЬ
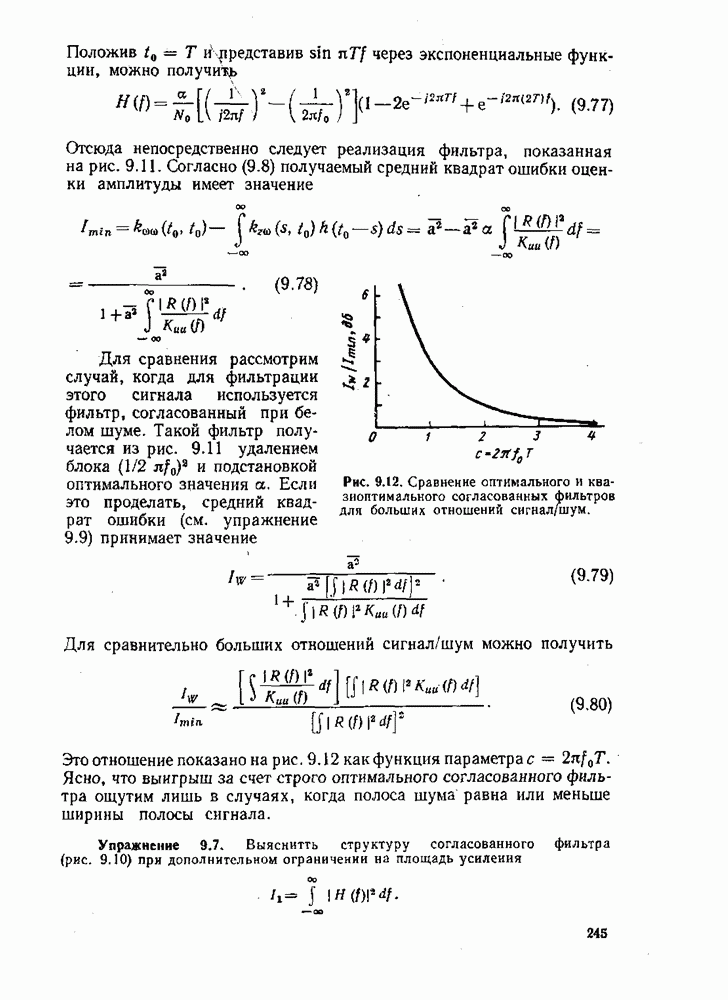
- 2.3. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 2.4. НОРМИРОВАННЫЕ ЛИНЕИНЫЕ ПРОСТРАНСТВА
- 2.5. ПРОСТРАНСТВА СО СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ
- 2.6. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
- 3. ДИСКРЕТНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
- 3.1. ПОДПРОСТРАНСТВА ИЗ L2(T)
- 3.2. ПОЛНЫЕ ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ
- 3.3. ПРИМЕРЫ ПОЛНЫХ ОРТОНОРМАЛЬНЫХ СИСТЕМ
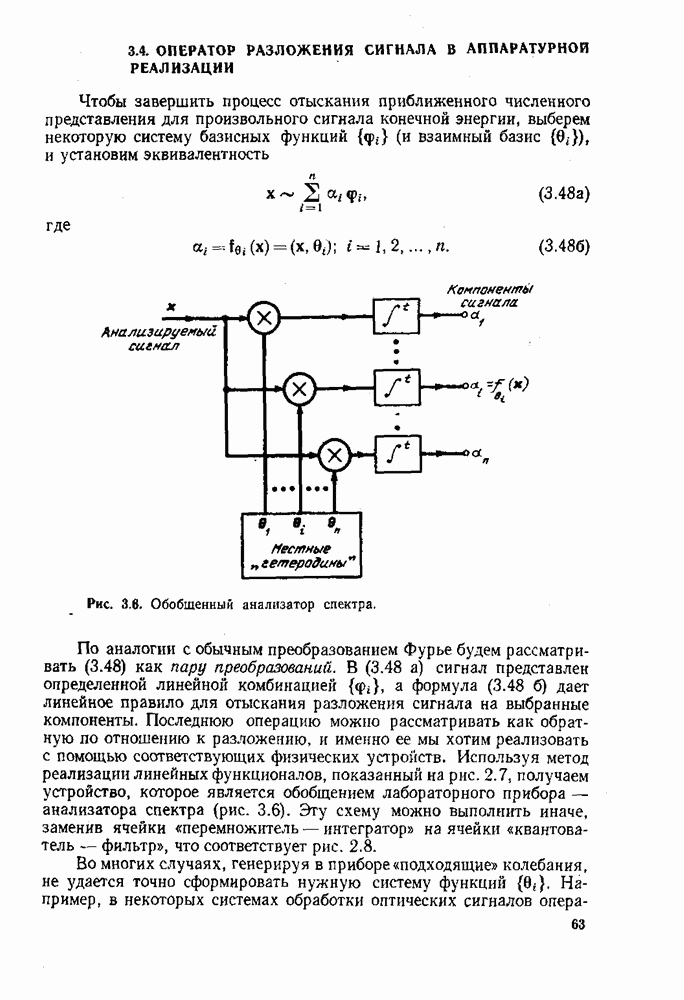
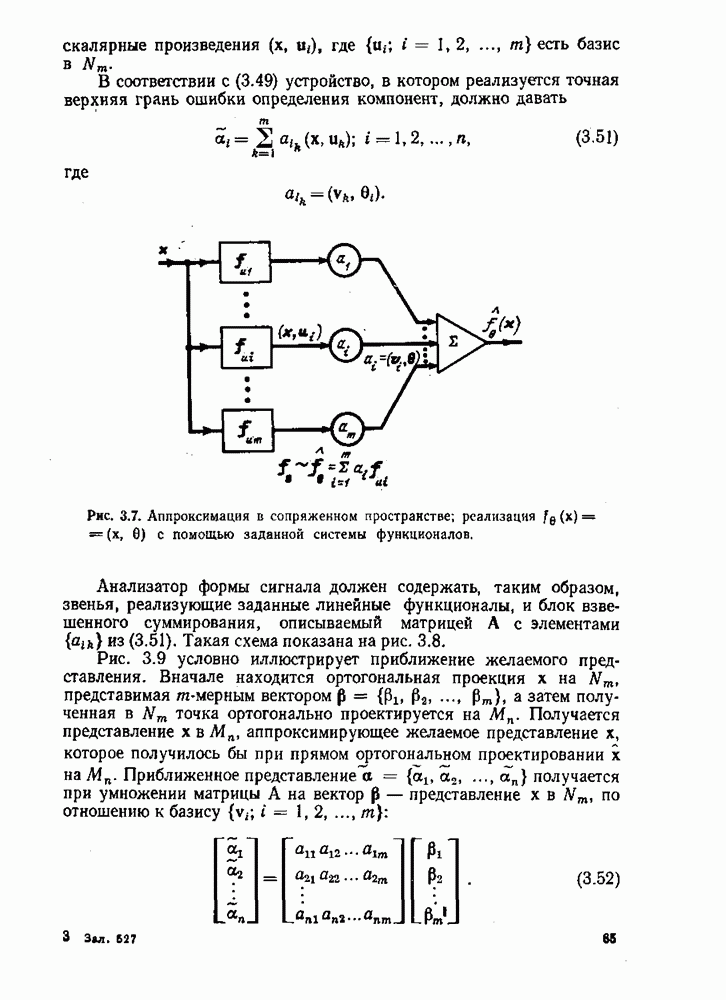
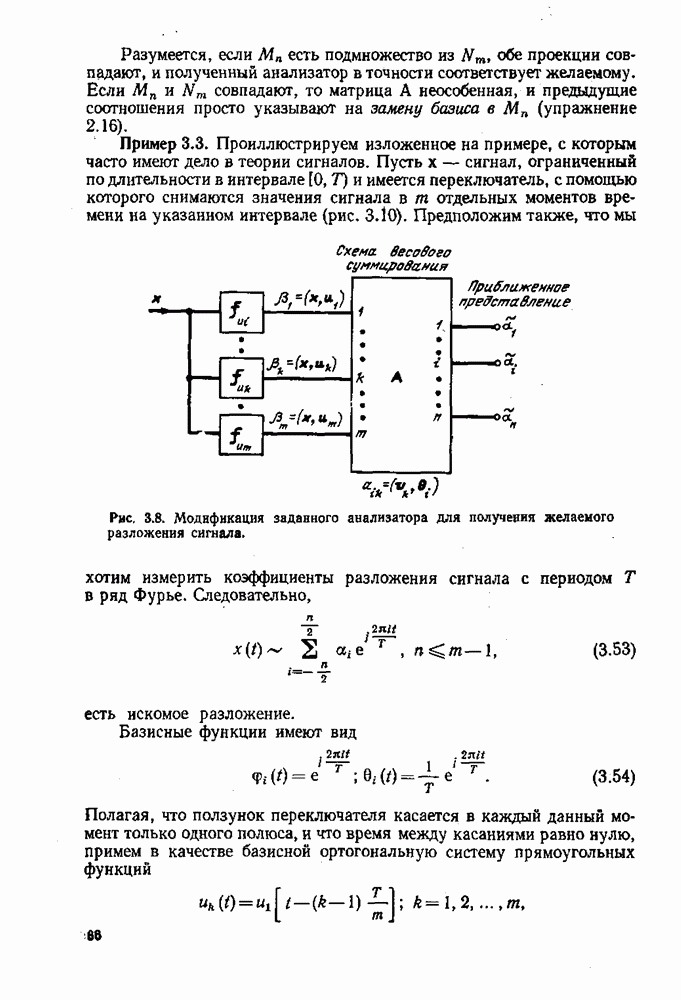
- 3.4. ОПЕРАТОР РАЗЛОЖЕНИЯ СИГНАЛА В АППАРАТУРНОЙ РЕАЛИЗАЦИИ
- 4. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
- 4.2. БАЗИСНЫЕ И СОПРЯЖЕННЫЕ БАЗИСНЫЕ ЯДРА
- 4.3. ПРЕОБРАЗОВАНИЯ ФУРЬЕ, ГИЛЬБЕРТА И ДРУГИЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРЕДСТАВЛЕНИЕ УЗКОПОЛОСНЫХ СИГНАЛОВ
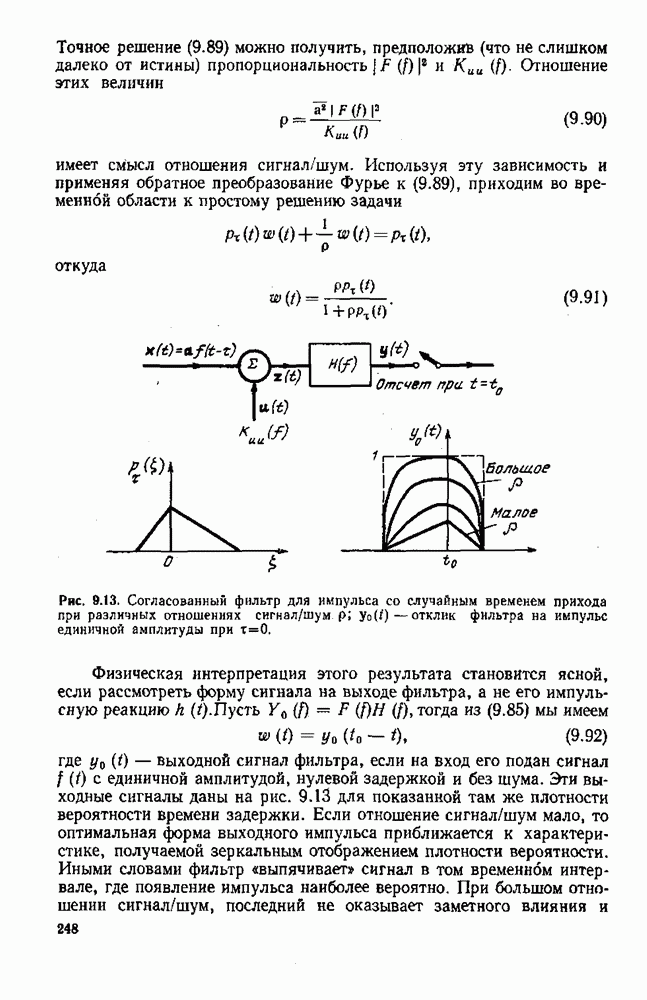
- Полосовая фильтрация
- Радиолокационная функция неопределенности
- 5. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ
- 5.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
- 5.3. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ, ДЕЙСТВУЮЩИХ В КОНЕЧНОМЕРНОМ ПРОСТРАНСТВЕ
- 5.4 ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ, ДЕЙСТВУЮЩИХ В ПРОСТРАНСТВЕ L2(T)
- 5.5. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ, ДЕЙСТВУЮЩИХ В L2(T)
- 5.6 РЕАЛИЗАЦИЯ ВЫРОЖДЕННЫХ ОПЕРАТОРОВ
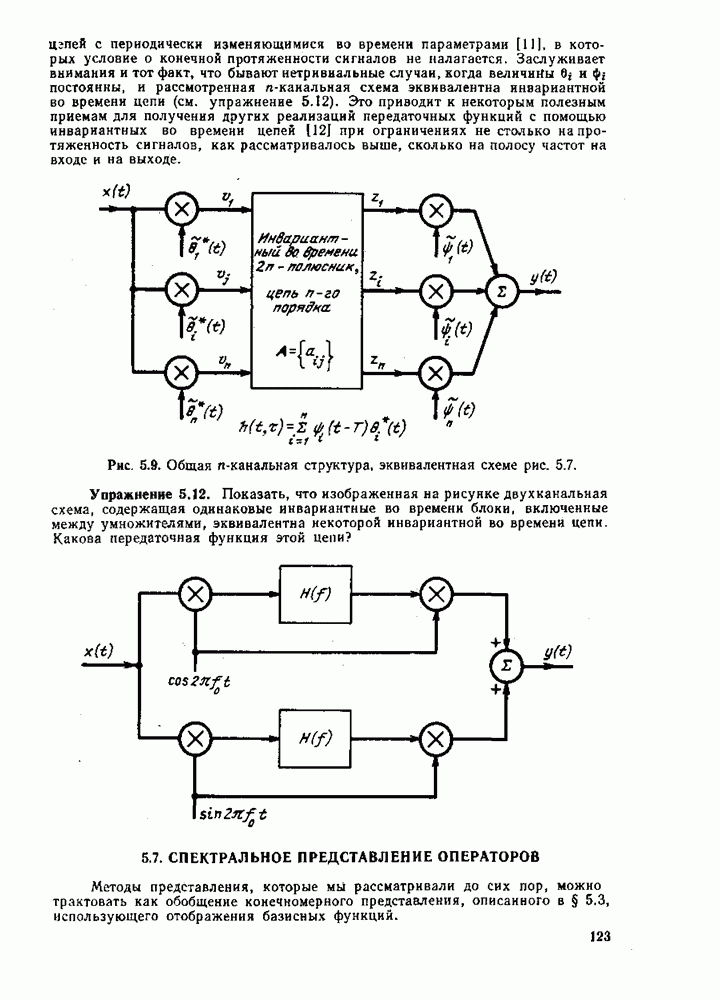
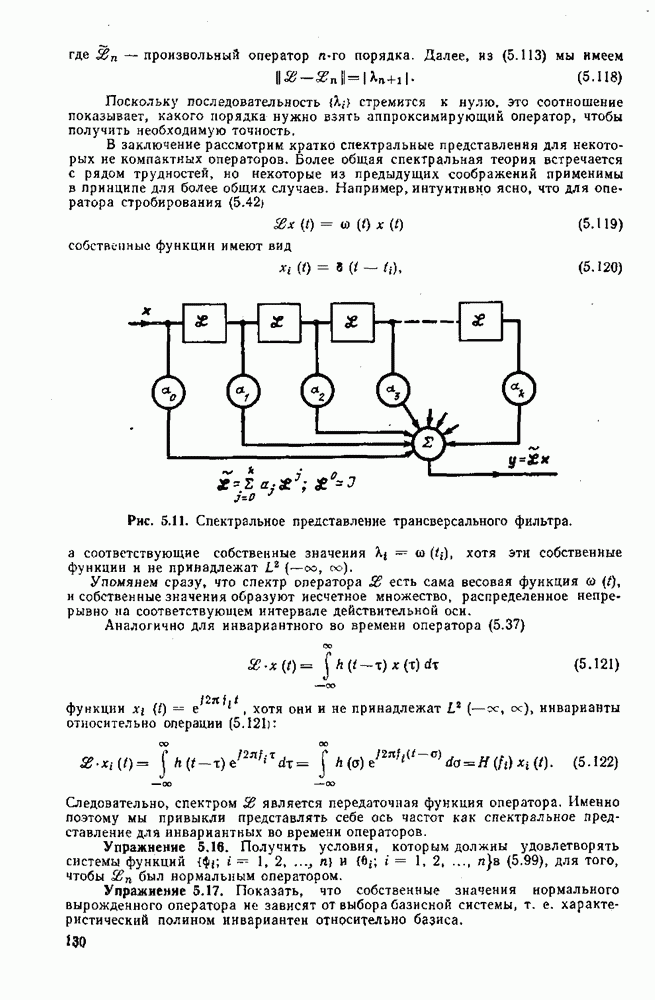
- 5.7. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ
- Собственные значения и собственные пространства
- Сопряженный оператор
- Спектральное представление нормальных вырожденных операторов
- Спектральное представление нормальных компактных операторов
- 6. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ
- 6.2. КВАДРАТИЧНЫЕ ФУНКЦИОНАЛЫ
- 6.3. НЕКОТОРЫЕ ХАРАКТЕРНЫЕ КВАДРАТИЧНЫЕ ФУНКЦИОНАЛЫ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
- 6.4. ВАРИАЦИОННАЯ ЗАДАЧА БЕЗ ОГРАНИЧЕНИЙ
- 6.5. ВАРИАЦИОННАЯ ЗАДАЧА ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
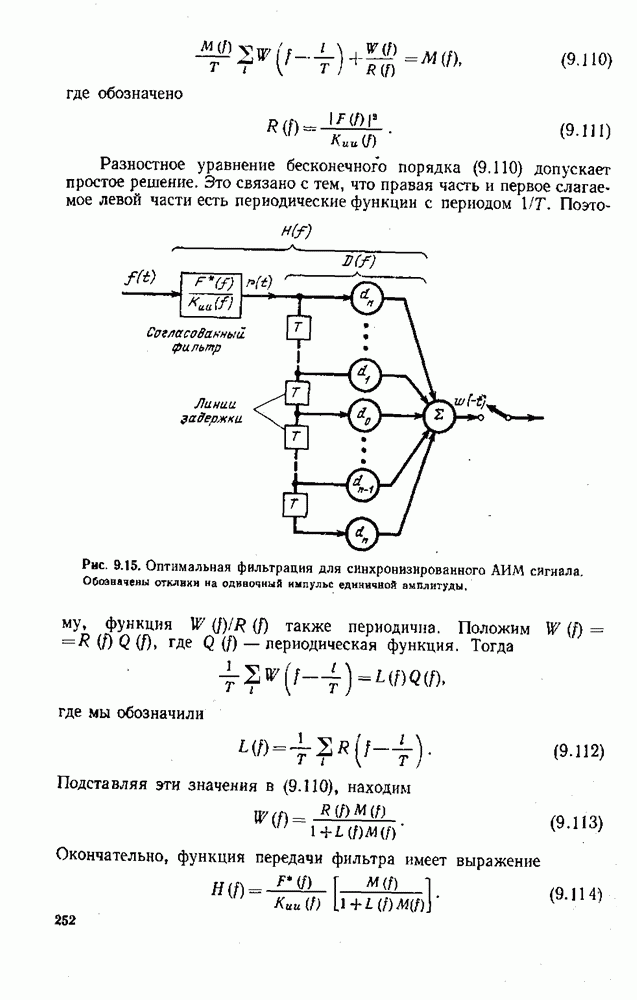
- 6.6. НЕКОТОРЫЕ ПРИМЕРЫ
- 6.7. ОБЛАСТЬ, ЗАНИМАЕМАЯ СИГНАЛОМ НА ПЛОСКОСТИ ВРЕМЯ-ЧАСТОТА
- Межсимвольные искажения
- Синхронные импульсные последовательности, критерий Найквиста, теорема отсчетов
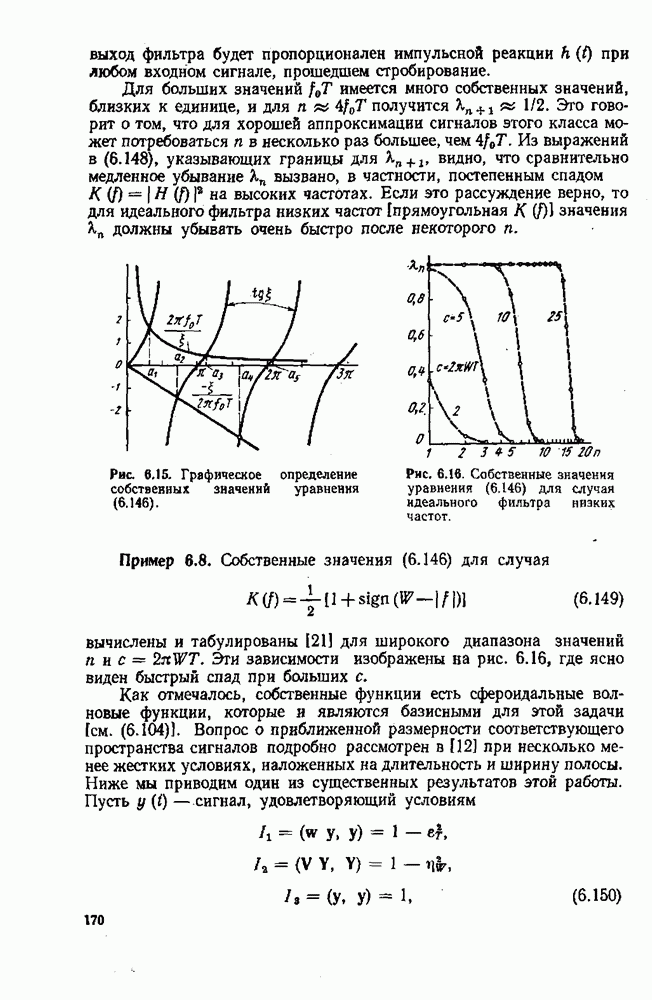
- 6.8. ПРИБЛИЖЕННОЕ ЧИСЛО ИЗМЕРЕНИЙ ПРОСТРАНСТВА СИГНАЛОВ
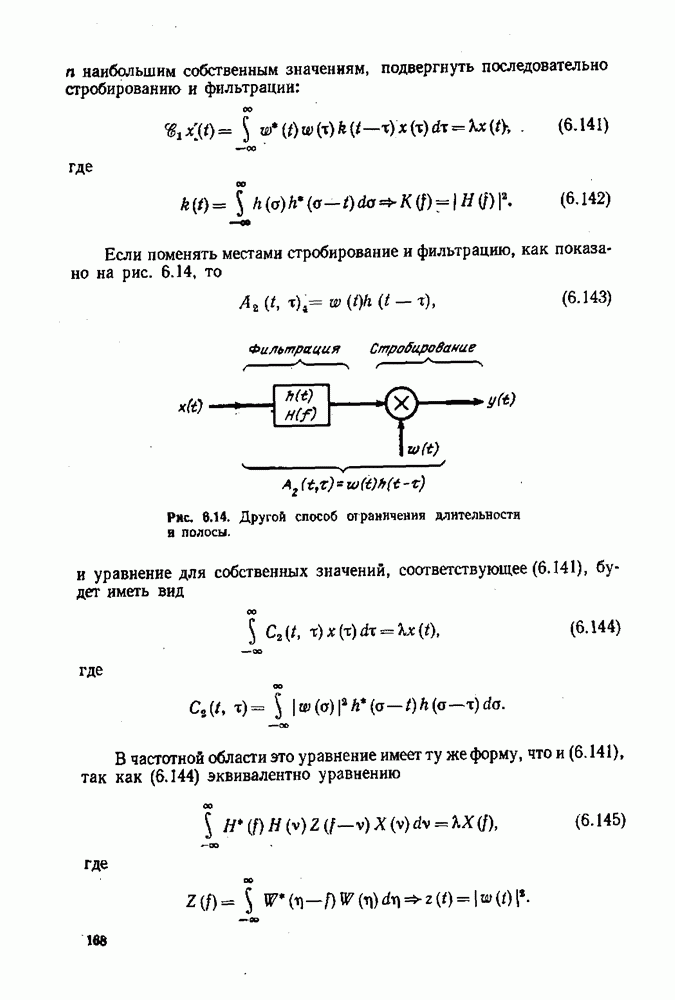
- Стробирование и фильтрация
- 7. ПРЕДСТАВЛЕНИЯ СЛУЧАЙНЫХ СИГНАЛОВ
- 7.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ОЖИДАНИЯ
- 7.3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 7.4. ДВУМЕРНЫЕ КОМПЛЕКСНЫЕ ПРОЦЕССЫ
- Спектральная плотность мощности
- 7.5. КОНЕЧНОМЕРНЫЕ ПРЕДСТАВЛЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА
- 7.6. УЗКОПОЛОСНЫЕ ПРОЦЕССЫ
- 8. МОДЕЛИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 8.2. ИМПУЛЬСНЫЕ СИГНАЛЫ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ И СЛУЧАЙНЫМ ВРЕМЕНЕМ ПРИХОДА
- 8.3. ПРОЦЕССЫ С ЦИКЛИЧЕСКОЙ СТАЦИОНАРНОСТЬЮ
- 8.4. ВЛИЯНИЕ КОДИРОВАНИЯ НА СПЕКТРАЛЬНУЮ ПЛОТНОСТЬ
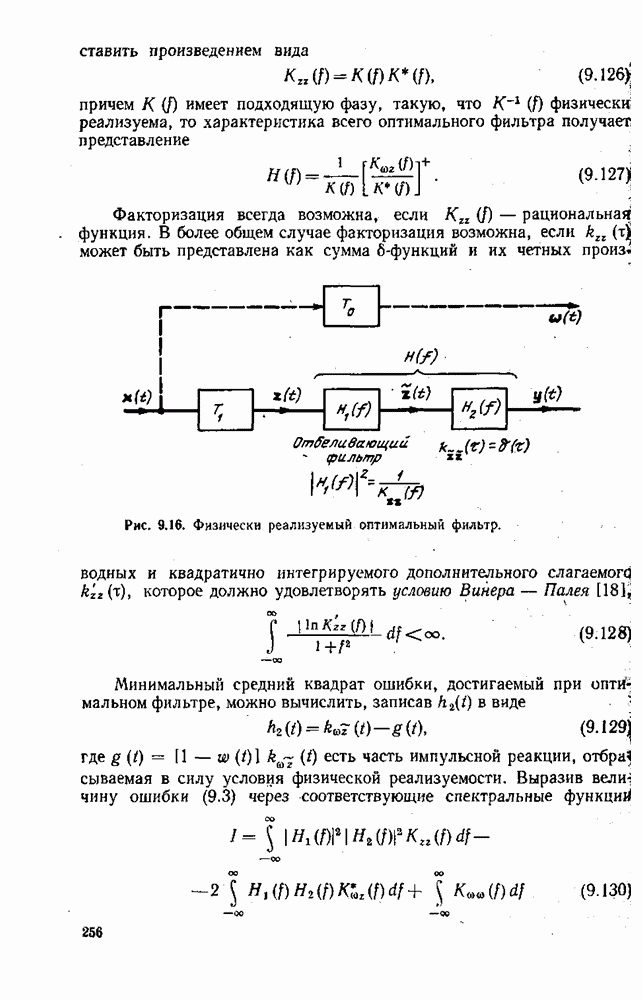
- 8.5. АИМ СИГНАЛЫ С ВРЕМЕННОЙ НЕСТАБИЛЬНОСТЬЮ
- 8.6. СИГНАЛЫ С ВРЕМЕННЫМ УПЛОТНЕНИЕМ
- 8.7. ПРОЦЕССЫ, СВЯЗАННЫЕ С ПУАССОНОВСКИМИ
- 9. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ
- 9.2. МИНИМИЗАЦИЯ СРЕДНЕГО КВАДРАТА ОШИБКИ ПРИ ОЦЕНКЕ ПАРАМЕТРА
- 9.3 НЕПРЕРЫВНАЯ ОЦЕНКА ФОРМЫ СИГНАЛА
- 9.4. ОЦЕНКА ИМПУЛЬСНЫХ АМПЛИТУД
- 9.5. ПЕРИОДИЧЕСКАЯ ОЦЕНКА ФОРМЫ СИГНАЛА
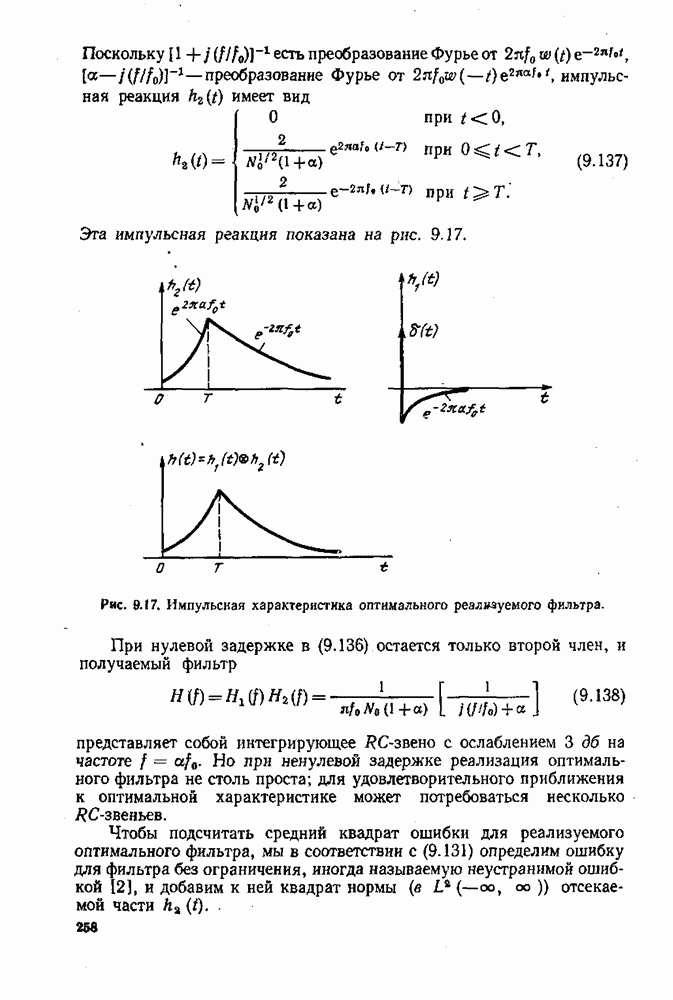
- 9.6. УСЛОВИЕ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ
- 10. ОБНАРУЖЕНИЕ СИГНАЛОВ
- 10.2. КРИТЕРИЙ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
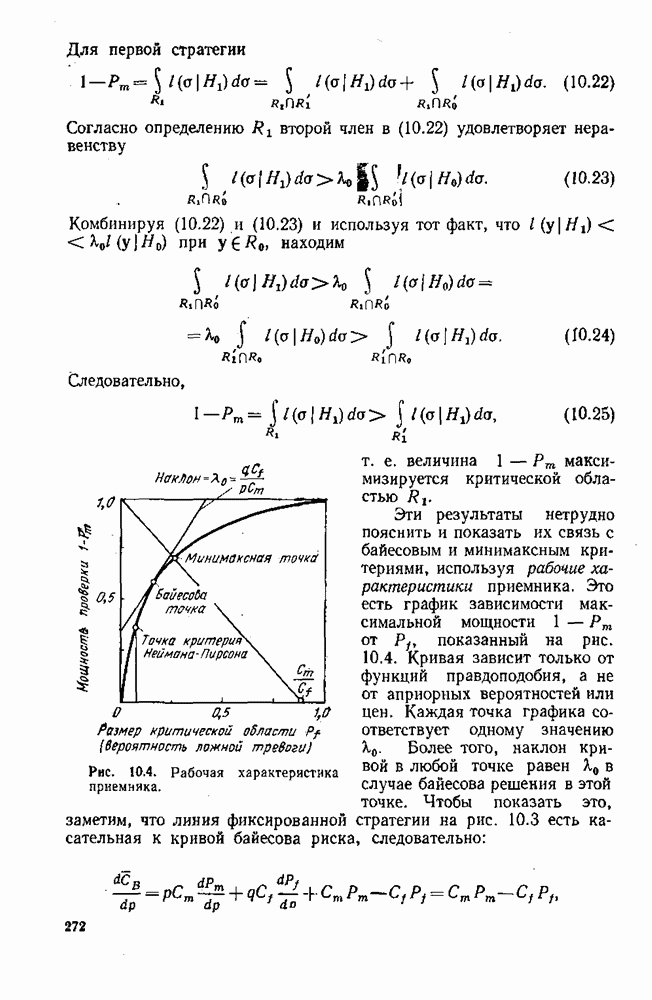
- 10.3. КРИТЕРИИ НЕЙМАНА—ПИРСОНА
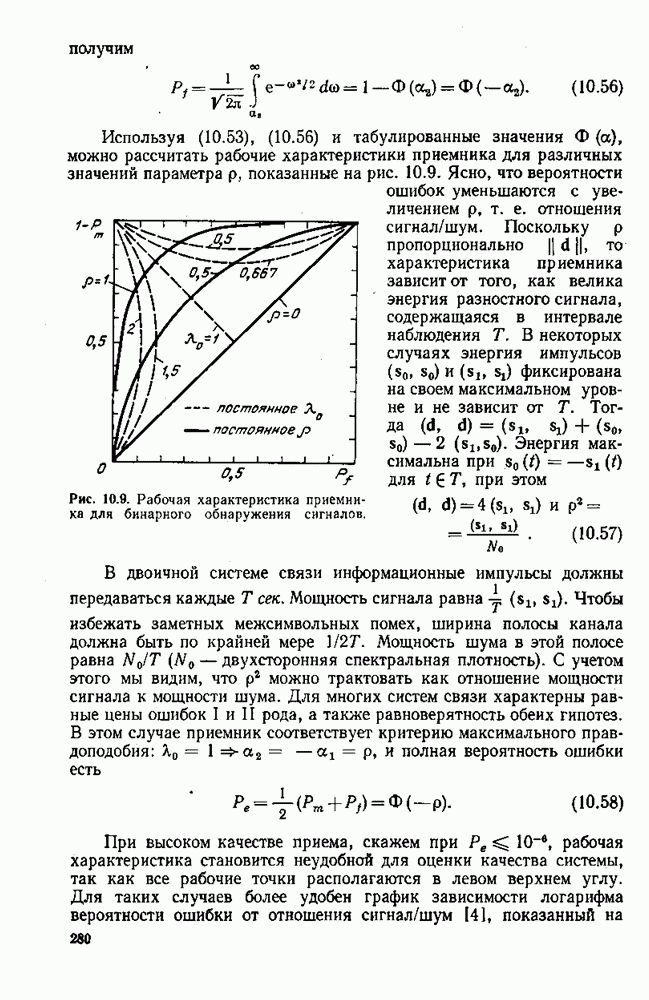
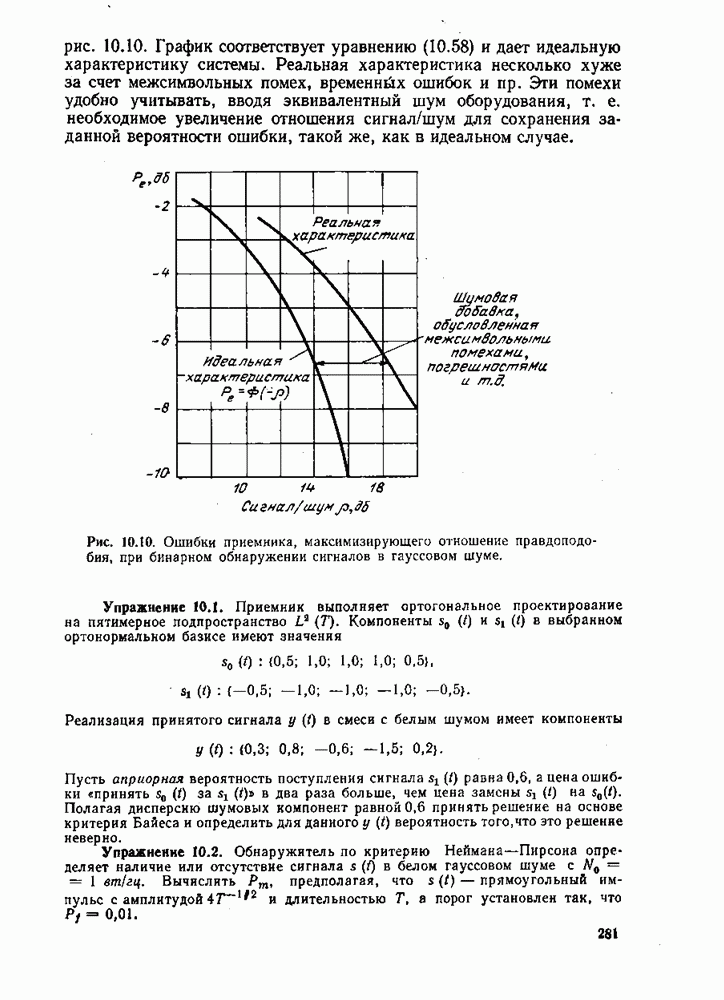
- 10.4. ОБНАРУЖЕНИЕ БИНАРНЫХ СИГНАЛОВ В БЕЛОМ ГАУССОВОМ ШУМЕ
- 10.5. ДВОИЧНОЕ ОБНАРУЖЕНИЕ СИГНАЛОВ В ОКРАШЕННОМ ГАУССОВОМ ШУМЕ
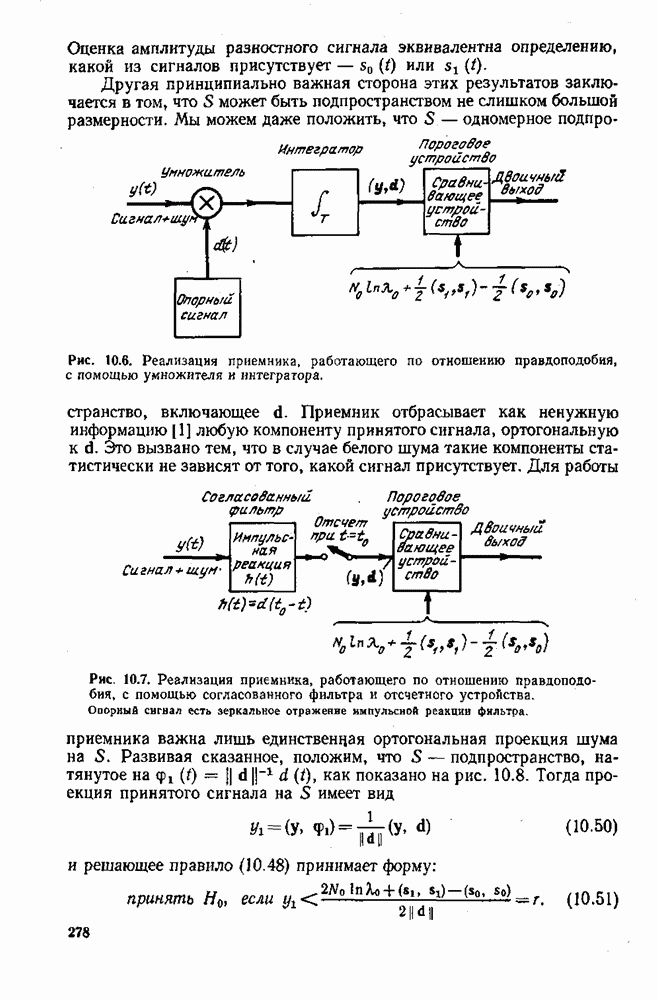
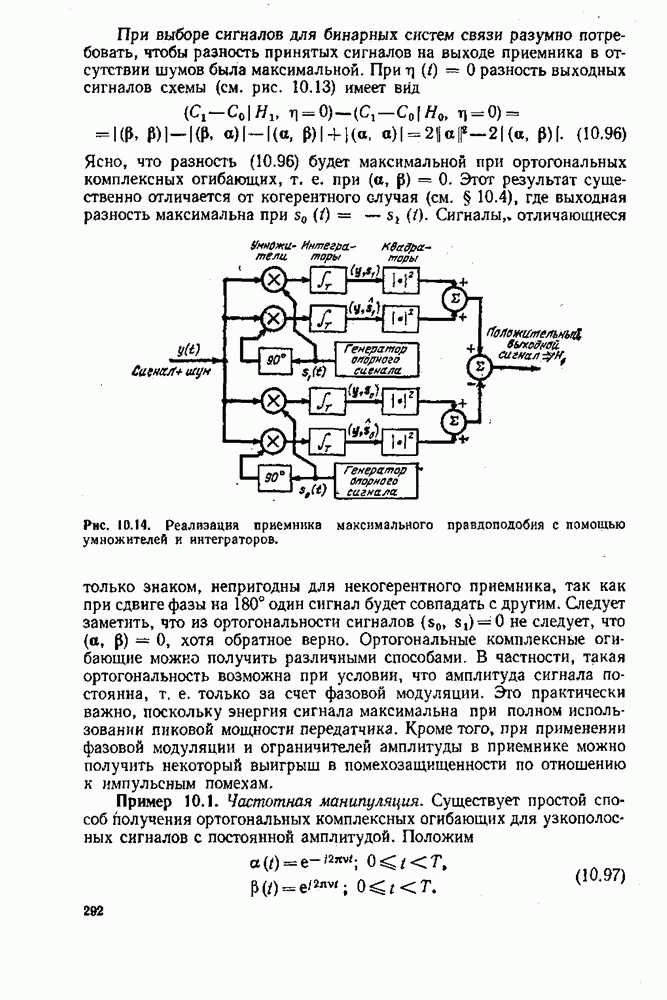
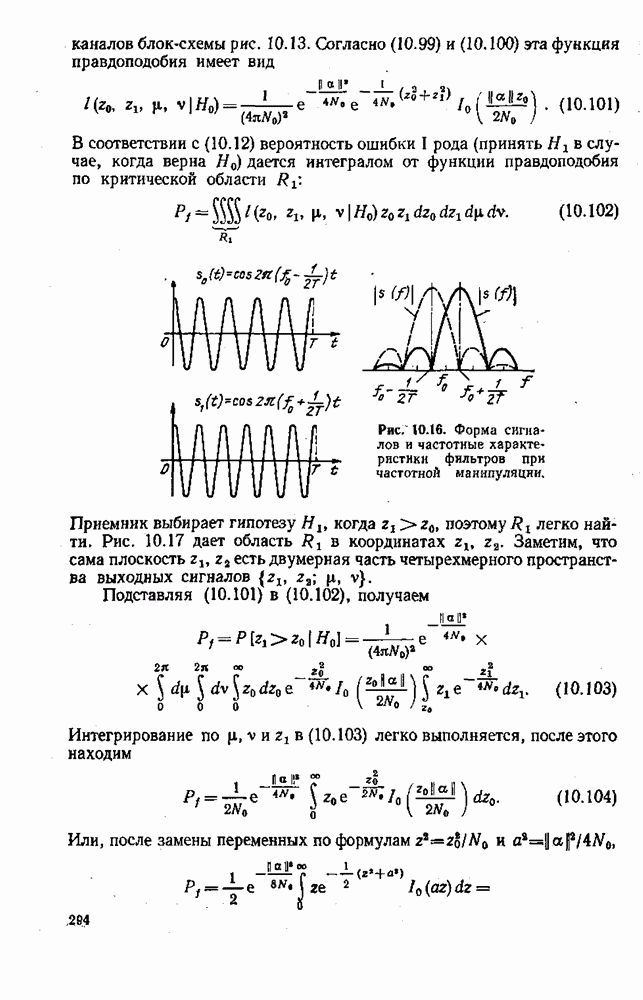
- 10.6. УЗКОПОЛОСНЫЕ СИГНАЛЫ — НЕКОГЕРЕНТНОЕ ОБНАРУЖЕНИЕ
- РЕШЕНИЯ ЗАДАЧ