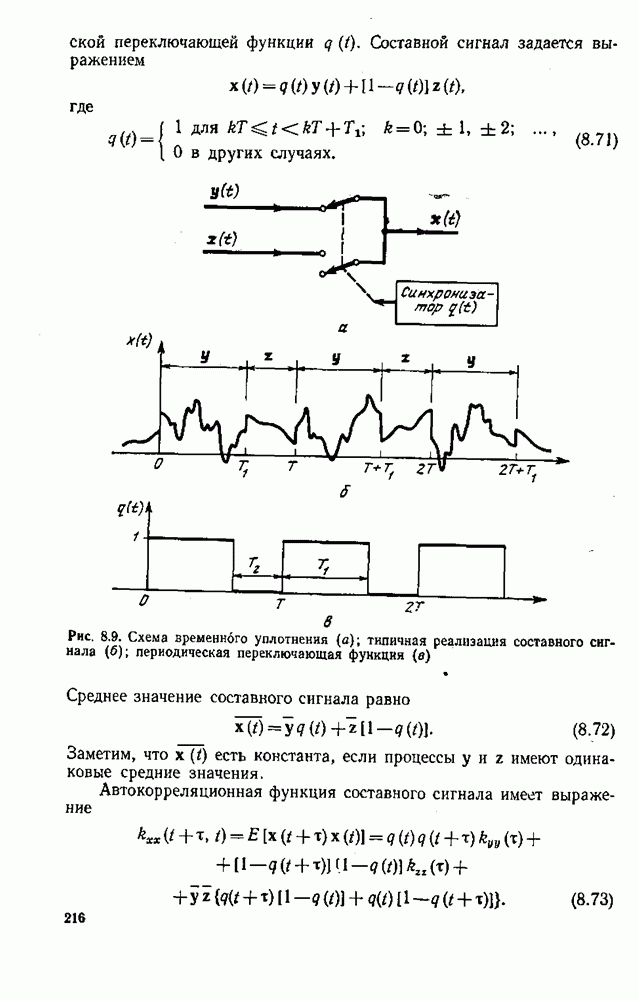
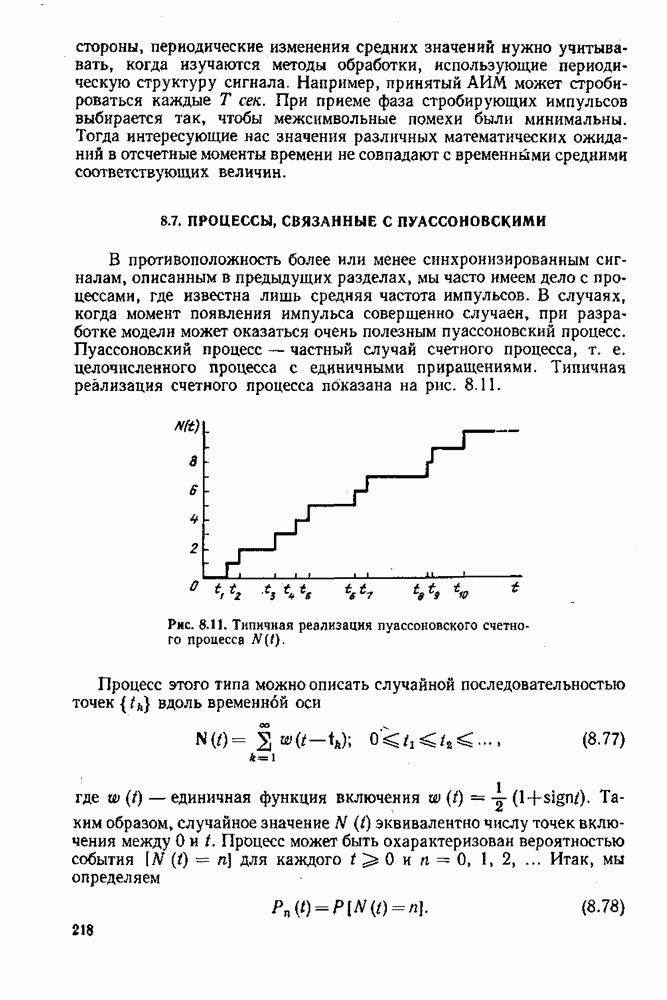
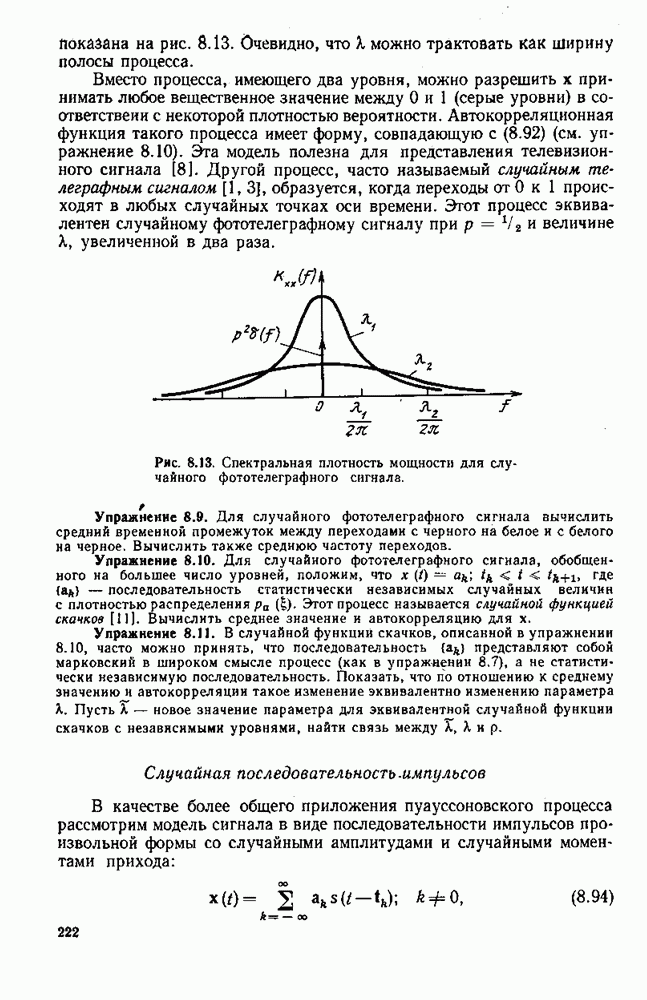
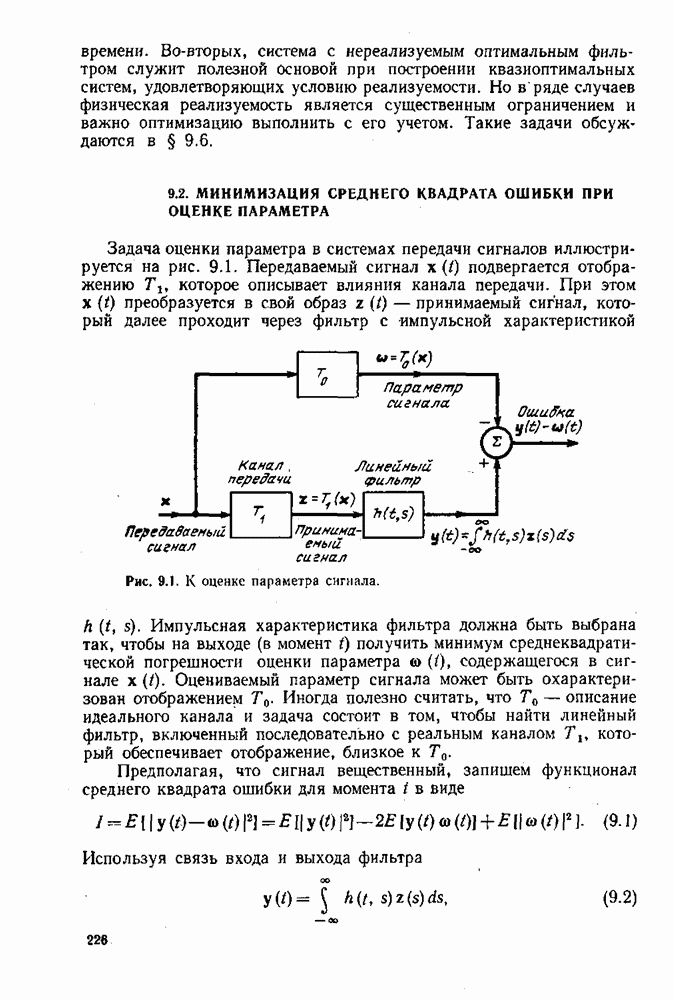
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РЕШЕНИЯ ЗАДАЧ
(см. скан)
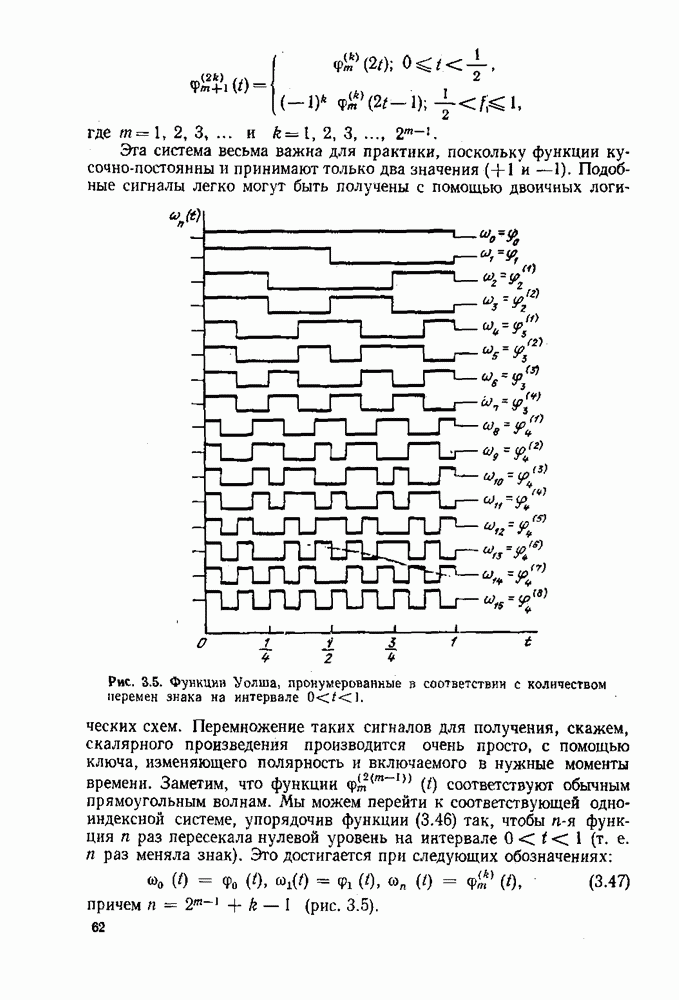
Для примера укажем, что две функции времени принадлежит одному в то  же множеству эквивалентности, если у них совпадают первые
же множеству эквивалентности, если у них совпадают первые  членов разложения в ряд Фурье.
членов разложения в ряд Фурье.
К упр. 1.10. Для  мы имеем
мы имеем  для
для  и можно представить
и можно представить  рядом Фурье на интервале
рядом Фурье на интервале 

где

Поскольку  равна нулю при
равна нулю при  можно также записать
можно также записать

Поэтому, делая замену  получаем
получаем

Обратное преобразование Фурье дает далее

Выполнив интегрирование, приходим к (1.34).
К упр. 1,11. Заметим, что  — периодическая функция с периодом
— периодическая функция с периодом  Разложим эту функцию в ряд Фурье:
Разложим эту функцию в ряд Фурье:

где

Положим  и проинтегрируем почленно, тогда
и проинтегрируем почленно, тогда

Таким образом, мы можем записать

Поэтому, если —  при
при  то
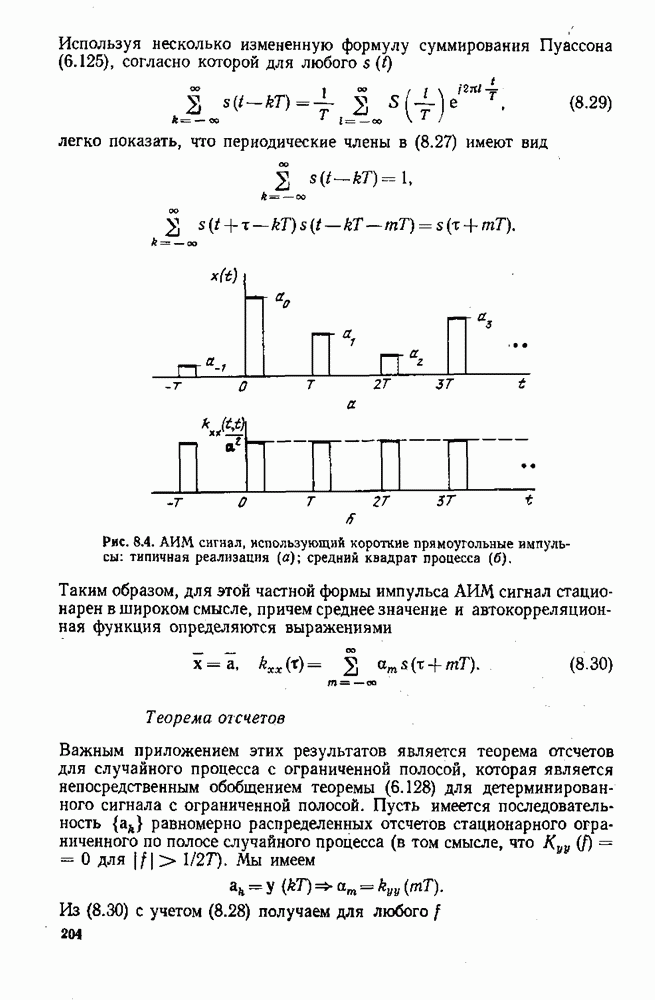
то

В частности, при  для
для 

Мы получили критерий Найквиста для интерполирующих импульсов.
К упр. 2.1. Пусть  — псевдометрика, покажем, что имеет место отношение эквивалентности, определяемое соотношением
— псевдометрика, покажем, что имеет место отношение эквивалентности, определяемое соотношением  . Действительно, условия (1.12) удовлетворяются:
. Действительно, условия (1.12) удовлетворяются:
а)  , следовательно,
, следовательно, 
б)  следовательно,
следовательно,  ;
;
в)  следовательно, если
следовательно, если 
Теперь рассмотрим множество (пространство) содержащее все образованные таким образом множества эквивалентности. Мы можем определить метрику  на множестве
на множестве  следующим образом:
следующим образом:

Вначале мы должны показать, что  определено однозначно. Пусть х — произвольная точка в
определено однозначно. Пусть х — произвольная точка в  и у — произвольная точка в
и у — произвольная точка в  тогда
тогда

С другой стороны, 
Отсюда мы заключаем, что  Итак, метрика
Итак, метрика  однозначна.
однозначна.
Теперь покажем, что  является метрикой:
является метрикой:

Рассмотрим в качестве примера

как в уравнении (2.5); здесь  есть псевдометрика, так как имеются разные функции времени, для которых
есть псевдометрика, так как имеются разные функции времени, для которых  (см. рис. К10). Рассматривая же
(см. рис. К10). Рассматривая же  метрику, мы в действительности говорим, что элементами метрического пространства
метрику, мы в действительности говорим, что элементами метрического пространства  являются не отдельные функции, а, скорее множества функций, эквивалентных почти всюду. Мы впредь будем трактовать эти множества эквивалентности как элементы функционального пространства. Это необходимо, например, для того, чтобы можно было говорить об «обратном преобразовании Фурье».
являются не отдельные функции, а, скорее множества функций, эквивалентных почти всюду. Мы впредь будем трактовать эти множества эквивалентности как элементы функционального пространства. Это необходимо, например, для того, чтобы можно было говорить об «обратном преобразовании Фурье».
К упр. 2.2, Чтобы показать, что  есть псевдометрика, проверим условия, приведенные в упражнении 2.1:
есть псевдометрика, проверим условия, приведенные в упражнении 2.1:
a)  по определению модуля действительных чисел, и
по определению модуля действительных чисел, и  поскольку функционал есть однозначное
поскольку функционал есть однозначное
(см. скан)

Теперь предположим, что значение с выбрано достаточно большим, таким, что для некоторого в О имеет место

а значение 6 выберем достаточно малым, таким, что

Тогда для  имеем
имеем

Здесь учтено, что последний интеграл равен единице, поскольку  Таким образом, мы показали, что
Таким образом, мы показали, что  — непрерывная функция.
— непрерывная функция.
Для вещественных сигналов можно показать, что  — четная функция, так как
— четная функция, так как

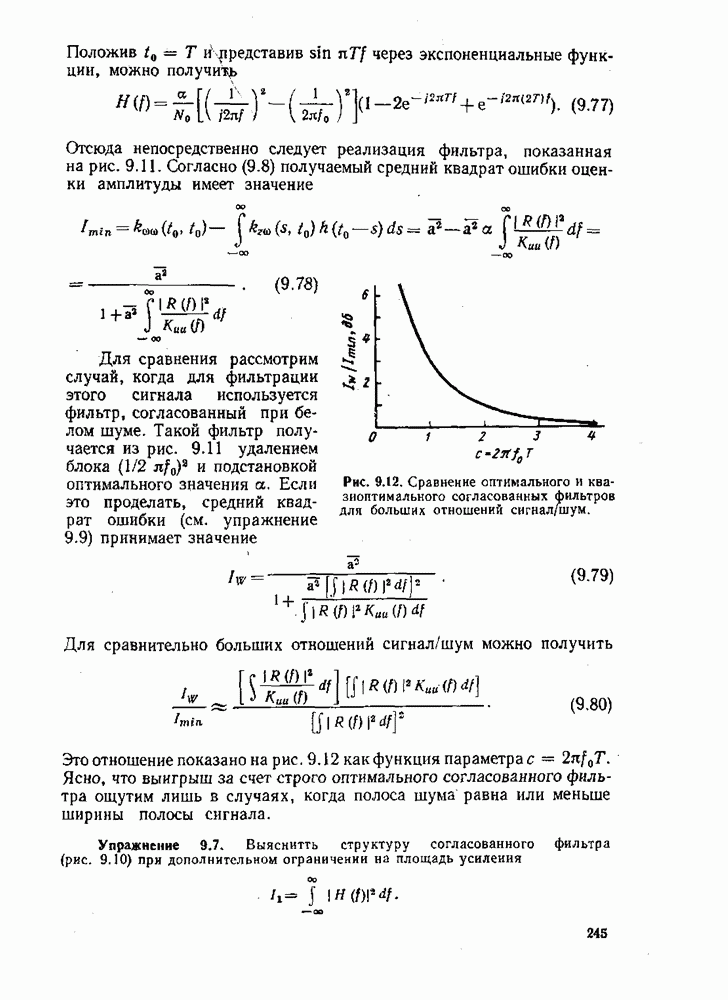
Здесь сделана замена переменной  . Снова, применяя неравенство Шварца, получаем
. Снова, применяя неравенство Шварца, получаем

таким образом, 
К упр. 2.15. Процедура Грама—Шмидта. Воспользуемся схемой (2,50), предположив, что множество ортонормальных векторов  уже получено. Покажем, что при этом следующий вектор
уже получено. Покажем, что при этом следующий вектор  получаемый по этой схеме, ортонормален ко всем предыдущим (доказательство по индукции)
получаемый по этой схеме, ортонормален ко всем предыдущим (доказательство по индукции)

Но мы приняли, что для  следовательно,
следовательно,

Таким образом, при  мы получаем желаемый результат:
мы получаем желаемый результат:

При подсчете нормирующих коэффициентов в процедуре Грама—Шмидта полезно следующее соотношение:

Поскольку  три последних члена совпадают (без учета знаков) и мы имеем
три последних члена совпадают (без учета знаков) и мы имеем

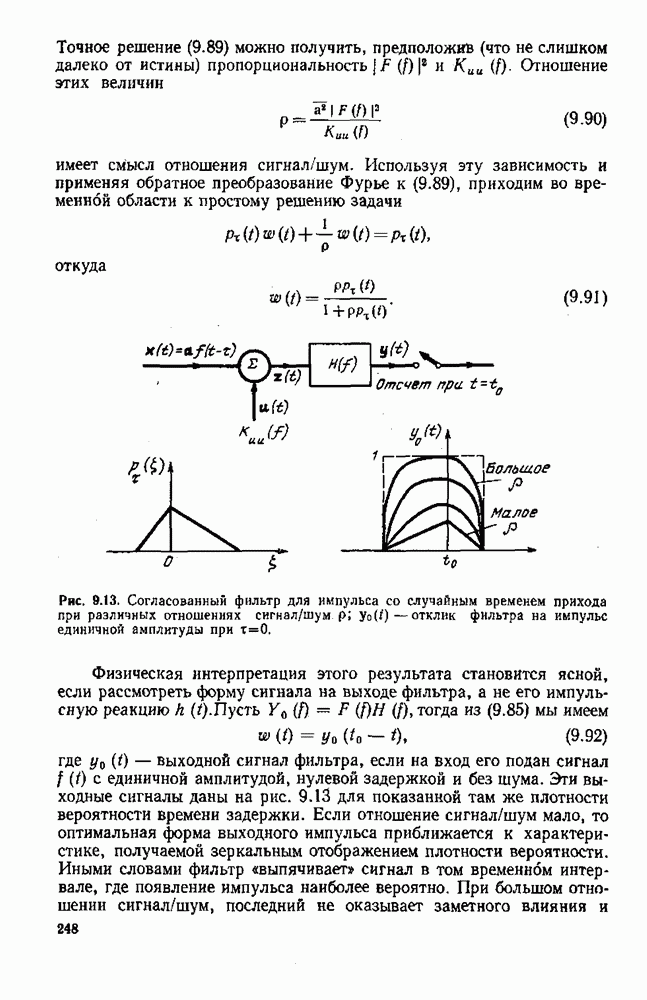
Чтобы сформировать  скалярных уравнений, возьмем скалярное произведение обеих частей этого равенства на
скалярных уравнений, возьмем скалярное произведение обеих частей этого равенства на 

Но, так как  получаем
получаем

Это может быть записано в матричной форме  где
где  матрица Г имеет в
матрица Г имеет в  строке и
строке и  столбце член
столбце член 
К упр. 3.1, Предположим, что

Тогда при  (почти всюду) и, поскольку
(почти всюду) и, поскольку  линейно независимы, мы имеем
линейно независимы, мы имеем  для всех
для всех  Следовательно, представление (3,1) единственно.
Следовательно, представление (3,1) единственно.
К упр. 3.2. Покажем, что разложение  где
где  единственно тогда и только тогда, когда
единственно тогда и только тогда, когда 
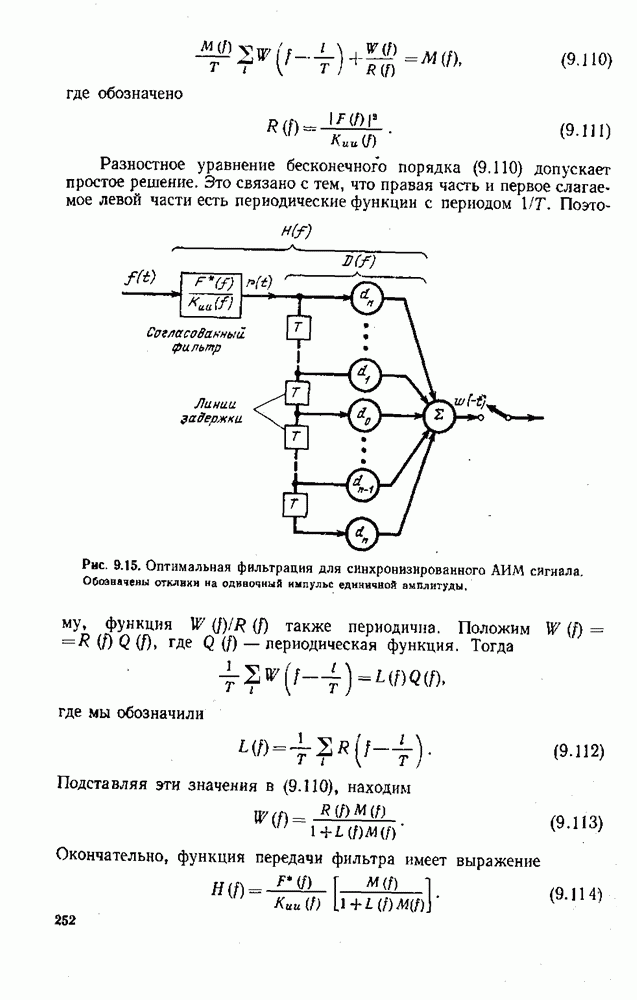
а) Пусть  и предположим, что
и предположим, что 
Тогда  а поскольку
а поскольку  — единственный общий вектор для М и то
— единственный общий вектор для М и то  т. е. разложение единственно.
т. е. разложение единственно.
б) С другой стороны, предположим, что существует такой  , для которого справедливо
, для которого справедливо  Тогда можно записать
Тогда можно записать  или
или  и разложение не единственно.
и разложение не единственно.
Итак, в а) и б) мы доказали, что
 - единственно
- единственно 
Поскольку  — базис для
— базис для 
— базис для М и
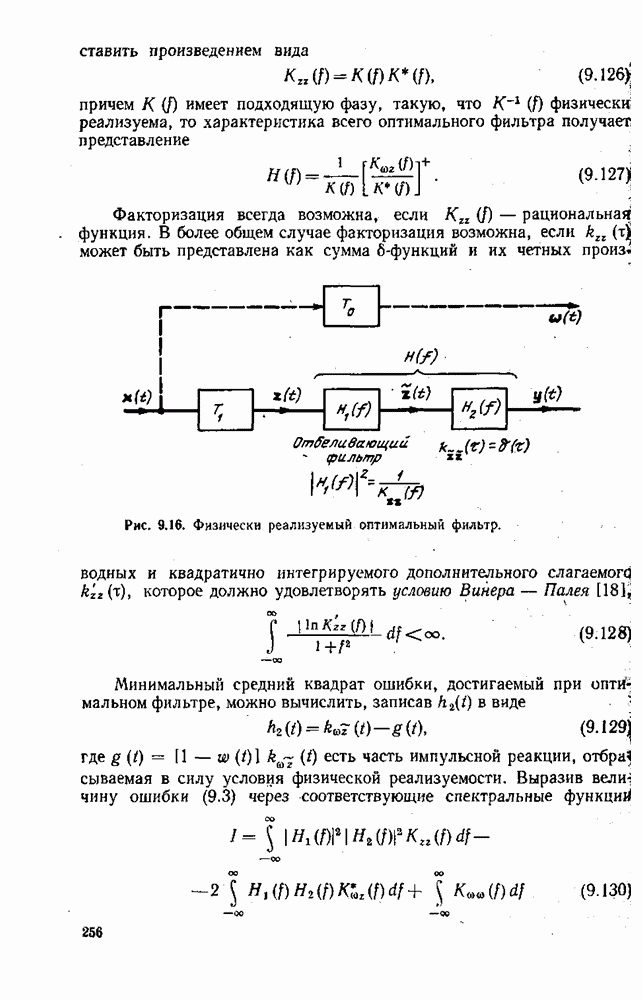
 базис для
базис для  а также
а также  линейно-независимая система, мы можем утверждать, что
линейно-независимая система, мы можем утверждать, что  в единственным образом записать
в единственным образом записать

Заметим, однако, что

не всегда равно нулю при  Поэтому нельзя утверждать, что
Поэтому нельзя утверждать, что  при
при  следовательно,
следовательно,  не обязатель но является взаимным базисом в М, Если
не обязатель но является взаимным базисом в М, Если  — ортонормальная система, то она самосопряженная, и
— ортонормальная система, то она самосопряженная, и  есть взаимный базис для М.
есть взаимный базис для М.
Это один из важнейших доводов в пользу применения в качестве базиса для  ортонормальных систем.
ортонормальных систем.
К упр. 3.5. Поскольку  полная ортонормальная система, мы можем записать:
полная ортонормальная система, мы можем записать:

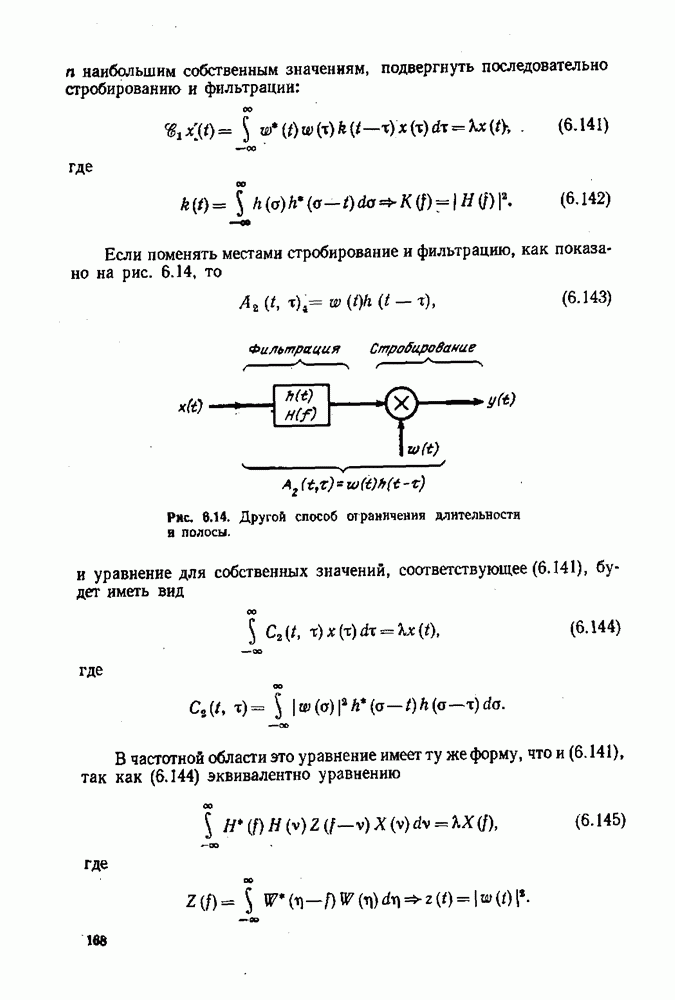
Тогда

Таким образом, доказано равенство Парсеваля.
К упр. 3.6. Учитывая указание и условие  имеем
имеем

Поскольку  и
и  — взаимные базисы, из (3.12) мы имеем
— взаимные базисы, из (3.12) мы имеем

но, так как  — ортонормальная система, то из (3.53) с учетом
— ортонормальная система, то из (3.53) с учетом  находим
находим

Наконец, подставив  получим
получим

Теперь, если мы хотим выполнить условие

то должны выбрать  достаточно большим, так чтобы
достаточно большим, так чтобы

Выполнив разложение в ряд по степеням  найдем
найдем 
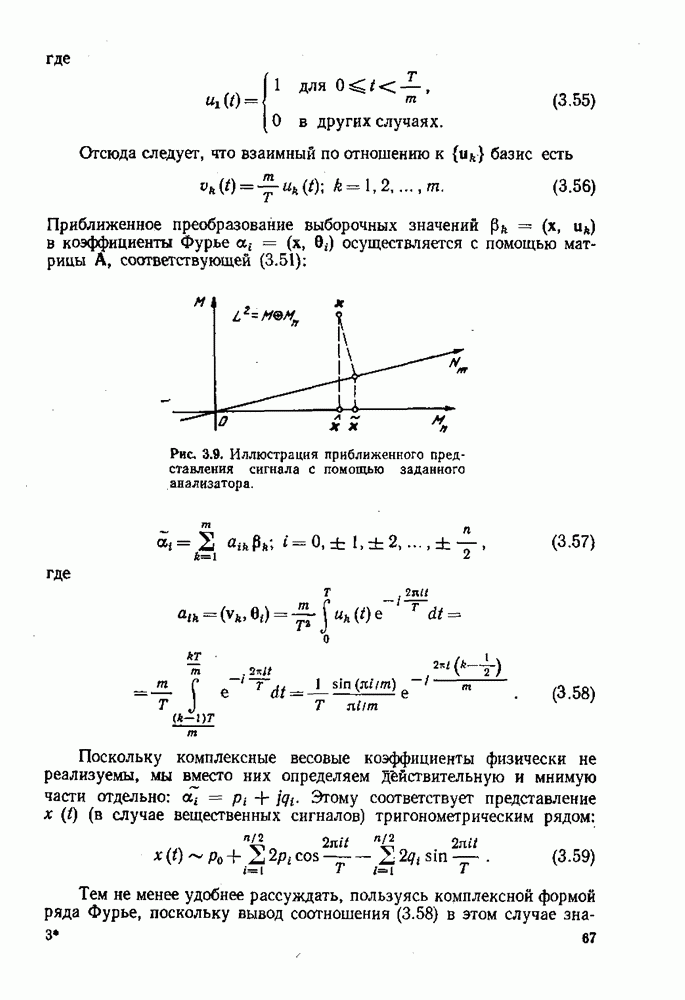
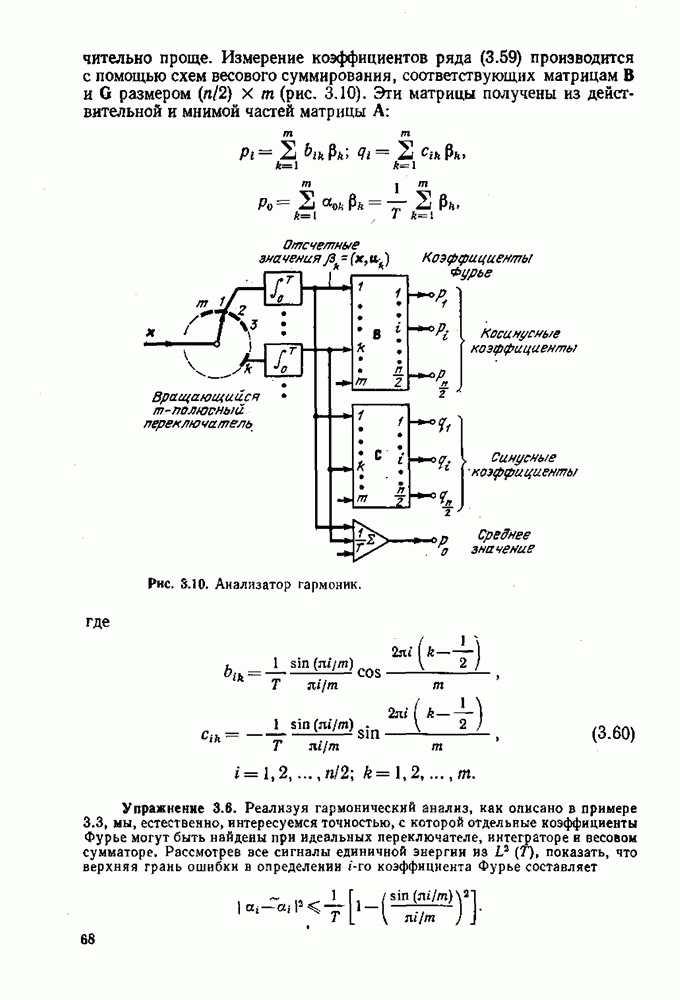
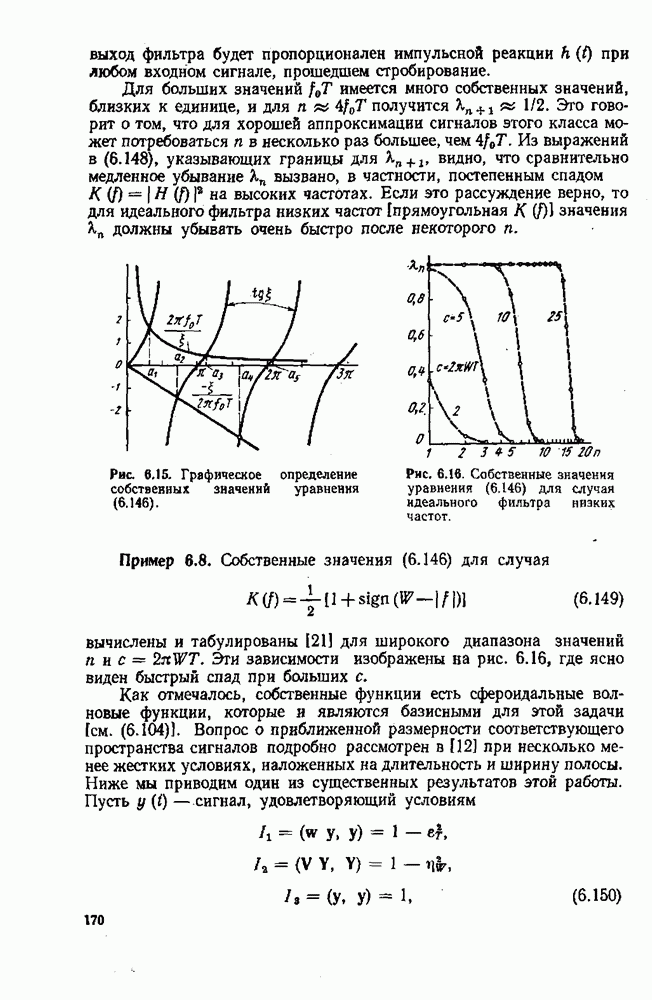
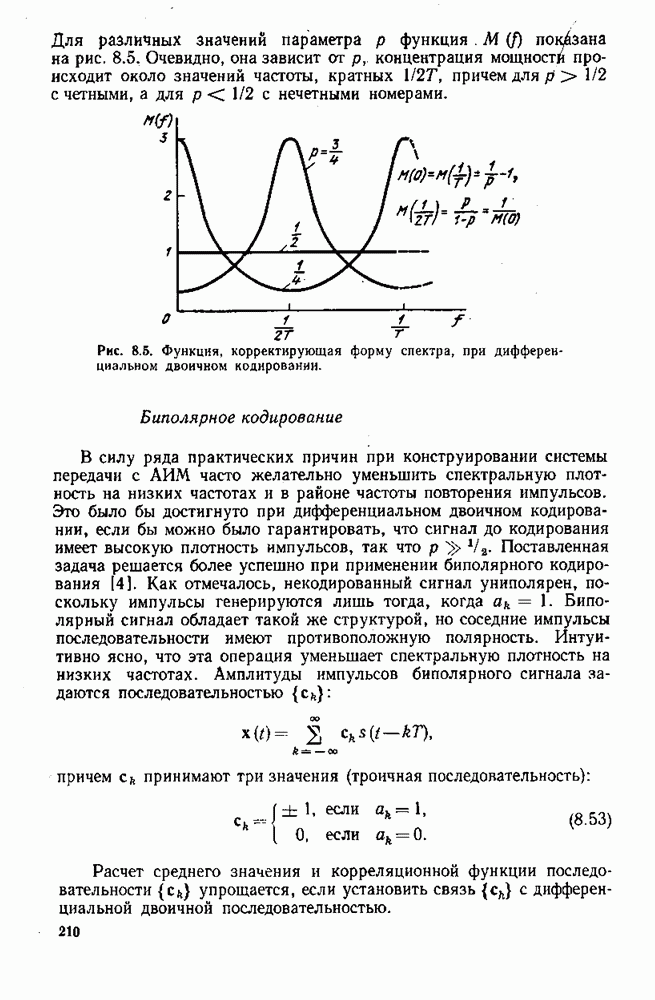
На первый взгляд может показаться, что при уменьшении времени нахождения переключателя на каждом контакте вдвое верхняя граница ошибки определения коэффициентов Фурье соответственно уменьшается. Однако, повторив предыдущий анализ для такого случая, получим

Таким образом, верхняя граница ошибки определения коэффициентов Фурье существенно не уменьшается, даже при очень больших т. Физически это объясняется тем» что могут встретиться сигналы, сконцентрированные в тех отрезках времени, когда переключатель не находится ни на одном контакте. В этом случае не приходится ждать хороших результатов спектрального анализа.
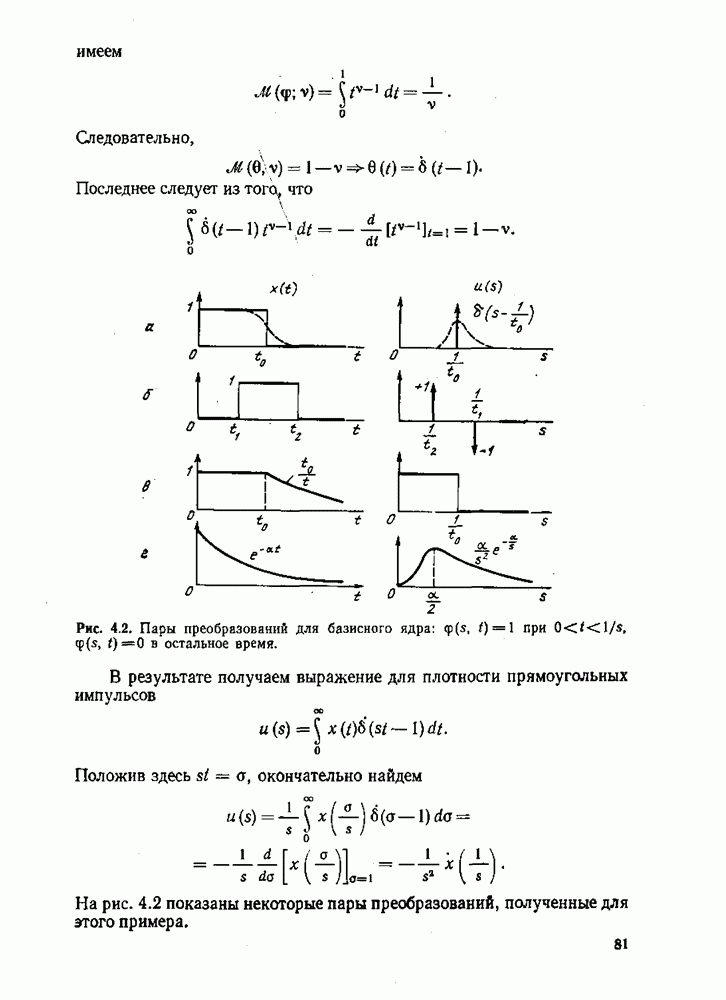
К упр. 4,1, Чтобы найти значение  как обобщенной функции, нужно проанализировать порождаемый ею линейный функционал в
как обобщенной функции, нужно проанализировать порождаемый ею линейный функционал в  Итак, пусть Т есть интервал времени
Итак, пусть Т есть интервал времени  и
и

Сделав замену переменной:  мы получим
мы получим

Но по определению  имеем
имеем

Отсюда заключаем, что для обобщенной функции  имеет место зависимость
имеет место зависимость

К упр. 4.3. Для анализа величины  мы вначале разложим в ряд Фурье периодический множитель
мы вначале разложим в ряд Фурье периодический множитель

где

Такам образом, мы имеем

Теперь вычислим почленно преобразование Фурье:

В силу свойства дуальности

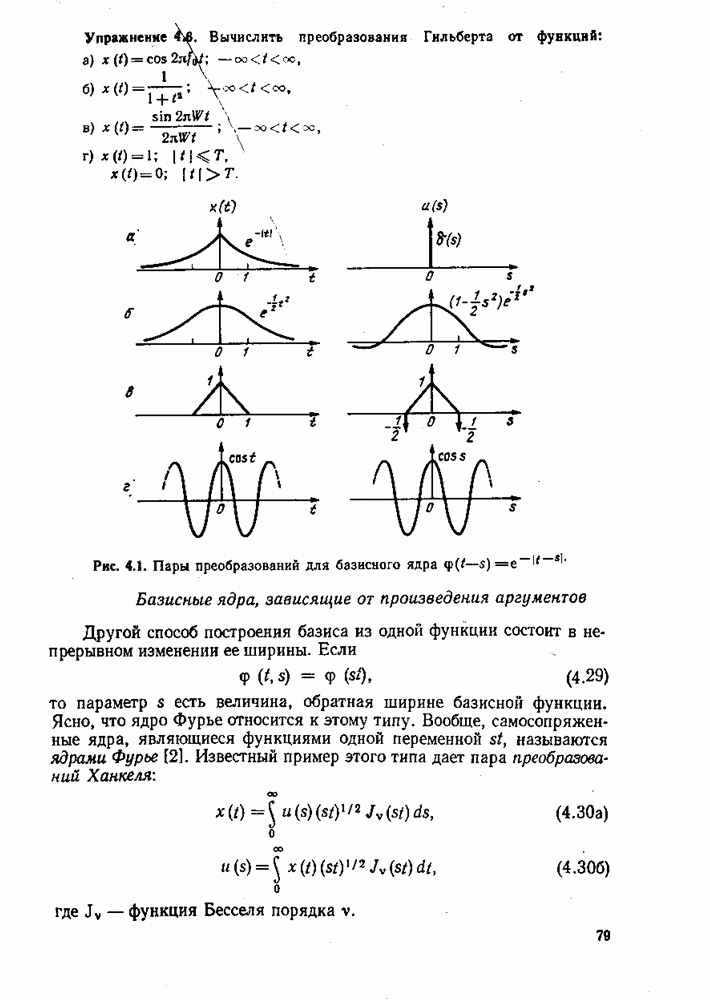
Одним из применений этого общего результата является вывод формул преобразования Фурье для различных «последовательностей импульсивных функций»
а) Пусть  тогда имеем
тогда имеем 
б) Пусть и  тогда имеем
тогда имеем 

К упр. 4.4. В выражении  положим
положим  и используем результаты упражнения 4.3. Тогда
и используем результаты упражнения 4.3. Тогда

Теперь вычислим почленно обратное преобразование Фурье. Мы получим

В частности, при  получается обычная формула суммирования Пуассона:
получается обычная формула суммирования Пуассона:

Можно воспользоваться дуальным соотношением 
Положив  получим
получим

(кликните для просмотра скана)
Далее, если  для
для  то
то

Пусть  тогда
тогда  (см. упр. 4.5), и
(см. упр. 4.5), и  При этом
При этом 
К упр. 4.8. 
Но согласно  и в соответствии с упр. 4.5 а
и в соответствии с упр. 4.5 а

Следовательно,

Отсюда

Пусть, например, мы положили 

или

К упр. 5.5. Пусть инвариантный во времени оператор характеризуется импульсной реакцией  (отклик на единичный импульс» поступивший в момент
(отклик на единичный импульс» поступивший в момент  ).
).
Случай А: инвариантный во времени оператбр стоит первым:

По определению:  Ядра преобразования по отношению к другим базисам получаются из
Ядра преобразования по отношению к другим базисам получаются из  согласно (5.31), (5.34) и (5.36):
согласно (5.31), (5.34) и (5.36):

Случай Б: оператор стробирования стоит первым:

Снова по определению:

Согласно (5.31), (5.34) и (5.36) для этого случая получаем остальные ядра:

К упр. 5,6. Для вырожденного оператора с импульсной реакцией

применив (5.21), получим выражение для ядра в частотной области:

Следовательно, разделимость сохранилась и в этом ядре. Разделимость является свойством данного оператора независимо от выбора базисных ядер. Чтобы это показать, выберем произвольные базисы для пространства входов и пространства выходов, скажем,  соответственно. Тогда согласно (5.32) имеем
соответственно. Тогда согласно (5.32) имеем

где

Подставив последнее выражение в  , получим условие разделимости:
, получим условие разделимости:

где

К упр. 5.7. Отображения, получаемые с помощью вырожденного оператора с импульсной реакцией (5.52), всегда являются линейными комбинациями  следовательно область значений данного оператора есть линейное подпространство
следовательно область значений данного оператора есть линейное подпространство  натянутое на множество этих
натянутое на множество этих  векторов. Из (5.33) мы видим, что отображение у равно нулю тогда и только тогда, когда все скалярные произведения
векторов. Из (5.33) мы видим, что отображение у равно нулю тогда и только тогда, когда все скалярные произведения  равны нулю для
равны нулю для 
Следовательно, нуль-пространство для вырожденного оператора есть ортогональное дополнение подпространства  натянутого на
натянутого на 
К упр. 6.1 Для направляющего вектора имеем:

Теперь мы можем записать  где
где  — вещественные скаляры, и производная может быть получена согласно (6.34) для вещественного пространства
— вещественные скаляры, и производная может быть получена согласно (6.34) для вещественного пространства

где 
Воспользовавшись (6.31), получаем производную по направлению

Теперь, чтобы выразить результат через скалярные произведения с и, запишем

Следовательно,  , где векторы
, где векторы  и
и  определяются
определяются  дующим образом:
дующим образом:

К упр. 6.2, Согласно (6.33) производную по направлению от квадратичного функционала можно записать в виде

Чтобы убедиться в непрерывности  как функционала
как функционала  запишем
запишем

Здесь использовано неравенство Шварца, Поскольку — ограниченный оператор, можно найти такое вещественное положительное число  что
что

Подставив это неравенство в предыдущее, получим

Отсюда сразу же следует, что  — непрерывный функционал, поскольку это неравенство имеет место для любого
— непрерывный функционал, поскольку это неравенство имеет место для любого  и любого направляющего вектора и.
и любого направляющего вектора и.
К упр. 6.3, Пусть задано  (и, следовательно,
(и, следовательно,  ) и пусть
) и пусть  — сигнал, ограниченный по длительности в интервале
— сигнал, ограниченный по длительности в интервале  Пусть теперь Т становится весьма малым по сравнению с
Пусть теперь Т становится весьма малым по сравнению с  Тогда, независимо от формы
Тогда, независимо от формы  на интервале
на интервале  входной сигнал приближается к импульсивному, т. е.
входной сигнал приближается к импульсивному, т. е.

В этом предельном случае максимум выходной энергии просто соответствует максимуму а, если  имеет единичную энергию. Найдем максимум
имеет единичную энергию. Найдем максимум  при ограничении
при ограничении  . Пусть
. Пусть  , полагая
, полагая  получаем
получаем  — постоянная величина в интервале
— постоянная величина в интервале  входной сигнал есть прямоугольный импульс.
входной сигнал есть прямоугольный импульс.

К упр. 6.4. В этой задаче надо максимизировать  при ограничении
при ограничении  Оба квадратичных функционала содержат самосопряженные операторы, таким образом, положив градиент функционала
Оба квадратичных функционала содержат самосопряженные операторы, таким образом, положив градиент функционала  равным нулю, получим
равным нулю, получим


Ядро находим по табл. 6.1:

Заметим, что

К упр. 5.5. Мы имеем  но в согласованном случае
но в согласованном случае

Последнее равенство записано, исходя из (2.40) для вещественных сигналов.
К упр. 8.8. Для вещественных сигналов преобразование Фурье функции автокорреляции согласно (2.41) имеет вид

таким образом,  также имеет ограниченную полосу
также имеет ограниченную полосу  Согласно равенству Парсеваля
Согласно равенству Парсеваля

а применение неравенства Шварца дает

или

Равенство достигается, когда  есть константа на участке
есть константа на участке  таким образом, импульс, обеспечивающий минимум радиуса корреляции, есть
таким образом, импульс, обеспечивающий минимум радиуса корреляции, есть

К упр. 6.7. Максимизируем  при ограничения
при ограничения  при
при 
Пусть

тогда

т. е.

К упр. 6.8. Максимизируем —  при ограничении
при ограничении  Используя функционалы в частотной области, имеем
Используя функционалы в частотной области, имеем

где

Пусть  Полагая
Полагая  заметим, что
заметим, что  не является самосопряженным оператором, поэтому
не является самосопряженным оператором, поэтому

Тогда

Следовательно,

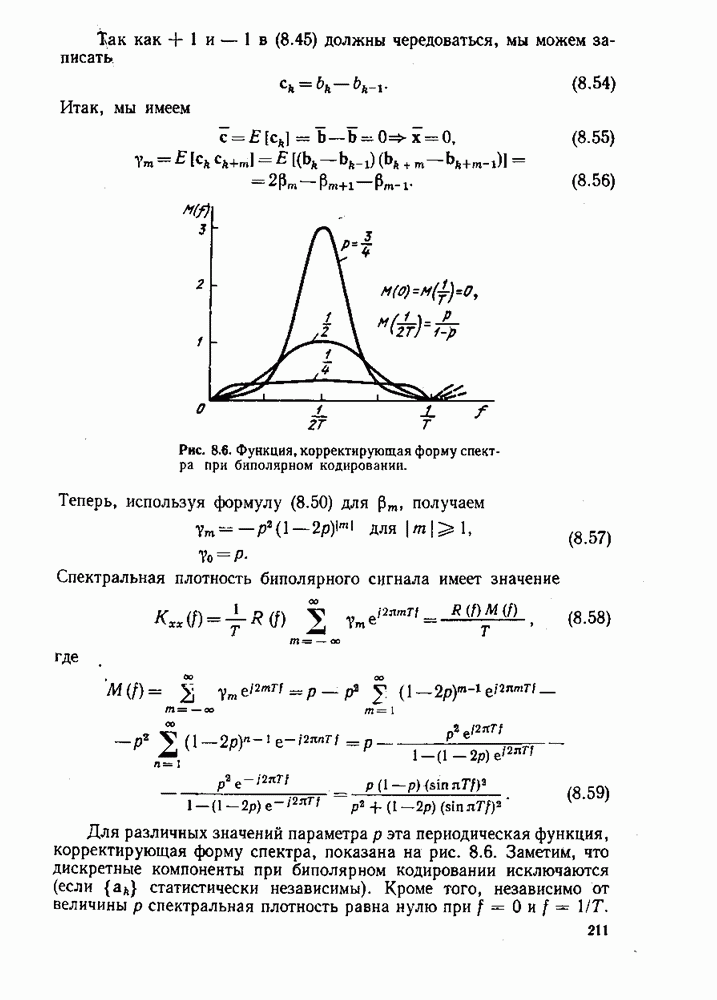
Постоянный множитель  следует определить из условия нормировки энергии на входе. Учитывая, что
следует определить из условия нормировки энергии на входе. Учитывая, что  получаем
получаем


К упр. 6-9, В частотной области задача формулируется так. Надо минимизировать  а при ограничении
а при ограничении  где
где  заданные функции частоты:
заданные функции частоты:

Заметим, что оператор  самосопряженный.
самосопряженный.
Берем  и полагаем
и полагаем  отсюда получаем искомый результат
отсюда получаем искомый результат

где X должно быть выбрано так, чтобы удовлетворить условию  Если соответствующее значение X достаточно мало, то
Если соответствующее значение X достаточно мало, то  , т. е. мы получаем тот же результат, что в задаче без ограничений. Наиболее интересен случай,
, т. е. мы получаем тот же результат, что в задаче без ограничений. Наиболее интересен случай,  содержится в полосе
содержится в полосе  Заметим, что при
Заметим, что при  результат получается таким же, как в примере 6,4.
результат получается таким же, как в примере 6,4.
К упр. 6.10. Например, пусть  и
и  (при этом мы попадаем на линию
(при этом мы попадаем на линию  на рис. 6.10). Положим
на рис. 6.10). Положим  где
где  прямоугольный импульс длительности
прямоугольный импульс длительности  , а
, а  — импульс вида
— импульс вида  имеющий полосу
имеющий полосу 
Далее, подберем такие амплитуды, что  , Теперь, не изменяя
, Теперь, не изменяя  положим
положим  . Тогда
. Тогда  . Заметим также, что
. Заметим также, что  так что
так что 

К упр. 7.1, Рассмотрим вещественный процесс  на выходе фильтра. Согласно
на выходе фильтра. Согласно  для него
для него

Пусть  — белый шум со спектральной плотностью
— белый шум со спектральной плотностью  для всех
для всех  и пусть
и пусть

 — произвольная вещественная функция из
— произвольная вещественная функция из  (вообще говоря, это условие также не обязательно). Тогда
(вообще говоря, это условие также не обязательно). Тогда

и, следовательно,  есть временная функция неопределенности фильтра
есть временная функция неопределенности фильтра 

К упр. 7.2. Непрерывность  вытекает из следующего. Мы имеем
вытекает из следующего. Мы имеем 

Далее, если  непрерывна в нуле, то для любого
непрерывна в нуле, то для любого  найдется такое малое
найдется такое малое  что
что

Следовательно,  непрерывна при всех
непрерывна при всех  .
.
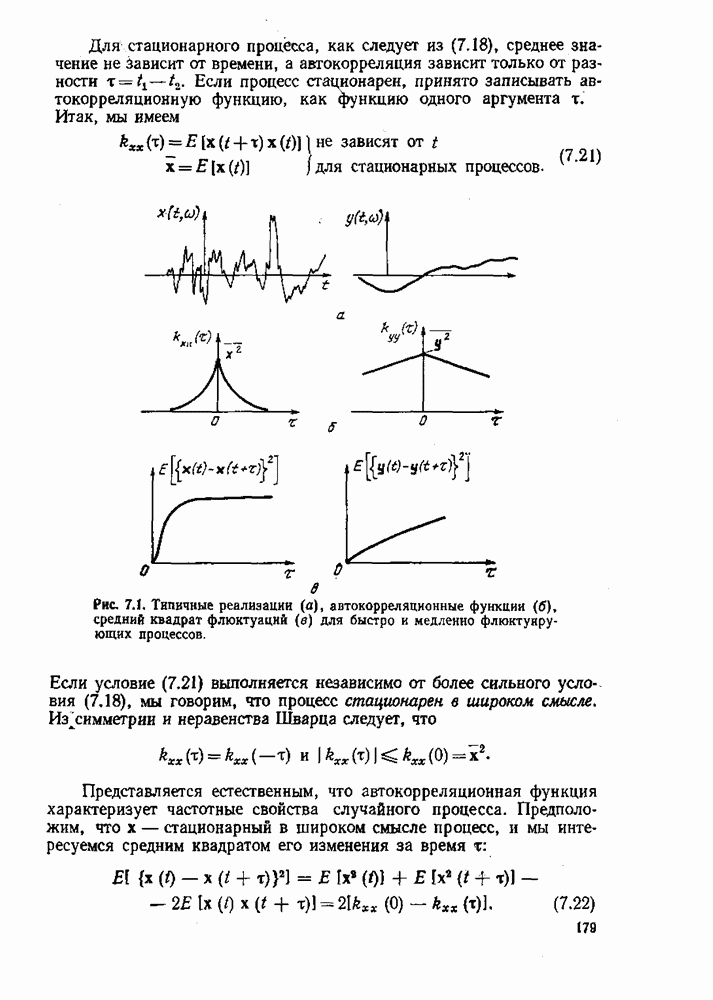
К упр. 7.3. Согласно (7.22) средний квадрат флюктуаций имеет значение

Следовательно, средний квадрат флюктуаций меньше, чем  Мы имеем также
Мы имеем также

Но  при
при  Поэтому
Поэтому

Также» если  то
то

К упр. 7.4.


Среднее значение представляет собой квадратичную форму  типа (6.16) с ядром вида
типа (6.16) с ядром вида 
Следовательно, оператор: 1) инвариантен во времени (оператор свертки); 2) положительно-определен, так как при любой  самосопряжен
самосопряжен  так как
так как


(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
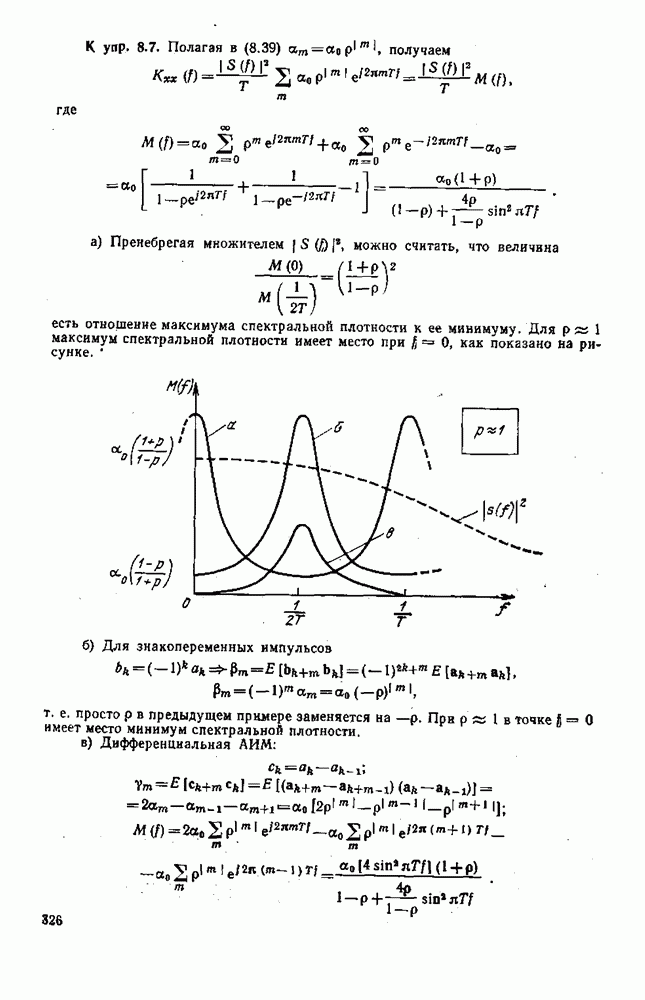
Эти условия показывают» что если  разложить в ряд Фурье на интервале
разложить в ряд Фурье на интервале  , то члены, содержащие первую к вторую гармоники, должны обратиться в нуль (конечно, при условии
, то члены, содержащие первую к вторую гармоники, должны обратиться в нуль (конечно, при условии  Очевидно распределение
Очевидно распределение  дает процесс стационарный в широкой смысле. Но такая стационарность возможна и при других распределениях. Например, процесс
дает процесс стационарный в широкой смысле. Но такая стационарность возможна и при других распределениях. Например, процесс  стационарен в широком смысле, если распределения фазы соответствуют одному из следующих рисунков.
стационарен в широком смысле, если распределения фазы соответствуют одному из следующих рисунков.

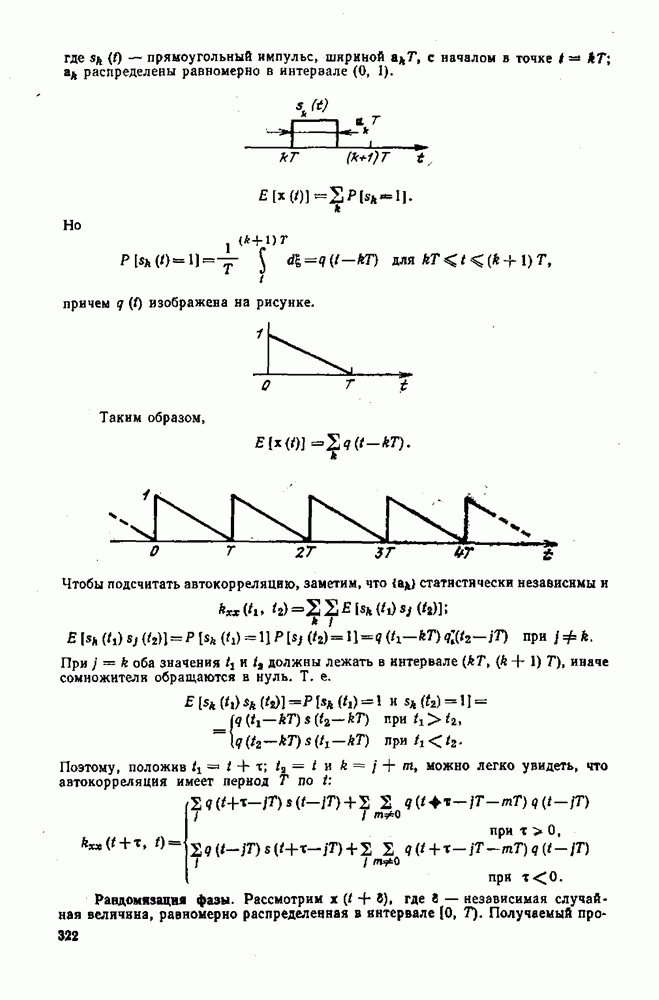
К упр. 8.2, Квантованный процесс

причем  стационарен в широком смысле.
стационарен в широком смысле.


Рассмотрим каждое слагаемое отдельно:

поскольку при  слагаемые в двойной сумме обращаются в нуль.
слагаемые в двойной сумме обращаются в нуль.

Следовательно»

т. е. средний квадрат ошибки периодичен во времени и имеет период  Усредняя за период, получаем
Усредняя за период, получаем

«Постоянная составляющая», т. е. процесс вида  где а — случайная величина, имеет постоянную автокорреляцию и средний квадрат ошибки в этом случае равен нулю.
где а — случайная величина, имеет постоянную автокорреляцию и средний квадрат ошибки в этом случае равен нулю.
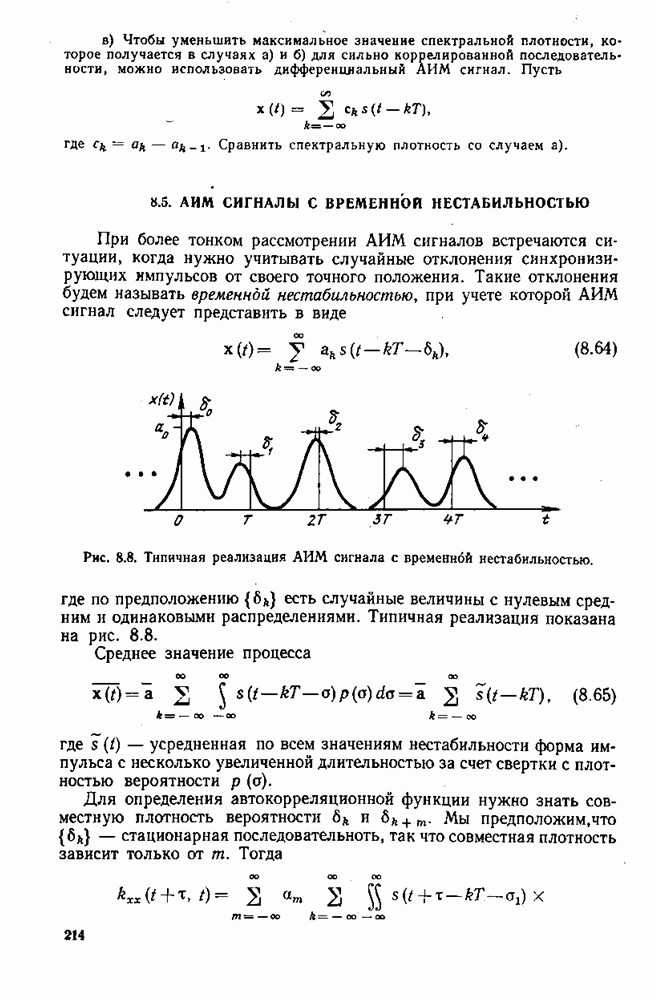
К упр. 8.3. Широтно-импульсная модуляция. Мы можем представить процесс в виде


(кликните для просмотра скана)

(кликните для просмотра скана)
В качестве проверки этого результата заметим, что для рассматриваемого процесса  поэтому мы должны получить
поэтому мы должны получить  Как следует из предыдущего,
Как следует из предыдущего, 
К упр. 8.4. Пусть

где

 — случайная величина, равномерно распределенная в интервале
— случайная величина, равномерно распределенная в интервале  ,
,

Пусть далее

и при всех 

Тогда

Можно переписать это выражение, выделив периодическую составляющую:

Замечая, что

запишем спектральную плотность мощности в виде


(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
Далее, согласно (9.11) оптимальный фильтр имеет передаточную функцию

Таким образом, мы просто даем наилучшую оценку для  [см. (9,16)] и достигаем этого путем «сглаживания», характеризуемого множителем
[см. (9,16)] и достигаем этого путем «сглаживания», характеризуемого множителем 
К упр. 9.2, Установим прежде всего вид ограничения на величину нормы в  Мы имеем
Мы имеем

где учтено, что  не случайная функция,
не случайная функция,  имеет нулевое среднее значение. Взяв преобразование Фурье, получим далее
имеет нулевое среднее значение. Взяв преобразование Фурье, получим далее

Теперь, применяя равенство Парсеваля в  можем записать функционал ограничения в виде
можем записать функционал ограничения в виде

Выполняя это ограничение, мы хотим найти такую  чтобы дисперсия
чтобы дисперсия  ошибки
ошибки  была минимальной, причем
была минимальной, причем

Здесь учтено, что

а шум и  имеет нулевое среднее значение. Поэтому
имеет нулевое среднее значение. Поэтому

Теперь, положив  будем варьировать
будем варьировать  и приравняем градиент функционала
и приравняем градиент функционала  нулю. Мы получаем
нулю. Мы получаем

Следовательно,

где множитель Лагранжа 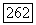 выбирается так, чтобы удовлетворять ограничению
выбирается так, чтобы удовлетворять ограничению

К упр. 9.3. Положив в примере 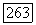 мы имеем
мы имеем

Фаза функции 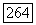 в данной задаче несущественна. Обозначим
в данной задаче несущественна. Обозначим 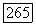 Нам нужно найти градиент функционала
Нам нужно найти градиент функционала 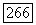 который в данном случае не является квадратичным. Рассмотрим производную по направлению функционала
который в данном случае не является квадратичным. Рассмотрим производную по направлению функционала

Поэтому согласно (6.34) имеем

Пусть теперь

что совпадает с результатом (9.32).
К упр. 9.4. Эта задача лишь незначительно отличается от примера 9.2. Здесь мы хотим минимизировать функционал

при ограничении на передаваемую мощность

где

Повторяя преобразования, аналогичные 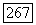 мы положим градиент функционала
мы положим градиент функционала 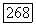 равным нулю при вариациях как по отношению
равным нулю при вариациях как по отношению 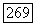 так и
так и 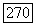 Полученные два уравнения умножим на
Полученные два уравнения умножим на 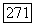 соответственно. Тогда условия стационарности принимают вид
соответственно. Тогда условия стационарности принимают вид

Как и ранее, можно видеть» что X должно быть неотрицательным, и, кроне того, заключать, что


(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- 1. ВВЕДЕНИЕ
- 1.1. СИСТЕМЫ ОБРАБОТКИ СИГНАЛОВ
- 1.2. МНОЖЕСТВА СИГНАЛОВ
- 1.3. ОТОБРАЖЕНИЯ И ФУНКЦИОНАЛЫ
- 2 ПРОСТРАНСТВА СИГНАЛОВ
- 2.1. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
- 2.2. СХОДИМОСТЬ И НЕПРЕРЫВНОСТЬ
- 2.3. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 2.4. НОРМИРОВАННЫЕ ЛИНЕИНЫЕ ПРОСТРАНСТВА
- 2.5. ПРОСТРАНСТВА СО СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ
- 2.6. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
- 3. ДИСКРЕТНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
- 3.1. ПОДПРОСТРАНСТВА ИЗ L2(T)
- 3.2. ПОЛНЫЕ ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ
- 3.3. ПРИМЕРЫ ПОЛНЫХ ОРТОНОРМАЛЬНЫХ СИСТЕМ
- 3.4. ОПЕРАТОР РАЗЛОЖЕНИЯ СИГНАЛА В АППАРАТУРНОЙ РЕАЛИЗАЦИИ
- 4. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
- 4.2. БАЗИСНЫЕ И СОПРЯЖЕННЫЕ БАЗИСНЫЕ ЯДРА
- 4.3. ПРЕОБРАЗОВАНИЯ ФУРЬЕ, ГИЛЬБЕРТА И ДРУГИЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРЕДСТАВЛЕНИЕ УЗКОПОЛОСНЫХ СИГНАЛОВ
- Полосовая фильтрация
- Радиолокационная функция неопределенности
- 5. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ
- 5.2. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
- 5.3. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ, ДЕЙСТВУЮЩИХ В КОНЕЧНОМЕРНОМ ПРОСТРАНСТВЕ
- 5.4 ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ, ДЕЙСТВУЮЩИХ В ПРОСТРАНСТВЕ L2(T)
- 5.5. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ, ДЕЙСТВУЮЩИХ В L2(T)
- 5.6 РЕАЛИЗАЦИЯ ВЫРОЖДЕННЫХ ОПЕРАТОРОВ
- 5.7. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАТОРОВ
- Собственные значения и собственные пространства
- Сопряженный оператор
- Спектральное представление нормальных вырожденных операторов
- Спектральное представление нормальных компактных операторов
- 6. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ
- 6.2. КВАДРАТИЧНЫЕ ФУНКЦИОНАЛЫ
- 6.3. НЕКОТОРЫЕ ХАРАКТЕРНЫЕ КВАДРАТИЧНЫЕ ФУНКЦИОНАЛЫ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
- 6.4. ВАРИАЦИОННАЯ ЗАДАЧА БЕЗ ОГРАНИЧЕНИЙ
- 6.5. ВАРИАЦИОННАЯ ЗАДАЧА ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
- 6.6. НЕКОТОРЫЕ ПРИМЕРЫ
- 6.7. ОБЛАСТЬ, ЗАНИМАЕМАЯ СИГНАЛОМ НА ПЛОСКОСТИ ВРЕМЯ-ЧАСТОТА
- Межсимвольные искажения
- Синхронные импульсные последовательности, критерий Найквиста, теорема отсчетов
- 6.8. ПРИБЛИЖЕННОЕ ЧИСЛО ИЗМЕРЕНИЙ ПРОСТРАНСТВА СИГНАЛОВ
- Стробирование и фильтрация
- 7. ПРЕДСТАВЛЕНИЯ СЛУЧАЙНЫХ СИГНАЛОВ
- 7.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ОЖИДАНИЯ
- 7.3. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 7.4. ДВУМЕРНЫЕ КОМПЛЕКСНЫЕ ПРОЦЕССЫ
- Спектральная плотность мощности
- 7.5. КОНЕЧНОМЕРНЫЕ ПРЕДСТАВЛЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА
- 7.6. УЗКОПОЛОСНЫЕ ПРОЦЕССЫ
- 8. МОДЕЛИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 8.2. ИМПУЛЬСНЫЕ СИГНАЛЫ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ И СЛУЧАЙНЫМ ВРЕМЕНЕМ ПРИХОДА
- 8.3. ПРОЦЕССЫ С ЦИКЛИЧЕСКОЙ СТАЦИОНАРНОСТЬЮ
- 8.4. ВЛИЯНИЕ КОДИРОВАНИЯ НА СПЕКТРАЛЬНУЮ ПЛОТНОСТЬ
- 8.5. АИМ СИГНАЛЫ С ВРЕМЕННОЙ НЕСТАБИЛЬНОСТЬЮ
- 8.6. СИГНАЛЫ С ВРЕМЕННЫМ УПЛОТНЕНИЕМ
- 8.7. ПРОЦЕССЫ, СВЯЗАННЫЕ С ПУАССОНОВСКИМИ
- 9. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ
- 9.2. МИНИМИЗАЦИЯ СРЕДНЕГО КВАДРАТА ОШИБКИ ПРИ ОЦЕНКЕ ПАРАМЕТРА
- 9.3 НЕПРЕРЫВНАЯ ОЦЕНКА ФОРМЫ СИГНАЛА
- 9.4. ОЦЕНКА ИМПУЛЬСНЫХ АМПЛИТУД
- 9.5. ПЕРИОДИЧЕСКАЯ ОЦЕНКА ФОРМЫ СИГНАЛА
- 9.6. УСЛОВИЕ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ
- 10. ОБНАРУЖЕНИЕ СИГНАЛОВ
- 10.2. КРИТЕРИЙ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
- 10.3. КРИТЕРИИ НЕЙМАНА—ПИРСОНА
- 10.4. ОБНАРУЖЕНИЕ БИНАРНЫХ СИГНАЛОВ В БЕЛОМ ГАУССОВОМ ШУМЕ
- 10.5. ДВОИЧНОЕ ОБНАРУЖЕНИЕ СИГНАЛОВ В ОКРАШЕННОМ ГАУССОВОМ ШУМЕ
- 10.6. УЗКОПОЛОСНЫЕ СИГНАЛЫ — НЕКОГЕРЕНТНОЕ ОБНАРУЖЕНИЕ
- РЕШЕНИЯ ЗАДАЧ