| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Краевые задачи для конечного отрезка
1. Постановка краевых задач. Постановку краевых задач мы формулируем для случая 1 § 1, когда изучаемое уравнение можно рассматривать как уравнение теплопроводности.
Другие физические задачи приводят по большей части к тем же краевым условиям.
Мы рассмотрим уравнение

при заданном начальном распределении температур

и при граничных условиях следующих типов:
Первая краевая задача: на границах стержня заданы температуры как функции времени:

Вторая краевая задача: заданы тепловые потоки, проходящие через торцевые сечения стержня. Так как тепловые потоки пропорциональны частным производным по х, то можно задать:

Третья краевая задача: на торцах стержня происходит теплообмен с окружающей средой, имеющей заданную температуру, являющуюся известной функцией от времени:

Встречаются и смешанные задачи, когда на разных концах стержня задаются условия различных типов.
Четвертая краевая задача: рассматривается кольцевой стержень длиной  краевые условия заменяются условиями периодичности:
краевые условия заменяются условиями периодичности:

Первые три краевые задачи называются однородными, если  равны нулю.
равны нулю.
2. Метод разделения переменных (метод Фурье). Начнем с решения однородного уравнения

при однородных краевых условиях.
Положим и  и подставим в уравнение (6.15); разделяя переменные, получим:
и подставим в уравнение (6.15); разделяя переменные, получим:

откуда

Краевые условия определяются граничными условиями для функции у, которая должна быть решением краевой задачи Штурма-Лиувилля (см. гл. II).
Обозначая через  собственные значения краевой задачи, а через
собственные значения краевой задачи, а через  собственные функции, получим:
собственные функции, получим:

Решением будет ряд

При  используя начальные условия, будем иметь:
используя начальные условия, будем иметь:

откуда

если собственные функции нормированы, и

где

если собственные функции не нормированы. Предполагается, что функция  удовлетворяет обычным требованиям, обеспечивающим разложимость по собственным функциям. (Достаточно, чтобы она была кусочно гладкой и удовлетворяла граничным условиям.)
удовлетворяет обычным требованиям, обеспечивающим разложимость по собственным функциям. (Достаточно, чтобы она была кусочно гладкой и удовлетворяла граничным условиям.)
Подставляя найденные значения  в формулу (6.17), придадим ей вид
в формулу (6.17), придадим ей вид

где

Функция  называется функцией мгновенного источника (или функцией Грина). Чтобы выяснить ее физический смысл, рассмотрим начальное распределение температур в виде
называется функцией мгновенного источника (или функцией Грина). Чтобы выяснить ее физический смысл, рассмотрим начальное распределение температур в виде  -функции (функции Дирака), отличающейся
-функции (функции Дирака), отличающейся  нуля в одной точке
нуля в одной точке  в которой она равна бесконечности, причем интеграл от этой функции равен единице. Тогда
в которой она равна бесконечности, причем интеграл от этой функции равен единице. Тогда

Следовательно,  температура, созданная в точке
температура, созданная в точке  в момент
в момент  тепловым источником единичной интенсивности, сосредоточенным в точке
тепловым источником единичной интенсивности, сосредоточенным в точке  в момент
в момент  Функция
Функция  симметрична относительно переменных
симметрична относительно переменных  и
и
Перейдем к решению неоднородного уравнения

с начальным условием  при
при  и однородными граничными условиями.
и однородными граничными условиями.
Решение будем искать в виде ряда по собственным функциям

где  подлежат определению. Функцию
подлежат определению. Функцию  также представим рядом
также представим рядом

где  коэффициенты разложения, определяемые по формулам
коэффициенты разложения, определяемые по формулам

где 
Подставляя в уравнение, будем иметь:

откуда с учетом того, что  при
при  получим:
получим:

и, следовательно,

Решение можно представить также в следующей форме: 

где

Физический смысл решения таков: его можно рассматривать как результат суммирования действия мгновенных источников, распределенных по длине стержня (интегрирование по  и распределенных по времени (интегрирование по
и распределенных по времени (интегрирование по 
Решение неоднородного уравнения при любых начальных условиях получается суммированием:

Неоднородные граничные условия сводятся к однородным заменой

где  любая дважды дифференцируемая функция, удовлетворяющая неоднородным граничным условиям. Для
любая дважды дифференцируемая функция, удовлетворяющая неоднородным граничным условиям. Для  получаем уравнение с измененной правой частью. Если уравнение для определения и записать в виде
получаем уравнение с измененной правой частью. Если уравнение для определения и записать в виде  то уравнение для
то уравнение для  будет иметь вид
будет иметь вид  граничные условия для функции
граничные условия для функции  будут однородными, а начальное условие при
будут однородными, а начальное условие при  будет следующим:
будет следующим: 
Таким образом, получив решение однородной краевой задачи для однородного уравнения и составив выражение для функции источника, можно получить решения неоднородных задач в квадратурах.
3. Интеграл Дюгамеля. Пусть  есть решение неоднородной краевой задачи при условиях
есть решение неоднородной краевой задачи при условиях 
 и при однородных начальных условиях; тогда функция
и при однородных начальных условиях; тогда функция

будет решением следующей краевой задачи:

при однородных граничных условиях. Формула (6.28) называется интегральной формулой Дюгамеля. Аналогично краевая задача

сводится к краевой задаче

4. Частный случай постоянных  В силу сказанного выше рассматриваем только однородное уравнение
В силу сказанного выше рассматриваем только однородное уравнение

полагая  получим:
получим:

откуда

Первая краевая задача. Собственные значения: 
Собственные функции (ненормированные):

Неоднородные граничные условия можно привести к однородным заменой

Вторая краевая задача. В этом случае  также является собственным значением, а
также является собственным значением, а  -соответствующей собственной функцией; собственные значения для
-соответствующей собственной функцией; собственные значения для  Собственные функции;
Собственные функции; 

Неоднородные граничные условия сводятся к однородным заменой

Третья краевая задача. Собственные значения определяются через корни  уравнения
уравнения

где 
Собственные функции:

Сведение неоднородных граничных условий к однородным может быть достигнуто заменой

Четвертая краевая задача. Имеется собственное значение  соответствующая собственная функция:
соответствующая собственная функция: 
Собственные значения  где
где  целое число; каждому собственному значению, кроме нулевого, соответствуют две собственных функции:
целое число; каждому собственному значению, кроме нулевого, соответствуют две собственных функции:

5. Функция Грина и функция Якоби. В теории эллиптических функций встречается функция

называемая функцией Якоби. Первый ряд быстро сходится при больших  второй — при малых
второй — при малых 
Через эту функцию легко выражаются функции Грина некоторых из рассмотренных краевых задач. Первая краевая задача:

Решение первой краевой задачи при неоднородных  ничных условиях также выражается через функцию Якоби. При однородных начальных условиях
ничных условиях также выражается через функцию Якоби. При однородных начальных условиях

Вторая краевая задача:

Третья краевая задача:

Смешанные краевые задачи:

6. Некоторые смешанные краевые задачи.
а) Граничные условия:

Собственные функции;

б) Граничные условия:

Собственные значения  определяются через корни уравнения
определяются через корни уравнения  где
где  Собственные функции:
Собственные функции:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОБЩИЕ СВЕДЕНИЯ О ЛИНЕЙНЫХ УРАВНЕНИЯХ В ЧАСТНЫХ ПРОИЗВОДНЫХ
- § 2. Классификация и канонические формы уравнений второго порядка с двумя независимыми переменными
- § 3. Классификация и канонические формы уравнений второго порядка с n независимыми переменными
- § 4. Задача Коши
- ГЛАВА II. ГИПЕРБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. Понятие о гиперболическом уравнении второго порядка. Простейшие примеры гиперболических уравнений
- § 2. Гиперболическое уравнение с двумя независимыми переменными
- § 3. Метод Фурье в случае двух переменных
- § 4. Волновое уравнение
- § 5. Метод Фурье для многих независимых переменных
- § 6. Сведения о более общих гиперболических уравнениях второго порядка
- § 7. Системы линейных гиперболических уравнений
- ГЛАВА III. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
- 2. Простейшие задачи, приводящие к уравнениям Лапласа и Пуассона.
- 3. Уравнение Лапласа в криволинейных координатах.
- 4. Фундаментальные решения уравнения Лапласа.
- § 2. Интегральные формулы
- § 3. Основные свойства гармонических функций
- § 4. Основные краевые задачи для уравнений Лапласа и Пуассона
- § 5. Решение краевых задач
- § 6. Функция Грина (функция источника)
- § 7. Сведения о более общих уравнениях эллиптического типа
- § 8. Потенциалы
- ГЛАВА IV. УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
- § 2. Разделение переменных в двумерном уравнении
- § 3. Разделение переменных в трехмерном уравнении
- § 4. Координаты, в которых переменные разделяются
- § 5. Решение краевых задач для неоднородного уравнения Гельмгольца
- ГЛАВА V. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОБЩИХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ
- § 2. Методы теории потенциала
- § 3. Обобщенные решения краевых задач
- § 4. Уравнения второго порядка с малым параметром при старших производных
- § 5. Уравнения высших порядков с малым параметром при старших производных
- ГЛАВА VI. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. Некоторые задачи, приводящие к уравнениям параболического типа с двумя независимыми переменными
- § 2. Общие свойства решений уравнений параболического типа
- § 3. Краевые задачи для конечного отрезка
- § 4. Решение уравнения теплопроводности на бесконечной прямой
- § 5. Задачи без начальных условий
- § 6. Понятие о параболической системе
- § 7. Фундаментальная матрица параболической системы
- § 8. Задача Коши и смешанная задача для параболической системы
- § 9. Теория потенциала для одного параболического уравнения второго порядка
- § 10. Свойства решений параболических систем
- ГЛАВА VII. ВЫРОЖДАЮЩИЕСЯ ГИПЕРБОЛИЧЕСКИЕ И ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. Задача Коши для гиперболических уравнений с двумя независимыми переменными и с начальными данными на линии параболичности
- § 2. Задача Коши для гиперболических уравнений, вырождающихся на начальной плоскости
- § 3. Смешанная задача для гиперболических уравнений, вырождающихся на начальной плоскости
- § 4. Смешанная задача для гиперболических уравнений, вырождающихся на части боковой границы области
- § 5. Краевые задачи для эллиптических уравнений, вырождающихся на границе области
- § 6. Применение функциональных методов исследования эллиптических уравнений, вырождающихся на части границы
- ГЛАВА VIII. УРАВНЕНИЯ СМЕШАННОГО ЭЛЛИПТИКО-ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 2. Постановка смешанных краевых задач для уравнения С. А. Чаплыгина
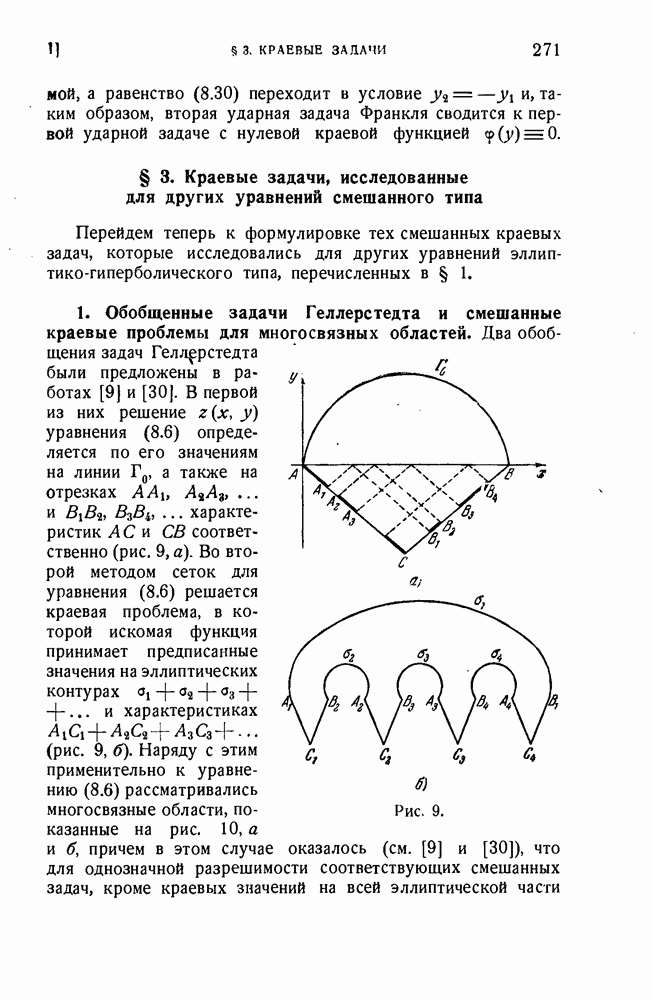
- § 3. Краевые задачи, исследованные для других уравнений смешанного типа
- § 4. Теоремы единственности и методы их доказательства
- § 5. Теоремы существования для смешанных краевых задач
- ГЛАВА IX. МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ ДИФРАКЦИИ И РАСПРОСТРАНЕНИЯ ВОЛН
- § 2. Плоские волны
- § 3. Точечные источники колебаний для уравнений теории упругости и уравнений Максвелла в случае неограниченного пространства. Задача Коши для уравнений теории упругости
- § 4. Установившиеся колебания
- § 5. Точечные источники для полуплоскости и полупространства
- § 6. Дифракция от угла и полуплоскости
- § 7. Задачи стационарной дифракции в случае цилиндрических и сферических границ раздела
- § 8. Задачи нестационарной дифракции в случае цилиндрических и сферических границ раздела
- § 9. Приближенные и асимптотические методы в задачах дифракции
- § 10. Литературные указания по другим задачам дифракции