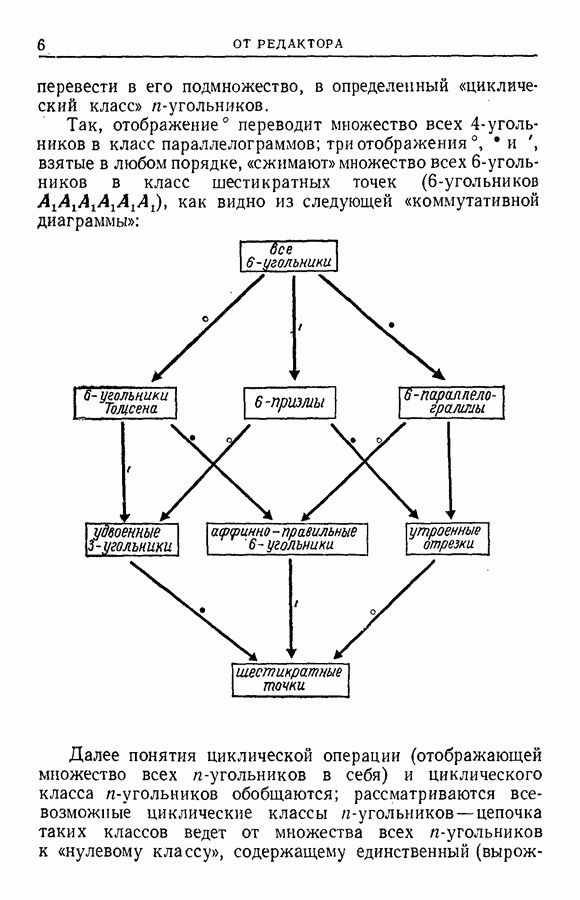
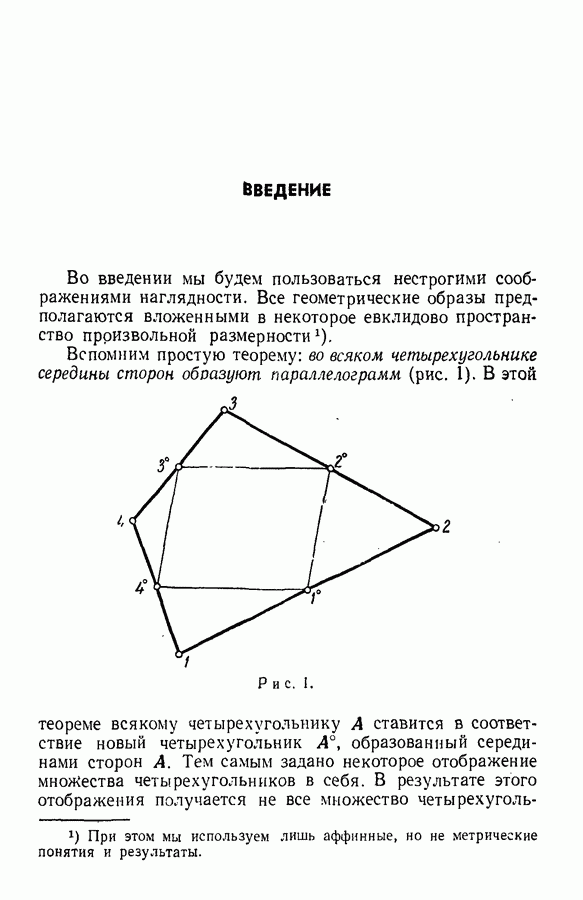
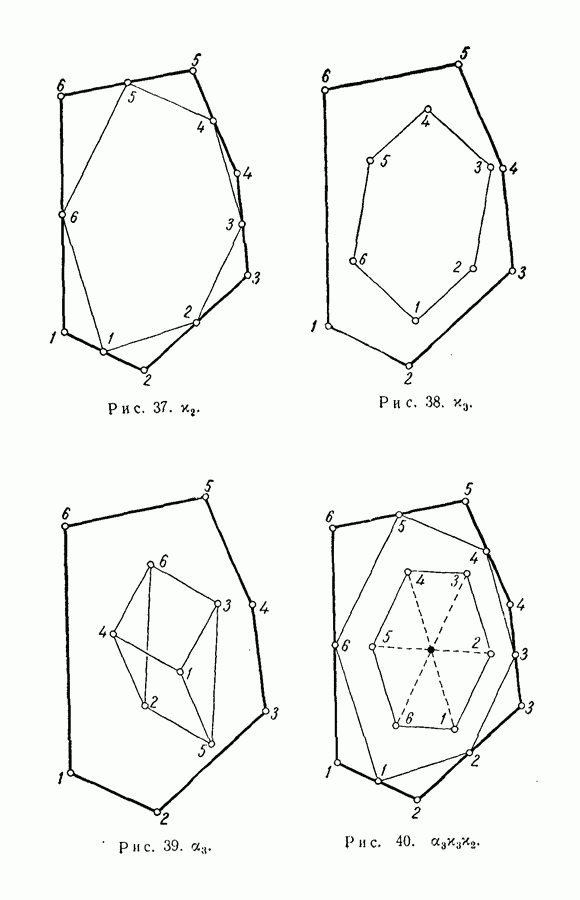
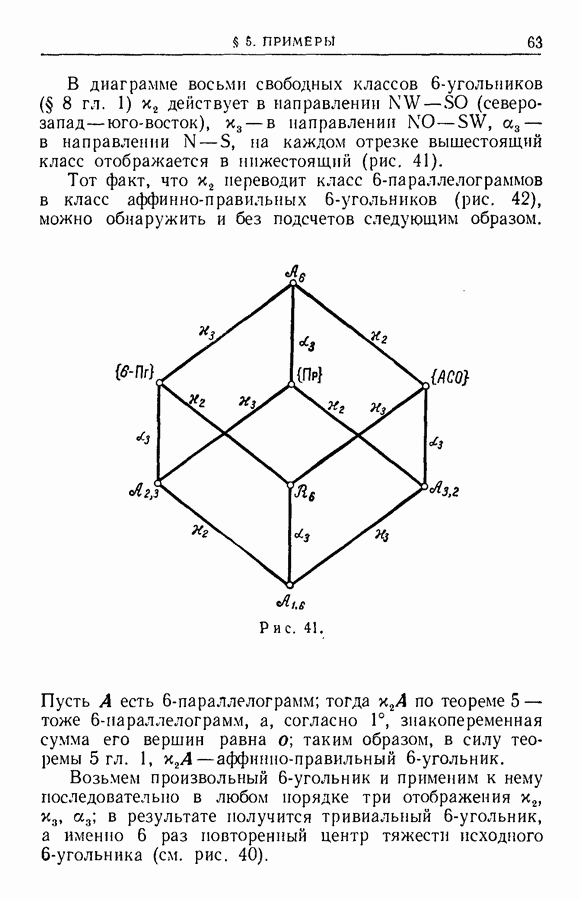
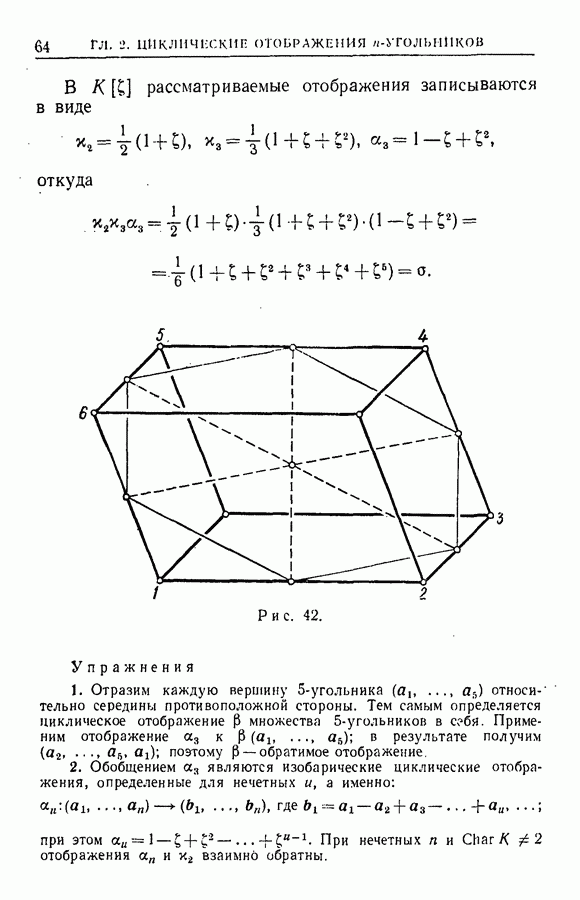
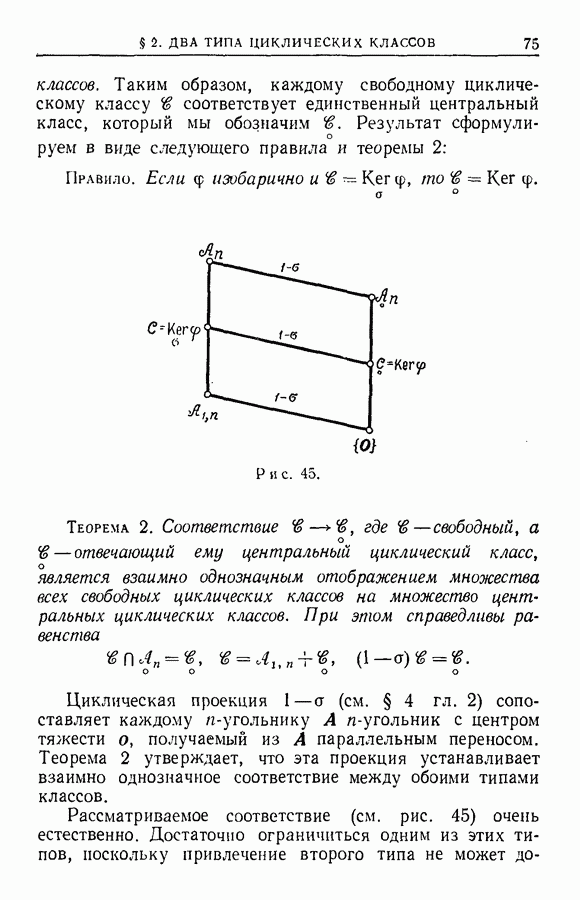
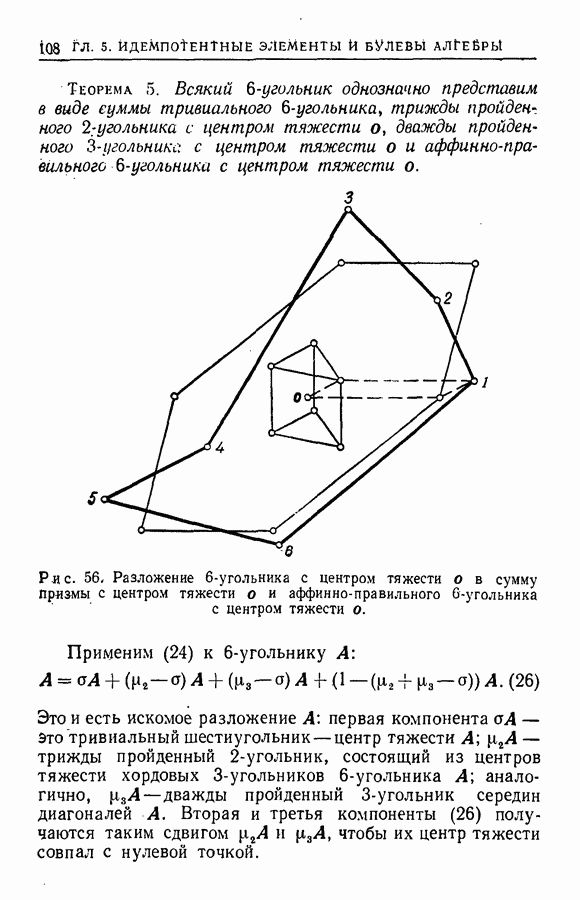
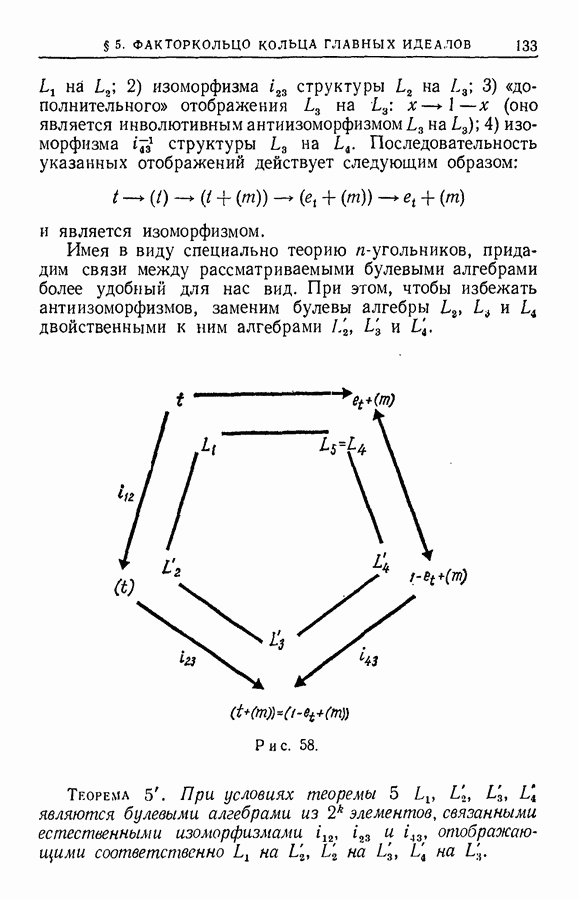
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 3. ОСНОВНАЯ ТЕОРЕМА О ЦИКЛИЧЕСКИХ КЛАССАХ
§ 1. Сравнения в кольце главных идеалов
Пусть  коммутативное кольцо с 1. Единицы (или обратимые элементы) кольца
коммутативное кольцо с 1. Единицы (или обратимые элементы) кольца  образуют по умножению абелеву группу
образуют по умножению абелеву группу  Элементы
Элементы  называются ассоциированными, если существует такой элемент и
называются ассоциированными, если существует такой элемент и  что
что  (в таком случае мы пишем
(в таком случае мы пишем  Ассоциированность является отношением эквивалентности в
Ассоциированность является отношением эквивалентности в  Класс ассоциированных с а элементов обозначим через
Класс ассоциированных с а элементов обозначим через 
Порожденный элементом а главный идеал  мы будем, как обычно, обозначать через
мы будем, как обычно, обозначать через  Очевидно, что
Очевидно, что  следует
следует  (но не наоборот!).
(но не наоборот!).
Лемма. Пусть  идемпотентные элементы коммутативного кольца с 1. Тогда следующие утверждения эквивалентны:
идемпотентные элементы коммутативного кольца с 1. Тогда следующие утверждения эквивалентны:

Отсюда следует, что класс ассоциированных элементов содержит не более одного идемпотентного элемента.
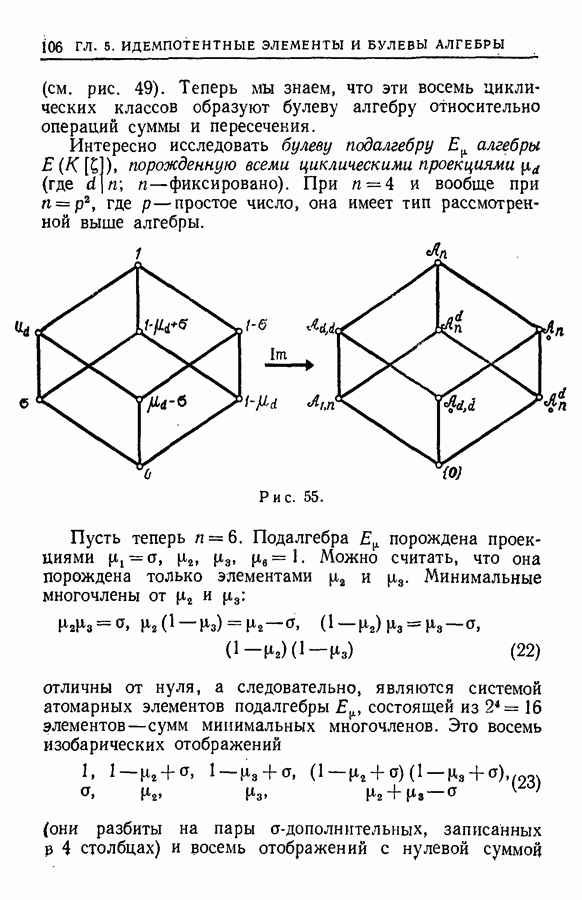
Доказательство. Очевидно, что 1) 2) и 3) 1); таким образом, остается доказать, что 2) 3).
Множество  состоит из элементов
состоит из элементов  где
где  Так как
Так как  —идемпотент, то
—идемпотент, то  умножение на
умножение на  не меняет элементов из
не меняет элементов из  В частности, если
В частности, если  то
то  Аналогично
Аналогично  Отсюда в силу коммутативности кольца следует, что
Отсюда в силу коммутативности кольца следует, что 
Кольцом главных идеалов называется область целостности с 1, в которой всякий идеал является главным. Известные примеры колец главных идеалов: кольцо целых чисел, кольцо многочленов над произвольным телом.
В кольце главных идеалов всякий отличный от нуля элемент, не являющийся единицей кольца, представим в виде произведения простых элементов — и это представление единственно с точностью до порядка сомножителей и замены их ассоциированными.
Пусть теперь  кольцо главных идеалов, и пусть задан элемент
кольцо главных идеалов, и пусть задан элемент  Будем говорить, что а сравним с
Будем говорить, что а сравним с  по модулю
по модулю 

Сравнение является отношением эквивалентности в  согласованным со сложением и умножением элементов
согласованным со сложением и умножением элементов 
Элемент  назовем идемпотентным по модулю
назовем идемпотентным по модулю  если
если  или, что то же самое,
или, что то же самое,  Если
Если  идемпотентен
идемпотентен  то
то  тоже идемпотентен
тоже идемпотентен  Произведение и булева сумма двух элементов, идемпотентных
Произведение и булева сумма двух элементов, идемпотентных  тоже идемпотентны
тоже идемпотентны 
Элемент  из
из  назовем свободным от квадратов, если он представим в виде произведения попарно неассоциированных простых элементов:
назовем свободным от квадратов, если он представим в виде произведения попарно неассоциированных простых элементов:

Для случая, когда  свободен от квадратов, мы докажем две теоремы об идемпотентных
свободен от квадратов, мы докажем две теоремы об идемпотентных  элементах. При этом мы будем пользоваться простейшими свойствами сравнений, знакомыми читателю из элементарной теории чисел и справедливыми для любого кольца главных идеалов.
элементах. При этом мы будем пользоваться простейшими свойствами сравнений, знакомыми читателю из элементарной теории чисел и справедливыми для любого кольца главных идеалов.
Итак, пусть  имеет вид
имеет вид  Нам понадобятся следующие утверждения:
Нам понадобятся следующие утверждения:
1°.  тогда и только тогда, когда
тогда и только тогда, когда  для всех
для всех 
2°. Элемент  тогда и только тогда идемпотентен
тогда и только тогда идемпотентен  когда для каждого
когда для каждого  он сравним
он сравним  либо с 0, либо с 1.
либо с 0, либо с 1.
Доказательство. Следующие соотношения эквивалентны:
 для всех
для всех  для каждого
для каждого  либо
либо  либо
либо 
3°. («Китайская конструкция».) Для всякого  существует элемент
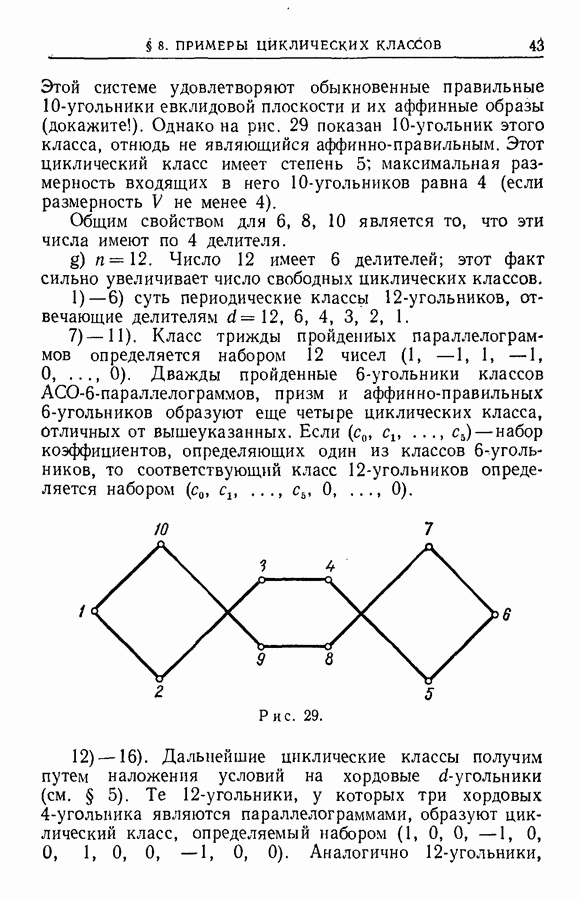
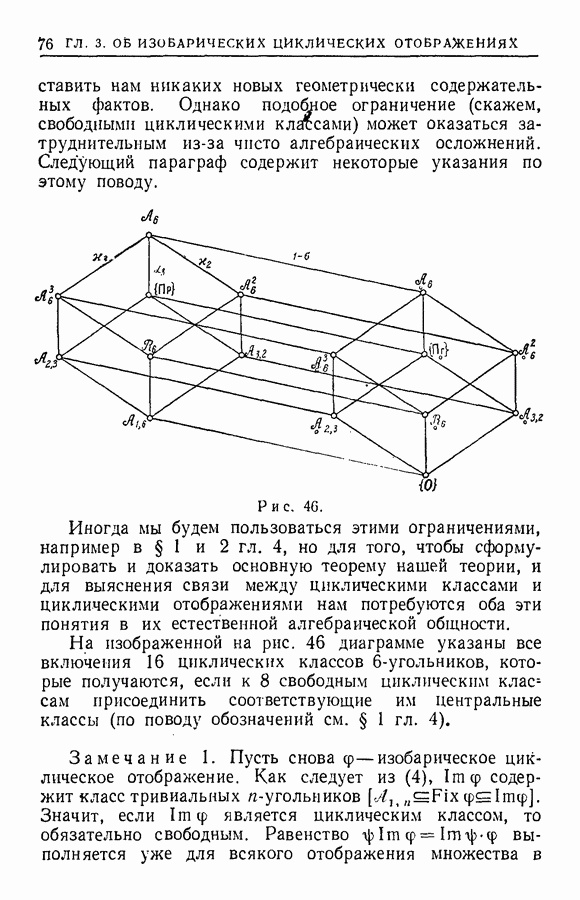
существует элемент  такой, что
такой, что

Из (2) следует

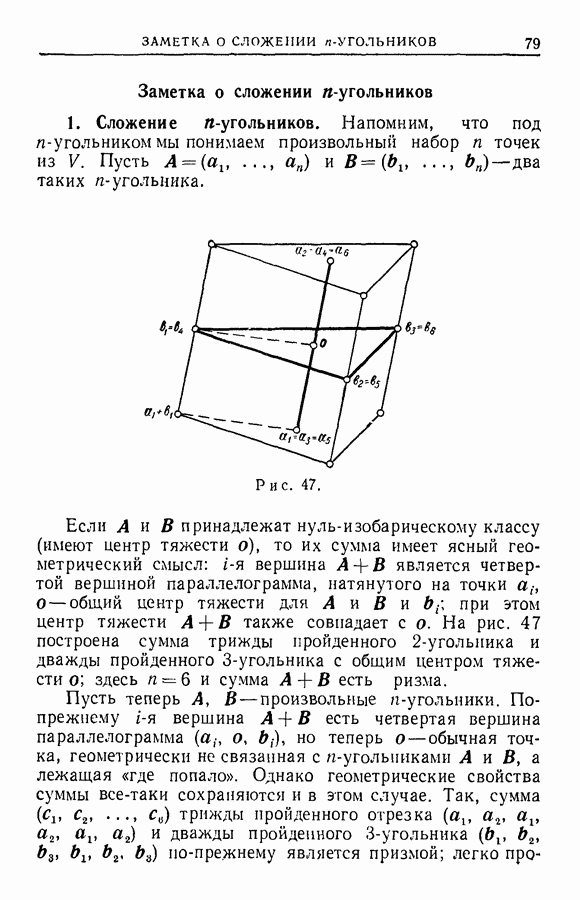
В силу 2°,  идемпотентен
идемпотентен  а в силу 1°,
а в силу 1°,  однозначно определен
однозначно определен  Справедливы равенства
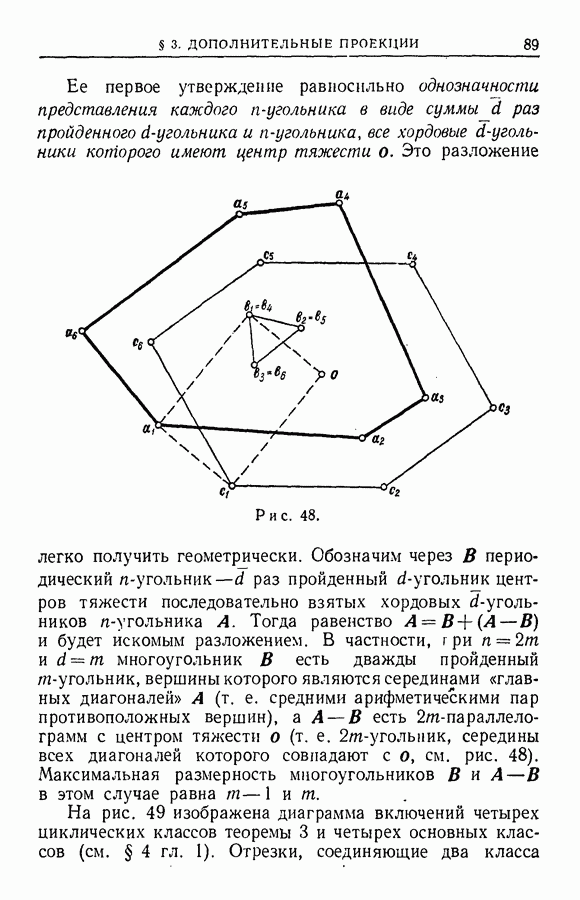
Справедливы равенства

Доказательство. Так как  и — взаимно просты, то сравнение —
и — взаимно просты, то сравнение —  разрешимо. Обозначим
разрешимо. Обозначим  через
через  левую часть этого сравнения, в котором вместо
левую часть этого сравнения, в котором вместо  стоит некоторое его решение. Очевидно,
стоит некоторое его решение. Очевидно,  удовлетворяет сравнениям (1), (2), а следовательно, и (2). Сравнения (3), (4) удовлетворяются по модулю всех
удовлетворяет сравнениям (1), (2), а следовательно, и (2). Сравнения (3), (4) удовлетворяются по модулю всех  а в силу 1° и
а в силу 1° и  частичных сумм выражения
частичных сумм выражения  идемпотентны и попарно не сравнимы
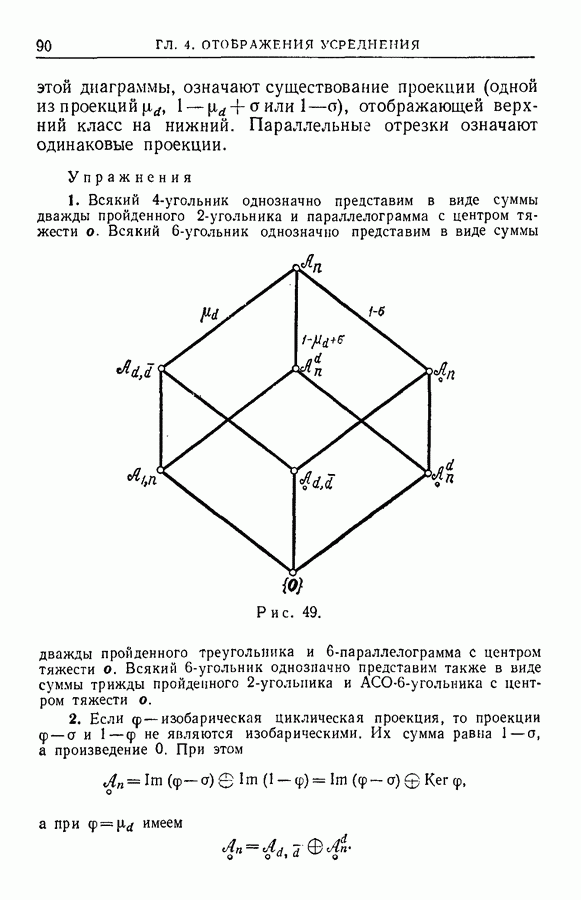
идемпотентны и попарно не сравнимы  Всякий идемпотентный
Всякий идемпотентный  элемент сравним с одной из этих частичных сумм.
элемент сравним с одной из этих частичных сумм.
Доказательство. Если  -подмножество множества
-подмножество множества  то, согласно (1) и (2),
то, согласно (1) и (2),

Это означает, что частичные суммы  идемпотентны
идемпотентны  (утверждение 2°). Всякие две формально различные частичные суммы несравнимы
(утверждение 2°). Всякие две формально различные частичные суммы несравнимы  если
если  например, присутствует в одной из них и отсутствует
например, присутствует в одной из них и отсутствует
в другой, то первая сумма сравнима с единицей, вторая — с нулем  Если
Если  произвольный идемпотентный
произвольный идемпотентный  элемент, то в силу 2° существует подмножество
элемент, то в силу 2° существует подмножество  множества
множества  такое, что
такое, что  для
для  для
для  Отсюда следует, что
Отсюда следует, что  для всех
для всех  а значит,
а значит, 
Итак, доказана
Теорема 1. Пусть  кольцо главных идеалов и
кольцо главных идеалов и  свободный от квадратов элемент вида
свободный от квадратов элемент вида  существует ровно
существует ровно  идемпотентных по модулю
идемпотентных по модулю  элементов, попарно не сравнимых
элементов, попарно не сравнимых  между собой и таких, что каждый идемпотентный
между собой и таких, что каждый идемпотентный  элемент сравним
элемент сравним  ровно с одним из этих
ровно с одним из этих  элементов.
элементов.
Теорема 2. Пусть  кольцо главных идеалов и
кольцо главных идеалов и  свободен от квадратов. Всякий элемент из
свободен от квадратов. Всякий элемент из  ассоциирован по модулю
ассоциирован по модулю  с некоторым идемпотентным по модулю
с некоторым идемпотентным по модулю  элементом.
элементом.
Скажем точнее: для всякого  существуют идемпотентный по модулю
существуют идемпотентный по модулю  элемент
элемент  и элемент и, такие, что
и элемент и, такие, что

Доказательство. Пусть  имеет вид
имеет вид  идемпотентные по модулю
идемпотентные по модулю  элементы «китайской конструкции». Разобьем все простые элементы
элементы «китайской конструкции». Разобьем все простые элементы  на две группы: те, которые делят
на две группы: те, которые делят  и те, которые а не делят. Пусть
и те, которые а не делят. Пусть  Положим
Положим

Элемент  идемпотентен по модулю
идемпотентен по модулю  Как и в доказательстве 4°,
Как и в доказательстве 4°,

Отсюда следует, что  для всех
для всех  первый сомножитель, а при
первый сомножитель, а при  а второй сравнимы с нулем
а второй сравнимы с нулем  Таким образом,
Таким образом,  или
или

[Последнее сравнение следует из того, что  Положим а
Положим а  Тогда справедливо сравнение (5) и
Тогда справедливо сравнение (5) и

Это означает, что ни один из простых  не делит и. Следовательно,
не делит и. Следовательно,  взаимно просты и сравнение (6) разрешимо. Теорема доказана.
взаимно просты и сравнение (6) разрешимо. Теорема доказана.
Замечание. Идемпотентным и ассоциированным с  элементом является
элементом является  а не
а не  Такие обозначения выбраны потому, что, как показано в доказательстве, элемент
Такие обозначения выбраны потому, что, как показано в доказательстве, элемент  ассоциирован
ассоциирован  а не с
а не с 
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА
- ПРЕДЫСТОРИЯ КНИГИ
- ВВЕДЕНИЕ
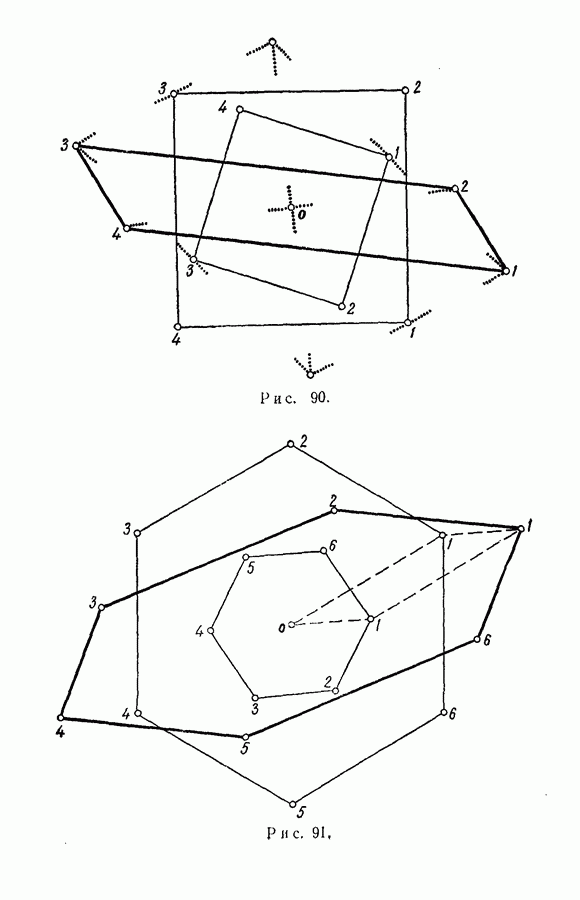
- ГЛАВА 1. ЦИКЛИЧЕСКИЕ КЛАССЫ n-УГОЛЬНИКОВ
- § 1. n-угольники, пространство n-угольников
- § 2. Циклические классы
- § 3. Центр тяжести n-угольника. Нуль-изобарический класс
- § 4. Два типа циклических классов
- § 5. Периодические классы
- § 6. Степень свободы циклического класса
- § 7. Размерность n-угольника
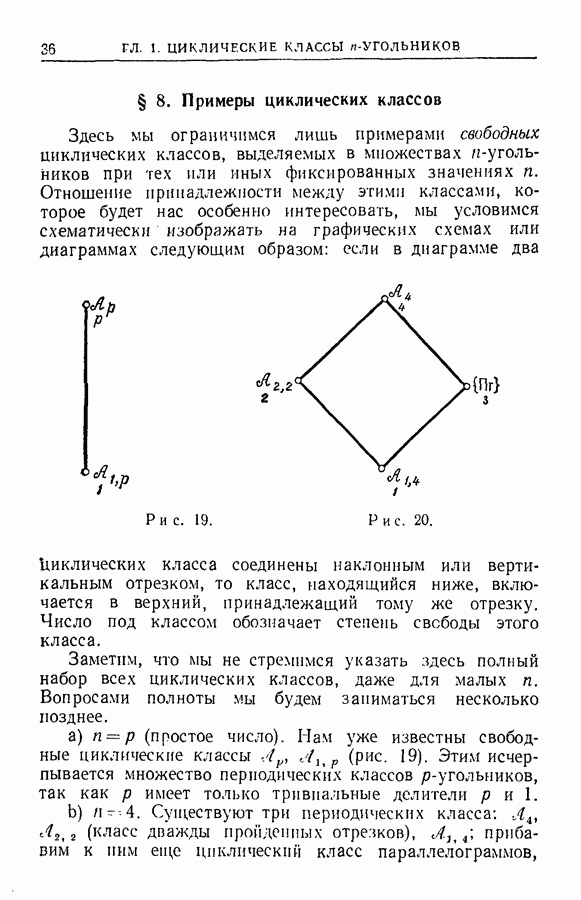
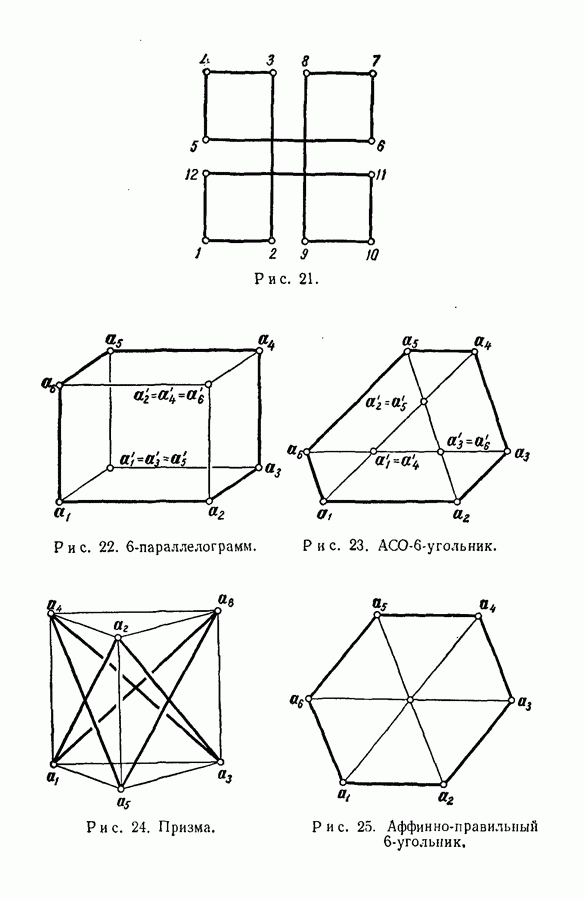
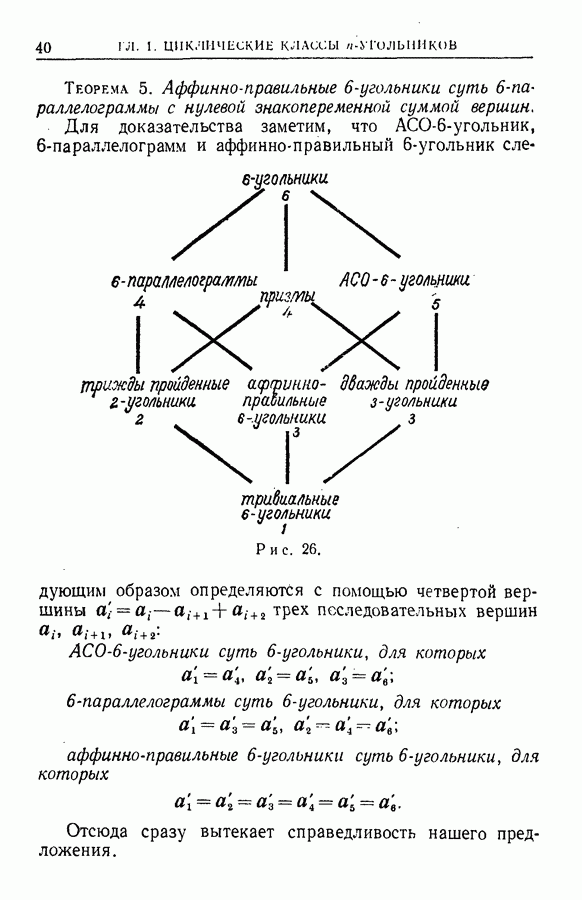
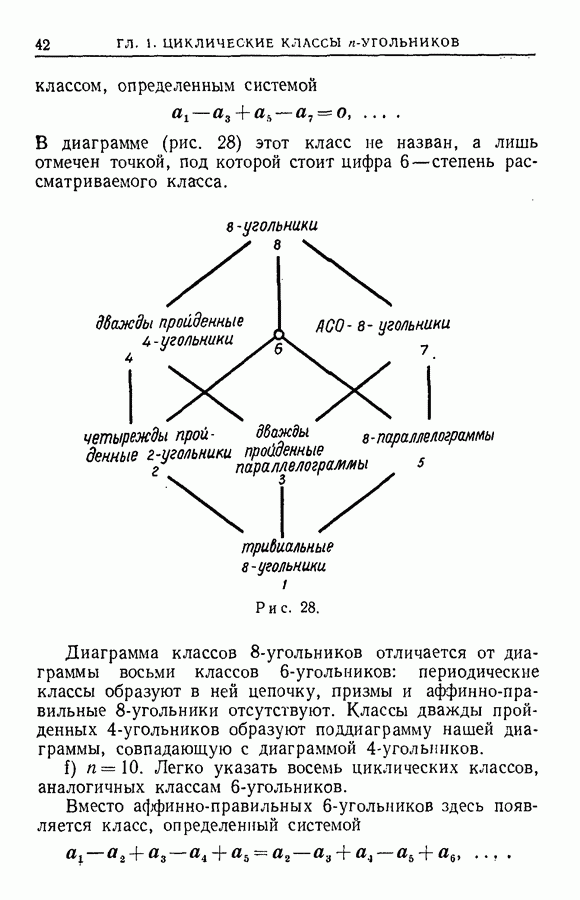
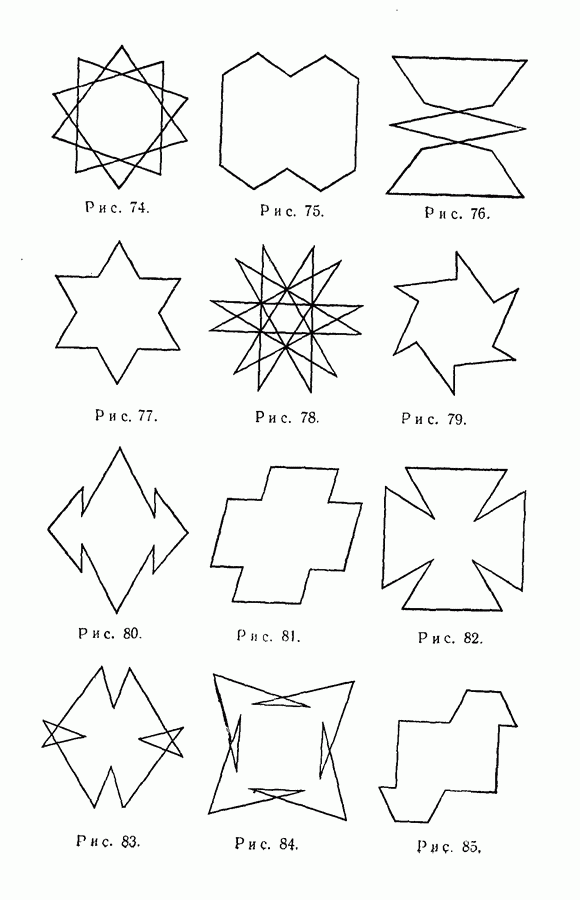
- § 8. Примеры циклических классов
- ГЛАВА 2. ЦИКЛИЧЕСКИЕ ОТОБРАЖЕНИЯ n-УГОЛЬНИКОВ
- § 2. Алгебра циклических отображений
- § 3. Сумма коэффициентов циклического отображения
- § 4. Проекции
- § 5. Примеры
- § 6. Циклическая квазипроекция
- § 7. Изобарические циклические проекции для n=4
- § 8. Циклические матрицы
- ГЛАВА 3. ОБ ИЗОБАРИЧЕСКИХ ЦИКЛИЧЕСКИХ ОТОБРАЖЕНИЯХ
- § 2. Два типа циклических классов
- § 3. Об изобарических циклических отображениях
- Заметка о сложении n-угольников
- ГЛАВА 3. ОТОБРАЖЕНИЯ УСРЕДНЕНИЯ
- § 1. Изобарически распадающиеся n-угольники
- § 2. Хордовые усреднения
- § 3. Дополнительные проекции
- § 4. Последовательные усреднения
- ГЛАВА 3. ИДЕМПОТЕНТНЫЕ ЭЛЕМЕНТЫ И БУЛЕВЫ АЛГЕБРЫ
- § 1. Идемпотентные элементы кольца
- § 2. Булевы алгебры, порожденные конечным числом элементов
- § 3. Идемпотентные эндоморфизмы абелевой группы; Im-вложения
- § 4. Булева алгебра циклических проекций
- § 5. Примеры Im-вложений
- ГЛАВА 3. ОСНОВНАЯ ТЕОРЕМА О ЦИКЛИЧЕСКИХ КЛАССАХ
- § 1. Сравнения в кольце главных идеалов
- § 2. Основные теоремы о циклических отображениях и циклических классах
- § 3. Простые делители многочлена х^n-1 и атомарные циклические классы
- ГЛАВА 7. ИДЕМПОТЕНТ-ВЛОЖЕНИЕ. ФАКТОРКОЛЬЦО КОЛЬЦА ГЛАВНЫХ ИДЕАЛОВ
- § 1. R-модули
- § 2. Идемпотент-вложение
- § 3. Частный случай идемпотент-вложения
- § 4. Идеалы и делимость в кольце главных идеалов
- § 5. Факторкольцо кольца главных идеалов
- § 6. Факторкольцо как сумма факторколец
- ГЛАВА 11. БУЛЕВЫ АЛГЕБРЫ n-УГОЛЬНИКОВ (ТЕОРИЯ I)
- § 2. Делители многочлена х^n-1 и циклические классы
- § 3. Спектр
- § 4. Примеры определения циклических классов по делителям многочлена x^n-1
- ГЛАВА 9. БУЛЕВЫ АЛГЕБРЫ n-УГОЛЬНИКОВ (ТЕОРИЯ II)
- § 1. Соответствие Галуа между аннуляторами и ядрами
- § 2. Идеал-вложение
- § 3. Второе доказательство основной теоремы. Основная диаграмма
- § 4. Градуировка. Степень свободы циклического класса
- § 5. Смешанные задачи
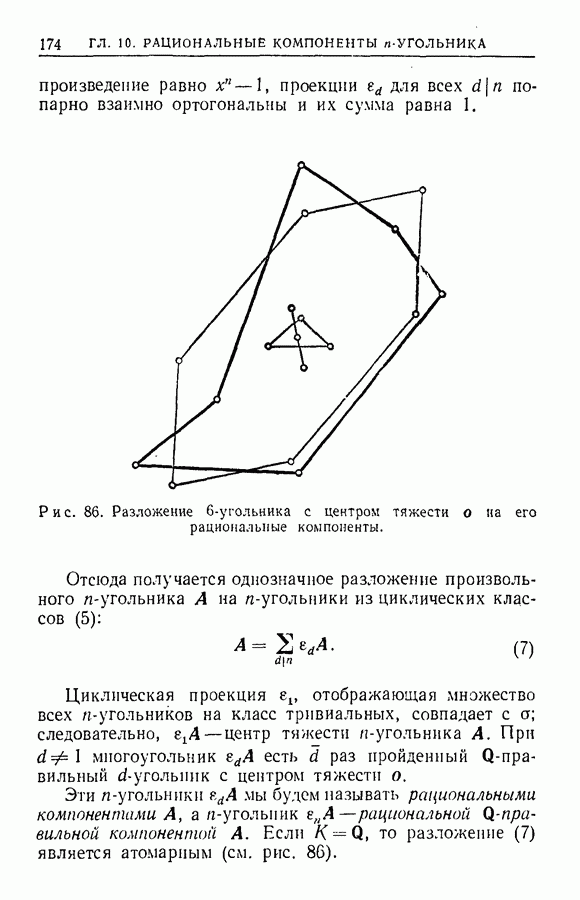
- ГЛАВА 16. РАЦИОНАЛЬНЫЕ КОМПОНЕНТЫ n-УГОЛЬНИКА
- § 2. Циклические классы, определенные многочленами деления круга
- § 3. Рациональные компоненты n-угольника
- § 4. Булева алгебра, порожденная хордовыми усреднениями, и ее атомарные элементы
- § 5. К построению рациональных компонент n-угольника
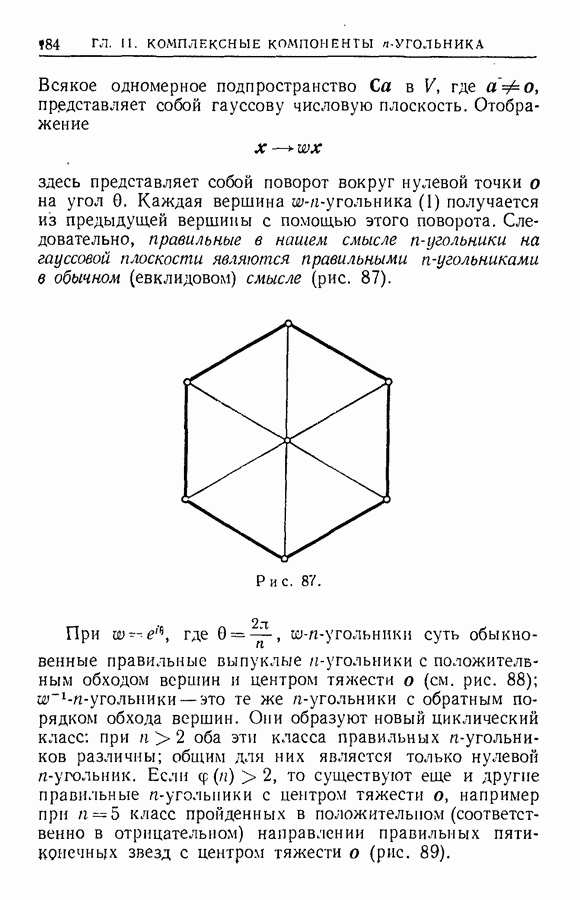
- ГЛАВА 11. КОМПЛЕКСНЫЕ КОМПОНЕНТЫ n-УГОЛЬНИКА
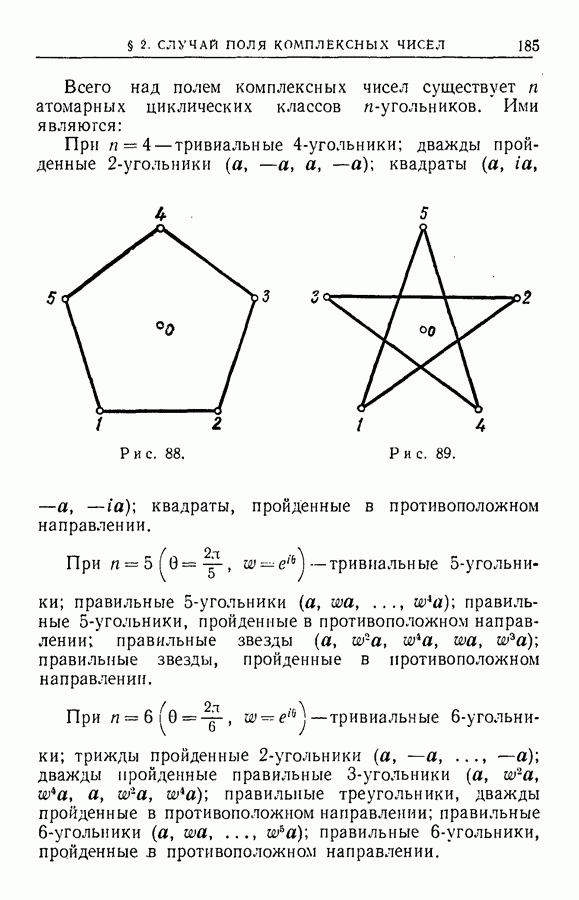
- § 2. Случай поля комплексных чисел
- § 3. Комплексные компоненты n-угольника
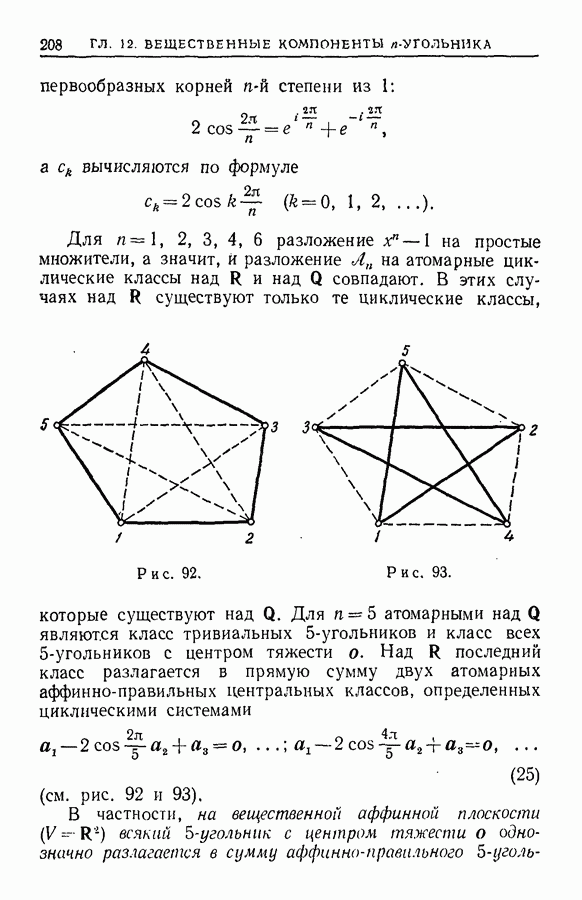
- ГЛАВА 12. ВЕЩЕСТВЕННЫЕ КОМПОНЕНТЫ n-УГОЛЬНИКА
- § 2. Специальный тип циклических систем уравнений
- § 3. Аффинно-правильные n-угольники
- § 4. Три крайних случая булевых алгебр циклических классов n-угольников
- § 5. Вещественные компоненты n-угольника
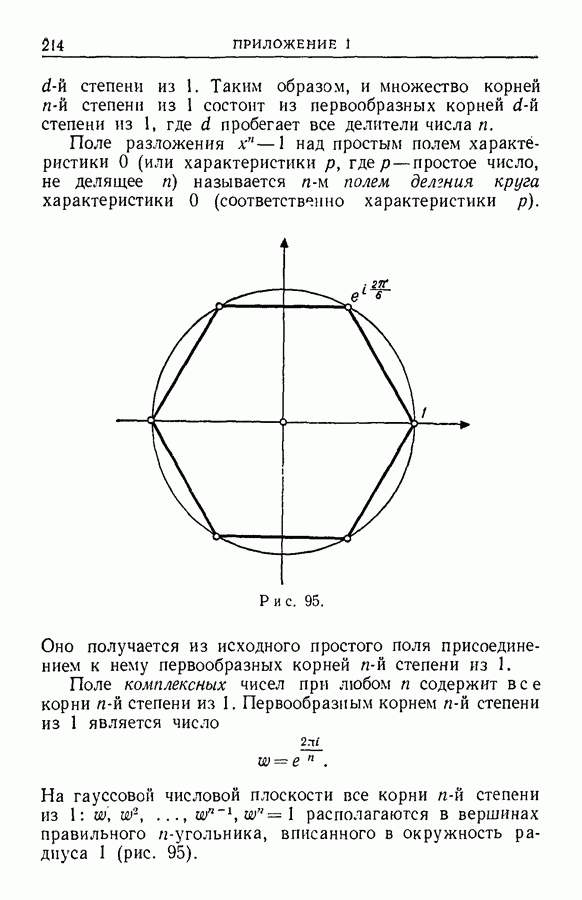
- ПРИЛОЖЕНИЕ I. МНОГОЧЛЕНЫ ДЕЛЕНИЯ КРУГА
- § 2. Многочлены деления круга
- § 3. Теорема Редеи
- § 4. Многочлены деления круга над простыми конечными полями
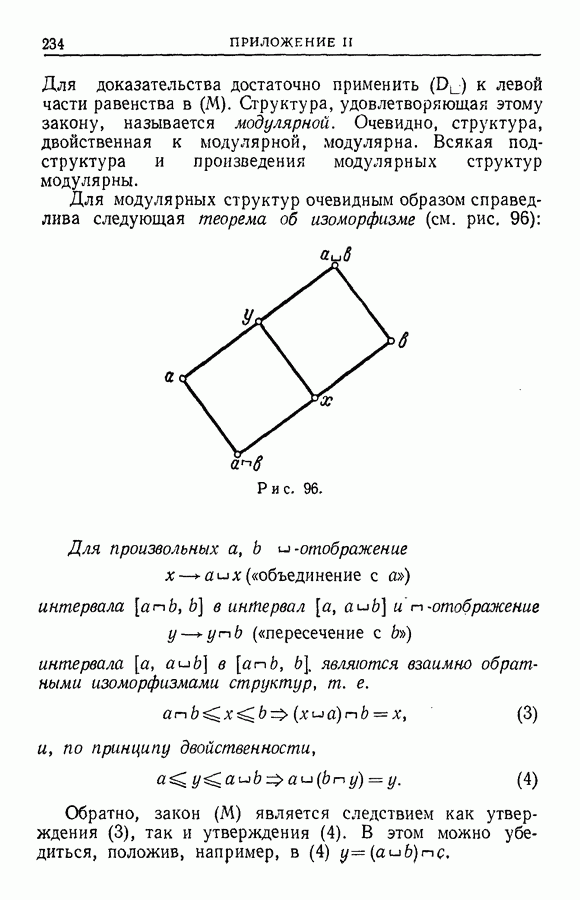
- ПРИЛОЖЕНИЕ II. СТРУКТУРЫ