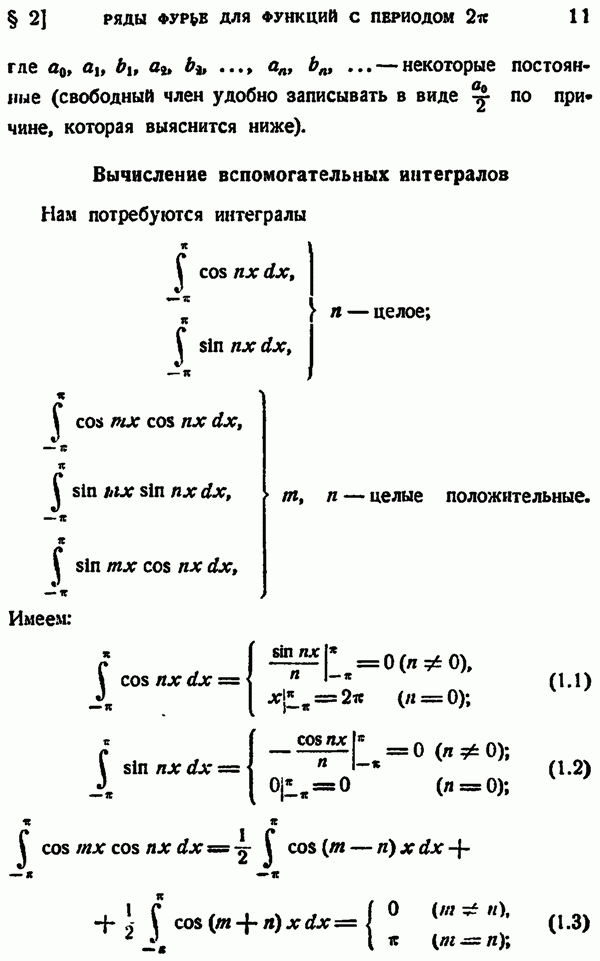
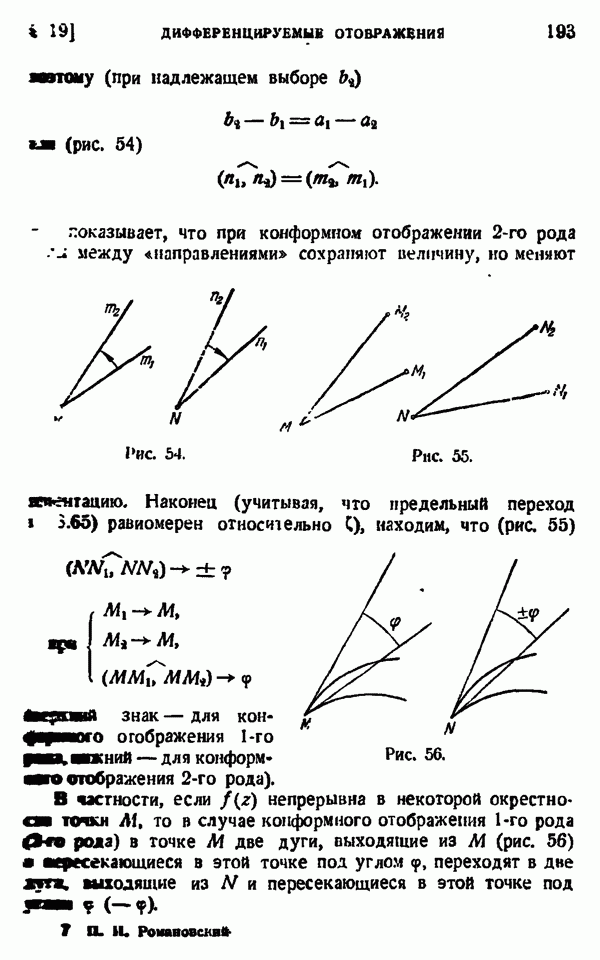
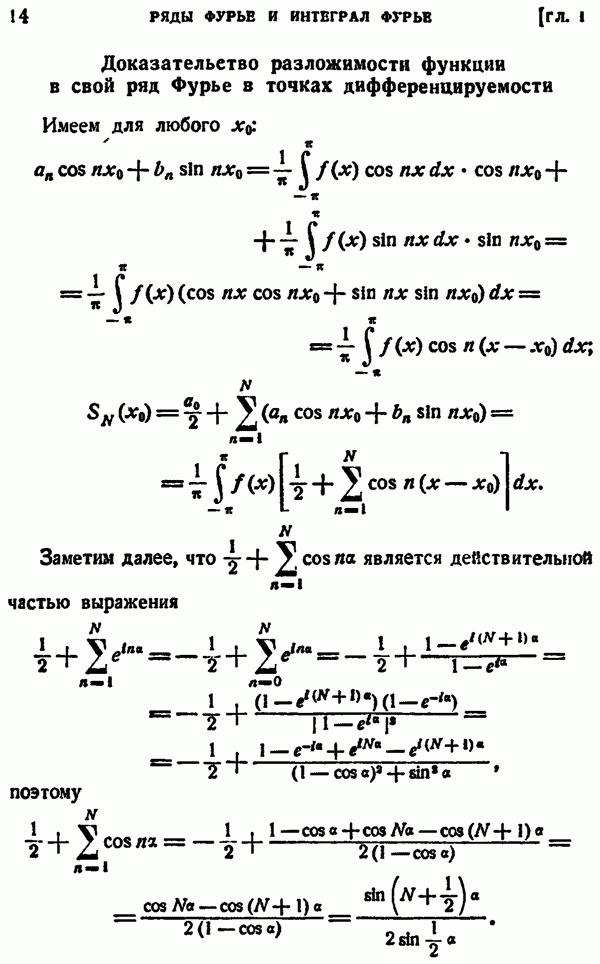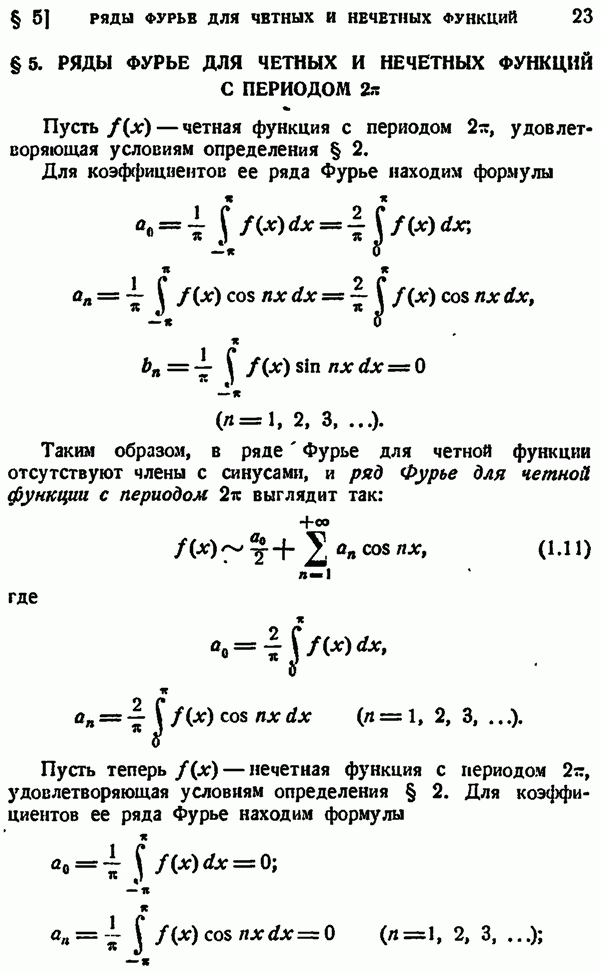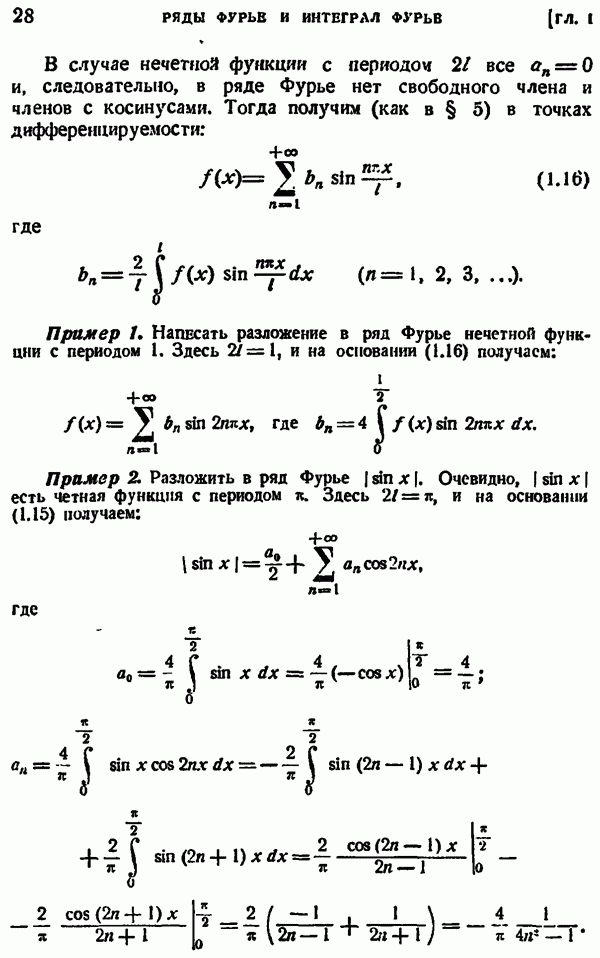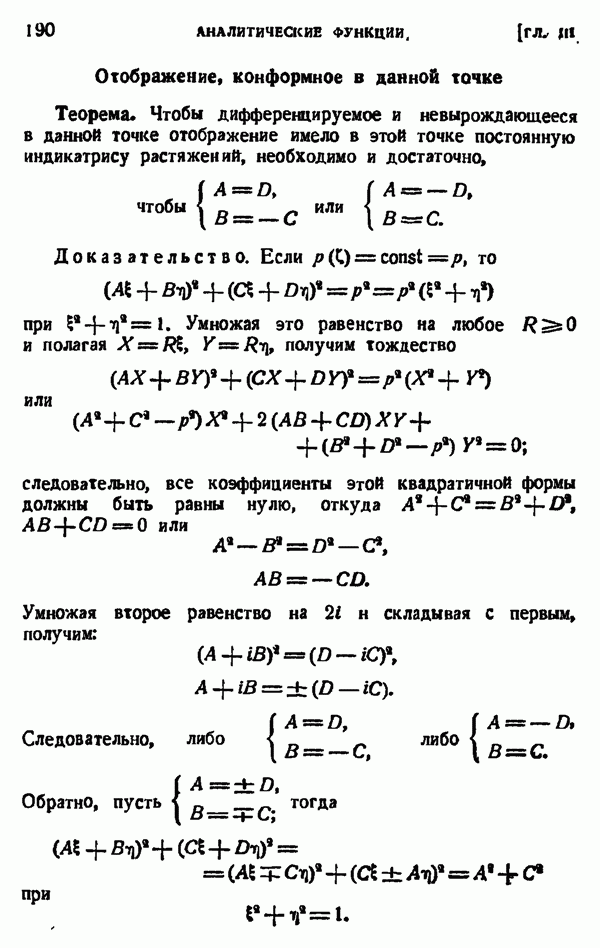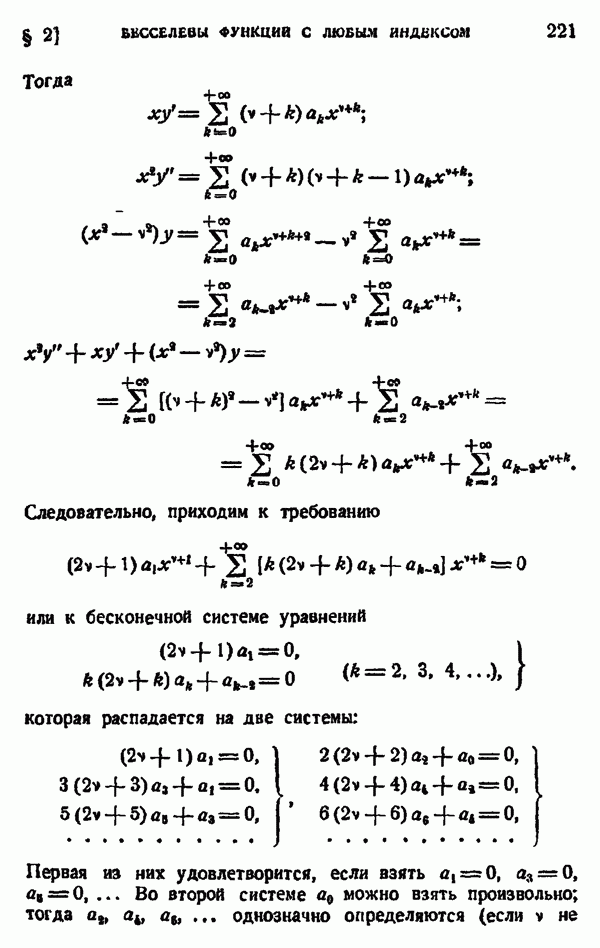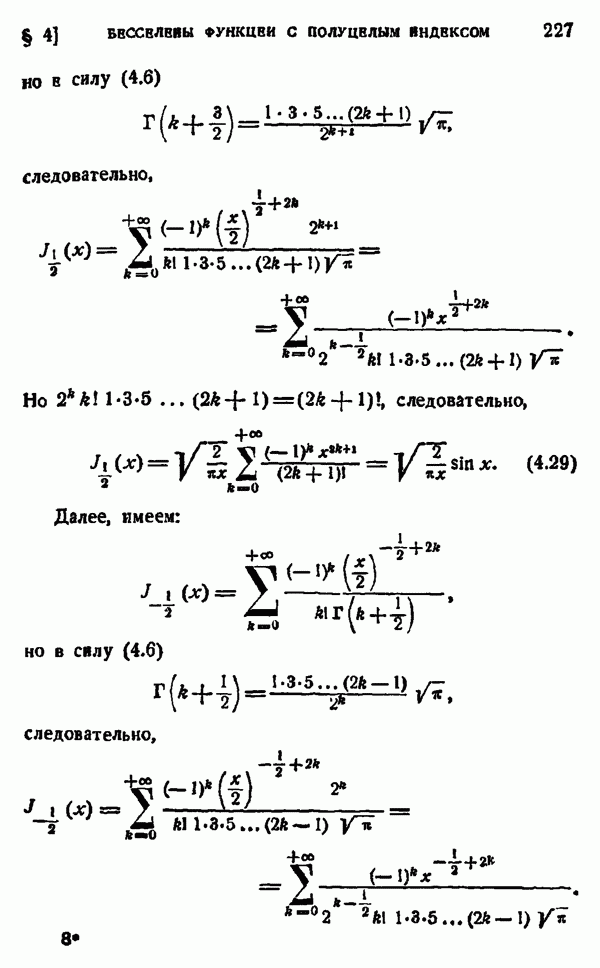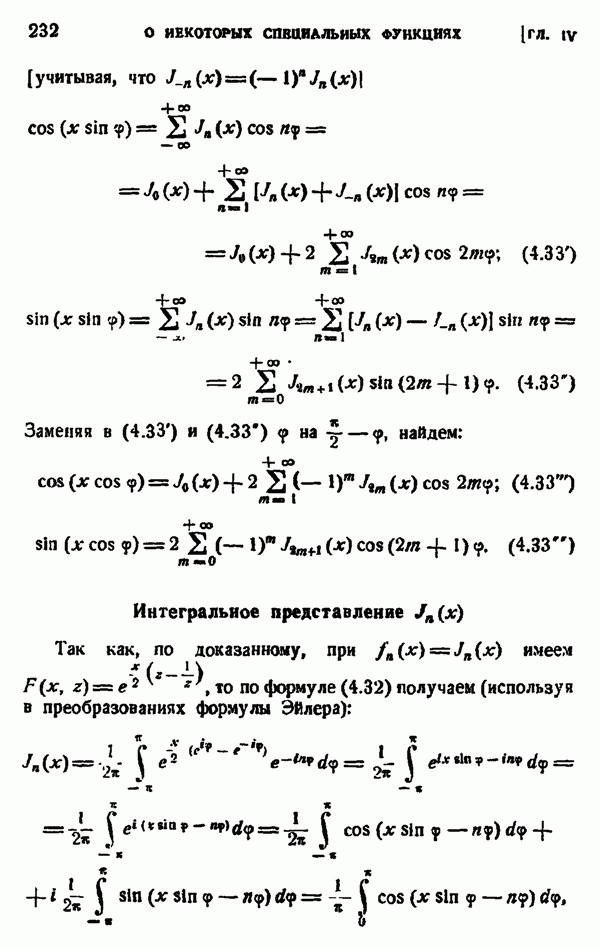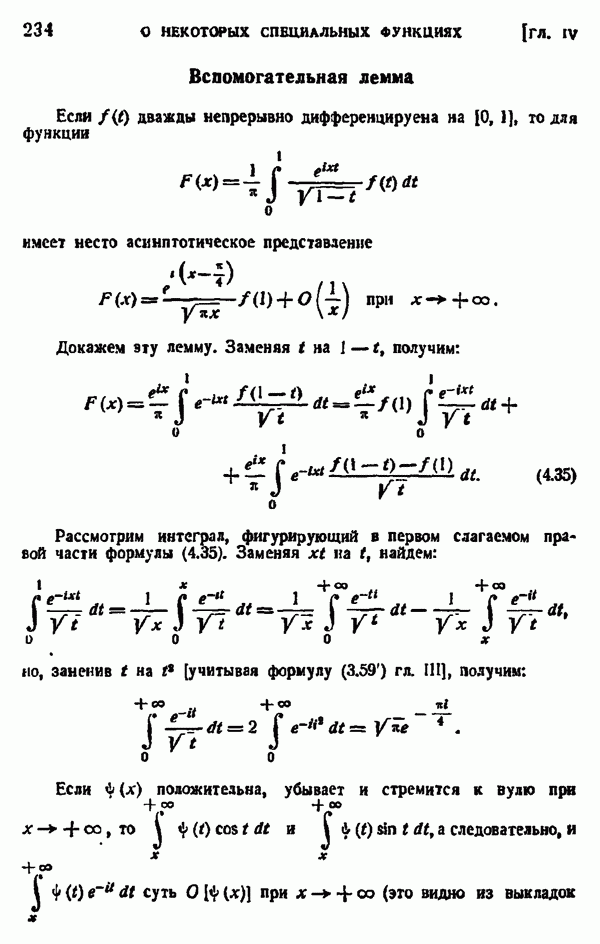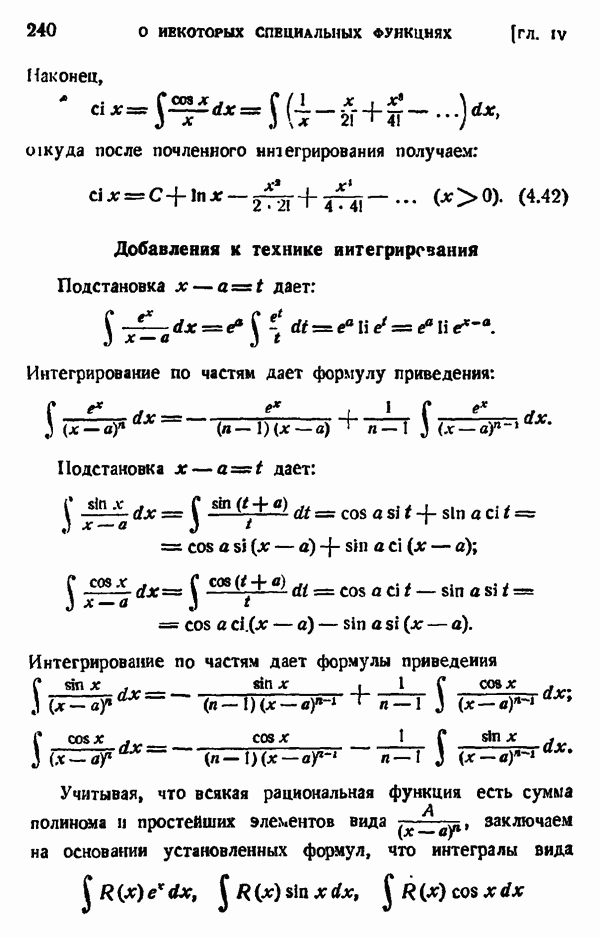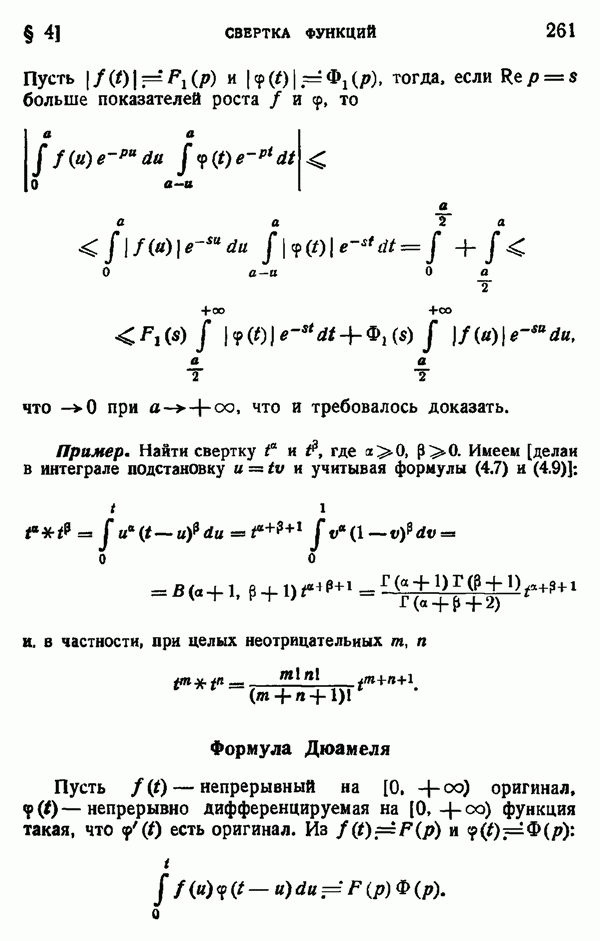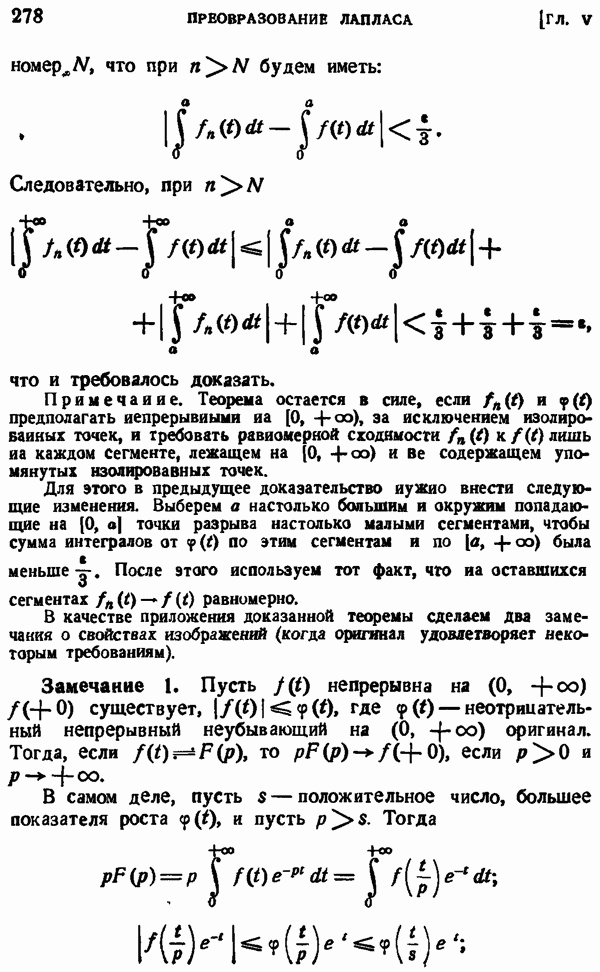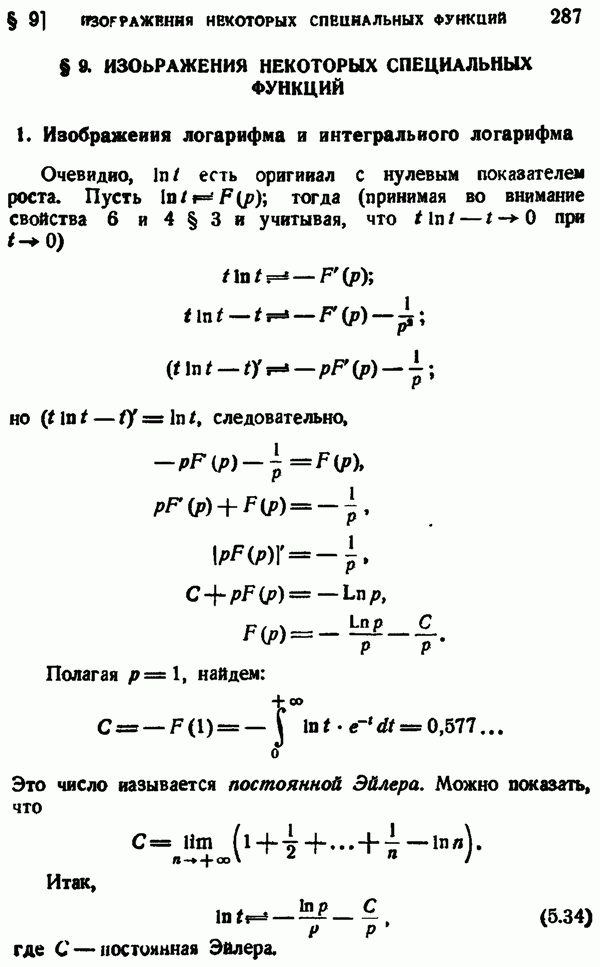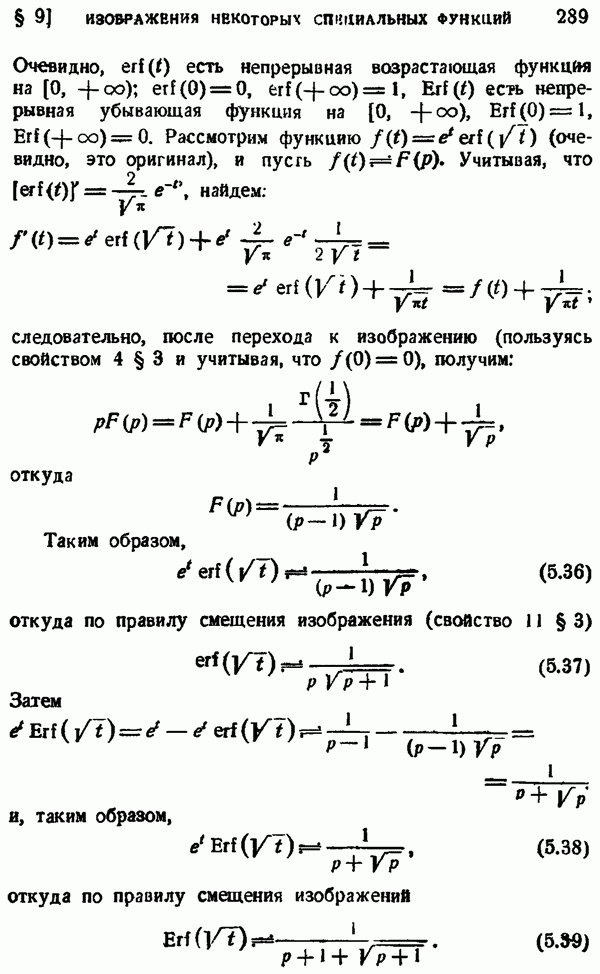| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Дугу кривой называют гладкой, еслв функции, фигурирующие в ее параметрических уравнениях, непрерывно дифференцируемы. Дугу называют кусочно-гладкой, если ее можно разбить на конечное число гладких дуг.
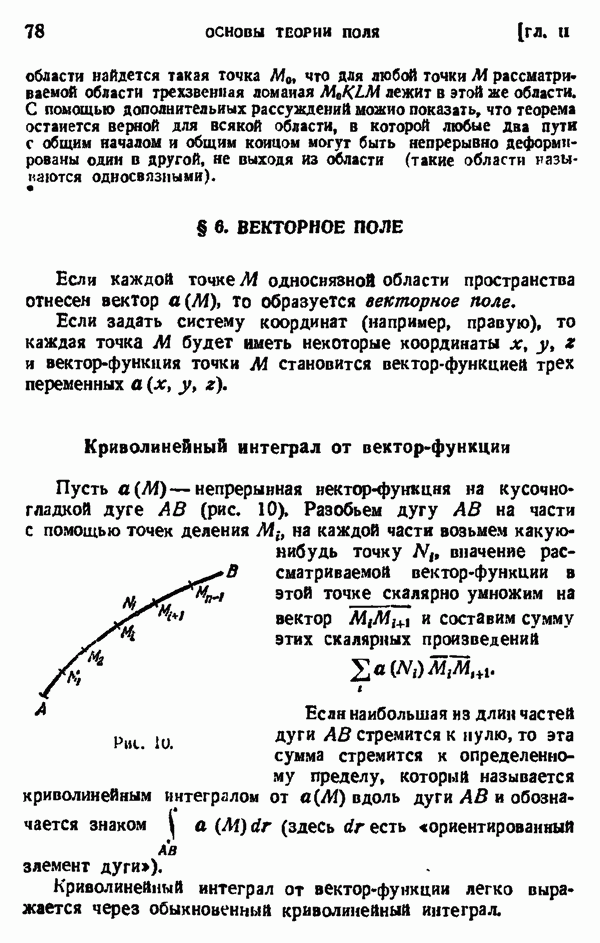
Пусть  непрерывная функция на кусочногладкой дуге
непрерывная функция на кусочногладкой дуге  (рис. 3). Разобьем дугу
(рис. 3). Разобьем дугу  на части с помощью точек деления
на части с помощью точек деления  На каждой части
На каждой части  возьмем какую-нибудь точку
возьмем какую-нибудь точку  значение рассматриваемой функции в этой точке умножнм на
значение рассматриваемой функции в этой точке умножнм на  и составим сумму таких произведений
и составим сумму таких произведений


Рис. 3.
Если наибольшая  длин частей дуги
длин частей дуги  стремится к нулю, то эта сумма стремится к определенному пределу, который называется криволинейным интегралом от
стремится к нулю, то эта сумма стремится к определенному пределу, который называется криволинейным интегралом от  вдоль дуги
вдоль дуги  по переменному х и обозначается знаком
по переменному х и обозначается знаком  Аналогично определяются криволинейные интегралы по переменным
Аналогично определяются криволинейные интегралы по переменным  Таким образом,
Таким образом,

где  — непрерывные функции на дуге
— непрерывные функции на дуге 
Далее вводим понятие комбинироианного криволинейного интеграла

Из определения криволинейного интеграла непосредственно следует, что при перемене направления дуги интеграл лишь меняет свой знак


Рис. 4
Далее, если дугу разбить на части, то интеграл вдоль всей дуги равен сумме интегралов вдоль ее частей, например (рис. 4),

Отсюда следует, что интеграл вдоль замкнутой кривой не вависнт от выбора начальной точки, а зависит лишь от направления обхода кривой. В самом деле (рис. 5),

откуда (так как правые части этих равенств одинаковы)


Рис. 5.
Из определения криволинейного интеграла сразу следует, что постоянные множители выносятся за знак интеграла,  суммы равен сумме интегралов. Из (2.18) видно, что
суммы равен сумме интегралов. Из (2.18) видно, что
 если дуга
если дуга  расположена в плоскости
расположена в плоскости 
Аналогично из (2.19) и (2.20) следует, что  когда
когда  расположена и плоскости
расположена и плоскости  когда
когда  расположена в плоскости
расположена в плоскости 
Преобразование криволинейного иитеграла в простой интеграл
Пусть даны параметрвческие уравнения дуги 

(мы предполагаем, что все три функции непрерывно дифференцируемы). По теореме Лагранжа (рис. 6)

где  лежит между
лежит между  и
и 

Рис. 6
Пусть  — точка кривой, соответствующая значению параметра
— точка кривой, соответствующая значению параметра  — точка кривой, соответствующая вначению параметра
— точка кривой, соответствующая вначению параметра  тогда
тогда

откуда и пределе при стремлении к нулю наибольшей из разностей 

Заметим, что  выкладки не только дают выражение криволинейиого интеграла через простой, но и доказывают существование криволинейного интеграла [в случае непрерывно дифференцируемых
выкладки не только дают выражение криволинейиого интеграла через простой, но и доказывают существование криволинейного интеграла [в случае непрерывно дифференцируемых  ], если считать существование простого интеграла от непрерывной функции известный.
], если считать существование простого интеграла от непрерывной функции известный.
Аналогичные формулы имеют место для  .
.
Мы видим, что для преобразоиакия криволинейного интеграла в простой интеграл следует взять параметрические уравнения пути интегрирования, затем всюду под знаком криволинейного интеграла заменить  их выражениями через параметр и после этого рассматривать интеграл как простой по параметру, взятый в пределах изменения параметра.
их выражениями через параметр и после этого рассматривать интеграл как простой по параметру, взятый в пределах изменения параметра.
Если, например, имеем дугу

то (беря х за параметр) получим:

Условие независимости криволинейного интеграла от формы пути
Будем говорить, что криволинейный интеграл

не зависит от формы пути в некоторой области (в которой  предполагаются непрерывными), если этот интеграл, клоль всяких двух кусочно-гладких дуг (лежащих в рассматриваемой области) с общим началом и общим концом, имеет одинаковую величину. В этом случае при обозначении интеграла достаточно лишь указывать начальную и конечную точку пути (не называя самого путы) и употреблять запись
предполагаются непрерывными), если этот интеграл, клоль всяких двух кусочно-гладких дуг (лежащих в рассматриваемой области) с общим началом и общим концом, имеет одинаковую величину. В этом случае при обозначении интеграла достаточно лишь указывать начальную и конечную точку пути (не называя самого путы) и употреблять запись  (где выписаны координаты точек
(где выписаны координаты точек  )
)
Если подынтегральное выражение в (2.24) есть полный дифференциал некоторой функции и  , то для какой иибудь гладкой дуги с параметрическими уравнениями
, то для какой иибудь гладкой дуги с параметрическими уравнениями

получим (учитывая свойство инвариантности дифференциального обозначения):

То же будет для кусочно-гладкой дуги  и следовательно, криволинейный интеграл не вависит от формы пути.
и следовательно, криволинейный интеграл не вависит от формы пути.
Обратно, предположим, что криволинейный интеграл (2.24) не зависит от формы пути и положим

Тогда

Беря в последнем интеграле за путь интегрирования прямолинейный отрезок и преобразуя кризолинейный интеграл в простой, получим:

Так как

при  , то следрвательно, существует и
, то следрвательно, существует и 
Аналогично найдем, что существуют  причем
причем 
Отсюда видно, что

т. е. подынтегральное выражение в (2.24) есть полный дифференциал.
Итак, для независимости криволинейного интеграла от формы пути (в некоторой области) необходимо и достаточно, чтобы подынтегральное выражение было полним дифференциалом некоторой функции (в упомянутой области).

Рис. 7.

Рис. 8.
Заметим, что независимость криволинейного интеграла (2.24) от формы пути в некоторой области равносильна равенству нулю этою интрала вдоль всякого замкнутого пути, лежащего в рассматрлваемой области. В самом деле, пусть имеем независимость от формы  -нибудь замкнутый путь; тогда (рис. 7)
-нибудь замкнутый путь; тогда (рис. 7)

Обратно, пусть имеем равенство нулю интегралов вдоль замкнутых путей, и пусть  — два пути с общим началом и общим концом; тогда (рис. 8)
— два пути с общим началом и общим концом; тогда (рис. 8)

Условия, при которых выражение  есть полный дифференциал
есть полный дифференциал
Если это выражение (предполагается, что  имеют непрерывные частные производные первого порядка)
имеют непрерывные частные производные первого порядка)  полным дифференциал некоторой функции и
полным дифференциал некоторой функции и 
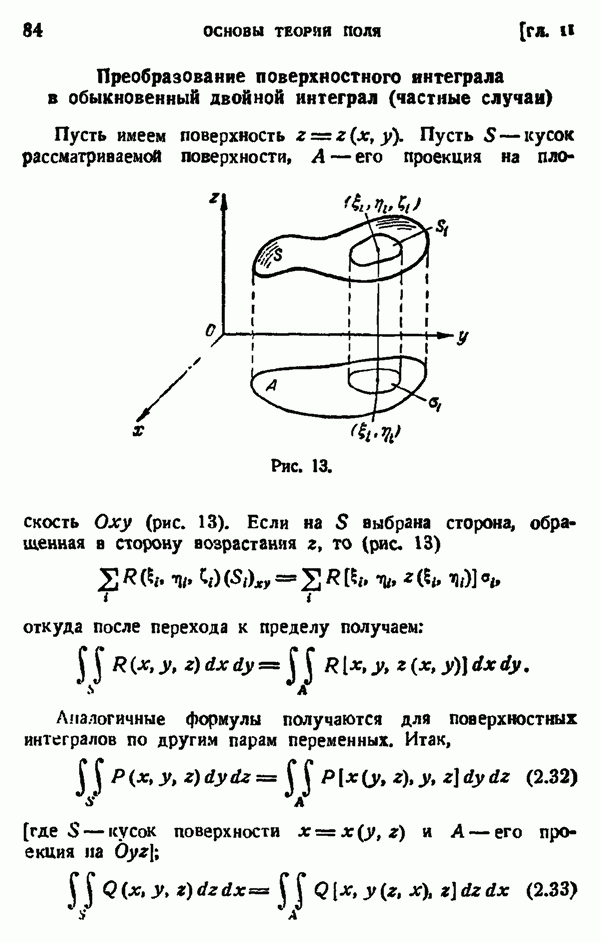
(в рассматрвваемой области), то

следовательно,

откуда, учитывая независимость частных производных от последовательности дифференцирования, получаем:


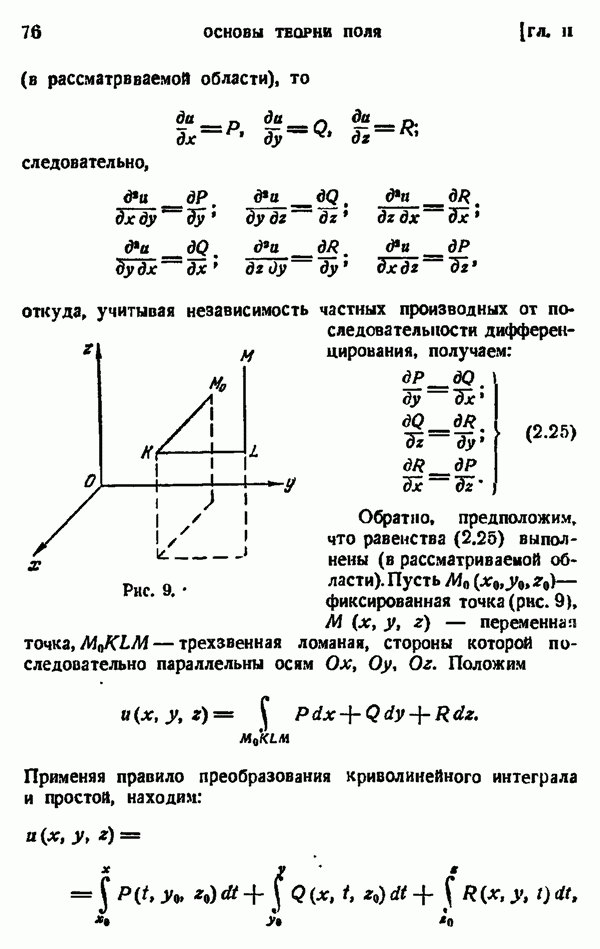
Рис. 9.
Обратно, предположим, что равенства (2.25) выполнены (в рассматриваемой области). Пусть  фиксированная точка (рис. 9),
фиксированная точка (рис. 9),  — переменная точка,
— переменная точка,  — трехзвенная ломаная, стороны которой последовательно параллельны осям
— трехзвенная ломаная, стороны которой последовательно параллельны осям  Положим
Положим

Применяя правило преобразования криволинейного интеграла и простой, находим:

откуда с помощью правила дифференцировании интеграла с переменным верхним пределом и правила дифференцирования под знаком интеграла с учетом (2.25) получаем:

и, следовательно,

Итак,  того чтобы выражение
того чтобы выражение  было полным дифференциалом (в рассматриваемой области), необходимо и достаточно, чтобы выполнялись равенства
было полным дифференциалом (в рассматриваемой области), необходимо и достаточно, чтобы выполнялись равенства

(в рассматриваемой области).
В доказательстве теоремы о том, что если выполнены условия (2.25), то выражение  есть полный дифференциал некоторой функции, молчаливо преднола) алось, что в рассматриваемой
есть полный дифференциал некоторой функции, молчаливо преднола) алось, что в рассматриваемой
области найдется такая точка  что для любой точки М рассматриваемой области трехзвениая ломаная
что для любой точки М рассматриваемой области трехзвениая ломаная  лежит в этой же области. С помощью дополнительных рассуждений можно показать, что теорема останется верной для всякой области, в которой любые два пут с общим началом и общим концом могут быть непрерывно деформированы один в другой, не выходя из области (такие области называются односвязными).
лежит в этой же области. С помощью дополнительных рассуждений можно показать, что теорема останется верной для всякой области, в которой любые два пут с общим началом и общим концом могут быть непрерывно деформированы один в другой, не выходя из области (такие области называются односвязными).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
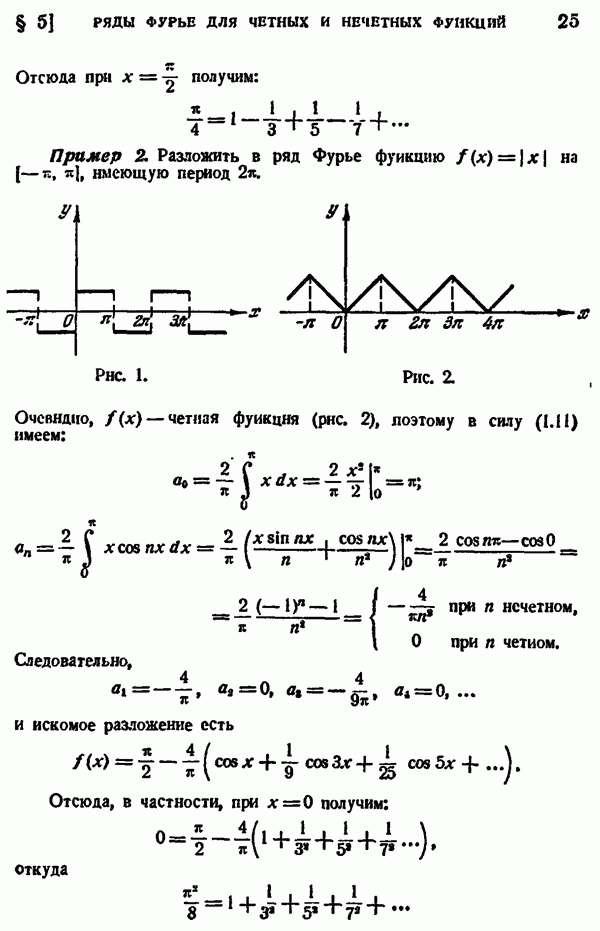
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 6. ВЕКТОРНОЕ ПОЛЕ
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
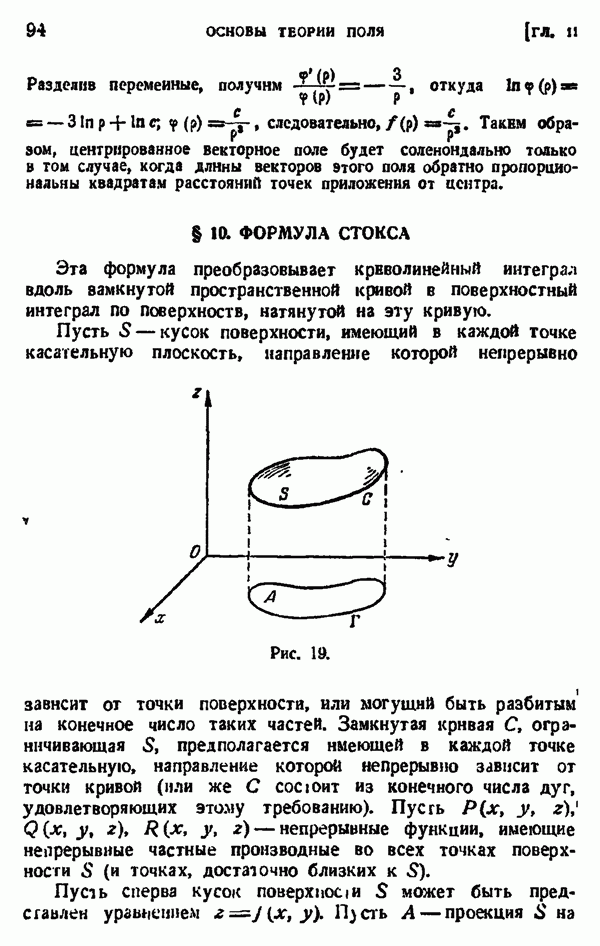
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
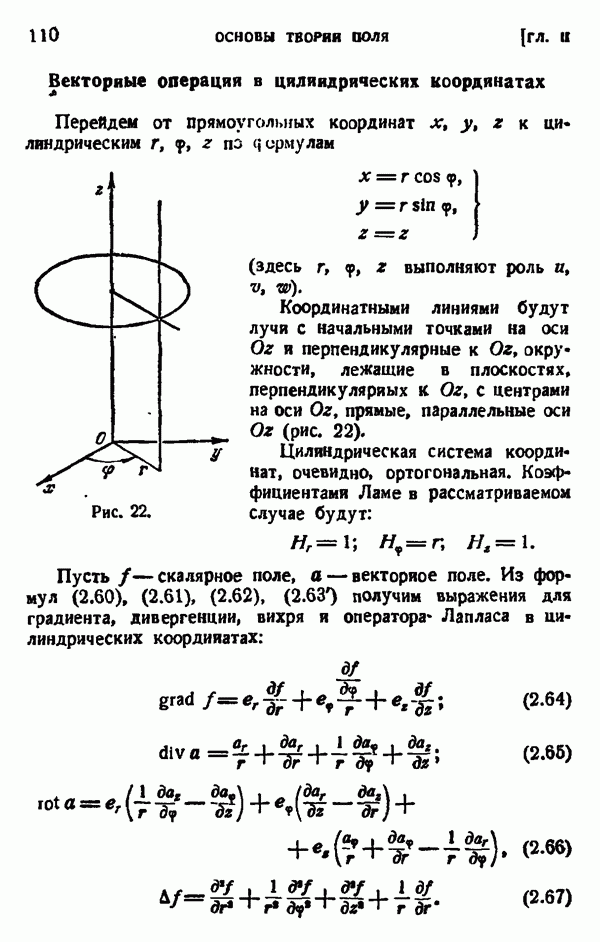
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
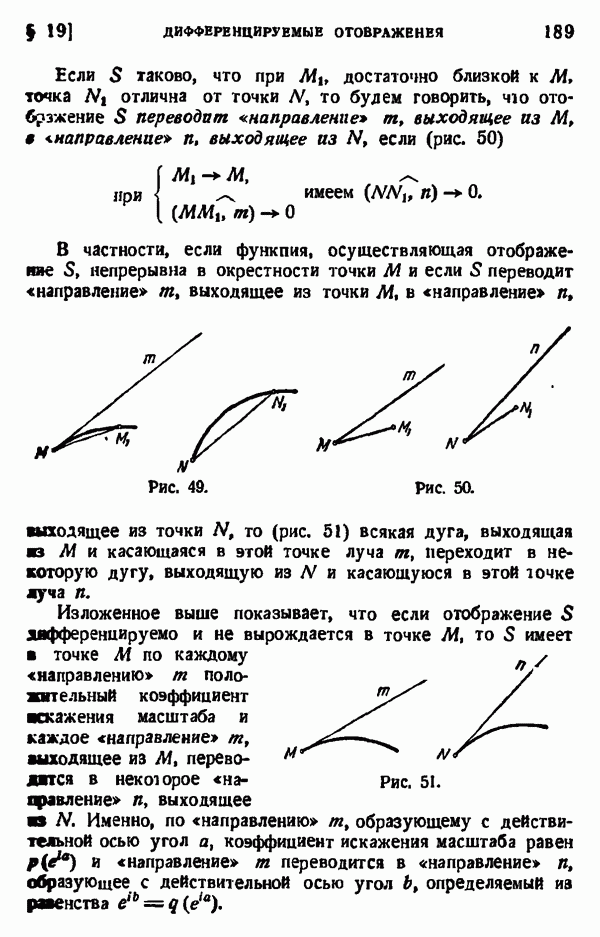
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
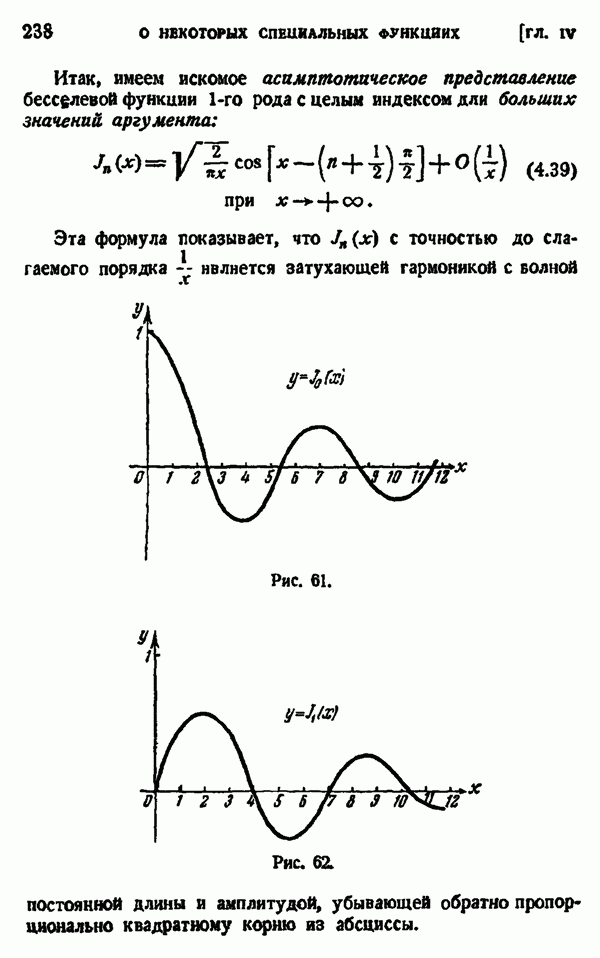
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
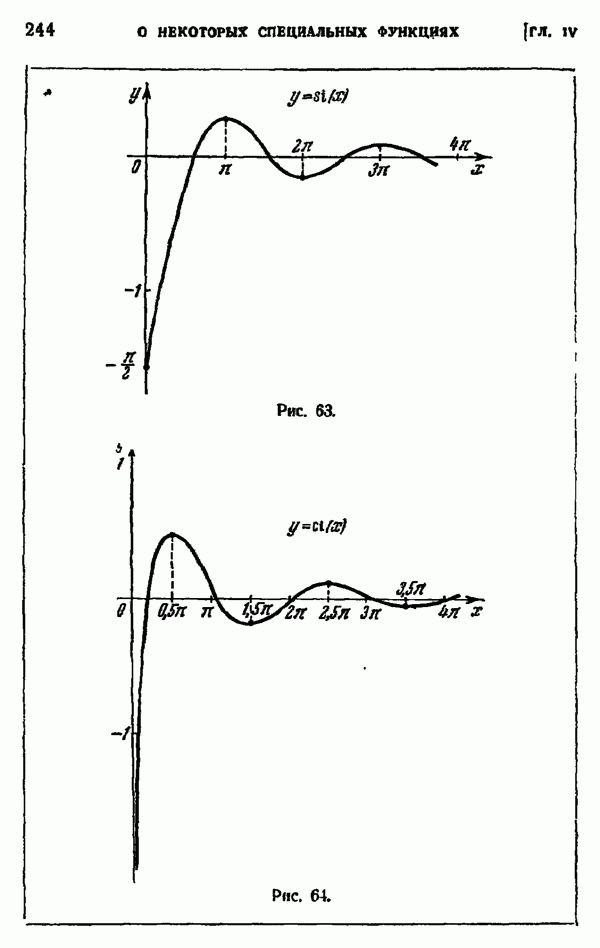
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ