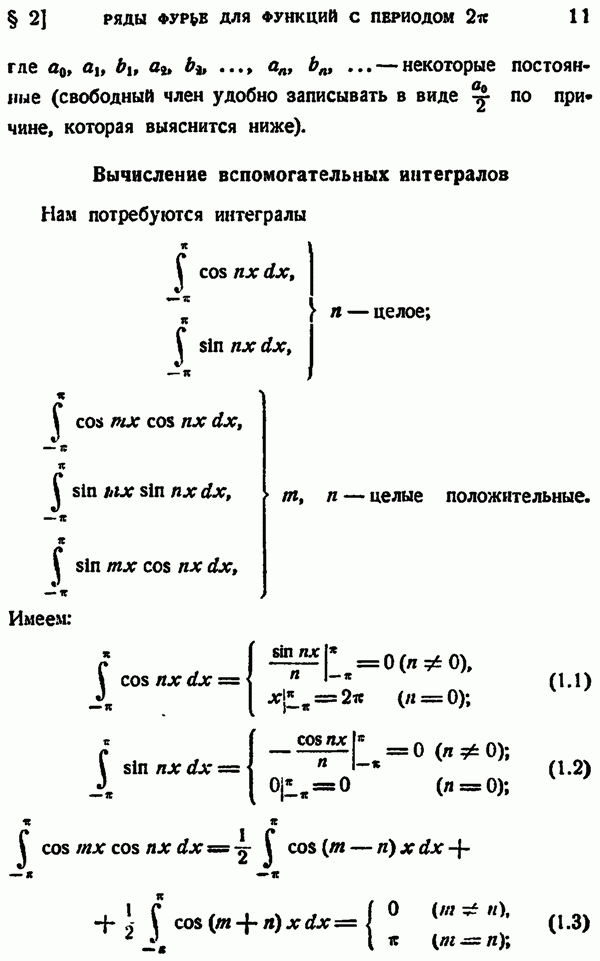
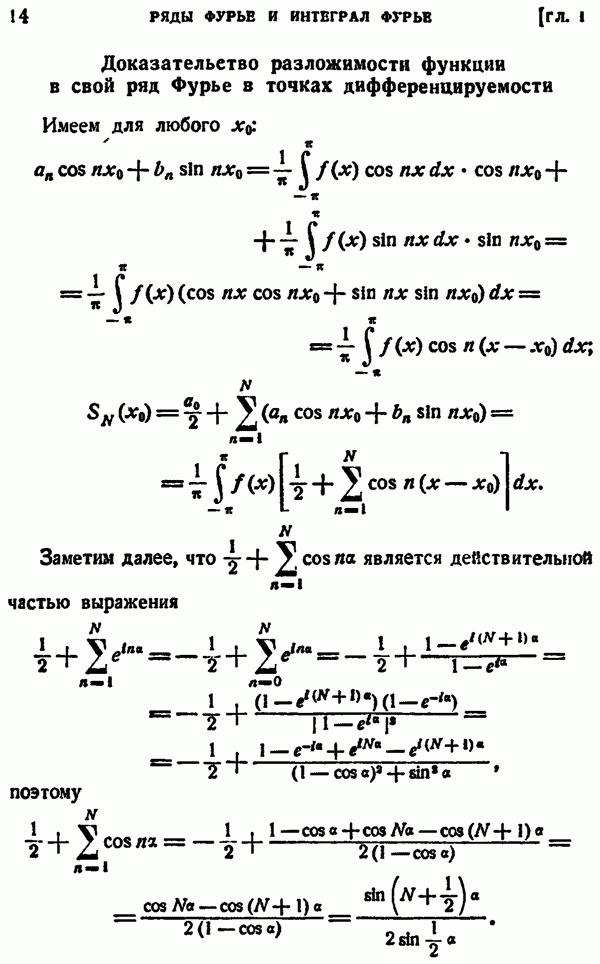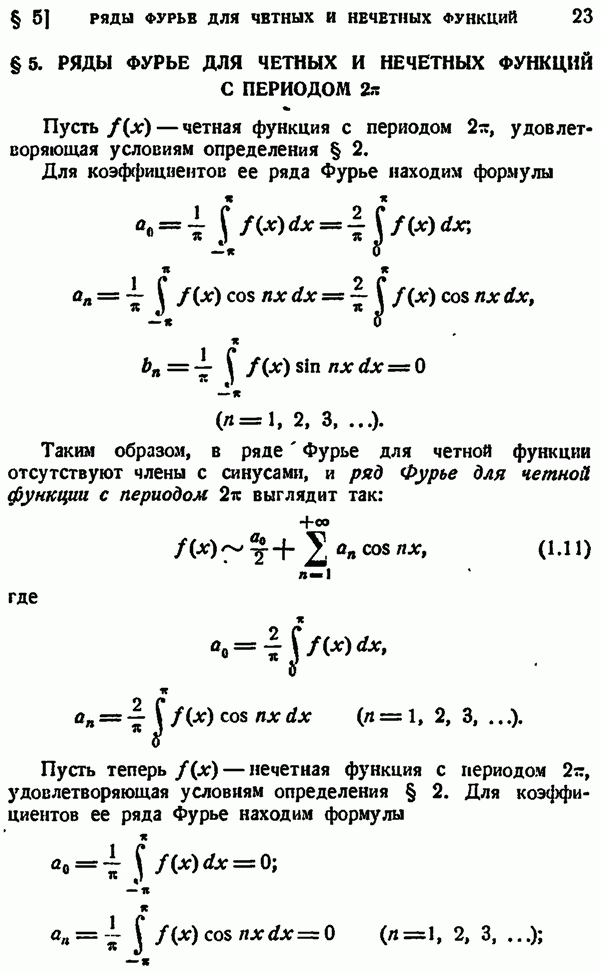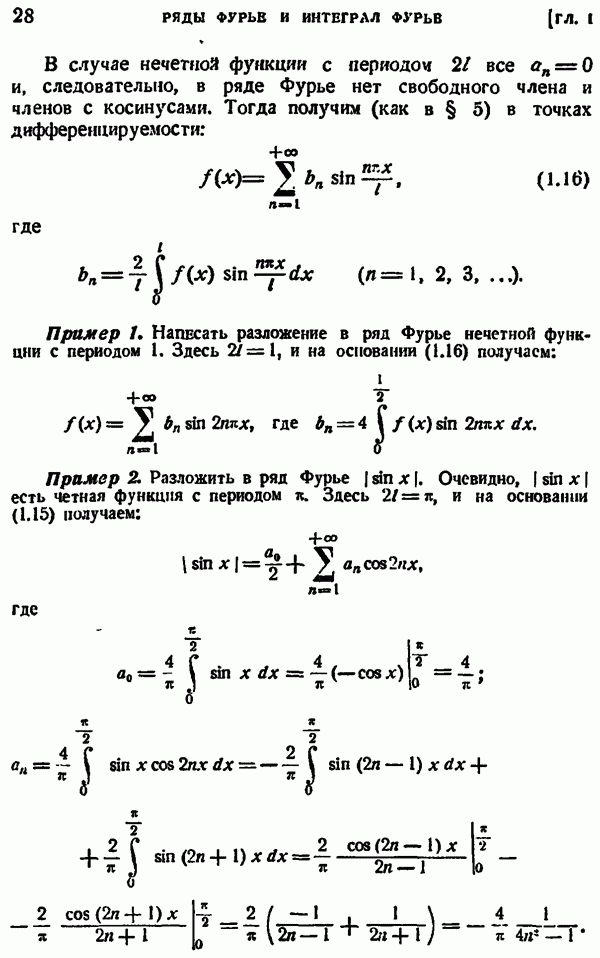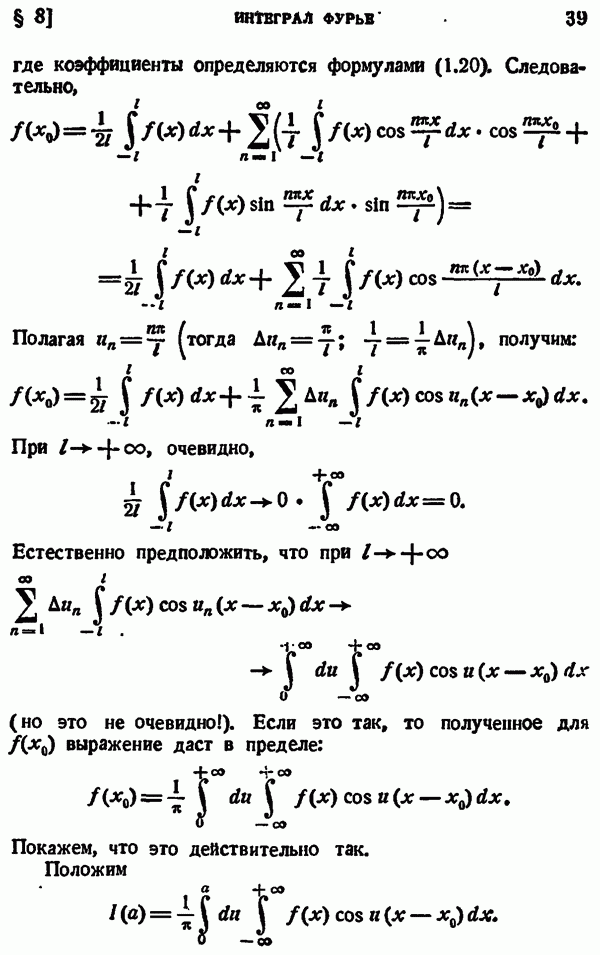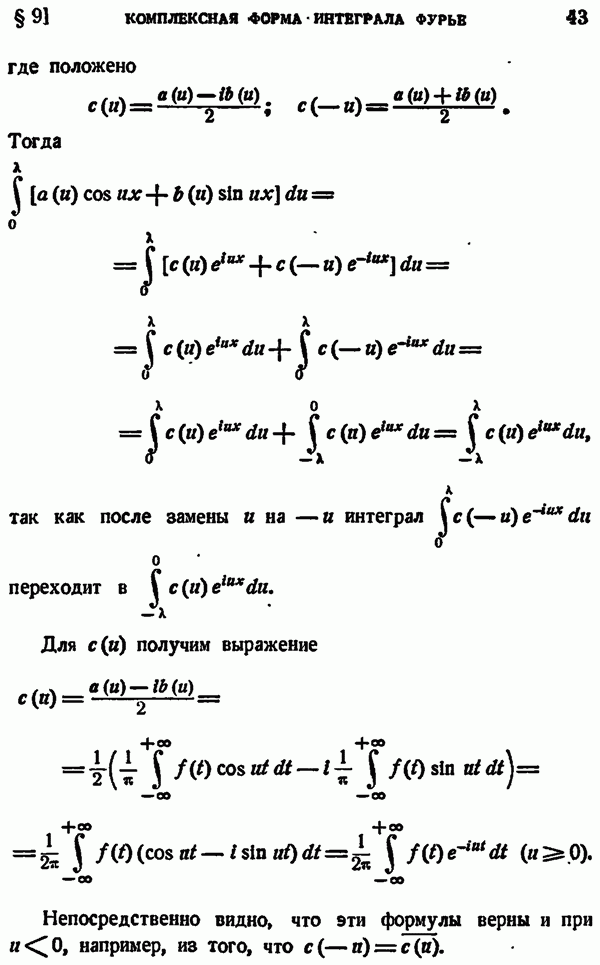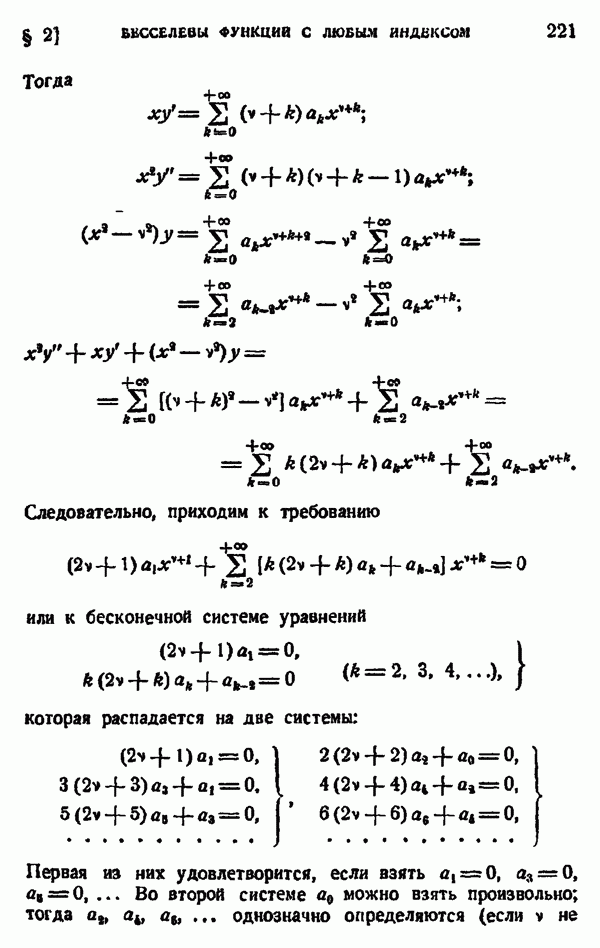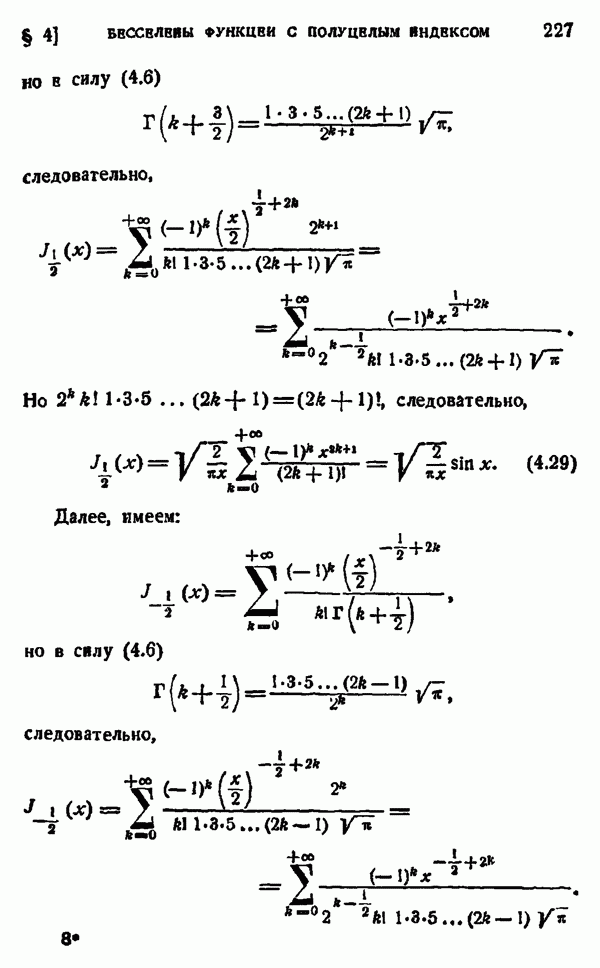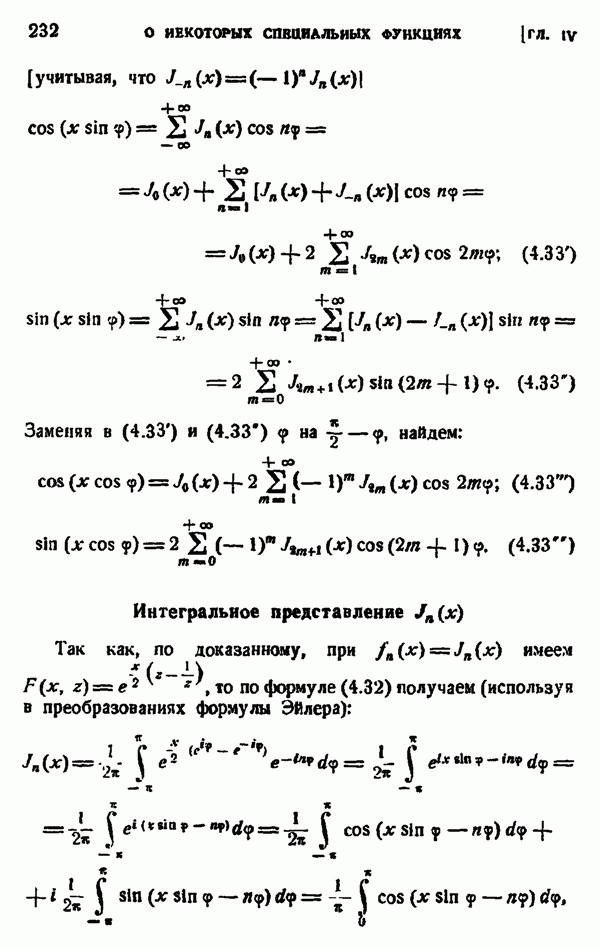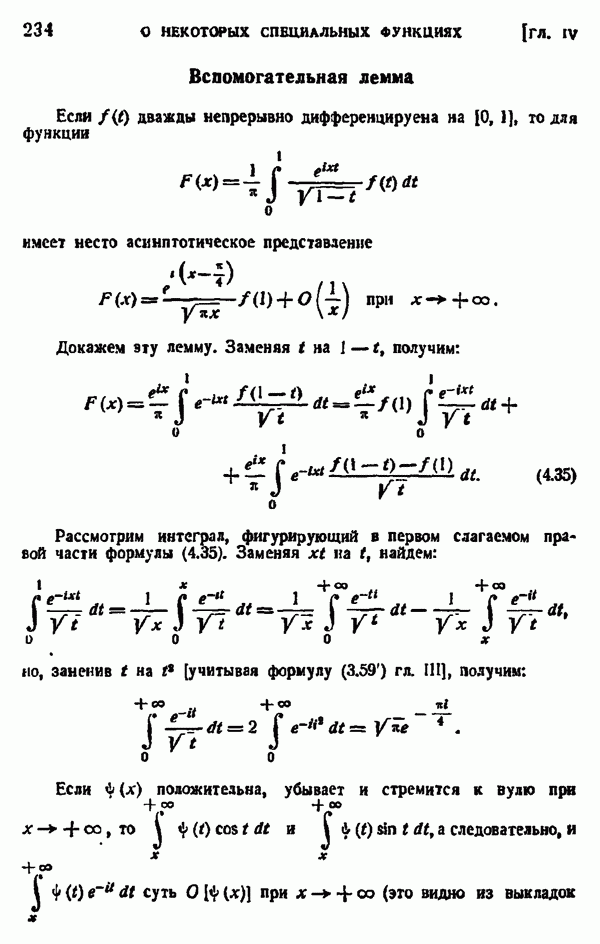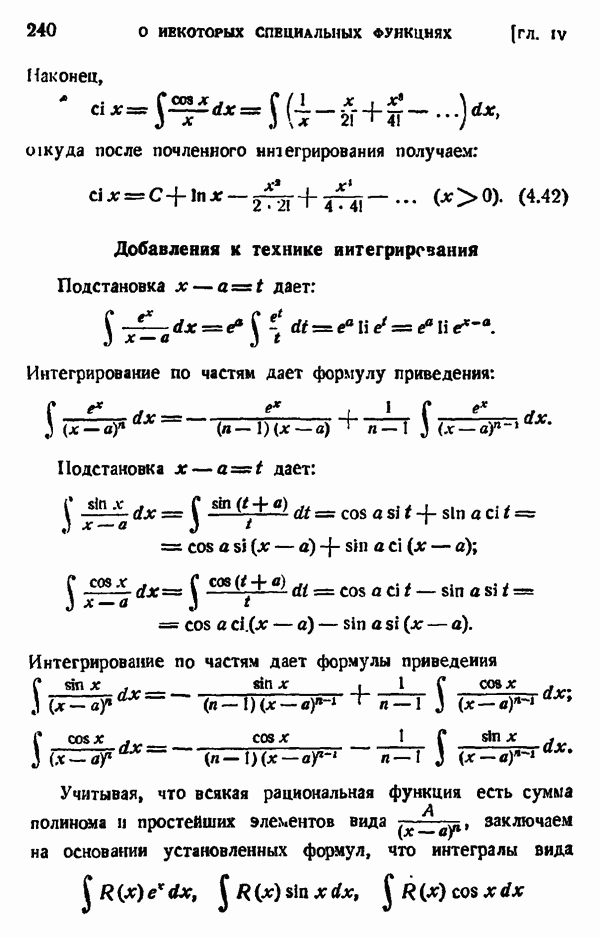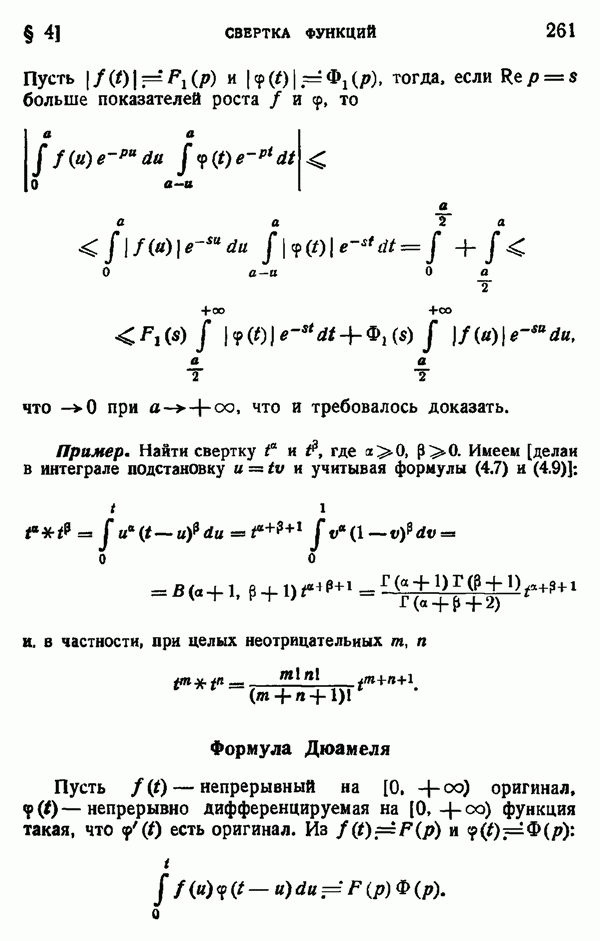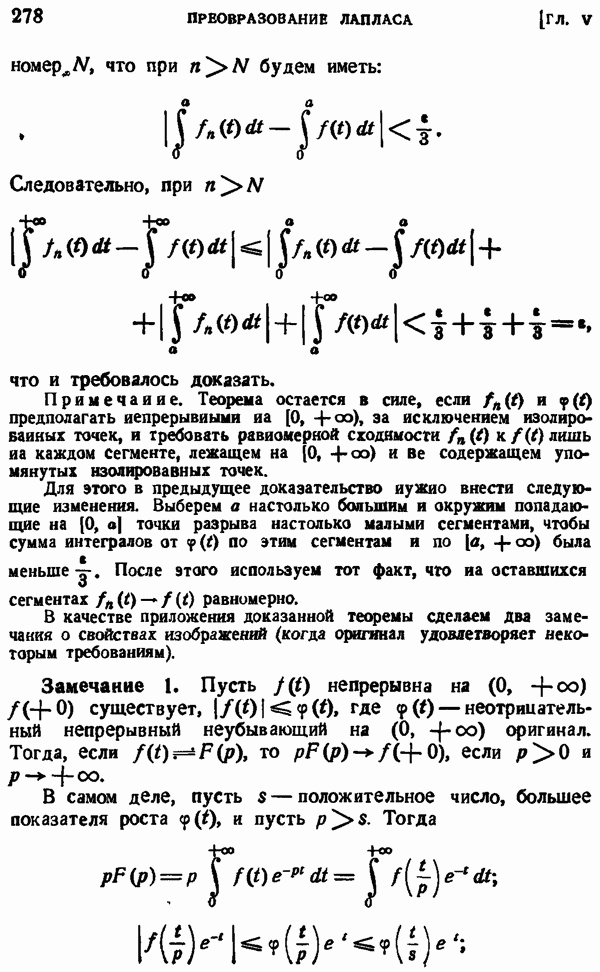| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
О предельном переходе под знаком несобственного интеграла
Теорема. Пусть  — комелекснозначные непрерывные функции на
— комелекснозначные непрерывные функции на  причем
причем  где
где  — такая действительная неотрицательная непрерывная функция на
— такая действительная неотрицательная непрерывная функция на  что
что  сходится. Пусть затем
сходится. Пусть затем  на
на  и притом равномерно на каждом сегменте
и притом равномерно на каждом сегменте  , где
, где  Тогда
Тогда

Доказательства Из условий теоремы видно, что  непрерывна и
непрерывна и  Пусть
Пусть  - произвольное положительное число. Так как несобственный интеграл
- произвольное положительное число. Так как несобственный интеграл  сходится, то найдется такое
сходится, то найдется такое  что
что  Так как
Так как  на [0, а) равномерно, то
на [0, а) равномерно, то  , следовательно, найдется такой
, следовательно, найдется такой
номерам, что при  будем иметь:
будем иметь:

Следовательно, при 

что и требовалось доказать.
Примечание. Теорема остается в силе, если  предполагать непрерывными на
предполагать непрерывными на  за исключением изолированных точек, и требовать равномерной сходимости
за исключением изолированных точек, и требовать равномерной сходимости  лишь на каждом сегменте, лежащем на
лишь на каждом сегменте, лежащем на  содержащем упомянутых нзолировавных точек.
содержащем упомянутых нзолировавных точек.
Для этого в предыдущее доказательство иужио внести следующие изменения. Выберем а настолько большим и окружим попадающие на  точки разрыва настолько малыми сегментами, чтобы сумма интегралов от
точки разрыва настолько малыми сегментами, чтобы сумма интегралов от  по этим сегментам и по
по этим сегментам и по  была меньше
была меньше  . После этого используем тот факт, что на оставшихся сегментах
. После этого используем тот факт, что на оставшихся сегментах  равномерно.
равномерно.
В качестве приложения доказанной теоремы сделаем два замечания о свойствах изображений (когда оригинал удовлетворяет некоторым требованиям).
Замечание 1. Пусть  непрерывна на
непрерывна на  существует,
существует,  где
где  — неотрицательный непрерывный неубывающий на
— неотрицательный непрерывный неубывающий на  оригинал. Тогда, если
оригинал. Тогда, если  то
то  если
если 
В самом деле, пусть  — положительное число, большее показателя роста
— положительное число, большее показателя роста  и пусть
и пусть  Тогда
Тогда

интеграл

сходится; при  равномерно на каждом сегменте
равномерно на каждом сегменте  где
где  Следовательно, в свлу доказанной теоремы
Следовательно, в свлу доказанной теоремы

что и требовалось доказать.
Замечание 2. Пусть  непрерывна на
непрерывна на  существует,
существует,  где
где  — неотрицательный, непрерывный, невозрастающий на
— неотрицательный, непрерывный, невозрастающий на  оригинал. Тогда, если
оригинал. Тогда, если  то
то  еслв
еслв 
Сперва заметим, что показатель роста  и подавно показатель роста
и подавно показатель роста  не более нуля в потому
не более нуля в потому  имеет смысл при всех
имеет смысл при всех  Пусть Огде
Пусть Огде  Тогда
Тогда

 сходится; кроме того,
сходится; кроме того,  при
при  равномерно на каждом сегменте
равномерно на каждом сегменте  где
где  Следовательно, в силу доказанной теоремы
Следовательно, в силу доказанной теоремы

что  требовалось доказать.
требовалось доказать.
Целые функции экспоненциального типа
Определение. Целая функция  комплексного переменного
комплексного переменного  называется целой функцией экспоненциального типа, если можно найти такие положительные числа С, а, что для всех комплексных значений
называется целой функцией экспоненциального типа, если можно найти такие положительные числа С, а, что для всех комплексных значений  выполняется неравенство
выполняется неравенство

Лемма. Для того чтобы степенной ряд  изображал целую функцию экспоненциального типа, необходимо и достаточно, чтобы для некоторых положительных чисел
изображал целую функцию экспоненциального типа, необходимо и достаточно, чтобы для некоторых положительных чисел  выполнялись неравенства
выполнялись неравенства

Доказательство необходимости Пусть  — целая функция экспоненциального типа. Тогда
— целая функция экспоненциального типа. Тогда  при всех
при всех  где
где  — некоторые положительные числа. В силу неравенства (3.48) для модулей коэффициентов ряда Тейлора (гл. III, § 14) находим при всех
— некоторые положительные числа. В силу неравенства (3.48) для модулей коэффициентов ряда Тейлора (гл. III, § 14) находим при всех 

Беря  получим
получим

поэтому, полагая  будем иметь
будем иметь

Доказательство достаточности. Пусть  — некоторые положительные числа Тогда, очевидно, степенной ряд
— некоторые положительные числа Тогда, очевидно, степенной ряд  сходится для всех
сходится для всех  в
в
изображает целую функцию  причем для всех
причем для всех  имеем:
имеем:

что и требовалось доказать.
Заметим, что операции линейного комбинирования, умножения на независимое переменное, умножения на показательную функцию, линейного преобразования независимого переменного, дифференцирования и интегрирования, примененные к целым функциям экспоненциального типа, приводи снова к целым функциям экспоненциального типа.
Необходимое и достаточное условие регулярности изображения в бесконечности
Теорема. Для того чтобы изображение было регулярным в бесконечно удаленной точке, необходимо и достаточно, чтобы оригинал являлся целой функцией экспоненциального типа.
Доказательство достаточности. Пусть оригинал  есть целая функция экспоненциального типа [точнее,
есть целая функция экспоненциального типа [точнее,  заданная на
заданная на  продолжаема до целой функции экспоненциального типа]. Тогда, в частности при
продолжаема до целой функции экспоненциального типа]. Тогда, в частности при  будем иметь:
будем иметь:

Очевидно, при  имеем:
имеем:

интеграл  сходится;
сходится;  равномерно на каждом [0, а], где
равномерно на каждом [0, а], где 
доватедьно, на основании теоремы о предельном переходе под знаком несобственного интеграла

или

но

следовательно,

причем ряд в правой части сходится при  и изображает аналитическую функцию в окрестности бесконечно удаленной точки. Это доказывает, что изображение
и изображает аналитическую функцию в окрестности бесконечно удаленной точки. Это доказывает, что изображение  после аналитического продолжения на окрестность бесконечно удаленной точки становится регулярным в ней и
после аналитического продолжения на окрестность бесконечно удаленной точки становится регулярным в ней и

Таким образом, если  — целая функция экспоненциального типа и если ее разложение в ряд Тейлора есть
— целая функция экспоненциального типа и если ее разложение в ряд Тейлора есть  то изображение
то изображение  определяется формулой
определяется формулой

Доказательство необходимости. Пусть изображение  оригинала
оригинала  после аналитического продолжения оказалось регулярным в бесконечно удаленной
после аналитического продолжения оказалось регулярным в бесконечно удаленной
точке. Лорановское разложение  в окрестности
в окрестности  [учитывается, что
[учитывается, что  при
при  имеет вид
имеет вид

Пусть положительное число  лежит в области сходимости этого ряда. Тогда ряд сходится; следовательно, сходится и ряд
лежит в области сходимости этого ряда. Тогда ряд сходится; следовательно, сходится и ряд  поэтому его члены ограничены, т. е.
поэтому его члены ограничены, т. е.  где С — некоторое положительное число, откуда следовательно,
где С — некоторое положительное число, откуда следовательно,  — целая функция экспоненциального типа. По доказанному
— целая функция экспоненциального типа. По доказанному

отсюда (так как оригинал вполне определяется своим изображением) заключаем, что

что и требовалось доказать.
Заметим, что всякая регулярная в бесконечности аналитическая функция, равная нулю в бесконечности, является изображением некоторой целой функции экспоненциальною типа.
Таким образом, с помощью преобразования Лапласа устанавливается взаимно однозначное соответствие между всеми целыми функциями экспоненциального типа и всеми аналитическими функииями, регулярными в бесконечно удаленной точке и равными в ней нулю.
Нахождение оригинала по его изображению (когда оно регулярно в бесконечности)
Предыдущие выкладки показывают, что если  какая-нибудь аналитическая функция, регулярная в бесконечно удаленной точке и равная в ней нулю, и если ее лорановское разложение в окрестности
какая-нибудь аналитическая функция, регулярная в бесконечно удаленной точке и равная в ней нулю, и если ее лорановское разложение в окрестности  есть
есть

то

будет оригиналом, имеющим изображение 
Изображения бесселевых функций
При  [см. гл IV, § 2, формулу (4.30)] функция
[см. гл IV, § 2, формулу (4.30)] функция

будет целой функцией экспоненциального типа.
В самом деле, модуль коэффициента при  в правой части равен
в правой части равен

но  [Это неравенство проверяется методом
[Это неравенство проверяется методом  при
при  оно верно; если оно верно для некоторого к, то переход к
оно верно; если оно верно для некоторого к, то переход к  сводится к умножению левой и
сводится к умножению левой и  частей соответственно на
частей соответственно на  )
)  но
но  Следовательно, неравенство будет верно и для
Следовательно, неравенство будет верно и для  Таким образом, при всех комплексных
Таким образом, при всех комплексных 

и, следовательно,  целая функция экспоненциального типа.
целая функция экспоненциального типа.
В силу (5.27)

где  — любое действительное неотрицательное число.
— любое действительное неотрицательное число.
При  отсюда находим:
отсюда находим:

но биномиальное разложение показывает, что

следовательно,

Покажем методом индукции, что

При  это следует из (5.30). Далее, в сяду свойства 4 § 3
это следует из (5.30). Далее, в сяду свойства 4 § 3

и, следовательно, при  доказываемая формула также верна. Пусть теперь эта формула верна для всех неотрицательных целых индексов, меньших
доказываемая формула также верна. Пусть теперь эта формула верна для всех неотрицательных целых индексов, меньших  тогда
тогда
|см. гл. IV, § 3, формулу (4.27)], учитывая, что  находим:
находим:

Таким образом, формула (5.31) доказана.
Рассмотрим теперь функцию

Эта функция регулярна в бесконечно удаленной точке и  следовательно, она является изображением некоторой целой функции экспоненциального типа
следовательно, она является изображением некоторой целой функции экспоненциального типа  Так как
Так как

то в силу (5.28)

но [см. гл. IV, § 2, формулу (4.20)]

следовательно,

Таким образом,

и, в частности, при 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
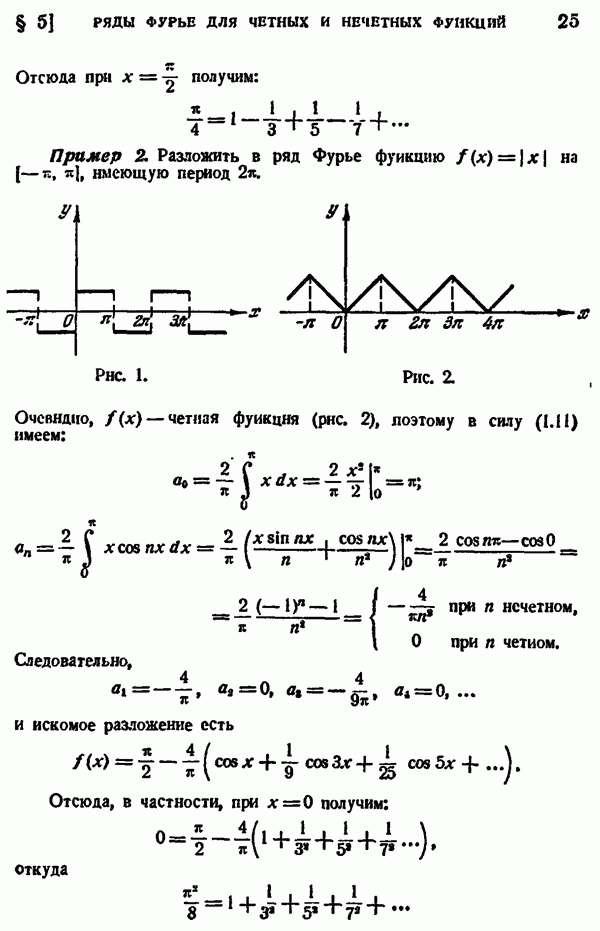
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
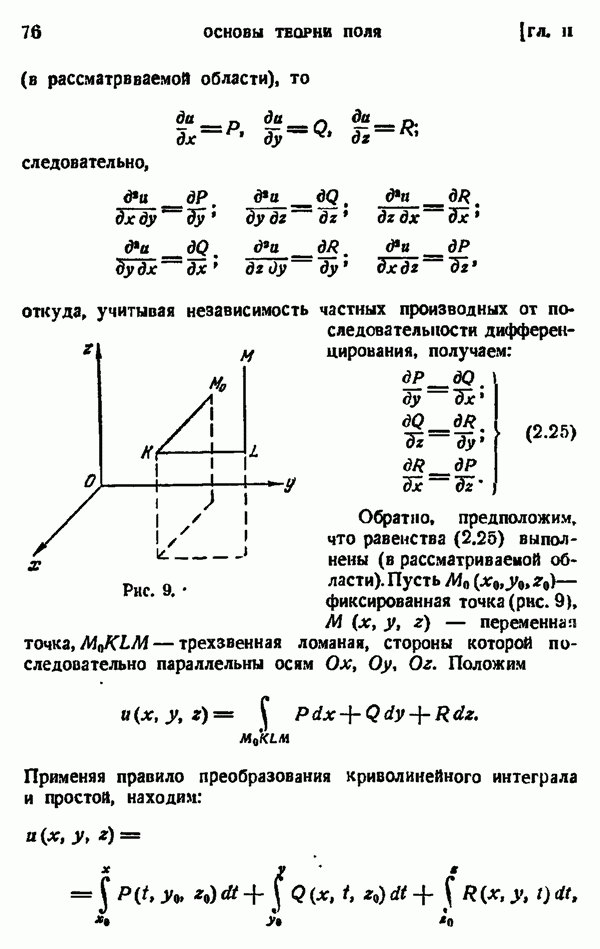
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 6. ВЕКТОРНОЕ ПОЛЕ
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
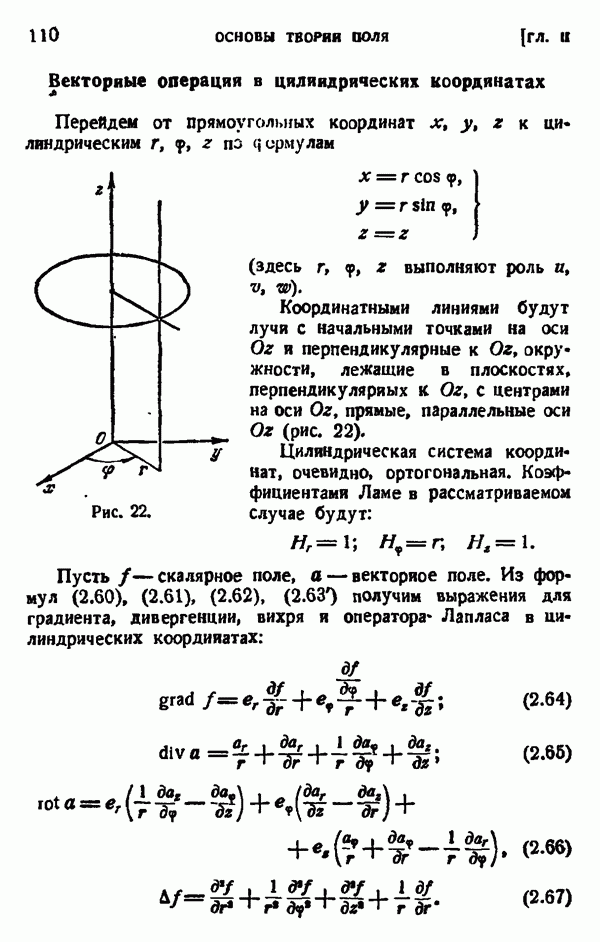
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
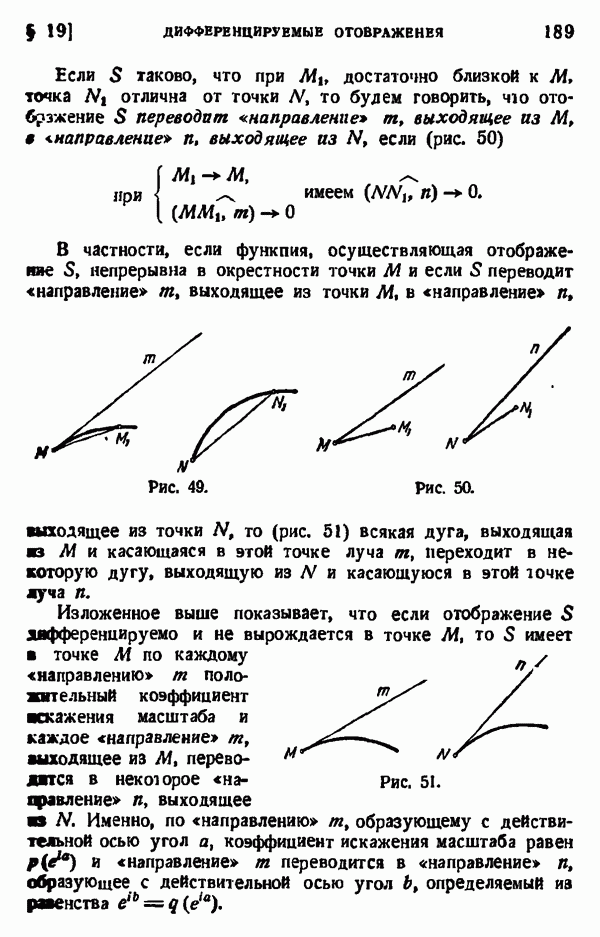
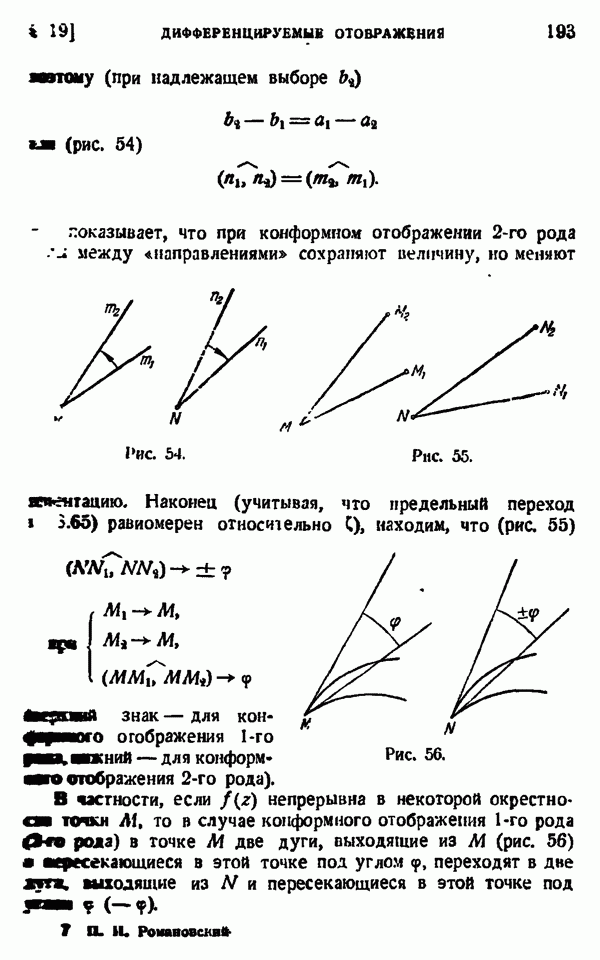
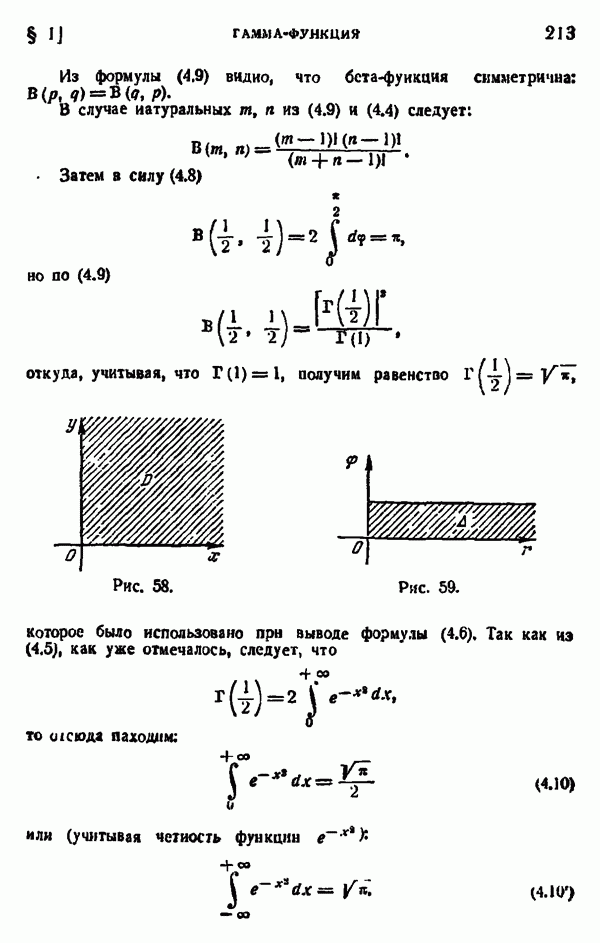
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
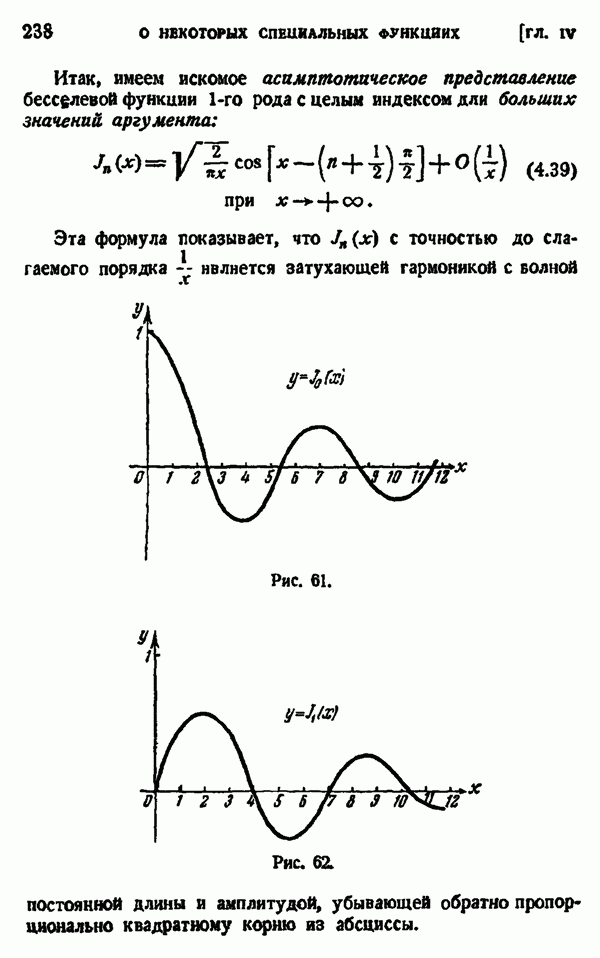
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
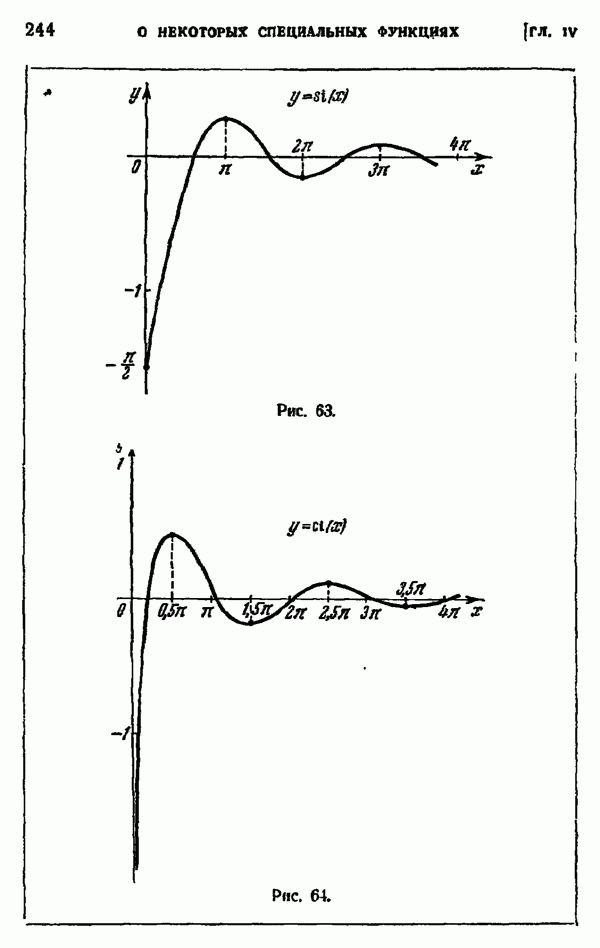
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ