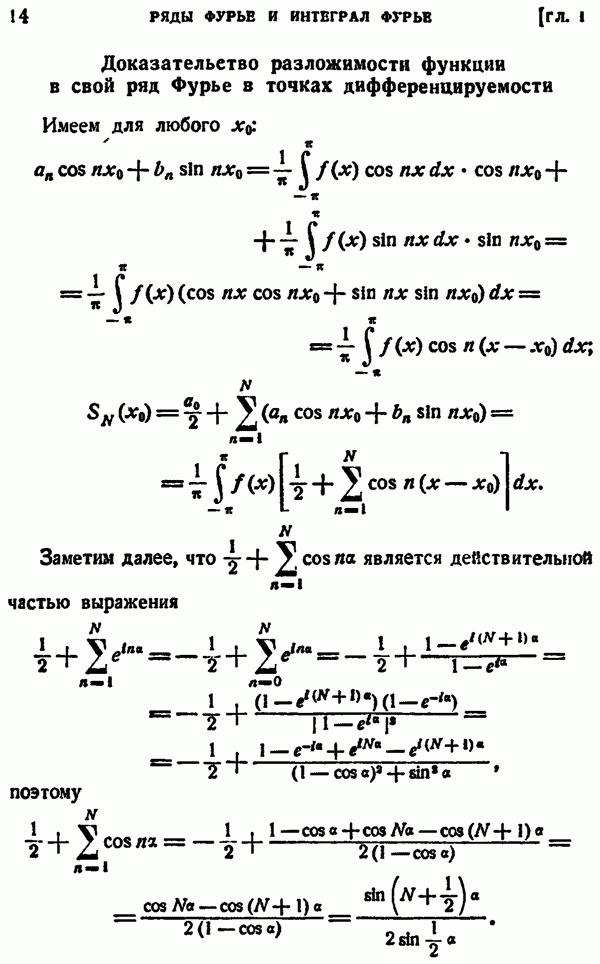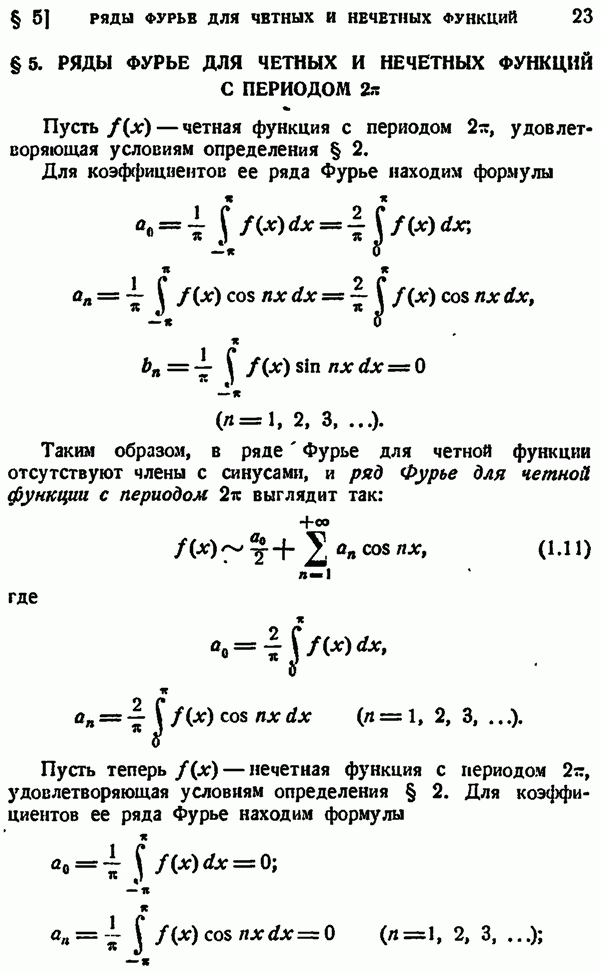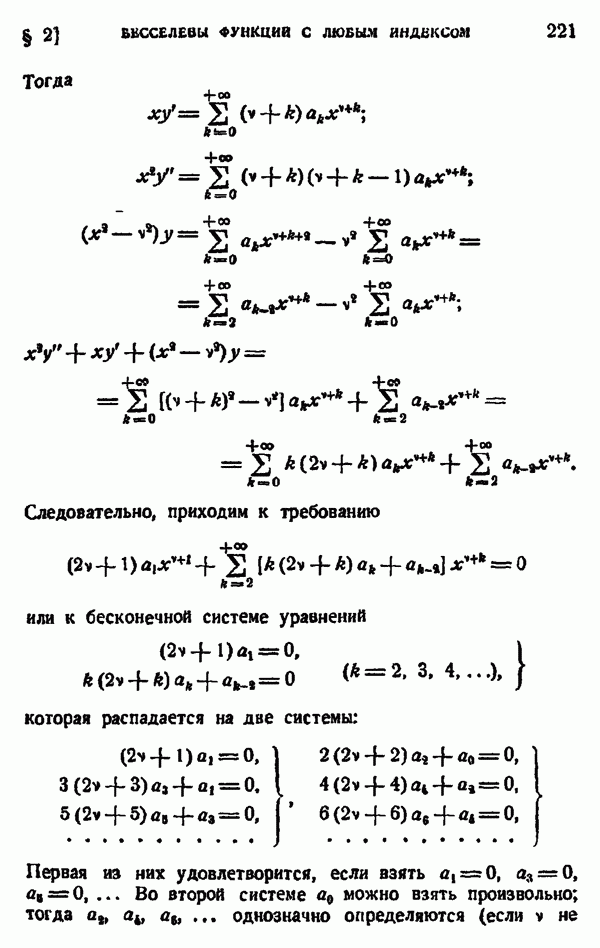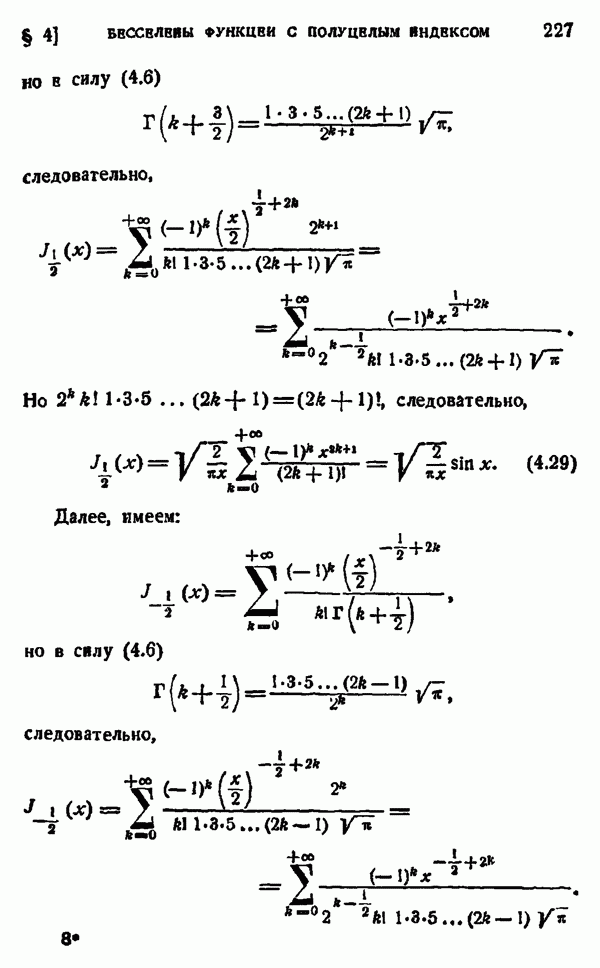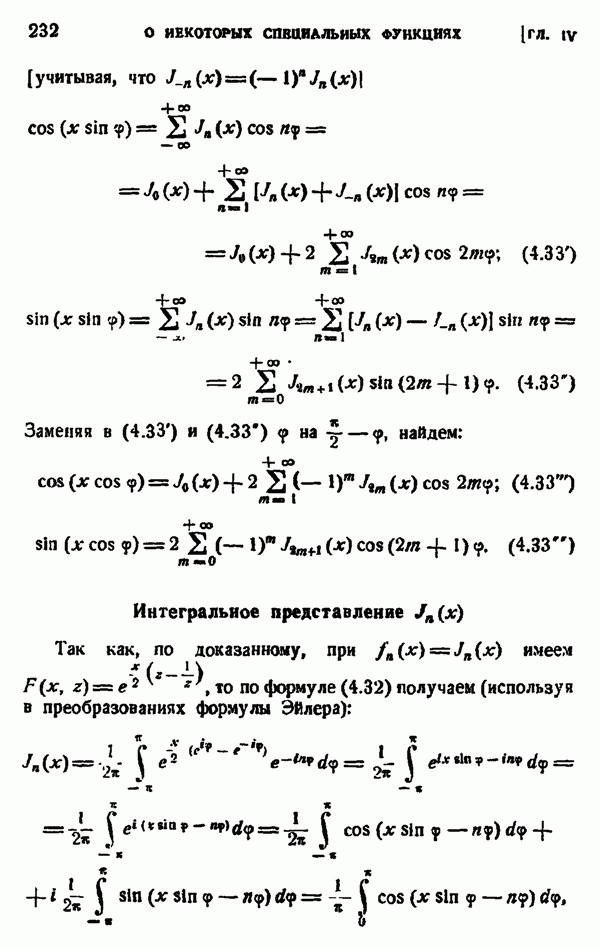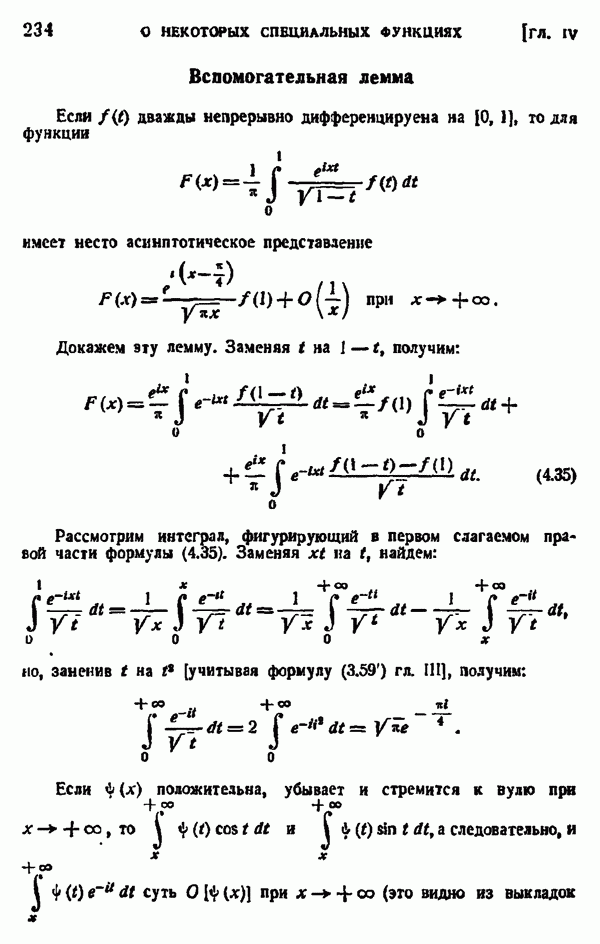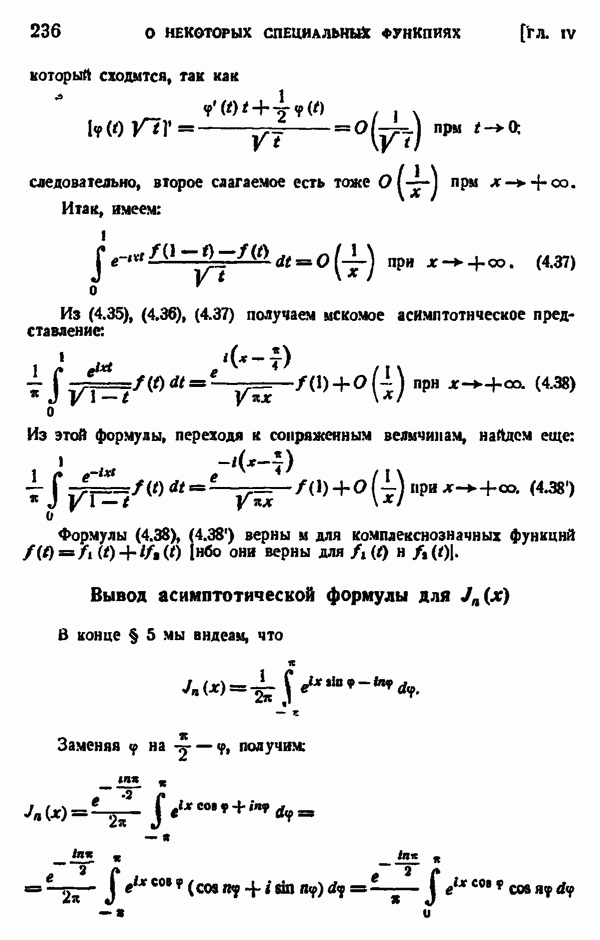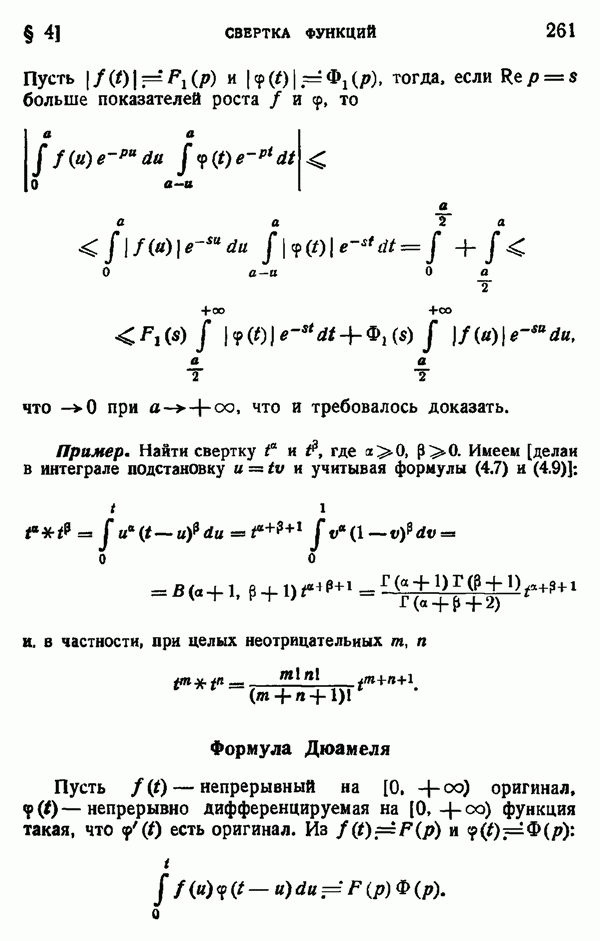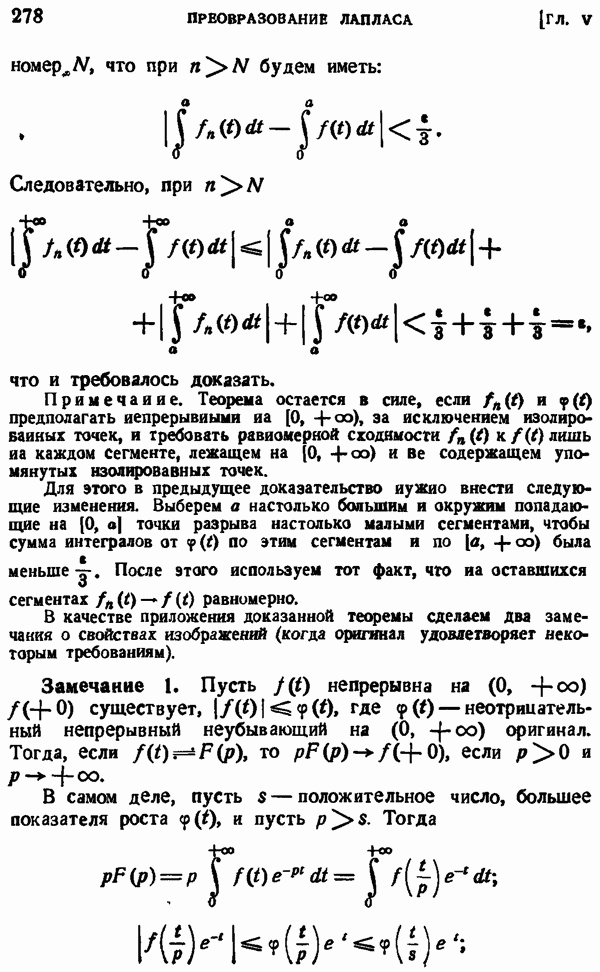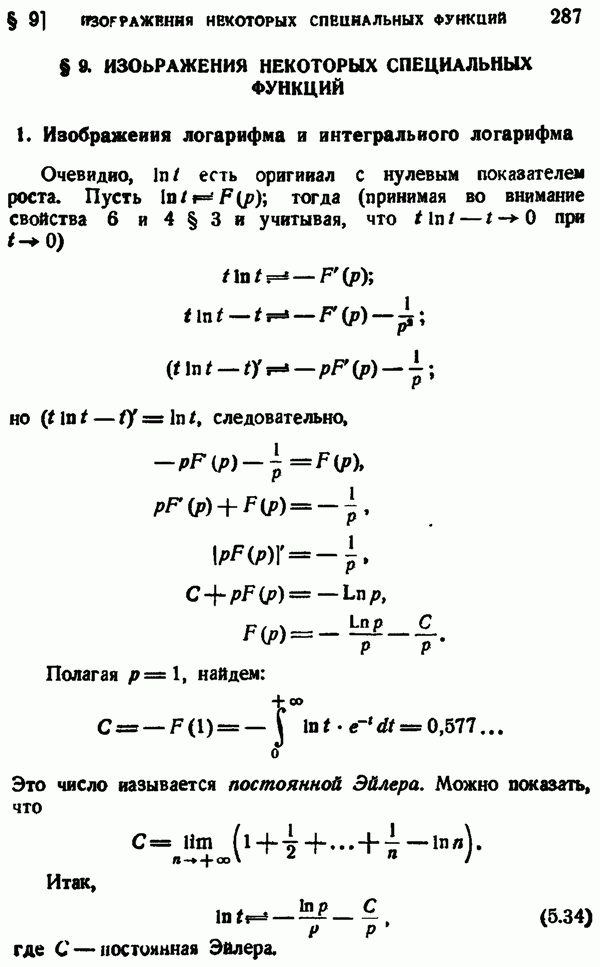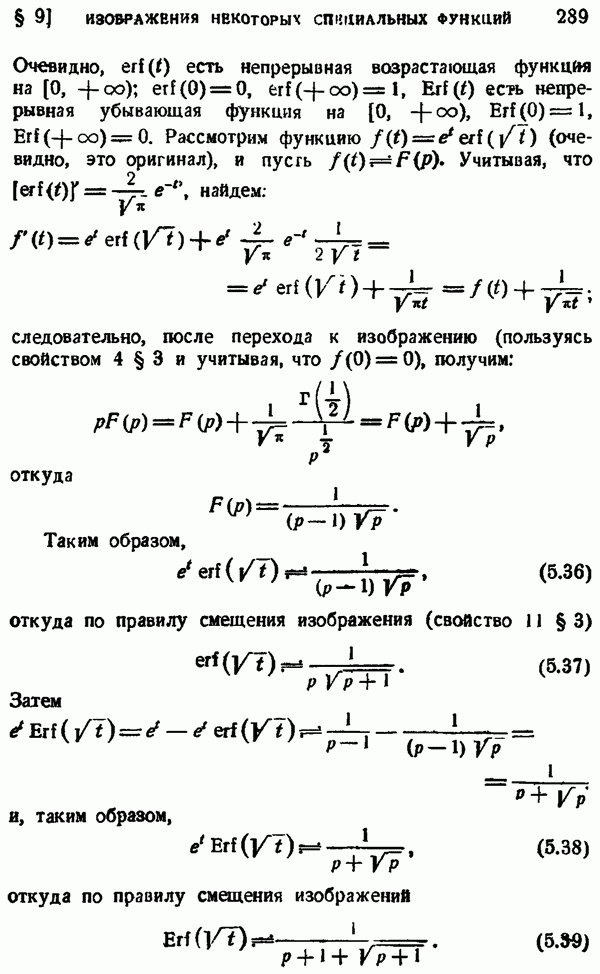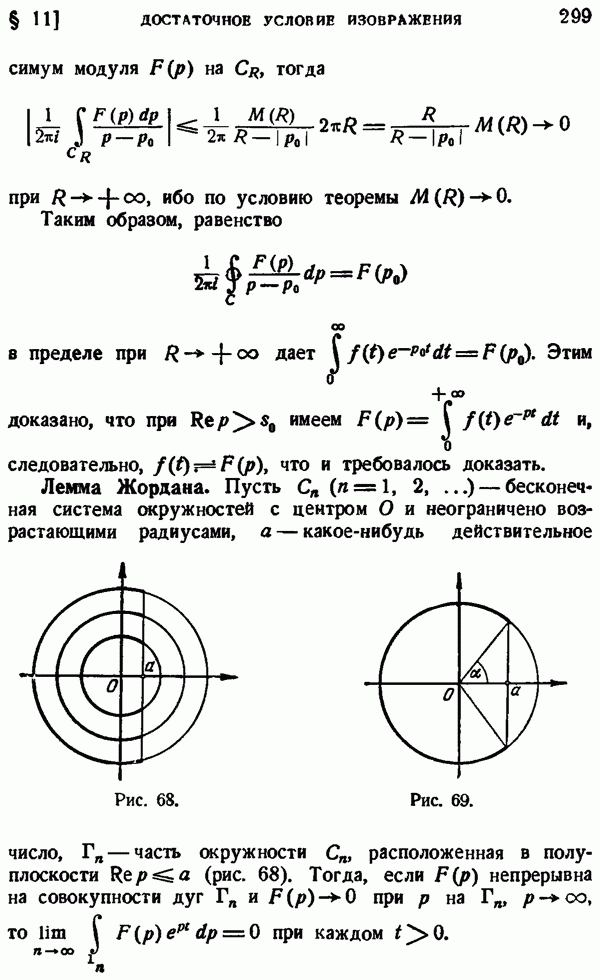| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Будем говорить, что последовательность функций

определенных в некоторой области  сходится равномерно внутри области
сходится равномерно внутри области  если она сходится равномерно на каждой ограниченной замкнутой области, лежащей в
если она сходится равномерно на каждой ограниченной замкнутой области, лежащей в 
Теорема. Если последовательность аналитических функций в области 

сходится равномерно внутри области  к функции
к функции  то
то  — функция, аналитическая в области
— функция, аналитическая в области  причем последовательность производных
причем последовательность производных

равномерно сходится внутри области  к производной предельной функции,
к производной предельной функции, 
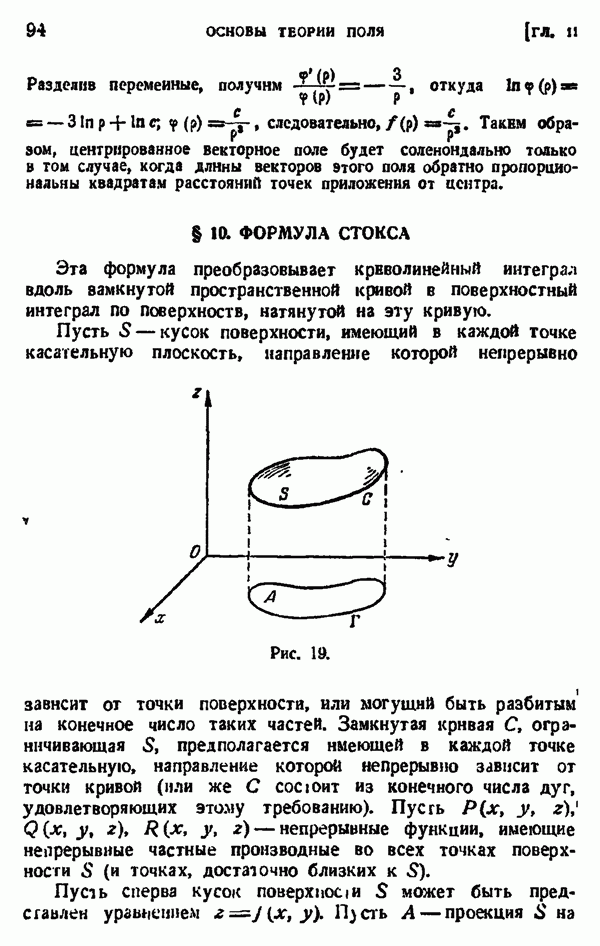
Пусть С — замкнутый контур, лежащий вместе с внутренностью в  и
и  точка внутри С. Тогда по формуле Коши
точка внутри С. Тогда по формуле Коши

Но  равномерно на С, следовательно,
равномерно на С, следовательно,

равномерно на С (при фиксированном  ); поэтому на основании правила предельного перехода (3.38)
); поэтому на основании правила предельного перехода (3.38)


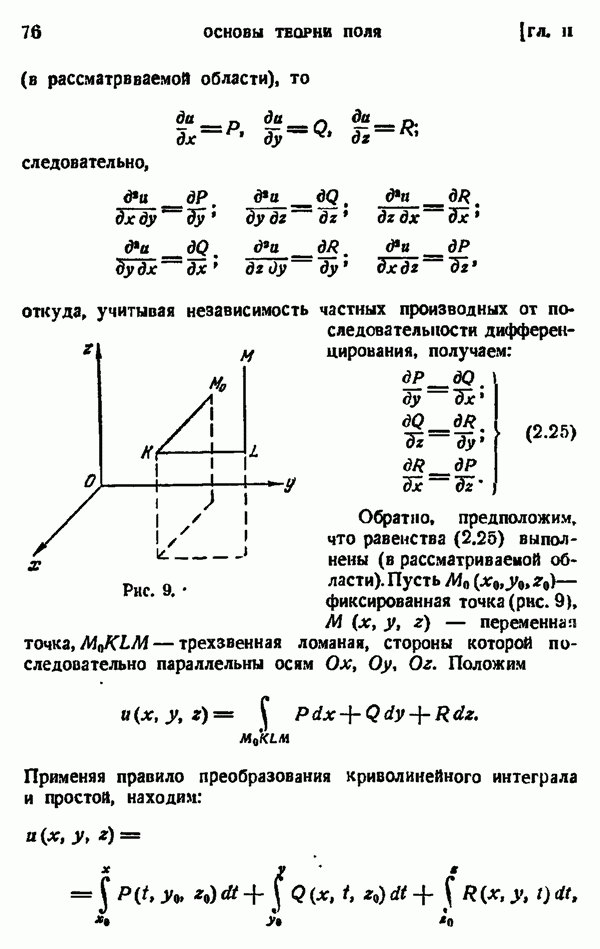
Рис. 35.
Таким образом, внутри С предельная функция  выражается интегралом типа Коши, следовательно, является аналитической. Но любую точку области
выражается интегралом типа Коши, следовательно, является аналитической. Но любую точку области  можно окружить таким контуром С, следовательно, предельная функция
можно окружить таким контуром С, следовательно, предельная функция  аналитична во всей области
аналитична во всей области  Пусть теперь
Пусть теперь  — какая-нибудь ограниченная замкнутая область (рис. 35), лежащая в
— какая-нибудь ограниченная замкнутая область (рис. 35), лежащая в  и С — вамкнутый контур длины
и С — вамкнутый контур длины  лежащий вместе с внутренностью в
лежащий вместе с внутренностью в  и такой, что
и такой, что  лежит внутри С. Пусть
лежит внутри С. Пусть  — расстояние между С и А (т. е. наименьшее из расстояний точек на С от точек в Д). Имеем при
— расстояние между С и А (т. е. наименьшее из расстояний точек на С от точек в Д). Имеем при  лежащем в
лежащем в  [в силу формул (3.44) для
[в силу формул (3.44) для  ]:
]:

Но  на С равномерно, следовательно, для всякого
на С равномерно, следовательно, для всякого  найдется такой номер
найдется такой номер  что при
что при  будем иметь
будем иметь  при всех С на С. Тогда из последней формулы найдем (по правилу оценки модуля интеграла);
при всех С на С. Тогда из последней формулы найдем (по правилу оценки модуля интеграла);

при  и любом
и любом  на А. Этим доказано, что
на А. Этим доказано, что  равномерно на любой ограниченной аамкнутой области А, лежащей в
равномерно на любой ограниченной аамкнутой области А, лежащей в 
Замечание. Мы видим, что последовательность производных  находится в таких же условиях, как последовательность функций
находится в таких же условиях, как последовательность функций  поэтому к ней также применима доказанная теорема.
поэтому к ней также применима доказанная теорема.
Таким образом, если последовательность аналитических функций  в области
в области  равномерно сходится внутри
равномерно сходится внутри  к
к  то последовательность производных любого порядка от
то последовательность производных любого порядка от  равномерно сходится внутри
равномерно сходится внутри  к производной такого же порядка от
к производной такого же порядка от 
Пусть теперь имеем функциональный ряд

члены которого суть аналитические функции в области  Из доказанного следует, что если этот ряд разномерно сходится внутри
Из доказанного следует, что если этот ряд разномерно сходится внутри  то его сумма аналитична в
то его сумма аналитична в  и ряд можно сколько угодно раз почленно дифференцировать, причем все получающиеся ряды равномерно сходятся внутри
и ряд можно сколько угодно раз почленно дифференцировать, причем все получающиеся ряды равномерно сходятся внутри 
Аналитичность суммы степенного ряда
Пусть — степенной ряд и  — его радиус сходимости. Пусть
— его радиус сходимости. Пусть  . Точка
. Точка  как лежащая внутри круга сходимости (рис. 36), есть точка абсолютной сходимости степенного ряда, т. е. ряд
как лежащая внутри круга сходимости (рис. 36), есть точка абсолютной сходимости степенного ряда, т. е. ряд  сходится. Но при
сходится. Но при  имеем
имеем  поэтому степенной ряд
поэтому степенной ряд  равномерно сходится на круге
равномерно сходится на круге  т. Так как любая замкнутая область, лежащая внутри круга сходимости, может быть заключена в круг
т. Так как любая замкнутая область, лежащая внутри круга сходимости, может быть заключена в круг  при надлежащем выборе числа
при надлежащем выборе числа  то приходим к следующему заключению: всякий степенной ряд равномерно сходится внутри круга сходимости.
то приходим к следующему заключению: всякий степенной ряд равномерно сходится внутри круга сходимости.

Рис. 36.
Примечание. На внутренности круга сходимости сходимость может быть неравномерной.
Так как члены степенного ряда  являются аналитическими функциями, то из доказанной теоремы следует, что сумма степенного ряда есть аналитическая функция внутри круга сходимости и что степенной ряд можно любое число раз почленно дифференцировать внутри круга сходимости. Следовательно, получающиеся в результате этого степенные ряды имеют не меньший радиус сходимости (на самом деле — тот же радиус сходимости).
являются аналитическими функциями, то из доказанной теоремы следует, что сумма степенного ряда есть аналитическая функция внутри круга сходимости и что степенной ряд можно любое число раз почленно дифференцировать внутри круга сходимости. Следовательно, получающиеся в результате этого степенные ряды имеют не меньший радиус сходимости (на самом деле — тот же радиус сходимости).

Рис. 37.

Рис. 38.
Аналогично, степенной ряд  равномерно сходится внутри круга с центром в точке а (рис. 37), а его сумма есть аналитическая функция внутри этого круга; ряд
равномерно сходится внутри круга с центром в точке а (рис. 37), а его сумма есть аналитическая функция внутри этого круга; ряд  имеющий кольцо сходимости (рис. 38), равномерно сходится внутри кольца и его сумма есть аналитическая функция внутри этого кольца. При этом законно почленное дифференцирование любое число раз.
имеющий кольцо сходимости (рис. 38), равномерно сходится внутри кольца и его сумма есть аналитическая функция внутри этого кольца. При этом законно почленное дифференцирование любое число раз.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
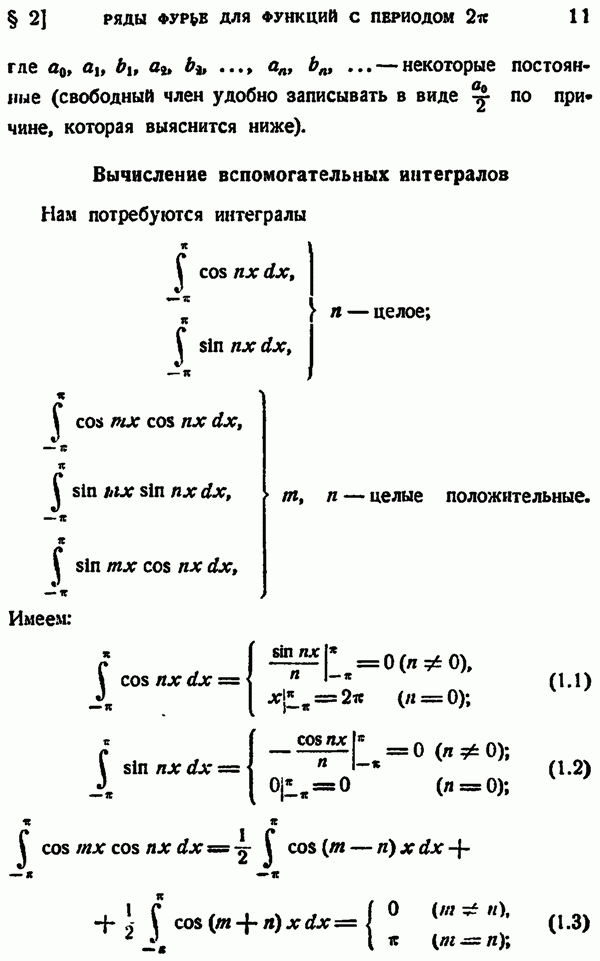
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
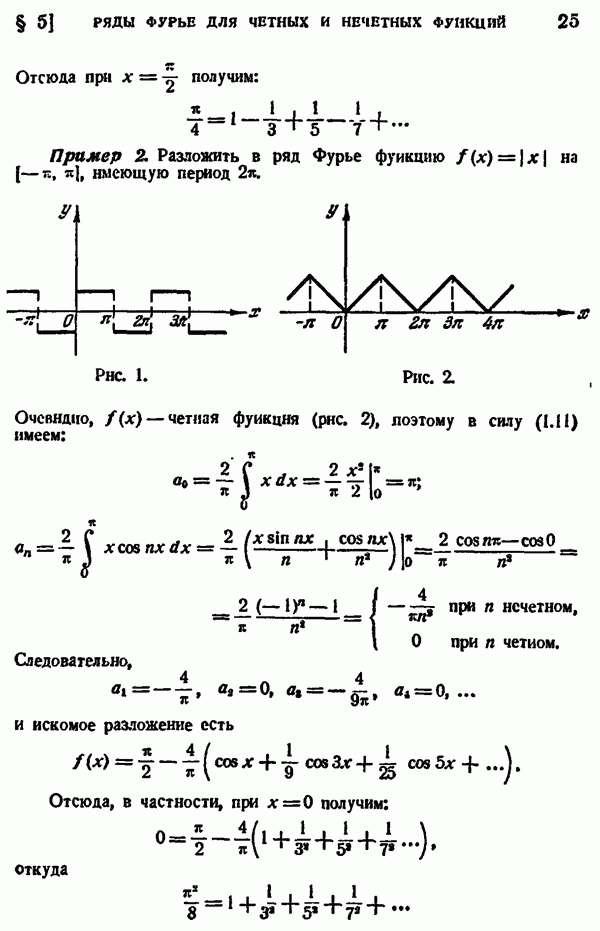
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 6. ВЕКТОРНОЕ ПОЛЕ
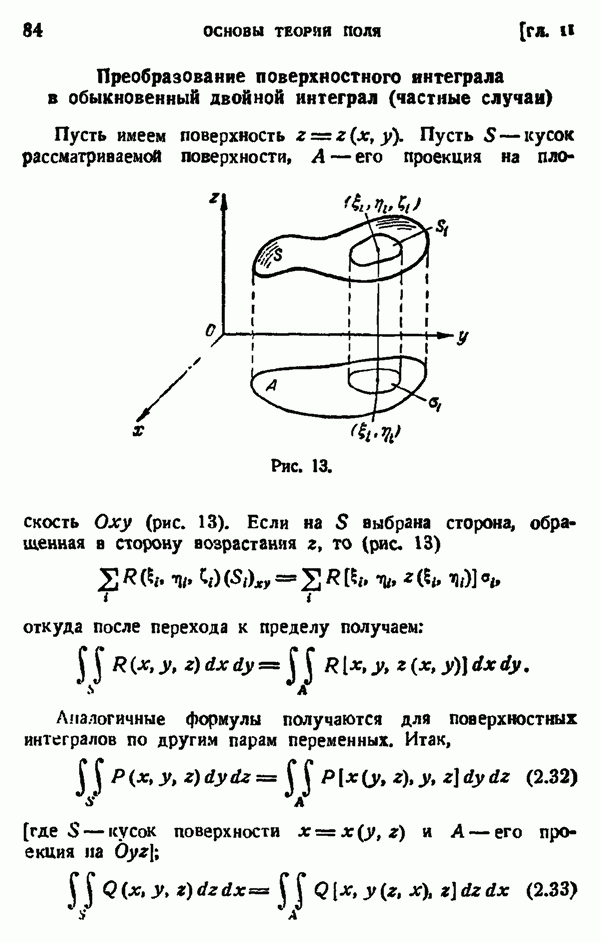
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
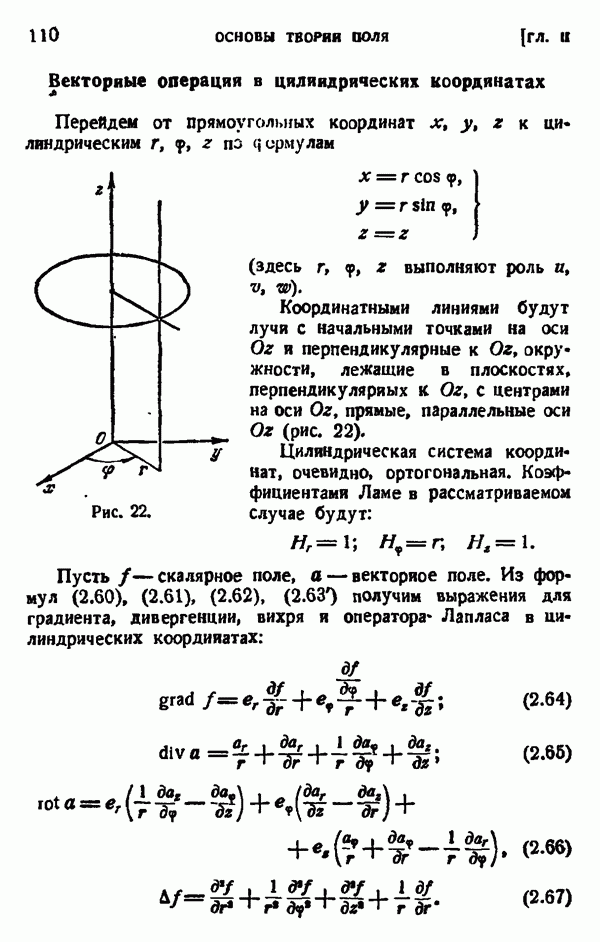
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
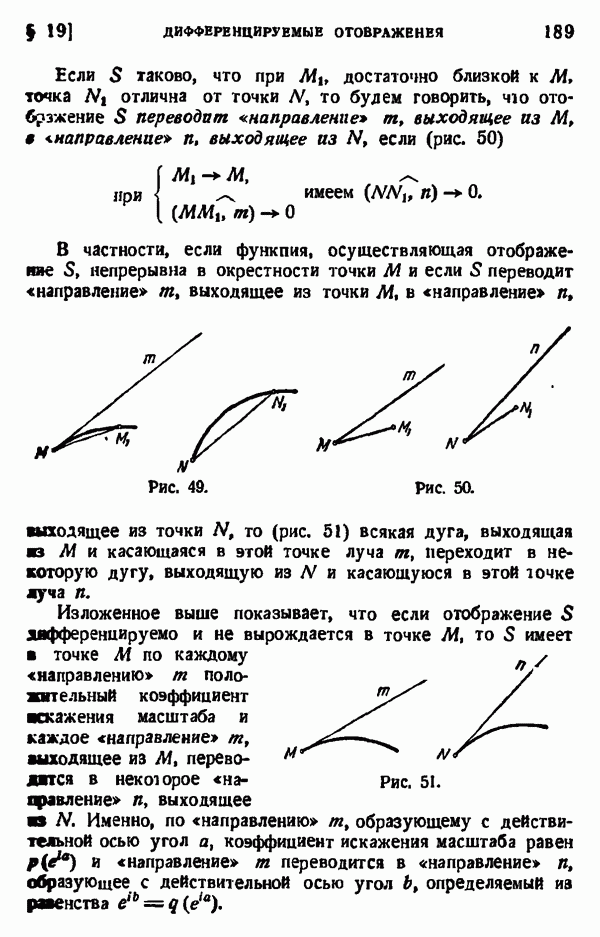
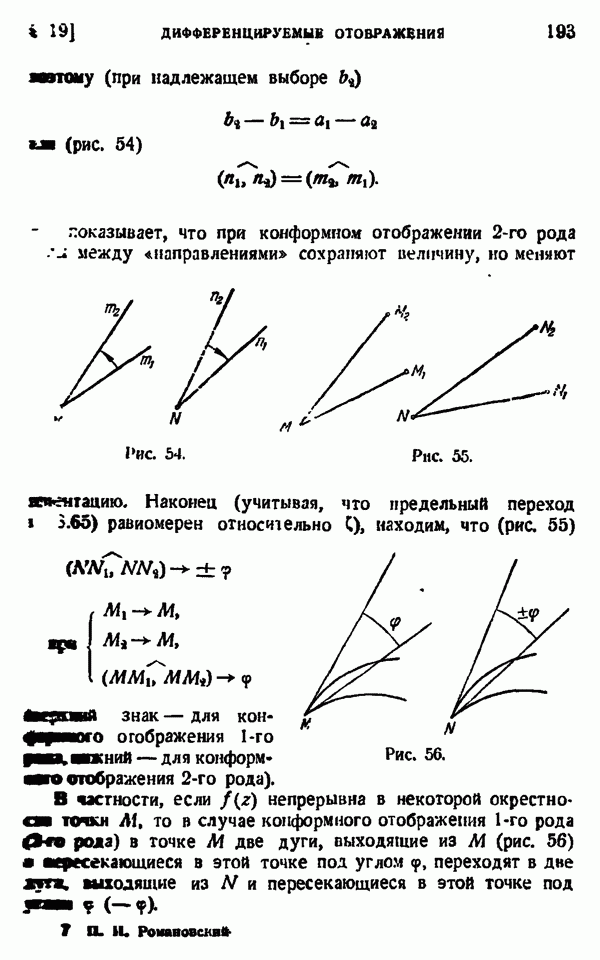
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
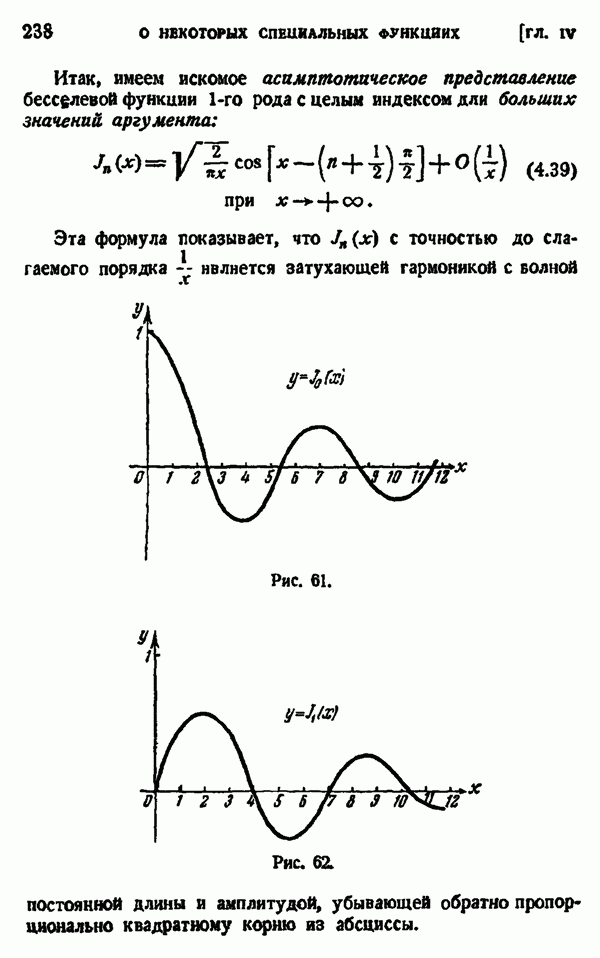
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
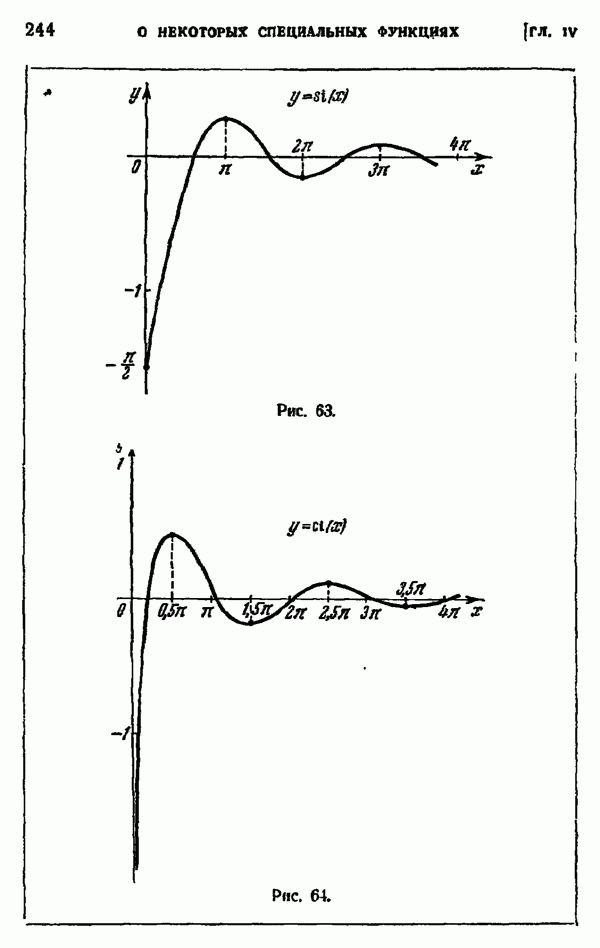
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ