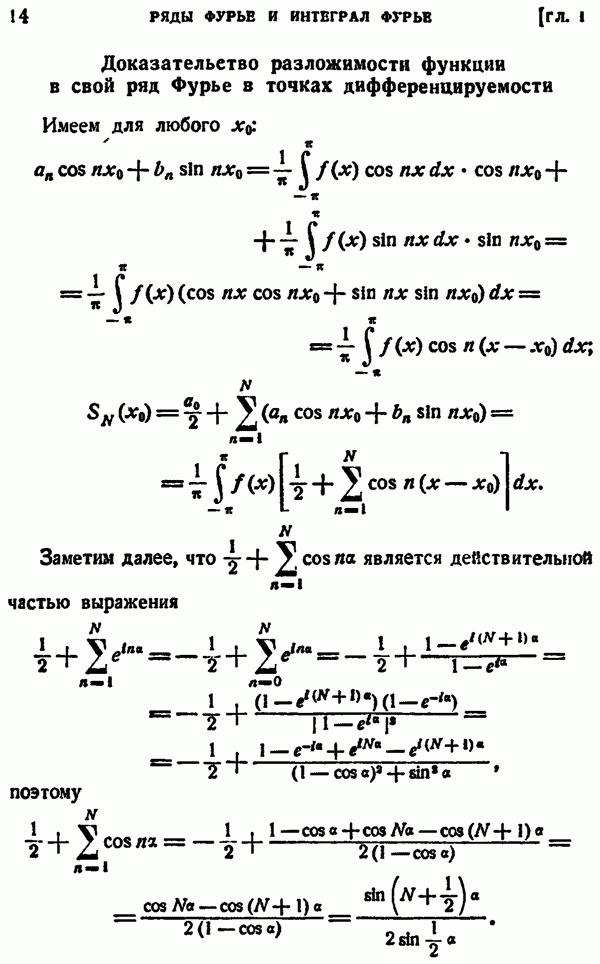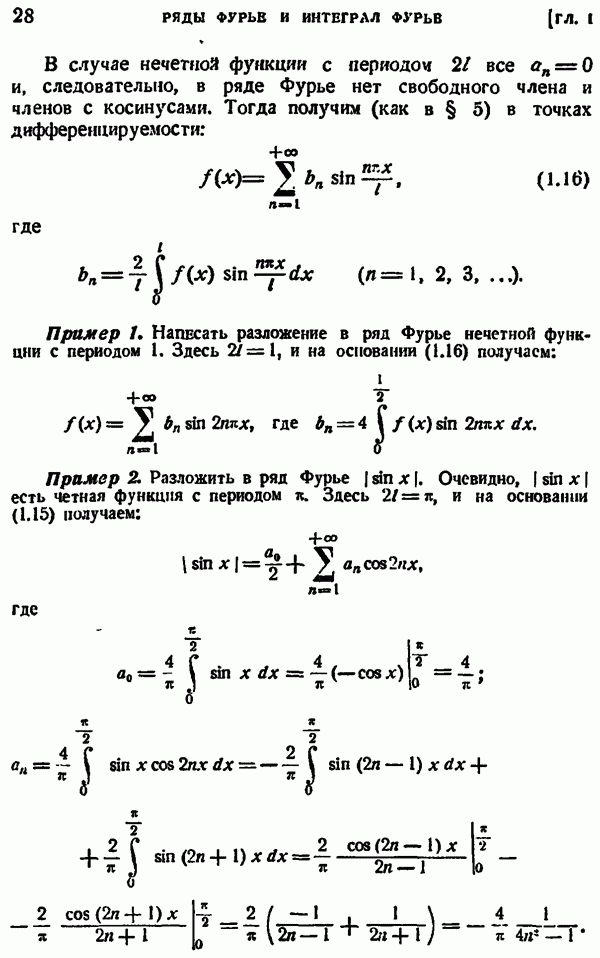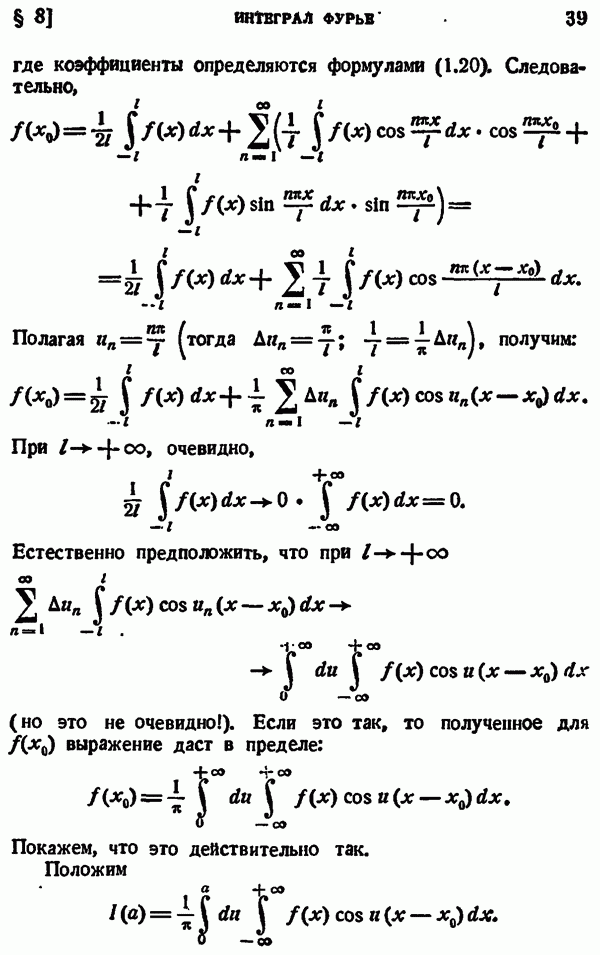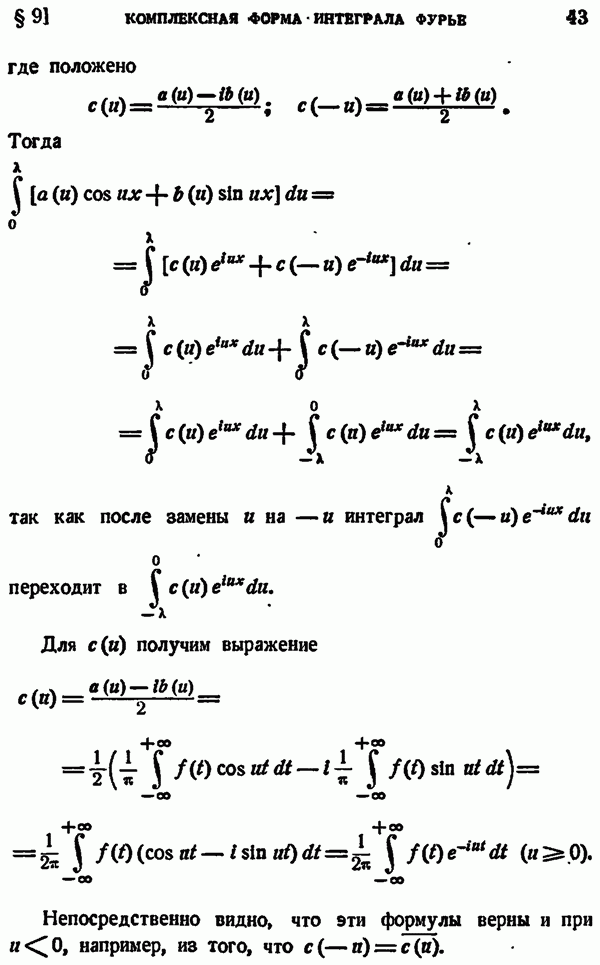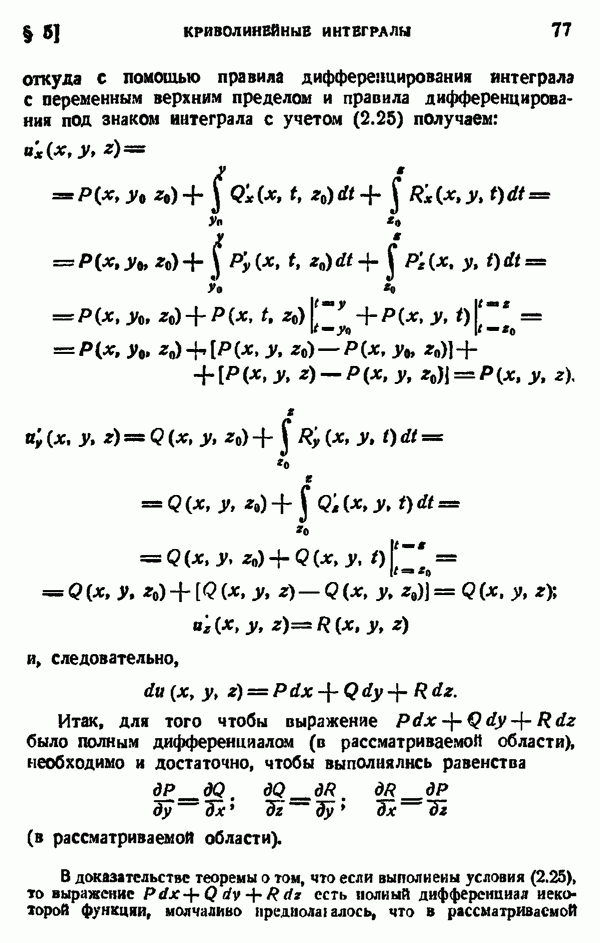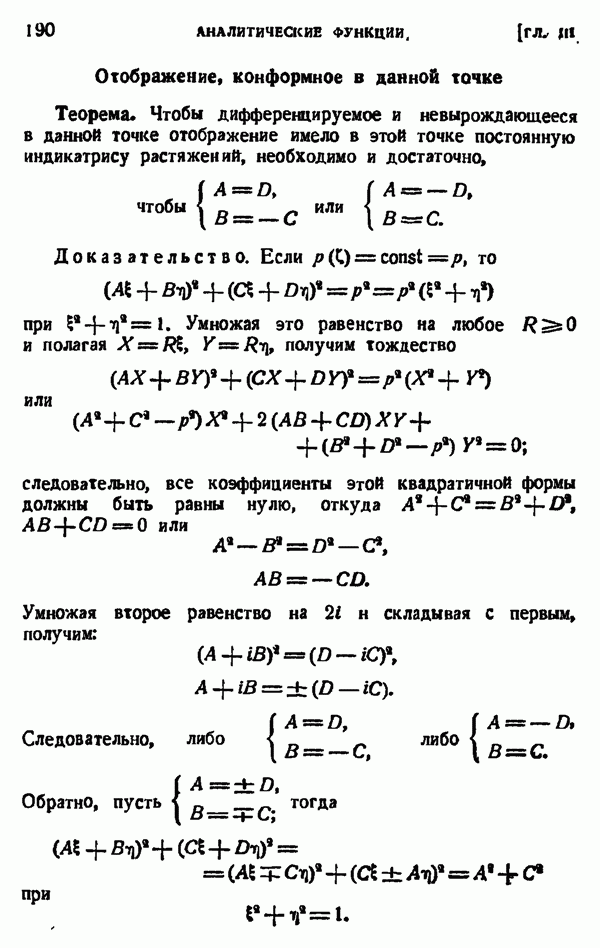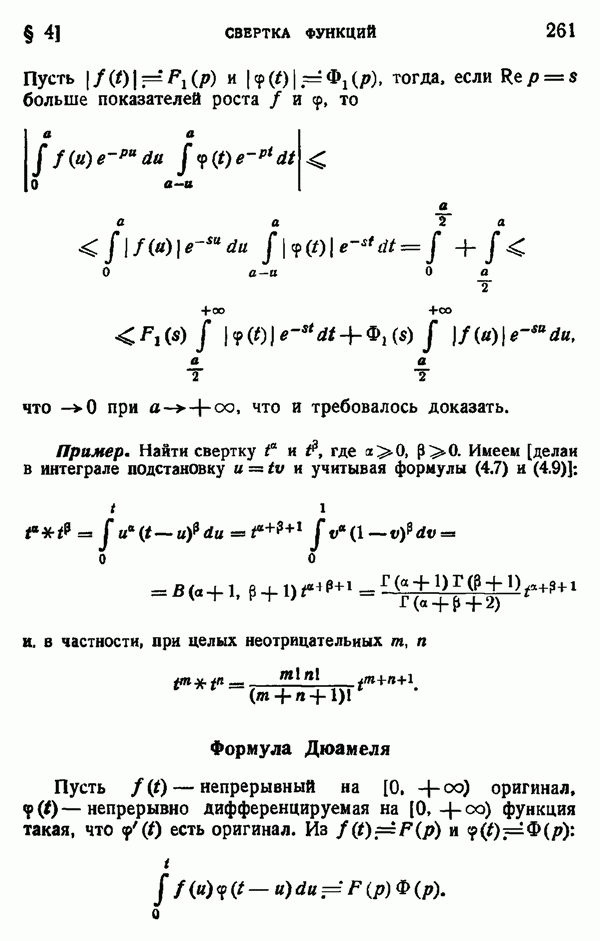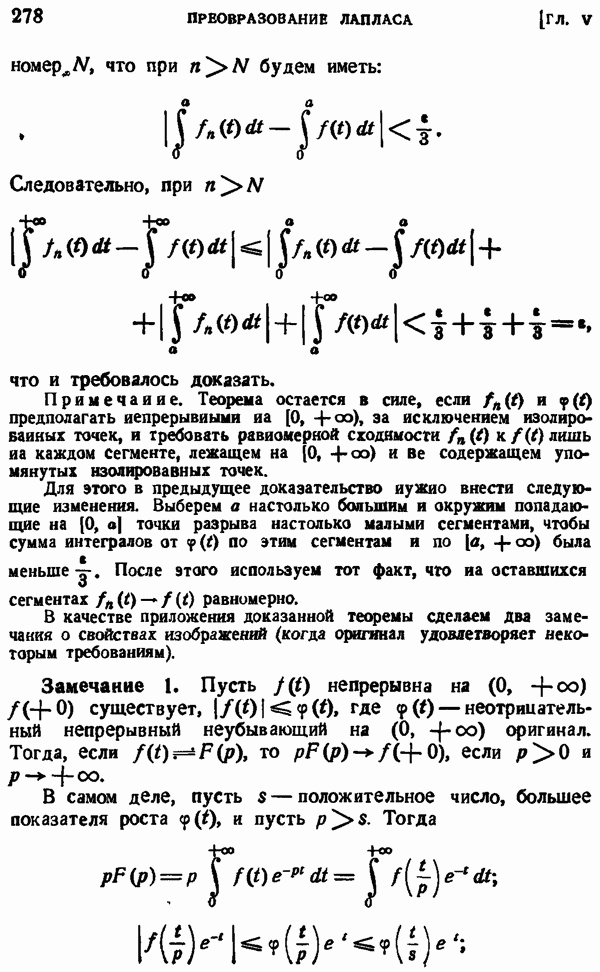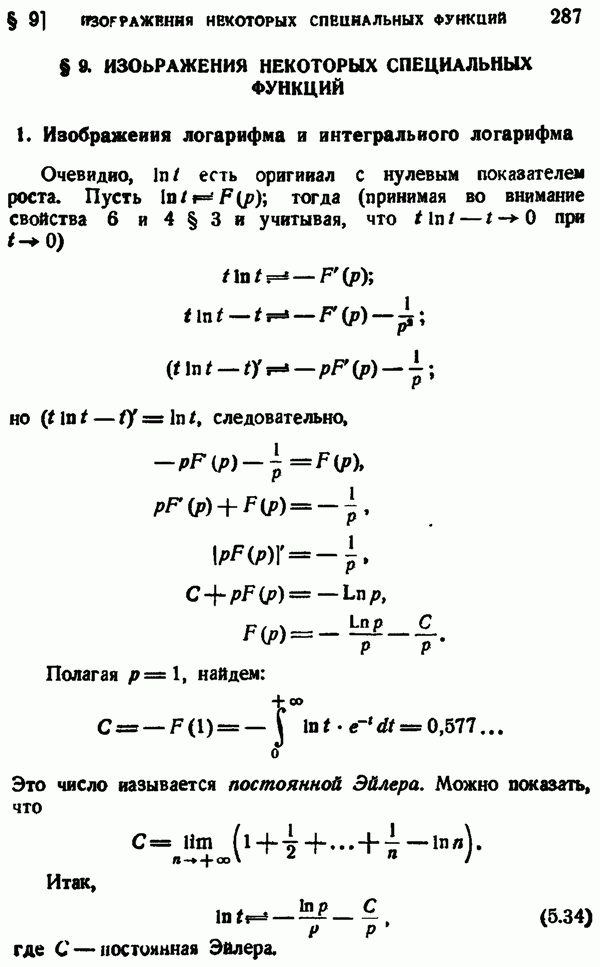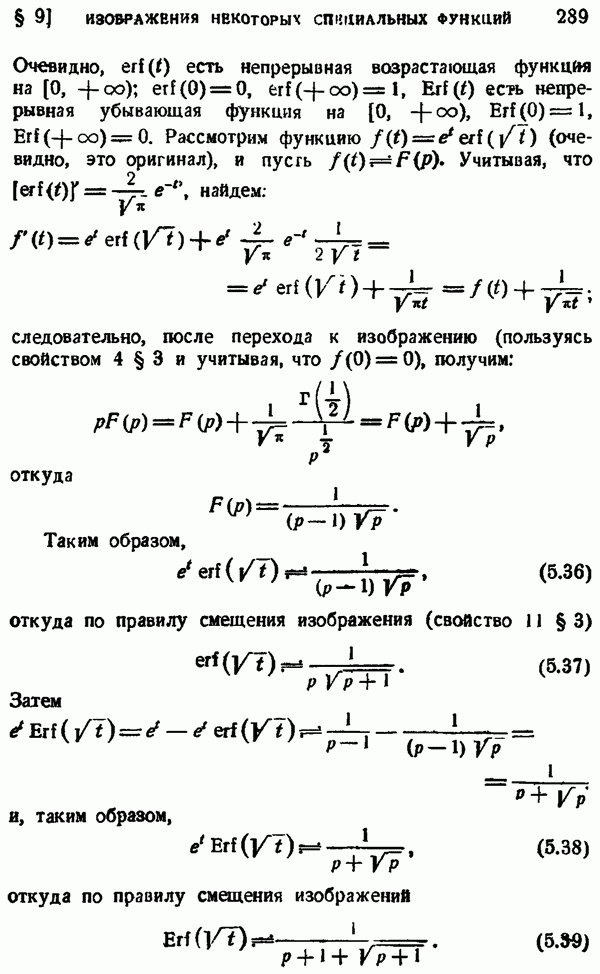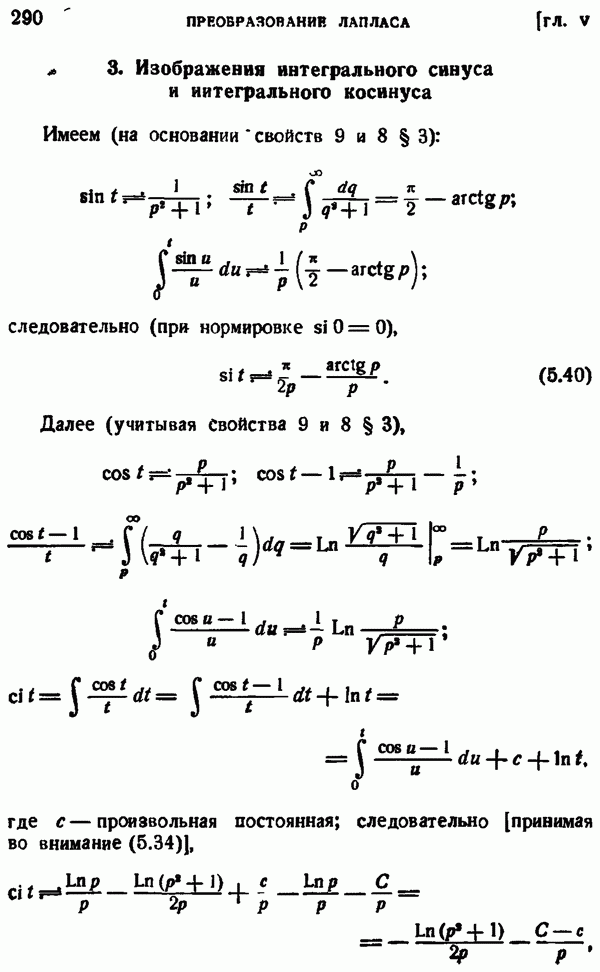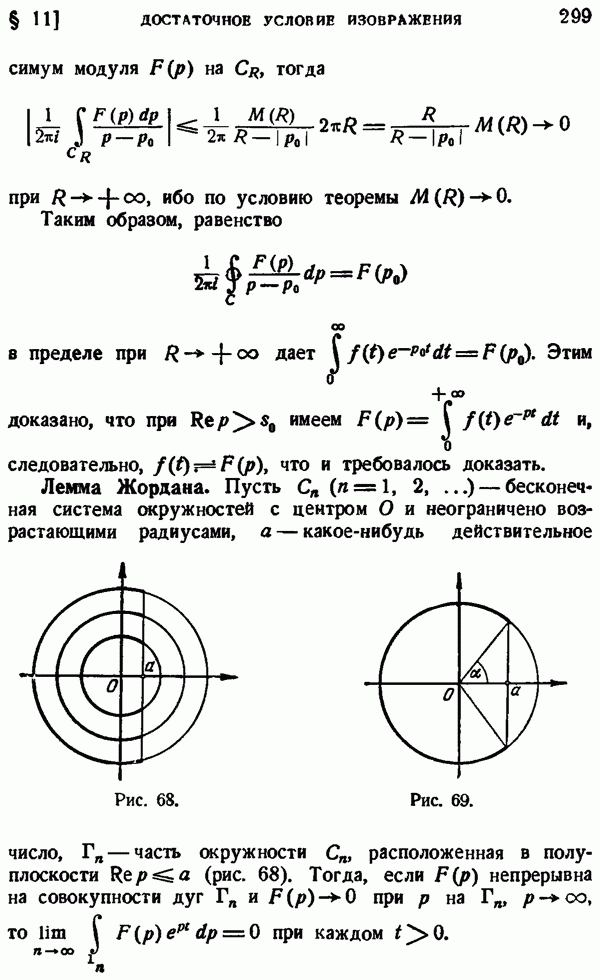| << Предыдущий параграф | Следующий параграф >> |
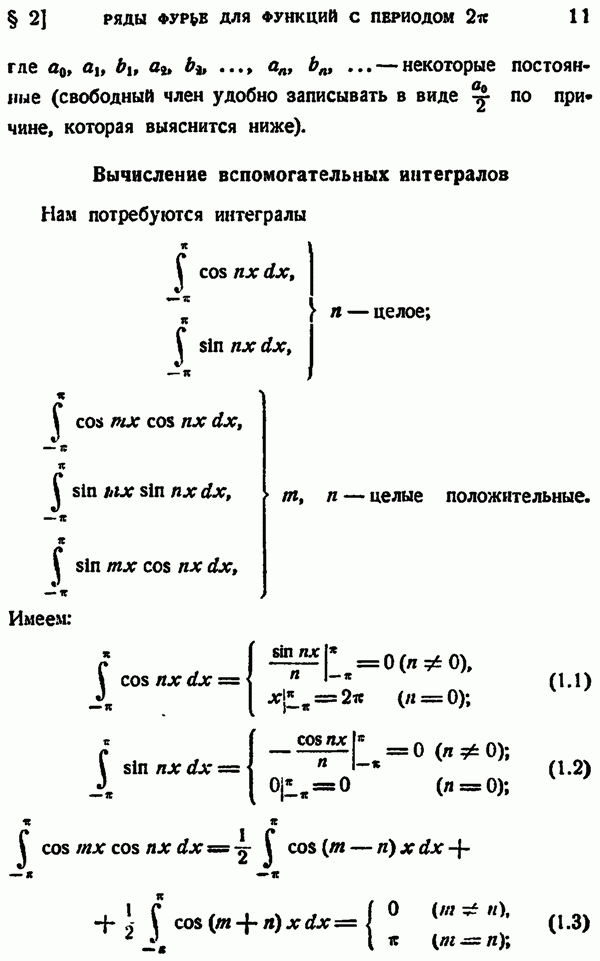
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
§ 1. ГАММА-ФУНКЦИЯ
Гамма-функция, или эйлеров интеграл  рода, определяется (для положительных значений независимого переменного
рода, определяется (для положительных значений независимого переменного  формулой
формулой

Интеграл в правой части является несобственным при верхнем пределе и, кроме того, в случае  несобственным при нижнем пределе. Сходимость интеграла (4.1) при всех
несобственным при нижнем пределе. Сходимость интеграла (4.1) при всех  обеспечена, так как при
обеспечена, так как при  показательная функция
показательная функция  растет быстрее любой степенной функции и так как интеграл с нижним пределом
растет быстрее любой степенной функции и так как интеграл с нижним пределом  при
при  сходится.
сходится.
Формула приведения для гамма-функции (первая основная формула)
Интегрирование по частям дает:

Таким образом, получаем формулу приведения

Отсюда заключаем, что

и вообще

а тогда при натуральном 

но

следовательно,

Формула приведения (4.2) позволяет выразить значения гамма-функции для любого положительного  черев ее значения для
черев ее значения для  лежащего между 0 и 1.
лежащего между 0 и 1.
Второе выражение гамма-функции
Делая подстановку  получим:
получим:

или, заменяя  на х,
на х,

откуда, в частности,

Ниже будет показано, что  (см. стр. 213), откуда с помощью (4.3) найдем для любого натурального я:
(см. стр. 213), откуда с помощью (4.3) найдем для любого натурального я:

Бета-функция
Бета-функция, или эйлеров интеграл 1-го рода, определяется (для положительных значении независимых переменных  формулой
формулой

Этот интеграл является несобственным при нижием пределе в случае  и несобственным при верхнем пределе в случае
и несобственным при верхнем пределе в случае 
Делая подстановку  получим второе выражение для бета-функции:
получим второе выражение для бета-функции:

Бета-функция может быть легко выражена через Г-функцию посредством формулы

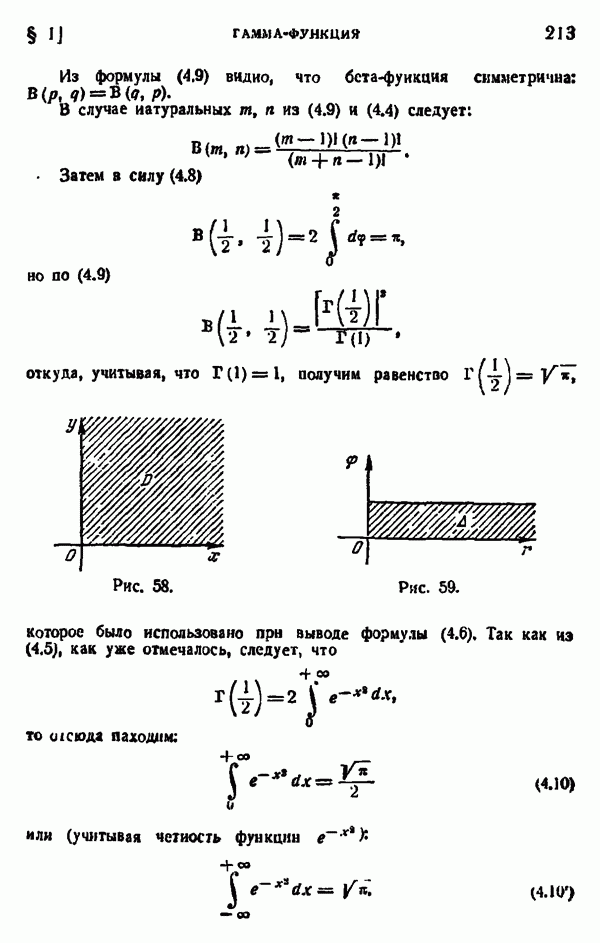
Действительно, перемножая равенства

и переходя в получающемся двойном интеграле к полярным координатам

получим (рис. 58 и 59):

откуда и вытекает формула (4.9).
Из формулы (4.9) видно, что бета-функция симметрична: 
В случае натуральных  из (4.9) и (4.4) следует:
из (4.9) и (4.4) следует:

Затем в силу (4.8) но по (4.9)

но по (4.9)

откуда, учитывая, что  подучим равенство
подучим равенство  которое было использовано при выводе формулы (4.6).
которое было использовано при выводе формулы (4.6).

Рис. 58.

Рис. 59.
Так как  как уже отмечалось, следует, что
как уже отмечалось, следует, что

то отсюда находим:

или (учитывая четность функции 

Интеграл, фигурирующий в формулах (4.10) или (4.10), называется интегрелом Гауссе.
Если  — любое положительное,
— любое положительное,  — натуральное, то из (4.9), (4.4), (4.3) находим:
— натуральное, то из (4.9), (4.4), (4.3) находим:

Делая в формуле (4.7) подстановку

(и меняя затем у на  получим третье выражение для бета-функции:
получим третье выражение для бета-функции:

откуда

или, учитывая (4.9),

Вычисление интеграла  где
где 
Пусть сперва я — рациональное число вида  где
где  — четное,
— четное,  — нечетное,
— нечетное,  Подстановка
Подстановка  даст:
даст:

Используя правило вычисления несобственных интегралов с помощью вычетом (см. гл. III, § 17), подучим:

где а — полюсы рациональной дроби 

лежащие в верхней полуплоскости, т. е. корни уравнения  имеющие положительный коэффициент при
имеющие положительный коэффициент при  Имеем:
Имеем:

Из эти  значений
значений  положительный коэффициент при
положительный коэффициент при  имеют значения, соответствующие
имеют значения, соответствующие  Следовательно, все значения а суть
Следовательно, все значения а суть

С помощью правила вычисления вычета относительно простого полюса находим:

Таким образом, имеем при  (используя в процессе преобразований суммирование геометрической прогрессии и выражение синуса через показательную функцию по формуле Эйлера):
(используя в процессе преобразований суммирование геометрической прогрессии и выражение синуса через показательную функцию по формуле Эйлера):

где

и, следовательно,  Но левая часть нашей цепочки равенств и коэффициент при
Но левая часть нашей цепочки равенств и коэффициент при  положительны, поэтому
положительны, поэтому  Таким образом, имеем при
Таким образом, имеем при  равенство
равенство

по левая и правая части этого равенства суть непрерывные функции от  на иитерваяе
на иитерваяе  (мы не останавливаемся здесь на обосновании непрерывности левой части), а так как каждое действительное число этого интервала можно представить как предел последовательности правильных рациональных дробей вида
(мы не останавливаемся здесь на обосновании непрерывности левой части), а так как каждое действительное число этого интервала можно представить как предел последовательности правильных рациональных дробей вида  где
где  — четное,
— четное,  — нечетное, для которых упомянутое равенство доказано, то в пределе найдем справедливость его для всех
— нечетное, для которых упомянутое равенство доказано, то в пределе найдем справедливость его для всех  Итак,
Итак,

Вторая основная формула для гамма-функции
Из (4.12) и (4.13) находим:

Формула (4.14) позволяет пыразнть значение гамма-функцни для  лежащих между
лежащих между  и 1, через ее значения для
и 1, через ее значения для  лежащих между 0 и
лежащих между 0 и 
Гамма-функция как предел произведения
Учитывая, что  при
при  найдем:
найдем:

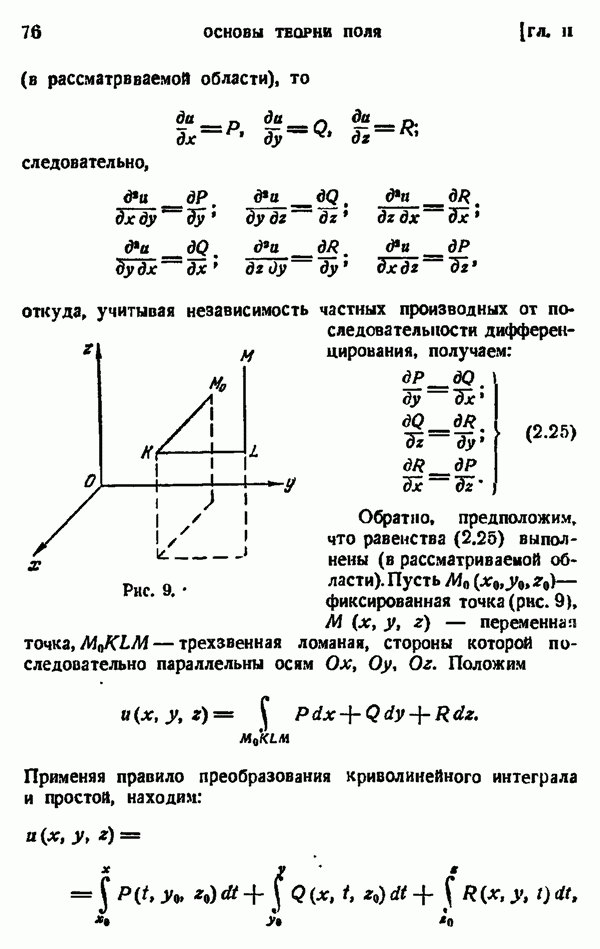
(законность этого предельного перехода легко установить, но на этом мы не останавливаемся). Положим:

Интегрирование по частям дает:

значит, применяя последовятельно эту формулу и учи тывая, что

найдем:

Таким образом,

Можно показать, что предел, стоящий в правой части формулы (4.15), существует для всех комплексных чисел  (конечный для всех
(конечный для всех  отличных от нуля и отрицательных целых чисел). Выражение (4.15) может служить определением гамма-функции для любого комплексного значения
отличных от нуля и отрицательных целых чисел). Выражение (4.15) может служить определением гамма-функции для любого комплексного значения 
Если формула (4.16) принята за определение гамма-функции, то формулу приведения (4.2) можно доказать следующим образом:

Гамма-функция является аналитической на всей плоскости комплексного переменного, за исключением точек 0, —1, - 2, -3..... являющихся для нее простыми полюсами.
Гамма-фуикция, как это можно установить, нигде в иуль не обращается.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
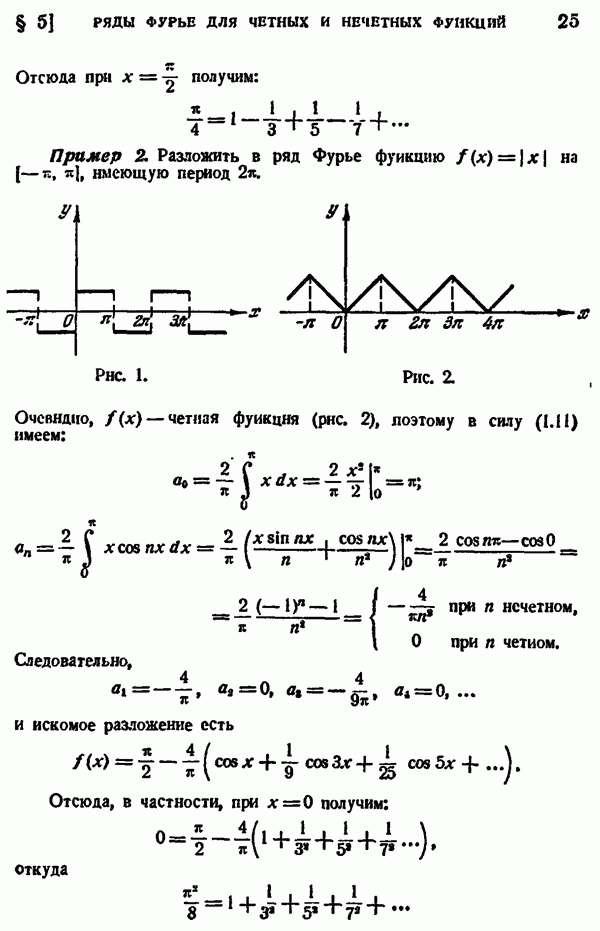
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
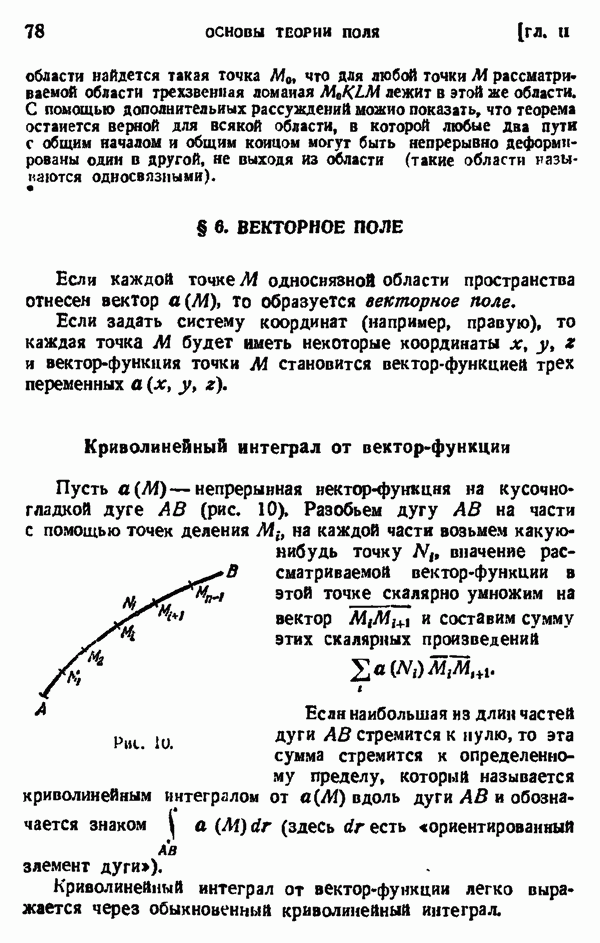
- § 6. ВЕКТОРНОЕ ПОЛЕ
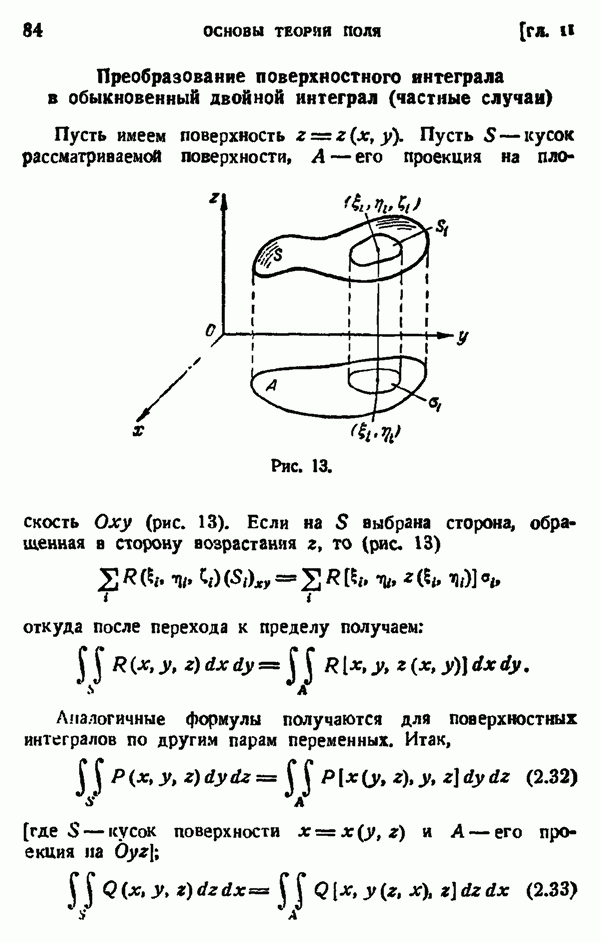
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
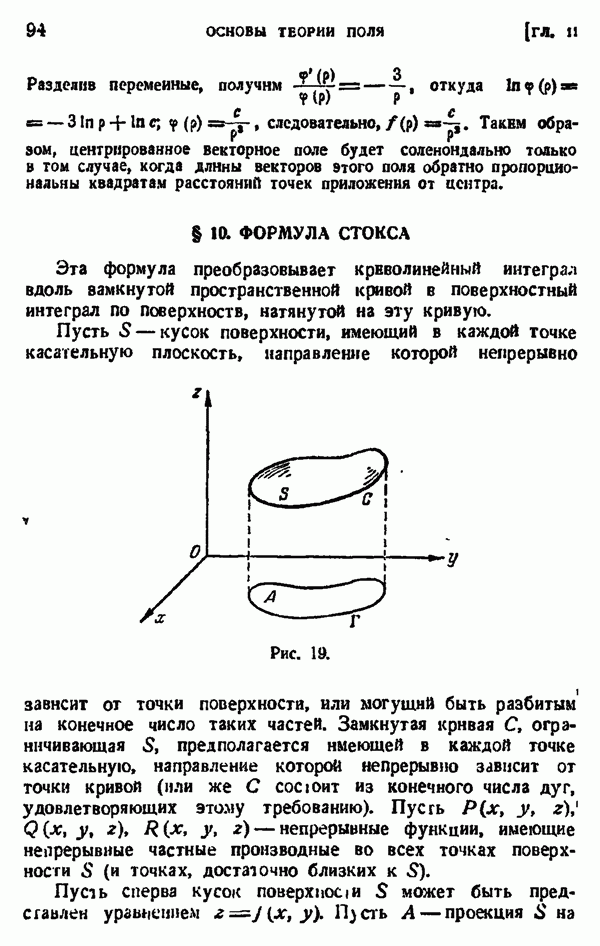
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
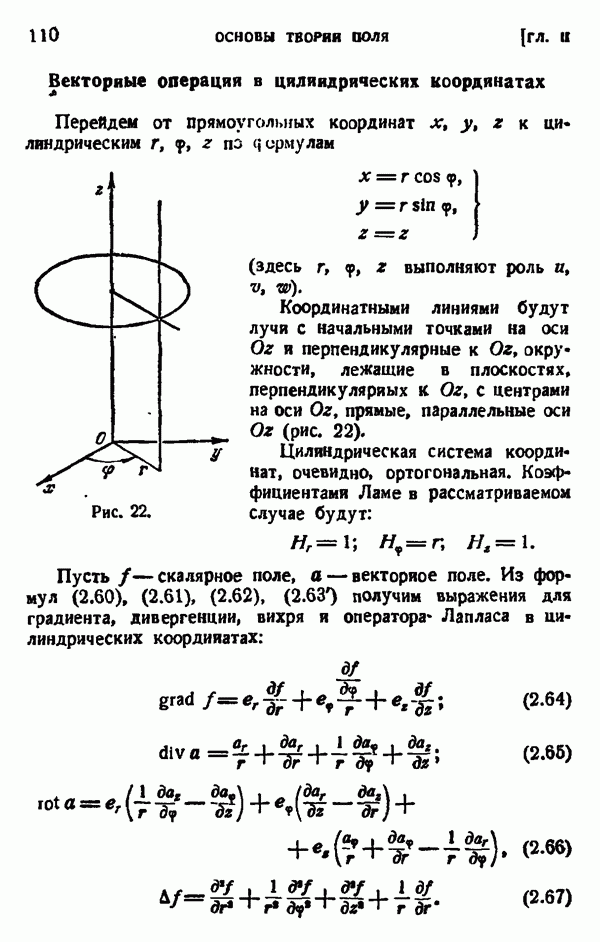
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
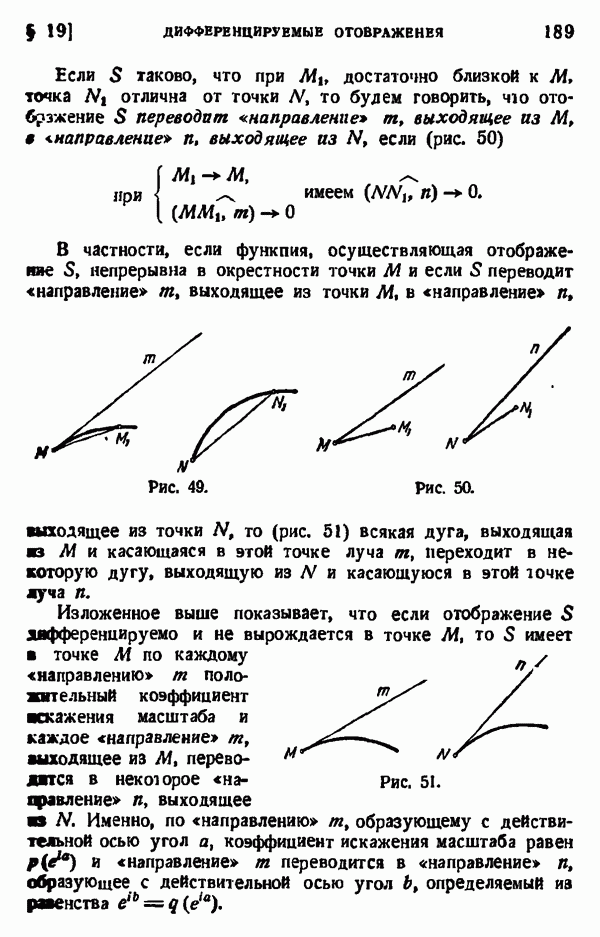
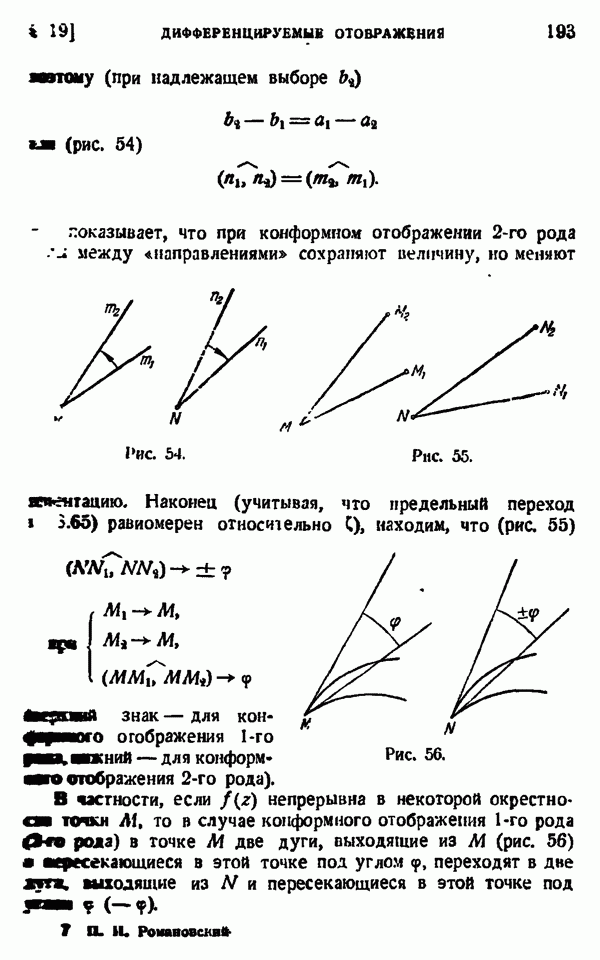
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
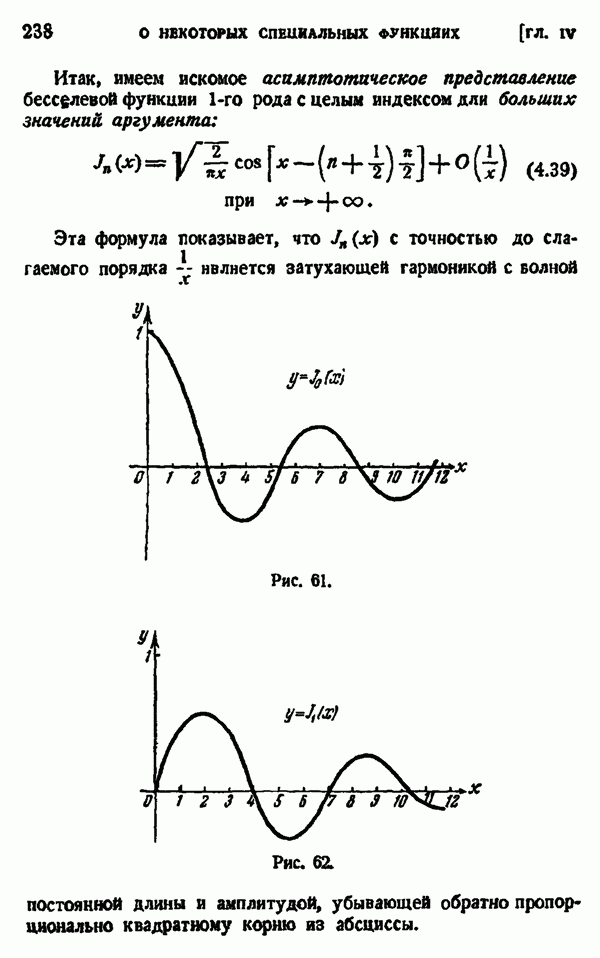
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
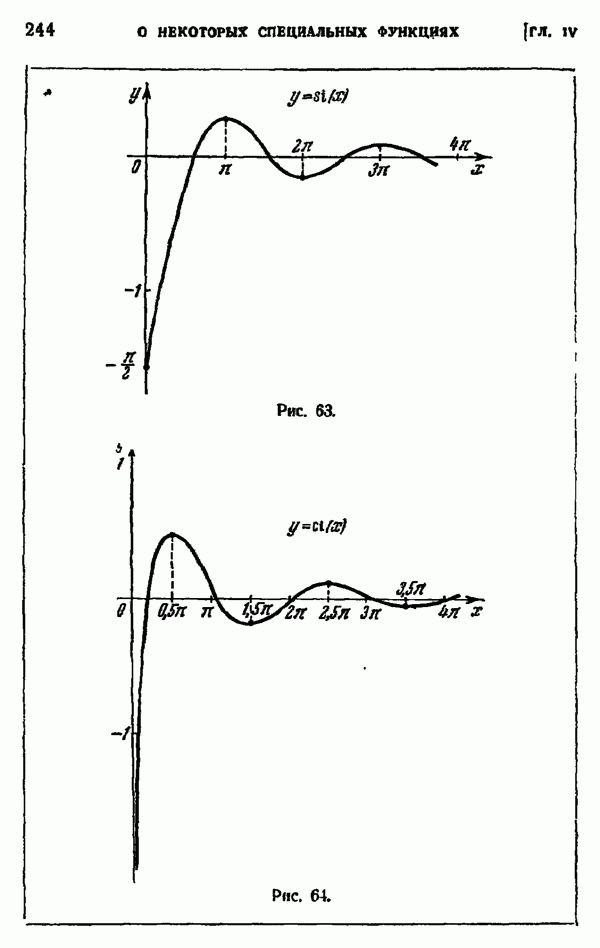
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ