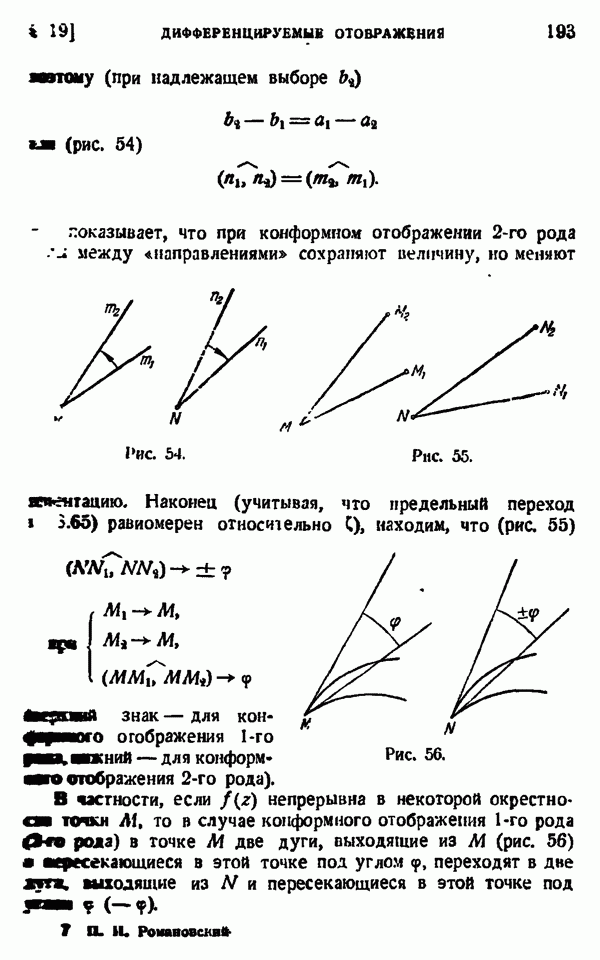
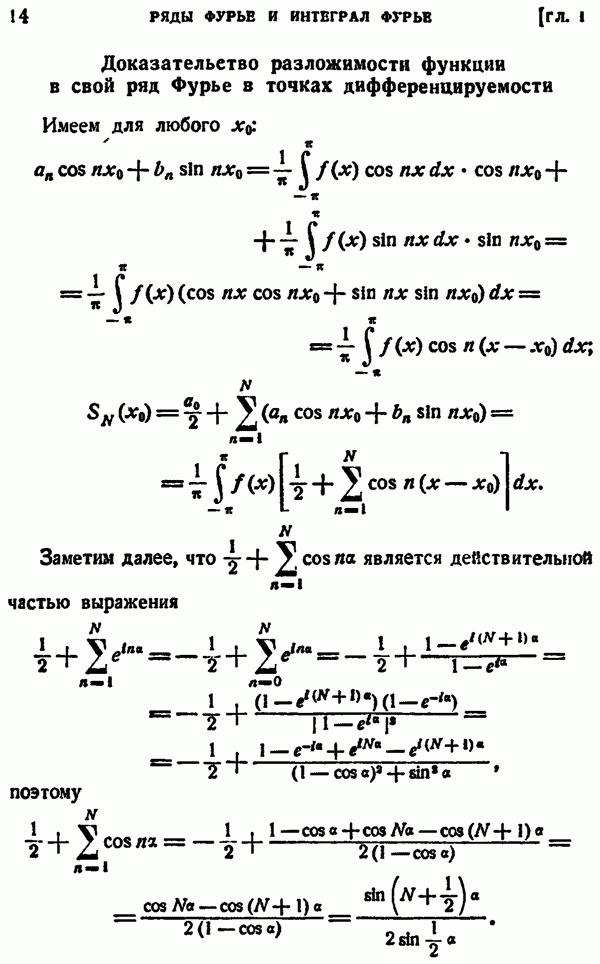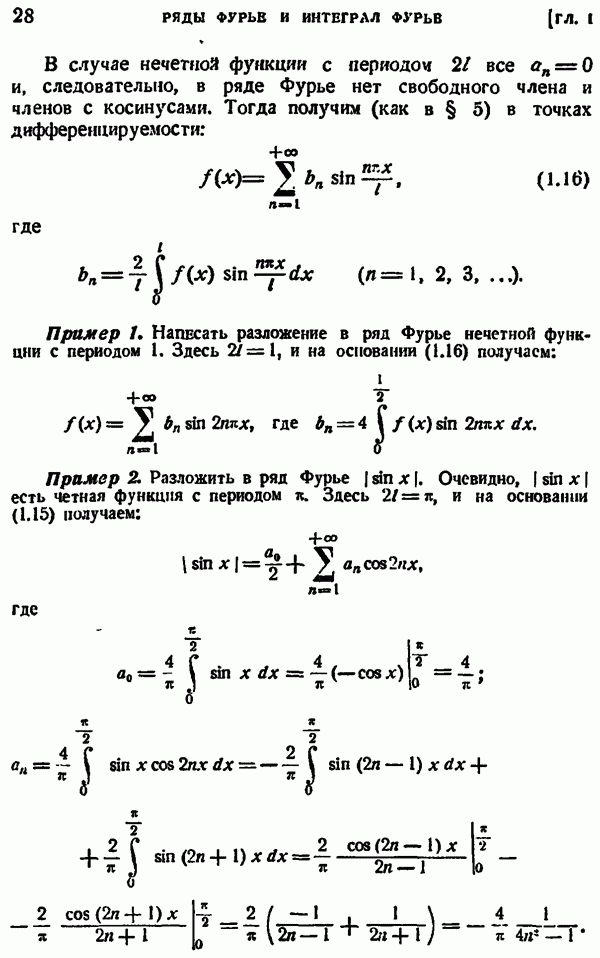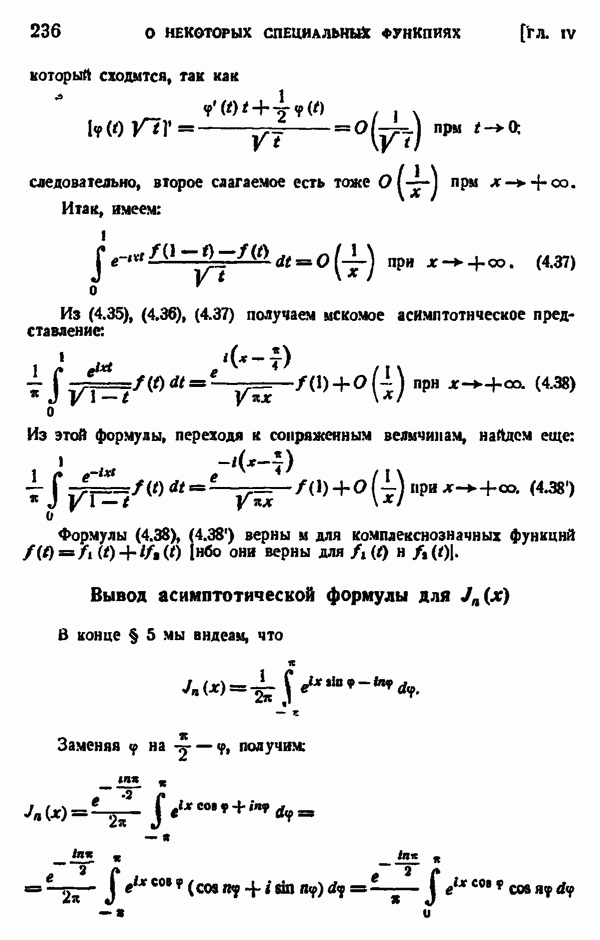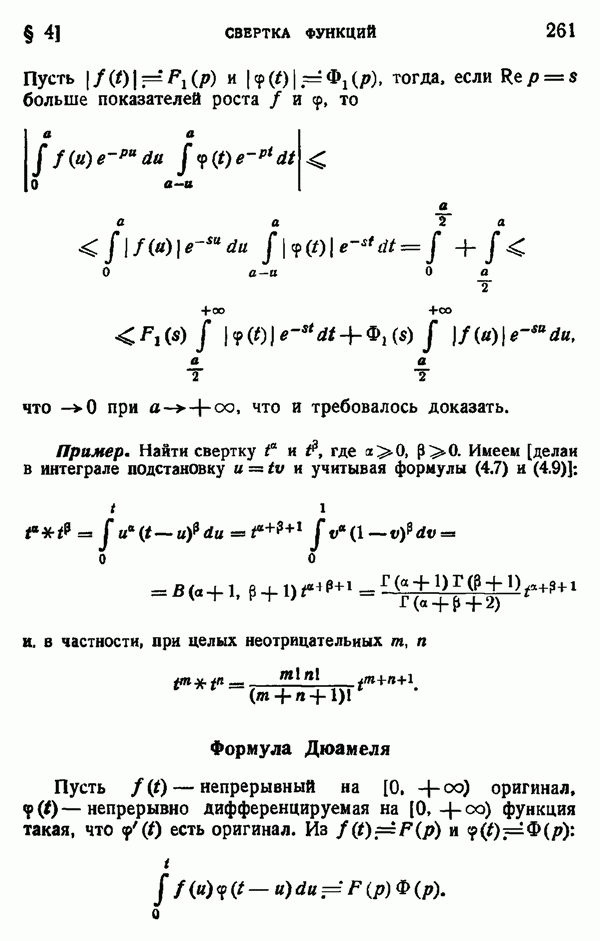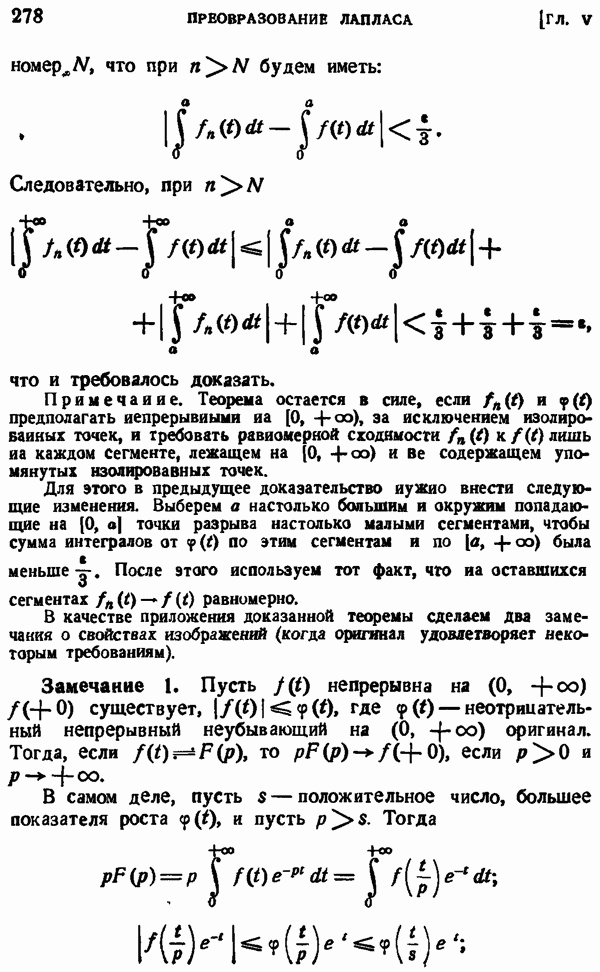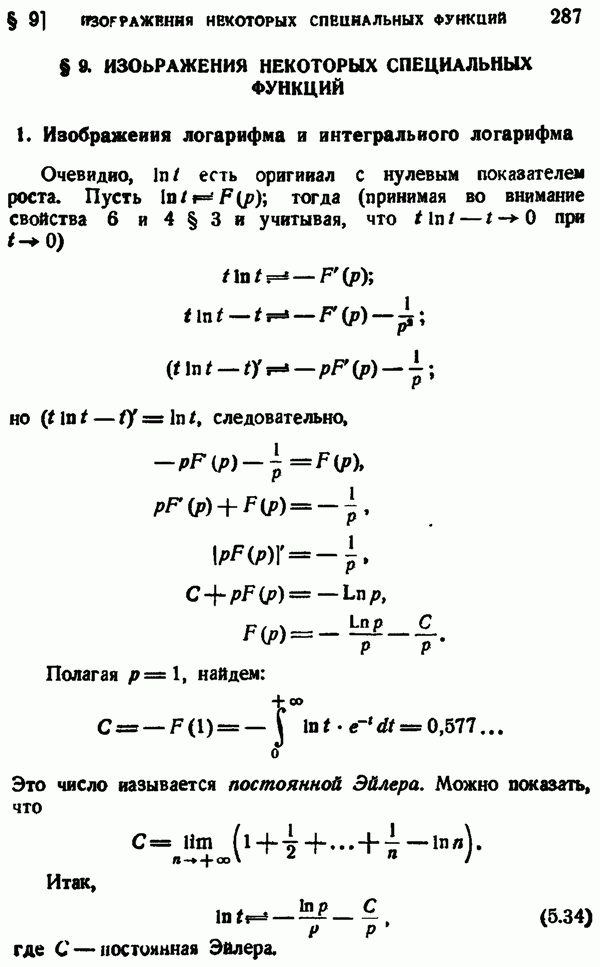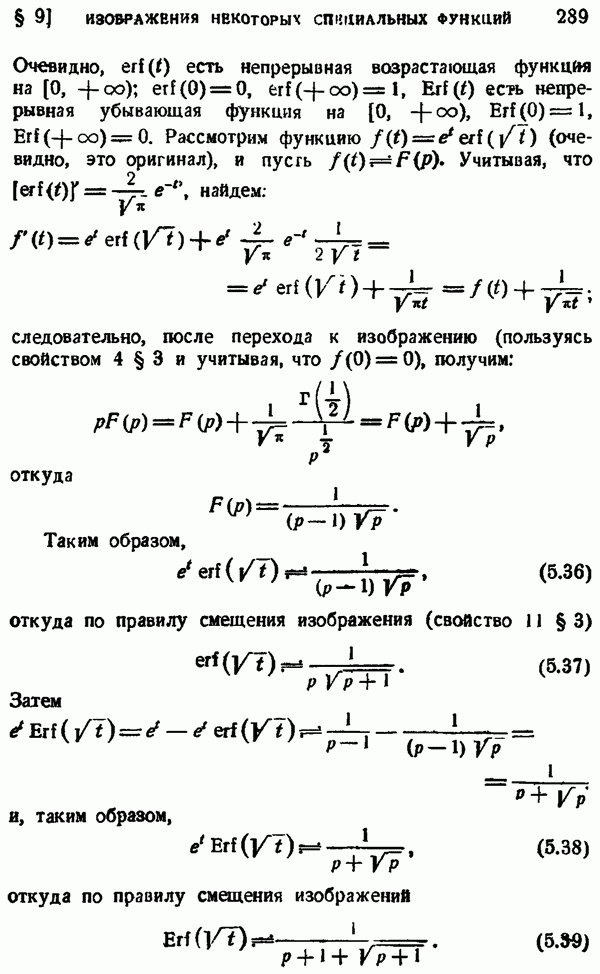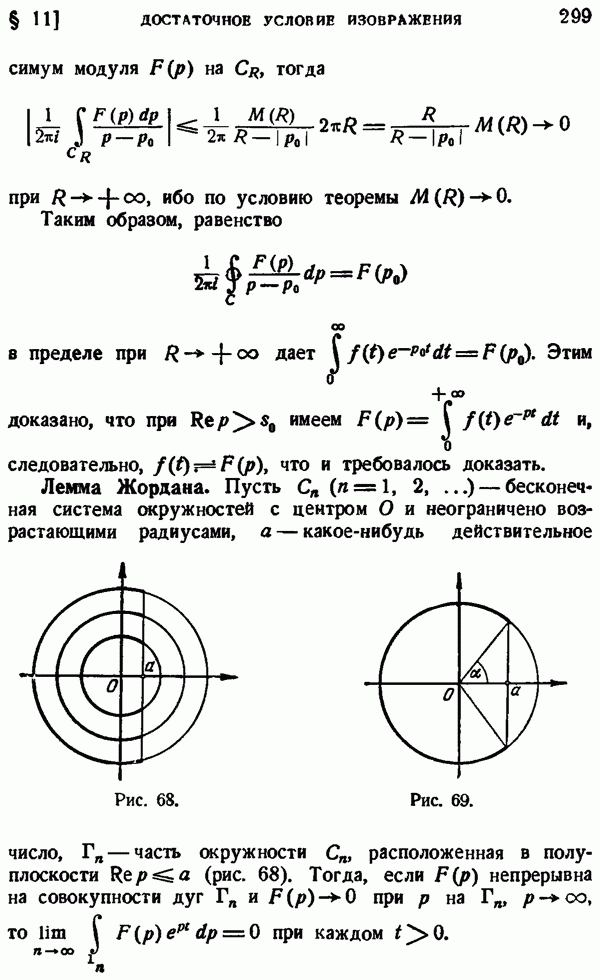| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
Будем рассматривать действительные функции  на каком-нибудь интервале (закрытом, открытом или полуоткрытом) с концами
на каком-нибудь интервале (закрытом, открытом или полуоткрытом) с концами  (а конечно или равно
(а конечно или равно  конечно или равно
конечно или равно  на котором фиксирована некоторая положительная непрерывная функция
на котором фиксирована некоторая положительная непрерывная функция  (весовая функция). Будем предполагать функции
(весовая функция). Будем предполагать функции  непрерывными на рассматриваемом интервале и такими, что
непрерывными на рассматриваемом интервале и такими, что

Для таких функций  положим
положим 

Этот интеграл имеет смысл, так как 
Определение. Функции  (удовлетворяющие указанным выше требованиям) называются ортогональными относительно веса
(удовлетворяющие указанным выше требованиям) называются ортогональными относительно веса  на данном интервале, если
на данном интервале, если

Ортогональность не нарушается при умножении функций на постоянные множители.
Определение. Функция  (удовлетворяющая указанным требованиям) называется нормированной относительно веса
(удовлетворяющая указанным требованиям) называется нормированной относительно веса  на данном интервале, если
на данном интервале, если

Не исчезающую тождественно  можно сделать нормированной, умножив на подходящий постоянный множитель X (нормирующий множитель). Этот множитель X следует выбрать так, чтобы
можно сделать нормированной, умножив на подходящий постоянный множитель X (нормирующий множитель). Этот множитель X следует выбрать так, чтобы

откуда

Например, для х на [0, 1] при единичном весе

Рассмотрим бесконечную систему функций

(удовлетворяющих отмеченным в начале параграфа требованиям). Назовем систему  ортогональной относительно веса
ортогональной относительно веса  на данном интервале, если все функции этой системы не исчезают тождественно и попарно ортогональны относительно веса
на данном интервале, если все функции этой системы не исчезают тождественно и попарно ортогональны относительно веса  на рассматриваемом интервале, т. е. если
на рассматриваемом интервале, т. е. если

Назовем систему  ортонормированной относительно веса
ортонормированной относительно веса  на данном интервале, если она ортогональная и все (ее функции нормированные относительно названного веса на
на данном интервале, если она ортогональная и все (ее функции нормированные относительно названного веса на
рассматриваемом интервале, т. е. если

Если некоторая функция  допускает разложение
допускает разложение

то, умножая это равенство на  и интегрируя затем почленно в пределах от а до
и интегрируя затем почленно в пределах от а до  (если это законно), получим:
(если это законно), получим:

Откуда

Определение. Рядом Фурье какой-нибудь функции  (удовлетворяющей отмеченным в начале параграфа требованиям) относительно ортогональной системы
(удовлетворяющей отмеченным в начале параграфа требованиям) относительно ортогональной системы  называется ряд
называется ряд

коэффициенты которого определяются по формулам (1.47).
Разумеется, из этого определения не следует, что  должна непременно разлагаться в свой ряд Фурье.
должна непременно разлагаться в свой ряд Фурье.
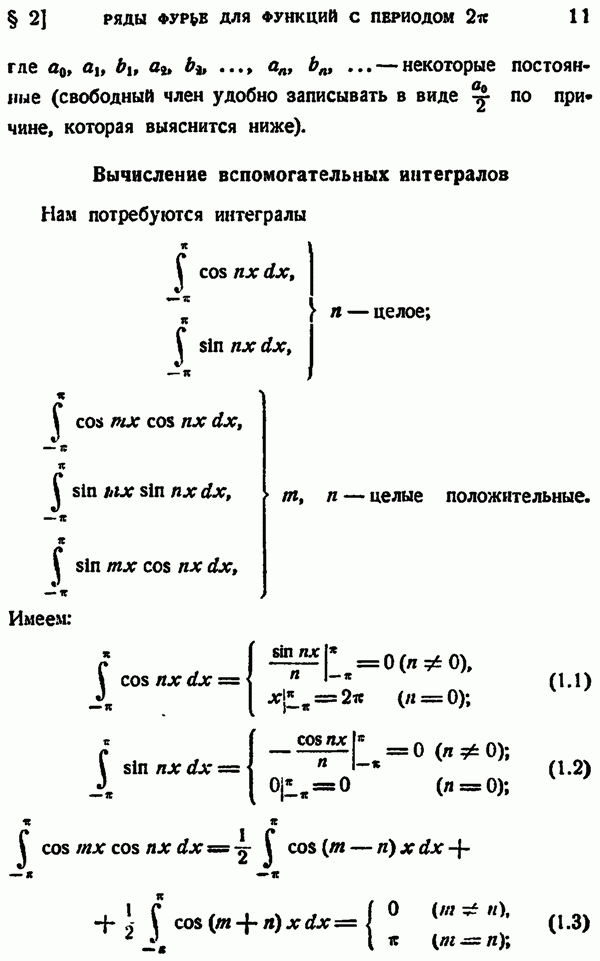
Пример. На сегменте  система функций
система функций

ортогональна относительно единичного веса (см. вычисление вспомогательных интегралов § 2). Обозначая коэффициенты Фурье какой-нибудь функции  на
на  относительно системы
относительно системы  через
через

найдем по формулам (1.47):

которые в данном случае превращаются в формулы (1.7) § 2.
Тригонометрические ряды Фурье являются частным случаем рядов Фурье относительно ортогональных систем функций.
Если функции, составляющие какую-нибудь ортогональную систему  умножить на какие-нибудь постоянные
умножить на какие-нибудь постоянные  , то получим снона ортогональную систему. Коэффициенты Фурье какой-нибудь функции при этом разделятся на
, то получим снона ортогональную систему. Коэффициенты Фурье какой-нибудь функции при этом разделятся на  [как видно из формул (1.47)], члены же ряда Фурье не изменятся
[как видно из формул (1.47)], члены же ряда Фурье не изменятся  . В случае ортонормированной системы
. В случае ортонормированной системы  формулы (1.47) принимают вид
формулы (1.47) принимают вид

Ортогонализация системы функций
Пусть  - бесконечная система линейно независимых функций (удовлетворяющих отмеченным в начале параграфа требованиям). Взяв произвольные действительные числа
- бесконечная система линейно независимых функций (удовлетворяющих отмеченным в начале параграфа требованиям). Взяв произвольные действительные числа  последовательно построим функции
последовательно построим функции

По индукции видно, что каждая функция  есть линейная комбинация функций
есть линейная комбинация функций  с коэффициентом 1 при
с коэффициентом 1 при  откуда следует, что функции
откуда следует, что функции  линейно независимы. В частности, каждая
линейно независимы. В частности, каждая  не исчезает тождественно.
не исчезает тождественно.
Покажем, что можно (единственным образом) подобрать числа так, что система функций  станет ортогональной относительно веса
станет ортогональной относительно веса  на данном интервале (процесс построения таких называется ортогонализацией системы линейно независимых функций
на данном интервале (процесс построения таких называется ортогонализацией системы линейно независимых функций  Требование
Требование

дает

Пусть теперь  при
при  уже определены и
уже определены и  попарно ортогональны. Тогда требования
попарно ортогональны. Тогда требования

дают  и таким образом все
и таким образом все  при
при  определены и функции
определены и функции  попарно ортогональны. И как, индукция проведена, и утверждение доказано.
попарно ортогональны. И как, индукция проведена, и утверждение доказано.
Ортогональные полиномы
Наложим на весовую функцию  добавочное условие:
добавочное условие:

Тогда функции  будут удовлетворять отмеченным в начале параграфа требованиям. Применяя процесс ортогонализации относительно веса
будут удовлетворять отмеченным в начале параграфа требованиям. Применяя процесс ортогонализации относительно веса  на рассматриваемом интервале к системе степенных функций
на рассматриваемом интервале к системе степенных функций  получим последовательность полиномов
получим последовательность полиномов

степеней  с единичными старшими коэффициентами, образующих ортогональную (относительно веса
с единичными старшими коэффициентами, образующих ортогональную (относительно веса  на данном интервале) систему.
на данном интервале) систему.
Отметим некоторые свойства этих полиномов.
Если  - произвольный полином степени
- произвольный полином степени  то
то  ибо, разлагая
ибо, разлагая  по полиномам
по полиномам  получим
получим

откуда

Покажем, что полиномы  удовлетворяют простым рекуррентным соотношениям. Очевидно,
удовлетворяют простым рекуррентным соотношениям. Очевидно,  — некоторое число). Разлагая при
— некоторое число). Разлагая при  полином
полином  (его степень, очевидно,
(его степень, очевидно,  по
по
 получим
получим

 — некоторые числа), откуда при
— некоторые числа), откуда при 

Но

что при  равно нулю, следовательно,
равно нулю, следовательно,  затем, разлагай
затем, разлагай  по
по  найдем
найдем

( -некоторые числа), поэтому
-некоторые числа), поэтому  Следовательно, полагая
Следовательно, полагая  получим:
получим:

Таким образом, всякий интервал и всякая заданная на нем весовая функция  порождают такую последовательность положительных чисел
порождают такую последовательность положительных чисел  и такую последовательность действительных чисел
и такую последовательность действительных чисел  что соответствующие ортогональные полиномы удовлетворяют соотношениям
что соответствующие ортогональные полиномы удовлетворяют соотношениям

Отметим интервалы и заданные на них весовые функции, порождающие классические ортогональные полиномы

Различные аналитические выражения для упомянутых в этой таблице полиномов мы здесь не рассматриваем.
Свойства нулей ортогональных полиномов
При любом интервале и любом заданном на нем весе нули ортогональных полиномов обладают нижеследующими свойствами:
1) Все нули полиномов  действительные, простые и лежат в интервале
действительные, простые и лежат в интервале 
Доказательство. Пусть  те из нулей
те из нулей  которые действительны, лежат на
которые действительны, лежат на  и имеют нечетную кратность. Пусть
и имеют нечетную кратность. Пусть  . Если
. Если  то
то  но это невозможно, так как
но это невозможно, так как  сохраняет постоянный знак на
сохраняет постоянный знак на  Следовательно, должно быть
Следовательно, должно быть  Отсюда видно, что
Отсюда видно, что  имеет на
имеет на  нулей, поэтому все они простые и других нулей
нулей, поэтому все они простые и других нулей  не имеет.
не имеет.
2) Полиномы  с соседними индексами не имеют общих нулей.
с соседними индексами не имеют общих нулей.
В самом деле, из (1.48) нидно, что общий нуль днух полиномон с соседними индексами был бы нулем нсех поли номон с меньшими индексами (ибо все  ), то это невозможно, так как
), то это невозможно, так как 
3) В каждом нуле полинома  полиномы
полиномы  имеют разные знаки.
имеют разные знаки.
Это нидно из (1.48) (ибо нее  ).
).
4) Между нсякими днумя соседними нулями полинома  лежит один нуль полинома
лежит один нуль полинома 
Доказательство. Доказываемое предложение справедлино при  ибо в нуле полинома
ибо в нуле полинома  полином
полином  отрицателен, так как там
отрицателен, так как там  будучи тождественной единицей, положителен; следонательно, нули квадратного трехчлена
будучи тождественной единицей, положителен; следонательно, нули квадратного трехчлена  лежат по разные стороны от нуля линейной функции
лежат по разные стороны от нуля линейной функции  Предположим теперь, что доказываемое предложение спранедливо для
Предположим теперь, что доказываемое предложение спранедливо для  (т. е. между нсякими двумя соседними нулями полинома
(т. е. между нсякими двумя соседними нулями полинома  лежит один нуль полинома
лежит один нуль полинома  . В нулях полинома
. В нулях полинома  значения
значения  знакочередуются (в силу простоты нулей
знакочередуются (в силу простоты нулей  и силу сделанного предположения), следовательно, на основании
и силу сделанного предположения), следовательно, на основании  значения
значения  также знакочередуются. Отсюда видно, что между нсякими соседними нулями полинома
также знакочередуются. Отсюда видно, что между нсякими соседними нулями полинома  находится нуль полинома
находится нуль полинома  (что дает
(что дает  нуля). Затем, пранее большего и ленее меньшего из нулей
нуля). Затем, пранее большего и ленее меньшего из нулей  найдется по нулю полинома
найдется по нулю полинома  ибо знак
ибо знак  и названных нулях
и названных нулях  противоположен тому знаку, какой имеет
противоположен тому знаку, какой имеет  соответственно нблизи
соответственно нблизи  и вблизи а. Полученные
и вблизи а. Полученные  нулей полинома
нулей полинома  исчерпывают его нули и обеспечивают искомое взаиморасположение нулей
исчерпывают его нули и обеспечивают искомое взаиморасположение нулей  Итак, индукция проведена и предложение доказано.
Итак, индукция проведена и предложение доказано.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
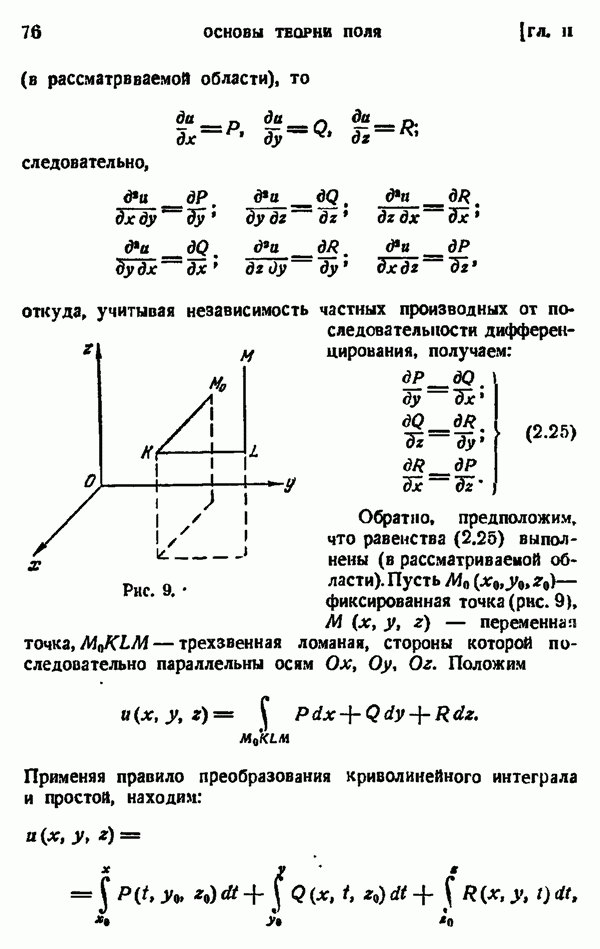
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 6. ВЕКТОРНОЕ ПОЛЕ
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
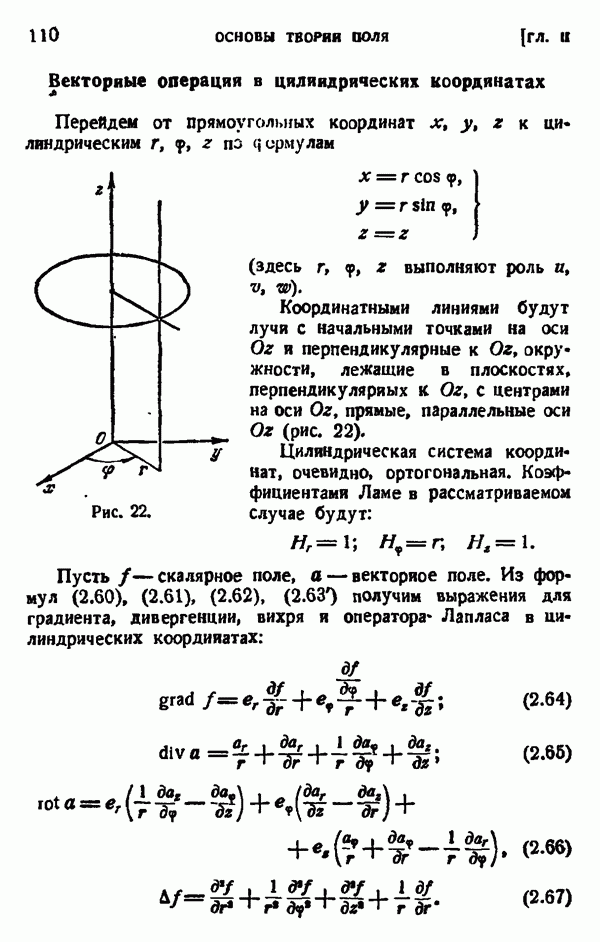
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
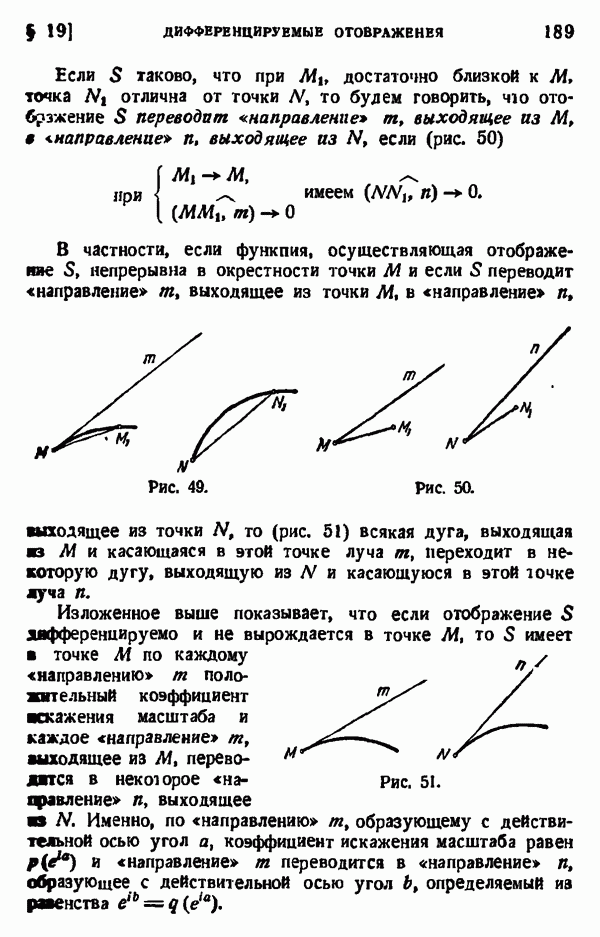
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
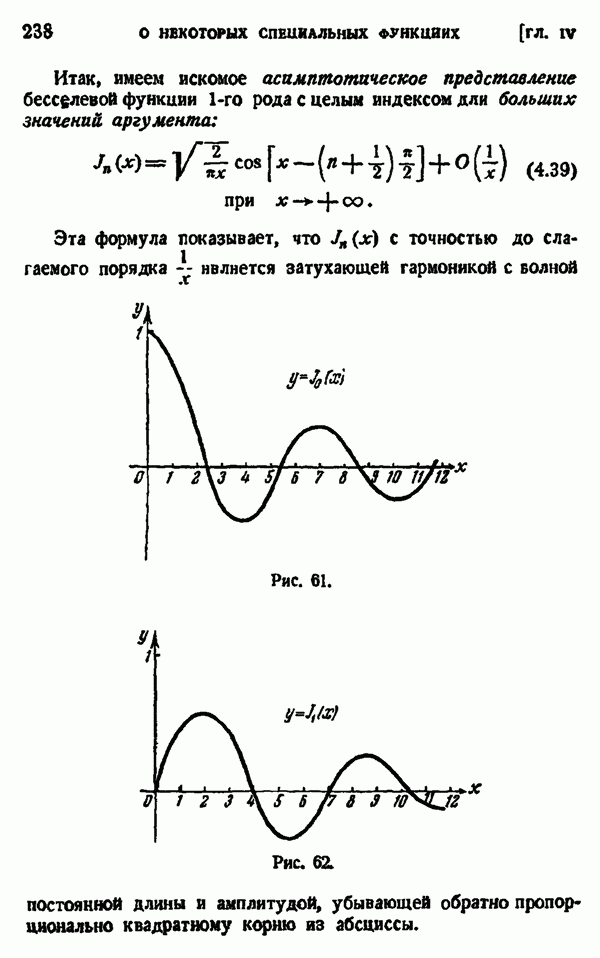
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
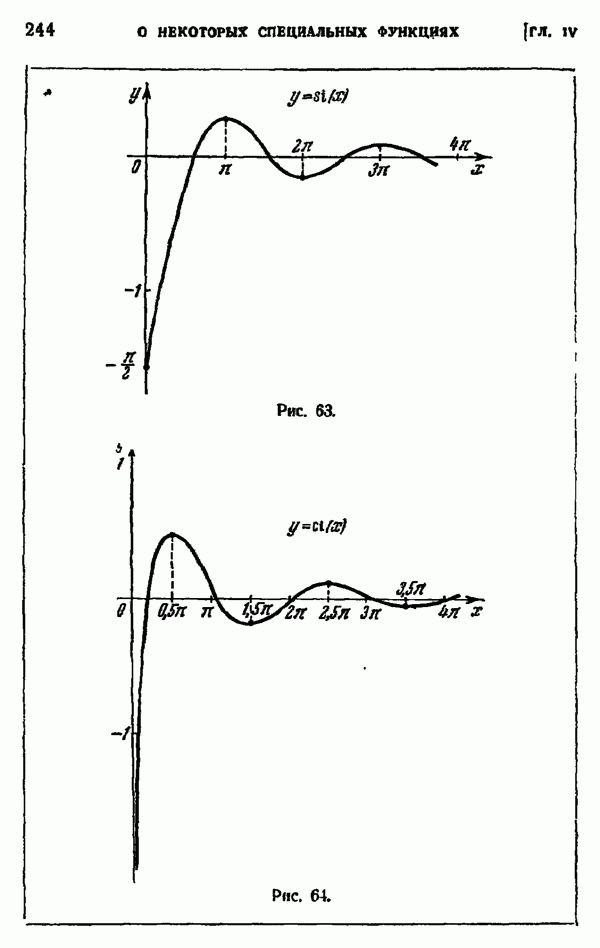
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ