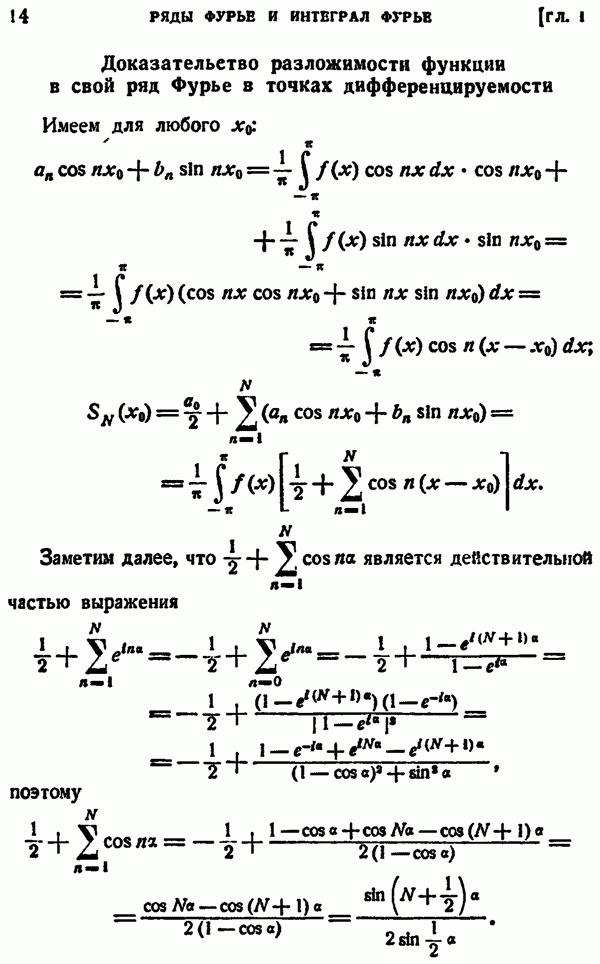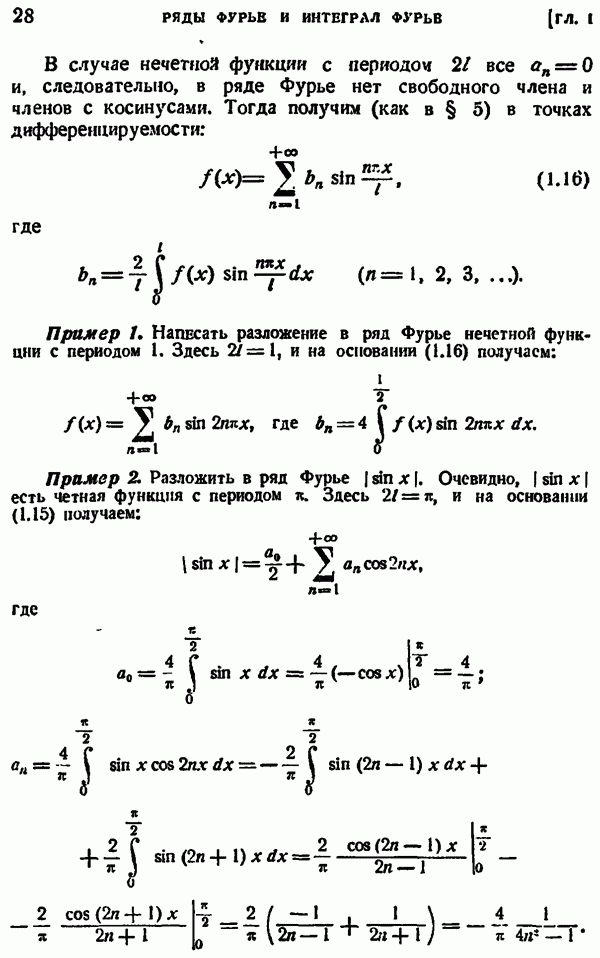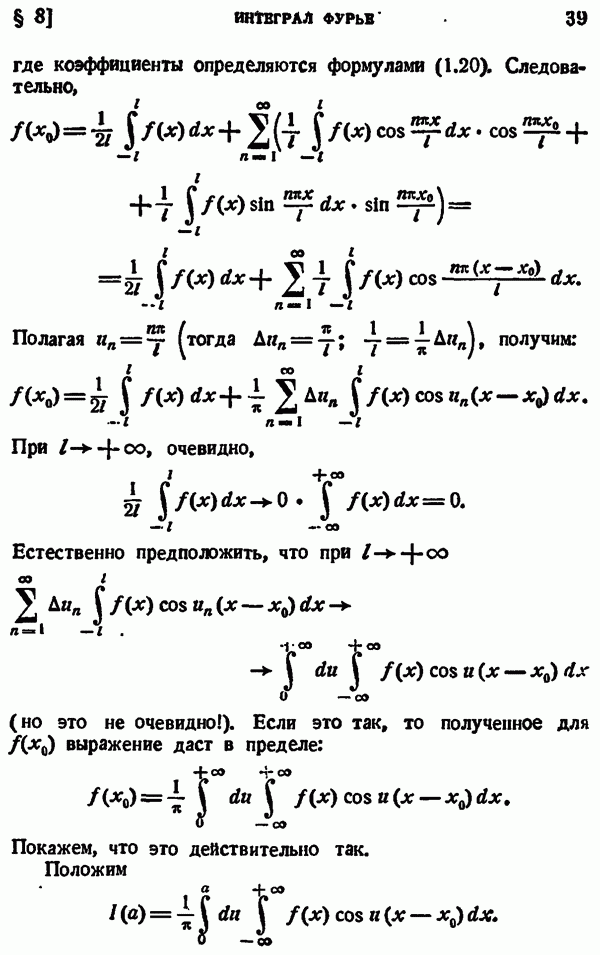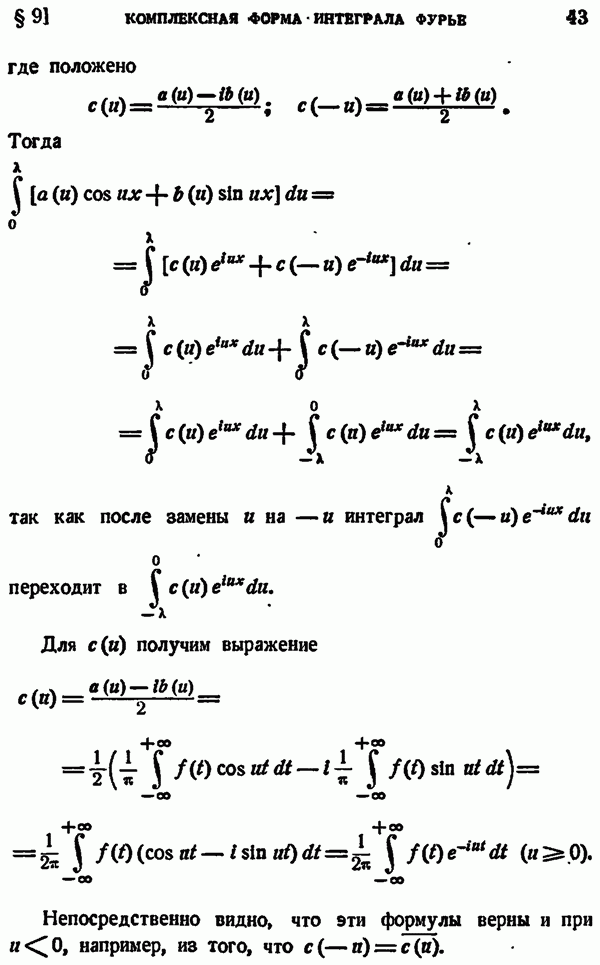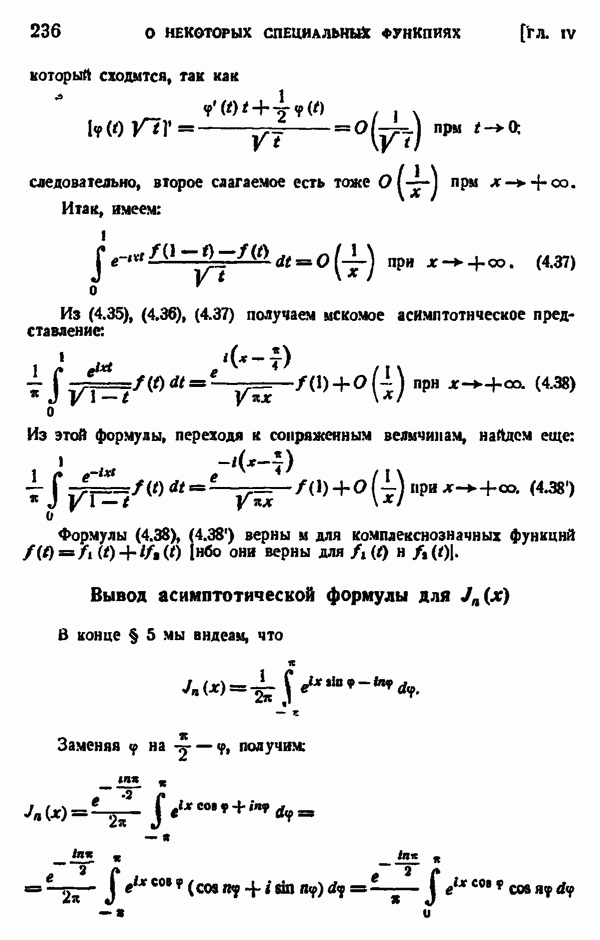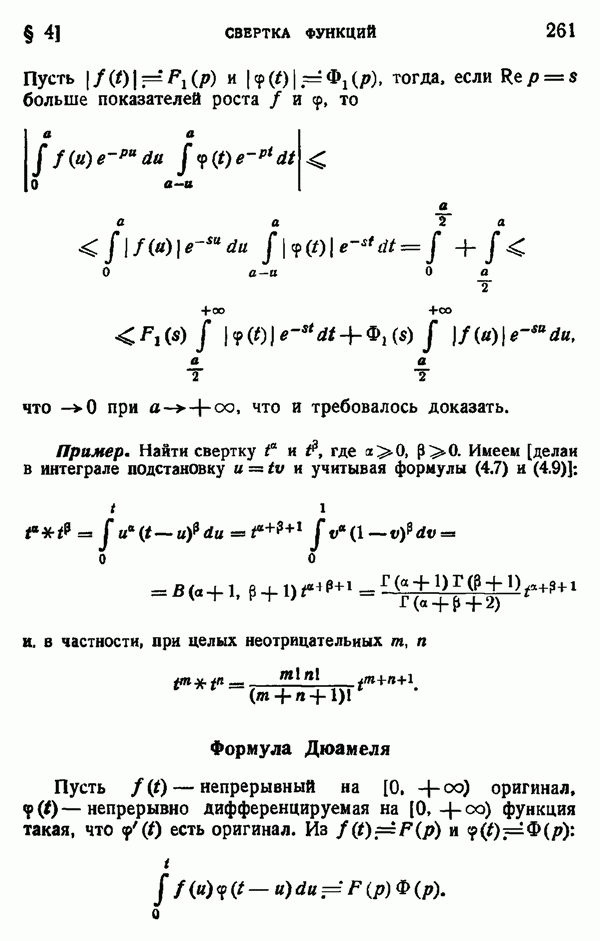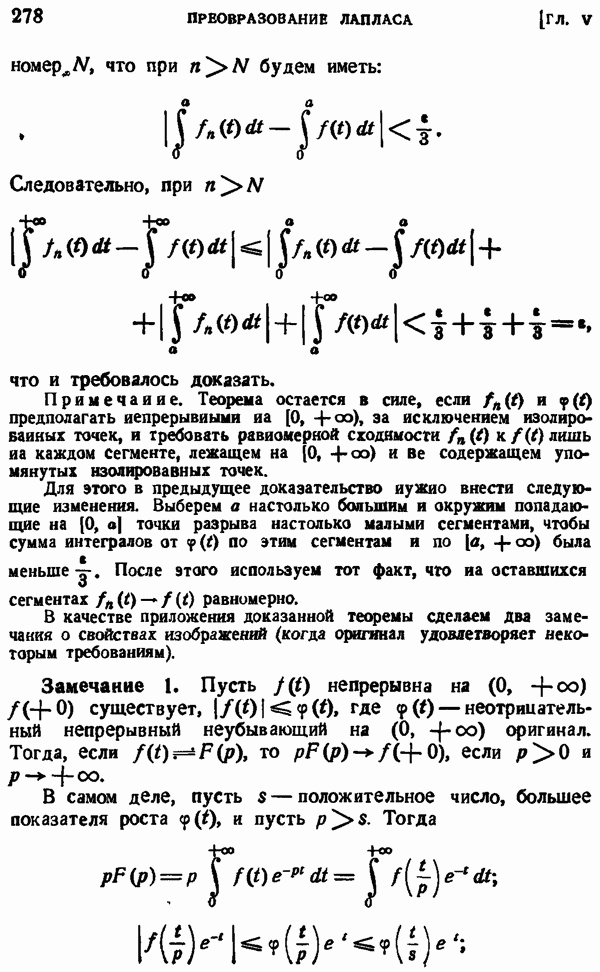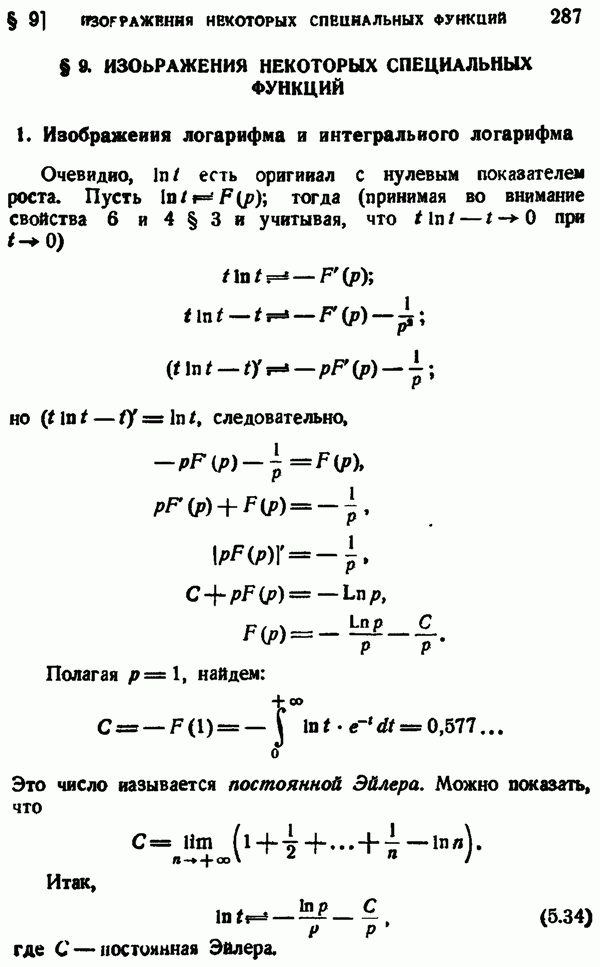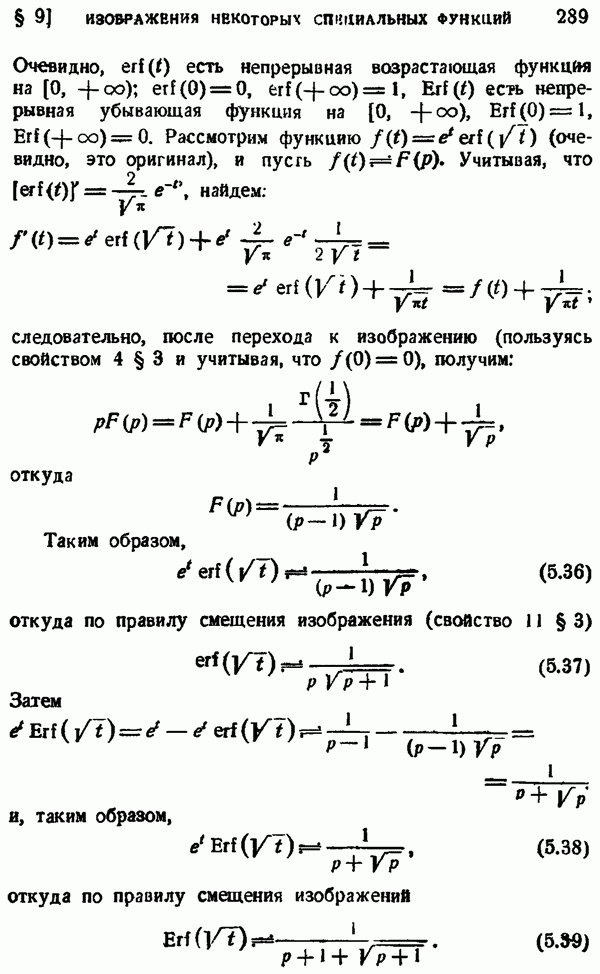| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
Поставим вадачу: разложить сложную периодическую функцию на простые периодические функции. Под «простыми периодическими функциями» естественно понимать простые гармоники, т. е. функции вида

или, что равносильно, функции вида

Эта простая гармоника имеет период 
Если мы хотим разложить функцию с периодом  на простые гармоники, то их частоты следует выбирать так, чтобы каждая из этих гармоник имела
на простые гармоники, то их частоты следует выбирать так, чтобы каждая из этих гармоник имела  в качестве одного из своих периодов. Таким образом, частоты
в качестве одного из своих периодов. Таким образом, частоты  следует брать так, чтобы
следует брать так, чтобы  (
( - целое) или
- целое) или  т. е. в качестве составляющих следует брать гармоники с целыми частотами.
т. е. в качестве составляющих следует брать гармоники с целыми частотами.
Допуская в качестве составляющей еще постоянную, для которой всякое число служит периодом, приходим к такой задаче: разложить функцию  с периодом
с периодом  в ряд вида
в ряд вида

или, короче, в ряд вида

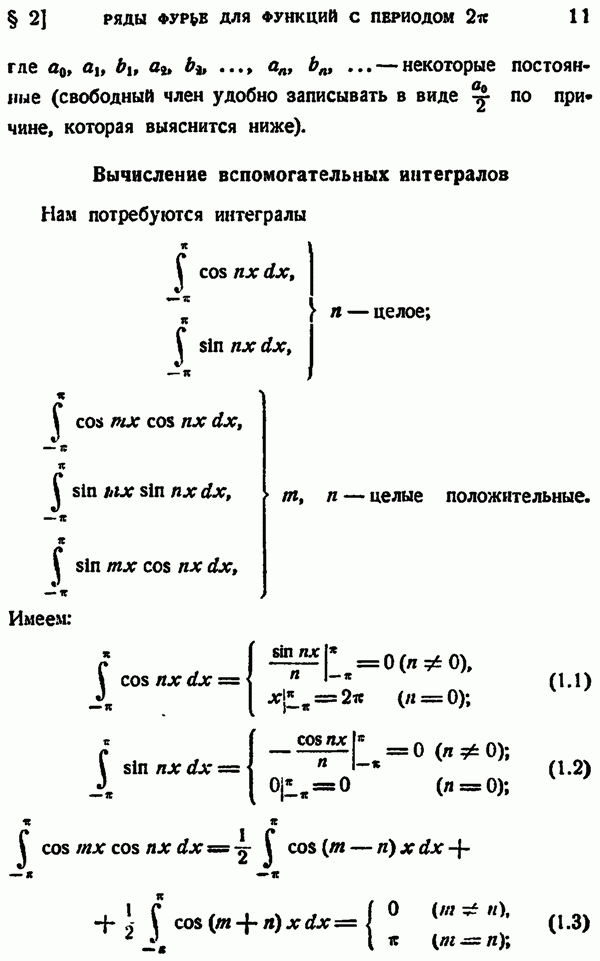
где  некоторые постоянные (свободный член удобно записывать в виде у по при чине, которая выяснится ниже).
некоторые постоянные (свободный член удобно записывать в виде у по при чине, которая выяснится ниже).
Вычисление вспомогательных интегралов Нам потребуются интегралы

Имеем:


причем при выводе формул (1.3) и (1.4) использовалась формула (1.1), при выводе (1.5) использовалась (1.2).
Предположим теперь, что функция  оказалась такой, что для нее нашлось разложение в равномерно сходящийся ряд указанного выше вида:
оказалась такой, что для нее нашлось разложение в равномерно сходящийся ряд указанного выше вида:

Почленное интегрирование в пределах от  до
до  (законное в силу предположенной равномерной сходимости) с учетом
(законное в силу предположенной равномерной сходимости) с учетом  и (1.2) дает:
и (1.2) дает:

Умножая (1.6) на  и интегрируя почленно от
и интегрируя почленно от  до
до  с учетом (1.1), (1.3) и (1.5), получим:
с учетом (1.1), (1.3) и (1.5), получим:

Аналогично, умножая (1.6) на  и интегрируя почленно
и интегрируя почленно  до
до  и учитывая (1.2), (1.4), (1.5), получим;
и учитывая (1.2), (1.4), (1.5), получим;

Таким образом,

Определение. Пусть  — функция с периодом
— функция с периодом  имеющая на сегменте
имеющая на сегменте  не более конечного числа точек разрыва и абсолютно интегрируемая на этом сегменте (тогда она будет абсолютно интегрируема на всяком сегменте). Рядом Фурье этой функции называется ряд
не более конечного числа точек разрыва и абсолютно интегрируемая на этом сегменте (тогда она будет абсолютно интегрируема на всяком сегменте). Рядом Фурье этой функции называется ряд

коэффициенты которого определяются по формулам (1.7). При этом пишут:

Примечание. Вместо функций с периодом  можно рассматривать функции, определенные лишь на сегменте
можно рассматривать функции, определенные лишь на сегменте  и удовлетворяющие отмеченным требованиям. Определение ряда Фурье для такой функции будет то же самое.
и удовлетворяющие отмеченным требованиям. Определение ряда Фурье для такой функции будет то же самое.
Необходимо отметить, что из определения ряда Фурье отнюдь не следует, что функция должна разлагаться в свой ряд Фурье. Из сказанного выше следует только, что если некоторая функция допускает разложение в равномерно сходящийся ряд вида  то этот ряд будет ее рядом Фурье.
то этот ряд будет ее рядом Фурье.
Доказательство разложимости функции в свой ряд Фурье в точках дифференцируемости
Имеем для любого 

Заметим далее, что  является действительной частью выражения
является действительной частью выражения

поэтому

Следовательно, при любом  имеем:
имеем:

(второй интеграл получек из первого заменой  на
на  с учетом периодичности
с учетом периодичности  Применяя эту формулу к случаю
Применяя эту формулу к случаю  получим:
получим:

Ужножая (1.8) на  и вычитая из
и вычитая из  , найдем при любом
, найдем при любом 

Для дальнейшего нам потребуется
Лемма Римана. Если  непрерывна на сегменте
непрерывна на сегменте  за исключением, быть может, конечного числа точек, и абсолютно интегрируема на этом сегменте, то
за исключением, быть может, конечного числа точек, и абсолютно интегрируема на этом сегменте, то  при
при 
Доказательство. Так как

при  то лемма Римана верна для
то лемма Римана верна для  и поэтому верна для любой линейной функции
и поэтому верна для любой линейной функции  Отсюда следует, что лемма верна для любой
Отсюда следует, что лемма верна для любой  ичейной функции (т. е. функции, график которой есть ломангя линии), ибо если
ичейной функции (т. е. функции, график которой есть ломангя линии), ибо если  кусочно-линейна на
кусочно-линейна на  то найдутся такие числа
то найдутся такие числа  что
что  линейна на каждом
линейна на каждом  ; а тогда
; а тогда

ибо по доказанному каждое слагаемое правой части стремится к нулю. Далее заметим, что любая непрерывная функция на  может быть как угодно хорошо аппроксимирована кусочнолинейной функцией. Действительно, если
может быть как угодно хорошо аппроксимирована кусочнолинейной функцией. Действительно, если  непрерывна на
непрерывна на  то она равномерно непрерывна на
то она равномерно непрерывна на  т. е. для любого
т. е. для любого  найдется такое
найдется такое  что при любых
что при любых  на
на  из
из  следует
следует  Возьмем числа
Возьмем числа  так, что все
так, что все  и пусть
и пусть  обозначает функцию, график которой есть вписанная в график функции
обозначает функцию, график которой есть вписанная в график функции  ломаная, вершины которой имеют абсциссы
ломаная, вершины которой имеют абсциссы  тогда для любого х на
тогда для любого х на  будет
будет  так как есля число х попадает на частичный сегмент
так как есля число х попадает на частичный сегмент  то
то  лежит между
лежит между  (ибо
(ибо  линейна и, следовательно, монотонна на
линейна и, следовательно, монотонна на  поэтому число
поэтому число  лежит между
лежит между  модули которых
модули которых  и поэтому тоже будет иметь модуль
и поэтому тоже будет иметь модуль 
Теперь легко показать, что лемма Римана справедлив для любой непрерывной функции  на
на  . В самом деле, по доказанному для любого
. В самом деле, по доказанному для любого  найдется такая кусочнолинейная функция
найдется такая кусочнолинейная функция  что
что  Так как для кусочно-линейной функции лемма Римана справедлива, то при достаточно большом
Так как для кусочно-линейной функции лемма Римана справедлива, то при достаточно большом  будем иметь:
будем иметь:

но тогда

и, следовательно,

Пусть теперь  имеет одну точку разрыва
имеет одну точку разрыва  Так как
Так как  абсолютно интегрируема на
абсолютно интегрируема на  то для любого
то для любого  найдется такое
найдется такое  что
что

Так как лемма Римана для непрерывной функции справедлива, то при достаточно большом у будем иметь:

но тогда

следовательно,  при
при  Аналогичное рассуждение проводится в случае, когда
Аналогичное рассуждение проводится в случае, когда  имеет несколько точек разрыва на
имеет несколько точек разрыва на  Лемма Римана доказана.
Лемма Римана доказана.
Предположим теперь, что  дифференцируема в точке
дифференцируема в точке  Тогда из
Тогда из  находим:
находим:

а так как

при  то после надлежащего доопределения в точке
то после надлежащего доопределения в точке  функция
функция  становится непрерывной в этой точке и, очевидно, находится в условиях применимости леммы Римана на
становится непрерывной в этой точке и, очевидно, находится в условиях применимости леммы Римана на  Поэтому
Поэтому

Пусть теперь  дифференцируема в точке
дифференцируема в точке  имея в ней какое угодно значение. Положим
имея в ней какое угодно значение. Положим  Тогда частичные суммы ряда Фурье этой функции будут
Тогда частичные суммы ряда Фурье этой функции будут

Так как  дифференцируема в точке
дифференцируема в точке  то по доказанному
то по доказанному

т. е.

и следовательно,

Итак, доказана
Теорема. Если функция  с периодом 2 имеет на сегменте
с периодом 2 имеет на сегменте  не более конечного числа точек разрыва и абсолютно интегрируема на этом сегменте, то эта функция
не более конечного числа точек разрыва и абсолютно интегрируема на этом сегменте, то эта функция
разлагается в свой ряд Фурье в каждой точке, в которой она дифференцируема.
Примечание. Доказанное достаточное условие представимости функции своим рядом Фурье отнюдь не является необходимым. Представление функции своим рядом Фурье будет иметь место и при значительно более общих предположениях. Отмстим, например, без доказательства, что если  удовлетворяет условию Дирихле на
удовлетворяет условию Дирихле на  то
то  разлагается в свой ряд Фурье в каждой точке непрерывности, а в точках разрыва х ряд Фурье сходится к
разлагается в свой ряд Фурье в каждой точке непрерывности, а в точках разрыва х ряд Фурье сходится к  Отсюда следует, что разложение рассматриваемой функции в ряд Фурье имеет место во всех правильных точках, т. е. в точках х, где
Отсюда следует, что разложение рассматриваемой функции в ряд Фурье имеет место во всех правильных точках, т. е. в точках х, где

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
- § 2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi
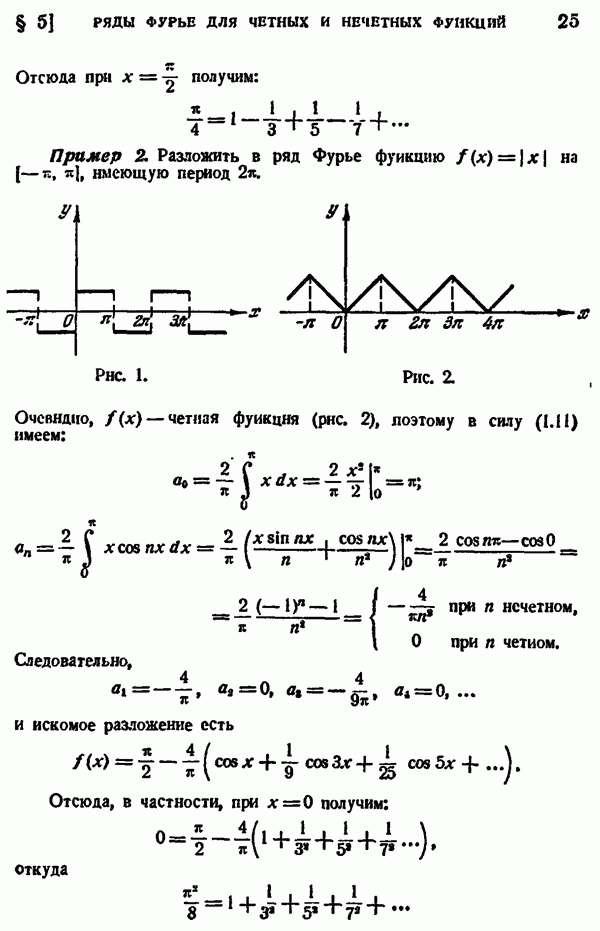
- § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
- § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi
- § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ
- § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ
- § 8. ИНТЕГРАЛ ФУРЬЕ
- § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ
- § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
- § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ
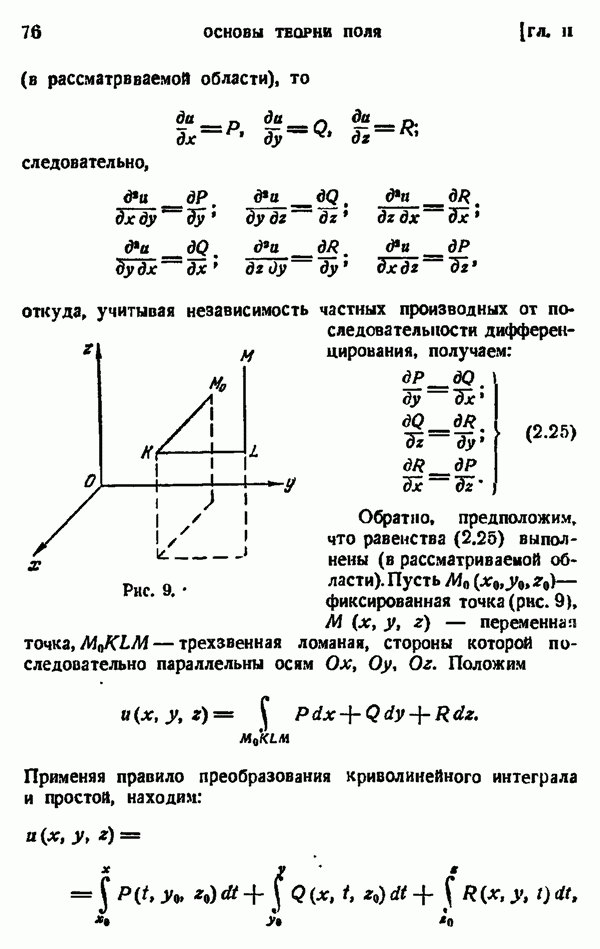
- ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ
- § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО
- § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ
- § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
- § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
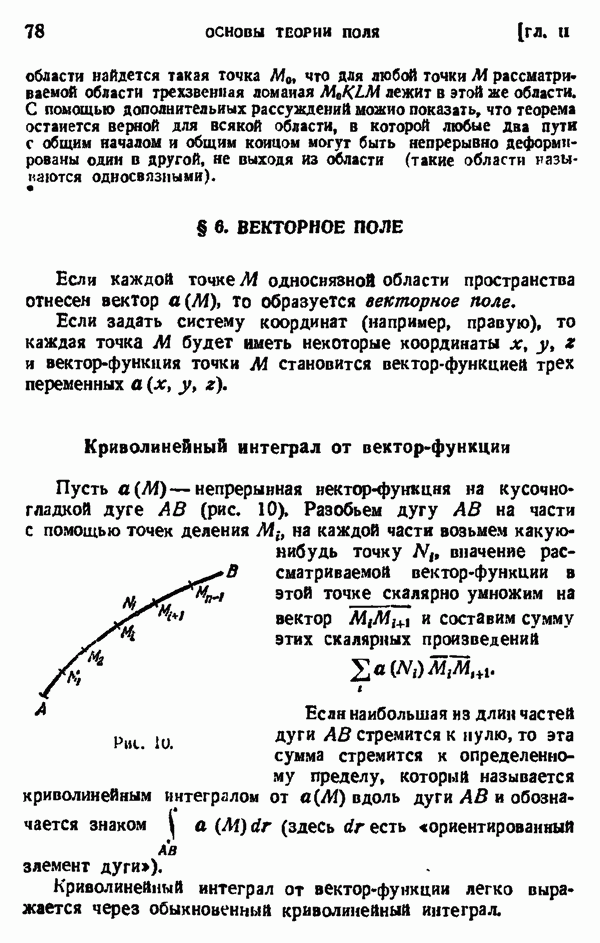
- § 6. ВЕКТОРНОЕ ПОЛЕ
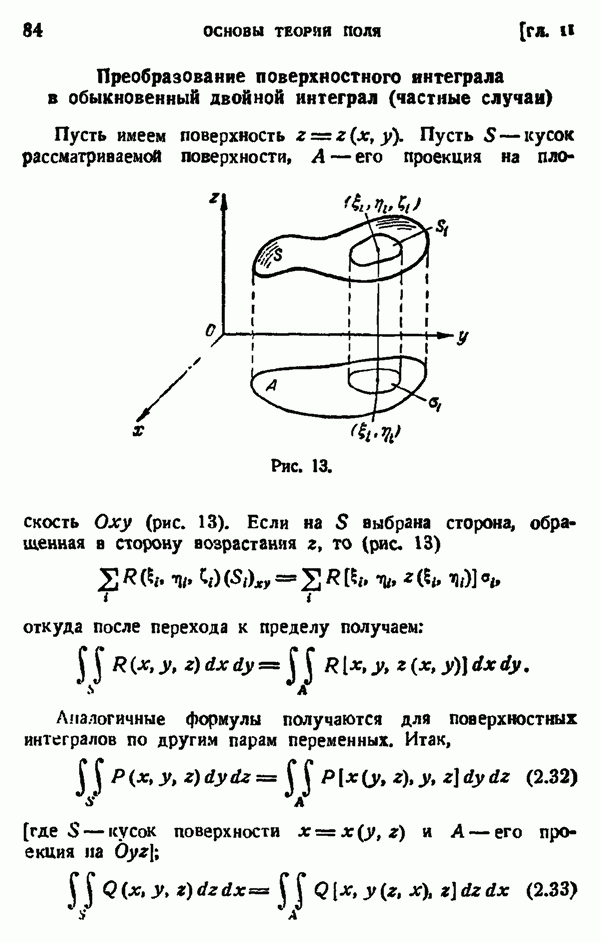
- § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 8. ФОРМУЛА ОСТРОГРАДСКОГО
- § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
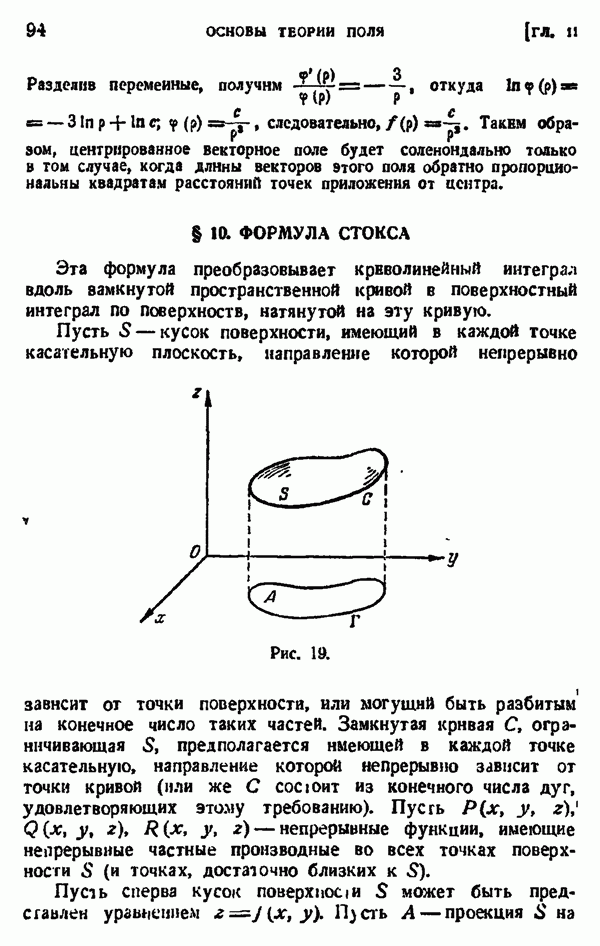
- § 10. ФОРМУЛА СТОКСА
- § 11. ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ
- § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА
- § 13. СИМВОЛИКА ГАМИЛЬТОНА
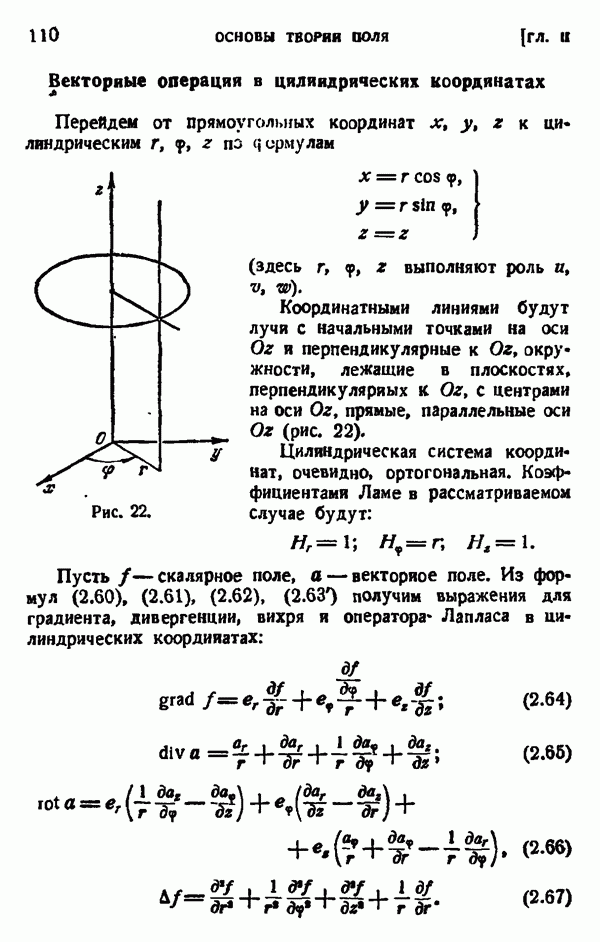
- § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ
- § 1. КОМПЛЕКСНЫЕ ЧИСЛА
- § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
- § 3. СТЕПЕННЫЕ РЯДЫ
- § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
- § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ
- § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
- § 11. ИНТЕГРАЛ ТИПА КОШИ
- § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- § 14. РЯД ТЕЙЛОРА
- § 15. РЯД ЛОРАНА
- § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
- § 17. ВЫЧЕТЫ
- § 18. ПРИНЦИП АРГУМЕНТА
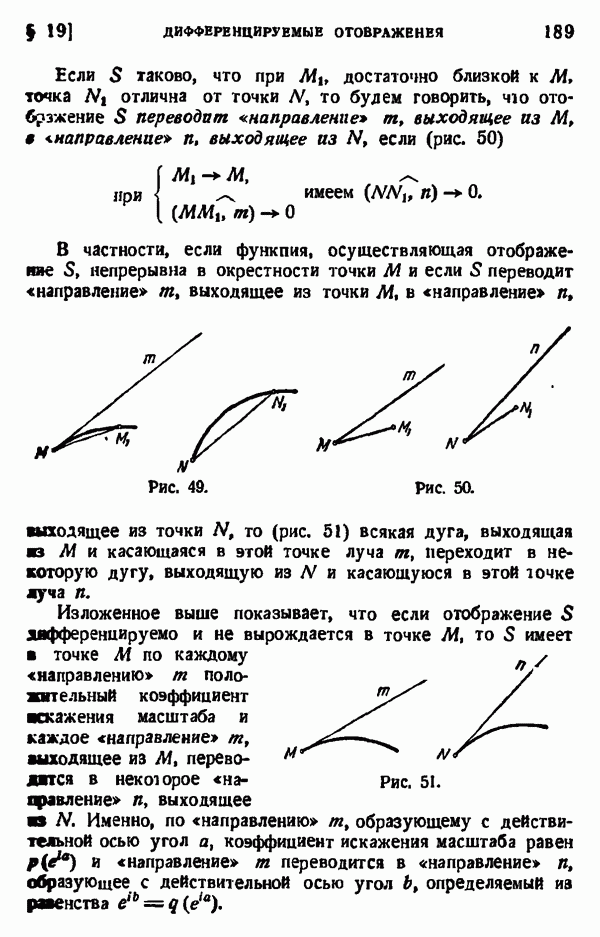
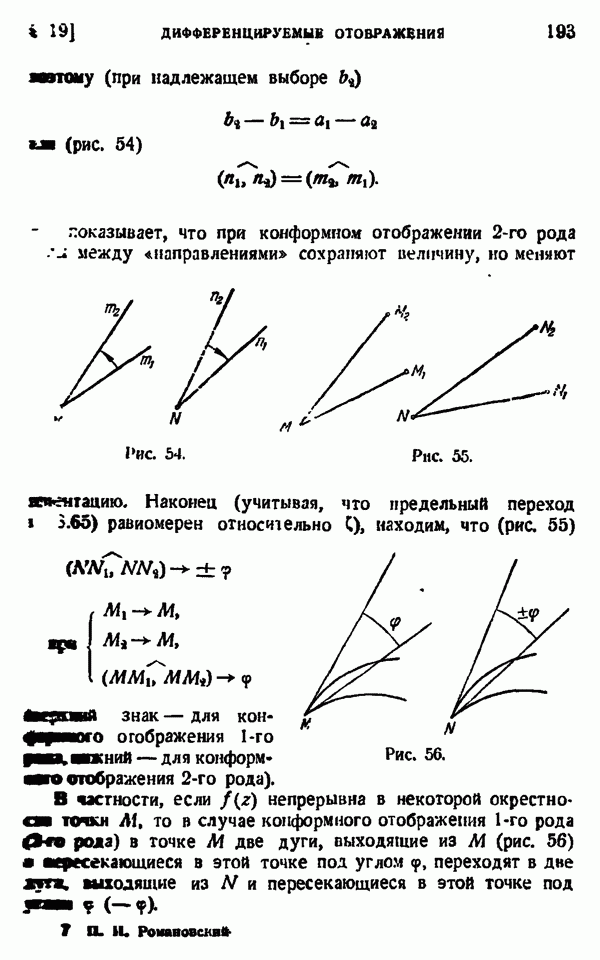
- § 19. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- Отображение, конформное в данной точке
- § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ
- Конформное отображение области на область
- Линейные преобразования
- Конформные отображения односвязных областей
- ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ
- § 1. ГАММА-ФУНКЦИЯ
- § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ
- § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ
- § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ
- § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ
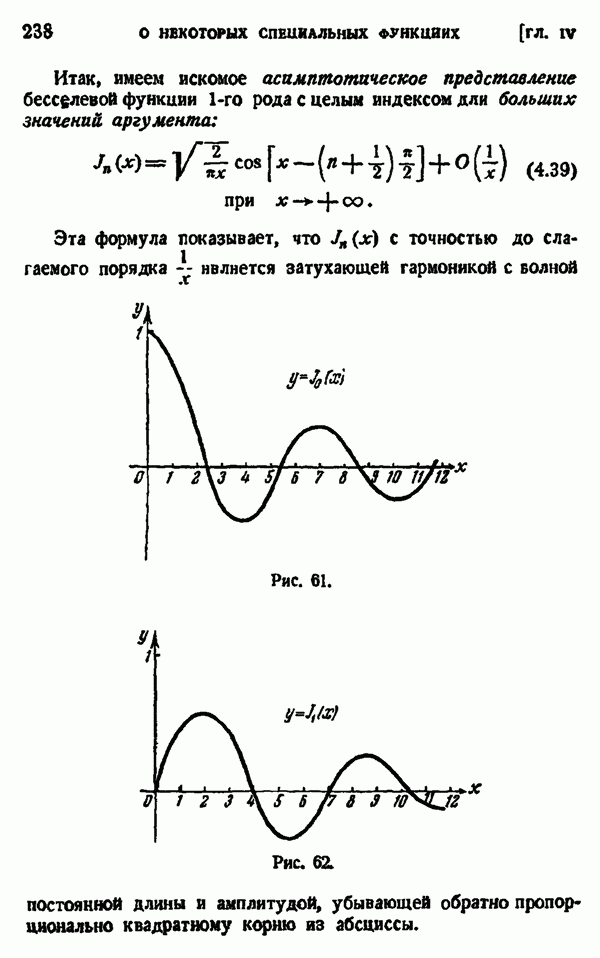
- § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА
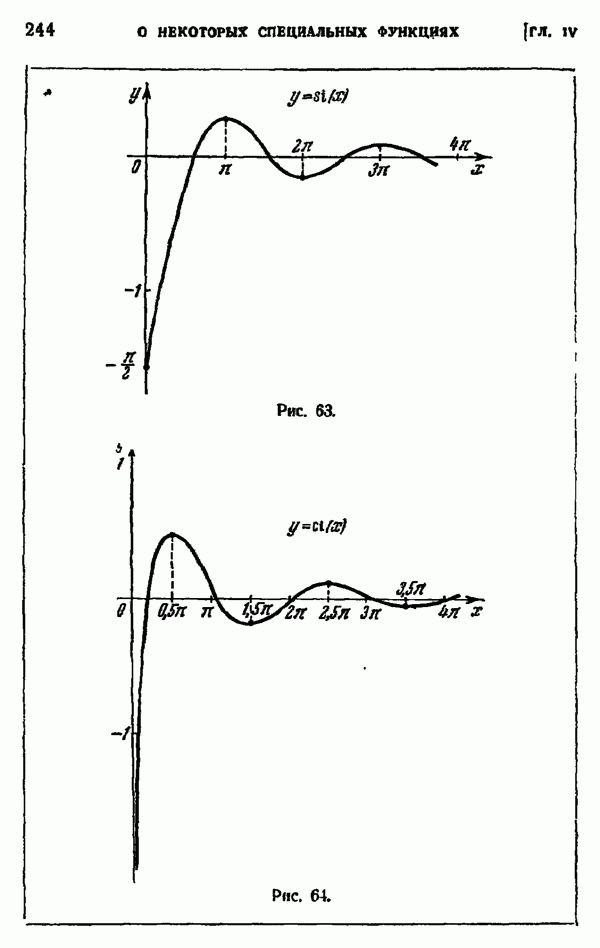
- § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 4. СВЕРТКА ФУНКЦИЙ
- § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ
- § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ
- § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
- 2. Изображения функций, связанных с интегралом вероятностей
- 3. Изображения интегрального синуса и интегрального косинуса
- 4. Изображения интегралов Френеля
- § 10. ФОРМУЛЫ ОБРАЩЕНИЯ
- § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ