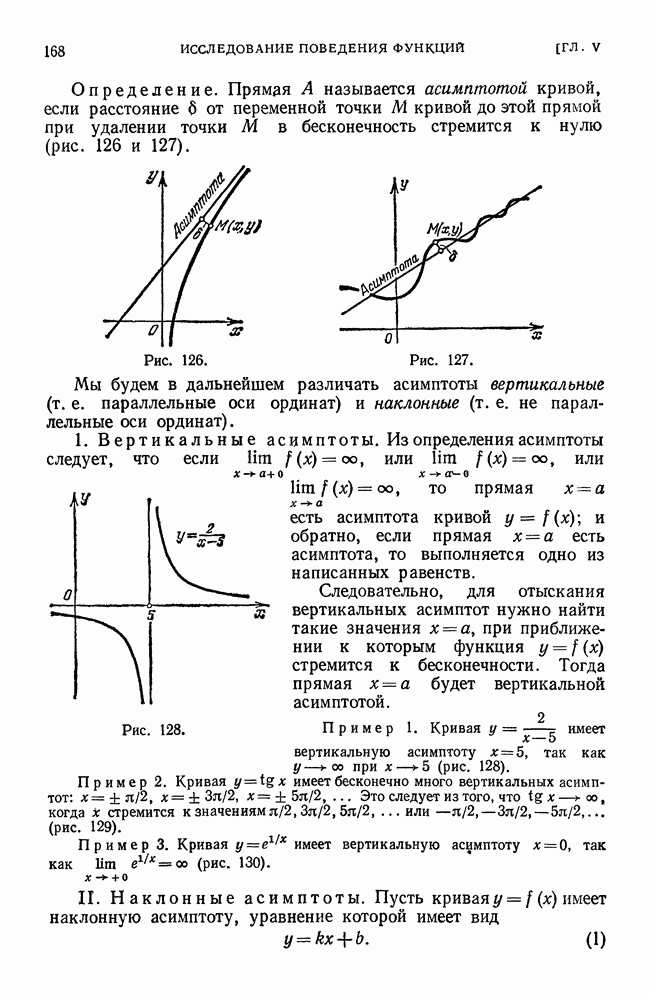
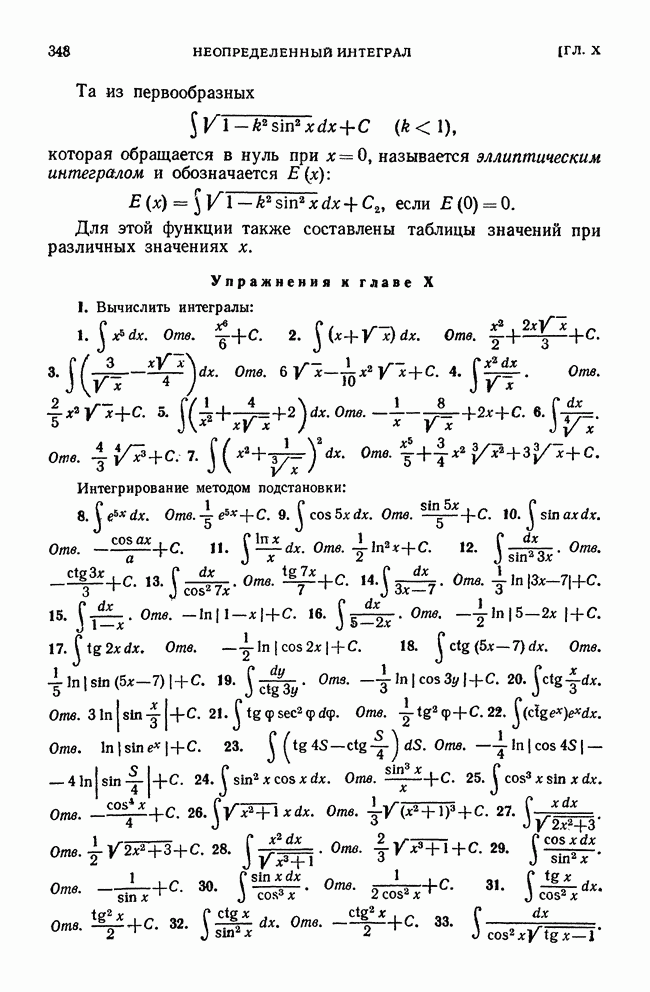| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
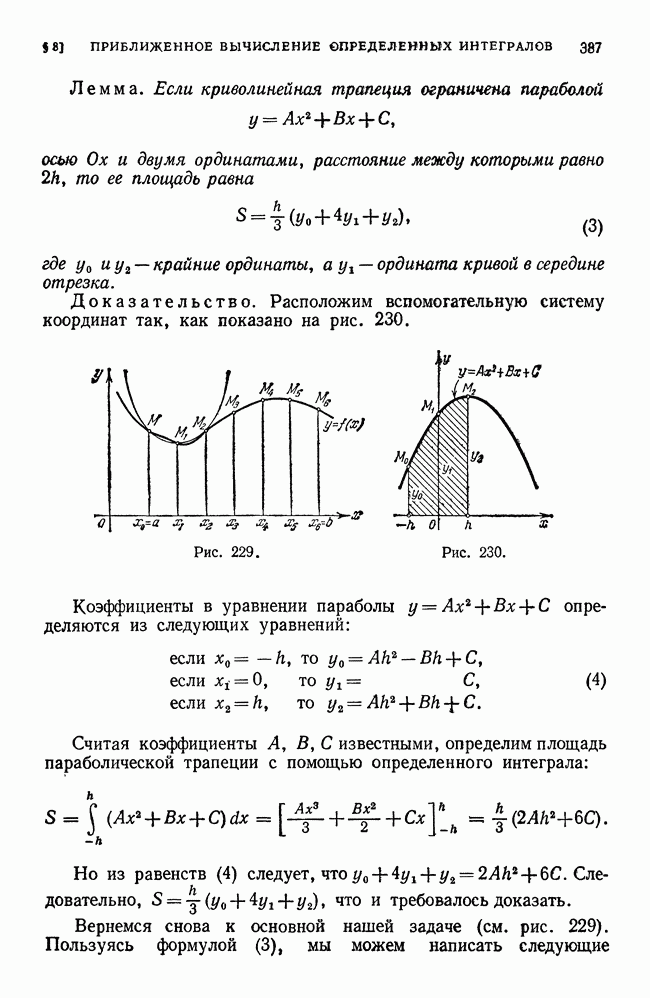
§ 2. Определенный интеграл. Теорема о существовании определенного интеграла
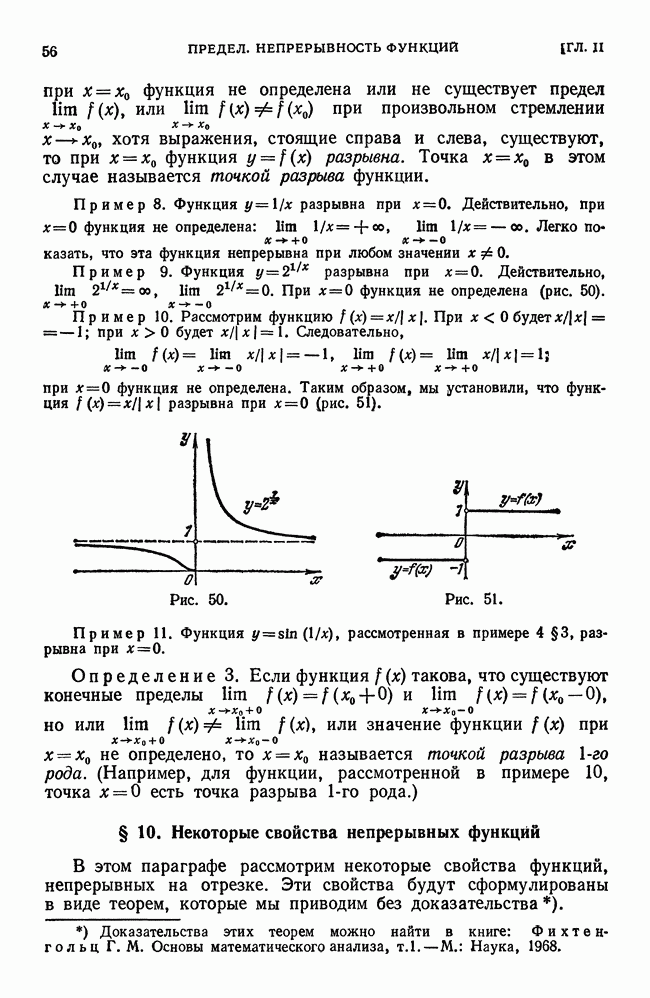
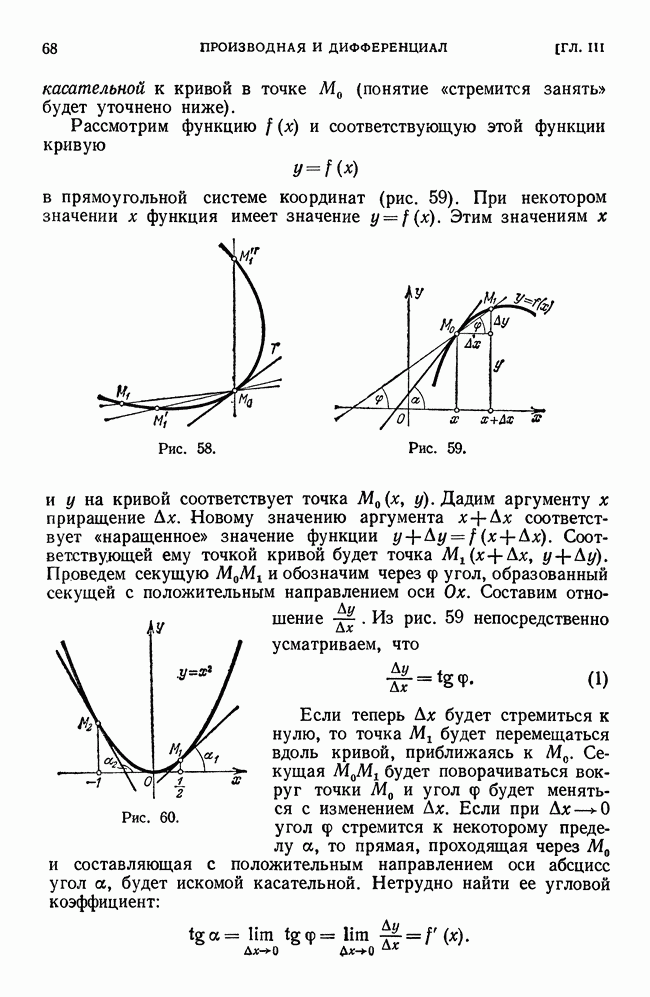
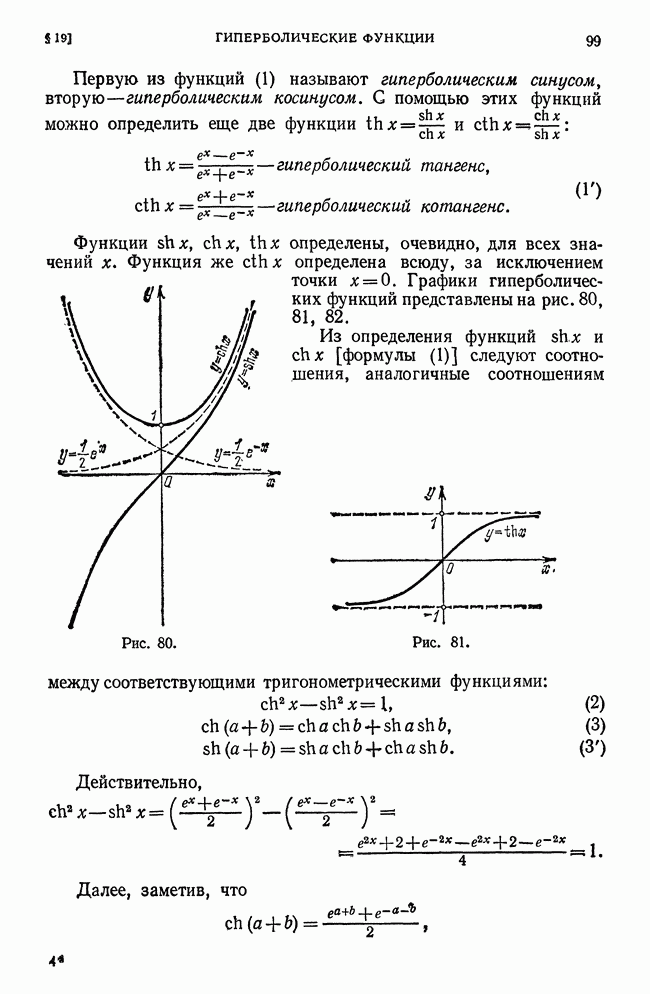
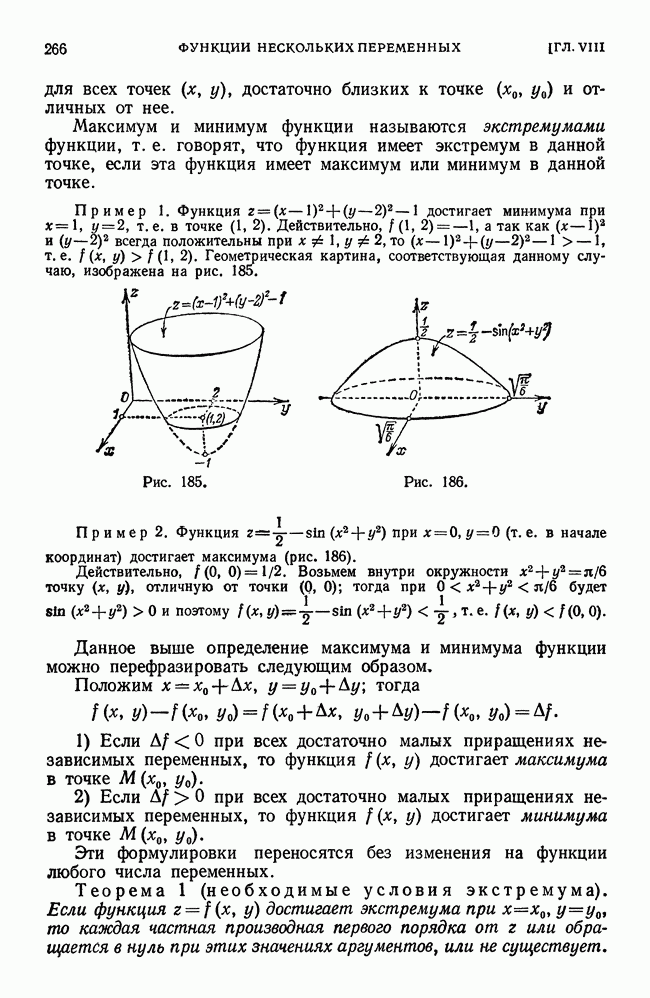
Продолжим рассмотрение вопроса предыдущего параграфа. В каждом из отрезков  возьмем по точке, которые обозначим
возьмем по точке, которые обозначим  (рис. 213):
(рис. 213):  ,
,

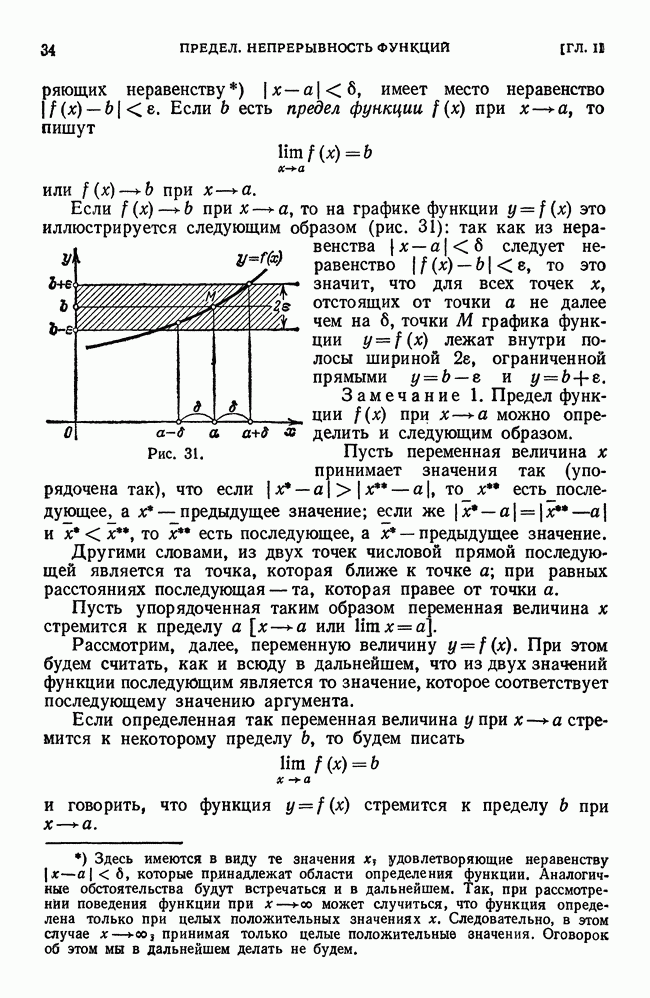
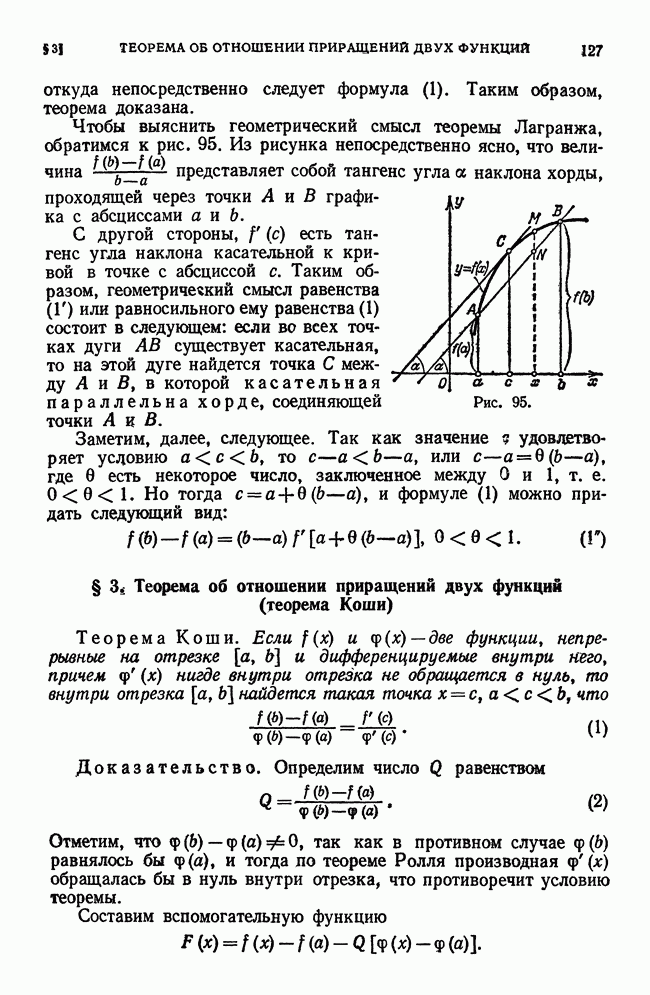
Рис. 213.
В каждой из этих точек вычислим значение функции  Составим сумму
Составим сумму

Эта сумма называется интегральной суммой для функции  на отрезке
на отрезке  . Так как при произвольном
. Так как при произвольном  принадлежащем отрезку
принадлежащем отрезку  будет
будет  и все
и все  , то
, то

следовательно,

или

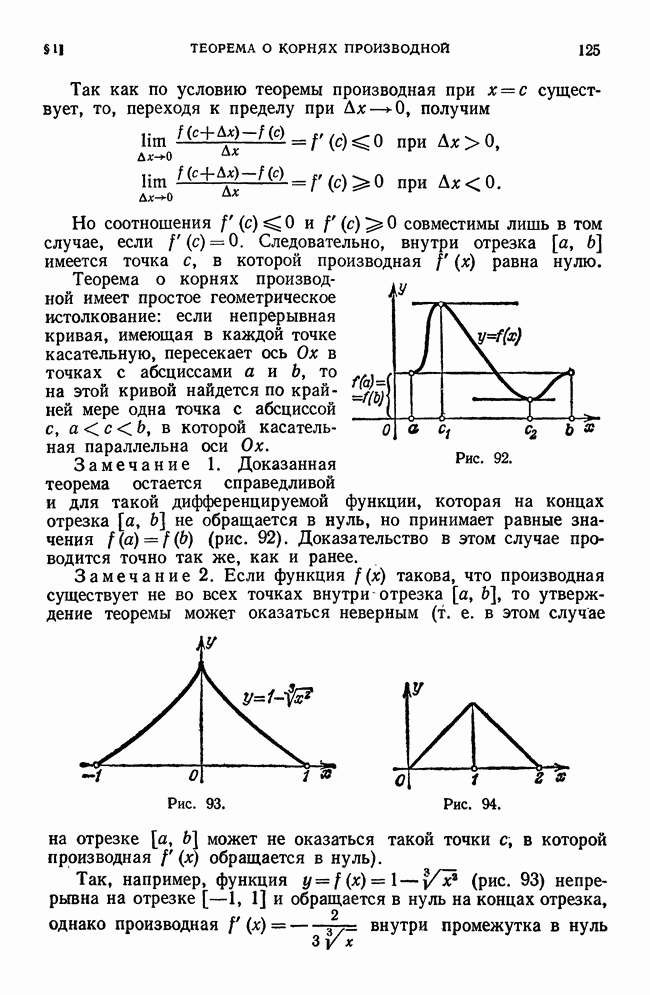
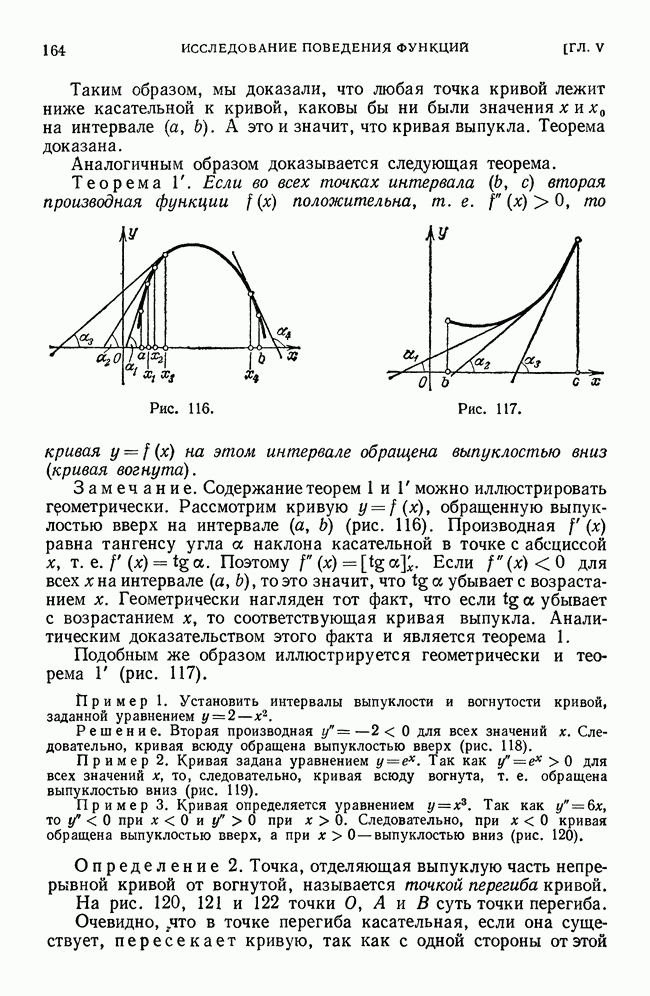
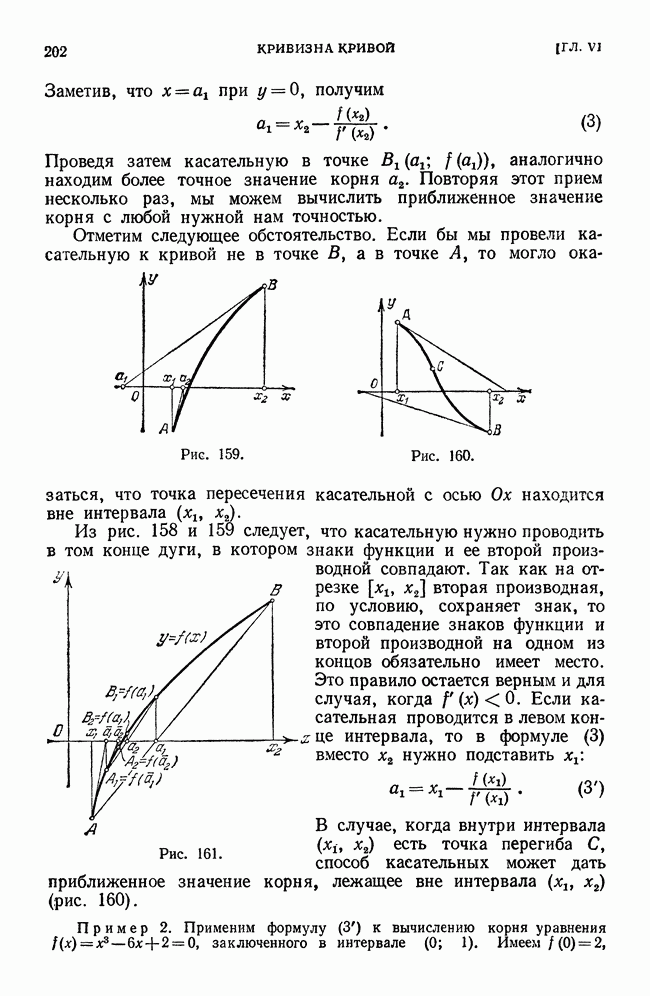
Геометрический смысл последнего неравенства при  состоит в том, что фигура, площадь которой равна
состоит в том, что фигура, площадь которой равна  ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
Сумма  зависит от способа разделения отрезка
зависит от способа разделения отрезка  на отрезки
на отрезки  и от выбора точек внутри получающихся отрезков.
и от выбора точек внутри получающихся отрезков.
Обозначим теперь через  наибольшую из длин отрезков
наибольшую из длин отрезков  Рассмотрим различные разбиения отрезка
Рассмотрим различные разбиения отрезка  на отрезки
на отрезки  такие, что
такие, что  Очевидно, что при этом число отрезков
Очевидно, что при этом число отрезков  в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения
в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения  можно составить интегральную сумму
можно составить интегральную сумму

Рассмотрим некоторую последовательность разбиений, при которых  при этом
при этом  При каждом разбиении выбираем значения Предположим, что эта последовательность интегральных сумм s стремится к некоторому пределу
При каждом разбиении выбираем значения Предположим, что эта последовательность интегральных сумм s стремится к некоторому пределу

Теперь мы можем сформулировать следующее
Определение 1. Если при любых разбиениях отрезка  таких, что
таких, что  и при любом выборе точек на отрезках
и при любом выборе точек на отрезках  интегральная сумма
интегральная сумма

стремится к одному и тому же пределу s, то этот предел называют определенным интегралом от функции  на отрезке
на отрезке  и обозначают
и обозначают

Таким образом, по определению

Число а называется нижним пределом интеграла, b — верхним пределом интеграла. Отрезок  называется отрезком интегрирования, х — переменной интегрирования.
называется отрезком интегрирования, х — переменной интегрирования.
Определение 2. Если для функции  предел (6) существует, то функцию называют интегрируемой на отрезке
предел (6) существует, то функцию называют интегрируемой на отрезке 
Заметим, что нижняя интегральная сумма  и верхняя интегральная сумма
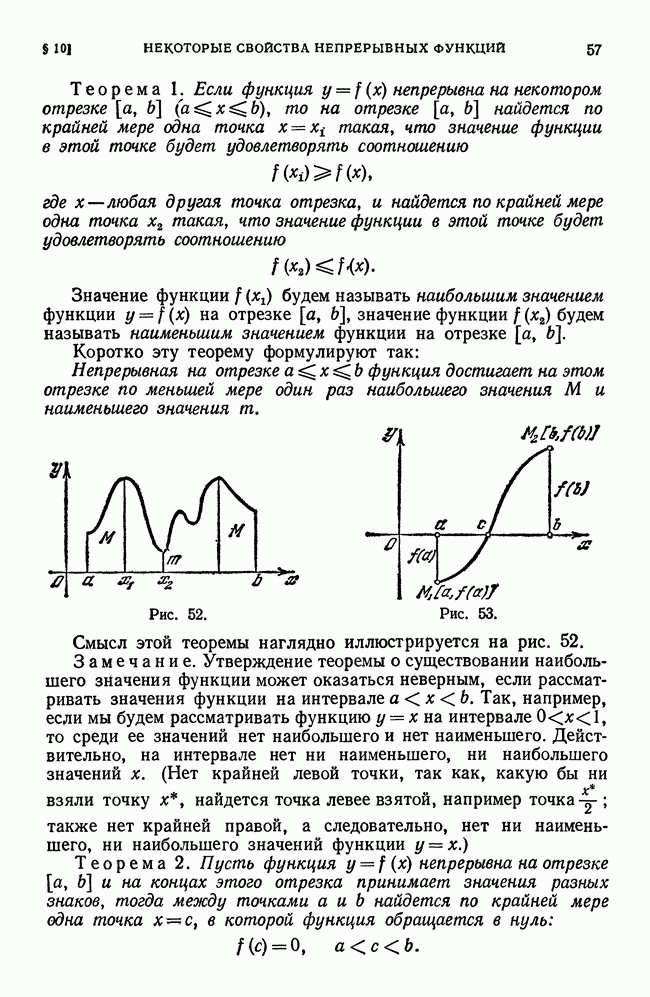
и верхняя интегральная сумма  являются частными случаями интегральной суммы (5), поэтому если
являются частными случаями интегральной суммы (5), поэтому если  интегрируема, то нижняя и верхняя интегральные суммы стремятся к тому же пределу s, и потому на основании равенства (6) можем написать
интегрируема, то нижняя и верхняя интегральные суммы стремятся к тому же пределу s, и потому на основании равенства (6) можем написать

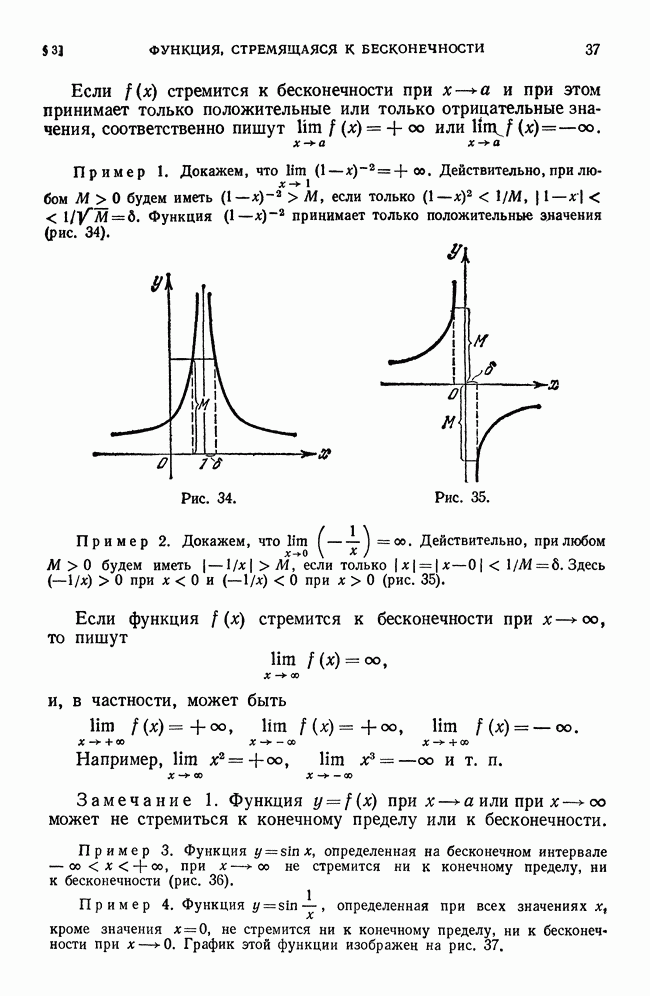
Если построить график подынтегральной функции y = f(x), то в случае  интеграл
интеграл

будет численно равен площади так называемой криволинейной трапеции, ограниченной указанной кривой, прямыми  и осью
и осью 

Рис. 214.
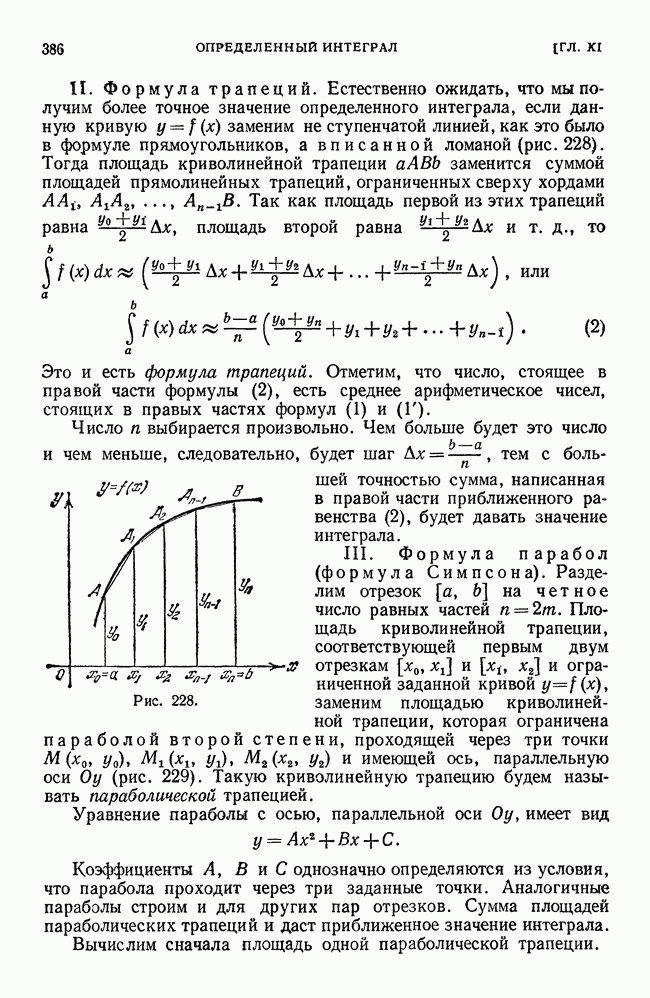
Поэтому если требуется вычислить площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми  и осью
и осью  то эта площадь Q вычисляется с помощью интеграла:
то эта площадь Q вычисляется с помощью интеграла:

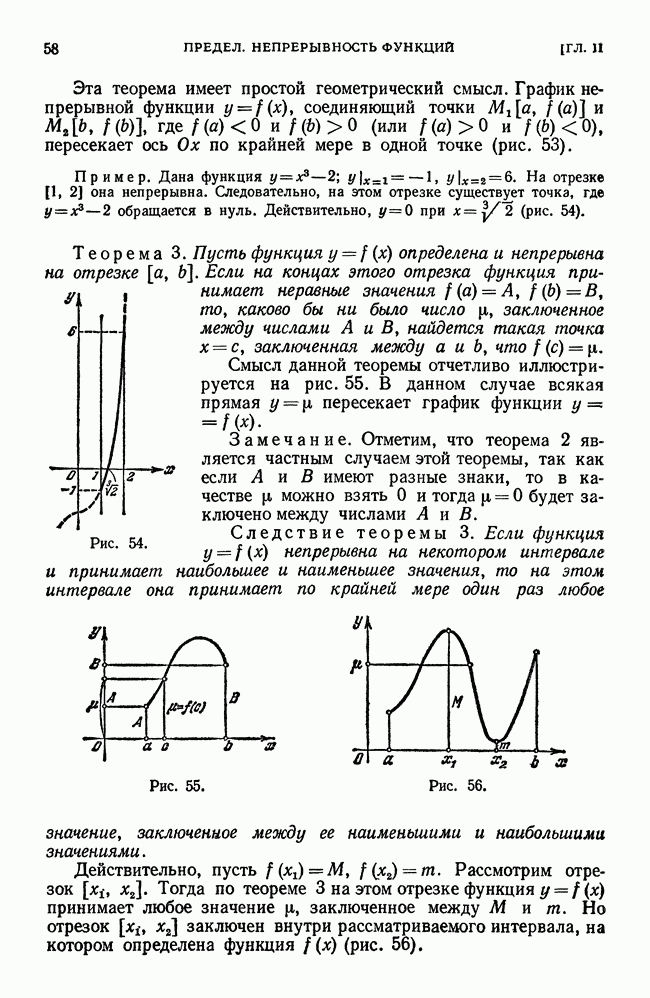
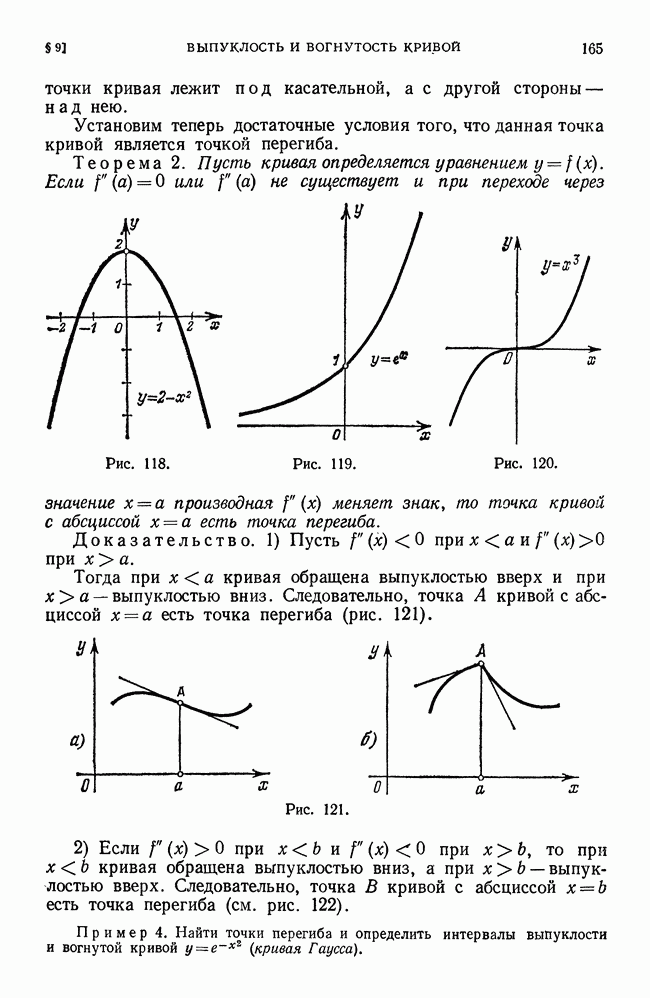
Докажем следующую важную теорему. Теорема 1. Если функция  непрерывна на отрезке
непрерывна на отрезке  то она интегрируется на этом отрезке.
то она интегрируется на этом отрезке.
Доказательство. Снова разобьем отрезок  на отрезки
на отрезки  Составим нижнюю и верхнюю интегральные суммы:
Составим нижнюю и верхнюю интегральные суммы:

Для дальнейшего установим некоторые свойства верхних и нижних интегральных сумм.
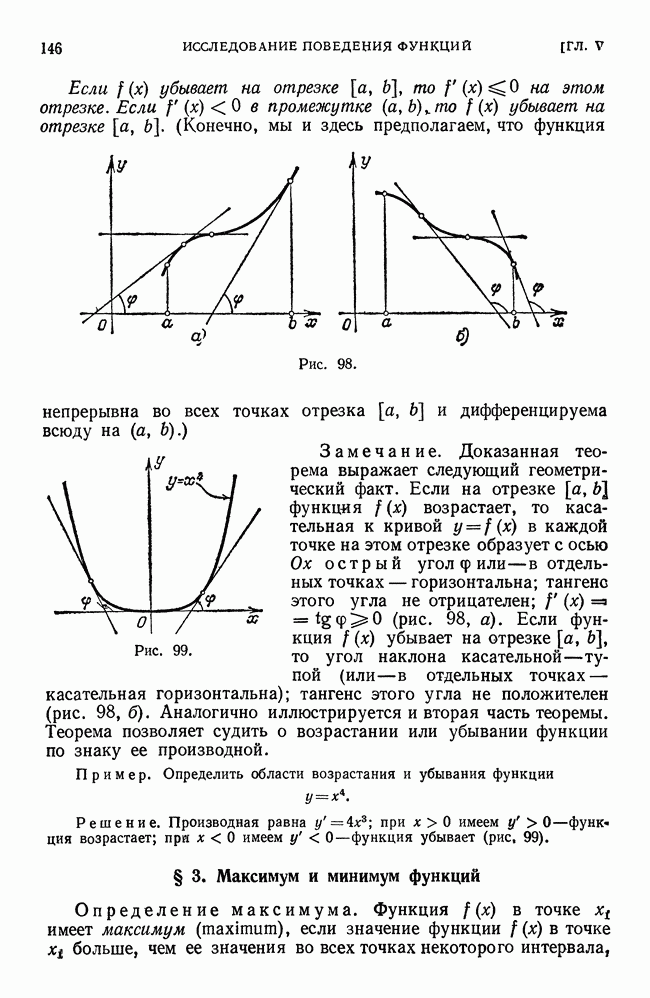
Свойство 1. При увеличении числа отрезков, на которые мы разбиваем отрезок  путем добавления новых точек деления, нижняя интегральная сумма может только возрастать, а верхняя интегральная сумма только убывать.
путем добавления новых точек деления, нижняя интегральная сумма может только возрастать, а верхняя интегральная сумма только убывать.
Доказательство. Пусть отрезок  разбит на
разбит на  отрезков путем добавления новых точек
отрезков путем добавления новых точек  Если какой-то отрезок
Если какой-то отрезок  будет разбит на несколько отрезков, например, на
будет разбит на несколько отрезков, например, на  отрезков, то в новой нижней интегральной сумме
отрезков, то в новой нижней интегральной сумме  отрезку
отрезку  будет соответствовать
будет соответствовать  слагаемых, которые мы обозначим через
слагаемых, которые мы обозначим через  . В сумме
. В сумме  этому отрезку соответствует одно слагаемое
этому отрезку соответствует одно слагаемое  Но для суммы и величины
Но для суммы и величины  справедливо неравенство, аналогичное неравенству (4) § 1. Мы можем написать
справедливо неравенство, аналогичное неравенству (4) § 1. Мы можем написать

Написав соответствующие неравенства для каждого отрезка и суммируя левые и правые части, получим

Свойство 1 доказано.
Свойство 2. Нижняя интегрируемая сумма (9) и верхняя интегральная сумма (10) при неограниченном увеличении числа отрезков путем добавления новых точек деления стремятся к некоторым пределам 
Доказательство. На основании неравенства (6) § 1 можем написать:

т. е.  ограничена при всех n. На основании свойств
ограничена при всех n. На основании свойств  монотонно возрастает при возрастании n. Следовательно, на основании теоремы
монотонно возрастает при возрастании n. Следовательно, на основании теоремы  о пределах (см. § 5 гл. II) эта переменная величина имеет предел; обозначим его через
о пределах (см. § 5 гл. II) эта переменная величина имеет предел; обозначим его через 

Аналогично устанавливается, что  ограничена снизу и монотонно убывает. Следовательно,
ограничена снизу и монотонно убывает. Следовательно,  имеет предел, который мы обозначим через
имеет предел, который мы обозначим через 

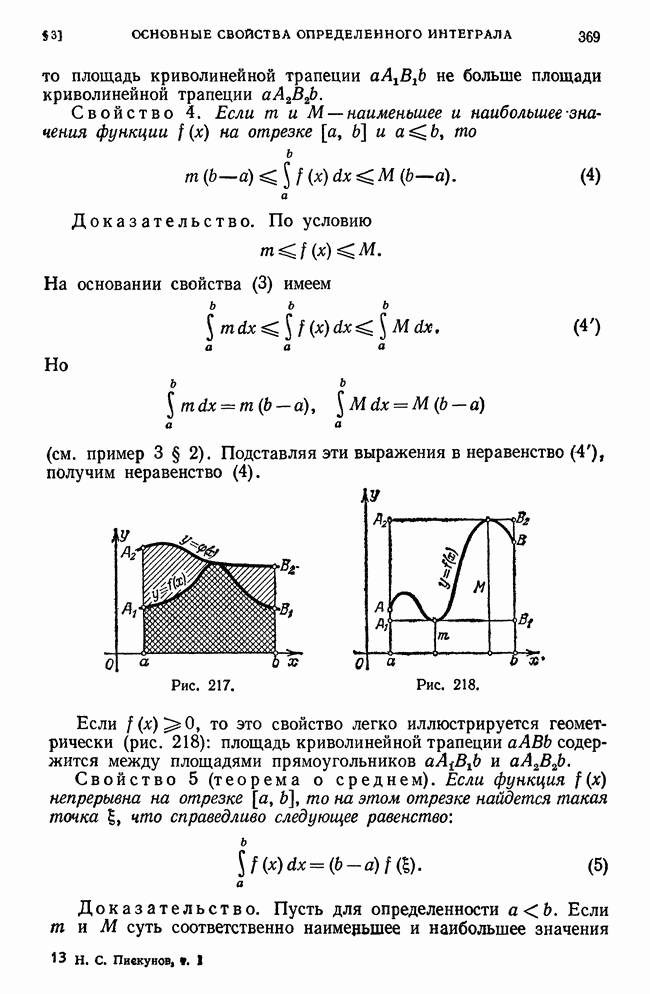
Свойство 3. Если функция  непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке  , то пределы
, то пределы  , определенные в свойстве 2 при условии, что
, определенные в свойстве 2 при условии, что  равны.
равны.
Этот общий предел обозначим через 

Доказательство. Рассмотрим разность верхней и нижней интегральной суммы:

Обозначим через  наибольшую из разностей
наибольшую из разностей  при данном разбиении:
при данном разбиении:

Можно доказать (на чем мы останавливаться не будем), что если функция  непрерывна на замкнутом отрезке, то при любом
непрерывна на замкнутом отрезке, то при любом
способе разбиения отрезка  если только
если только 

Свойство непрерывной функции на замкнутом отрезке, выражаемое равенством (15), называется разномерной непрерывностью функции.
Итак, мы будем пользоваться теоремой: Непрерывная функция на замкнутом отрезке равномерно непрерывна на этом отрезке.
Вернемся к равенству (14). Каждую разность  в правой части заменим не меньшей величиной
в правой части заменим не меньшей величиной  Получаем неравенство
Получаем неравенство

Переходя к пределу при  получаем
получаем

т. е.

или  что и требовалось доказать.
что и требовалось доказать.
Свойство 4. Пусть  и
и  -нижняя и верхняя интегральные суммы, соответствующие разбиениям отрезка
-нижняя и верхняя интегральные суммы, соответствующие разбиениям отрезка  на
на  и соответственно на
и соответственно на  отрезков. Тогда имеет место неравенство
отрезков. Тогда имеет место неравенство

при любых 
Доказательство. Рассмотрим разбиение отрезка  на
на  отрезков, где точками деления будут точки деления первого и второго разбиений.
отрезков, где точками деления будут точки деления первого и второго разбиений.
На основании неравенства (3) § 1 имеем

На основании свойства I имеем

Пользуясь соотношениями (20) и (21), можно расширить неравенство (19):

или

что и требовалось доказать.
Свойство 5. Если функция  непрерывна на отрезке
непрерывна на отрезке  то при любой последовательности разбиений отрезка
то при любой последовательности разбиений отрезка  на отрезки
на отрезки  не обязательно путем присоединения новых точек деления, если только
не обязательно путем присоединения новых точек деления, если только  нижняя интегральная сумма 4 и верхняя интегральная сумма стремятся к пределу s, определенному в свойстве 3.
нижняя интегральная сумма 4 и верхняя интегральная сумма стремятся к пределу s, определенному в свойстве 3.
Доказательство. Рассмотрим последовательность разбиений последовательности верхних интегральных сумм  определенных в свойстве 2. При любых значениях пит (на основании неравенства (18)) можем написать
определенных в свойстве 2. При любых значениях пит (на основании неравенства (18)) можем написать 
Переходя к пределу при  на основании (15) можем написать
на основании (15) можем написать 
Аналогичным способом докажем Итак,

или

Рассмотрим предел разности  Так как функция
Так как функция  непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке  то (так же как и при доказательстве свойства 3) докажем (см. равенство (16)), что
то (так же как и при доказательстве свойства 3) докажем (см. равенство (16)), что 
Перепишем последнее соотношение так:

На основании (22) каждая из разностей, стоящих в квадратных скобках, неотрицательна. Следовательно,

и окончательно получаем

что и требовалось доказать.
Теперь можно доказать и сформулированную выше теорему. Пусть  непрерывна на отрезке
непрерывна на отрезке  Рассмотрим произвольную
Рассмотрим произвольную
последовательность интегральных сумм  , - такую, что
, - такую, что  - произвольная точка отрезка
- произвольная точка отрезка 
Для данной последовательности разбиений рассмотрим соответствующие последовательности верхних и нижних интегральных сумм  Для каждого разбиения будут справедливы соотношения (2):
Для каждого разбиения будут справедливы соотношения (2):

Переходя к пределу при  и пользуясь равенствами (23) и теоремой 4 § 5 гл. II, получаем
и пользуясь равенствами (23) и теоремой 4 § 5 гл. II, получаем  где s — предел, определенный в свойстве 3.
где s — предел, определенный в свойстве 3.
Этот предел, как уже говорилось выше, и называется определенным интегралом  Итак, если
Итак, если  непрерывна на отрезке
непрерывна на отрезке  то
то

Отметим, что среди разрывных функций есть как интегрируемые, так и: неинтегрируемые.
Замечание 1. Отметим, что определенный интеграл зависит только от вида функции  и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой. Шэтому, не изменяя величины определенного интеграла, можно заменить букву
и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой. Шэтому, не изменяя величины определенного интеграла, можно заменить букву  любой другой буквой:
любой другой буквой:

Замечание 2. При введении понятия определенного интеграла  мы предполагали, что
мы предполагали, что  . В случае
. В случае  примем по определению
примем по определению

Так, например, 
Замечание 3. В случае  полагаем по определению, что для любой функции
полагаем по определению, что для любой функции  имеет место
имеет место

Это естественно и с геометрической точки зрения. В самом деле, основание криволинейной трапеции имеет длину, равную нулю, следовательно, и площадь этой криволинейной трапеции равна нулю.
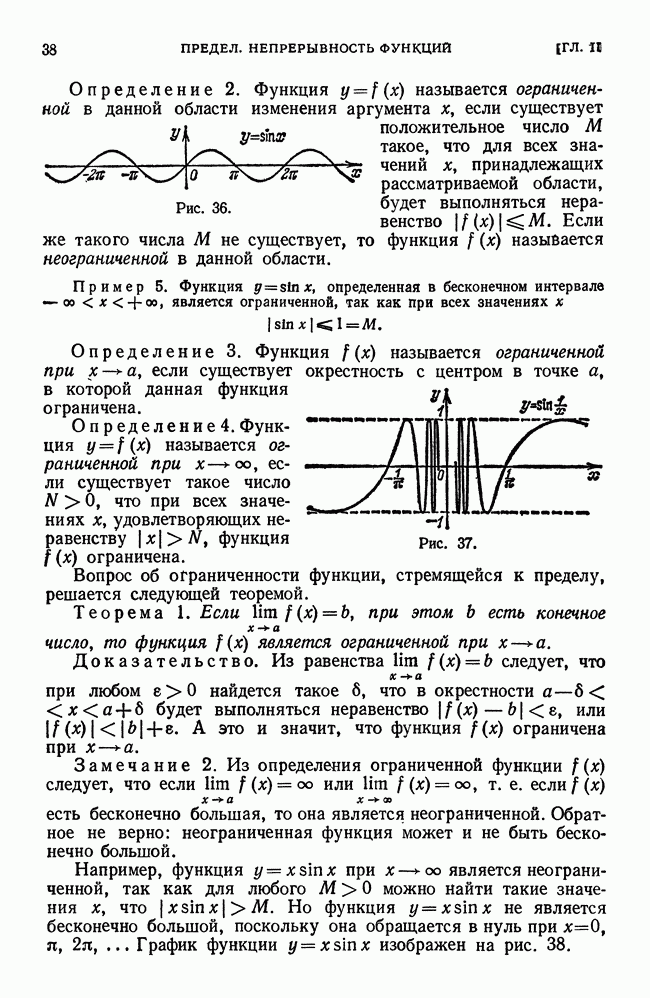
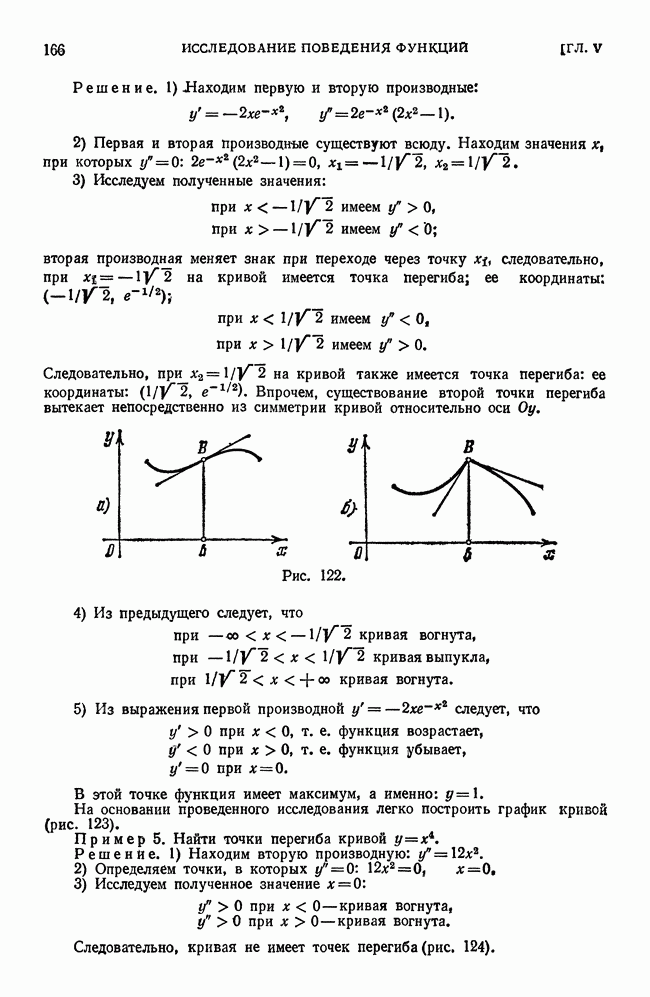
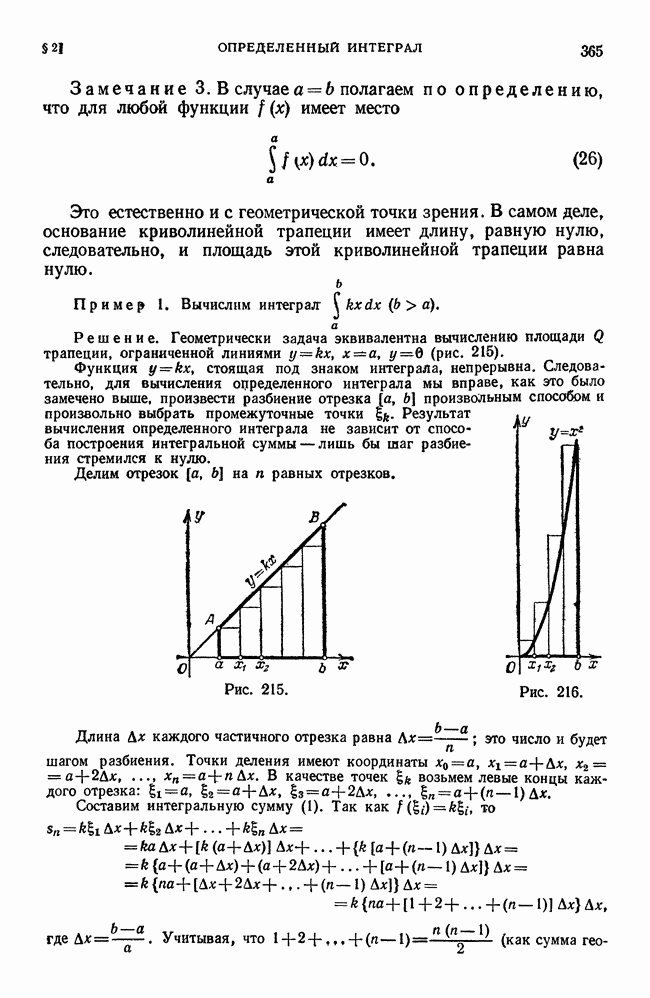
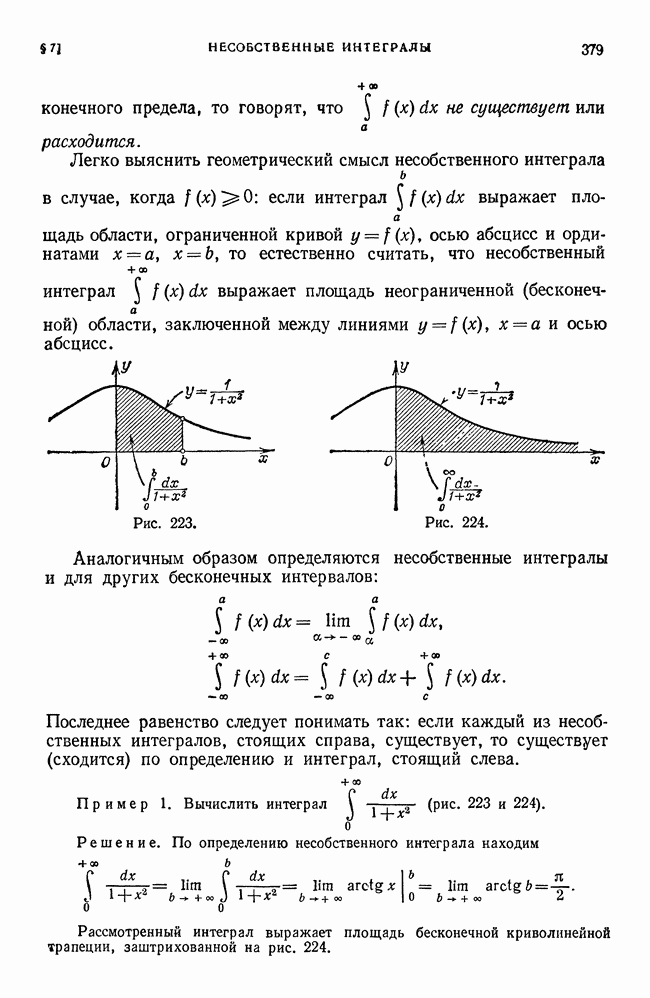
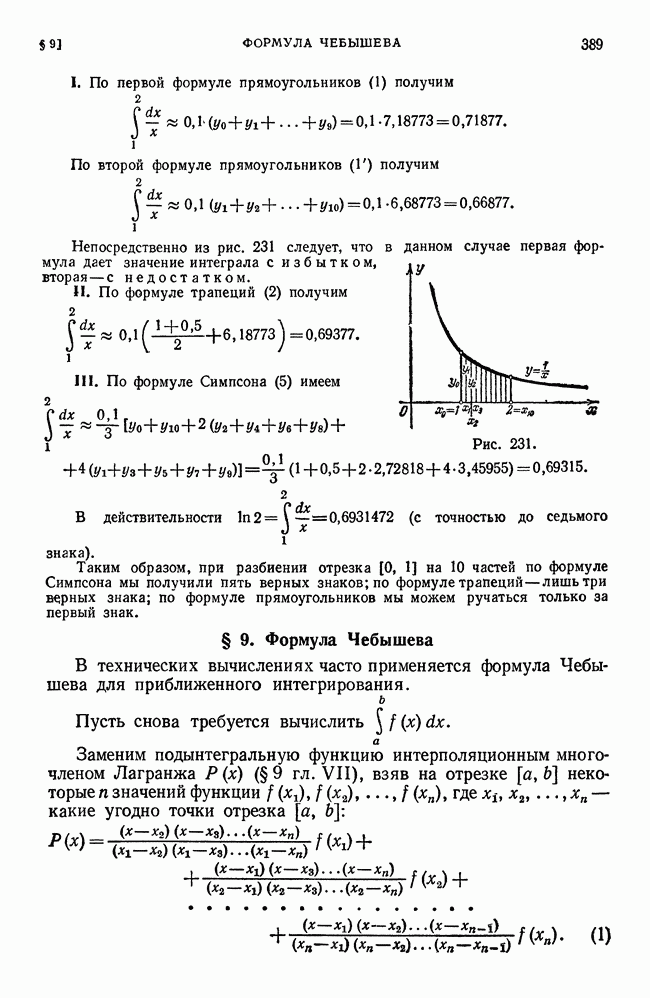
Пример 1. Вычислим  .
.
Решение. Геометрически задача эквивалентна вычислению площади  трапеции, ограниченной линиями
трапеции, ограниченной линиями 
Функция  стоящая под знаком интеграла, непрерывна. Следовательно, для вычисления определенного интеграла мы вправе, как это было замечено выше, произвести разбиение отрезка
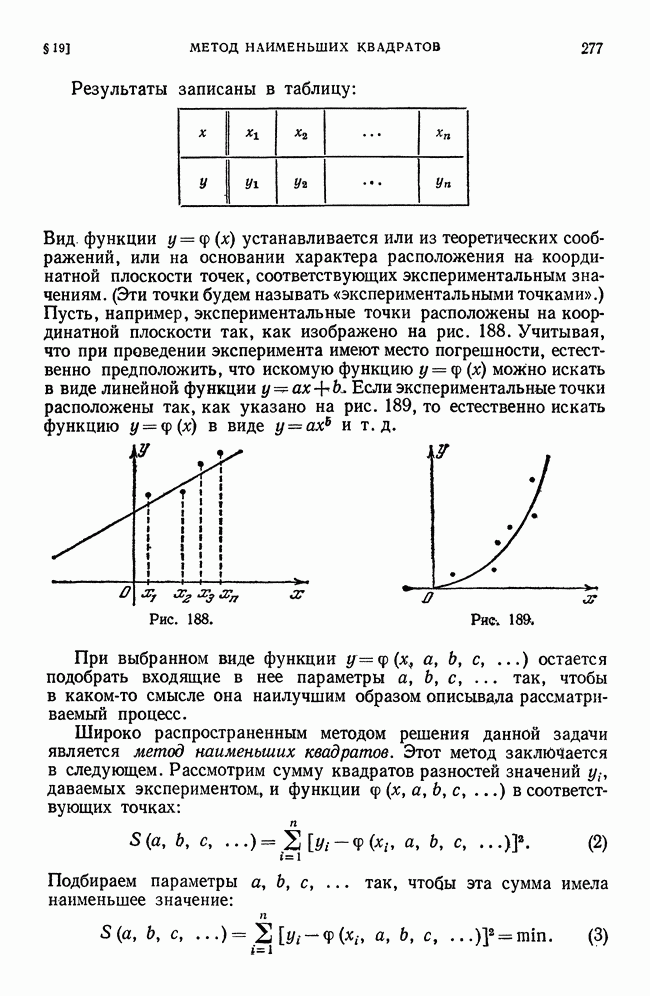
стоящая под знаком интеграла, непрерывна. Следовательно, для вычисления определенного интеграла мы вправе, как это было замечено выше, произвести разбиение отрезка  произвольным способом и произвольно выбрать промежуточные точки
произвольным способом и произвольно выбрать промежуточные точки  . Результат вычисления определенного интеграла не зависит от способа построения интегральной суммы — лишь бы шаг разбиения стремился к нулю.
. Результат вычисления определенного интеграла не зависит от способа построения интегральной суммы — лишь бы шаг разбиения стремился к нулю.
Делим отрезок  на
на  равных отрезков.
равных отрезков.

Рис. 215.

Рис. 216.
Длина  каждого частичного отрезка равна
каждого частичного отрезка равна  это число и будет шагом разбиения. Точки деления имеют координаты
это число и будет шагом разбиения. Точки деления имеют координаты  . В качестве точек возьмем левые концы каждого отрезка:
. В качестве точек возьмем левые концы каждого отрезка:  .
.
Составим интегральную сумму (1). Так как 

где  Учитывая, что
Учитывая, что  сумма
сумма
геометрической прогрессии), получим

Так как 
Итак, 
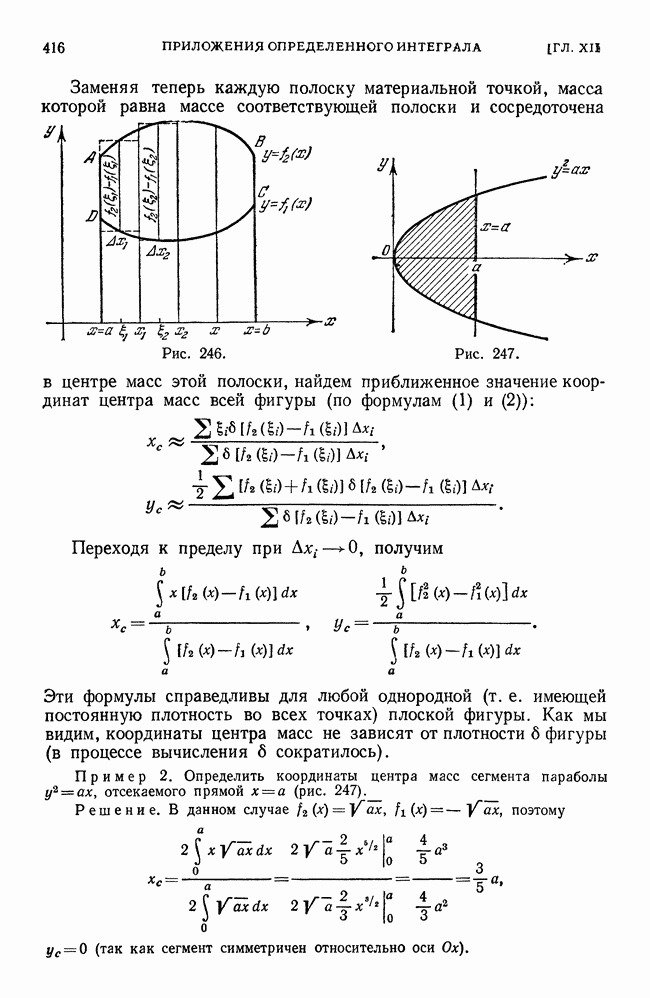
Площадь  (рис. 215) легко вычислить методами элементарной геометрии.
(рис. 215) легко вычислить методами элементарной геометрии.
Результат получится тот же.
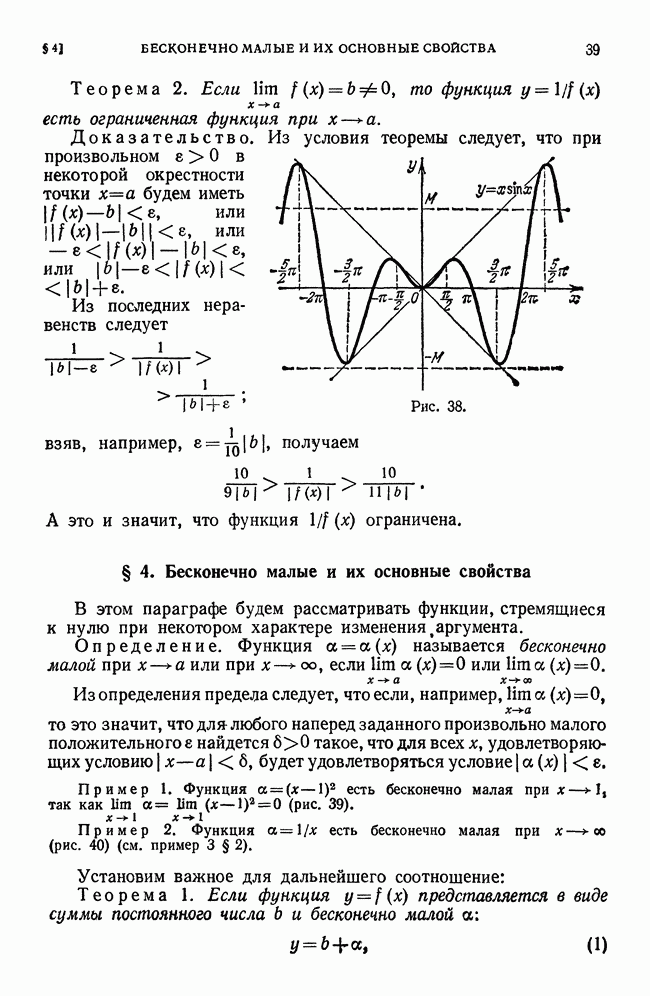
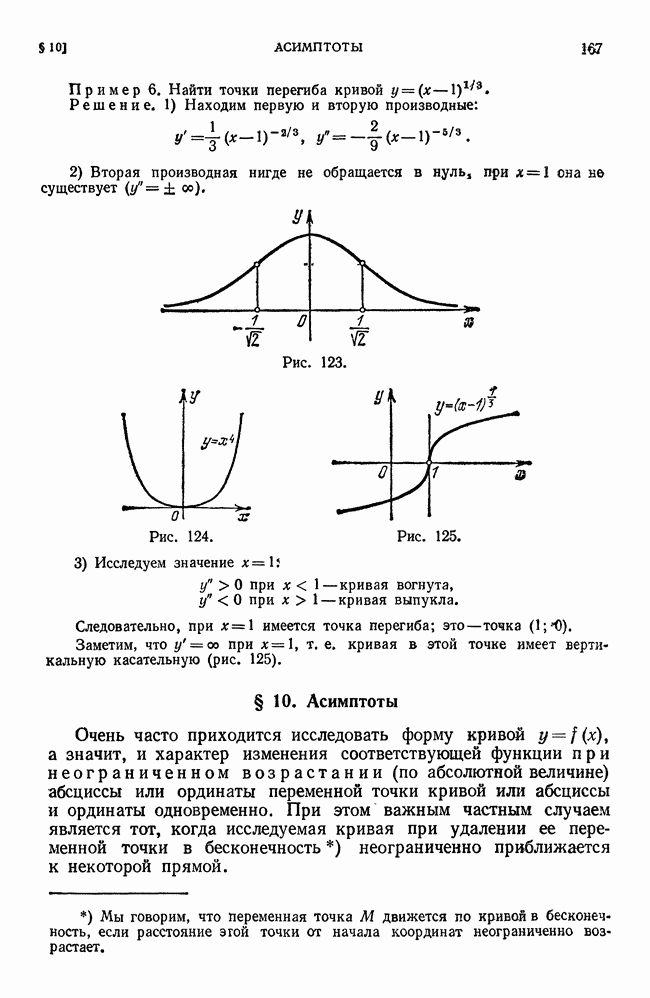
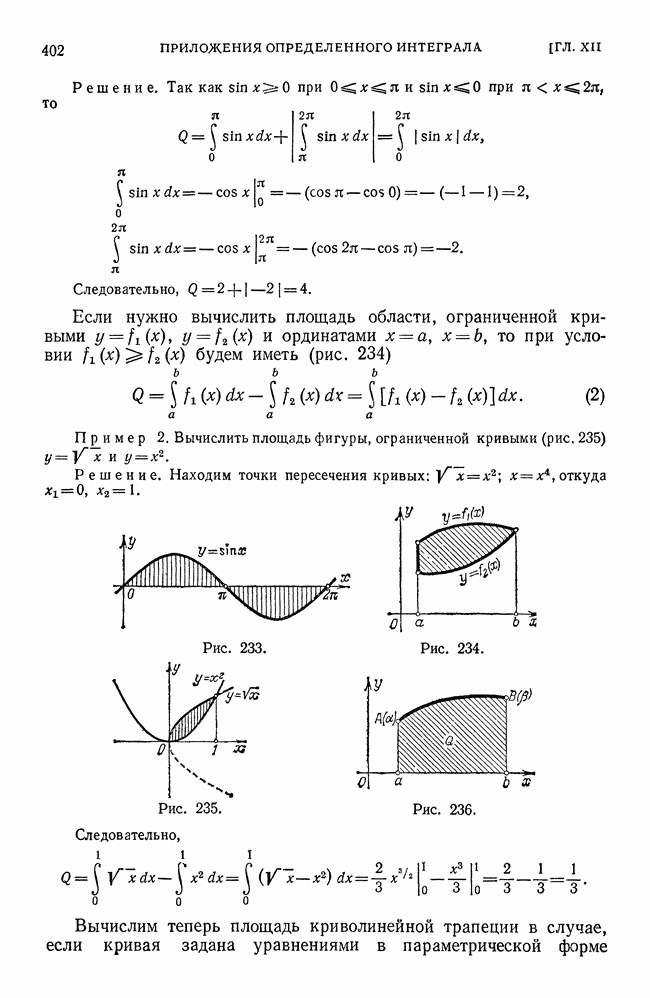
Пример 2. Вычислить 
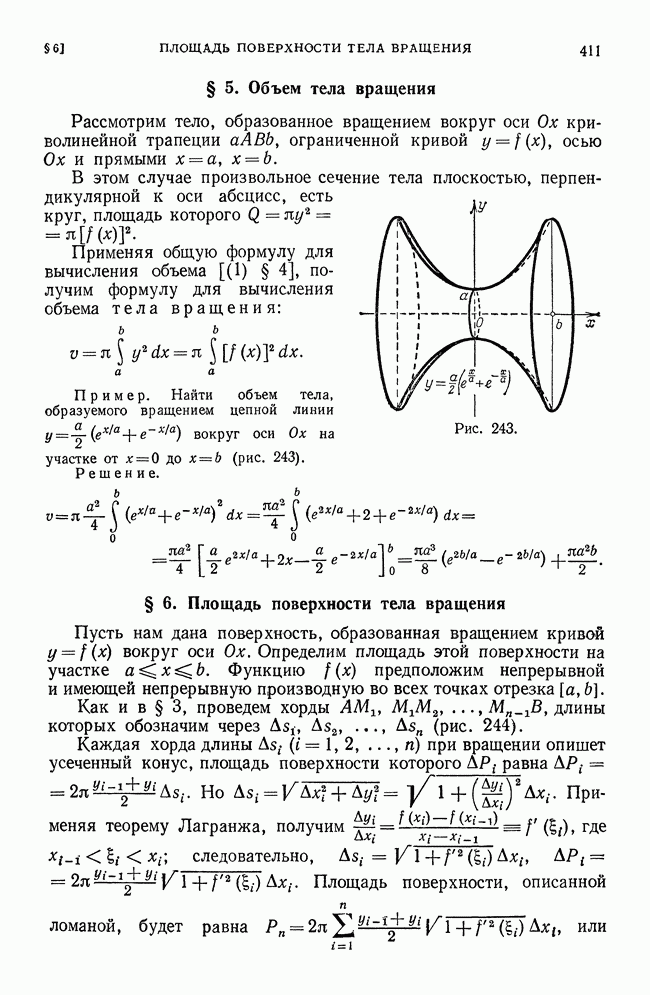
Решение. Данный интеграл равен площади Q криволинейной трапеции, ограниченной параболой  ординатой
ординатой  и прямой
и прямой 
Разобьем отрезок  на
на  равных частей точками
равных частей точками 
За точки возьмем крайние правые точки каждого  отрезков. Составим интегральную сумму:
отрезков. Составим интегральную сумму:

Как известно,  поэтому
поэтому 

Пример 3. Вычислить 
Решение.

Здесь  есть сумма длин отрезков, на которые разбит отрезок
есть сумма длин отрезков, на которые разбит отрезок 
При любом способе разбиения эта сумма равна длине отрезка 
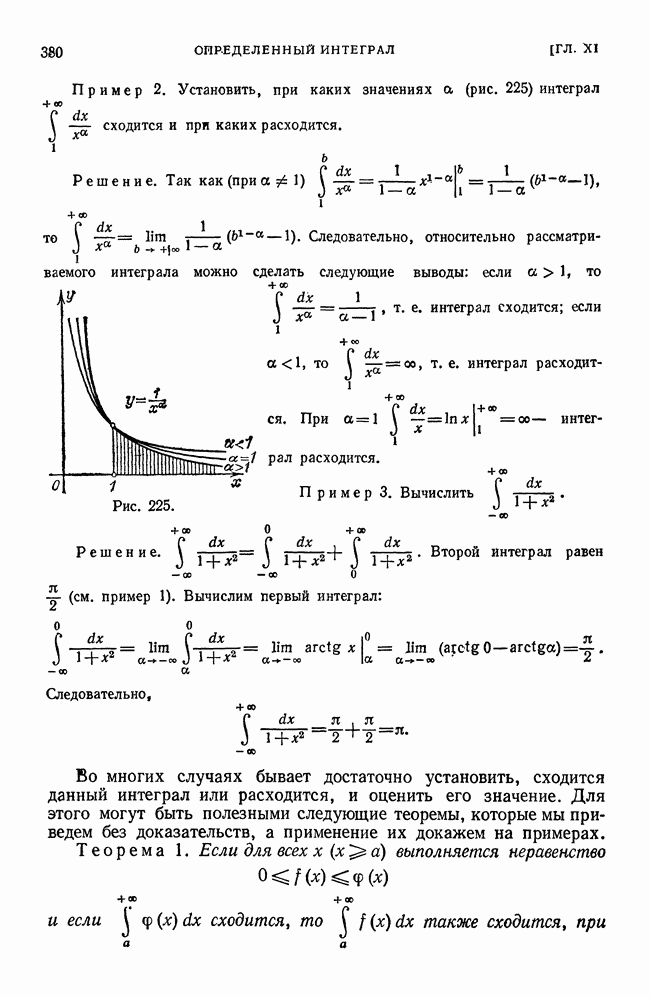
Пример 4. Вычислить 
Решение. Снова разделим отрезок  на
на  равных частей:
равных частей: 
За точки  возьмем левые крайние
возьмем левые крайние
точки. Составим интегральную сумму:

Выражение в скобках есть геометрическая прогрессия со знаменателем  дпервым членом 1, поэтому
дпервым членом 1, поэтому  Далее, имеем
Далее, имеем  правилу Лопиталя
правилу Лопиталя  Таким образом,
Таким образом, 
Замечание 4. Только что рассмотренные примеры показывают, что непосредственное вычисление определенных интегралов как пределов интегральных сумм связано с большими трудностями. Даже в тех случаях, когда подынтегральные функции являются очень простыми  , этот способ требует громоздких подсчетов. Нахождение же определенных интегралов от более сложных функций приводит к еще большим трудностям. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Этот метод, открытый Ньютоном и Лейбницем, использует глубокую связь, существующую между интегрированием и дифференцированием. Изложению и обоснованию этого метода посвящены следующие параграфы настоящей главы.
, этот способ требует громоздких подсчетов. Нахождение же определенных интегралов от более сложных функций приводит к еще большим трудностям. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Этот метод, открытый Ньютоном и Лейбницем, использует глубокую связь, существующую между интегрированием и дифференцированием. Изложению и обоснованию этого метода посвящены следующие параграфы настоящей главы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
- § 1. Действительные числа.
- § 2. Абсолютная величина действительного числа
- § 3. Переменные и постоянные величины
- § 4. Область изменения переменной величины
- § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина
- § 6. Функция
- § 7. Способы задания функции
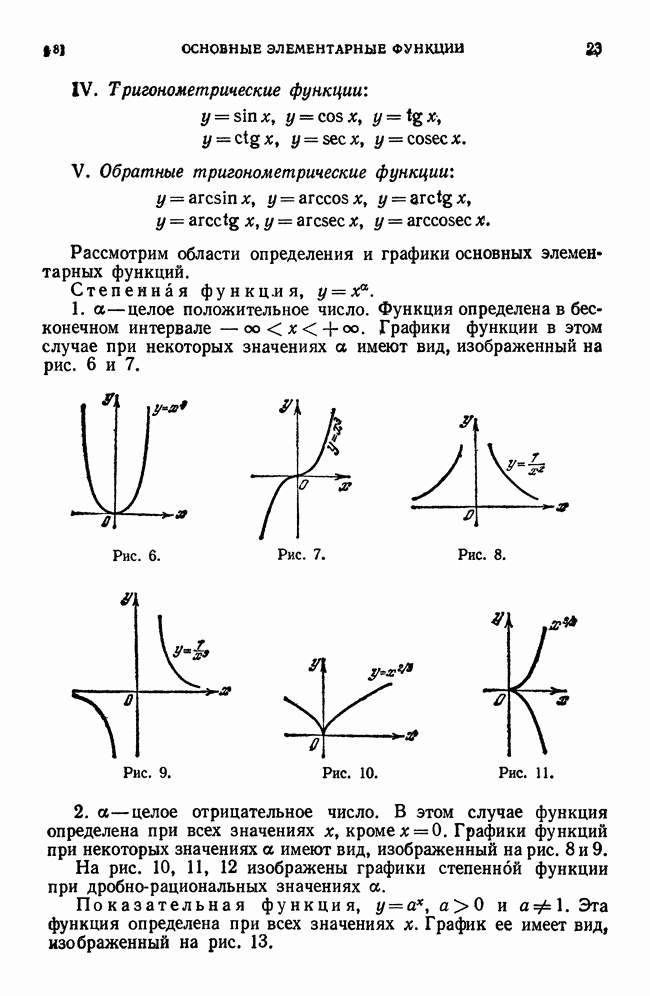
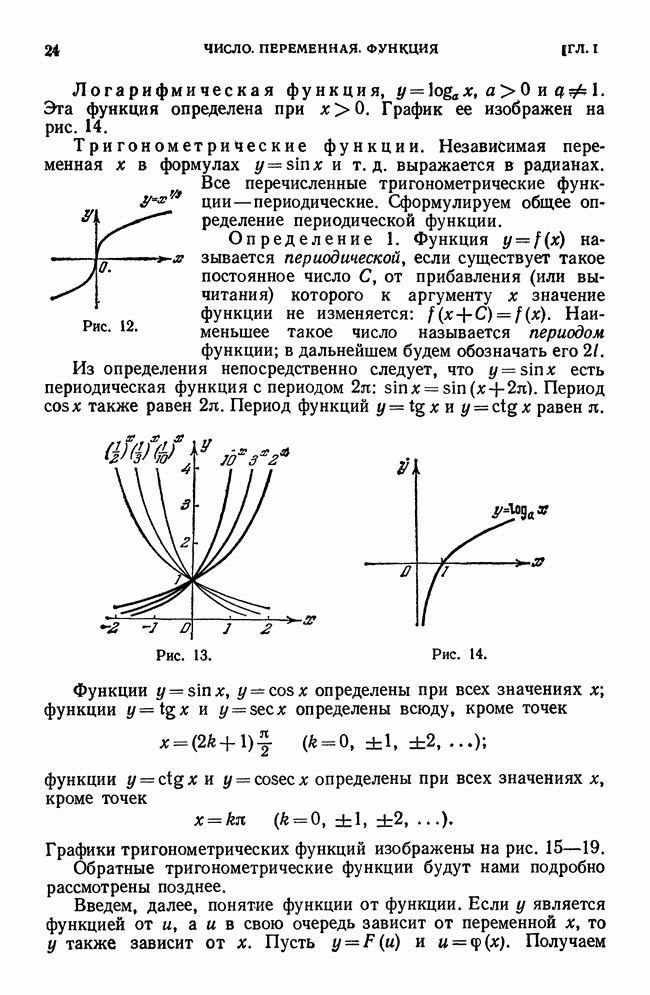
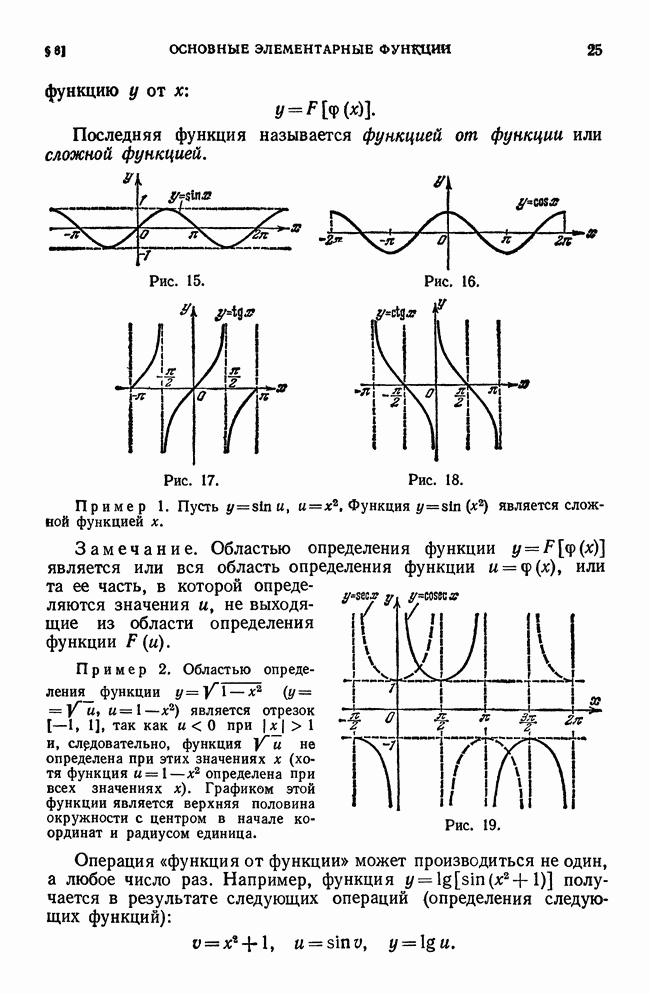
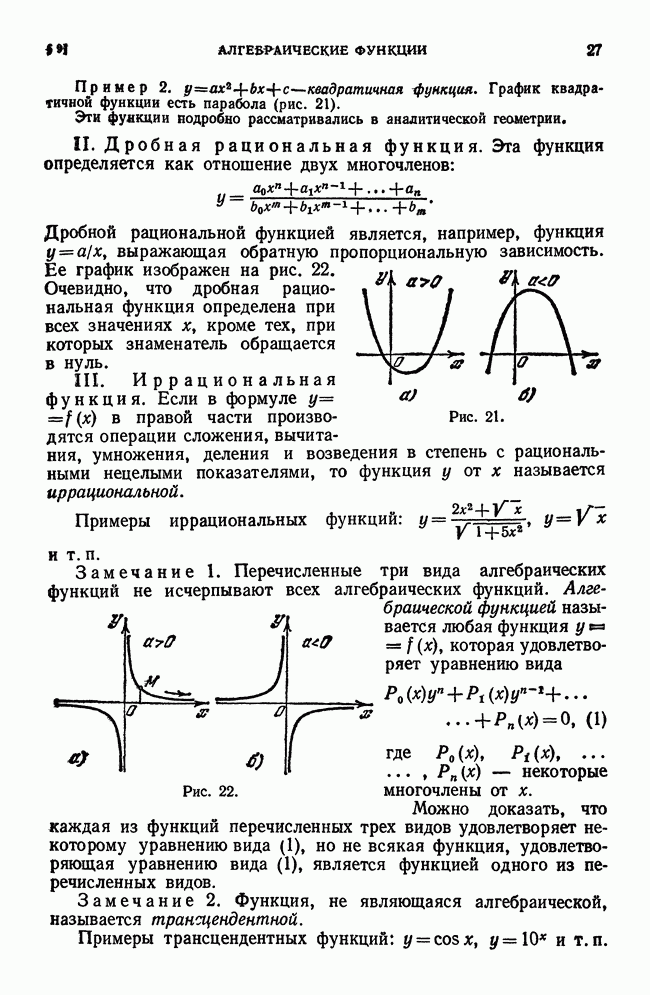
- § 8. Основные элементарные функции. Элементарные функции
- § 9. Алгебраические функции
- § 10. Полярная система координат
- Упражнения к главе I
- ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
- § 1. Предел переменной величины. Бесконечно большая переменная величина
- § 2. Предел функции
- § 3. Функция, стремящаяся к бесконечности. Ограниченные функции
- § 4. Бесконечно малые и их основные свойства
- § 5. Основные теоремы о пределах
- § 6. Предел функции (sin x)/x при x->0
- § 7. Число e
- § 8. Натуральные логарифмы
- § 9. Непрерывность функций
- § 10. Некоторые свойства непрерывных функций
- § 11. Сравнение бесконечно малых
- Упражнения к главе II
- ГЛАВА III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
- § 2. Определение производной
- § 3. Геометрическое значение производной
- § 4. Дифференцируемость функций
- § 5. Производная от функции y = x^n при n целом и положительном
- § 6. Производные от функций y = sinx; y = cosx
- § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного
- § 8. Производная логарифмической функции
- § 9. Производная от сложной функции
- § 10. Производные функций y = tgx, y = ctgx, y = ln|x|
- § 11. Неявная функция и ее дифференцирование
- § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции
- § 13. Обратная функция и ее дифференцирование
- § 14. Обратные тригонометрические функции и их дифференцирование
- § 15. Таблица основных формул дифференцирования
- § 16. Параметрическое задание функции
- § 17. Уравнения некоторых кривых в параметрической форме
- § 18. Производная функции, заданной параметрически
- § 19. Гиперболические функции
- § 20. Дифференциал
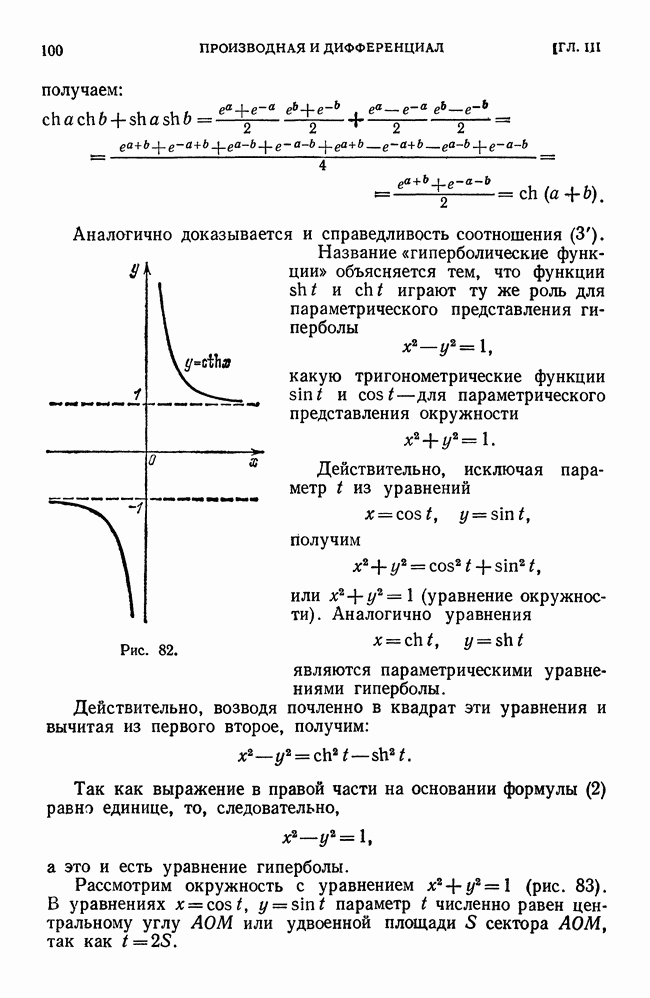
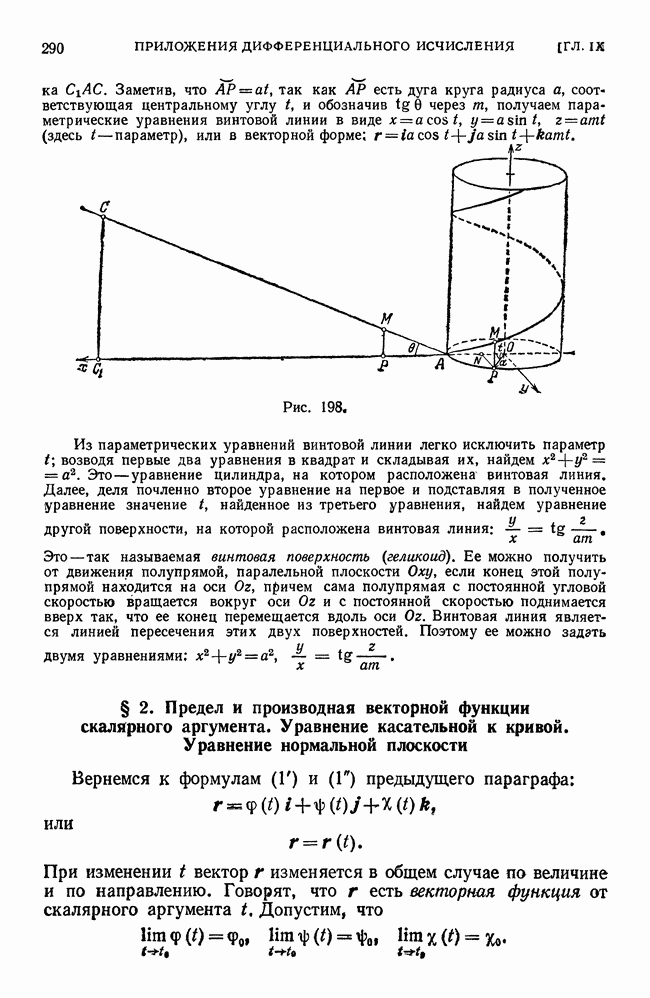
- § 21. Геометрическое значение дифференциала Рассмотрим функцию
- § 22. Производные различных порядков
- § 23. Дифференциалы различных порядков
- § 24. Производные различных порядков от неявных функций и функций, заданных параметрически
- § 25. Механическое значение второй производной
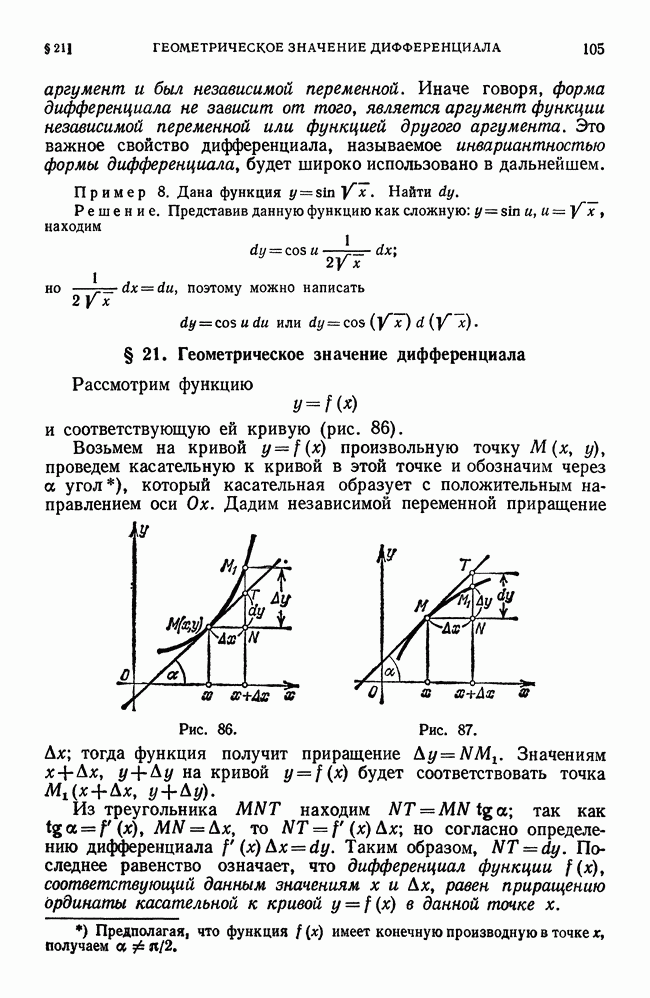
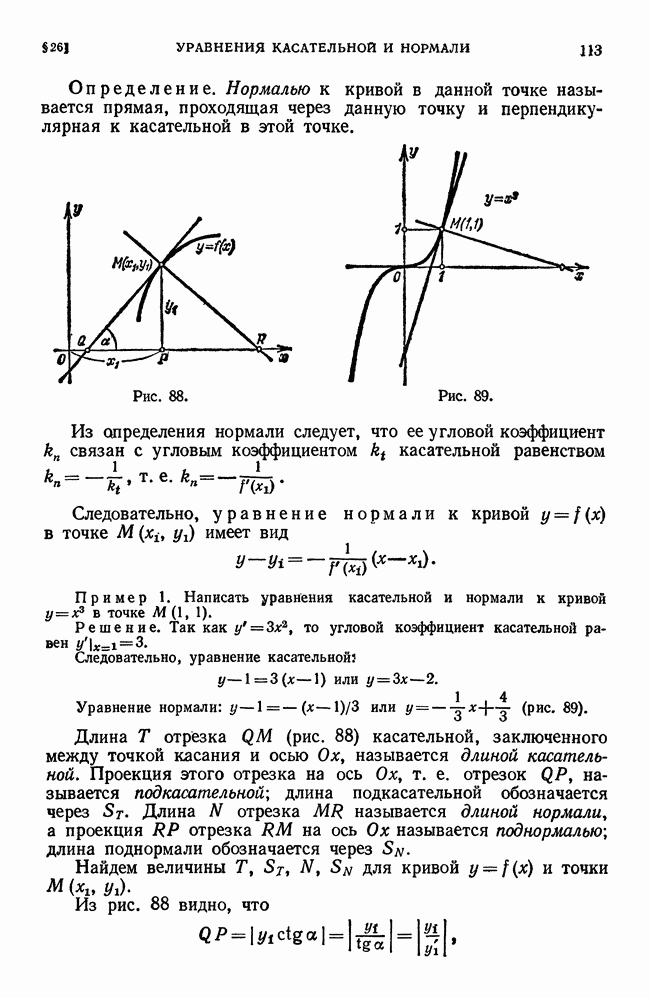
- § 26. Уравнения касательной и нормали. Длины подкасательной и поднормали
- § 27. Геометрическое значение производной радиус-вектора по полярному углу
- Упражнения к главе III
- ГЛАВА IV. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- § 1. Теорема о корнях производной (теорема Ролля)
- § 2. Теорема о конечных приращениях (теорема Лагранжа)
- § 3. Теорема об отношении приращений двух функций (теорема Коши)
- § 4. Предел отношения двух бесконечно малых величин «раскрытие неопределенностей вида 0/0»)
- § 5. Предел отношения двух бесконечно больших величин «раскрытие неопределенностей вида oo/oo»)
- § 6. Формула Тейлора
- § 7. Разложение по формуле Тейлора функций e^x, sin x, cos x
- Упражнения к главе IV
- ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
- § 2. Возрастание и убывание функции
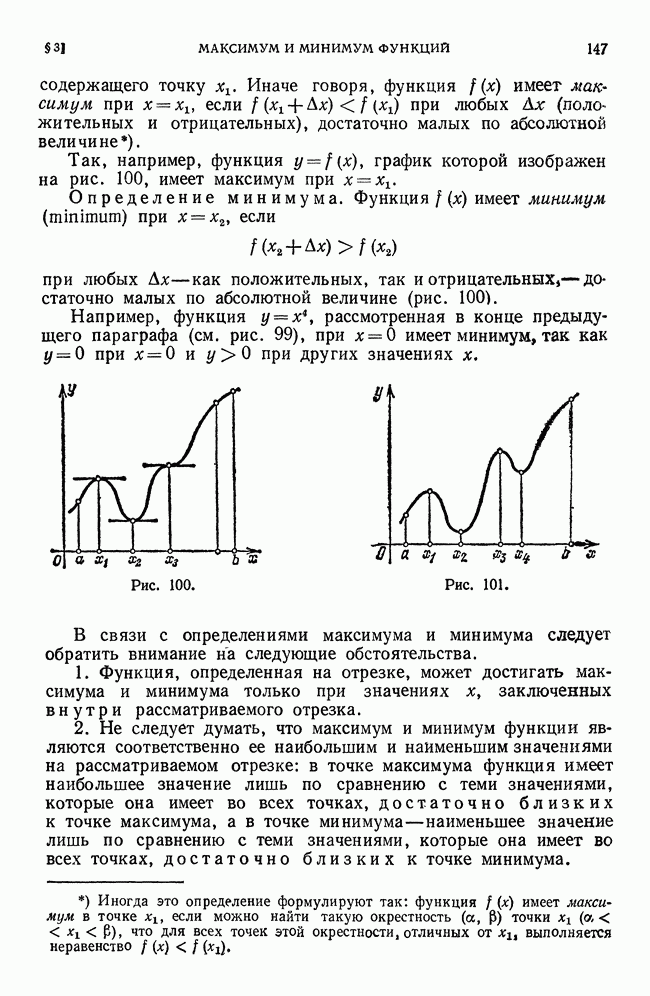
- § 3. Максимум и минимум функций
- § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной
- § 5. Исследование функции на максимум и минимум с помощью второй производной
- § 6. Наибольшее и наименьшее значения функции на отрезке
- § 7. Применение теории максимума и минимума функций к решению задач
- § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора
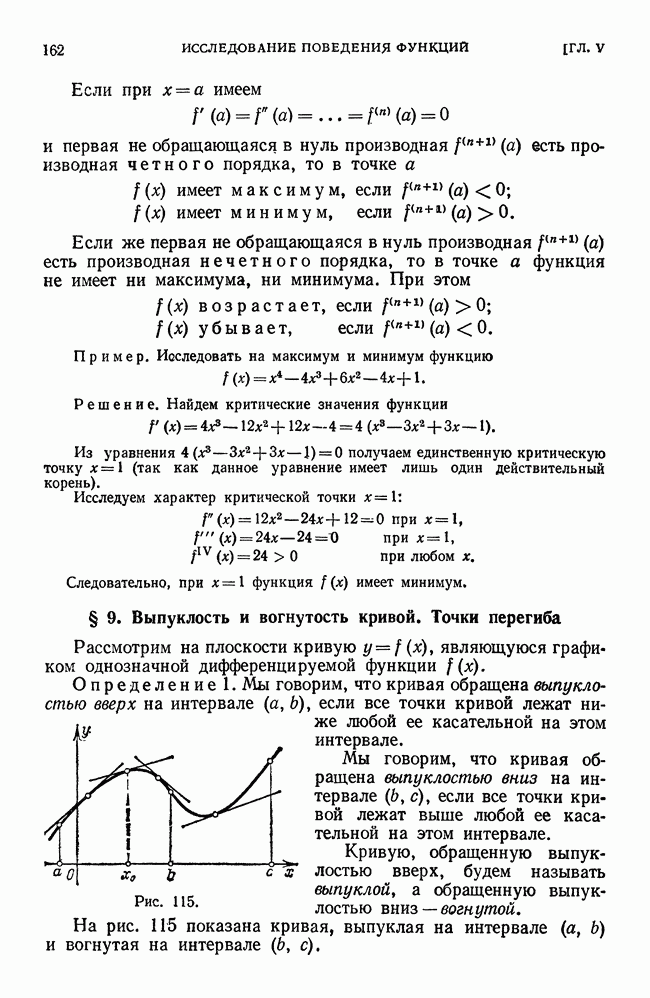
- § 9. Выпуклость и вогнутость кривой. Точки перегиба
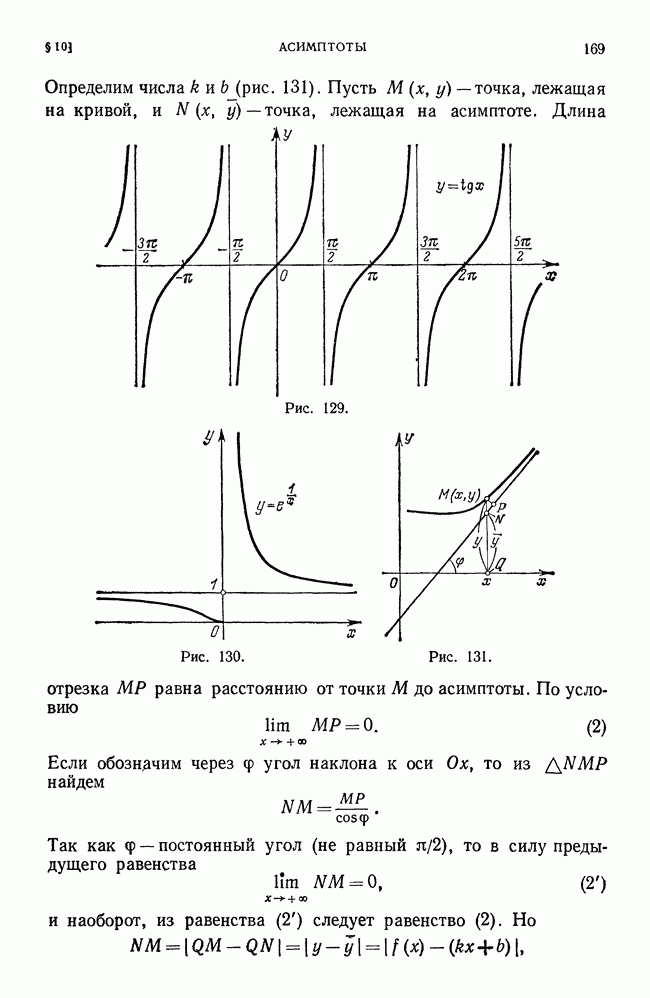
- § 10. Асимптоты
- § 11. Общий план исследования функций и построения графиков
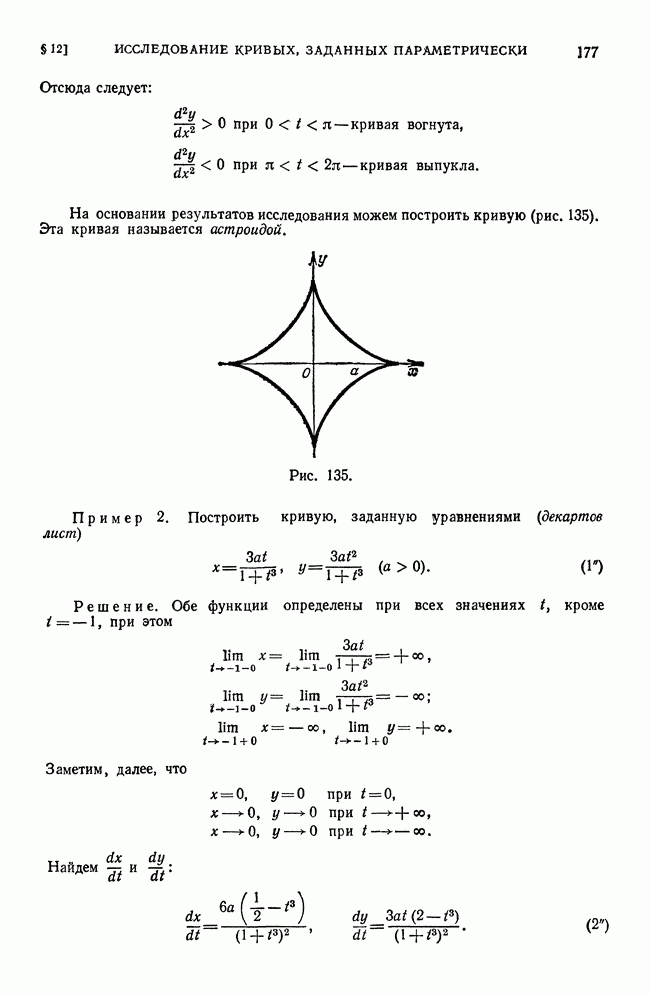
- § 12. Исследование кривых, заданных параметрически
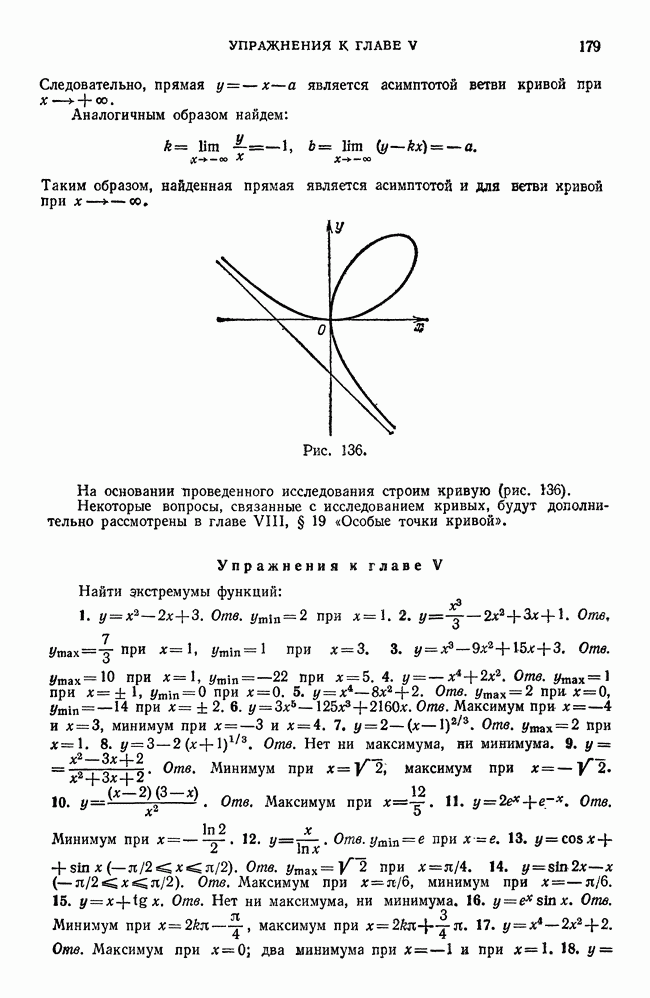
- Упражнения к главе V
- ГЛАВА VI. КРИВИЗНА КРИВОЙ
- § 1. Длина дуги и ее производная
- § 2. Кривизна
- § 3. Вычисление кривизны
- § 4. Вычисление кривизны линии, заданной параметрически
- § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах
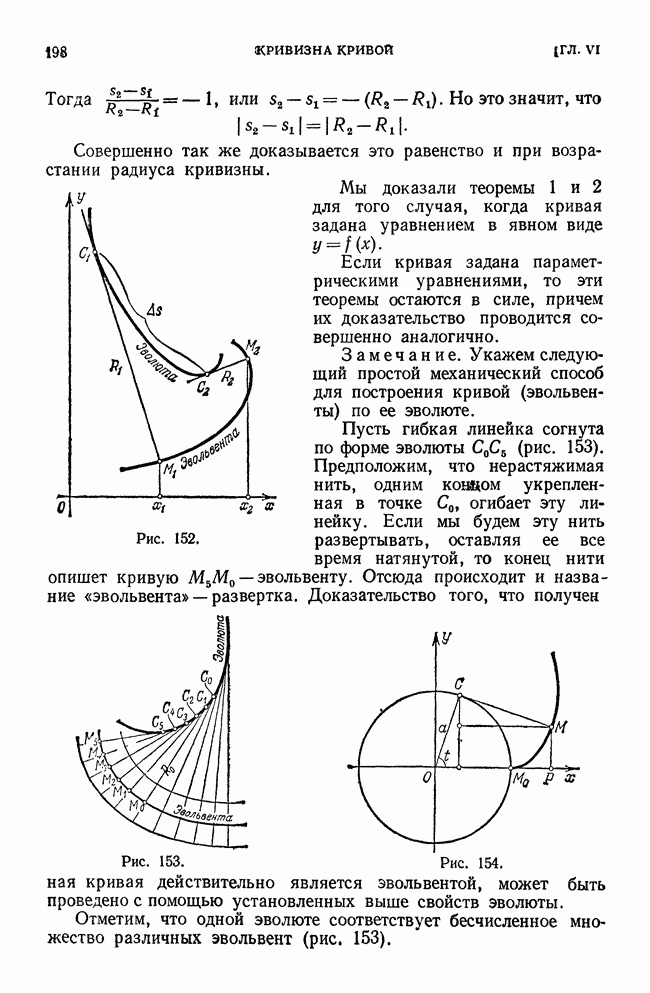
- § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
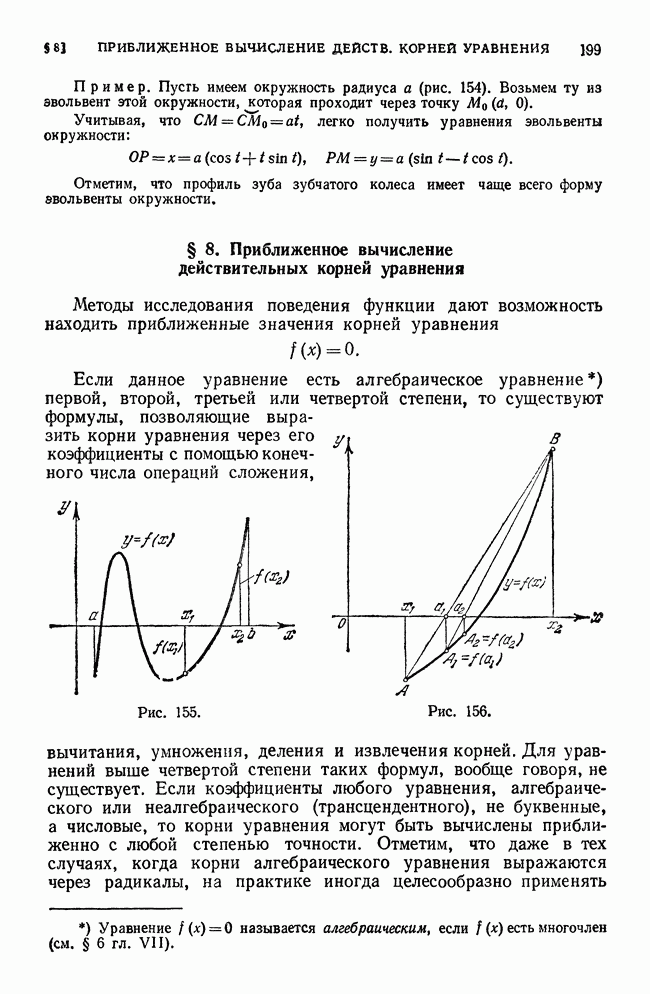
- § 7. Свойства эволюты
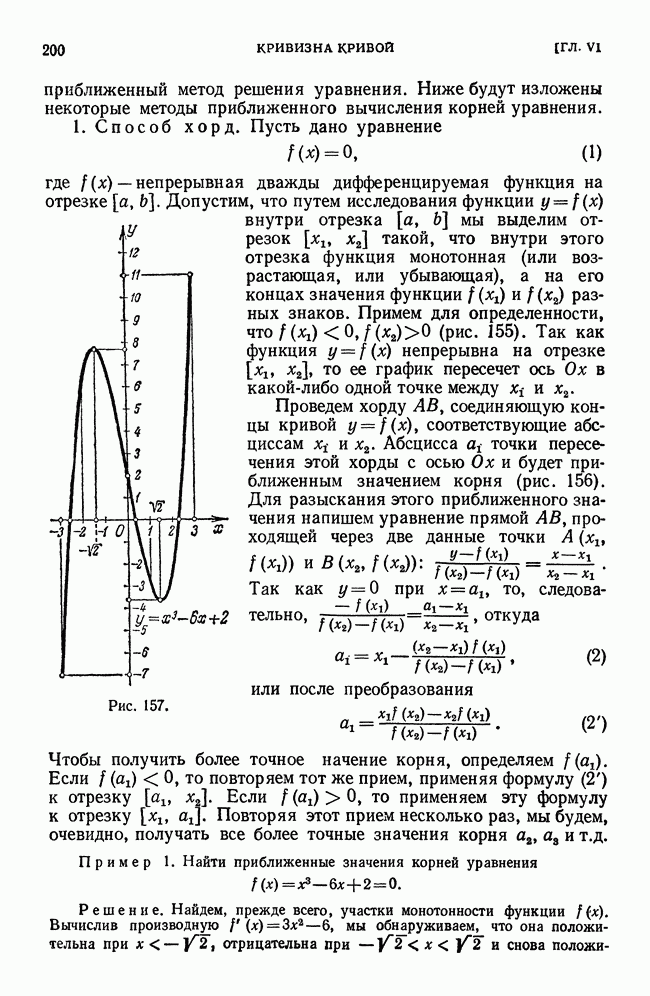
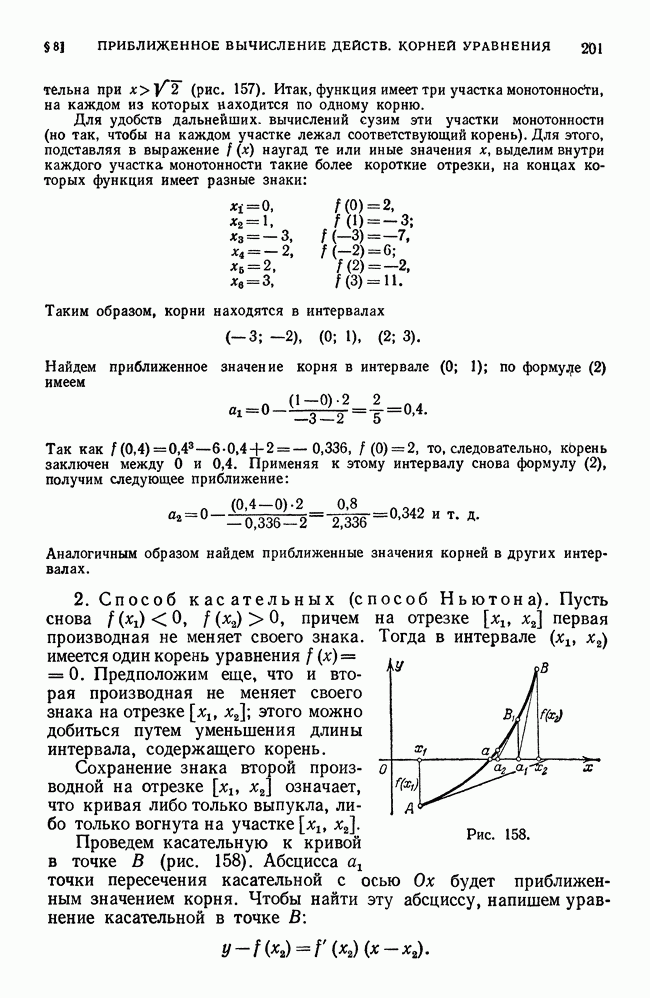
- § 8. Приближенное вычисление действительных корней уравнения
- Упражнения к главе VI
- ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ
- § 1. Комплексные числа. Исходные определения
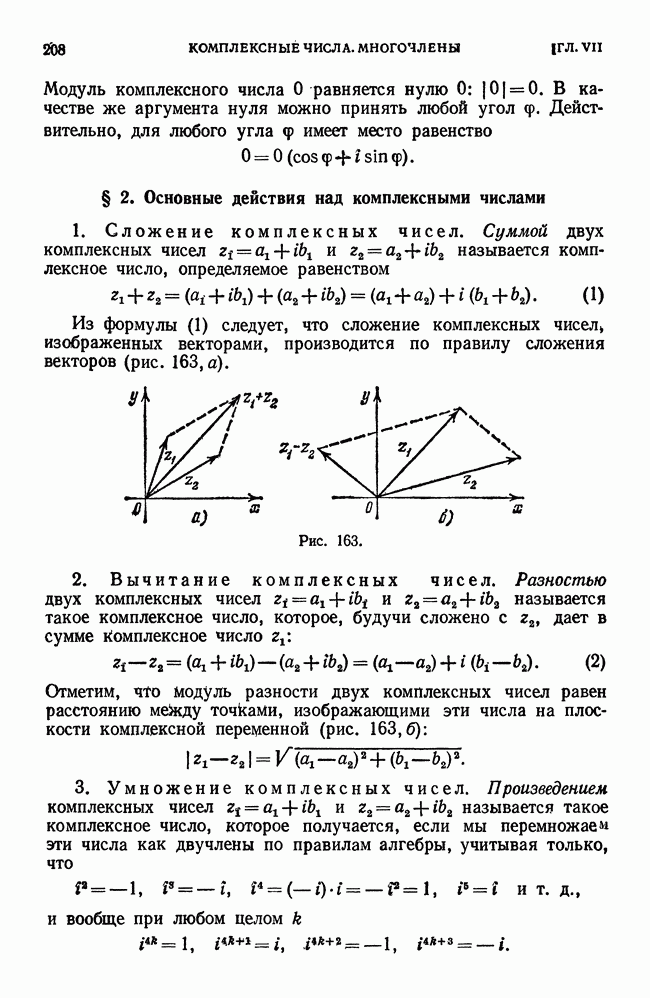
- § 2. Основные действия над комплексными числами
- § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа
- § 4. Показательная функция с комплексным показателем и ее свойства
- § 5. Формула Эйлера. Показательная форма комплексного числа
- § 6. Разложение многочлена на множители
- § 7. О кратных корнях многочлена
- § 8. Разложение многочлена на множители в случае комплексных корней
- § 9. Интерполирование. Интерполяционная формула Лагранжа
- § 10. Интерполяционная формула Ньютона
- § 11. Численное дифференцирование
- § 12. О наилучшем приближении функций многочленами. Теория Чебышева
- Упражнения к главе VII
- ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. Определение функции нескольких переменных
- § 2. Геометрическое изображение функции двух переменных
- § 3. Частное и полное приращение функции
- § 4. Непрерывность функции нескольких переменных
- § 5. Частные производные функции нескольких переменных
- § 6. Геометрическая интерпретация частных производных функции двух переменных
- § 7. Полное приращение и полный дифференциал
- § 8. Применение полного дифференциала в приближенных вычислениях
- § 9. Приложение дифференциала к оценке погрешности при вычислениях
- § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции
- § 11. Производная от функции, заданной неявно
- § 12. Частные производные различных порядков
- § 13. Поверхности уровня
- § 14. Производная по направлению
- § 15. Градиент
- § 16. Формула Тейлора для функции двух переменных
- § 17. Максимум и минимум функции нескольких переменных
- § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы)
- § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов
- § 20. Особые точки кривой
- Упражнения к главе VIII
- ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
- § 1. Уравнения кривой в пространстве
- § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости
- § 3. Правила дифференцирования векторов (векторных функций)
- § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении
- § 5. Соприкасающаяся плоскость. Бинормаль. Кручение.
- § 6. Касательная плоскость и нормаль к поверхности
- Упражнения к главе IX
- ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Первообразная и неопределенный интеграл
- § 2. Таблица интегралов
- § 3. Некоторые свойства неопределенного интеграла
- § 4. Интегрирование методом замены переменной или способом подстановки
- § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
- § 6. Интегрирование по частям
- § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- § 8. Разложение рациональной дроби на простейшие
- § 9. Интегрирование рациональных дробей
- § 10. Интегралы от иррациональных функций
- § 11. Интегралы вида …
- § 12. Интегрирование некоторых классов тригонометрических функций
- § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
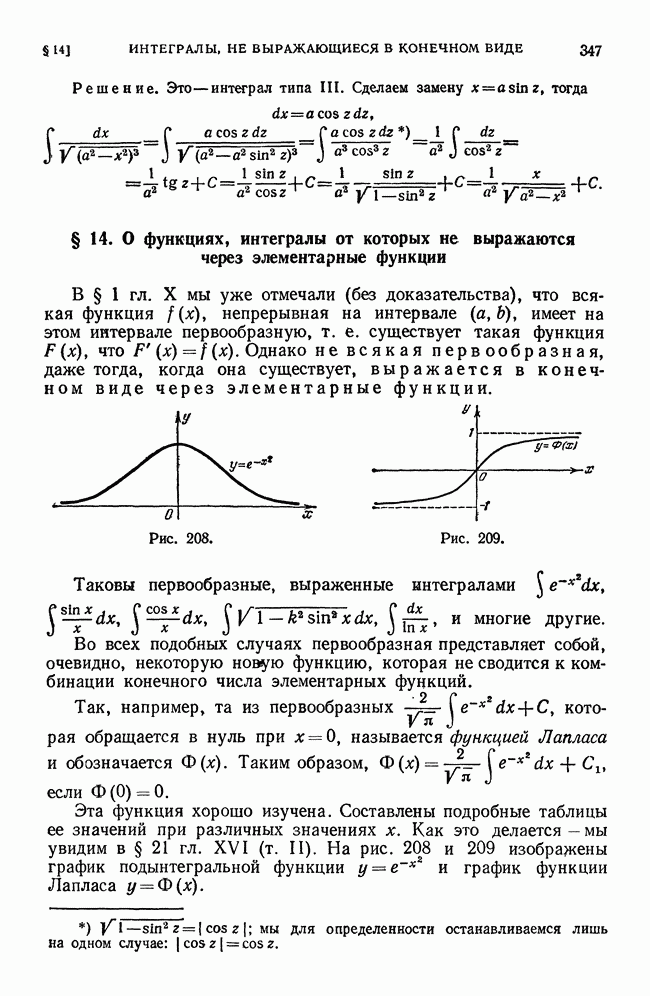
- § 14. О функциях, интегралы от которых не выражаются через элементарные функции
- Упражнения к главе X
- ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Постановка задачи. Нижняя и верхняя интегральные суммы
- § 2. Определенный интеграл. Теорема о существовании определенного интеграла
- § 3. Основные свойства определенного интеграла
- § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
- § 5. Замена переменной в определенном интеграле
- § 6. Интегрирование по частям
- § 7. Несобственные интегралы
- § 8. Приближенное вычисление определенных интегралов
- § 9. Формула Чебышева
- § 10. Интегралы, зависящие от параметра. Гамма-функция
- § 11. Интегрирование комплексной функции действительной переменной
- Упражнения кглаве XI
- ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. Вычисление площадей в прямоугольных координатах
- § 2. Площадь криволинейного сектора в полярных координатах
- § 3. Длина дуги кривой
- § 4. Вычисление объема тела по площадям параллельных сечений
- § 5. Объем тела вращения
- § 6. Площадь поверхности тела вращения
- § 7. Вычисление работы с помощью определенного интеграла
- § 8. Координаты центра масс
- § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла
- Упражнения к главе XII