| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
19. Комбинационные логические схемы
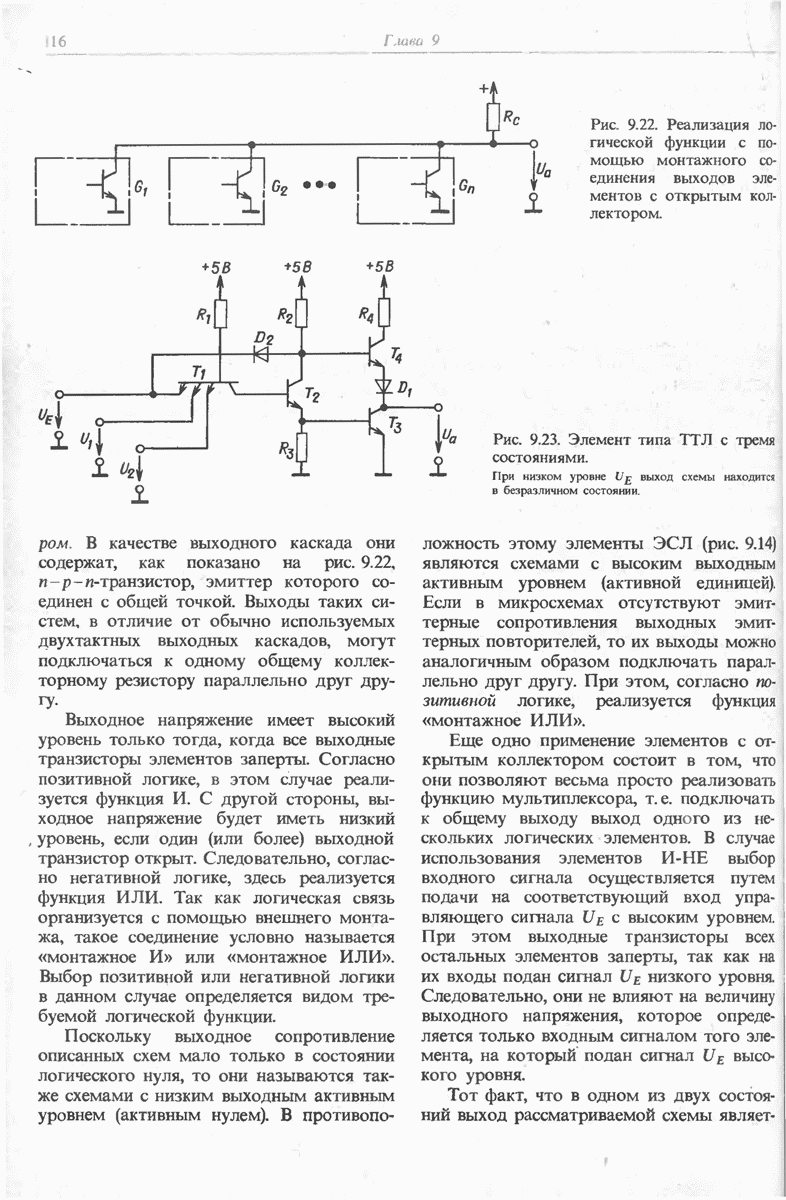
Под комбинационной логической схемой понимают цифровую схему без запоминания переменных (логические схемы без памяти). Согласно блок-схеме, представленной на рис. 19.1, выходные переменные однозначно определяются значениями входных переменных  В случае логических схем с памятью (схем последовательностного типа) выходные переменные зависят, кроме того, и от состояния системы в данный момент, т.е. от ее предыстории.
В случае логических схем с памятью (схем последовательностного типа) выходные переменные зависят, кроме того, и от состояния системы в данный момент, т.е. от ее предыстории.
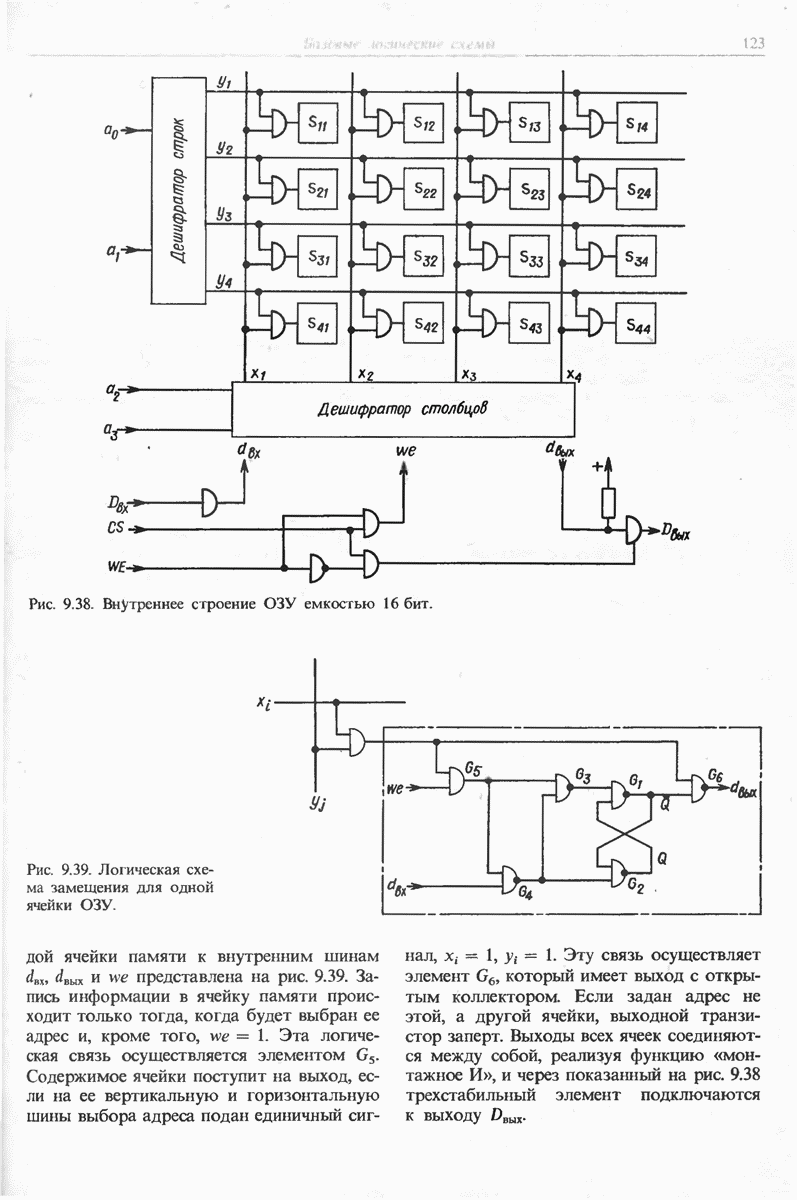
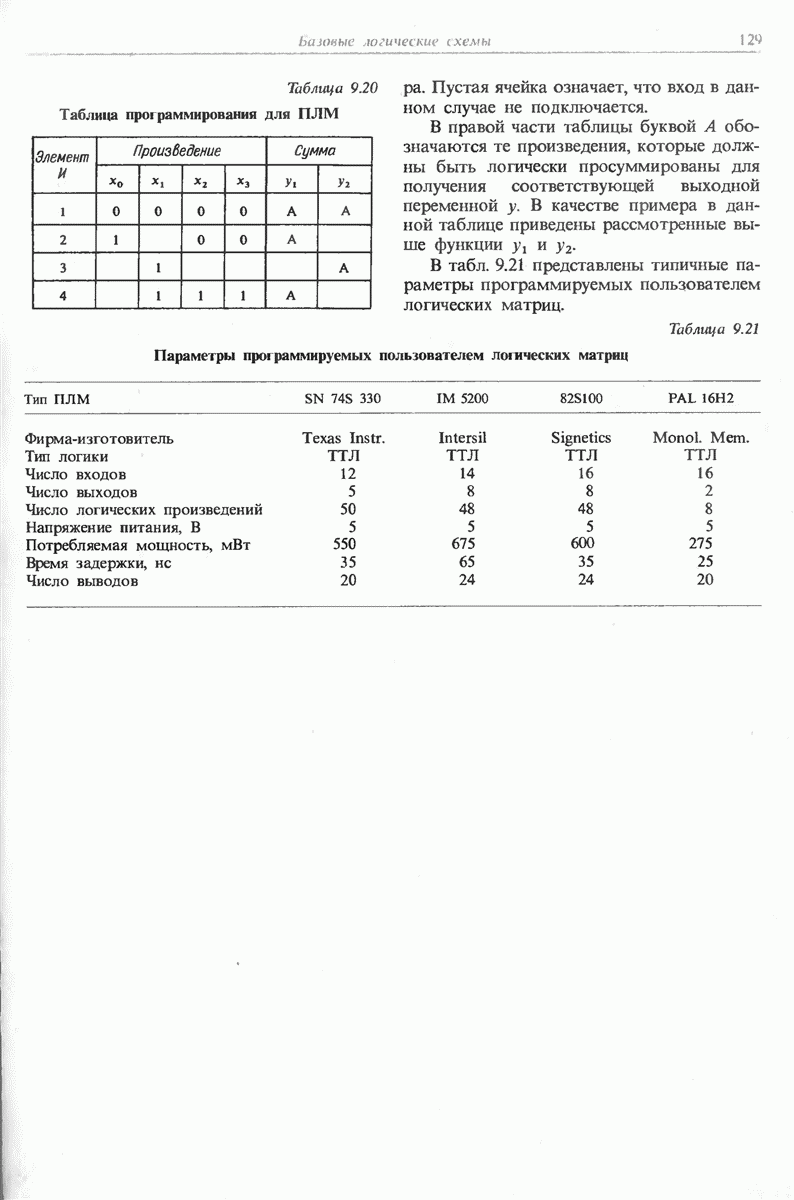
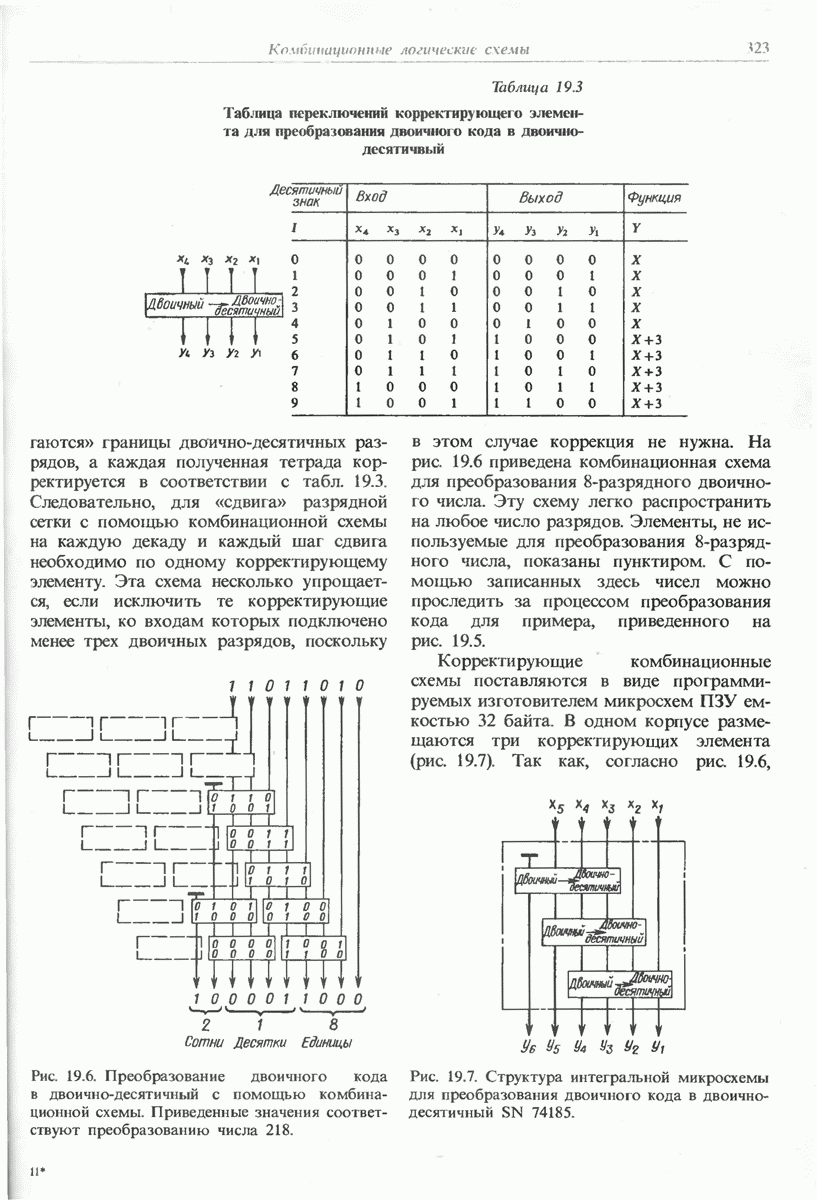
Связь между входными и выходными переменными задается с помощью таблиц переключений или булевых функций. Для их схемотехнической реализации можно использовать постоянные запоминающие устройства (ПЗУ), в которые непосредственно заносится таблица переключений. При этом входные переменные играют роль адреса. Вторая возможность заключается в использовании логических элементов, которыми реализуются булевы функции.
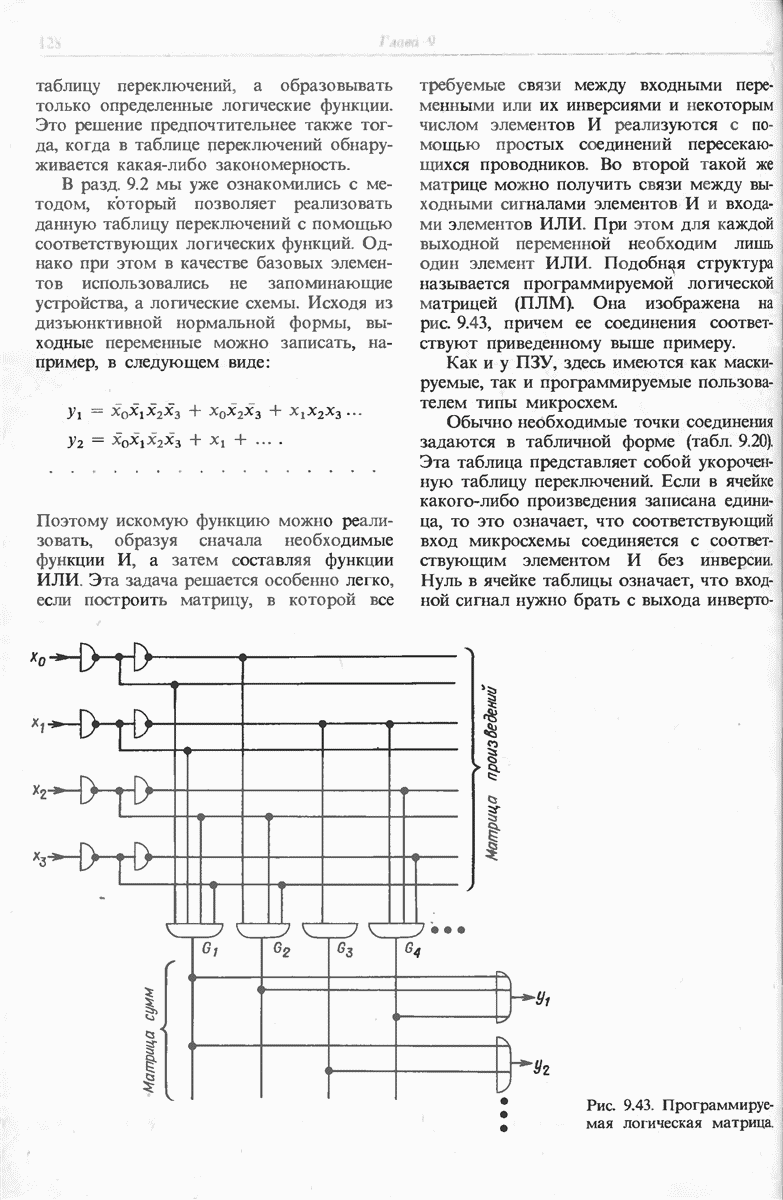
Если в таблице переключений для выходных переменных записано небольшое число логических единиц, более удобной является ее реализация с помощью логических элементов, поскольку в этом случае требуется незначительное количество монтажных соединений. Даже при большом числе входных переменных в этом случае можно обойтись лишь одной интегральной схемой, применив программируемую логическую матрицу (ПЛМ).

Рис. 19.1. Общий вид комбинационной схемы.
Если в таблице переключений стоит незначительное число нулей, то следует составить инверсные логические функции, как было описано в разд. 9.2. Рекомендации для использования различных способов построения комбинационных схем приведены на рис. 19.2.
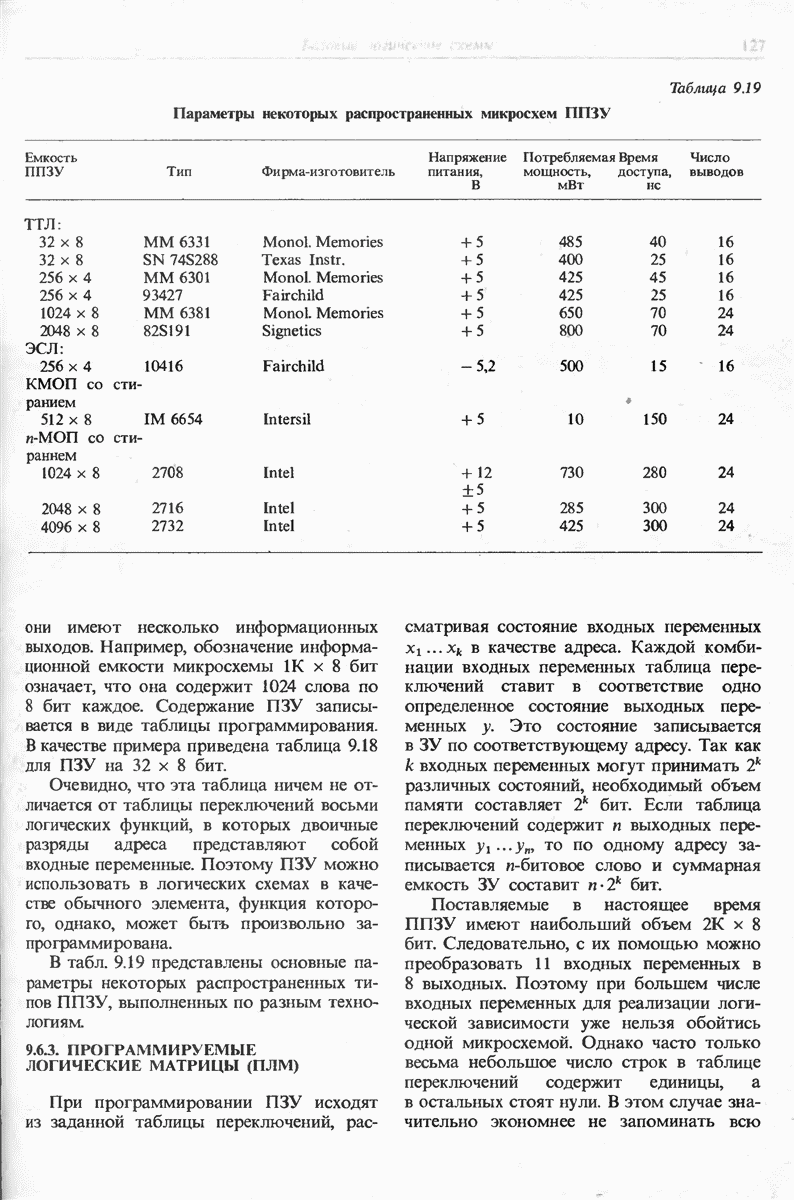
В следующих разделах рассмотрены вопросы построения и функционирования наиболее распространенных схем комбинационной логики. При этом особое внимание уделяется операциям над числами. Для того чтобы числа можно было представить с помощью логических переменных, нужно записать их в виде ряда цифр, принимающих только два значения. Двоичная цифра (или знак) называется битом. Одна из форм представления чисел с помощью двоичных знаков называется двоичной системой счисления или двоичным кодом. В этом случае разряды числа расставлены по возрастающим степеням числа 2. Цифра 1 соответствует логической единице, а цифра  логическому нулю. Логические переменные, характеризующие отдельные разряды, будем обозначать строчными буквами, а все число - прописными. Следовательно, запись
логическому нулю. Логические переменные, характеризующие отдельные разряды, будем обозначать строчными буквами, а все число - прописными. Следовательно, запись  -разрядного числа в двоичном коде имеет вид
-разрядного числа в двоичном коде имеет вид

Очевидно, что всегда надо четко различать, выполняется ли данная операция над числами, или имеется в виду функция логических переменных. Рассмотрим еще раз это различие на следующем пример». Пусть необходимо определить, чему будет равно  Рассматривая знак
Рассматривая знак  как операцию сложения в десятичной системе, получим следующий результат:
как операцию сложения в десятичной системе, получим следующий результат:


Рис. 19.2 Возможные способы реализации комбинационной схемы.
Напротив, если сложение выполняется в двоичной системе счисления, то

Если знак  рассматривать как дизъюнкцию логических переменных, то
рассматривать как дизъюнкцию логических переменных, то

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Часть I. Основные положения
- 1. Пояснение применяемых величин
- 2. Пассивные RC- и LRC- цепи
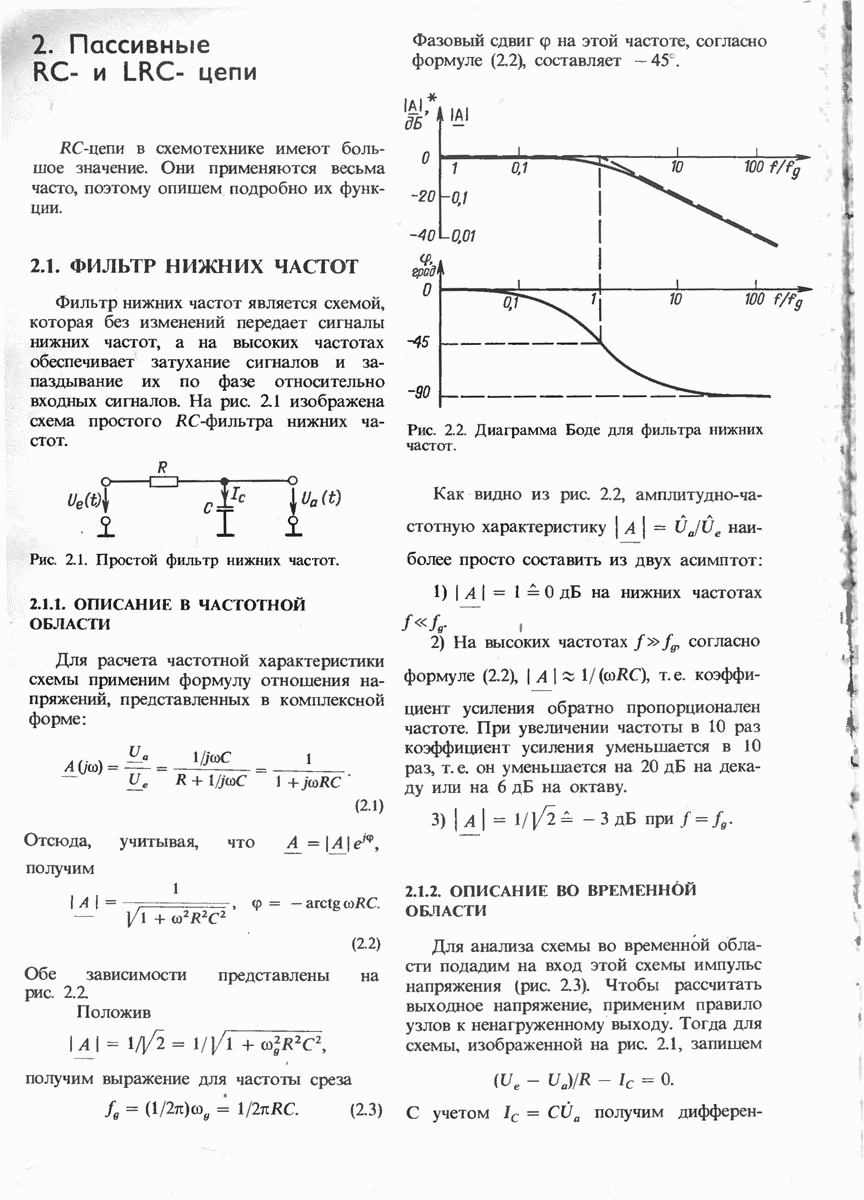
- 2.1. ФИЛЬТР НИЖНИХ ЧАСТОТ
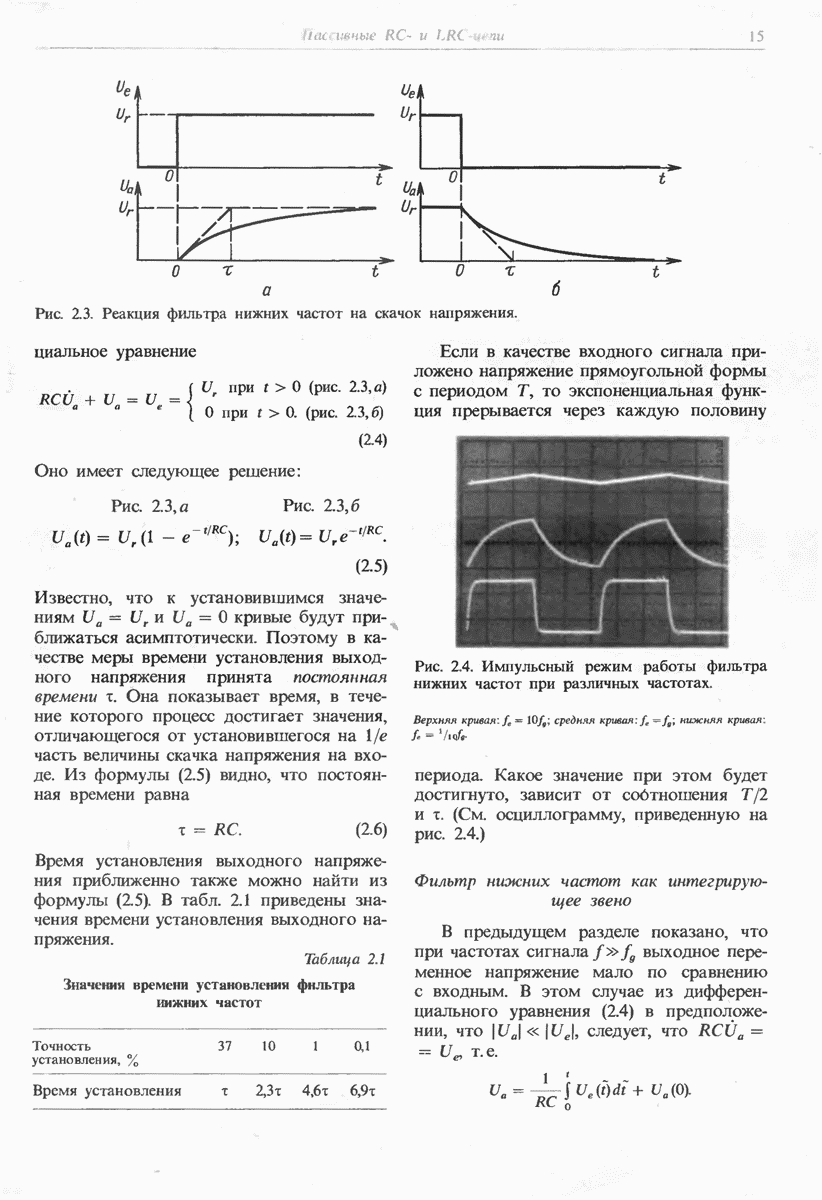
- 2.1.3. ДЛИТЕЛЬНОСТЬ ФРОНТА ИМПУЛЬСА И ЧАСТОТА СРЕЗА ФИЛЬТРА
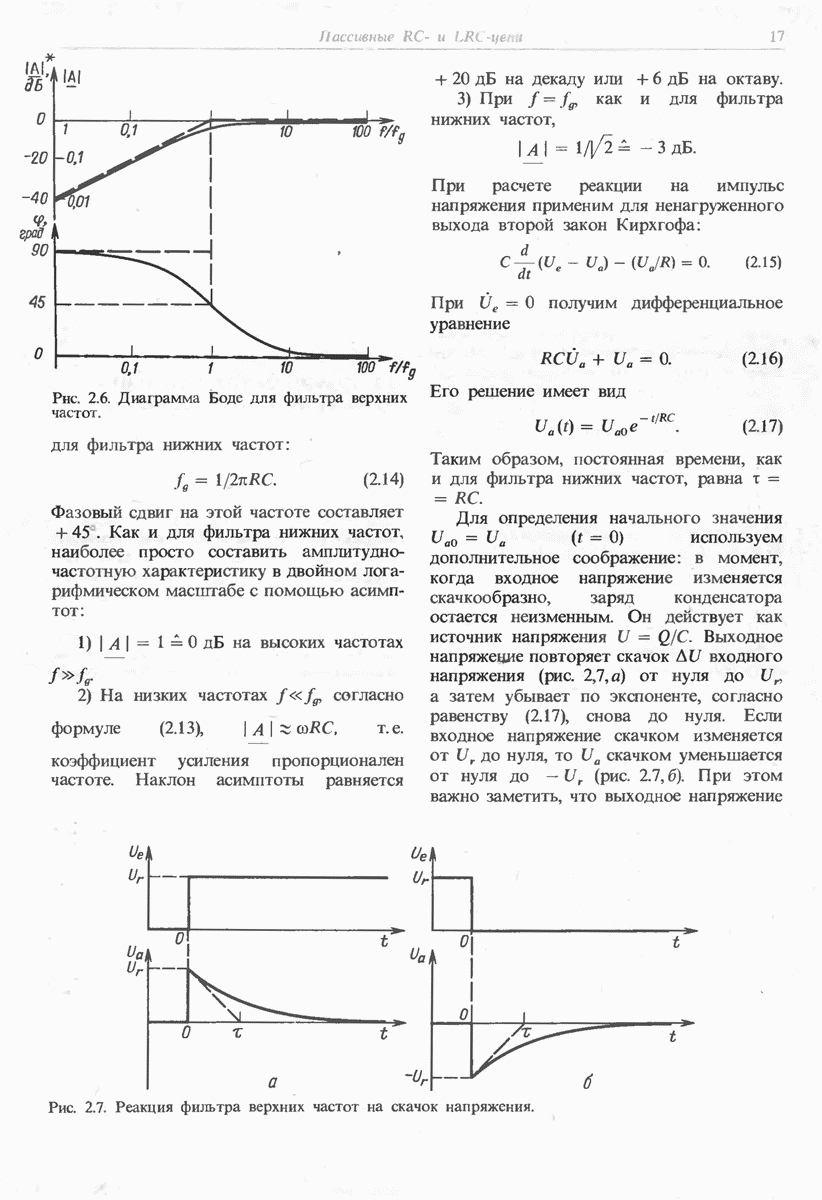
- 2.2. ФИЛЬТР ВЕРХНИХ ЧАСТОТ
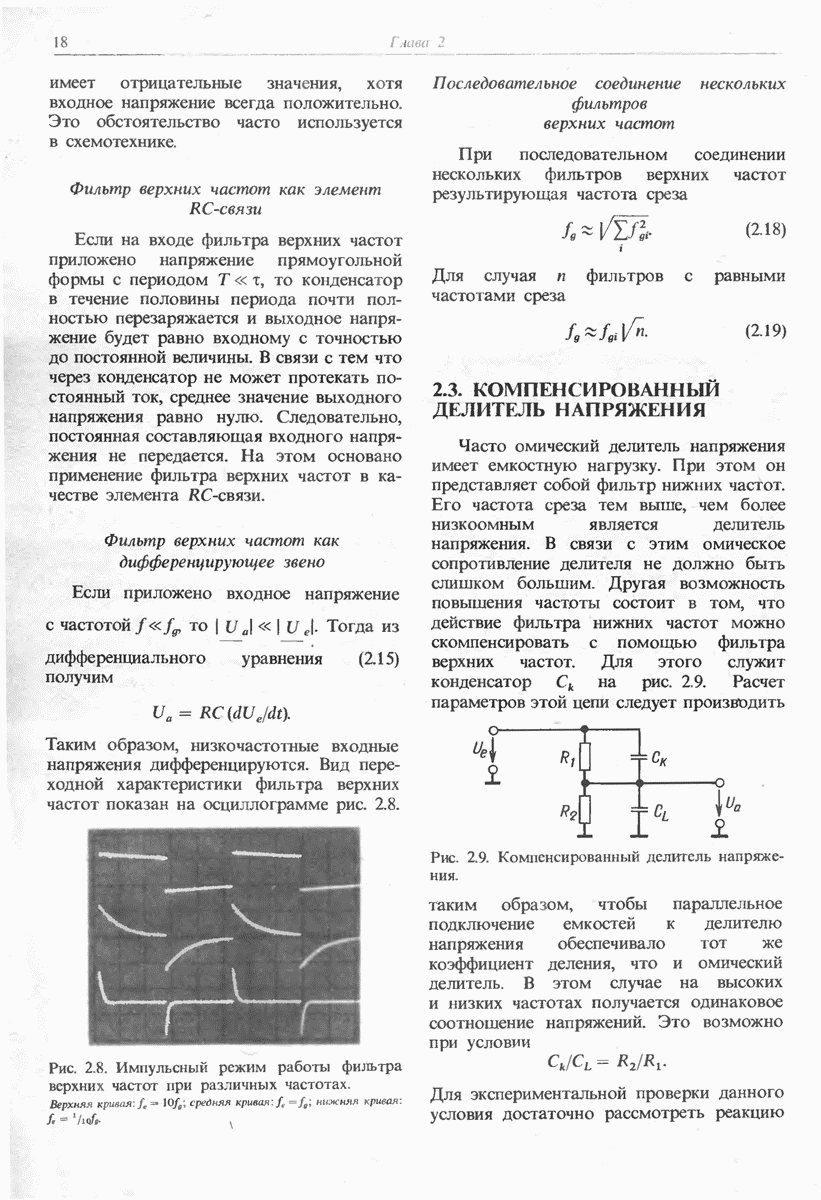
- 2.3. КОМПЕНСИРОВАННЫЙ ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
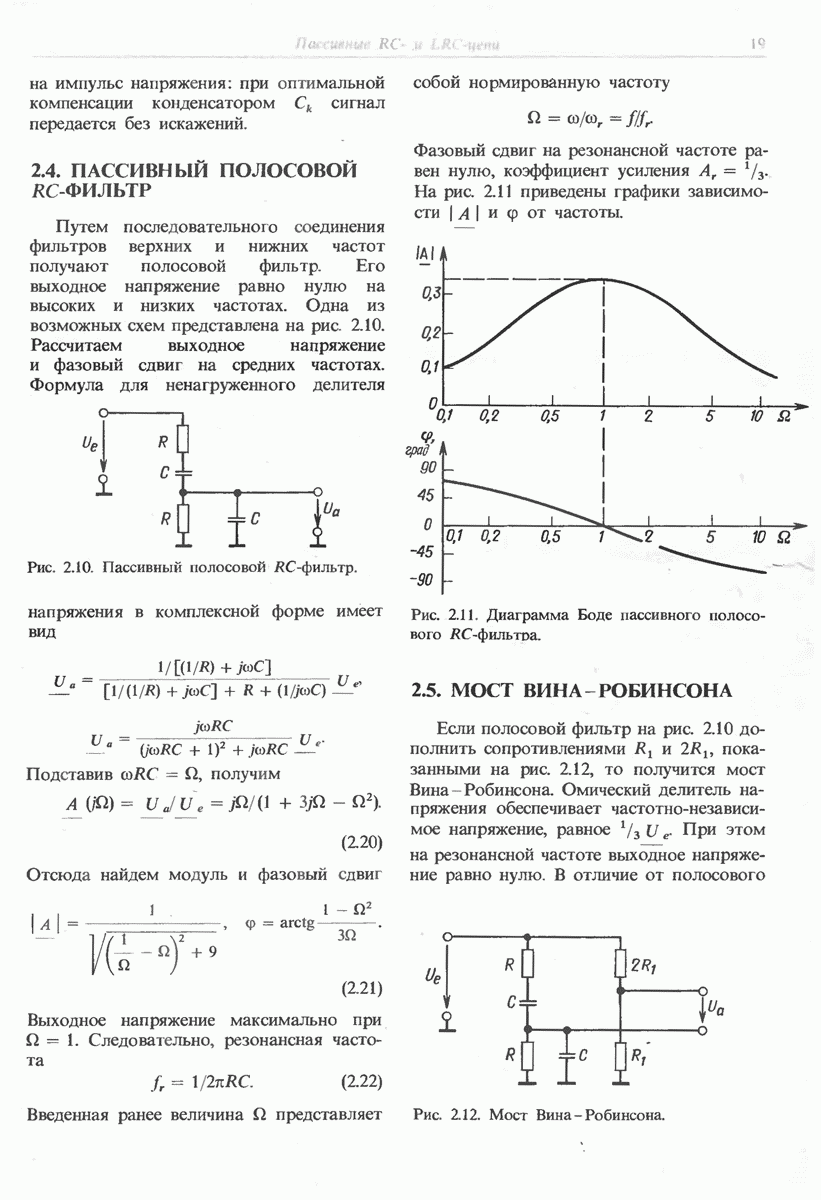
- 2.4. ПАССИВНЫЙ ПОЛОСОВОЙ RC-ФИЛЬТР
- 2.5. МОСТ ВИНА-РОБИНСОНА
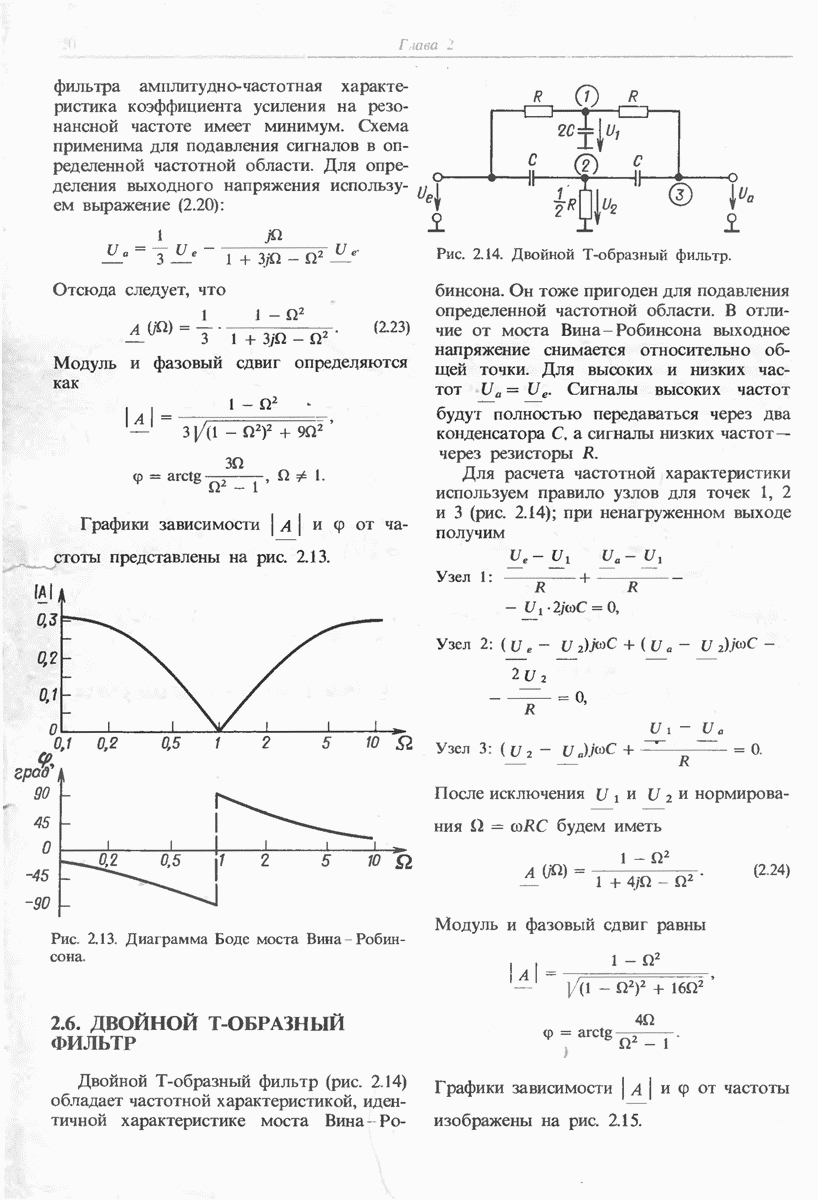
- 2.6. ДВОЙНОЙ Т-ОБРАЗНЫЙ ФИЛЬТР
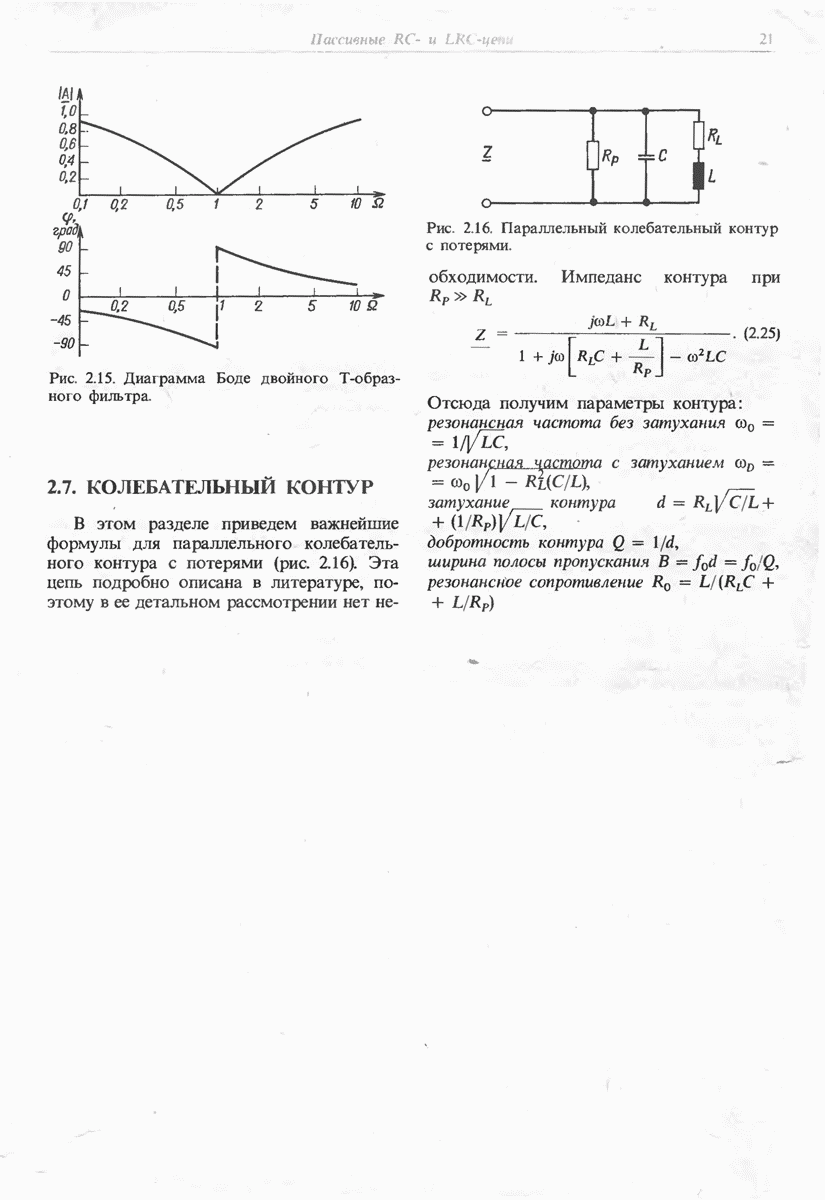
- 2.7. КОЛЕБАТЕЛЬНЫЙ КОНТУР
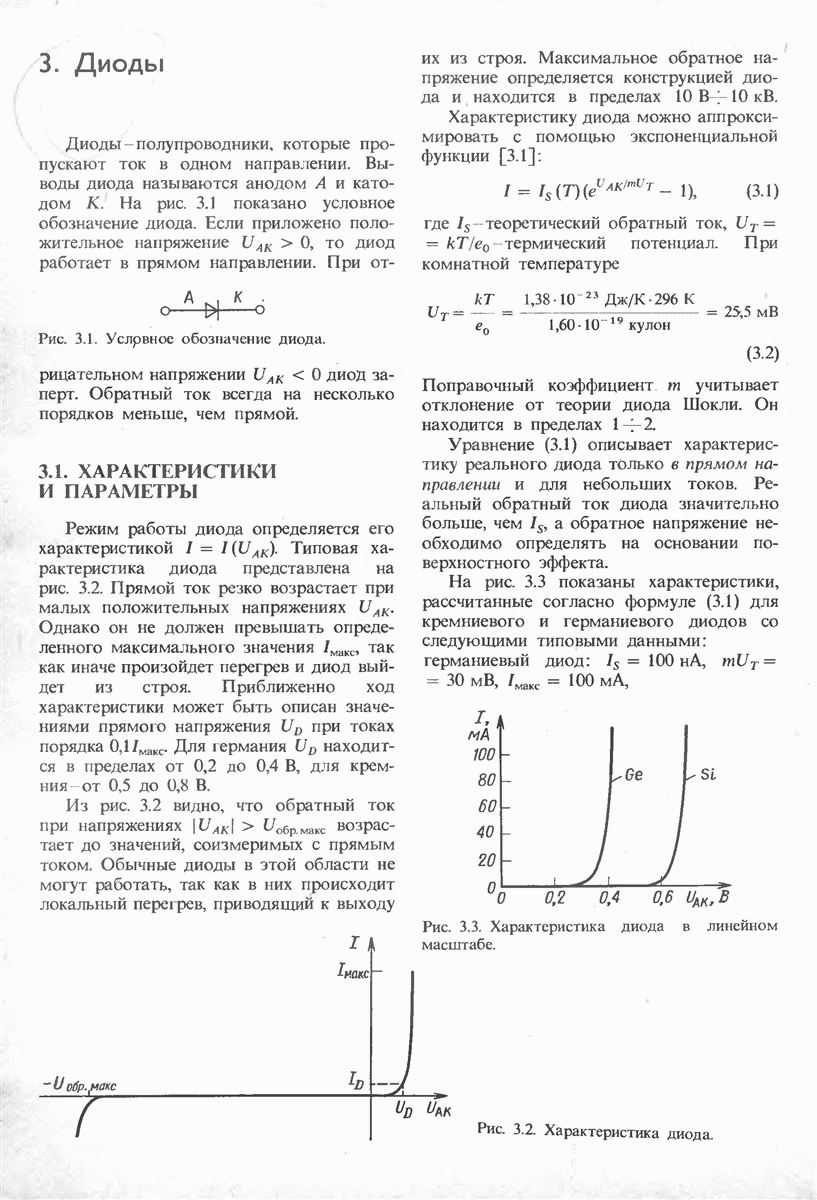
- 3. Диоды
- 3.2. СТАБИЛИТРОНЫ
- 3.3. ВАРИКАПЫ
- 4. Транзистор и схемы на его основе
- 4.2. СХЕМА С ОБЩИМ ЭМИТТЕРОМ
- 4.2.2. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 4.2.3. СХЕМА С ОБЩИМ ЭМИТТЕРОМ И ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.2.4. ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ ПО НАПРЯЖЕНИЮ
- 4.2.5. УСТАНОВКА РАБОЧЕЙ ТОЧКИ
- 4.3. СХЕМА С ОБЩЕЙ БАЗОЙ
- 4.4. СХЕМА С ОБЩИМ КОЛЛЕКТОРОМ, ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 4.5. ТРАНЗИСТОР КАК ИСТОЧНИК СТАБИЛЬНОГО ТОКА
- 4.5.2. БИПОЛЯРНЫЙ ИСТОЧНИК ПИТАНИЯ
- 4.5.3. СХЕМА «ТОКОВОГО ЗЕРКАЛА»
- 4.6. СХЕМА ДАРЛИНГТОНА
- 4.7. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛИ
- 4.7.2. РЕЖИМ БОЛЬШОГО СИГНАЛА
- 4.7.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.7.4. НАПРЯЖЕНИЕ РАЗБАЛАНСА
- 4.8. ИЗМЕРЕНИЕ НЕКОТОРЫХ ПАРАМЕТРОВ ПРИ МАЛОМ СИГНАЛЕ
- 4.9. ШУМЫ ТРАНЗИСТОРА
- 4.10. ПРЕДЕЛЬНЫЕ ПАРАМЕТРЫ
- 5. Полевые транзисторы
- 5.2. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ МАЛЫХ СИГНАЛОВ
- 5.3. ПРЕДЕЛЬНЫЕ ЭЛЕКТРИЧЕСКИЕ ПАРАМЕТРЫ
- 5.4. ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ
- 5.4.1. СХЕМА С ОБЩИМ ИСТОКОМ
- 5.4.2. СХЕМА С ОБЩИМ ЗАТВОРОМ
- 5.4.3. СХЕМА С ОБЩИМ СТОКОМ, ИСТОКОВЫЙ ПОВТОРИТЕЛЬ
- 5.5. ПОЛЕВОЙ ТРАНЗИСТОР КАК СТАБИЛИЗАТОР ТОКА
- 5.6. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- 5.7. ПОЛЕВОЙ ТРАНЗИСТОР В КАЧЕСТВЕ УПРАВЛЯЕМОГО СОПРОТИВЛЕНИЯ
- 6. Операционный усилитель
- 6.1. СВОЙСТВА ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 6.2. ПРИНЦИП ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ
- 6.3. НЕИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 6.4. ИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 7. Внутренняя структура операционных усилителей
- 7.2. ПРОСТЕЙШИЕ СХЕМЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 7.3. СТАНДАРТНАЯ СХЕМА ИНТЕГРАЛЬНОГО ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 7.4. КОРРЕКЦИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
- 7.4.2. ПОЛНАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
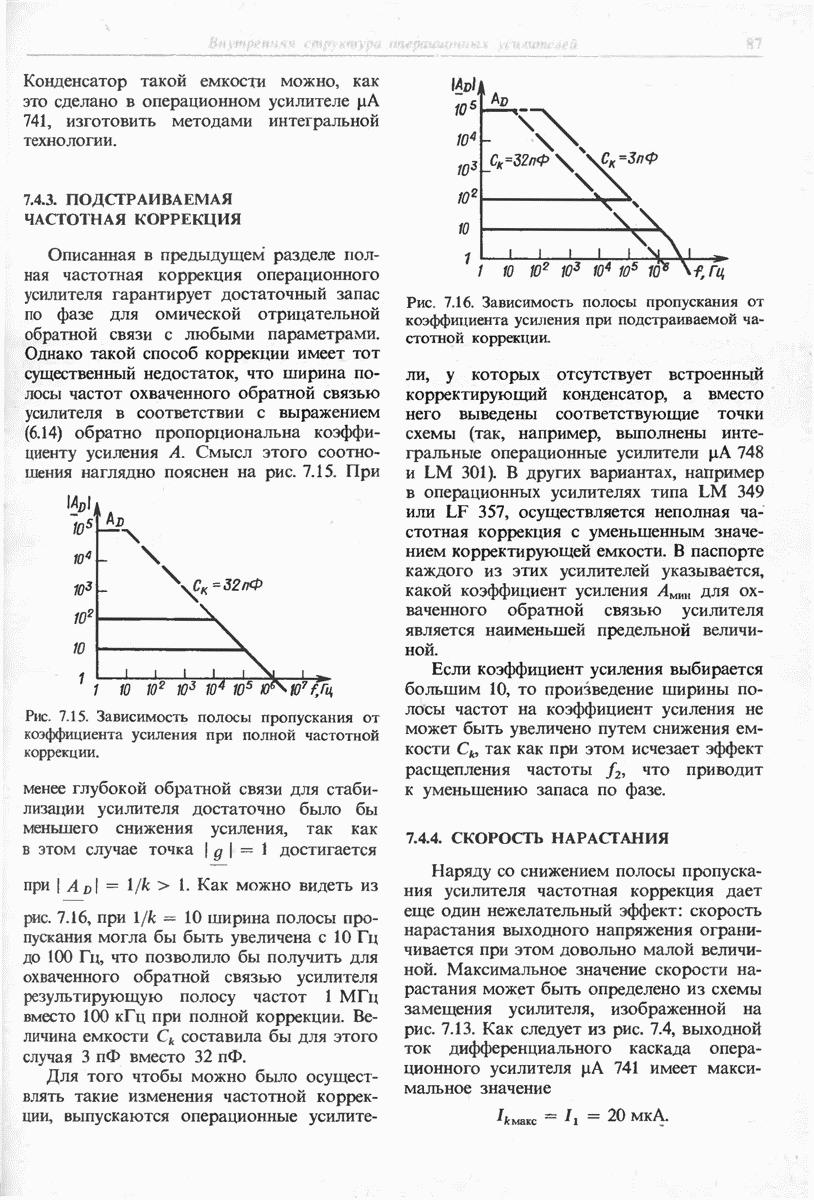
- 7.4.3. ПОДСТРАИВАЕМАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
- 7.4.4. СКОРОСТЬ НАРАСТАНИЯ
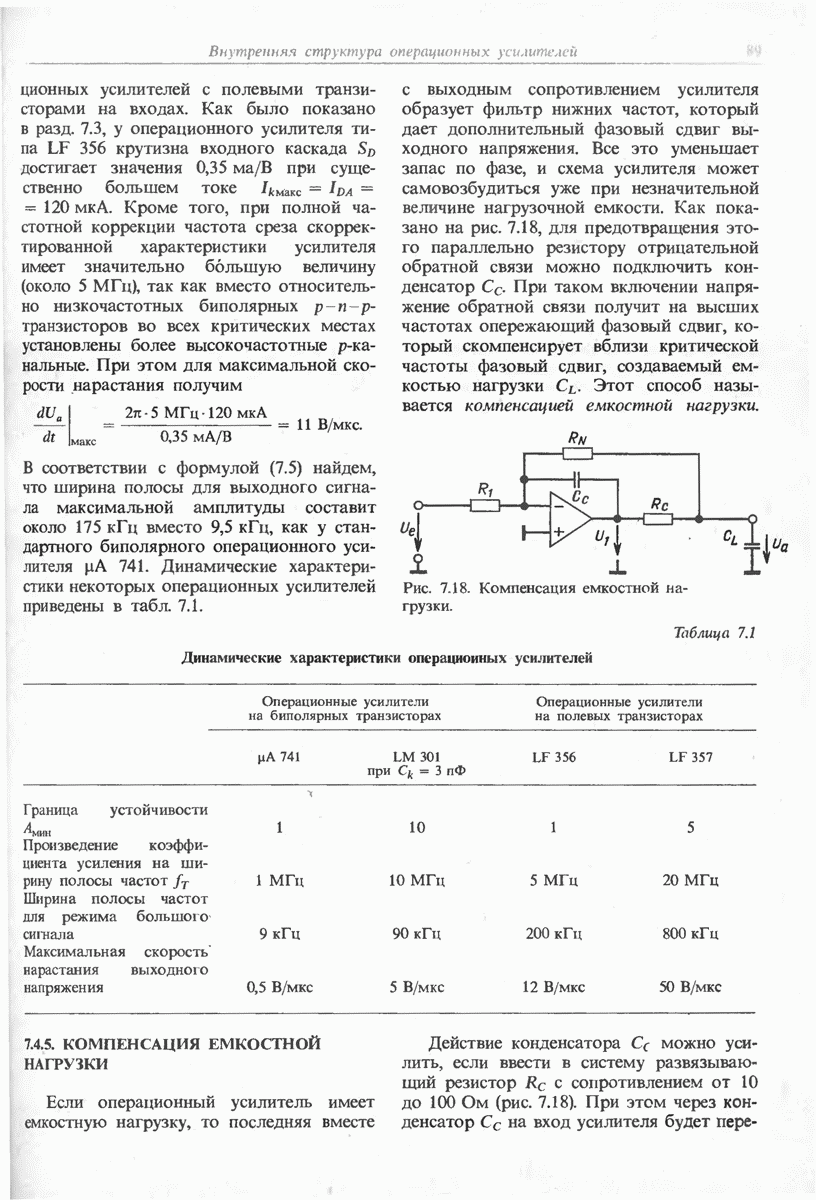
- 7.4.5. КОМПЕНСАЦИЯ ЕМКОСТНОЙ НАГРУЗКИ
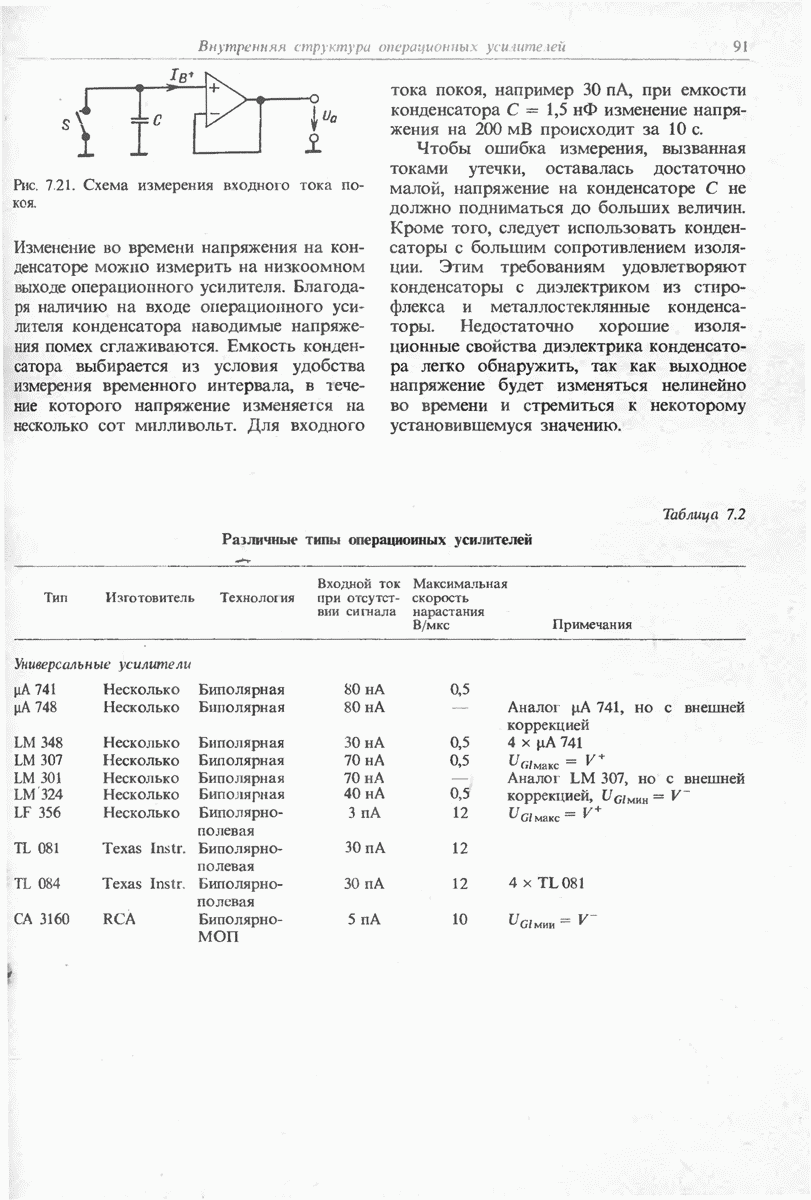
- 7.5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 8. Простейшие переключающие схемы
- 8.1. ТРАНЗИСТОРНЫЙ КЛЮЧ
- 8.2. БИСТАБИЛЬНЫЕ РЕЛАКСАЦИОННЫЕ СХЕМЫ
- 8.2.2. ТРИГГЕР ШМИТТА
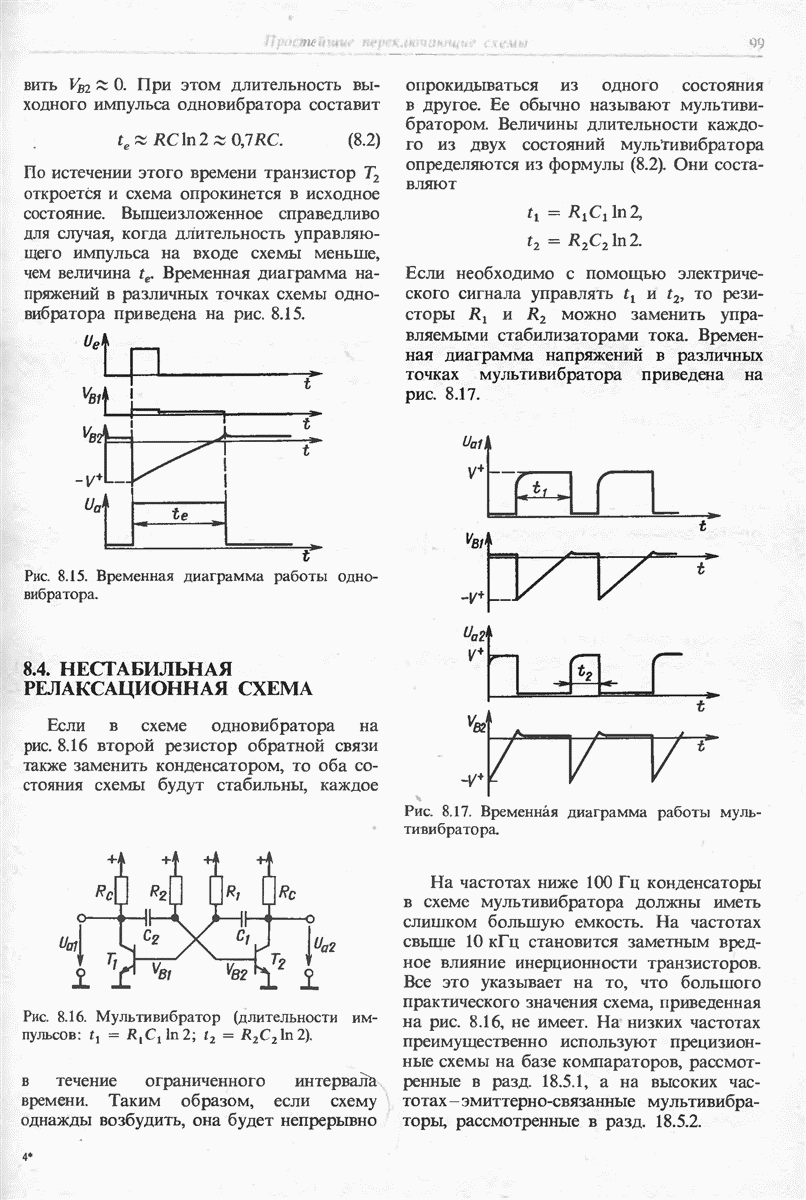
- 8.3. МОНОСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
- 8.4. НЕСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
- 9. Базовые логические схемы
- 9.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
- 9.2. СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.2.1. ТАБЛИЦА КАРНО
- 9.3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4.1. РЕЗИСТИВНО-ТРАНЗИСТОРНАЯ ЛОГИКА (РТЛ)
- 9.4.2. ДИОДНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ДТЛ)
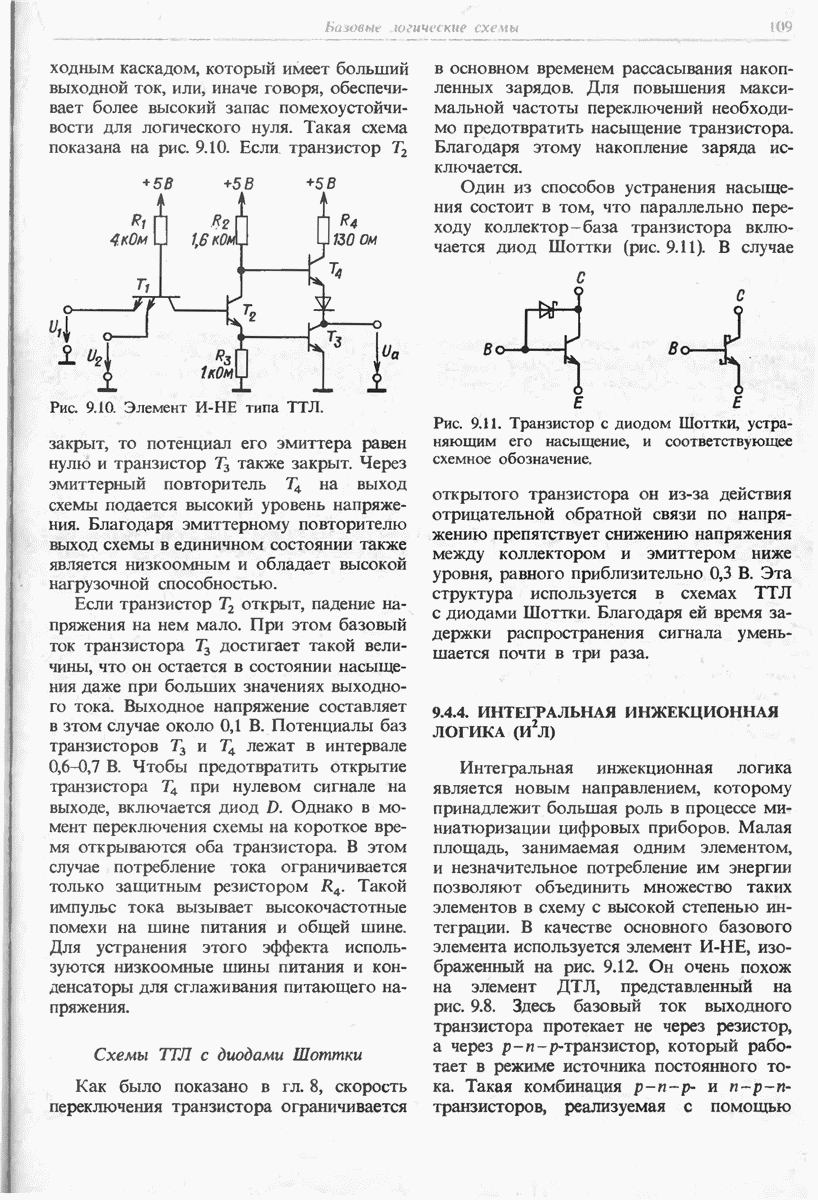
- 9.4.3. ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ТТЛ)
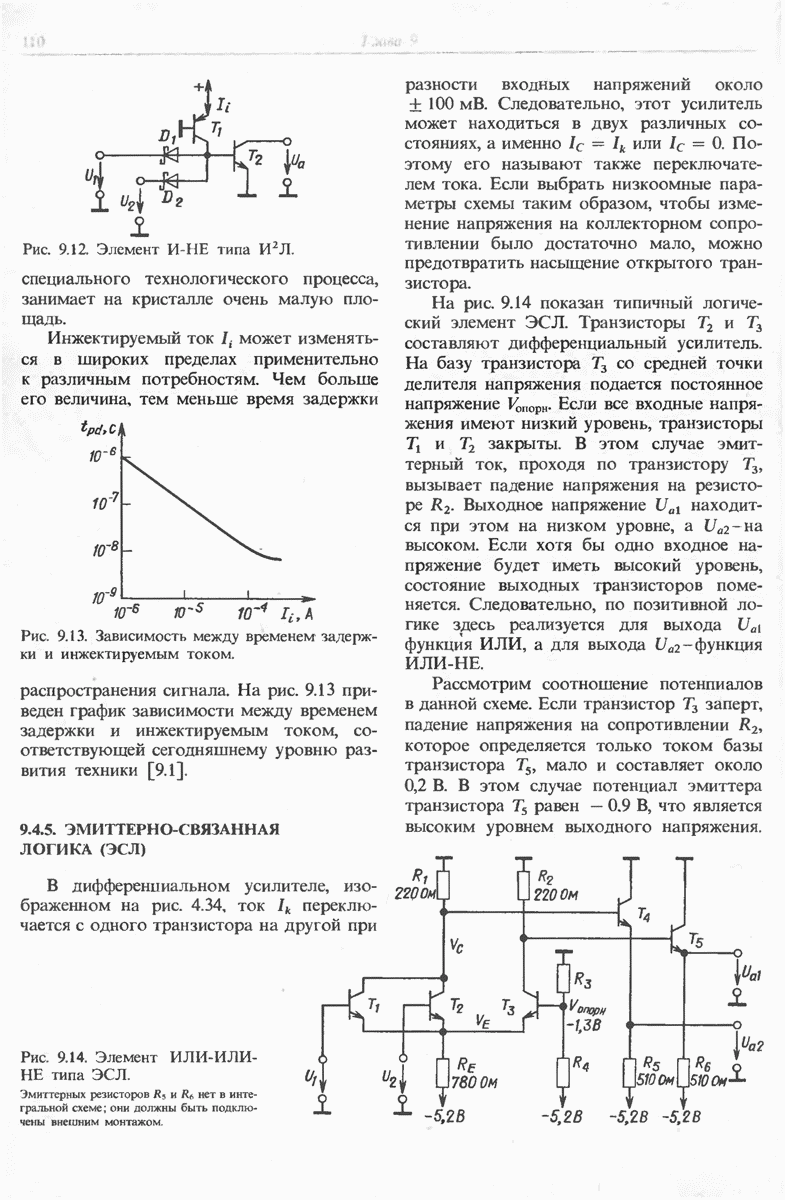
- 9.4.4. ИНТЕГРАЛЬНАЯ ИНЖЕКЦИОННАЯ ЛОГИКА
- 9.4.5. ЭМИТТЕРНО-СВЯЗАННАЯ ЛОГИКА (ЭСЛ)
- 9.4.6. n-КАНАЛЬНАЯ МОП-ЛОГИКА
- 9.4.7. КОМПЛЕМЕНТАРНАЯ МОП-ЛОГИКА (КМОП)
- 9.4.8. ОБЗОР
- 9.4.9. СПЕЦИАЛЬНЫЕ СХЕМЫ ВЫХОДНЫХ КАСКАДОВ
- 9.5. ИНТЕГРАЛЬНЫЕ ТРИГГЕРЫ
- 9.5.2. ТРИГГЕРЫ ТИПА M-S (MASTER-SLAVE)
- 9.5.3. ДИНАМИЧЕСКИЙ ТРИГГЕР
- 9.6. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 9.6.2. ПОСТОЯННЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА (ПЗУ)
- 9.6.3. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ (ПЛМ)
- 10. Оптоэлектронные приборы
- 10.1. ОСНОВНЫЕ ПОНЯТИЯ ФОТОМЕТРИИ
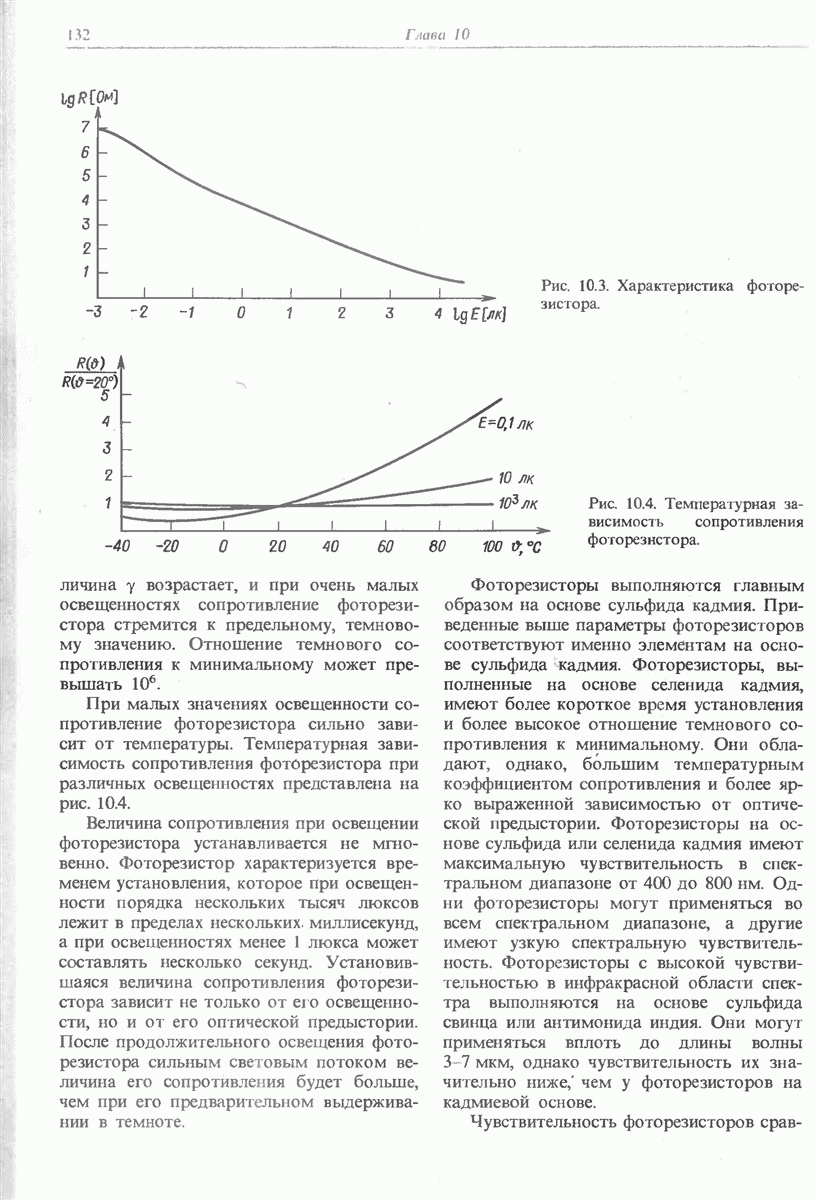
- 10.2. ФОТОРЕЗИСТОР
- 10.3. ФОТОДИОДЫ
- 10.4. ФОТОТРАНЗИСТОРЫ
- 10.5. СВЕТОДИОДЫ
- 10.6. ОПТРОНЫ
- Часть II. Применения
- 11. Линейные и нелинейные аналоговые вычислительные схемы
- 11.1. СХЕМА СУММИРОВАНИЯ
- 11.2. СХЕМЫ ВЫЧИТАНИЯ
- 11.2.2. СХЕМА ВЫЧИТАНИЯ НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 11.3. БИПОЛЯРНОЕ УСИЛИТЕЛЬНОЕ ЗВЕНО
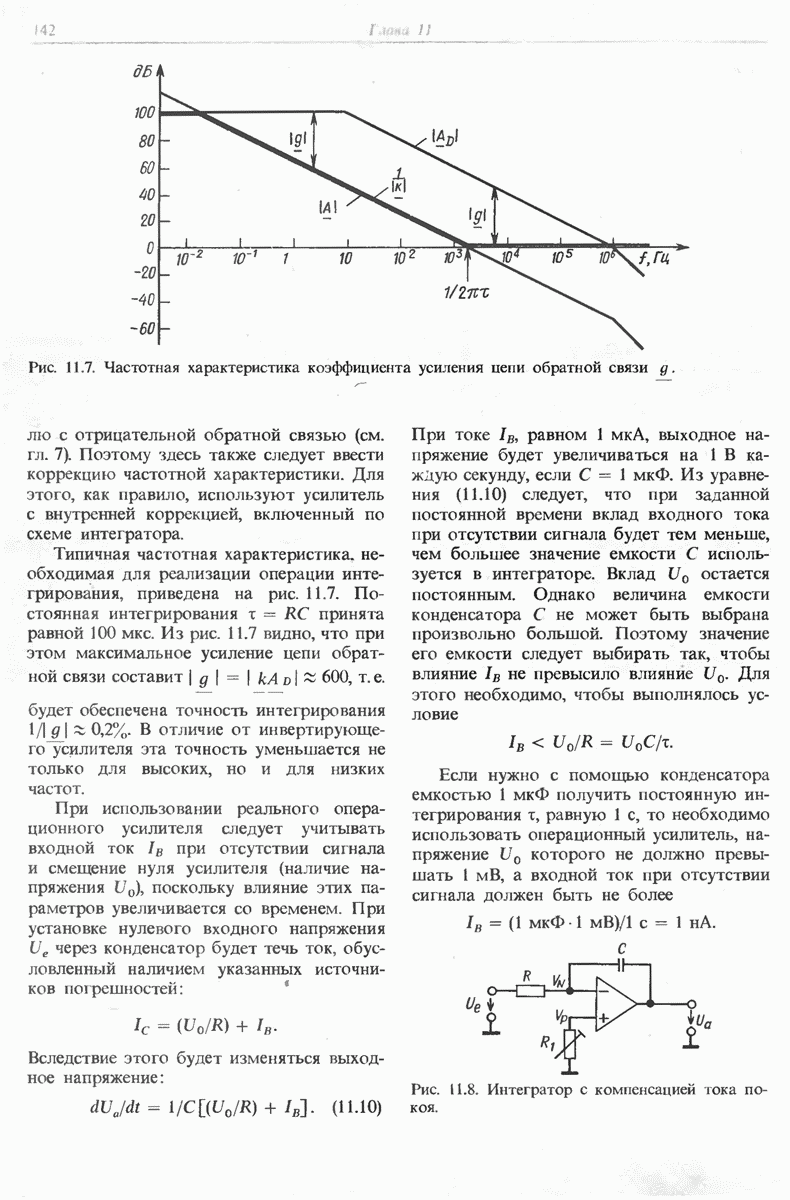
- 11.4. СХЕМЫ ИНТЕГРИРОВАНИЯ
- 11.4.1. ИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.2. ЗАДАНИЕ НАЧАЛЬНЫХ УСЛОВИЙ
- 11.4.3. СУММИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.4. НЕИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
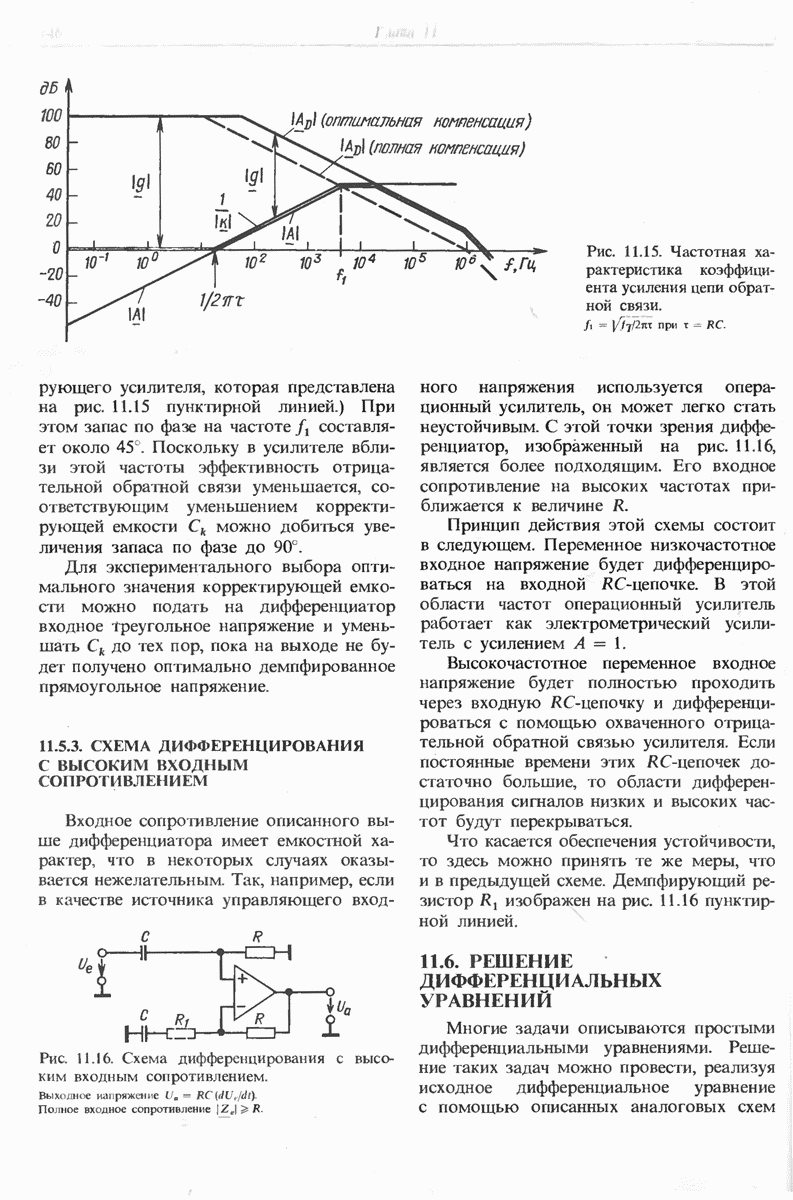
- 11.5. СХЕМЫ ДИФФЕРЕНЦИРОВАНИЯ
- 11.5.3. СХЕМА ДИФФЕРЕНЦИРОВАНИЯ С ВЫСОКИМ ВХОДНЫМ СОПРОТИВЛЕНИЕМ
- 11.6. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 11.7. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11.7.2. ЭКСПОНЕНТА
- 11.7.3. ВЫЧИСЛЕНИЕ СТЕПЕННЫХ ФУНКЦИЙ С ПОМОЩЬЮ ЛОГАРИФМОВ
- 11.7.4. ФУНКЦИИ SIN X И COS X
- 11.7.5. ПЕРЕСТРАИВАЕМЫЕ ФУНКЦИОНАЛЬНЫЕ СХЕМЫ
- 11.8. АНАЛОГОВЫЕ СХЕМЫ УМНОЖЕНИЯ
- 11.8.2. УМНОЖЕНИЕ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ ФУНКЦИОНАЛЬНЫХ ГЕНЕРАТОРОВ
- 11.8.3. СХЕМА УМНОЖЕНИЯ, ИСПОЛЬЗУЮЩАЯ ИЗМЕНЕНИЕ КРУТИЗНЫ ХАРАКТЕРИСТИКИ ТРАНЗИСТОРОВ
- 11.8.4. СХЕМА УМНОЖЕНИЯ С ИЗОЛИРОВАННЫМИ ЗВЕНЬЯМИ
- 11.8.5. БАЛАНСИРОВКА СХЕМ УМНОЖЕНИЯ
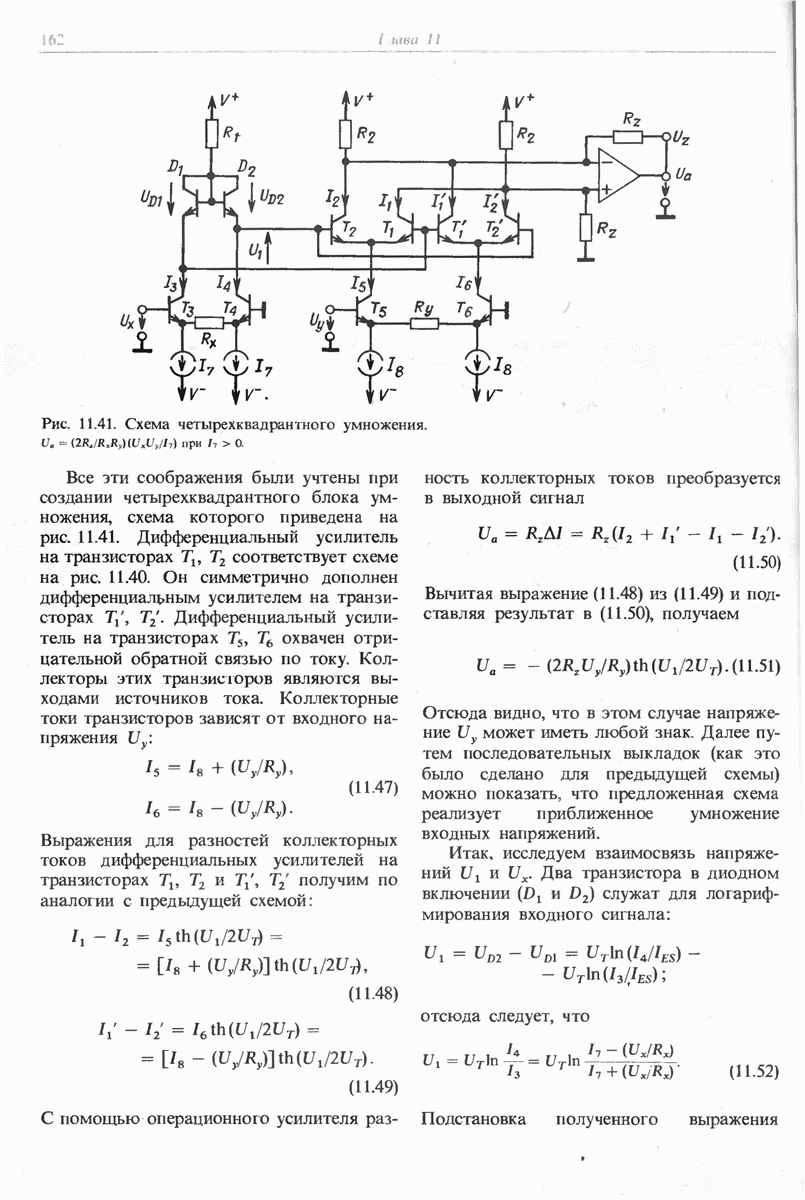
- 11.8.6. СХЕМЫ ЧЕТЫРЕХКВАДРАНТНОГО УМНОЖЕНИЯ
- 11.8.7. ПРИМЕНЕНИЕ СХЕМЫ УМНОЖЕНИЯ ДЛЯ ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- 11.9. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 11.9.2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ КООРДИНАТ В ПОЛЯРНЫЕ
- 12. Управляемые источники и схемы преобразования полного сопротивления
- 12.1. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.2. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ ТОКОМ
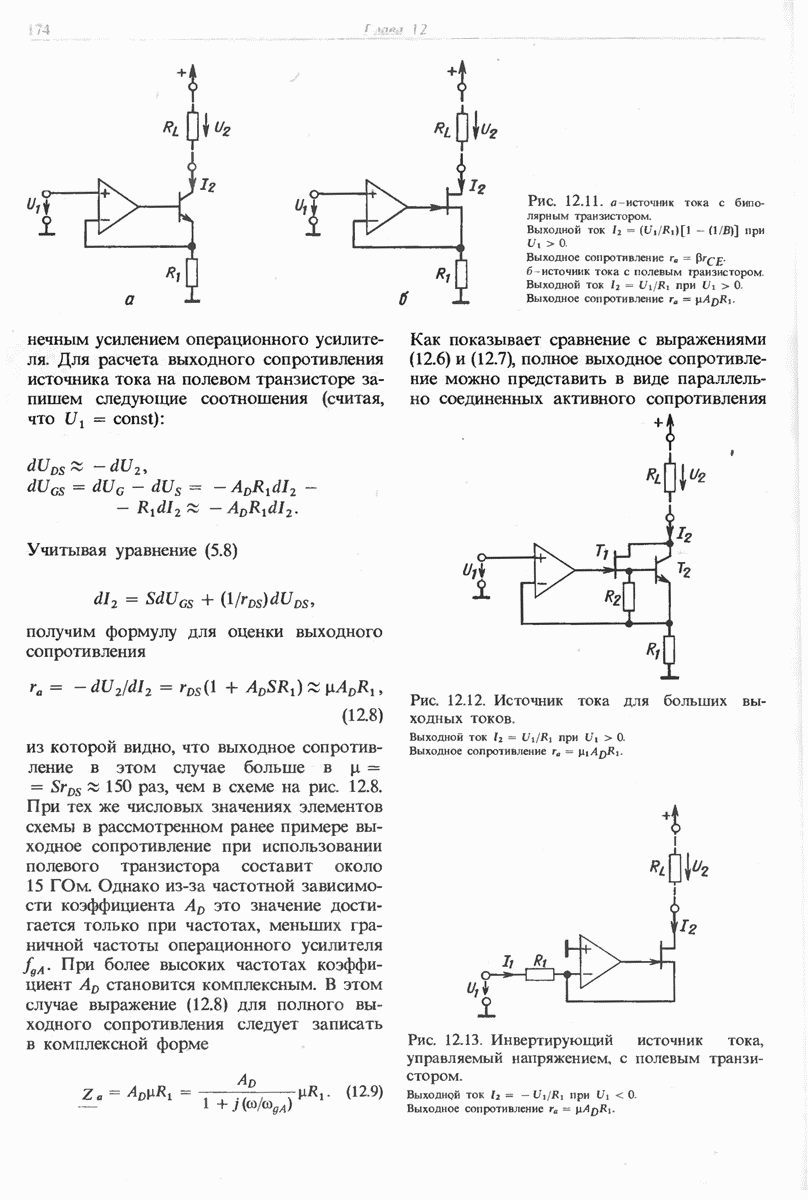
- 12.3. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.3.2. ИСТОЧНИКИ ТОКА С ЗАЗЕМЛЕННОЙ НАГРУЗКОЙ
- 12.3.3. ЭТАЛОННЫЕ ИСТОЧНИКИ ТОКА НА ТРАНЗИСТОРАХ
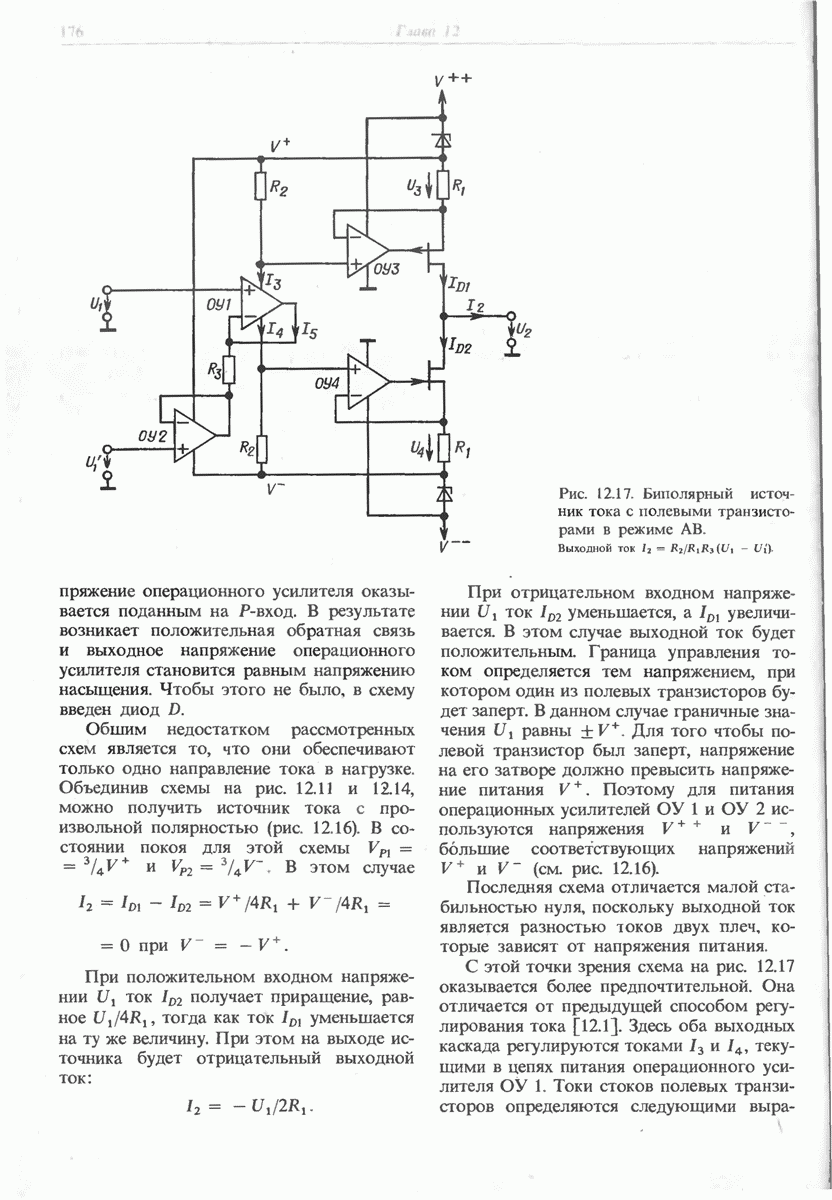
- 12.3.4. ПЛАВАЮЩИЕ ИСТОЧНИКИ ТОКА
- 12.4. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ ТОКОМ
- 12.5. ПРЕОБРАЗОВАТЕЛЬ ОТРИЦАТЕЛЬНОГО СОПРОТИВЛЕНИЯ (NIC)
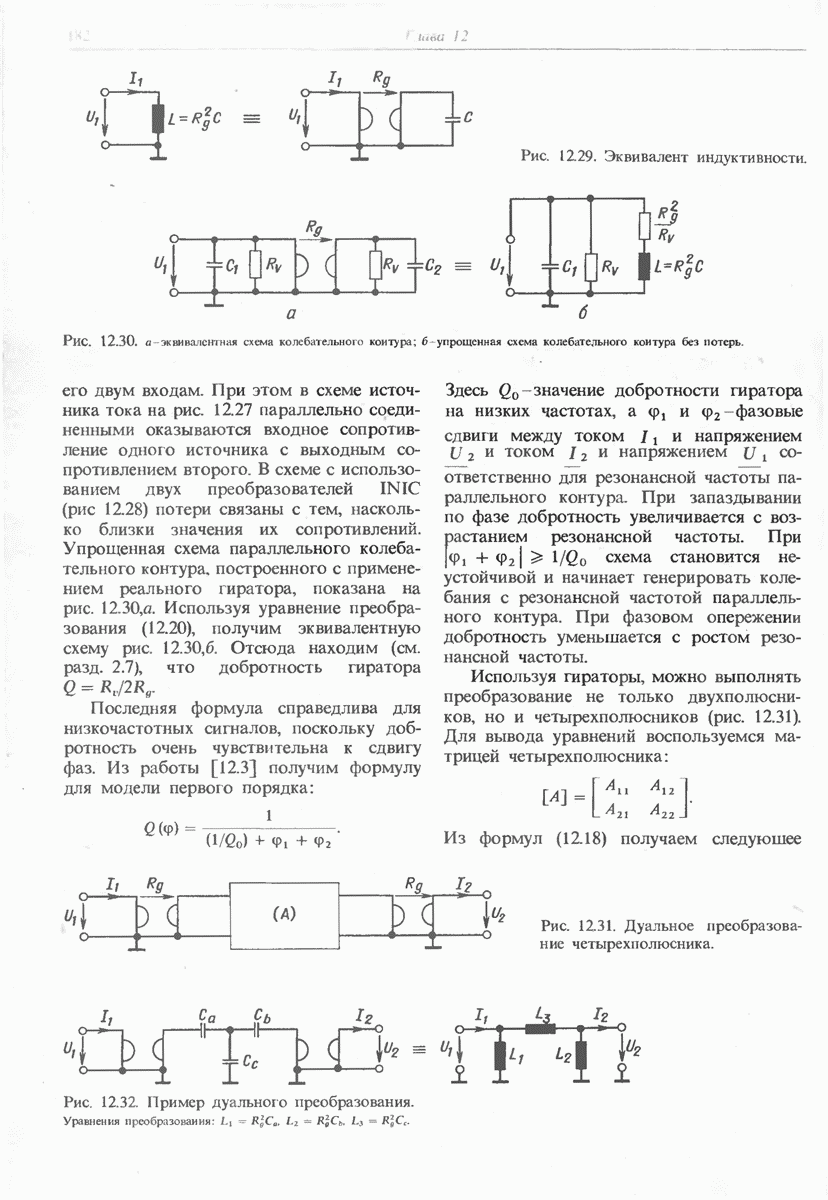
- 12.6. ГИРАТОР
- 12.7. ЦИРКУЛЯТОР
- 13. Активные фильтры
- 13.1. ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
- 13.1.1. ФИЛЬТР БАТТЕРВОРТА
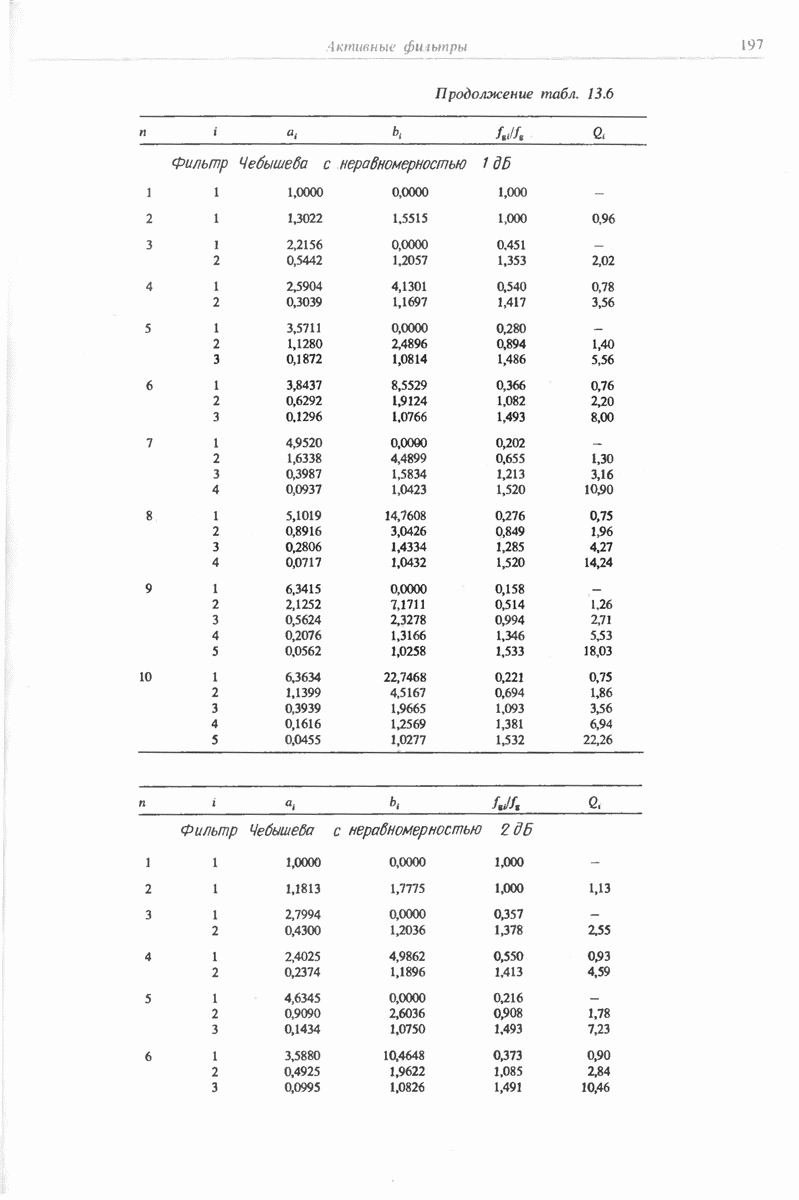
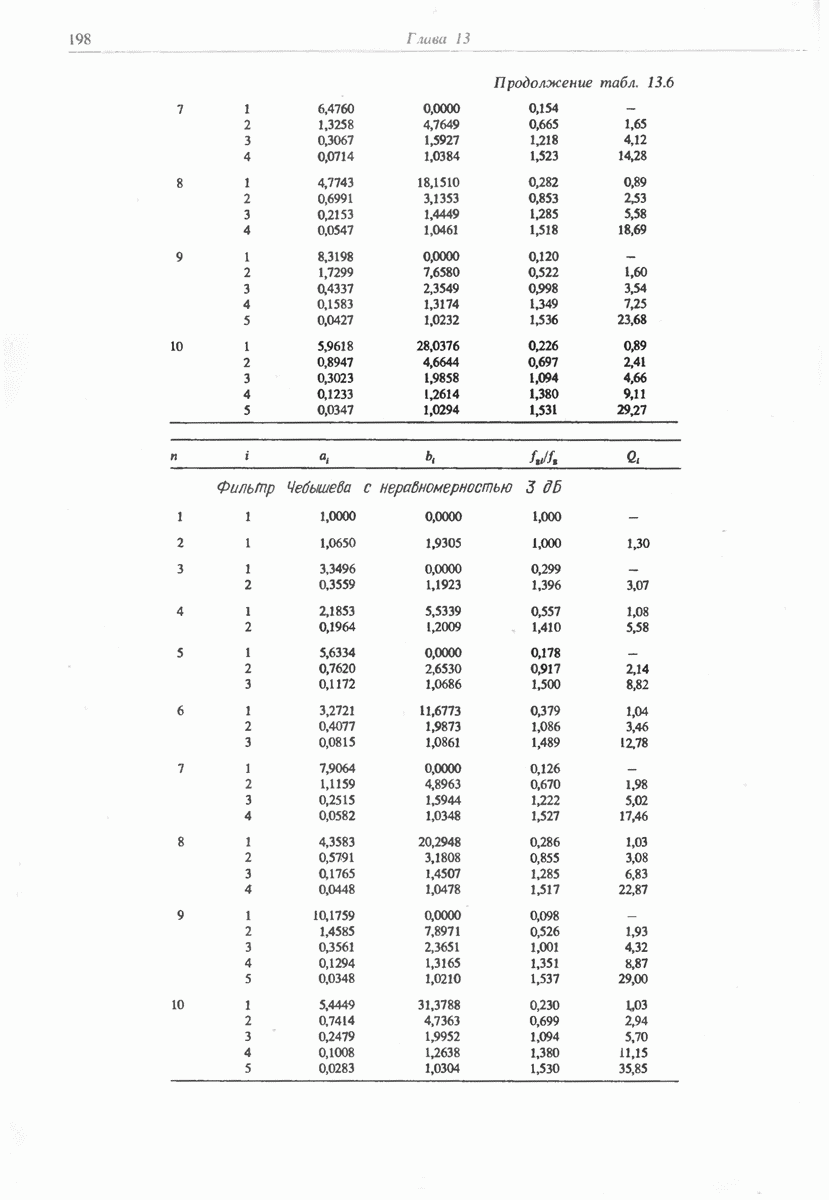
- 13.1.2. ФИЛЬТР ЧЕБЫШЕВА
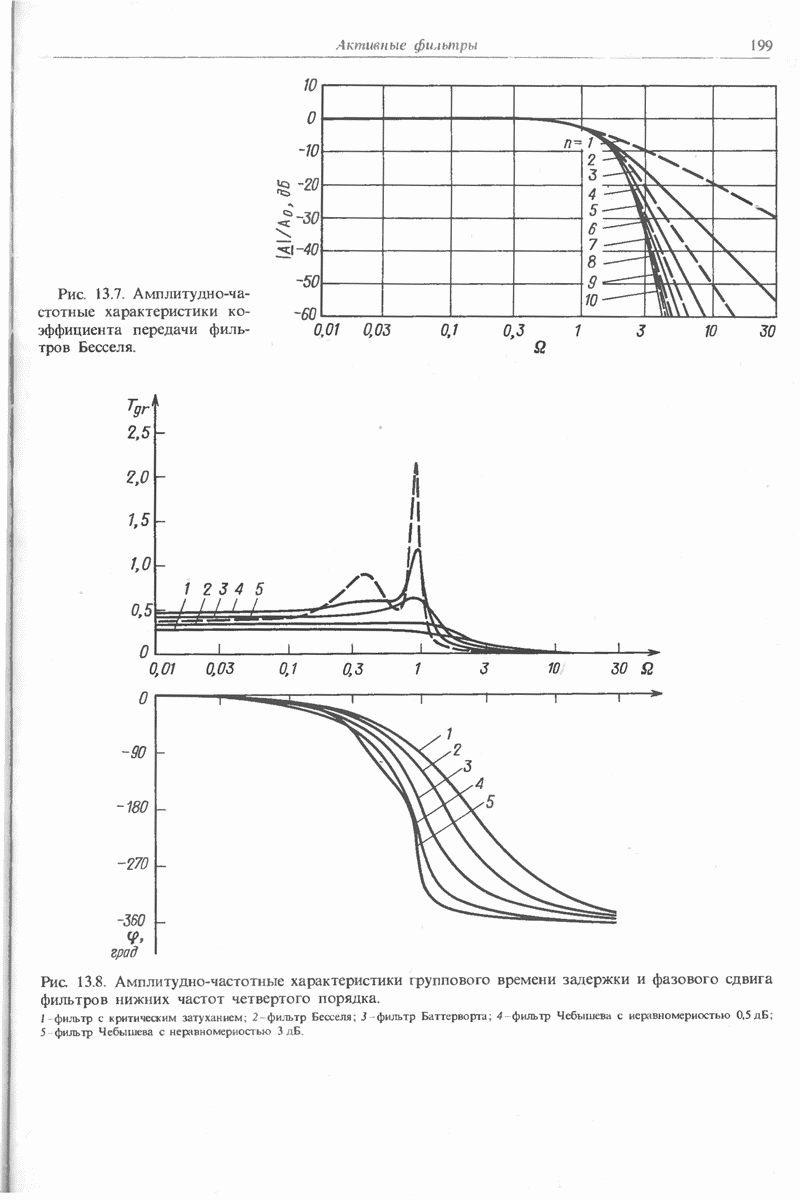
- 13.1.3. ФИЛЬТРЫ БЕССЕЛЯ
- 13.1.4. ОБОБЩЕННОЕ ОПИСАНИЕ ФИЛЬТРОВ
- 13.2. ПРЕОБРАЗОВАНИЕ НИЖНИХ ЧАСТОТ В ВЕРХНИЕ
- 13.3. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ПЕРВОГО ПОРЯДКА
- 13.4. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ВТОРОГО ПОРЯДКА
- 13.4.2. ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.3. ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.4. ФИЛЬТР НИЖНИХ ЧАСТОТ С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.5. РЕАЛИЗАЦИЯ ФИЛЬТРОВ ВЕРХНИХ И НИЖНИХ ЧАСТОТ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
- 13.6. ПРЕОБРАЗОВАНИЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ В ПОЛОСОВОЙ ФИЛЬТР
- 13.6.1. ПОЛОСОВОЙ ФИЛЬТР ВТОРОГО ПОРЯДКА
- 13.6.2. ПОЛОСОВОЙ ФИЛЬТР ЧЕТВЕРТОГО ПОРЯДКА
- 13.7. РЕАЛИЗАЦИЯ ПОЛОСОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.7.2. ПОЛОСОВОЙ ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.3. ПОЛОСОВОЙ ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.4. ПОЛОСОВОЙ ФИЛЬТР С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.8. ПРЕОБРАЗОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ В ЗАГРАЖДАЮЩИЕ ПОЛОСОВЫЕ ФИЛЬТРЫ
- 13.9. РЕАЛИЗАЦИЯ ЗАГРАЖДАЮЩИХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.9.1. ЗАГРАЖДАЮЩИЙ LRC-ФИЛЬТР
- 13.9.2. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С ДВОЙНЫМ Т-ОБРАЗНЫМ МОСТОМ
- 13.9.3. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С МОСТОМ ВИНА-РОБИНСОНА
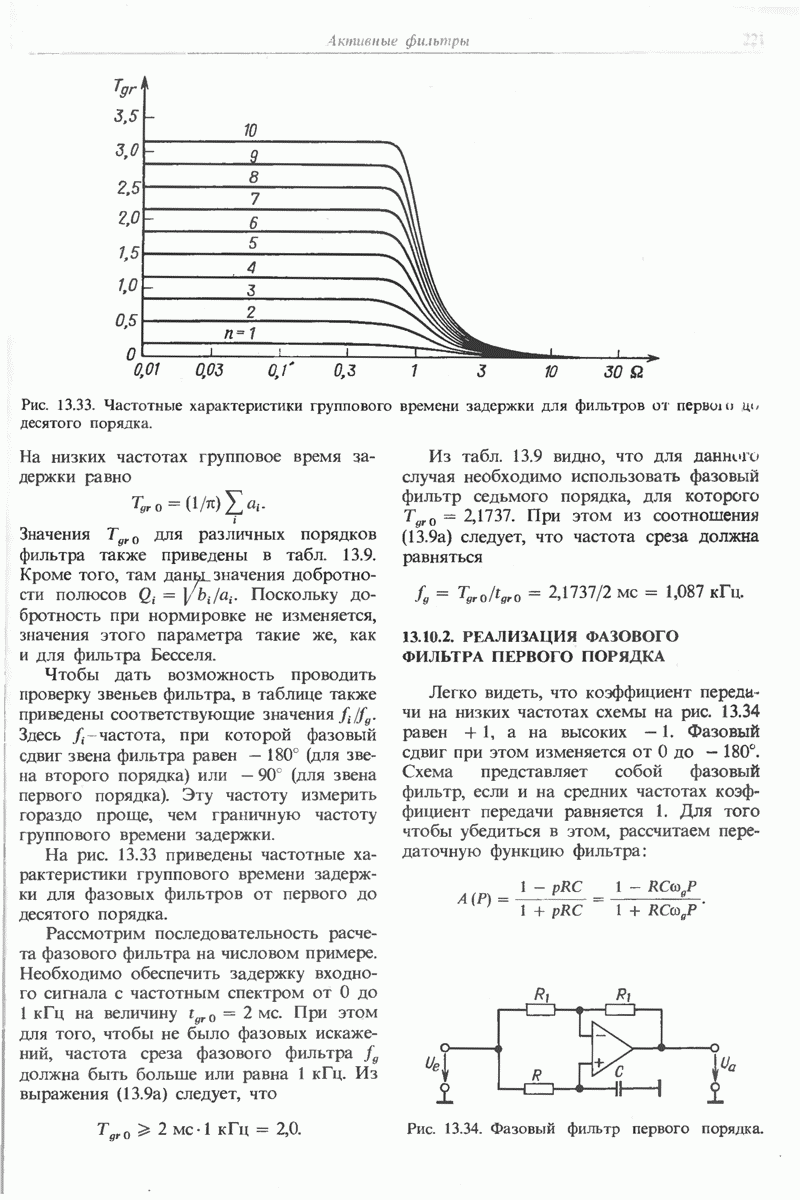
- 13.10. ФАЗОВЫЙ ФИЛЬТР
- 13.10.2. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ПЕРВОГО ПОРЯДКА
- 13.10.3. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ВТОРОГО ПОРЯДКА
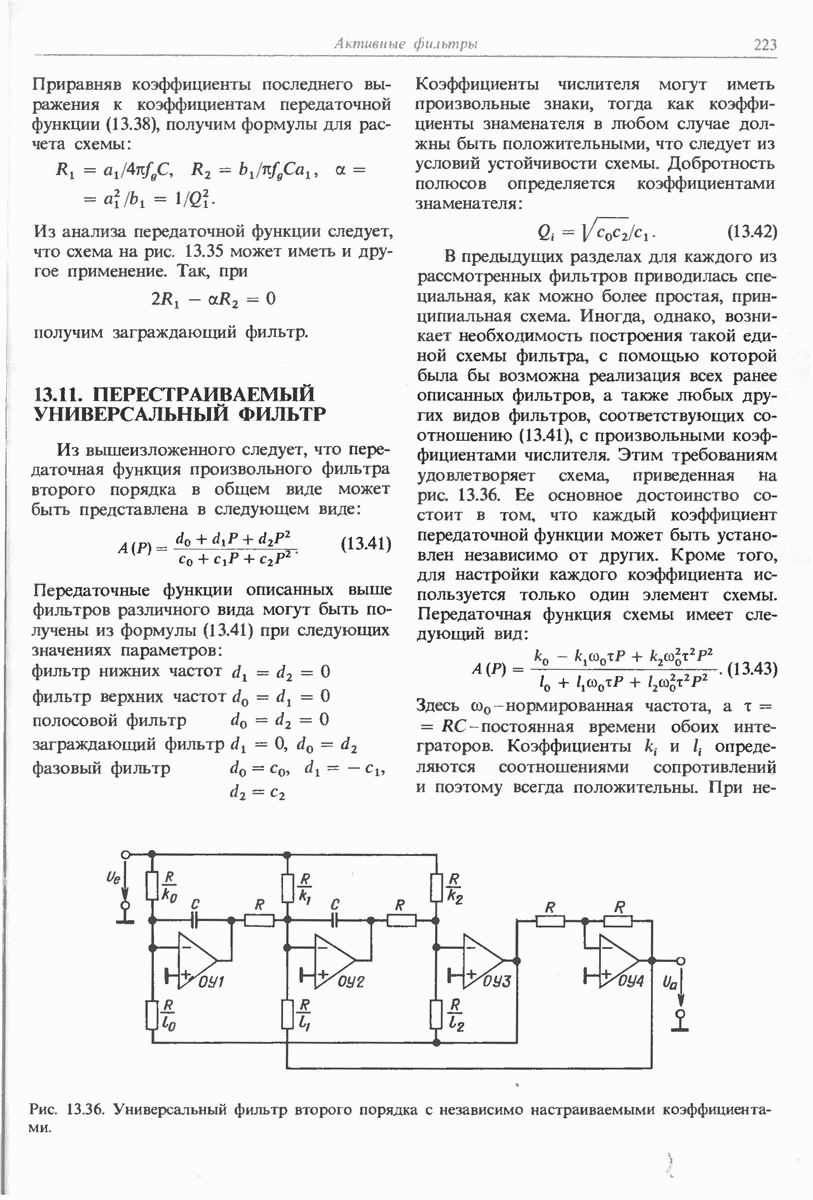
- 13.11. ПЕРЕСТРАИВАЕМЫЙ УНИВЕРСАЛЬНЫЙ ФИЛЬТР
- 14. Широкополосные усилители
- 14.1. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА УСИЛЕНИЯ ПО ТОКУ ОТ ЧАСТОТЫ
- 14.2. ВЛИЯНИЕ ВНУТРЕННИХ ЕМКОСТЕЙ ТРАНЗИСТОРА И ЕМКОСТЕЙ МОНТАЖА
- 14.3. КАСКОДНАЯ СХЕМА
- 14.4. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ КАК ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5. СИММЕТРИЧНЫЙ ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5.2. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ИНВЕРТОРОМ
- 14.5.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С КОМПЛЕМЕНТАРНОЙ КАСКОДНОЙ СХЕМОЙ
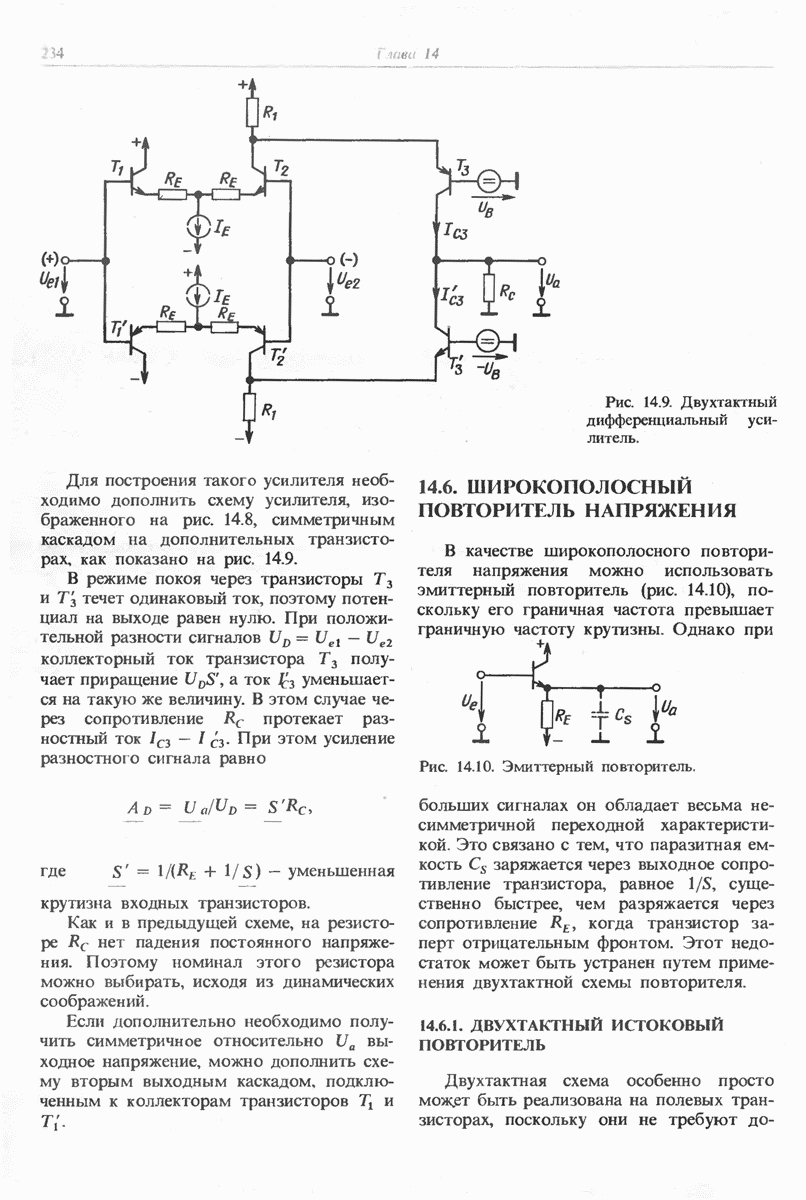
- 14.5.4. ДВУХТАКТНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ
- 14.6. ШИРОКОПОЛОСНЫЙ ПОВТОРИТЕЛЬ НАПРЯЖЕНИЯ
- 14.6.2. ДВУХТАКТНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
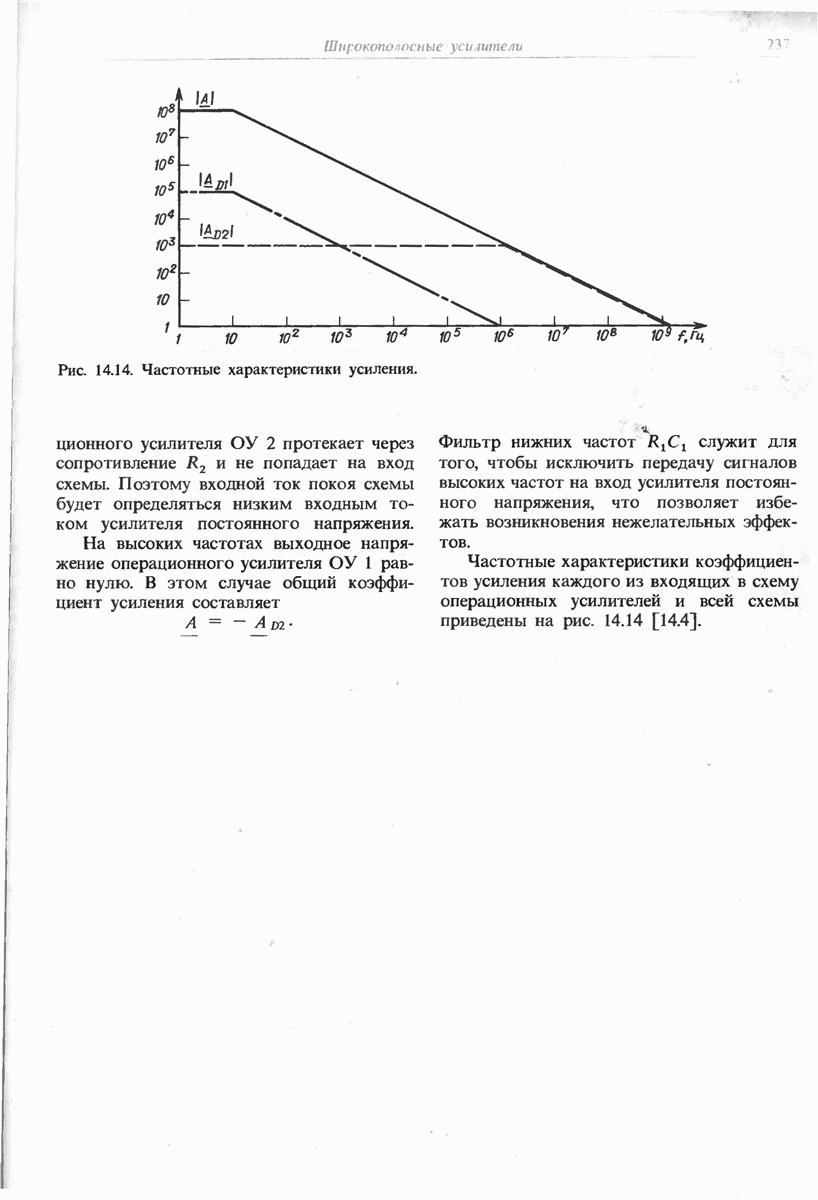
- 14.7. ШИРОКОПОЛОСНЫЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 15. Усилители мощности
- 15.1. ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ КАК УСИЛИТЕЛЬ МОЩНОСТИ
- 15.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 15.2.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ В РЕЖИМЕ AB
- 15.2.3. СПОСОБЫ ЗАДАНИЯ НАПРЯЖЕНИЯ СМЕЩЕНИЯ
- 15.3. СХЕМЫ ОГРАНИЧЕНИЯ ТОКА
- 15.4. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ ПО СХЕМЕ ДАРЛИНГТОНА
- 15.5. РАСЧЕТ МОЩНОГО ОКОНЕЧНОГО КАСКАДА
- 15.6. СХЕМЫ ПРЕДВАРИТЕЛЬНЫХ УСИЛИТЕЛЕЙ НАПРЯЖЕНИЯ
- 15.7. ПОВЫШЕНИЕ НАГРУЗОЧНОЙ СПОСОБНОСТИ ИНТЕГРАЛЬНЫХ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 16. Источники питания
- 16.1. СВОЙСТВА СЕТЕВЫХ ТРАНСФОРМАТОРОВ
- 16.2. ВЫПРЯМИТЕЛИ
- 16.2.1. ОДНОПОЛУПЕРИОДНЫЙ ВЫПРЯМИТЕЛЬ
- 16.2.2. МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 16.2.3. МОСТОВОЙ ВЫПРЯМИТЕЛЬ ДЛЯ ДВУХ СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ ВЫХОДНЫХ НАПРЯЖЕНИЙ
- 16.3. ПОСЛЕДОВАТЕЛЬНАЯ СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЯ
- 16.3.2. СХЕМА С РЕГУЛИРУЮЩИМ УСИЛИТЕЛЕМ
- 16.3.3. ИНТЕГРАЛЬНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 16.3.4. СТАБИЛИЗАТОР С МАЛЫМ НАПРЯЖЕНИЕМ ПОТЕРЬ
- 16.3.5. СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЙ, СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ
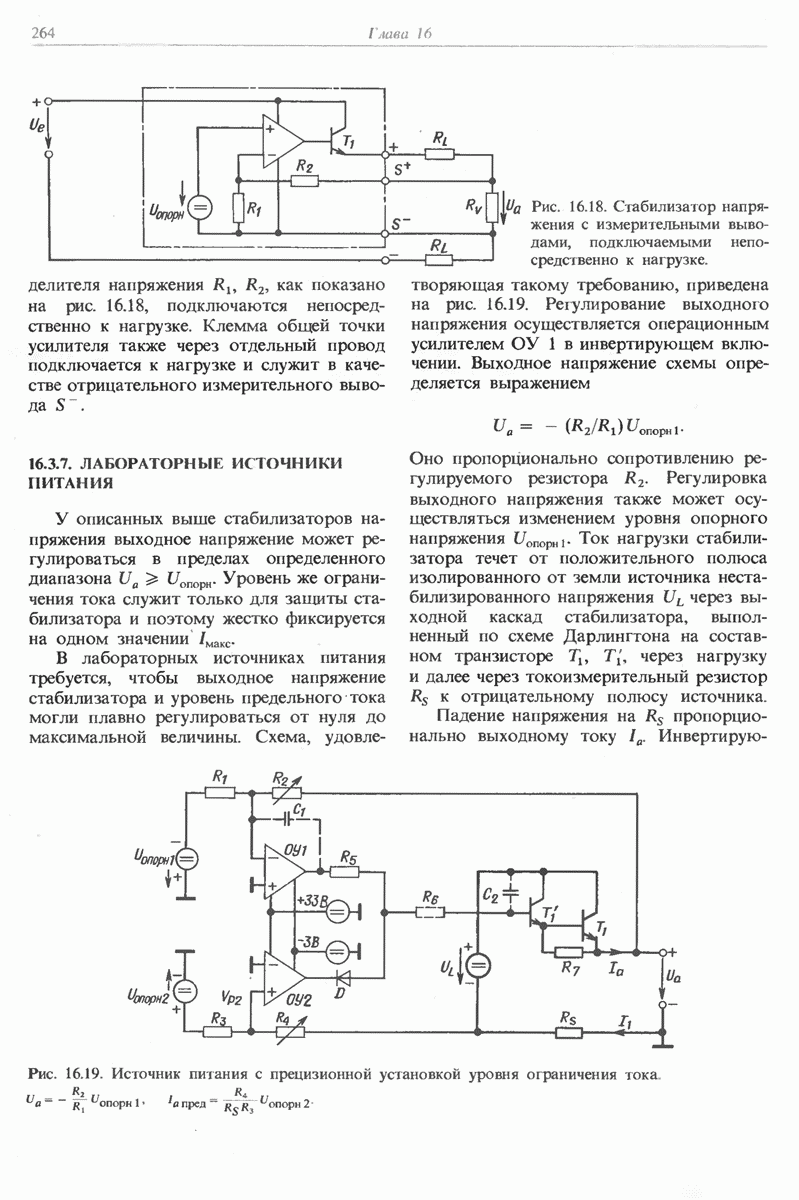
- 16.3.6. СТАБИЛИЗАТОР НАПРЯЖЕНИЯ С ИЗМЕРИТЕЛЬНЫМИ ВЫВОДАМИ
- 16.3.7. ЛАБОРАТОРНЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 16.3.8. ОКОНЕЧНЫЙ КАСКАД ЛАБОРАТОРНОГО ИСТОЧНИКА ПИТАНИЯ С БОЛЬШОЙ ВЫХОДНОЙ МОЩНОСТЬЮ
- 16.4. ПОЛУЧЕНИЕ ОПОРНОГО НАПРЯЖЕНИЯ
- 16.4.2. ПОЛУЧЕНИЕ МАЛЫХ ОПОРНЫХ НАПРЯЖЕНИЙ
- 16.5. ИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ
- 16.5.2. ПЕРВИЧНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 17. Аналоговые коммутаторы и компараторы
- 17.2. ЭЛЕКТРОННЫЕ КОММУТАТОРЫ
- 17.2.2. ДИОДНЫЙ КОММУТАТОР
- 17.2.3. КОММУТАТОР НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
- 17.3. АНАЛОГОВЫЕ КОММУТАТОРЫ НА БАЗЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 17.3.2. КОММУТАТОР НА ПОЛЕВОМ ТРАНЗИСТОРЕ С ПЕРЕМЕНОЙ ЗНАКА ВЫХОДНОГО НАПРЯЖЕНИЯ
- 17.3.3. КОММУТАТОР НА БАЗЕ ДИФФЕРЕНЦИАЛЬНОГО УСИЛИТЕЛЯ
- 17.4. АНАЛОГОВЫЕ КОММУТАТОРЫ С ПАМЯТЬЮ
- 17.5. КОМПАРАТОРЫ
- 17.5.2. КОМПАРАТОР С ПРЕЦИЗИОННЫМ ВЫХОДНЫМ НАПРЯЖЕНИЕМ
- 17.5.3. ДВУХПОРОГОВЫЙ КОМПАРАТОР
- 17.6. ТРИГГЕР ШМИТТА
- 17.6.1. ИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.2. НЕИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.3. ПРЕЦИЗИОННЫЙ ТРИГГЕР ШМИТТА
- 18. Генераторы сигналов
- 18.1. LC-ГЕНЕРАТОРЫ
- 18.1.2. ГЕНЕРАТОР С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ (СХЕМА МАЙССНЕРА)
- 18.1.3. ТРЕХТОЧЕЧНАЯ СХЕМА С ИНДУKТИВНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА ХАРТЛИ)
- 18.1.4. ТРЕХТОЧЕЧНАЯ СХЕМА С ЕМКОСТНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА КОЛПИТЦА)
- 18.1.5. LC-ГЕНЕРАТОР С ЭМИТТЕРНОЙ СВЯЗЬЮ
- 18.1.6. ДВУХТАКТНЫЕ ГЕНЕРАТОРЫ
- 18.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ
- 18.2.1. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КВАРЦЕВОГО РЕЗОНАТОРА
- 18.2.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ С LC-КОЛЕБАТЕЛЬНЫМ КОНТУРОМ
- 18.2.3. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ БЕЗ LC-КОНТУРА
- 18.3. СИНУСОИДАЛЬНЫЕ RC-ГЕНЕРАТОРЫ
- 18.3.2. МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 18.4. ГЕНЕРАТОРЫ СИГНАЛОВ СПЕЦИАЛЬНОЙ ФОРМЫ (ФУНКЦИОНАЛЬНЫЕ ГЕНЕРАТОРЫ)
- 18.4.2. ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР С УПРАВЛЯЕМОЙ ЧАСТОТОЙ ВЫХОДНОГО СИГНАЛА
- 18.4.3. ВЫСОКОЧАСТОТНЫЙ ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР
- 18.5. МУЛЬТИВИБРАТОРЫ
- 18.5.1. НИЗКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 18.5.2. ВЫСОКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 19. Комбинационные логические схемы
- 19.1. ПРЕОБРАЗОВАТЕЛИ КОДОВ
- 19.1.2. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 19.1.3. КОД ГРЕЯ
- 19.2. МУЛЬТИПЛЕКСОР И ДЕМУЛЬТИПЛЕКСОР
- 19.3. КОМБИНАЦИОННОЕ УСТРОЙСТВО СДВИГА
- 19.4. КОМПАРАТОРЫ
- 19.5. СУММАТОРЫ
- 19.5.1. ПОЛУСУММАТОР
- 19.5.2. ПОЛНЫЙ СУММАТОР
- 19.5.3. СУММАТОРЫ С ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ
- 19.5.4. СЛОЖЕНИЕ ДВОИЧНО-ДЕСЯТИЧНЫХ ЧИСЕЛ
- 19.5.5. ВЫЧИТАНИЕ
- 19.5.6. СЛОЖЕНИЕ ЧИСЕЛ С ЛЮБЫМИ ЗНАКАМИ
- 19.6. УМНОЖИТЕЛИ
- 19.7. ЦИФРОВЫЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 20. Интегральные схемы со структурами последовательностного типа
- 20.1. ДВОИЧНЫЕ СЧЕТЧИКИ
- 20.1.1. АСИНХРОННЫЙ (ПОСЛЕДОВАТЕЛЬНЫЙ) СЧЕТЧИК
- 20.1.2. СИНХРОННЫЙ (ПАРАЛЛЕЛЬНЫЙ) СЧЕТЧИК
- 20.2. ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК В КОДЕ 8421
- 20.2.1. АСИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.2.2. СИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.3. СЧЕТЧИК С ПРЕДВАРИТЕЛЬНОЙ УСТАНОВКОЙ
- 20.4. РЕГИСТРЫ СДВИГА
- 20.4.2. КОЛЬЦЕВОЙ РЕГИСТР
- 20.4.3. РЕГИСТР СДВИГА С ПАРАЛЛЕЛЬНЫМ ВВОДОМ
- 20.4.4. РЕГИСТР СДВИГА С ПЕРЕКЛЮЧАЕМЫМ НАПРАВЛЕНИЕМ СДВИГА
- 20.5. ПОЛУЧЕНИЕ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- 20.6. ПЕРВОНАЧАЛЬНАЯ ОБРАБОТКА АСИНХРОННОГО СИГНАЛА
- 20.6.2. СИНХРОНИЗАЦИЯ ИМПУЛЬСОВ
- 20.6.3. СИНХРОННЫЙ ОДНОВИБРАТОР
- 20.6.4. СИНХРОННЫЙ ДЕТЕКТОР ИЗМЕНЕНИЙ
- 20.6.5. СИНХРОННЫЙ ТАКТОВЫЙ ПЕРЕКЛЮЧАТЕЛЬ
- 20.7. СИСТЕМАТИЧЕСКИЙ СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ
- 20.7.2. ПРИМЕР СИНТЕЗА ПЕРЕКЛЮЧАЕМОГО СЧЕТЧИКА
- 20.7.3. СОКРАЩЕНИЕ ЕМКОСТИ ПАМЯТИ
- 21. Микро-ЭВМ
- 21.1. ОСНОВНАЯ СТРУКТУРА МИКРО-ЭВМ
- 21.2. ПРИНЦИП ДЕЙСТВИЯ МИКРОПРОЦЕССОРА
- 21.3. НАБОР КОМАНД
- 21.4. ОТЛАДОЧНЫЕ СРЕДСТВА
- 21.5. ОБЗОР МИКРОПРОЦЕССОРОВ РАЗЛИЧНОГО ТИПА
- 21.6. МОДУЛЬНОЕ ПОСТРОЕНИЕ МИКРО-ЭВМ
- 21.7. ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА
- 21.7.1. ПАРАЛЛЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.2. ПОСЛЕДОВАТЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.3. ИНТЕРФЕЙС МАГИСТРАЛИ «ОБЩАЯ ШИНА»
- 21.7.4. ПРОГРАММИРУЕМЫЙ СЧЕТЧИК
- 21.7.5. ПОДКЛЮЧЕНИЕ ПЕРИФЕРИЙНЫХ МОДУЛЕЙ СЕМЕЙСТВА 8080 К МАГИСТРАЛЯМ СЕМЕЙСТВА 6800
- 21.7.6. ОБЗОР ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
- 21.8. МИНИМАЛЬНЫЕ СИСТЕМЫ
- 21.8.2. ОДНОКРИСТАЛЬНАЯ МИКРО-ЭВМ
- 22. Цифровые фильтры
- 22.1. ТЕОРЕМА О ДИСКРЕТИЗАЦИИ (ТЕОРЕМА О ВЫБОРКАХ)
- 22.1.2. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 22.2. ЦИФРОВАЯ ФУНКЦИЯ ПЕРЕДАЧИ ФИЛЬТРА
- 22.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
- 22.4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ
- 22.4.2. СТРУКТУРА ЦИФРОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 22.4.3. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 23. Передача данных и индикация
- 23.1. СОЕДИНИТЕЛЬНЫЕ ЛИНИИ
- 23.2. ЗАЩИТА ДАННЫХ
- 23.2.2. КОД ХЕММИНГА
- 23.3. СТАТИЧЕСКИЕ ЦИФРОВЫЕ ИНДИКАТОРЫ
- 23.3.1. ДВОИЧНЫЕ ИНДИКАТОРЫ НА СВЕТОДИОДАХ
- 23.3.2. ДЕКАДНЫЕ ИНДИКАТОРЫ
- 23.3.3. ИНДИКАЦИЯ В ШЕСТНАДЦАТЕРИЧНОМ КОДЕ
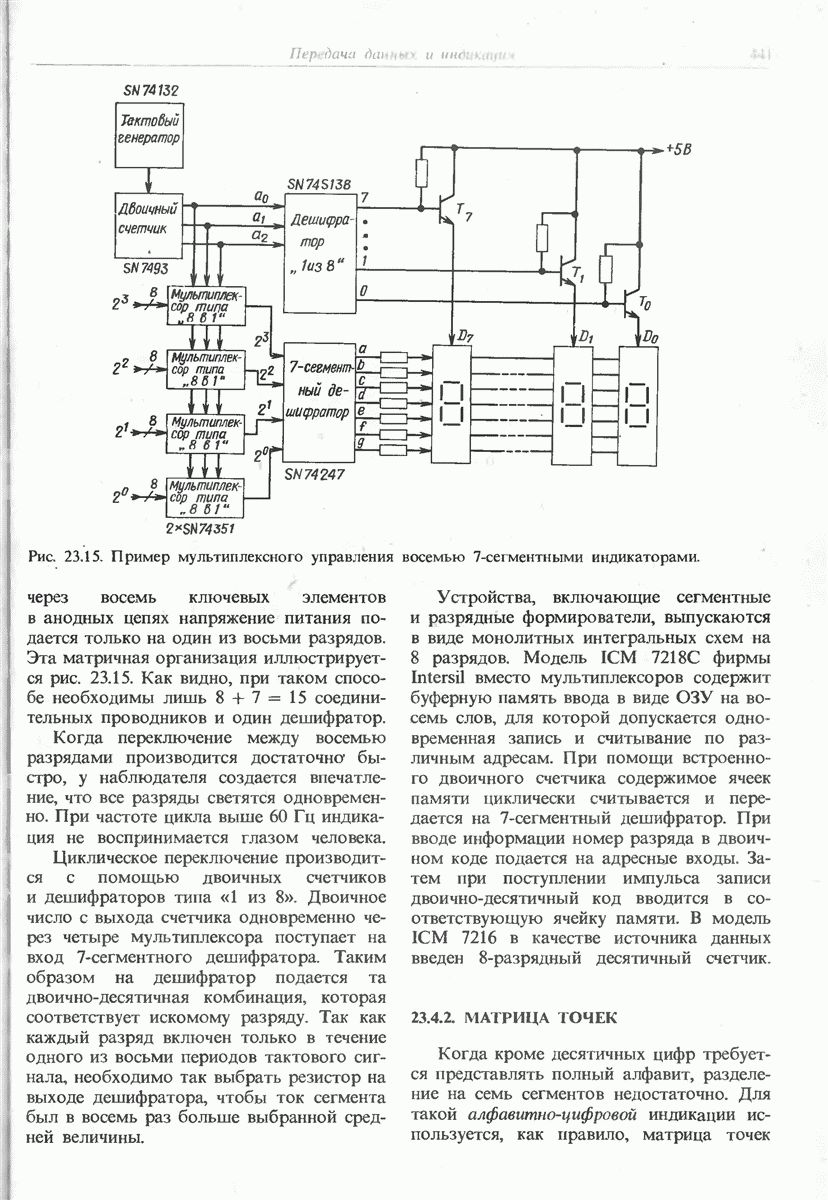
- 23.4. МУЛЬТИПЛЕКСНЫЕ ИНДИКАТОРЫ
- 23.4.1. МНОГОРАЗРЯДНЫЕ 7-СЕГМЕНТНЫЕ ИНДИКАТОРЫ
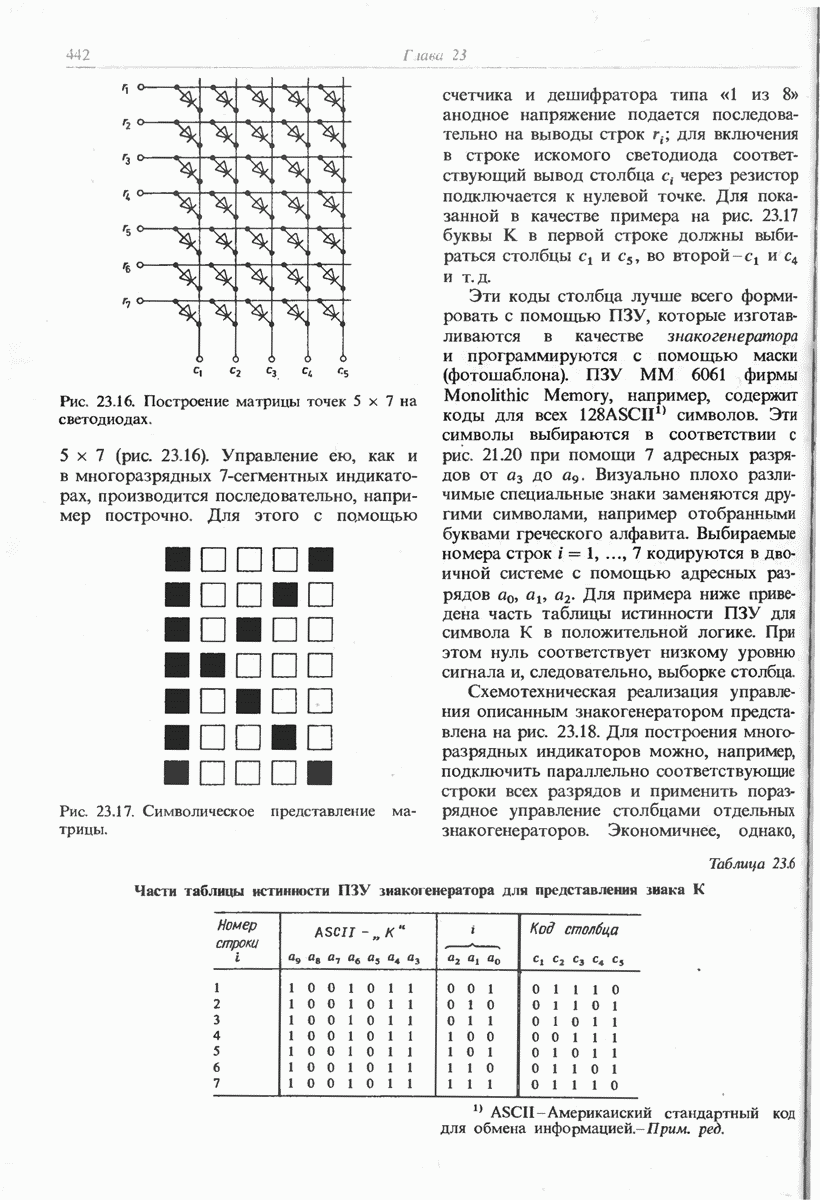
- 23.4.2. МАТРИЦА ТОЧЕК
- 24. Цифро-аналоговые и аналого-цифровые преобразователи
- 24.1. СХЕМОТЕХНИЧЕСКИЕ ПРИНЦИПЫ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.1.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ПЕРЕКИДНЫМИ КЛЮЧАМИ
- 24.1.3. РЕЗИСТИВНАЯ МАТРИЦА ПОСТОЯННОГО ИМПЕДАНСА (МАТРИЦА ТИПА R-2R)
- 24.1.4. РЕЗИСТИВНАЯ МАТРИЦА ДЛЯ ДЕКАДНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
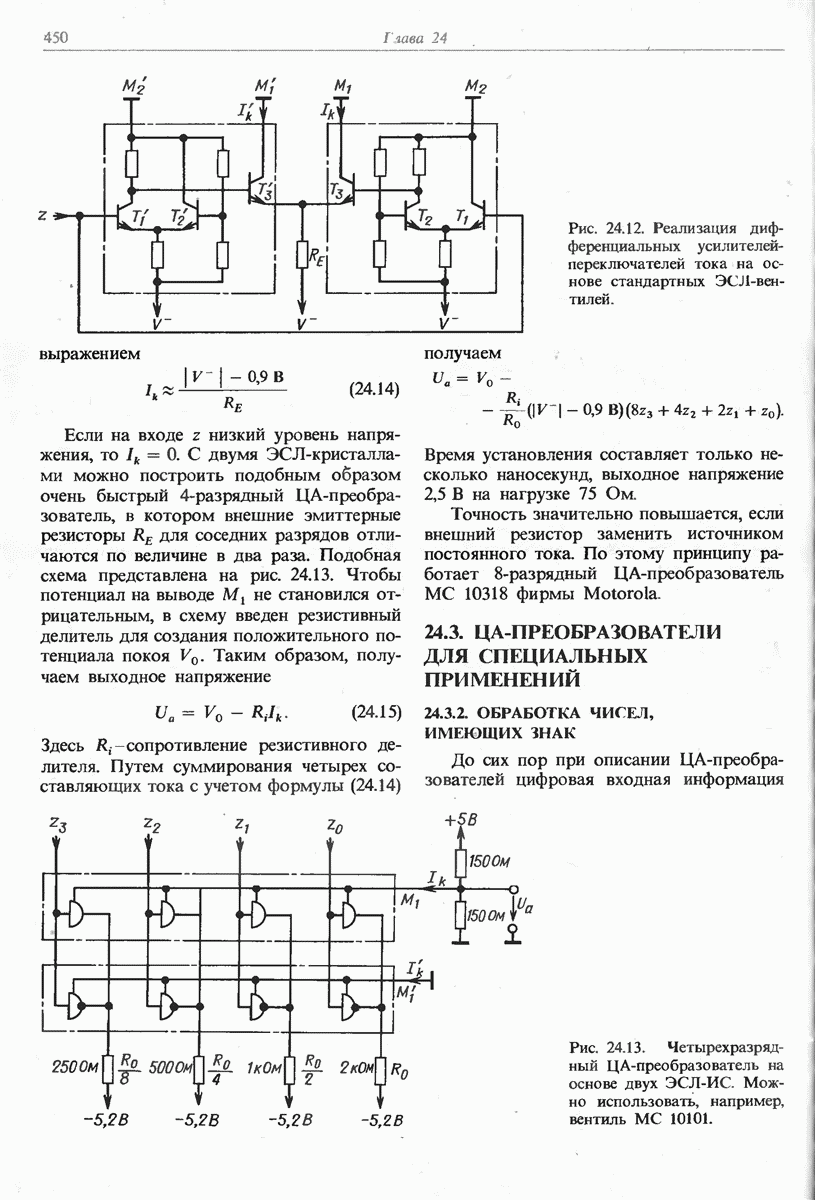
- 24.2. ПОСТРОЕНИЕ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ С ЭЛЕКТРОННЫМИ КЛЮЧАМИ
- 24.2.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ТОКОВЫМИ КЛЮЧАМИ
- 24.3. ЦА-ПРЕОБРАЮВАТЕЛИ ДЛЯ СПЕЦИАЛЬНЫХ ПРИМЕНЕНИЙ
- 24.3.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ДЕЛЕНИЯ
- 24.3.3. ЦА-ПРЕОБРАЗОВАТЕЛЬ КАК ГЕНЕРАТОР ФУНКЦИЙ
- 24.4. ОСНОВНЫЕ ПРИНЦИПЫ АЦ-ПРЕОБРАЗОВАНИЯ
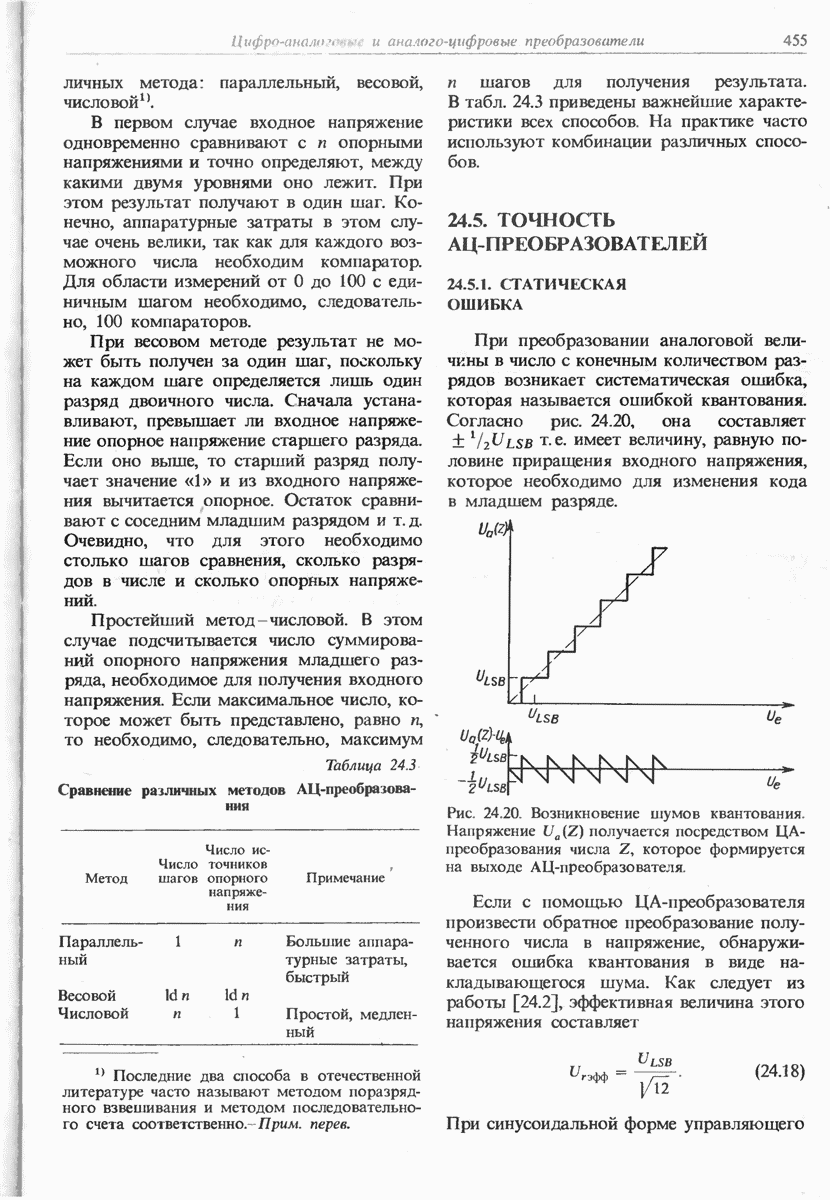
- 24.5. ТОЧНОСТЬ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.6. ПОСТРОЕНИЕ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 25. Измерительные схемы
- 25.1. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ
- 25.1.2. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- 25.1.3. ИЗОЛИРОВАННЫЙ УСИЛИТЕЛЬ
- 25.2. ИЗМЕРЕНИЕ ТОКА
- 25.2.1. ИЗОЛИРОВАННЫЕ ОТ ЗЕМЛИ АМПЕРМЕТРЫ С МАЛЫМ ПАДЕНИЕМ НАПРЯЖЕНИЯ
- 25.2.2. ИЗМЕРЕНИЕ ТОКА ПРИ ВЫСОКОМ ПОТЕНЦИАЛЕ
- 25.3. ИЗМЕРИТЕЛЬНЫЙ ВЫПРЯМИТЕЛЬ
- 25.3.2. ИЗМЕРЕНИЕ ЭФФЕКТИВНОГО ЗНАЧЕНИЯ
- 25.3.3. ИЗМЕРЕНИЕ АМПЛИТУДНЫХ ЗНАЧЕНИЙ
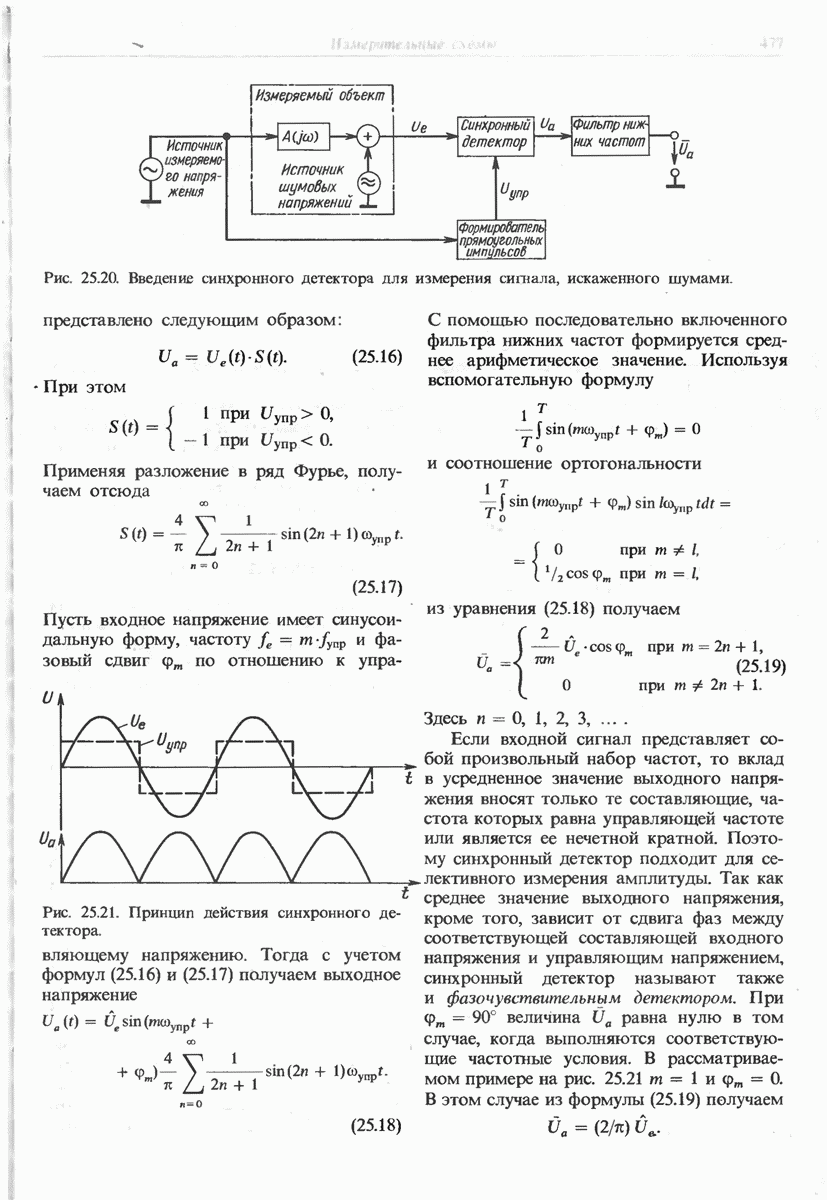
- 25.3.4. СИНХРОННЫЙ ДЕТЕКТОР
- 26. Электронные регуляторы
- 26.2. ТИПЫ РЕГУЛЯТОРОВ
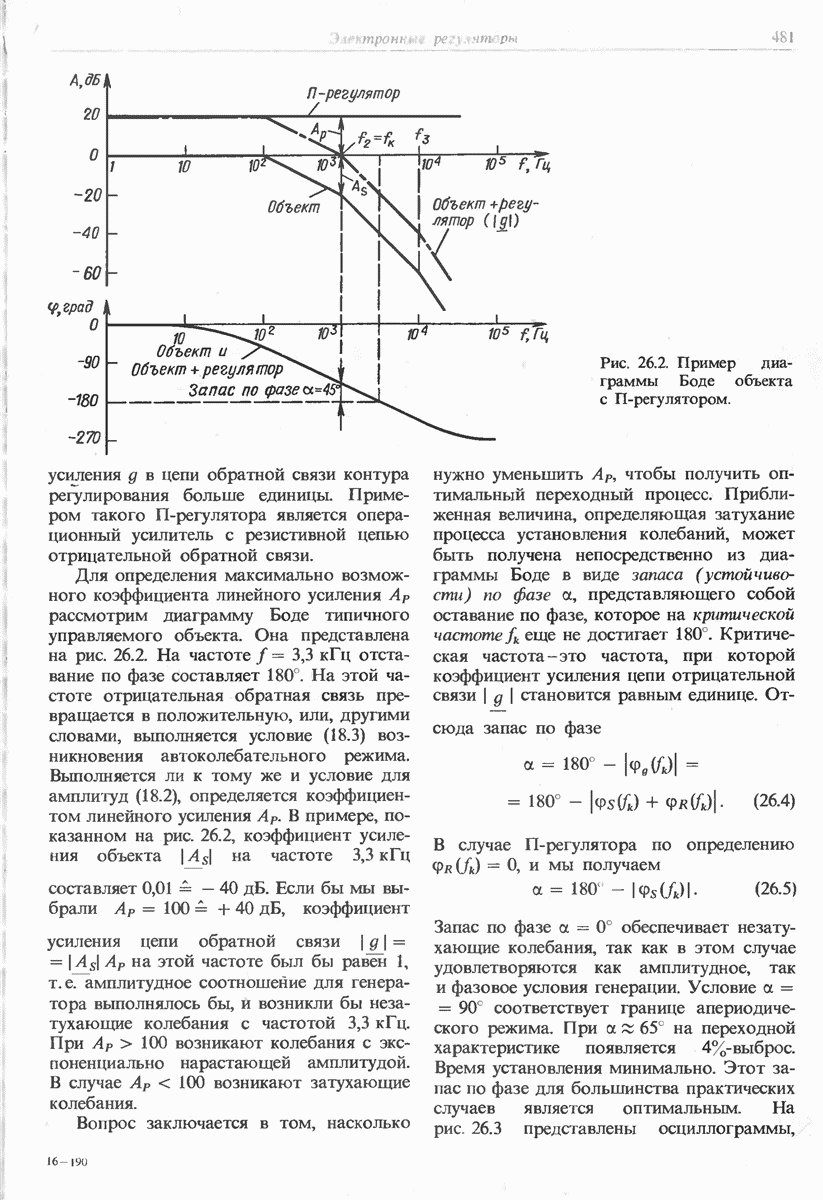
- 26.2.1. П-РЕГУЛЯТОР
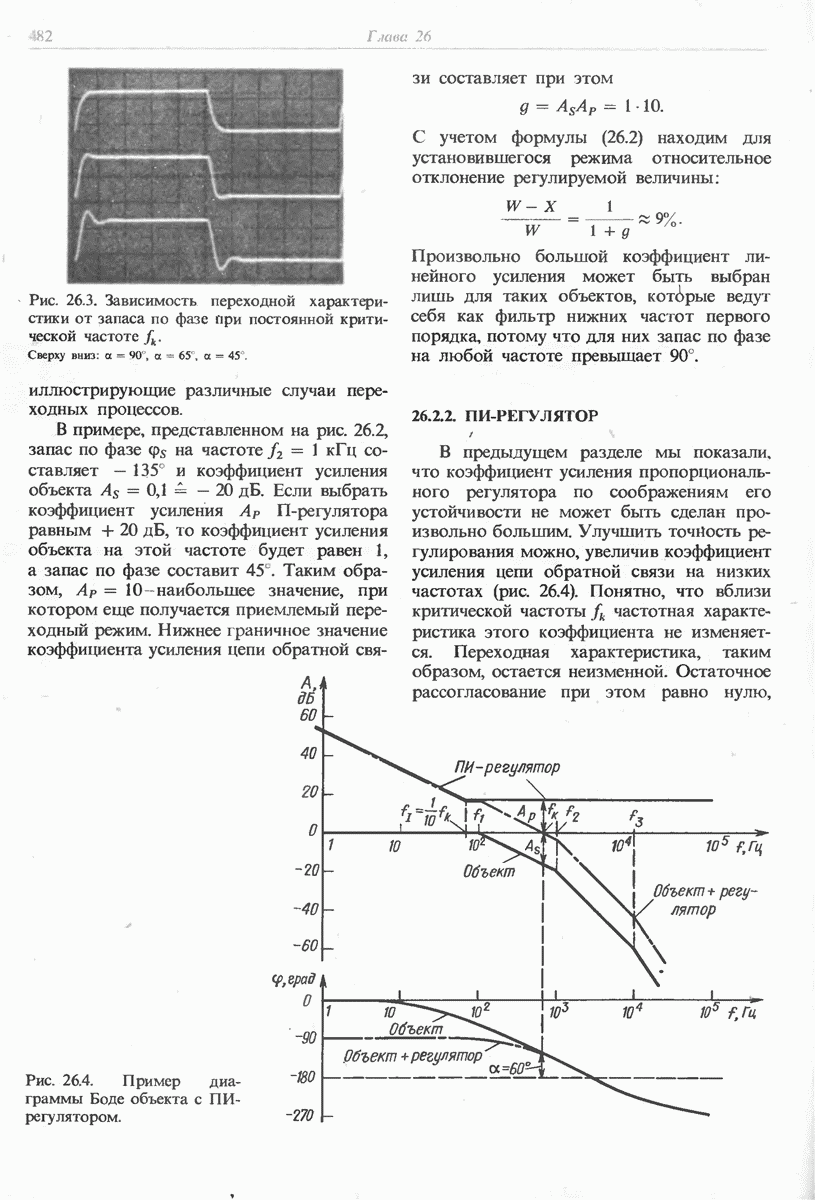
- 26.2.2. ПИ-РЕГУЛЯТОР
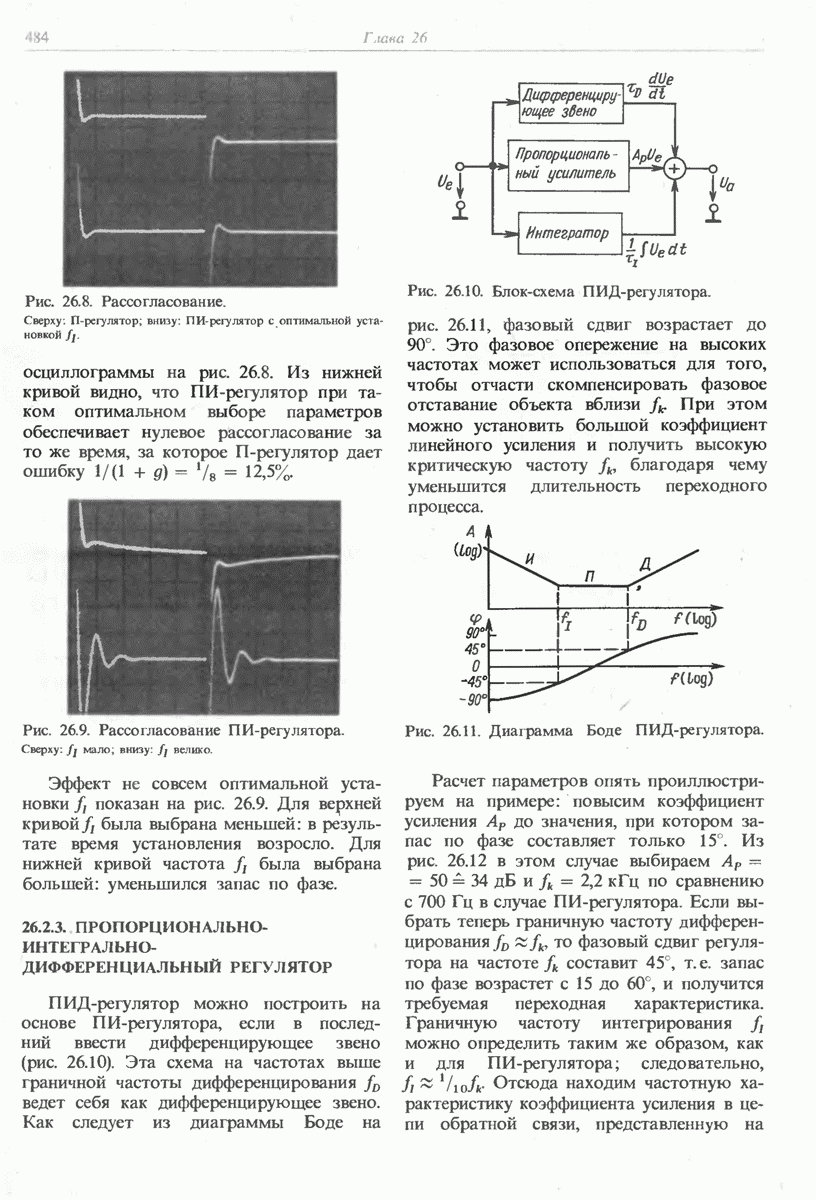
- 26.2.3. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР
- 26.2.4. НАСТРАИВАЕМЫЕ ПИД-РЕГУЛЯТОРЫ
- 26.3. УПРАВЛЕНИЕ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ
- 26.4. ОТСЛЕЖИВАЮЩАЯ СИНХРОНИЗАЦИЯ (АВТОПОДСТРОЙКА)
- 26.4.1. ЭЛЕМЕНТЫ ВЫБОРКИ-ХРАНЕНИЯ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
- 26.4.2. СИНХРОННЫЙ ВЫПРЯМИТЕЛЬ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
- 26.4.3. ЧАСТОТНО-ЧУВСТВИТЕЛЬНЫЙ ФАЗОВЫЙ ДЕТЕКТОР
- 26.4.4. ФАЗОВЫЙ ДЕТЕКТОР С ПРОИЗВОЛЬНО УВЕЛИЧИВАЕМЫМ ДИАПАЗОНОМ ИЗМЕРЕНИЙ
- 26.4.5. ФАЗОРЕГУЛЯТОР В КАЧЕСТВЕ ПЕРЕМНОЖИТЕЛЯ ЧАСТОТ