| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
19.1.2. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
Ввод и вывод чисел в десятичной системе счисления невозможен с помощью обычного двоичного кода. Для этой цели
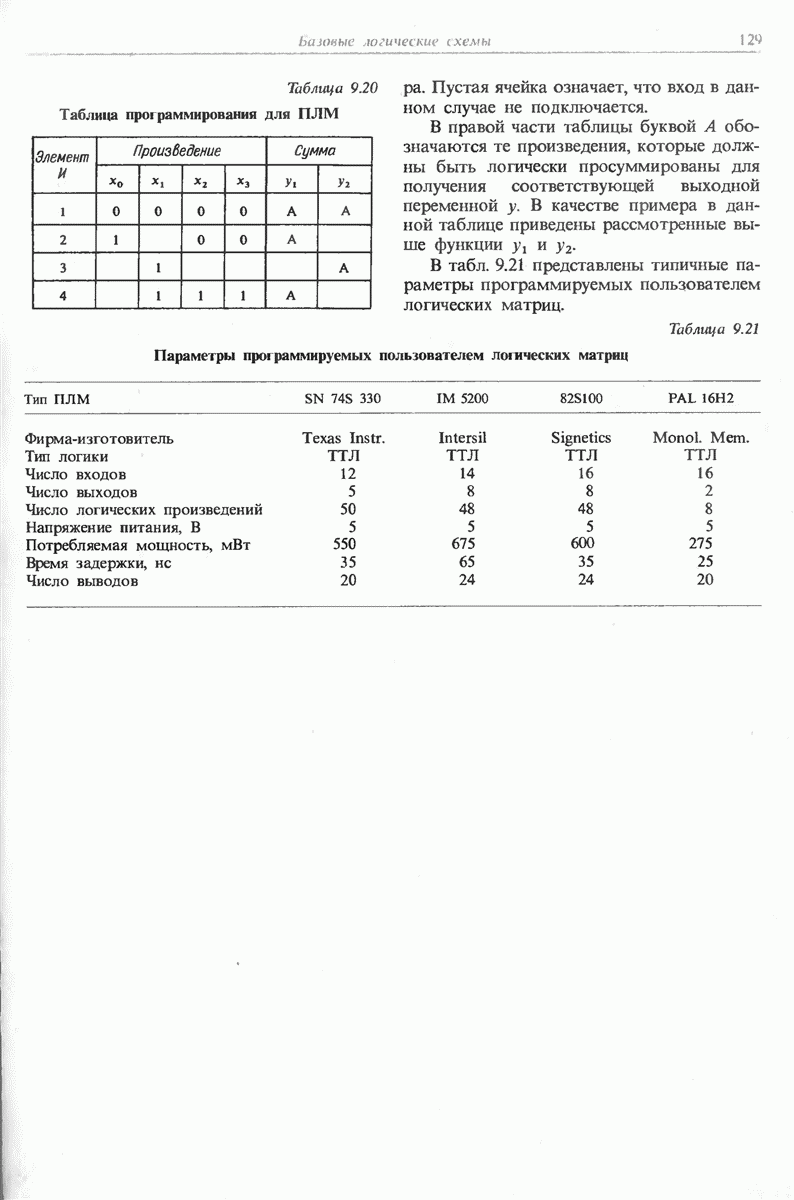
Таблица 19.2 (см. скан)
был предложен двоично-десятичный код. В таком коде каждая отдельная десятичная цифра представлена с помощью двоичных знаков, в частности в виде соответствующего двоичного числа. В таком случае получим, например,

Записанное таким образом десятичное число более точно следует называть двоично-десятичным числом в коде 8421 или в натуральном двоично-десятичном коде. Десятичные цифры можно представить и с помощью других комбинаций двоичных знаков, содержащих 4 и более разрядов. Однако, поскольку двоично-десятичный код 8421 является самым распространенным, его называют просто двоично-десятичным кодом. Ниже используется этот термин, а отличные от натурального двоично-десятичные коды будем оговаривать особо.
Одно четырехразрядное двоичное число позволяет представить десятичные числа от 0 до 15. В случае двоично-десятичного кода из них используется только 10 комбинаций Следовательно, для записи двоично-десятичного числа требуется больше разрядов, чем для записи двоичного.
При выполнении операций в десятичном коде можно получить результат, включающий десятичную «цифру» от  до
до  . Подобные, не предусмотренные этим кодом цифры называются псевдотетрадами. Для исправления записи псевдотетрад следует уменьшить их на
. Подобные, не предусмотренные этим кодом цифры называются псевдотетрадами. Для исправления записи псевдотетрад следует уменьшить их на  и следующий по старшинству разряд увеличить на 1. Данный результат можно получить и другим способом, добавив к псевдотетраде число
и следующий по старшинству разряд увеличить на 1. Данный результат можно получить и другим способом, добавив к псевдотетраде число  как показано в следующем примере:
как показано в следующем примере:

Преобразование двоичного кода в двоично-десятичный
В предыдущем примере мы уже познакомились с процедурой преобразования четырехразрядного двоичного числа в двоично-десятичное:
Числа до 8 включительно остаются без изменения.
Числа свыше 9, представляющие собой псевдотетрады, подвергаются коррекции.
Двоичные числа, содержащие более 4 разрядов, можно преобразовать
аналогичным образом. Для этого двоичное число, начиная со старшего разряда, «вдвигается» справа налево в двоично-десятичную разрядную сетку, как показано на рис. 19.5. Когда какая-либо единица пересекает границу между двоично-десятичными разрядами, возникает ошибка. Действительно, в случае двоичного числа разрядное значение этой единицы при сдвиге увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно возрастает от 8 до 10. Поэтому на этом этапе двоично-десятичное число как бы уменьшается на 6. Следовательно, для коррекции необходимо прибавлять 6 к числу во всех случаях, когда единица пересекает границу между двоично-десятичными разрядами. К числу десятков надо прибавить 6, если единица перейдет в разряд сотен, и т.д. Составленное таким образом двоично-десятичное число имеет правильное значение, однако оно может еще содержать псевдотетрады. Чтобы этого не было, возникающие псевдотетрады корректируют непосредственно после каждого шага сдвига, прибавляя 6 к соответствующей декаде с переносом 1 в следующую. Следовательно, обе указанные коррекции производятся с помощью одной. и той же операции, а именно путем прибавления 6.
Вместо того чтобы прибавлять после сдвига 6, с тем же успехом можно перед сдвигом прибавлять 3. Необходимость такой коррекции можно также определить перед сдвигом. Если значение тетрады меньше или равно  то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
Если значение тетрады составляет 8 или 9, необходимо корректировать переход единицы через границу между декадами. Поэтому после каждого сдвига появляются правильные тетрады 6 или 7 либо 8 или 9. При такой коррекции псевдотетрад полученное значение каждой тетрады не может быть более 9. Этим исчерпываются все возможности, и мы получим таблицу коррекции 19.3.
Преобразование двоичного числа в соответствующее двоично-десятичное можно реализовать, сдвигая влево двоичное число, записанное в регистре сдвига, разделенном на четырехразрядные секции. Каждая секция должна включать корректирующий элемент, который преобразует содержание регистра перед каждым последующим сдвигом в соответствии с таблицей переключений 19.3.
Наряду с подобным способом реализации преобразования кодов с помощью схем с памятью можно использовать комбинационные схемы, в которых операция сдвига проводится с помощью соответствующей логики. Эта схема представлена на рис. 19.6. Вместо сдвига числа справа налево здесь слева направо

Рис. 19.5. Преобразование двоичного кода в двоично-десятичный; в качестве примера взято число 218.
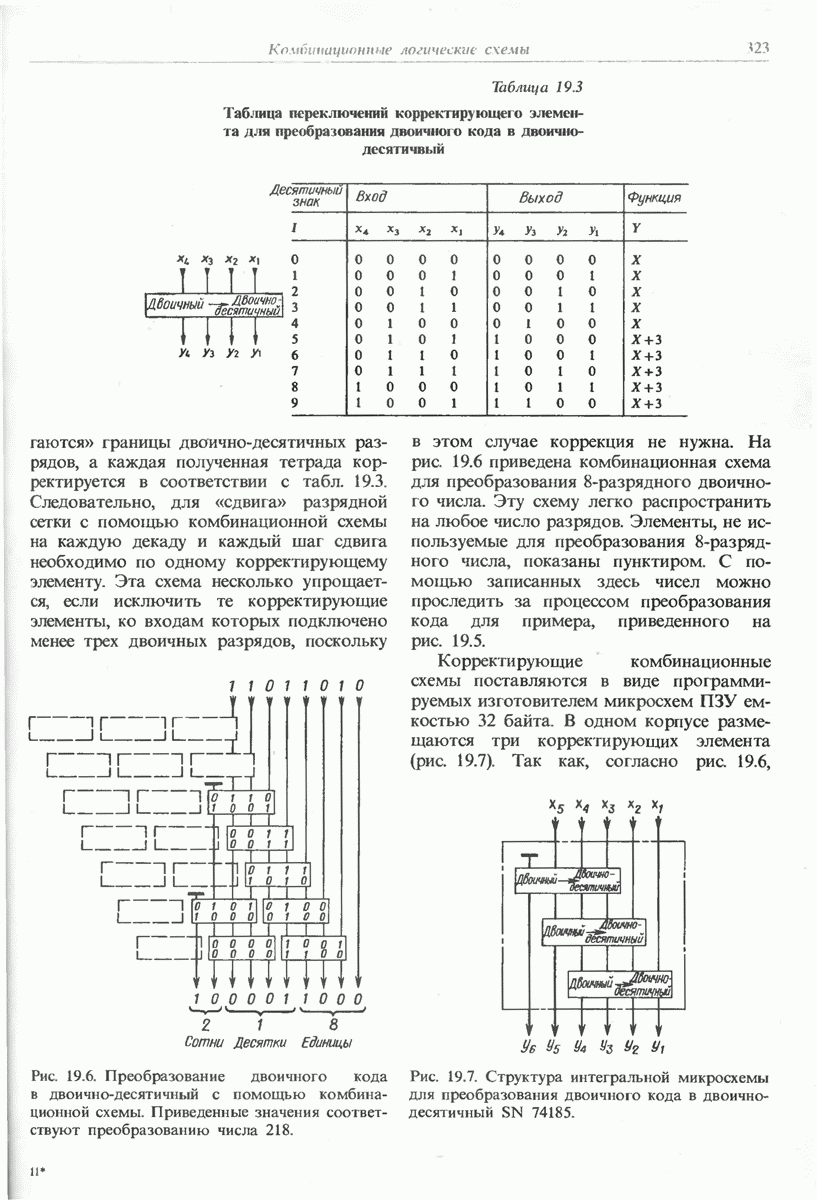
Таблица 19.3 (см. скан) Таблица переключений корректирующего элемента для преобразования двоичного кода в двоично-десятичвый
«сдвигаются» границы двоично-десятичных разрядов, а каждая полученная тетрада корректируется в соответствии с табл. 19.3. Следовательно, для «сдвига» разрядной сетки с помощью комбинационной схемы на каждую декаду и каждый шаг сдвига необходимо по одному корректирующему элементу. Эта схема несколько упрощается, если исключить те корректирующие элементы, ко входам которых подключено менее трех двоичных разрядов, поскольку в этом случае коррекция не нужна. На рис. 19.6 приведена комбинационная схема для преобразования 8-разрядного двоичного числа. Эту схему легко распространить на любое число разрядов. Элементы, не используемые для преобразования 8-разрядного числа, показаны пунктиром. С помощью записанных здесь чисел можно проследить за процессом преобразования кода для примера, приведенного на рис. 19.5.
Корректирующие комбинационные схемы поставляются в виде программируемых изготовителем микросхем ПЗУ емкостью 32 байта. В одном корпусе размещаются три корректирующих элемента (рис. 19.7). Так как, согласно рис. 19.6,

Рис. 19.6. Преобразование двоичного кода в двоично-десятичный с помощью комбинационной схемы. Приведенные значения соответствуют преобразованию числа 218.

Рис. 19.7. Структура интегральной микросхемы для преобразования двоичного кода в двоично-десятичный 
младший разряд не подается на корректирующую схему, то с помощью одной ИС можно преобразовать  -разрядное двоичное число, а для 8-разрядного числа нужны три таких ИС.
-разрядное двоичное число, а для 8-разрядного числа нужны три таких ИС.
Преобразование двоично-десятичного кода в двоичный
Во многих случаях двоично-десятичный код можно достаточно просто получить непосредственно, например с помощью двоично-десятичных счетчиков Как будет показано ниже, в двоично-десятичном коде также можно выполнять многие вычислительные операции. Однако в некоторых случаях необходимо все же провести преобразование его в двоичный код. Это можно сделать путем последовательного деления числа на 2. Для этого десятичиое число делится на 2. Если оно нечетное, то в остатке получится 1, т.е. в разряде 2° записывается 1. Затем частное от деления еще раз делится на 2, и, если остаток равен нулю, в разряде 21 записывается 0. Если остаток равен 1, то в этом разряде записывается 1. Аналогично получают и более старшие разряды двоичного числа. Деление двоично-десятичного числа на 2 очень просто можно провести путем сдвига вправо на один разряд, так как отдельные цифры уже представлены в двоичном коде. Самый правый бит, выдвинутый из двоично-десятичной разрядной сетки, и является искомым значением разряда. Но если при сдвиге единица пересекает границу между декадами, то возникает ошибка: при переходе от десятков к единицам значение разряда должно уменьшиться наполовину - от десяти до пяти. Однако в случае двоичного числа эта величина становится равной восьми. Поэтому, для коррекции нужно вычесть 3. Из этого вытекает следующее правило коррекции: если старший разряд в декаде равен единице, то необходимо данную декаду уменьшить на три. Таким образом можно непосредственно составить таблицу переключений для корректирующего элемента 19.4. Процесс преобразования закапчивается, если все двоично-десятичное число будет выдвинуто из разрядной сетки.
На рис. 19.8 приведена комбинационная схема для преобразования  -разрядного двоично-десятичного числа. Здесь, так же как и в схеме на рис. 19.6, сдвиг двоично-десятичных разрядов достигается путем соответствующего соединения одинаковых комбинационных схем. Чтобы наглядно продемонстрировать структуру этой
-разрядного двоично-десятичного числа. Здесь, так же как и в схеме на рис. 19.6, сдвиг двоично-десятичных разрядов достигается путем соответствующего соединения одинаковых комбинационных схем. Чтобы наглядно продемонстрировать структуру этой
Таблица 19.4 (см. скан) Таблица переключений корректирующего элемента для преобразования двоично-десятичного кода в двоичный

Рис. 19.8. Преобразование двоично-десятичного кода в двоичный с помощью комбинационной схемы. Приведенные значения соответствуют преобразованию числа 218.

Рис. 19.9. Структура интегральной микросхемы для преобразования двоично-десятичного кода в двоичный.
схемы, на рис. 19.8 изображены все три корректирующих элемента для каждой ступени кодопреобразователя. В действительности если старший разряд корректирующего элемента не используется, то, согласно табл. 19.4, коррекция не нужна и данный элемент можно исключить. На рис. 19.8 такие элементы изображены пунктирной линией.
Корректирующие схемы составляются из отдельных секций, содержащих по два элемента (рис. 19.9). Каждая секция представляет собой одну интегральную микросхему ПЗУ на 32 байта, программируемую изготовителем. Такая микросхема (типа  ) имеет пять входов и пять выходов.
) имеет пять входов и пять выходов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Часть I. Основные положения
- 1. Пояснение применяемых величин
- 2. Пассивные RC- и LRC- цепи
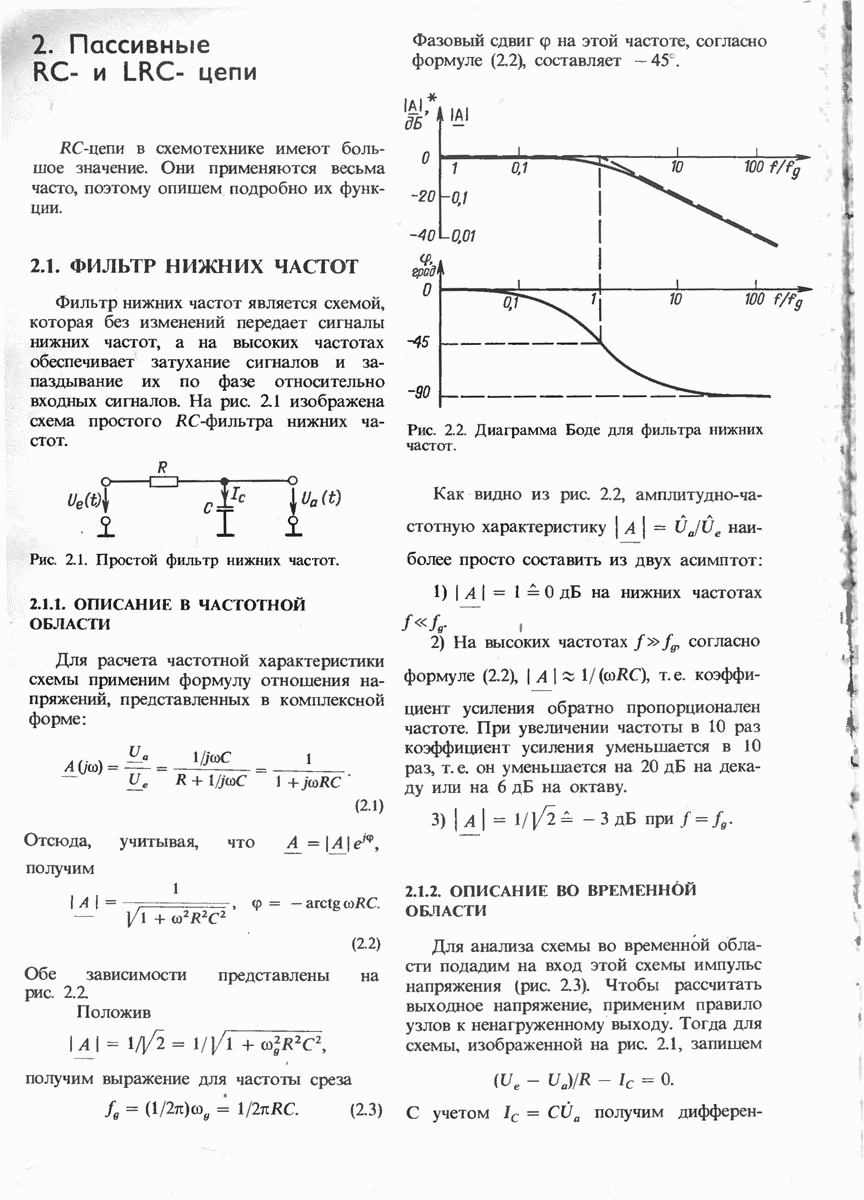
- 2.1. ФИЛЬТР НИЖНИХ ЧАСТОТ
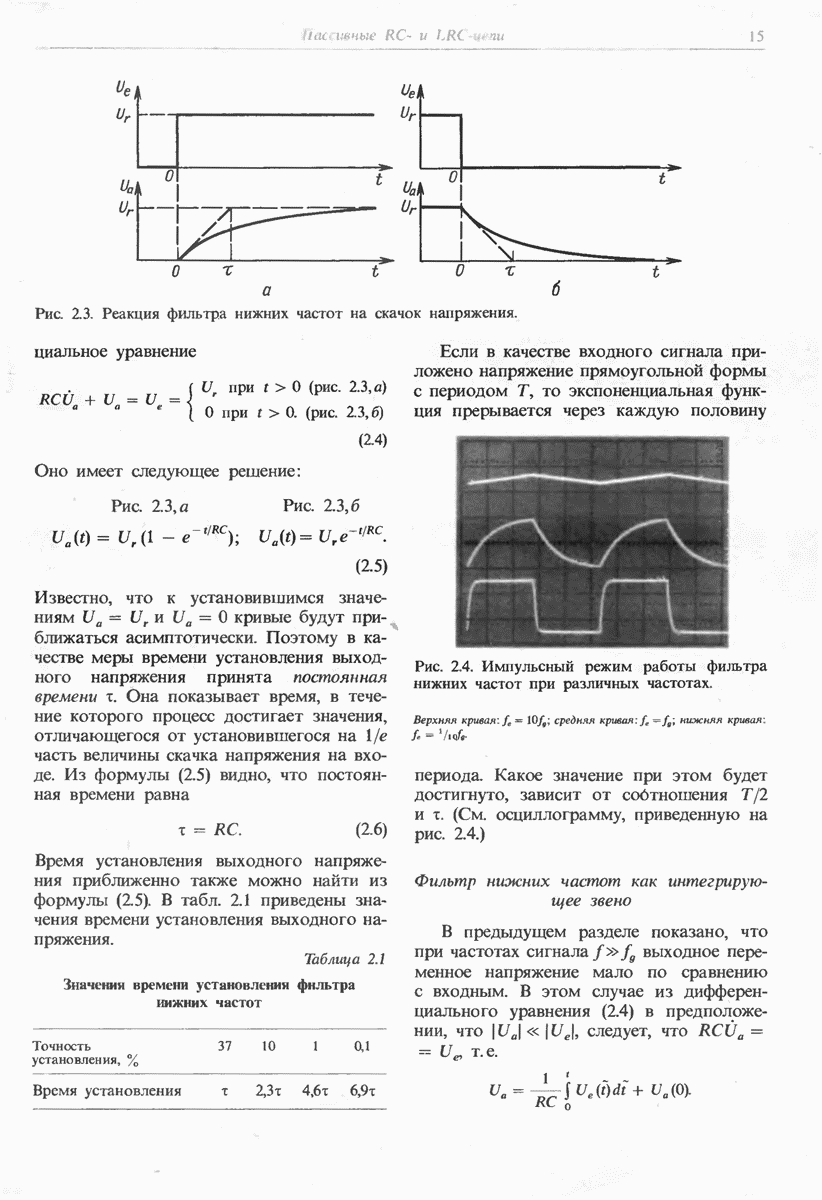
- 2.1.3. ДЛИТЕЛЬНОСТЬ ФРОНТА ИМПУЛЬСА И ЧАСТОТА СРЕЗА ФИЛЬТРА
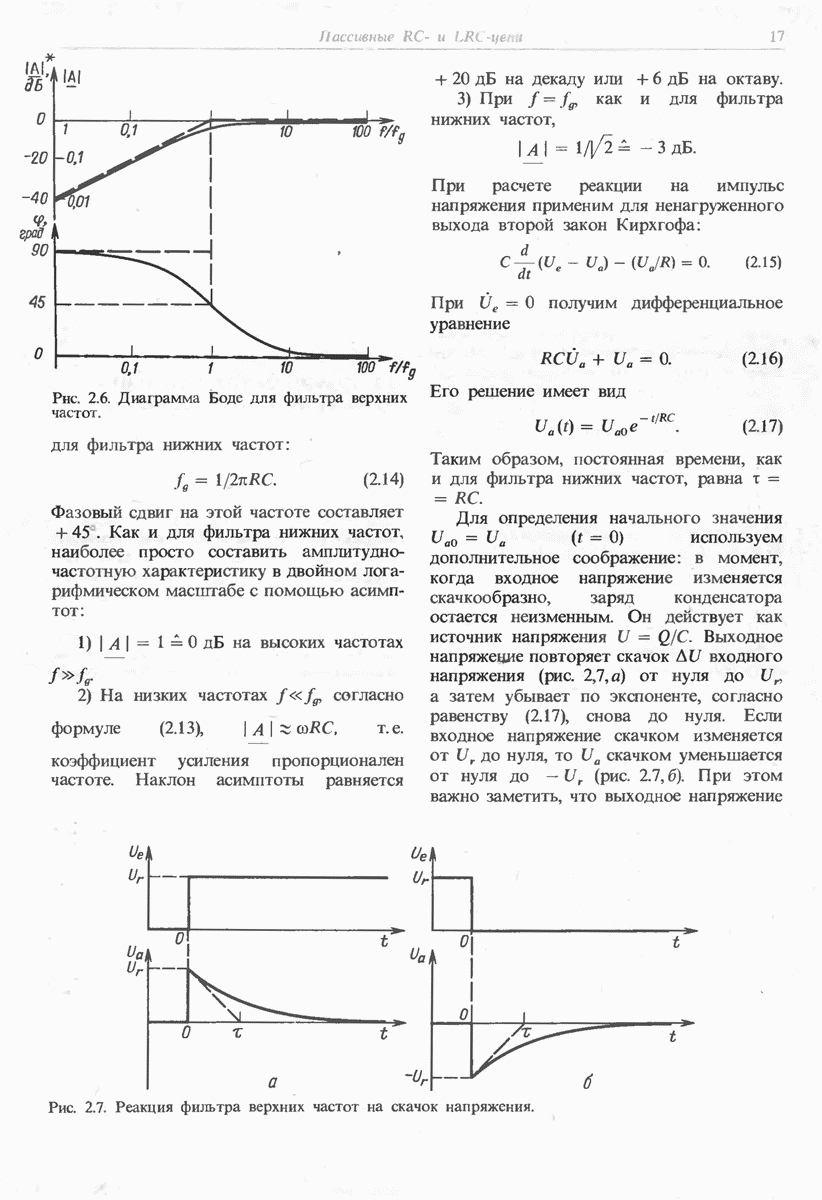
- 2.2. ФИЛЬТР ВЕРХНИХ ЧАСТОТ
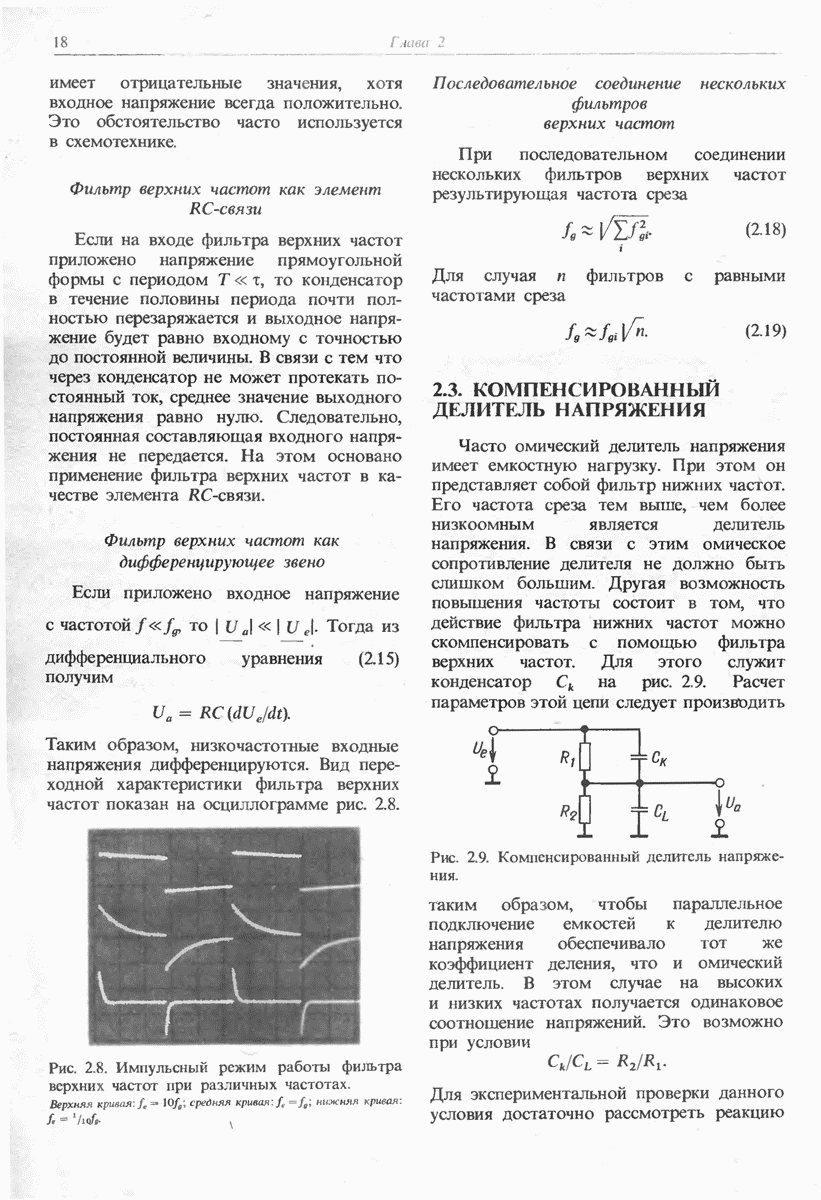
- 2.3. КОМПЕНСИРОВАННЫЙ ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
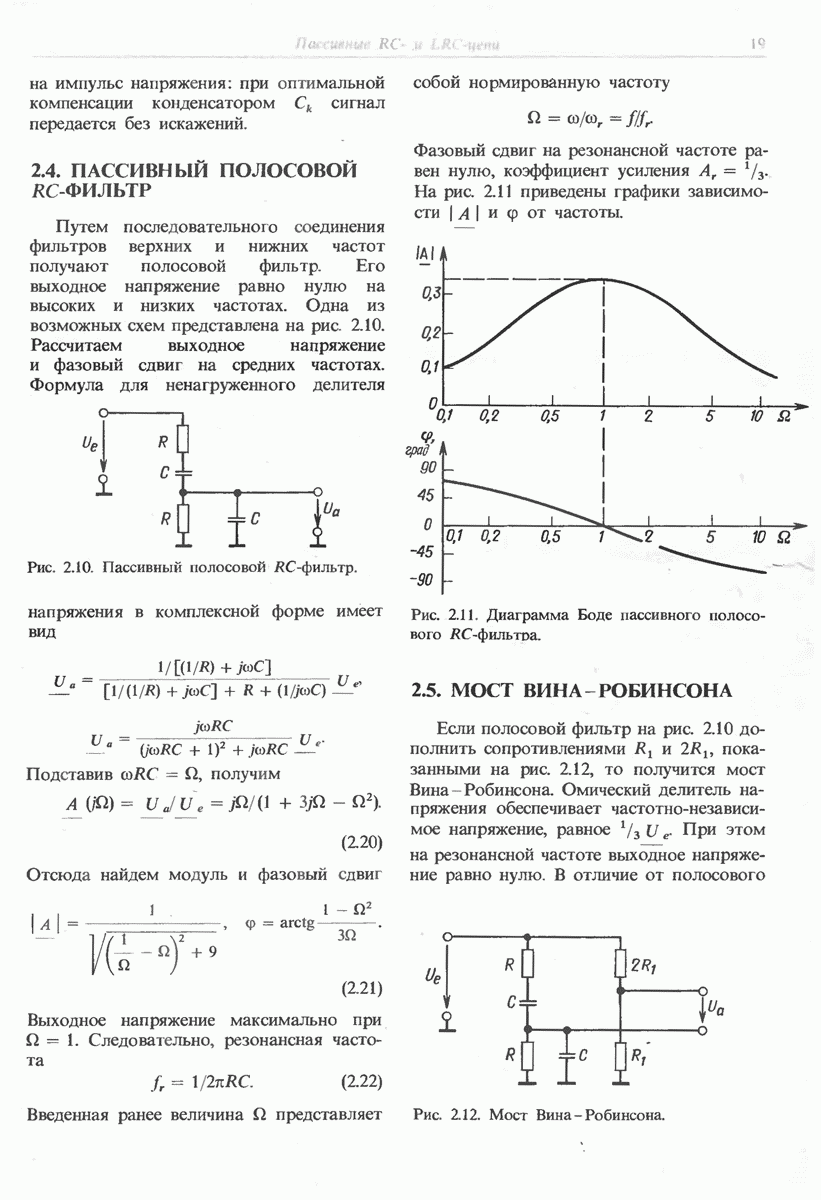
- 2.4. ПАССИВНЫЙ ПОЛОСОВОЙ RC-ФИЛЬТР
- 2.5. МОСТ ВИНА-РОБИНСОНА
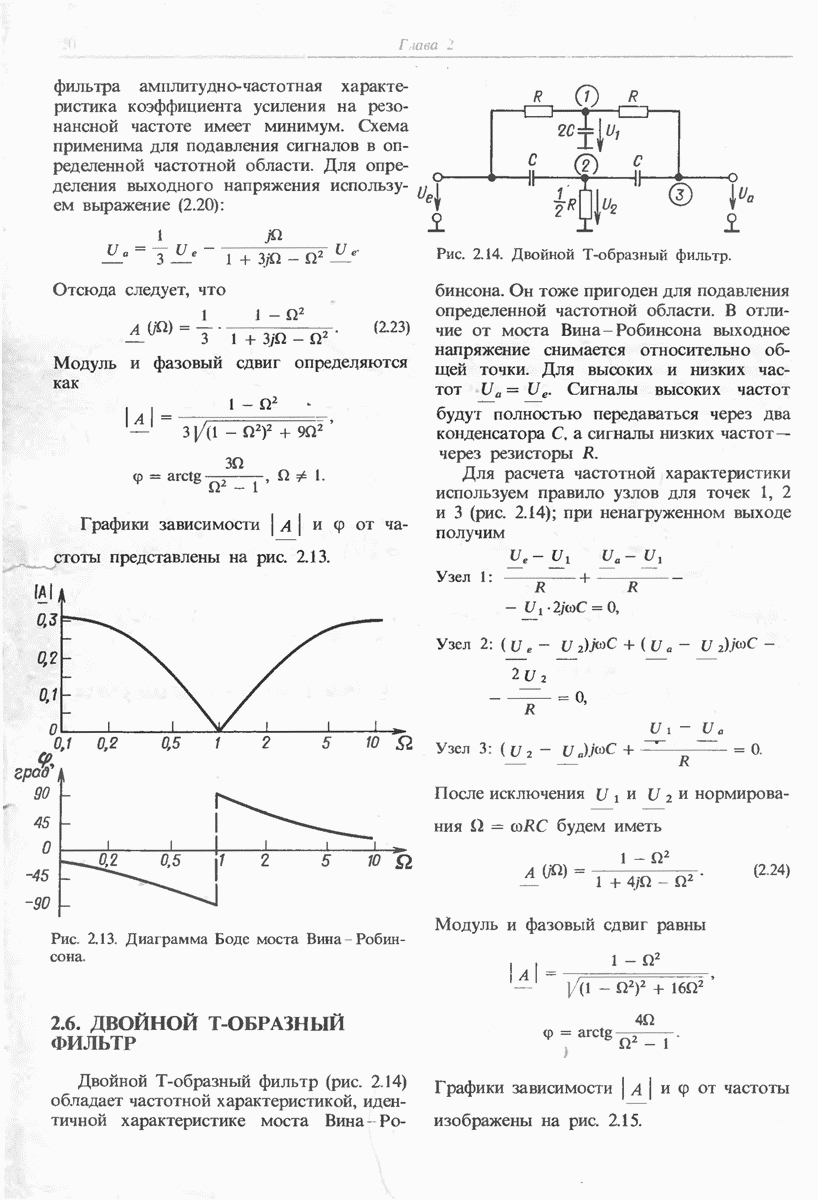
- 2.6. ДВОЙНОЙ Т-ОБРАЗНЫЙ ФИЛЬТР
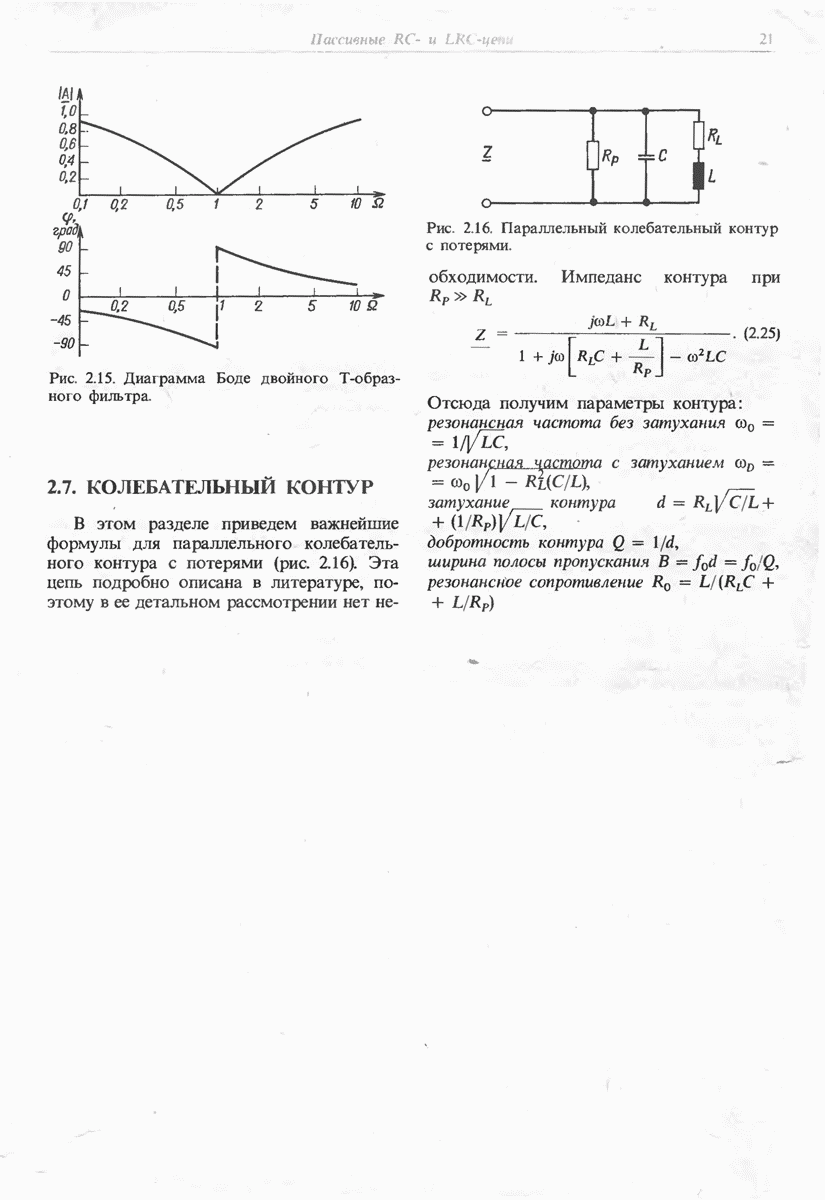
- 2.7. КОЛЕБАТЕЛЬНЫЙ КОНТУР
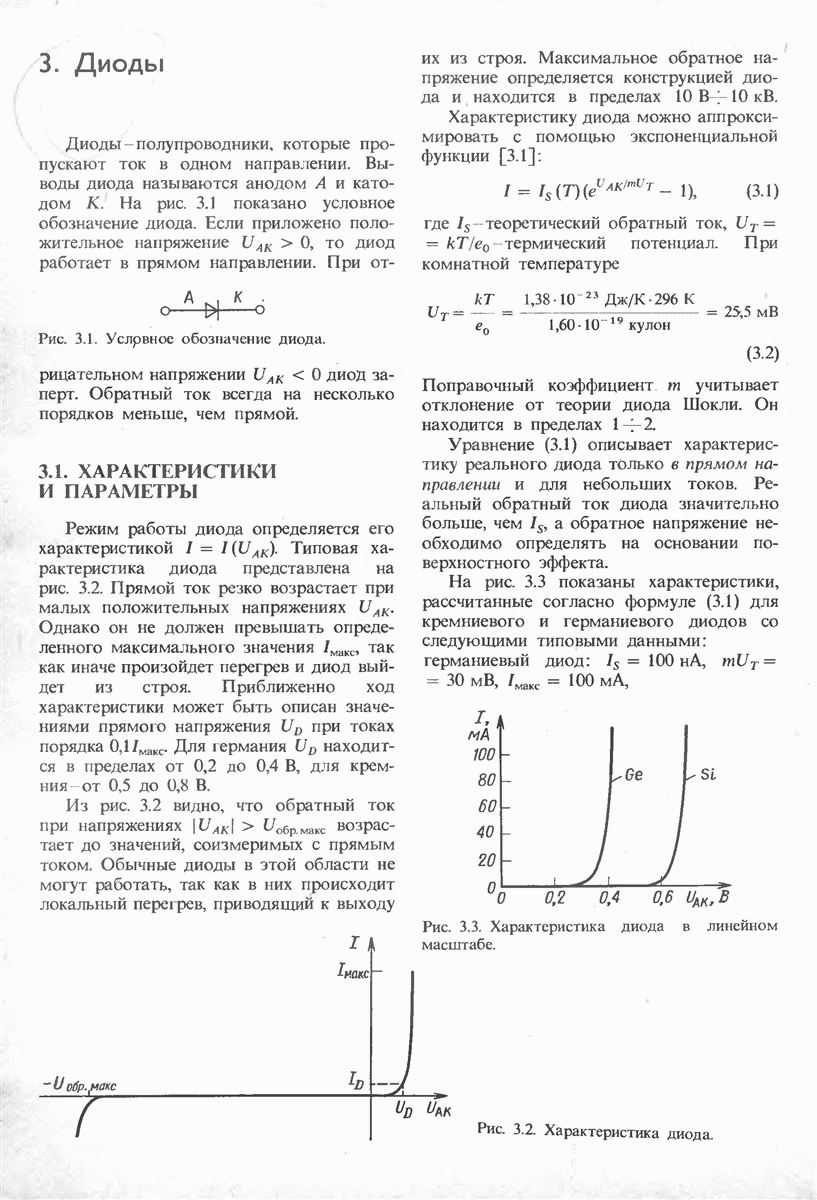
- 3. Диоды
- 3.2. СТАБИЛИТРОНЫ
- 3.3. ВАРИКАПЫ
- 4. Транзистор и схемы на его основе
- 4.2. СХЕМА С ОБЩИМ ЭМИТТЕРОМ
- 4.2.2. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 4.2.3. СХЕМА С ОБЩИМ ЭМИТТЕРОМ И ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.2.4. ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ ПО НАПРЯЖЕНИЮ
- 4.2.5. УСТАНОВКА РАБОЧЕЙ ТОЧКИ
- 4.3. СХЕМА С ОБЩЕЙ БАЗОЙ
- 4.4. СХЕМА С ОБЩИМ КОЛЛЕКТОРОМ, ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 4.5. ТРАНЗИСТОР КАК ИСТОЧНИК СТАБИЛЬНОГО ТОКА
- 4.5.2. БИПОЛЯРНЫЙ ИСТОЧНИК ПИТАНИЯ
- 4.5.3. СХЕМА «ТОКОВОГО ЗЕРКАЛА»
- 4.6. СХЕМА ДАРЛИНГТОНА
- 4.7. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛИ
- 4.7.2. РЕЖИМ БОЛЬШОГО СИГНАЛА
- 4.7.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.7.4. НАПРЯЖЕНИЕ РАЗБАЛАНСА
- 4.8. ИЗМЕРЕНИЕ НЕКОТОРЫХ ПАРАМЕТРОВ ПРИ МАЛОМ СИГНАЛЕ
- 4.9. ШУМЫ ТРАНЗИСТОРА
- 4.10. ПРЕДЕЛЬНЫЕ ПАРАМЕТРЫ
- 5. Полевые транзисторы
- 5.2. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ МАЛЫХ СИГНАЛОВ
- 5.3. ПРЕДЕЛЬНЫЕ ЭЛЕКТРИЧЕСКИЕ ПАРАМЕТРЫ
- 5.4. ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ
- 5.4.1. СХЕМА С ОБЩИМ ИСТОКОМ
- 5.4.2. СХЕМА С ОБЩИМ ЗАТВОРОМ
- 5.4.3. СХЕМА С ОБЩИМ СТОКОМ, ИСТОКОВЫЙ ПОВТОРИТЕЛЬ
- 5.5. ПОЛЕВОЙ ТРАНЗИСТОР КАК СТАБИЛИЗАТОР ТОКА
- 5.6. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- 5.7. ПОЛЕВОЙ ТРАНЗИСТОР В КАЧЕСТВЕ УПРАВЛЯЕМОГО СОПРОТИВЛЕНИЯ
- 6. Операционный усилитель
- 6.1. СВОЙСТВА ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 6.2. ПРИНЦИП ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ
- 6.3. НЕИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 6.4. ИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 7. Внутренняя структура операционных усилителей
- 7.2. ПРОСТЕЙШИЕ СХЕМЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 7.3. СТАНДАРТНАЯ СХЕМА ИНТЕГРАЛЬНОГО ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 7.4. КОРРЕКЦИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
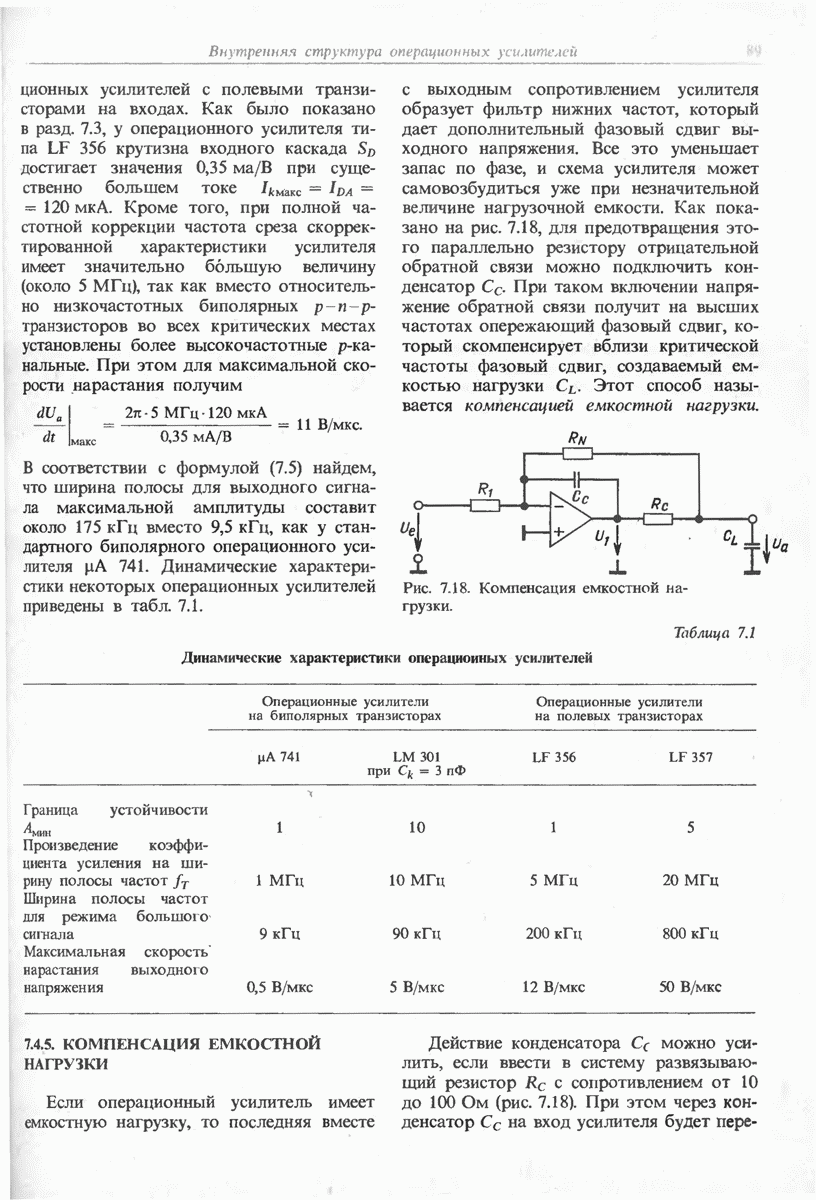
- 7.4.2. ПОЛНАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
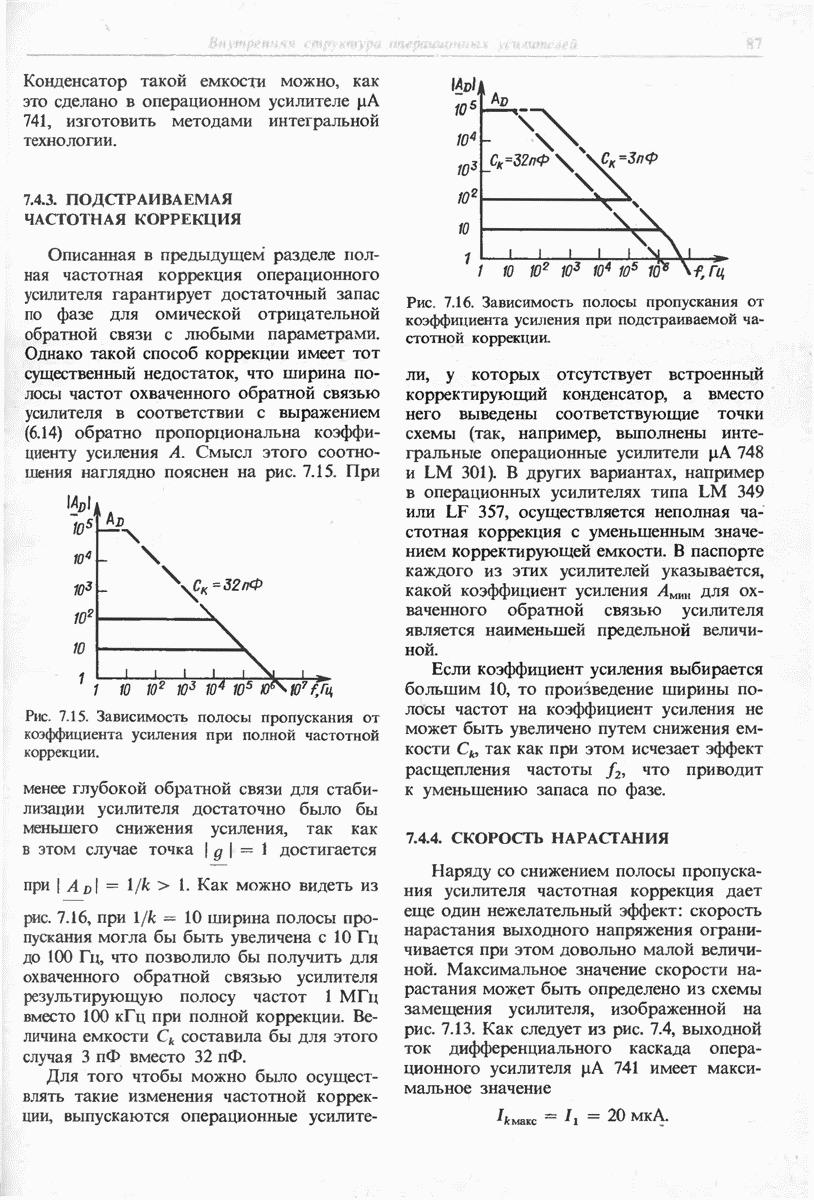
- 7.4.3. ПОДСТРАИВАЕМАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
- 7.4.4. СКОРОСТЬ НАРАСТАНИЯ
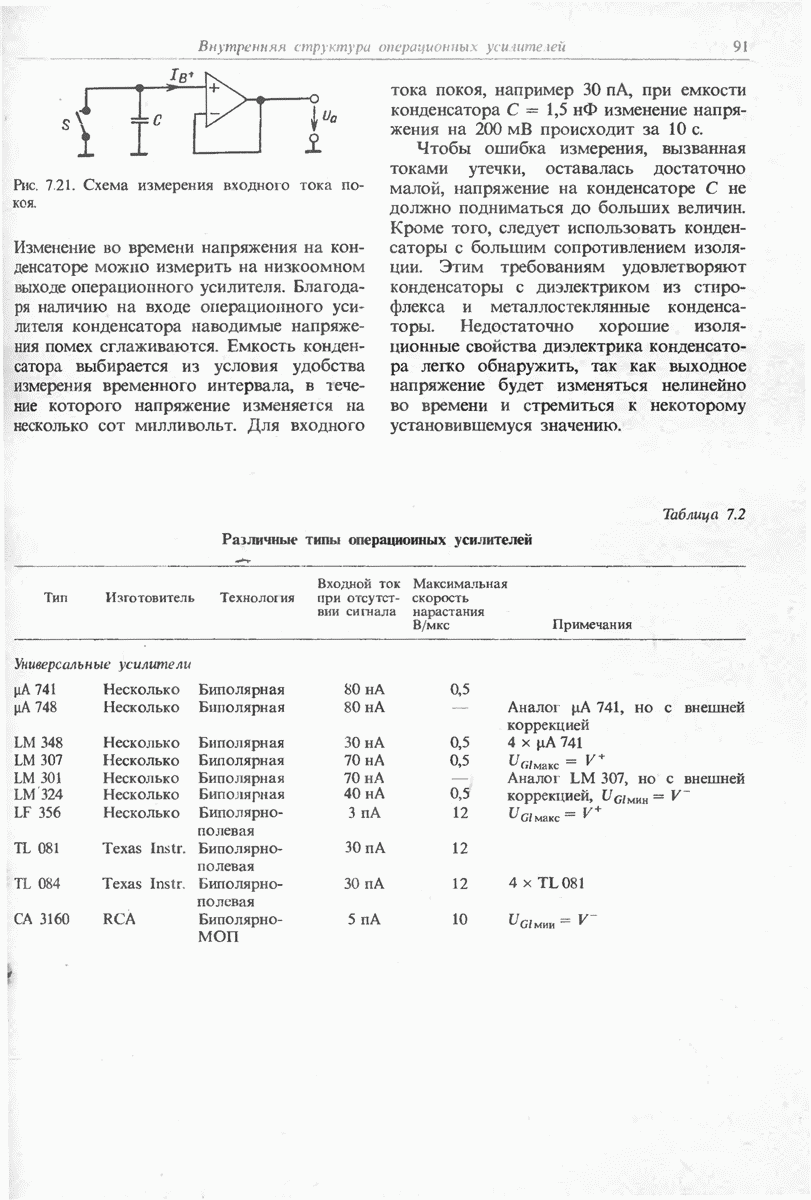
- 7.4.5. КОМПЕНСАЦИЯ ЕМКОСТНОЙ НАГРУЗКИ
- 7.5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
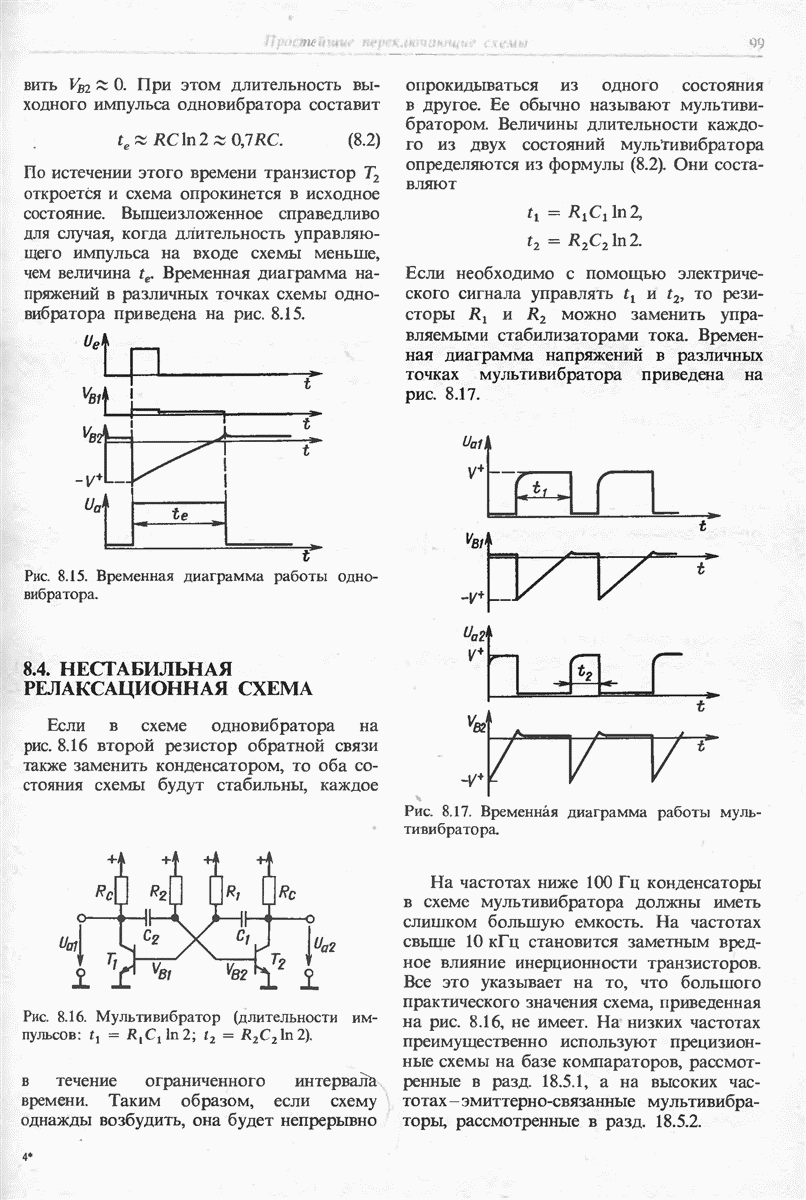
- 8. Простейшие переключающие схемы
- 8.1. ТРАНЗИСТОРНЫЙ КЛЮЧ
- 8.2. БИСТАБИЛЬНЫЕ РЕЛАКСАЦИОННЫЕ СХЕМЫ
- 8.2.2. ТРИГГЕР ШМИТТА
- 8.3. МОНОСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
- 8.4. НЕСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
- 9. Базовые логические схемы
- 9.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
- 9.2. СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.2.1. ТАБЛИЦА КАРНО
- 9.3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4.1. РЕЗИСТИВНО-ТРАНЗИСТОРНАЯ ЛОГИКА (РТЛ)
- 9.4.2. ДИОДНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ДТЛ)
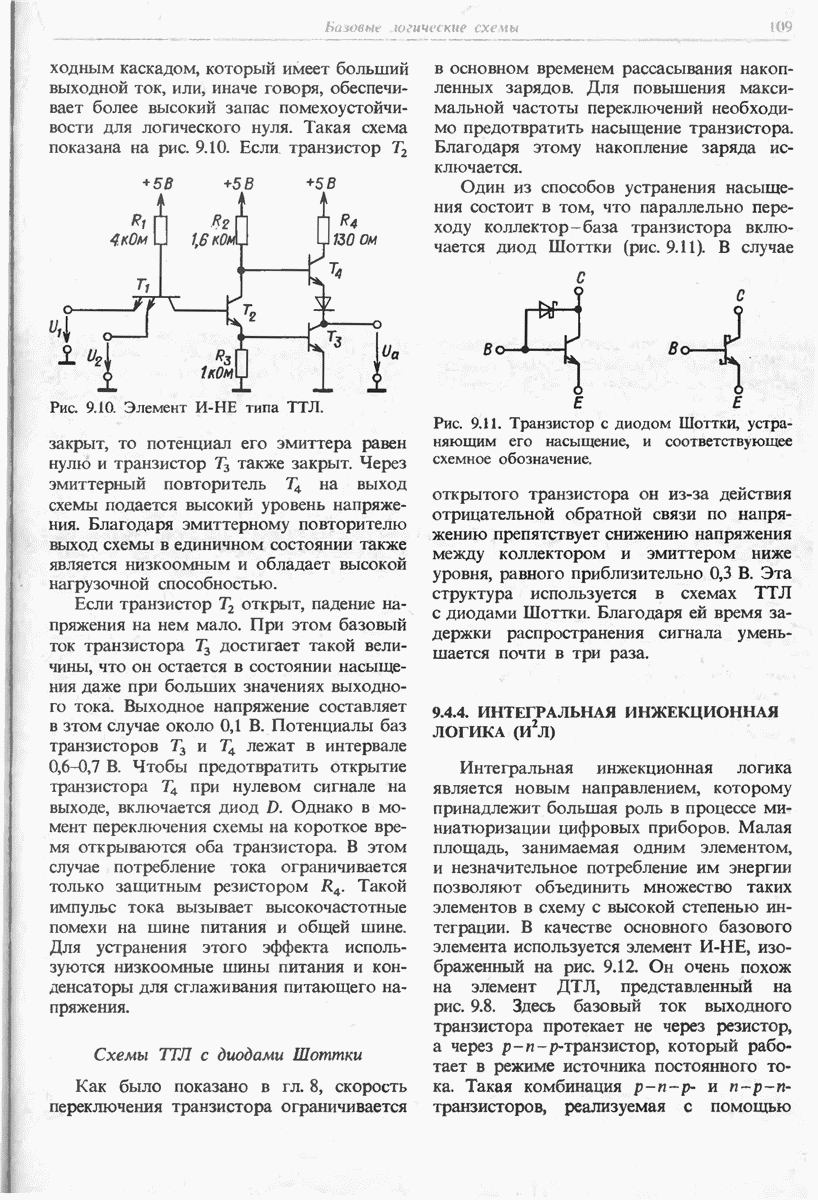
- 9.4.3. ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ТТЛ)
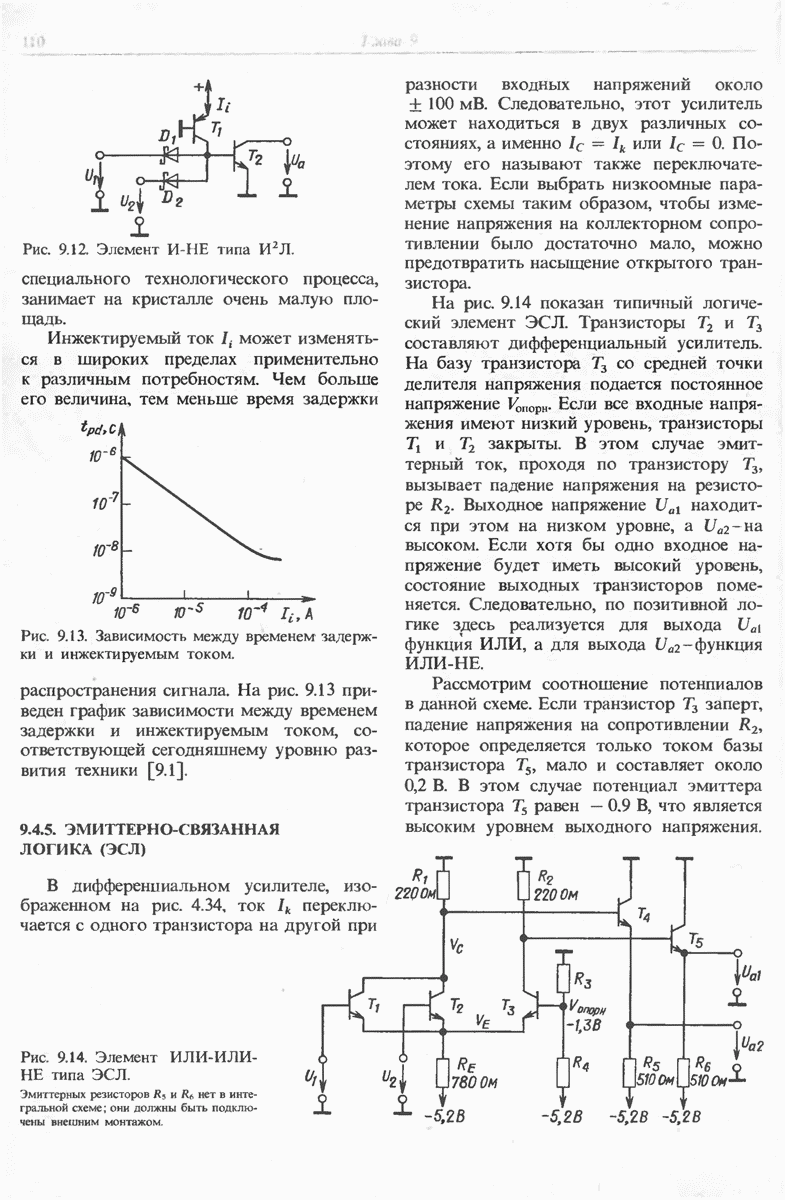
- 9.4.4. ИНТЕГРАЛЬНАЯ ИНЖЕКЦИОННАЯ ЛОГИКА
- 9.4.5. ЭМИТТЕРНО-СВЯЗАННАЯ ЛОГИКА (ЭСЛ)
- 9.4.6. n-КАНАЛЬНАЯ МОП-ЛОГИКА
- 9.4.7. КОМПЛЕМЕНТАРНАЯ МОП-ЛОГИКА (КМОП)
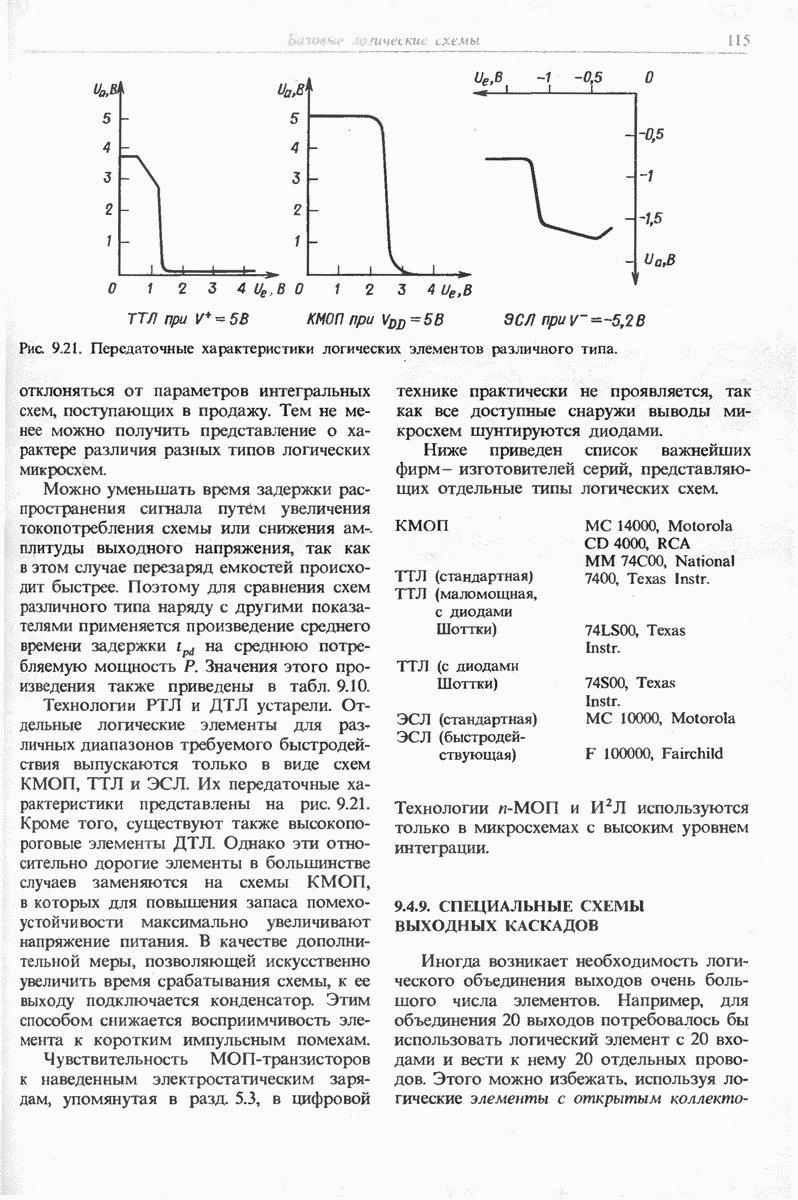
- 9.4.8. ОБЗОР
- 9.4.9. СПЕЦИАЛЬНЫЕ СХЕМЫ ВЫХОДНЫХ КАСКАДОВ
- 9.5. ИНТЕГРАЛЬНЫЕ ТРИГГЕРЫ
- 9.5.2. ТРИГГЕРЫ ТИПА M-S (MASTER-SLAVE)
- 9.5.3. ДИНАМИЧЕСКИЙ ТРИГГЕР
- 9.6. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 9.6.2. ПОСТОЯННЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА (ПЗУ)
- 9.6.3. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ (ПЛМ)
- 10. Оптоэлектронные приборы
- 10.1. ОСНОВНЫЕ ПОНЯТИЯ ФОТОМЕТРИИ
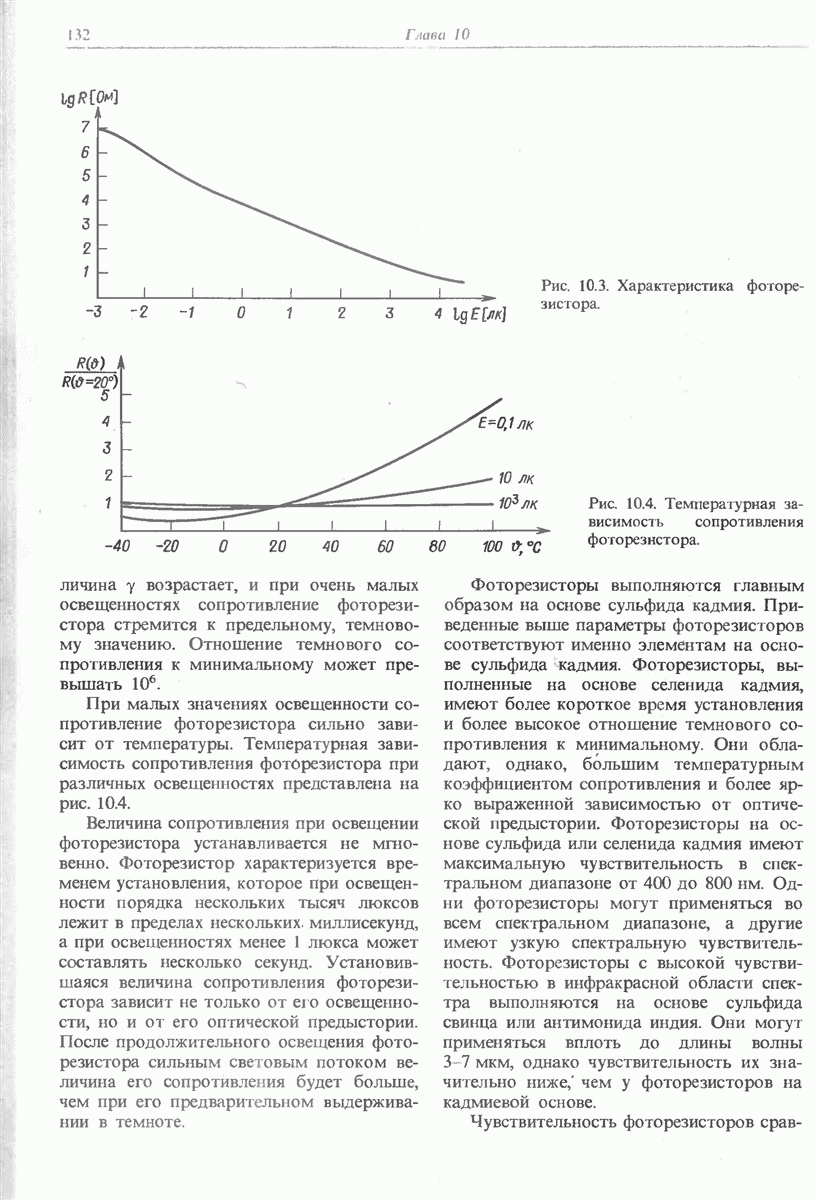
- 10.2. ФОТОРЕЗИСТОР
- 10.3. ФОТОДИОДЫ
- 10.4. ФОТОТРАНЗИСТОРЫ
- 10.5. СВЕТОДИОДЫ
- 10.6. ОПТРОНЫ
- Часть II. Применения
- 11. Линейные и нелинейные аналоговые вычислительные схемы
- 11.1. СХЕМА СУММИРОВАНИЯ
- 11.2. СХЕМЫ ВЫЧИТАНИЯ
- 11.2.2. СХЕМА ВЫЧИТАНИЯ НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 11.3. БИПОЛЯРНОЕ УСИЛИТЕЛЬНОЕ ЗВЕНО
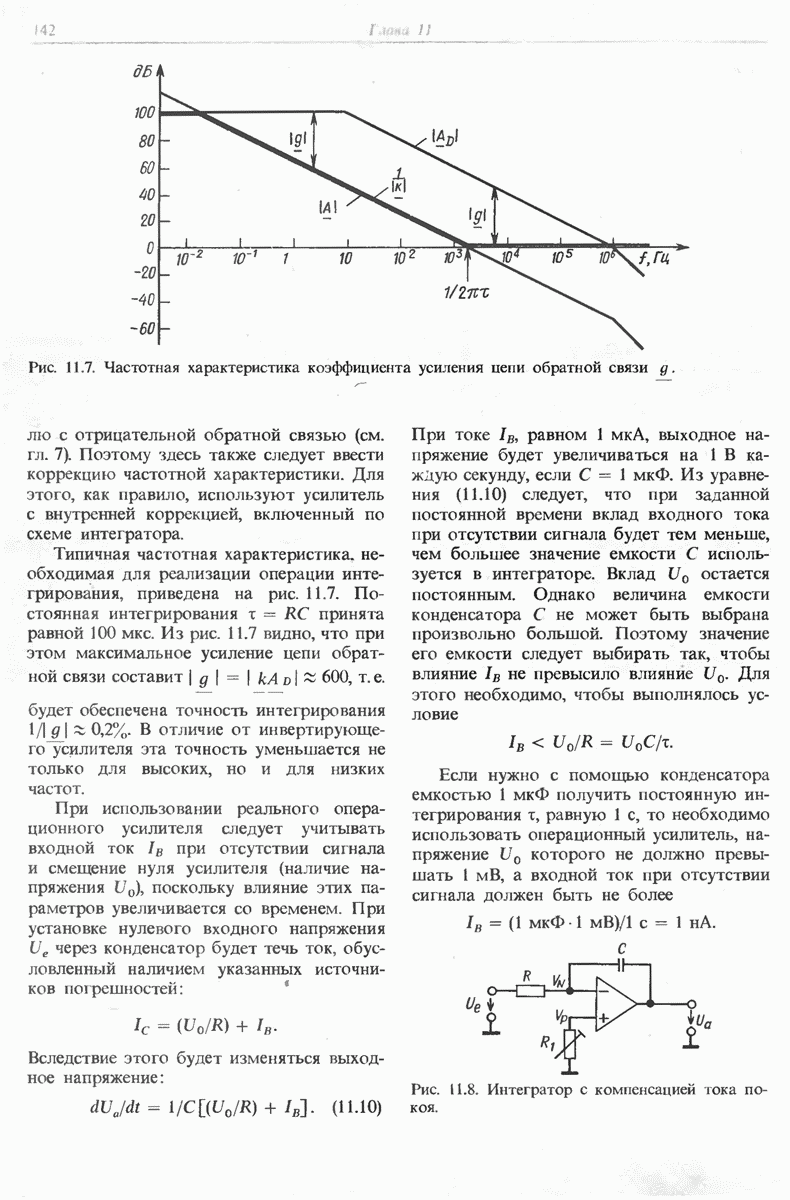
- 11.4. СХЕМЫ ИНТЕГРИРОВАНИЯ
- 11.4.1. ИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.2. ЗАДАНИЕ НАЧАЛЬНЫХ УСЛОВИЙ
- 11.4.3. СУММИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.4. НЕИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
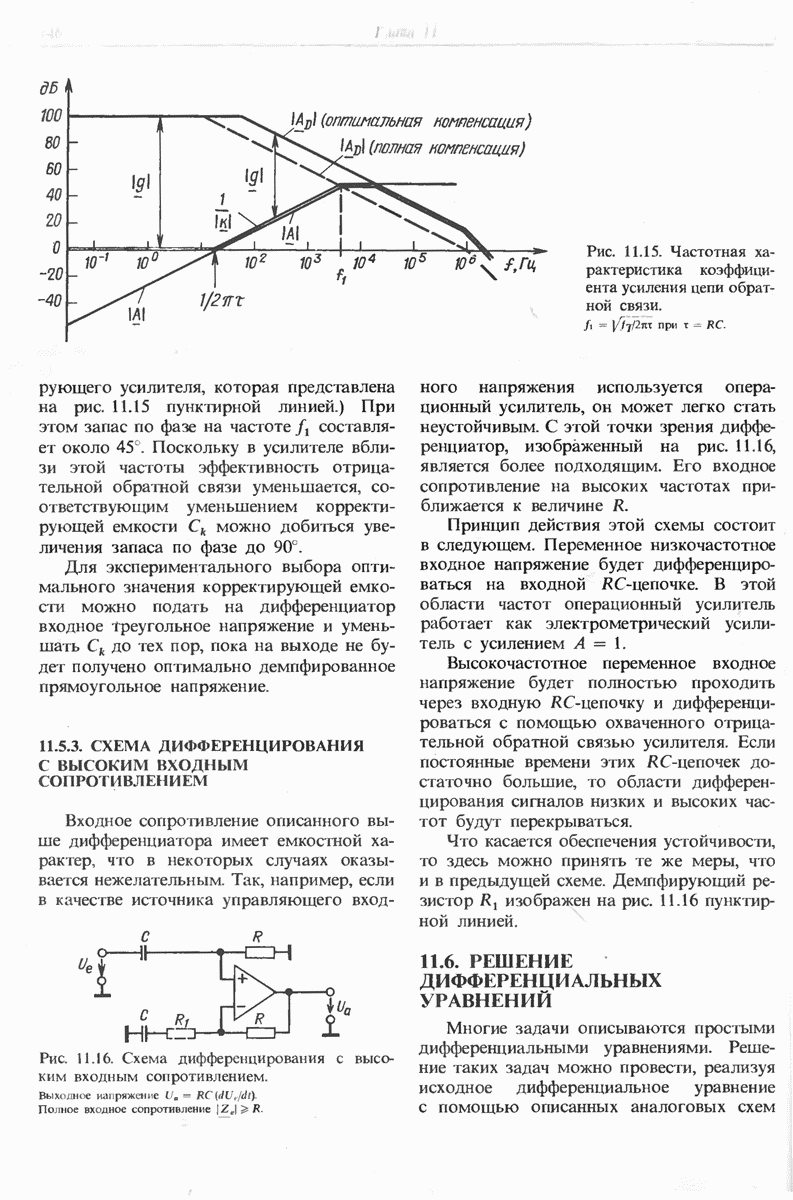
- 11.5. СХЕМЫ ДИФФЕРЕНЦИРОВАНИЯ
- 11.5.3. СХЕМА ДИФФЕРЕНЦИРОВАНИЯ С ВЫСОКИМ ВХОДНЫМ СОПРОТИВЛЕНИЕМ
- 11.6. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 11.7. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11.7.2. ЭКСПОНЕНТА
- 11.7.3. ВЫЧИСЛЕНИЕ СТЕПЕННЫХ ФУНКЦИЙ С ПОМОЩЬЮ ЛОГАРИФМОВ
- 11.7.4. ФУНКЦИИ SIN X И COS X
- 11.7.5. ПЕРЕСТРАИВАЕМЫЕ ФУНКЦИОНАЛЬНЫЕ СХЕМЫ
- 11.8. АНАЛОГОВЫЕ СХЕМЫ УМНОЖЕНИЯ
- 11.8.2. УМНОЖЕНИЕ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ ФУНКЦИОНАЛЬНЫХ ГЕНЕРАТОРОВ
- 11.8.3. СХЕМА УМНОЖЕНИЯ, ИСПОЛЬЗУЮЩАЯ ИЗМЕНЕНИЕ КРУТИЗНЫ ХАРАКТЕРИСТИКИ ТРАНЗИСТОРОВ
- 11.8.4. СХЕМА УМНОЖЕНИЯ С ИЗОЛИРОВАННЫМИ ЗВЕНЬЯМИ
- 11.8.5. БАЛАНСИРОВКА СХЕМ УМНОЖЕНИЯ
- 11.8.6. СХЕМЫ ЧЕТЫРЕХКВАДРАНТНОГО УМНОЖЕНИЯ
- 11.8.7. ПРИМЕНЕНИЕ СХЕМЫ УМНОЖЕНИЯ ДЛЯ ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- 11.9. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 11.9.2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ КООРДИНАТ В ПОЛЯРНЫЕ
- 12. Управляемые источники и схемы преобразования полного сопротивления
- 12.1. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.2. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ ТОКОМ
- 12.3. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.3.2. ИСТОЧНИКИ ТОКА С ЗАЗЕМЛЕННОЙ НАГРУЗКОЙ
- 12.3.3. ЭТАЛОННЫЕ ИСТОЧНИКИ ТОКА НА ТРАНЗИСТОРАХ
- 12.3.4. ПЛАВАЮЩИЕ ИСТОЧНИКИ ТОКА
- 12.4. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ ТОКОМ
- 12.5. ПРЕОБРАЗОВАТЕЛЬ ОТРИЦАТЕЛЬНОГО СОПРОТИВЛЕНИЯ (NIC)
- 12.6. ГИРАТОР
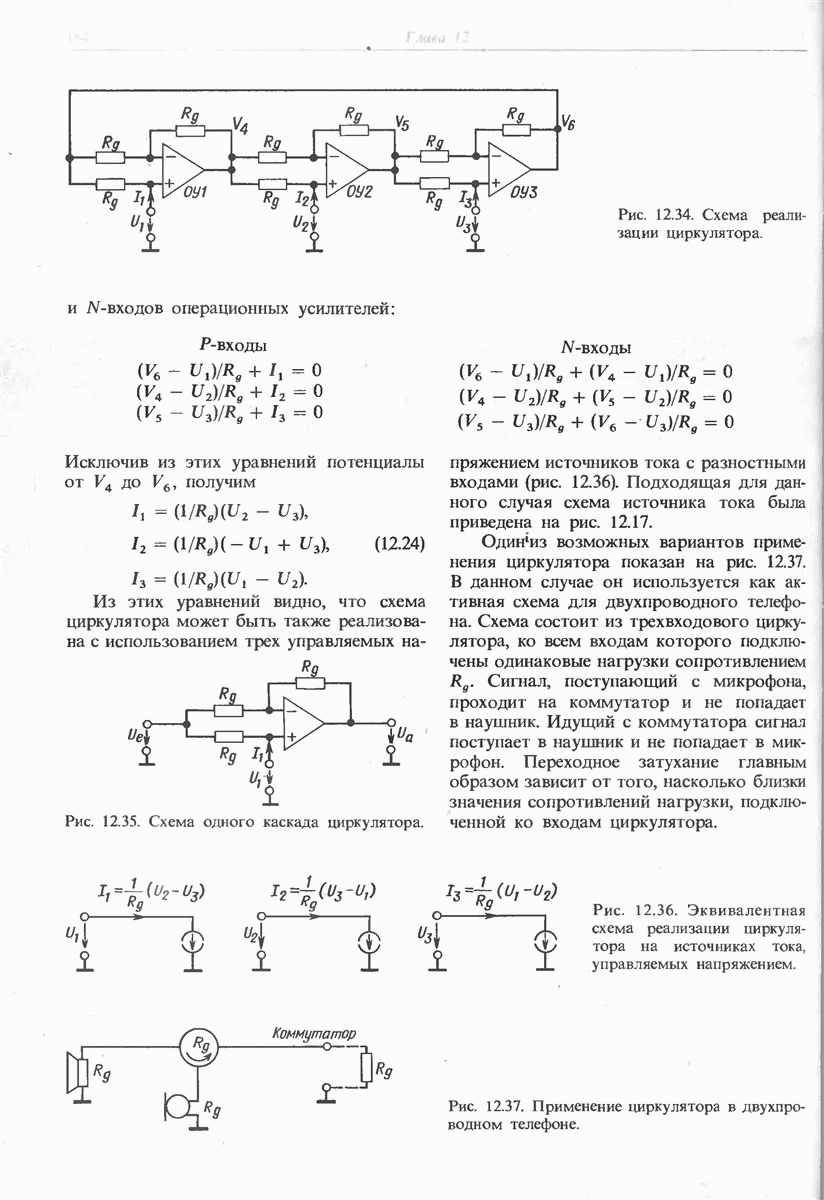
- 12.7. ЦИРКУЛЯТОР
- 13. Активные фильтры
- 13.1. ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
- 13.1.1. ФИЛЬТР БАТТЕРВОРТА
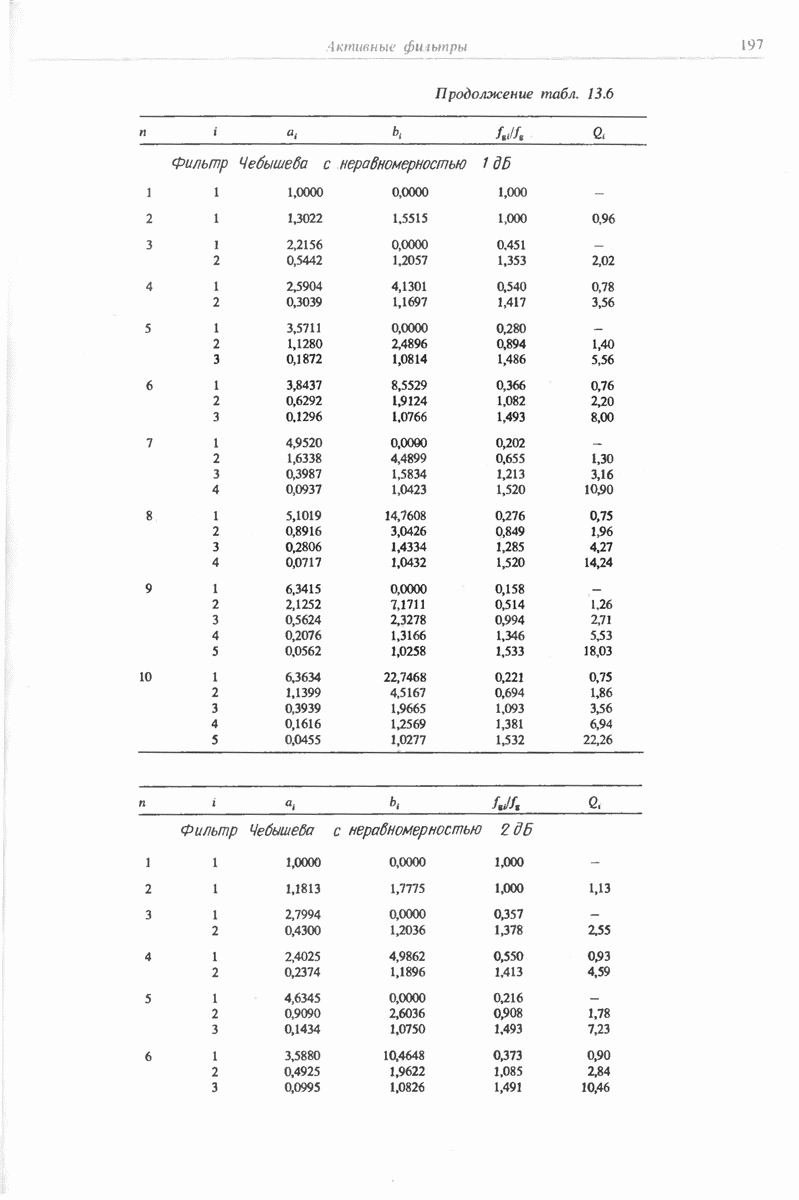
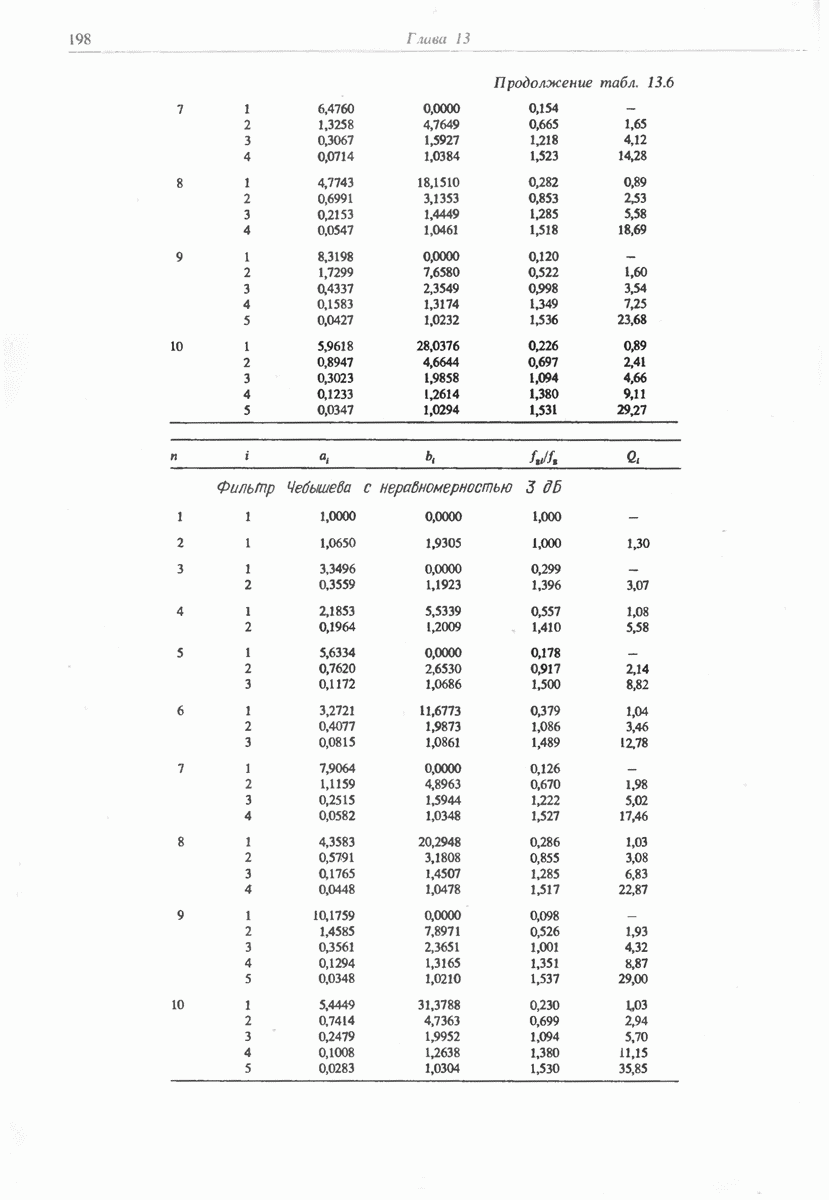
- 13.1.2. ФИЛЬТР ЧЕБЫШЕВА
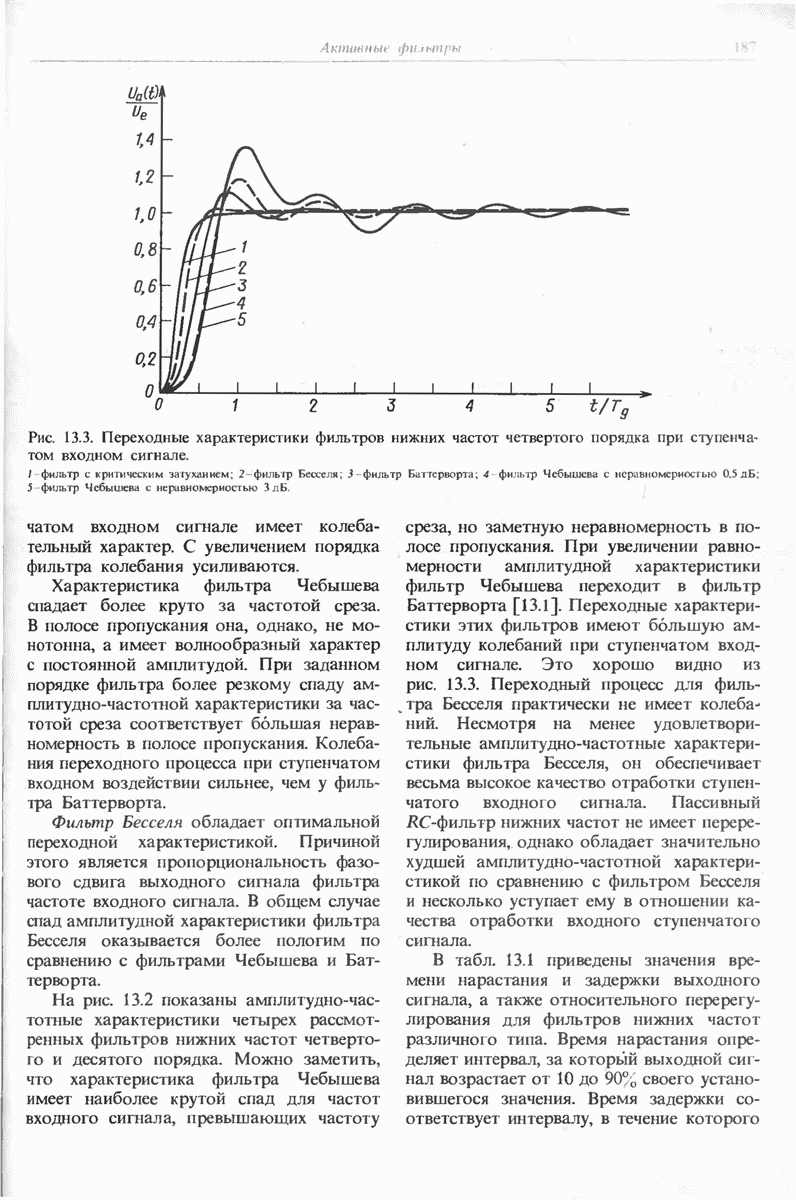
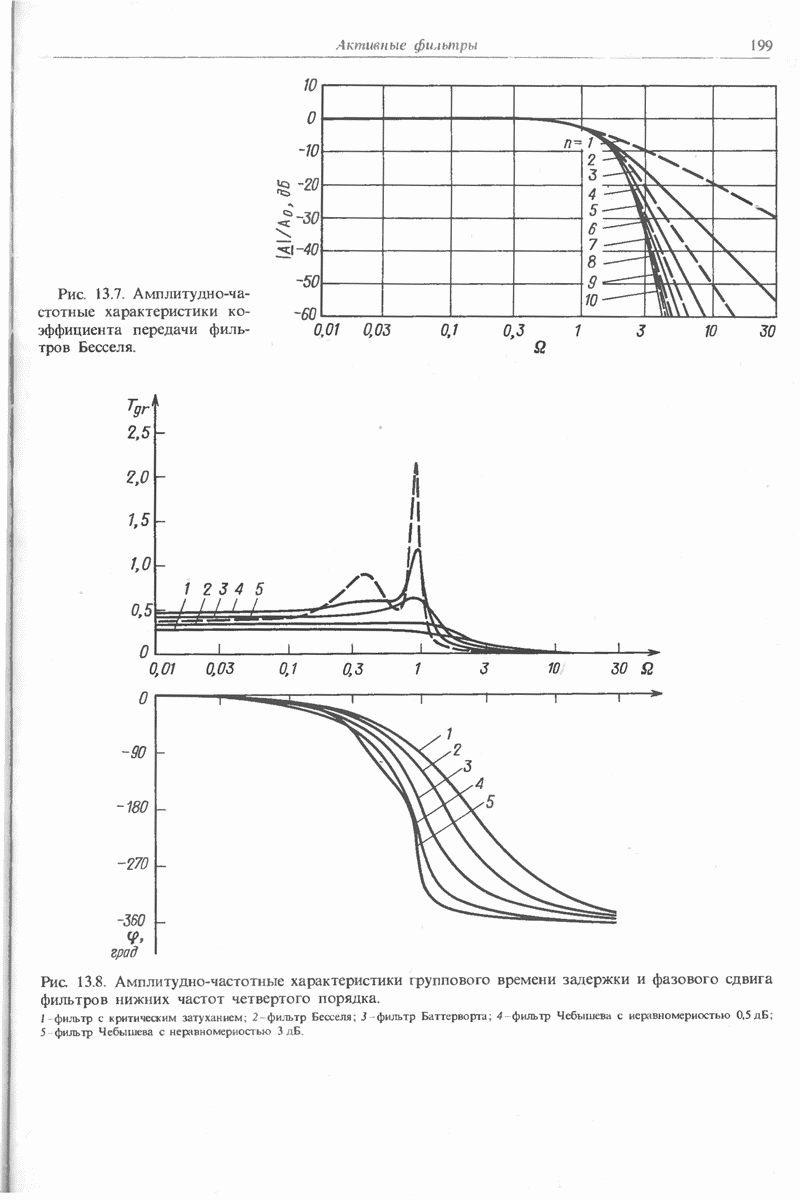
- 13.1.3. ФИЛЬТРЫ БЕССЕЛЯ
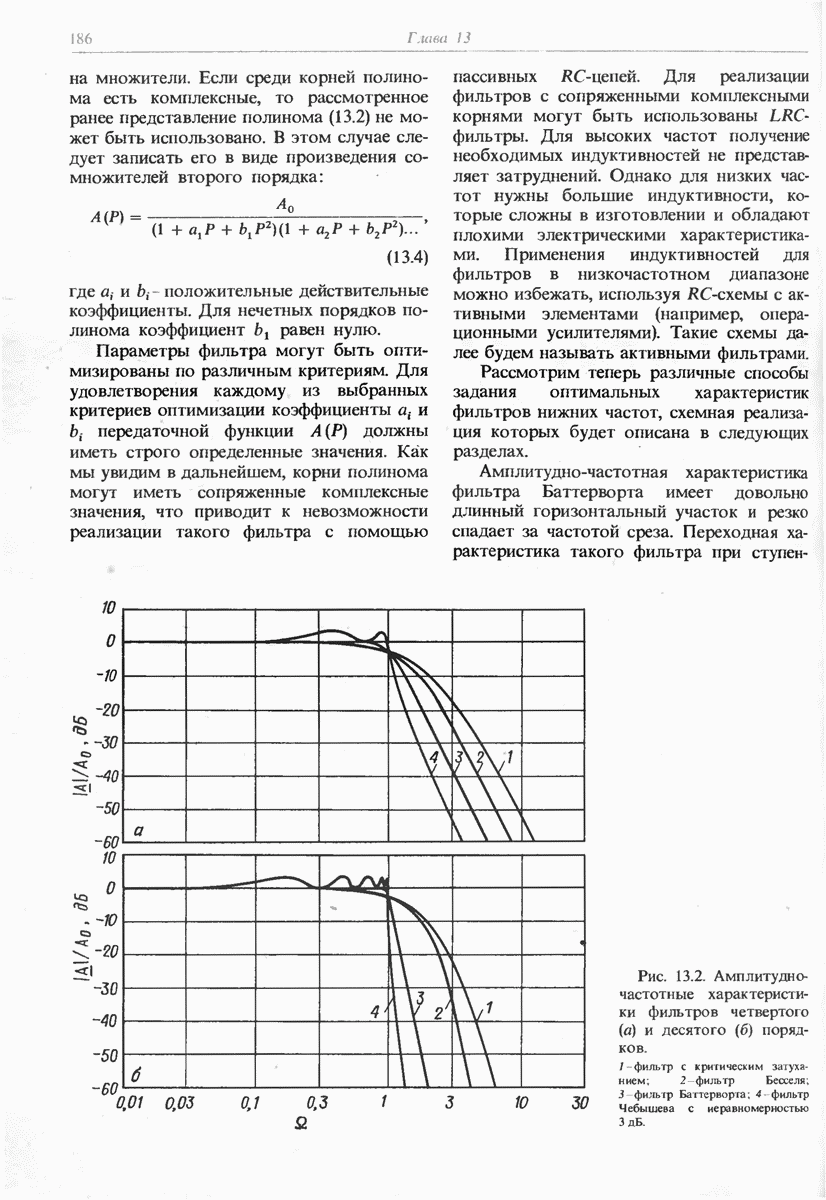
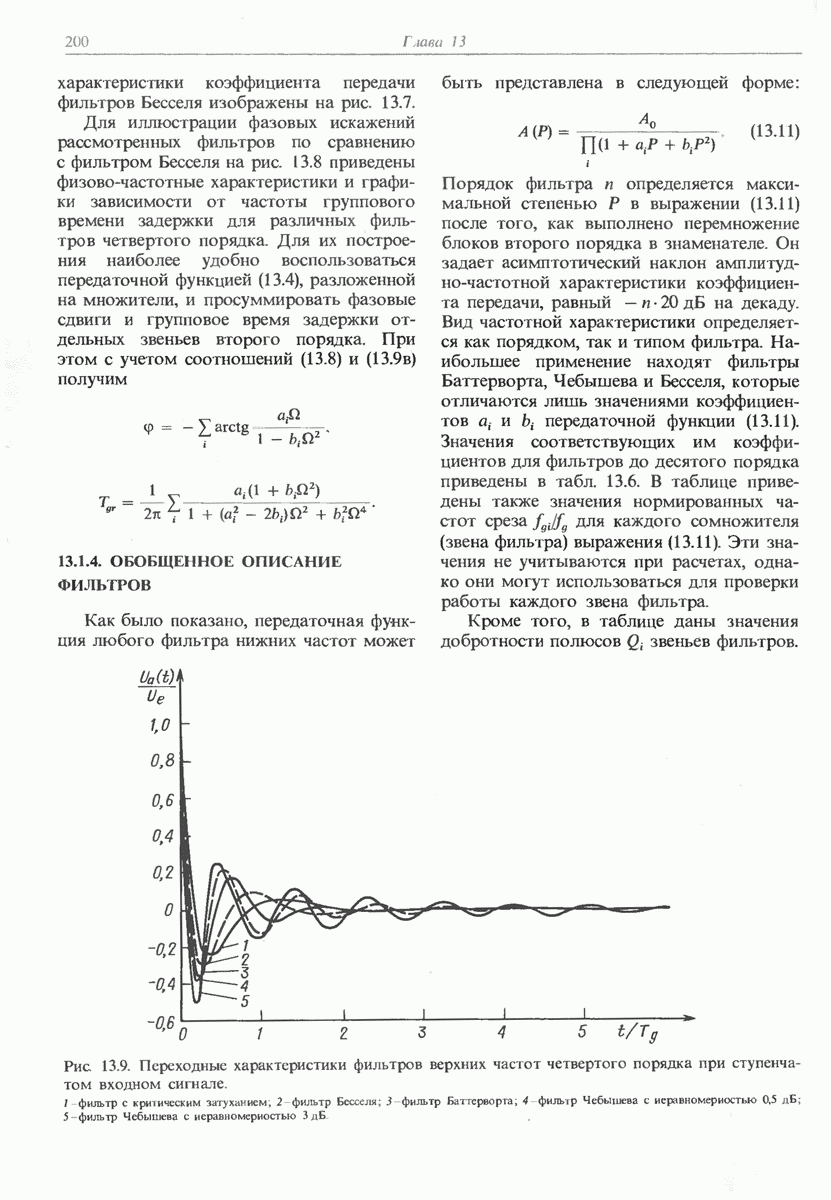
- 13.1.4. ОБОБЩЕННОЕ ОПИСАНИЕ ФИЛЬТРОВ
- 13.2. ПРЕОБРАЗОВАНИЕ НИЖНИХ ЧАСТОТ В ВЕРХНИЕ
- 13.3. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ПЕРВОГО ПОРЯДКА
- 13.4. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ВТОРОГО ПОРЯДКА
- 13.4.2. ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.3. ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.4. ФИЛЬТР НИЖНИХ ЧАСТОТ С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.5. РЕАЛИЗАЦИЯ ФИЛЬТРОВ ВЕРХНИХ И НИЖНИХ ЧАСТОТ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
- 13.6. ПРЕОБРАЗОВАНИЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ В ПОЛОСОВОЙ ФИЛЬТР
- 13.6.1. ПОЛОСОВОЙ ФИЛЬТР ВТОРОГО ПОРЯДКА
- 13.6.2. ПОЛОСОВОЙ ФИЛЬТР ЧЕТВЕРТОГО ПОРЯДКА
- 13.7. РЕАЛИЗАЦИЯ ПОЛОСОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.7.2. ПОЛОСОВОЙ ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.3. ПОЛОСОВОЙ ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.4. ПОЛОСОВОЙ ФИЛЬТР С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.8. ПРЕОБРАЗОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ В ЗАГРАЖДАЮЩИЕ ПОЛОСОВЫЕ ФИЛЬТРЫ
- 13.9. РЕАЛИЗАЦИЯ ЗАГРАЖДАЮЩИХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.9.1. ЗАГРАЖДАЮЩИЙ LRC-ФИЛЬТР
- 13.9.2. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С ДВОЙНЫМ Т-ОБРАЗНЫМ МОСТОМ
- 13.9.3. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С МОСТОМ ВИНА-РОБИНСОНА
- 13.10. ФАЗОВЫЙ ФИЛЬТР
- 13.10.2. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ПЕРВОГО ПОРЯДКА
- 13.10.3. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ВТОРОГО ПОРЯДКА
- 13.11. ПЕРЕСТРАИВАЕМЫЙ УНИВЕРСАЛЬНЫЙ ФИЛЬТР
- 14. Широкополосные усилители
- 14.1. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА УСИЛЕНИЯ ПО ТОКУ ОТ ЧАСТОТЫ
- 14.2. ВЛИЯНИЕ ВНУТРЕННИХ ЕМКОСТЕЙ ТРАНЗИСТОРА И ЕМКОСТЕЙ МОНТАЖА
- 14.3. КАСКОДНАЯ СХЕМА
- 14.4. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ КАК ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5. СИММЕТРИЧНЫЙ ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5.2. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ИНВЕРТОРОМ
- 14.5.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С КОМПЛЕМЕНТАРНОЙ КАСКОДНОЙ СХЕМОЙ
- 14.5.4. ДВУХТАКТНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ
- 14.6. ШИРОКОПОЛОСНЫЙ ПОВТОРИТЕЛЬ НАПРЯЖЕНИЯ
- 14.6.2. ДВУХТАКТНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 14.7. ШИРОКОПОЛОСНЫЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 15. Усилители мощности
- 15.1. ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ КАК УСИЛИТЕЛЬ МОЩНОСТИ
- 15.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 15.2.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ В РЕЖИМЕ AB
- 15.2.3. СПОСОБЫ ЗАДАНИЯ НАПРЯЖЕНИЯ СМЕЩЕНИЯ
- 15.3. СХЕМЫ ОГРАНИЧЕНИЯ ТОКА
- 15.4. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ ПО СХЕМЕ ДАРЛИНГТОНА
- 15.5. РАСЧЕТ МОЩНОГО ОКОНЕЧНОГО КАСКАДА
- 15.6. СХЕМЫ ПРЕДВАРИТЕЛЬНЫХ УСИЛИТЕЛЕЙ НАПРЯЖЕНИЯ
- 15.7. ПОВЫШЕНИЕ НАГРУЗОЧНОЙ СПОСОБНОСТИ ИНТЕГРАЛЬНЫХ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 16. Источники питания
- 16.1. СВОЙСТВА СЕТЕВЫХ ТРАНСФОРМАТОРОВ
- 16.2. ВЫПРЯМИТЕЛИ
- 16.2.1. ОДНОПОЛУПЕРИОДНЫЙ ВЫПРЯМИТЕЛЬ
- 16.2.2. МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 16.2.3. МОСТОВОЙ ВЫПРЯМИТЕЛЬ ДЛЯ ДВУХ СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ ВЫХОДНЫХ НАПРЯЖЕНИЙ
- 16.3. ПОСЛЕДОВАТЕЛЬНАЯ СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЯ
- 16.3.2. СХЕМА С РЕГУЛИРУЮЩИМ УСИЛИТЕЛЕМ
- 16.3.3. ИНТЕГРАЛЬНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 16.3.4. СТАБИЛИЗАТОР С МАЛЫМ НАПРЯЖЕНИЕМ ПОТЕРЬ
- 16.3.5. СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЙ, СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ
- 16.3.6. СТАБИЛИЗАТОР НАПРЯЖЕНИЯ С ИЗМЕРИТЕЛЬНЫМИ ВЫВОДАМИ
- 16.3.7. ЛАБОРАТОРНЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 16.3.8. ОКОНЕЧНЫЙ КАСКАД ЛАБОРАТОРНОГО ИСТОЧНИКА ПИТАНИЯ С БОЛЬШОЙ ВЫХОДНОЙ МОЩНОСТЬЮ
- 16.4. ПОЛУЧЕНИЕ ОПОРНОГО НАПРЯЖЕНИЯ
- 16.4.2. ПОЛУЧЕНИЕ МАЛЫХ ОПОРНЫХ НАПРЯЖЕНИЙ
- 16.5. ИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ
- 16.5.2. ПЕРВИЧНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 17. Аналоговые коммутаторы и компараторы
- 17.2. ЭЛЕКТРОННЫЕ КОММУТАТОРЫ
- 17.2.2. ДИОДНЫЙ КОММУТАТОР
- 17.2.3. КОММУТАТОР НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
- 17.3. АНАЛОГОВЫЕ КОММУТАТОРЫ НА БАЗЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 17.3.2. КОММУТАТОР НА ПОЛЕВОМ ТРАНЗИСТОРЕ С ПЕРЕМЕНОЙ ЗНАКА ВЫХОДНОГО НАПРЯЖЕНИЯ
- 17.3.3. КОММУТАТОР НА БАЗЕ ДИФФЕРЕНЦИАЛЬНОГО УСИЛИТЕЛЯ
- 17.4. АНАЛОГОВЫЕ КОММУТАТОРЫ С ПАМЯТЬЮ
- 17.5. КОМПАРАТОРЫ
- 17.5.2. КОМПАРАТОР С ПРЕЦИЗИОННЫМ ВЫХОДНЫМ НАПРЯЖЕНИЕМ
- 17.5.3. ДВУХПОРОГОВЫЙ КОМПАРАТОР
- 17.6. ТРИГГЕР ШМИТТА
- 17.6.1. ИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.2. НЕИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.3. ПРЕЦИЗИОННЫЙ ТРИГГЕР ШМИТТА
- 18. Генераторы сигналов
- 18.1. LC-ГЕНЕРАТОРЫ
- 18.1.2. ГЕНЕРАТОР С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ (СХЕМА МАЙССНЕРА)
- 18.1.3. ТРЕХТОЧЕЧНАЯ СХЕМА С ИНДУKТИВНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА ХАРТЛИ)
- 18.1.4. ТРЕХТОЧЕЧНАЯ СХЕМА С ЕМКОСТНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА КОЛПИТЦА)
- 18.1.5. LC-ГЕНЕРАТОР С ЭМИТТЕРНОЙ СВЯЗЬЮ
- 18.1.6. ДВУХТАКТНЫЕ ГЕНЕРАТОРЫ
- 18.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ
- 18.2.1. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КВАРЦЕВОГО РЕЗОНАТОРА
- 18.2.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ С LC-КОЛЕБАТЕЛЬНЫМ КОНТУРОМ
- 18.2.3. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ БЕЗ LC-КОНТУРА
- 18.3. СИНУСОИДАЛЬНЫЕ RC-ГЕНЕРАТОРЫ
- 18.3.2. МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 18.4. ГЕНЕРАТОРЫ СИГНАЛОВ СПЕЦИАЛЬНОЙ ФОРМЫ (ФУНКЦИОНАЛЬНЫЕ ГЕНЕРАТОРЫ)
- 18.4.2. ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР С УПРАВЛЯЕМОЙ ЧАСТОТОЙ ВЫХОДНОГО СИГНАЛА
- 18.4.3. ВЫСОКОЧАСТОТНЫЙ ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР
- 18.5. МУЛЬТИВИБРАТОРЫ
- 18.5.1. НИЗКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 18.5.2. ВЫСОКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 19. Комбинационные логические схемы
- 19.1. ПРЕОБРАЗОВАТЕЛИ КОДОВ
- 19.1.2. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 19.1.3. КОД ГРЕЯ
- 19.2. МУЛЬТИПЛЕКСОР И ДЕМУЛЬТИПЛЕКСОР
- 19.3. КОМБИНАЦИОННОЕ УСТРОЙСТВО СДВИГА
- 19.4. КОМПАРАТОРЫ
- 19.5. СУММАТОРЫ
- 19.5.1. ПОЛУСУММАТОР
- 19.5.2. ПОЛНЫЙ СУММАТОР
- 19.5.3. СУММАТОРЫ С ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ
- 19.5.4. СЛОЖЕНИЕ ДВОИЧНО-ДЕСЯТИЧНЫХ ЧИСЕЛ
- 19.5.5. ВЫЧИТАНИЕ
- 19.5.6. СЛОЖЕНИЕ ЧИСЕЛ С ЛЮБЫМИ ЗНАКАМИ
- 19.6. УМНОЖИТЕЛИ
- 19.7. ЦИФРОВЫЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 20. Интегральные схемы со структурами последовательностного типа
- 20.1. ДВОИЧНЫЕ СЧЕТЧИКИ
- 20.1.1. АСИНХРОННЫЙ (ПОСЛЕДОВАТЕЛЬНЫЙ) СЧЕТЧИК
- 20.1.2. СИНХРОННЫЙ (ПАРАЛЛЕЛЬНЫЙ) СЧЕТЧИК
- 20.2. ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК В КОДЕ 8421
- 20.2.1. АСИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.2.2. СИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.3. СЧЕТЧИК С ПРЕДВАРИТЕЛЬНОЙ УСТАНОВКОЙ
- 20.4. РЕГИСТРЫ СДВИГА
- 20.4.2. КОЛЬЦЕВОЙ РЕГИСТР
- 20.4.3. РЕГИСТР СДВИГА С ПАРАЛЛЕЛЬНЫМ ВВОДОМ
- 20.4.4. РЕГИСТР СДВИГА С ПЕРЕКЛЮЧАЕМЫМ НАПРАВЛЕНИЕМ СДВИГА
- 20.5. ПОЛУЧЕНИЕ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- 20.6. ПЕРВОНАЧАЛЬНАЯ ОБРАБОТКА АСИНХРОННОГО СИГНАЛА
- 20.6.2. СИНХРОНИЗАЦИЯ ИМПУЛЬСОВ
- 20.6.3. СИНХРОННЫЙ ОДНОВИБРАТОР
- 20.6.4. СИНХРОННЫЙ ДЕТЕКТОР ИЗМЕНЕНИЙ
- 20.6.5. СИНХРОННЫЙ ТАКТОВЫЙ ПЕРЕКЛЮЧАТЕЛЬ
- 20.7. СИСТЕМАТИЧЕСКИЙ СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ
- 20.7.2. ПРИМЕР СИНТЕЗА ПЕРЕКЛЮЧАЕМОГО СЧЕТЧИКА
- 20.7.3. СОКРАЩЕНИЕ ЕМКОСТИ ПАМЯТИ
- 21. Микро-ЭВМ
- 21.1. ОСНОВНАЯ СТРУКТУРА МИКРО-ЭВМ
- 21.2. ПРИНЦИП ДЕЙСТВИЯ МИКРОПРОЦЕССОРА
- 21.3. НАБОР КОМАНД
- 21.4. ОТЛАДОЧНЫЕ СРЕДСТВА
- 21.5. ОБЗОР МИКРОПРОЦЕССОРОВ РАЗЛИЧНОГО ТИПА
- 21.6. МОДУЛЬНОЕ ПОСТРОЕНИЕ МИКРО-ЭВМ
- 21.7. ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА
- 21.7.1. ПАРАЛЛЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.2. ПОСЛЕДОВАТЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.3. ИНТЕРФЕЙС МАГИСТРАЛИ «ОБЩАЯ ШИНА»
- 21.7.4. ПРОГРАММИРУЕМЫЙ СЧЕТЧИК
- 21.7.5. ПОДКЛЮЧЕНИЕ ПЕРИФЕРИЙНЫХ МОДУЛЕЙ СЕМЕЙСТВА 8080 К МАГИСТРАЛЯМ СЕМЕЙСТВА 6800
- 21.7.6. ОБЗОР ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
- 21.8. МИНИМАЛЬНЫЕ СИСТЕМЫ
- 21.8.2. ОДНОКРИСТАЛЬНАЯ МИКРО-ЭВМ
- 22. Цифровые фильтры
- 22.1. ТЕОРЕМА О ДИСКРЕТИЗАЦИИ (ТЕОРЕМА О ВЫБОРКАХ)
- 22.1.2. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 22.2. ЦИФРОВАЯ ФУНКЦИЯ ПЕРЕДАЧИ ФИЛЬТРА
- 22.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
- 22.4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ
- 22.4.2. СТРУКТУРА ЦИФРОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 22.4.3. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 23. Передача данных и индикация
- 23.1. СОЕДИНИТЕЛЬНЫЕ ЛИНИИ
- 23.2. ЗАЩИТА ДАННЫХ
- 23.2.2. КОД ХЕММИНГА
- 23.3. СТАТИЧЕСКИЕ ЦИФРОВЫЕ ИНДИКАТОРЫ
- 23.3.1. ДВОИЧНЫЕ ИНДИКАТОРЫ НА СВЕТОДИОДАХ
- 23.3.2. ДЕКАДНЫЕ ИНДИКАТОРЫ
- 23.3.3. ИНДИКАЦИЯ В ШЕСТНАДЦАТЕРИЧНОМ КОДЕ
- 23.4. МУЛЬТИПЛЕКСНЫЕ ИНДИКАТОРЫ
- 23.4.1. МНОГОРАЗРЯДНЫЕ 7-СЕГМЕНТНЫЕ ИНДИКАТОРЫ
- 23.4.2. МАТРИЦА ТОЧЕК
- 24. Цифро-аналоговые и аналого-цифровые преобразователи
- 24.1. СХЕМОТЕХНИЧЕСКИЕ ПРИНЦИПЫ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.1.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ПЕРЕКИДНЫМИ КЛЮЧАМИ
- 24.1.3. РЕЗИСТИВНАЯ МАТРИЦА ПОСТОЯННОГО ИМПЕДАНСА (МАТРИЦА ТИПА R-2R)
- 24.1.4. РЕЗИСТИВНАЯ МАТРИЦА ДЛЯ ДЕКАДНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 24.2. ПОСТРОЕНИЕ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ С ЭЛЕКТРОННЫМИ КЛЮЧАМИ
- 24.2.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ТОКОВЫМИ КЛЮЧАМИ
- 24.3. ЦА-ПРЕОБРАЮВАТЕЛИ ДЛЯ СПЕЦИАЛЬНЫХ ПРИМЕНЕНИЙ
- 24.3.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ДЕЛЕНИЯ
- 24.3.3. ЦА-ПРЕОБРАЗОВАТЕЛЬ КАК ГЕНЕРАТОР ФУНКЦИЙ
- 24.4. ОСНОВНЫЕ ПРИНЦИПЫ АЦ-ПРЕОБРАЗОВАНИЯ
- 24.5. ТОЧНОСТЬ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.6. ПОСТРОЕНИЕ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 25. Измерительные схемы
- 25.1. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ
- 25.1.2. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- 25.1.3. ИЗОЛИРОВАННЫЙ УСИЛИТЕЛЬ
- 25.2. ИЗМЕРЕНИЕ ТОКА
- 25.2.1. ИЗОЛИРОВАННЫЕ ОТ ЗЕМЛИ АМПЕРМЕТРЫ С МАЛЫМ ПАДЕНИЕМ НАПРЯЖЕНИЯ
- 25.2.2. ИЗМЕРЕНИЕ ТОКА ПРИ ВЫСОКОМ ПОТЕНЦИАЛЕ
- 25.3. ИЗМЕРИТЕЛЬНЫЙ ВЫПРЯМИТЕЛЬ
- 25.3.2. ИЗМЕРЕНИЕ ЭФФЕКТИВНОГО ЗНАЧЕНИЯ
- 25.3.3. ИЗМЕРЕНИЕ АМПЛИТУДНЫХ ЗНАЧЕНИЙ
- 25.3.4. СИНХРОННЫЙ ДЕТЕКТОР
- 26. Электронные регуляторы
- 26.2. ТИПЫ РЕГУЛЯТОРОВ
- 26.2.1. П-РЕГУЛЯТОР
- 26.2.2. ПИ-РЕГУЛЯТОР
- 26.2.3. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР
- 26.2.4. НАСТРАИВАЕМЫЕ ПИД-РЕГУЛЯТОРЫ
- 26.3. УПРАВЛЕНИЕ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ
- 26.4. ОТСЛЕЖИВАЮЩАЯ СИНХРОНИЗАЦИЯ (АВТОПОДСТРОЙКА)
- 26.4.1. ЭЛЕМЕНТЫ ВЫБОРКИ-ХРАНЕНИЯ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
- 26.4.2. СИНХРОННЫЙ ВЫПРЯМИТЕЛЬ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
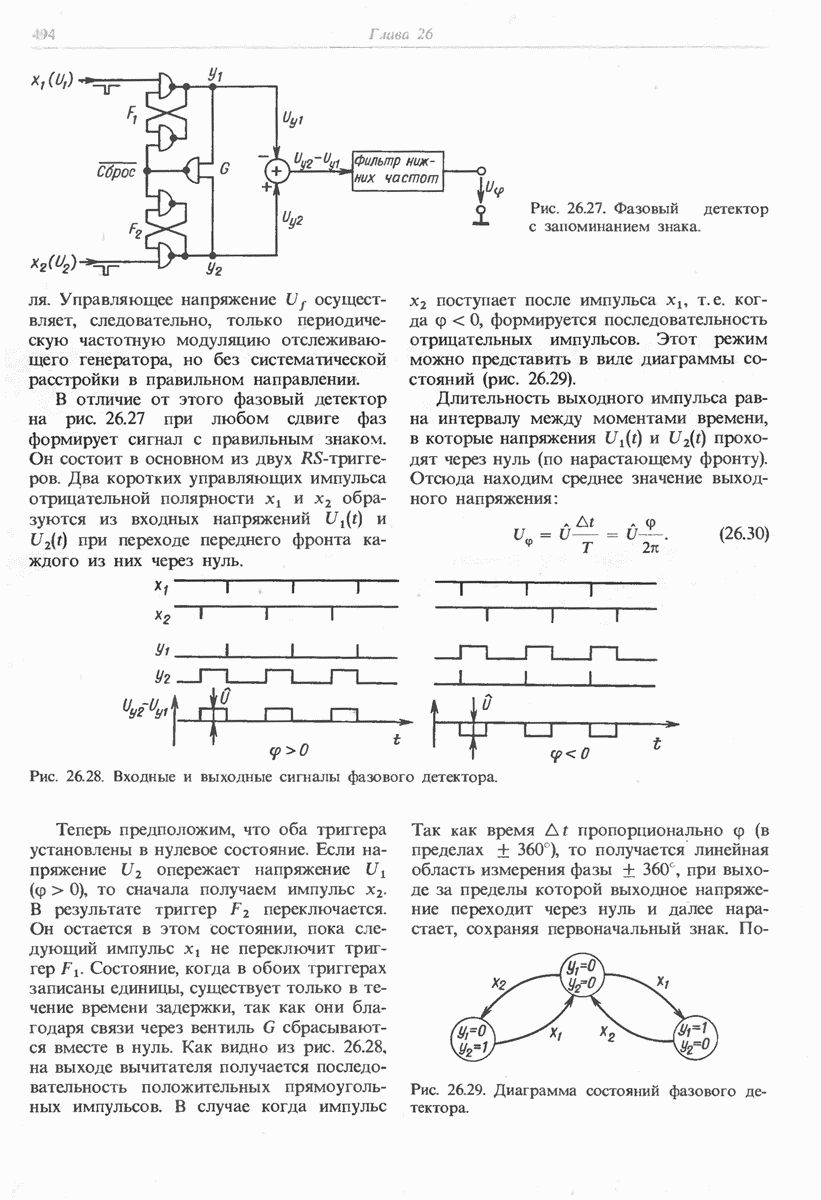
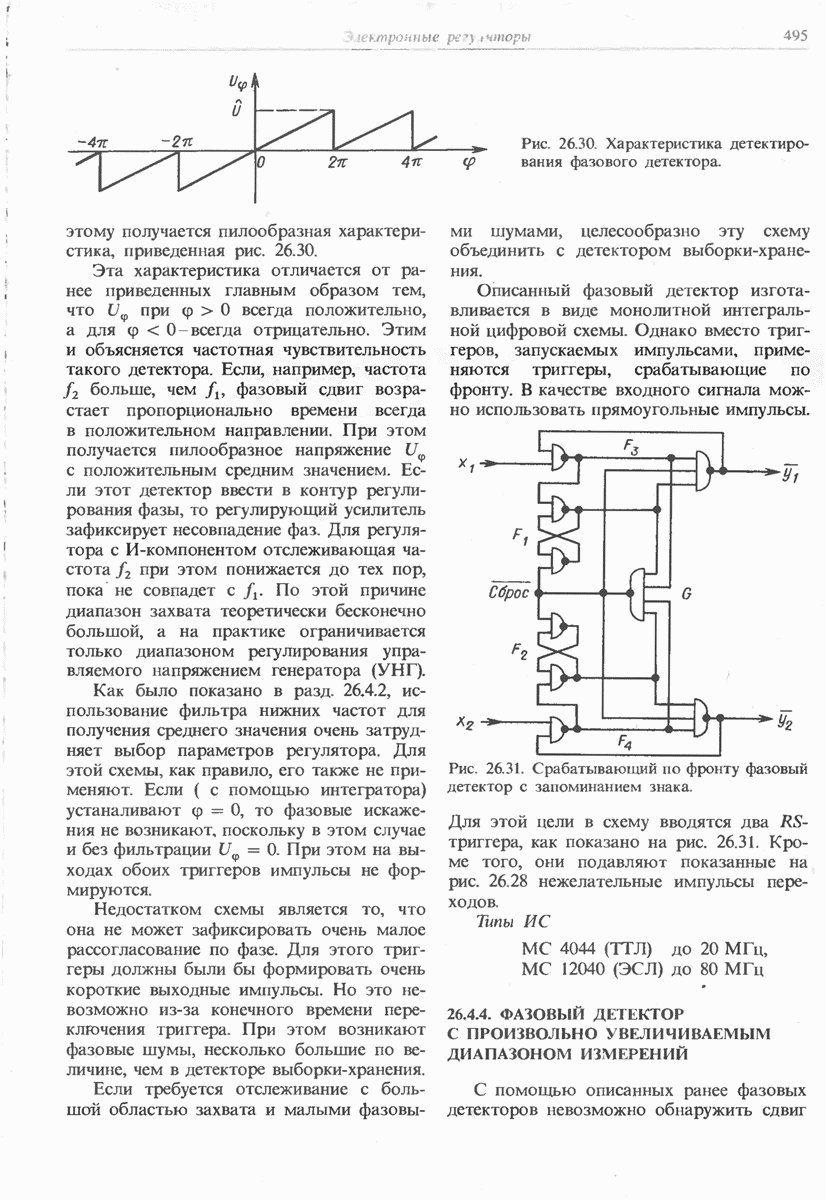
- 26.4.3. ЧАСТОТНО-ЧУВСТВИТЕЛЬНЫЙ ФАЗОВЫЙ ДЕТЕКТОР
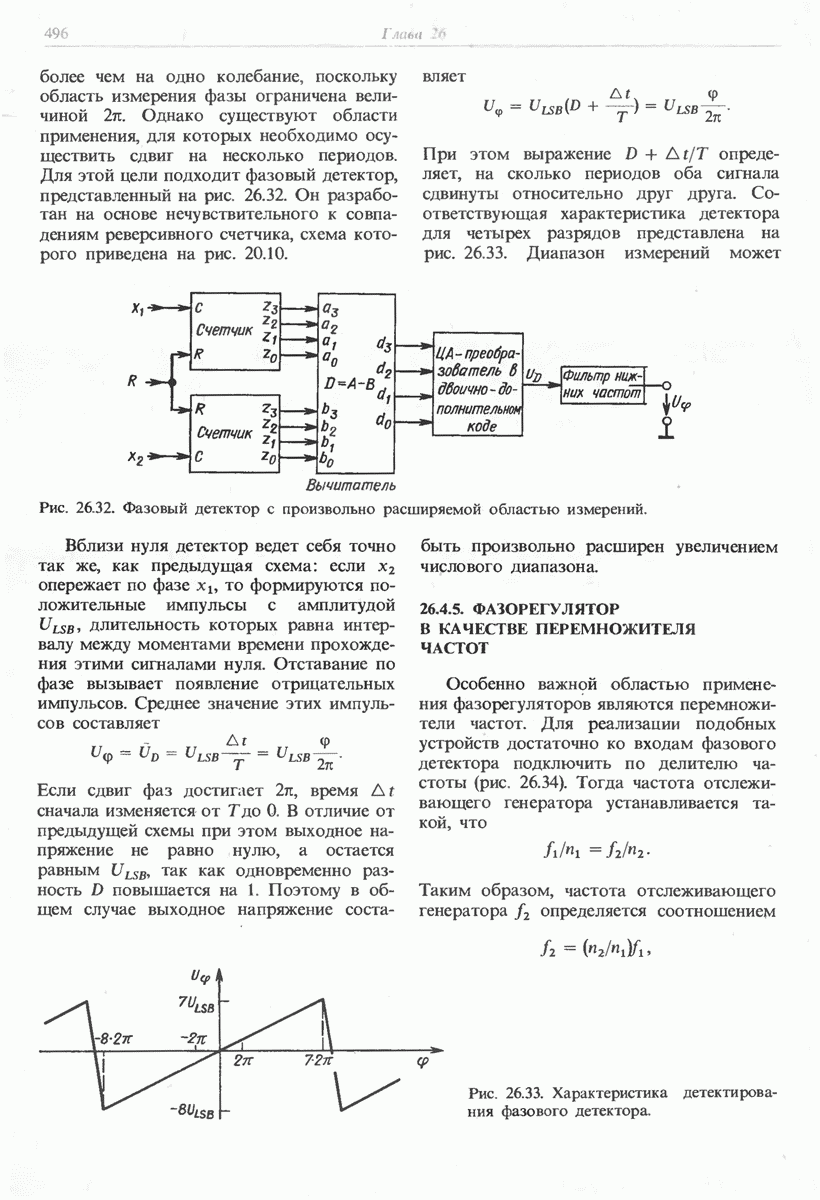
- 26.4.4. ФАЗОВЫЙ ДЕТЕКТОР С ПРОИЗВОЛЬНО УВЕЛИЧИВАЕМЫМ ДИАПАЗОНОМ ИЗМЕРЕНИЙ
- 26.4.5. ФАЗОРЕГУЛЯТОР В КАЧЕСТВЕ ПЕРЕМНОЖИТЕЛЯ ЧАСТОТ