| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.4. СХЕМЫ ИНТЕГРИРОВАНИЯ
Наиболее важное значение для аналоговых вычислителей имеет применение операционных усилителей для реализации операций интегрирования, В общем случае интегратор описывается выражением

11.4.1. ИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
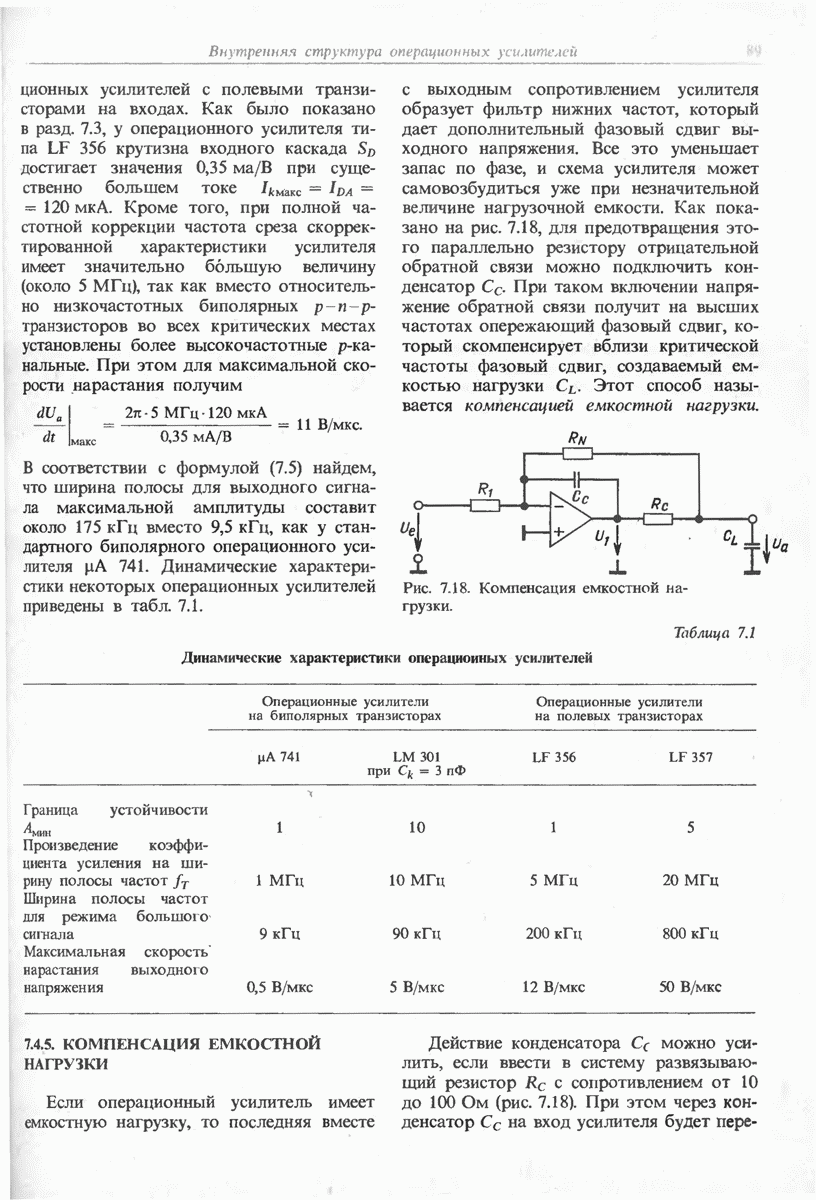
Интегратор на рис. 11.6 построен на основе инвертирующего усилителя, в котором резистор обратной связи  заменен конденсатором С. В этом случае выходное напряжение описывается выражением
заменен конденсатором С. В этом случае выходное напряжение описывается выражением

где  величина заряда, которая была на конденсаторе к моменту начала интегрирования
величина заряда, которая была на конденсаторе к моменту начала интегрирования  Учитывая, что
Учитывая, что  можно записать
можно записать

Постоянный член  определяет начальное условие интегрирования:
определяет начальное условие интегрирования:  . С помощью специальных мер можно реализовать любые начальные условия.
. С помощью специальных мер можно реализовать любые начальные условия.
Рассмотрим два особых случая. Если входное напряжение  постоянно, то изменение выходного сигнала описывается формулой
постоянно, то изменение выходного сигнала описывается формулой

т. е. выходной сигнал линейно возрастает со временем. Поэтому рассмотренная схема оказывается пригодной для формирования пилообразного напряжения.

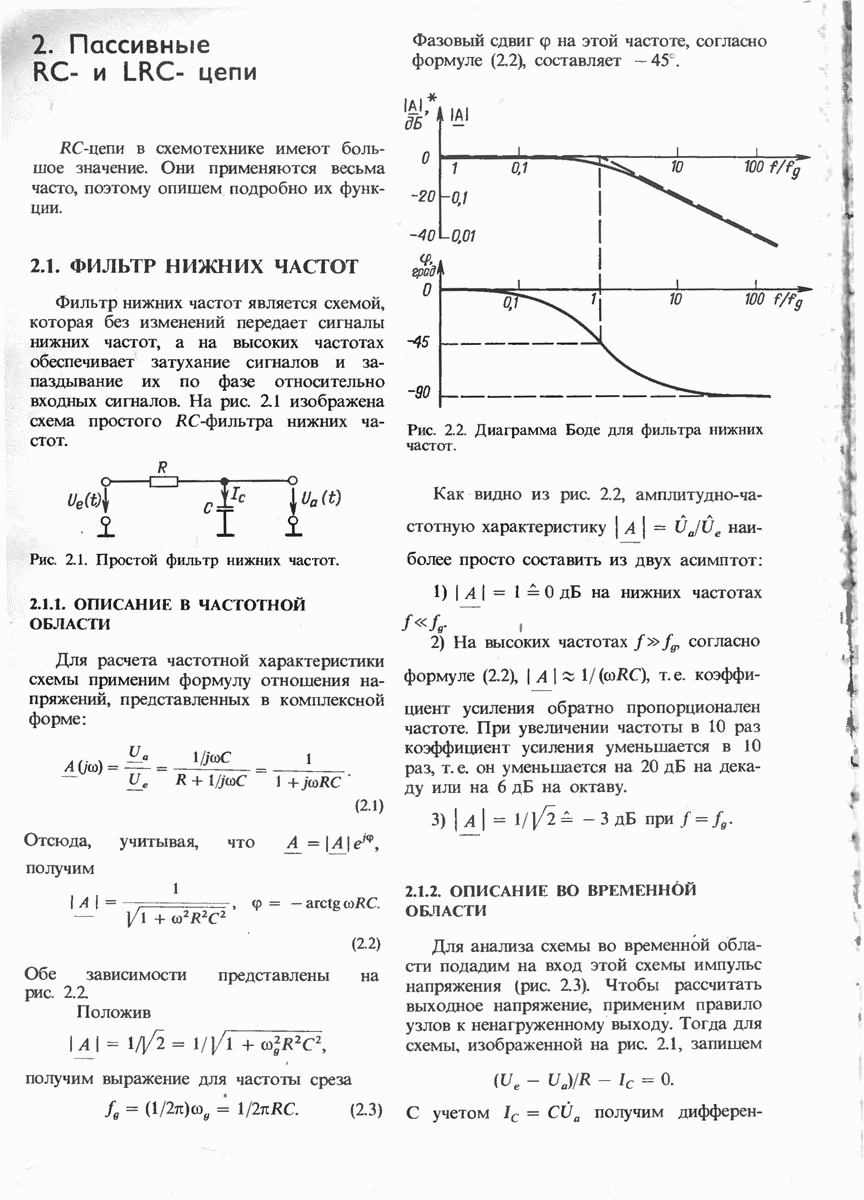
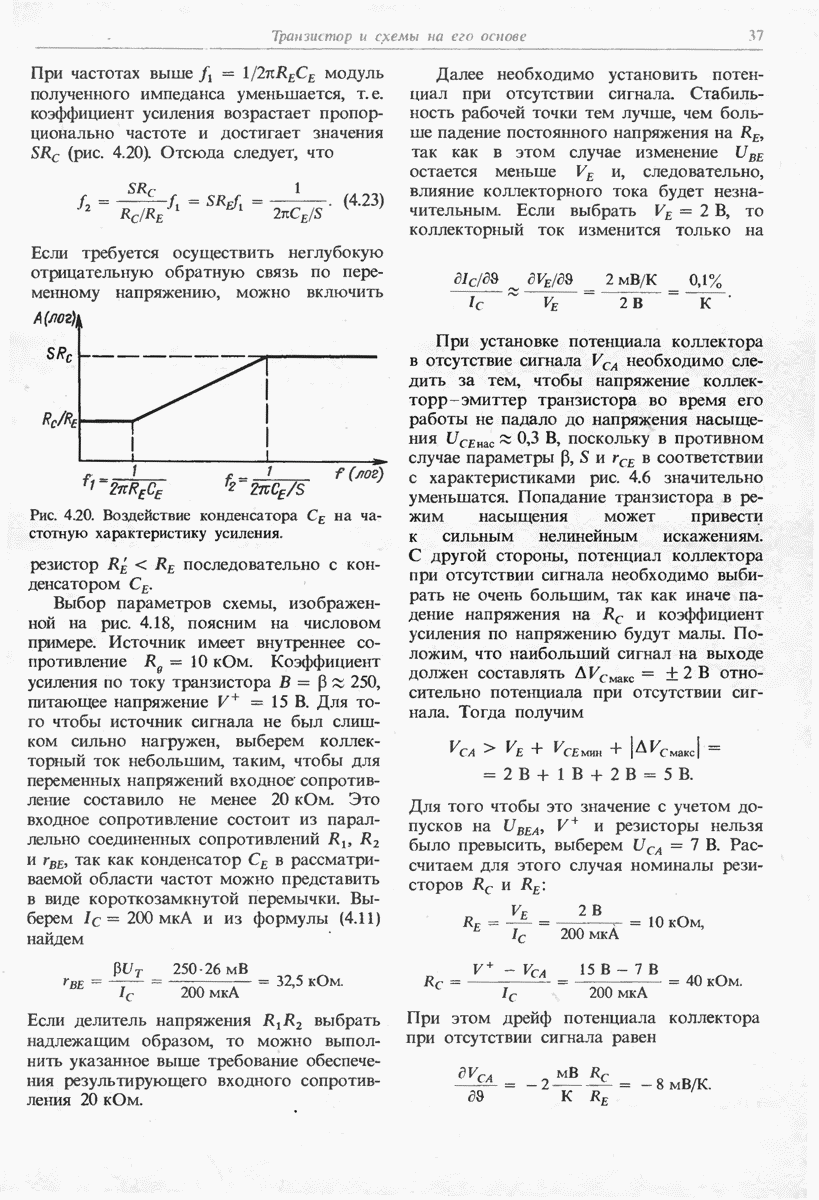
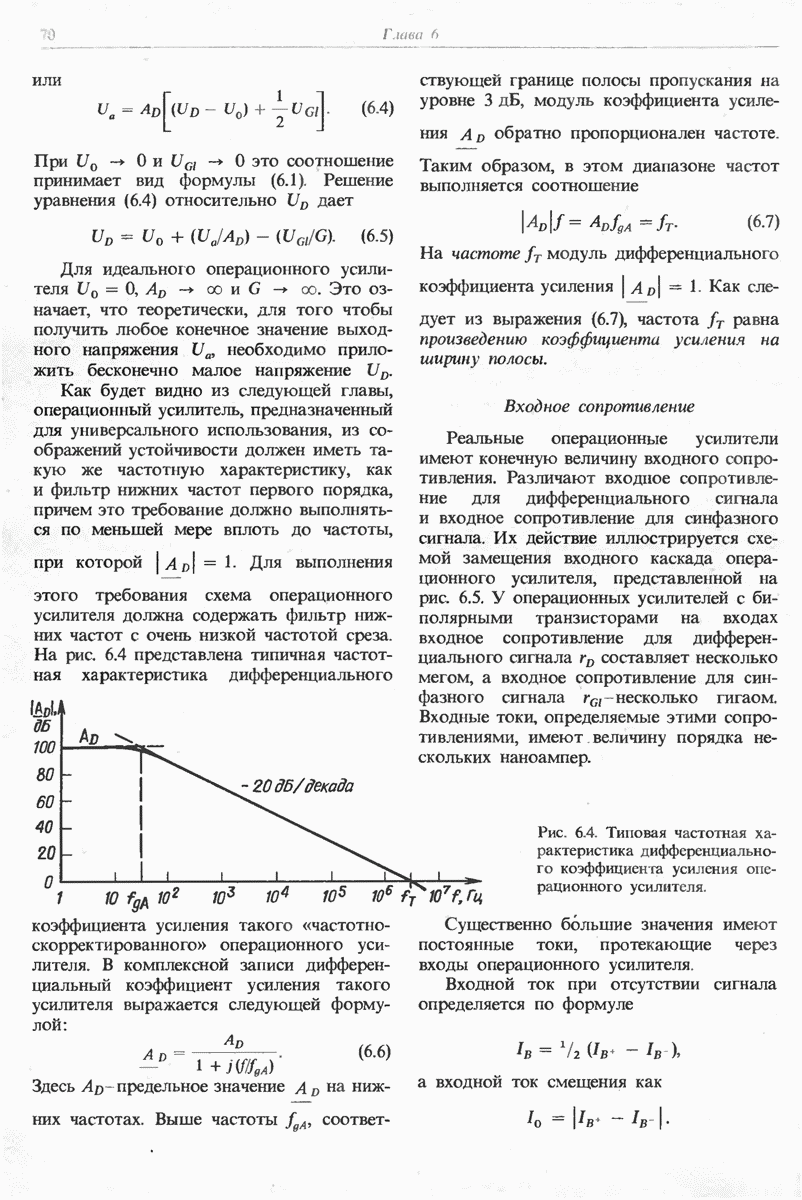
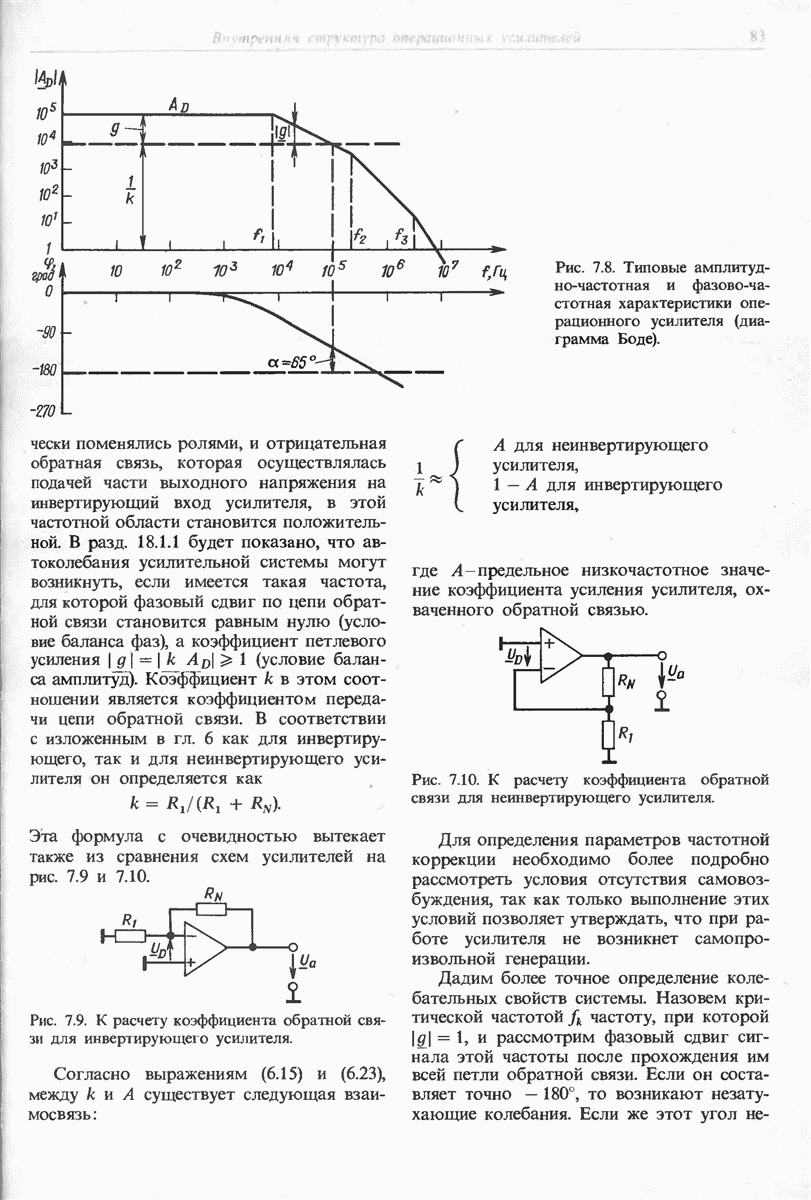
Рис. 11.6. Инвертирующий интегратор. Выходное напряжение 
Если входной сигнал представляет собой переменное напряжение, изменяющееся по косинусоидальному закону, т.е.  то формула для выходного напряжения будет иметь следующий вид:
то формула для выходного напряжения будет иметь следующий вид:

Как видно из этого выражения, амплитуда выходного сигнала обратно пропорциональна круговой частоте  . Амплитудно-частотная характеристика в логарифмическом масштабе имеет вид прямой с наклоном
. Амплитудно-частотная характеристика в логарифмическом масштабе имеет вид прямой с наклоном  на октаву. Это является простым критерием, с помощью которого можно определить, является ли схема интегратором.
на октаву. Это является простым критерием, с помощью которого можно определить, является ли схема интегратором.
Такая амплитудно-частотная характеристика интегратора может быть получена непосредственно при использовании символического представления реактивных сопротивлений в виде комплексных чисел:

Отсюда можно получить соотношение для расчета амплитуды выходного сигнала:

Оценивая стабильность схемы, следует отметить, что в противоположность ранее рассмотренным схемам отрицательная обратная связь в этом случае вызывает фазовый сдвиг, т. е. коэффициент обратной связи будет комплексным:

Для высоких частот  и его фазовый сдвиг будет нулевым. В этой частотной области к схеме предъявляются те же требования, что и к инвертирующему усилителю
и его фазовый сдвиг будет нулевым. В этой частотной области к схеме предъявляются те же требования, что и к инвертирующему усилителю

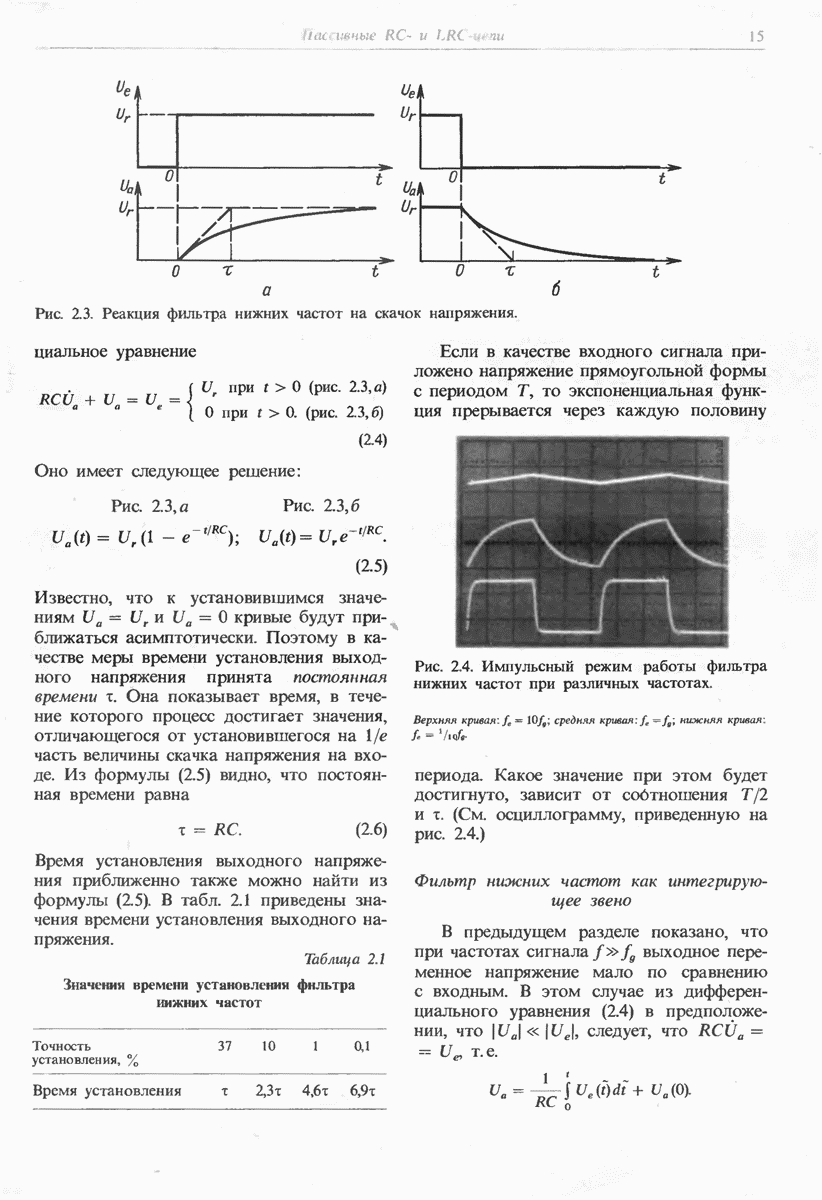
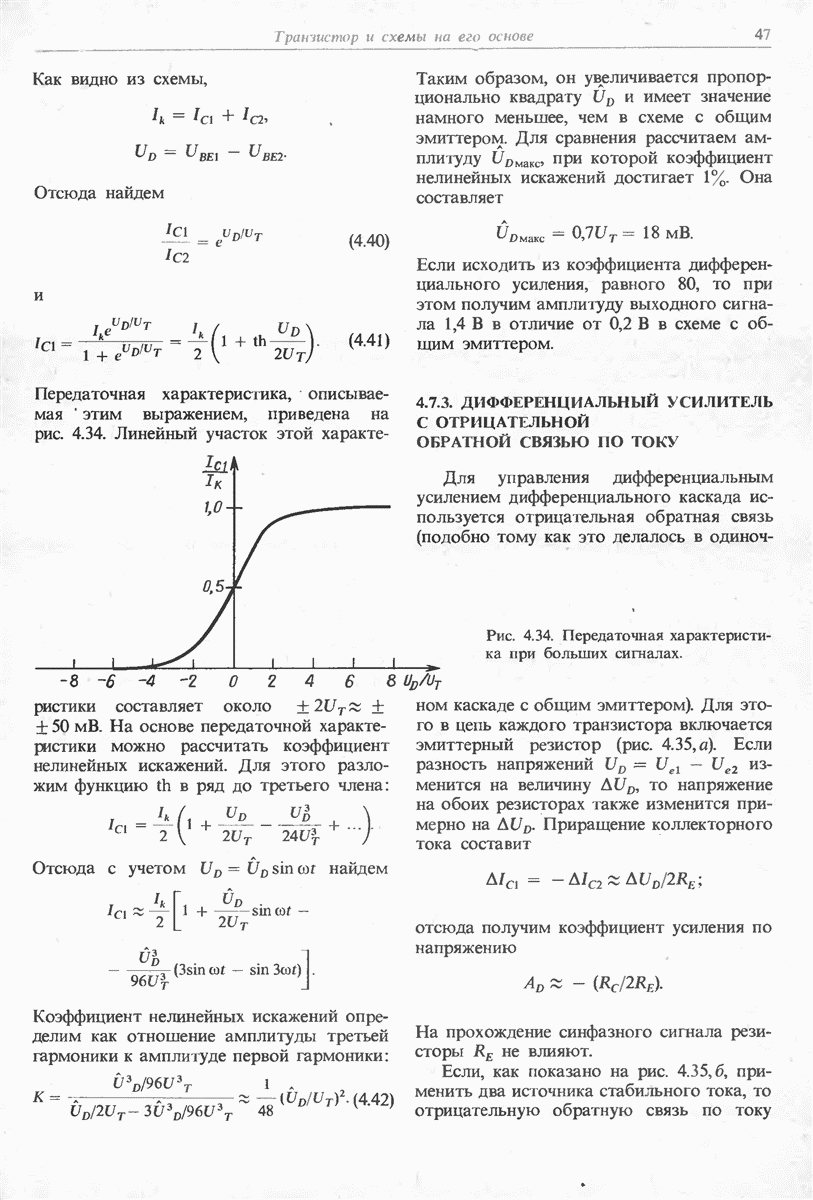
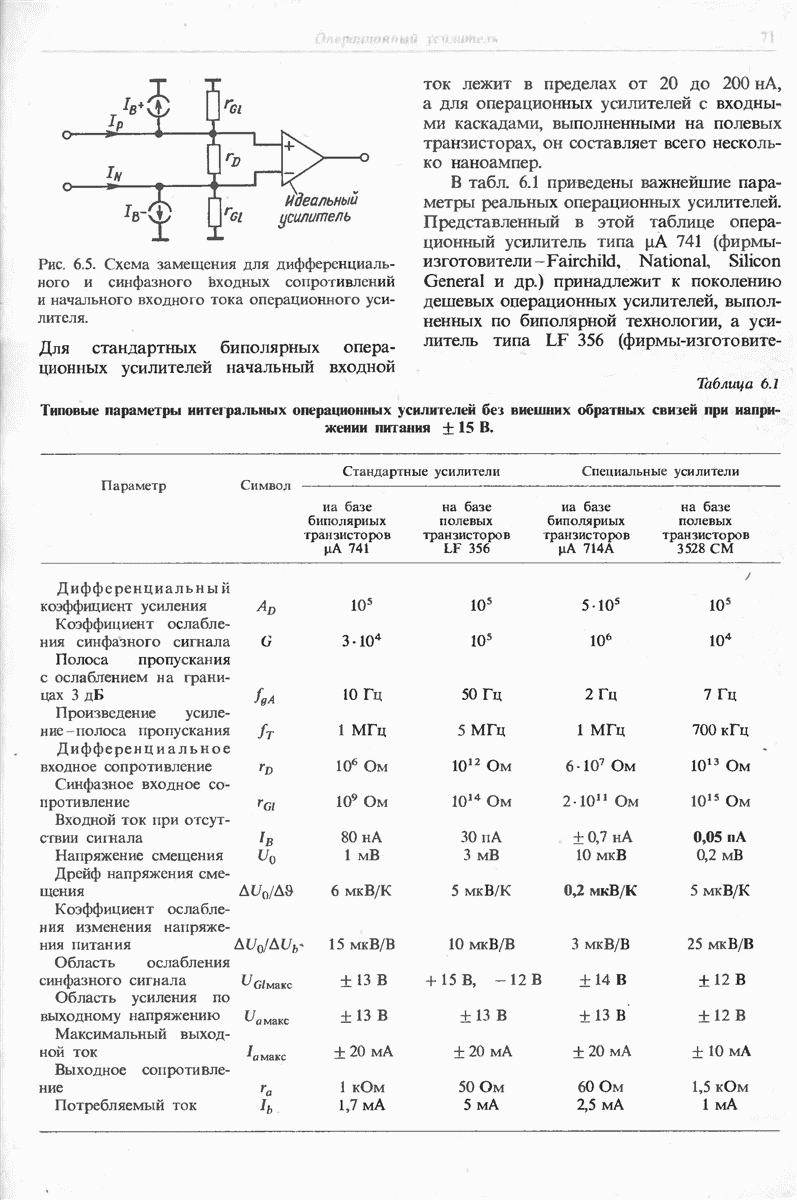
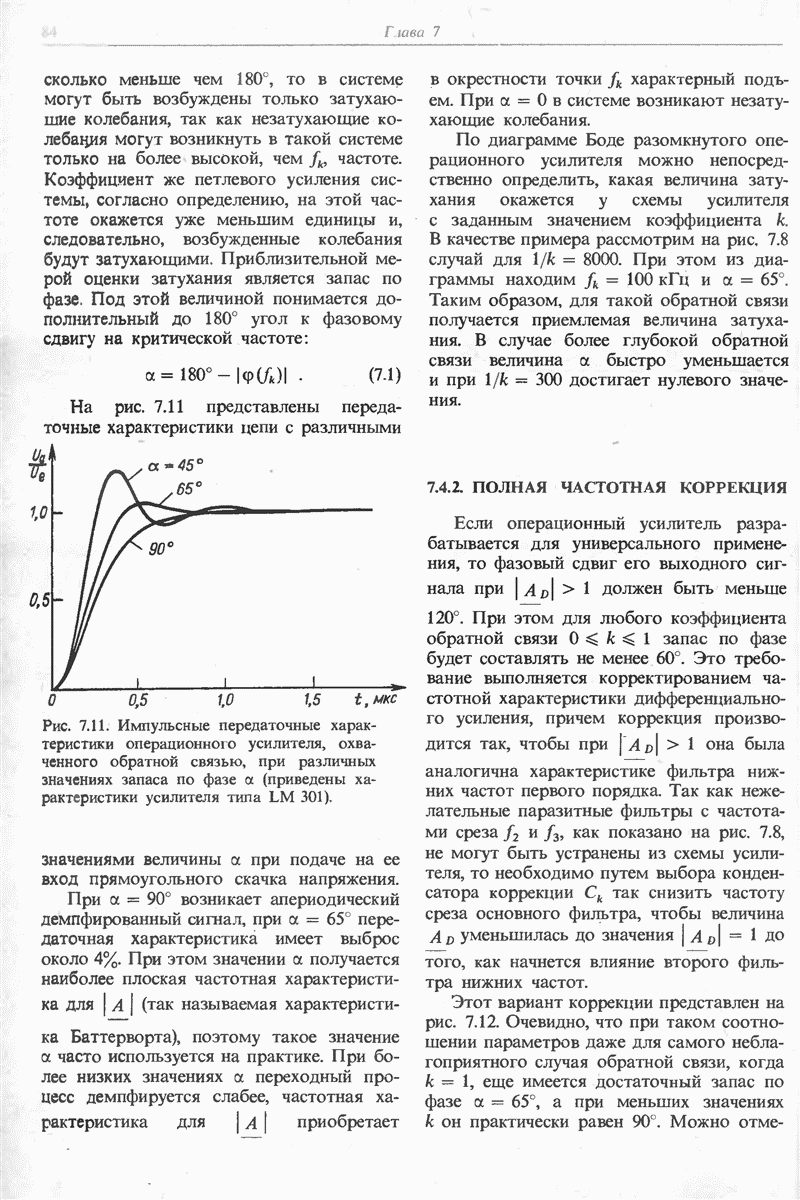
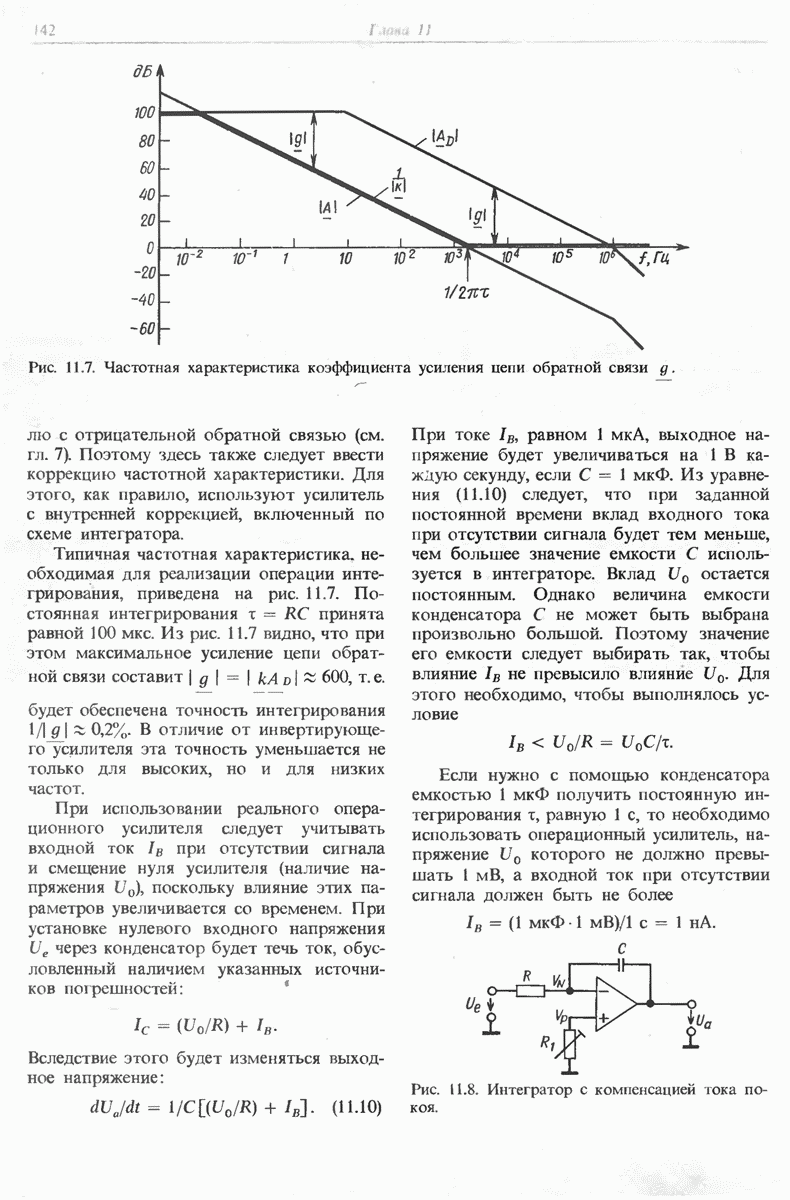
Рис. 11.7. Частотная характеристика коэффициента усиления цепи обратной связи 
с отрицательной обратной связью (см. гл. 7). Поэтому здесь также следует ввести коррекцию частотной характеристики. Для этого, как правило, используют усилитель с внутренней коррекцией, включенный по схеме интегратора.
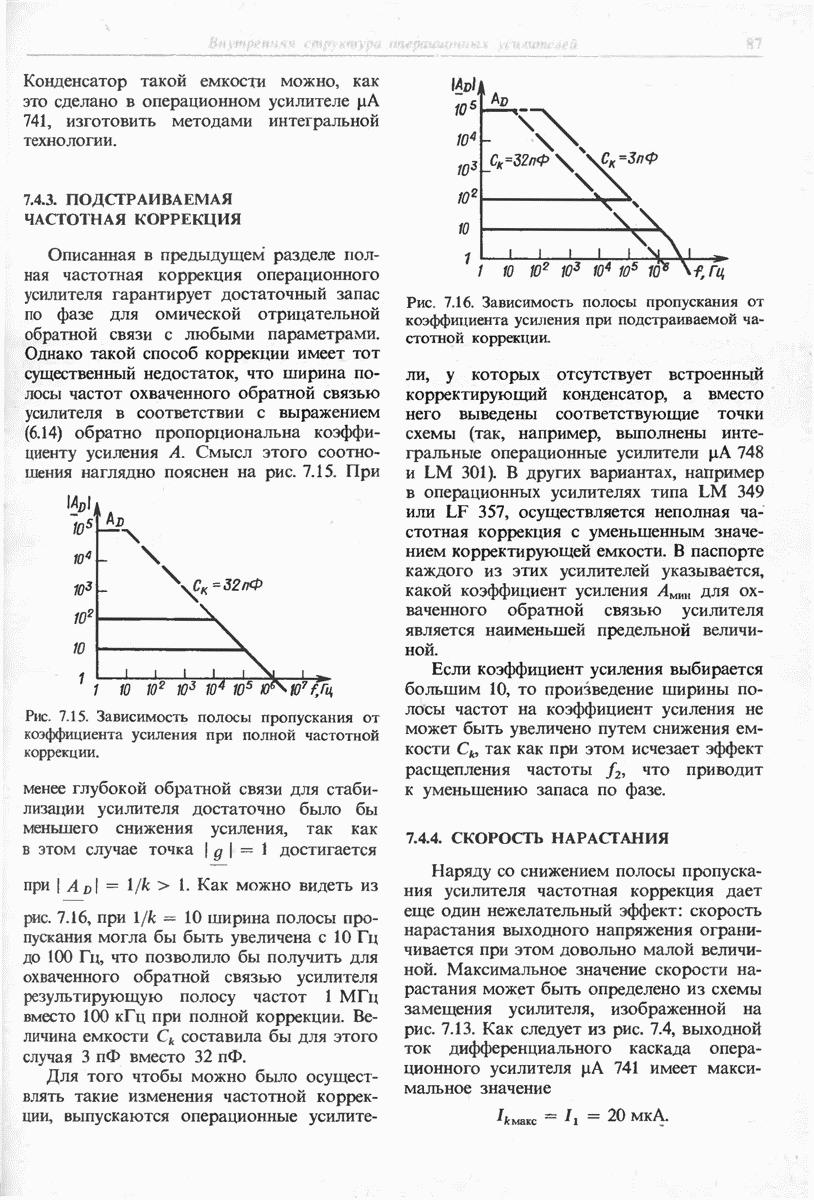
Типичная частотная характеристика, необходимая для реализации операции интегрирования, приведена на рис. 11.7. Постоянная интегрирования  принята равной
принята равной  Из рис. 11.7 видно, что при этом максимальное усиление цепи обратной связи составит
Из рис. 11.7 видно, что при этом максимальное усиление цепи обратной связи составит  , т. е. будет обеспечена точность интегрирования
, т. е. будет обеспечена точность интегрирования  . В отличие от инвертирующего усилителя эта точность уменьшается не только для высоких, но и для низких частот.
. В отличие от инвертирующего усилителя эта точность уменьшается не только для высоких, но и для низких частот.
При использовании реального операционного усилителя следует учитывать входной ток  при отсутствии сигнала и смещение нуля усилителя (наличие напряжения
при отсутствии сигнала и смещение нуля усилителя (наличие напряжения  поскольку влияние этих параметров увеличивается со временем. При установке нулевого входного напряжения
поскольку влияние этих параметров увеличивается со временем. При установке нулевого входного напряжения  через конденсатор будет течь ток, обусловленный наличием указанных источников погрешностей:
через конденсатор будет течь ток, обусловленный наличием указанных источников погрешностей:

Вследствие этого будет изменяться выходное напряжение:

При токе  равном
равном  выходное напряжение будет увеличиваться на 1 В каждую секунду, если
выходное напряжение будет увеличиваться на 1 В каждую секунду, если  Из уравнения (11.10) следует, что при заданной постоянной времени вклад входного тока при отсутствии сигнала будет тем меньше, чем большее значение емкости С используется в интеграторе. Вклад
Из уравнения (11.10) следует, что при заданной постоянной времени вклад входного тока при отсутствии сигнала будет тем меньше, чем большее значение емкости С используется в интеграторе. Вклад  остается постоянным. Однако величина емкости конденсатора С не может быть выбрана произвольно большой. Поэтому значение его емкости следует выбирать так, чтобы влияние
остается постоянным. Однако величина емкости конденсатора С не может быть выбрана произвольно большой. Поэтому значение его емкости следует выбирать так, чтобы влияние  не превысило влияние
не превысило влияние  Для этого необходимо, чтобы выполнялось условие
Для этого необходимо, чтобы выполнялось условие

Если нужно с помощью конденсатора емкостью  получить постоянную интегрирования
получить постоянную интегрирования  равную 1 с, то необходимо использовать операционный усилитель, напряжение
равную 1 с, то необходимо использовать операционный усилитель, напряжение  которого не должно превышать
которого не должно превышать  а входной ток при отсутствии сигнала должен быть не более
а входной ток при отсутствии сигнала должен быть не более


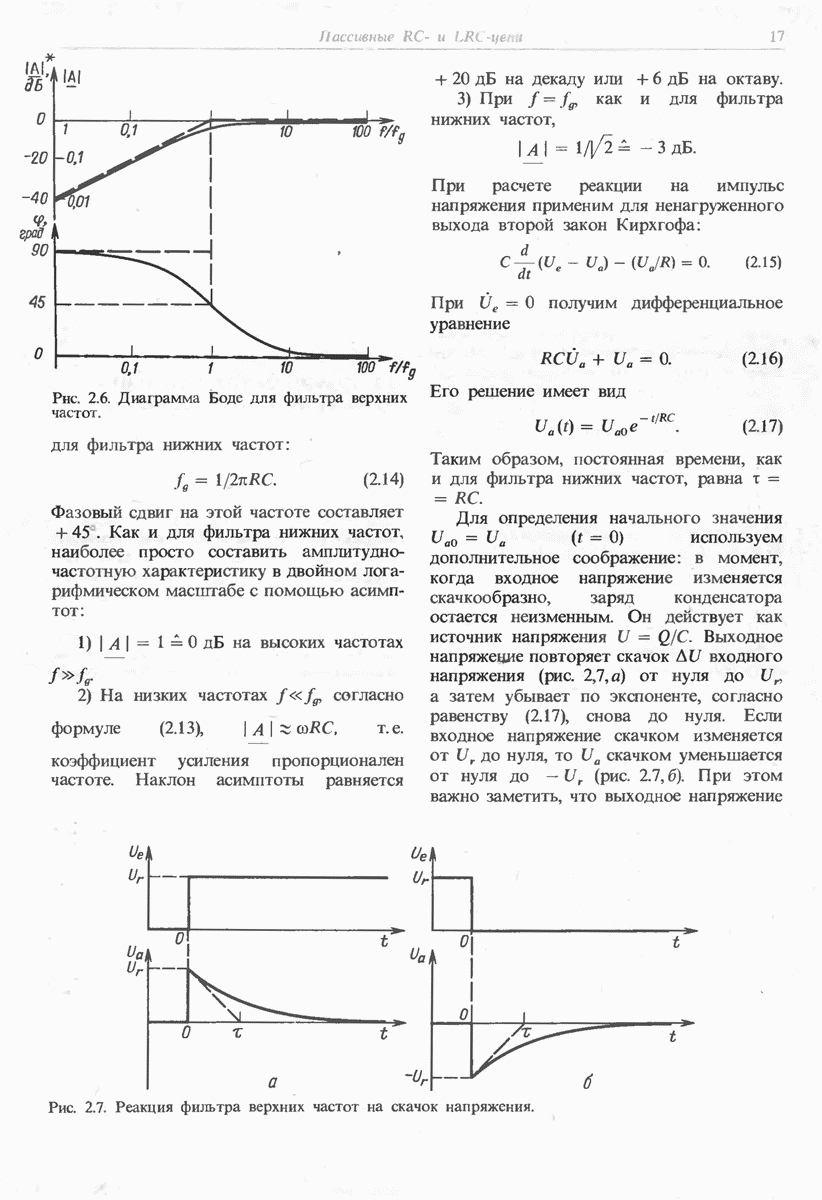
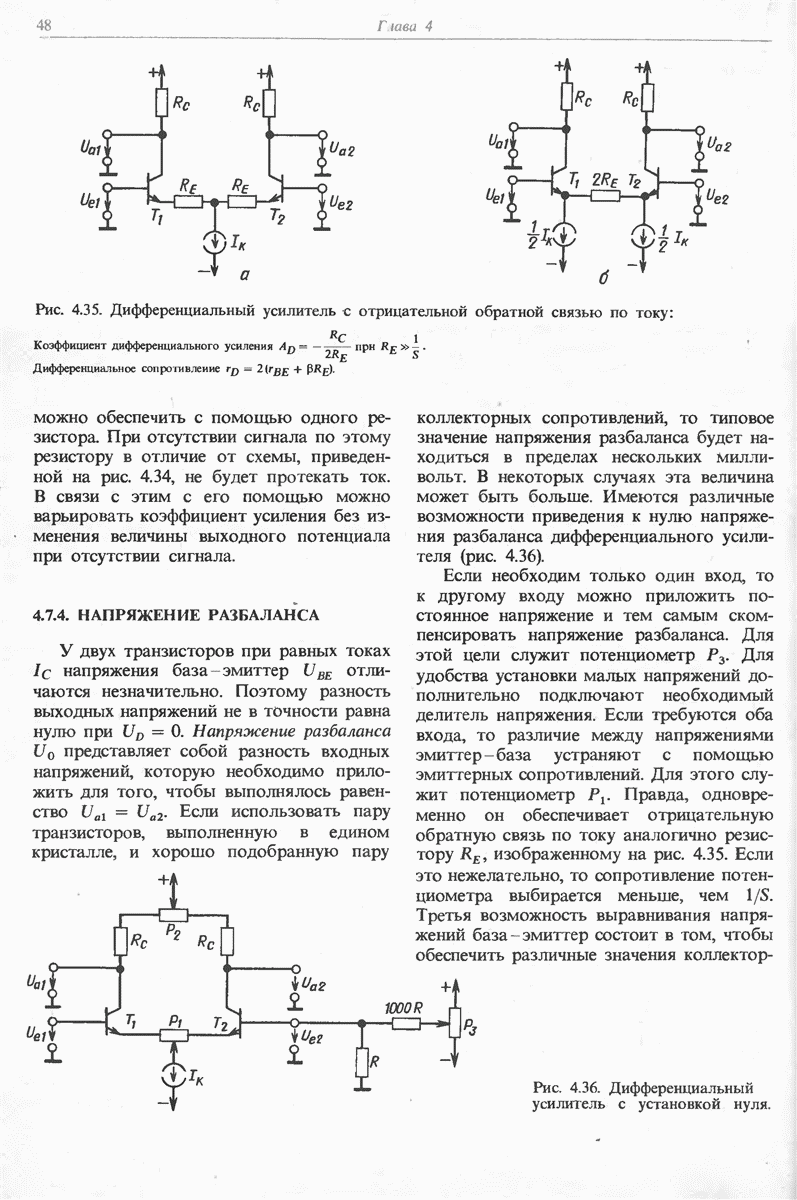
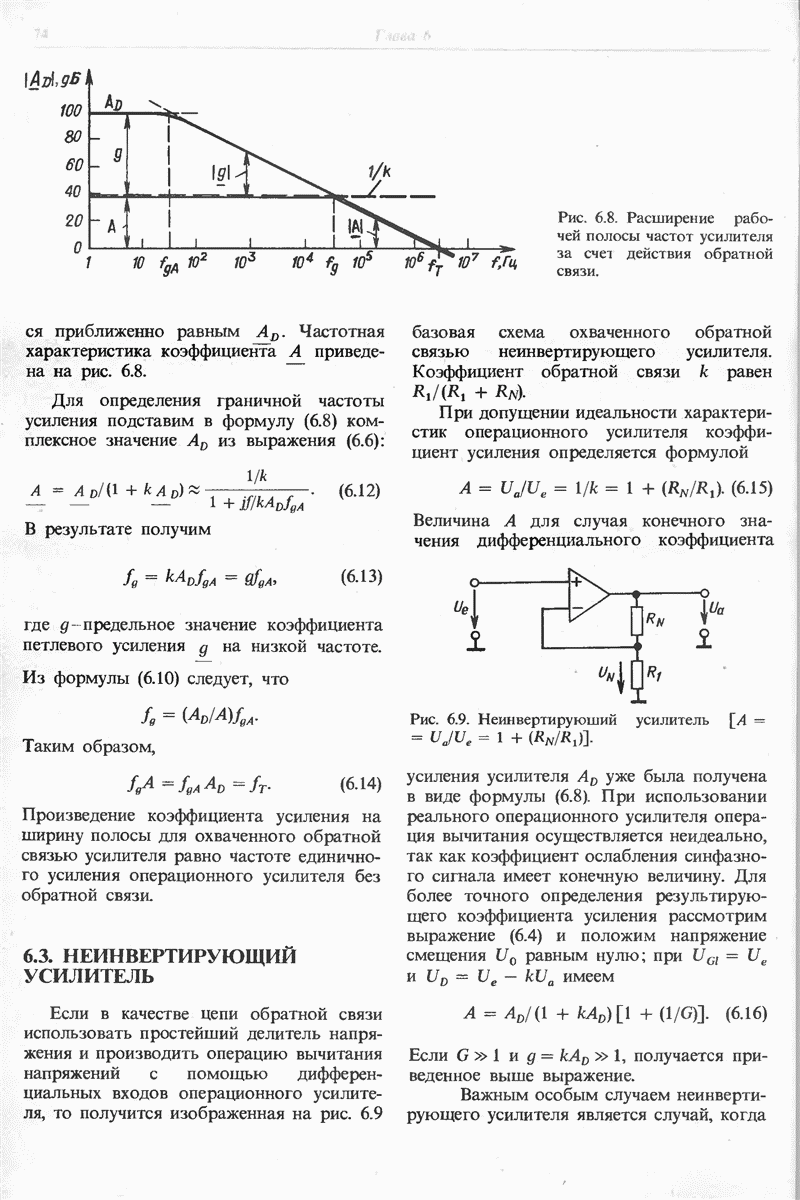
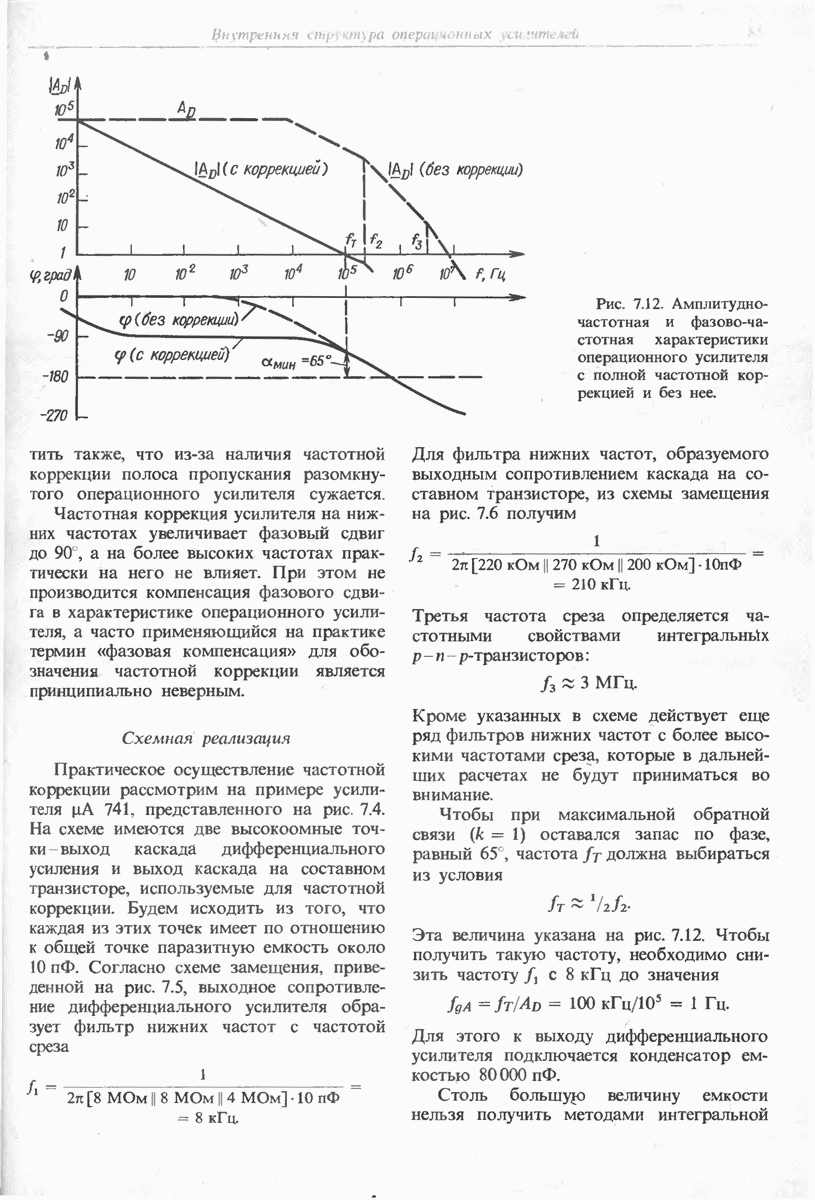
Рис. 11.8. Интегратор с компенсацией тока покоя.
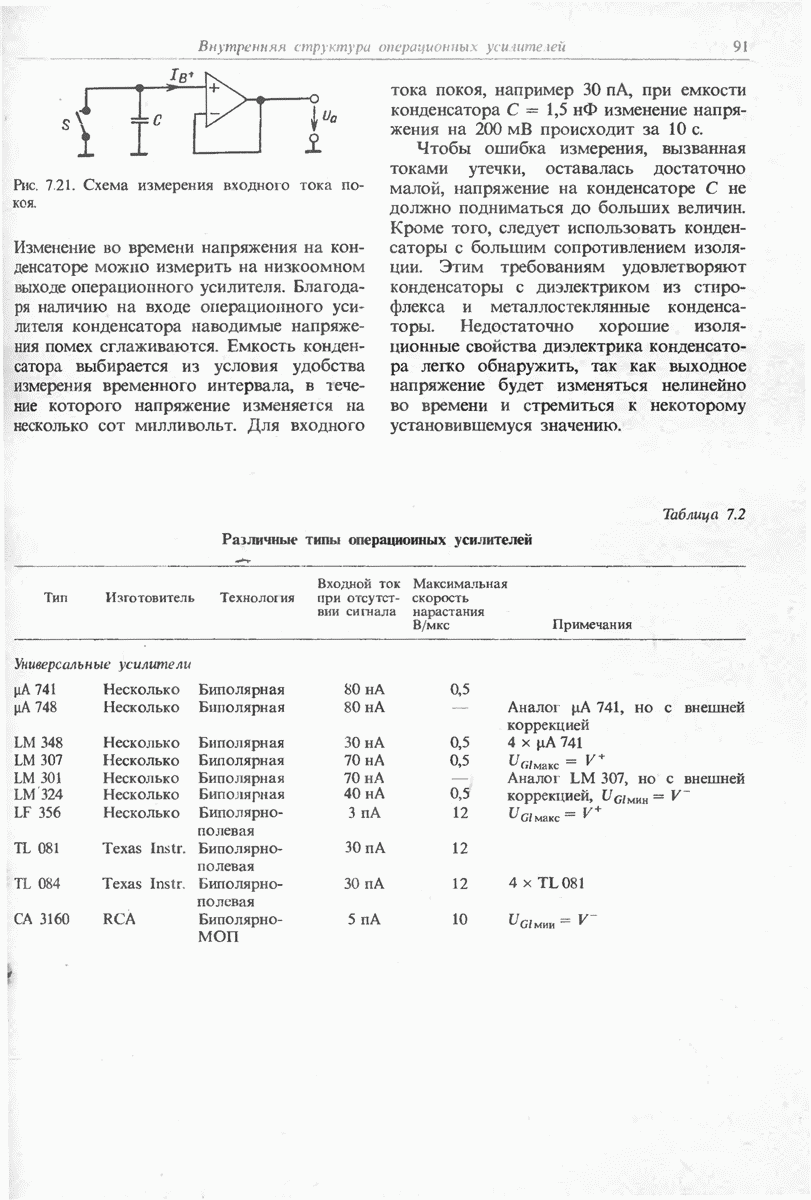
Операционный усилитель с биполярными транзисторами на входе вряд ли будет иметь такое низкое значение тока при отсутствии сигнала. Поэтому остается единственный выход компенсировать этот ток (рис. 11.8). Величина сопротивления  должна быть того же порядка, что и сопротивление
должна быть того же порядка, что и сопротивление  Падение напряжения на этом сопротивлении будет равно
Падение напряжения на этом сопротивлении будет равно  Если
Если  то вследствие того что
то вследствие того что  через сопротивление
через сопротивление  будет течь ток
будет течь ток

При этом ток через конденсатор С будет равен нулю. Теперь остается скомпенсировать таким же образом небольшой сдвиг входных токов, соответствующий сдвигу входного напряжения, с помощью незначительного изменения сопротивления  Нескомпенсированным остается лишь дрейф сдвига входных токов, который для операционных усилителей на биполярных транзисторах может быть достаточно большим. Поэтому лучше всего применить операционный усилитель с полевыми транзисторами на входе, для которого входной ток при отсутствии сигнала настолько мал, что нет необходимости в компенсации.
Нескомпенсированным остается лишь дрейф сдвига входных токов, который для операционных усилителей на биполярных транзисторах может быть достаточно большим. Поэтому лучше всего применить операционный усилитель с полевыми транзисторами на входе, для которого входной ток при отсутствии сигнала настолько мал, что нет необходимости в компенсации.
Еще один источник погрешности интегратора ток утечки конденсатора обратной связи. У электролитических конденсаторов ток утечки порядка микроампер, поэтому их использование в интеграторах недопустимо. Можно рекомендовать для этих целей металлобумажные конденсаторы, однако их использование при емкости свыше 10 мкФ крайне неудобно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Часть I. Основные положения
- 1. Пояснение применяемых величин
- 2. Пассивные RC- и LRC- цепи
- 2.1. ФИЛЬТР НИЖНИХ ЧАСТОТ
- 2.1.3. ДЛИТЕЛЬНОСТЬ ФРОНТА ИМПУЛЬСА И ЧАСТОТА СРЕЗА ФИЛЬТРА
- 2.2. ФИЛЬТР ВЕРХНИХ ЧАСТОТ
- 2.3. КОМПЕНСИРОВАННЫЙ ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
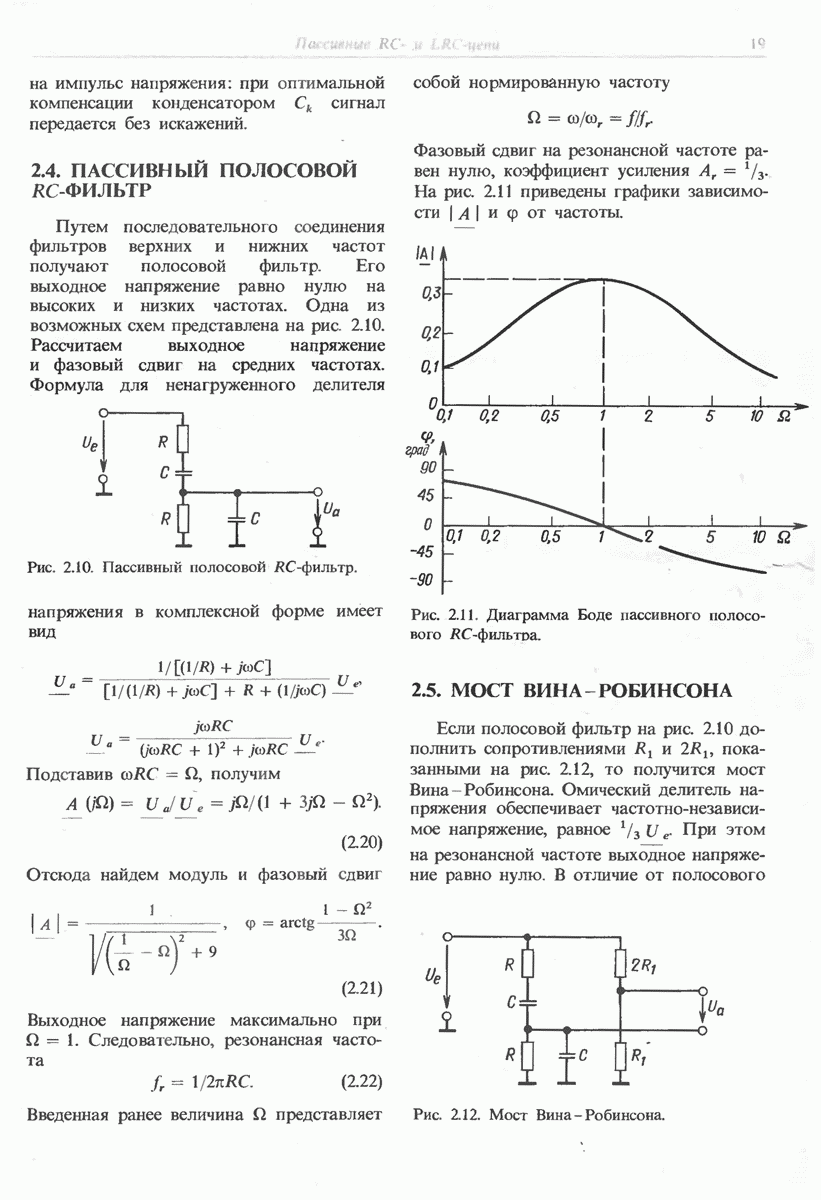
- 2.4. ПАССИВНЫЙ ПОЛОСОВОЙ RC-ФИЛЬТР
- 2.5. МОСТ ВИНА-РОБИНСОНА
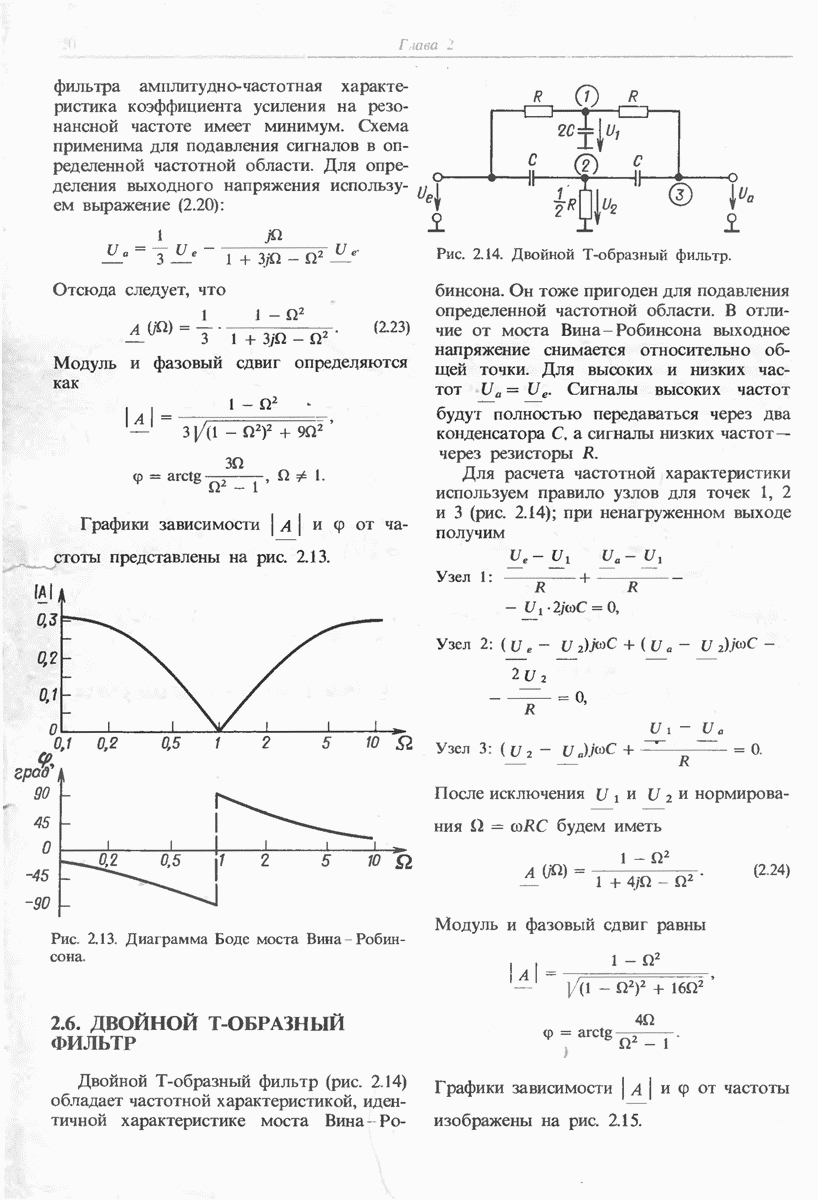
- 2.6. ДВОЙНОЙ Т-ОБРАЗНЫЙ ФИЛЬТР
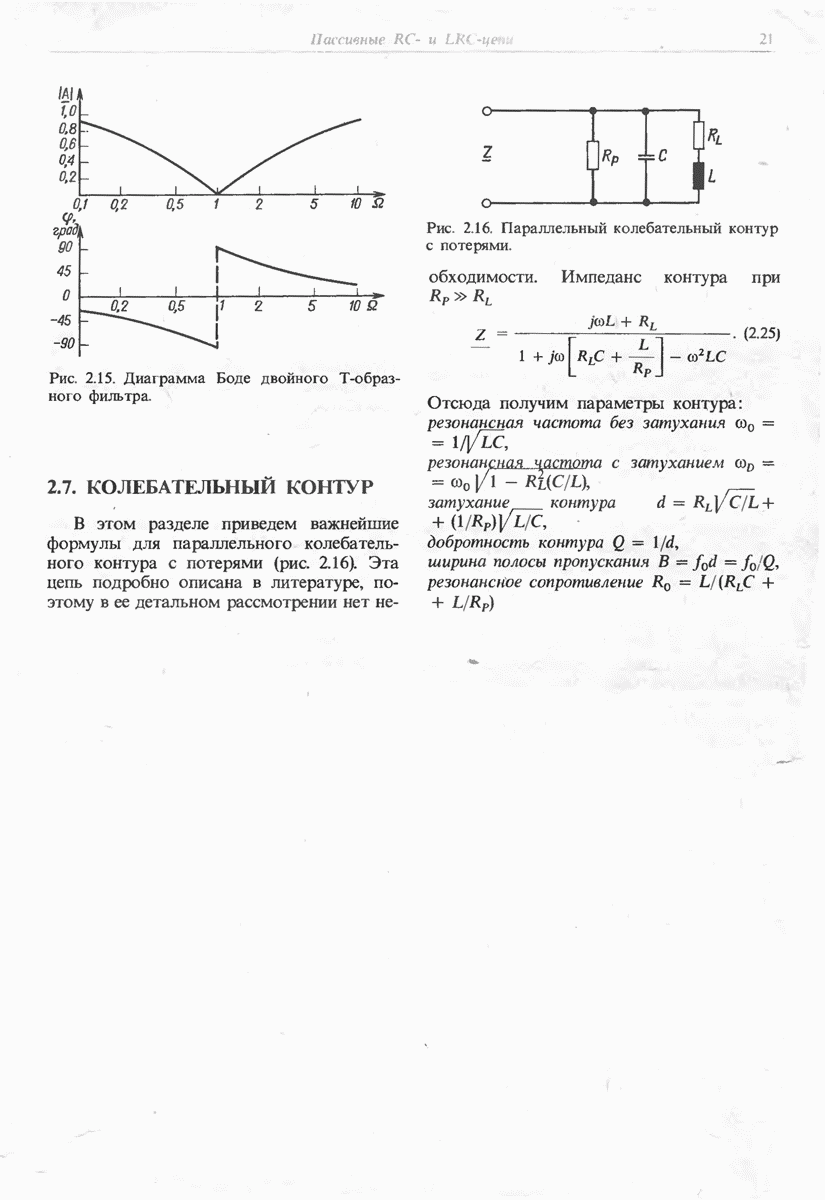
- 2.7. КОЛЕБАТЕЛЬНЫЙ КОНТУР
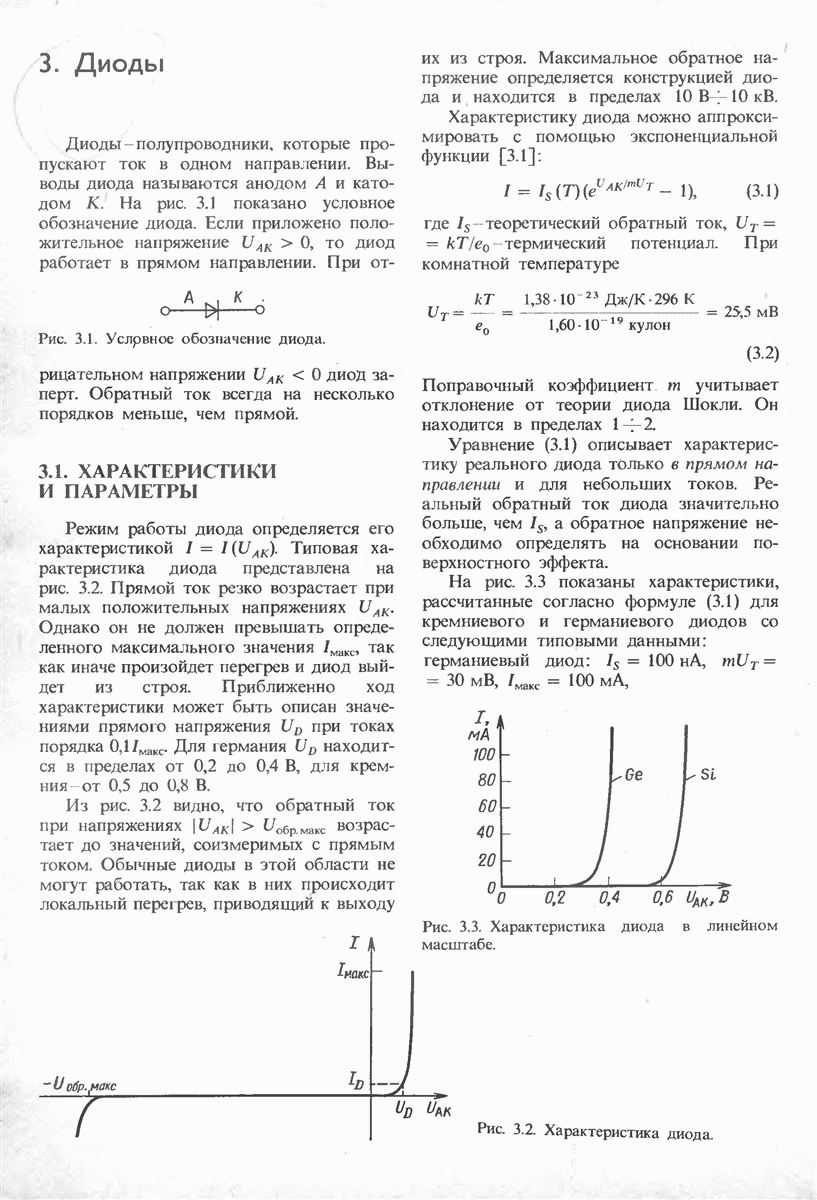
- 3. Диоды
- 3.2. СТАБИЛИТРОНЫ
- 3.3. ВАРИКАПЫ
- 4. Транзистор и схемы на его основе
- 4.2. СХЕМА С ОБЩИМ ЭМИТТЕРОМ
- 4.2.2. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
- 4.2.3. СХЕМА С ОБЩИМ ЭМИТТЕРОМ И ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.2.4. ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ ПО НАПРЯЖЕНИЮ
- 4.2.5. УСТАНОВКА РАБОЧЕЙ ТОЧКИ
- 4.3. СХЕМА С ОБЩЕЙ БАЗОЙ
- 4.4. СХЕМА С ОБЩИМ КОЛЛЕКТОРОМ, ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 4.5. ТРАНЗИСТОР КАК ИСТОЧНИК СТАБИЛЬНОГО ТОКА
- 4.5.2. БИПОЛЯРНЫЙ ИСТОЧНИК ПИТАНИЯ
- 4.5.3. СХЕМА «ТОКОВОГО ЗЕРКАЛА»
- 4.6. СХЕМА ДАРЛИНГТОНА
- 4.7. ДИФФЕРЕНЦИАЛЬНЫЕ УСИЛИТЕЛИ
- 4.7.2. РЕЖИМ БОЛЬШОГО СИГНАЛА
- 4.7.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ ПО ТОКУ
- 4.7.4. НАПРЯЖЕНИЕ РАЗБАЛАНСА
- 4.8. ИЗМЕРЕНИЕ НЕКОТОРЫХ ПАРАМЕТРОВ ПРИ МАЛОМ СИГНАЛЕ
- 4.9. ШУМЫ ТРАНЗИСТОРА
- 4.10. ПРЕДЕЛЬНЫЕ ПАРАМЕТРЫ
- 5. Полевые транзисторы
- 5.2. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ МАЛЫХ СИГНАЛОВ
- 5.3. ПРЕДЕЛЬНЫЕ ЭЛЕКТРИЧЕСКИЕ ПАРАМЕТРЫ
- 5.4. ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ
- 5.4.1. СХЕМА С ОБЩИМ ИСТОКОМ
- 5.4.2. СХЕМА С ОБЩИМ ЗАТВОРОМ
- 5.4.3. СХЕМА С ОБЩИМ СТОКОМ, ИСТОКОВЫЙ ПОВТОРИТЕЛЬ
- 5.5. ПОЛЕВОЙ ТРАНЗИСТОР КАК СТАБИЛИЗАТОР ТОКА
- 5.6. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ НА ПОЛЕВЫХ ТРАНЗИСТОРАХ
- 5.7. ПОЛЕВОЙ ТРАНЗИСТОР В КАЧЕСТВЕ УПРАВЛЯЕМОГО СОПРОТИВЛЕНИЯ
- 6. Операционный усилитель
- 6.1. СВОЙСТВА ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 6.2. ПРИНЦИП ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ
- 6.3. НЕИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 6.4. ИНВЕРТИРУЮЩИЙ УСИЛИТЕЛЬ
- 7. Внутренняя структура операционных усилителей
- 7.2. ПРОСТЕЙШИЕ СХЕМЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 7.3. СТАНДАРТНАЯ СХЕМА ИНТЕГРАЛЬНОГО ОПЕРАЦИОННОГО УСИЛИТЕЛЯ
- 7.4. КОРРЕКЦИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
- 7.4.2. ПОЛНАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
- 7.4.3. ПОДСТРАИВАЕМАЯ ЧАСТОТНАЯ КОРРЕКЦИЯ
- 7.4.4. СКОРОСТЬ НАРАСТАНИЯ
- 7.4.5. КОМПЕНСАЦИЯ ЕМКОСТНОЙ НАГРУЗКИ
- 7.5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 8. Простейшие переключающие схемы
- 8.1. ТРАНЗИСТОРНЫЙ КЛЮЧ
- 8.2. БИСТАБИЛЬНЫЕ РЕЛАКСАЦИОННЫЕ СХЕМЫ
- 8.2.2. ТРИГГЕР ШМИТТА
- 8.3. МОНОСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
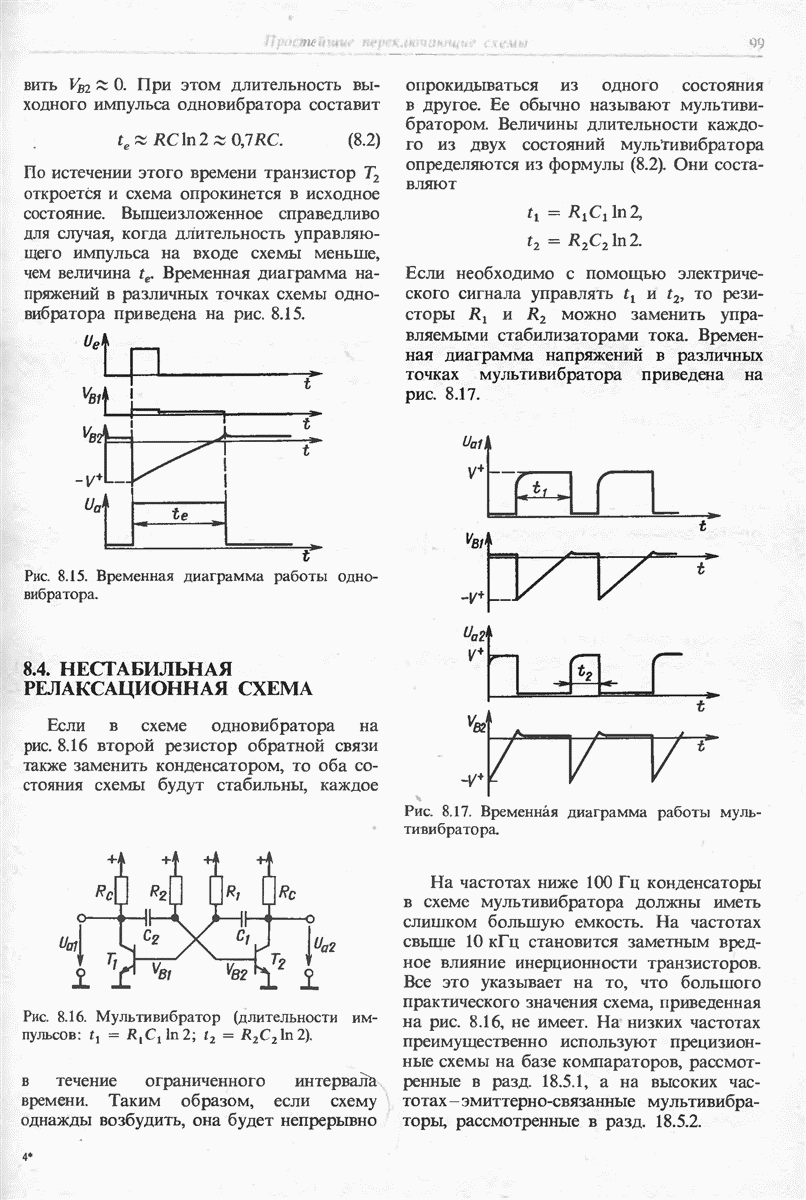
- 8.4. НЕСТАБИЛЬНАЯ РЕЛАКСАЦИОННАЯ СХЕМА
- 9. Базовые логические схемы
- 9.1. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ
- 9.2. СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.2.1. ТАБЛИЦА КАРНО
- 9.3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 9.4.1. РЕЗИСТИВНО-ТРАНЗИСТОРНАЯ ЛОГИКА (РТЛ)
- 9.4.2. ДИОДНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ДТЛ)
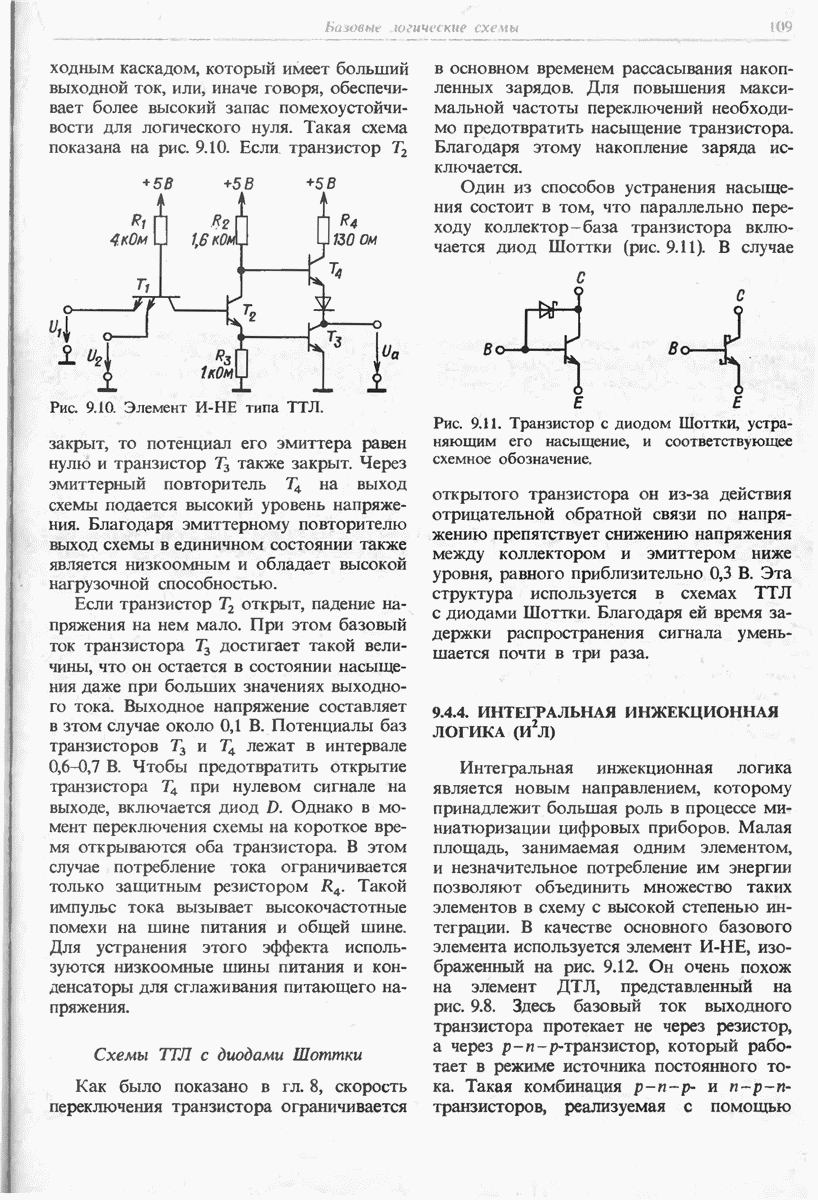
- 9.4.3. ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ТТЛ)
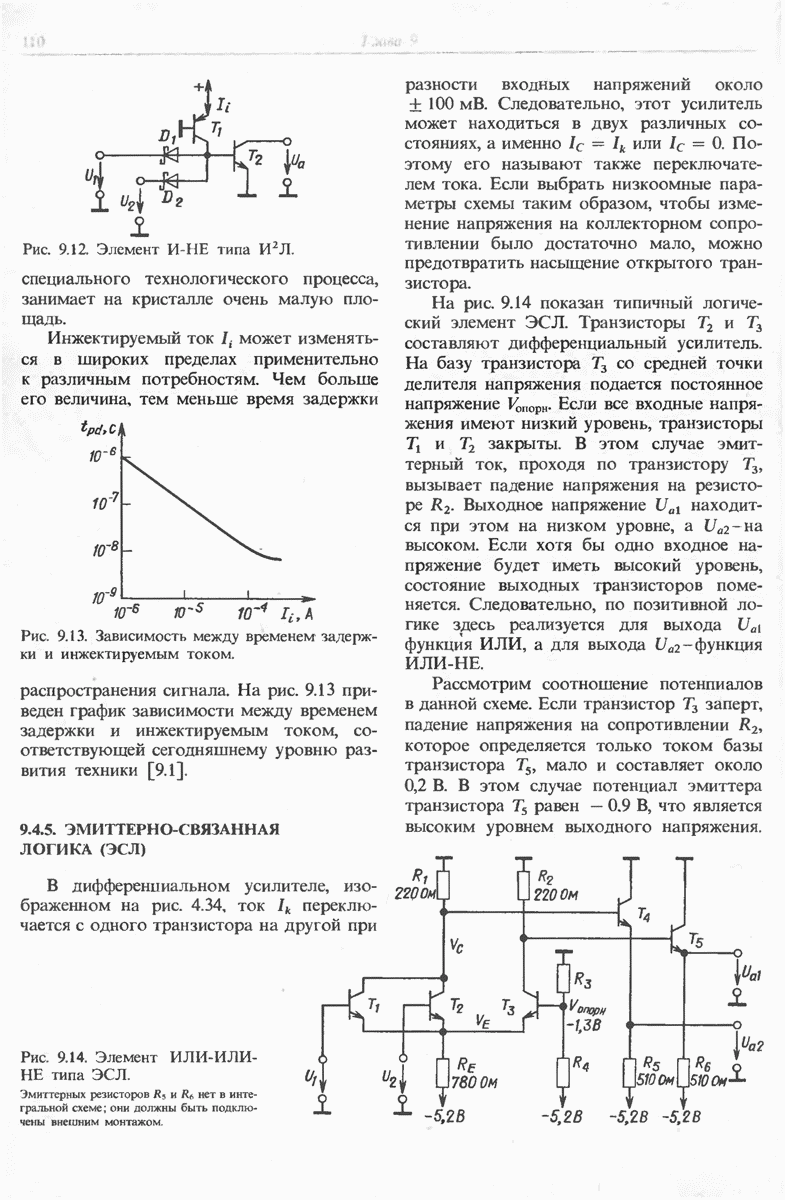
- 9.4.4. ИНТЕГРАЛЬНАЯ ИНЖЕКЦИОННАЯ ЛОГИКА
- 9.4.5. ЭМИТТЕРНО-СВЯЗАННАЯ ЛОГИКА (ЭСЛ)
- 9.4.6. n-КАНАЛЬНАЯ МОП-ЛОГИКА
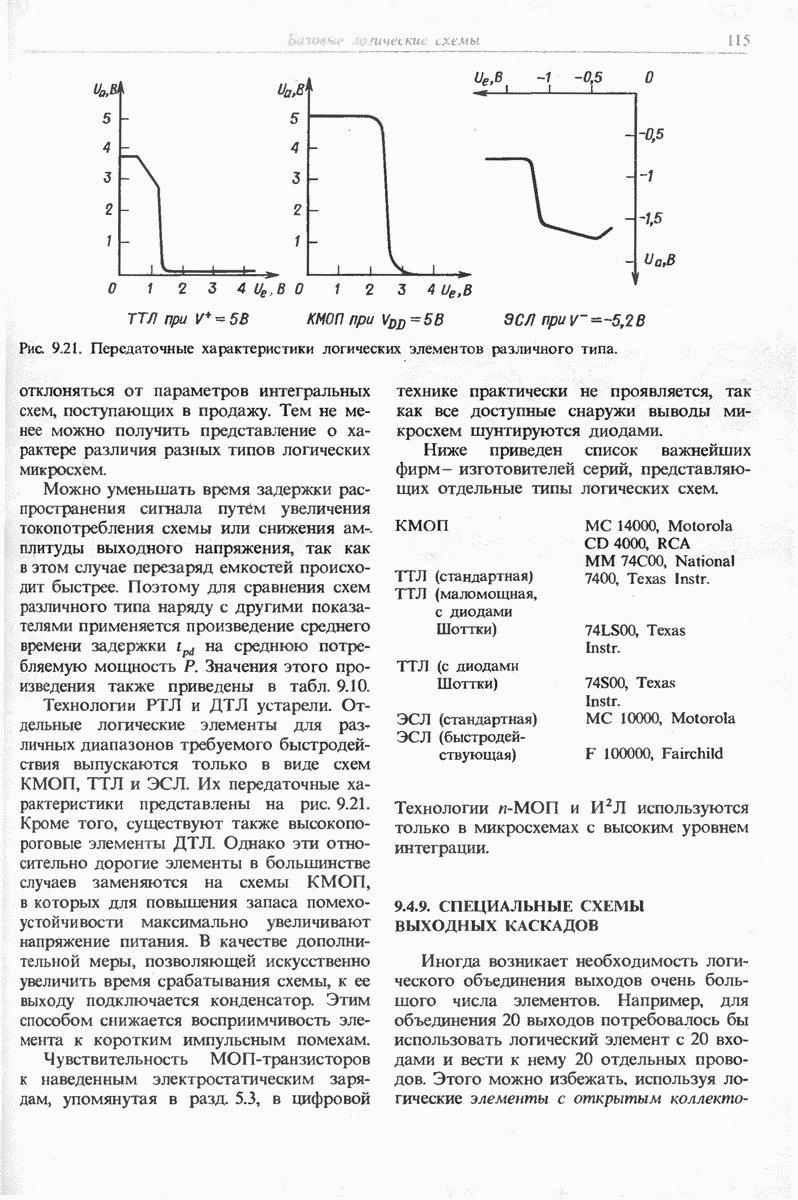
- 9.4.7. КОМПЛЕМЕНТАРНАЯ МОП-ЛОГИКА (КМОП)
- 9.4.8. ОБЗОР
- 9.4.9. СПЕЦИАЛЬНЫЕ СХЕМЫ ВЫХОДНЫХ КАСКАДОВ
- 9.5. ИНТЕГРАЛЬНЫЕ ТРИГГЕРЫ
- 9.5.2. ТРИГГЕРЫ ТИПА M-S (MASTER-SLAVE)
- 9.5.3. ДИНАМИЧЕСКИЙ ТРИГГЕР
- 9.6. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 9.6.2. ПОСТОЯННЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА (ПЗУ)
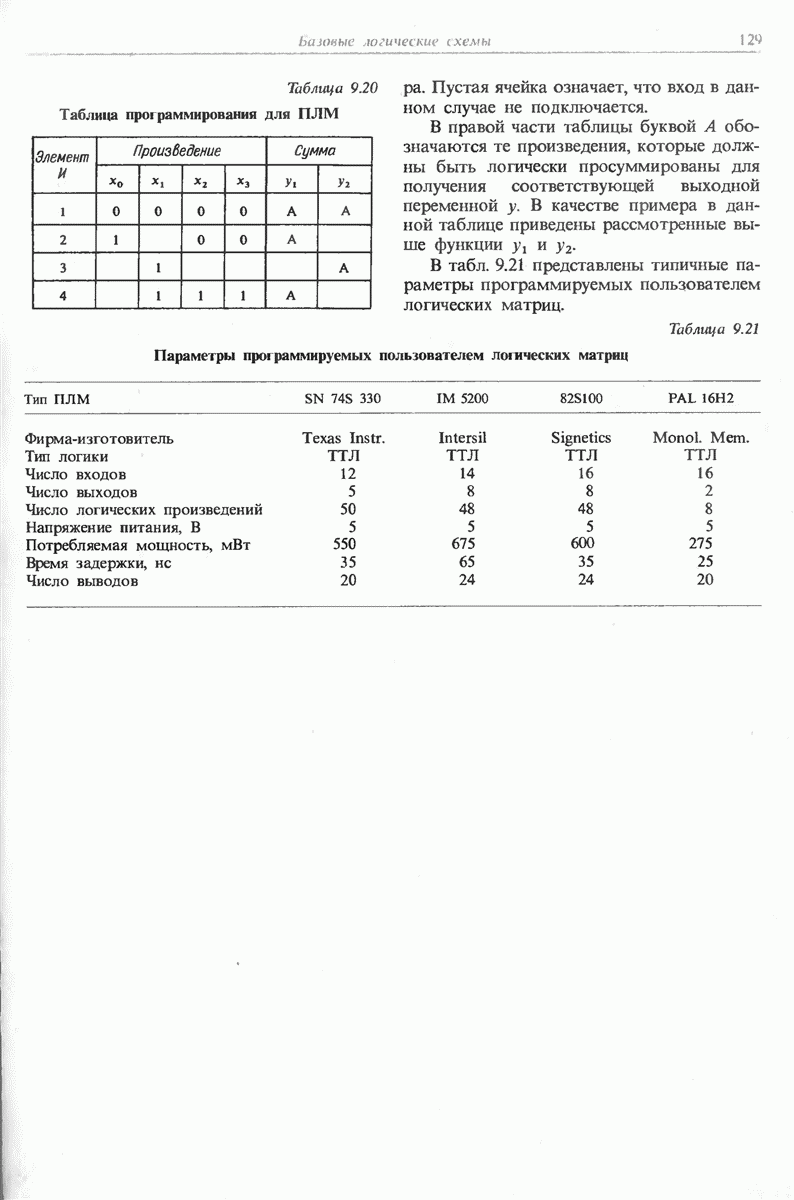
- 9.6.3. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ (ПЛМ)
- 10. Оптоэлектронные приборы
- 10.1. ОСНОВНЫЕ ПОНЯТИЯ ФОТОМЕТРИИ
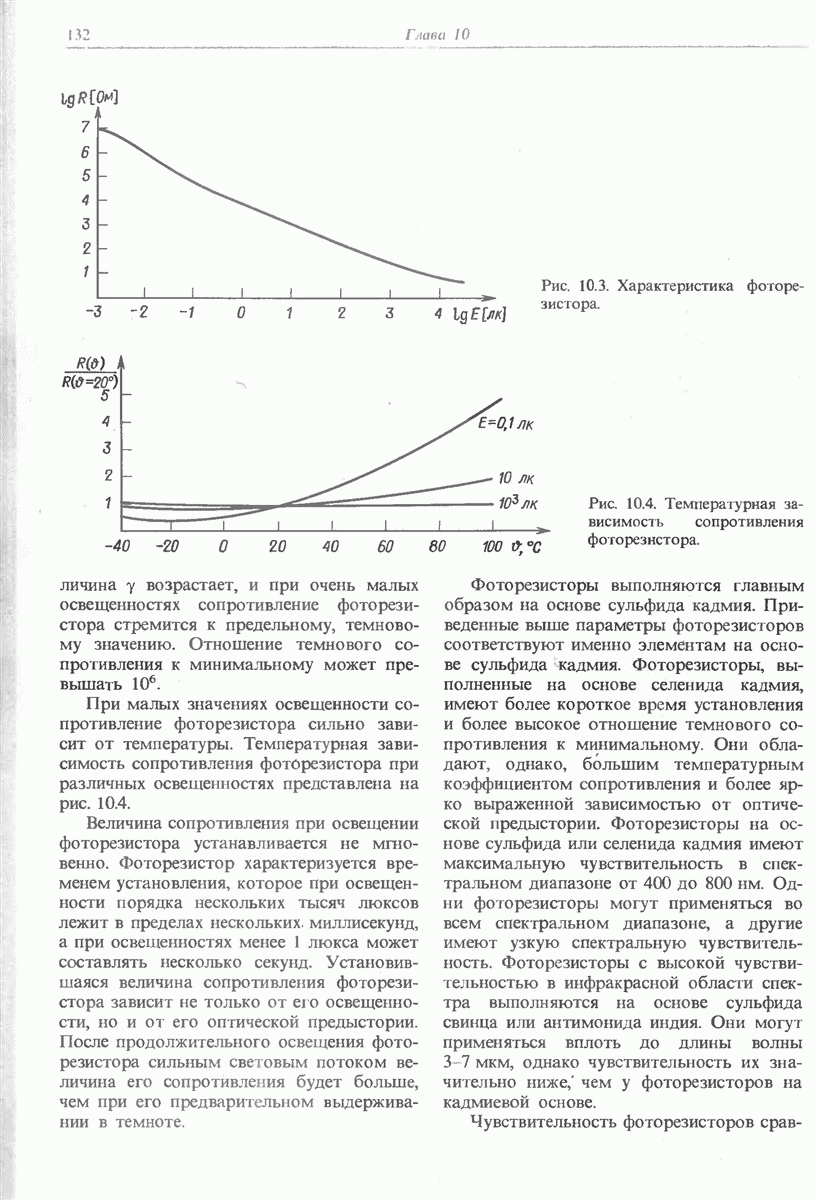
- 10.2. ФОТОРЕЗИСТОР
- 10.3. ФОТОДИОДЫ
- 10.4. ФОТОТРАНЗИСТОРЫ
- 10.5. СВЕТОДИОДЫ
- 10.6. ОПТРОНЫ
- Часть II. Применения
- 11. Линейные и нелинейные аналоговые вычислительные схемы
- 11.1. СХЕМА СУММИРОВАНИЯ
- 11.2. СХЕМЫ ВЫЧИТАНИЯ
- 11.2.2. СХЕМА ВЫЧИТАНИЯ НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ
- 11.3. БИПОЛЯРНОЕ УСИЛИТЕЛЬНОЕ ЗВЕНО
- 11.4. СХЕМЫ ИНТЕГРИРОВАНИЯ
- 11.4.1. ИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.2. ЗАДАНИЕ НАЧАЛЬНЫХ УСЛОВИЙ
- 11.4.3. СУММИРУЮЩИЙ ИНТЕГРАТОР
- 11.4.4. НЕИНВЕРТИРУЮЩИЙ ИНТЕГРАТОР
- 11.5. СХЕМЫ ДИФФЕРЕНЦИРОВАНИЯ
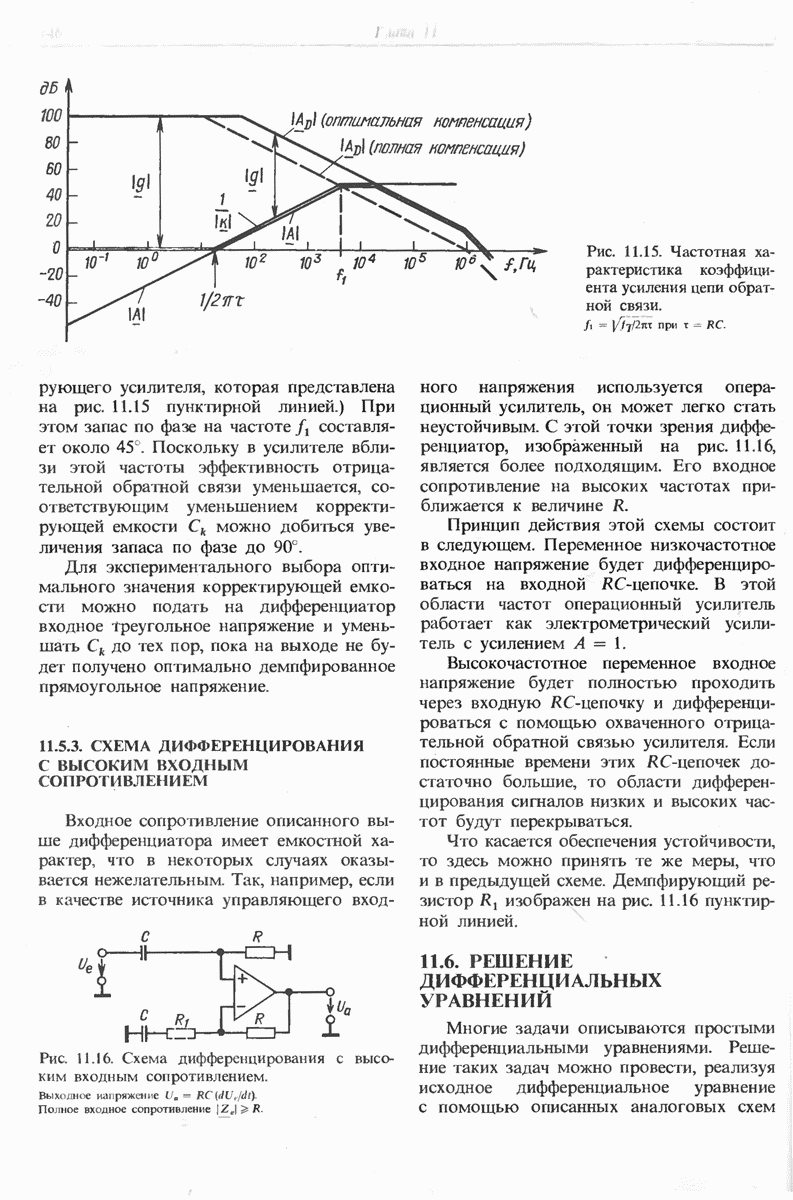
- 11.5.3. СХЕМА ДИФФЕРЕНЦИРОВАНИЯ С ВЫСОКИМ ВХОДНЫМ СОПРОТИВЛЕНИЕМ
- 11.6. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 11.7. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11.7.2. ЭКСПОНЕНТА
- 11.7.3. ВЫЧИСЛЕНИЕ СТЕПЕННЫХ ФУНКЦИЙ С ПОМОЩЬЮ ЛОГАРИФМОВ
- 11.7.4. ФУНКЦИИ SIN X И COS X
- 11.7.5. ПЕРЕСТРАИВАЕМЫЕ ФУНКЦИОНАЛЬНЫЕ СХЕМЫ
- 11.8. АНАЛОГОВЫЕ СХЕМЫ УМНОЖЕНИЯ
- 11.8.2. УМНОЖЕНИЕ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ ФУНКЦИОНАЛЬНЫХ ГЕНЕРАТОРОВ
- 11.8.3. СХЕМА УМНОЖЕНИЯ, ИСПОЛЬЗУЮЩАЯ ИЗМЕНЕНИЕ КРУТИЗНЫ ХАРАКТЕРИСТИКИ ТРАНЗИСТОРОВ
- 11.8.4. СХЕМА УМНОЖЕНИЯ С ИЗОЛИРОВАННЫМИ ЗВЕНЬЯМИ
- 11.8.5. БАЛАНСИРОВКА СХЕМ УМНОЖЕНИЯ
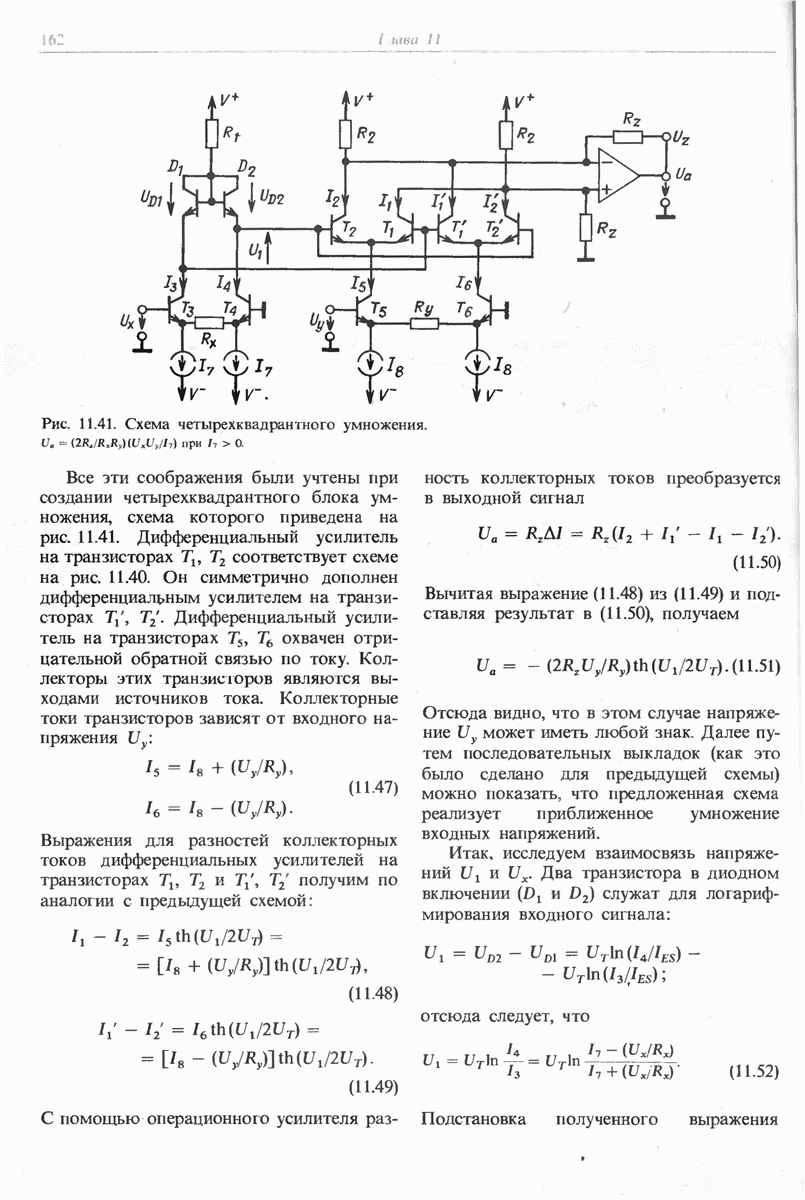
- 11.8.6. СХЕМЫ ЧЕТЫРЕХКВАДРАНТНОГО УМНОЖЕНИЯ
- 11.8.7. ПРИМЕНЕНИЕ СХЕМЫ УМНОЖЕНИЯ ДЛЯ ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
- 11.9. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 11.9.2. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ КООРДИНАТ В ПОЛЯРНЫЕ
- 12. Управляемые источники и схемы преобразования полного сопротивления
- 12.1. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.2. ИСТОЧНИКИ НАПРЯЖЕНИЯ, УПРАВЛЯЕМЫЕ ТОКОМ
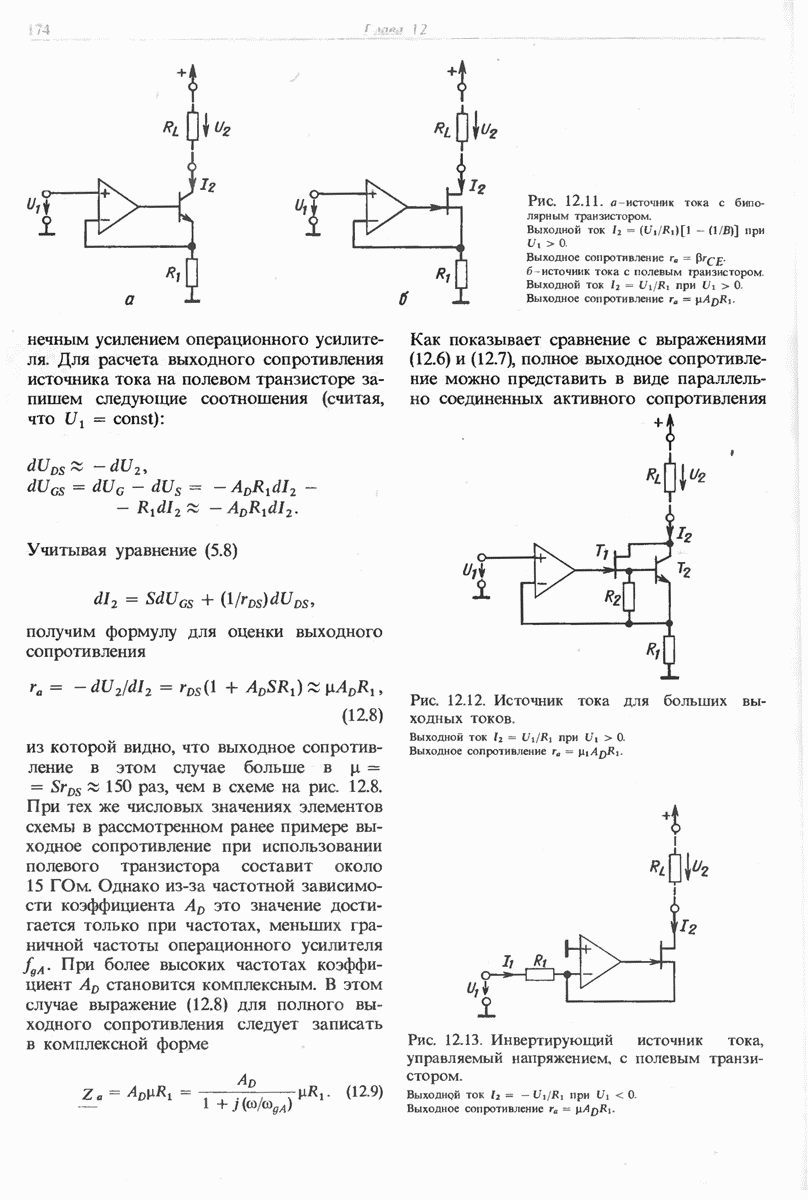
- 12.3. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ НАПРЯЖЕНИЕМ
- 12.3.2. ИСТОЧНИКИ ТОКА С ЗАЗЕМЛЕННОЙ НАГРУЗКОЙ
- 12.3.3. ЭТАЛОННЫЕ ИСТОЧНИКИ ТОКА НА ТРАНЗИСТОРАХ
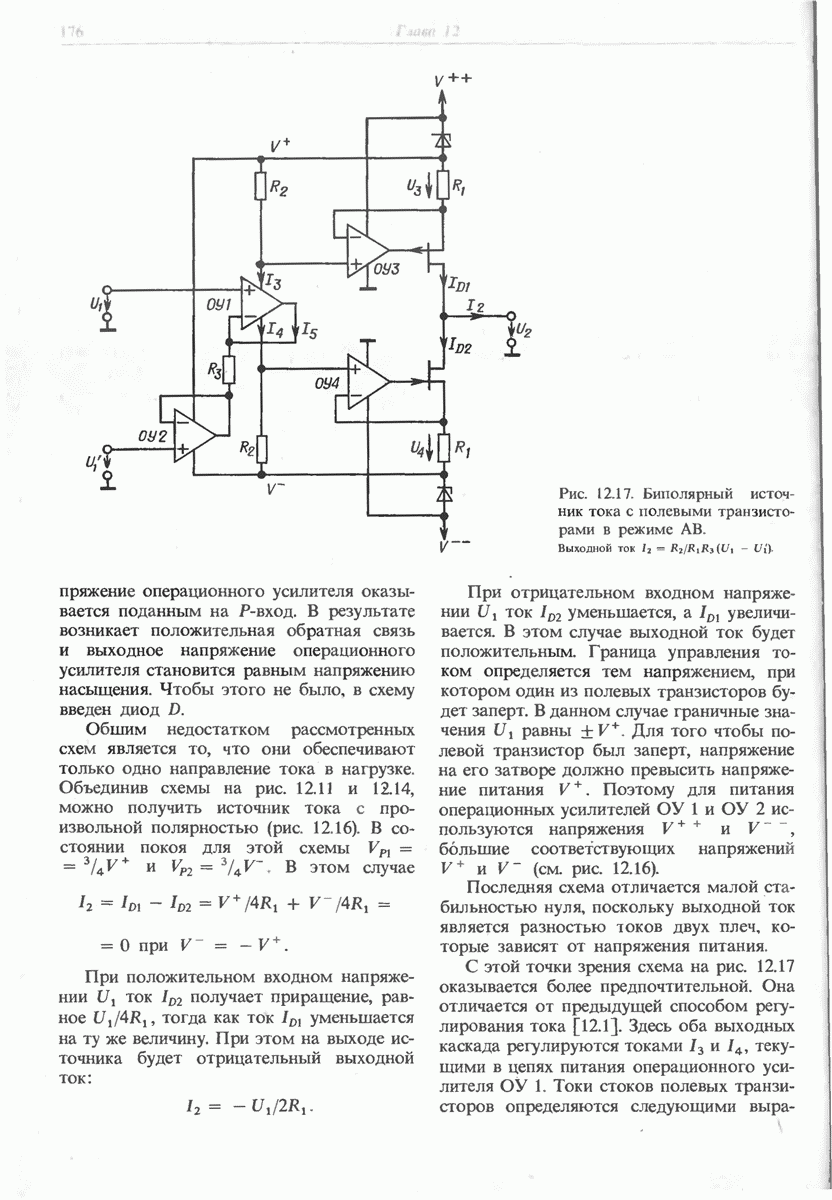
- 12.3.4. ПЛАВАЮЩИЕ ИСТОЧНИКИ ТОКА
- 12.4. ИСТОЧНИКИ ТОКА, УПРАВЛЯЕМЫЕ ТОКОМ
- 12.5. ПРЕОБРАЗОВАТЕЛЬ ОТРИЦАТЕЛЬНОГО СОПРОТИВЛЕНИЯ (NIC)
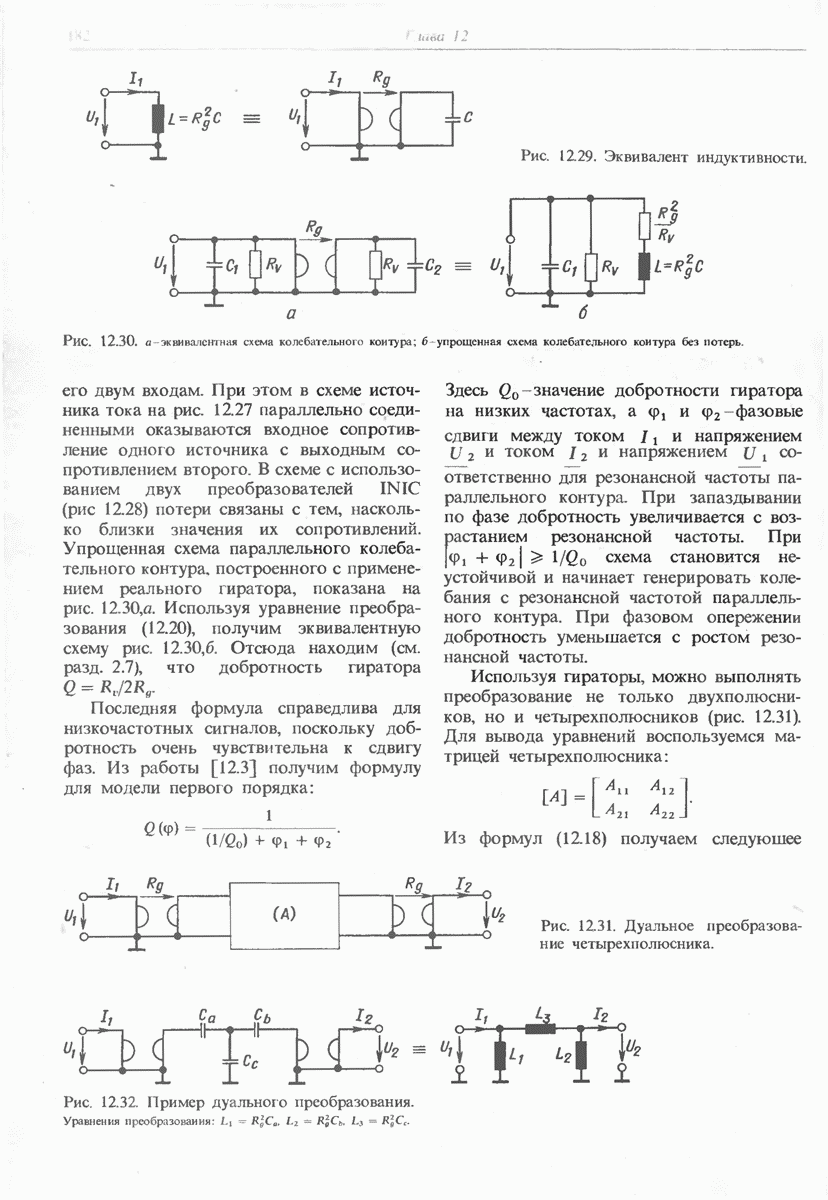
- 12.6. ГИРАТОР
- 12.7. ЦИРКУЛЯТОР
- 13. Активные фильтры
- 13.1. ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
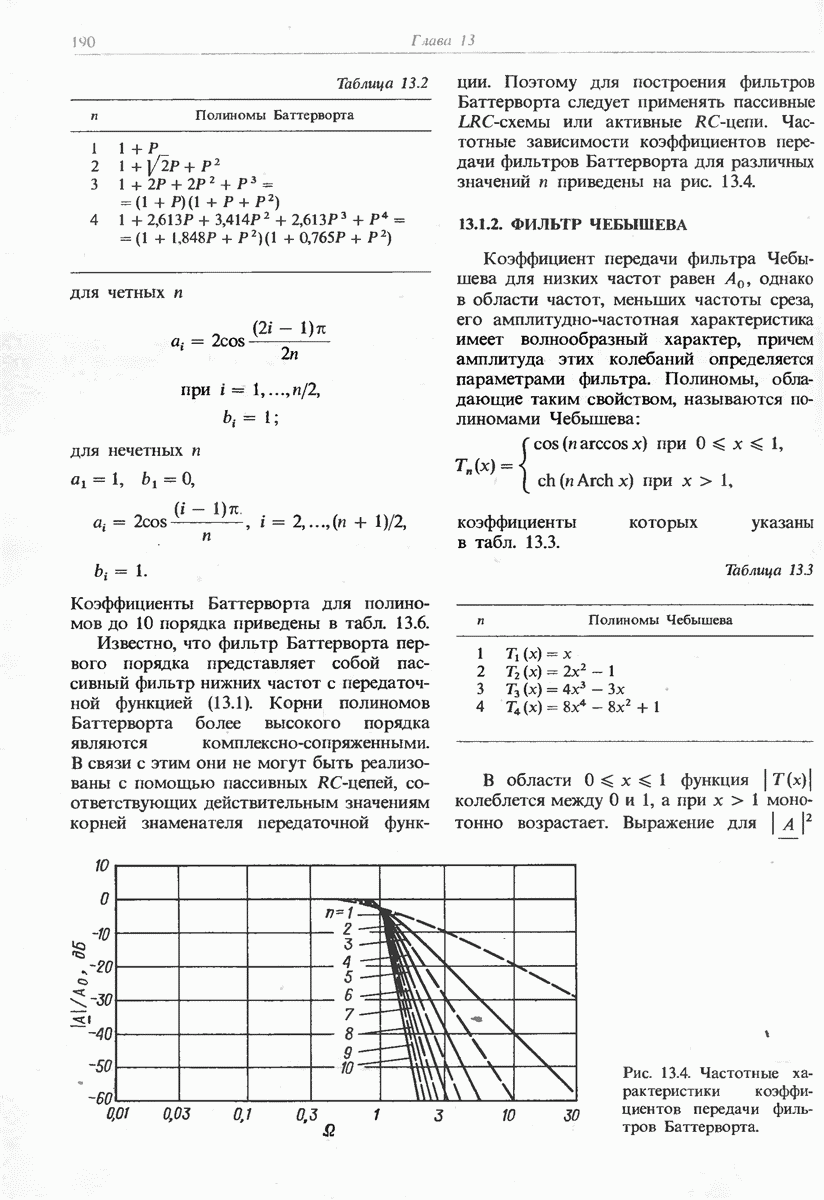
- 13.1.1. ФИЛЬТР БАТТЕРВОРТА
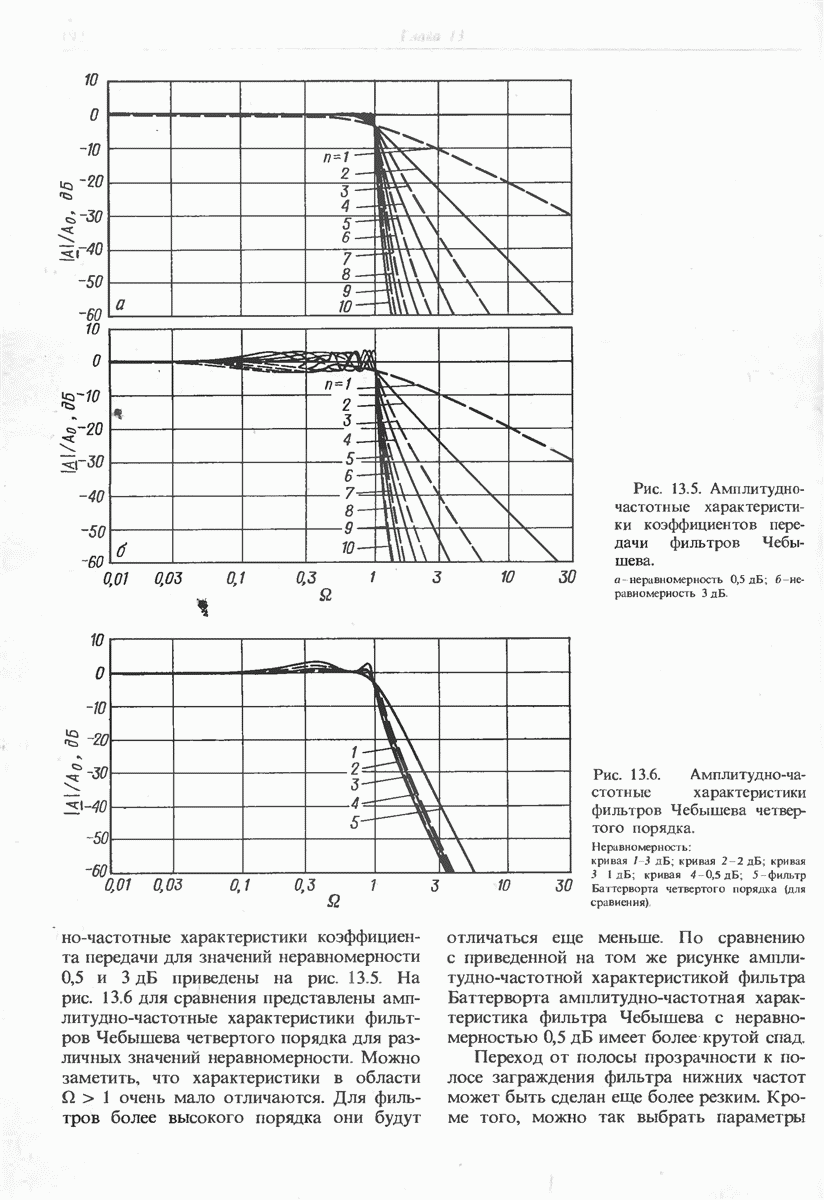
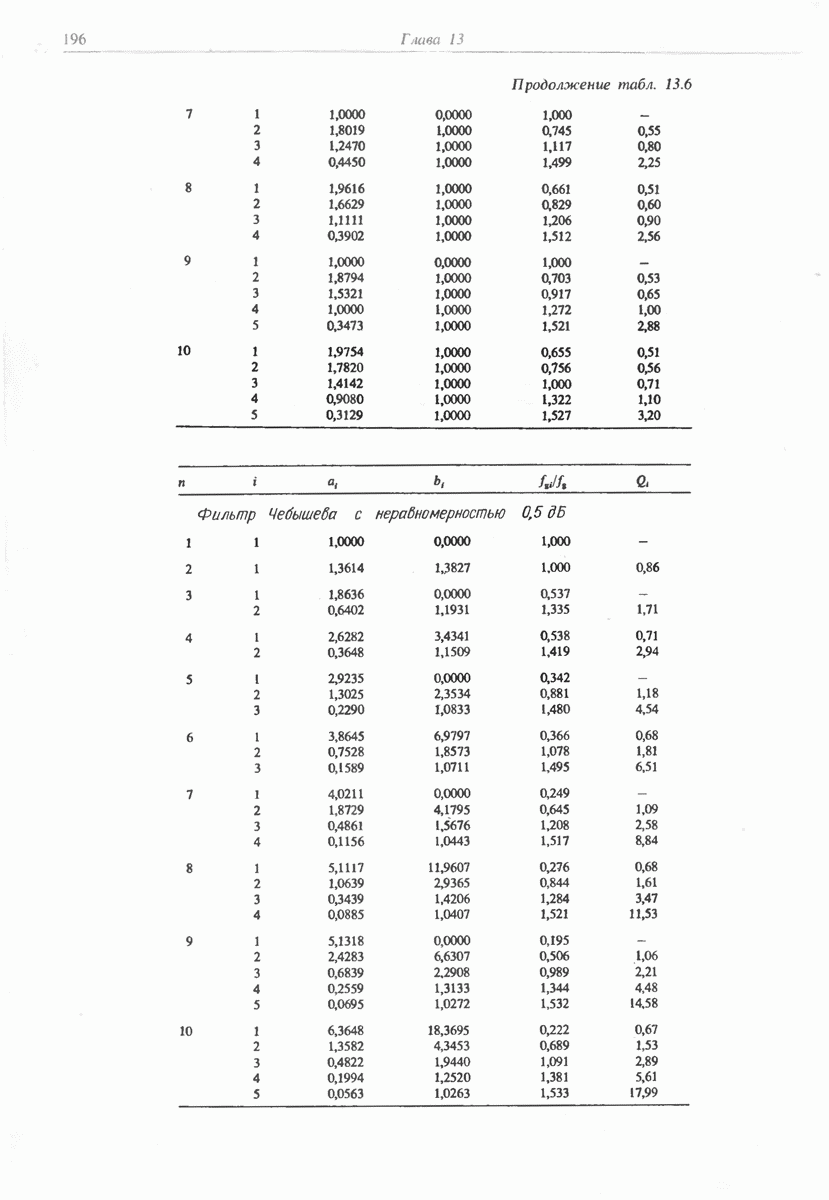
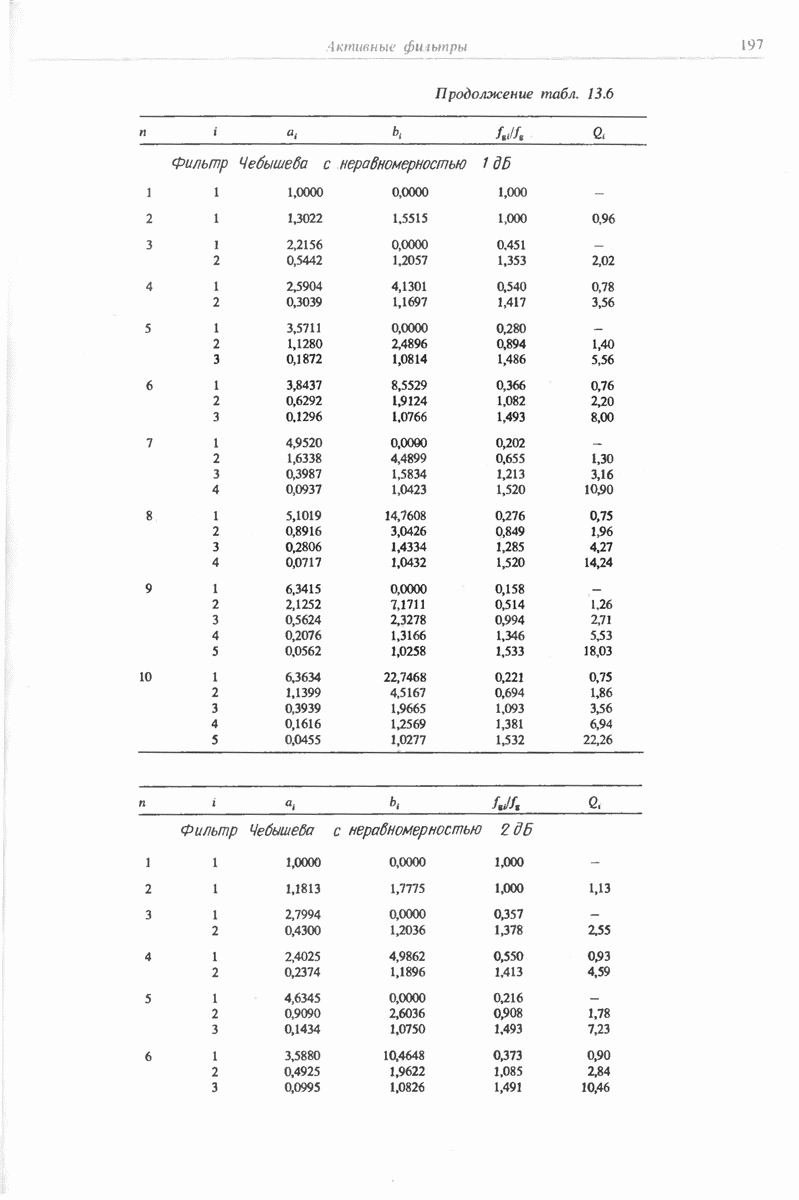
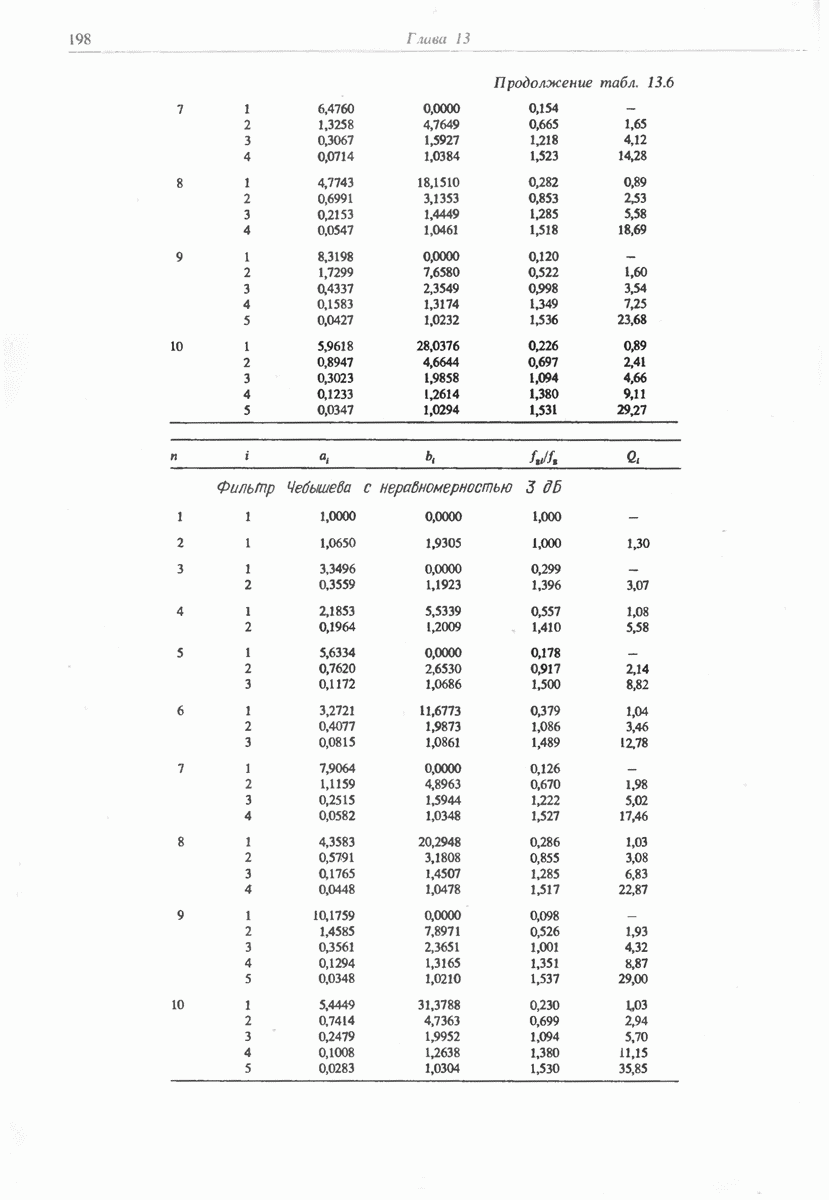
- 13.1.2. ФИЛЬТР ЧЕБЫШЕВА
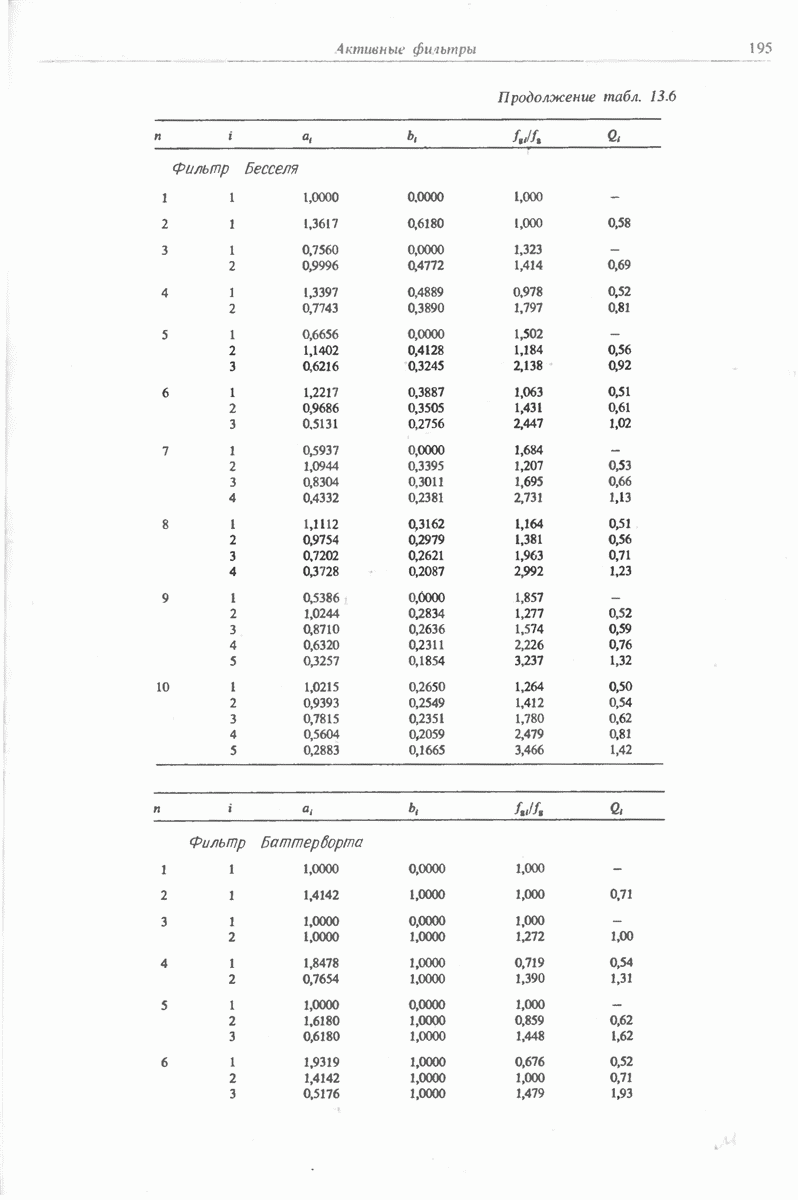
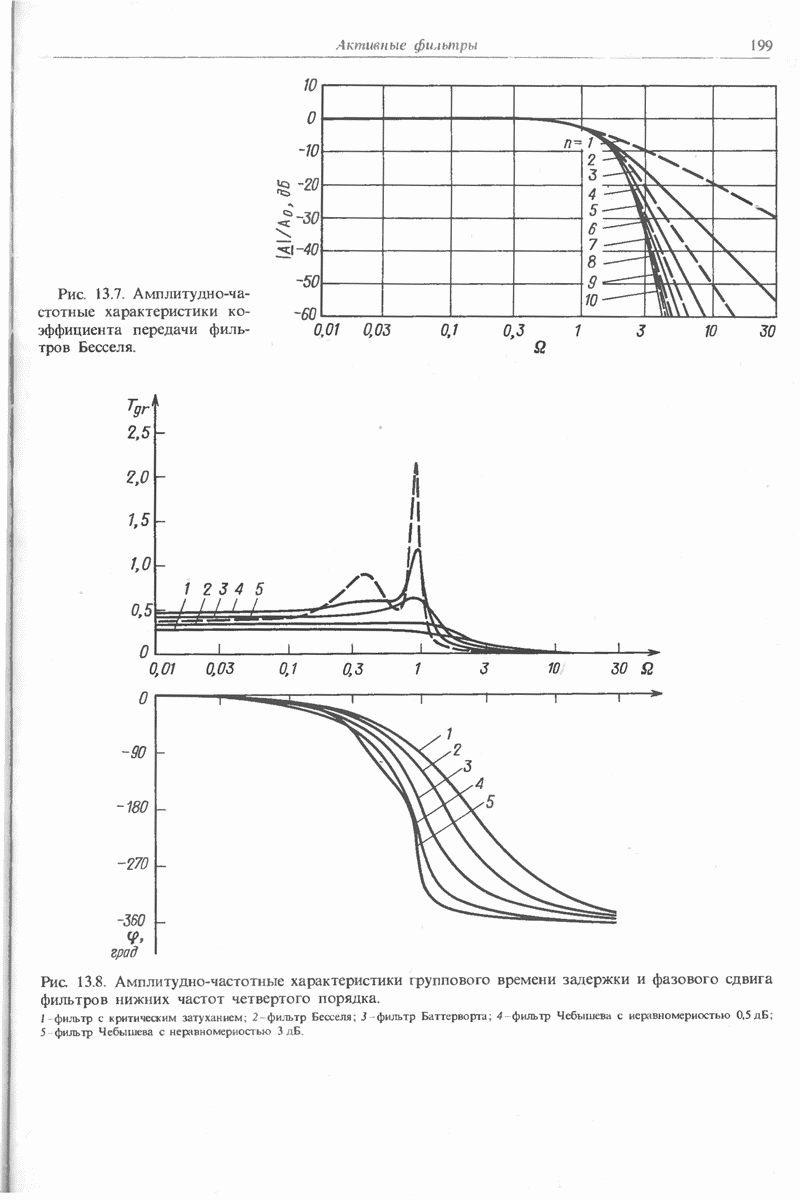
- 13.1.3. ФИЛЬТРЫ БЕССЕЛЯ
- 13.1.4. ОБОБЩЕННОЕ ОПИСАНИЕ ФИЛЬТРОВ
- 13.2. ПРЕОБРАЗОВАНИЕ НИЖНИХ ЧАСТОТ В ВЕРХНИЕ
- 13.3. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ПЕРВОГО ПОРЯДКА
- 13.4. РЕАЛИЗАЦИЯ ФИЛЬТРОВ НИЖНИХ И ВЕРХНИХ ЧАСТОТ ВТОРОГО ПОРЯДКА
- 13.4.2. ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.3. ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.4.4. ФИЛЬТР НИЖНИХ ЧАСТОТ С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.5. РЕАЛИЗАЦИЯ ФИЛЬТРОВ ВЕРХНИХ И НИЖНИХ ЧАСТОТ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
- 13.6. ПРЕОБРАЗОВАНИЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ В ПОЛОСОВОЙ ФИЛЬТР
- 13.6.1. ПОЛОСОВОЙ ФИЛЬТР ВТОРОГО ПОРЯДКА
- 13.6.2. ПОЛОСОВОЙ ФИЛЬТР ЧЕТВЕРТОГО ПОРЯДКА
- 13.7. РЕАЛИЗАЦИЯ ПОЛОСОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.7.2. ПОЛОСОВОЙ ФИЛЬТР СО СЛОЖНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.3. ПОЛОСОВОЙ ФИЛЬТР С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.7.4. ПОЛОСОВОЙ ФИЛЬТР С ОМИЧЕСКОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
- 13.8. ПРЕОБРАЗОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ В ЗАГРАЖДАЮЩИЕ ПОЛОСОВЫЕ ФИЛЬТРЫ
- 13.9. РЕАЛИЗАЦИЯ ЗАГРАЖДАЮЩИХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 13.9.1. ЗАГРАЖДАЮЩИЙ LRC-ФИЛЬТР
- 13.9.2. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С ДВОЙНЫМ Т-ОБРАЗНЫМ МОСТОМ
- 13.9.3. АКТИВНЫЙ ЗАГРАЖДАЮЩИЙ ФИЛЬТР С МОСТОМ ВИНА-РОБИНСОНА
- 13.10. ФАЗОВЫЙ ФИЛЬТР
- 13.10.2. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ПЕРВОГО ПОРЯДКА
- 13.10.3. РЕАЛИЗАЦИЯ ФАЗОВОГО ФИЛЬТРА ВТОРОГО ПОРЯДКА
- 13.11. ПЕРЕСТРАИВАЕМЫЙ УНИВЕРСАЛЬНЫЙ ФИЛЬТР
- 14. Широкополосные усилители
- 14.1. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА УСИЛЕНИЯ ПО ТОКУ ОТ ЧАСТОТЫ
- 14.2. ВЛИЯНИЕ ВНУТРЕННИХ ЕМКОСТЕЙ ТРАНЗИСТОРА И ЕМКОСТЕЙ МОНТАЖА
- 14.3. КАСКОДНАЯ СХЕМА
- 14.4. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ КАК ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5. СИММЕТРИЧНЫЙ ШИРОКОПОЛОСНЫЙ УСИЛИТЕЛЬ
- 14.5.2. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С ИНВЕРТОРОМ
- 14.5.3. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ С КОМПЛЕМЕНТАРНОЙ КАСКОДНОЙ СХЕМОЙ
- 14.5.4. ДВУХТАКТНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬ
- 14.6. ШИРОКОПОЛОСНЫЙ ПОВТОРИТЕЛЬ НАПРЯЖЕНИЯ
- 14.6.2. ДВУХТАКТНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 14.7. ШИРОКОПОЛОСНЫЙ ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
- 15. Усилители мощности
- 15.1. ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ КАК УСИЛИТЕЛЬ МОЩНОСТИ
- 15.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ
- 15.2.2. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ В РЕЖИМЕ AB
- 15.2.3. СПОСОБЫ ЗАДАНИЯ НАПРЯЖЕНИЯ СМЕЩЕНИЯ
- 15.3. СХЕМЫ ОГРАНИЧЕНИЯ ТОКА
- 15.4. КОМПЛЕМЕНТАРНЫЙ ЭМИТТЕРНЫЙ ПОВТОРИТЕЛЬ ПО СХЕМЕ ДАРЛИНГТОНА
- 15.5. РАСЧЕТ МОЩНОГО ОКОНЕЧНОГО КАСКАДА
- 15.6. СХЕМЫ ПРЕДВАРИТЕЛЬНЫХ УСИЛИТЕЛЕЙ НАПРЯЖЕНИЯ
- 15.7. ПОВЫШЕНИЕ НАГРУЗОЧНОЙ СПОСОБНОСТИ ИНТЕГРАЛЬНЫХ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 16. Источники питания
- 16.1. СВОЙСТВА СЕТЕВЫХ ТРАНСФОРМАТОРОВ
- 16.2. ВЫПРЯМИТЕЛИ
- 16.2.1. ОДНОПОЛУПЕРИОДНЫЙ ВЫПРЯМИТЕЛЬ
- 16.2.2. МОСТОВОЙ ВЫПРЯМИТЕЛЬ
- 16.2.3. МОСТОВОЙ ВЫПРЯМИТЕЛЬ ДЛЯ ДВУХ СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ ВЫХОДНЫХ НАПРЯЖЕНИЙ
- 16.3. ПОСЛЕДОВАТЕЛЬНАЯ СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЯ
- 16.3.2. СХЕМА С РЕГУЛИРУЮЩИМ УСИЛИТЕЛЕМ
- 16.3.3. ИНТЕГРАЛЬНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 16.3.4. СТАБИЛИЗАТОР С МАЛЫМ НАПРЯЖЕНИЕМ ПОТЕРЬ
- 16.3.5. СТАБИЛИЗАЦИЯ НАПРЯЖЕНИЙ, СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ЗЕМЛИ
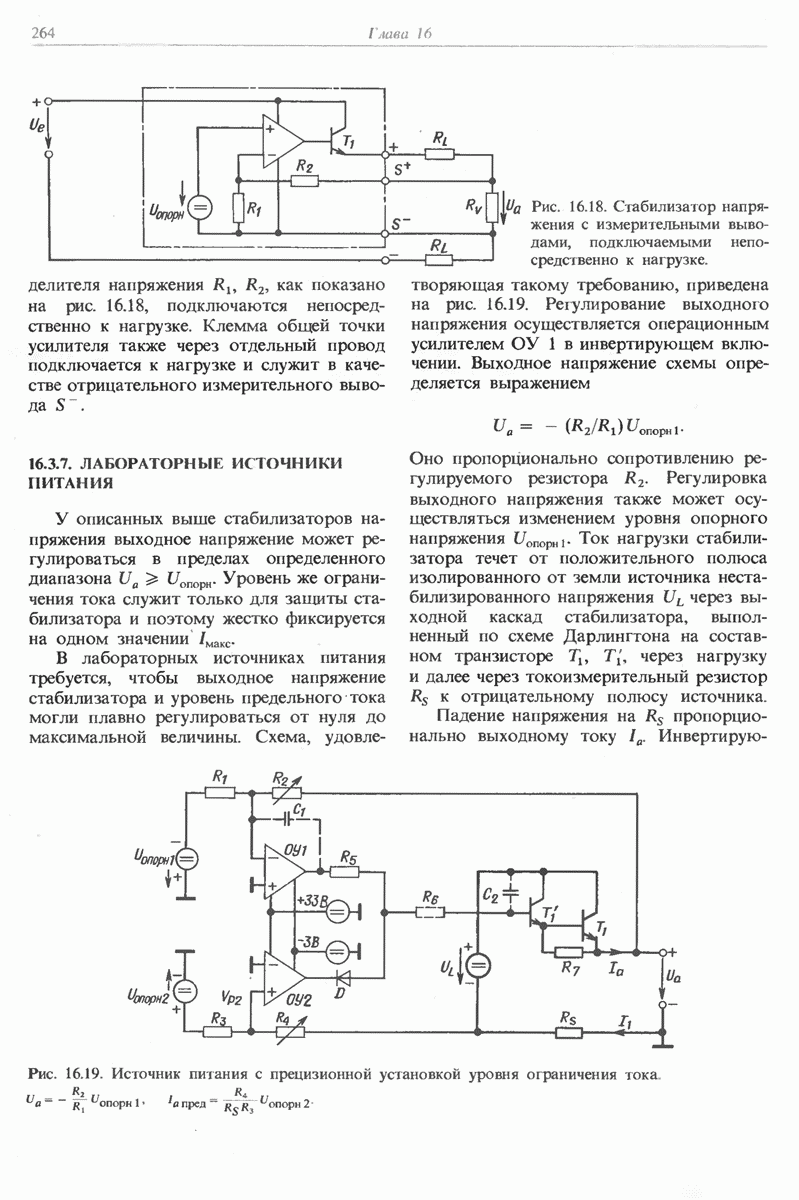
- 16.3.6. СТАБИЛИЗАТОР НАПРЯЖЕНИЯ С ИЗМЕРИТЕЛЬНЫМИ ВЫВОДАМИ
- 16.3.7. ЛАБОРАТОРНЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 16.3.8. ОКОНЕЧНЫЙ КАСКАД ЛАБОРАТОРНОГО ИСТОЧНИКА ПИТАНИЯ С БОЛЬШОЙ ВЫХОДНОЙ МОЩНОСТЬЮ
- 16.4. ПОЛУЧЕНИЕ ОПОРНОГО НАПРЯЖЕНИЯ
- 16.4.2. ПОЛУЧЕНИЕ МАЛЫХ ОПОРНЫХ НАПРЯЖЕНИЙ
- 16.5. ИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ
- 16.5.2. ПЕРВИЧНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- 17. Аналоговые коммутаторы и компараторы
- 17.2. ЭЛЕКТРОННЫЕ КОММУТАТОРЫ
- 17.2.2. ДИОДНЫЙ КОММУТАТОР
- 17.2.3. КОММУТАТОР НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
- 17.3. АНАЛОГОВЫЕ КОММУТАТОРЫ НА БАЗЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 17.3.2. КОММУТАТОР НА ПОЛЕВОМ ТРАНЗИСТОРЕ С ПЕРЕМЕНОЙ ЗНАКА ВЫХОДНОГО НАПРЯЖЕНИЯ
- 17.3.3. КОММУТАТОР НА БАЗЕ ДИФФЕРЕНЦИАЛЬНОГО УСИЛИТЕЛЯ
- 17.4. АНАЛОГОВЫЕ КОММУТАТОРЫ С ПАМЯТЬЮ
- 17.5. КОМПАРАТОРЫ
- 17.5.2. КОМПАРАТОР С ПРЕЦИЗИОННЫМ ВЫХОДНЫМ НАПРЯЖЕНИЕМ
- 17.5.3. ДВУХПОРОГОВЫЙ КОМПАРАТОР
- 17.6. ТРИГГЕР ШМИТТА
- 17.6.1. ИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.2. НЕИНВЕРТИРУЮЩИЙ ТРИГГЕР ШМИТТА
- 17.6.3. ПРЕЦИЗИОННЫЙ ТРИГГЕР ШМИТТА
- 18. Генераторы сигналов
- 18.1. LC-ГЕНЕРАТОРЫ
- 18.1.2. ГЕНЕРАТОР С ТРАНСФОРМАТОРНОЙ СВЯЗЬЮ (СХЕМА МАЙССНЕРА)
- 18.1.3. ТРЕХТОЧЕЧНАЯ СХЕМА С ИНДУKТИВНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА ХАРТЛИ)
- 18.1.4. ТРЕХТОЧЕЧНАЯ СХЕМА С ЕМКОСТНОЙ ОБРАТНОЙ СВЯЗЬЮ (СХЕМА КОЛПИТЦА)
- 18.1.5. LC-ГЕНЕРАТОР С ЭМИТТЕРНОЙ СВЯЗЬЮ
- 18.1.6. ДВУХТАКТНЫЕ ГЕНЕРАТОРЫ
- 18.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ
- 18.2.1. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КВАРЦЕВОГО РЕЗОНАТОРА
- 18.2.2. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ С LC-КОЛЕБАТЕЛЬНЫМ КОНТУРОМ
- 18.2.3. КВАРЦЕВЫЕ ГЕНЕРАТОРЫ БЕЗ LC-КОНТУРА
- 18.3. СИНУСОИДАЛЬНЫЕ RC-ГЕНЕРАТОРЫ
- 18.3.2. МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 18.4. ГЕНЕРАТОРЫ СИГНАЛОВ СПЕЦИАЛЬНОЙ ФОРМЫ (ФУНКЦИОНАЛЬНЫЕ ГЕНЕРАТОРЫ)
- 18.4.2. ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР С УПРАВЛЯЕМОЙ ЧАСТОТОЙ ВЫХОДНОГО СИГНАЛА
- 18.4.3. ВЫСОКОЧАСТОТНЫЙ ФУНКЦИОНАЛЬНЫЙ ГЕНЕРАТОР
- 18.5. МУЛЬТИВИБРАТОРЫ
- 18.5.1. НИЗКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 18.5.2. ВЫСОКОЧАСТОТНЫЕ МУЛЬТИВИБРАТОРЫ
- 19. Комбинационные логические схемы
- 19.1. ПРЕОБРАЗОВАТЕЛИ КОДОВ
- 19.1.2. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 19.1.3. КОД ГРЕЯ
- 19.2. МУЛЬТИПЛЕКСОР И ДЕМУЛЬТИПЛЕКСОР
- 19.3. КОМБИНАЦИОННОЕ УСТРОЙСТВО СДВИГА
- 19.4. КОМПАРАТОРЫ
- 19.5. СУММАТОРЫ
- 19.5.1. ПОЛУСУММАТОР
- 19.5.2. ПОЛНЫЙ СУММАТОР
- 19.5.3. СУММАТОРЫ С ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ
- 19.5.4. СЛОЖЕНИЕ ДВОИЧНО-ДЕСЯТИЧНЫХ ЧИСЕЛ
- 19.5.5. ВЫЧИТАНИЕ
- 19.5.6. СЛОЖЕНИЕ ЧИСЕЛ С ЛЮБЫМИ ЗНАКАМИ
- 19.6. УМНОЖИТЕЛИ
- 19.7. ЦИФРОВЫЕ ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 20. Интегральные схемы со структурами последовательностного типа
- 20.1. ДВОИЧНЫЕ СЧЕТЧИКИ
- 20.1.1. АСИНХРОННЫЙ (ПОСЛЕДОВАТЕЛЬНЫЙ) СЧЕТЧИК
- 20.1.2. СИНХРОННЫЙ (ПАРАЛЛЕЛЬНЫЙ) СЧЕТЧИК
- 20.2. ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК В КОДЕ 8421
- 20.2.1. АСИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.2.2. СИНХРОННЫЙ ДВОИЧНО-ДЕСЯТИЧНЫЙ СЧЕТЧИК
- 20.3. СЧЕТЧИК С ПРЕДВАРИТЕЛЬНОЙ УСТАНОВКОЙ
- 20.4. РЕГИСТРЫ СДВИГА
- 20.4.2. КОЛЬЦЕВОЙ РЕГИСТР
- 20.4.3. РЕГИСТР СДВИГА С ПАРАЛЛЕЛЬНЫМ ВВОДОМ
- 20.4.4. РЕГИСТР СДВИГА С ПЕРЕКЛЮЧАЕМЫМ НАПРАВЛЕНИЕМ СДВИГА
- 20.5. ПОЛУЧЕНИЕ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- 20.6. ПЕРВОНАЧАЛЬНАЯ ОБРАБОТКА АСИНХРОННОГО СИГНАЛА
- 20.6.2. СИНХРОНИЗАЦИЯ ИМПУЛЬСОВ
- 20.6.3. СИНХРОННЫЙ ОДНОВИБРАТОР
- 20.6.4. СИНХРОННЫЙ ДЕТЕКТОР ИЗМЕНЕНИЙ
- 20.6.5. СИНХРОННЫЙ ТАКТОВЫЙ ПЕРЕКЛЮЧАТЕЛЬ
- 20.7. СИСТЕМАТИЧЕСКИЙ СИНТЕЗ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ
- 20.7.2. ПРИМЕР СИНТЕЗА ПЕРЕКЛЮЧАЕМОГО СЧЕТЧИКА
- 20.7.3. СОКРАЩЕНИЕ ЕМКОСТИ ПАМЯТИ
- 21. Микро-ЭВМ
- 21.1. ОСНОВНАЯ СТРУКТУРА МИКРО-ЭВМ
- 21.2. ПРИНЦИП ДЕЙСТВИЯ МИКРОПРОЦЕССОРА
- 21.3. НАБОР КОМАНД
- 21.4. ОТЛАДОЧНЫЕ СРЕДСТВА
- 21.5. ОБЗОР МИКРОПРОЦЕССОРОВ РАЗЛИЧНОГО ТИПА
- 21.6. МОДУЛЬНОЕ ПОСТРОЕНИЕ МИКРО-ЭВМ
- 21.7. ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА
- 21.7.1. ПАРАЛЛЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.2. ПОСЛЕДОВАТЕЛЬНЫЙ ИНТЕРФЕЙС
- 21.7.3. ИНТЕРФЕЙС МАГИСТРАЛИ «ОБЩАЯ ШИНА»
- 21.7.4. ПРОГРАММИРУЕМЫЙ СЧЕТЧИК
- 21.7.5. ПОДКЛЮЧЕНИЕ ПЕРИФЕРИЙНЫХ МОДУЛЕЙ СЕМЕЙСТВА 8080 К МАГИСТРАЛЯМ СЕМЕЙСТВА 6800
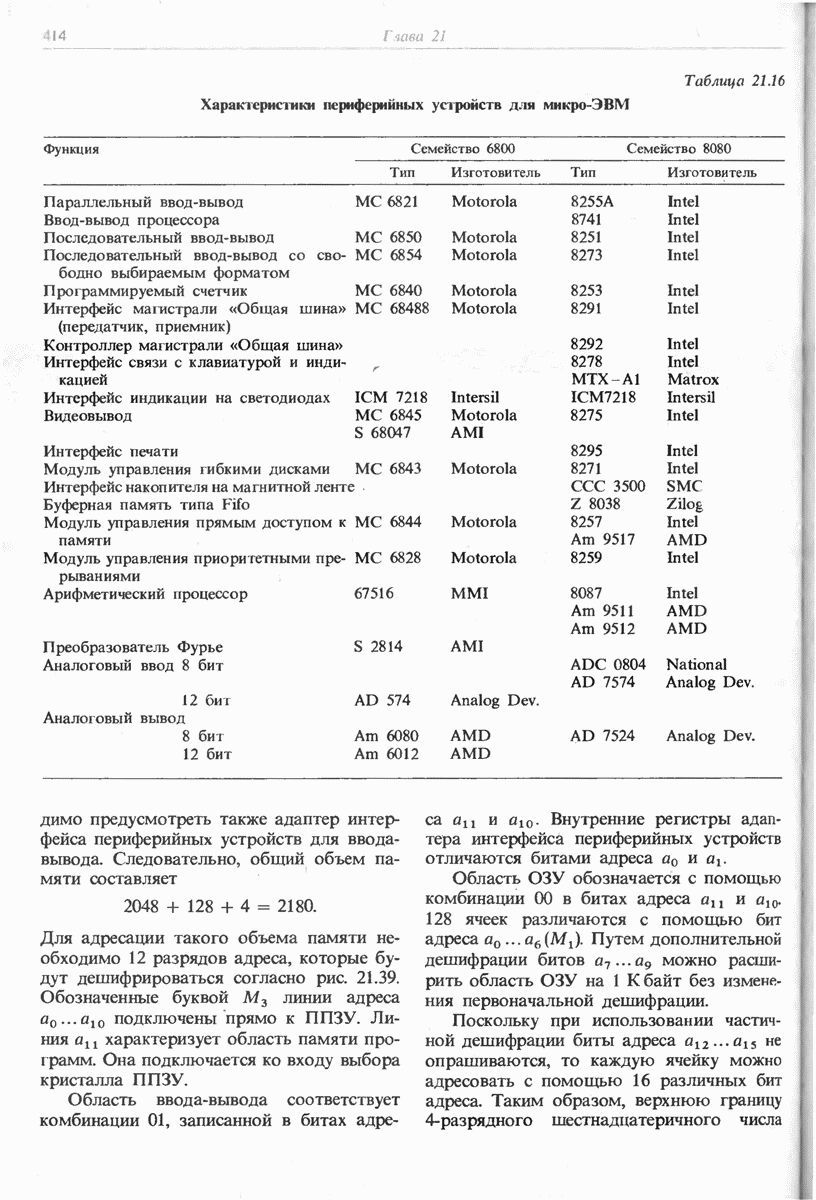
- 21.7.6. ОБЗОР ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
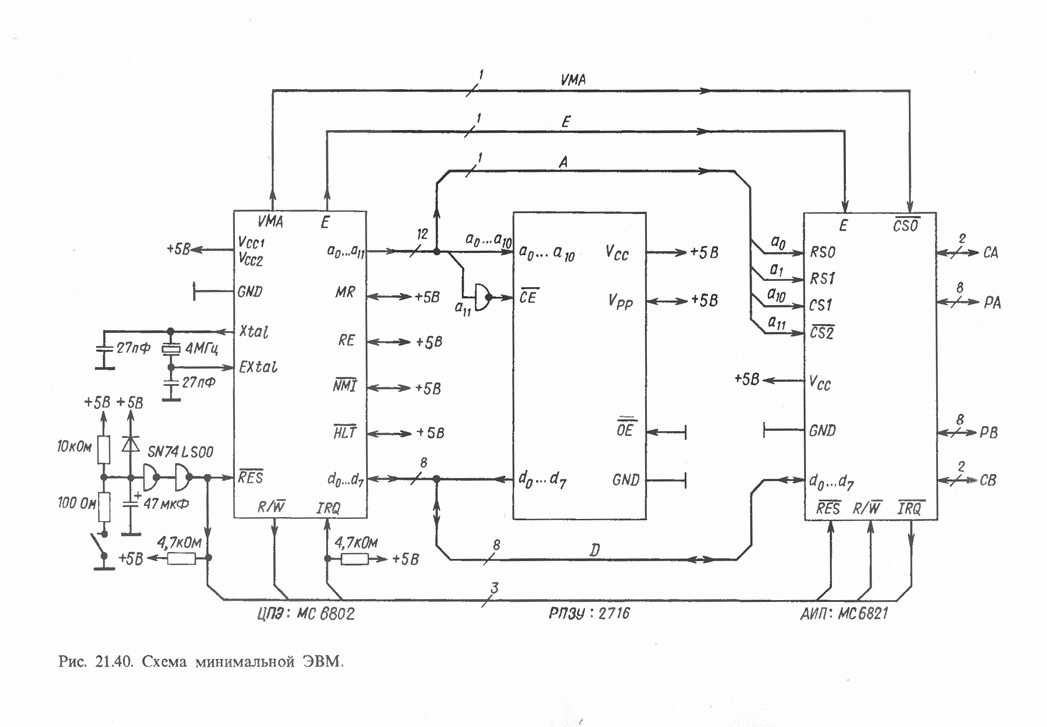
- 21.8. МИНИМАЛЬНЫЕ СИСТЕМЫ
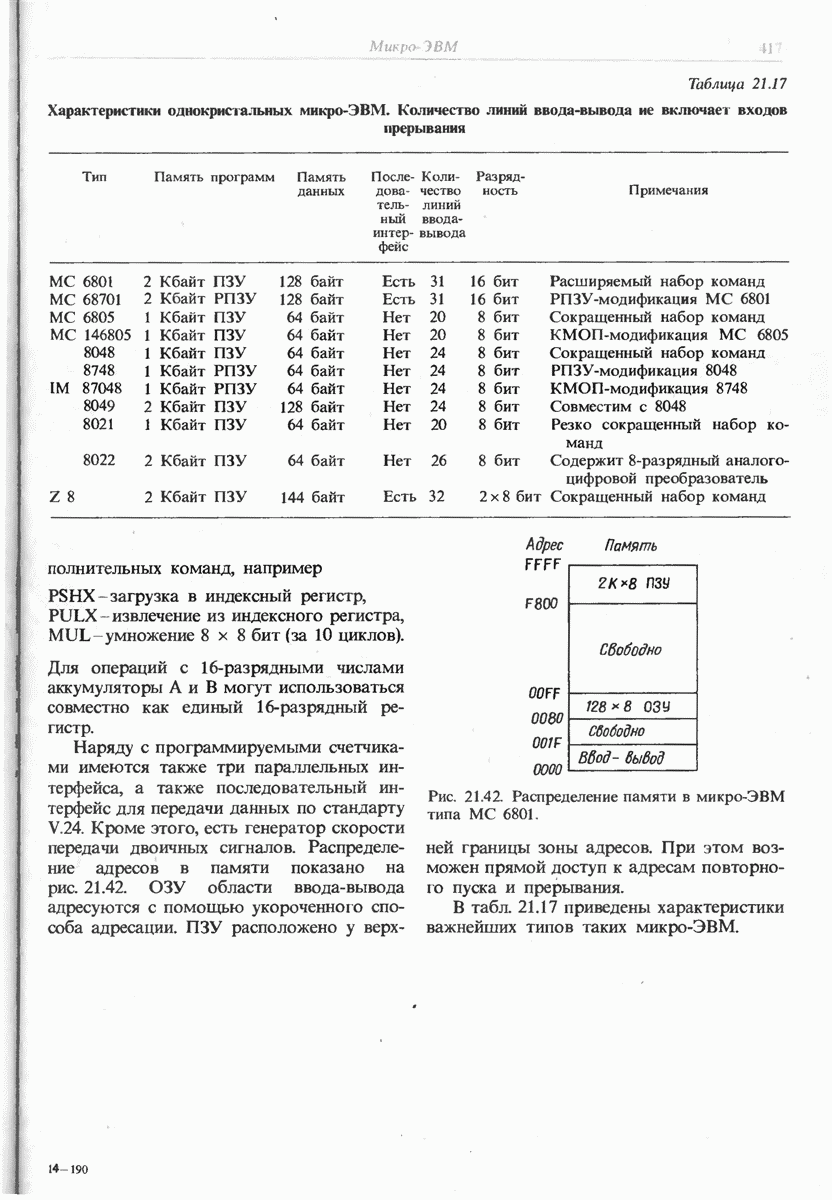
- 21.8.2. ОДНОКРИСТАЛЬНАЯ МИКРО-ЭВМ
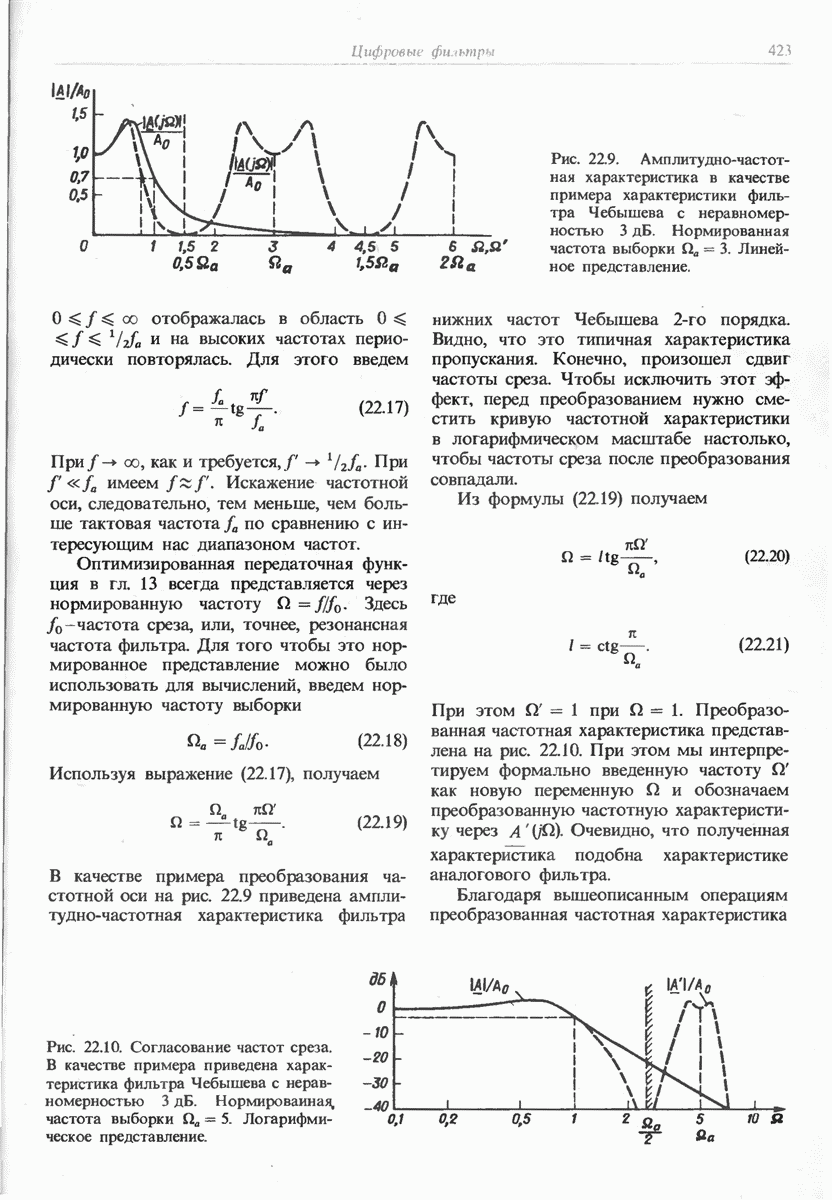
- 22. Цифровые фильтры
- 22.1. ТЕОРЕМА О ДИСКРЕТИЗАЦИИ (ТЕОРЕМА О ВЫБОРКАХ)
- 22.1.2. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 22.2. ЦИФРОВАЯ ФУНКЦИЯ ПЕРЕДАЧИ ФИЛЬТРА
- 22.3. БИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
- 22.4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ
- 22.4.2. СТРУКТУРА ЦИФРОВЫХ ФИЛЬТРОВ ВТОРОГО ПОРЯДКА
- 22.4.3. ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
- 23. Передача данных и индикация
- 23.1. СОЕДИНИТЕЛЬНЫЕ ЛИНИИ
- 23.2. ЗАЩИТА ДАННЫХ
- 23.2.2. КОД ХЕММИНГА
- 23.3. СТАТИЧЕСКИЕ ЦИФРОВЫЕ ИНДИКАТОРЫ
- 23.3.1. ДВОИЧНЫЕ ИНДИКАТОРЫ НА СВЕТОДИОДАХ
- 23.3.2. ДЕКАДНЫЕ ИНДИКАТОРЫ
- 23.3.3. ИНДИКАЦИЯ В ШЕСТНАДЦАТЕРИЧНОМ КОДЕ
- 23.4. МУЛЬТИПЛЕКСНЫЕ ИНДИКАТОРЫ
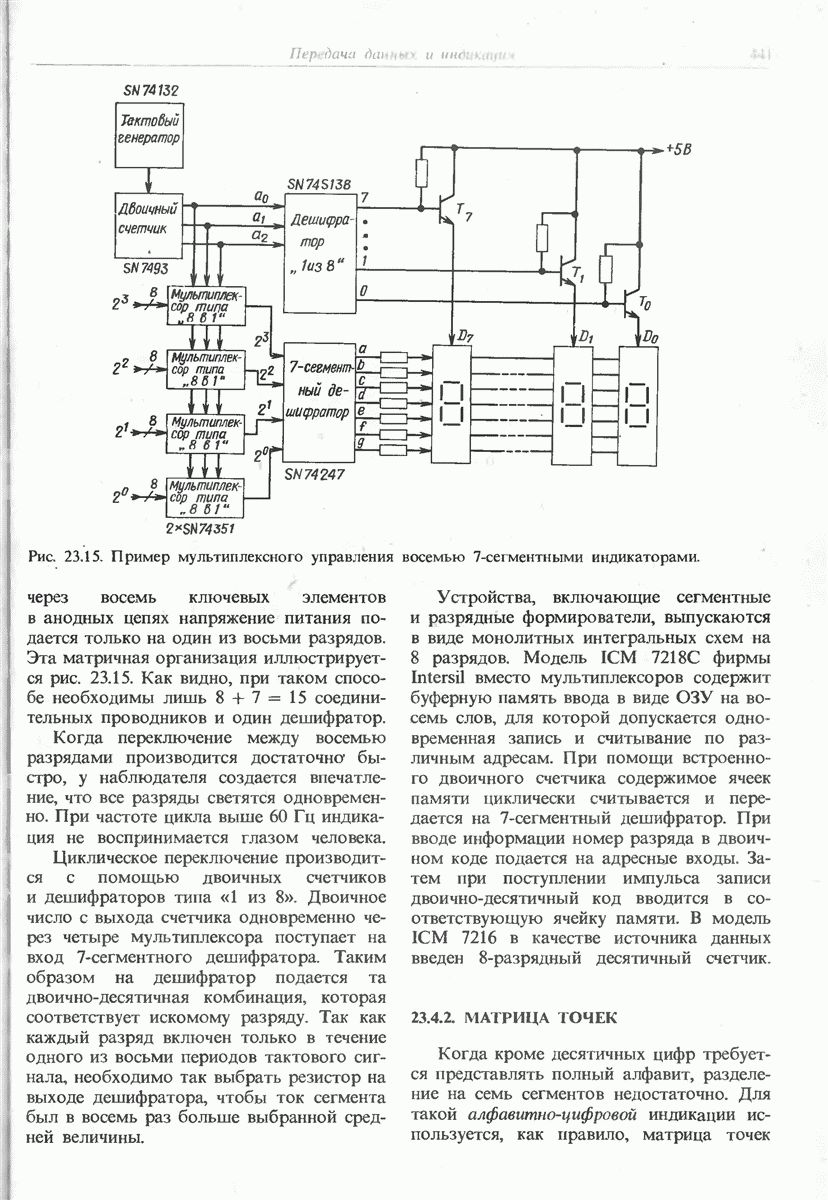
- 23.4.1. МНОГОРАЗРЯДНЫЕ 7-СЕГМЕНТНЫЕ ИНДИКАТОРЫ
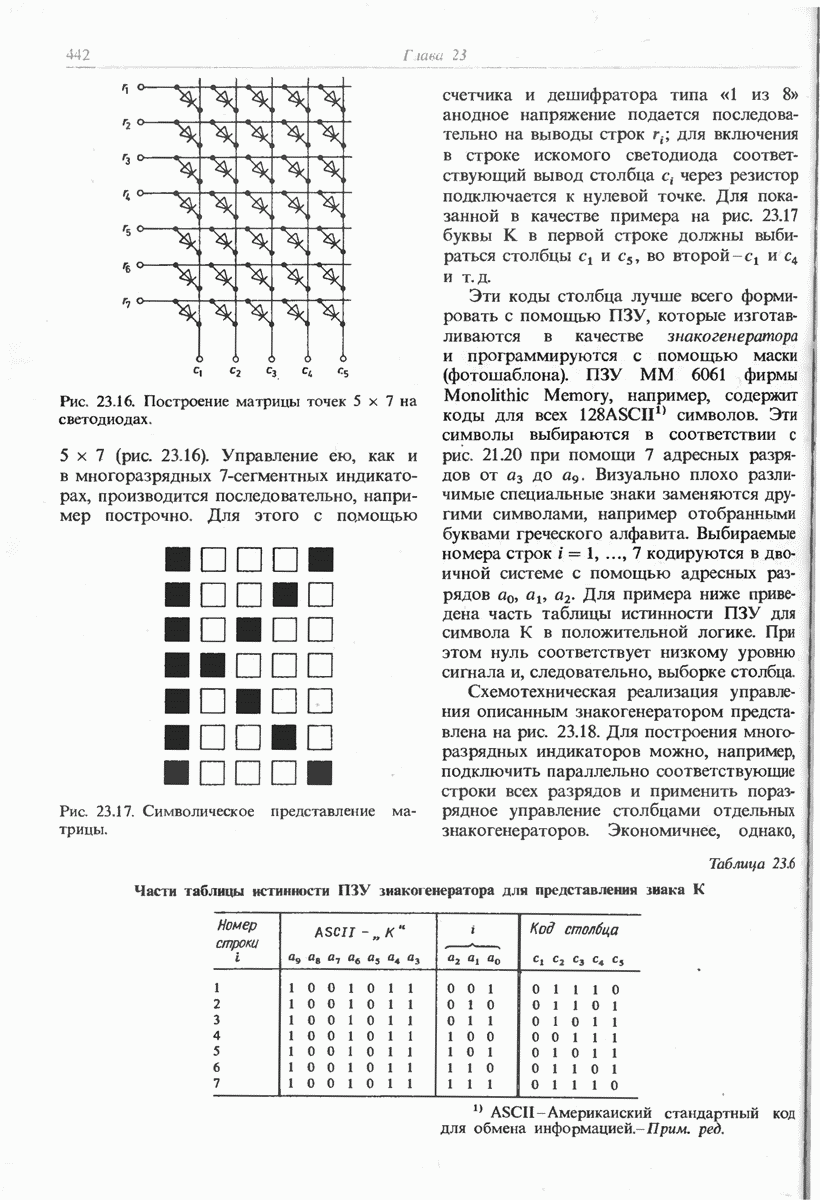
- 23.4.2. МАТРИЦА ТОЧЕК
- 24. Цифро-аналоговые и аналого-цифровые преобразователи
- 24.1. СХЕМОТЕХНИЧЕСКИЕ ПРИНЦИПЫ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.1.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ПЕРЕКИДНЫМИ КЛЮЧАМИ
- 24.1.3. РЕЗИСТИВНАЯ МАТРИЦА ПОСТОЯННОГО ИМПЕДАНСА (МАТРИЦА ТИПА R-2R)
- 24.1.4. РЕЗИСТИВНАЯ МАТРИЦА ДЛЯ ДЕКАДНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 24.2. ПОСТРОЕНИЕ ЦА-ПРЕОБРАЗОВАТЕЛЕЙ С ЭЛЕКТРОННЫМИ КЛЮЧАМИ
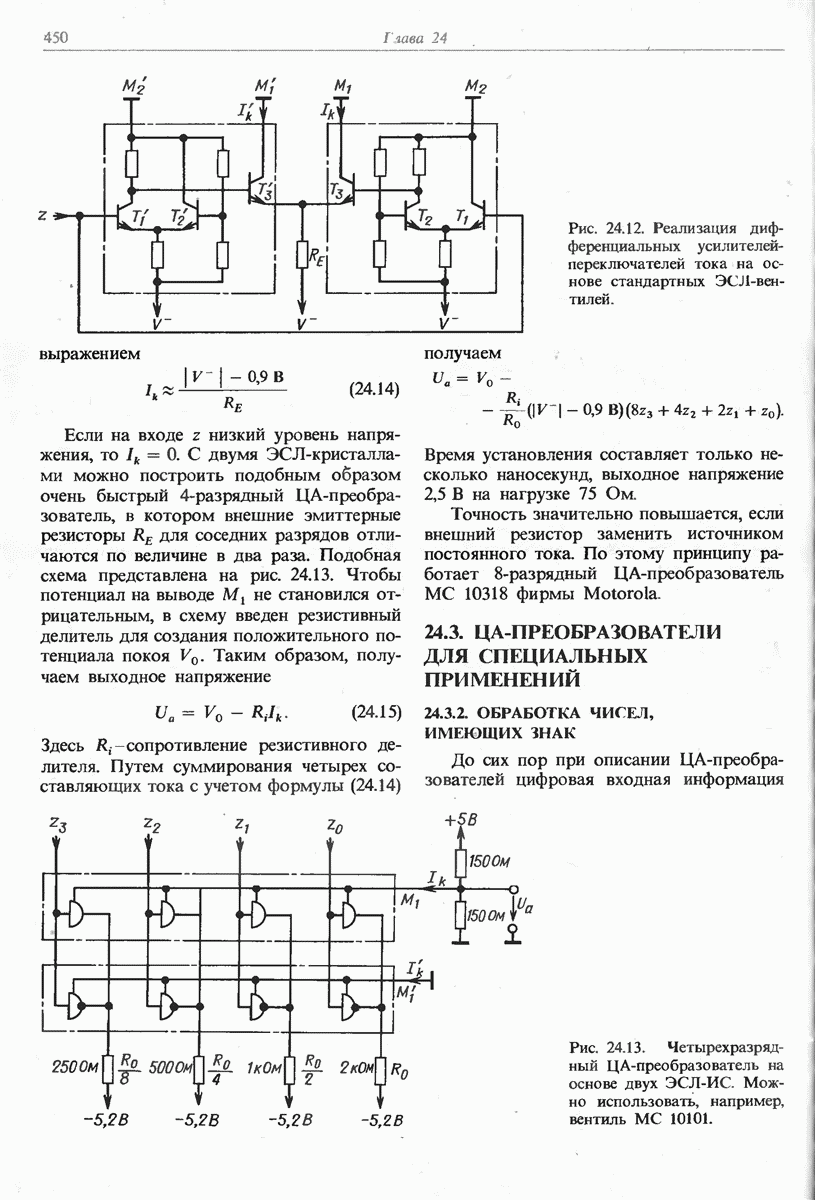
- 24.2.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ С ТОКОВЫМИ КЛЮЧАМИ
- 24.3. ЦА-ПРЕОБРАЮВАТЕЛИ ДЛЯ СПЕЦИАЛЬНЫХ ПРИМЕНЕНИЙ
- 24.3.2. ЦА-ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ДЕЛЕНИЯ
- 24.3.3. ЦА-ПРЕОБРАЗОВАТЕЛЬ КАК ГЕНЕРАТОР ФУНКЦИЙ
- 24.4. ОСНОВНЫЕ ПРИНЦИПЫ АЦ-ПРЕОБРАЗОВАНИЯ
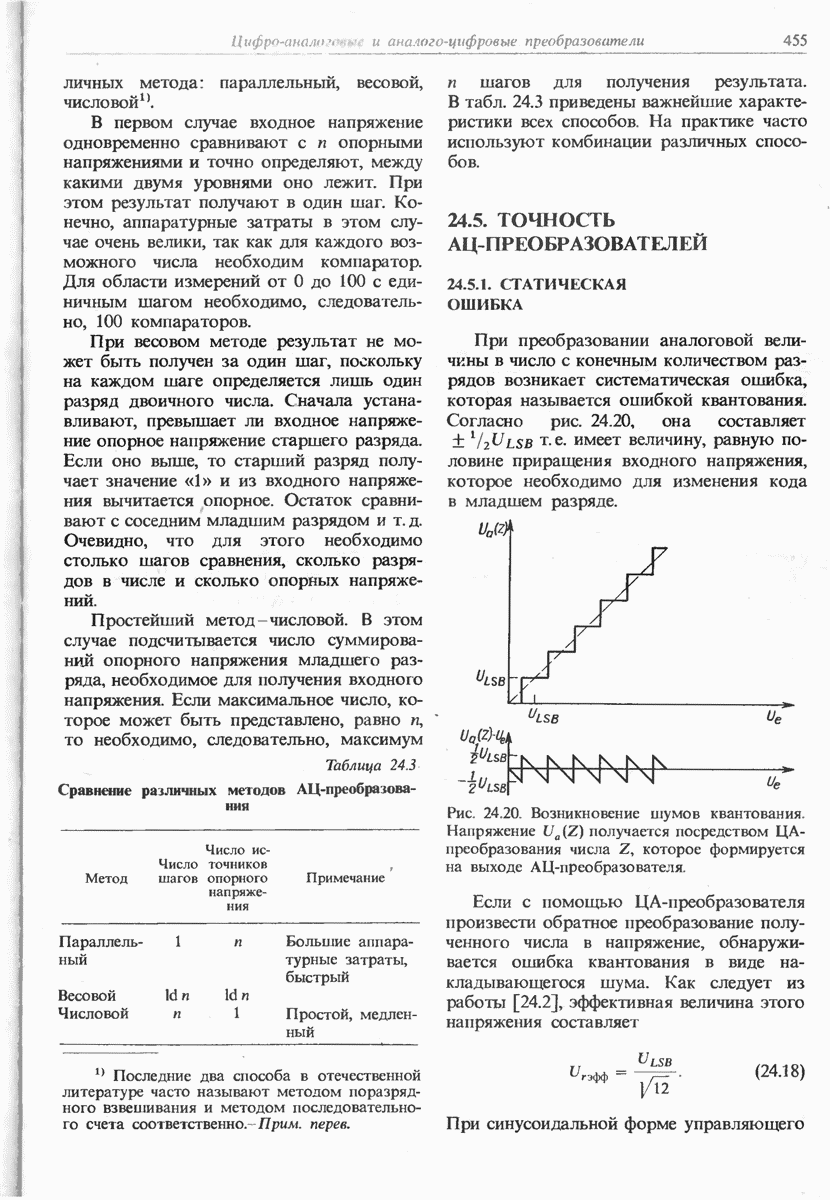
- 24.5. ТОЧНОСТЬ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 24.6. ПОСТРОЕНИЕ АЦ-ПРЕОБРАЗОВАТЕЛЕЙ
- 25. Измерительные схемы
- 25.1. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ
- 25.1.2. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
- 25.1.3. ИЗОЛИРОВАННЫЙ УСИЛИТЕЛЬ
- 25.2. ИЗМЕРЕНИЕ ТОКА
- 25.2.1. ИЗОЛИРОВАННЫЕ ОТ ЗЕМЛИ АМПЕРМЕТРЫ С МАЛЫМ ПАДЕНИЕМ НАПРЯЖЕНИЯ
- 25.2.2. ИЗМЕРЕНИЕ ТОКА ПРИ ВЫСОКОМ ПОТЕНЦИАЛЕ
- 25.3. ИЗМЕРИТЕЛЬНЫЙ ВЫПРЯМИТЕЛЬ
- 25.3.2. ИЗМЕРЕНИЕ ЭФФЕКТИВНОГО ЗНАЧЕНИЯ
- 25.3.3. ИЗМЕРЕНИЕ АМПЛИТУДНЫХ ЗНАЧЕНИЙ
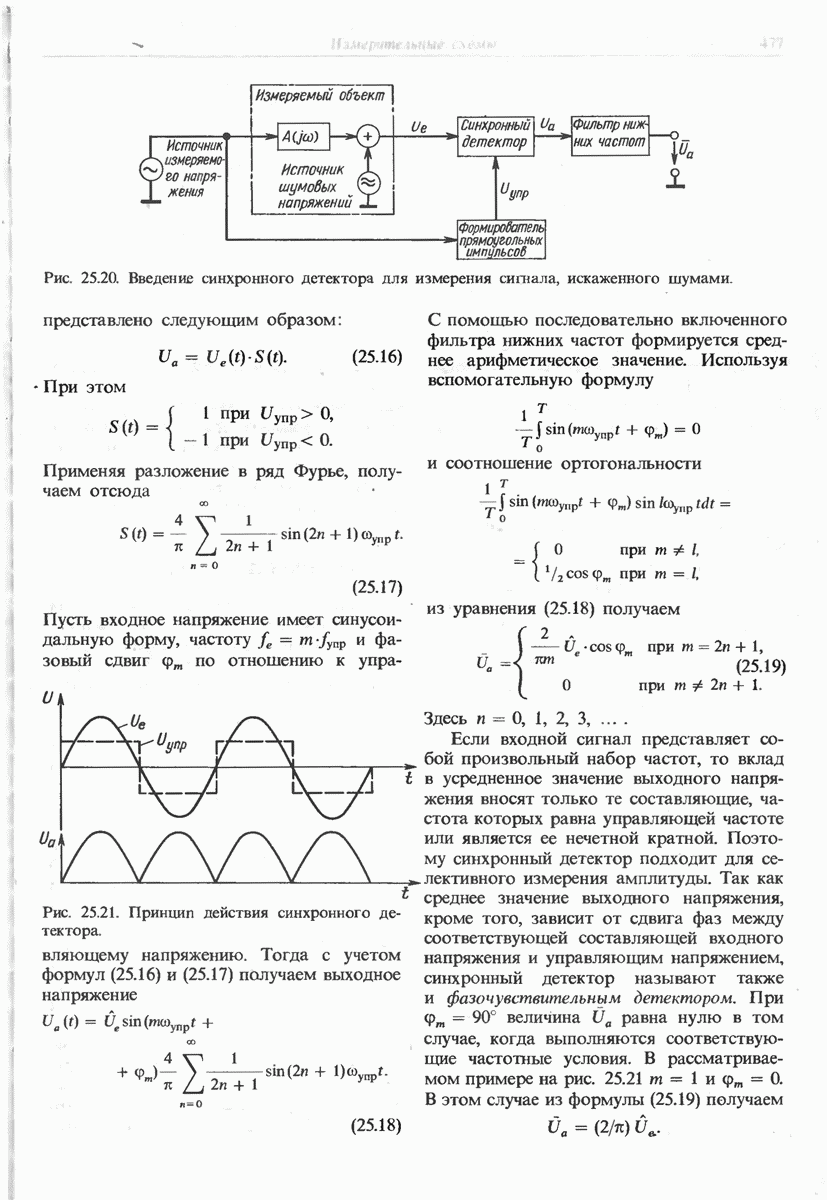
- 25.3.4. СИНХРОННЫЙ ДЕТЕКТОР
- 26. Электронные регуляторы
- 26.2. ТИПЫ РЕГУЛЯТОРОВ
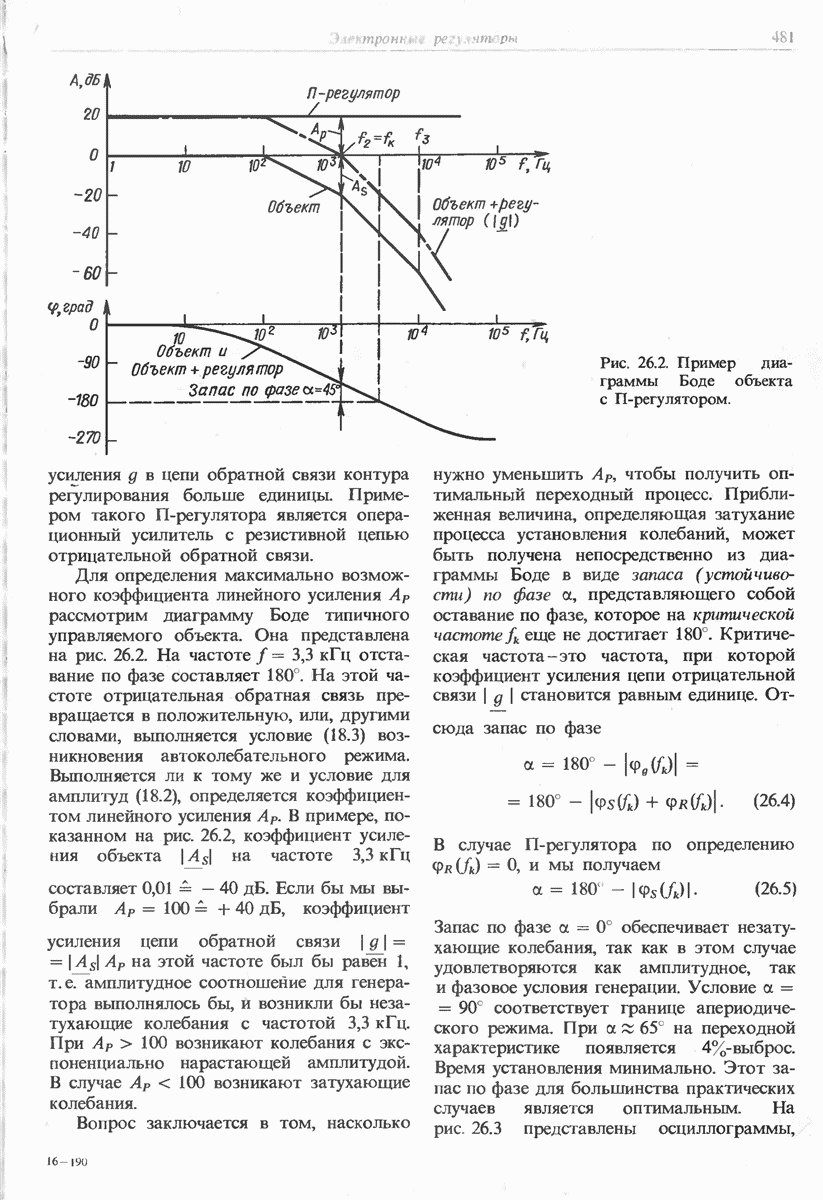
- 26.2.1. П-РЕГУЛЯТОР
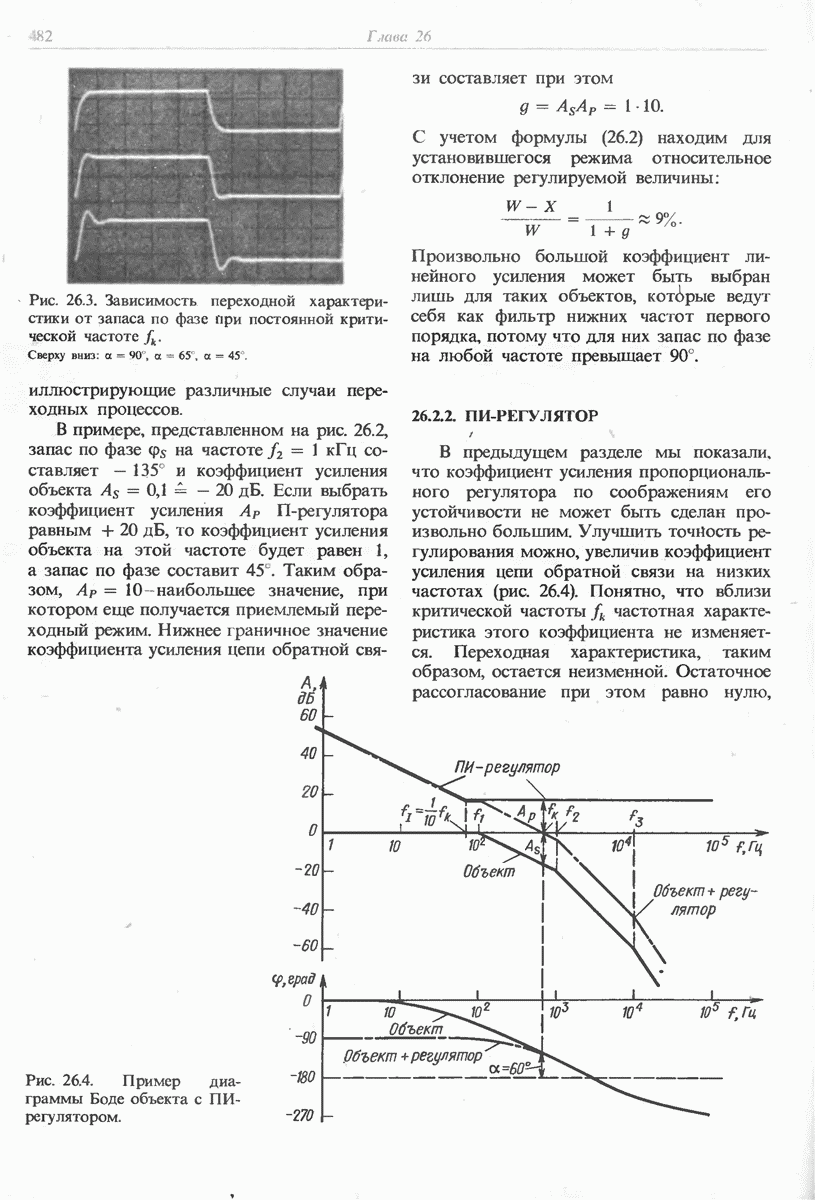
- 26.2.2. ПИ-РЕГУЛЯТОР
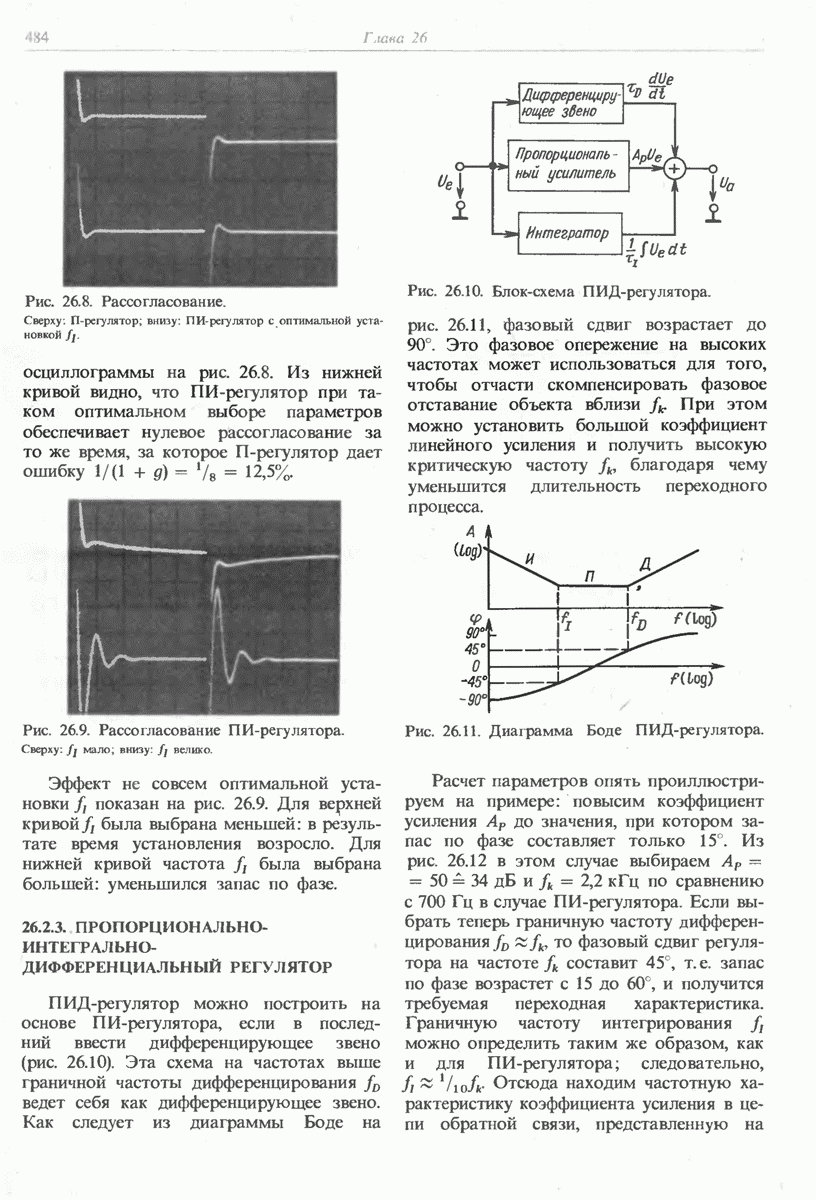
- 26.2.3. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР
- 26.2.4. НАСТРАИВАЕМЫЕ ПИД-РЕГУЛЯТОРЫ
- 26.3. УПРАВЛЕНИЕ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ
- 26.4. ОТСЛЕЖИВАЮЩАЯ СИНХРОНИЗАЦИЯ (АВТОПОДСТРОЙКА)
- 26.4.1. ЭЛЕМЕНТЫ ВЫБОРКИ-ХРАНЕНИЯ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
- 26.4.2. СИНХРОННЫЙ ВЫПРЯМИТЕЛЬ В КАЧЕСТВЕ ФАЗОВОГО ДЕТЕКТОРА
- 26.4.3. ЧАСТОТНО-ЧУВСТВИТЕЛЬНЫЙ ФАЗОВЫЙ ДЕТЕКТОР
- 26.4.4. ФАЗОВЫЙ ДЕТЕКТОР С ПРОИЗВОЛЬНО УВЕЛИЧИВАЕМЫМ ДИАПАЗОНОМ ИЗМЕРЕНИЙ
- 26.4.5. ФАЗОРЕГУЛЯТОР В КАЧЕСТВЕ ПЕРЕМНОЖИТЕЛЯ ЧАСТОТ