| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
В основном эта глава посвящена обсуждению свойств теории: Янга—Миллса, описывающей изотопический триплет безмассовых: векторных полей, взаимодействующих с сохраняющимся током. Прежде чем приступить к описанию теории Янга—Миллса, сделаем некоторые замечания о классификации симметрий и рассмотрим несколько теорий, более простых, чем теория Янга — Миллса. Все симметрии можно разделить на две большие группы: глобальные симметрии и локальные симметрии.
Глобальная абелева симметрия U(1)
Простейшим примером глобальной симметрии является сохранение заряда, выражающееся в виде инвариантности лагранжиана относительно преобразования типа

где  — заряд частицы, описываемой полем
— заряд частицы, описываемой полем  произвольное число, не зависящее от пространственно-временных координат частицы. В роли заряда могут выступать не только электрический заряд
произвольное число, не зависящее от пространственно-временных координат частицы. В роли заряда могут выступать не только электрический заряд  но и другие заряды (барионный В, лептониый
но и другие заряды (барионный В, лептониый  и т. п.). Группа таких фазовых преобразований называется
и т. п.). Группа таких фазовых преобразований называется 
Различные преобразования группы  коммутируют между собой. Такую группу называют абелевой. Если параметр а независит от
коммутируют между собой. Такую группу называют абелевой. Если параметр а независит от  то группу называют глобальной. Итак, мы рассмотрели глобальную абелеву симметрию
то группу называют глобальной. Итак, мы рассмотрели глобальную абелеву симметрию 
Глобальная неабелева симметрия SU(2)
Другим примером глобальной симметрии является обычнаж изотопическая инвариантность. При изотопическом преобразовании.

где Т — матрицы,  параметры, как и в предыдущем случае, не зависящие от координат. Значение а — одно и то же и в Москве, и в Нью-Йорке, и на Луне. Именно поэтому симметрия называется глобальной. В случае простейшего нетривиального
параметры, как и в предыдущем случае, не зависящие от координат. Значение а — одно и то же и в Москве, и в Нью-Йорке, и на Луне. Именно поэтому симметрия называется глобальной. В случае простейшего нетривиального
изотопического мультиплета — дублета

где  — три матрицы Паули:
— три матрицы Паули:

Поскольку матрицы  не коммутируют между собой, симметрия
не коммутируют между собой, симметрия  называется неабелевой.
называется неабелевой.
Локальная абелева симметрия U(1)
Рассмотрим теперь лагранжиан квантовой электродинамики, описывающей электроны, фотоны и их взаимодействия:

Здесь  - заряд электрона,
- заряд электрона,  Если ввести так называемую ковариантную, или обобщенную (или в просторечии — длинную), производную
Если ввести так называемую ковариантную, или обобщенную (или в просторечии — длинную), производную

то лагранжиан примет вид

Легко убедиться, что этот лагранжиан инвариантен относительно лреобразования

тде  - параметр, зависящий от мировой точки
- параметр, зависящий от мировой точки  При этом
При этом

Напряженность поля

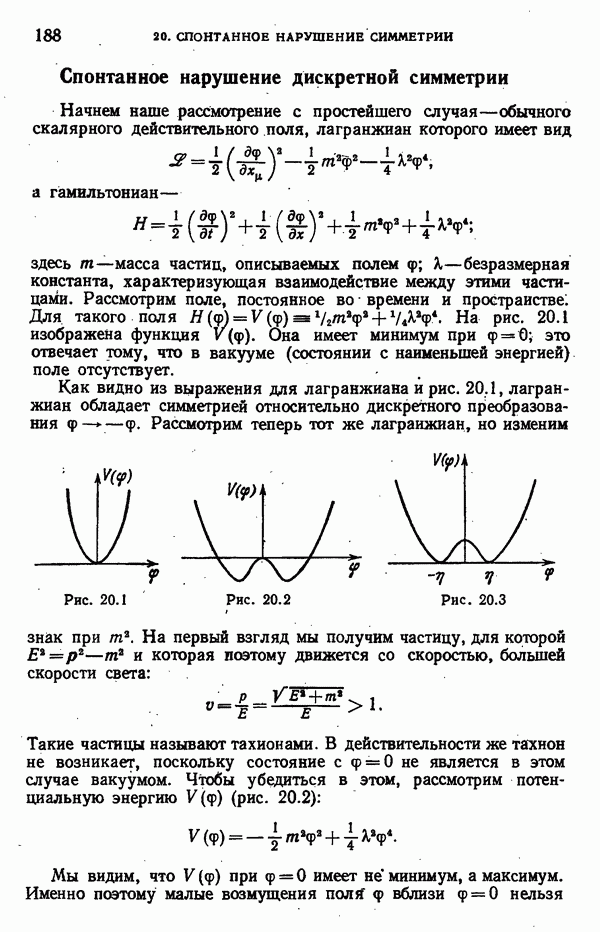
инвариантна относительно этого преобразования. Следует подчеркнуть, что если бы у фотона была масса, то локальная  -инвариантность нарушилась бы, так как член
-инвариантность нарушилась бы, так как член  не переходит сам в себя при добавлении к А слагаемого
не переходит сам в себя при добавлении к А слагаемого  .
.
Мы видим, что для локальной инвариантности необходимо, чтобы сохраняющийся заряд являлся источником безмассового векторного поля. В этом пункте имеется радикальное отличие электрического заряда, генерирующего фотоны, от барионного, лептонного, мюоиного зарядов, с которыми, насколько можно судить, не связаны специфические безмассовые векторные поля:
барионные, лептонные или мюонные «фотоны». Поэтому этим зарядам отвечают глобальные, но не локальные  (
( -симметрии.
-симметрии.
При калибровочных преобразованиях физические (наблюдаемые) поперечные компоненты фотонного поля  не преобразуются (импульс фотона
не преобразуются (импульс фотона  направлен по оси
направлен по оси  а преобразуются лишь нефизические продольные компоненты фотонного 4-вектора:
а преобразуются лишь нефизические продольные компоненты фотонного 4-вектора:  Сохранение векторного тока обеспечивает ненаблюдаемость этих компонент.
Сохранение векторного тока обеспечивает ненаблюдаемость этих компонент.
Чисто формально локальную инвариантность можно было бы обеспечить нефизическим (без  продольным полем, не вводя наблюдаемых векторных полей и не интерпретируя продольное поле как нефизическую часть векторного поля. Мы, однако, в соответствии с принятой в литературе терминологией будем называть локальной такую теорию, в которой есть безмассовое векторное калибровочное поле.
продольным полем, не вводя наблюдаемых векторных полей и не интерпретируя продольное поле как нефизическую часть векторного поля. Мы, однако, в соответствии с принятой в литературе терминологией будем называть локальной такую теорию, в которой есть безмассовое векторное калибровочное поле.
Отступление о барионных и лептонных фотонах
Выше мы сделали замечание о том, что барионные фотоны не существуют. Поясним это утверждение.
Легко показать, что если барионные фотоны существуют, то их взаимодействие с барионами должно быть очень слабым:  (это следует сравнивать с
(это следует сравнивать с  для обычных фотонов). Такое ограничение вытекает из равенства инертной и гравитационной масс, проверенного с точностью до
для обычных фотонов). Такое ограничение вытекает из равенства инертной и гравитационной масс, проверенного с точностью до  . Указанное ограничение на
. Указанное ограничение на  следует из того, что барионные фотоны создали бы вокруг Земли своеобразное «кулоново» поле, которое, отталкивало бы барионы от Земли. Сила этого отталкивания была бы пропорциональна числу барионов в образце, а не его массе, и была бы различна, скажем, для свинцового и медного образцов с одинаковыми массами. Сила, действующая на образец
следует из того, что барионные фотоны создали бы вокруг Земли своеобразное «кулоново» поле, которое, отталкивало бы барионы от Земли. Сила этого отталкивания была бы пропорциональна числу барионов в образце, а не его массе, и была бы различна, скажем, для свинцового и медного образцов с одинаковыми массами. Сила, действующая на образец  с массой
с массой  содержащий А; нуклонов, равна
содержащий А; нуклонов, равна

где М — масса Земли, А — число нуклонов в Земле  — гравитационная константа.
— гравитационная константа.
Аналогичная формула описывала бы в этом случае и притяжение тел к Солнцу. Это очевидное замечание сделано потому, что притяжение тел к Солнцу измерено с более высокой точностью, чем к Земле.
Масса нуклона в ядре свинца примерно на 1 МэВ больше, чем в ядре меди 
Из опыта следует, что

откуда

Аналогичное рассуждение можно провести и для  - константы взаимодействия гипотетических лептонных «фотонов» с электронами. В этом случае
- константы взаимодействия гипотетических лептонных «фотонов» с электронами. В этом случае

и, следовательно,

Из-за нестабильнссти мюона верхний предел для  — кон станты взаимодействия гипотетических мюонных «фотонов» с
— кон станты взаимодействия гипотетических мюонных «фотонов» с  онным зарядом на
онным зарядом на  порядков хуже (выше), чем для
порядков хуже (выше), чем для 
Основываясь на приведенных выше оценках, естественно заключить, что безмассовых векторных частиц, связанных с лептонным и барионным зарядами, нет. Возможно, что с этими зарядами связаны массивные векторные частицы.
В 80-х годах широко сбсуждалась возможность того, что барионные и/или лептонные фотоиы не безмассовы, но очень легки, так что их комптонсвская длина волны составляет величину, скажем, порядка километра. В этом случае ограничения на  и/или на
и/или на  не столь жесткие, как обсуждалось выше. Некоторые авторы сообщали о наблюдении ими в опытах типа опыта Этвеша так называемой пятой силы с подобным радиусом действия. Последующие опыты не подтвердили этих первых сообщений. Но на более высоком уровне точности экспериментальные поиски пятой силы продолжаются.
не столь жесткие, как обсуждалось выше. Некоторые авторы сообщали о наблюдении ими в опытах типа опыта Этвеша так называемой пятой силы с подобным радиусом действия. Последующие опыты не подтвердили этих первых сообщений. Но на более высоком уровне точности экспериментальные поиски пятой силы продолжаются.
Локальная SU(2)-симметрия
Обратимся теперь к теории Янга—Миллса, которая представляет собой локальную реализацию изотопической инвариантности.
В этой теории имеет место инвариантность относительно локальных изотопических поворотов:

Здесь  — три матрицы изотопических поворотов,
— три матрицы изотопических поворотов,  три параметра этих поворотов, вообще говоря, различные в различных мировых точках. Для реализации такой симметрии необходимо существование триплета векторных безмассовых полей 4, взаимодействующих с полями
три параметра этих поворотов, вообще говоря, различные в различных мировых точках. Для реализации такой симметрии необходимо существование триплета векторных безмассовых полей 4, взаимодействующих с полями 
Лагранжиан имеет вид

где  - ковариантная производная. В отличие от абелева случая
- ковариантная производная. В отличие от абелева случая  представляет собой матрицу
представляет собой матрицу

Конкретный вид матрицы Т и, следовательно,  определяется тем, по какому представлению группы
определяется тем, по какому представлению группы  преобразуется поле, от которого берется длинная производная; если поле
преобразуется поле, от которого берется длинная производная; если поле  -изодублет, то
-изодублет, то

если поле  —изотриплет, то
—изотриплет, то

Изовектор напряженности поля имеет вид

(Обычно в качестве матриц Т в этом случае выбирают  Из этого выражения (оно будет пояснено ниже) мы видим, что, в отличие от абелева случая, напряженность неабелева калибровочного поля есть нелинейная функция поля. (В абелевом случае коммутатор
Из этого выражения (оно будет пояснено ниже) мы видим, что, в отличие от абелева случая, напряженность неабелева калибровочного поля есть нелинейная функция поля. (В абелевом случае коммутатор  равен нулю.) В результате лагранжиан свободного поля Янга—Миллса, наряду с членами
равен нулю.) В результате лагранжиан свободного поля Янга—Миллса, наряду с членами  содержит
содержит  . В отличие от обычных фотонов, янг-миллсовские фотоны несут изовекторные «заряды» и сами себя излучают. Это как бы «светящийся свет». Аналогичным свойством обладают гравитоны—кванты гравитационного поля.
. В отличие от обычных фотонов, янг-миллсовские фотоны несут изовекторные «заряды» и сами себя излучают. Это как бы «светящийся свет». Аналогичным свойством обладают гравитоны—кванты гравитационного поля.
Хорошо известно, что источником гравитонов является тензор энергии-импульса. Поэтому даже безмассовые частицы, например, фотоны, взаимодействуют с гравитационным полем, и тем сильнее, чем выше их энергия.

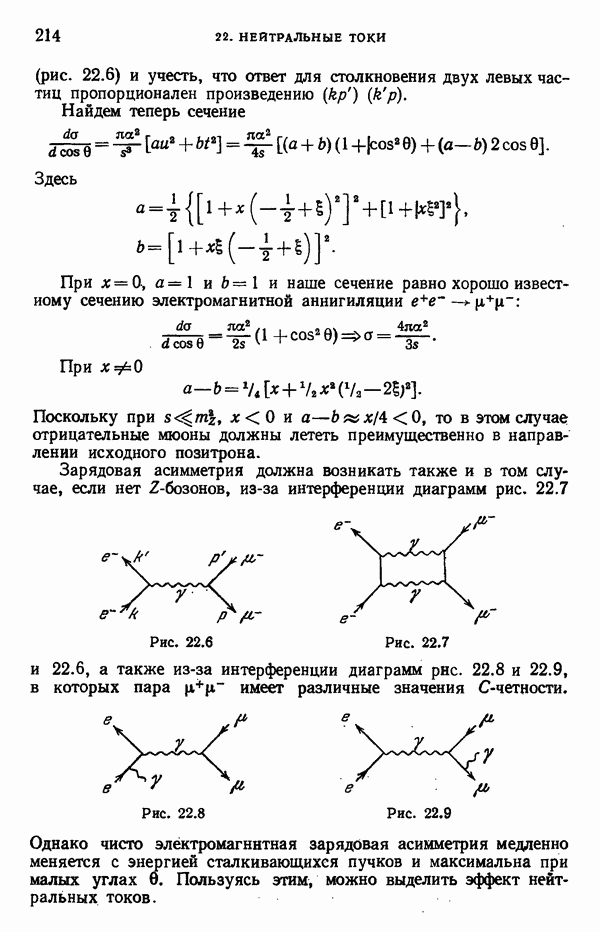
Рис. 19.1
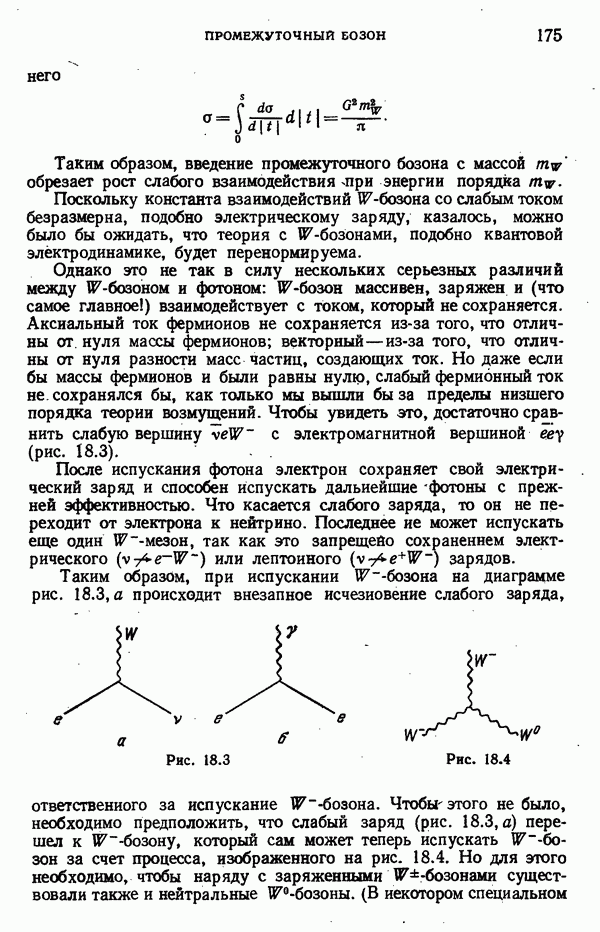
Вершина взаимодействия фотона с гравитоном изображена на рис. 19.1, а. Поскольку гравитон сам имеет энергию и импульс, он также должен испускать гравитоны (рис. 19.1,6). Для обычного абелевого фотона подобной тройной вершины  нет, а для неабелевого — вершина
нет, а для неабелевого — вершина  отлична
отлична
от нуля. Эта вершина описывает рассеяние  -«фотонов» на поле
-«фотонов» на поле  аннигиляцию
аннигиляцию  и другие процессы, связанные с указанными кроссингом. Напомним, что вершина именно такого типа понадобилась нам для того, чтобы сделать слабый ток сохраняющимся в высоких порядках теории возмущений (см. гл. 18).
и другие процессы, связанные с указанными кроссингом. Напомним, что вершина именно такого типа понадобилась нам для того, чтобы сделать слабый ток сохраняющимся в высоких порядках теории возмущений (см. гл. 18).
Как преобразуются  Чтобы установить, каким образом преобразуется поле
Чтобы установить, каким образом преобразуется поле  рассмотрим, например, выражение
рассмотрим, например, выражение  Пусть
Пусть  Как должно выглядеть
Как должно выглядеть  , чтобы выражение
, чтобы выражение  было калибровочно инвариантным, т. е. чтобы при калибровочном преобразовании
было калибровочно инвариантным, т. е. чтобы при калибровочном преобразовании

Очевидно, для этого необходимо и достаточно, чтобы

Напомним, что в абелевом случае

Так что отличие неабелева поля заключается в том, что оно сна чала изотопически поворачивается и только потом удлиняется на член —  . В случае, когда калибровочная матрица
. В случае, когда калибровочная матрица  близка к единичной, т. е. когда угол поворота а
близка к единичной, т. е. когда угол поворота а  мал, наглядным является выражение для преобразования поля не в матричной форме, использованной выше, а в обычной изовекторной форме. В этом случае
мал, наглядным является выражение для преобразования поля не в матричной форме, использованной выше, а в обычной изовекторной форме. В этом случае  их
их 

(Мы воспользовались тем, что

а также тем, что при малых  )
)
Что касается напряженности поля  , то из определения
, то из определения

сразу же следует, что

Таким образом,  преобразуется, как обычный изовектор. В частности, при малых а:
преобразуется, как обычный изовектор. В частности, при малых а:

Напряженность Оустроена таким хитрым способом, что она одинаково преобразуется как при глобальных, так и при локальных изотопических поворотах. Следствием этого является калибровочная инвариантность члена  в лагранжиане.
в лагранжиане.
Похвальное слово теории Янга—Миллса
Мы привыкли к тому, что симметрии налагают определенные ограничения на массы частиц и на константы, характеризующие их взаимодействия. Например, изотопическая инвариантность сильного взаимодействия требует, чтобы массы протона и нейтрона были равны, а их взаимодействие с  -мезонами характеризовалось одной и той же константой. Замечательным свойством неабелевой калибровочной симметрии является то, что она не только накладывает ограничения на массы частиц и константы связи, но и определяет динамику взаимодействия калибровочных полей (нелинейности типа
-мезонами характеризовалось одной и той же константой. Замечательным свойством неабелевой калибровочной симметрии является то, что она не только накладывает ограничения на массы частиц и константы связи, но и определяет динамику взаимодействия калибровочных полей (нелинейности типа  Калибровочные неабелевы поля являются носителями «изотопического заряда», и их взаимодействия друг с другом и с другими полями определяются этим зарядом. Калибровочная симметрия однозначно задает вид этих взаимодействий.
Калибровочные неабелевы поля являются носителями «изотопического заряда», и их взаимодействия друг с другом и с другими полями определяются этим зарядом. Калибровочная симметрия однозначно задает вид этих взаимодействий.
В этом смысле теория Янга—Миллса очень похожа на общую теорию относительности, в которой динамика гравитационного взаимодействия в значительной степени определяется требованием инвариантности относительно наиболее общих преобразований координат. Так что аналогия между нелинейными взаимодействиями неабелевых фотонов и гравитонов, отмеченная выше, является лишь одним из частных проявлений глубокого сходства этих теорий. Теория Янга—Миллса является достаточно простой моделью, на которой можно попытаться понять некоторые особенности квантования такой существенно нелинейной теории, как общая теория относительности. Задача построения квантовой теории гравитации привлекает к себе все большее внимание.
В 60-е годы теория Янга—Миллса была подвергнута тщательному теоретическому анализу. Для нее были сформулированы правила построения фейнмановских графиков и была доказана перенормируемость. Перенормируемость теории Янга—Миллса является следствием безразмерности константы  сохранения изотопических токов и безмассовости неабелевых «фотонов».
сохранения изотопических токов и безмассовости неабелевых «фотонов».
Поля Янга—Миллса из теоретического курьеза (каковыми они казались при своем рождении) превратились сегодня в центральный. объект теоретических исследований-. По существу, все наши надежды на построение теории элементарных частиц связаны с неабелевыми калибровочными полями. Это относится и к единой теории слабых и электромагнитных взаимодействий, и к глюонной теории сильного взаимодействия, и, наконец, к возможному будущему синтезу этих теорий. (Напомним, что теория
цветных глюонов, взаимодействующих с цветными кварками, обладает локальной  -симметрией.)
-симметрией.)
В этом месте вдумчивый читатель должен был бы прервать этот панегирик и задать естественный вопрос: как учесть массы?
Как учесть массы?
В первую очередь возникает вопрос, как внести в теорию массы промежуточных бозонов. Ведь из эксперимента мы знаем, что эти частицы должны иметь массы (и довольно большие!) в то время как янг-миллсовские калибровочные поля безмассовы. На первый взгляд кажется, что ничего страшного не произойдет, если ввести в лагранжиан массовый член  , что называется «руками». В случае абелевых калибровочных полей это не приводит
, что называется «руками». В случае абелевых калибровочных полей это не приводит  к чему плохому, как мы убедились, обсуждая вопрос о массе фотона. Для фотона существует «мягкий» переход от
к чему плохому, как мы убедились, обсуждая вопрос о массе фотона. Для фотона существует «мягкий» переход от  квантовая электродинамика остается перенормируемой.
квантовая электродинамика остается перенормируемой.
Легко убедиться, что для неабелевых калибровочных полей это не так: включение массы «руками» разрушает перенормируемость. Рассмотрим амплитуду испускания  фотонов:
фотонов:

В абелевом случае матричный элемент  поперечен по любой комбинации индексов. Например:
поперечен по любой комбинации индексов. Например:

и т. д. При этом  может быть как равным нулю, так и отличным от нуля, т. е. фотоны могут быть как реальными, так и виртуальными. В отличие от этого, в неабелевом случае поперечность по любому из «фотонов» имеет место лишь тогда, когда все остальные «фотоны» реальны (находятся на массовой поверхности), и их испускание явно учтено в амплитуде их волновыми функциями:
может быть как равным нулю, так и отличным от нуля, т. е. фотоны могут быть как реальными, так и виртуальными. В отличие от этого, в неабелевом случае поперечность по любому из «фотонов» имеет место лишь тогда, когда все остальные «фотоны» реальны (находятся на массовой поверхности), и их испускание явно учтено в амплитуде их волновыми функциями:

Во всех остальных случаях поперечности нет (в частности,  ). Это связано с тем, что неабелевы фотоны несут изотопический заряд. Виртуальный неабелев фотон по определению переносит этот заряд из одной части фейнмановской диаграммы в другую. Рассматривая диаграмму, в которой один из «фотонных» концов виртуален, мы рассматриваем, по существу, лишь кусок физической диаграммы, для которого нет сохранения изотопического тока и, следовательно, поперечности. (Обычные (абелевы) фотоны электрически нейтральны, и поэтому для них этого явления нет.)
). Это связано с тем, что неабелевы фотоны несут изотопический заряд. Виртуальный неабелев фотон по определению переносит этот заряд из одной части фейнмановской диаграммы в другую. Рассматривая диаграмму, в которой один из «фотонных» концов виртуален, мы рассматриваем, по существу, лишь кусок физической диаграммы, для которого нет сохранения изотопического тока и, следовательно, поперечности. (Обычные (абелевы) фотоны электрически нейтральны, и поэтому для них этого явления нет.)
Вспомним теперь, как выглядит продольная часть волновой функции массивной векторной частицы:

здесь  , k — масса, энергия, импульс частицы,
, k — масса, энергия, импульс частицы,  -им-пульс. Отсюда следует, что амплитуда испускания
-им-пульс. Отсюда следует, что амплитуда испускания  продольных абелевых фотонов стремится к нулю, как
продольных абелевых фотонов стремится к нулю, как  при
при  . В отличие от этого, амплитуда испускания продольных неабелевых фотонов ведет себя как
. В отличие от этого, амплитуда испускания продольных неабелевых фотонов ведет себя как  и неограниченно растет при
и неограниченно растет при  если
если  Действительно, умножая матричный элемент на волновые функции, мы лишь в одной из них оставим часть
Действительно, умножая матричный элемент на волновые функции, мы лишь в одной из них оставим часть  , а в остальных
, а в остальных  волновых функциях оставим
волновых функциях оставим  . Тогда
. Тогда

Таким образом, в неабелевом случае мы по-прежнему имеем дело с иеперенормируемой теорией.
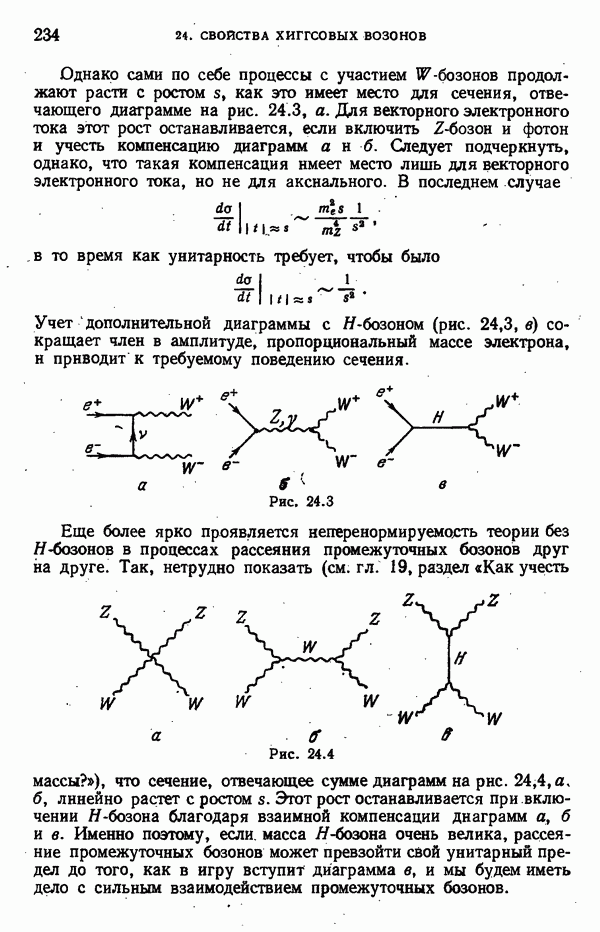
Калибровочное происхождение промежуточных бозонов позволило лишь на две степени энергии улучшить поведение амплитуд при высоких энергиях, уменьшить их рост. Для того чтобы избавиться от этого роста полностью, необходимо, чтобы с появлением у промежуточных бозонов массы, в лагранжиане появлялись дополнительные поля, вклад которых компенсировал обсуждаемые расходимости. Такое «мягкое» включение массы промежуточных бозонов возникает при спонтанном нарушении калибровочной симметрии, которое мы рассмотрим в следующей главе. В ней на ряде примеров мы увидим, что в механизме спонтанного нарушения калибровочной симметрии центральную роль играют скалярные поля. Ожидаемые физические свойства частиц, отвечающих этим полям, так называемых хиггсовых бозонов, будут обсуждены в гл. 24.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
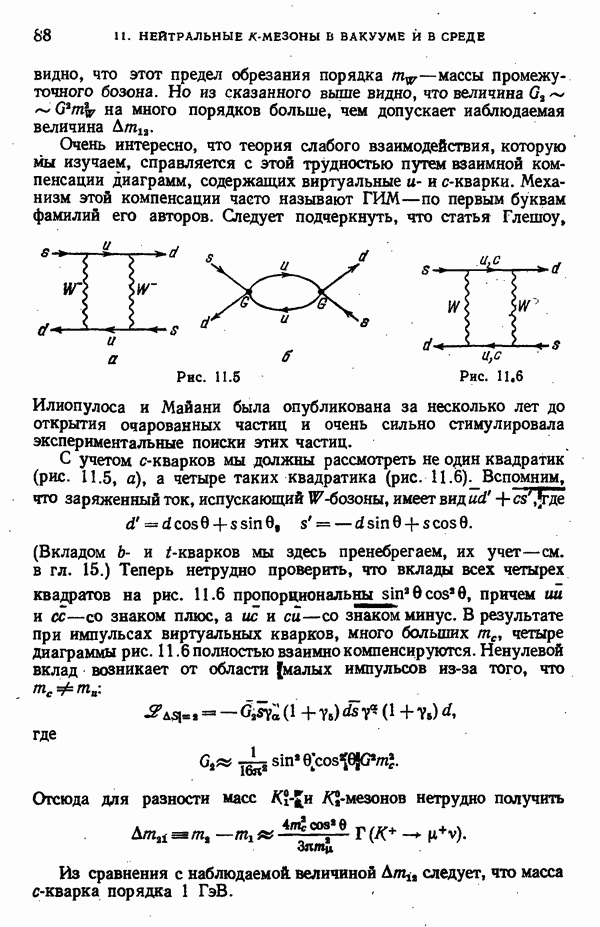
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
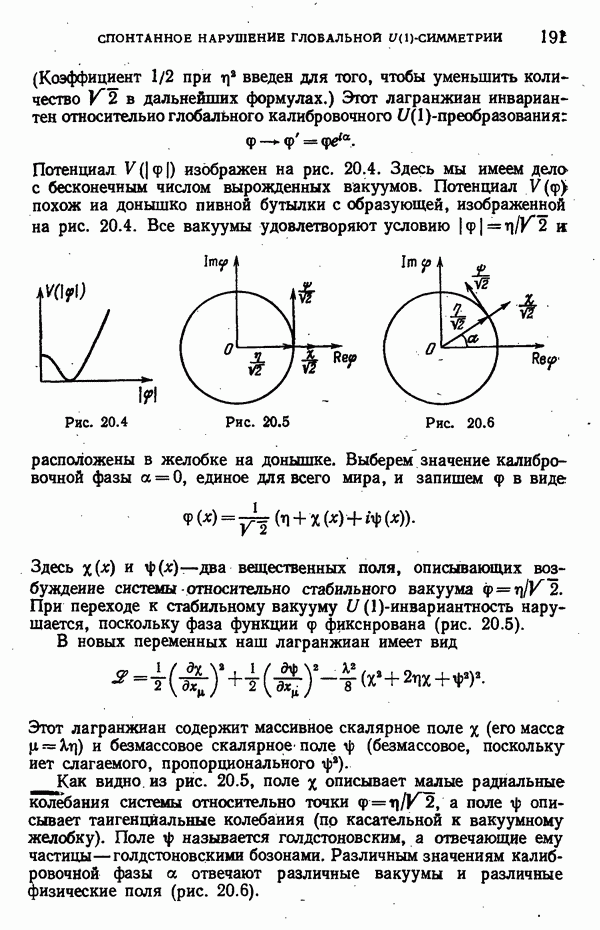
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
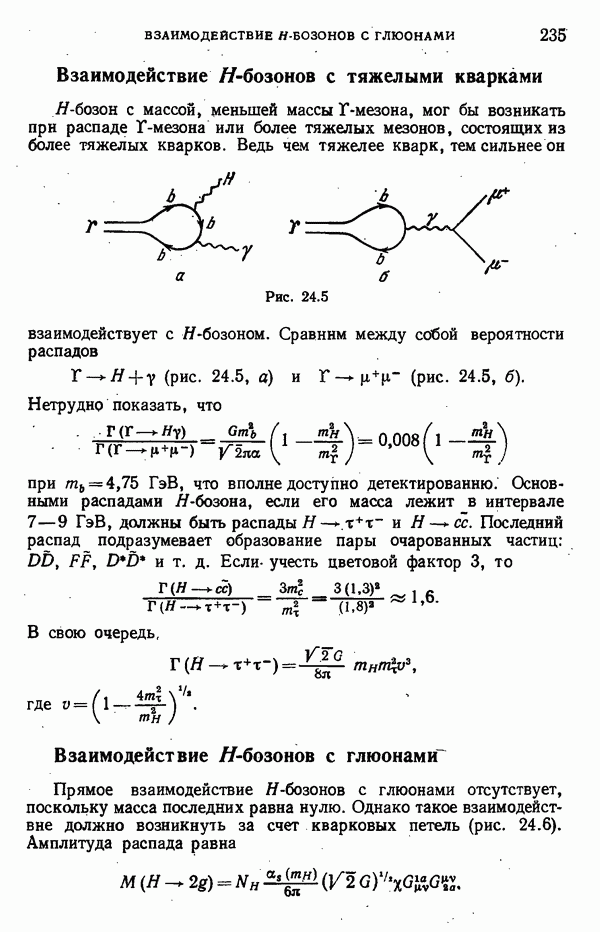
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
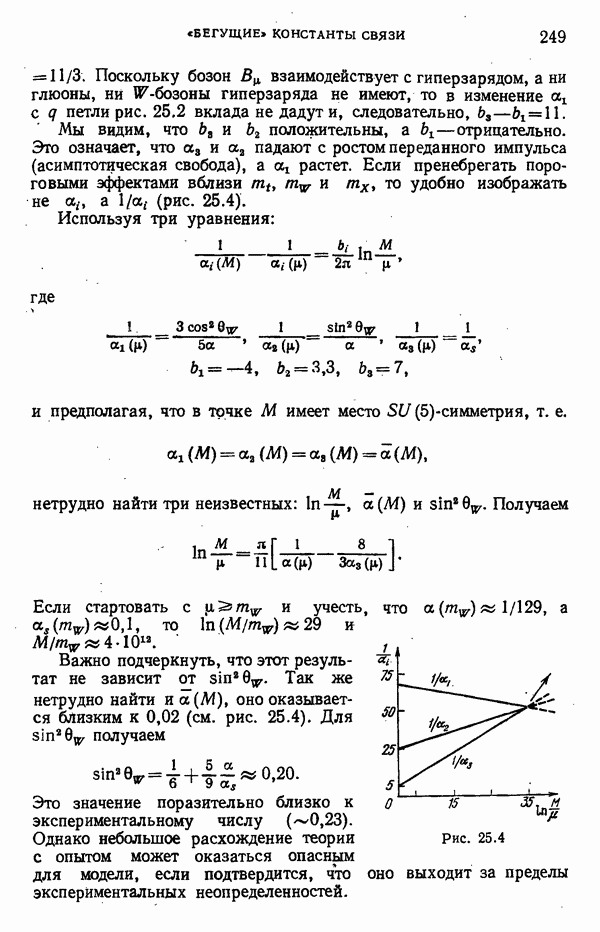
- «Бегущие» константы связи
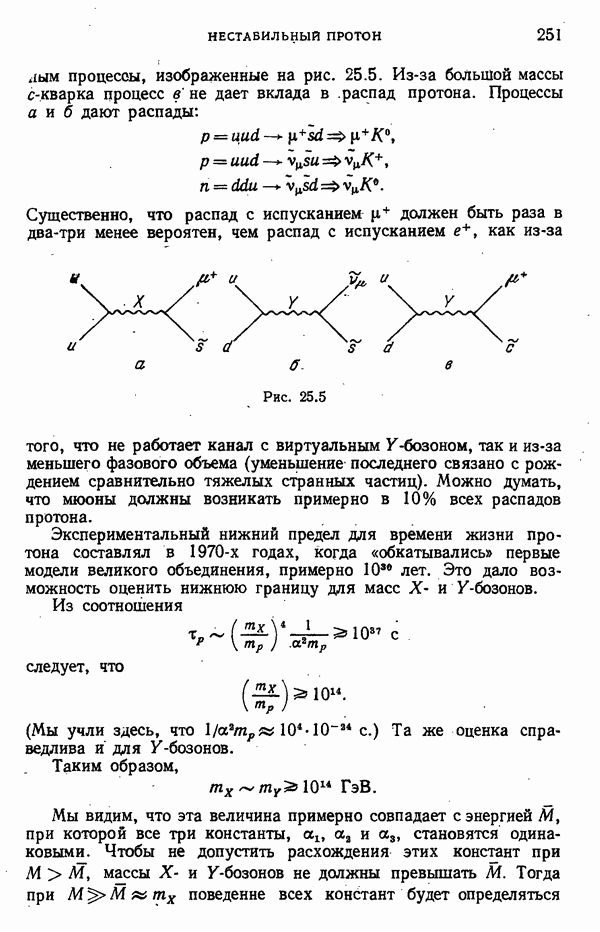
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
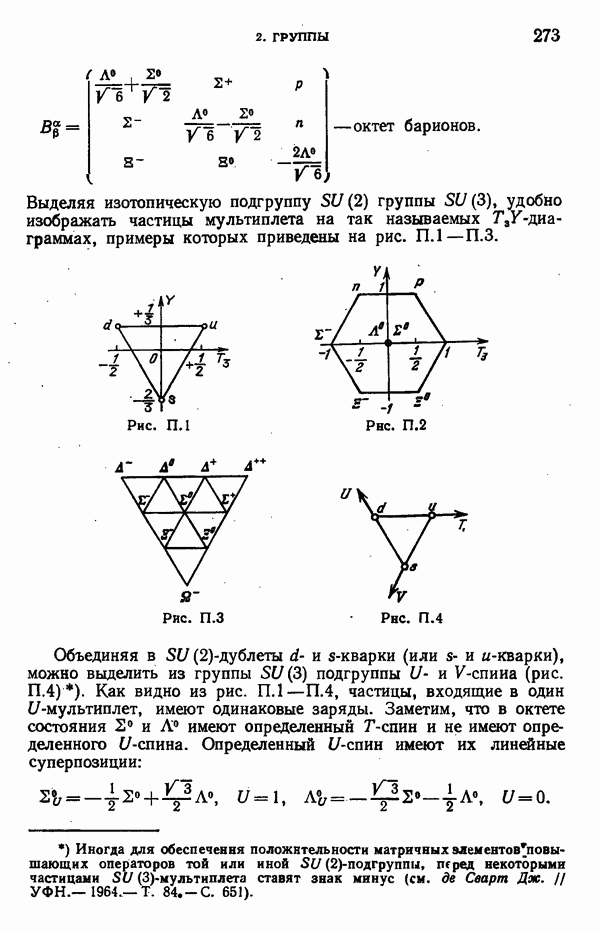
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей