| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Кварковые диаграммы для распадов
В качестве примера вычислим амплитуду распадов  исходя из эффективного нелептонного взаимодействия
исходя из эффективного нелептонного взаимодействия  (напомним, что остальные члены эффективного нелептонного лагранжиана, рассмотренного в гл. 7, удовлетворяют правилу отбора
(напомним, что остальные члены эффективного нелептонного лагранжиана, рассмотренного в гл. 7, удовлетворяют правилу отбора  и поэтому вклада в распад
и поэтому вклада в распад  не дают). Для удобства, чтобы иметь дело с
не дают). Для удобства, чтобы иметь дело с  -кварком а не
-кварком а не  -кварком, будем рассматривать распад
-кварком, будем рассматривать распад  амплитуда которого равна амплитуде распада
амплитуда которого равна амплитуде распада 

Рис. 10.1
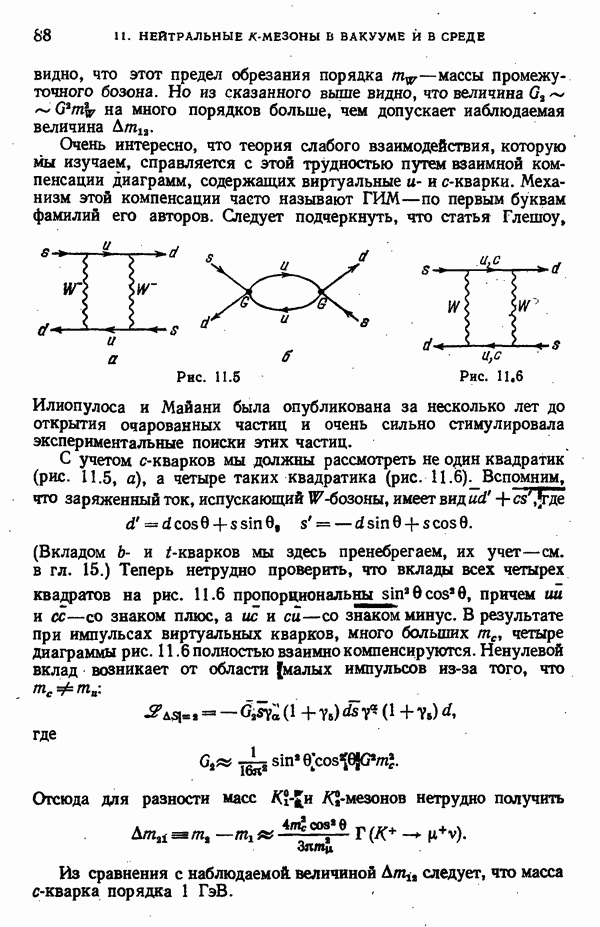
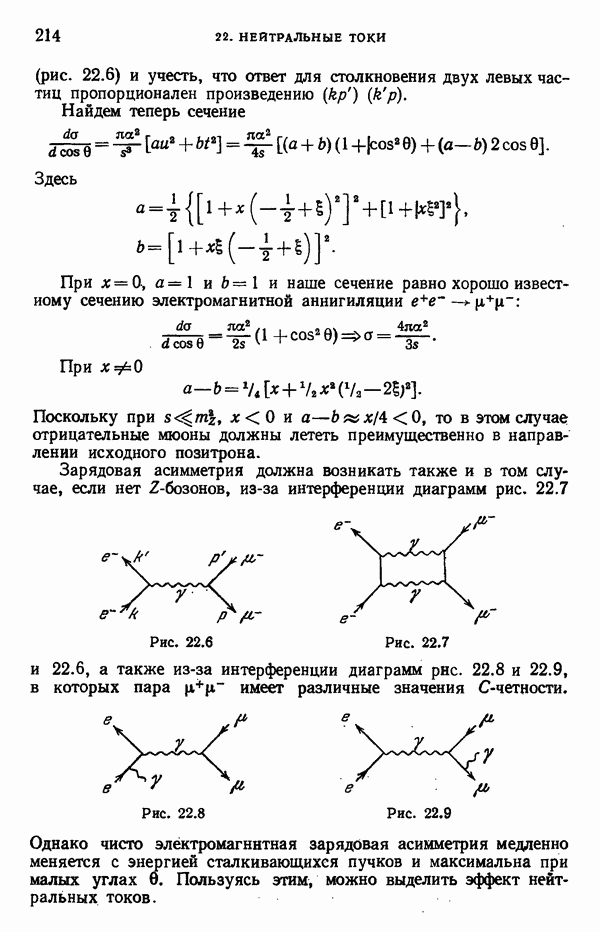
Легко убедиться, что диаграммы аннигиляционного типа, изображенные на рис. 10.1, дают нулевой вклад в амплитуду. Дело в том, что в диаграммах а и  -мезон возникает с противоположными знаками (один раз из
-мезон возникает с противоположными знаками (один раз из  , а другой — из
, а другой — из  ).
).

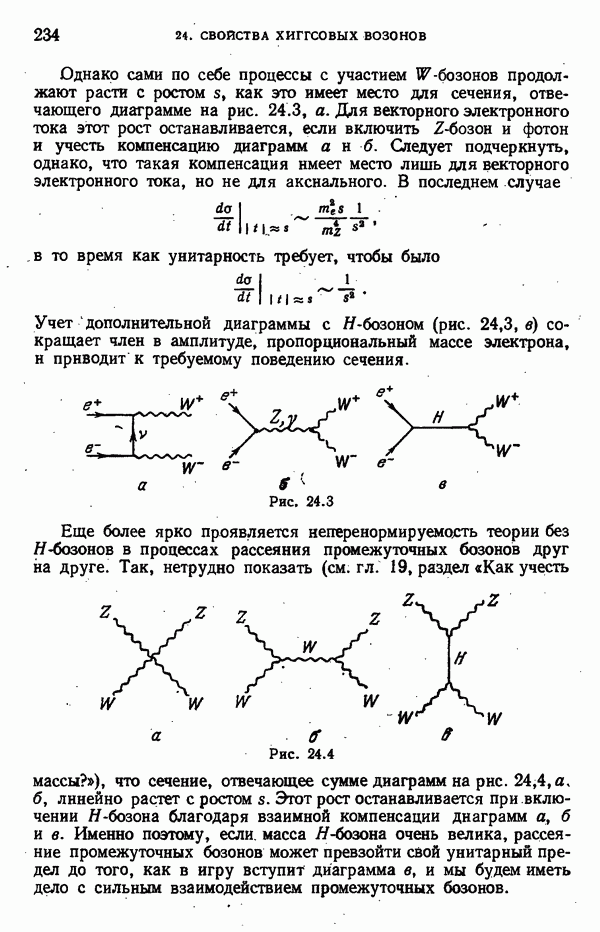
Рис. 10.2
Если учесть теперь, что в распаде два пиона возникают в симметричном состоянии (на диаграммах этому отвечает симметрия верх—низ), то сразу же видно, что диаграммы а и б взаимно гасят друг друга.
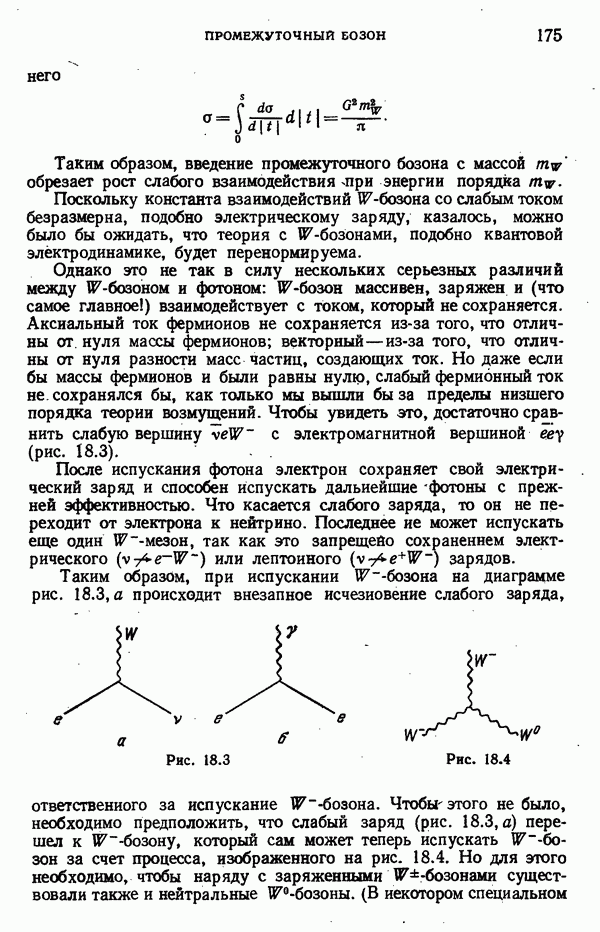
Рассмотрим теперь внешние диаграммы, в которых  -кварк испускает пион (рис. 10.2).
-кварк испускает пион (рис. 10.2).
Напомним (см. конец гл. 7), что

Факторизуем сначала амплитуду, отвечающую диаграмме 2, а.
Вклад в эту амплитуду первого слагаемого из  равен
равен

Вклад второго слагаемого из  в амплитуду 2, а найдем с помощью преобразования Фирца (см. гл. 28, п. 3.4 и гл. 7 и 9)
в амплитуду 2, а найдем с помощью преобразования Фирца (см. гл. 28, п. 3.4 и гл. 7 и 9)

Легко видеть, что вклад в амплитуду 2, а третьего слагаемого из  равен нулю: в этом слагаемом нет
равен нулю: в этом слагаемом нет  -кварковых операторов. Суммарный вклад оператора
-кварковых операторов. Суммарный вклад оператора  в амплитуду, отвечающую диаграмме 2, а, равен
в амплитуду, отвечающую диаграмме 2, а, равен

Аналогичное рассмотрение диаграммы  дает
дает 

Так что

Наконец, рассмотрим амплитуду, отвечающую диаграмме 2, с. В нее дает вклад только последнее слагаемое из 

Если мы учтем теперь, что

то увидим, что диаграммы 2, а, 2, b и 2, с дают одинаковые вклады. Окончательно имеем

Мы учли здесь (см. гл. 5 и 6), что

где  - импульс
- импульс  -мезона, и
-мезона, и  - импульсы
- импульсы  и
и  -мезонов соответственно. В распаде
-мезонов соответственно. В распаде  Если пренебречь
Если пренебречь  по сравнению с
по сравнению с  (дополнительно принимая во внимание, что
(дополнительно принимая во внимание, что  то
то

- Вспомним теперь, что

где  (см. конец гл. 7). Тогда для амплитуды распада получаем
(см. конец гл. 7). Тогда для амплитуды распада получаем

Сравним это с тем, что дает опыт:

Мы видим, что экспериментальное значение для  примерно в полтора раза меньше того, что дает теоретический расчет, учитывающий вклад жестких виртуальных глюонов (т. е. поправки за счет сильного взаимодействия на малых расстояниях).
примерно в полтора раза меньше того, что дает теоретический расчет, учитывающий вклад жестких виртуальных глюонов (т. е. поправки за счет сильного взаимодействия на малых расстояниях).
Напомним, что данные по распадам  также указывают на то, что
также указывают на то, что  примерно в полтора раза меньше, чем дает теоретический расчет. Можно думать, что неудовлетворительность последнего связана с тем, что учитываются лишь главные логарифмические члеиы. Кроме того, не учтен вклад промежуточных расстояний (большие расстояния учтены в волновых функциях мезонов).
примерно в полтора раза меньше, чем дает теоретический расчет. Можно думать, что неудовлетворительность последнего связана с тем, что учитываются лишь главные логарифмические члеиы. Кроме того, не учтен вклад промежуточных расстояний (большие расстояния учтены в волновых функциях мезонов).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
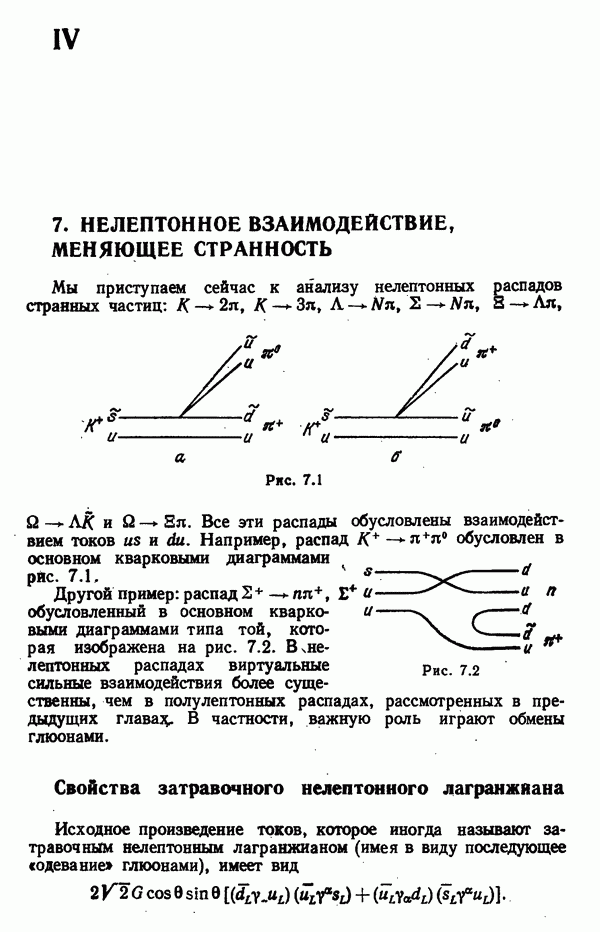
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
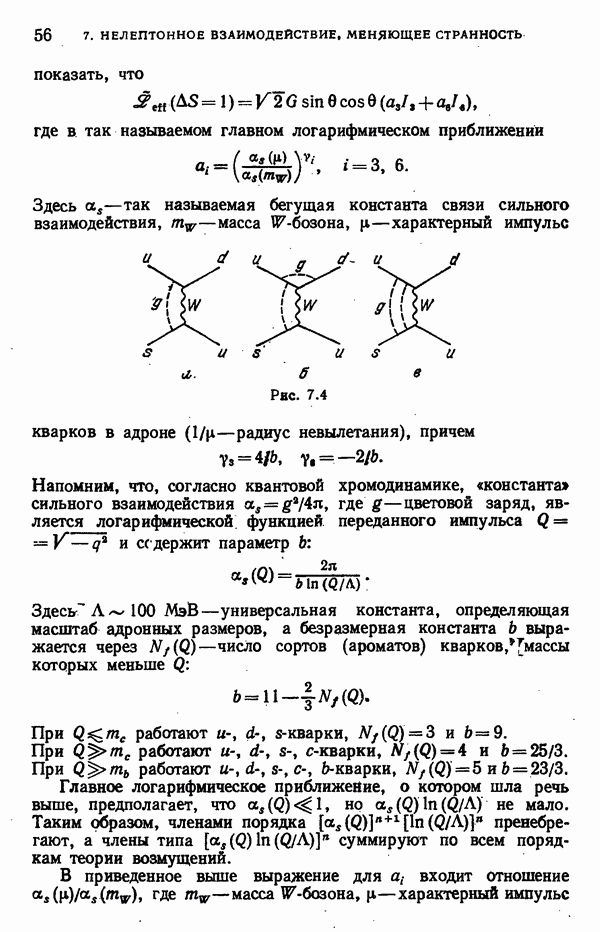
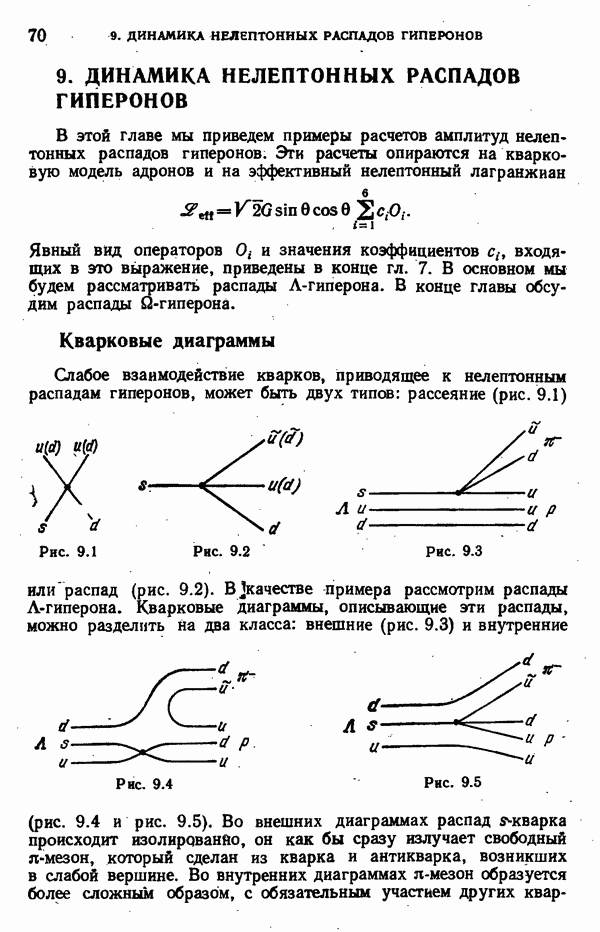
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
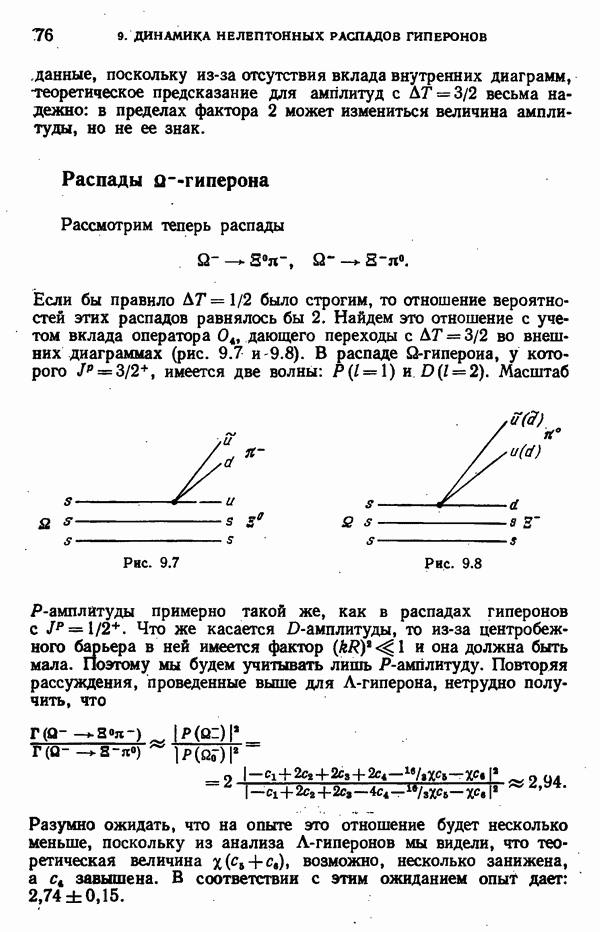
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
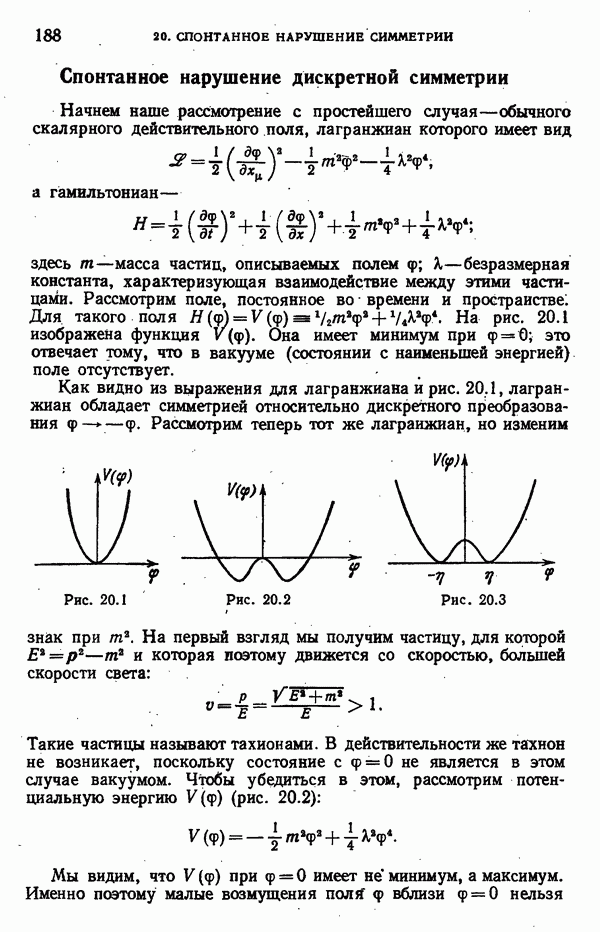
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
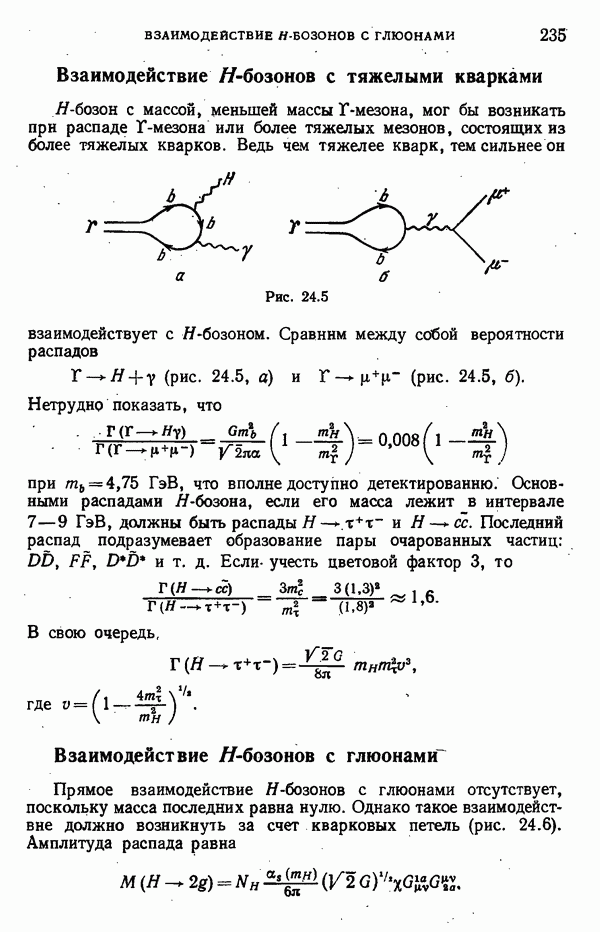
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
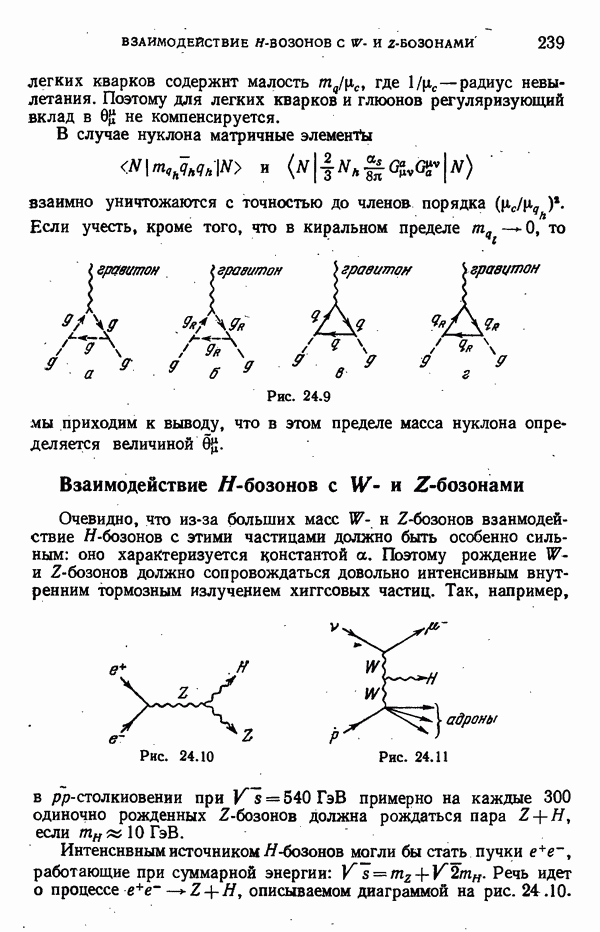
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
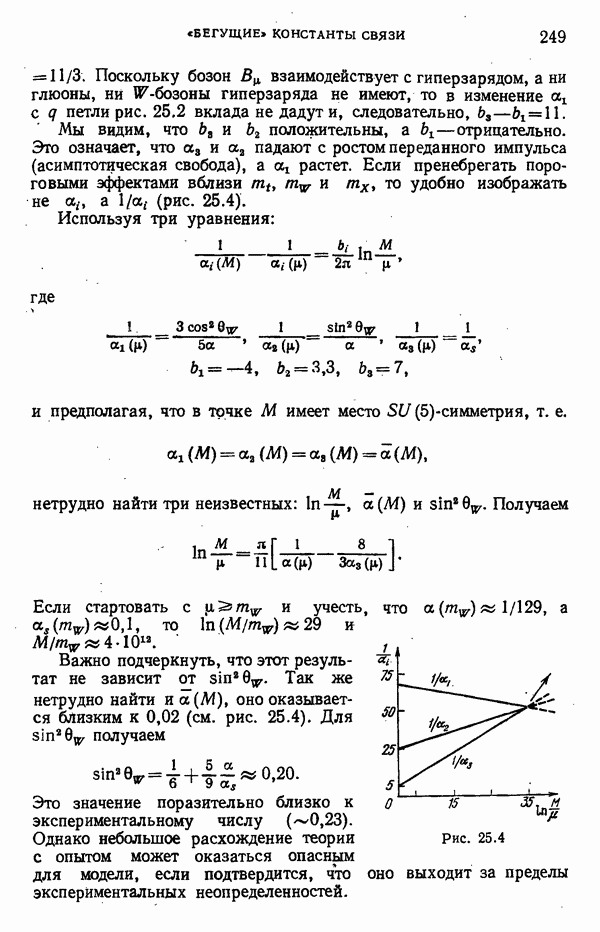
- «Бегущие» константы связи
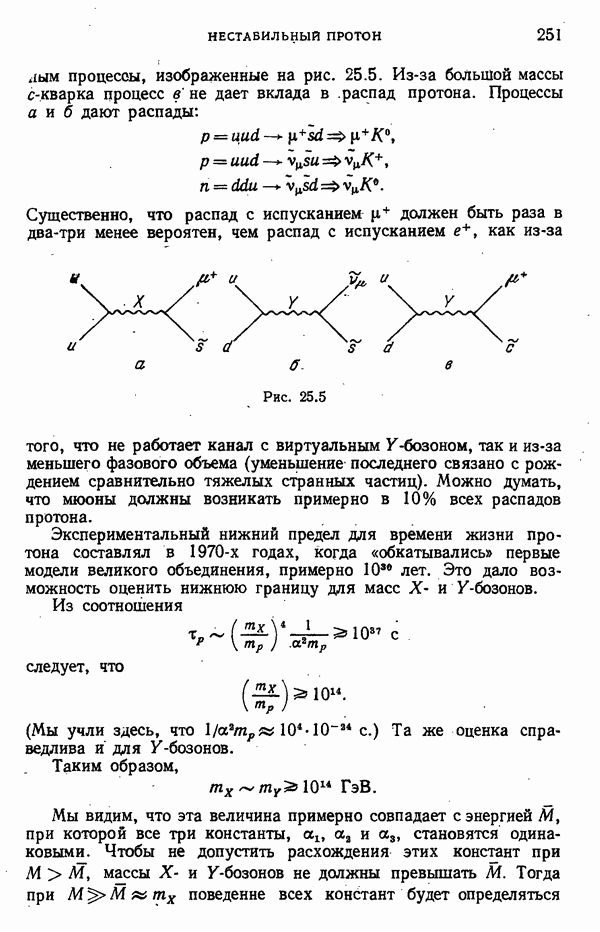
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
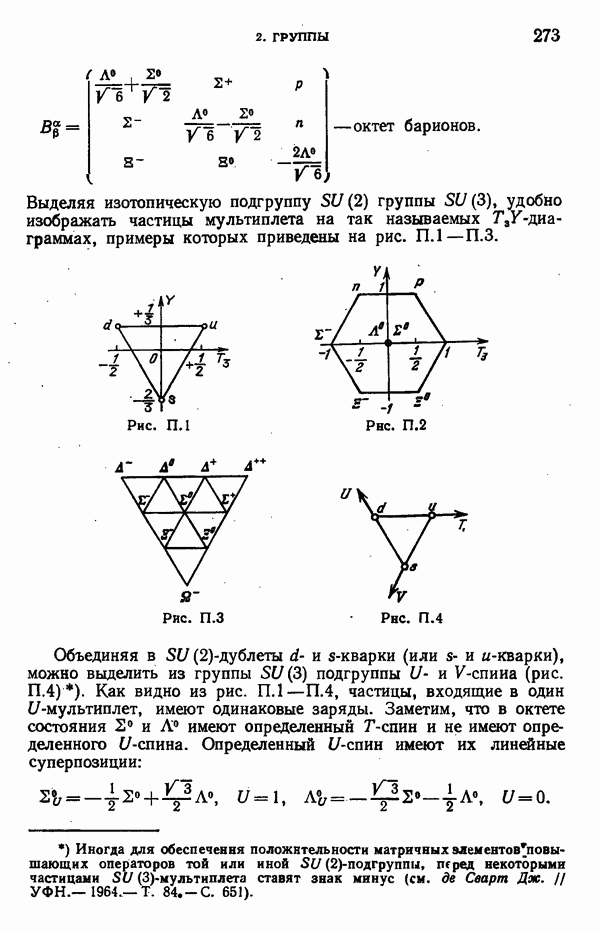
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей