| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глюонный монополь и «пингвины»
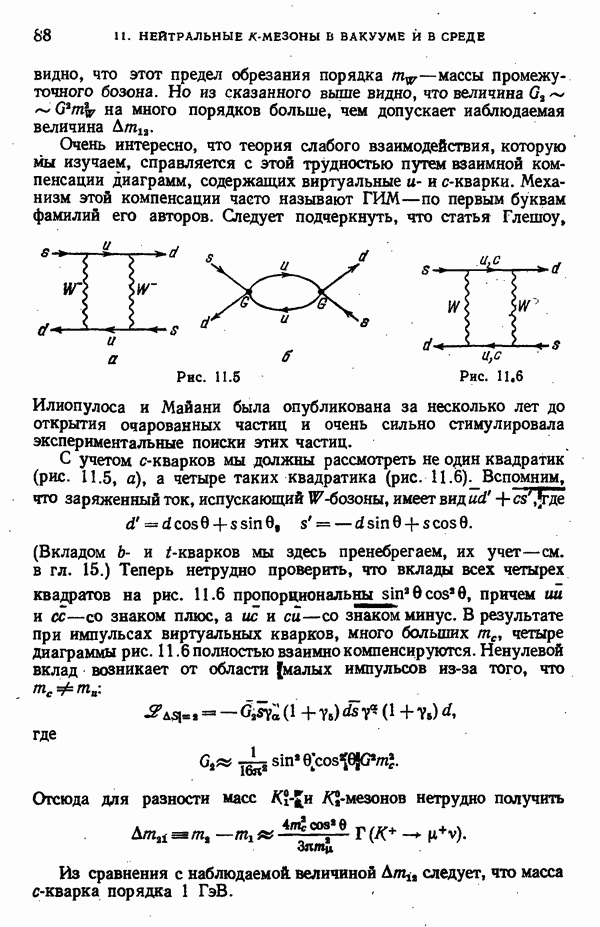
При учете виртуальных глюонов возможен еще один класс диаграмм, которые мы до сих пор не учитывали. Речь идет о диаграммах, в которых виртуальный Р-бозон испускается и поглощается одной и той же кварковой линией, а связь с другими кварками осуществляется глюонами.

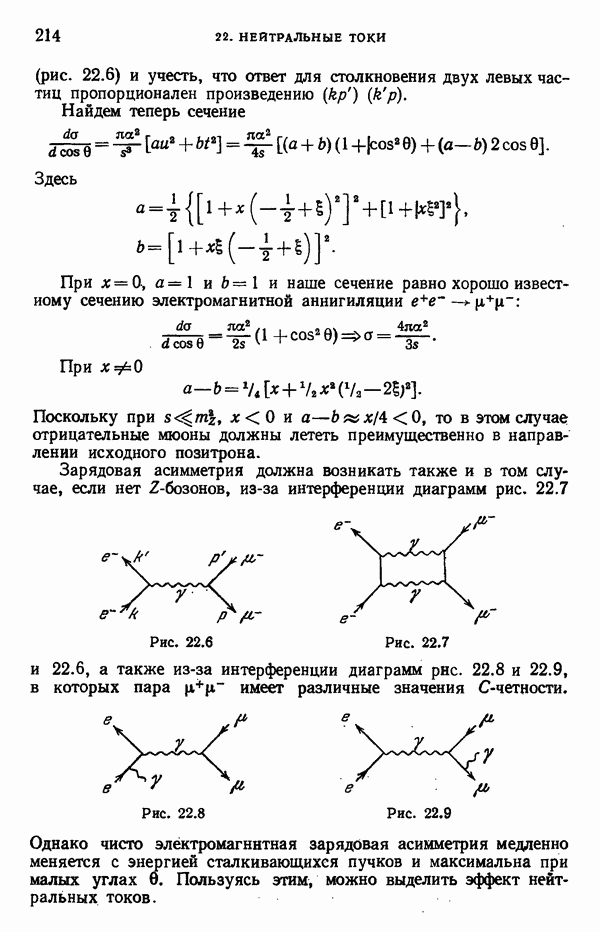
Рис. 7.5
На рис. 7.5, а, б изображены простейшие диаграммы такого типа. Мы сейчас вычислим их вклад. В главном логарифмическом приближении можно учесть одевание этих диаграмм бесконечным числом глюонов, но это не сильно изменит результат.
Если пренебречь перемешиванием  и
и  -кварков с
-кварков с  -кварками, то заряженные токи имеют вид
-кварками, то заряженные токи имеют вид

В результате, если бы массы и- и с-кварков были одинаковыми, диаграммы рис. 7.5, а и 7.5, б взаимно скомпенсировались бы.

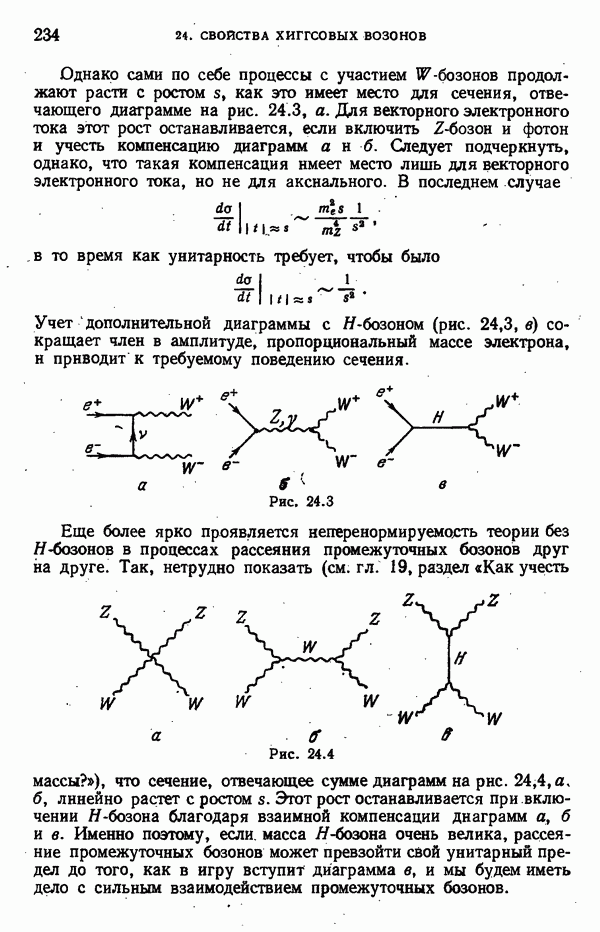
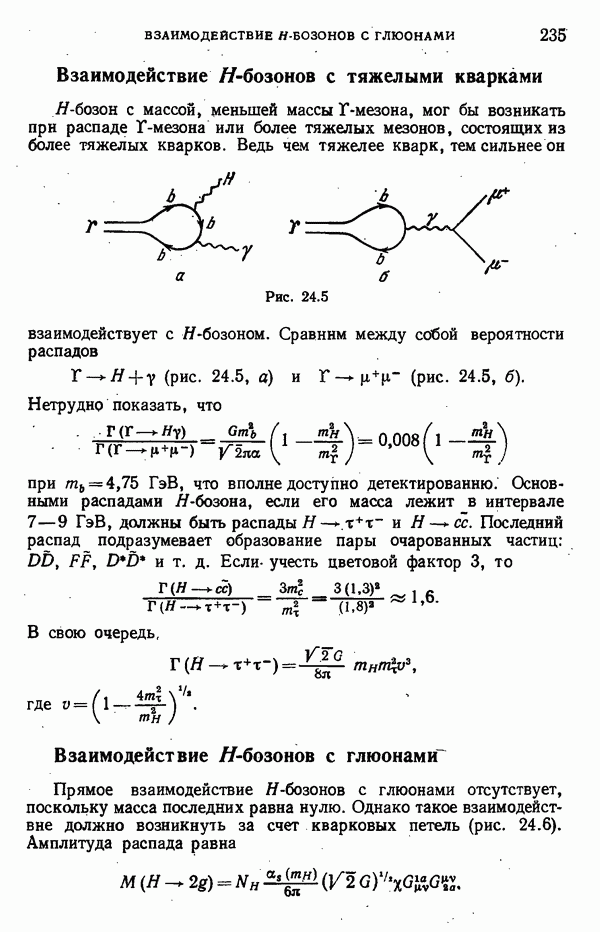
Рис. 7.6
В действительности  и компенсация происходит лишь при импульсах виртуальных частиц, больших чем те. При меньших импульсах доминирует диаграмма 5, а. Учитывая это, можно прийти к выводу, что сумма диаграмм 5, а и 5, б примерно равна вкладу первой из них с импульсами виртуальных частиц, образующих петлю 5, а, обрезанными при
и компенсация происходит лишь при импульсах виртуальных частиц, больших чем те. При меньших импульсах доминирует диаграмма 5, а. Учитывая это, можно прийти к выводу, что сумма диаграмм 5, а и 5, б примерно равна вкладу первой из них с импульсами виртуальных частиц, образующих петлю 5, а, обрезанными при  Учитывая, что
Учитывая, что  мы можем вернуться в диаграмме 5, а к точечному четырехфермионному взаимодействию (рис. 7.6, а). Просвет в четырехфермионной вершине на рис. 7.6, а отделяет друг от друга два белых
мы можем вернуться в диаграмме 5, а к точечному четырехфермионному взаимодействию (рис. 7.6, а). Просвет в четырехфермионной вершине на рис. 7.6, а отделяет друг от друга два белых  -тока, стоящих в скобках в выражении
-тока, стоящих в скобках в выражении

где греческие индексы—дираковы, а латинские — цветовые. Для упрощения дальнейшего расчета удобно произвести преобразование Фирца так, чтобы операторы и, и вошли в одну скобку, а  другую (рис. 7.6, б). Воспользуемся тем (см. гл. 28, пп. 2.6 и 3.4), что
другую (рис. 7.6, б). Воспользуемся тем (см. гл. 28, пп. 2.6 и 3.4), что

и учтем, что фермиоиные операторы антикоммутируют. Тогда

Теперь наша задача свелась к вычислению  -кварковой петли на рис. 7.6, б г Верхняя вершина (испускание глюона) в этой петле имеет вид
-кварковой петли на рис. 7.6, б г Верхняя вершина (испускание глюона) в этой петле имеет вид

Поскольку при вычислении петли надо взять след по дираковским и цветовым индексам, то в нижней вершине член
 даст нулевой вклад, а в члене
даст нулевой вклад, а в члене  даст ненулевой вклад лишь слагаемое
даст ненулевой вклад лишь слагаемое 
За исключением дополнительных цветовых матриц наша петля в точности такая, какая встречается в квантовой электродинамике при расчете поляризации вакуума:

где  , q-4-импульс, уносимый глюоном (см. рис. 7.6, б), массой
, q-4-импульс, уносимый глюоном (см. рис. 7.6, б), массой  -кварка мы пренебрегли, поскольку
-кварка мы пренебрегли, поскольку 
Знак минус перед всем выражением возникает от следующих стандартных сомножителей, обсуждение которых можно найти в любом учебнике по квантовой теории поля:  для замкнутой фермионной петли,
для замкнутой фермионной петли,  для каждого фермионного пропагатора,
для каждого фермионного пропагатора,  для каждого пропагатора векторной частицы,
для каждого пропагатора векторной частицы,  для каждой вершины,
для каждой вершины,  из-за перехода в
из-за перехода в  от
от  к
к  . Кроме того, следует учесть связь
. Кроме того, следует учесть связь  -матрицы с Г-матрицей:
-матрицы с Г-матрицей:  и с лагранжианом:
и с лагранжианом: 
Вид интеграла с точностью до безразмерного коэффициента  определяется условием поперечности (оно, в частности, требует зануления квадратичной расходимости). Чтобы найти
определяется условием поперечности (оно, в частности, требует зануления квадратичной расходимости). Чтобы найти  умножим левую и правую части на
умножим левую и правую части на  Тогда
Тогда

поскольку

Таким образом,

где верхний предел интеграла мы выбрали равным  так как при
так как при  происходит компенсация диаграмм рис. 7.5, а и
происходит компенсация диаграмм рис. 7.5, а и  а нижний — равным
а нижний — равным  поскольку при
поскольку при  свободный кварковый пропагатор должен модифицироваться из-за невылетания кварка. В результате вклад диаграммы рис. 7.6, а оказывается равным
свободный кварковый пропагатор должен модифицироваться из-за невылетания кварка. В результате вклад диаграммы рис. 7.6, а оказывается равным

Заметим, что множитель  в пропагаторе глюона скомпенсировался множителем
в пропагаторе глюона скомпенсировался множителем  который дала кварковая петля. Так что эффективное четырехкварковое взаимодействие, отвечающее диаграмме рис. 7.6, а, локальное. Поскольку эффективная вершина испускания глюона при переходе
который дала кварковая петля. Так что эффективное четырехкварковое взаимодействие, отвечающее диаграмме рис. 7.6, а, локальное. Поскольку эффективная вершина испускания глюона при переходе  -кварка в
-кварка в  -кварк обращается в нуль при
-кварк обращается в нуль при  где
где  -ймпульс глюона, то ее можно назвать монопольной по аналогии с монопольными электромагнитными переходами в ядрах, в которых запрещено испускание реальных квантов с
-ймпульс глюона, то ее можно назвать монопольной по аналогии с монопольными электромагнитными переходами в ядрах, в которых запрещено испускание реальных квантов с  и происходит испускание пары
и происходит испускание пары  . (Более точно,
. (Более точно,  -вершина является суммой монополя
-вершина является суммой монополя  и анаполя
и анаполя  ).
).
Поясним теперь, почему мы подставили в полученное выше выражение  Буквально диаграммам рис. 7.6 отвечает
Буквально диаграммам рис. 7.6 отвечает  поскольку именно в точке те происходит обрезание петли. Можно показать, однако, что если учесть одевание диаграмм рис. 7.6 дополнительными глюонами, то войдет перенормировочный множитель
поскольку именно в точке те происходит обрезание петли. Можно показать, однако, что если учесть одевание диаграмм рис. 7.6 дополнительными глюонами, то войдет перенормировочный множитель  где
где  , и в интересующем нас выражении
, и в интересующем нас выражении  заменится на
заменится на  (Напомним, что выше мы условились, что
(Напомним, что выше мы условились, что  Если ввести обозначение
Если ввести обозначение

то при  получим, что
получим, что  Таким образом,
Таким образом,  очень мало:
очень мало:

Тем не менее вклад диаграмм типа рис. 7.6 оказывается весьма существенным из-за особой спиновой структуры оператора

Дело в том, что этот оператор представляет собой сумму двух слагаемых:

Первое из этих слагаемых содержит лишь левые спиноры и из-за малости коэффициента перед ним играет меньшую роль, чем операторы  имеющие ту же спиральную структуру. Поэтому при грубом расчете этим оператором можно пренебречь. Второй оператор — мы назовем его
имеющие ту же спиральную структуру. Поэтому при грубом расчете этим оператором можно пренебречь. Второй оператор — мы назовем его  -содержит, наряду с левыми спинорами, - правые. Это обстоятельство, как мы увидим в гл. 9, в ряде случаев может сильно увеличить его вклад в амплитуды нелептонных распадов.
-содержит, наряду с левыми спинорами, - правые. Это обстоятельство, как мы увидим в гл. 9, в ряде случаев может сильно увеличить его вклад в амплитуды нелептонных распадов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
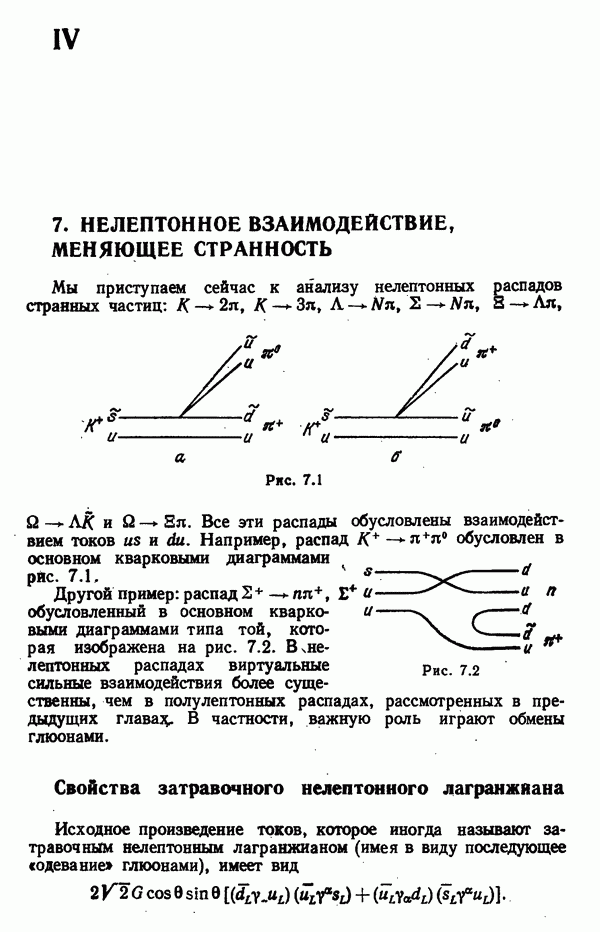
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
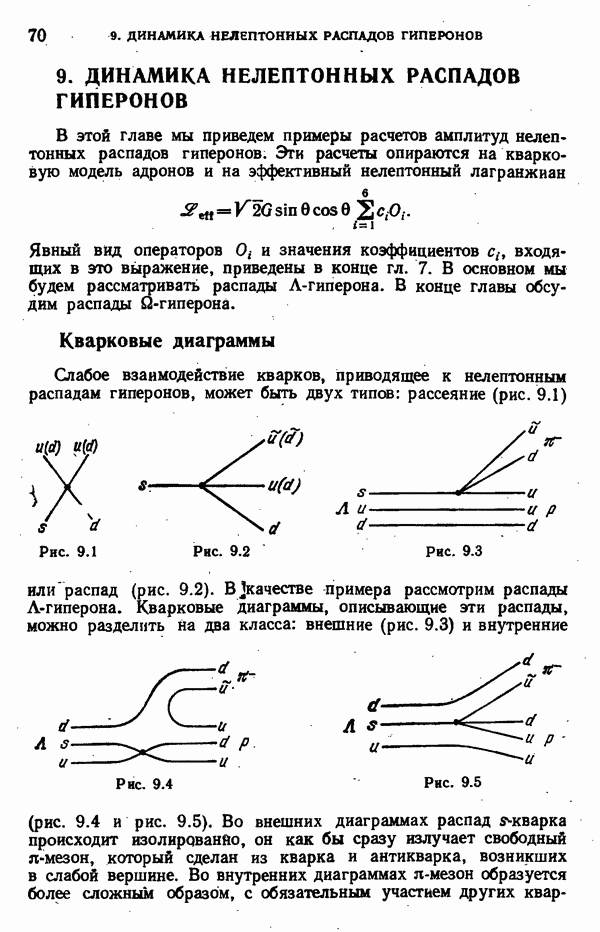
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
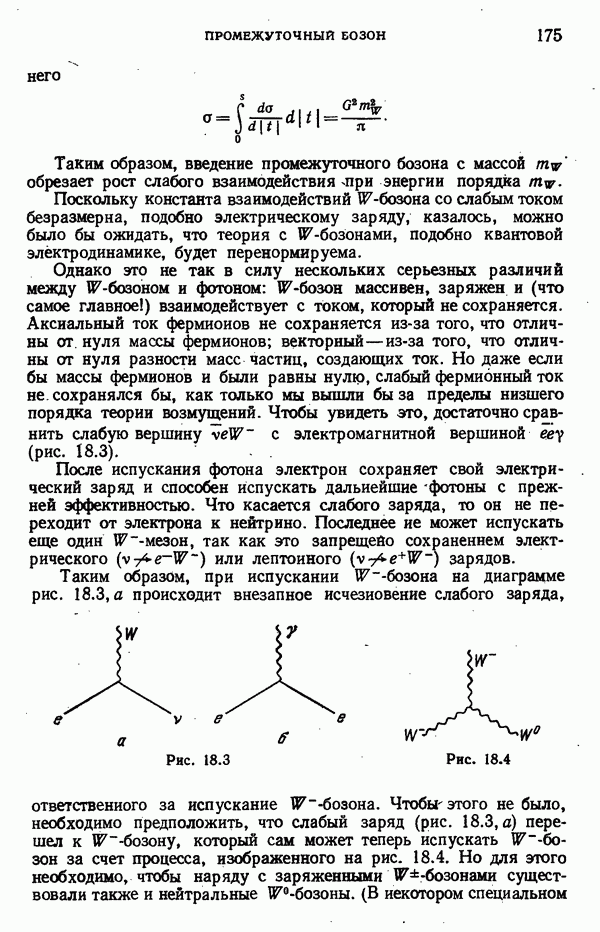
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
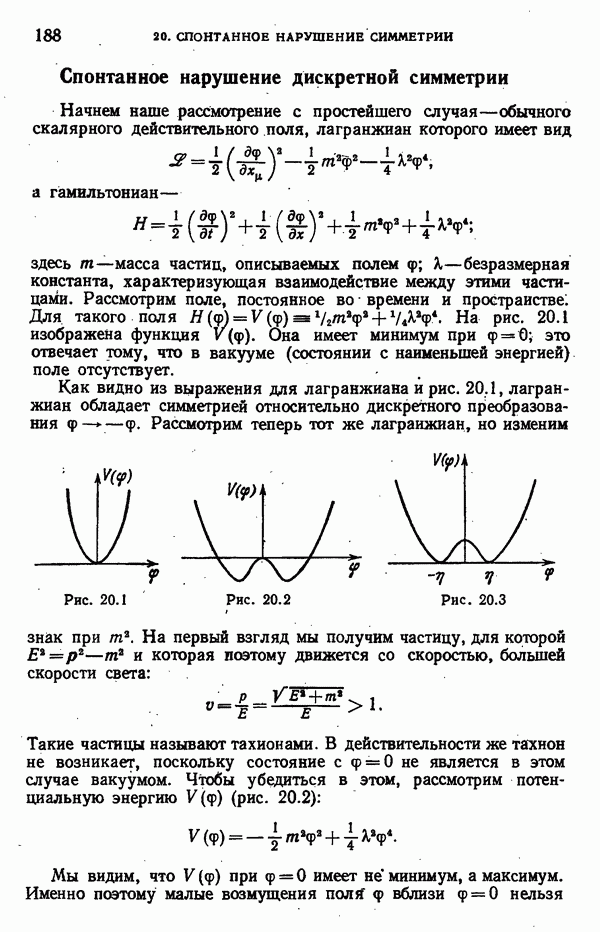
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
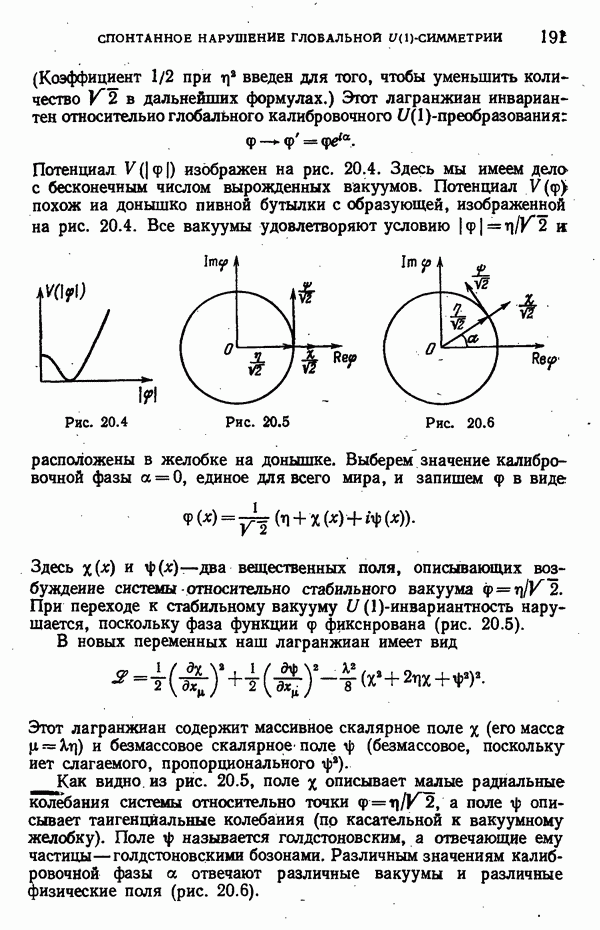
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
- «Бегущие» константы связи
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей