| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Свойства матриц Дирака
3.1. Матрицы  Матрицы удовлетворяют условию
Матрицы удовлетворяют условию

Мы используем представление

или, что то же:

(В определении знака матрицы  - единственное отличие наших обозначений от обозначений известной книги Бьёркена и Дрелла.)
- единственное отличие наших обозначений от обозначений известной книги Бьёркена и Дрелла.)

«Скалярное произведение» матриц у и 4-вектора 

Умножая  на
на  получим соответственно
получим соответственно

Если последнее равенство умножить справа на  где
где  - произвольное матричное выражение, то получится
- произвольное матричное выражение, то получится

Отсюда получаем:

3.2. След матриц у. След  -сумма диагональных элементов матрицы:
-сумма диагональных элементов матрицы:

По определению

Отсюда, используя соотношения  легко получить, что след произведения нечетного числа матриц равен.
легко получить, что след произведения нечетного числа матриц равен.

Если воспользоваться соотношением  то аналогичным приемом для случая, когда
то аналогичным приемом для случая, когда  четно, нетрудно получить следующую редукционную формулу:
четно, нетрудно получить следующую редукционную формулу:

Для  и
и  имеем
имеем

Из определения  следует, что
следует, что

где  - полностью антисимметричный тензор четвертого ранга
- полностью антисимметричный тензор четвертого ранга

Если умножить это на  то получим
то получим

(Мы использовали при этом, что 
Аналогично получаются соотношения

3.3. Дираковский биспииор. Уравнение Дирака для свободной частицы с массой  и 4-импульсом
и 4-импульсом  имеет вид
имеет вид

где  — четырехкомпонентный спинор (биспшор):
— четырехкомпонентный спинор (биспшор):

Определим сопряженный биспинор следующим образом:

Он удовлетворяет уравнению

3.4. Четырехфермионные инварианты и тождества Фирца для матриц Дирака. Из биспиноров а и  описывающих, вообще говоря, две разные частицы, можно составить 16 билинейных комбинаций, которые группируются в пять различных лоренц-ковариантных величин:
описывающих, вообще говоря, две разные частицы, можно составить 16 билинейных комбинаций, которые группируются в пять различных лоренц-ковариантных величин:

Здесь

Множитель  в определении тензора введен для того, чтобы каждая из шести компонент тензора была нормирована на единицу (точнее на —1):
в определении тензора введен для того, чтобы каждая из шести компонент тензора была нормирована на единицу (точнее на —1):

Так же нормированы остальные коварианты:

Можно было бы иметь полное единообразие, если ввести в определение тензора и аксиала множитель  но по традиции этого обычно не делают.
но по традиции этого обычно не делают.
Из четырех биспиноров  лоренцев скаляр можно построить пятью способами:
лоренцев скаляр можно построить пятью способами:

16 матриц  образуют полную систему, поэтому любой из вариантов может быть представлен как линейная суперпозиция вариантов с измененным порядком спиноров:
образуют полную систему, поэтому любой из вариантов может быть представлен как линейная суперпозиция вариантов с измененным порядком спиноров:

где 
Можно показать (см. следующий раздел), что коэффициенты  имеют значения, приведенные в таблице.
имеют значения, приведенные в таблице.
Матрица Фирца

Отметим, что таблица симметрична по отношению к отражениям относительно центральной клетки  . Отметим также, что таблицу следует читать слева направо, но не сверху вниз; это связано с тем, что пять инвариантных амплитуд, по которым производится разложение, не ортогональны друг другу: матрица Фирца не является матрицей ортогонального поворота. Глядя на
. Отметим также, что таблицу следует читать слева направо, но не сверху вниз; это связано с тем, что пять инвариантных амплитуд, по которым производится разложение, не ортогональны друг другу: матрица Фирца не является матрицей ортогонального поворота. Глядя на  рицу Фирца, легко проверить, что при перестановке
рицу Фирца, легко проверить, что при перестановке  две комбинации вариантов переходят сами в себя со знаком плюс, а три — со знаком минус (если предположить, что биспиноры коммутируют):
две комбинации вариантов переходят сами в себя со знаком плюс, а три — со знаком минус (если предположить, что биспиноры коммутируют):

В нерелятивистском пределе симметричные комбинации переходят в выражение  а антисимметричные — в
а антисимметричные — в  . (Действительно, в нерелятивистском пределе
. (Действительно, в нерелятивистском пределе 
Напомним, что для системы двух спиноров выражение  является проекционным оператором состояния с полным спииом
является проекционным оператором состояния с полным спииом  равным единице, а выражение
равным единице, а выражение  -проекционный оператор состояния с
-проекционный оператор состояния с  Это легко увидеть, если возвести в квадрат равенство
Это легко увидеть, если возвести в квадрат равенство 

Мы видим, таким образом, что имеется полное согласие между нерелятивистскими и релятивистскими свойствами симметрии: ведь состояние с  антисимметрично при перестановке образующих его спиноров, а состояние с
антисимметрично при перестановке образующих его спиноров, а состояние с  симметрично.
симметрично.
До сих пор мы рассматривали пять лоренцевых скаляров. Точно такая же матрица Фирца связывает между собой пять лореицевых псевдоскаляров. В этом легко убедиться, если в рассмотренных выше четырехфермионных выражениях заменить, скажем,  на
на 
В расчетах слабых процессов особенно часто встречаются два соотношения:

Эти соотношения легко получаются из фирцевского разложения  -варианта. Для получения первого надо сделать замены:
-варианта. Для получения первого надо сделать замены:

Для получения второго надо сделать замены:

3.5. Вывод тождеств Фирца для матриц Дирака. В этом разделе приведем явный вывод матрицы Фирца. Рассмотрим сначала» некоторые вспомогательные соотношения. Разложим произвольную  -матрицу y по 16 матрицам
-матрицу y по 16 матрицам 

Тогда

где

Легко проверить, что

Таким образом,

или, явно выписывая матричные индексы,

Последнее равенство будет иметь место, если

Сделав в этом выражении замену  и умножив его на тензор
и умножив его на тензор  где
где  и
и  -некоторые матричные выражения, получим основное соотношение, с помощью которого вычисляются коэффициенты матрицы Фирца:
-некоторые матричные выражения, получим основное соотношение, с помощью которого вычисляются коэффициенты матрицы Фирца:

Если рассмотреть это выражение в спинорных обкладках а  то получится именно то, что нам нужно: при переходе от левой части равенства к правой спиноры
то получится именно то, что нам нужно: при переходе от левой части равенства к правой спиноры  меняют своих партнеров. Рассмотрим теперь, как получаются отдельные строки матрицы Фирца.
меняют своих партнеров. Рассмотрим теперь, как получаются отдельные строки матрицы Фирца.
Скалярный вариант. В этом случае  Отрицательные значения
Отрицательные значения  обеспечивают правильный знак в скалярном произведении
обеспечивают правильный знак в скалярном произведении  Отрицательный знак
Отрицательный знак  обусловлен тем, что
обусловлен тем, что  Отрицательный знак
Отрицательный знак  легко проверить, если учесть, что в сумму
легко проверить, если учесть, что в сумму  слагаемое
слагаемое  входит со знаком минус (из-за псевдоевклидовой метрики).
входит со знаком минус (из-за псевдоевклидовой метрики).
Псевдоскалярный вариант.  Из-за антикоммутации у с
Из-за антикоммутации у с 
Векторный вариант.  Коэффициенты второй строки матрицы Фирца определяются следующими
Коэффициенты второй строки матрицы Фирца определяются следующими
соотношениями:

Аксиальный вариант  . Выкладки аналогичны предыдущему случаю.
. Выкладки аналогичны предыдущему случаю.
Тензорный вариант  При получении коэффициентов использованы соотношения:
При получении коэффициентов использованы соотношения:

Чтобы получить соотношения Фирца для продольных спиноров, надо взять 

или

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
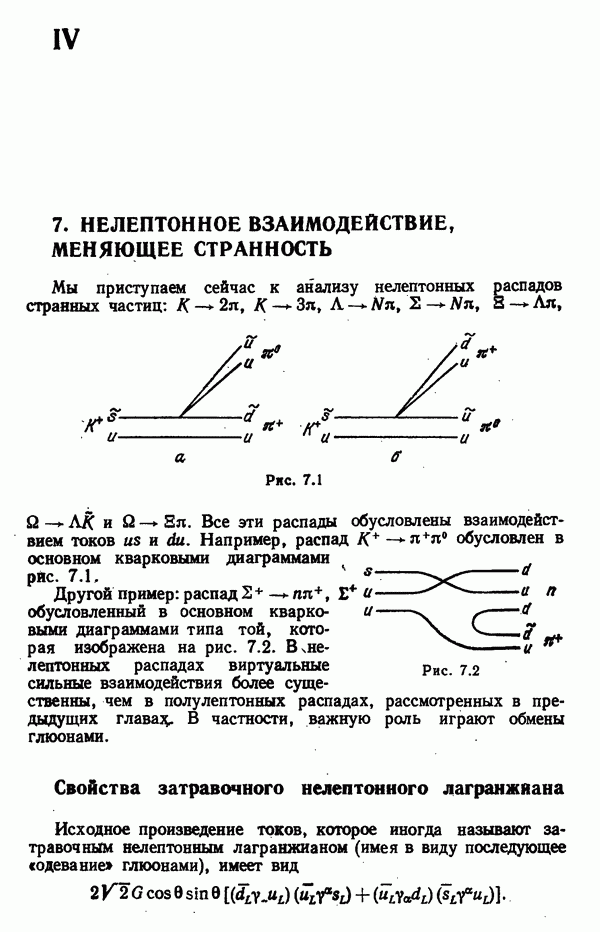
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
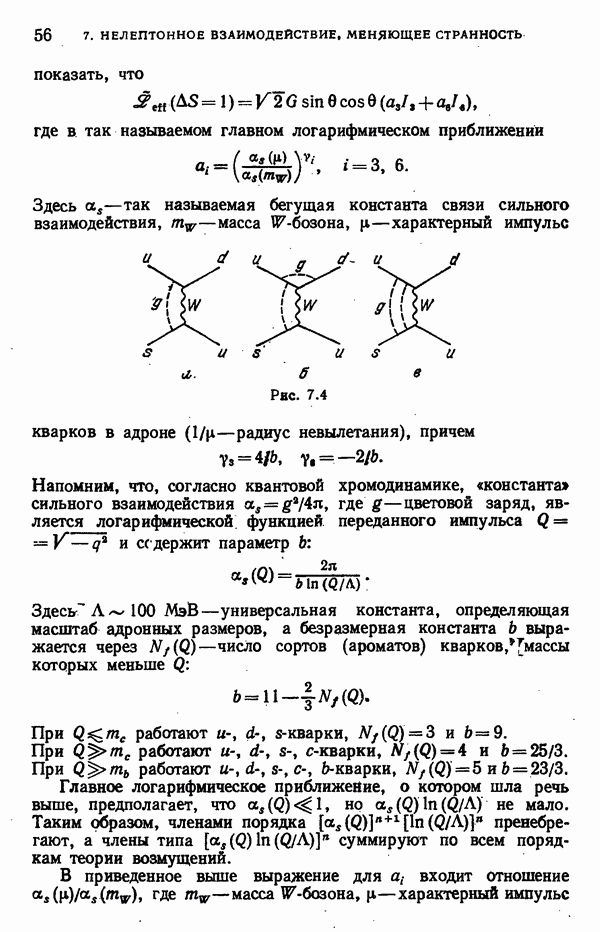
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
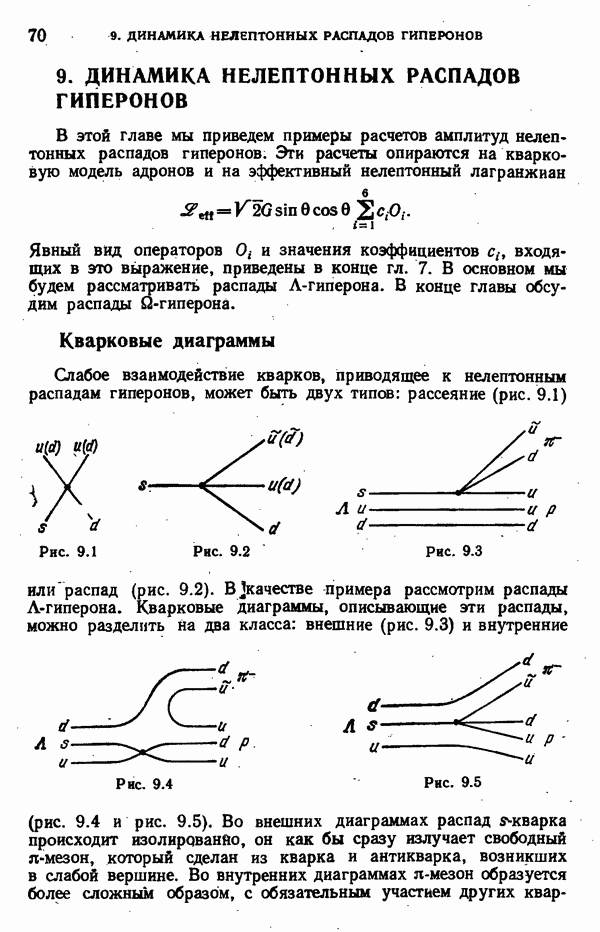
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
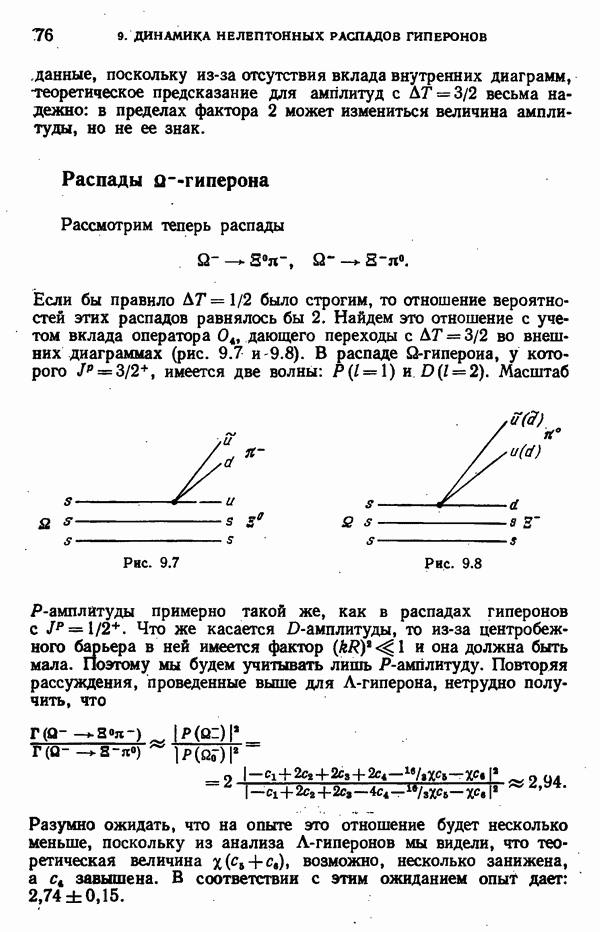
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
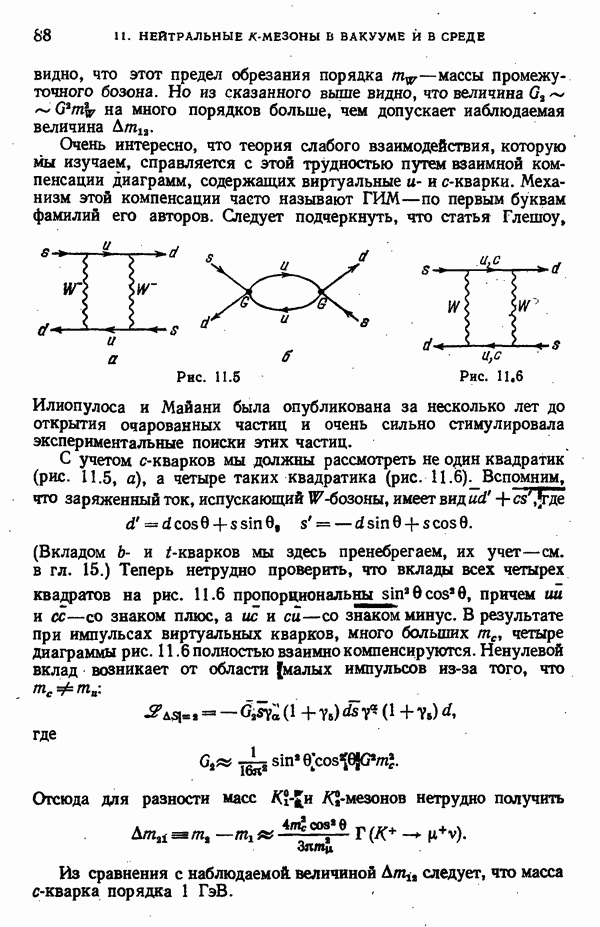
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
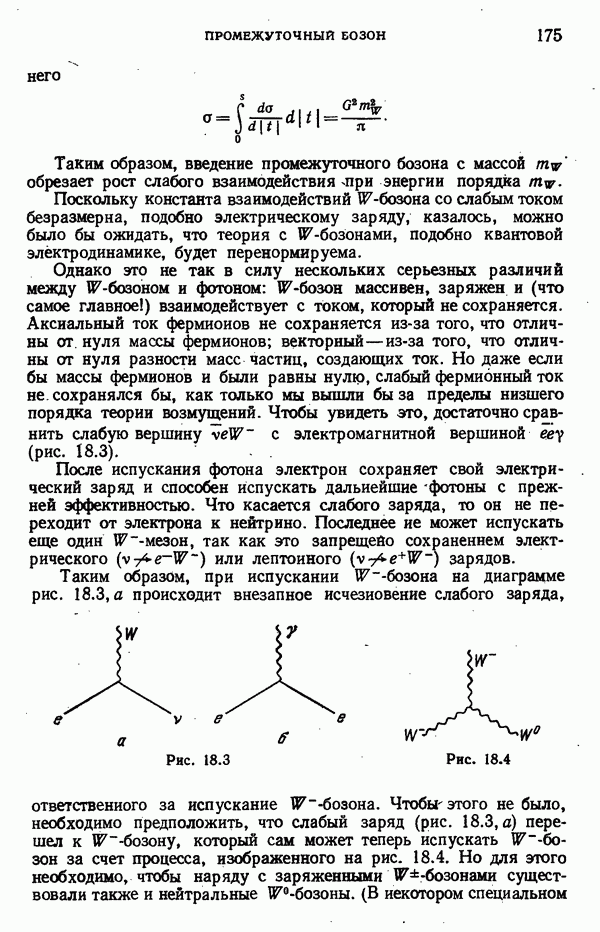
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
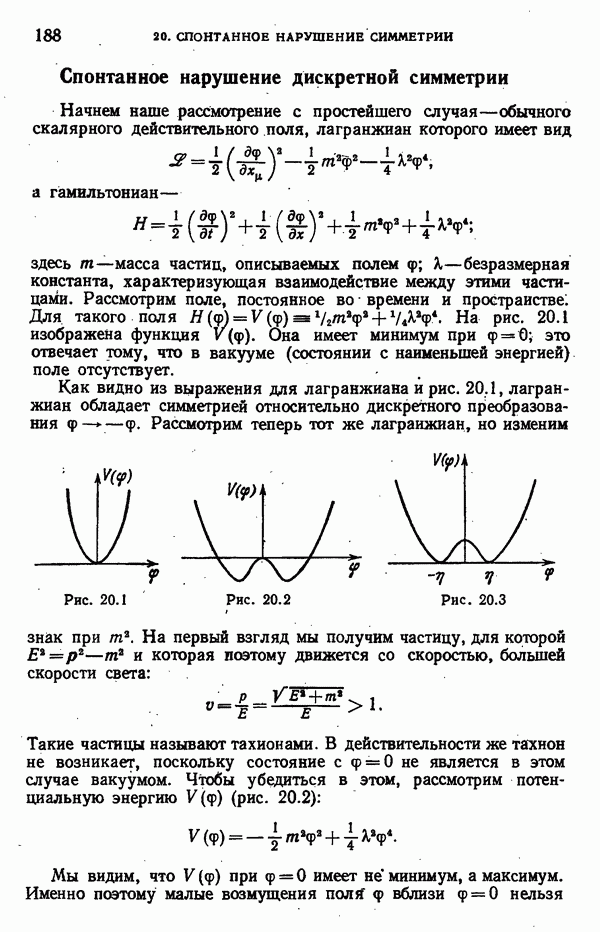
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
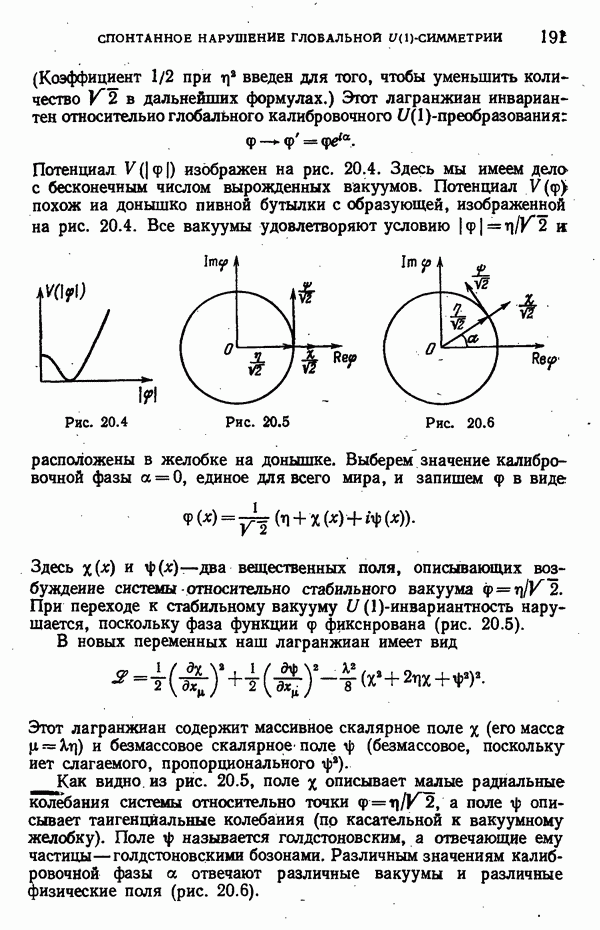
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
- «Бегущие» константы связи
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей