| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. СТРУКТУРА СЛАБЫХ ТОКОВ
Во Введении была дана качественная картина слабого взаимодействия «с птичьего полета». Сейчас мы перейдем к количественному описанию свойств слабых токов. Как уже говорилось, слабые процессы при низких энергиях прекрасно описываются эффективным четырехфермионным лагранжианом, содержащим два слагаемых:

Здесь  — лагранжиан взаимодействия заряженных токов,
— лагранжиан взаимодействия заряженных токов,  — нейтральных:
— нейтральных:

 — заряженный ток (он уменьшает заряд частиц на единицу),
— заряженный ток (он уменьшает заряд частиц на единицу),  -эрмитово-сопряженный ток (он увеличивает заряд частиц на единицу),
-эрмитово-сопряженный ток (он увеличивает заряд частиц на единицу),  -нейтральный ток (он диагонален, т. е. переводит частицы в самое себя). Как уже говорилось, константа Ферми
-нейтральный ток (он диагонален, т. е. переводит частицы в самое себя). Как уже говорилось, константа Ферми  множитель
множитель  выделяют, следуя традиции. Согласно стандартной теории электрослабого взаимодействия
выделяют, следуя традиции. Согласно стандартной теории электрослабого взаимодействия  {см. гл. 22). Экспериментальные данные согласуются с этой величиной в пределах экспериментальных погрешностей порядка процента.
{см. гл. 22). Экспериментальные данные согласуются с этой величиной в пределах экспериментальных погрешностей порядка процента.
Токи в лагранжианах  и взаимодействуют локально: это значит, что взаимодействие происходит тогда, когда операторы обоих токов действуют в одной и той же мировой точке. Иногда четырехфермионное слабое взаимодействие называют универсальным, имея в виду при этом, что взаимодействия различных токов характеризуются одной и той же константой
и взаимодействуют локально: это значит, что взаимодействие происходит тогда, когда операторы обоих токов действуют в одной и той же мировой точке. Иногда четырехфермионное слабое взаимодействие называют универсальным, имея в виду при этом, что взаимодействия различных токов характеризуются одной и той же константой  Однако утверждение об универсальности слабого взаимодействия нуждается в серьезных оговорках и разъяснениях, которые мы дадим ниже.
Однако утверждение об универсальности слабого взаимодействия нуждается в серьезных оговорках и разъяснениях, которые мы дадим ниже.
Левые заряженные токи
Во всех случаях, когда удалось экспериментально установить пространственно-временную структуру заряженных токов, она оказывалась типа

где  - операторы начальной и конечной частиц — представляют собой дираковские биспиноры,
- операторы начальной и конечной частиц — представляют собой дираковские биспиноры,  , а матрица
, а матрица  имеет вид
имеет вид

Напомним, что  где
где  (сведения о дираковских матрицах у см. гл. 8, п. 3). Величина
(сведения о дираковских матрицах у см. гл. 8, п. 3). Величина  представляет собой разность вектора
представляет собой разность вектора  и аксиального вектора
и аксиального вектора  Поэтому о взаимодействиях заряженных токов говорят как об универсальном
Поэтому о взаимодействиях заряженных токов говорят как об универсальном  -взаимодействии.
-взаимодействии.
В силу антикоммутации матриц и 

Воспользовавшись этим, мы можем записать:

где

Здесь индекс  указывает на то, что
указывает на то, что  представляют собой так называемые левые компоненты дираковских биспиноров. Чтобы пояснить смысл этого термина, рассмотрим волновую функцию
представляют собой так называемые левые компоненты дираковских биспиноров. Чтобы пояснить смысл этого термина, рассмотрим волновую функцию

где  удовлетворяет уравнению Дирака
удовлетворяет уравнению Дирака

(как обычно,  для любого 4-вектора
для любого 4-вектора  ). Выражая биспинор
). Выражая биспинор  через двухкомпонентные спиноры
через двухкомпонентные спиноры 

получаем, что уравнение Дирака дает связь между 

Теперь, используя явный вид матрицы  находим, что
находим, что

 содержит только комбинацию
содержит только комбинацию  и не содержит комбинацию
и не содержит комбинацию  . Используя выражение для
. Используя выражение для  мы видим, что
мы видим, что

В ультрарелятивистском пределе, когда  получаем
получаем

где  — единичный вектор, направленный по импульсу частицы. Направим координатную ось
— единичный вектор, направленный по импульсу частицы. Направим координатную ось  по
по  , тогда
, тогда

Учтем теперь, что двухкомпонентный спинор  описывает частицу, спин которой направлен по оси
описывает частицу, спин которой направлен по оси  — частицу с противоположным направлением спина. Тогда получим, что
— частицу с противоположным направлением спина. Тогда получим, что  если
если  если
если  Таким образом,
Таким образом,  описывает частицу, спин которой направлен против ее импульса. Про такую частицу говорят, что она имеет левую спиральность или что она левополяризована. Если спин частицы направлен по ее импульсу, то говорят, что она имеет правую спиральность или что она правополяризована. Понятие спиральности не является лоренц-инвариантным, если частица обладает ненулевой массой. Для такой частицы спиральность зависит от того, в какой системе координат находится наблюдатель. Если мы устремимся вдогонку частице со скоростью, превышающей скорость частицы, то в нашей системе координат ее спиральность изменит знак. Чем больше скорость частицы, тем труднее ее обогнать и тем лучшим квантовым числом является спиральность. Спиральность безмассовых нейтрино — точное квантовое число.
описывает частицу, спин которой направлен против ее импульса. Про такую частицу говорят, что она имеет левую спиральность или что она левополяризована. Если спин частицы направлен по ее импульсу, то говорят, что она имеет правую спиральность или что она правополяризована. Понятие спиральности не является лоренц-инвариантным, если частица обладает ненулевой массой. Для такой частицы спиральность зависит от того, в какой системе координат находится наблюдатель. Если мы устремимся вдогонку частице со скоростью, превышающей скорость частицы, то в нашей системе координат ее спиральность изменит знак. Чем больше скорость частицы, тем труднее ее обогнать и тем лучшим квантовым числом является спиральность. Спиральность безмассовых нейтрино — точное квантовое число.
Из вида заряженного тока следует, что в нем участвуют только левые компоненты биспинорных операторов. Это отвечает тому, что при  частицы входят в него только с левыми спиральностями, а античастицы — только с правыми. Никаким слабым процессом нельзя породить или поглотить правое нейтрино или левое антинейтрино, если нейтрино участвует только в левых токах, а антинейтрино — только в правых, и если массы этих частиц равны нулю.
частицы входят в него только с левыми спиральностями, а античастицы — только с правыми. Никаким слабым процессом нельзя породить или поглотить правое нейтрино или левое антинейтрино, если нейтрино участвует только в левых токах, а антинейтрино — только в правых, и если массы этих частиц равны нулю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
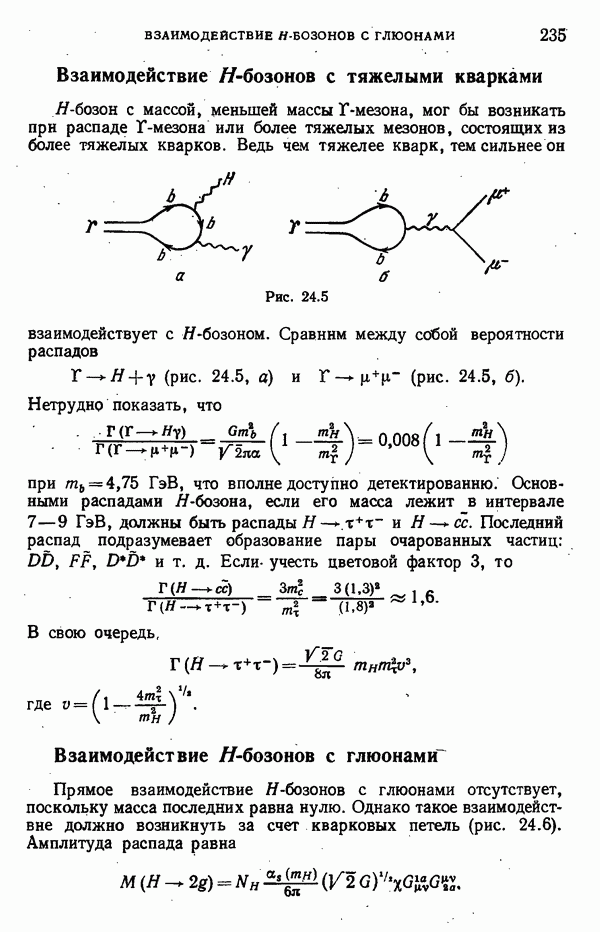
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
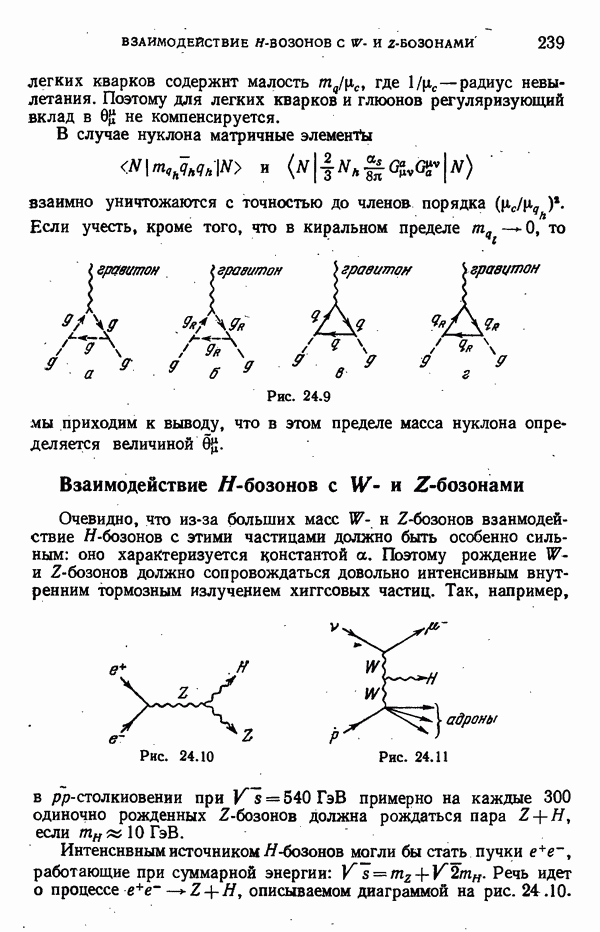
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
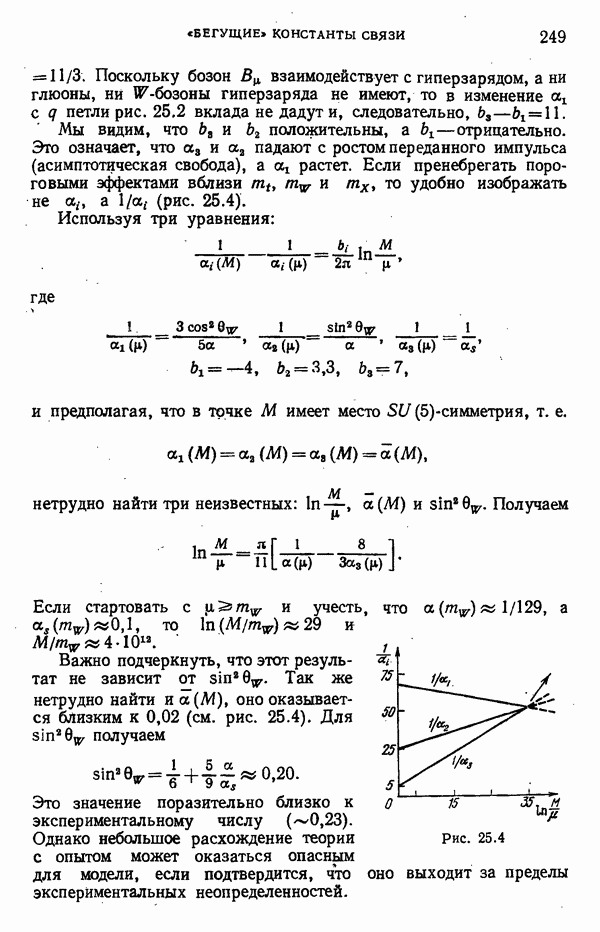
- «Бегущие» константы связи
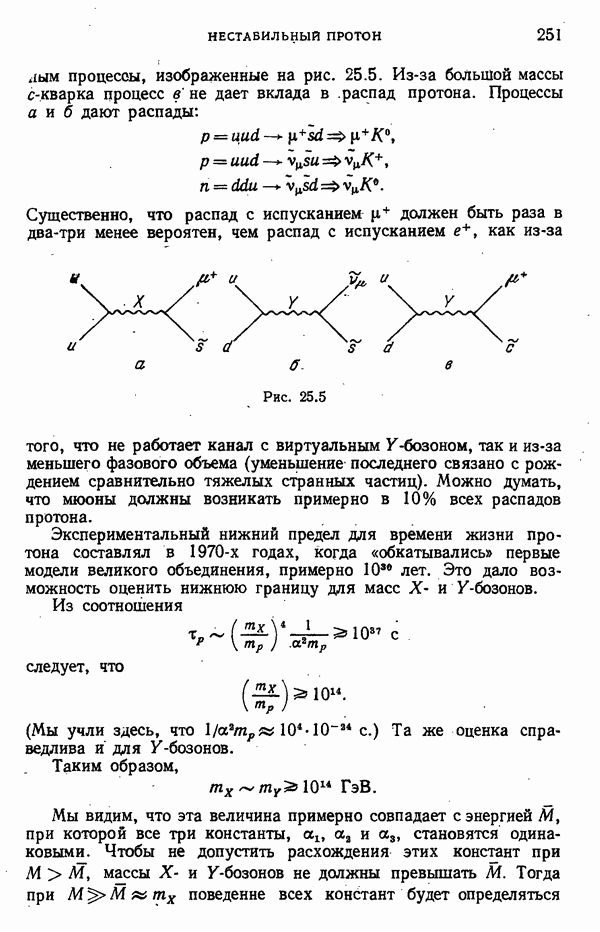
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
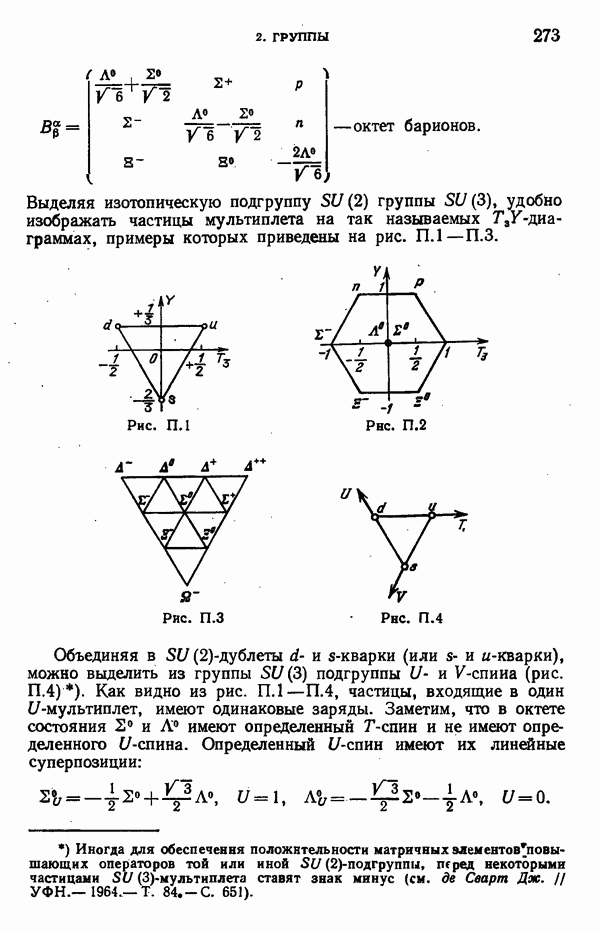
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей