| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
В этой главе мы рассмотрим следующие лептонные распада адронов: распады  -мезонов
-мезонов  где
где  или
или  -распад нейтрона
-распад нейтрона  - захват
- захват  Кроме того, мы кратко обсудим распады
Кроме того, мы кратко обсудим распады  которые также обусловлены
которые также обусловлены  -током.
-током.
Распады ....
Начнем с распада  Кварковая диаграмма этого распада изображена на рис. 5.1. Вершина, отмеченная точкой на диаграмме, представляет собой условное изображение того, что
Кварковая диаграмма этого распада изображена на рис. 5.1. Вершина, отмеченная точкой на диаграмме, представляет собой условное изображение того, что  состоит из и
состоит из и  . В матричном элементе На векторная часть равна нулю,
. В матричном элементе На векторная часть равна нулю,  мы запишем в виде
мы запишем в виде  где
где  -волновая функция пиона,
-волновая функция пиона,  — его 4-импульс и
— его 4-импульс и  представляет собой параметр размерности массы (иногда вместо
представляет собой параметр размерности массы (иногда вместо  исполь. зуюг константу
исполь. зуюг константу  Амплитуда процесса имеет вид
Амплитуда процесса имеет вид


Рис. 5.1
Во многих статьях и книгах волновая функция пиона  не включается в выражение для амплитуда, поскольку она не несет никаких лоренцевых или спинорных индексов (в отличие от волновых функций частиц с ненулевым спином скажем, фотона или электрона), и при используемой нами нормировке ее значение равно единице. Мы, тем не менее, явно выписываем ее, чтобы
не включается в выражение для амплитуда, поскольку она не несет никаких лоренцевых или спинорных индексов (в отличие от волновых функций частиц с ненулевым спином скажем, фотона или электрона), и при используемой нами нормировке ее значение равно единице. Мы, тем не менее, явно выписываем ее, чтобы
каждая частица, участвующая в процессе, была представлена в амплитуде своей волновой функцией, и, кроме того, чтобы было явно видно, что  - является аксиальным 4-вектором, поскольку
- является аксиальным 4-вектором, поскольку  -псевдоскаляр. Воспользуемся сохранением 4-импульса
-псевдоскаляр. Воспользуемся сохранением 4-импульса

и уравнением Дирака  и перепишем М в следующем виде:
и перепишем М в следующем виде:

Мы видим, что амплитуда пропорциональна  и зануляется при
и зануляется при  . Это зануление связано с тем, что как мы уже отмечали раньше, слабое взаимодействие сохраняет спиральность, а распад мезона с нулевым спином на левое нейтрино и правый антилептон, летящие в противоположные стороны, запрещен сохранением углового момента. Стандартным образом находим
. Это зануление связано с тем, что как мы уже отмечали раньше, слабое взаимодействие сохраняет спиральность, а распад мезона с нулевым спином на левое нейтрино и правый антилептон, летящие в противоположные стороны, запрещен сохранением углового момента. Стандартным образом находим

где  — масса пиона,
— масса пиона,  -энергия нейтрино в системе покоя пиона
-энергия нейтрино в системе покоя пиона 
Запишем вероятность распада в виде

где Ф — фазовый объем:

Чтобы не усложнять обозначений, в последнем равенстве одной и той же буквой  обозначены как подынтегральная переменная, так и фиксированная кинематикой распада (
обозначены как подынтегральная переменная, так и фиксированная кинематикой распада ( -функцией) величина, вошедшая в результат интегрирования. Думаю, что это не смутит читателя. В результате получаем
-функцией) величина, вошедшая в результат интегрирования. Думаю, что это не смутит читателя. В результате получаем

Сравнивая это выражение с известной из опыта вероятностью распада находим, что  МэВ. Как мы увидим в дальнейшем, эта величина входит во все соотношения, получаемые на основе
МэВ. Как мы увидим в дальнейшем, эта величина входит во все соотношения, получаемые на основе  Отношение вероятностей распадов
Отношение вероятностей распадов  не зависит от величины
не зависит от величины  и равно
и равно

Следует подчеркнуть, что величина  для обоих распадов строго одна и та же. Это обусловлено тем, что матричный элемент
для обоих распадов строго одна и та же. Это обусловлено тем, что матричный элемент  -тока зависит от суммарного 4-импульса лептонов, но не от 4-импульса каждого из лептонов в отдельности.
-тока зависит от суммарного 4-импульса лептонов, но не от 4-импульса каждого из лептонов в отдельности.
Распад ...
Распад  изображается суммой кварковых диаграмм (рис. 5.2). Амплитуда этого распада имеет вид
изображается суммой кварковых диаграмм (рис. 5.2). Амплитуда этого распада имеет вид

где

Здесь  - волновые функции
- волновые функции  -мезонов, и
-мезонов, и  - их 4-импульсы,
- их 4-импульсы,  .
.

Рис. 5.2
Скалярные безразмерные параметры  являются, вообще говоря, функциями
являются, вообще говоря, функциями  однако, поскольку энерговыделение в
однако, поскольку энерговыделение в  распаде мало, можно считать, что во всей физической области
распаде мало, можно считать, что во всей физической области  формфакторы
формфакторы  постоянны:
постоянны: 
В силу сохранения векторного тока

Это равенство должно выполняться в пределе строгой изотопической инвариантности при выключенном электромагнитном взаимодействии. В этом пределе  и условие поперечности имеет вид
и условие поперечности имеет вид

отсюда следует, что  Что касается
Что касается  то ее величина фиксируется тем, что векторный
то ее величина фиксируется тем, что векторный  -ток входит в один триплет с изовекторным электромагнитным током. Как было показано в предыдущей главе,
-ток входит в один триплет с изовекторным электромагнитным током. Как было показано в предыдущей главе,  представляет собой слабый векторный заряд, величина которого в переходе
представляет собой слабый векторный заряд, величина которого в переходе  равна
равна  Это значение
Это значение  легко получить и «на пальцах», глядя на диаграммы рис. 5.2, если учесть, что слабые заряда в переходах кварка
легко получить и «на пальцах», глядя на диаграммы рис. 5.2, если учесть, что слабые заряда в переходах кварка  и антикварка
и антикварка
 равны соответственно
равны соответственно  Интересующий нас матричный элемент имеет вид
Интересующий нас матричный элемент имеет вид

Итак, амплитуда  -распада
-распада

Упражнение. Вычислить с этой амплитудой ширину  -распада.
-распада.
Ответ:

Здесь  при расчете пренебрегалось более высокими степенями отношений
при расчете пренебрегалось более высокими степенями отношений  Вычисленная нами вероятность
Вычисленная нами вероятность  -распада составляет примерно
-распада составляет примерно  от полной ширины
от полной ширины  -мезона. Эксперименты подтверждают теоретическое предсказание для
-мезона. Эксперименты подтверждают теоретическое предсказание для 
b-распад нейтрона
В распаде  отличны от нуля как
отличны от нуля как  так и
так и  . В наиболее общем виде можно записать:
. В наиболее общем виде можно записать:

Все шесть формфакторов  являются функциями
являются функциями  где
где  Характерный масштаб значений
Характерный масштаб значений  на которых меняются эти функции, составляет величину порядка
на которых меняются эти функции, составляет величину порядка  Исключением является
Исключением является  для которой эта величина гораздо меньше, — порядка
для которой эта величина гораздо меньше, — порядка  ГэВ. В любом случае энергия, выделяемая в Р-распаде, настолько мала, что можно рассматривать все шесть формфакторов, как константы. На опыте зависимость функций
ГэВ. В любом случае энергия, выделяемая в Р-распаде, настолько мала, что можно рассматривать все шесть формфакторов, как константы. На опыте зависимость функций  от
от  измеряется в нейтринных экспериментах:
измеряется в нейтринных экспериментах:

Мы будем говорить о них в гл. 17.
Векторные формфакторы
Рассмотрим сначала векторные формфакторы  Из сохранения векторного тока следует, что слабый заряд
Из сохранения векторного тока следует, что слабый заряд  Это можно конечно, пелучить, складывая кварковые амплитуды
Это можно конечно, пелучить, складывая кварковые амплитуды
диаграмм рис. 5.3. Однако в данном случае проще сразу прибегнуть к общей формуле, согласно которой слабый заряд равен  Для перехода
Для перехода  имеем
имеем  , следовательно,
, следовательно,  и слабый заряд в переходах
и слабый заряд в переходах  равен слабому заряду в переходах
равен слабому заряду в переходах 

Рис. 5.3
Данные по Р-распаду нейтрона и сверхразрешенным переходам в ядрах (обусловленных именно слабым векторным зарядом, см. гл. 4) дают при этом значение 
В главе о распаде мюона мы уже отмечали, что измерение времени жизни мюона дает наиболее точное значение константы 

С другой стороны, данные по сверхразрешенным Р-переходам в ядрах  обусловленных векторным током, дают
обусловленных векторным током, дают

(Неопределенность в этой величине примерно в равной степени связана с экспериментальными ошибками и с теоретическими неоднозначностями в учете радиационной, кулоновой и слабой поправок.) Сравнивая  с
с  находим
находим

Независимое определение величины  дают лептонные распады странных частиц:
дают лептонные распады странных частиц:

Величину  обычно называют слабым магнетизмом. Сходство слабого и электромагнитного токов позволяет предсказать значение
обычно называют слабым магнетизмом. Сходство слабого и электромагнитного токов позволяет предсказать значение  Действительно, электромагнитные нуклонные вершины имеют вид
Действительно, электромагнитные нуклонные вершины имеют вид

Эго значит, что изоскалярная вершина равна

а изовекторная

Поскольку изовекторный электромагнитный ток входит в один триплет со слабым векторным током, то последнее выражение справедливо и для  Учитывая, что
Учитывая, что  получаем
получаем  Заодно мы получаем также, что
Заодно мы получаем также, что  Член
Член  называют обычно эффективным скаляром. Это название связано с тем, что его можно записать в виде скаляра:
называют обычно эффективным скаляром. Это название связано с тем, что его можно записать в виде скаляра:

Есть две причины, по которым  Во-первых, поперечность
Во-первых, поперечность  следует, что
следует, что  , во-вторых, то обстоятельство что
, во-вторых, то обстоятельство что  должно быть
должно быть  -четно, а изовекторный скаляр - G - нечетен. Наилучшие, экспериментальные ограничения на величину
-четно, а изовекторный скаляр - G - нечетен. Наилучшие, экспериментальные ограничения на величину  дает процесс
дает процесс  -захвата
-захвата 

Рис. 5.4
Возвращаясь к слабому магнетизму, отметим, что непосредственно в  -распаде нейтрона наблюдать вклад этого члена очень трудно из-за малости последнего. Он существенно больше в
-распаде нейтрона наблюдать вклад этого члена очень трудно из-за малости последнего. Он существенно больше в  -переходах ядер с большим энерговыделением, например в изотопически зеркальных
-переходах ядер с большим энерговыделением, например в изотопически зеркальных  -переходах бора и азота (рис. 5.4). Величина слабого магнетизма в этих переходах выражается через величину магнитного матричного элемента в радиационном распаде возбужденного уровня
-переходах бора и азота (рис. 5.4). Величина слабого магнетизма в этих переходах выражается через величину магнитного матричного элемента в радиационном распаде возбужденного уровня  входящего в один изотопический триплет с основными состояниями
входящего в один изотопический триплет с основными состояниями  (у всех трех уровней
(у всех трех уровней 
Аксиальные формфакторы
Три аксиальных формфактора носят следующие названия:  -аксиальный заряд,
-аксиальный заряд,  -слабый электризм, эффективный псевдоскаляр. Начнем с члена
-слабый электризм, эффективный псевдоскаляр. Начнем с члена  -эгкгт член аналогичен электрическому дипольйому моменту нейтрона. Подобно последнему, который запрещен в силу СР-инвариантности электромагнитного взаимодействия, слабый электризм также запрещен. Причиной запрета является то, что этот член имеет положительную
-эгкгт член аналогичен электрическому дипольйому моменту нейтрона. Подобно последнему, который запрещен в силу СР-инвариантности электромагнитного взаимодействия, слабый электризм также запрещен. Причиной запрета является то, что этот член имеет положительную  -четность, в то время как аксиальный ток
-четность, в то время как аксиальный ток  -нечетен. Члены
-нечетен. Члены  являются
являются  -нечетньми и, следовательно, не запрещены.
-нечетньми и, следовательно, не запрещены.
Между ними существует связь, налагаемая частичным сохранением аксиального тока  . В пределе безмассовых пионов аксиальный ток сохраняется и матричный элемент поперечен:
. В пределе безмассовых пионов аксиальный ток сохраняется и матричный элемент поперечен:

Сам по себе член  не поперечен, поскольку отличны от нуля массы нуклонов:
не поперечен, поскольку отличны от нуля массы нуклонов:

Чтобы сделать матричный элемент поперечным, умножим его на поперечное выражение  Получившееся выражение
Получившееся выражение  при умножении на
при умножении на  дает нуль, однако это выражение, наряду с членом
дает нуль, однако это выражение, наряду с членом  содержит еще одно слагаемое, в котором трудно не узнать эффективный псевдоскаляр:
содержит еще одно слагаемое, в котором трудно не узнать эффективный псевдоскаляр:

(Мы воспользовались тем, что рпип  и приближенно положили,
и приближенно положили,  Видно, что формфактор эффективного псевдоскаляра содержит
Видно, что формфактор эффективного псевдоскаляра содержит  -мезонный полюс при
-мезонный полюс при  (напомним, что массой
(напомним, что массой  -мезона мы пока, пренебрегаем). Феноменологически этот полюс отвечает диаграмме рис. 5.5. Константы
-мезона мы пока, пренебрегаем). Феноменологически этот полюс отвечает диаграмме рис. 5.5. Константы  и
и  определяющие величину диаграммы, нам известны. Величина
определяющие величину диаграммы, нам известны. Величина  характеризует распад
характеризует распад  , как мы выяснили в начале этой главы,
, как мы выяснили в начале этой главы,  МэВ. Константа
МэВ. Константа  характеризует сильное взаимодействие
характеризует сильное взаимодействие  -мезонов с нуклонами. Если записать вершину
-мезонов с нуклонами. Если записать вершину  в виде
в виде

то известное из опыта значение  таково, что
таково, что  да 14. Чтобы окончательно договориться о нормировке, заметим, что в электродинамике аналогичная величина
да 14. Чтобы окончательно договориться о нормировке, заметим, что в электродинамике аналогичная величина 

Рис. 5.5
Когда-то константа  для сильного взаимодействия считалась столь же фундаментальной константой, как
для сильного взаимодействия считалась столь же фундаментальной константой, как  -для электромагнитного. Сегодня мы знаем, что
-для электромагнитного. Сегодня мы знаем, что  -величина чисто феноменологическая и в фундаментальный лагранжиан сильного взаимодействия не входит.
-величина чисто феноменологическая и в фундаментальный лагранжиан сильного взаимодействия не входит.
Константа  характеризует вершину
характеризует вершину  в условиях, когда все три частицы находятся на массовой поверхности. Например, она равна вычету пионного полюса в амплитуде нуклон-нуклонного рассеяния или вычету нуклонного полюса в амплитудах пион-нуклонного
в условиях, когда все три частицы находятся на массовой поверхности. Например, она равна вычету пионного полюса в амплитуде нуклон-нуклонного рассеяния или вычету нуклонного полюса в амплитудах пион-нуклонного
рассеяния и фоторождения пионов. В рассматриваемый аксиальный формфактор нуклона величина  входит как вычет пионного полюса.
входит как вычет пионного полюса.
Перепишем  -нуклонную вершину в градиентном виде:
-нуклонную вершину в градиентном виде:

тогда  МэВ. (Введенную здесь величину
МэВ. (Введенную здесь величину  не следует путать с введенными ранее величинами
не следует путать с введенными ранее величинами  и с величиной
и с величиной  часто используемой в литературе.) Мы видим, что полюсной член в амплитуде, описываемой диаграммой рис. 5.5, должен равняться
часто используемой в литературе.) Мы видим, что полюсной член в амплитуде, описываемой диаграммой рис. 5.5, должен равняться

С другой стороны, умножение матричного элемента  на Дало нам выше
на Дало нам выше

Следовательно,

Это так называемое соотношение Голдбергера—Треймана. Если подставить в него числовые значения  то получим
то получим  что хорошо согласуется с известным из опыта значением
что хорошо согласуется с известным из опыта значением  (В литературе часто используются обозначения:
(В литературе часто используются обозначения:  вместо нашего
вместо нашего  вместо нашего
вместо нашего  иногда через
иногда через  обозначают —
обозначают —  Следует учесть, что экспериментальные
Следует учесть, что экспериментальные  определяются при
определяются при  при
при  Мы предполагаем, что при сдвиге на
Мы предполагаем, что при сдвиге на  ГэВ эти величины меняются мало.
ГэВ эти величины меняются мало.
Появление пионного полюса в матричном элементе аксиального тока является следствием спонтанного нарушения киральной симметрии, выражающегося в том, что из безмассовых кварков возникают массивные нуклоны. Как уже отмечалось в предыдущей главе, из-за наличия у нуклонов массы киральная симметрия реализуется нелинейным образом, за счет возникновения изотопического триплета безмассовых псевдоскалярных частиц. Такие частицы со спином, равным нулю, и нулевой массой, сопровождающие спонтанное нарушение симметрии, носят название голдстоновских мезонов. На примере  -распада мы видим, каким образом полюсной член, отвечающий безмассовому голдстоновскому мезону
-распада мы видим, каким образом полюсной член, отвечающий безмассовому голдстоновскому мезону

обеспечивает сохранение аксиального тока (поперечность  После умножения на лептонную скобку этот член дает эффективный
После умножения на лептонную скобку этот член дает эффективный
псевдоскаляр:

Для ( -распада эффективный псевдоскаляр очень мал из-за малой массы электрона. Он значительно больше в реакции
-распада эффективный псевдоскаляр очень мал из-за малой массы электрона. Он значительно больше в реакции  -захвата.
-захвата.
При обсуждении численной величины эффективного псевдоскаляра мы уже не можем игнорировать то обстоятельство, что  -мезон не безмассов. Обычно массу пиона учитывают по-простецки, вставляя в пропагатор «руками», так что «константа» эффективного псевдоскаляра
-мезон не безмассов. Обычно массу пиона учитывают по-простецки, вставляя в пропагатор «руками», так что «константа» эффективного псевдоскаляра  приобретает вид
приобретает вид

Мы видим, что  меняется с изменением
меняется с изменением  . В процессе
. В процессе  практически всю энергию (порядка
практически всю энергию (порядка  уносит нейтрино, а нуклон получает импульс порядка
уносит нейтрино, а нуклон получает импульс порядка  так что
так что  . Учитывая это, получаем, что
. Учитывая это, получаем, что  Опыты по
Опыты по  -захвату согласуются с такой большой величиной эффективного псевдоскаляра.
-захвату согласуются с такой большой величиной эффективного псевдоскаляра.
Вероятность b-распада. Угловые корреляции
Мы уже упоминали, что лагранжиан взаимодействия лептонных токов с токами легких кварков CP-инвариантен (более подробно об этом гойорится в гл. 12). В силу СРТ-теоремы, из этого следует, что этот лагранжиан инвариантен также и относительно обращения времени Т. Можно показать, что Г-инвариантность лагранжиана приводит к действительности формфакторов  в матричном элементе Р-распада нейтрона. То же относится и к формфакторам в распадах пионов.
в матричном элементе Р-распада нейтрона. То же относится и к формфакторам в распадах пионов.
Итак, мы закончили рассмотрение всех шести формфакторов в Р-распаде нейтрона. Основной вклад в этот процесс дают векторный и аксиальный заряды, так что амплитуда распада может быть записана в виде

где

Упражнения.
(см. скан)
(см. скан)
Распады ...
В распадах  странность не меняется и, следовательно, они обусловлены
странность не меняется и, следовательно, они обусловлены  -током. Общий вид V и
-током. Общий вид V и  для этих распадов такой же, как и для
для этих распадов такой же, как и для  -распада нейтрона, но в связи с тем, что
-распада нейтрона, но в связи с тем, что  и
и  -гипероны не входят в один изотопический мультиплет,
-гипероны не входят в один изотопический мультиплет,  . В этом проще всего убедиться, если воспользоваться условием
. В этом проще всего убедиться, если воспользоваться условием  . При этом получится, что
. При этом получится, что

и, следовательно,  при
при  . В результате доминирующим членом в
. В результате доминирующим членом в  является
является  где
где  а величина
а величина  определяет ширину
определяет ширину  -гиперона относительно распада
-гиперона относительно распада  (Полным электромагнитным аналогом распада
(Полным электромагнитным аналогом распада  является распад
является распад  ) Поскольку
) Поскольку  то величина
то величина  мала и вклад
мала и вклад  в полную вероятность распадов
в полную вероятность распадов
 пренебрежимо мал. Что касается аксиального матричного элемента
пренебрежимо мал. Что касается аксиального матричного элемента  то в нем
то в нем  и вероятность распадов
и вероятность распадов  определяется величиной
определяется величиной  которая для обоих распадов одна и та же. Поскольку
которая для обоих распадов одна и та же. Поскольку  МэВ, а
МэВ, а 

Экспериментальные данные согласуются с этим числом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
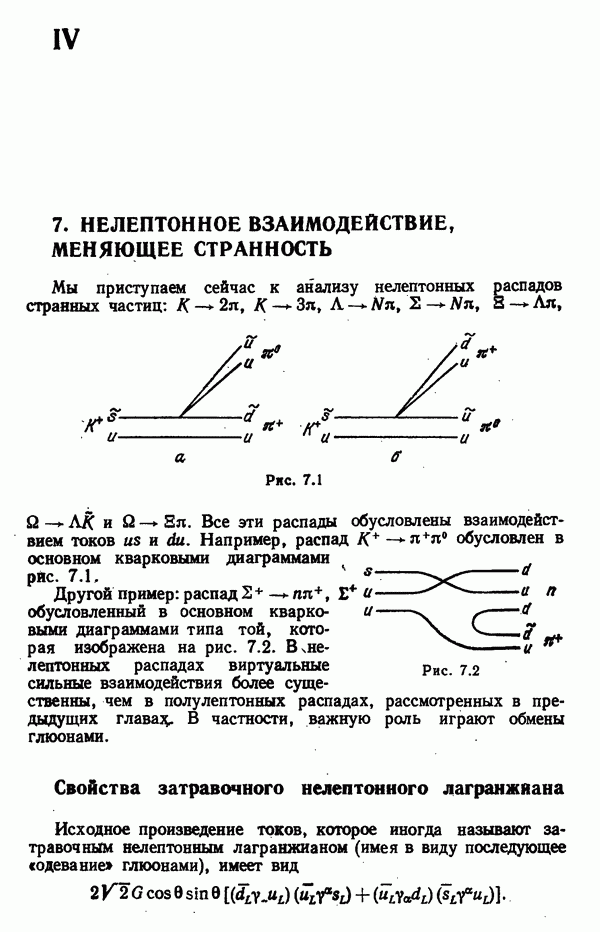
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
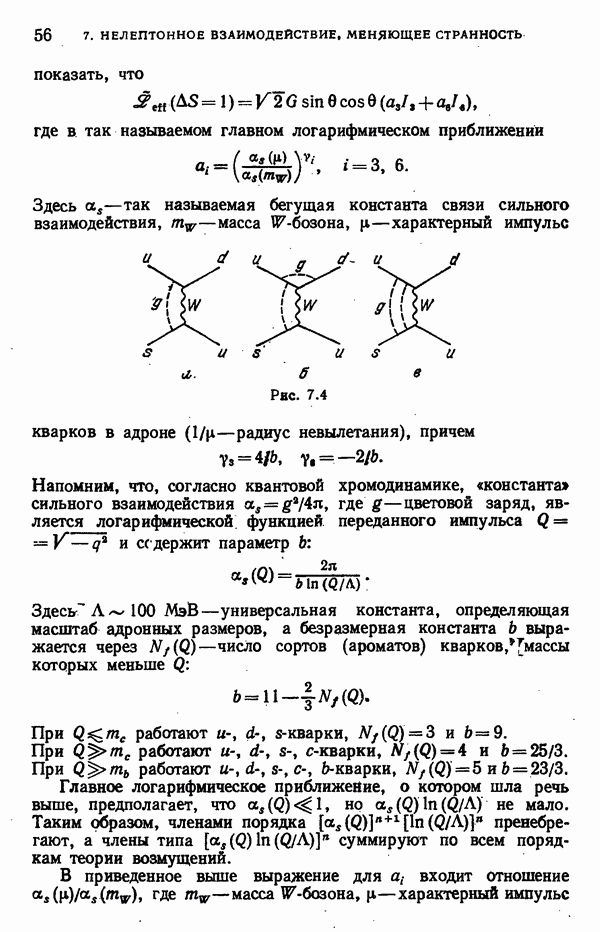
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
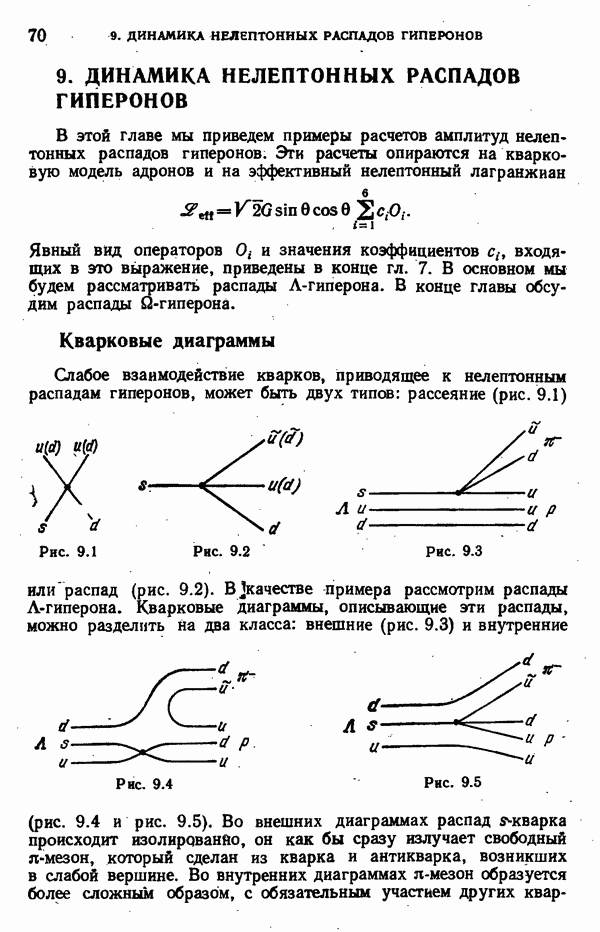
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
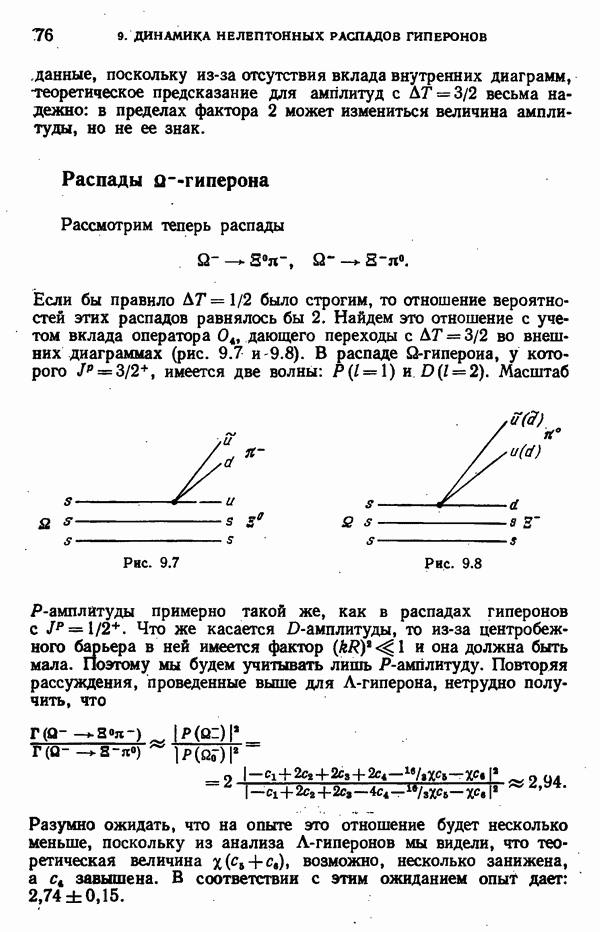
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
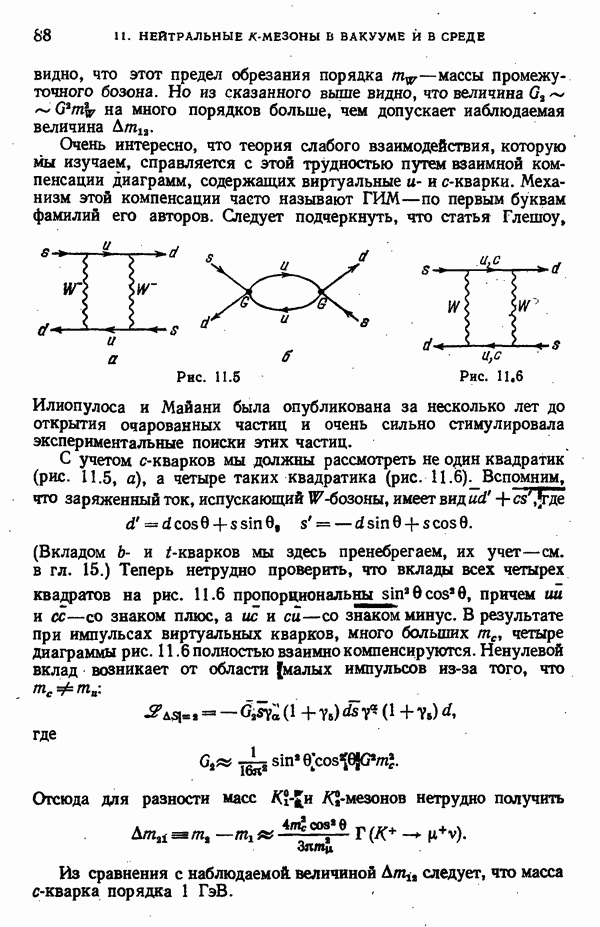
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
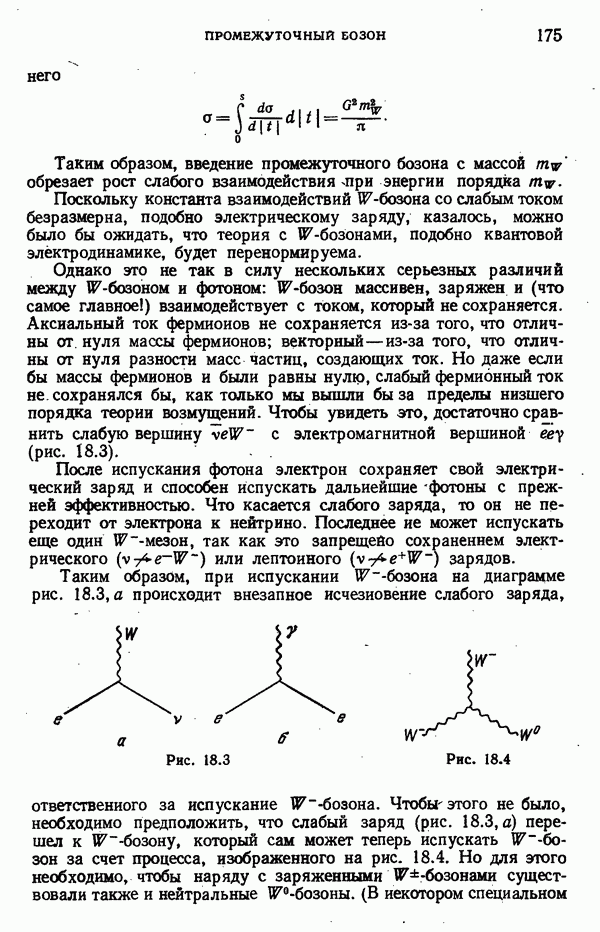
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
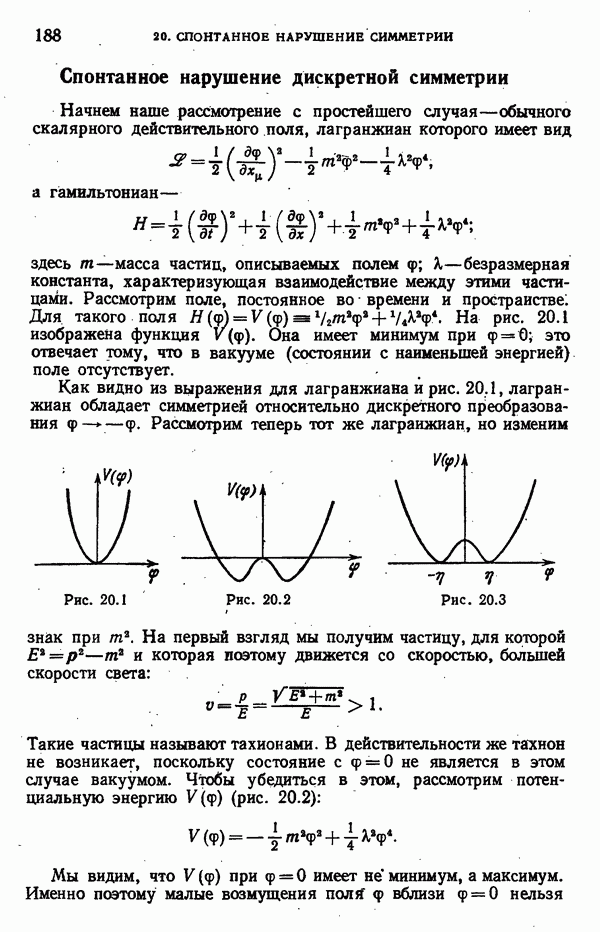
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
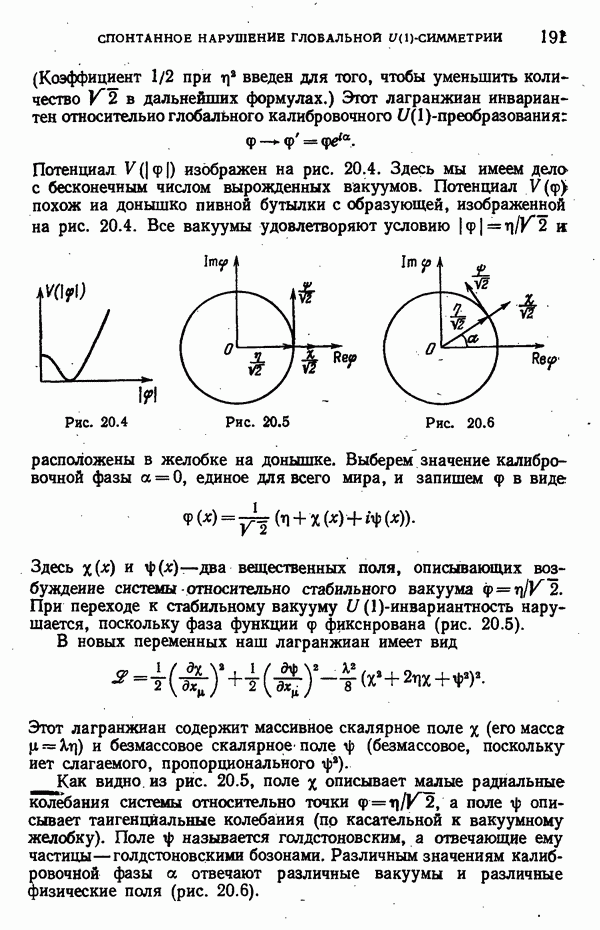
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
- «Бегущие» константы связи
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей