| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Группы
2.1. Некоторые определения. Группой  называется множество элементов, в котором определены операция ассоциативного умножения, единичный элемент и каждому элементу отвечает обратный элемент. Если все элементы коммутируют между собой, то группа называется абелевой. Представлением
называется множество элементов, в котором определены операция ассоциативного умножения, единичный элемент и каждому элементу отвечает обратный элемент. Если все элементы коммутируют между собой, то группа называется абелевой. Представлением  группы 3 называется группа линейных преобразований (матриц) в некотором линейном пространстве (базисе представления, мультиплете), элементы которой находятся в однозначном соответствии с элементами группы
группы 3 называется группа линейных преобразований (матриц) в некотором линейном пространстве (базисе представления, мультиплете), элементы которой находятся в однозначном соответствии с элементами группы  Группы, элементы которых аналитически зависят от конечного числа параметров, называются группами Ли. Число независимых параметров называется размерностью группы. Генераторами для данного представления называются операторы
Группы, элементы которых аналитически зависят от конечного числа параметров, называются группами Ли. Число независимых параметров называется размерностью группы. Генераторами для данного представления называются операторы  с помощью которых осуществляются преобразования, сколь угодно близкие к единичным:
с помощью которых осуществляются преобразования, сколь угодно близкие к единичным:  Максимальное число коммутирующих между собой операторов называется рангом группы. Число линейно независимых векторов в базисе (число компонент мультиплета) называется размерностью представления (размерность представления равна порядку матриц, его реализующих). Если при некотором выборе базиса представление разбивается на сумму независимых подгрупп, то оно называется приводимым; если этого нельзя достичь никаким выбором базиса, то неприводимым. Фундаментальным называются представления, из которых с помощью перемножения можно построить все остальные представления группы. Размерность регулярного (присоединенного) представления равна порядку группы.
Максимальное число коммутирующих между собой операторов называется рангом группы. Число линейно независимых векторов в базисе (число компонент мультиплета) называется размерностью представления (размерность представления равна порядку матриц, его реализующих). Если при некотором выборе базиса представление разбивается на сумму независимых подгрупп, то оно называется приводимым; если этого нельзя достичь никаким выбором базиса, то неприводимым. Фундаментальным называются представления, из которых с помощью перемножения можно построить все остальные представления группы. Размерность регулярного (присоединенного) представления равна порядку группы.
2.2. Группы  .
.  (
( -группа комплексных матриц
-группа комплексных матриц  удовлетворяющих условию унитарности
удовлетворяющих условию унитарности  и унимодулярности
и унимодулярности  фундаментальным мультиплегом которой является
фундаментальным мультиплегом которой является  -компонентный спинор, а фундаментальным представлением матрицы
-компонентный спинор, а фундаментальным представлением матрицы  порядка.
порядка.
2.3. Группа  Фундаментальным представлением группы
Фундаментальным представлением группы  являются матрицы
являются матрицы

где  - матрицы Паули, а
- матрицы Паули, а  - три реальных параметра. Обозначение а; используется при описании спина частиц (при описании изоспина обычно эти же матрицы обозначают
- три реальных параметра. Обозначение а; используется при описании спина частиц (при описании изоспина обычно эти же матрицы обозначают  Матрицы Паули удовлетворяют коммутационным соотношениям:
Матрицы Паули удовлетворяют коммутационным соотношениям:

где  полностью антисимметричный единичный тензор. Компоненты этого тензора являются структурными константами группы
полностью антисимметричный единичный тензор. Компоненты этого тензора являются структурными константами группы  Обычно матрицы Паули выбирают в виде
Обычно матрицы Паули выбирают в виде

Матрицы Паули удовлетворяют условию

След матрицы 

Произвольное представление группы  имеет три генератора, удовлетворяющих условию
имеет три генератора, удовлетворяющих условию

Для регулярного (трехмерного) представления

Очевидно, что ненулевые матричные элементы этих генераторов могут быть записаны в виде

где а — номер столбца,  - номер строки.
- номер строки.
2.4. Тождества Фирца для матриц 

где  . Эти соотношения легко проверить, умножив оба равенства на
. Эти соотношения легко проверить, умножив оба равенства на  и на
и на  Из этих равенств следует, что
Из этих равенств следует, что

Действуя на произведения спиноров  первое из этих выражений дает состояние со спином 1, а второе — со спином 0. Это согласуется с тем, что оператор, зануляющий состояние со спином
первое из этих выражений дает состояние со спином 1, а второе — со спином 0. Это согласуется с тем, что оператор, зануляющий состояние со спином  имеет вид
имеет вид

2.5. Группа  Фундаментальным представлением группы
Фундаментальным представлением группы  являются матрицы
являются матрицы

где  -матрицы Гелл-Манна, а
-матрицы Гелл-Манна, а  - восемь реальных параметров. Обычно матрицы
- восемь реальных параметров. Обычно матрицы  выбирают в виде
выбирают в виде

Матрицы  , удовлетворяют следующим соотношениям:
, удовлетворяют следующим соотношениям:

Здесь  - структурные константы группы
- структурные константы группы  симметричны,
симметричны,  антисимметричны относительно перестановок любой пары индексов. Прямым вычислением легко найти 54 ненулевые константы
антисимметричны относительно перестановок любой пары индексов. Прямым вычислением легко найти 54 ненулевые константы  и 58 ненулевых констант
и 58 ненулевых констант 

 где
где  - число перестановок индексов
- число перестановок индексов  Заметим, что
Заметим, что  если среди
если среди  нечетное число раз встречаются индексы 2, 5, 7. Напротив,
нечетное число раз встречаются индексы 2, 5, 7. Напротив,  если индексы 2, 5, 7 встречаются четное число раз. Эта выделенность индексов 2, 5, 7 связана с тем, что соответствующие матрицы X антисимметричны.
если индексы 2, 5, 7 встречаются четное число раз. Эта выделенность индексов 2, 5, 7 связана с тем, что соответствующие матрицы X антисимметричны.
2.6. Тождества Фирца для матриц X. Пользуясь полнотой девяти трехрядных матриц  запишем, введя неопределенные коэффициенты:
запишем, введя неопределенные коэффициенты:

где  Умножив оба равенства на
Умножив оба равенства на  получим
получим

Умножив их же на  получим
получим

откуда следует

Теперь нетрудно найти, что

Действуя на произведение двух триплетных спиноров, первое из этих выражений отбирает состояние 6, а второе — (напомним, что 
2.7.  -мультиплеты. Контравариантный трехкомпонентный спинор
-мультиплеты. Контравариантный трехкомпонентный спинор  преобразуется матрицами
преобразуется матрицами  мы будем обозначать его 3. Ковариантный спинор
мы будем обозначать его 3. Ковариантный спинор  преобразуется по комплексно-сопряженному представлению:
преобразуется по комплексно-сопряженному представлению:  мы будем обозначать его 3. Пользуясь инвариантными тензорами
мы будем обозначать его 3. Пользуясь инвариантными тензорами  можно построить из 3 и 3 представления более высоких размерностей:
можно построить из 3 и 3 представления более высоких размерностей:

Произвольный тензор может быть записан в виде

где отдельно по всем верхним и по нижним индексам проведена симметризация, и след по любой паре равен нулю. Нетрудно найти  -полное число компонент мультиплета
-полное число компонент мультиплета 

Примеры физических  -мультиплетов:
-мультиплетов:
 - триплет кварков,
- триплет кварков,
 - (анти)триплет - антикварков,
- (анти)триплет - антикварков,
 — октет псевдоскалярных мезонов,
— октет псевдоскалярных мезонов,
 - октет барионов.
- октет барионов.
Выделяя изотопическую подгруппу  группы
группы  удобно изображать частицы мультиплета на так называемых
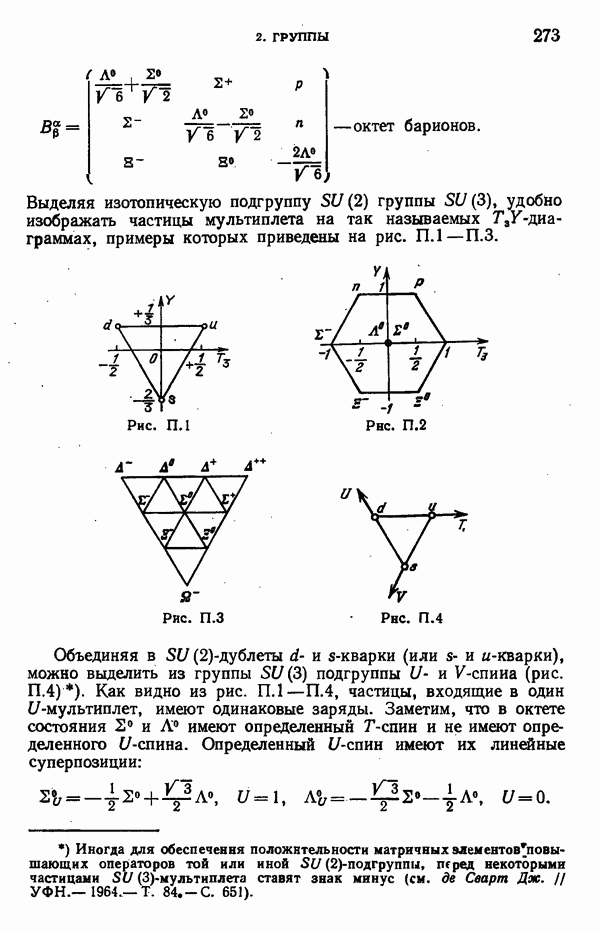
удобно изображать частицы мультиплета на так называемых  -диа-граммах, примеры которых приведены на рис. П.1-П.3.
-диа-граммах, примеры которых приведены на рис. П.1-П.3.

Рис. П.1

Рис. П.2

Рис. П.3

Рис. П.4
Объединяя в  -дублеты
-дублеты  и
и  -кварки (или
-кварки (или  и и-кварки), можно выделить из группы
и и-кварки), можно выделить из группы  подгруппы
подгруппы  и
и  -спина (рис. П.4). Как видно из рис. П.1-П.4, частицы, входящие в один (
-спина (рис. П.4). Как видно из рис. П.1-П.4, частицы, входящие в один ( -мультиплет, имеют одинаковые заряды. Заметим, что в октете состояния
-мультиплет, имеют одинаковые заряды. Заметим, что в октете состояния  имеют определенный Г-спин и не имеют определенного
имеют определенный Г-спин и не имеют определенного  -спина. Определенный
-спина. Определенный  -спин имеют их линейные суперпозиции:
-спин имеют их линейные суперпозиции:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
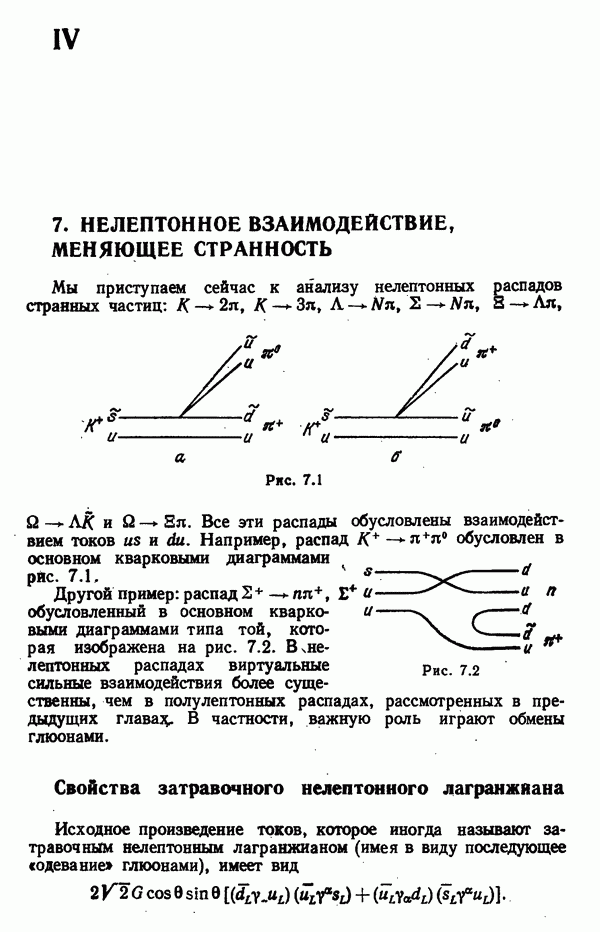
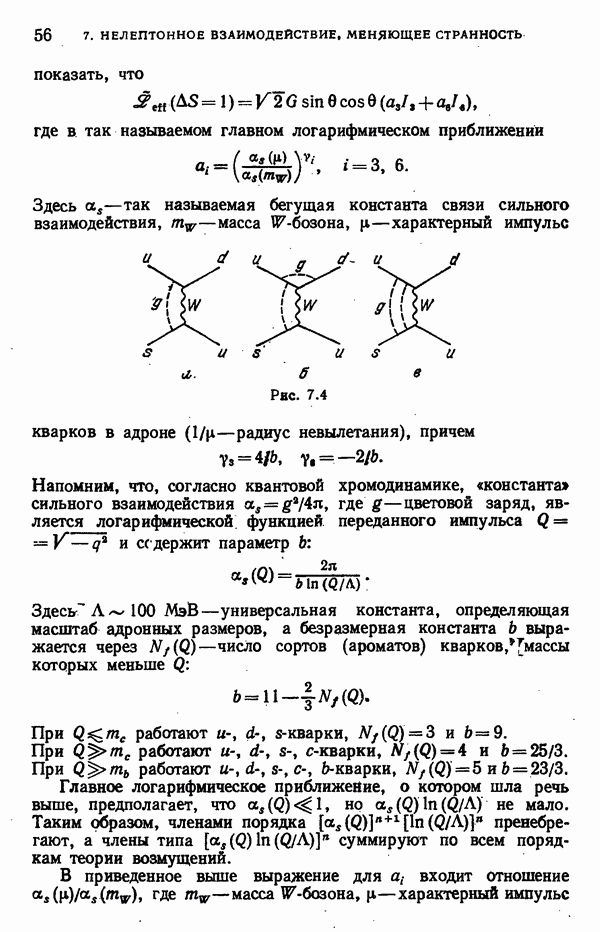
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
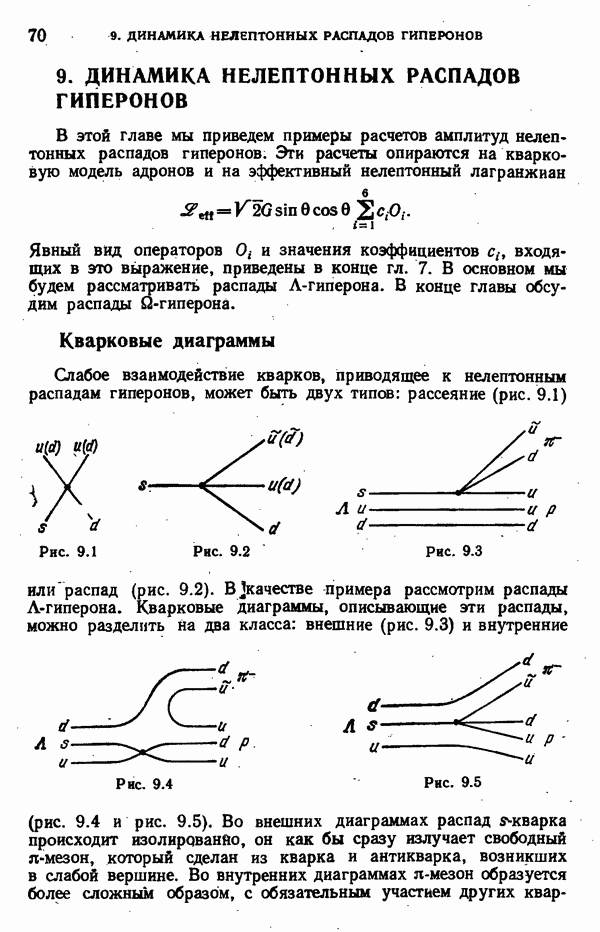
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
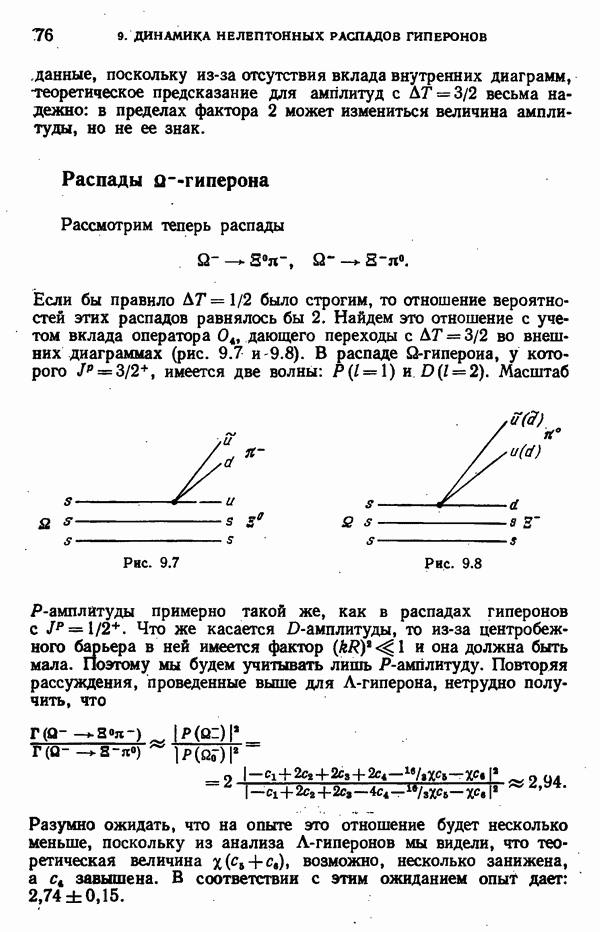
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
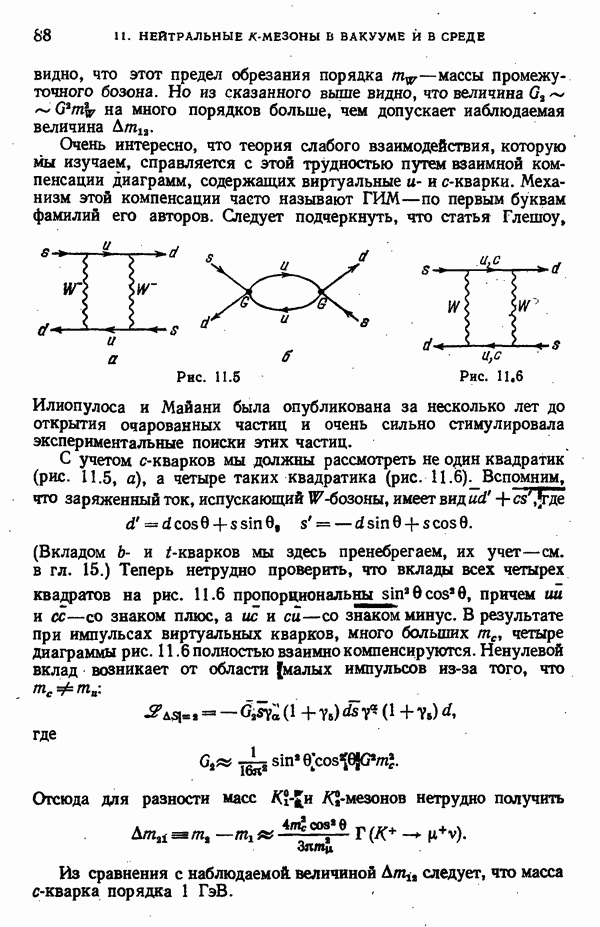
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
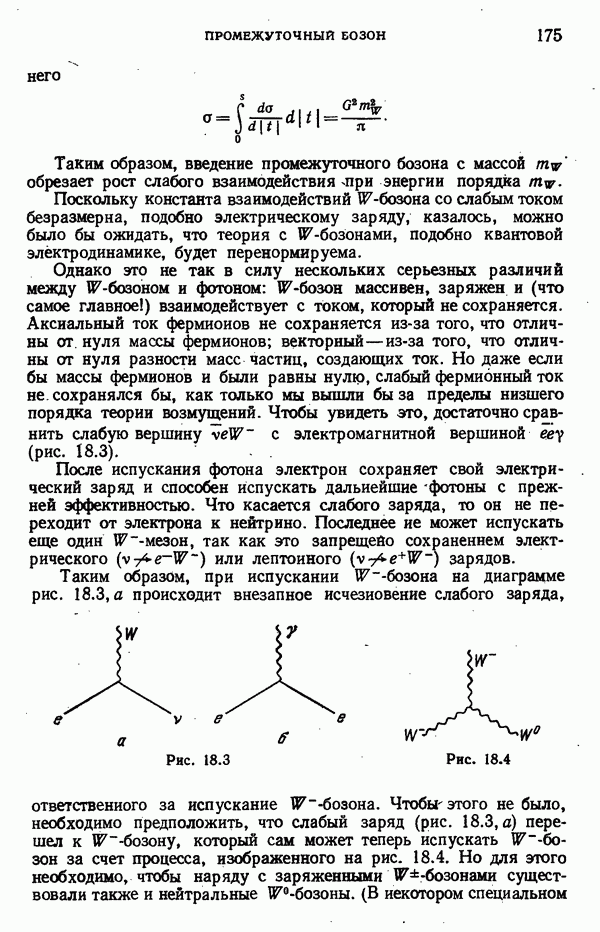
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
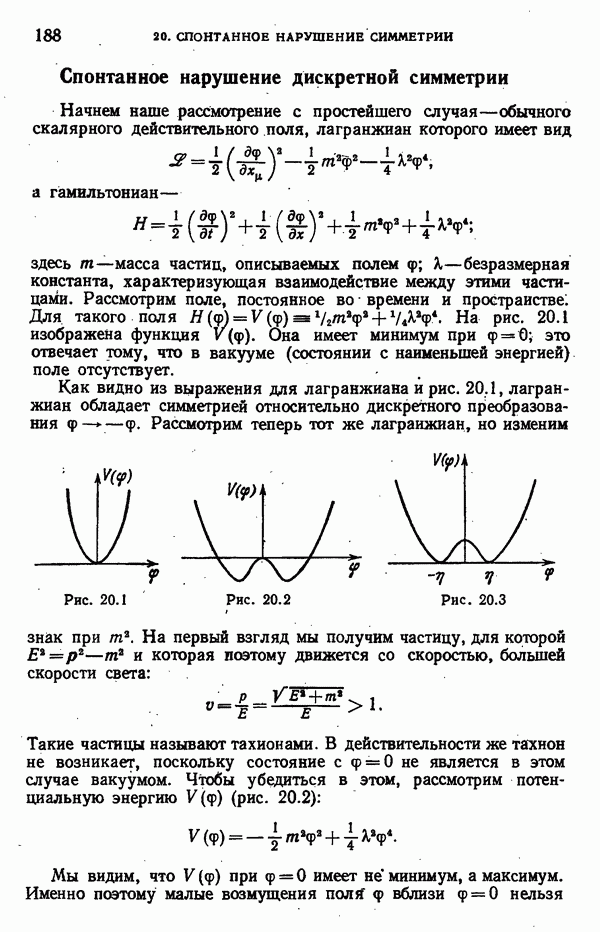
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
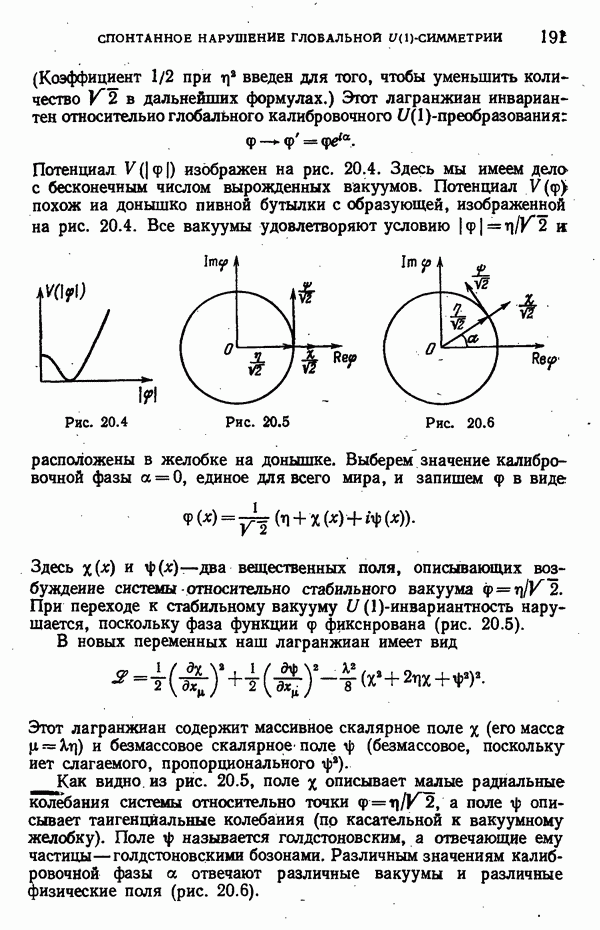
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
- «Бегущие» константы связи
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей