| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
О сохранении электрического заряда
То обстоятельство, что в рассмотренном выше примере заряженное скалярное поле  приобрело отличное от нуля вакуумное среднее, означает, что в этом примере нарушено сохранение электрического заряда. Чтобы более наглядно это продемонстрировать, предположим, что имеется взаимодействие поля
приобрело отличное от нуля вакуумное среднее, означает, что в этом примере нарушено сохранение электрического заряда. Чтобы более наглядно это продемонстрировать, предположим, что имеется взаимодействие поля  с лептонами —
с лептонами —
электроном и нейтрино:

В результате спонтанного нарушения симметрии этот член породит «недиагональную массу»  переводящую электрон в нейтрино:
переводящую электрон в нейтрино:  и нарушающее сохранение электрического заряда взаимодействие
и нарушающее сохранение электрического заряда взаимодействие  (Напомним, что поле
(Напомним, что поле  нейтрально.)
нейтрально.)
Как отмечалось выше, несохранение заряда сопровождается появлением у фотона ненулевой массы:  Что касается скалярного поля, то его масса
Что касается скалярного поля, то его масса  не может быть существенно больше, чем масса фотона. Дело в том, что если мы хотим, чтобы написанный нами лагранжиан имел физический смысл, то константа
не может быть существенно больше, чем масса фотона. Дело в том, что если мы хотим, чтобы написанный нами лагранжиан имел физический смысл, то константа  не должна превышать единицу (в противном случае простейшая диаграмма, описывающая рассеяние
не должна превышать единицу (в противном случае простейшая диаграмма, описывающая рассеяние  противоречит унитарности). Это ограничение на
противоречит унитарности). Это ограничение на  означает, что и, следовательно,
означает, что и, следовательно,  (напомним, что
(напомним, что  Итак, мы построили теорию, в которой массивное векторное поле (фотонное?) взаимодействует с несохраняющимся током (электрическим?) Можно показать, что теория эта перенормируема, что она обладает разумным поведением при асимптотически высоких энергиях, в отличие от теорий, в которых масса векторного поля изначально присутствует в лагранжиане.
Итак, мы построили теорию, в которой массивное векторное поле (фотонное?) взаимодействует с несохраняющимся током (электрическим?) Можно показать, что теория эта перенормируема, что она обладает разумным поведением при асимптотически высоких энергиях, в отличие от теорий, в которых масса векторного поля изначально присутствует в лагранжиане.
Прямое добавление к лагранжиану массового члёиа называют жестким введением массы. Появление массы за счет спонтанного нарушения симметрии называют мягким введением массы. При жестком введении массы теория неперенормируема, при мягком — перенормируема. Объяснение перенормируемости в том, что при высоких энергиях членом  в гамильтониане можно пренебречь. На другом языке это же выражается в том, что опасные члены, связанные с продольными степенями массивного векторного поля, компенсируются вкладом хиггсовых бозонов (см. гл. 24).
в гамильтониане можно пренебречь. На другом языке это же выражается в том, что опасные члены, связанные с продольными степенями массивного векторного поля, компенсируются вкладом хиггсовых бозонов (см. гл. 24).
На опыте сохранение электрического заряда проверено с гораздо худшей точностью, чем сохранение барионного заряда: нижняя граница времени жизни электрона по отношению к распадам типа  — лгу порядка
— лгу порядка  лет, в то время как нижняя граница времени жизни протона по отношению к распадам типа
лет, в то время как нижняя граница времени жизни протона по отношению к распадам типа  порядка
порядка  лет. Естественно задать вопрос: какое ограничение на величину константы
лет. Естественно задать вопрос: какое ограничение на величину константы  во взаимодействии
во взаимодействии  налагает то обстоятельство, что
налагает то обстоятельство, что  лет? Ответ на этот вопрос оказывается неожиданным. А именно, оказывается, что теория спонтанного нарушения локальной
лет? Ответ на этот вопрос оказывается неожиданным. А именно, оказывается, что теория спонтанного нарушения локальной 
 -симметрии, рассматриваемая в этом и предыдущем разделах, вообще не может служить реалистической моделью несохранения электрического заряда, не может быть навязана природе. Дело в том, что из существующей верхней границы
-симметрии, рассматриваемая в этом и предыдущем разделах, вообще не может служить реалистической моделью несохранения электрического заряда, не может быть навязана природе. Дело в том, что из существующей верхней границы
на массу фотона  следует, что величина
следует, что величина  также порядка
также порядка  и примерно такова же или еще меньше масса нейтрального хиггсова бозона
и примерно такова же или еще меньше масса нейтрального хиггсова бозона 
В земных условиях, даже работая с практически статическими полями, мы имеем дело с частотами, на много порядков превосходящими эти значения  . В этих условиях всеми этими величинами можно пренебречь, и, следовательно,
. В этих условиях всеми этими величинами можно пренебречь, и, следовательно,  -бозон и продольная компонента фотона испускаются когерентно в виде практически безмассовой заряженной скалярной частицы
-бозон и продольная компонента фотона испускаются когерентно в виде практически безмассовой заряженной скалярной частицы  (рис. 20.7). Но существование такой практически безмассовой заряженной частицы абсолютно исключено прекрасным согласием квантовой электродинамики с опытом. Ведь рождение пар таких частиц фотонами было бы самым ярким из всех электромагнитных эффектов.
(рис. 20.7). Но существование такой практически безмассовой заряженной частицы абсолютно исключено прекрасным согласием квантовой электродинамики с опытом. Ведь рождение пар таких частиц фотонами было бы самым ярким из всех электромагнитных эффектов.

Рис. 20.7
Итак, мягким образом нарушить сохранение электрического заряда не удается: этому препятствует практическая безмассовость фотона. В отличие от фотонов, промежуточные бозоны — очень тяжелые частицы, поэтому мягкое введение масс промежуточных бозонов вполне возможно. На пути к построению перенормируемой теории слабого взаимодействия нам осталось рассмотреть лишь спонтанное нарушение калибровочной неабелевой симметрии, при котором безмассовые неабелевы фотоны приобретут массу и превратятся в массивные промежуточные бозоны, не только нейтральные, но и заряженные.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
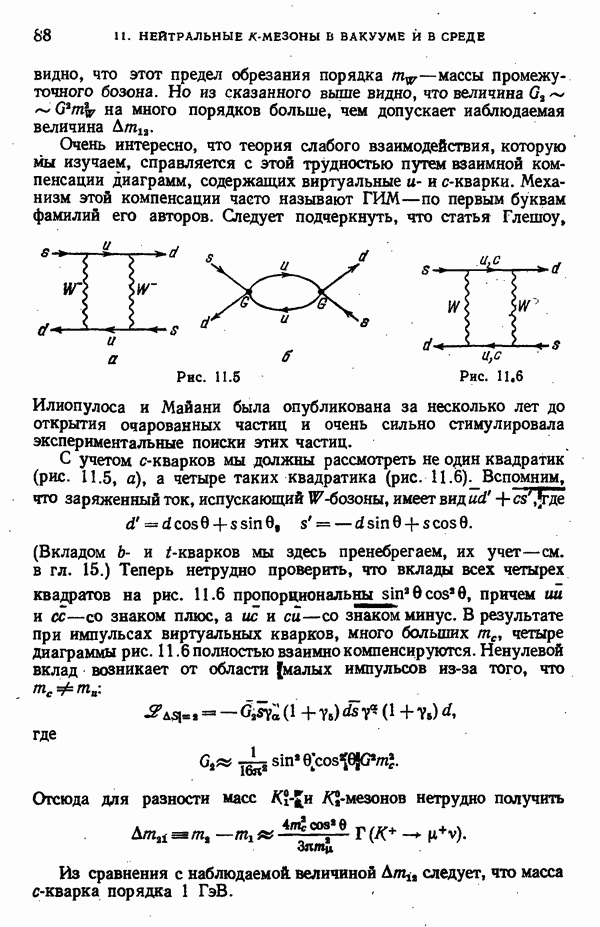
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
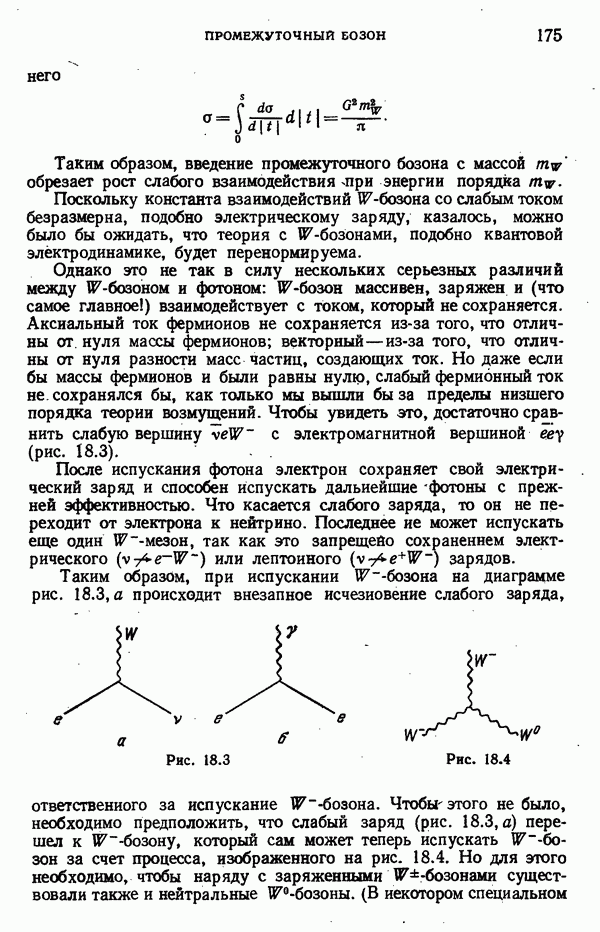
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
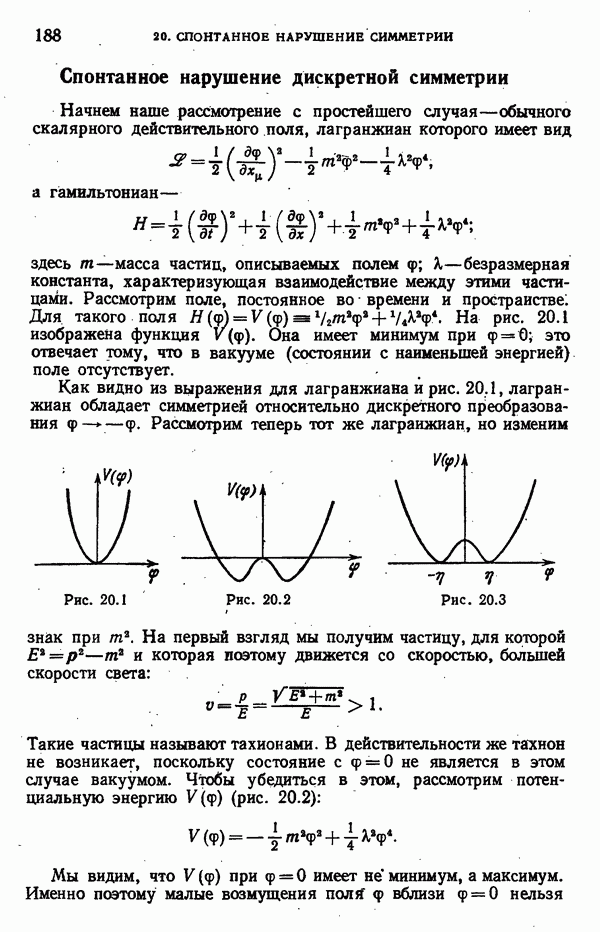
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
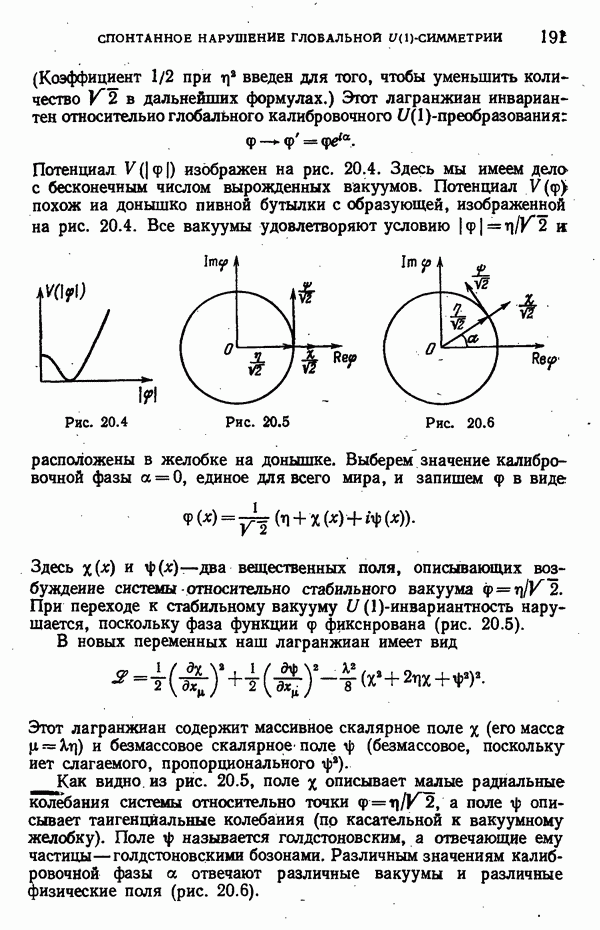
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
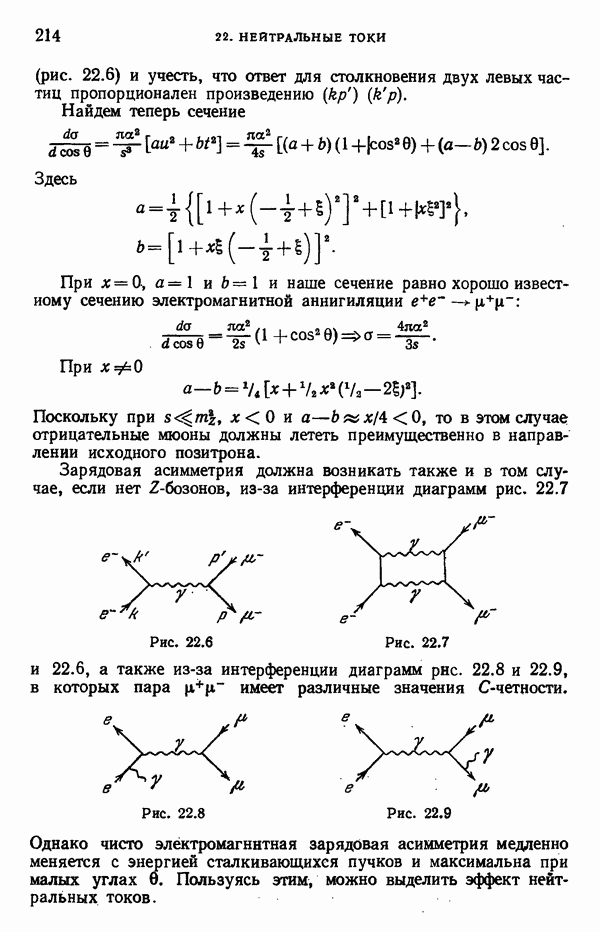
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
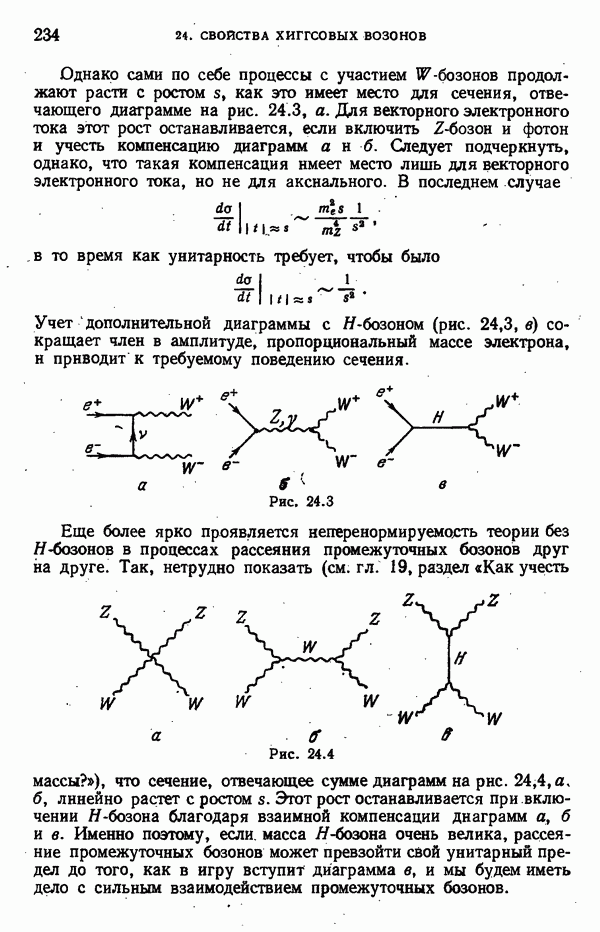
- Роль H-бозонов при высоких энергиях
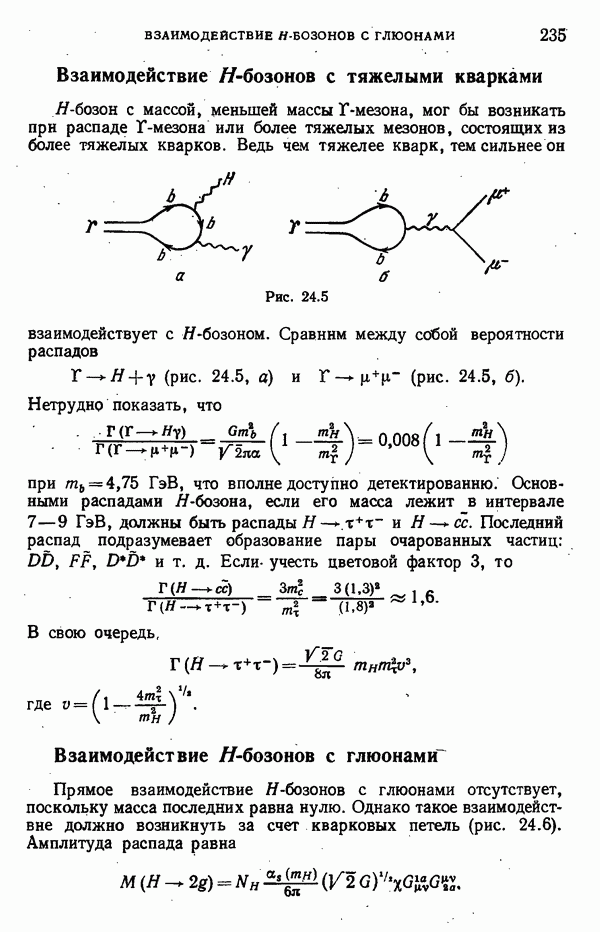
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
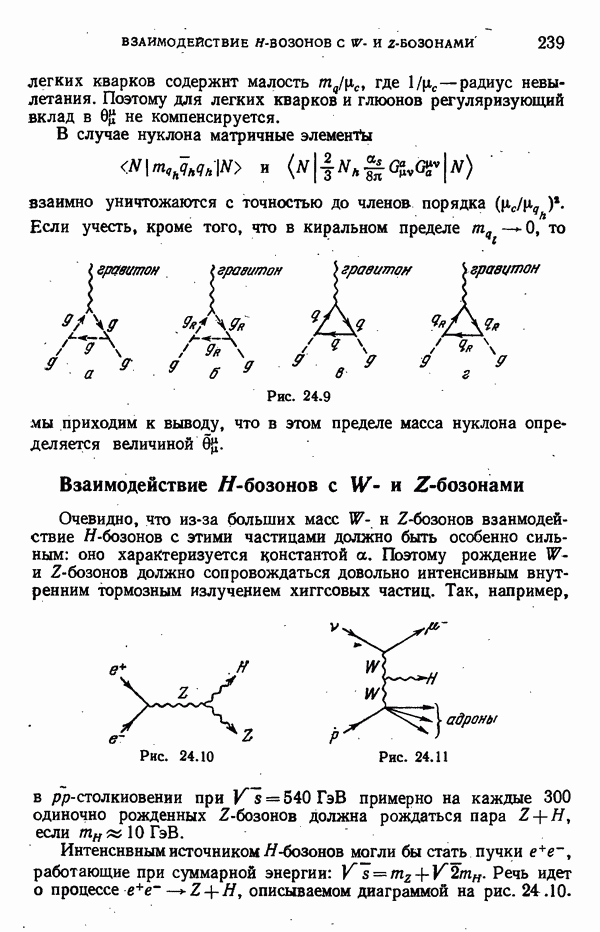
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
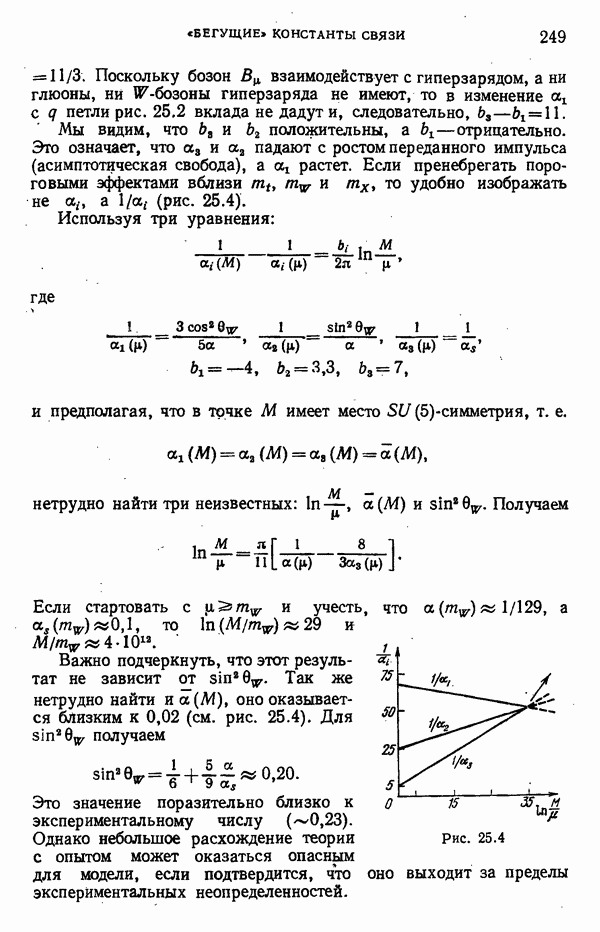
- «Бегущие» константы связи
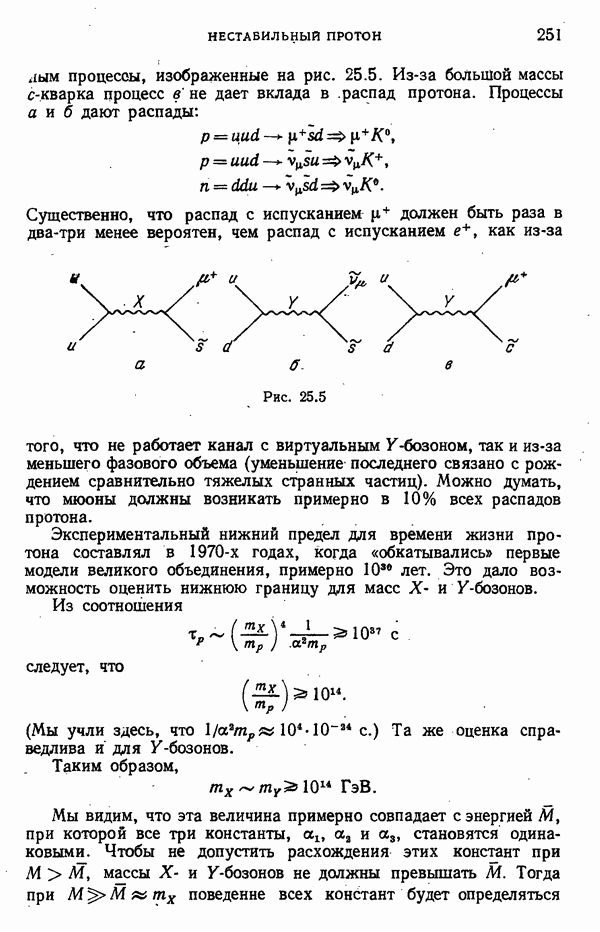
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
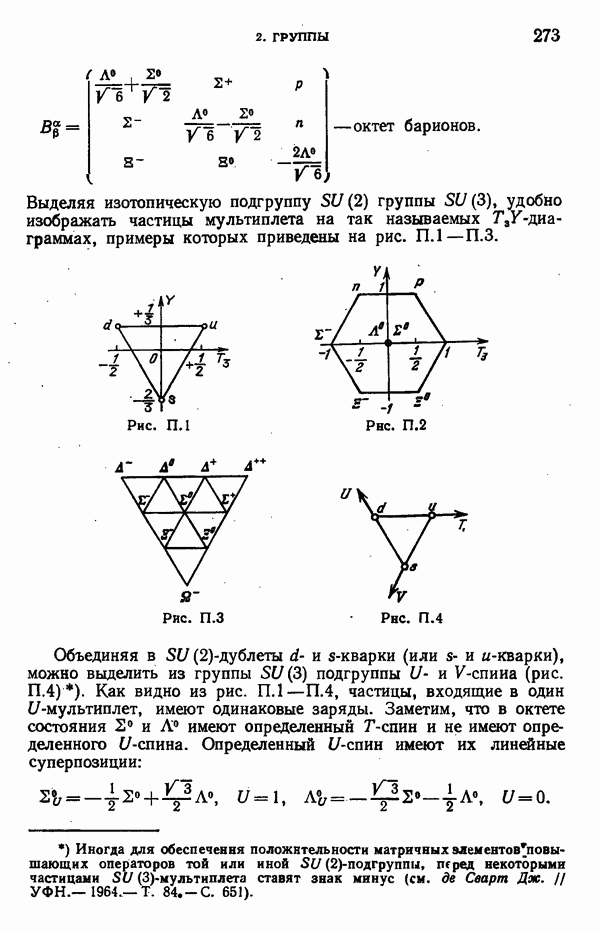
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей