| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
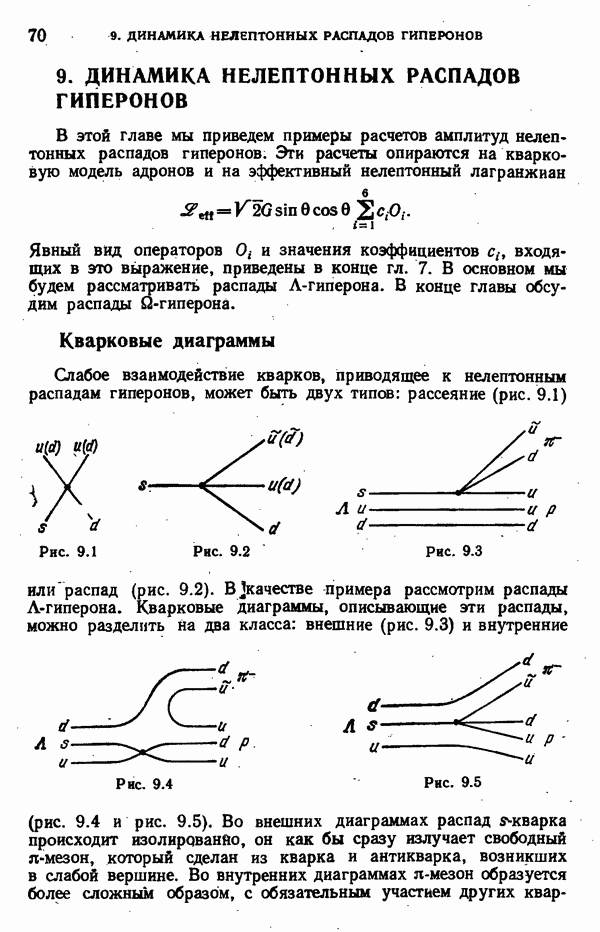
9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
В этой главе мы приведем примеры расчетов амплитуд нелептонных распадов гиперонов. Эти расчеты опираются на кварковую модель адронов и на эффективный нелептонный лагранжиан

Явный вид операторов  и значения коэффициентов
и значения коэффициентов  входящих в это выражение, приведены в конце гл. 7. В основном мы будем рассматривать распады
входящих в это выражение, приведены в конце гл. 7. В основном мы будем рассматривать распады  -гиперона. В конце главы обсудим распады
-гиперона. В конце главы обсудим распады  -гиперона.
-гиперона.
Кварковые диаграммы
Слабое взаимодействие кварков, приводящее к нелептонным распадам гиперонов, может быть двух типов: рассеяние (рис. 9.1) или распад (рис. 9.2).

Рис. 9.1

Рис. 9.2

Рис. 9.3
В качестве примера рассмотрим распады А-гиперона. Кварковые диаграммы, описывающие эти распады, можно разделить на два класса: внешние (рис. 9.3) и внутренние (рис. 9.4 и рис. 9.5).

Рис. 9.4

Рис. 9.5
Во внешних диаграммах распад шкварка происходит изолированно, он как бы сразу излучает свободный  -мезон, который сделан из кварка и антикварка, возникших в слабой вершине. Во внутренних диаграммах
-мезон, который сделан из кварка и антикварка, возникших в слабой вершине. Во внутренних диаграммах  -мезон образуется более сложным образом, с обязательным участием других
-мезон образуется более сложным образом, с обязательным участием других
кварков. Внутренние диаграммы более сложны, и мы пока что не умеем их рассчитывать. Однако легко видеть, что они обладают замечательным свойством: они дают переходы только с  . Возникновение такого запрета на переходы с
. Возникновение такого запрета на переходы с  легко понять, глядя как на упрощенный эффективный лагранжиан так и на полный эффективный лагранжиан (Вайнштейна, Захарова и Шифмана), с которым мы будем работать ниже. Напомним (см. гл. 7); что
легко понять, глядя как на упрощенный эффективный лагранжиан так и на полный эффективный лагранжиан (Вайнштейна, Захарова и Шифмана), с которым мы будем работать ниже. Напомним (см. гл. 7); что  состоит из трех слагаемых:
состоит из трех слагаемых:

Из трех слагаемых только  может давать переходы с
может давать переходы с  в то время как
в то время как  и
и  являются чистыми изотопическими спино рамн и, следовательно, дают переходы только с
являются чистыми изотопическими спино рамн и, следовательно, дают переходы только с  . Но именно
. Но именно  не может дать вклад во внешние диаграммы.
не может дать вклад во внешние диаграммы.
Дело в том, что оператор  симметризован по парам кварков. При рассеянии (рис. 9.1 и 9.4) симметризованы как начальные, так и конечные кварки; при распаде (рис. 9.2 и 9.5) симметризованы конечные кварки. В то же время в белом бар ионе любая пара кварков находится в антисимметричном по цвету состоянии, образуя антитриплет 3.
симметризован по парам кварков. При рассеянии (рис. 9.1 и 9.4) симметризованы как начальные, так и конечные кварки; при распаде (рис. 9.2 и 9.5) симметризованы конечные кварки. В то же время в белом бар ионе любая пара кварков находится в антисимметричном по цвету состоянии, образуя антитриплет 3.
Аналогичным образом, отсутствие переходов с  во внутренних диаграммах легко увидеть и в случае полного эффективного лагранжиана. Дело в том, что во внутренние диаграммы не дает вклада «симметричный» оператор
во внутренних диаграммах легко увидеть и в случае полного эффективного лагранжиана. Дело в том, что во внутренние диаграммы не дает вклада «симметричный» оператор  -единственный из шести операторов
-единственный из шести операторов  имеющий
имеющий  . (Заметим, что во внутренние диаграммы не дают также вклада «симметричные» операторы О, и
. (Заметим, что во внутренние диаграммы не дают также вклада «симметричные» операторы О, и  Доминирует в этих диаграммах
Доминирует в этих диаграммах  из-за большого коэффициента
из-за большого коэффициента 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
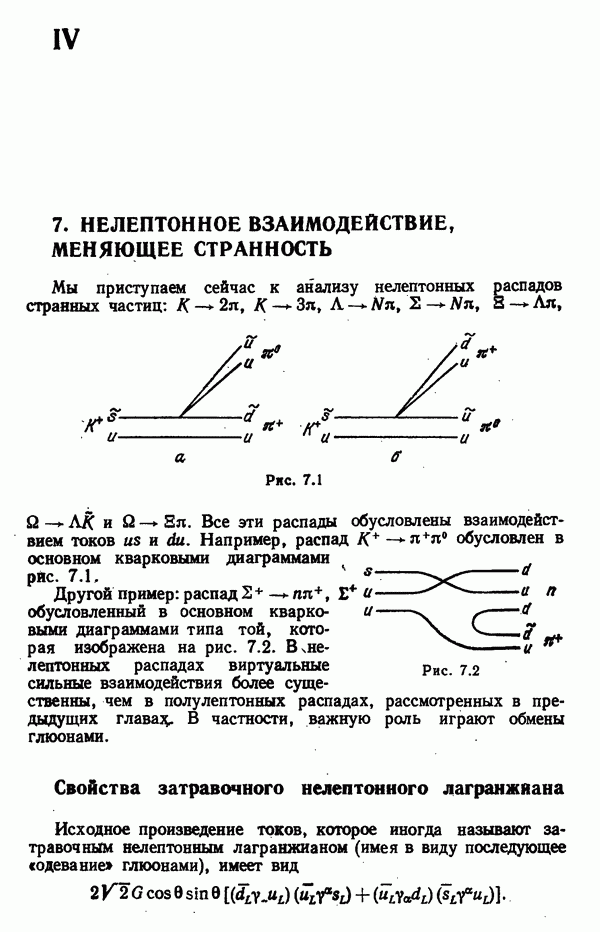
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
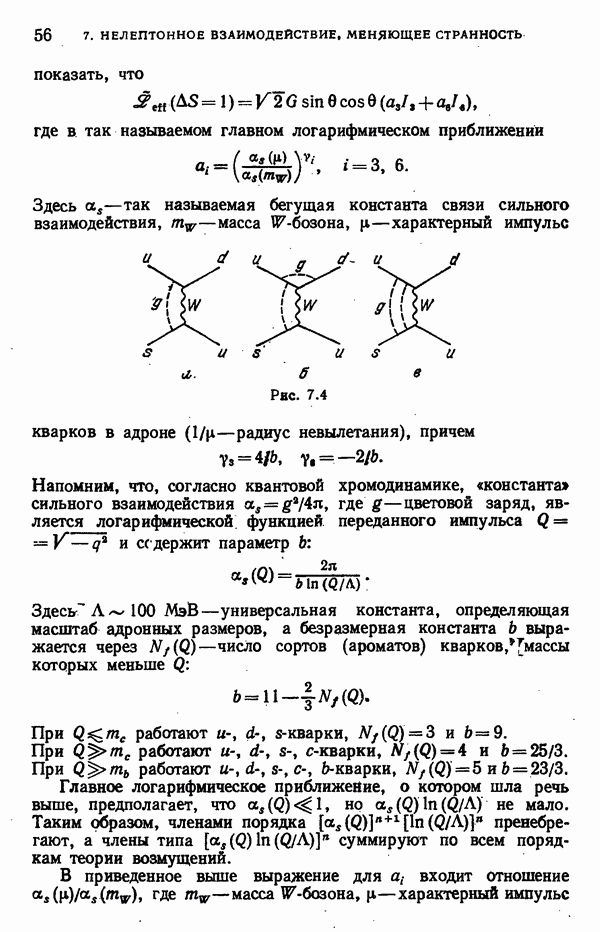
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
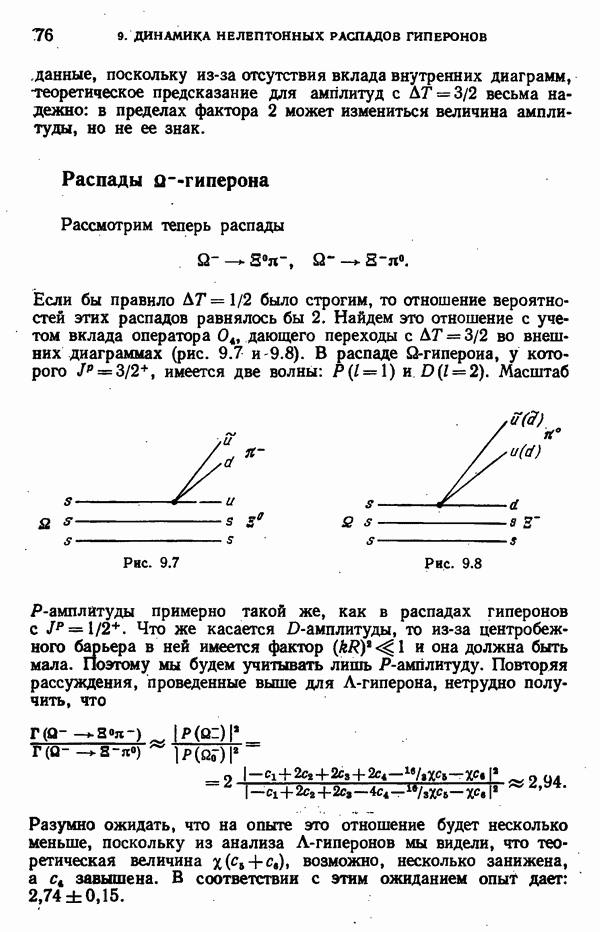
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
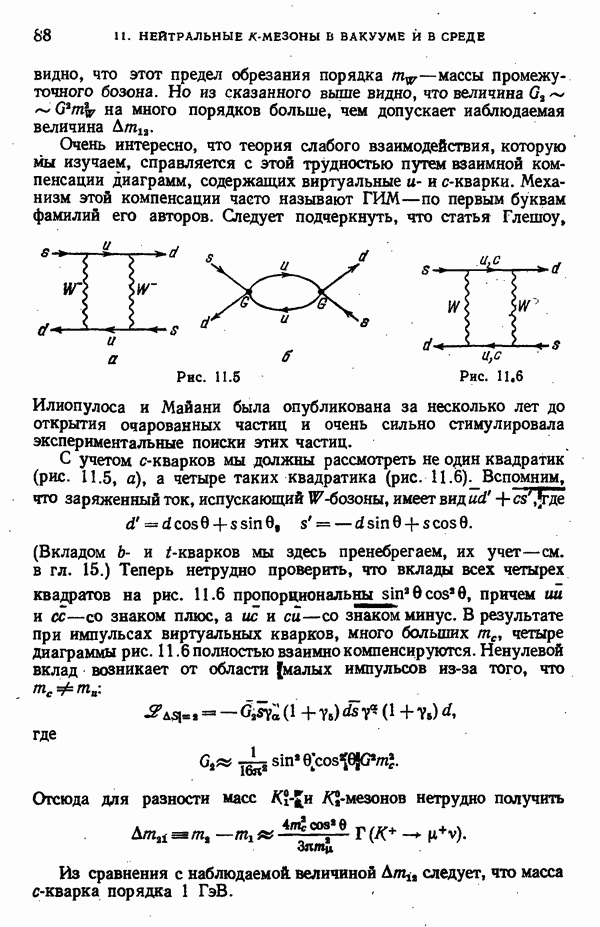
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
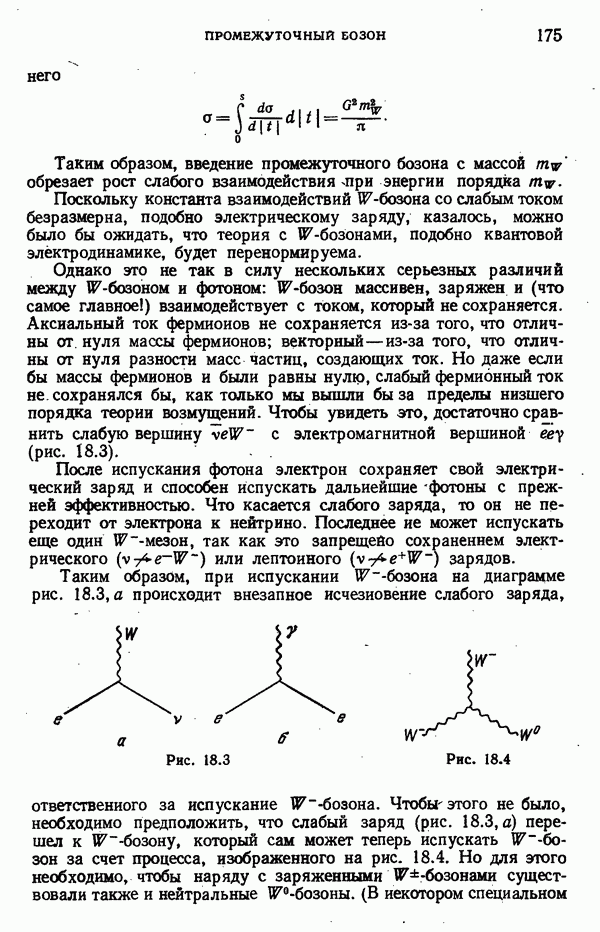
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
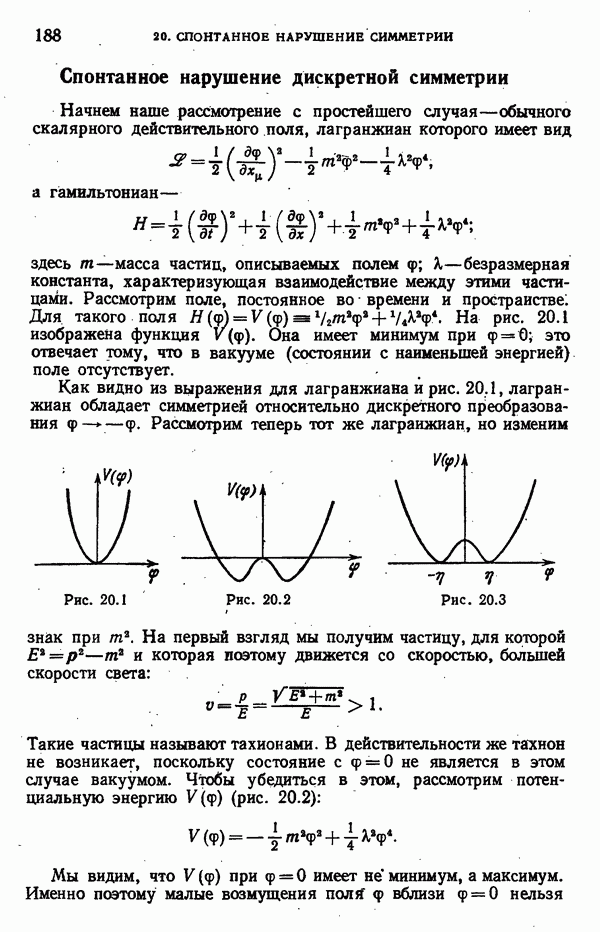
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
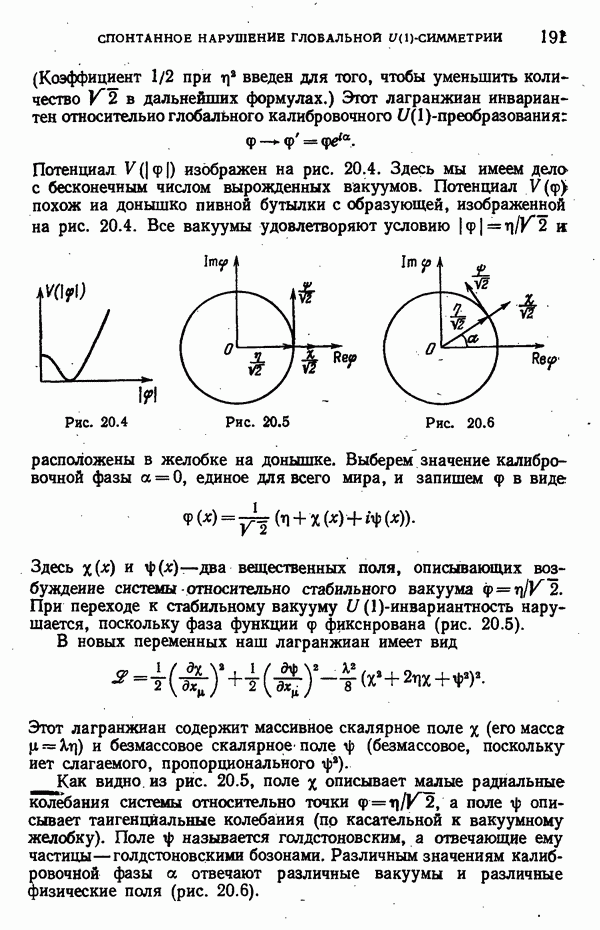
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
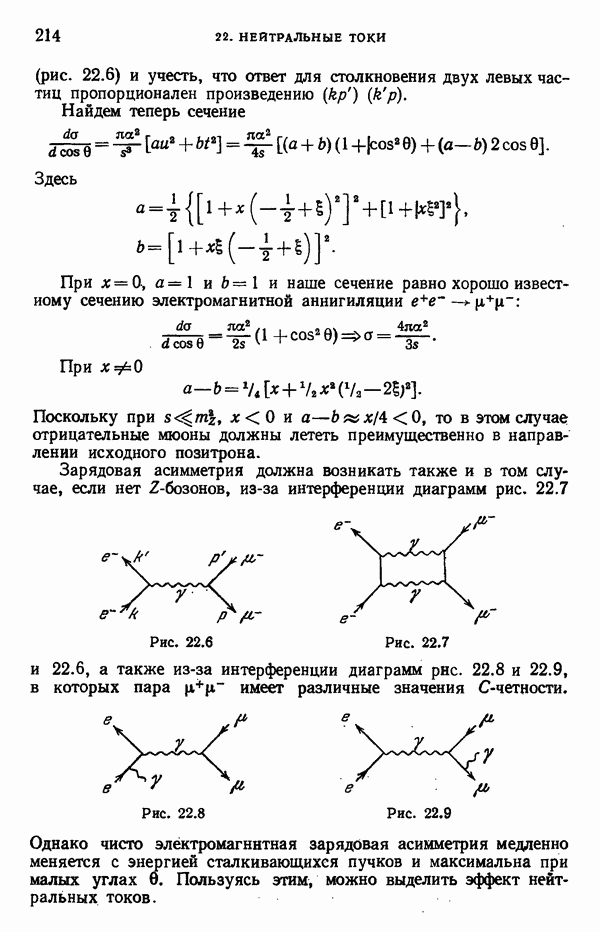
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
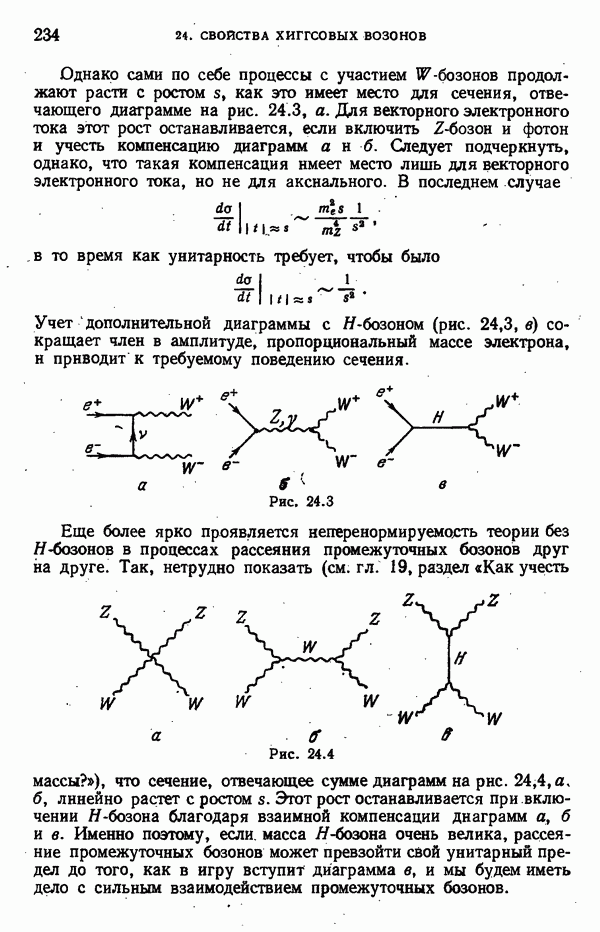
- Роль H-бозонов при высоких энергиях
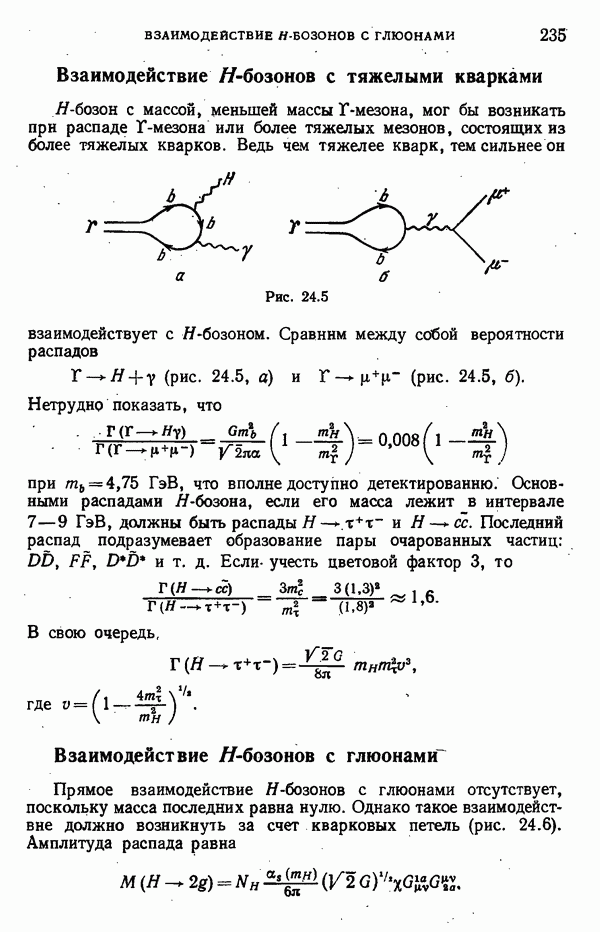
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
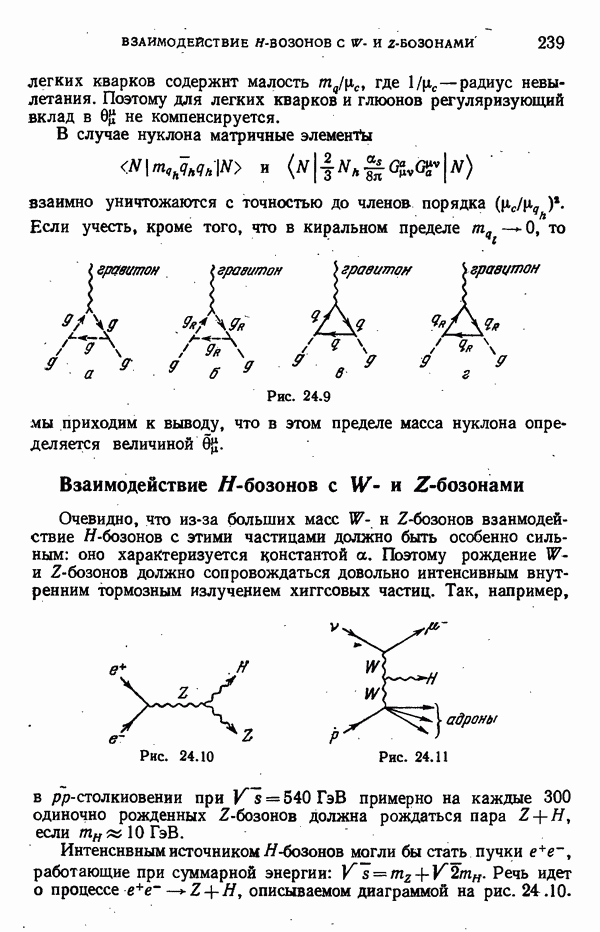
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
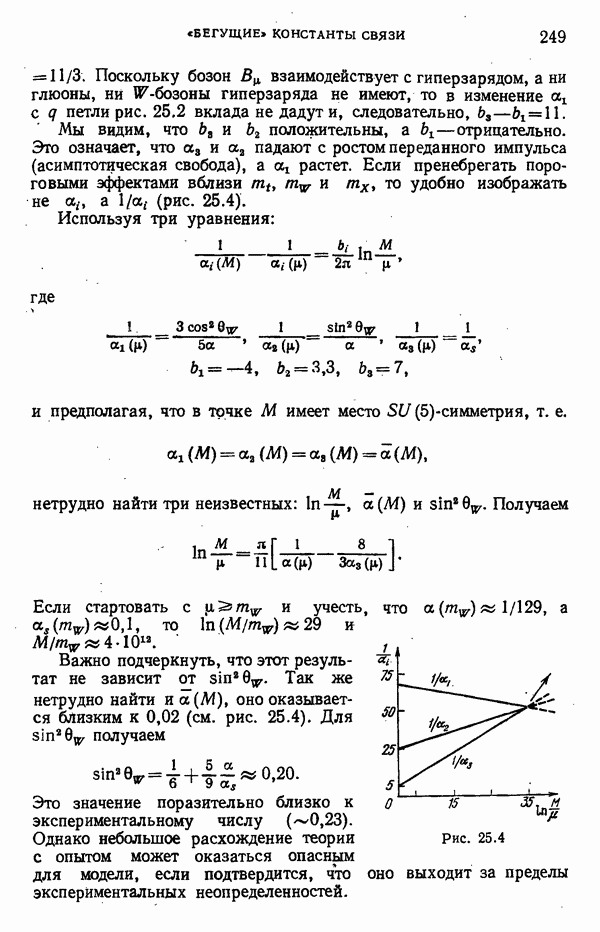
- «Бегущие» константы связи
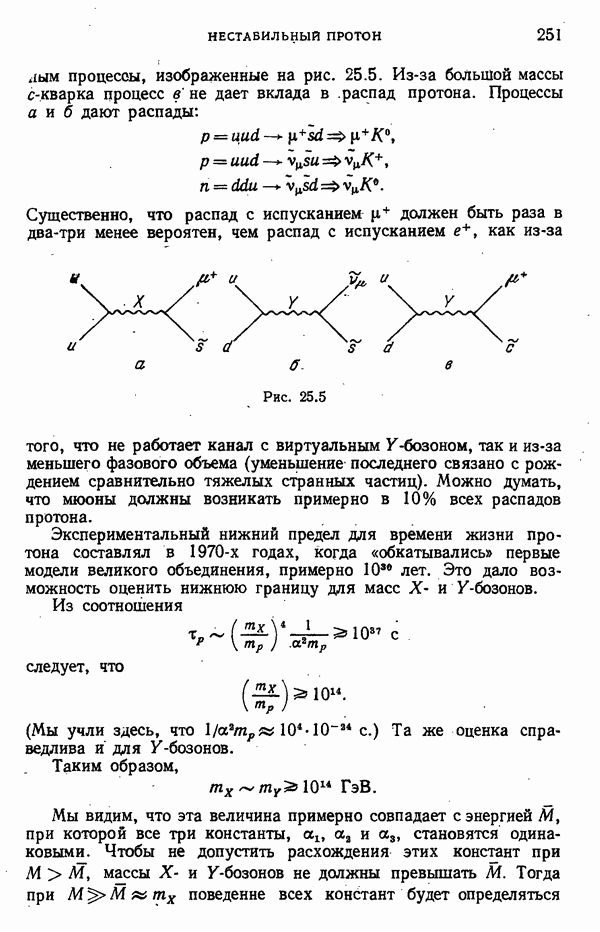
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
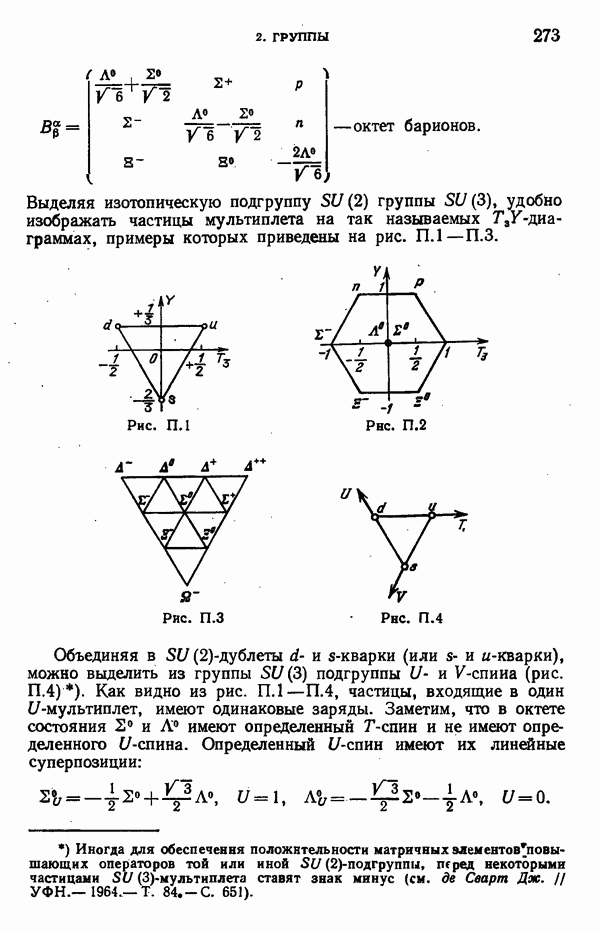
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей