| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Лептонные распады гиперонов
Получим соотношения между амплитудами лептонных распадов барионов, обусловленные  -симметрией сильного взаимодействия и тем обстоятельством, что токи
-симметрией сильного взаимодействия и тем обстоятельством, что токи  принадлежат одному октету токов. Рассмотрим октет барионов с
принадлежат одному октету токов. Рассмотрим октет барионов с  (см. гл. 28, п. 27):
(см. гл. 28, п. 27):

Здесь индекс  - номер строки,
- номер строки,  - номер столбца,
- номер столбца,  . След матрицы
. След матрицы  равен нулю:
равен нулю:  Мы будем изучать амплитуда
Мы будем изучать амплитуда

где нас будут интересовать токи

Ток  превращает
превращает  -кварк в
-кварк в  -кварк, ток
-кварк, ток  -кварк в
-кварк в  -кварк. В каждой из амплитуд нам надо перемножить три октета и получить скаляр. Учтем, что
-кварк. В каждой из амплитуд нам надо перемножить три октета и получить скаляр. Учтем, что  (см. гл. 28, п. 2.7) и что поэтому в произведении
(см. гл. 28, п. 2.7) и что поэтому в произведении  есть два различных скаляра: симметричный
есть два различных скаляра: симметричный  и антисимметричный
и антисимметричный  Запишем амплитуду в общем виде:
Запишем амплитуду в общем виде:

где  и
и  -скалярные параметры, различные, вообще говоря, для различных матричных элементов токов, т. е. для формфакторов
-скалярные параметры, различные, вообще говоря, для различных матричных элементов токов, т. е. для формфакторов  (см. гл. 5, где
(см. гл. 5, где  определены для
определены для  -распада нейтрона). Если начальные барионы описываются матрицей
-распада нейтрона). Если начальные барионы описываются матрицей  то конечные — описываются матрицей
то конечные — описываются матрицей  которая получается из
которая получается из  сопряжением каждого элемента и транспонированием. Умножение В на В удобно производить, не выписывая матрицу
сопряжением каждого элемента и транспонированием. Умножение В на В удобно производить, не выписывая матрицу
В, а глядя только на матрицу В. Выпишем матричные элементы тока 

Здесь выражение, пропорциональное  получено умноже нием первой строки матрицы В (с черточками над символами час
получено умноже нием первой строки матрицы В (с черточками над символами час  на вторую строку той же матрицы. (Это соответствует произведению поскольку первый столбец
на вторую строку той же матрицы. (Это соответствует произведению поскольку первый столбец  в матрице В получается транспонированием (и сопряжением) первой строки в матрице В.) Выражение, пропорциональное
в матрице В получается транспонированием (и сопряжением) первой строки в матрице В.) Выражение, пропорциональное  получено
получено
умножением второго столбца матрицы В (с черточками над символами частиц) на первый столбец той же матрицы. (Это соответствует произведению 
Аналогичным образом, выписав произведения первой строки на третью строку и третьего столбца на первый столбец, получим матричные элементы тока 

Глядя на полученные выражения, считываем с них шесть амплитуд для переходов с сохранением странности, и шесть амплитуд для переходов с изменением странности на единицу:

На опыте наблюдались три перехода с сохранением странности  и все переходы с изменением странности. (Распад
и все переходы с изменением странности. (Распад  наблюдать невозможно, так как он не может конкурировать с электромагнитным распадом
наблюдать невозможно, так как он не может конкурировать с электромагнитным распадом  но можно наблюдать реакцию
но можно наблюдать реакцию  имеющую тот же матричный элемент.)
имеющую тот же матричный элемент.)
Итак, двенадцать амплитуд выражаются через три параметра -  . Это относится к каждому из шести формфакторов, описывающих распад бариона:
. Это относится к каждому из шести формфакторов, описывающих распад бариона:  Основную роль в распадах барионов играют векторный формфактор
Основную роль в распадах барионов играют векторный формфактор  и аксиальный формфактор
и аксиальный формфактор  где
где  -импульс, уносимый лептонами. Поскольку где М — масса распадающегося бариона, то неплохим приближением является статический предел, и мы ограничимся рассмотрением векторного и аксиального зарядов:
-импульс, уносимый лептонами. Поскольку где М — масса распадающегося бариона, то неплохим приближением является статический предел, и мы ограничимся рассмотрением векторного и аксиального зарядов:  пренебрегая вкладом остальных формфакторов.
пренебрегая вкладом остальных формфакторов.
Обсудим теперь, чему должны равняться параметры  дающие
дающие  , и параметры
, и параметры  и
и  дающие
дающие  Поскольку векторные заряды
Поскольку векторные заряды  являются генераторами группы
являются генераторами группы
 то их матричные элементы между октетными состояниями
то их матричные элементы между октетными состояниями  и
и  равны структурным константам
равны структурным константам  группы
группы  (см. гл. 28, п. 2.5). В используемых нами обозначениях это означает, что
(см. гл. 28, п. 2.5). В используемых нами обозначениях это означает, что  Это заключение согласуется с тем, что мы получили в гл. 5, рассматривая изотопическую
Это заключение согласуется с тем, что мы получили в гл. 5, рассматривая изотопическую  (
( -подгруппу группы
-подгруппу группы  . Действительно, там мы пришли к выводу, что
. Действительно, там мы пришли к выводу, что  для распадов
для распадов  это означает, что
это означает, что  поскольку в этих распадах имеет место переход между частицами из разных изотопических мультиплетов. Там же мы установили, что
поскольку в этих распадах имеет место переход между частицами из разных изотопических мультиплетов. Там же мы установили, что  для
для  -распада нейтрона (переход
-распада нейтрона (переход  . В обозначениях данной главы это означает, что
. В обозначениях данной главы это означает, что 
Что касается  и
и  то оба эти параметра отличны
то оба эти параметра отличны  нуляг и их величина определяется из опыта. (В дальнейшем индекс А у них мы опускаем.) Выпишем матричные элементы основных распадов:
нуляг и их величина определяется из опыта. (В дальнейшем индекс А у них мы опускаем.) Выпишем матричные элементы основных распадов:

Совместная подгонка всех данных по спектрам, угловым распределениям и полным вероятностям лептонных распадов барионов дает

Заметим, что измерение  в распаде нейтрона фиксирует
в распаде нейтрона фиксирует  . Заметим также, что из данных по распадам
. Заметим также, что из данных по распадам  -мезонов получается несколько меньшее значение
-мезонов получается несколько меньшее значение 

Если вычислить отношение  в рамках нерелятивистской
в рамках нерелятивистской 
 -симметрии (симметрии между шестью состояниями трех нерелятивистских кварков:
-симметрии (симметрии между шестью состояниями трех нерелятивистских кварков:  где стрелка обозначает направление проекции спина кварка), то получится
где стрелка обозначает направление проекции спина кварка), то получится  что при
что при  дает:
дает:  Согласие экспериментальных данных с этим предсказанием представляется до странности хорошим, если учесть приближенный характер
Согласие экспериментальных данных с этим предсказанием представляется до странности хорошим, если учесть приближенный характер  -симметрии.
-симметрии.
К сожалению, значения  измерены пока лишь для четырех реакций распада:
измерены пока лишь для четырех реакций распада:

Хотя качественно 
 -симметричная картина полулептонных распадов подтверждена и кажется крайне маловероятным, чтобы с улучшением точности опытов здесь возникли серьезные расхождения с теорией, тем не менее точное измерение параметров
-симметричная картина полулептонных распадов подтверждена и кажется крайне маловероятным, чтобы с улучшением точности опытов здесь возникли серьезные расхождения с теорией, тем не менее точное измерение параметров  для различных распадов представляет большой интерес,
для различных распадов представляет большой интерес,
Упражнение. Найти выражения для спектра нейтронов в распаде  Расчет провести в нерелятивистском по скорости нейтрона приближении, когда можно пренебречь кинетической энергией нейтрона по сравнению с энергией, уносимой электроном и нейтрино. Если пренебречь массой электрона и взять интеграл по фазовому объему лептонов, то
Расчет провести в нерелятивистском по скорости нейтрона приближении, когда можно пренебречь кинетической энергией нейтрона по сравнению с энергией, уносимой электроном и нейтрино. Если пренебречь массой электрона и взять интеграл по фазовому объему лептонов, то

Здесь  - суммарный 4-импульс лептонов, —
- суммарный 4-импульс лептонов, —  - импульс нейтрона. Взяв интеграл по
- импульс нейтрона. Взяв интеграл по  и сравнивая полученное выражение
и сравнивая полученное выражение  с выражением для полной вероятности распада
с выражением для полной вероятности распада  (см. гл. 5), находим, что
(см. гл. 5), находим, что 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- 1. ВВЕДЕНИЕ
- Кварковые токи
- О цвете слабых токов
- Токи и процессы
- О плане книги
- 2. СТРУКТУРА СЛАБЫХ ТОКОВ
- Нарушение Р- и С-инвариантности
- Универсальность заряженного тока
- Нейтральный ток
- 3. РАСПАД МЮОНА
- Вероятность распада
- Распад поляризованного мюона
- Качественное обсуждение
- Замечания и упражнения
- 4. ЛЕПТОННЫЕ РАСПАДЫ АДРОНОВ С СОХРАНЕНИЕМ СТРАННОСТИ. СВОЙСТВА ud-TOKA
- Связь векторного тока ud с изовекторным электромагнитным током
- Слабый заряд
- Киральная инвариантность
- 5. ЛЕПТОННЫЕ РАСПАДЫ ПИОНОВ И НУКЛОНОВ
- 6. ЛЕПТОННЫЕ РАСПАДЫ K-МЕЗОНОВ И ГИПЕРОНОВ
- SU(3)- и SU(2)-свойства us-тока
- Распады Kl2
- Распады Ке3
- Распады …
- Распады Кl4
- Лептонные распады гиперонов
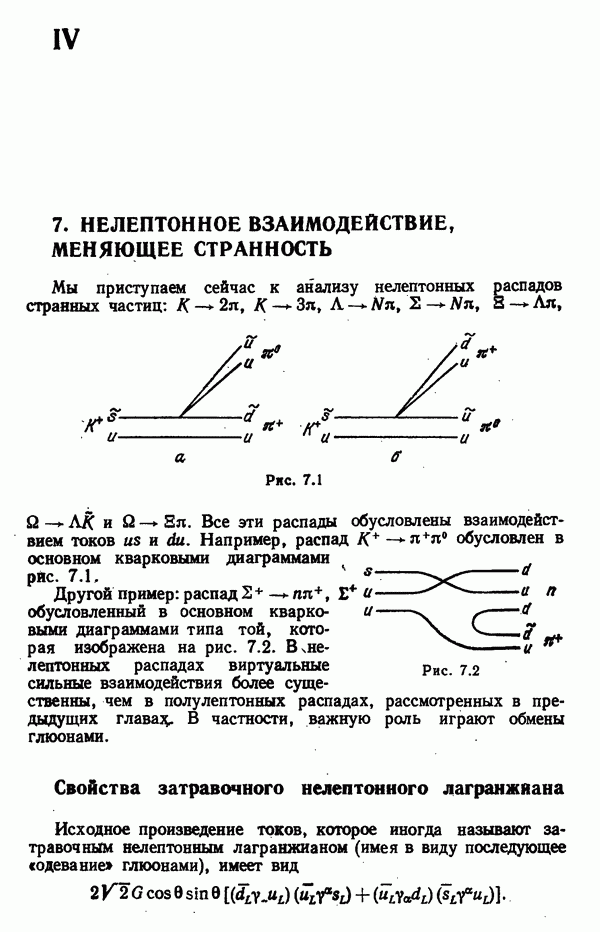
- 7. НЕЛЕПТОННОЕ ВЗАИМОДЕЙСТВИЕ, МЕНЯЮЩЕЕ СТРАННОСТЬ
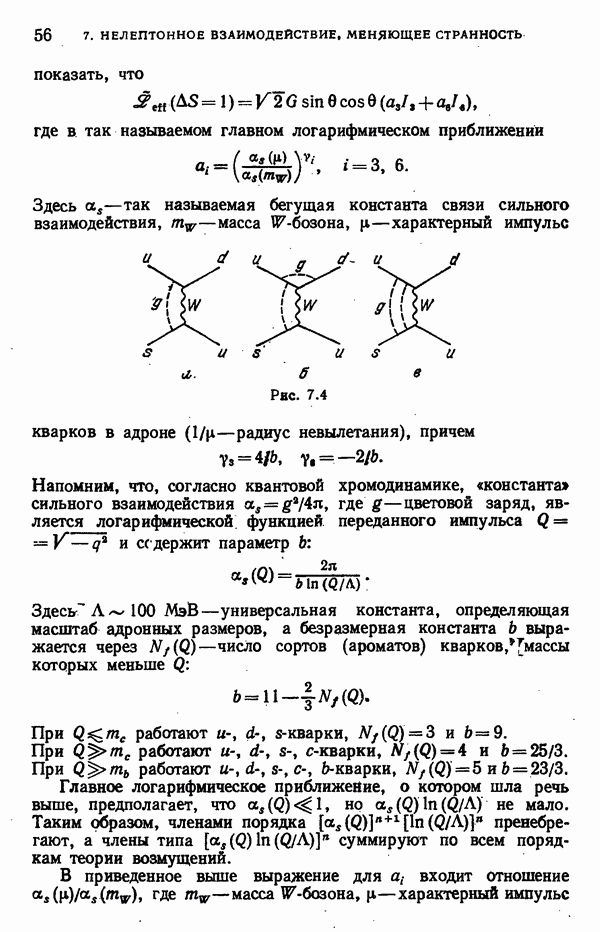
- Учет жестких глюонов
- Глюонный монополь и «пингвины»
- Эффективный нелептонный лагранжиан
- 8. ФЕНОМЕНОЛОГИЯ НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Нерелятивистская форма амплитуды
- Спиновыекорреляции при распаде гиперонов
- Изотопические амплитуды и правило
- Фазы S- и Р-амплитуд
- SU(3)-соотношение между амплитудами гиперонных распадов
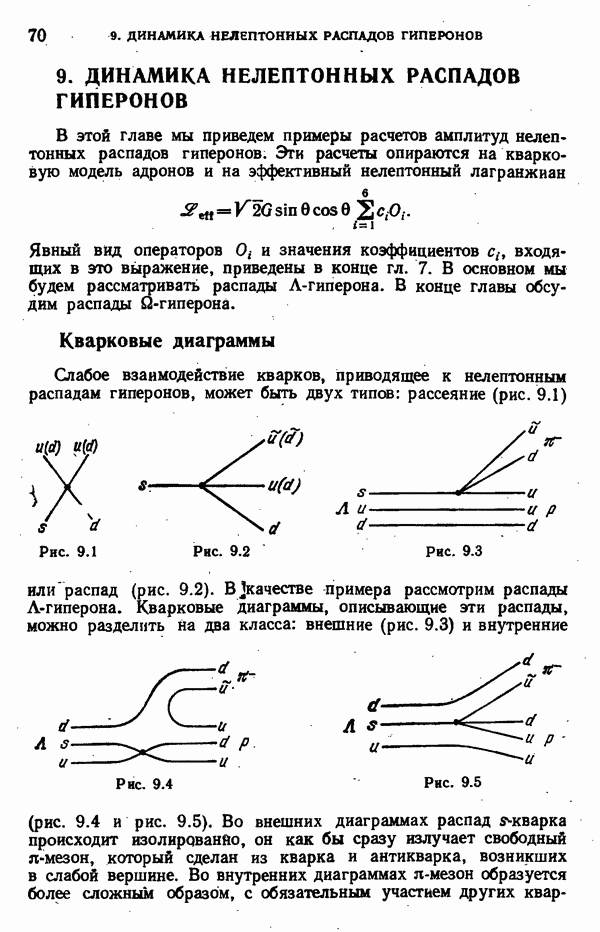
- 9. ДИНАМИКА НЕЛЕПТОННЫХ РАСПАДОВ ГИПЕРОНОВ
- Факторизация внешних диаграмм для распада
- Усиление вклада правых кварков
- Распад …
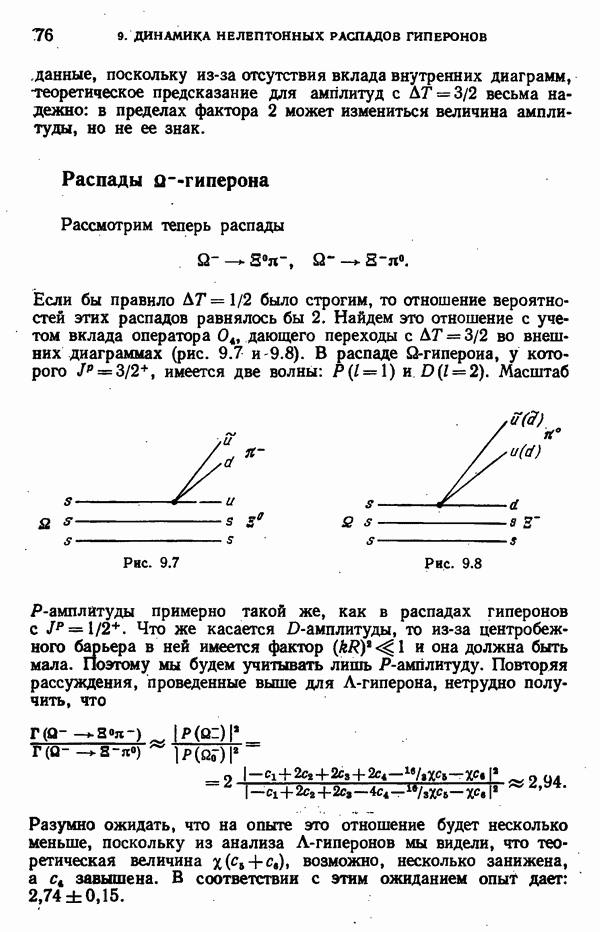
- Распады гиперона
- 10. НЕЛЕПТОННЫЕ РАСПАДЫ К-МЕЗОНОВ
- Изотопические соотношения для распадов
- Кварковые диаграммы для распадов
- Распады …
- 11. НЕЙТРАЛЬНЫЕ К-МЕЗОНЫ В ВАКУУМЕ И В СРЕДЕ
- Механизм Глешоу—Илиопулоса—Майани
- Как вычислить вклад «квадратика»
- Осцилляции странности
- Регенерация
- 12. НАРУШЕНИЕ CP-ИНВАРИАНТНОСТИ
- Другие наблюдавшиеся СР-неинвариантные эффекты
- Сверхслабое перемешивание
- О параметре …
- О распадах K-мезона
- Нарушение T-инвариантности и дипольный момент нейтрона
- Мысленные опыты
- 13. РАСПАДЫ «тау»-ЛЕПТОНА
- Полуадронные распады. Общие замечания
- Распад …
- Распад …
- Распады …
- Распады …
- Распады …
- Сводка результатов
- 14. РАСПАДЫ ОЧАРОВАННЫХ АДРОНОВ
- Грубая оценка времени жизни очарованных адронов
- Сравнение мезонов
- Роль виртуальных глюонов
- Роль «спектаторных» кварков
- Правила отбора по изоспину
- Следствия SU(3)-симметрии
- О секстетном усилении
- Двухчастичные лептонные распады D-мезонов
- Переходы …
- Зачем надо изучать слабые распады очарованных адронов?
- 15. КВАРКИ ТРЕТЬЕГО ПОКОЛЕНИЯ
- Матрица девяти кварковых токов
- Распады b-кварка
- Вклады t-кварков в переходы …
- Вклад t-кварка в переходы …, и b-кварка в переходы …
- О нарушении CP-инвариантности в переходах
- 16. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С ЭЛЕКТРОНОМ
- Сечение реакции …
- Сечение реакции …
- Упругое … и рассеяние под действием заряженного тока
- Общий вид сечений рассеяния
- Другие проявления ve-взаимодействия
- Рождение мюонной пары под действием нейтрино в кулоновом поле ядра
- 17. ВЗАИМОДЕЙСТВИЕ НЕЙТРИНО С НУКЛОНАМИ
- Квазиупругое рассеяние
- Партоны
- Кинематика столкновения лептона с партоном
- Сечения столкновения лептонов с партонами
- Распределения паргонов
- Сечения глубоко неупругих процессов
- Рождение странных и очарованных частиц
- Феноменология глубоко неупругих процессов
- Партонная модель и квантовая хромодинамика
- 18. ПЕРЕНОРМИРУЕМОСТЬ
- Унитарный предел
- Промежуточный бозон
- Волновая функция векторного бозона
- Отступление о массе фотона
- Пропагатор векторного бозона
- 19. КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
- 20. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ
- Спонтанное нарушение глобальной U(1)-симметрии
- Спонтанное нарушение глобальной SU(2)-симметрии
- Спонтанное нарушение калибровочной абелевой симметрии
- О сохранении электрического заряда
- Спонтанное нарушение локальной SU(2)-симметрии
- 21. СТАНДАРТНАЯ МОДЕЛЬ ЭЛЕКТРОСЛАБОГО ВЗАИМОДЕЙСТВИЯ
- Девять членов лагранжиана
- Массы W- и Z-бозонов
- Связь между электрическим зарядом и константами g и g’
- Связь между вакуумным средним и константой Ферми G
- Масса электрона
- Включение других лептонов и кварков
- 22. НЕЙТРАЛЬНЫЕ ТОКИ
- Рассеяние на электроне
- Рассеяние … на электроне
- Аннигиляция
- Нейтральные токи и взаимодействие нейтрино с нуклонами
- Изотопические свойства нейтрального тока
- Несохранение четности в рассеянии электронов нуклонами
- Нарушение четности в атомах
- Р-нечетные ядерные силы
- 23. СВОЙСТВА ПРОМЕЖУТОЧНЫХ БОЗОНОВ
- Распады W-бозонов
- Распады Z-бозонов
- Рождение Z-бозонов в столкновениях
- Рождение W- и Z-бозонов в pp-столкновениях
- W- и Z-бозоны и коллайдеры
- W-бозоны и проект ДЮМАНД
- 24. СВОЙСТВА ХИГГСОВЫХ БОЗОНОВ
- О массе H-бозонов
- Роль H-бозонов при высоких энергиях
- Взаимодействие H-бозонов с тяжелыми кварками
- Взаимодействие Н-бозонов с глюонами
- «Хиггсов заряд» нуклона
- Отступление о следе оператора энергии-импульса
- Взаимодействие H-бозонов с W- и Z-бозонами
- Взаимодействие H-бозонов с фотонами
- Общие замечания о хиггсовых бозонах
- 25. ВЕЛИКИЙ СИНТЕЗ
- Квиитет и декуплет в группе SU(5)
- 24 векторных бозона
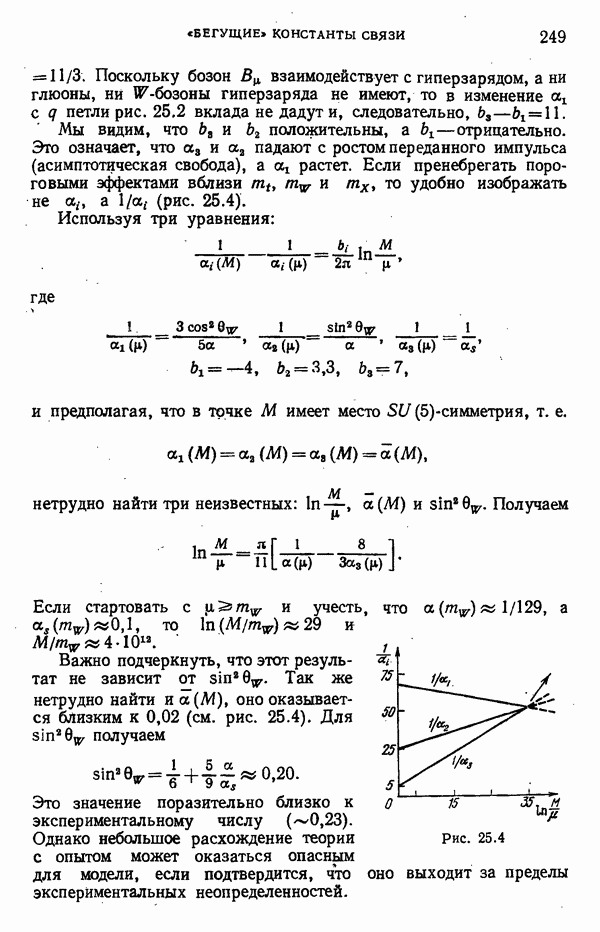
- «Бегущие» константы связи
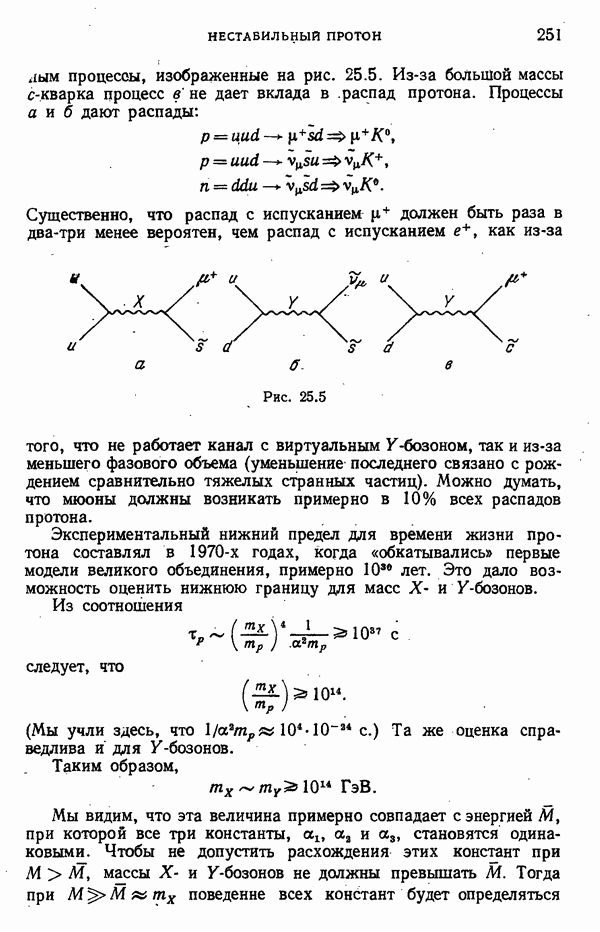
- Нестабильный протон
- Хиггсовы бозоны
- Группа SO(10)
- Исключительные группы
- 26. СУПЕРСИММЕТРИЯ
- Субкварки?
- 27. ЧАСТИЦЫ И ВСЕЛЕННАЯ
- Верхний предел для массы нейтрино
- О числе различных типов нейтрино
- Концентрация реликтовых кварков
- О барионной асимметрии Вселенной
- 28. ПРИЛОЖЕНИЕ (НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ)
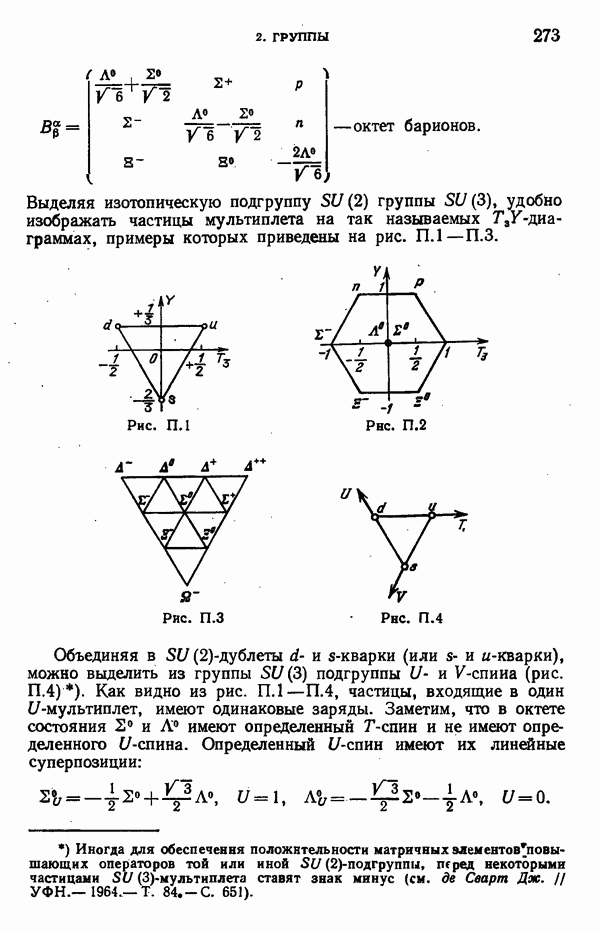
- 2. Группы
- 3. Свойства матриц Дирака
- 4. Правила расчета вероятностей