| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
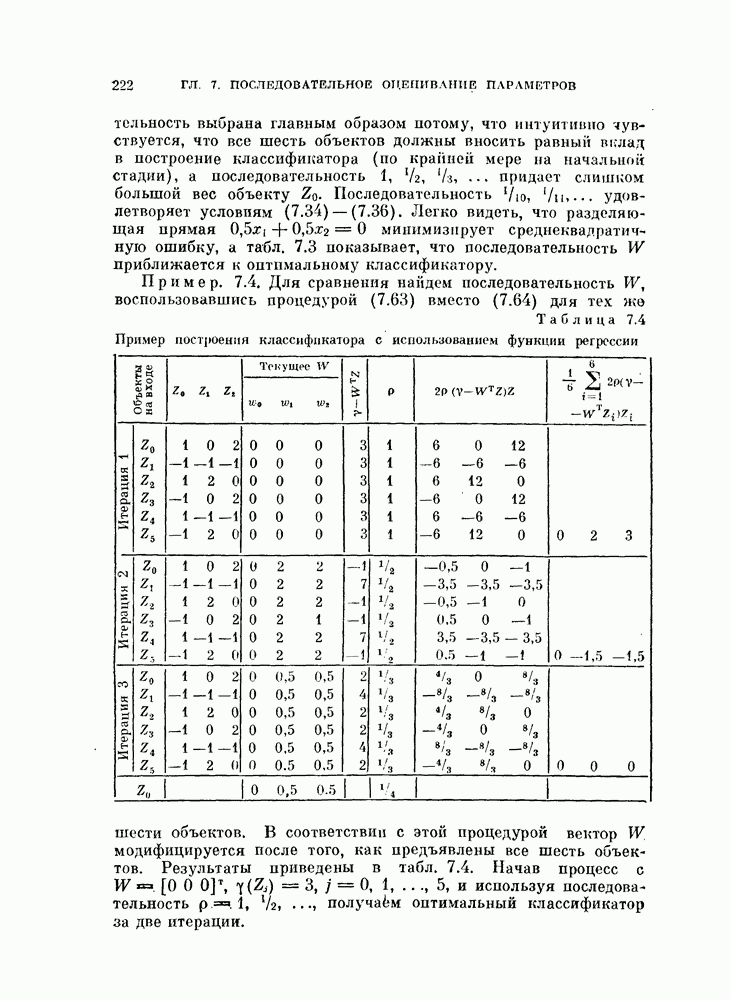
9.3.4. Случай многих классов.
Как уже говорилось в связи с дискриминантным анализом, ни один из критериев, взятых в отдельности, не является особенно хорошим индикатором разделимости в случае многих классов. Однако процедуру вычисления верхней границы вероятности ошибки можно обобщить на случай многих классов [Лайниотис, 1969]. Пусть 
Таблица 9.2. Качество оценки, найденной с помощью неравенства, Иенсена

 — общая вероятность ошибки и вероятность ошибки при разделении классов
— общая вероятность ошибки и вероятность ошибки при разделении классов  и
и  . В таком случае
. В таком случае

Так как верхняя граница гц определяется границей Чернова или границей Бхатачария, то комбинация этих границ и (9.110) дает верхнюю границу  в виде мм
в виде мм

где оптимальные значения  определяются соответствующими парами классов, но для простоты можно использовать
определяются соответствующими парами классов, но для простоты можно использовать  .
.
Воспользовавшись неравенством

можно определить верхнюю границу вероятности ошибки  следующим образом:
следующим образом:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
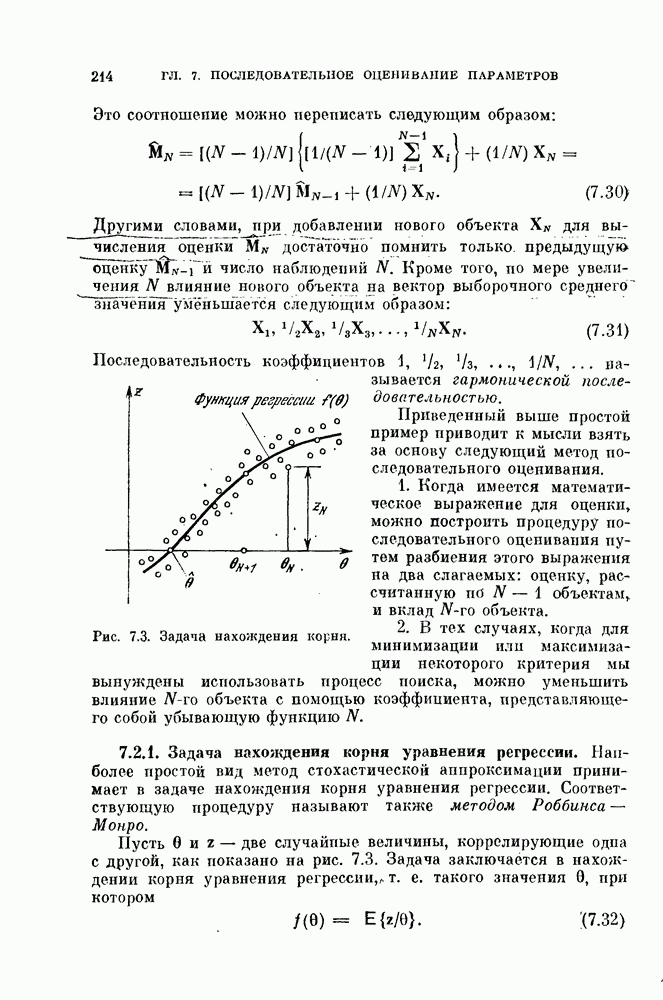
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
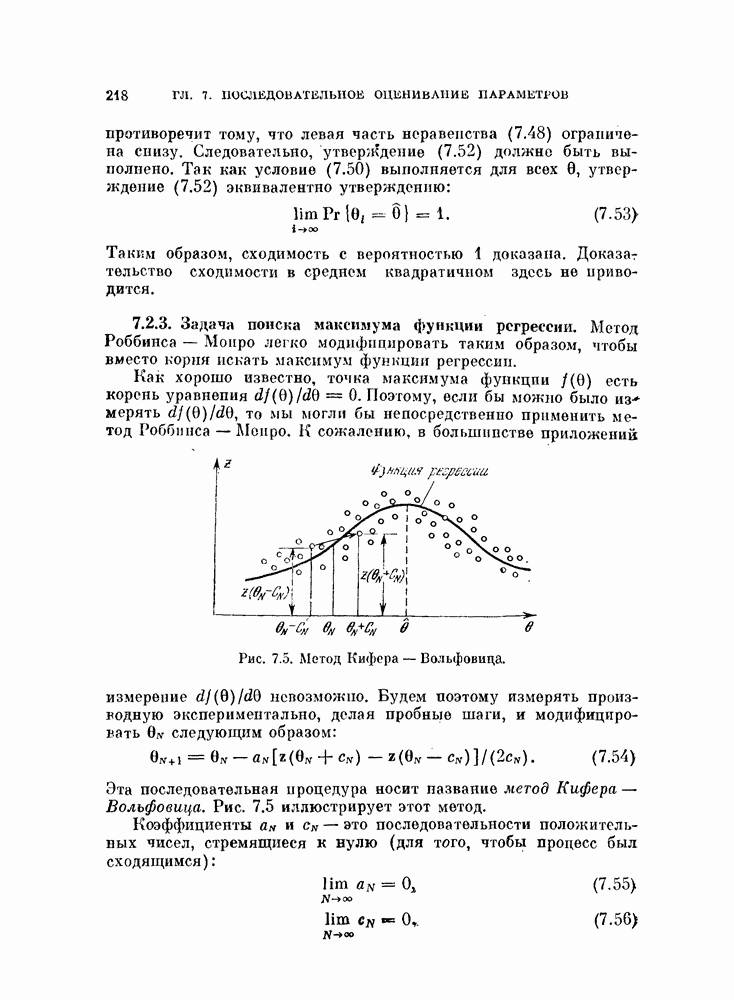
- 7.2.3. Задача поиска максимума функции регрессии.
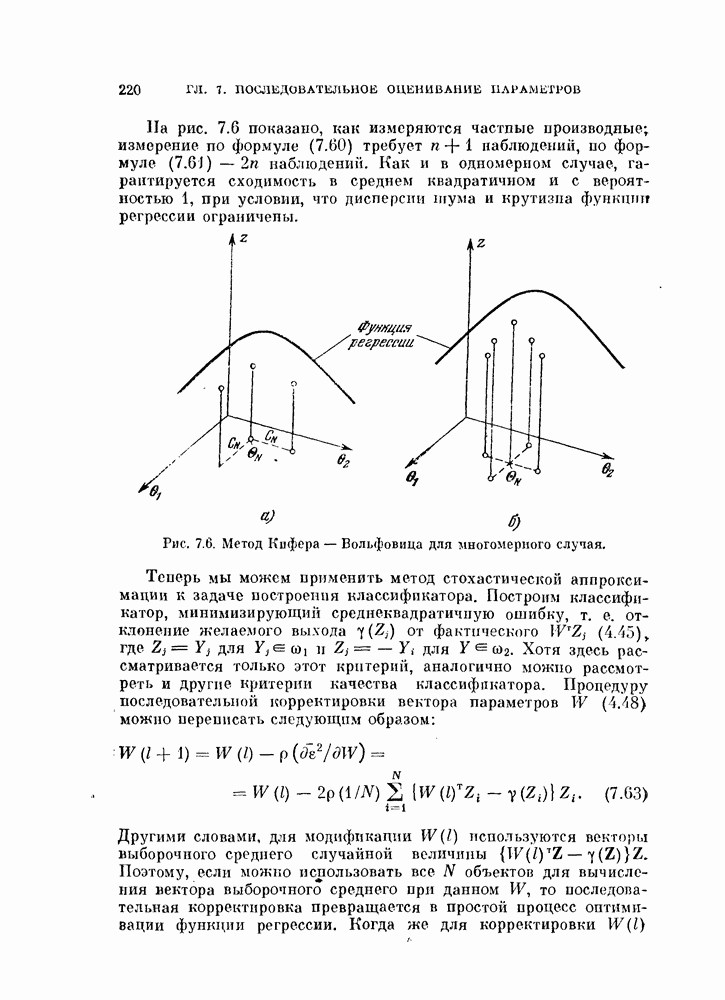
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
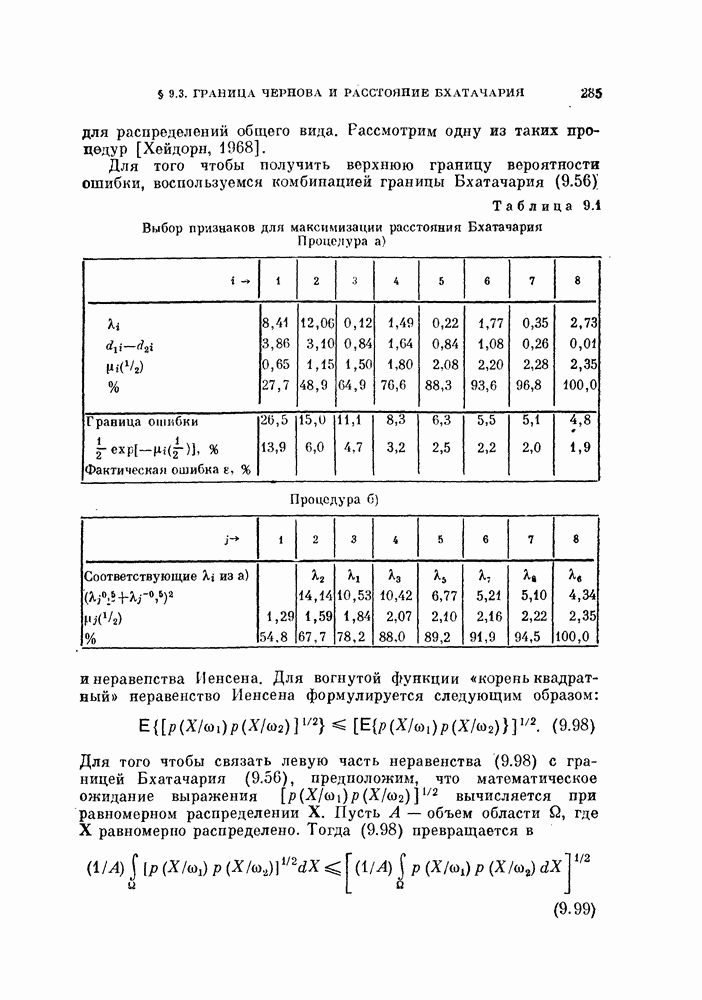
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
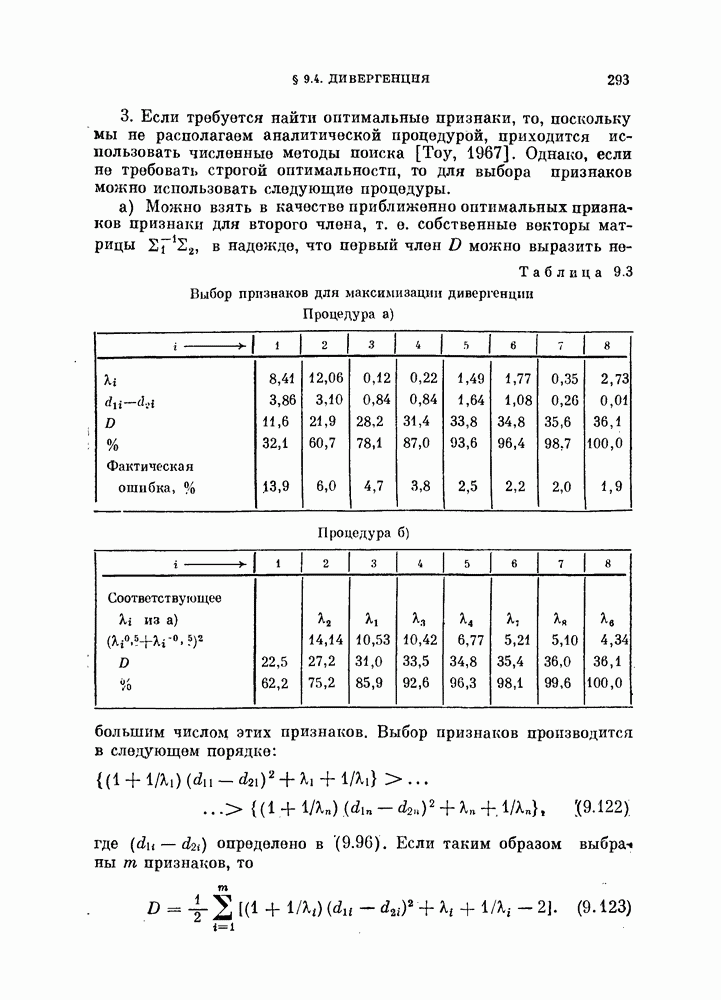
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА