| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
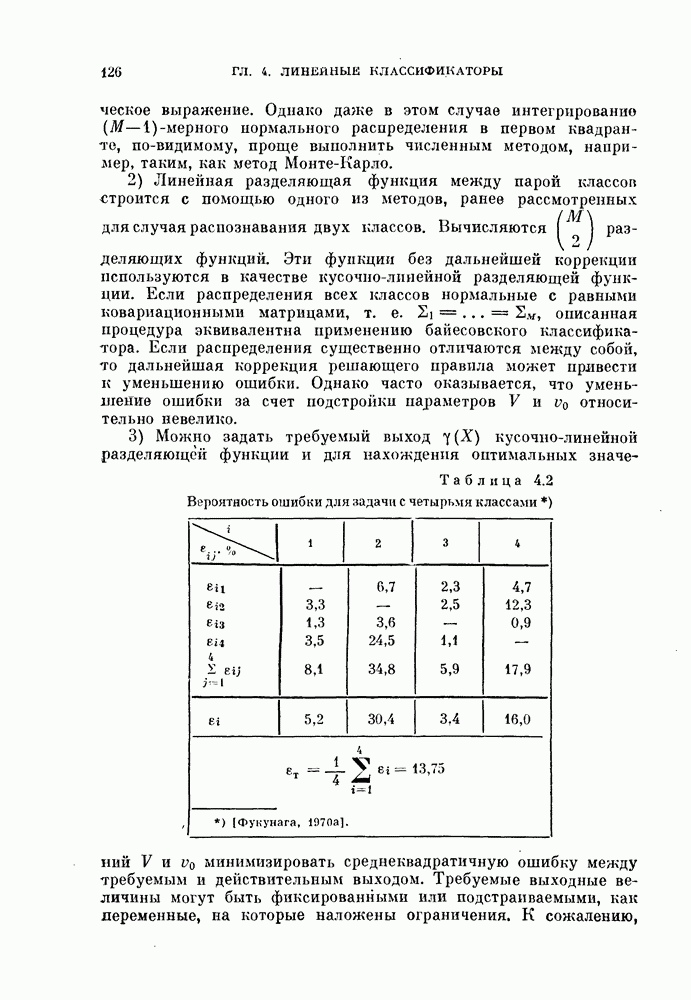
До сих пор при обсуждении вопроса о нахождении оптимальных признаков данного множества исходных данных рассматривались только линейные преобразования исходного пространства. К сожалению, линейное преобразование, как правило, не позволяет выделить минимальное число эффективных признаков. Несмотря на это, математические вопросы нелинейных отображений остаются неисследованными вследствие их сложности, и на практике эффективные признаки находят, в основном, за счет интуиции исследователя.
Трудности решения нелнпейных задач являются общими для всех технических дисциплин. Однако в задачах распознавания образов из-за большого числа переменных эти трудности особенно велики. В этой главе будут рассмотрены некоторые методы нелинейного преобразования исходного пространства, связанные с нахождением истинной размерности множества исходных данных, улучшением разделимости классов и двумерным отображением исходных данных без потери разделимости.
§ 10.1. Истинная размерность исходных данных
10.1.1. Локальные свойства распределения.
Всякий раз, когда мы имеем дело с большими множествами многомерных дапных, задача их обработки упрощается, если удается обнаружить или павязать этим данным некоторую структуру. Поэтому можно предположить, что исходные данные подчиняются закону, который характеризуется определенным числом основных параметров. Минимальное число параметров  , которые необходимо принять в расчет для объяснения наблюдаемых свойств исходных данных, называют истинной размерностью множества исходных данных или, что то же самое, истинной размерностью процесса, порождающего исходные данные. Геометрическая интерпретация этого определения заключается в том, что все множество исходных
, которые необходимо принять в расчет для объяснения наблюдаемых свойств исходных данных, называют истинной размерностью множества исходных данных или, что то же самое, истинной размерностью процесса, порождающего исходные данные. Геометрическая интерпретация этого определения заключается в том, что все множество исходных
данных лежит в топологическом подпространстве (на гиперповерхности) размерности 
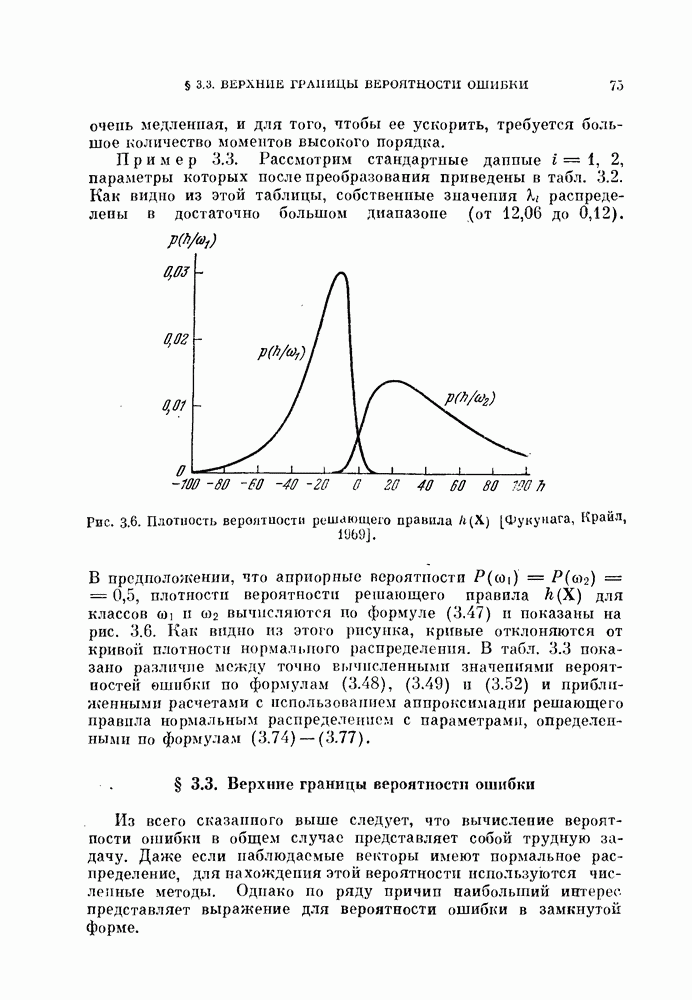
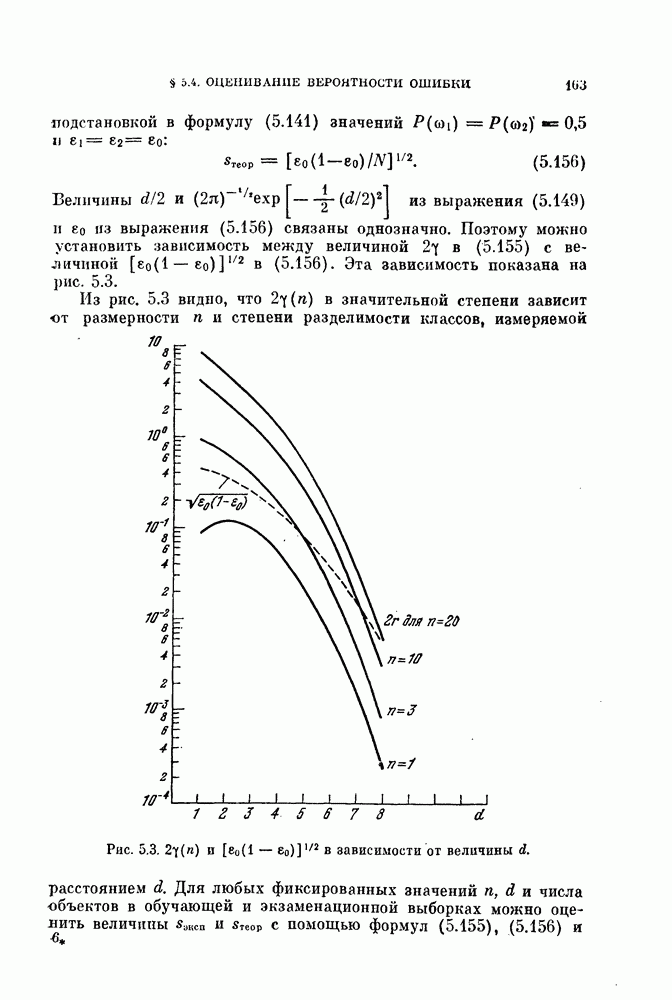
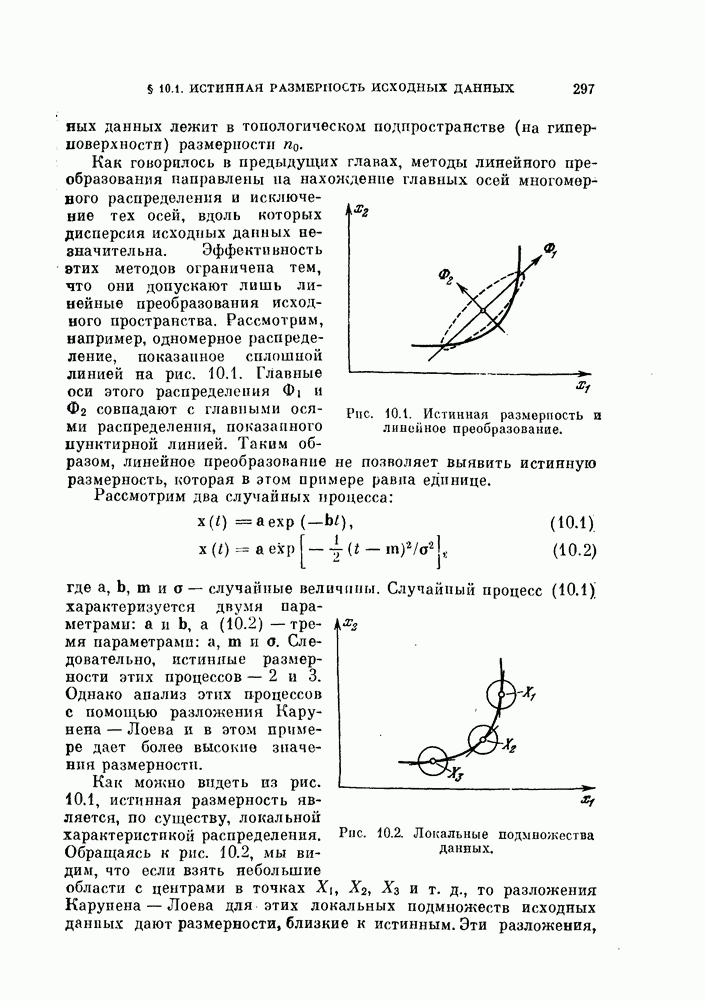
Как говорилось в предыдущих главах, методы линейного преобразования направлены на нахождение главных осей многомерного распределения и исключение тех осей, вдоль которых дисперсия исходных данных незначительна. Эффективность этих методов ограничена тем, что они допускают лишь линейные преобразования исходного пространства. Рассмотрим, например, одномерное распределение, показанное сплошной линией на рис. 10.1. Главные оси этого распределения  совпадают с главными осями распределения, показанного нунктирнох! линией. Таким образом, линейное преобразование не позволяет выявить истинную размерность, которая в этом примере равна единице.
совпадают с главными осями распределения, показанного нунктирнох! линией. Таким образом, линейное преобразование не позволяет выявить истинную размерность, которая в этом примере равна единице.
Рассмотрим два случайных процесса:

где  - случайные величины.
- случайные величины.

Рис. 10.1. Истинная размерность и линейное преобразование.

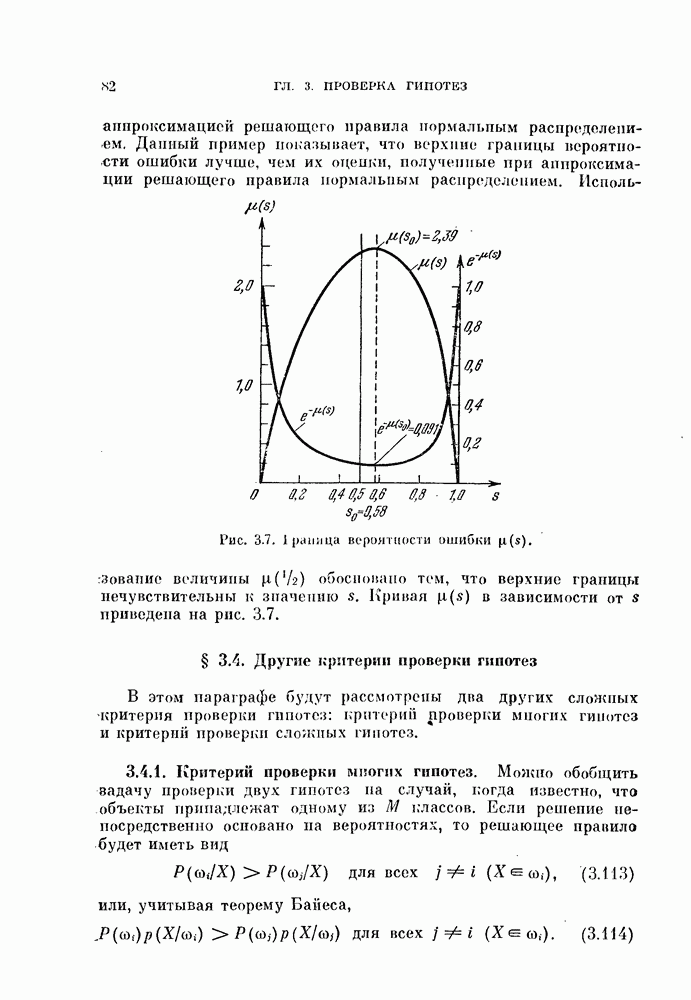
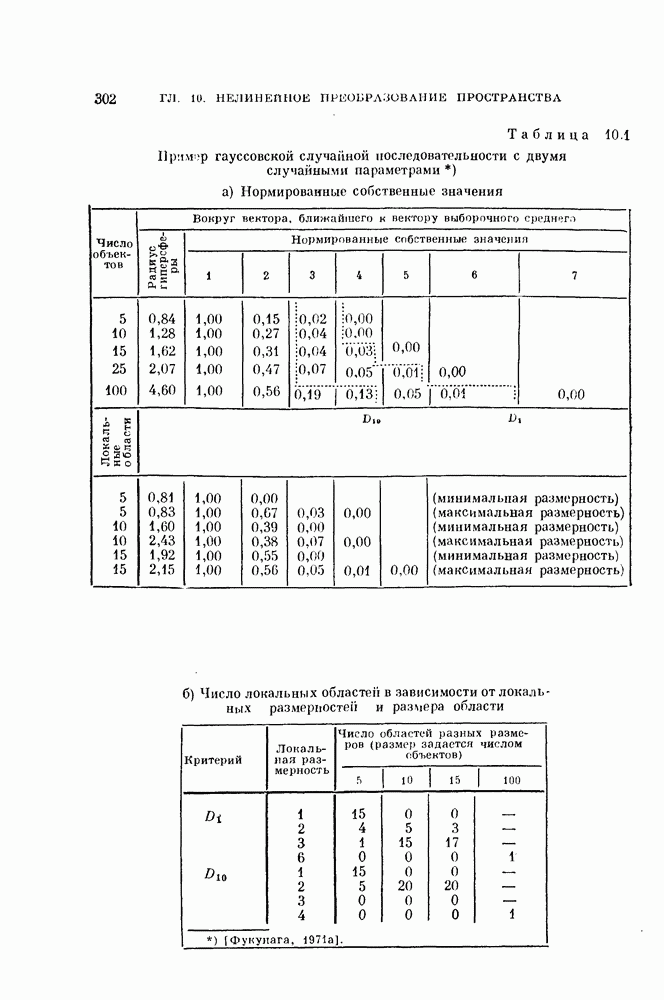
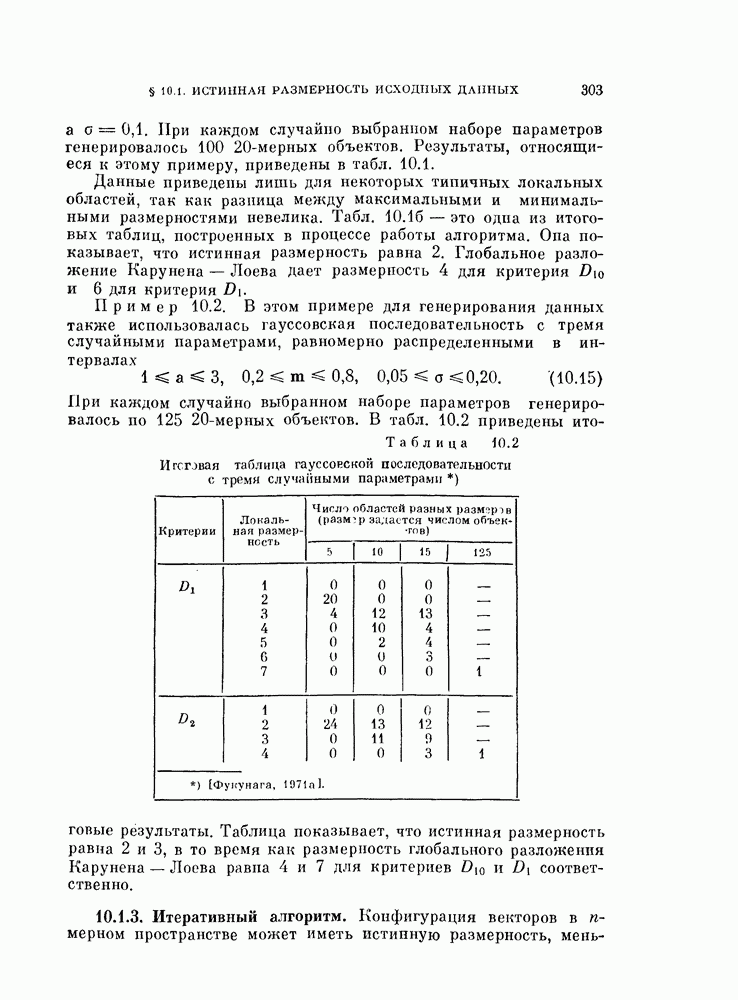
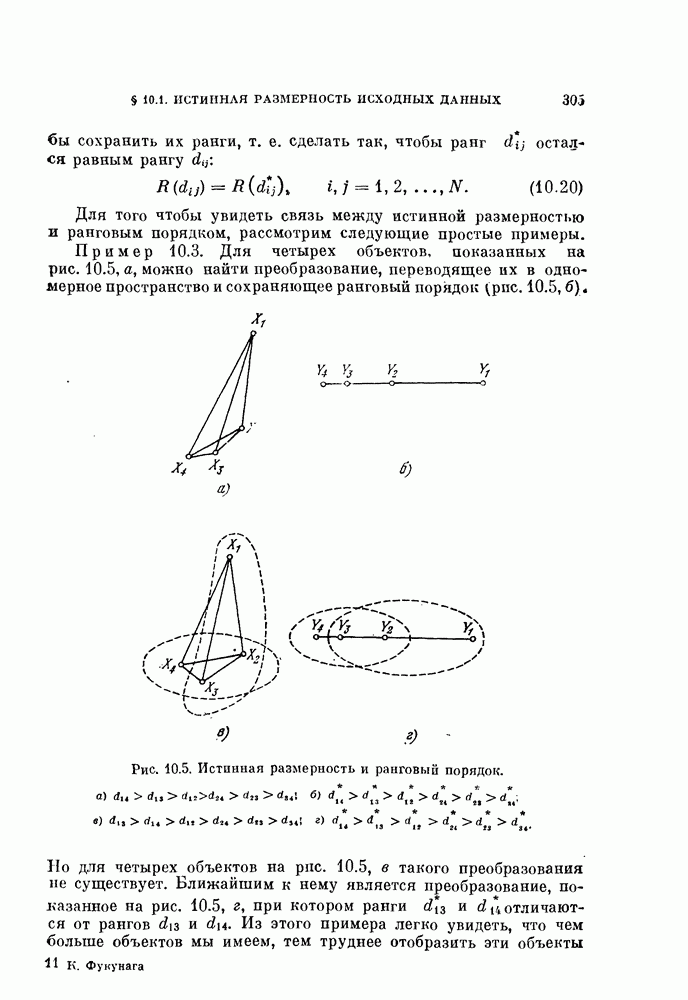
Рис. 10.2. Локальные подмножества данных.
Случайный процесс  характеризуется двумя параметрами: а и b, а
характеризуется двумя параметрами: а и b, а  — тремя параметрами:
— тремя параметрами:  . Следовательно, истинные размерности этих процессов — 2 и 3.
. Следовательно, истинные размерности этих процессов — 2 и 3.
Однако анализ этих процессов с помощью разложения Карунена — Лоева и в этом примере дает более высокие значения размерности.
Как можно видеть из рис. 10.1, истинная размерность является, по существу, локальной характеристикой распределения.
Обращаясь к рис. 10.2, мы видим, что если взять небольшие области с центрами в точках  то разложения Карунена — Лоева для этих локальных подмножеств исходных данных дают размерности, близкие к истинным. Эти разложения,
то разложения Карунена — Лоева для этих локальных подмножеств исходных данных дают размерности, близкие к истинным. Эти разложения,
кроме того, дают базисные векторы для локальных распределений.
Этот метод аналогичен методу локальной линеаризации нелинейных функций. Универсальное средство исследования локальных свойств — разложение в ряд Тейлора является общим средством. Для того чтобы применить это разложение, введем истинные случайные величины

где по — истинная размерность. Тогда наблюдаемый случайный вектор X, размерпость которого  больше истинной размерности
больше истинной размерности  является нелинейной функцией
является нелинейной функцией 

В случае случайного процесса эта зависимость записывается в виде

Например, для  . В пределах малой окрестности
. В пределах малой окрестности  вектор X можно представить усеченным рядом Тейлора:
вектор X можно представить усеченным рядом Тейлора:

где

и

Таким образом,  можно аппроксимировать линейным разложением по содержащим
можно аппроксимировать линейным разложением по содержащим  членов. То обстоятельство, что
членов. То обстоятельство, что  выражается через
выражается через  или меньшее число линейно независимых векторов, приводит к выводу, что ковариационная матрица
или меньшее число линейно независимых векторов, приводит к выводу, что ковариационная матрица  имеет ранг (или число ненулевых собственных значений) равный или меньший, чем
имеет ранг (или число ненулевых собственных значений) равный или меньший, чем  . В этом месте необходимо сделать следующие замечания.
. В этом месте необходимо сделать следующие замечания.
1. Так как разложение (10.6) является приближенным, фактическая ковариационная матрица наблюдаемых данных  имеет ранг
имеет ранг  , а не
, а не  . Но
. Но  или меньшее число собственных значений доминируют в области, где справедливо (10.6).
или меньшее число собственных значений доминируют в области, где справедливо (10.6).
2. К сожалению, базисные векторы  не являются взаимно ортогональными, а
не являются взаимно ортогональными, а  — некоррелированными. Это означает, что если базисные векторы ищутся по наблюдаемым данным
— некоррелированными. Это означает, что если базисные векторы ищутся по наблюдаемым данным  с помощью разложения Корунена — Лоева, то при этом будет получено другое разложение
с помощью разложения Корунена — Лоева, то при этом будет получено другое разложение

где

Так как  и
и  — собственные векторы и собственные значения ковариационной матрицы
— собственные векторы и собственные значения ковариационной матрицы  то
то  взаимно ортонормированы,
взаимно ортонормированы,  — нехшррелированы. Выражения (10.6) и
— нехшррелированы. Выражения (10.6) и  являются линейными выражениями относительно
являются линейными выражениями относительно  базисных векторов с
базисных векторов с  случайными коэффициентами. Поэтому
случайными коэффициентами. Поэтому  должны быть связаны с
должны быть связаны с  линейным преобразованием, хотя матрица преобразования неизвестна. Если бы можно было найти эту матрицу, то мы могли бы вычислить по
линейным преобразованием, хотя матрица преобразования неизвестна. Если бы можно было найти эту матрицу, то мы могли бы вычислить по  Так как — это частные производные от
Так как — это частные производные от  вычисленные значения
вычисленные значения  можно использовать для оценки вида функции
можно использовать для оценки вида функции 
3. Вообще говоря, нет гарантии, что в ряде Тейлора (10.6) доминируют члены первого порядка. Если минимальный размер локальной области ограничен по каким-либо техническим соображениям, доминирующими могут оказаться некоторые члены более высокого порядка или, другими словами, некоторые члены более низкого порядка могут быть малозначимыми. Поэтому упомянутая выше процедура эквивалентна подсчету числа значимых членов в ряде Тейлора, которое, как мы надеемся, близко к  Эта надежда, однако, подтверждается экспериментально, на примерах.
Эта надежда, однако, подтверждается экспериментально, на примерах.
4. На всех реальных ситуациях исходные данные искажены шумом. Поучительно рассмотреть влияние аддитивного белого шума. Так как белый шум имеет нулевое среднее значение, некоррелирован с сигналом  и имеет единичную ковариационную матрицу
и имеет единичную ковариационную матрицу  то ковариационная матрица
то ковариационная матрица  плюс шум равна
плюс шум равна

Буквой  обозначен вектор шума со спектральной плотностью 4, а
обозначен вектор шума со спектральной плотностью 4, а  определено в (10.10). Собственные векторы матрицы
определено в (10.10). Собственные векторы матрицы  идентичны собственным векторам матрицы
идентичны собственным векторам матрицы  Собственные значения матрицы
Собственные значения матрицы  равны
равны

Следовательно, если свободные от шума исходные данные имеют по доминирующих собственных значений и  несущественных, то зашумленные данные будут иметь такое же распределение собственных значений, каждое из которых лишь увеличивается на некоторую хшнстанту у. Это означает, что разность между собственными значениями с номерами
несущественных, то зашумленные данные будут иметь такое же распределение собственных значений, каждое из которых лишь увеличивается на некоторую хшнстанту у. Это означает, что разность между собственными значениями с номерами  не изменяется. Обнаружение факта, что
не изменяется. Обнаружение факта, что  собственных векторов
собственных векторов
являются доминирующими, означает, что эта разность значительна, и может быть использовано для выбора  собственных значений
собственных значений  при наличии шума.
при наличии шума.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
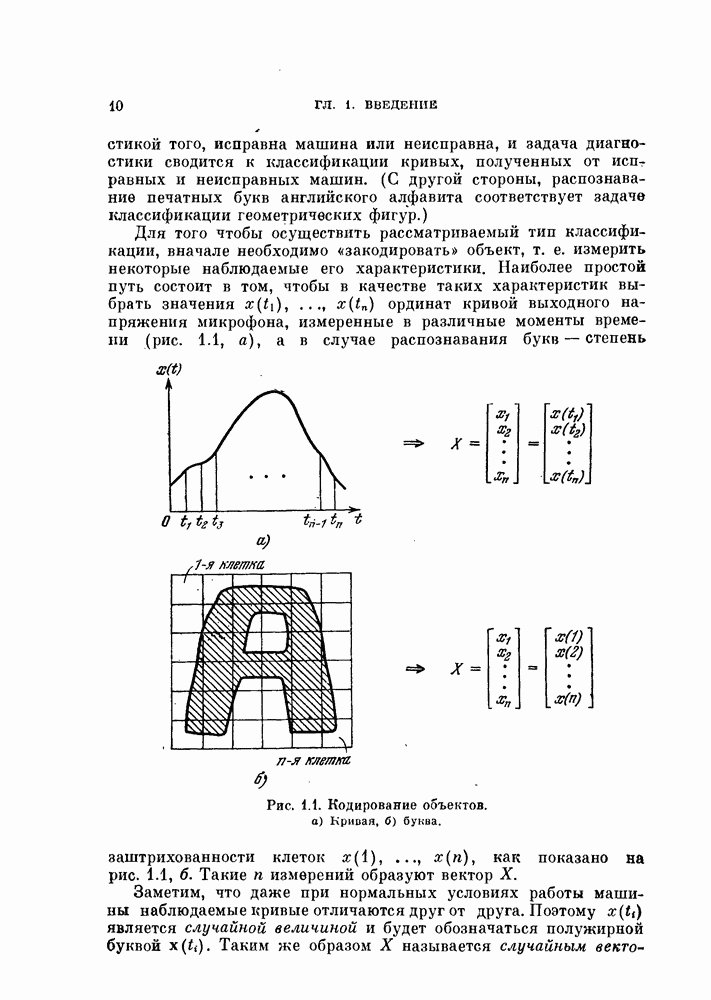
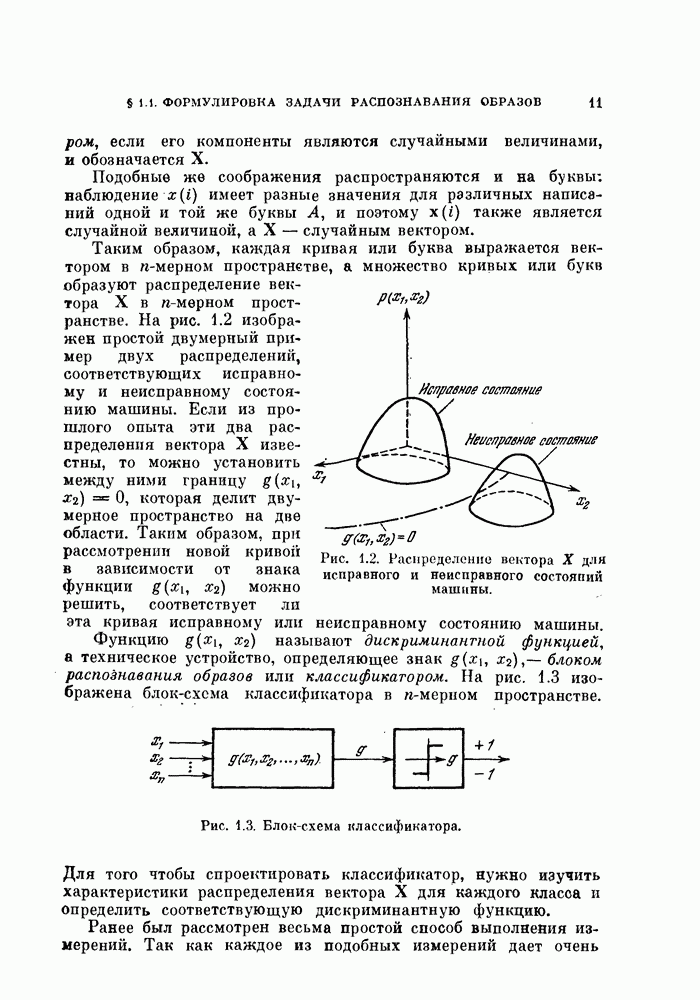
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
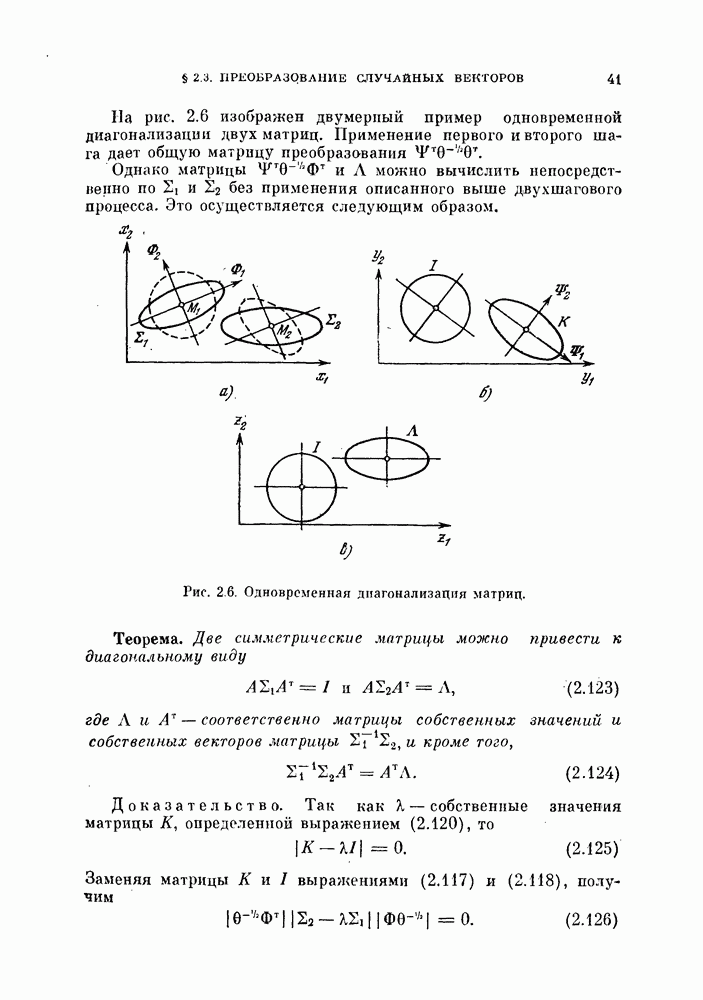
- 2.3.5. Одновременная диагонализация двух матриц.
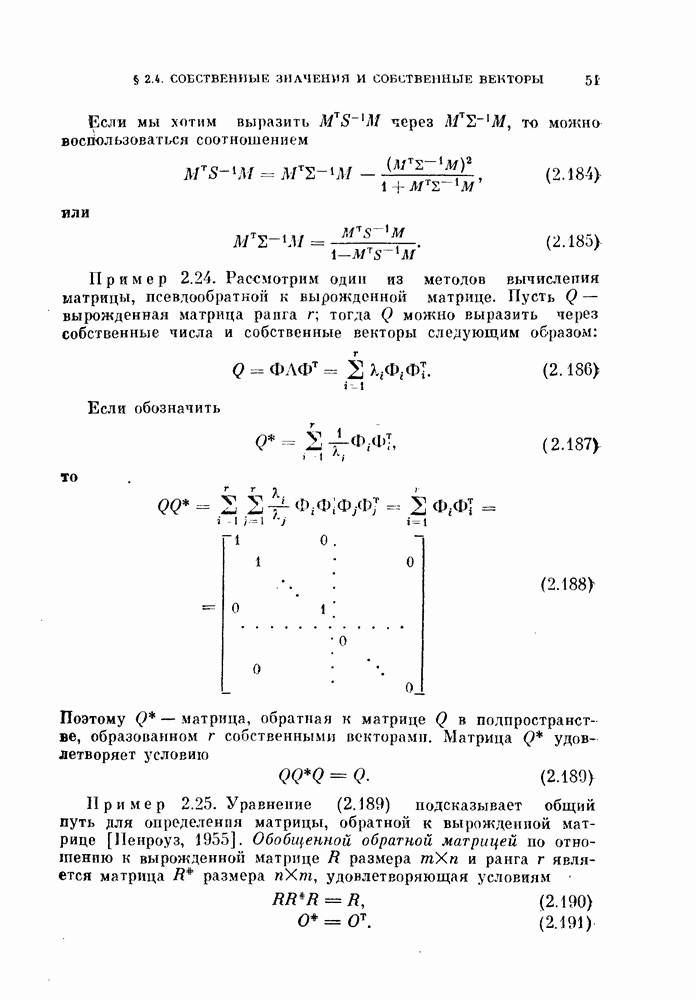
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
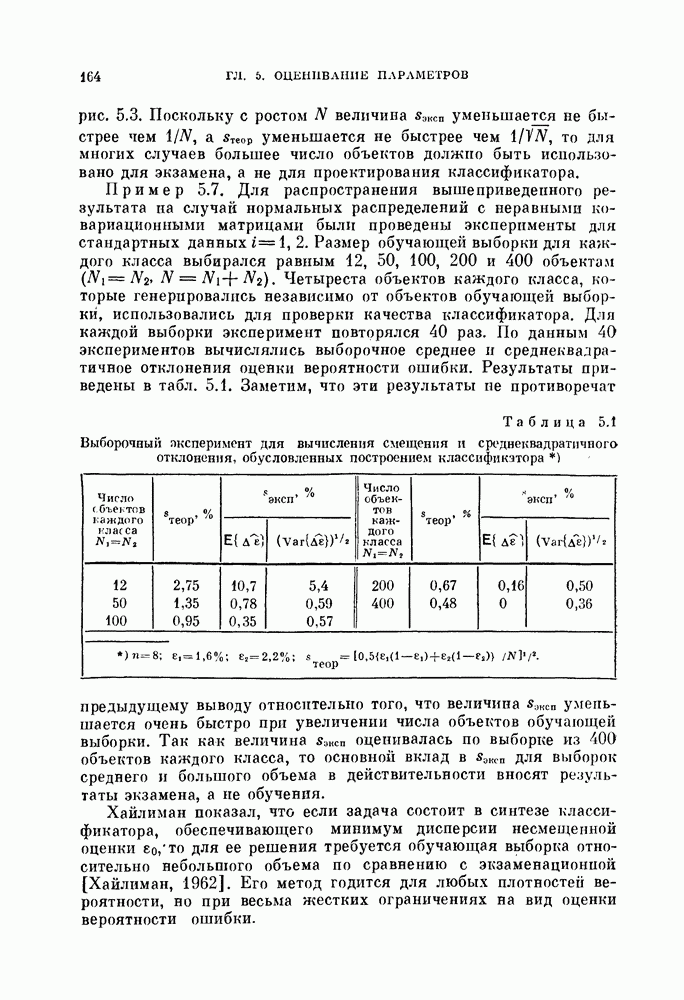
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
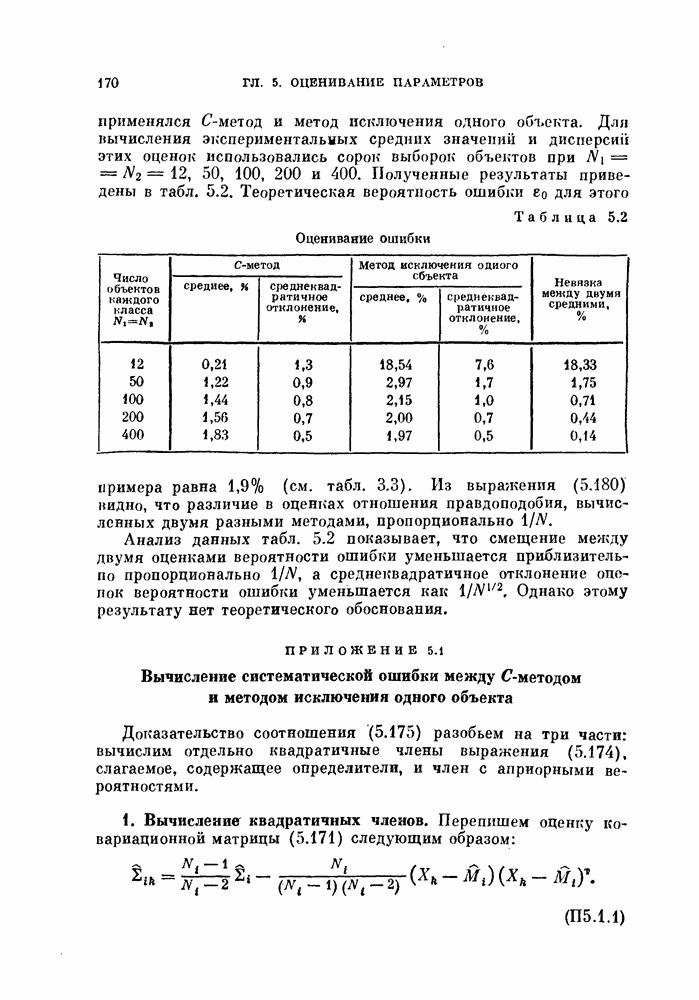
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
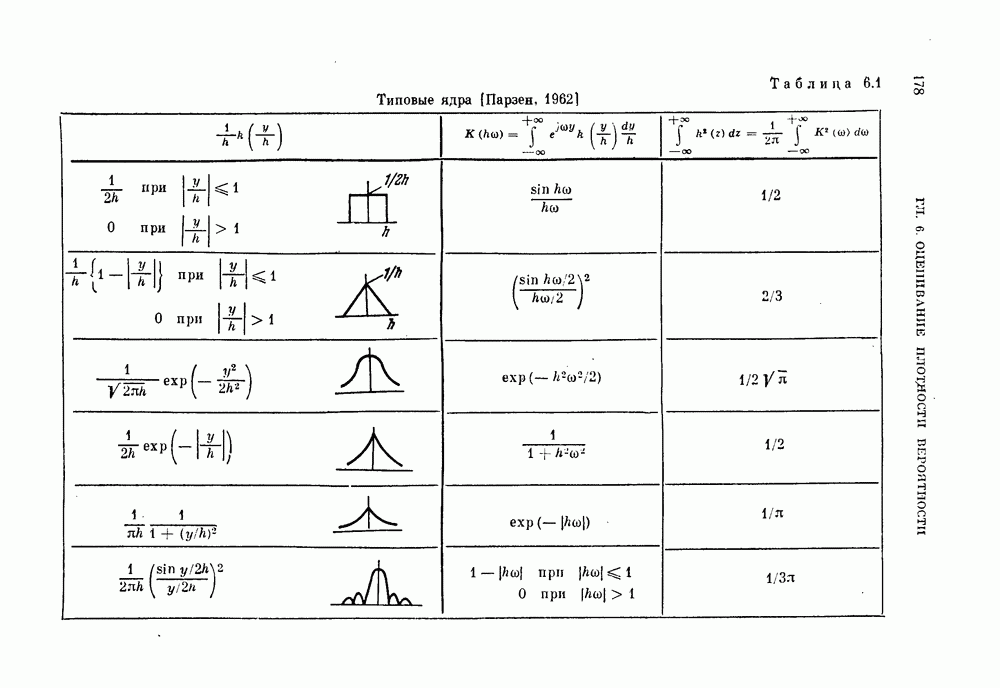
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
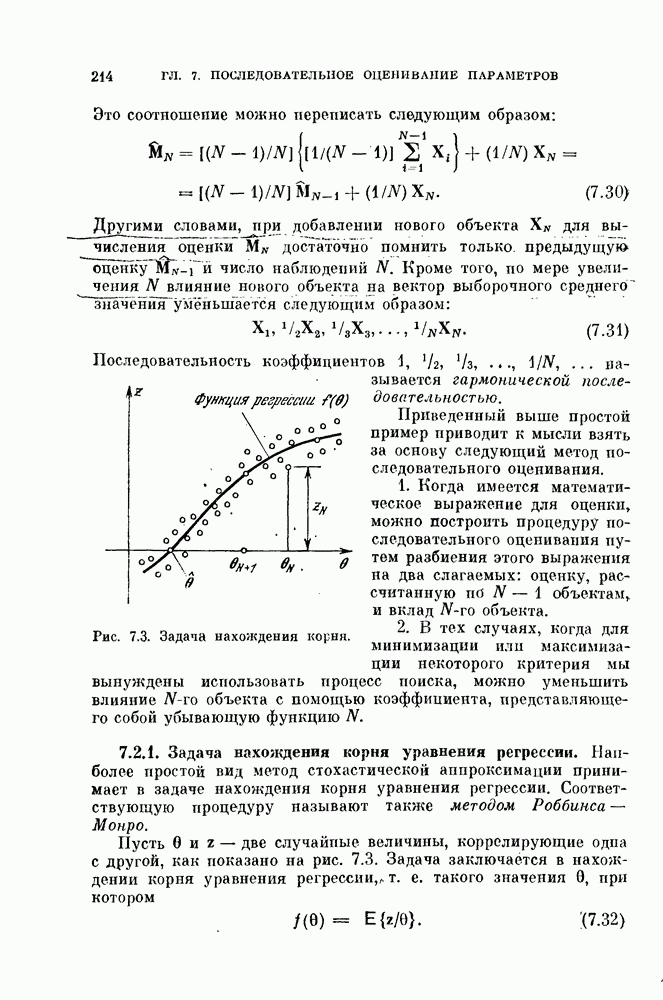
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
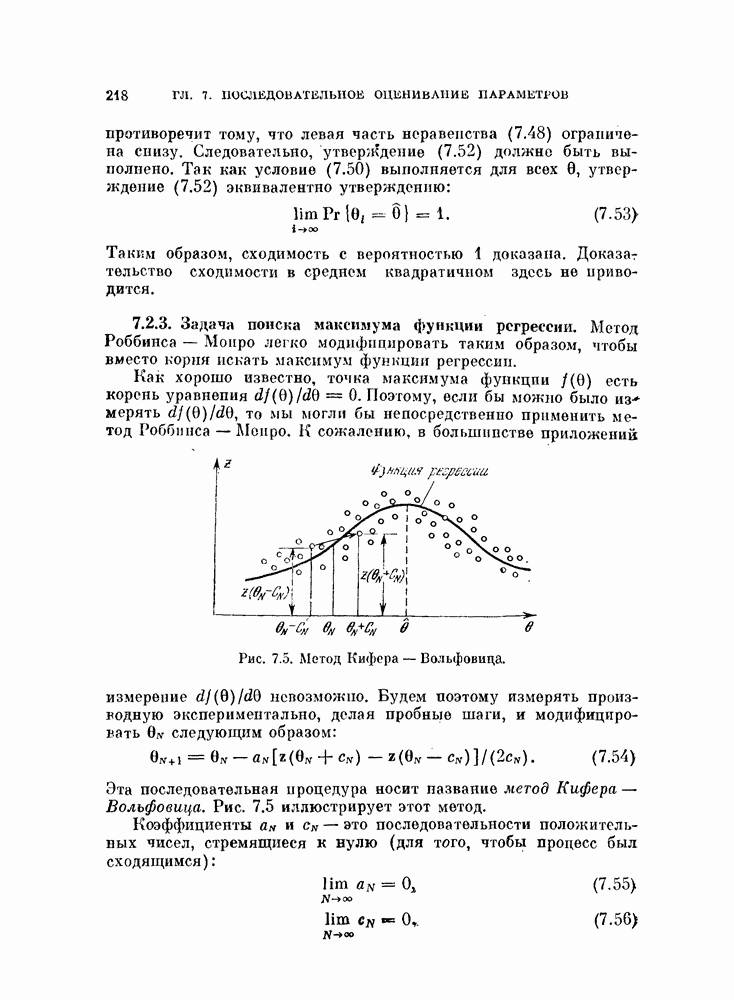
- 7.2.3. Задача поиска максимума функции регрессии.
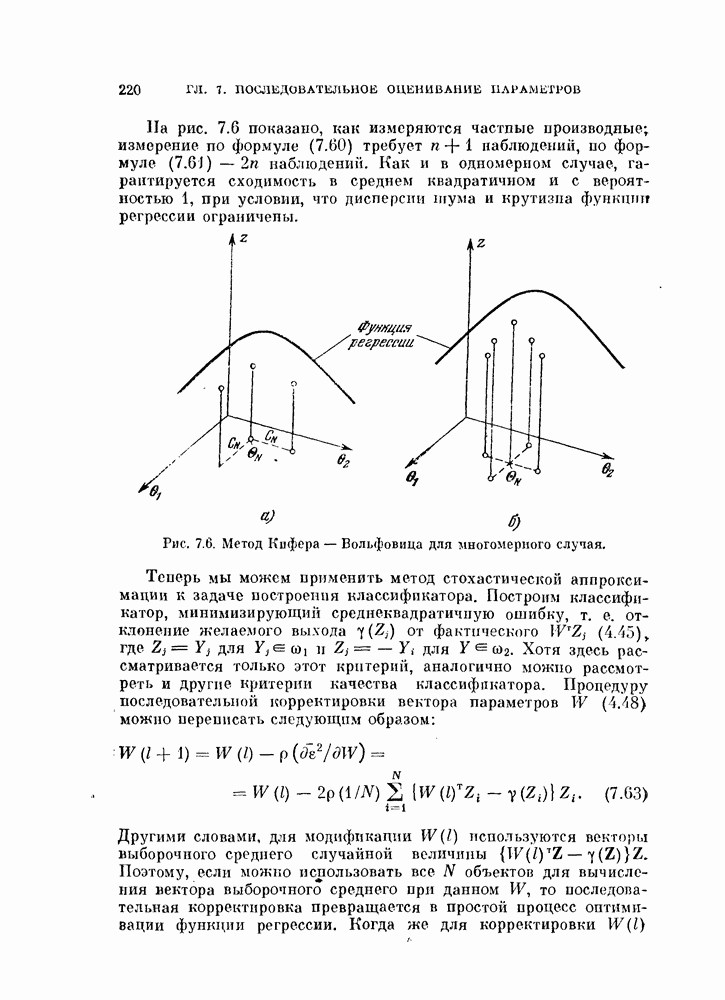
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
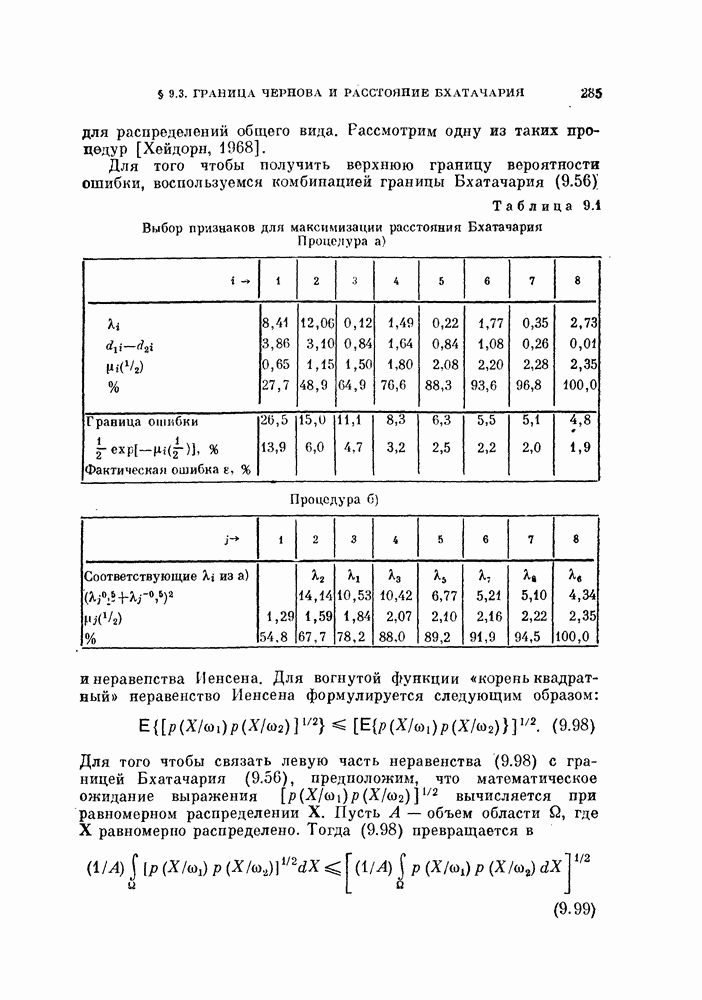
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
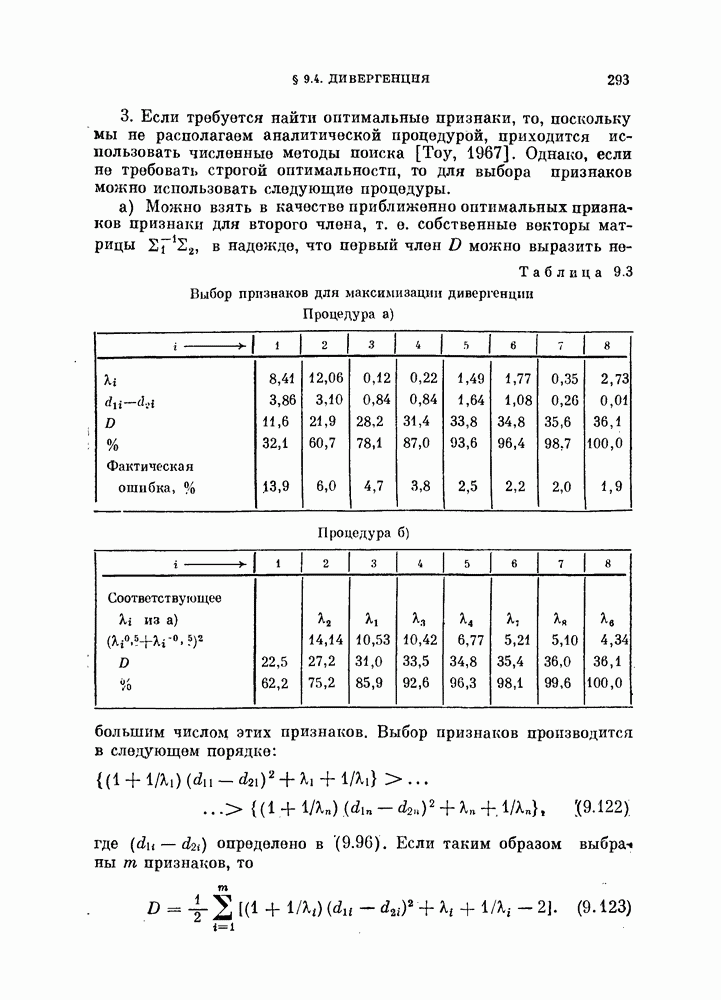
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА