| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.1.2. Определение числа классов.
До сих пор мы игнорировали проблему определения числа классов М. Хотелось бы, чтобы процедура автоматической классификации позволяла не только найти классификацию, но и определить М.
Пусть  — множество всех классификаций
— множество всех классификаций  объектов на М классов. Наш алгоритм автоматической классификации осуществляет поиск только среди классификаций
объектов на М классов. Наш алгоритм автоматической классификации осуществляет поиск только среди классификаций  Для большинства критериев
Для большинства критериев  алгоритм генерирует М непустых классов независимо от выбора М. Поэтому представляется необходимым иметь какой-либо метод выбора числа классов. К сожалению, единой общепринятой теории для определения М не существует. Поэтому нам остается довольствоваться описанием предложенных в разное время эвристических методов решения этой задачи.
алгоритм генерирует М непустых классов независимо от выбора М. Поэтому представляется необходимым иметь какой-либо метод выбора числа классов. К сожалению, единой общепринятой теории для определения М не существует. Поэтому нам остается довольствоваться описанием предложенных в разное время эвристических методов решения этой задачи.
Объединение и расщепление.
Основной алгоритм можно оиищить, введя в него процедуру образования и разрушения классов в ходе итерационного процесса. Можно или объединить два класса в один класс, или расщепить класс на два разных класса. Объединение и расщепление классов используется в хорошо известном алгоритме автоматической классификации, получившем наименование ISODATA [Болл, 1965а, б]. На каждой итерации этого алгоритма вначале происходит перебрасывание объектов из класса в класс без изменения числа классов. Затем к имеющимся на данный момент классам применяется процедура объединения или расщепления. Процедура объединения объединяет в один класс каждую пару классов, средние векторы которых находятся друг от друга на расстоянии, меньшем заданного порога. Процедура расщепления расщепляет или не расщепляет каждый класс в зависимости от плотности его заполнения и свойств выборочной матрицы коварнации.
Процедуры объединения и расщепления чередуются от итерации к итерации.
Само собой разумеется, что этот алгоритм является эвристическим. Его достоинство заключается в его эффективности и в том, что вмешательство человека в его работу сводится к минимуму.
Многократная дихотомия.
В некотором отношении более предпочтительными являются методы, зависящие целиком лишь от критерия классификации  Один такой метод предложен в [Ватанабе, 1969] и состоит в следующем.
Один такой метод предложен в [Ватанабе, 1969] и состоит в следующем.
Предположим, что при  имеется несколько разных классификаций, дающих почти минимальное значение
имеется несколько разных классификаций, дающих почти минимальное значение  Если эти классификации отличаются лишь классификацией нескольких объектов, то нет причины предполагать наличие белее чем двух классов. Однако, если классификации отличаются намного, то очевидно, что в действительности имеется несколько классов.
Если эти классификации отличаются лишь классификацией нескольких объектов, то нет причины предполагать наличие белее чем двух классов. Однако, если классификации отличаются намного, то очевидно, что в действительности имеется несколько классов.
На рис. 11.1 показаны две возможные дихотомии множества объектов, состоящего из трех классов  Первая дихотомия делит объекты на два класса
Первая дихотомия делит объекты на два класса  вторая — на классы
вторая — на классы  Таким образом, видно, что
Таким образом, видно, что  — это три разных класса (через А здесь обозначено дополнение множества А).
— это три разных класса (через А здесь обозначено дополнение множества А).
Рассмотрим теперь более общий случай, когда имеется к дихотомий совокупности объектов, состоящей из М классов. Каждая дихотомия разделяет эти объекты на две группы. Пусть  — множество всех объектов, отнесенных к группе
— множество всех объектов, отнесенных к группе  в результате
в результате  дихотомии
дихотомии  . Предположим, что выполняются следующие два условия:
. Предположим, что выполняются следующие два условия:
а) дихотомия относит каждый класс целиком в одну группу, т. е. классы нерасщепляются дихотомией;
б) для каждой пары классов имеется по крайней мере одна дихотомия, которая не относит оба класса к одной и той же группе.
Выберем по одной группе из каждой дихотомии и образуем подмножество С, являющееся пересечением всех к групп. По условию а), если подмножество С содержит один объект, то оно должно содержать все объекты того же класса. По условию б) для любого другого класса имеется по крайней мере одна из к выбранных групп, такая, что этот класс к ней не принадлежит. Поэтому, если С непусто, то С содержит один и только один класс. Следовательно, для того, чтобы построить все М классов, необходимо рассмотреть  подмножеств вида
подмножеств вида

где каждое  принимает значения 1 или 2. Каждое непустое множество С есть класс. Возвращаясь к нашему примеру, имеем
принимает значения 1 или 2. Каждое непустое множество С есть класс. Возвращаясь к нашему примеру, имеем

таким образом,

что согласуется с нашим предыдущим рассуждением.

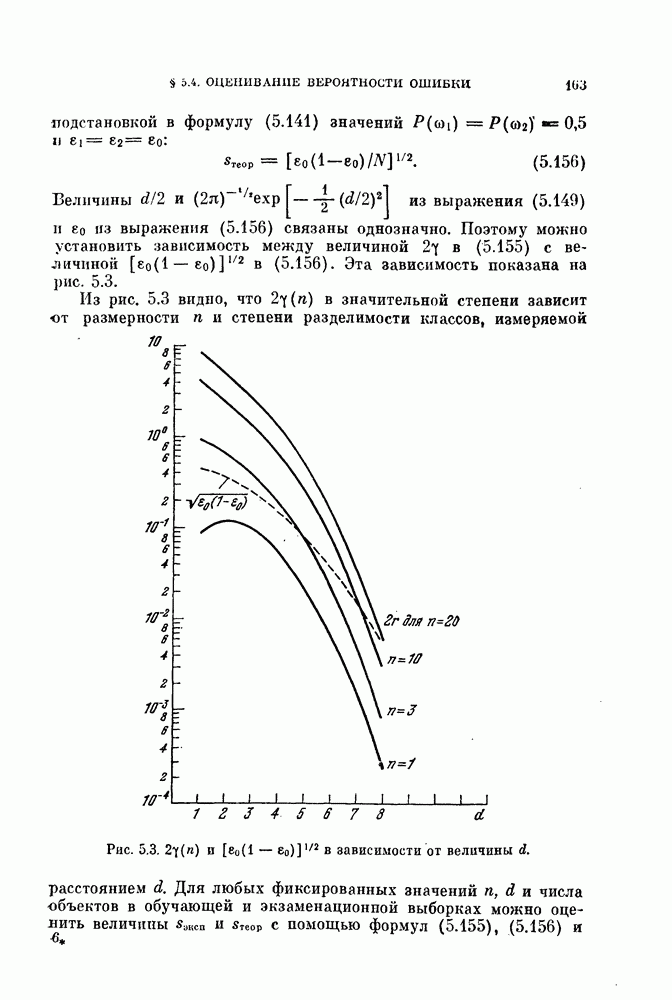
Рис. 11.1. Многократная дихотомия трех классов объектов.
Метод многократной дихотомии имеет более прочную теоретическую основу, чем процедура объединения и расщепления. Кроме того, он не использует никакого другого численного критерия, кроме  Однако практическая реализация метода многократной дихотомии может оказаться трудной, особенно в тех случаях, когда истинное число классов велико. Эта трудность может быть отчасти преодолена путем организации иерархической структуры на множестве классов. Объекты делятся на небольшое число классов, каждый класс делится в свою очередь, и т. д. При использовании этой стратегии не возникает необходимости
Однако практическая реализация метода многократной дихотомии может оказаться трудной, особенно в тех случаях, когда истинное число классов велико. Эта трудность может быть отчасти преодолена путем организации иерархической структуры на множестве классов. Объекты делятся на небольшое число классов, каждый класс делится в свою очередь, и т. д. При использовании этой стратегии не возникает необходимости
находить все возможные дихотомии всей совокупности объектов.
В этом месте мы отклонились от рассмотрения алгоритма автоматической классификации. Очевидно, это рассмотрение не закончено, однако основа для построения процедур автоматической классификации у нас уже есть. Нам недостает лишь той уверенности в правильности нашего метода, которая была у нас при решении задач распознавания образов с учителем. Обратимся поэтому к детальному рассмотрению критериев качества классификации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
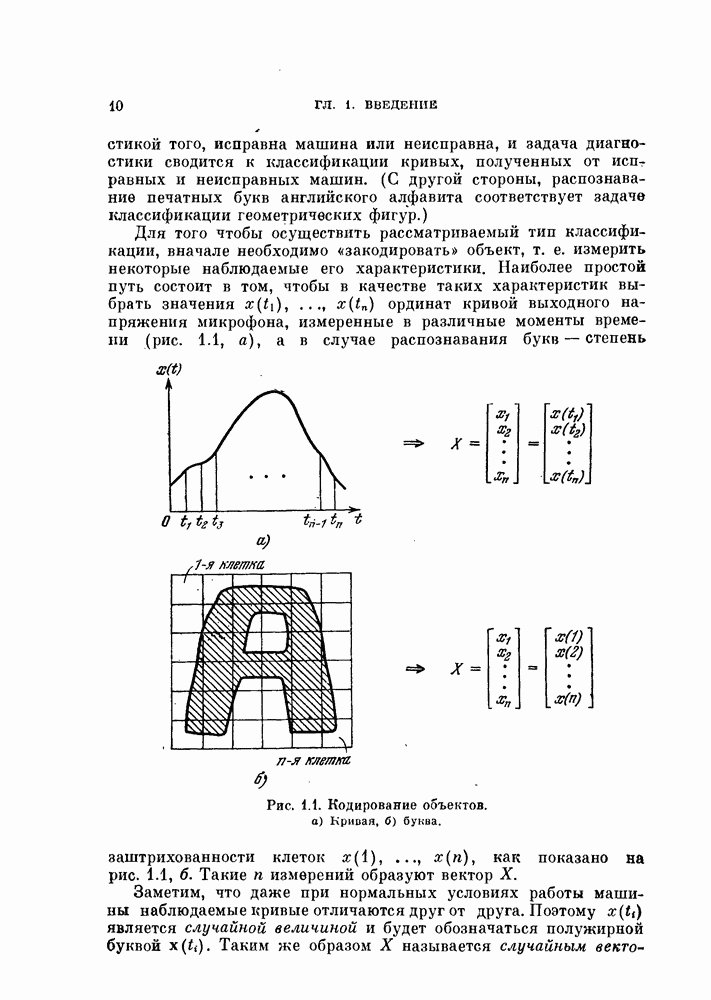
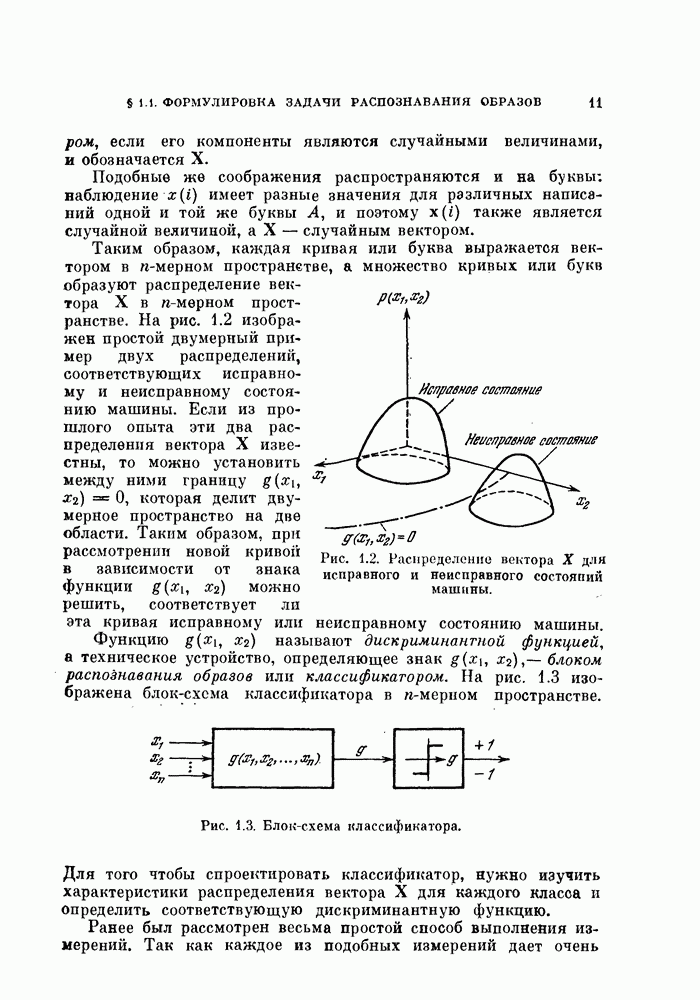
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
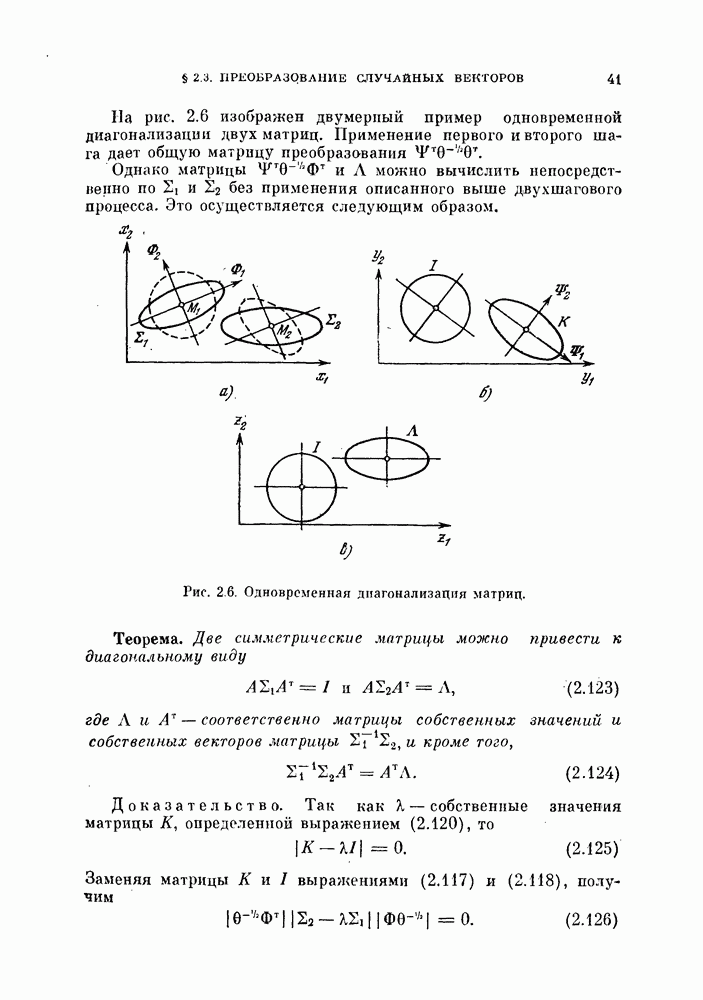
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
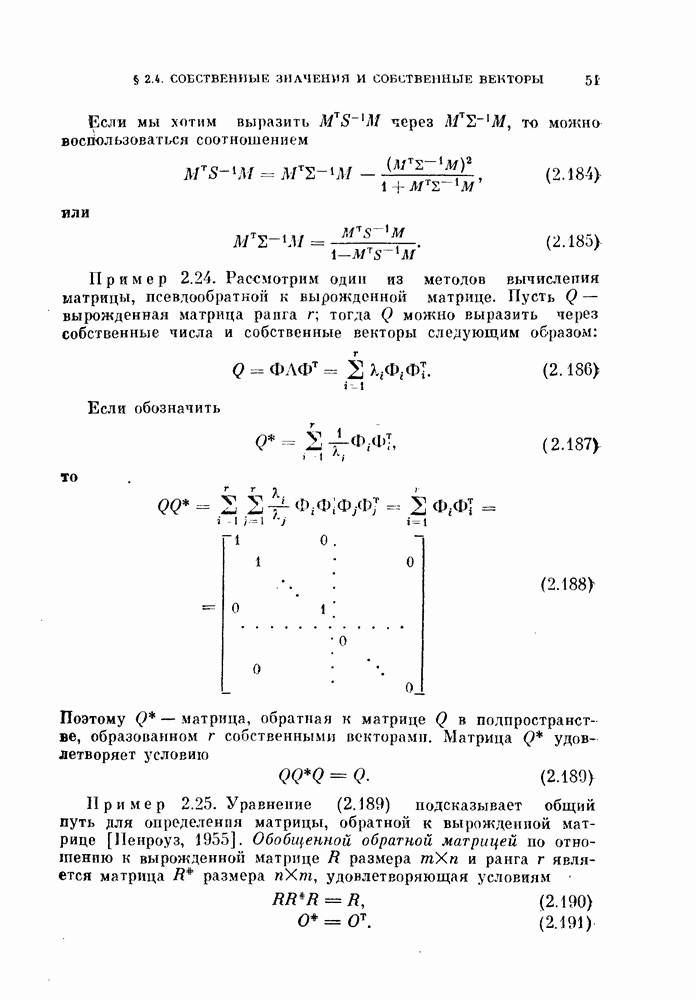
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
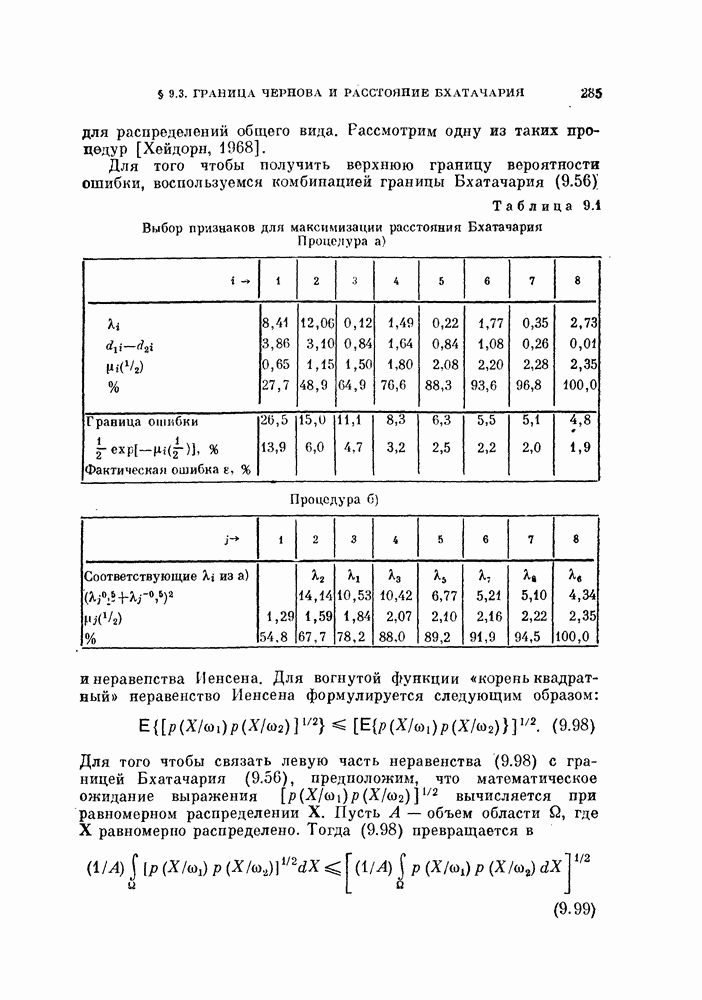
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
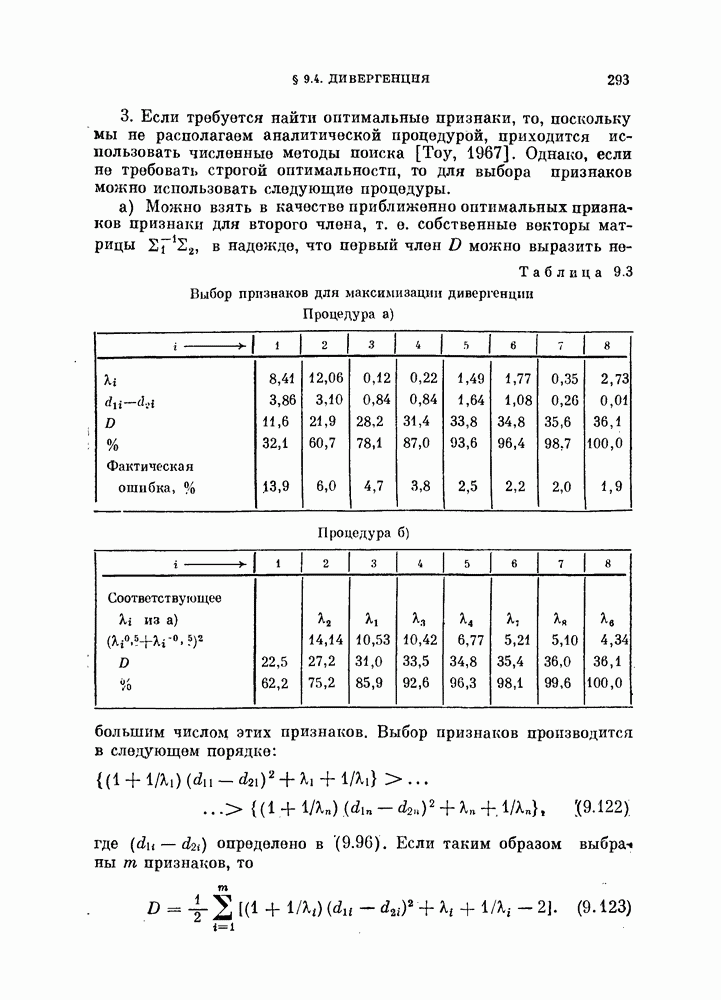
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА