| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7.3. Последовательное байесовское оценивание
Так как оценки параметров являются случайными векторами, полная информация о статистических свойствах оценок содержится в их совместной плотности вероятности, функции распределения вероятностей или характеристических функциях. В этом параграфе мы покажем, как плотность вероятностей оценки можег быть вычислена с помощью последовательной процедуры.
7.3.1. Оценивание в схеме с поощрением.
Пусть  объектов, которые используются для оценки плотности векторного параметра
объектов, которые используются для оценки плотности векторного параметра  Значения X поступают последовательно одно за другим. Воспользовавшись теоремой Байеса, можно получить рекуррентное выражение для условной плотности вероятности параметра
Значения X поступают последовательно одно за другим. Воспользовавшись теоремой Байеса, можно получить рекуррентное выражение для условной плотности вероятности параметра  при фиксированных
при фиксированных 

где априорная плотность вероятности  вектора
вектора  предполагается известной. Если числитель (7.82) известен, то знаменатель можно найти, интегрируя числитель:
предполагается известной. Если числитель (7.82) известен, то знаменатель можно найти, интегрируя числитель:

Таким образом, выражение (7.82) показывает, что если  известна, то
известна, то  может быть вычислена. Повторение этой операции до тех пор, пока
может быть вычислена. Повторение этой операции до тех пор, пока  не станет равным единице, показывает, что для того, чтобы начать эту последовательность вычислений, нужно знать только
не станет равным единице, показывает, что для того, чтобы начать эту последовательность вычислений, нужно знать только  Функция
Функция  является априорной плотностью вероятности 0 и отражает наше начальное знание о параметре
является априорной плотностью вероятности 0 и отражает наше начальное знание о параметре 
Оценивание вектора математического ожидания при известной ковариационной матрице.
Оценим вектор математического ожидания М нормального распределения с известной ковариационной матрицей Е. Плотность вероятности  предполагается нормальной с вектором математического ожидания
предполагается нормальной с вектором математического ожидания  и ковариационной матрицей
и ковариационной матрицей  Тогда, после наблюдения первого объекта
Тогда, после наблюдения первого объекта  имеем
имеем

где

Таким образом, плотность вероятности  также нормальна, а ее вектор математического ожидания и ковариационная матрица определяются формулами
также нормальна, а ее вектор математического ожидания и ковариационная матрица определяются формулами  Так как интеграл
Так как интеграл  в (7.84) не зависит от М, то С, и
в (7.84) не зависит от М, то С, и  являются константами, не зависящими от
являются константами, не зависящими от  и такими, что
и такими, что

Повторим тот же процесс, заменив параметры  плотности вероятности
плотности вероятности  параметрами
параметрами  плотности вероятности
плотности вероятности  Плотность вероятности
Плотность вероятности  также нормальна, а
также нормальна, а  вычисляются по формулам (7.85) и (7.86) с подстановкой
вычисляются по формулам (7.85) и (7.86) с подстановкой  вместо
вместо  Таким образом, после
Таким образом, после  итераций получим
итераций получим

где  обозначает нормальное распределение с вектором математического ожидания
обозначает нормальное распределение с вектором математического ожидания  и ковариационной матрицей 1. Значения
и ковариационной матрицей 1. Значения  определяются следующим образом:
определяются следующим образом:

С увеличением  влияние начальных значений
влияние начальных значений  уменьшается, и в пределе получим
уменьшается, и в пределе получим

Таким образом, при больших  оценкой математического ожидания является выборочное среднее, а дисперсия этой оценки равна
оценкой математического ожидания является выборочное среднее, а дисперсия этой оценки равна 
При описании этого вычислительного процесса мы постоянна обращали внимание на то, что как априорная, так и апостериорная плотности вероятности всегда нормальны. Вследствие этого мы рекуррентно вычисляли только параметры  и
и  а не сами плотности. Если апостериорная плотность вероятности в каждой итерации является членом того же семейства функций, что
а не сами плотности. Если апостериорная плотность вероятности в каждой итерации является членом того же семейства функций, что  априорная плотность вероятности, и изменяются лишь ее параметры, то мы называем такую плотность вероятности самосопряженной или воспроизводимой.
априорная плотность вероятности, и изменяются лишь ее параметры, то мы называем такую плотность вероятности самосопряженной или воспроизводимой.
Доказано, что, кроме упрощения вычислений, воспроизводимая плотность вероятности имеет то преимущество, что при  она становится все более «концентрированной» и сходится в определенном смысле к истинному вектору параметров
она становится все более «концентрированной» и сходится в определенном смысле к истинному вектору параметров  [Спрэджинс, 1963, 1965]. Многие хорошо известные плотности вероятности, которые вместе с тем являются и воспроизводимыми перечислены в [Спрэджинс, 1965].
[Спрэджинс, 1963, 1965]. Многие хорошо известные плотности вероятности, которые вместе с тем являются и воспроизводимыми перечислены в [Спрэджинс, 1965].
Оценивание ковариационной матрицы при пулевом векторе математического ожидания.
Последовательное оценивание ковариационпой матрицы нормально распределенного случайного вектора X может быть рассмотрено таким же образом, как оценивание вектора математического ожидания. Предполагается, что вектор математического ожидания известен и, без ограничения общности, — что он равен нулю. Ранее мы предположили, что априорная плотность вероятности  является нормальной. С другой стороны, известно, что выборочная ковариационная матрица имеет распределение Уишарта. Поэтому мы начнем с распределения выборочной ковариационной матрицы
является нормальной. С другой стороны, известно, что выборочная ковариационная матрица имеет распределение Уишарта. Поэтому мы начнем с распределения выборочной ковариационной матрицы  где
где  — число объектов и
— число объектов и  — начальное предположение об истинной ковариационной матрице. Значение
— начальное предположение об истинной ковариационной матрице. Значение  — это число объектов для начальной выборочной ковариационной матрицы, и его можно рассматривать как доверительную константу для начальной оценки
— это число объектов для начальной выборочной ковариационной матрицы, и его можно рассматривать как доверительную константу для начальной оценки  Далее, вместо вычисления
Далее, вместо вычисления  вычислим
вычислим  где
где  Это делается потому, что ковариационная матрица в случае нормального распределения всегда используется в обращенной форме. Тогда
Это делается потому, что ковариационная матрица в случае нормального распределения всегда используется в обращенной форме. Тогда  определяется следующим образом:
определяется следующим образом:

где

Используя (7.92) в качестве  и многократно применяя рекуррентную процедуру (7.82), получим для плотности вероятности
и многократно применяя рекуррентную процедуру (7.82), получим для плотности вероятности  снова распределение Уишарта с параметрами [Кишн, 1965]:
снова распределение Уишарта с параметрами [Кишн, 1965]:

Следовательно, с увеличением  оценка
оценка  приближается к выборочной ковариационной матрице
приближается к выборочной ковариационной матрице  с нулевым средним значением.
с нулевым средним значением.
Оценивание вектора математического ожидания и ковариационной матрицы.
Когда последовательно оцениваются как вектор математического ожидания, так и ковариационная матрица, необходимо
вычислить совместную апостериорную плотность вероятности  Когда М и
Когда М и  оцениваются выборочным средним и выборочной ковариационной матрицей,
оцениваются выборочным средним и выборочной ковариационной матрицей,  нормально распределенная случайная величина, плотность вероятности
нормально распределенная случайная величина, плотность вероятности  представляет собой распределение Гаусса — Уишарта:
представляет собой распределение Гаусса — Уишарта:

где  задается формулой (7.93). Значение
задается формулой (7.93). Значение  является доверительной константой для начальной оценки
является доверительной константой для начальной оценки  так же как значение
так же как значение  для оценки
для оценки  . И в этом случае, используя выражение (7.96) в качестве
. И в этом случае, используя выражение (7.96) в качестве  и многократно применяя рекуррентную процедуру (7.82), получим для плотности вероятности
и многократно применяя рекуррентную процедуру (7.82), получим для плотности вероятности  распределение Гаусса — Уишарта с параметрами [Кишн, 1965]:
распределение Гаусса — Уишарта с параметрами [Кишн, 1965]:

Оценивание в случае без поощрения. Предположим, что имеются два распределения, характеризуемые параметрами  При последовательном оценивании без поощрения ставится задача последовательно оценить параметры
При последовательном оценивании без поощрения ставится задача последовательно оценить параметры  предполагая, что нам неизвестны истинные распределения, в соответствии с которыми появляются объекты. Эту задачу называют также задачей обучения без учителя. Вследствие добавочной неопределенности, которую мы вводим, вычисление такой оценки оказывается более сложным. Однако разработка этого типа методов оправдывается надеждой, что после начального обучения с поощрением машина сможет улучшать качество распознавания без какого-либо внешнего вмешательства.
предполагая, что нам неизвестны истинные распределения, в соответствии с которыми появляются объекты. Эту задачу называют также задачей обучения без учителя. Вследствие добавочной неопределенности, которую мы вводим, вычисление такой оценки оказывается более сложным. Однако разработка этого типа методов оправдывается надеждой, что после начального обучения с поощрением машина сможет улучшать качество распознавания без какого-либо внешнего вмешательства.
Так как мы не знаем, к какому классу принадлежит объект  самое большое, что мы можем сказать, — это то, что X принадлежит классу
самое большое, что мы можем сказать, — это то, что X принадлежит классу  с вероятностью
с вероятностью  Поэтому априорная плотность вероятности (7.82) принимает вид
Поэтому априорная плотность вероятности (7.82) принимает вид

Следовательно, если нам известны априорная плотность вероятности каждого класса  и априорные вероятности классов
и априорные вероятности классов  то плотность вероятностей
то плотность вероятностей  можно вычислить по формуле (7.101), а
можно вычислить по формуле (7.101), а  — по формуле (7.83). Таким образом, мы получаем рекуррентное выражение для апостериорной плотности вероятности в виде
— по формуле (7.83). Таким образом, мы получаем рекуррентное выражение для апостериорной плотности вероятности в виде

Таким образом, процедура последовательного оценивания без поощрения (7.102) по смыслу не отличается от процедуры последовательного оценивания с поощрением (7.82). Но из-за того, что при вычислении априорной плотности вероятности используется суммирование, свойство воспроизводимости утрачивается для всех плотностей, включая нормальную, и уже нельзя ограничиться оценкой набора параметров: мы должны иметь дело с рекуррентным оцениванием многомерных функций.
Использование всех имеющихся объектов одновременно позволяет построить более удобные для практики методы оценивания и классификации без поощрения. Задача формулируется как задача нахождения «скоплений» (групп) данных объектов и естественных границ этих групп без использования информации о принадлежности объектов к тому или иному классу. Эта задача будет рассмотрена в гл. 11.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
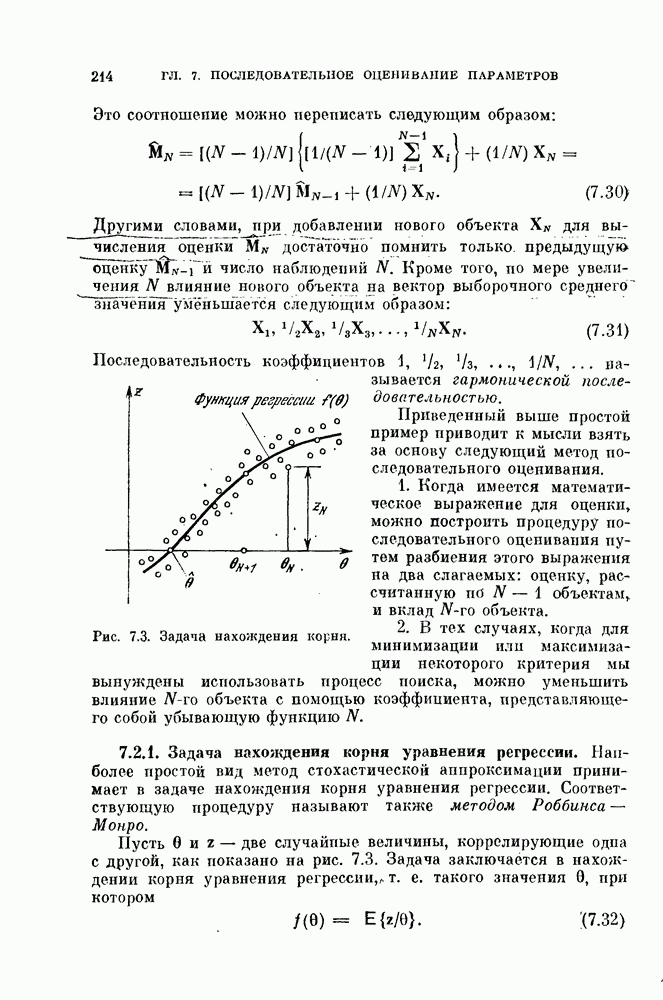
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
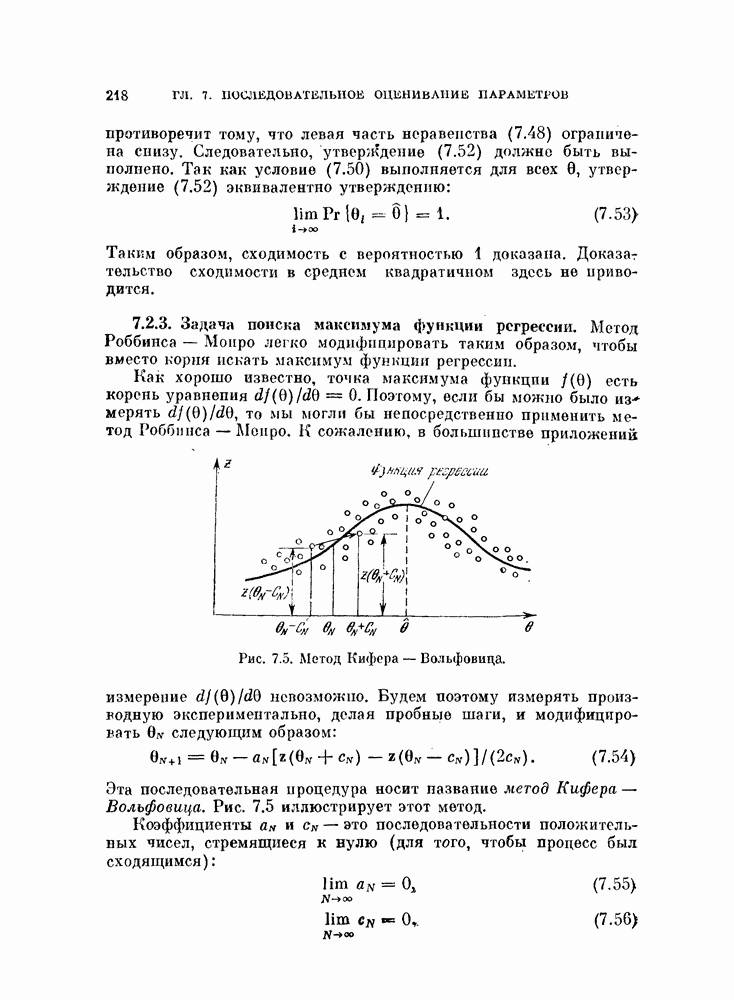
- 7.2.3. Задача поиска максимума функции регрессии.
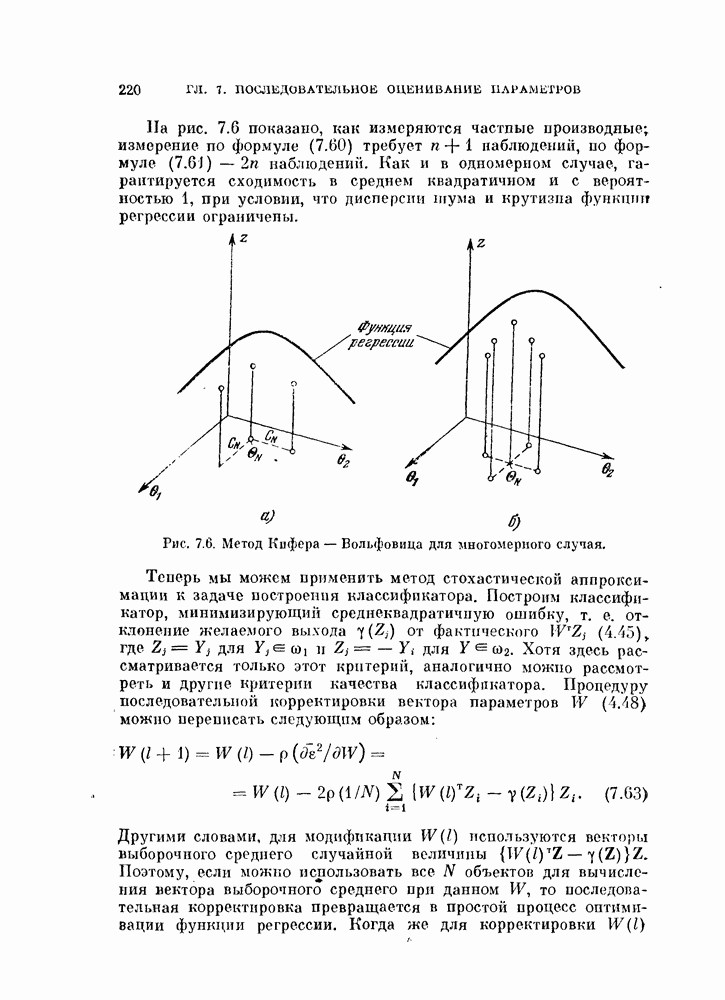
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
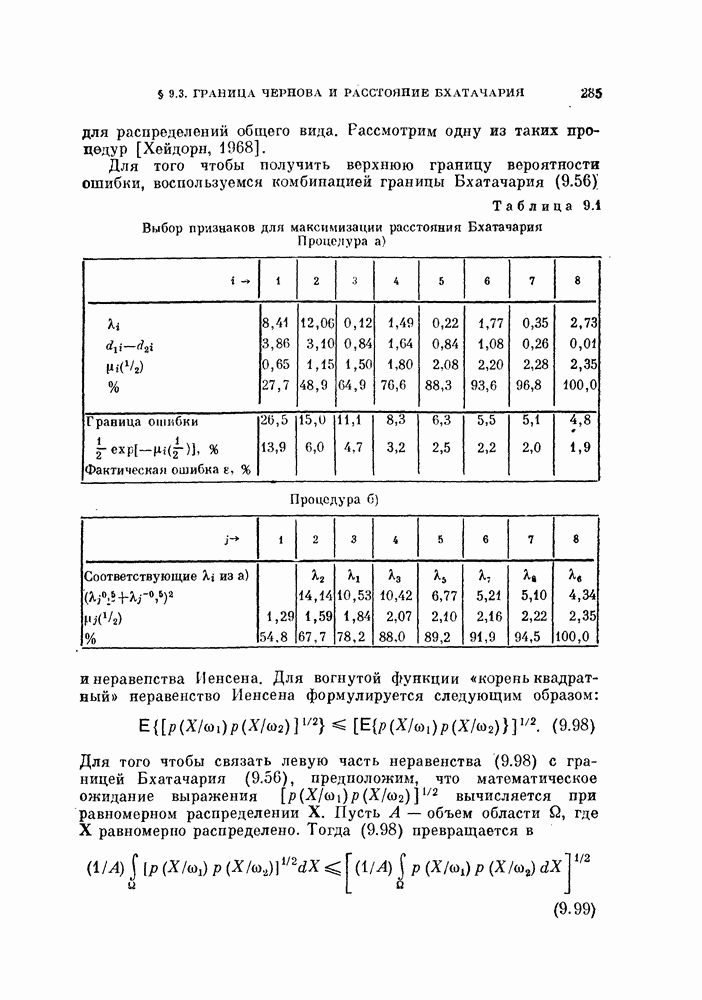
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
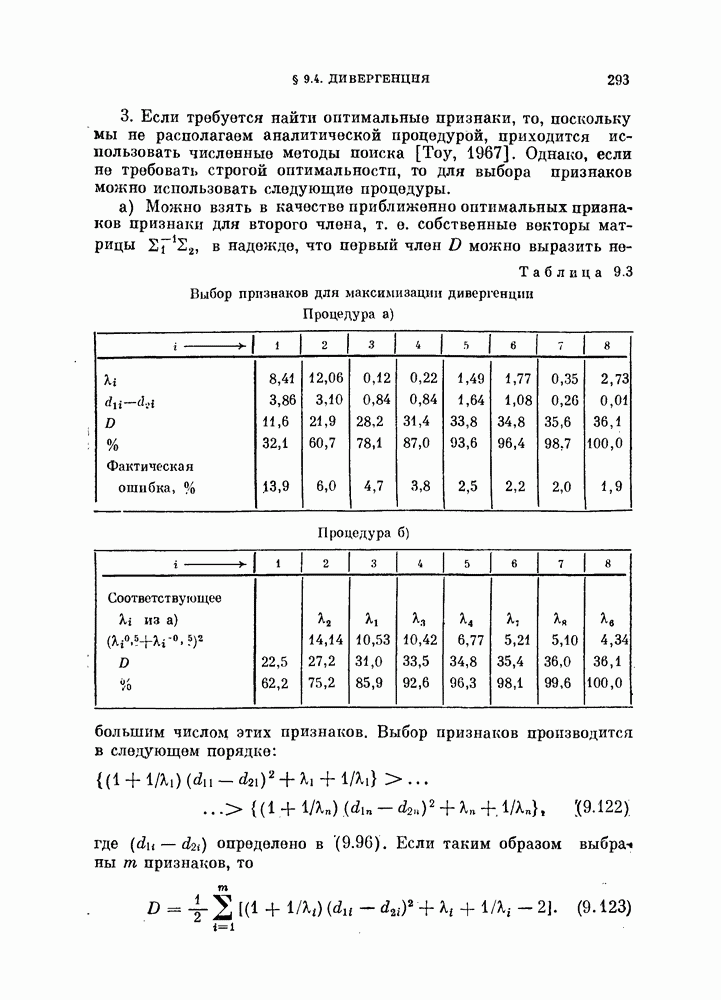
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА