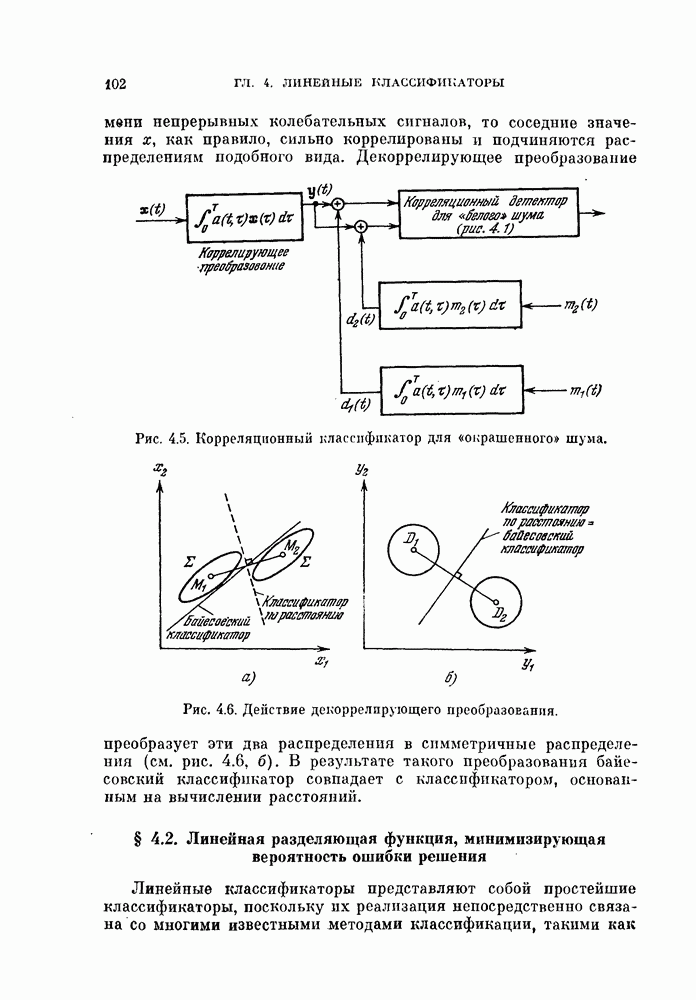
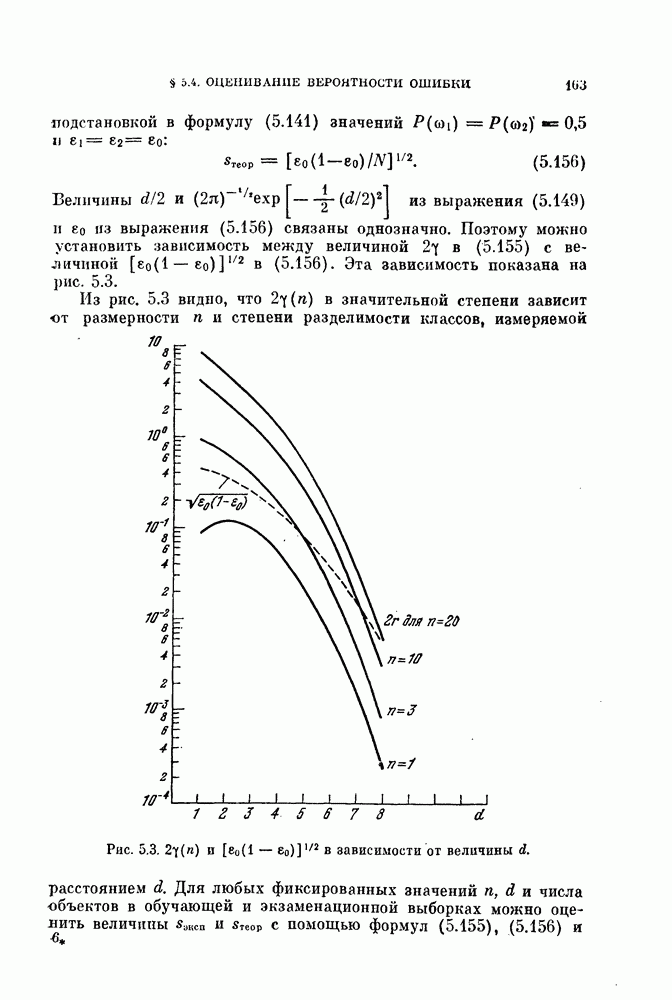
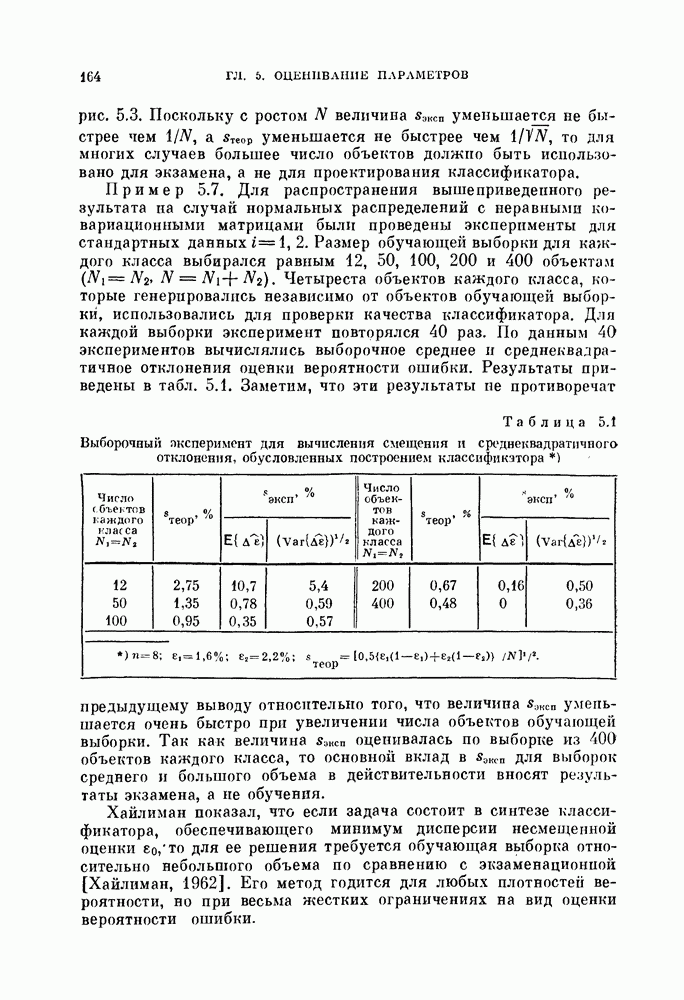
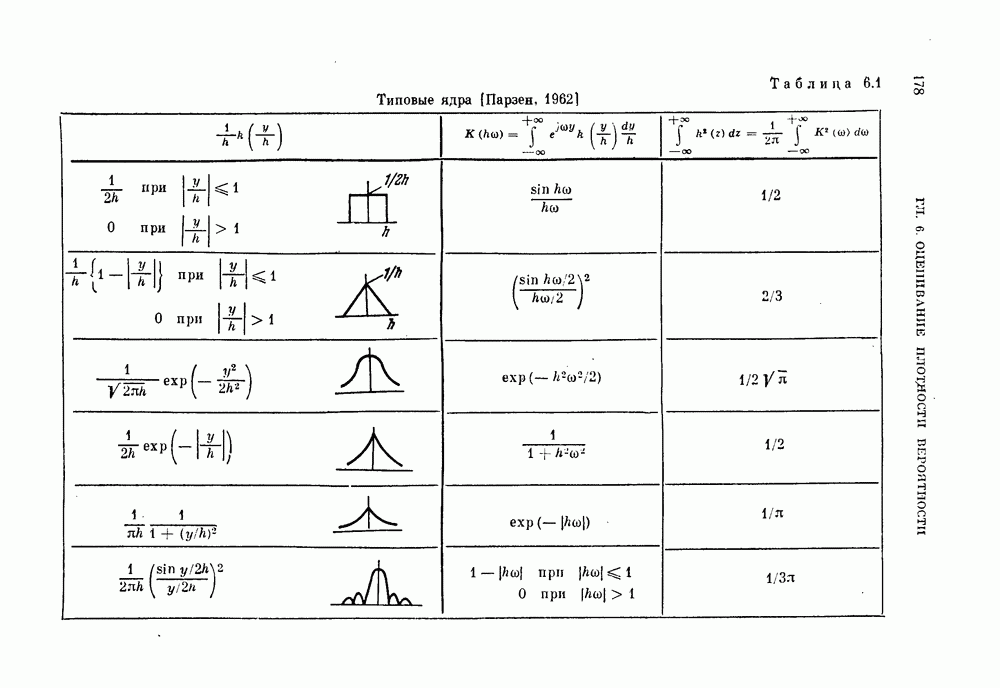
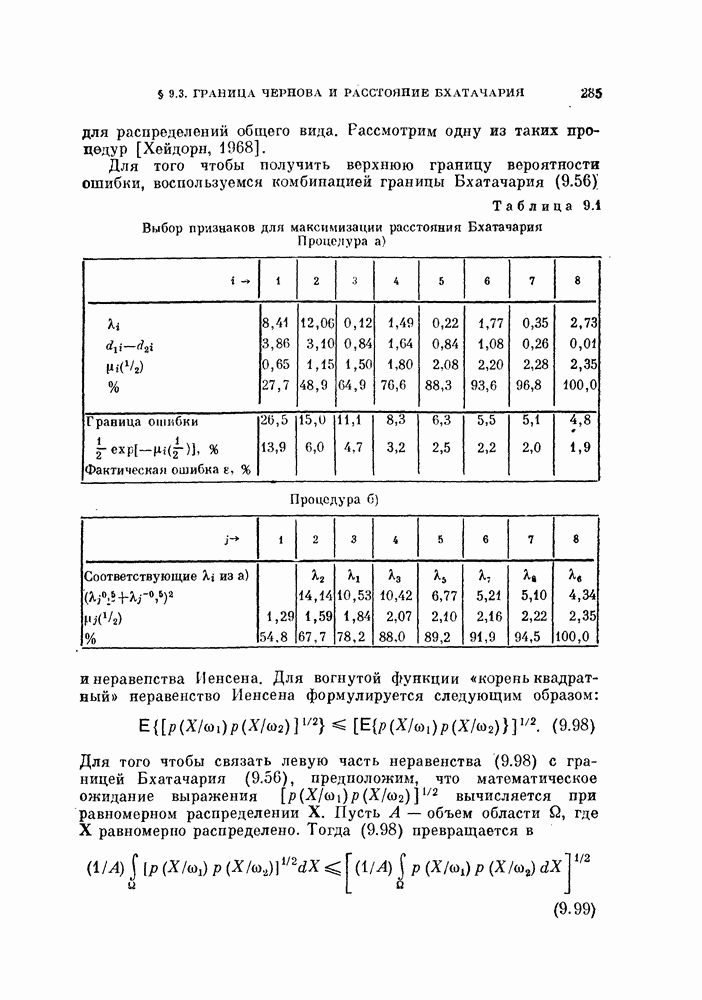
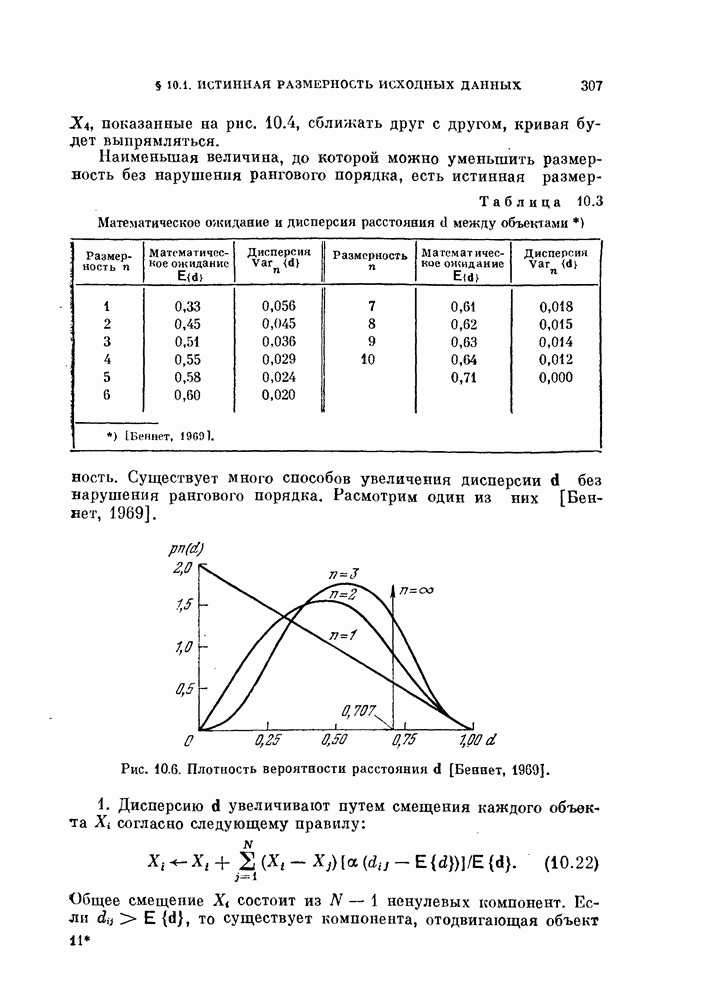
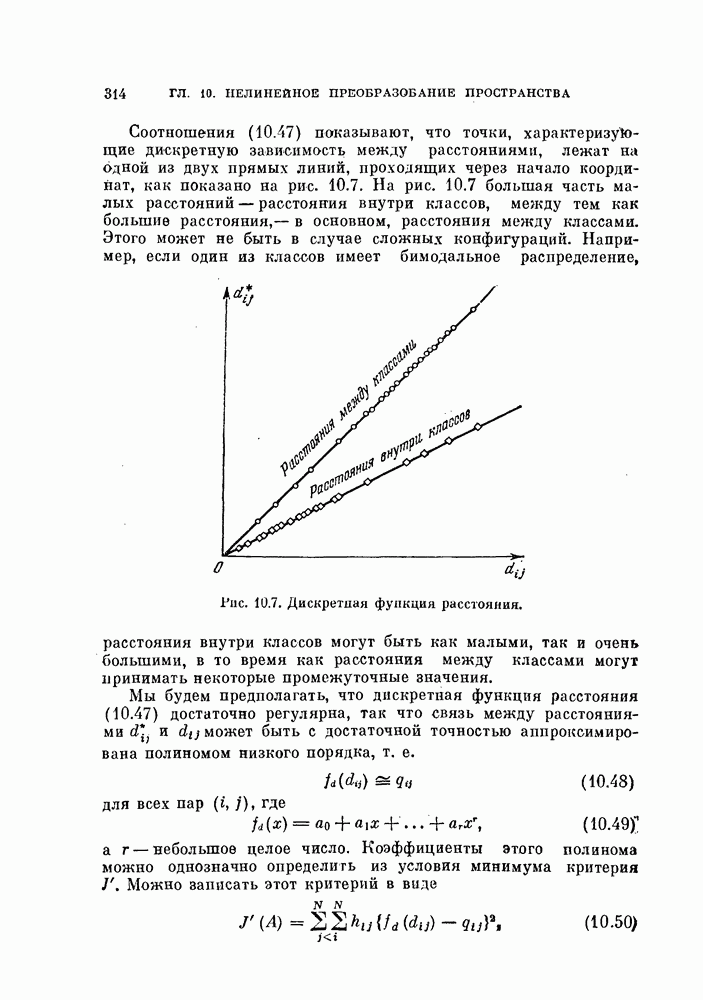
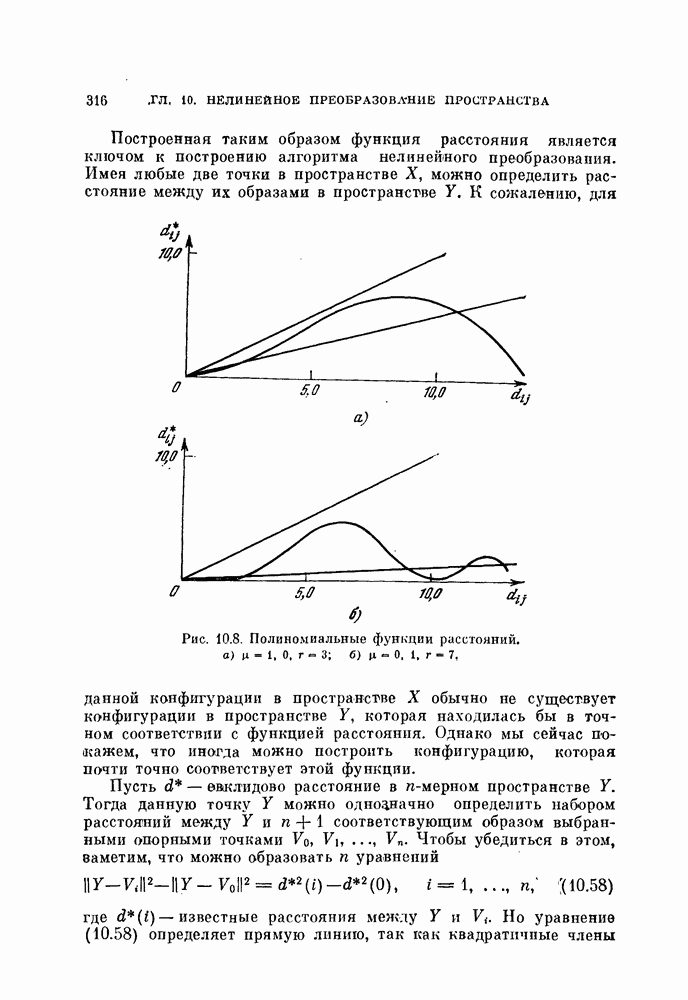
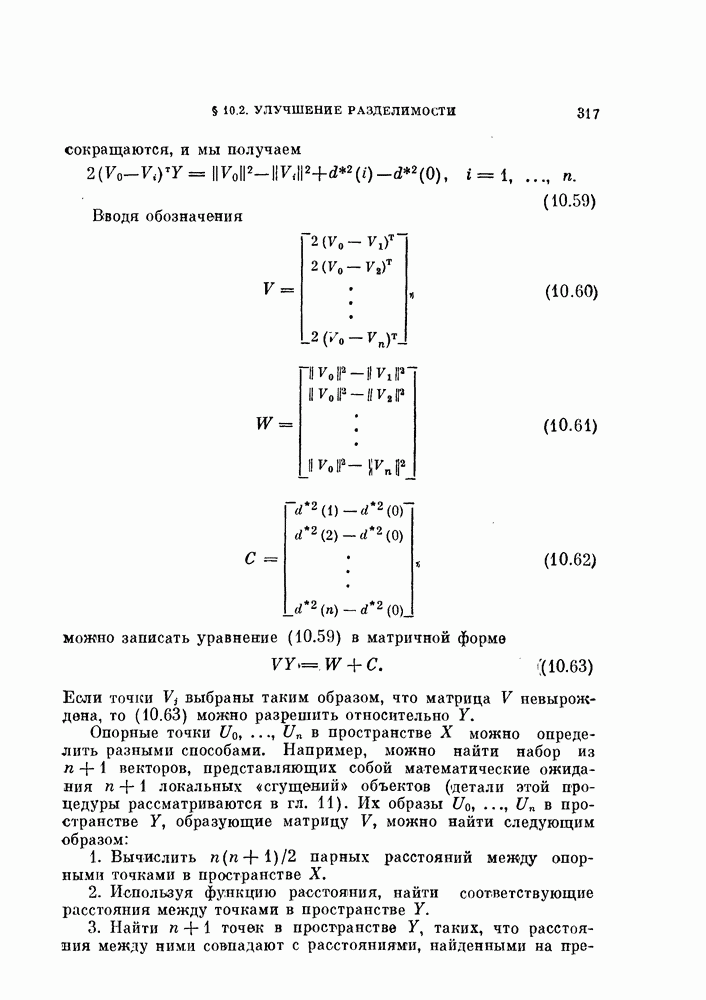
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5.2. Кусочно-линейные разделяющие функции.
Линейные разделяющие функции находят широкое применение в задачах.
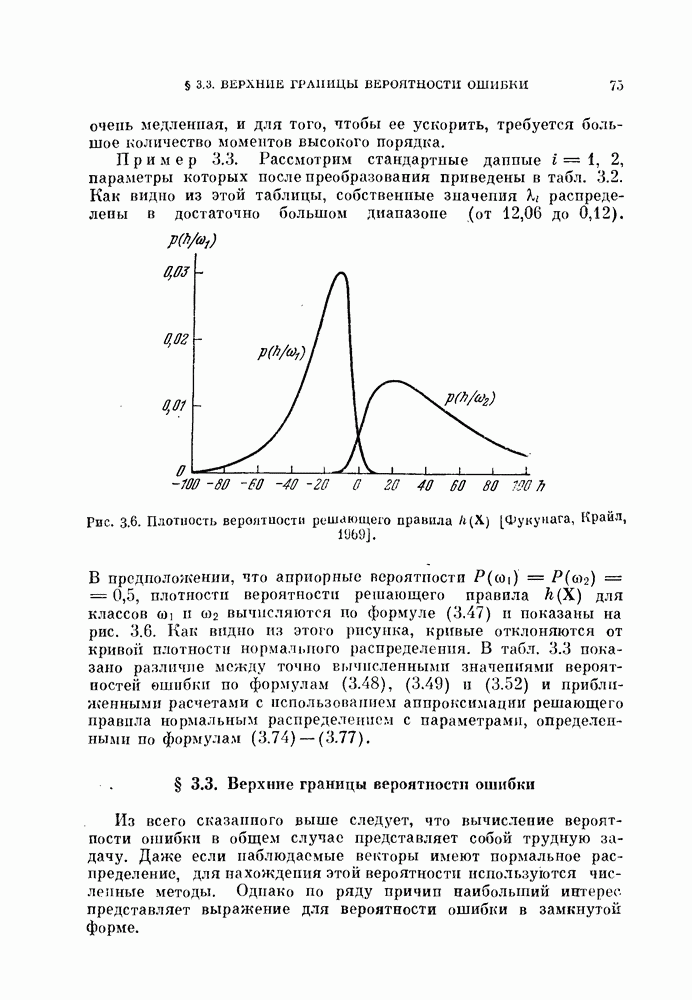
распознавания образов для случая двух классов, хотя при этом неизбежна некоторая потеря качества распознавания. Однако при трех или большем числе классов качество распознавания с использованием линейной разделяющей функции часто оказывается неприемлемым. Это может произойти и при двух классах, если каждый класс состоит из нескольких групп объектов.
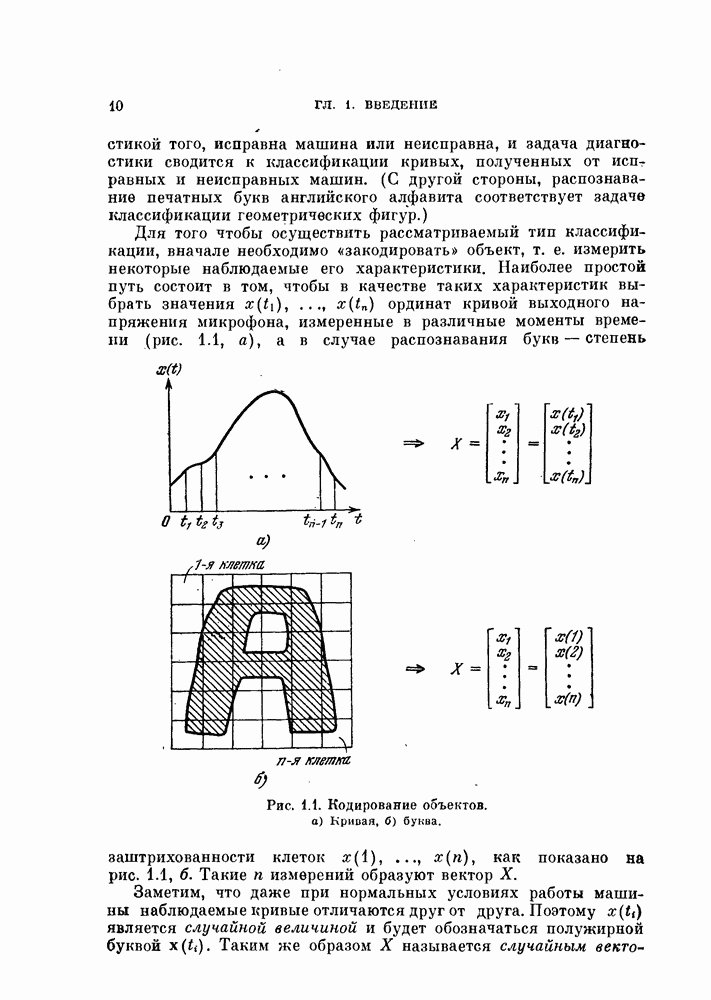
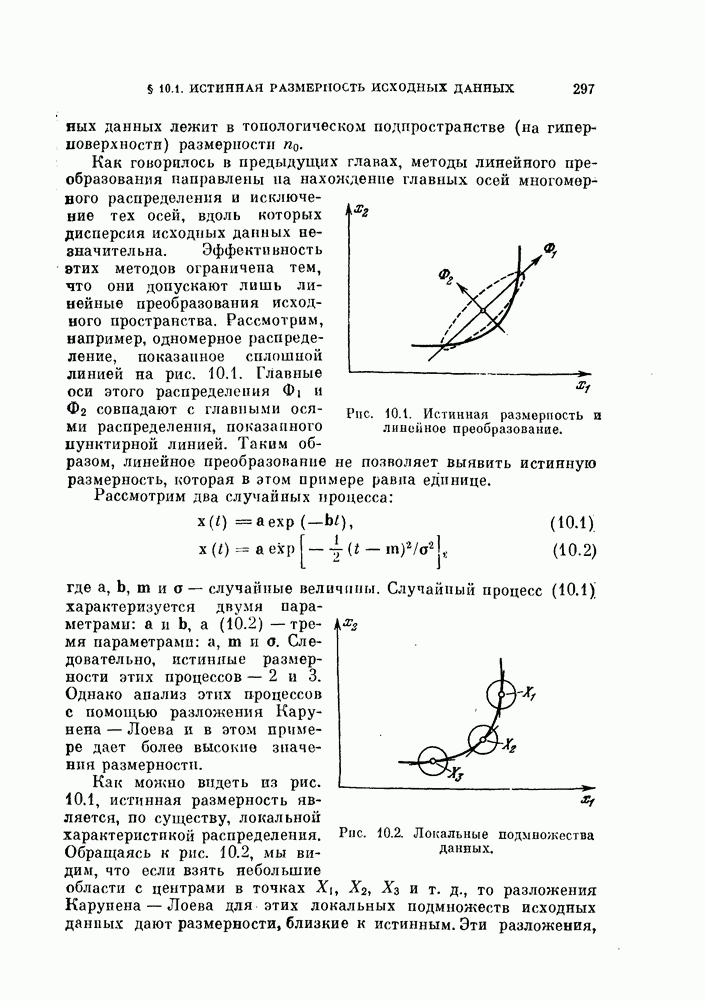
Если в этих случаях воспользоваться совокупностью линейных разделяющих функций, т. е. кусочно-линейной разделяющей функцией, то появляются дополнительные возможности улучшения качества распознавания. На рис. 4.11 изображен пример задачи распознавания при наличии четырех классов.

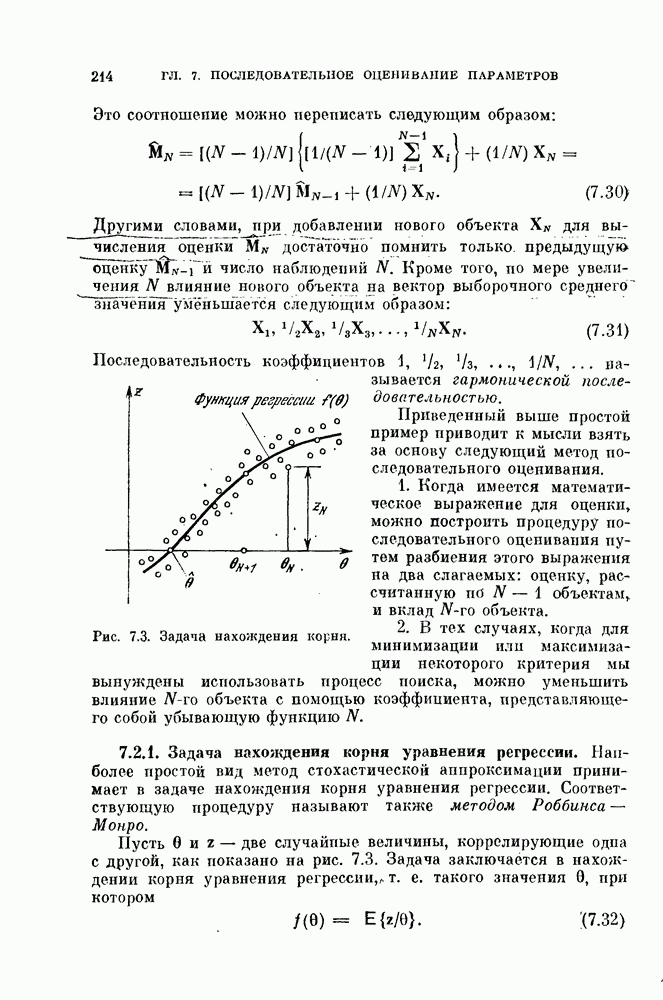
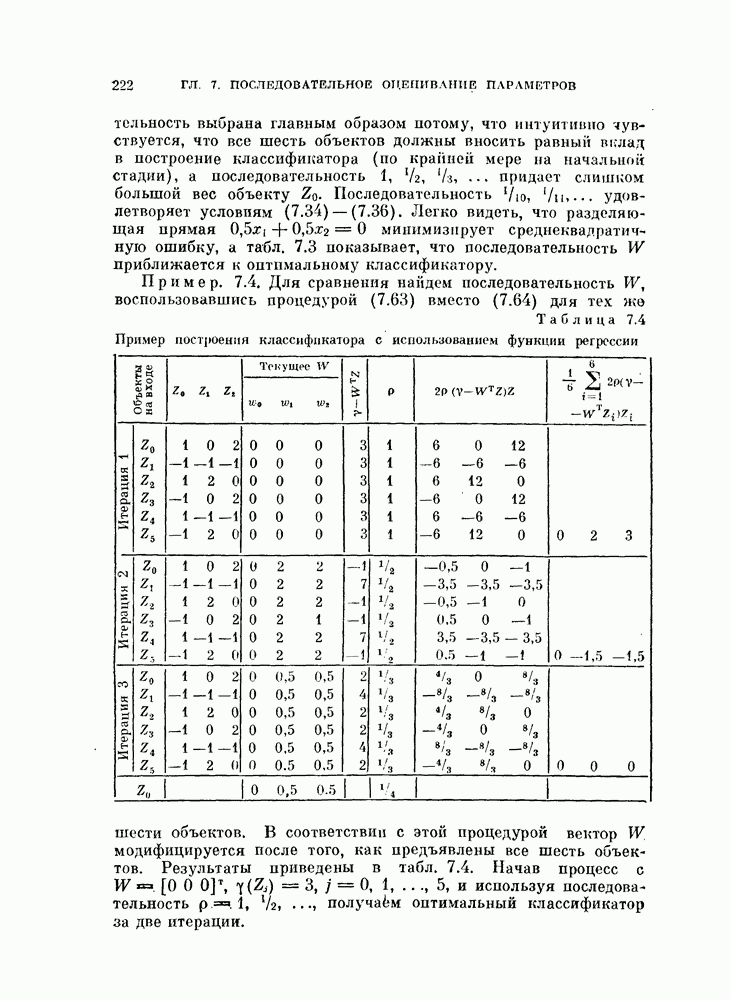
Рис. 4.11. Четыре распределения: а) байесовский классификатор; б) кусочно-линейный классификатор.
В задачах со многими классами критерии проверки многих гипотез дают наилучшее в байесовском смысле решающее правило, обеспечивающее минимум риска пли вероятности ошибки В соответствии с критерием проверки гипотез плотность вероятности каждого класса или ее логарифм следует сравнить с плотностями вероятности других классов, как следует из (3.114). На рис. 4.11, а изображены полученные таким образом границы. Если оценивание плотностей вероятности является слишком сложной задачей или границы, определяемые в соответствии с критерием проверки гипотез, достаточно «вычурные», то можно заменить эти сложные границы множеством простых линейных границ. Такая замена, конечно, приводит к некоторому ухудшению качества распознавания. Однако использование линейных границ особенно эффективно для задач распознавания многих классов, т. е. в тех случаях, когда сложность границ быстро возрастает с увеличением числа классов, и является желательным
некоторое упрощение процедуры синтеза классификатора. Например, на рис. 4.11, б показана замена байесовских границ (рис. 4.11, а) кусочно-линейными границами.
Множество линейных функций, соответствующее кусочно-линейной разделяющей функции, определяется следующим образом:

где М — число классов. Знаки  выбираются так, чтобы распределение класса
выбираются так, чтобы распределение класса  находилось в области положительных значений линейной функции
находилось в области положительных значений линейной функции  а распределение класса
а распределение класса  — в области отрицательных значений. Из этого требования следует, что
— в области отрицательных значений. Из этого требования следует, что

Предположим, что для каждого класса соответствующая область является выпуклой, как изображено на рис. 4.11,б. Тогда область класса  может быть просто определена следующим образом:
может быть просто определена следующим образом:

(функция  исключена из рассмотрения).
исключена из рассмотрения).

Рис. 4.12. Реализация кусочио-лниейиого классификатора.
Наличие заштрихованной области на рис. 4.11, б показывает, что М областей определяемые условиями (4.116), не обязательно покрывают  пространство. Если объект попадает в эту область, то кусочнолинейный классификатор не может принять решение о его
пространство. Если объект попадает в эту область, то кусочнолинейный классификатор не может принять решение о его
принадлежиости к определенному классу; эту область называют областью отказов. Решающее правило (4.116) состоит из  линейных разделяющих функций и логического элемента
линейных разделяющих функций и логического элемента  с
с  входами, которые принимают значения
входами, которые принимают значения 
Соответствующая блок-схема изображена на рис. 4.12. Поскольку каждая из параллельных цепей состоит из двух последовательно соединенных элементов, то такой кусочно-линейный классификатор иногда называют двуслойной машиной.
Если предположение о выпуклости областей не выполняется, то необходимо определить взаимные пересечения  гиперплоскостей и строить решающее правило в соответствии с этими пересечениями. Одиако при этом классификатор становится весьма сложным для решения практических задач. Поэтому в данной книге рассмотрение будет ограничено только выпуклыми областями.
гиперплоскостей и строить решающее правило в соответствии с этими пересечениями. Одиако при этом классификатор становится весьма сложным для решения практических задач. Поэтому в данной книге рассмотрение будет ограничено только выпуклыми областями.
Вероятность ошибки решения для каждого класса 8 можно выразить через  -мерную функцию распределения вероятности:
-мерную функцию распределения вероятности:

(функция  — исключена из рассмотрения). Тогда общая ошибка решения
— исключена из рассмотрения). Тогда общая ошибка решения

Задача теперь состоит в том, чтобы определить значения  для данного множества М распределений, при наличии информации о структуре кусочно-линейного классификатора. Вследствие сложности этой задачи ее решение не является таким наглядным, как для линейного классификатора.
для данного множества М распределений, при наличии информации о структуре кусочно-линейного классификатора. Вследствие сложности этой задачи ее решение не является таким наглядным, как для линейного классификатора.
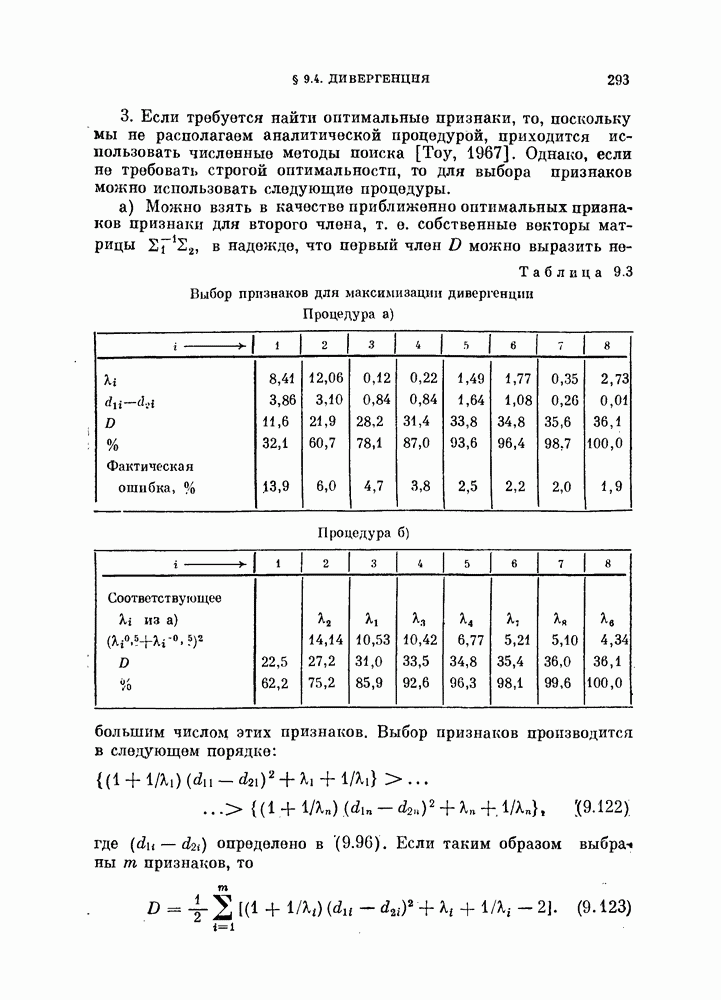
Кратко отметим три приближенных метода решения задачи.
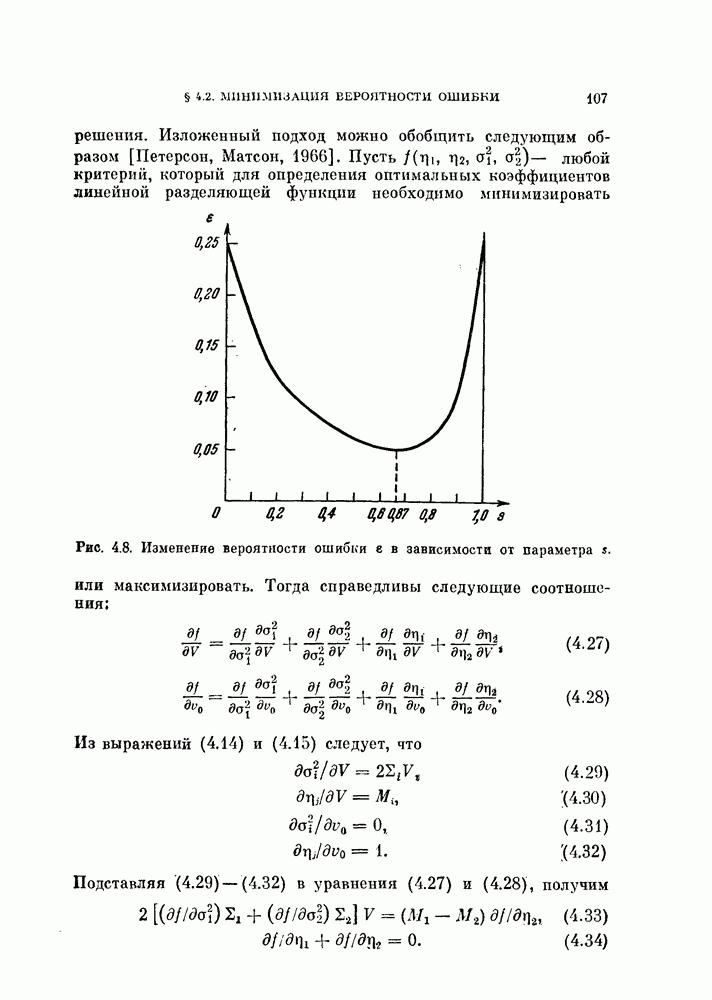
1) Можно подстраивать коэффициенты  так, чтобы минимизировать вероятность ошибки решения
так, чтобы минимизировать вероятность ошибки решения  определяемую формулой (4.118).
определяемую формулой (4.118).
Поскольку для в трудно получить явное математическое выражение, то 8 следует оценивать численными методами всякий раз, когда корректируются параметры V и  Если Случайные величины X для всех классов распределены по нормальному закону, то возможно некоторое упрощение решения, так как а этом случае разделяющие функции
Если Случайные величины X для всех классов распределены по нормальному закону, то возможно некоторое упрощение решения, так как а этом случае разделяющие функции  также распределены нормально, а для
также распределены нормально, а для  существует явное
существует явное
математическое выражение. Однако даже в этом случае интегрированно  -мерного нормального распределения в первом квадранте, по-видимому, проще выполнить численным методом, например, таким, как метод Монте-Карло.
-мерного нормального распределения в первом квадранте, по-видимому, проще выполнить численным методом, например, таким, как метод Монте-Карло.
2) Линейная разделяющая функция между парой классов строится с помощью одного из методов, ранее рассмотренных для случая распознавания двух классов. Вычисляются  разделяющих функций. Эти функции без дальнейшей коррекции используются в качестве кусочно-линейной разделяющей функции. Если распределения всех классов нормальные с равными ковариационными матрицами, т. е.
разделяющих функций. Эти функции без дальнейшей коррекции используются в качестве кусочно-линейной разделяющей функции. Если распределения всех классов нормальные с равными ковариационными матрицами, т. е.  описанная процедура эквивалентна применению байесовского классификатора. Если распределения существенно отличаются между собой, то дальнейшая коррекция решающего правила может прдвести к уменьшению ошибки. Однако часто оказывается, что уменьшение ошибки за счет подстройки параметров
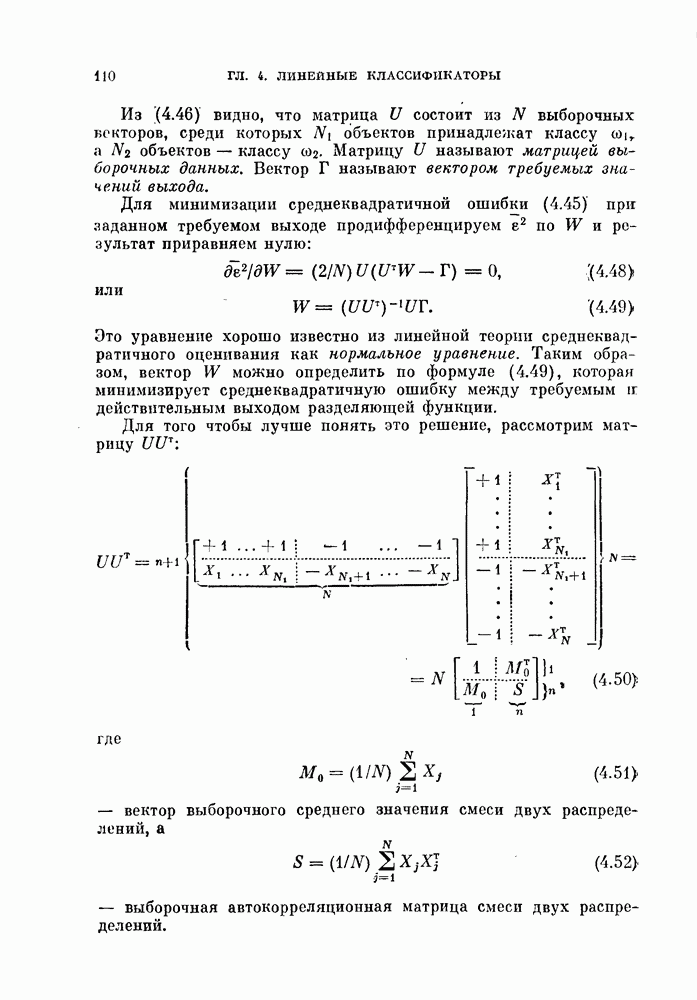
описанная процедура эквивалентна применению байесовского классификатора. Если распределения существенно отличаются между собой, то дальнейшая коррекция решающего правила может прдвести к уменьшению ошибки. Однако часто оказывается, что уменьшение ошибки за счет подстройки параметров  относительно невелико.
относительно невелико.
3) Можно задать требуемый выход  кусочно-линейной разделяющей функции и для нахождения оптимальных значений
кусочно-линейной разделяющей функции и для нахождения оптимальных значений  минимизировать среднеквадратичную ошибку между требуемым и действительным выходом.
минимизировать среднеквадратичную ошибку между требуемым и действительным выходом.
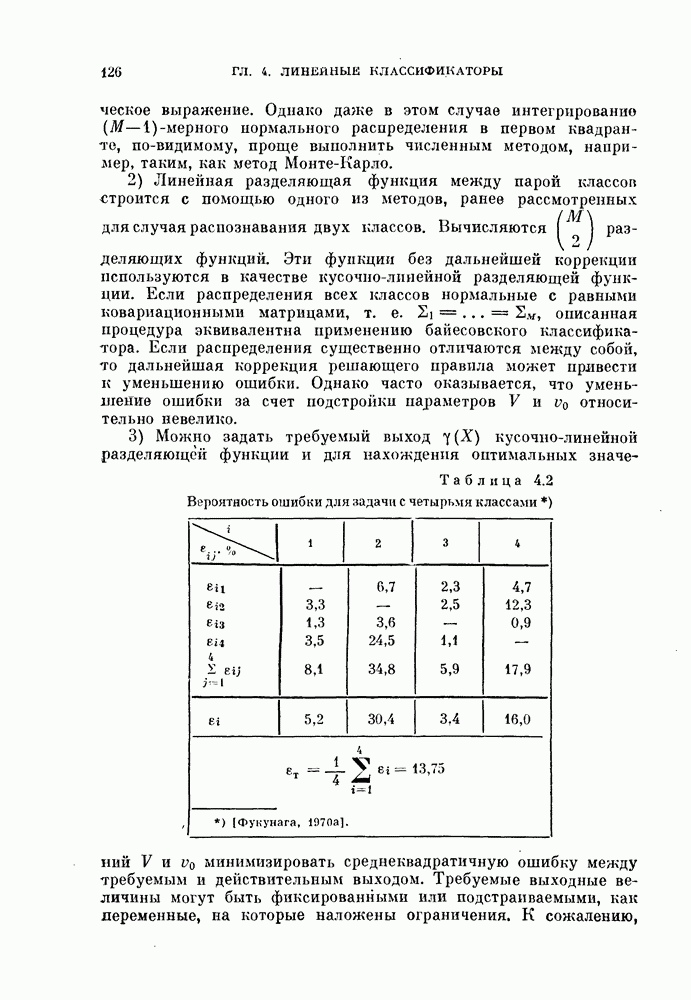
Таблица 4.2
Вероятность ошибки для задачи с четырьмя классами

Требуемые выходные величины могут быть фиксированными или подстраиваемыми, как переменные, на которые наложены ограничения. К сожалению,
даже для случая кусочно-линейной разделимости классов не существует доказательства сходимости этой процедуры.
Пример 4.5. Рассматривается задача с четырьмя классами, каждый из которых характеризуется нормальным распределением вероятностей. Эти распределения представлены в стандартных данных в гл. 2 (см. задания для составления программ). Поскольку все распределения нормальные, то можно для каждой пары классов определить линейный классификатор, оптимальный по критерию минимума вероятности ошибки.
В табл. 4.2 для различных пар классов приведены вероятности ошибок  обусловленных использованием соответствующих оптимальных линейных классификаторов. Кроме того, в табл. 4.2 приводится сумма вероятностен ошибок:
обусловленных использованием соответствующих оптимальных линейных классификаторов. Кроме того, в табл. 4.2 приводится сумма вероятностен ошибок:  . В случае, когда кусочно-линейный классификатор был синтезирован с помощью линейных классификаторов без дополнительной коррекции параметров, ошибка решения вычислялась по формулам (4.117) и (4.118) и обозначена в таблице 4.2 через
. В случае, когда кусочно-линейный классификатор был синтезирован с помощью линейных классификаторов без дополнительной коррекции параметров, ошибка решения вычислялась по формулам (4.117) и (4.118) и обозначена в таблице 4.2 через  .
.

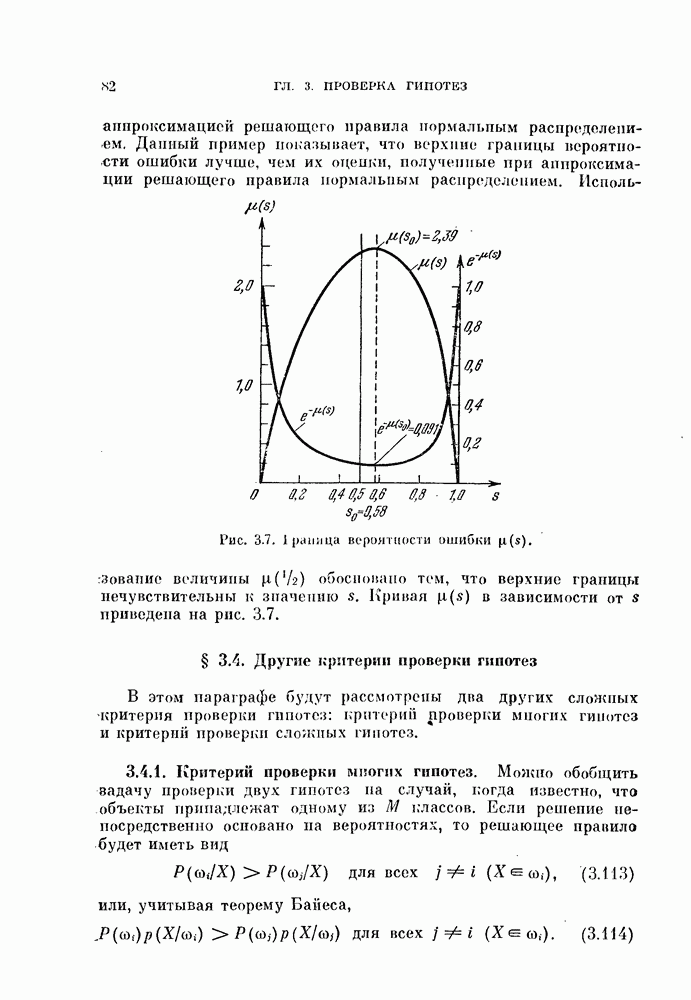
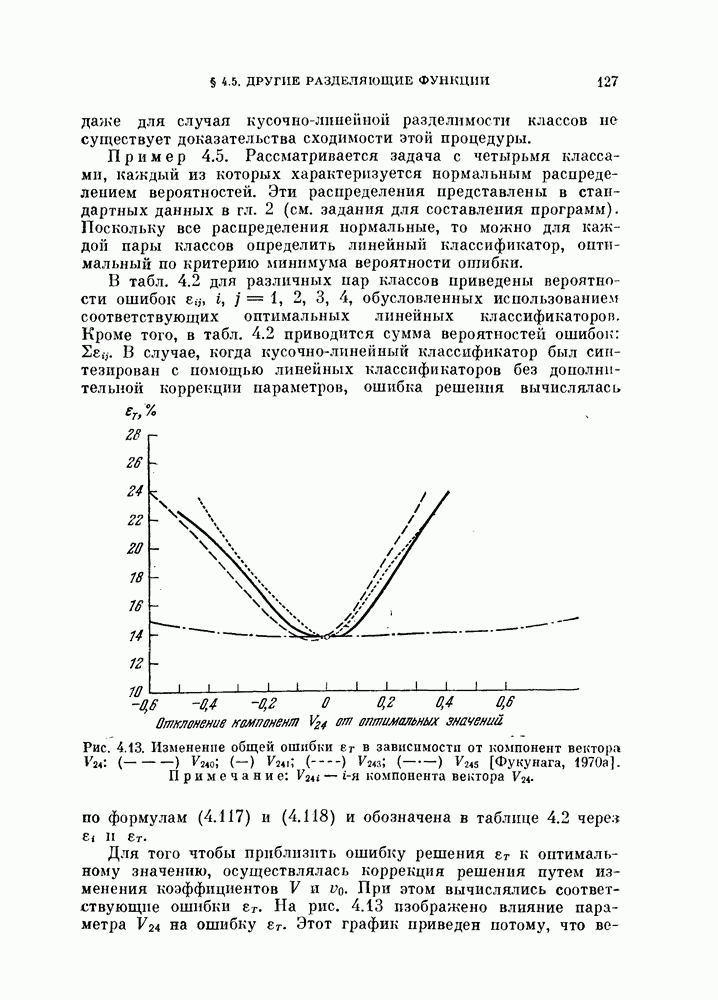
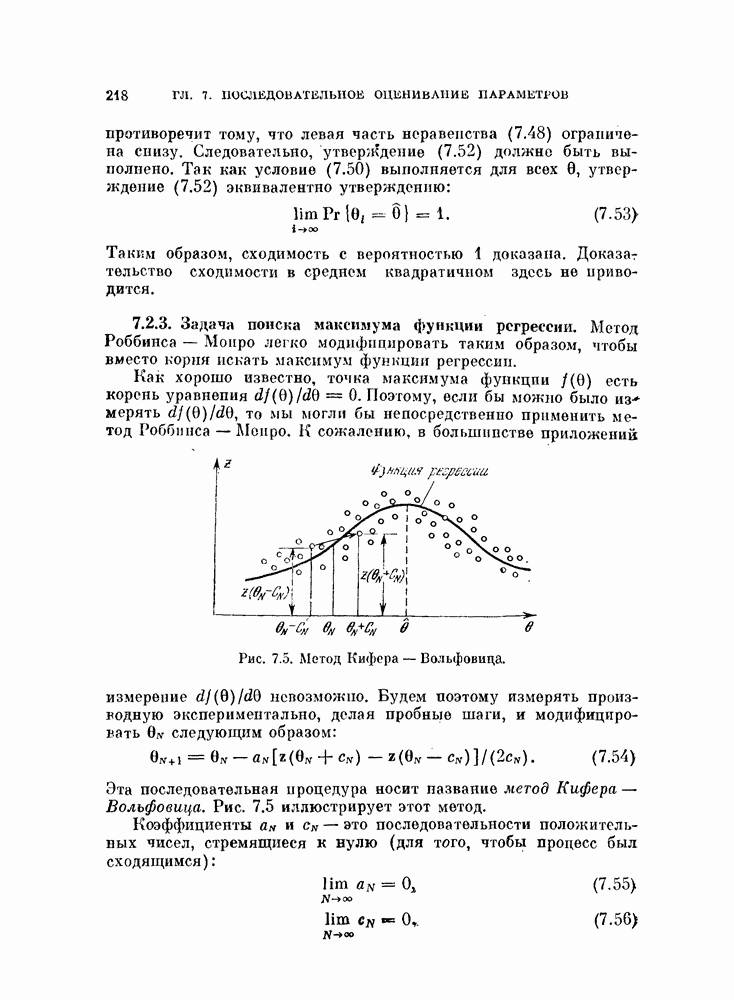
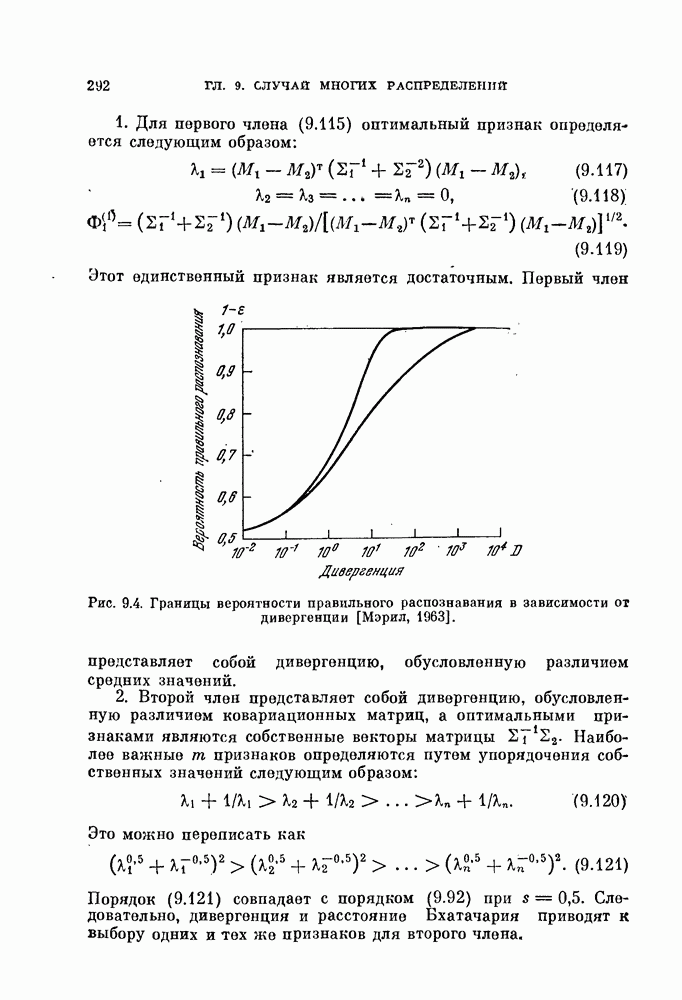
Рис. 4.13. Изменение общей ошибки  в зависимости от компонент вектора
в зависимости от компонент вектора  [Фукунага, 1970а]. Примечание:
[Фукунага, 1970а]. Примечание:  компонента вектора
компонента вектора 
Для того чтобы приблизить ошибку решения  к оптимальному значению, осуществлялась коррекция решения путем изменения коэффициентов
к оптимальному значению, осуществлялась коррекция решения путем изменения коэффициентов  При этом вычислялись соответствующие ошибки
При этом вычислялись соответствующие ошибки  . На рис. 4.13 изображено влияние параметра
. На рис. 4.13 изображено влияние параметра  на ошибку
на ошибку  . Этот график приведен потому, что
. Этот график приведен потому, что
вероятности  являются преобладающими слагаемыми в
являются преобладающими слагаемыми в  Как видно из рис. 4.13, оптимальное значение
Как видно из рис. 4.13, оптимальное значение  смещено относительно значения
смещено относительно значения  , соответствующего линейному классификатору для классов
, соответствующего линейному классификатору для классов  Однако при этом изменение ошибки
Однако при этом изменение ошибки  находится в пределах 0,3%. Влияние же других компонент вектора V намного меньше. Этот результат оправдывает для данного частного примера применение совокупности оптимальных классификаторов без дополнительной коррекции параметров.
находится в пределах 0,3%. Влияние же других компонент вектора V намного меньше. Этот результат оправдывает для данного частного примера применение совокупности оптимальных классификаторов без дополнительной коррекции параметров.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
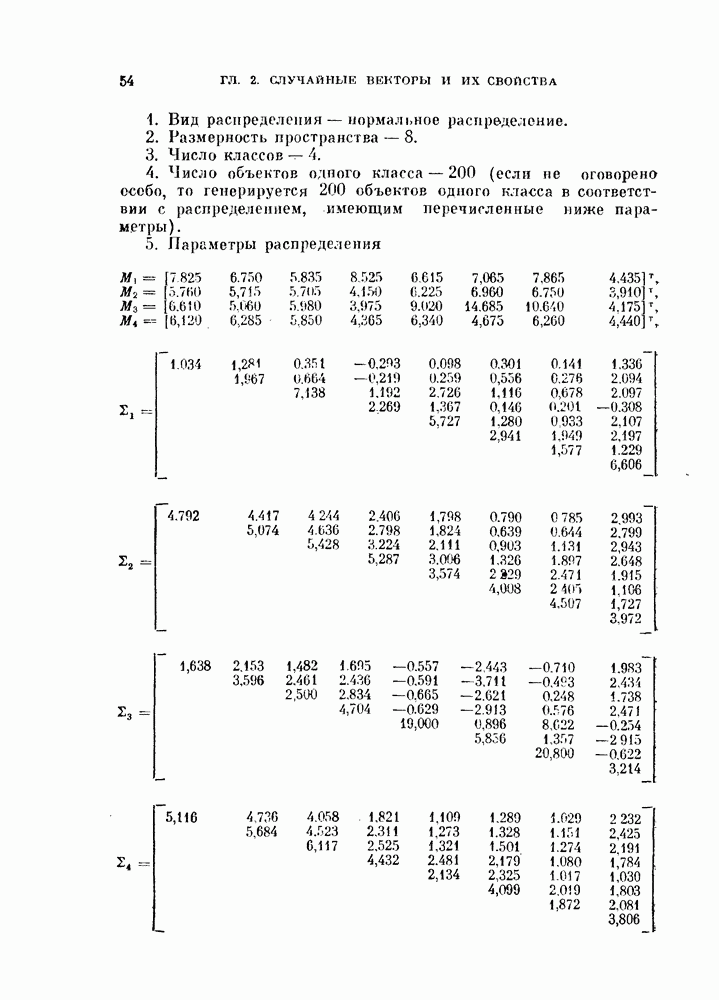
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
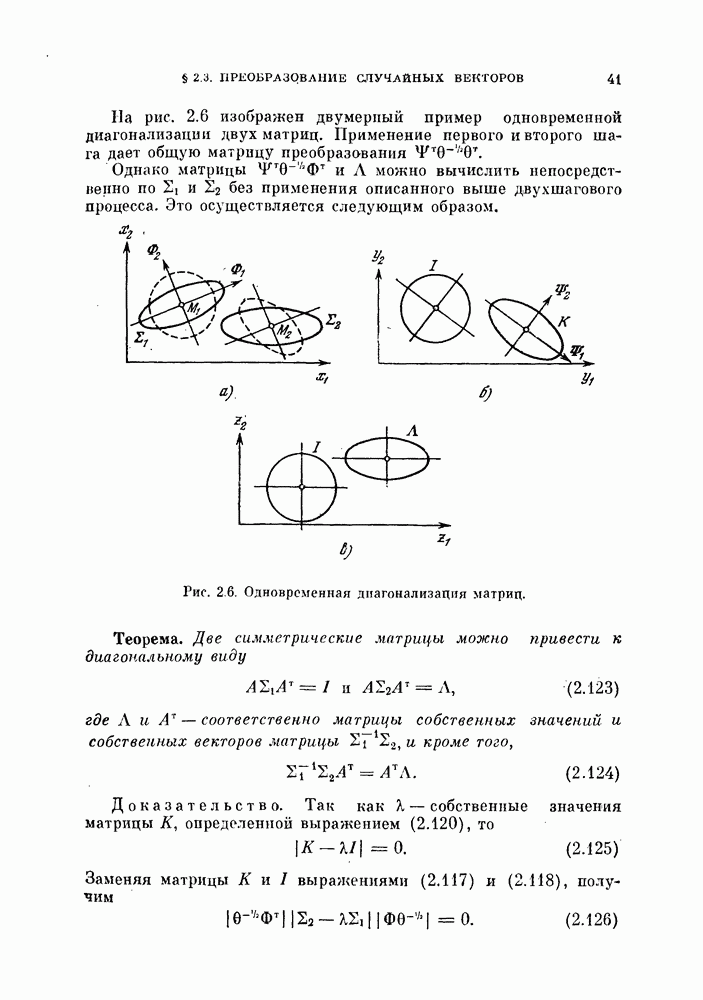
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
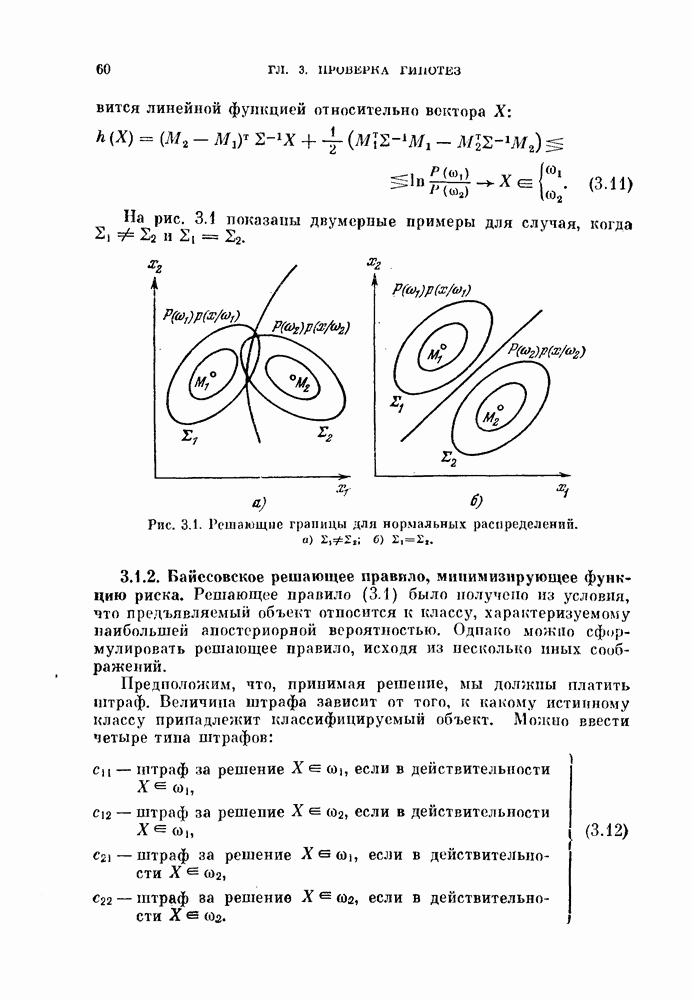
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
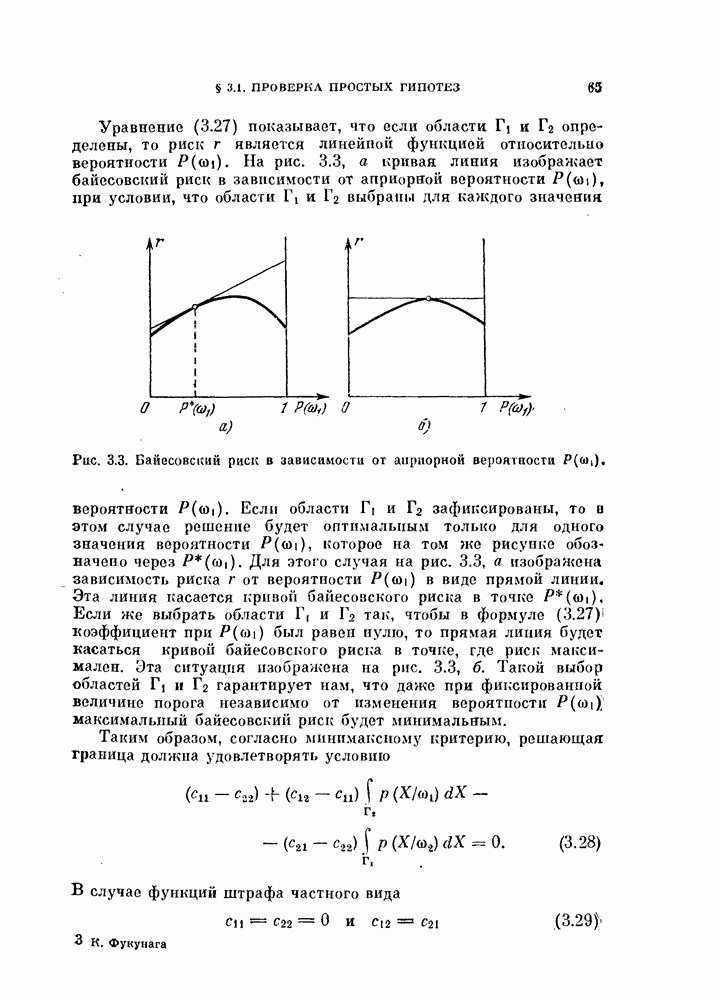
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
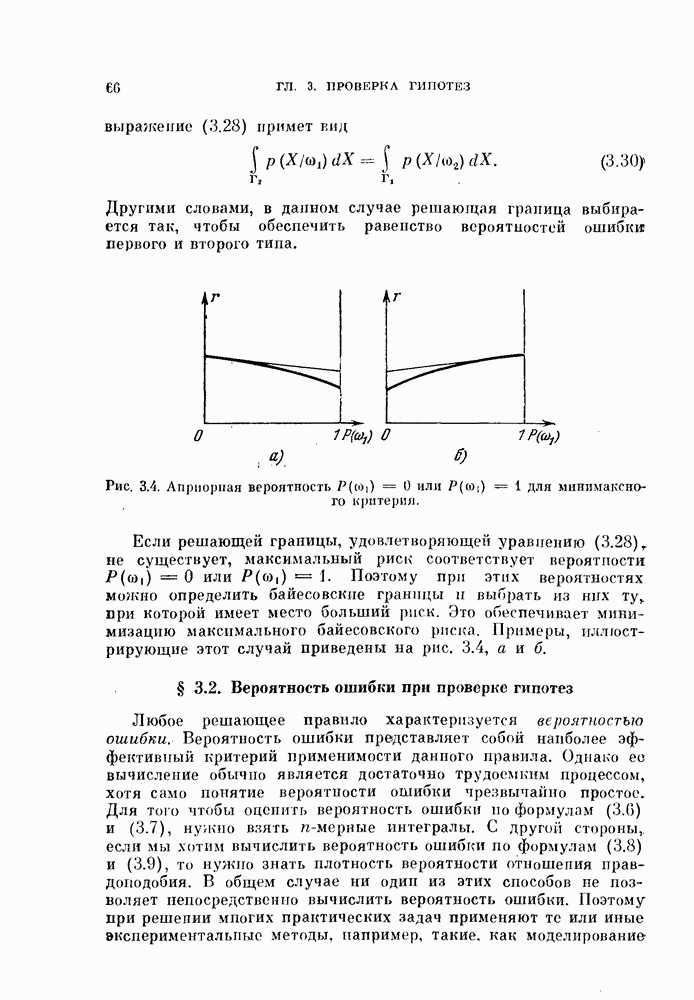
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
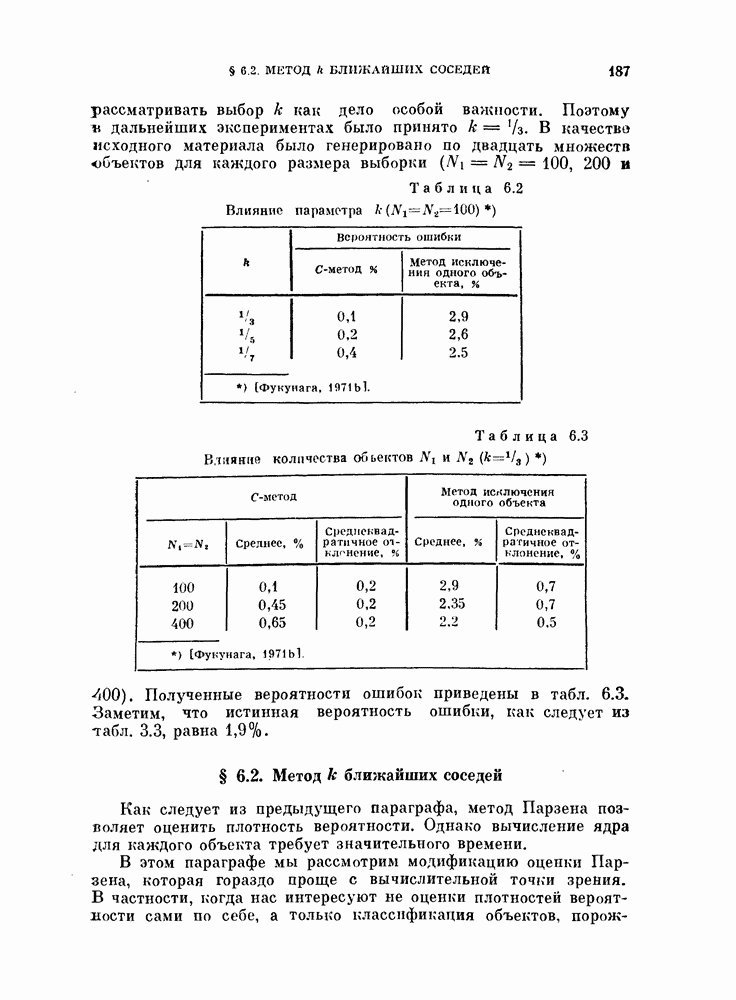
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
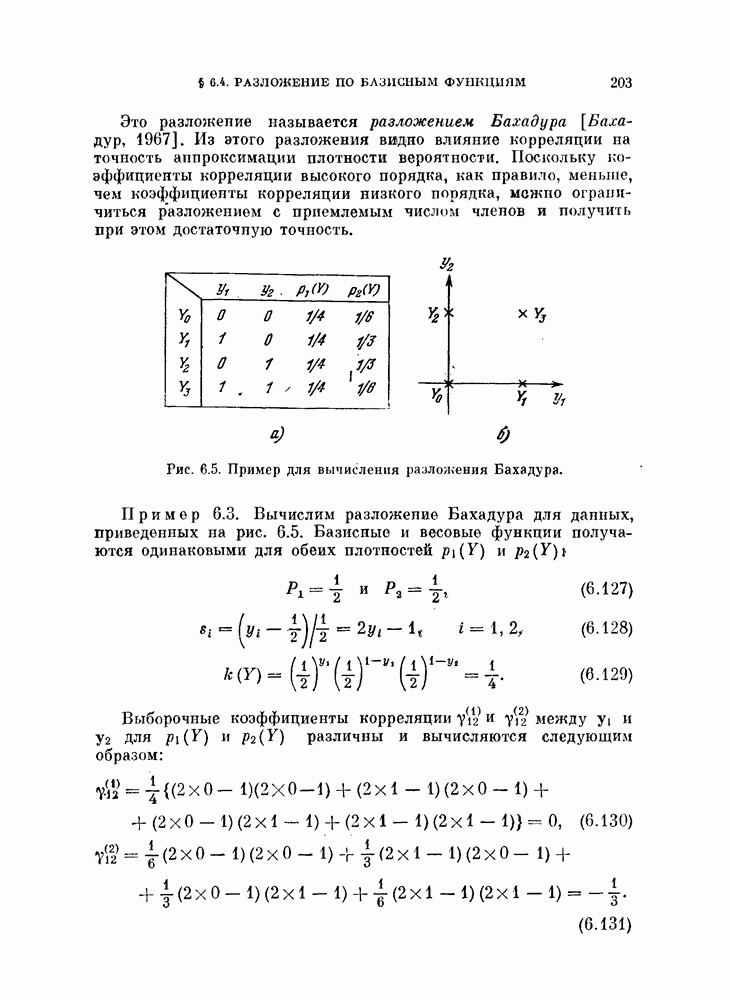
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
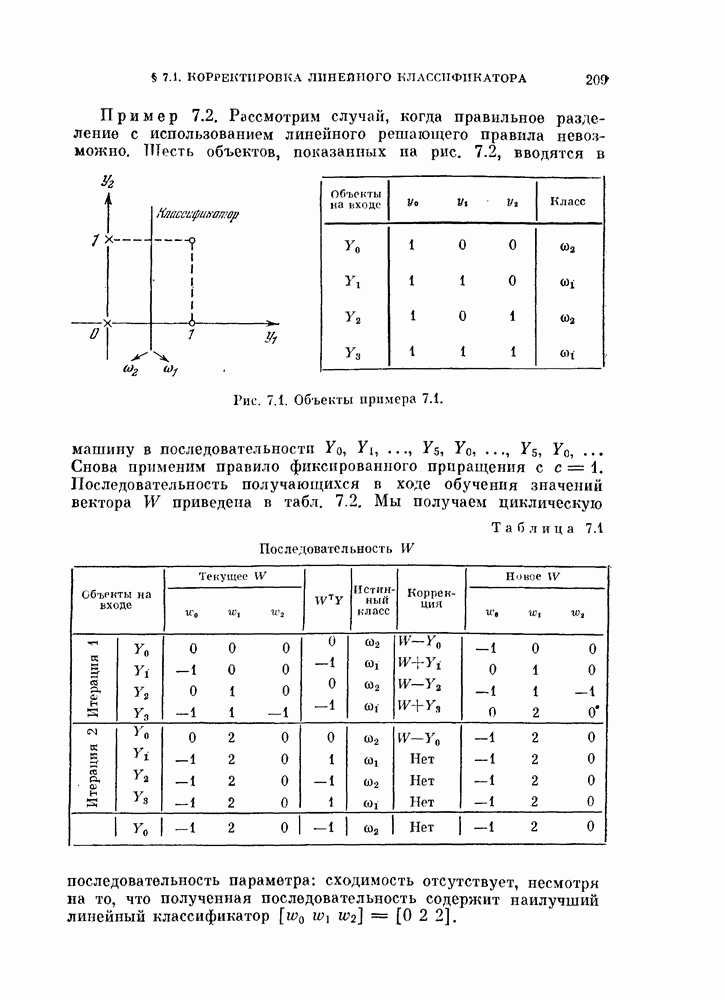
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
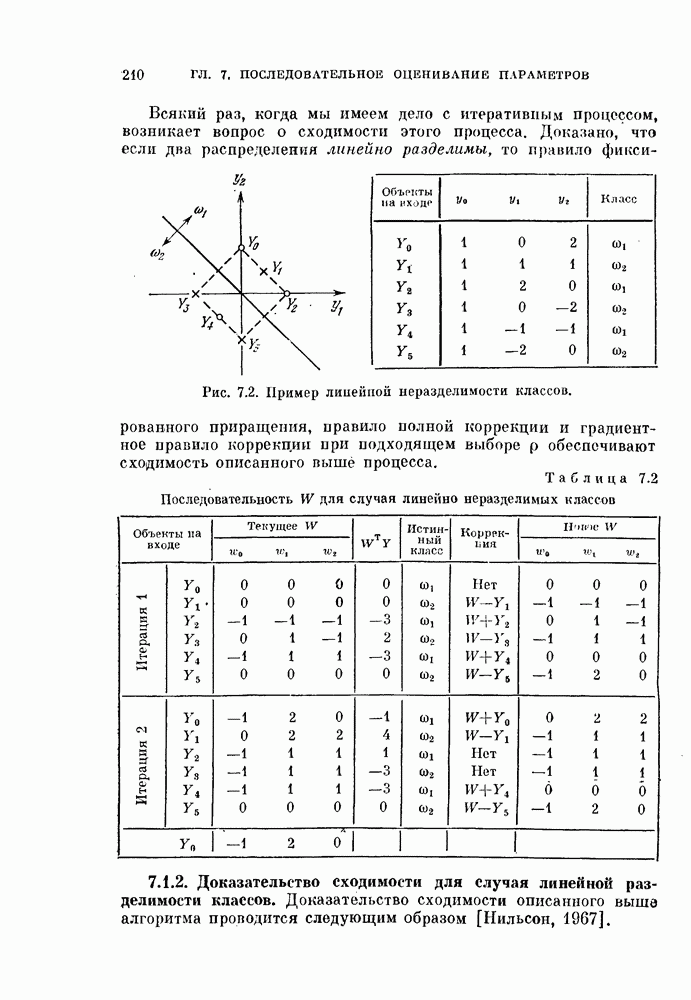
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
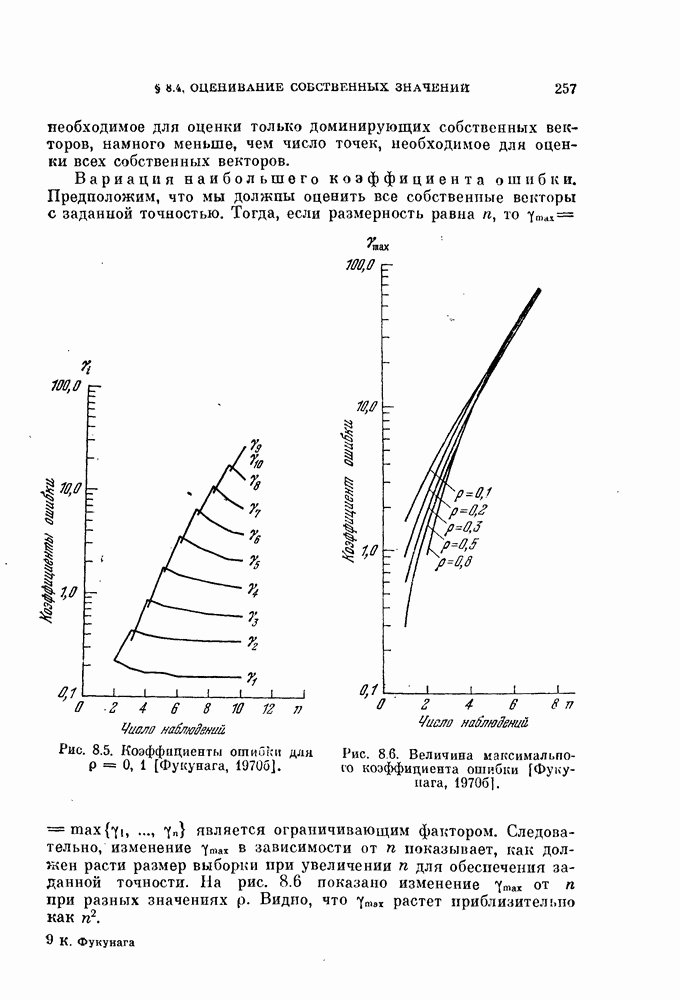
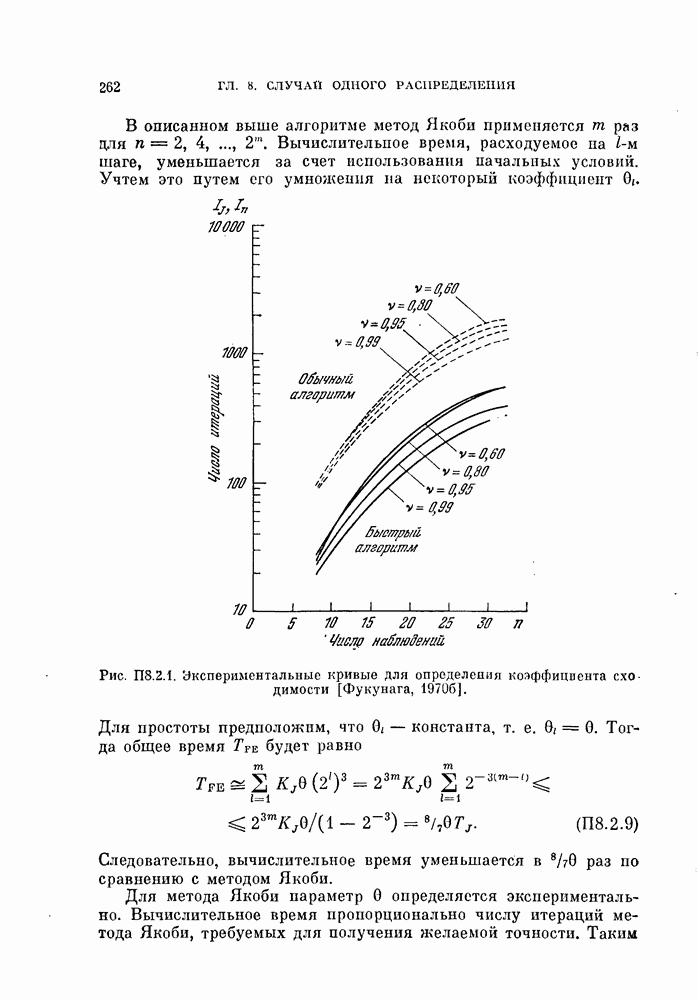
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
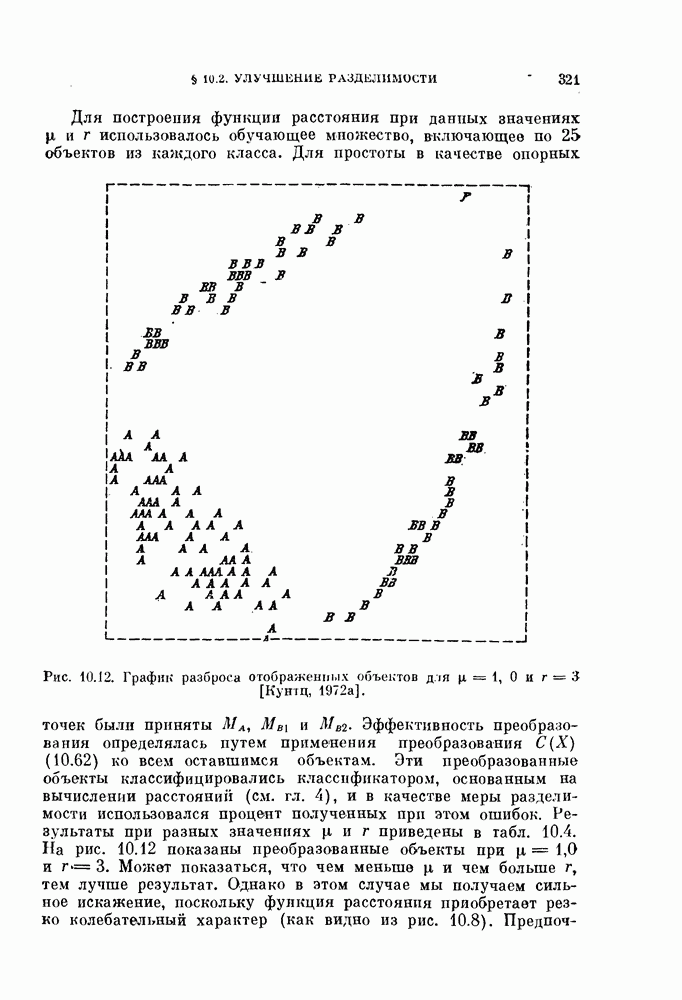
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
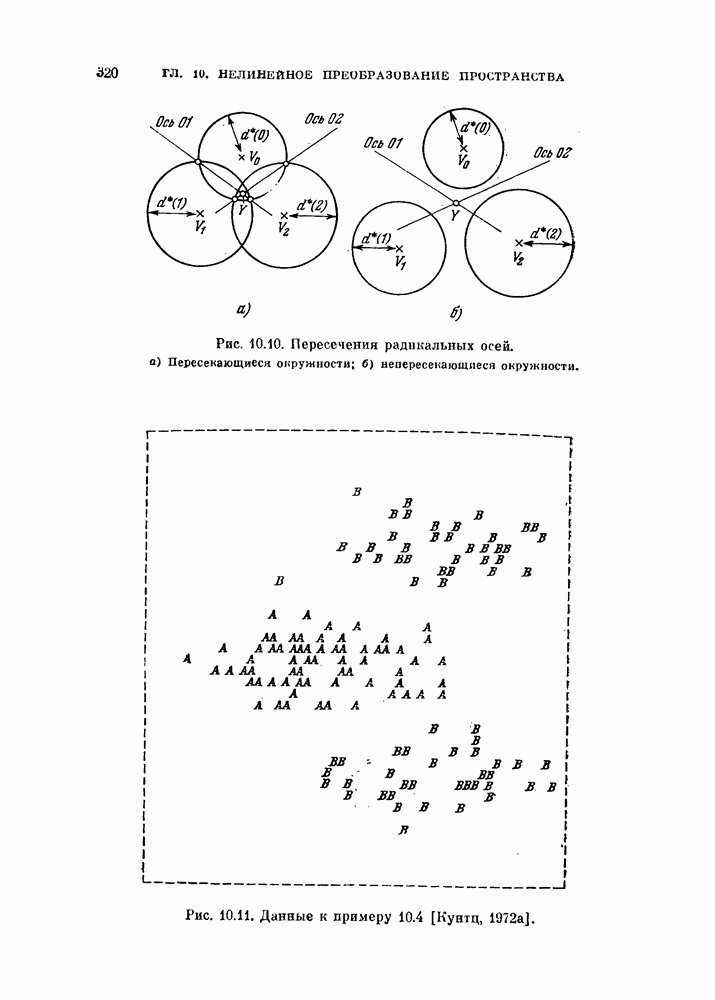
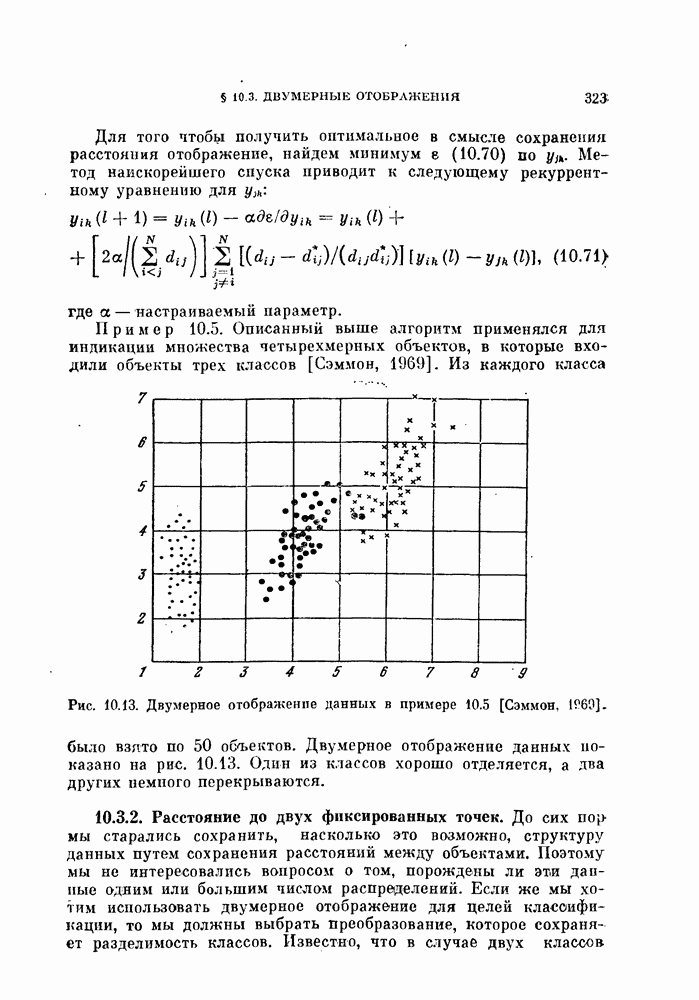
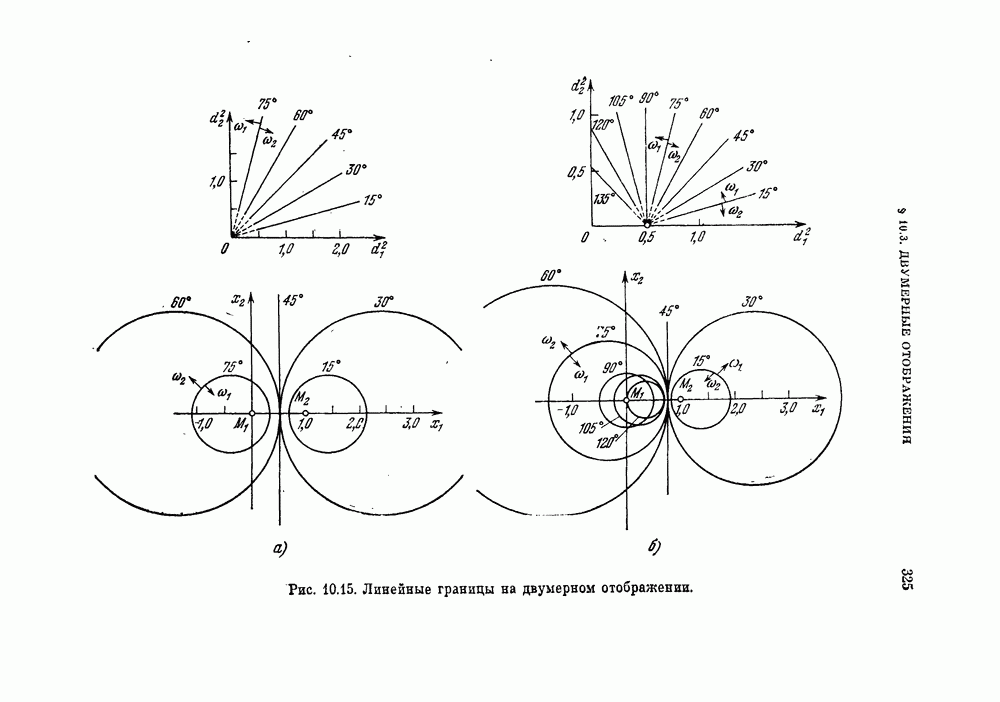
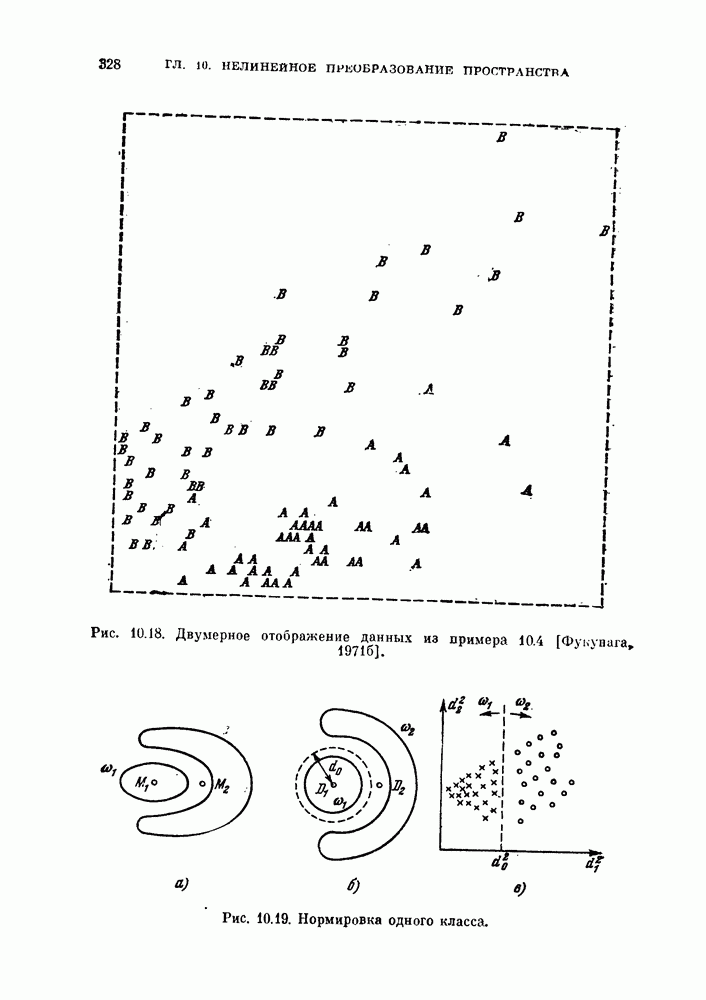
- § 10.3. Двумерные отображения
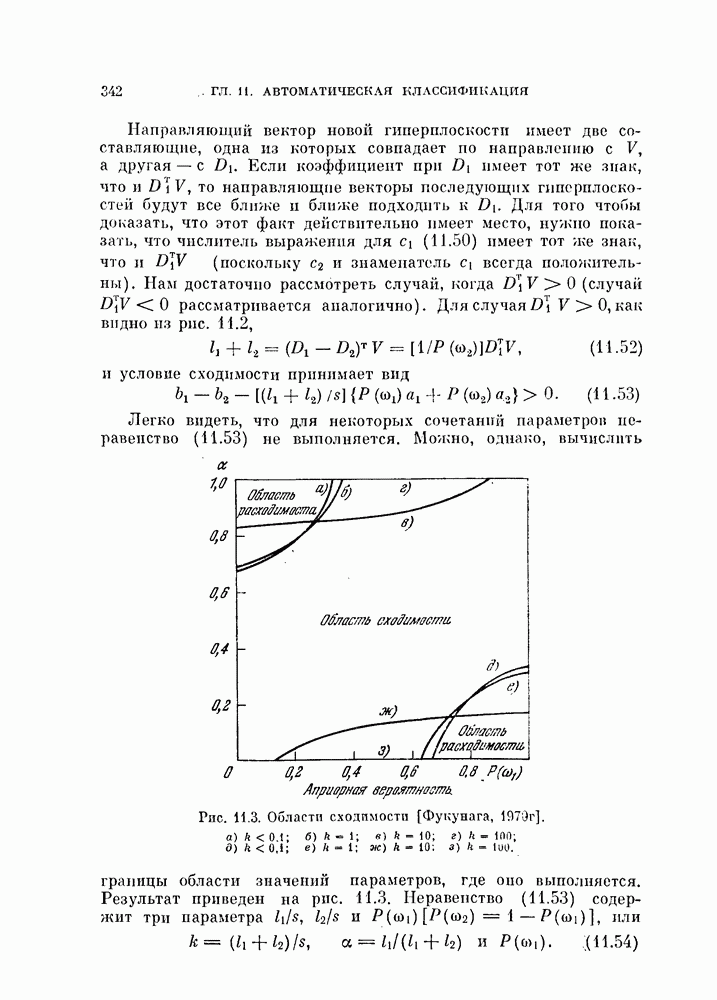
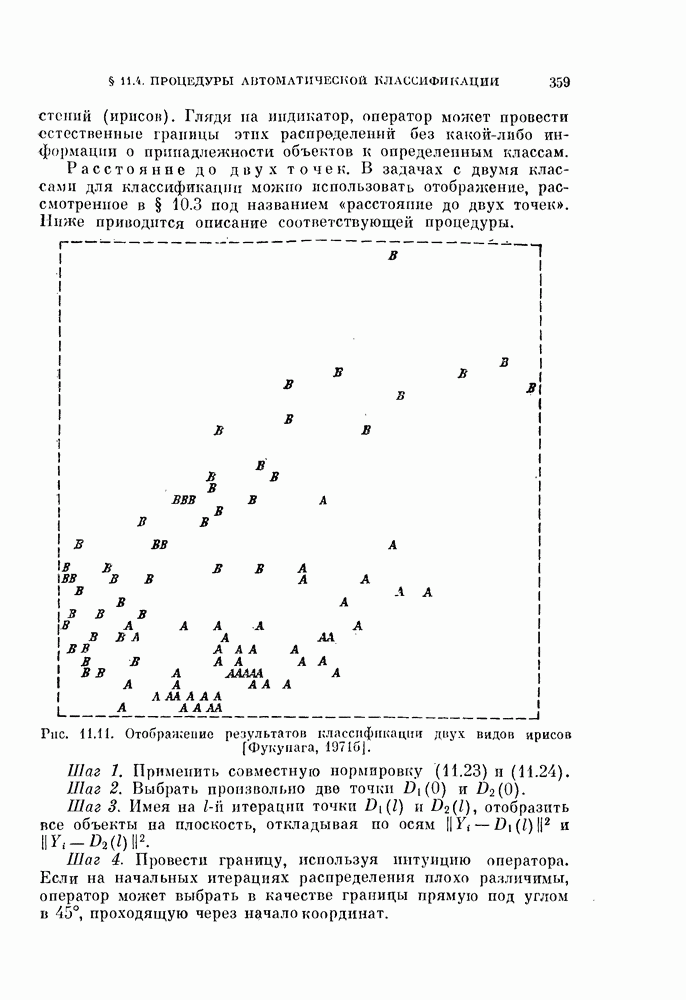
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
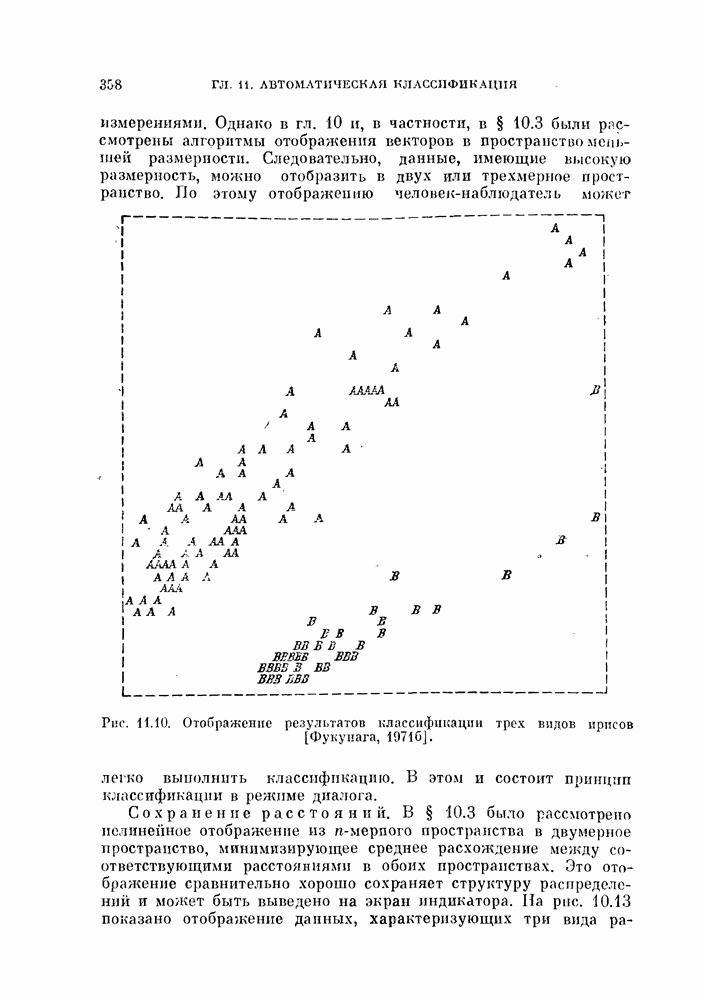
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА