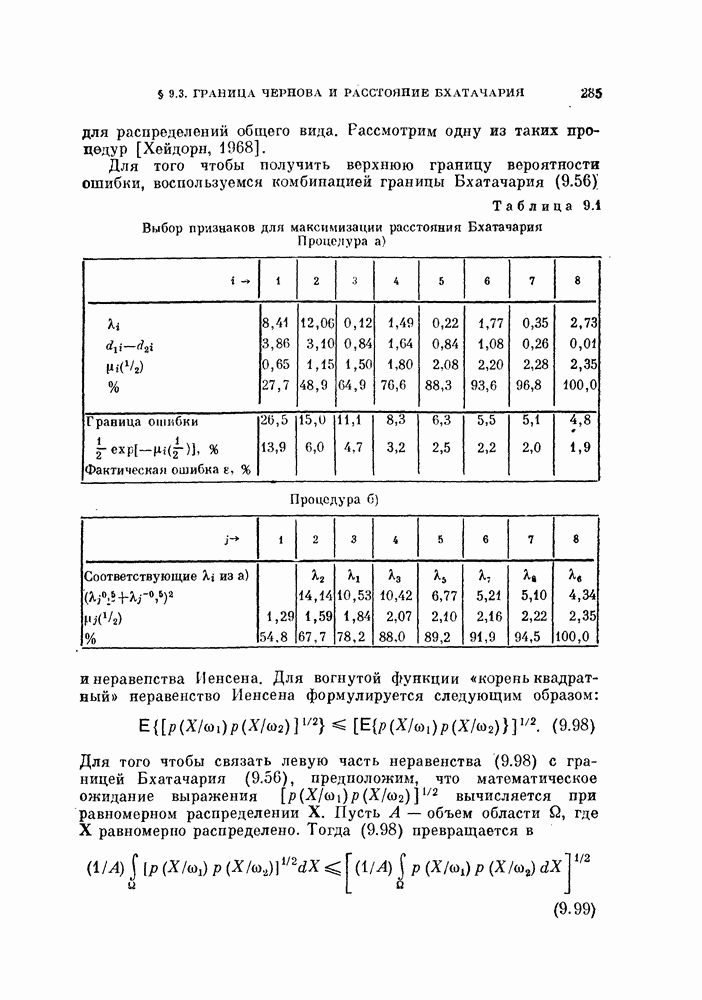
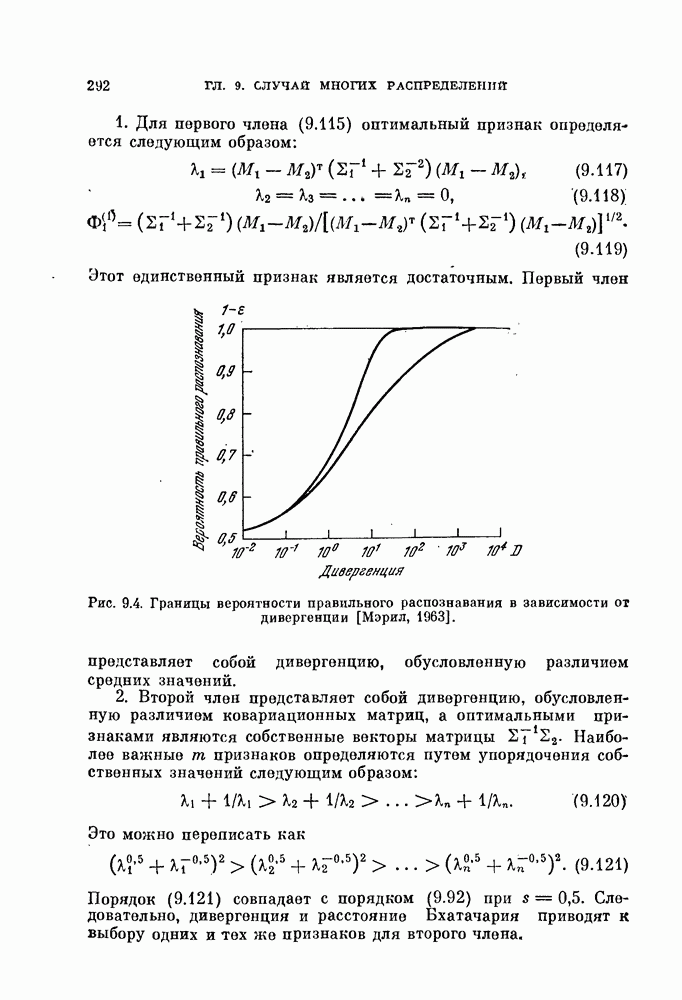
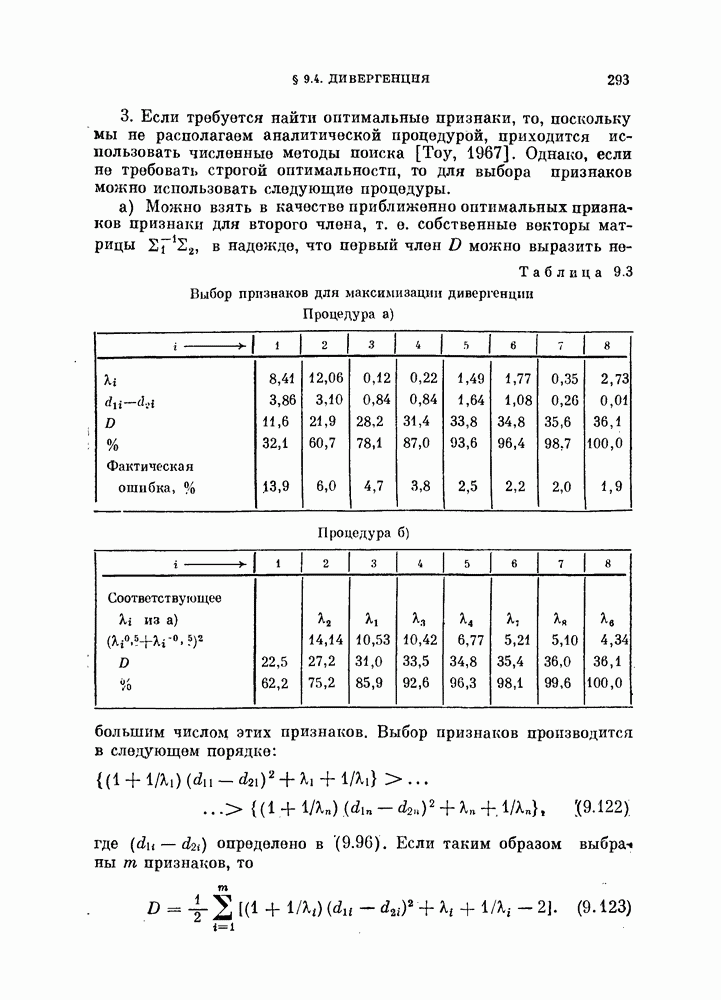
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
Полученные выше результаты приводят к следующей процедуре автоматической классификации [Фукунага, 1970 г].
1. Применить совместную нормировку.
2. Классифицировать объекты, используя правило ближайшего среднего.
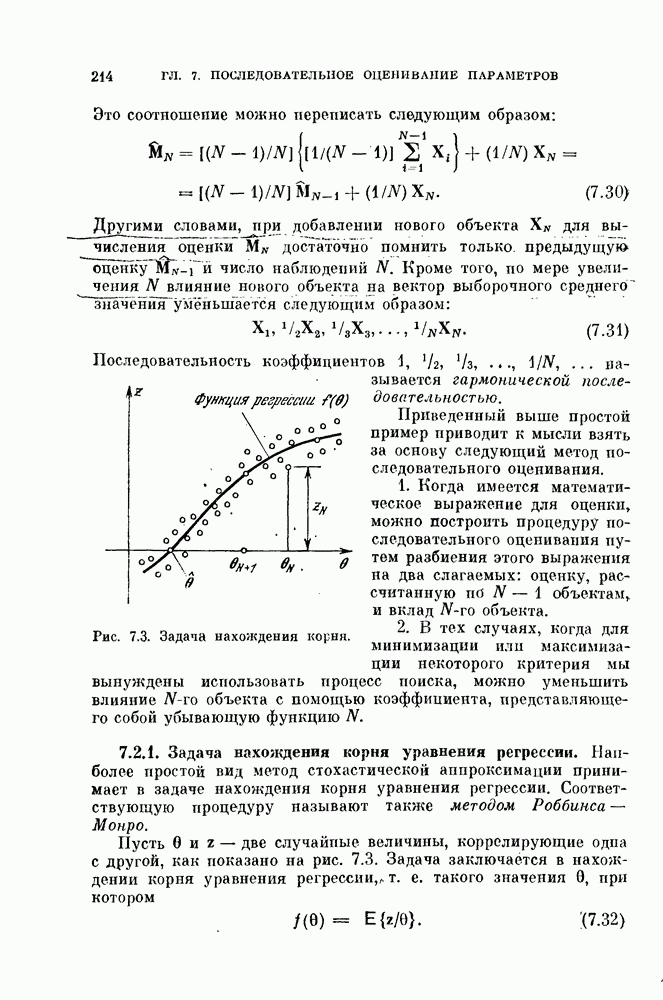
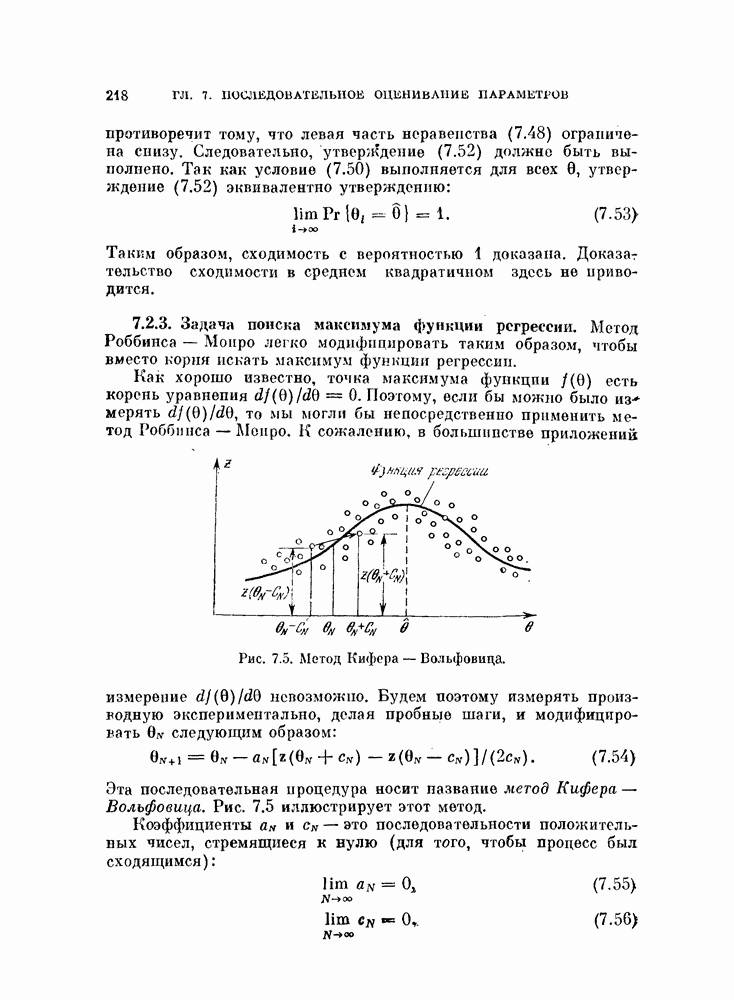
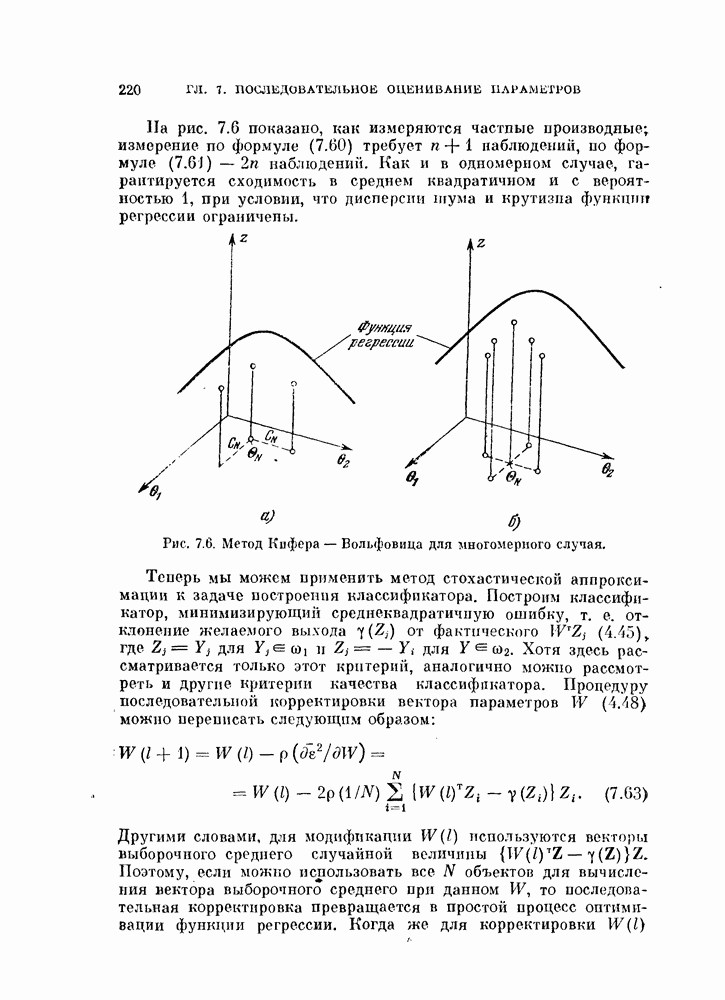
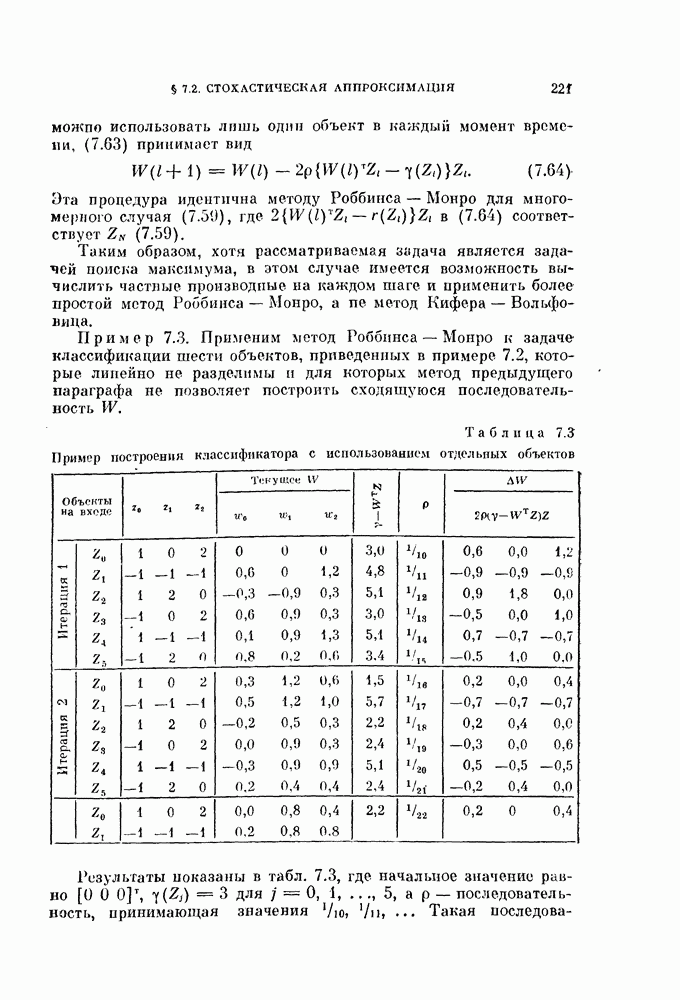
Эффективность этой процедуры можно оценить аналитически, если объекты генерируются в соответствии с двумя нормальными распределениями. Мы найдем условия, при которых разделяющая гиперплоскость сходится к гиперплоскости, перпендикулярной к вектору разности средних векторов этих распределений. В случае равных ковариационных матриц это будет байесовская оптимальная гиперплоскость.
Нормальные распределения с равными ковариационными матрицами.
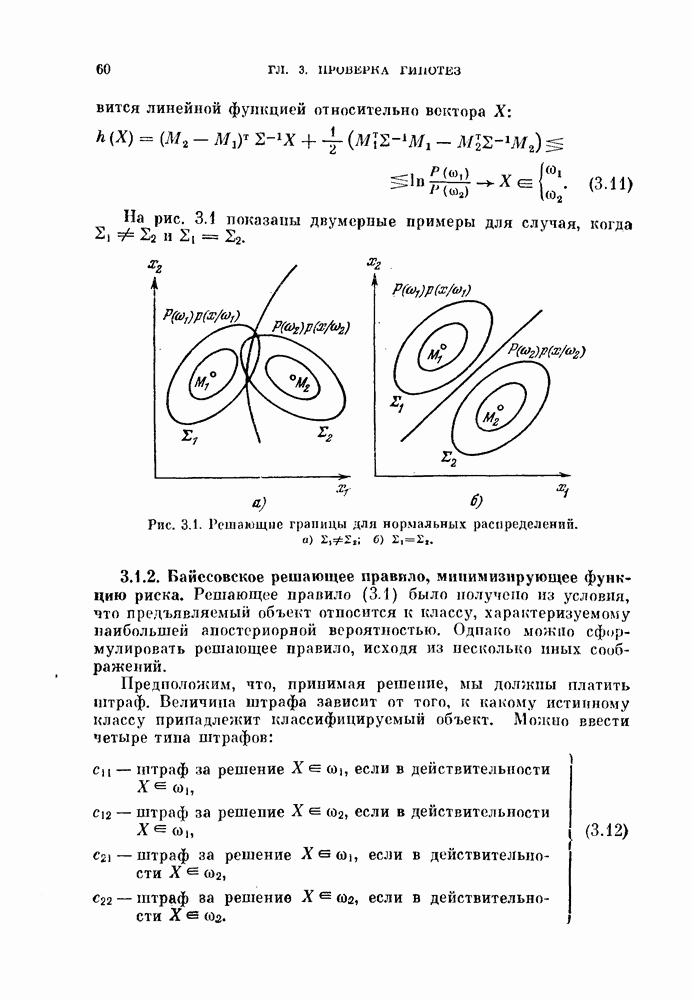
Если два нормальных распределения имеют одинаковые ковариационные матрицы  байесовская оптимальная разделяющая поверхность при условии совместной нормировки представляет собой гиперплоскость вида
байесовская оптимальная разделяющая поверхность при условии совместной нормировки представляет собой гиперплоскость вида

Действуя так же, как в (4.68), можно привести (11.36) к виду

Таким образом, в случае равных ковариационных матриц направляющий вектор оптимальной гиперплоскости совпадает по направлению с вектором  а следовательно, и с вектором разности
а следовательно, и с вектором разности
средних значений  Покажем, что правило ближайшего среднего устанавливает разделяющую гиперплоскость перпендикулярно к вектору разности средних значений. Это свойство, которым не обладает исходнаяг система координат, является значительным преимуществом нормированной системы координат. Для случая равных ковариационных матриц можно показать, что алгоритм сходится к разделяющей гиперплоскости, перпендикулярной
Покажем, что правило ближайшего среднего устанавливает разделяющую гиперплоскость перпендикулярно к вектору разности средних значений. Это свойство, которым не обладает исходнаяг система координат, является значительным преимуществом нормированной системы координат. Для случая равных ковариационных матриц можно показать, что алгоритм сходится к разделяющей гиперплоскости, перпендикулярной  в широком диапазоне начальных классификаций.
в широком диапазоне начальных классификаций.

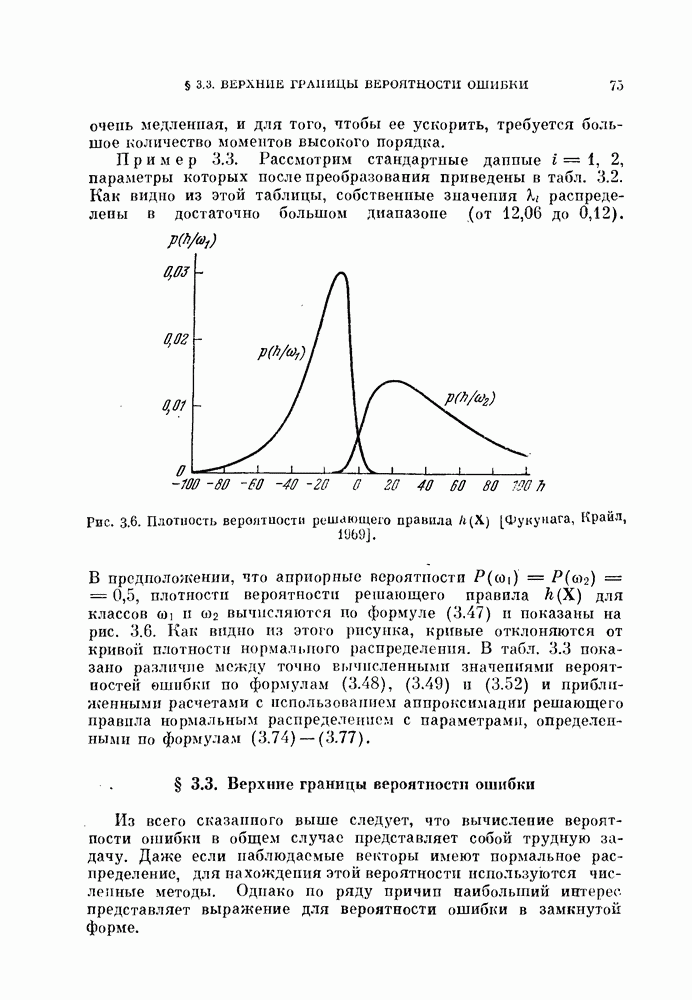
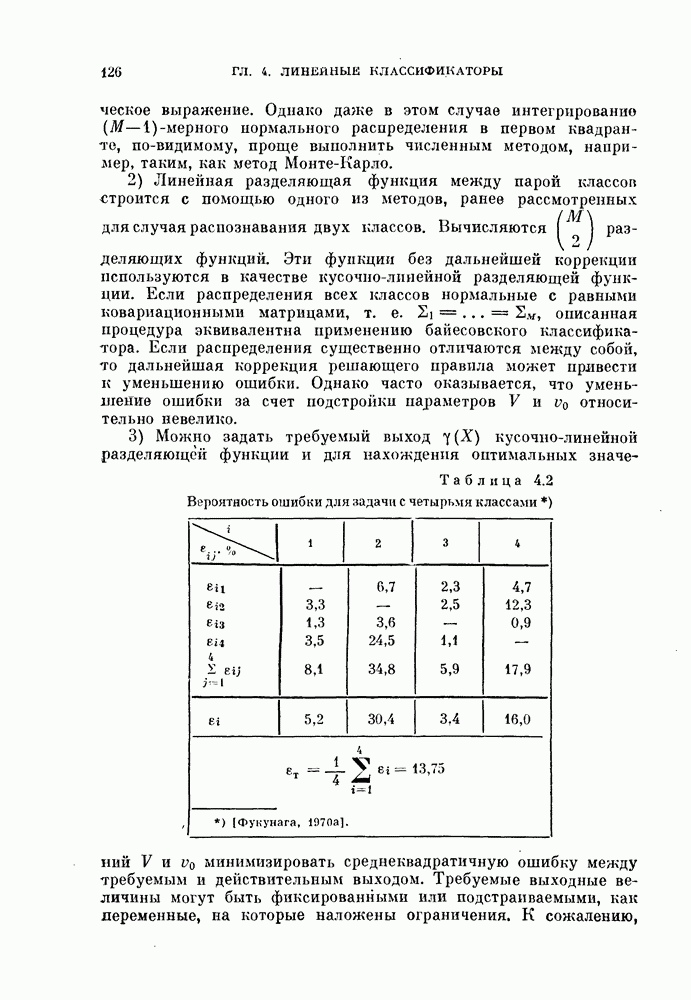
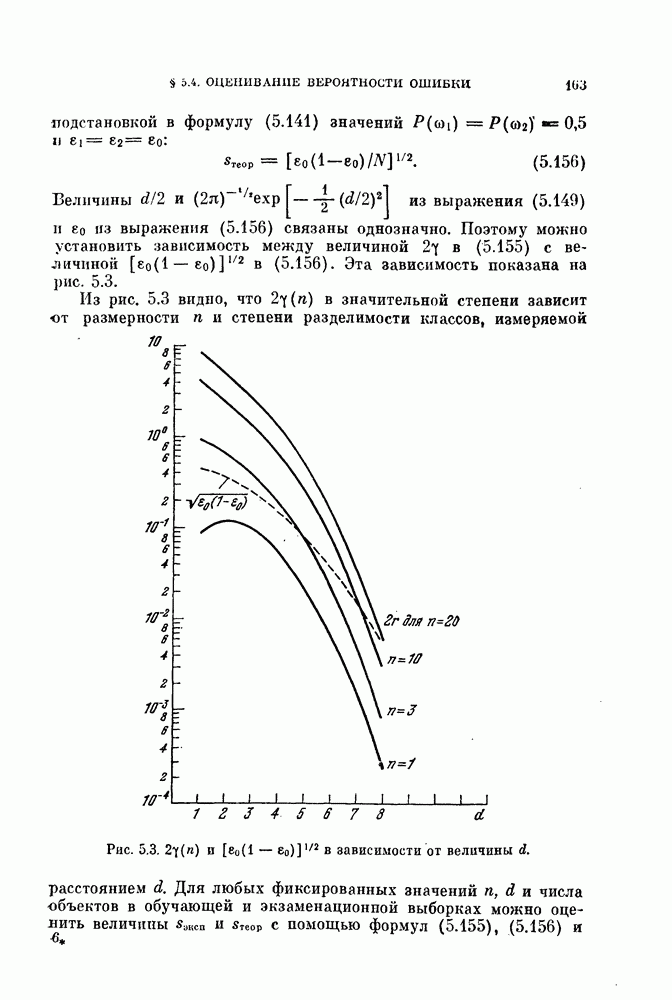
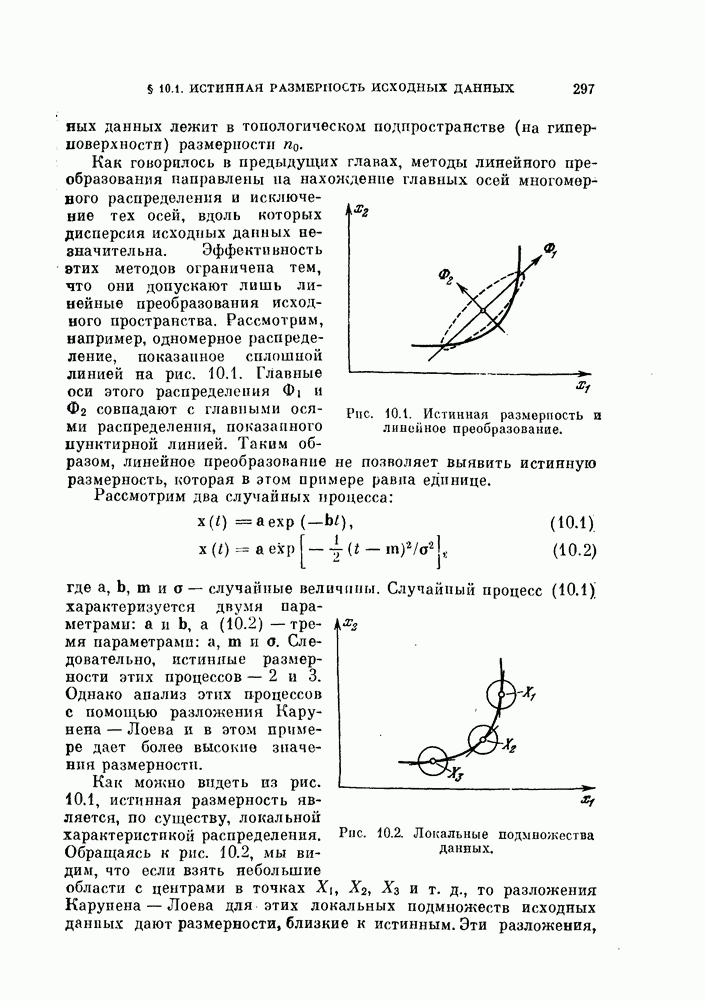
Рис. 11.2. Разделение двух распределений.
Пусть на некоторой итерации объекты разделяются гиперплоскостью с направляющим вектором  Предположим, что эта гиперплоскость находится на расстоянии
Предположим, что эта гиперплоскость находится на расстоянии  от
от  и на расстоянии
и на расстоянии  от
от  как показано на рис. 11.2. Пусть
как показано на рис. 11.2. Пусть  — центры «вероятностных масс», лежащих по обе стороны гиперплоскости. Тогда, в соответствии с правилом ближайшего среднего, направление следующей гиперплоскости будет совпадать с вектором
— центры «вероятностных масс», лежащих по обе стороны гиперплоскости. Тогда, в соответствии с правилом ближайшего среднего, направление следующей гиперплоскости будет совпадать с вектором 
На каждой итерации гиперплоскость делит каждое распределение на две части, лежащие по обе стороны гиперплоскости. Таким образом, имеем четыре вероятностные массы  (см. рис. 11.2). Центры
(см. рис. 11.2). Центры  и абсолютные значения
и абсолютные значения  этих четырех масс можно получить следующим образом:
этих четырех масс можно получить следующим образом:


где

(если  находится в области
находится в области  то используется положительный знак; если
то используется положительный знак; если  находится в
находится в  то — отрицательный знак) и
то — отрицательный знак) и

Здесь  — это центр масс
— это центр масс  — центр масс
— центр масс  и
и  . Следовательно,
. Следовательно,  можно вычислить следующим образом:
можно вычислить следующим образом:

Подставляя выражения (11.38) — (11.43) в (11.45) и (11.46), имеем

В случае равных ковариационных матриц

Далее, пользуясь условиями совместной нормировки (11.23) и (11.24) (или (4.62) и (4.63)), матрицы  можно выразить в виде функции от
можно выразить в виде функции от  Таким образом, (11.47) принимает вид
Таким образом, (11.47) принимает вид

где

Направляющий вектор новой гиперплоскости имеет две составляющие, одна из которых совпадает по направлению с V, а другая — с  Если коэффициент при
Если коэффициент при  имеет тот же знак, что и
имеет тот же знак, что и  то направляющие векторы последующих гиперплоскостей будут все ближе и ближе подходить к
то направляющие векторы последующих гиперплоскостей будут все ближе и ближе подходить к  Для того чтобы доказать, что этот факт действительно имеет место, нужно показать, что числитель выражения для
Для того чтобы доказать, что этот факт действительно имеет место, нужно показать, что числитель выражения для  (11.50) имеет тот же знак, что и
(11.50) имеет тот же знак, что и  (поскольку
(поскольку  и знаменатель
и знаменатель  всегда положительны), Нам достаточно рассмотреть случай, когда
всегда положительны), Нам достаточно рассмотреть случай, когда  (случай
(случай  рассматривается аналогично). Для случая
рассматривается аналогично). Для случая  , как видно из рис. 11.2,
, как видно из рис. 11.2,

и условие сходимости принимает вид

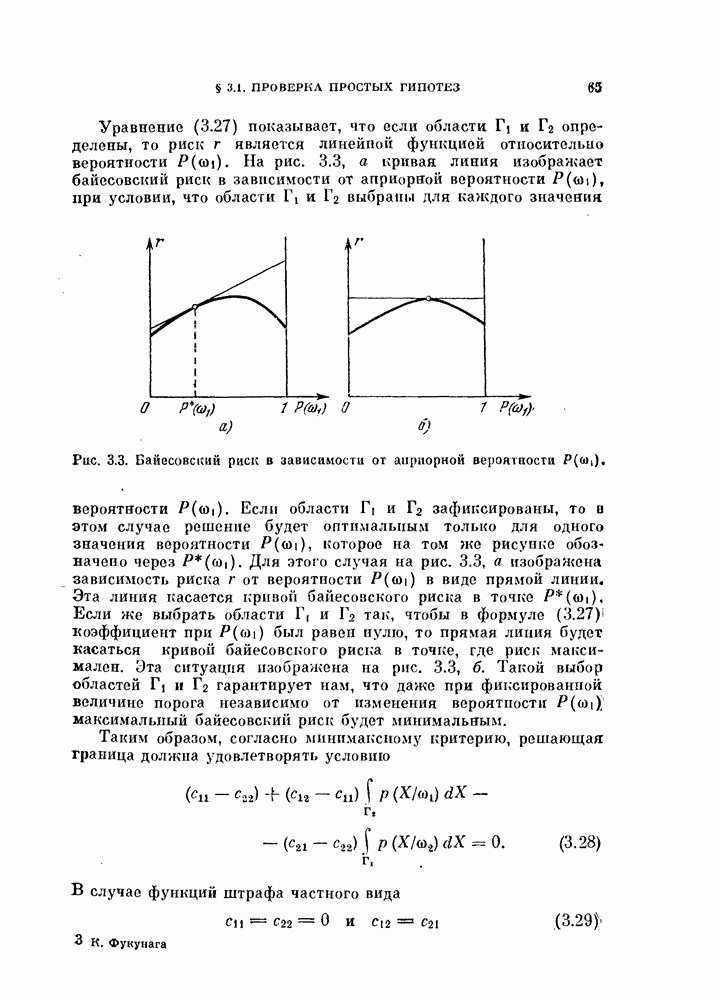
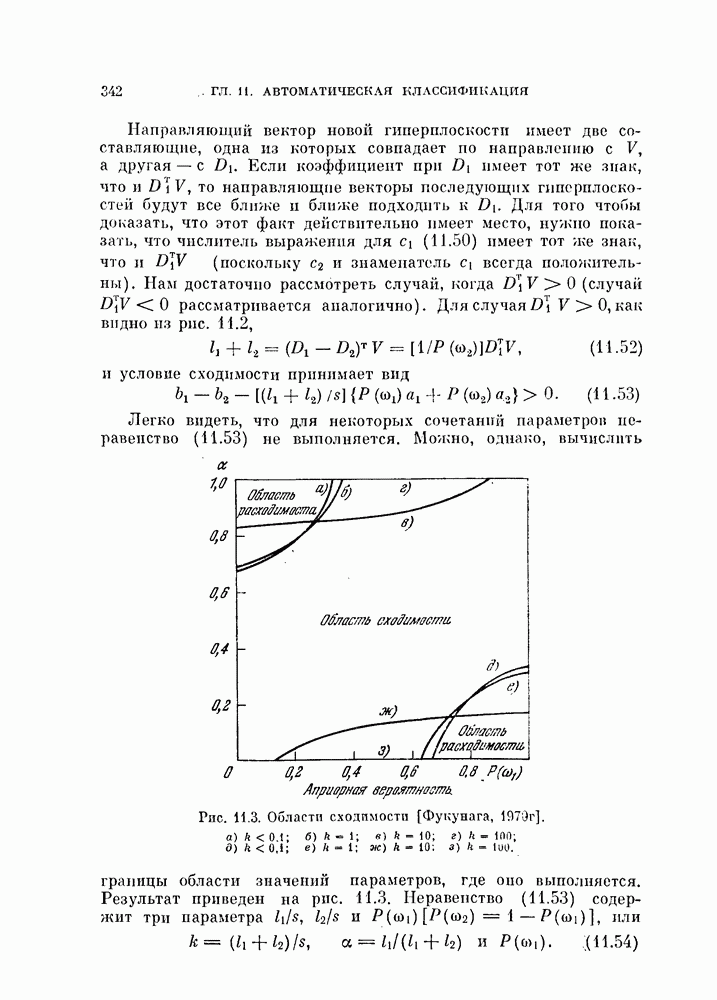
Легко видеть, что для некоторых сочетаний параметров неравенство (11.53) не выполняется.

Рис. 11.3. Области сходимости [Фукунага, 
Можно, однако, вычислить границы области значений параметров, где оно выполняется. Результат приведен на рис. 11.3. Неравенство (11.53) содержит три параметра  или
или

На рис. 11.3 показаны области сходимости в координатах  для различных к. Как видно из рисунка, область сходимости достаточно велика и не включает лишь крайние значения
для различных к. Как видно из рисунка, область сходимости достаточно велика и не включает лишь крайние значения  или а.
или а.
Сходимость в случае неравных ковариационных матриц.
Как уже говорилось ранее (см. рис. 4.10 и формулу (4.68)), гиперплоскость, перпендикулярная к вектору разности средних значений, дает приемлемое разделение двух нормальных распределений после совместной нормировки даже в том случае, когда ковариационные матрицы различны. Однако, когда  найти область сходимости, как мы это сделали выше, трудно. Сходимость можно доказать, если гиперплоскость проходит через определенную точку. Поэтому можно сказать, что некоторая область сходимости вблизи этой точки должна существовать.
найти область сходимости, как мы это сделали выше, трудно. Сходимость можно доказать, если гиперплоскость проходит через определенную точку. Поэтому можно сказать, что некоторая область сходимости вблизи этой точки должна существовать.
Предположим, что гиперплоскость проходит через точку, в которой

Тогда, подставляя (11.23) и (11.24) в (11.47), получим

Рассуждая так же, как мы это делали выше, получим следующее условие сходимости:

которое, используя (11.52) и (11.55), можно представить в виде

или

Это неравенство выполняется для всех 
Таким образом, если гиперплоскость проходит через точку, в которой выполняются соотношения (11.55), новый вектор разности средних  составляет меньший угол с вектором
составляет меньший угол с вектором  чем V, В окрестности этой точки должна существовать область сходимости (хотя теоретического обоснования этого утверждения мы не имеем).
чем V, В окрестности этой точки должна существовать область сходимости (хотя теоретического обоснования этого утверждения мы не имеем).
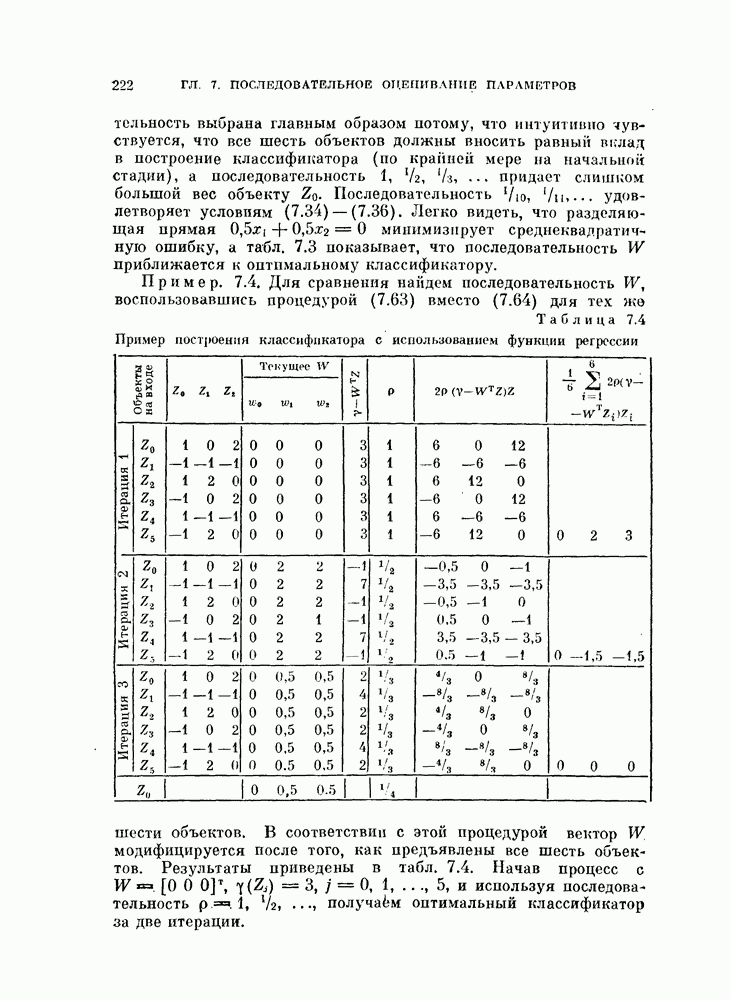
Пример 11.1. В дополнение к теоретическим исследованиям, рассмотрим результаты численных экспериментов.
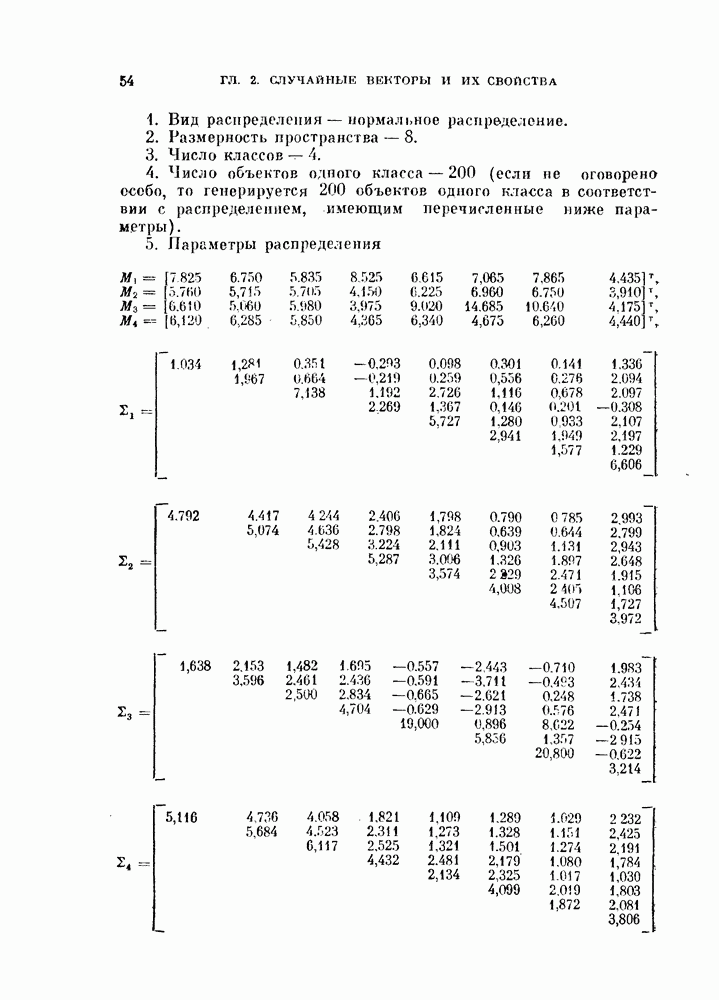
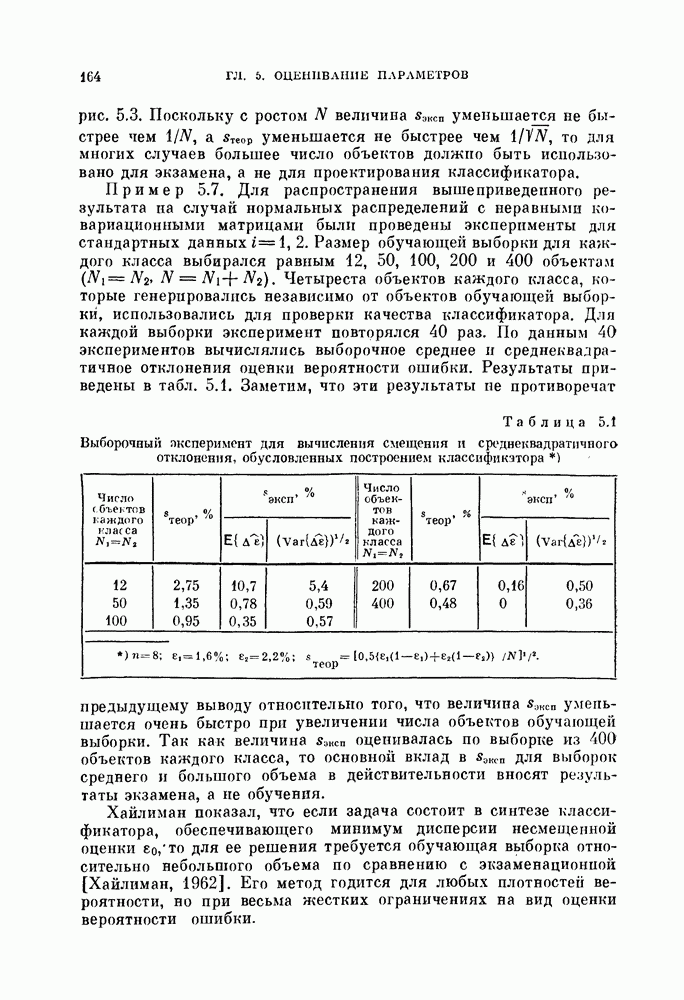
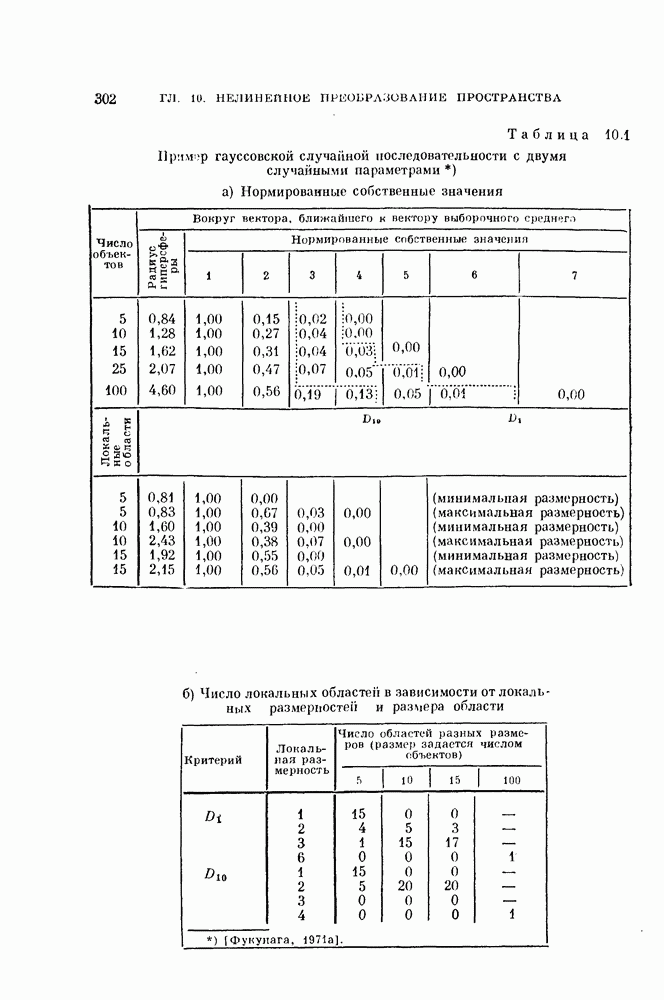
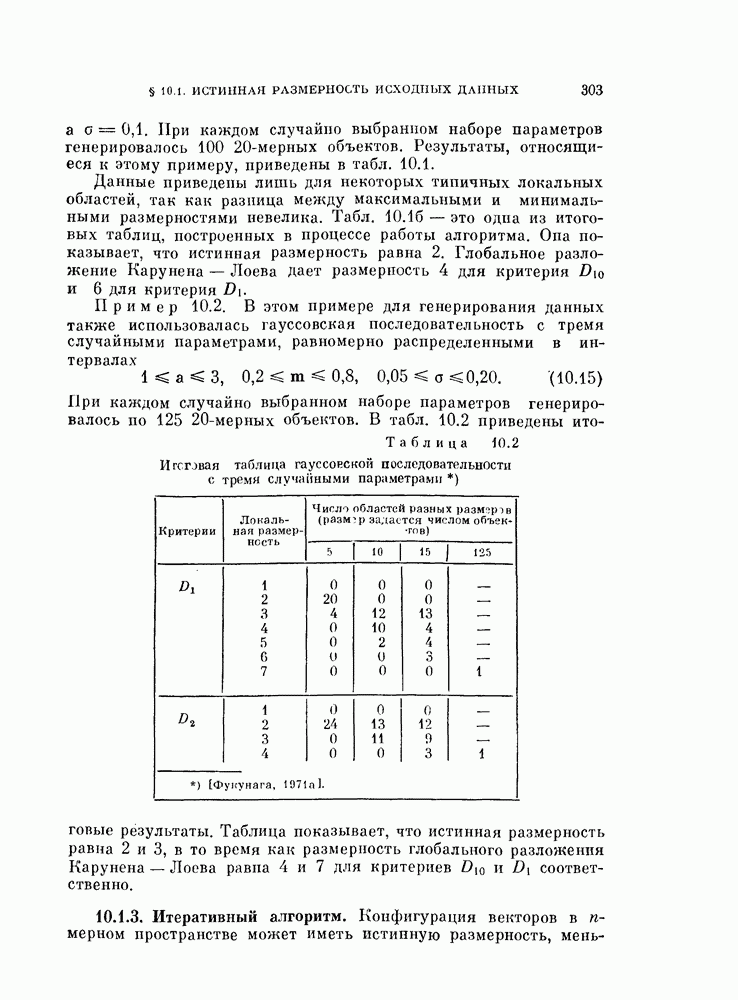
Таблица 11.1 (см. скан) Результаты классификации для стандартных данных 
В этих экспериментах объекты генерировались в соответствии с нормальными распределениями с заданными математическими ожиданиями и ковариационными матрицами. Математические ожидания и ковариации брались из стандартных данных.
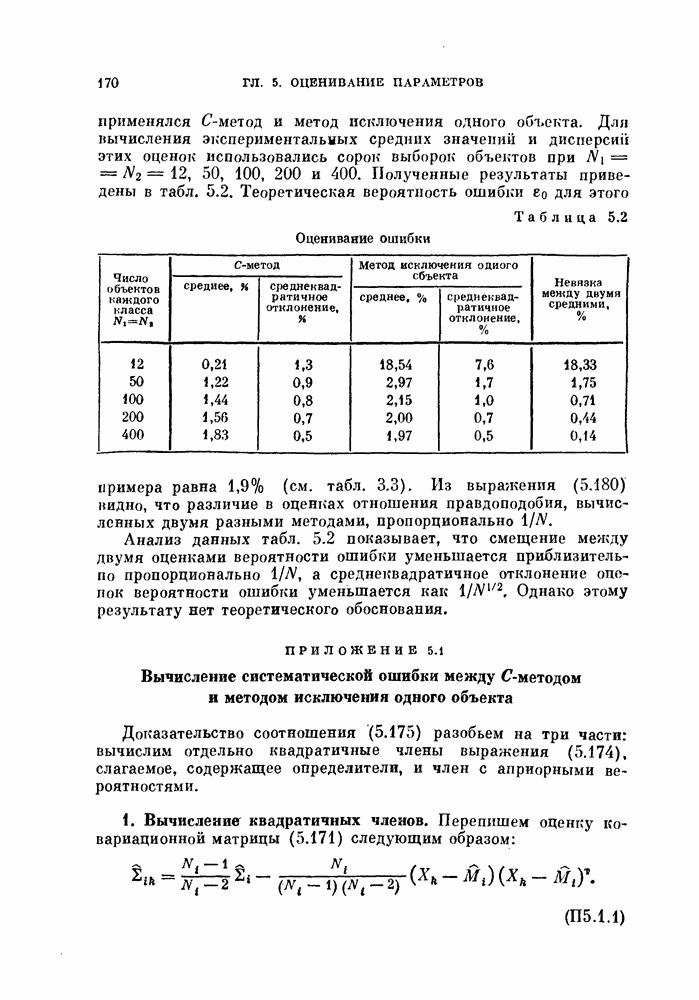
Таблица 11.2 (см. скан) Результаты классификации для стандартных данных 
Два класса. В первом эксперименте генерировалось по 100 объектов каждого класса в соответствии со стандартными данными,  Вначале объекты классифицировались в исходной системе координат в соответствии с решающим правилом
Вначале объекты классифицировались в исходной системе координат в соответствии с решающим правилом
ближайшего среднего. Затем производилась «совместная нормировка» объектов и они снова классифицировались.
В табл. 11.1 приведены матрицы, показывающие количество правильно и неправильно классифицированных объектов в каждом случае.

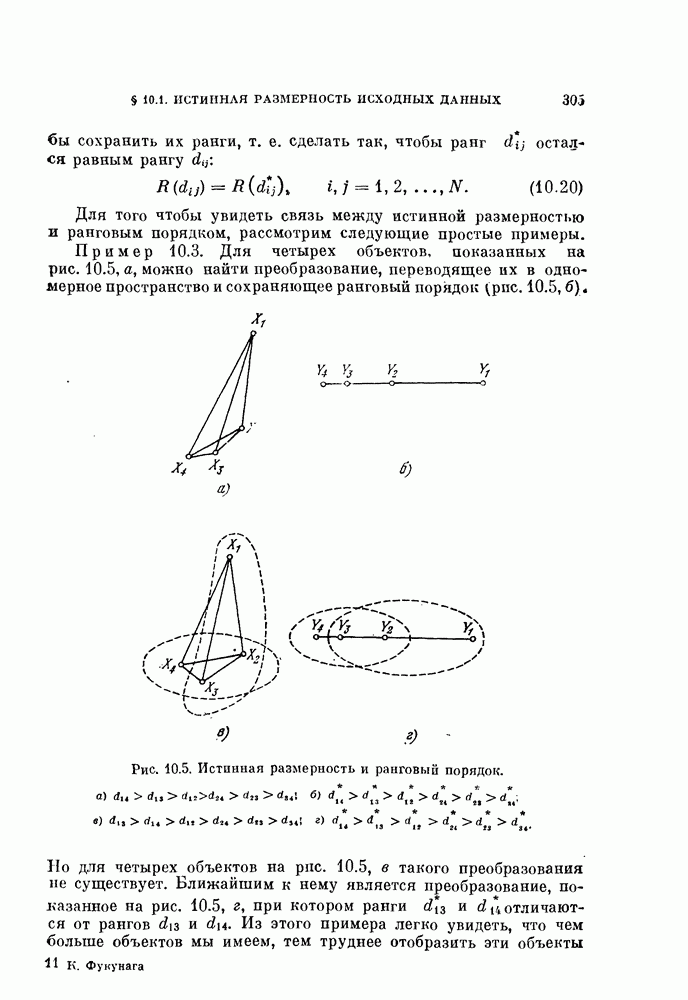
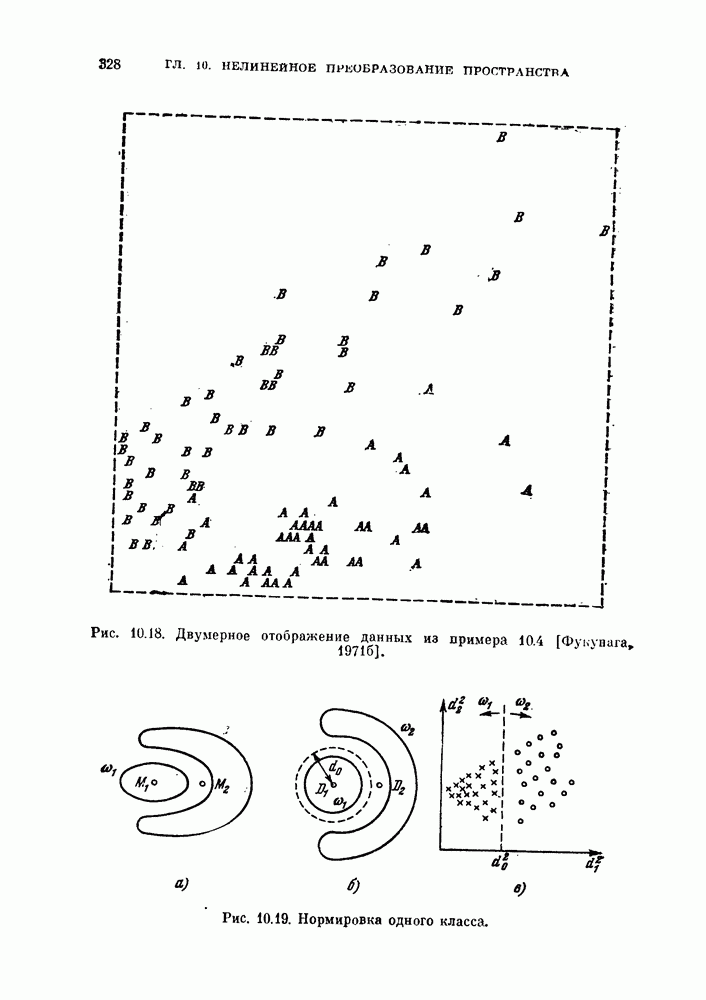
Рис. 11.4. График разброса экспериментальных объектов, а) Исходное распределение; 6) после совместной нормировки [Фукунага. 1970 г].
В случае, когда предварительно была сделана совместная нормировка, число неправильно классифицированных объектов оказалось меиыиим.
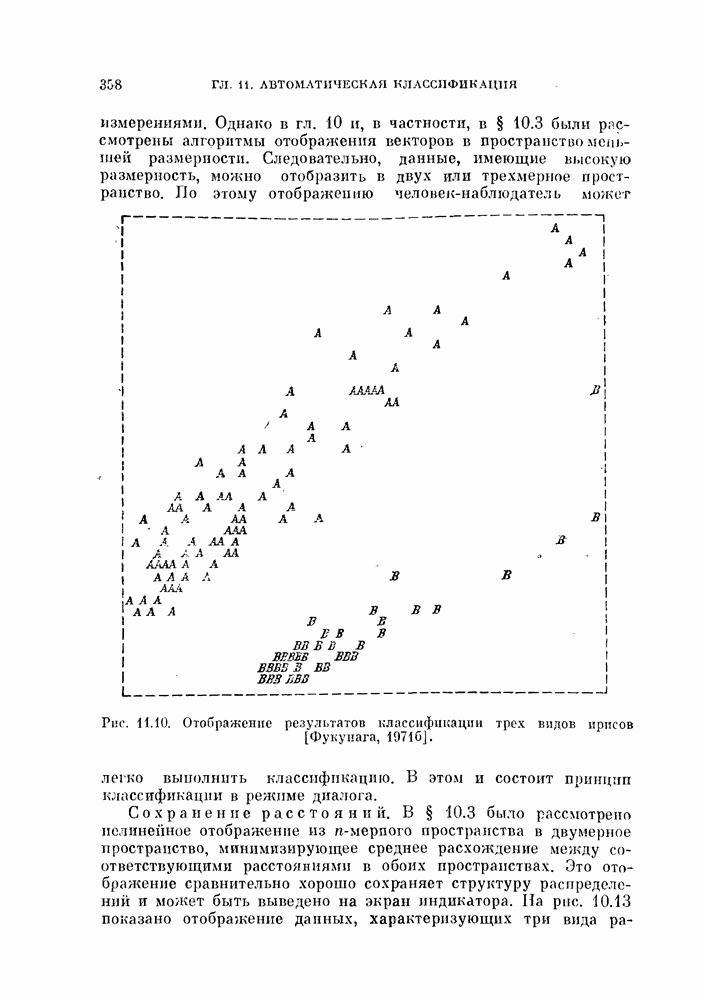
Три класса. В этом эксперименте генерировалось по 100 объектов каждого класса в соответствии со стандартными данными  . Далее применялась та же самая процедура. Результаты приведены в табл. 11.2. На рис. 11.4 показаны проекции данных на плоскость в исходной и нормированной системах координат.
. Далее применялась та же самая процедура. Результаты приведены в табл. 11.2. На рис. 11.4 показаны проекции данных на плоскость в исходной и нормированной системах координат.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
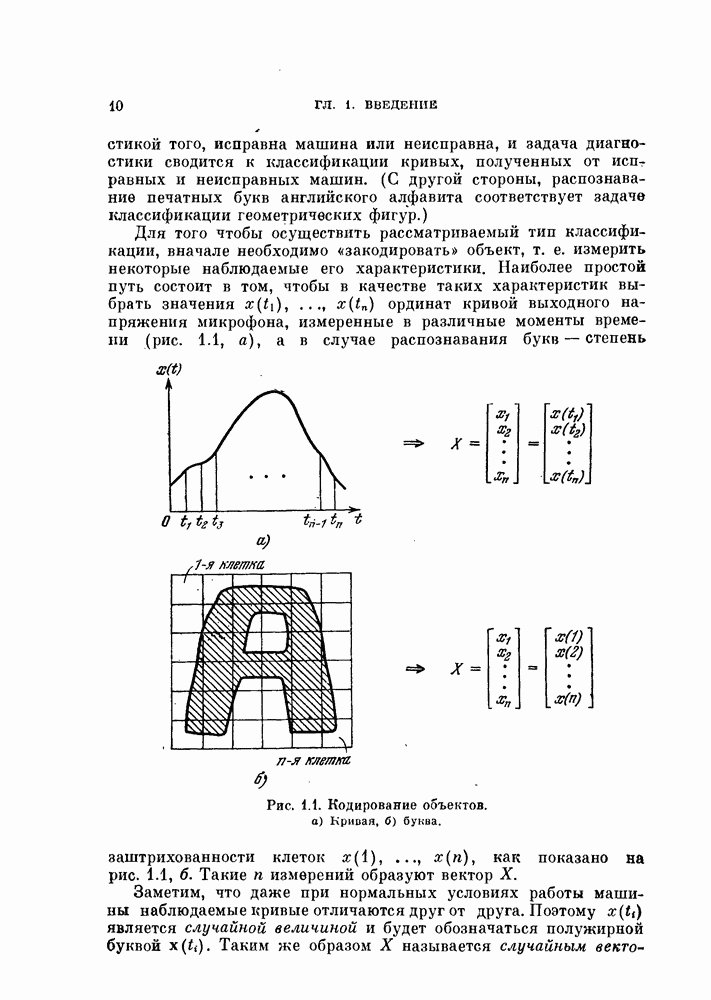
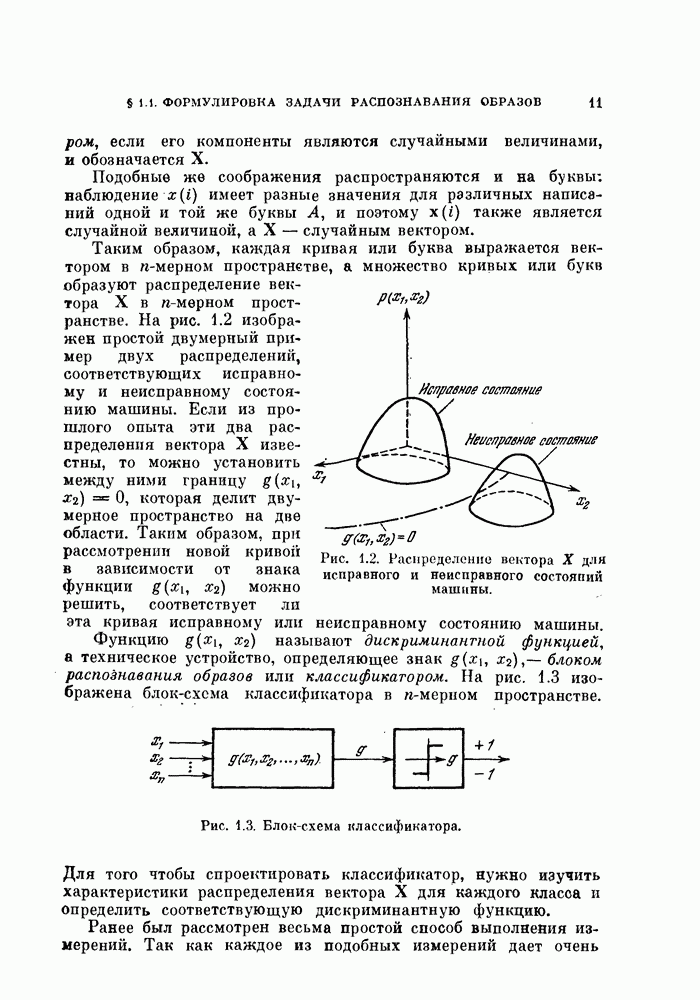
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
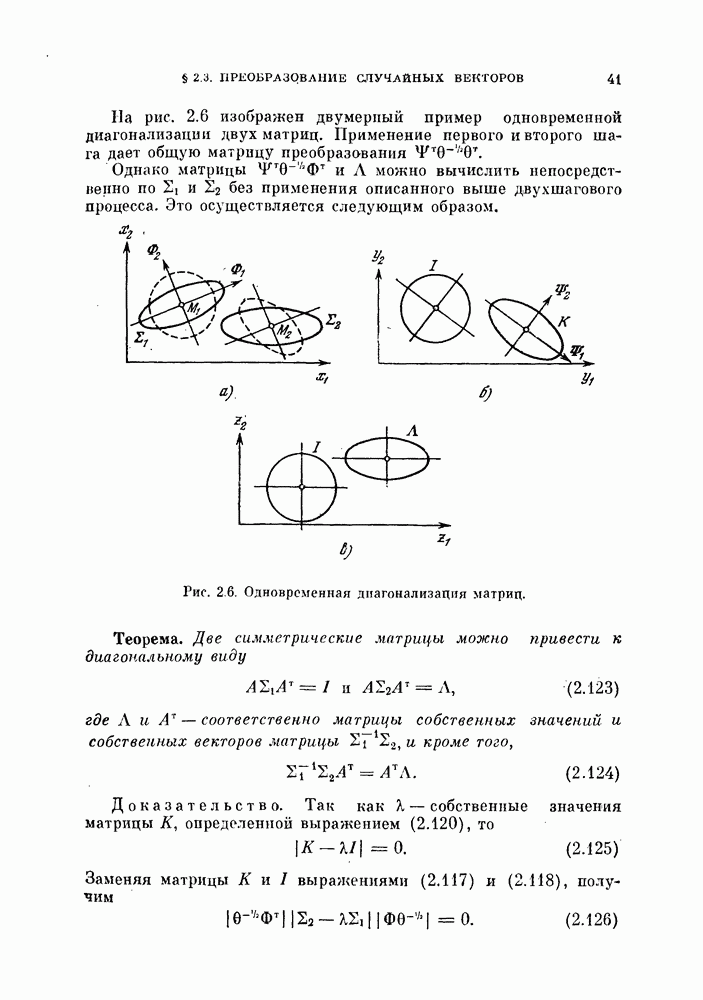
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
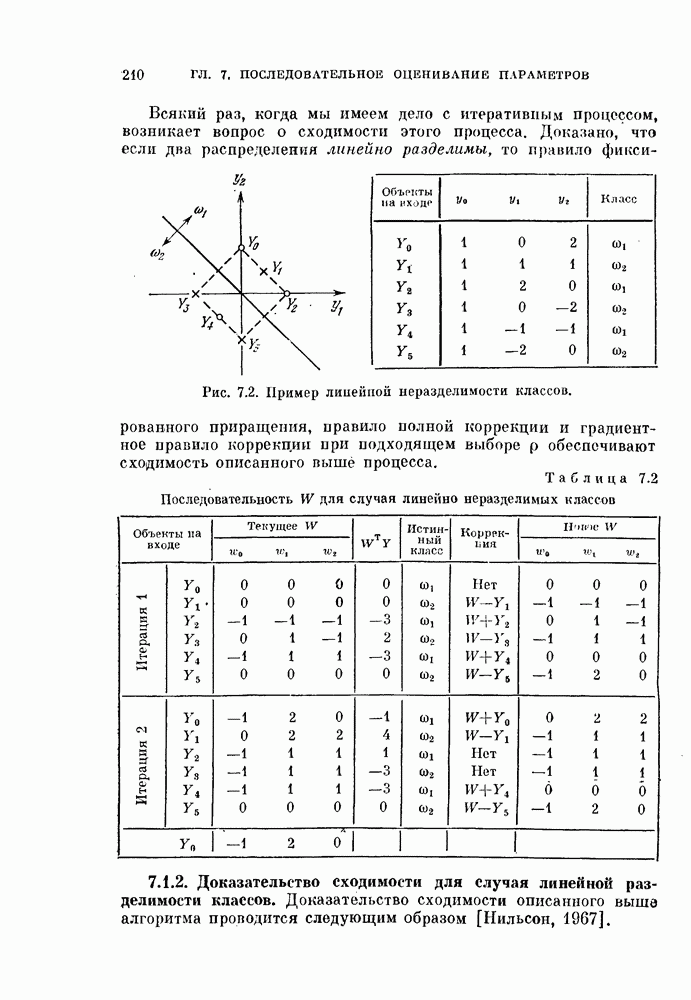
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
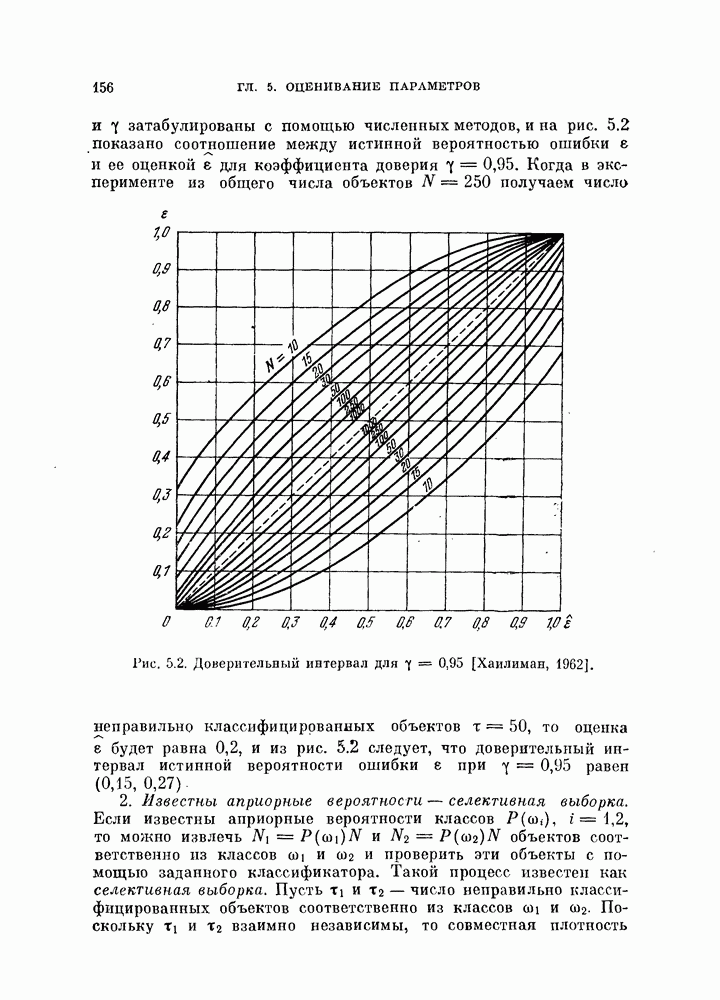
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
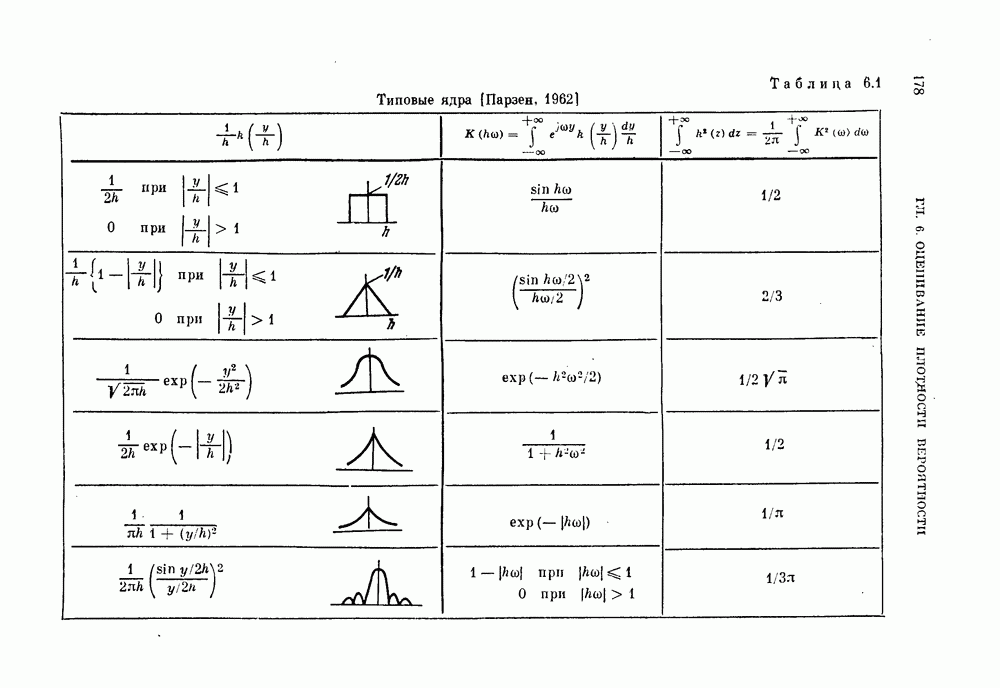
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
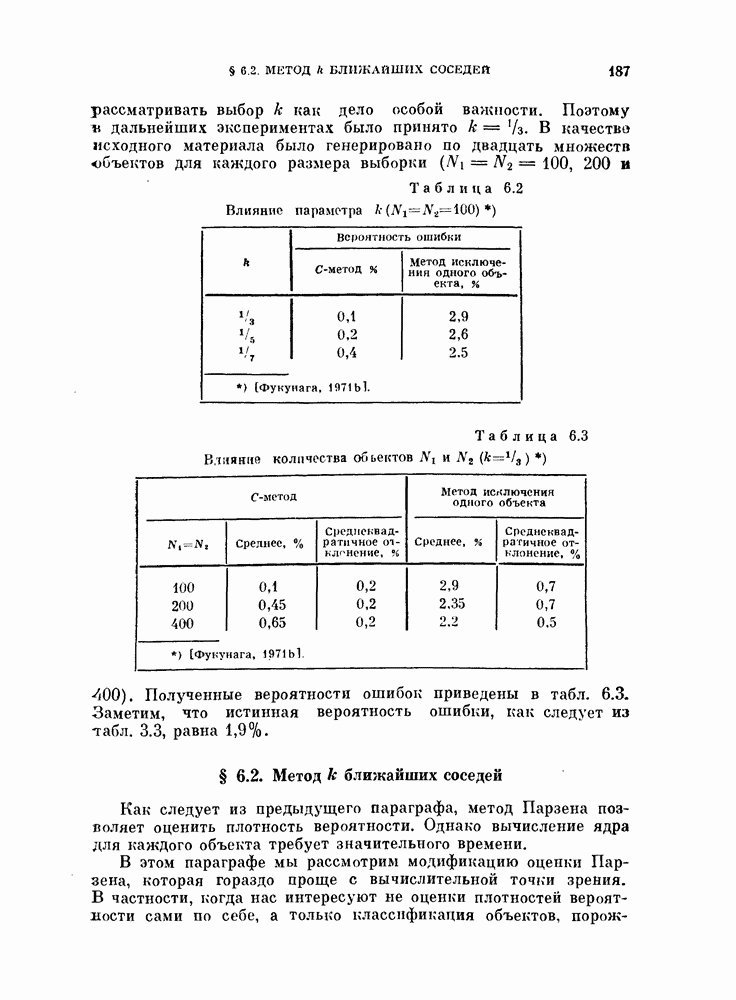
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
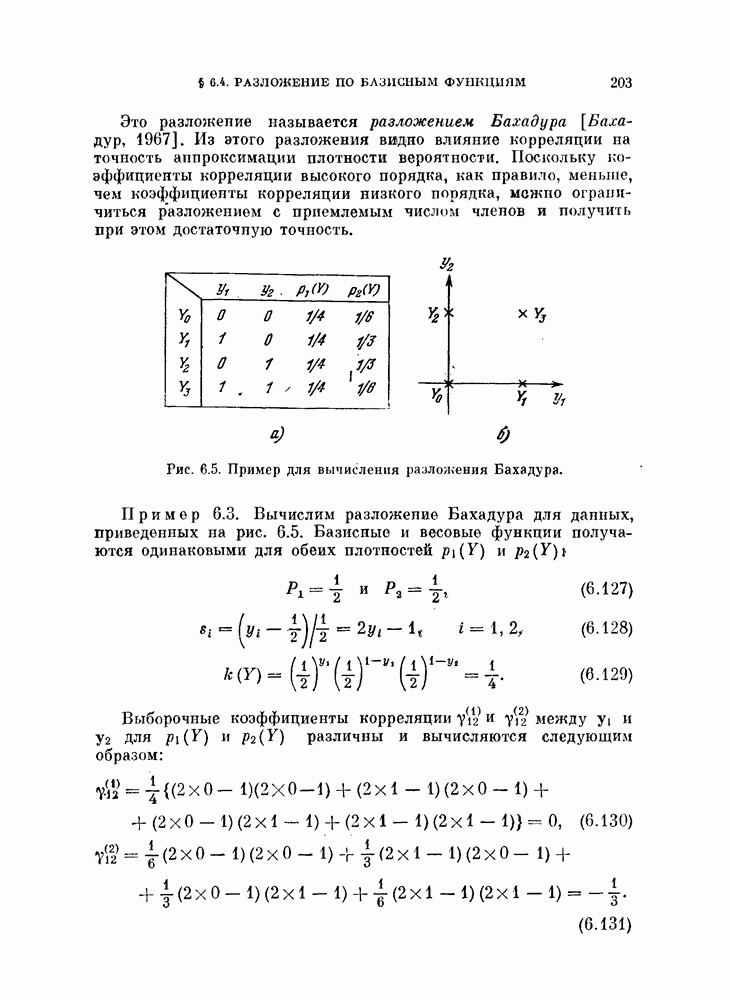
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
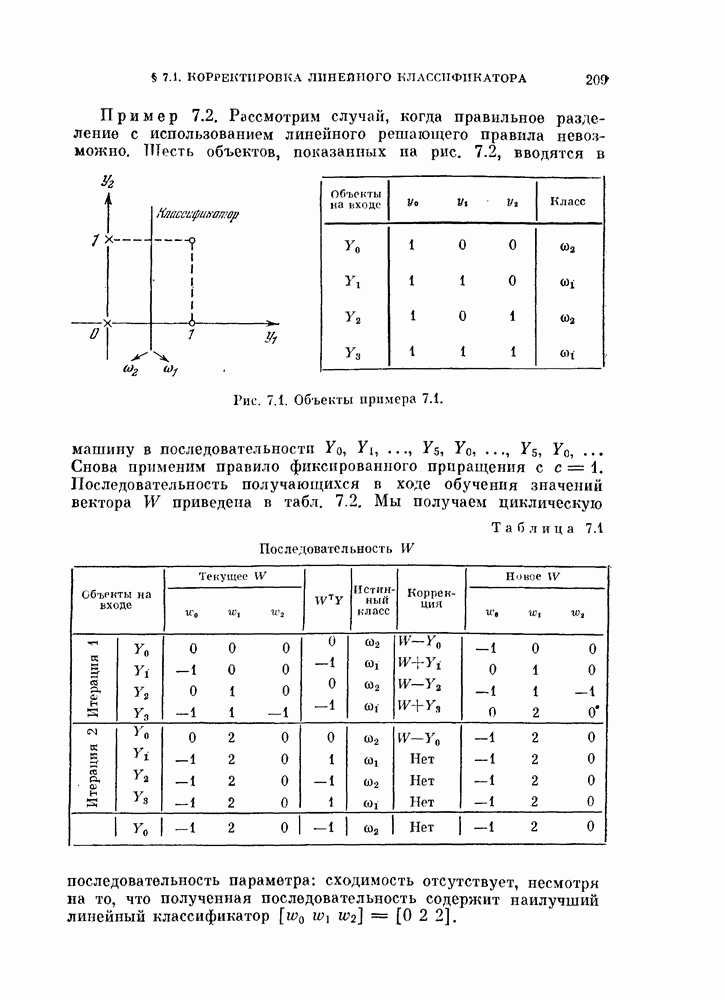
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
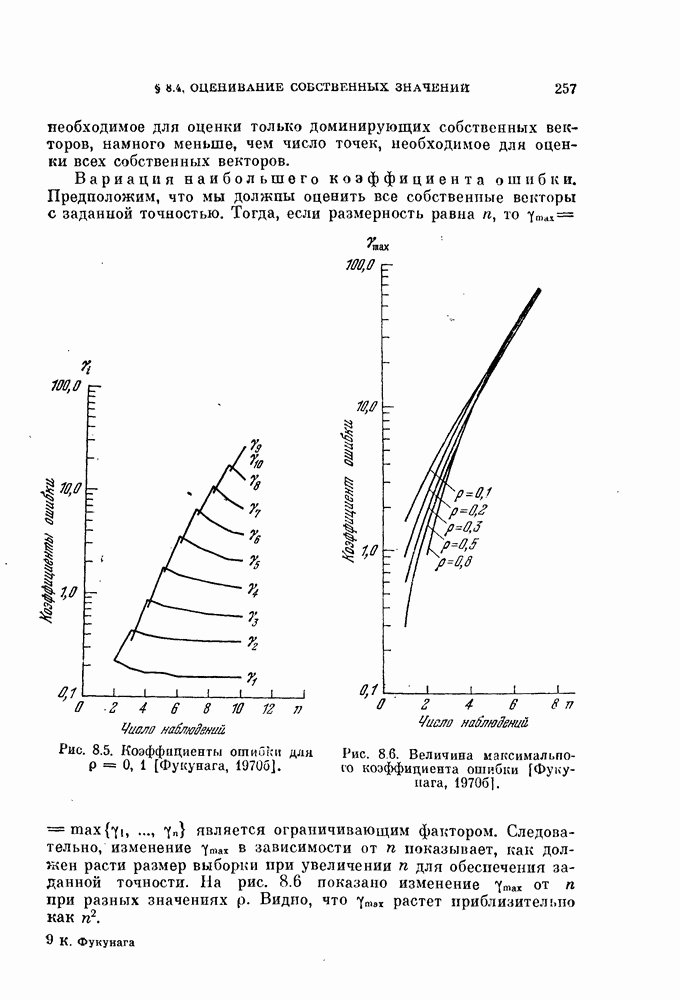
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
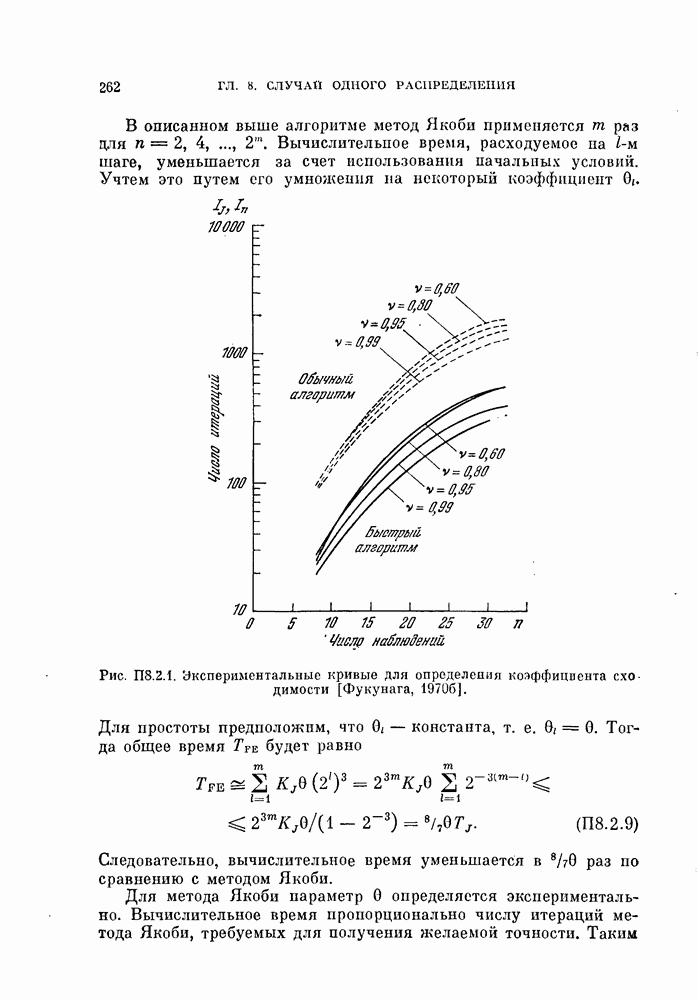
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
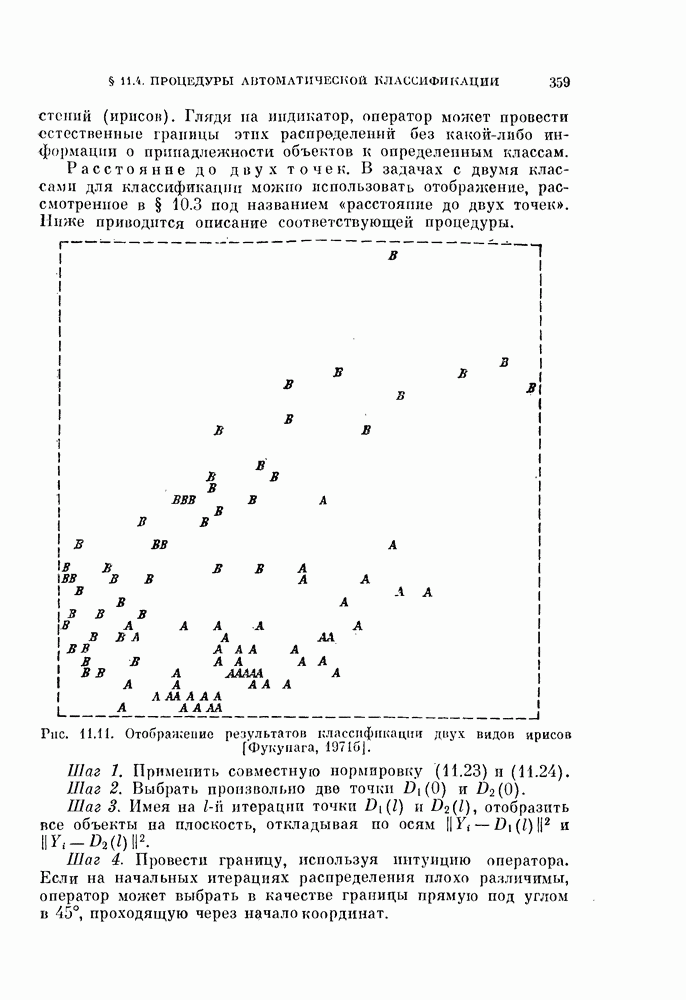
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА