| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8.1. Дискретное разложение Карунена — Лоева
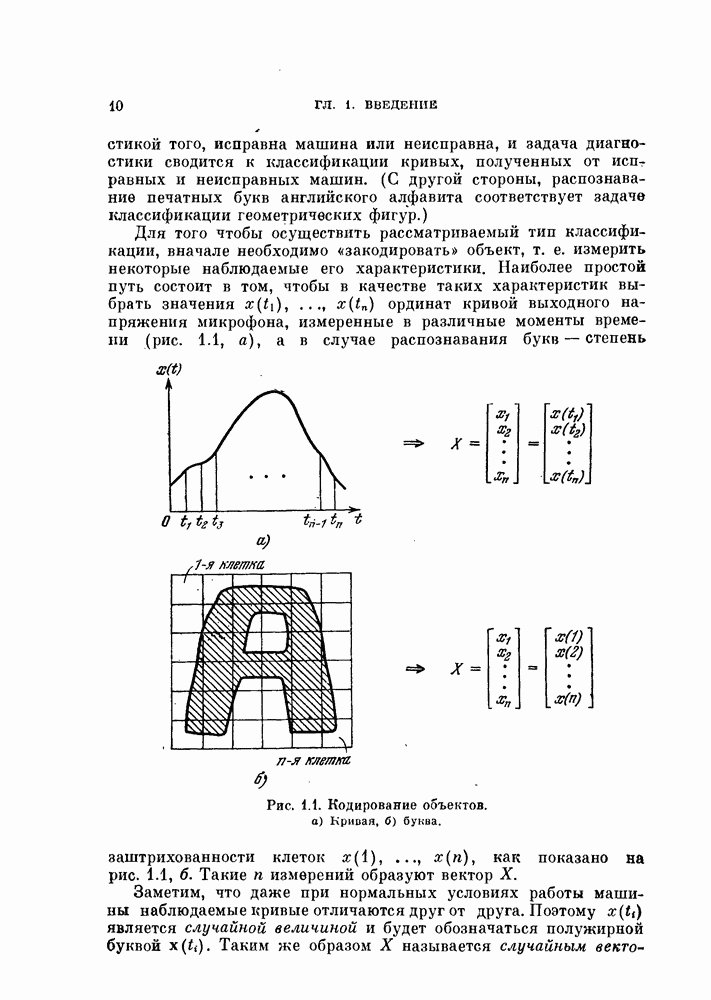
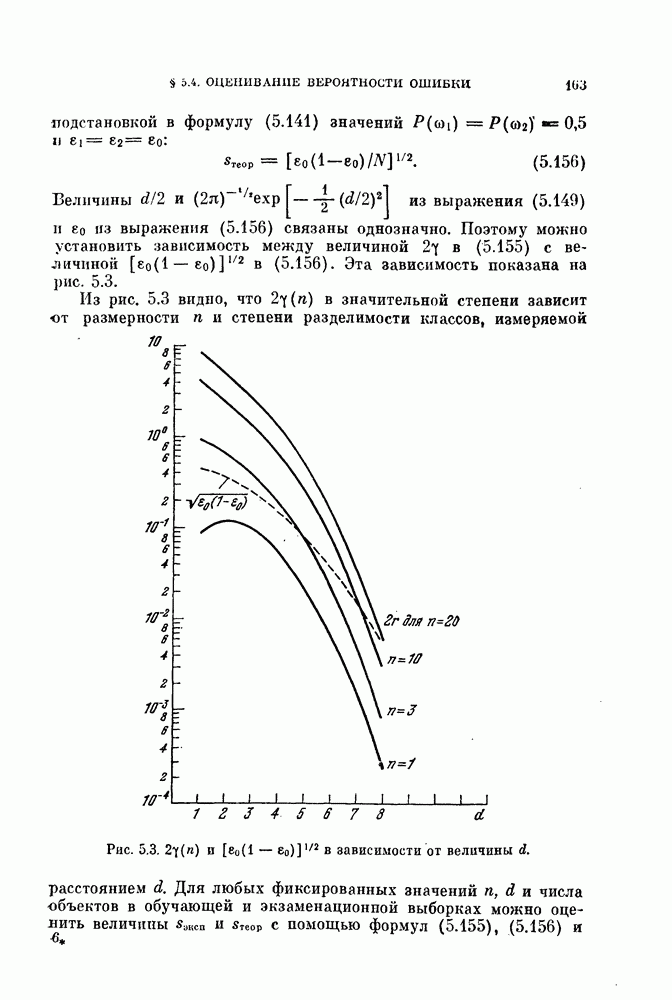
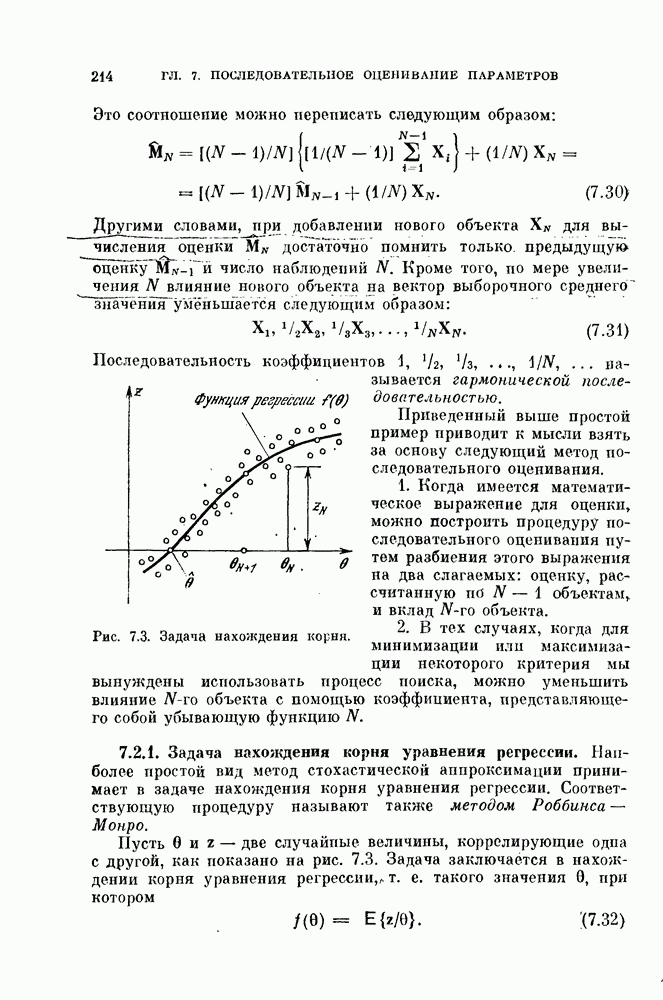
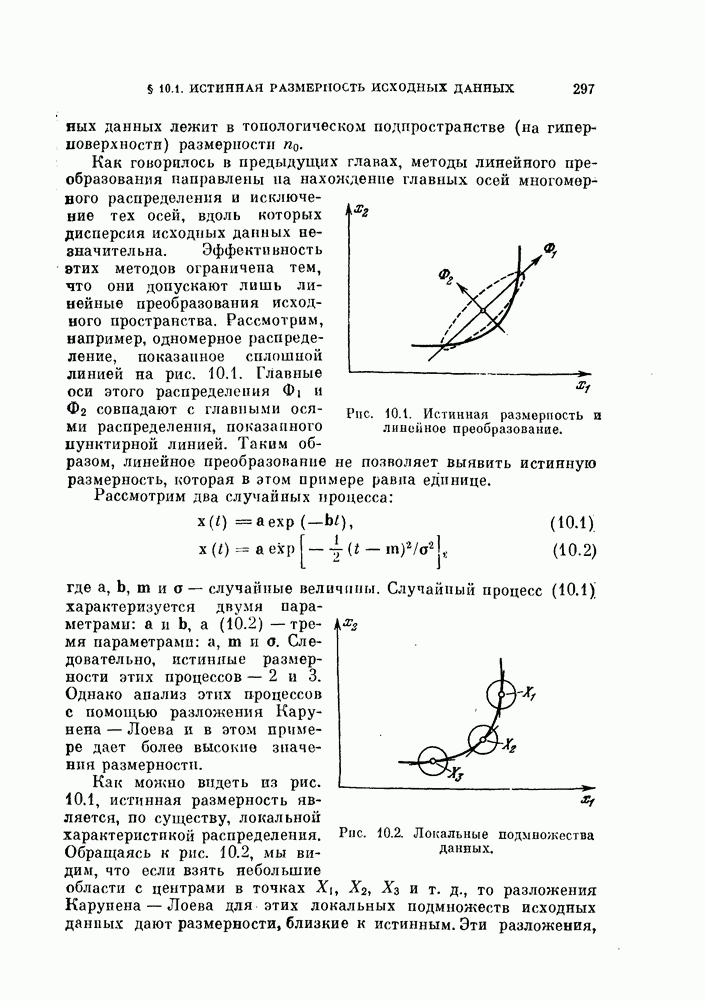
Рассмотрим вначале выбор признаков в случае одного распределения. При наличии только одного распределения нельзя говорить о разделимости классов, т. е. о задаче распознавания образов. Вместо этого мы рассмотрим, насколько точно можно описать объекты, генерированные в соответствии с распределеним с помощью набора признаков. Если с помощью небольшого числа признаков удается точно описать объекты, то можно сказать, что такие признаки эффективны. Хотя эта задача непосредственно не связана с распознаванием образов, знание характеристик отдельных распределений помогает отделить одно распределение от других. Кроме того, выбор признаков для случая одного распределения находит широкое применение в других областях, таких, как представление сигналов и сжатие данных в системах связи. Еще одно ограничение связано с тем, что ищутся только такие признаки, которые можно получить линейным преобразованием исходных переменных. Как видно из рис. 8.1, новый признак у весьма эффективен для представления данных объектов, но этот признак является нелинейной функцией относительно 

Рис. 8.1. Нелинейное преобразование.
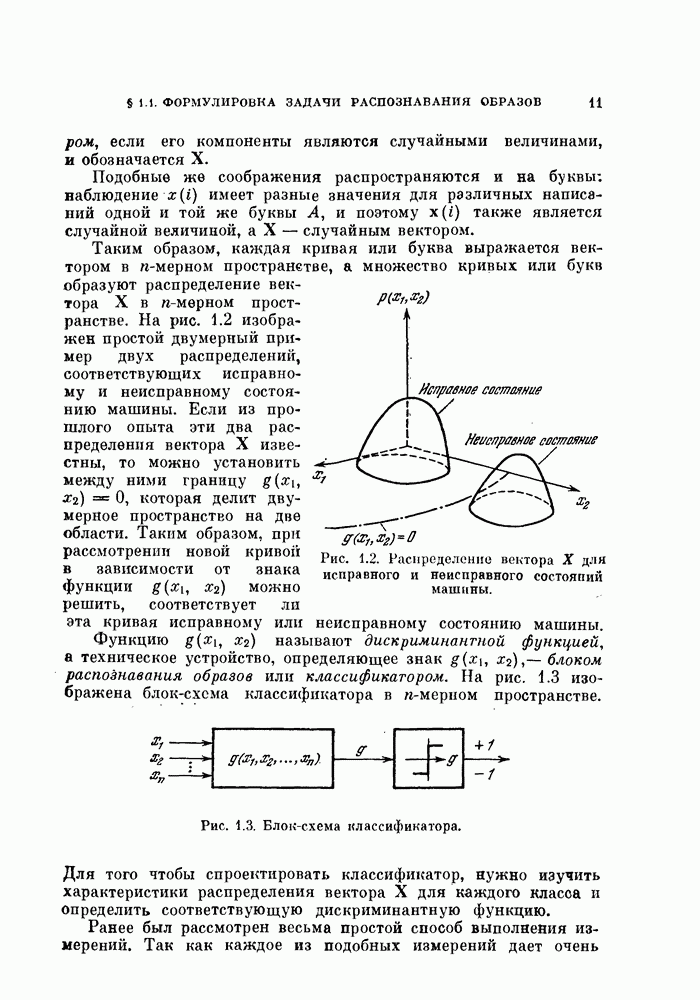
8.1.1. Критерий минимума среднеквадратичной ошибки.
Пусть X — n-мерный случайный вектор. Тогда X можно точно представить разложением

где

а

Матрица Ф является детерминированной и состоит из  линейно независимых векторов-столбцов, т. е.
линейно независимых векторов-столбцов, т. е.

Следовательно, линейные комбинации столбцов матрицы Ф образуют  -мерное пространство, содержащее X. Столбцы матрицы Ф называются базисными векторами. Далее можно предположить, что эти столбцы ортоиормированы, т. е.
-мерное пространство, содержащее X. Столбцы матрицы Ф называются базисными векторами. Далее можно предположить, что эти столбцы ортоиормированы, т. е.

Если условие ортонормированности выполнено, то компоненты вектора  определяются следующим образом:
определяются следующим образом:

Следовательно,  представляет собой ортогональное преобразование случайного вектора X и тоже является случайным вектором. Каждая компонента
представляет собой ортогональное преобразование случайного вектора X и тоже является случайным вектором. Каждая компонента  является признаком, который вносит вклад в представление наблюдаемого вектора X.
является признаком, который вносит вклад в представление наблюдаемого вектора X.
Предположим, что мы определили только  компонент вектора
компонент вектора  и все еще хотим если не точно представить, то по крайней мере оценить X. Это можно сделать, заменив заранее выбранными константами те компоненты
и все еще хотим если не точно представить, то по крайней мере оценить X. Это можно сделать, заменив заранее выбранными константами те компоненты  которые мы не вычисляем, и получить следующую оценку:
которые мы не вычисляем, и получить следующую оценку:

Без ограничения общности можно считать, что вычисляются только первые  компонент вектора у. Если используются не все признаки, то вектор X представляется с ошибкой, которая определяется выражением
компонент вектора у. Если используются не все признаки, то вектор X представляется с ошибкой, которая определяется выражением

Заметим, что как X, так и  являются случайными векторами. Используем среднюю величину квадрата
являются случайными векторами. Используем среднюю величину квадрата  в качестве критерия для измерейия эффективности подмножества, состоящего из
в качестве критерия для измерейия эффективности подмножества, состоящего из 
признаков:

Каждому набору базисных векторов и значений констант соответствует некоторое значение  Выберем их таким образом, чтобы минимизировать
Выберем их таким образом, чтобы минимизировать  Оптимальный выбор констант
Оптимальный выбор констант  производится следующим образом:
производится следующим образом:

Другими словами, мы должны заменить те  которые не измеряются, их математическими ожиданиями. Это легко показать, минимизируя
которые не измеряются, их математическими ожиданиями. Это легко показать, минимизируя  по
по 

Теперь среднеквадратичную ошибку можно записать следующим образом:

где  — ковариационная матрица случайного вектора X. Ниже будет показано, что оптимальный выбор матрицы Ф удовлетворяет условию
— ковариационная матрица случайного вектора X. Ниже будет показано, что оптимальный выбор матрицы Ф удовлетворяет условию

т. е. оптимальные базисные векторы — это собственные векторы ковариационной матрицы  Таким образом, минимальная среднеквадратичная ошибка равна
Таким образом, минимальная среднеквадратичная ошибка равна

Разложение случайного вектора по собственным векторам ковариационной матрицы представляет собой дискретный вариант разложения Карунена — Лоева.
В задачах распознавания образов коэффициенты  этого разложения рассматриваются как признаки, представляющий наблюдаемый вектор X. Эти признаки обладают некоторыми замечательными свойствами, которые мы здесь перечислим.
этого разложения рассматриваются как признаки, представляющий наблюдаемый вектор X. Эти признаки обладают некоторыми замечательными свойствами, которые мы здесь перечислим.
1. Эффекгвность каждого признака, т. е. его полезность с точки зрения представления X, определяется соответствующим собственным значением. Если некоторый признак, например, у» исключается из разложения, то среднеквадратичная ошибка увеличивается на  Поэтому, если мы хотим уменьшить число признаков, признак с наименьшим собственным значением следует исключить в первую очередь и т. д. Если собственные значения перенумерованы в порядке убывания.
Поэтому, если мы хотим уменьшить число признаков, признак с наименьшим собственным значением следует исключить в первую очередь и т. д. Если собственные значения перенумерованы в порядке убывания.

то признаки должны быть упорядочепы по важности таким же образом.
2. Рассматриваемые признаки взаимно иекоррелировапы, т. е. ковариационная матрица случайного вектора  диагональна:
диагональна:

В частном случае, когда случайный вектор X распределен нормально, признаки  взаимно независимы.
взаимно независимы.
3. Собственные векторы ковариационной матрицы дают наименьшее значение среднеквадратичной ошибки  среди всех ортонормированных базисных векторов. Неортогональные» линейные преобразования в зтой главе не рассматриваются: в случае одного распределения нас интересуют лишь те преобразования, которые сохраняют структуру распределения.
среди всех ортонормированных базисных векторов. Неортогональные» линейные преобразования в зтой главе не рассматриваются: в случае одного распределения нас интересуют лишь те преобразования, которые сохраняют структуру распределения.
Доказательство свойства 3. Предположим, что мы разложили случайный вектор X по столбцам другой ортогональной матрицы  Рассмотрим матрицу
Рассмотрим матрицу

диагональный элемент которой имеет вид

Разобьем матрицу Н на подматрицы следующим образом:

Тогда среднеквадратичная ошибка в случае, если измеряются
только  компопент вектора
компопент вектора  имеет вид
имеет вид

(в соответствии с равенством (8.12), которое было получена только из условия ортогональности Ф. Наша цель состоит  том, чтобы показать, что среднеквадратичная ошибка
том, чтобы показать, что среднеквадратичная ошибка  ограничена снизу значением
ограничена снизу значением  выражения (8.14).
выражения (8.14).
Пусть  — матрицы, составленные соответственно из собственных векторов и собственных значений ковариационной матрицы
— матрицы, составленные соответственно из собственных векторов и собственных значений ковариационной матрицы  Тогда можно записать
Тогда можно записать

Так как матрицы  ортогональны, матрица
ортогональны, матрица  также ортогональна, так как
также ортогональна, так как

Разобьем матрицу (8.21) аналогично (8.19):

Из этого следует, что

Тогда суть нашего доказательства состоит в том, чтобы показать:

Из ортогональности матрицы  имеем следующие тождества:
имеем следующие тождества:

Продолжим доказательство:

Первое неравенство следует из того, что  наименьшее собственное значение матрицы
наименьшее собственное значение матрицы  , a
, a  - наибольшее собственное значение матрицы
- наибольшее собственное значение матрицы  Мы воспользовались здесь матричным тождеством
Мы воспользовались здесь матричным тождеством  и тождествами (8.26) — (8.28). Подробное обоснование неравенства (8.29) оставлено в качестве упражнения. Когда
и тождествами (8.26) — (8.28). Подробное обоснование неравенства (8.29) оставлено в качестве упражнения. Когда  имеем
имеем  так что неравенство превращается в равенство.
так что неравенство превращается в равенство.

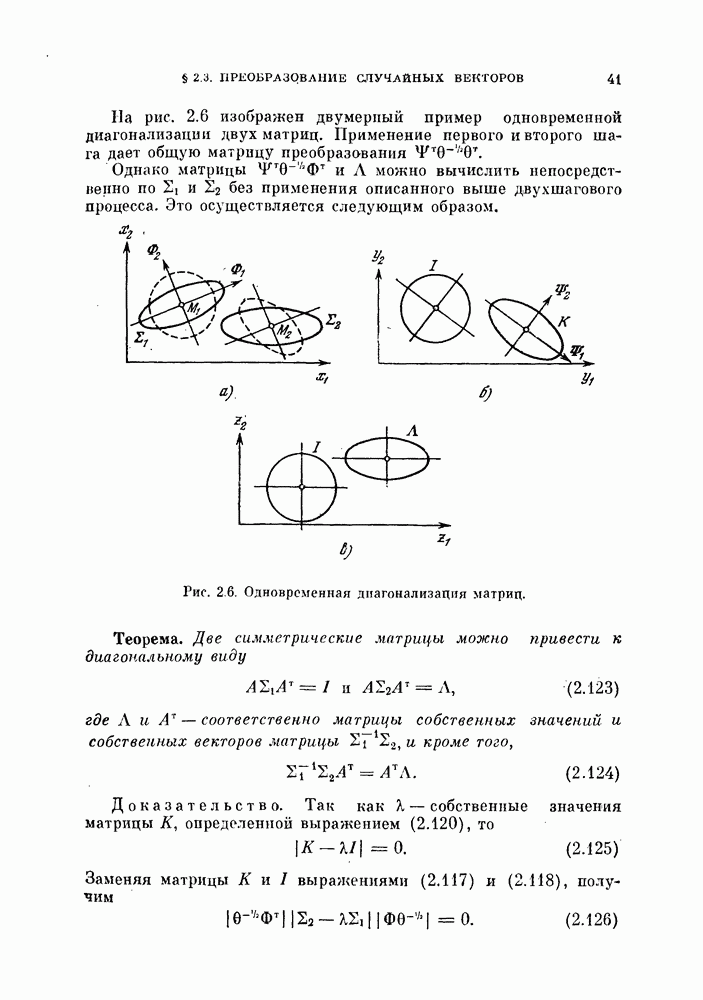
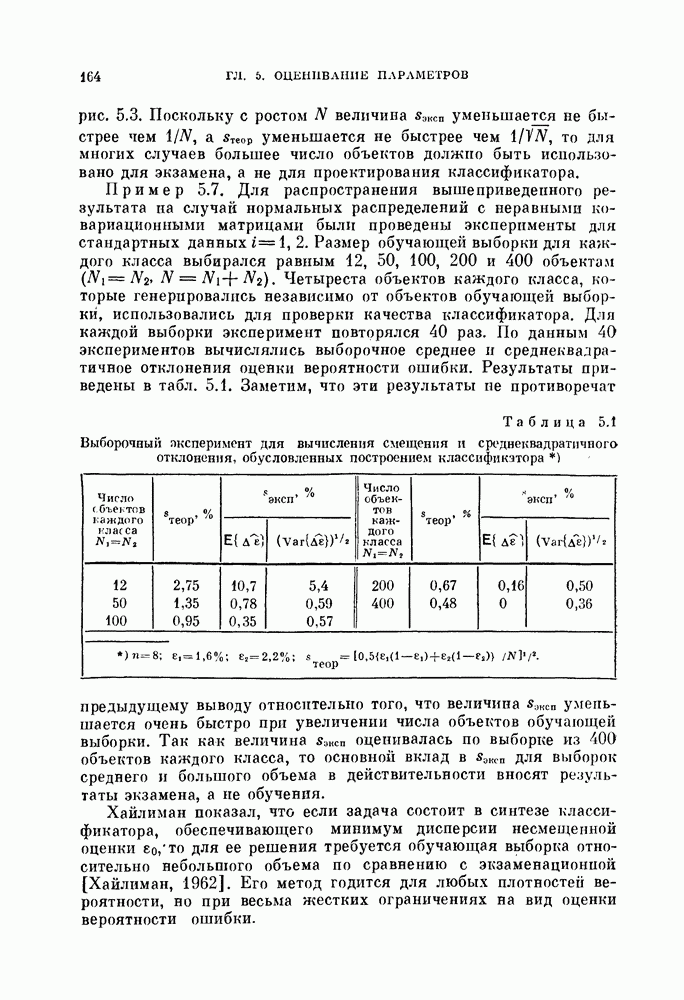
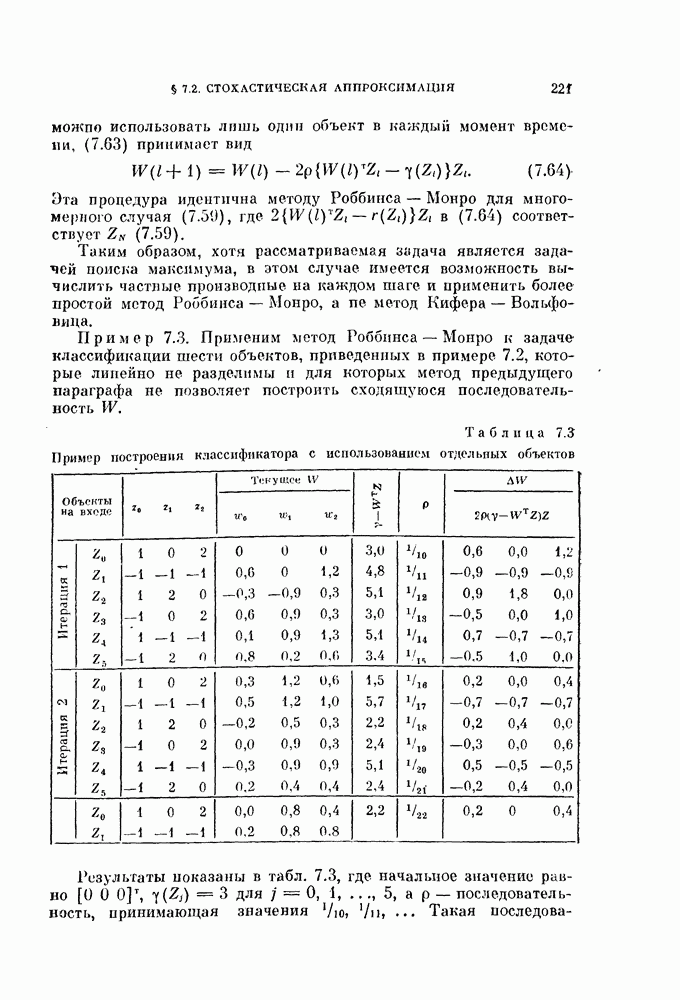
Рис. 8.2. Примеры разложения Карунена — Лоева.
Доказательство окончено.
Чтобы лучше почувствовать особенности разложения Карунена — Лоева, рассмотрим два простых примера.
Пример 8.1. Рассмотрим два мпожества дапных, показанные на рис. 8.2, а и б. В обоих случаях векторы математического ожидания равны нулю.
Во-первых, вычислим выборочную ковариационную матрицу  Для данных
Для данных  соответственно имеем:
соответственно имеем:

Во вторых, найдем собственные значения и собственные векторы матрицы 2

Таким образом, в обоих случаях базисные векторы повернуты на угол 45°, как показано на рис. 8.2.
Наконец, рассмотрим влияние исключения одного из  базисных векторов. Для данных а) собственное значенне
базисных векторов. Для данных а) собственное значенне  Поэтому, даже в том случае если исключить вектор
Поэтому, даже в том случае если исключить вектор  из раз ложения Карунена — Лоева, среднеквадратичная ошибка будет равна нулю.
из раз ложения Карунена — Лоева, среднеквадратичная ошибка будет равна нулю.
Рис. 8.2, а показывает, что все четыре объекта можно без ошибки выразить через первый базисный вектор  . С другой стороны, для данных б) собственное значение
. С другой стороны, для данных б) собственное значение  Поэтому мы ожидаем, что при исключении из разложения вектора
Поэтому мы ожидаем, что при исключении из разложения вектора  среднеквадратичная ошибка будет равна 1. Из рис.
среднеквадратичная ошибка будет равна 1. Из рис.  видног что объекты
видног что объекты  можно выразить через вектор
можно выразить через вектор  без ошибки, но объекты
без ошибки, но объекты  и
и  выражаются с ошибкой, равной
выражаются с ошибкой, равной  Поэтому сред неквадратичная ошибка равна
Поэтому сред неквадратичная ошибка равна

т. е. равна собственному значению 
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
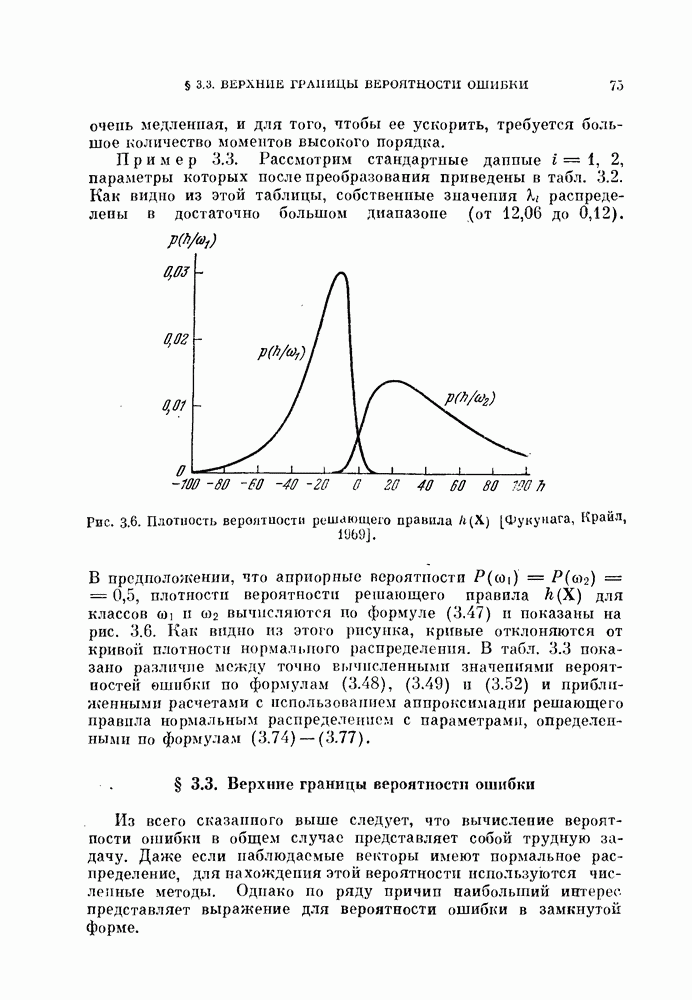
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
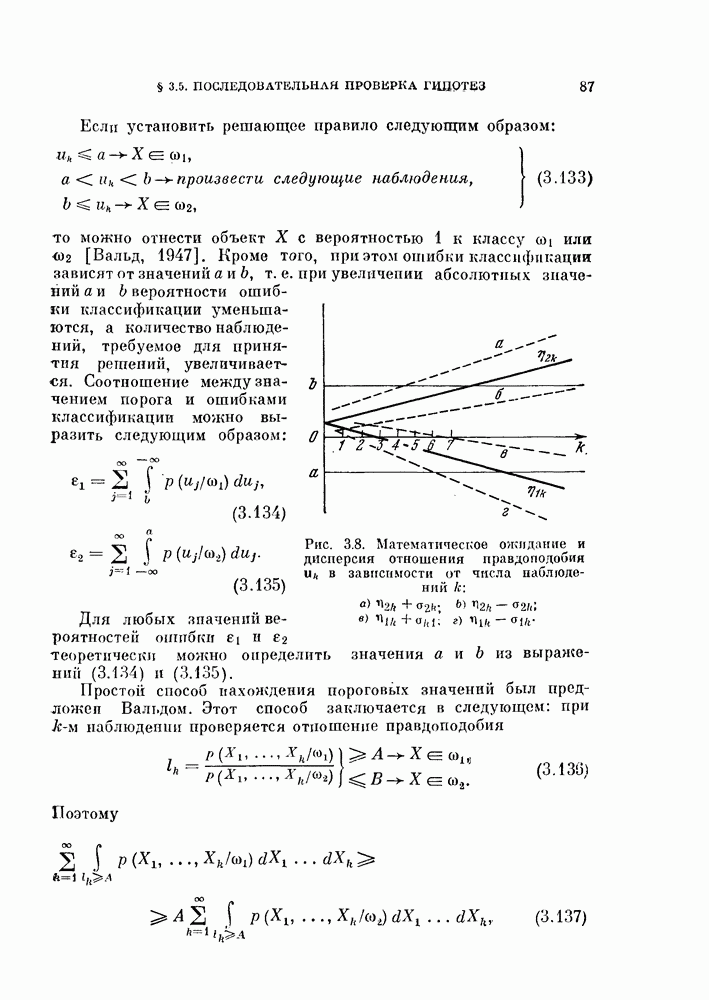
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
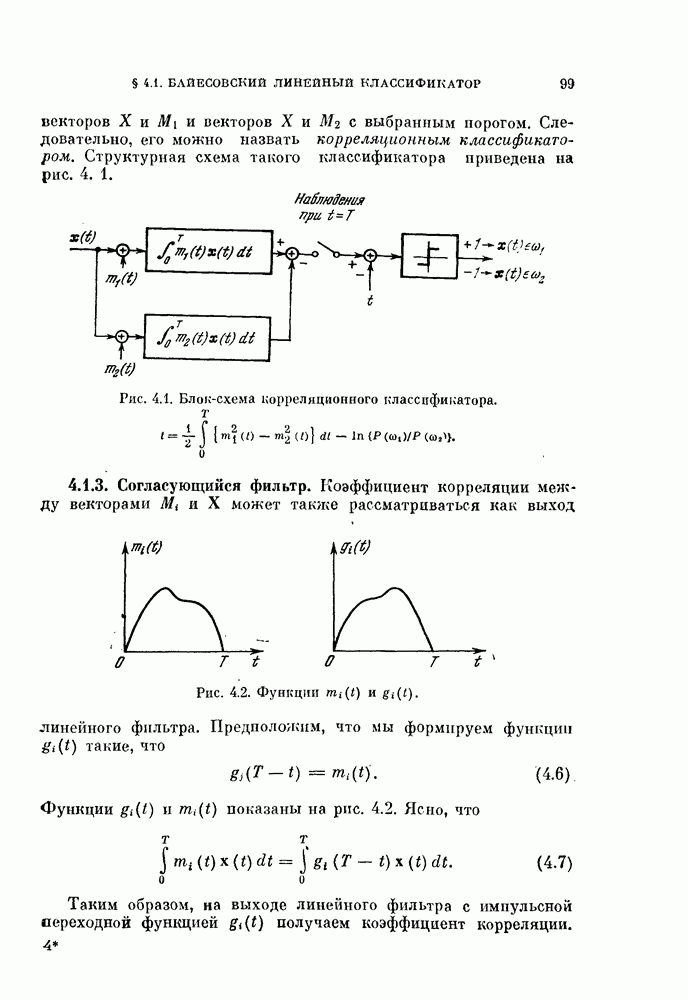
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА