| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
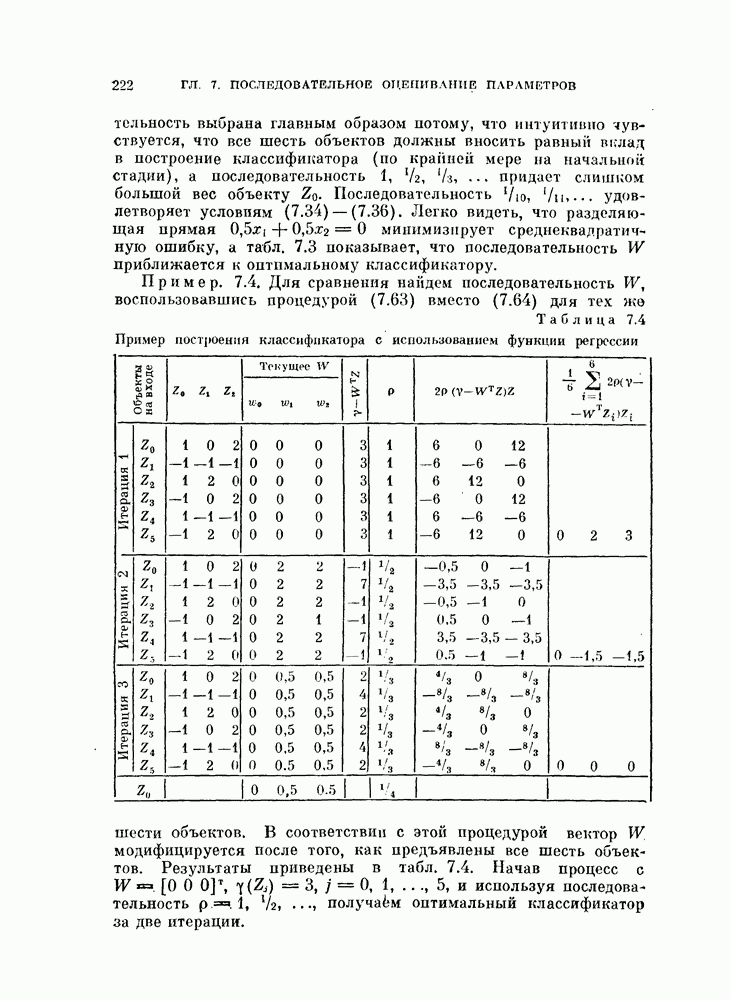
Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
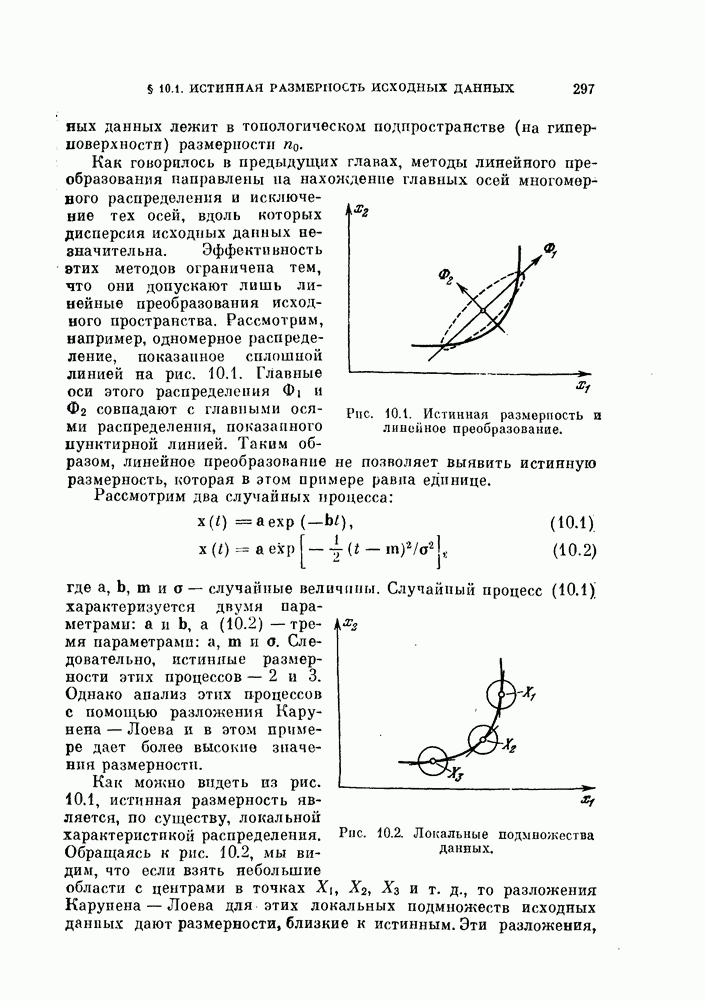
Как было показано в предыдущей главе, байесовский критерий отношения правдоподобия является оптимальным в том смысле, что он минимизирует риск или вероятность ошибки. Однако для получения отношения правдоподобия необходимо располагать для каждого класса условными плотностями вероятности. В большинстве приложений оценка этих плотностей осуществляется по конечному числу выборочных векторов наблюдений. Процедуры оценивания плотностей вероятности известны, но они являются очень сложными, либо требуют для получения точных результатов большого числа векторов наблюдений.
Однако даже при наличии плотностей вероятности метод, основанный на критерии отношения правдоподобия, на практике может оказаться трудно реализуемым, так как он может потребовать для классификации больших объемов памяти и машинного времени. В связи с этим часто мы вынуждены рассматривать более простые методы разработки классификаторов. В частности, можно задать математический вид классификатора с точностью до параметров, подлежащих определению.
Наиболее простым и общим видом является линейный или кусочно-линейный классификатор, изучению которого посвящена эта глава. Вначале рассматривается частный случай байесовского линейного классификатора. Далее будут приведены другие методы разработки «хороших» линейных классификаторов.
Читателю, однако, следует помнить, что байесовский классификатор во всех случаях является наилучшим. Никакой линейный классификатор не превосходит по качеству работы классификатор, полученный по критерию отношения правдоподобия.
§ 4.1. Байесовский линейный классификатор
Для двух нормально распределенных случайных величии байесовское решающее правило можно представить в виде квадратичной функции относительно вектора наблюдений X
следующим образом:

Если обе ковариационные матрицы одинаковы, т. е.  выражение (4.1) приобретает вид линейной функции относительно X:
выражение (4.1) приобретает вид линейной функции относительно X:

Сначала рассмотрим частный случай, при котором  а затем покажем, что выражение (4.2) представляет собой модификацию этого случая.
а затем покажем, что выражение (4.2) представляет собой модификацию этого случая.
4.1.1. Наблюдения — белый шум.
Если ковариационная мат рица равна единичной, то можно считать, что вектор X представ ляет собой наблюдение, искаженное белым шумом. Компоненты вектора X при этом некоррелированы и имеют единичную дисперсию, а байесовское решающее правило принимает вид

4.1.2. Корреляционный классификатор.
Произведение  называют коэффициентом корреляции между векторами
называют коэффициентом корреляции между векторами  и X. Если вектор X состоит из выборочных значений, полученных дискретизацией по времени замерами непрерывного случайного процесса, то можно записать коэффициент корреляции следующим образом:
и X. Если вектор X состоит из выборочных значений, полученных дискретизацией по времени замерами непрерывного случайного процесса, то можно записать коэффициент корреляции следующим образом:

В случае непрерывного времени коэффициент корреляции выражается через интеграл, т. е.

Легко видеть, что для принятия решения рассматриваемый; классификатор сравнивает разность коэффициентов корреляции
векторов X и  и векторов X и
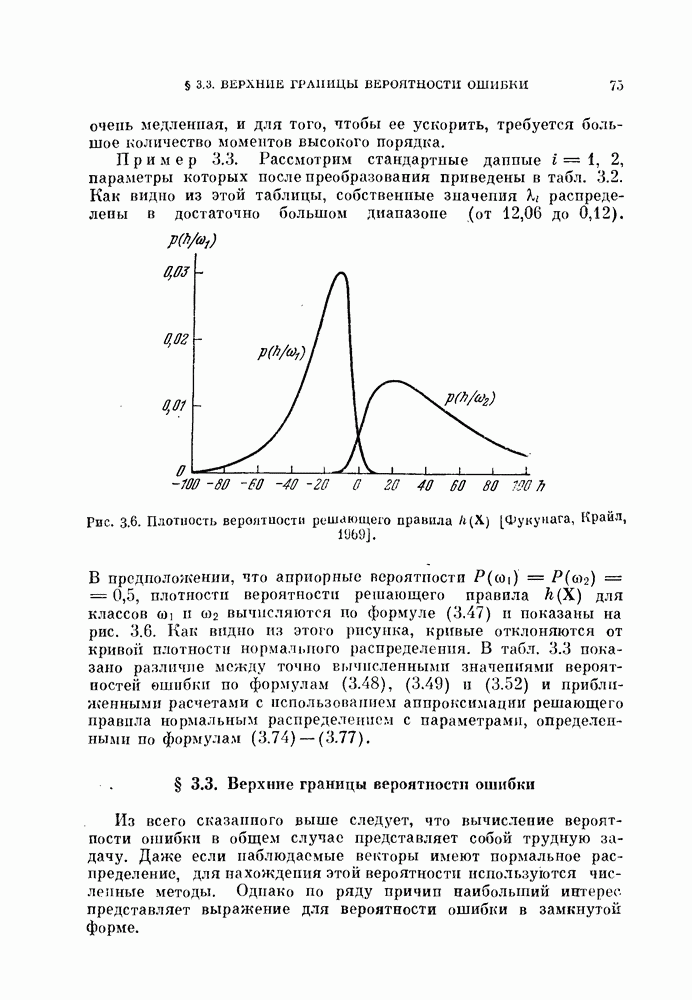
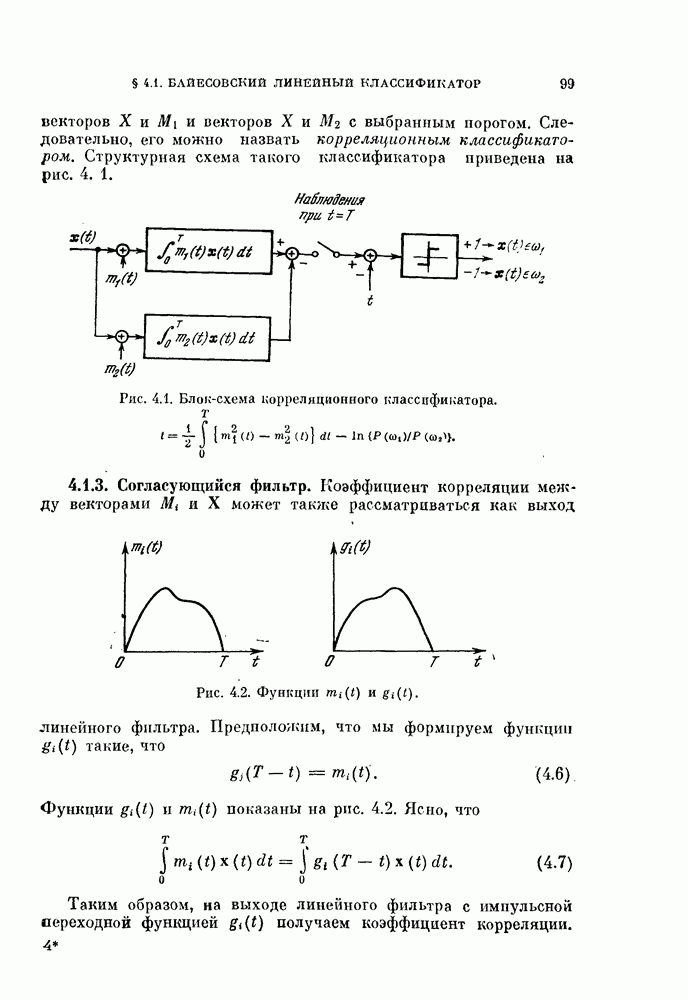
и векторов X и  с выбранным порогом. Следовательно, его можно назвать корреляционным классификатором. Структурная схема такого классификатора приведена на рис. 4. 1.
с выбранным порогом. Следовательно, его можно назвать корреляционным классификатором. Структурная схема такого классификатора приведена на рис. 4. 1.

Рис. 4.1. Блок-схема корреляционного классификатора. 
4.1.3. Согласующийся фильтр.
Коэффициент корреляции между векторами  и X может также рассматриваться как выход линейного фильтра.
и X может также рассматриваться как выход линейного фильтра.

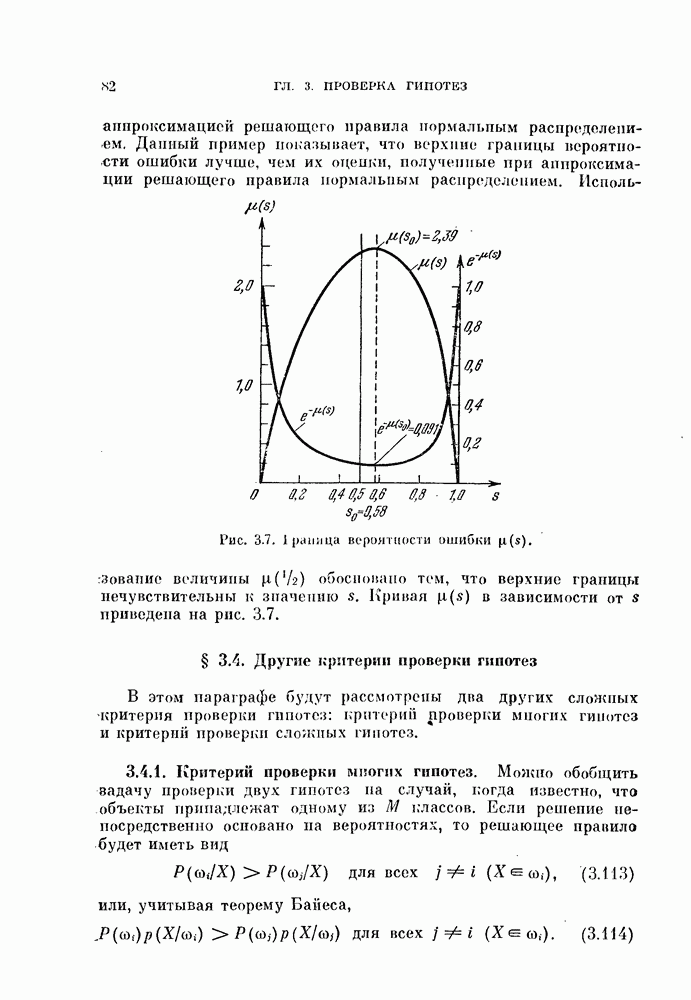
Рис. 4.2. Функции 
Предположим, что мы формируем функции  такие, что
такие, что

Функции  показаны на рис. 4.2. Ясно, что
показаны на рис. 4.2. Ясно, что

Таким образом, на выходе линейного фильтра с импульсной переходной функцией  получаем коэффициент корреляции.
получаем коэффициент корреляции.
Такой фильтр называют согласующимся фильтром. Классификатор, который основан на согласующемся фильтре и реализует ту же самую функцию, что и корреляционный классификатор, показан на рис. 4.3.

Рис. 4.3. Блок-схема согласующегося фильтра.
4.1.4. Классификатор, основанный на вычислении расстояния
Умножив выражение (4.3) на 2, а затем прибавив и вычтя  из левой части (4.3), получим решающее правило
из левой части (4.3), получим решающее правило

или

Полученному решающему правилу можно дать следующую геометрическую интерпретацию: сравниваются расстояния между вектором X и векторами  с порогом. Если априорные вероятности одинаковы,
с порогом. Если априорные вероятности одинаковы,  то решающая граница перпендикулярна к отрезку прямой, соединяющей векторы
то решающая граница перпендикулярна к отрезку прямой, соединяющей векторы  проходит через его середину, как показано на рис. 4.4.
проходит через его середину, как показано на рис. 4.4.
4.1.5. Наблюдения — не белый шум.
В общем случае, когда ковариационная матрица не равна единичной, т. е.  наблюдаемый шум является коррелированным, и его часто называют «окрашенным». В этом случае байесовский классификатор так легко не интерпретируется. Однако по-прежнему целесообразно в качестве решающего правила рассматривать корреляционный классификатор или классификатор, основанный на вычислении расстояния. Для этого введем декоррелирующее преобразование
наблюдаемый шум является коррелированным, и его часто называют «окрашенным». В этом случае байесовский классификатор так легко не интерпретируется. Однако по-прежнему целесообразно в качестве решающего правила рассматривать корреляционный классификатор или классификатор, основанный на вычислении расстояния. Для этого введем декоррелирующее преобразование  которое переводит коррелированный («окрашенный)))
которое переводит коррелированный («окрашенный)))
шум в белый:

Заметим, что пока ковариационная матрица 2 является положительно определенной, матрица А существует и невырождена. Таким образом, декоррелирующее преобразование обратимо, и наблюдения вектора  можно классифицировать такж эффективно, как и наблюдения вектора X. Вектор математического ожидания
можно классифицировать такж эффективно, как и наблюдения вектора X. Вектор математического ожидания  для класса
для класса  равен
равен

а ковариационная матрица  для обоих классов равна единичной матрице I. Следовательно, все рассуждения предыдущего раздела данного параграфа применимы и для вектора
для обоих классов равна единичной матрице I. Следовательно, все рассуждения предыдущего раздела данного параграфа применимы и для вектора  если заменить вектор
если заменить вектор  . В случае непрерывного времени декоррелирующее преобразование имеет интегральный вид
. В случае непрерывного времени декоррелирующее преобразование имеет интегральный вид


Рис. 4.4. Классификатор, основанный на вычислении евклидова расстояния.
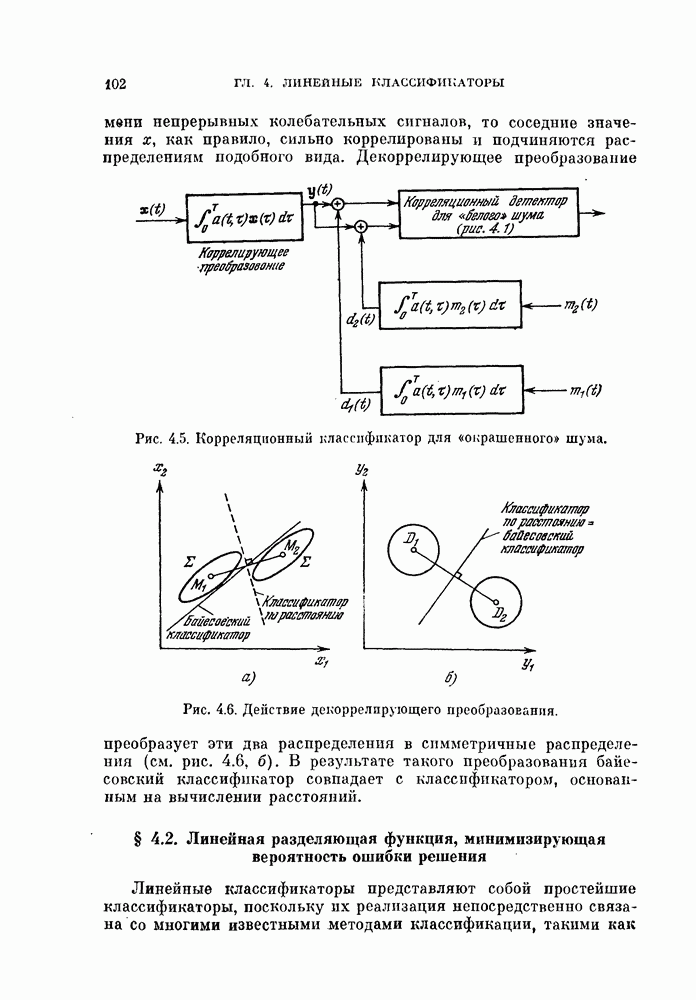
Ядро  можно рассматривать как импульсную переходную функцию декоррелирующего фильтра. Возможная структурная схема байесовского классификатора показана на рис. 4.5. Из схемы видно, что это корреляционный классификатор (см. рис. 4.1), модифицированный за счет добавления декоррелирующего фильтра.
можно рассматривать как импульсную переходную функцию декоррелирующего фильтра. Возможная структурная схема байесовского классификатора показана на рис. 4.5. Из схемы видно, что это корреляционный классификатор (см. рис. 4.1), модифицированный за счет добавления декоррелирующего фильтра.
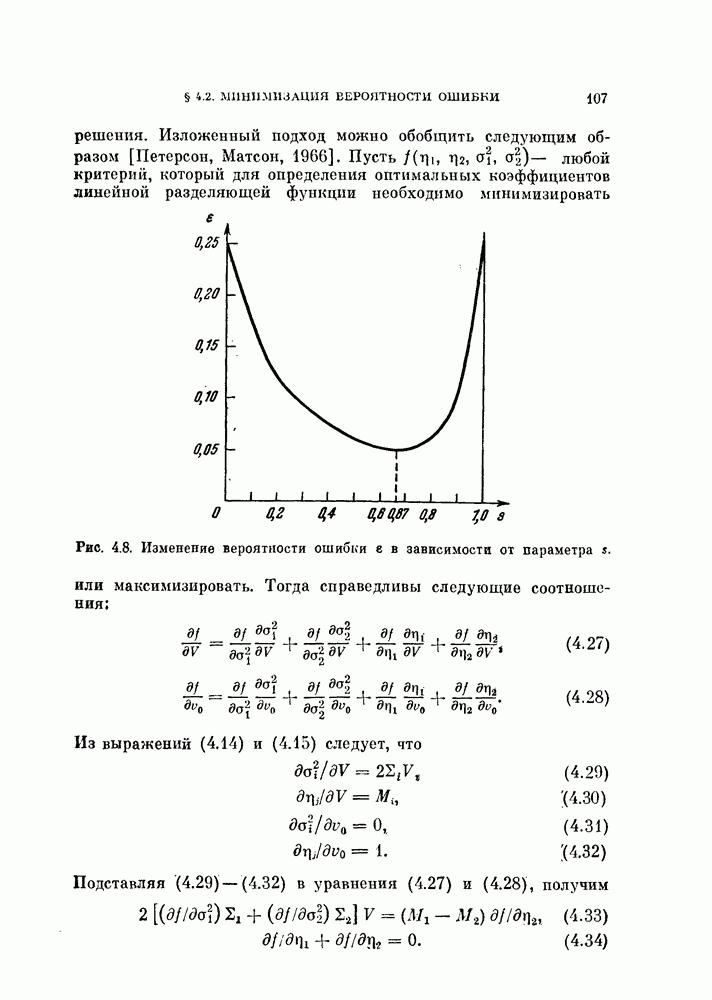
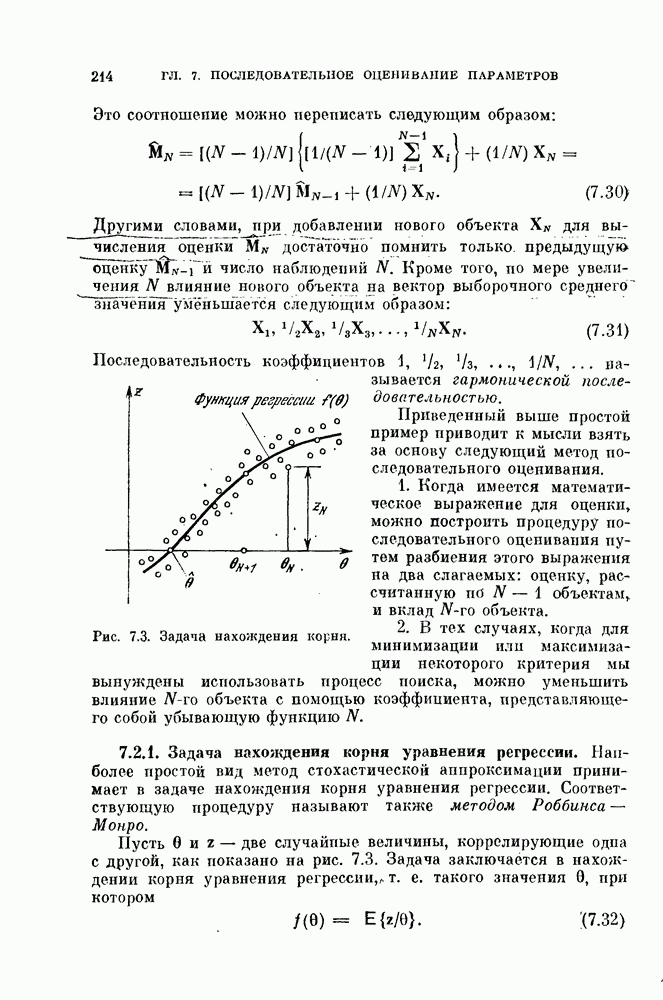
Пример 4.1. На рис. 4.6 изображен двумерный пример, для которого декоррелирующее преобразование является эффективным. Хотя два распределения на рис. 4.6, а хорошо разделимы байесовским классификатором решающее правило, основанное на вычислении расстояний, или простой корреляционный классификатор дают плохие результаты. На рис. 4.6, а изображены вытянутые распределения, соответствующие случаю сильной коррелированности величин  между собой. В частности, если
между собой. В частности, если  — выборочные значения, полученные дискретизацией по
— выборочные значения, полученные дискретизацией по
времени непрерывных колебательных сигналов, то соседние значения  как правило, сильно коррелированы и подчиняются распределениям подобного вида.
как правило, сильно коррелированы и подчиняются распределениям подобного вида.

Рис. 4.5. Корреляционный классификатор для «окрашенного» шума.

Рис. 4.6. Действие декоррелпрующего преобразования.
Декоррелирующее преобразование преобразует эти два распределения в симметричные распределения (см. рис. 4.6, б). В результате такого преобразования байесовский классификатор совпадает с классификатором, основанным на вычислении расстояний.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
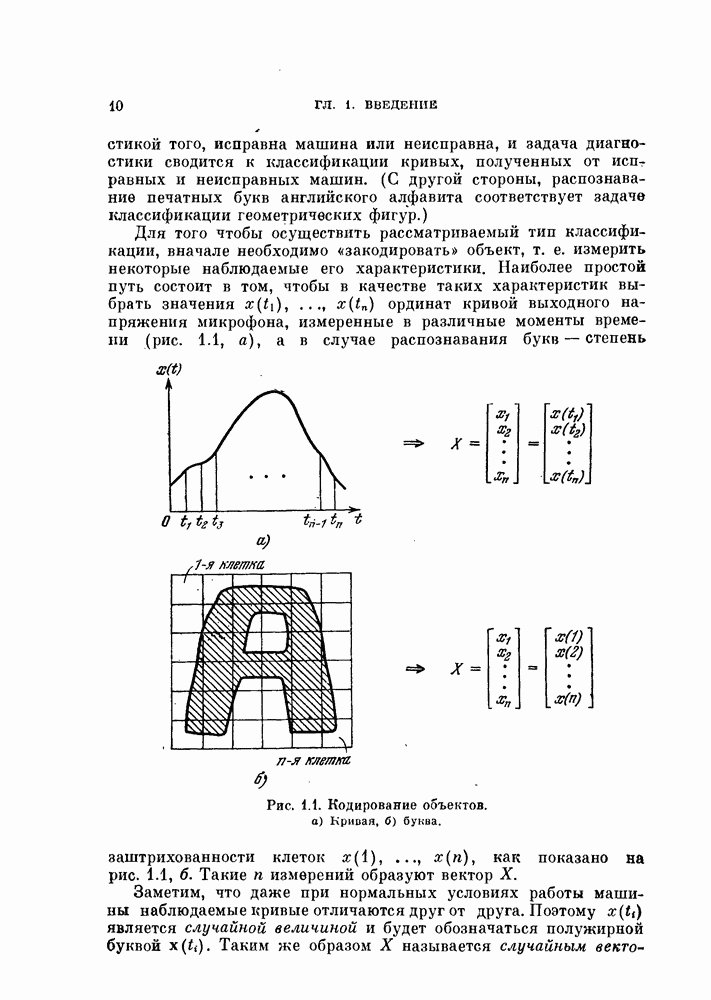
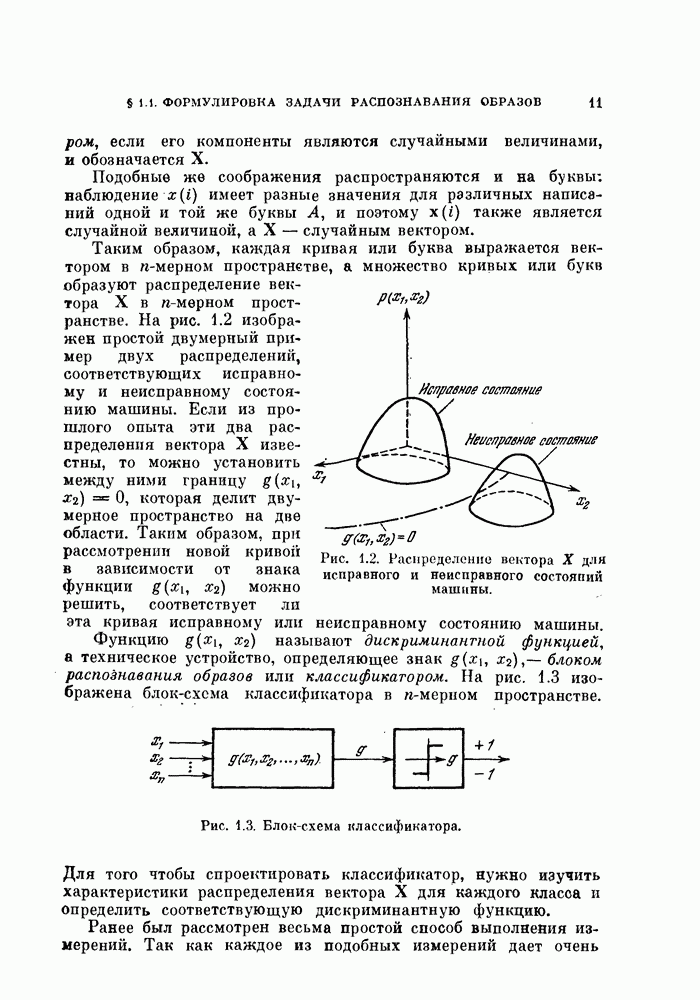
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
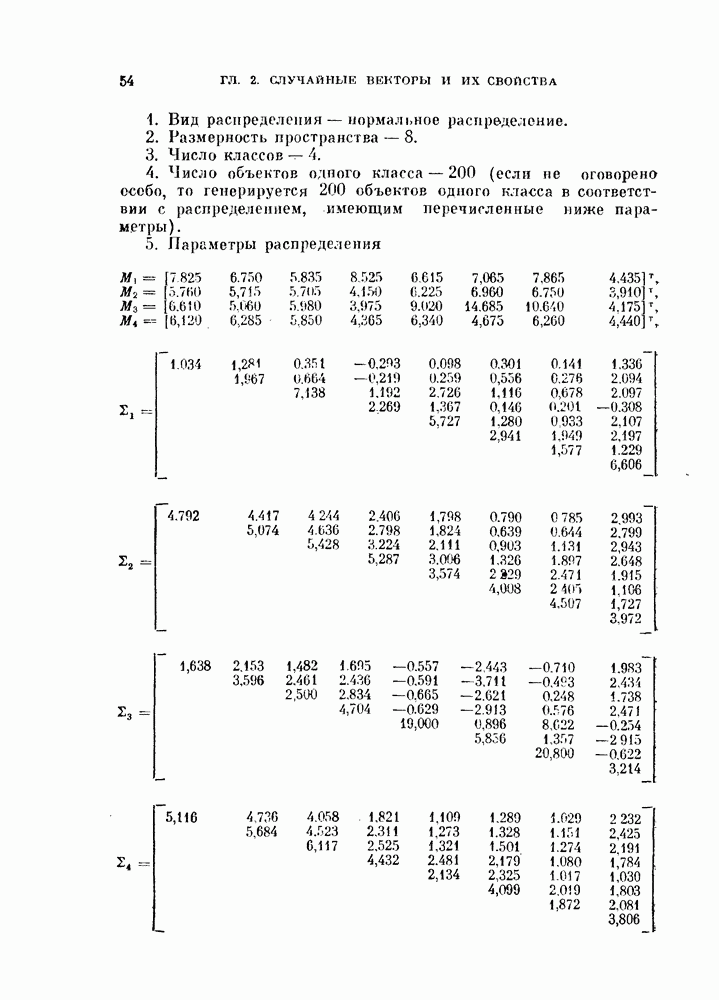
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
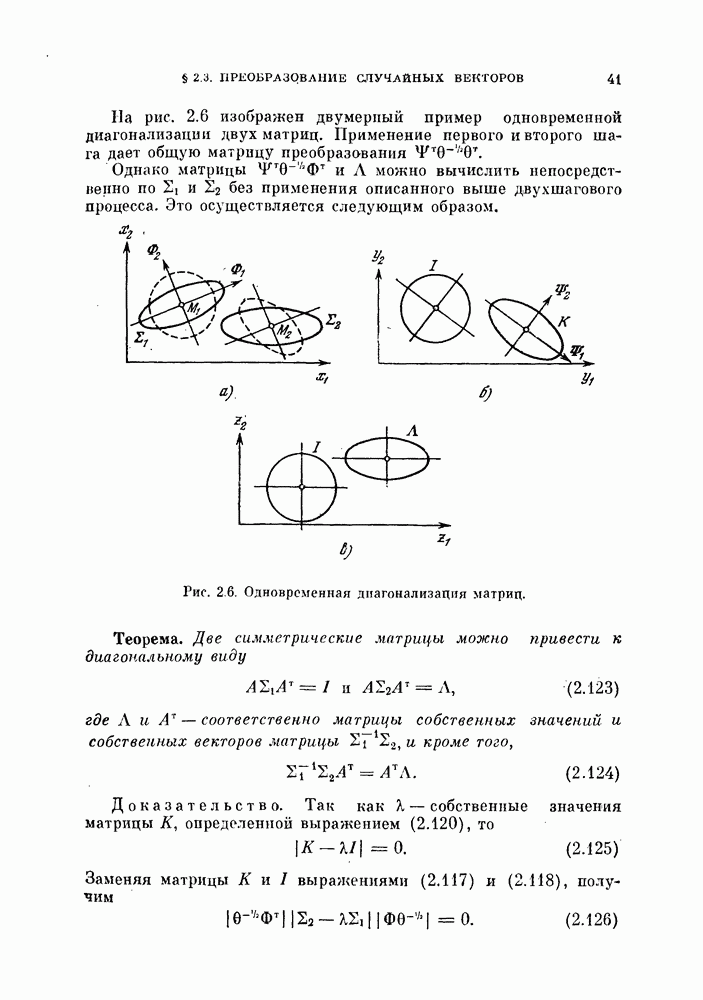
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
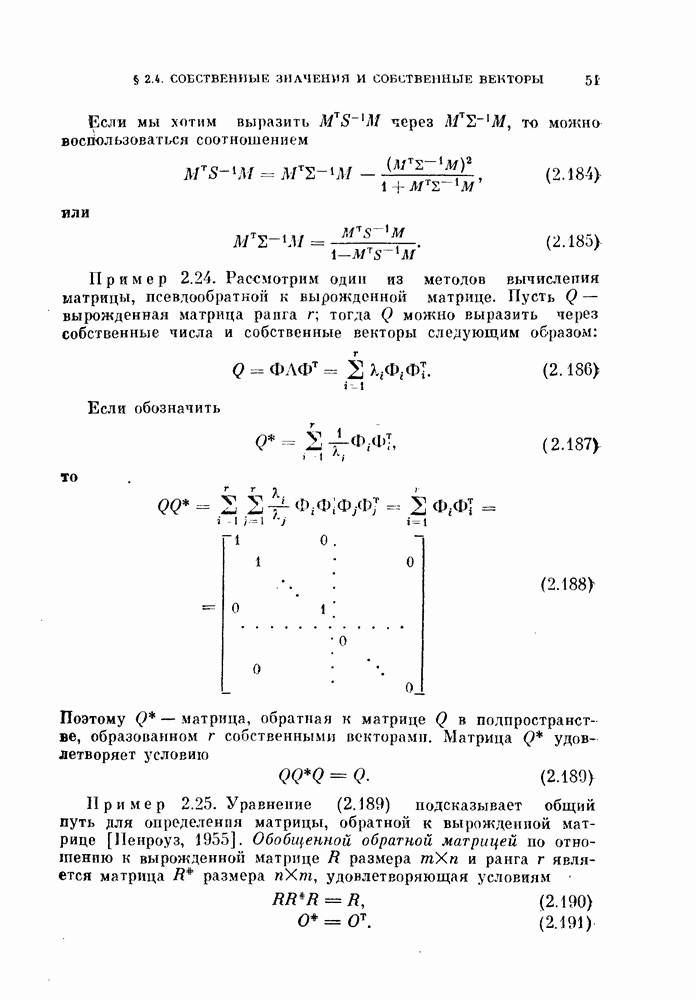
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
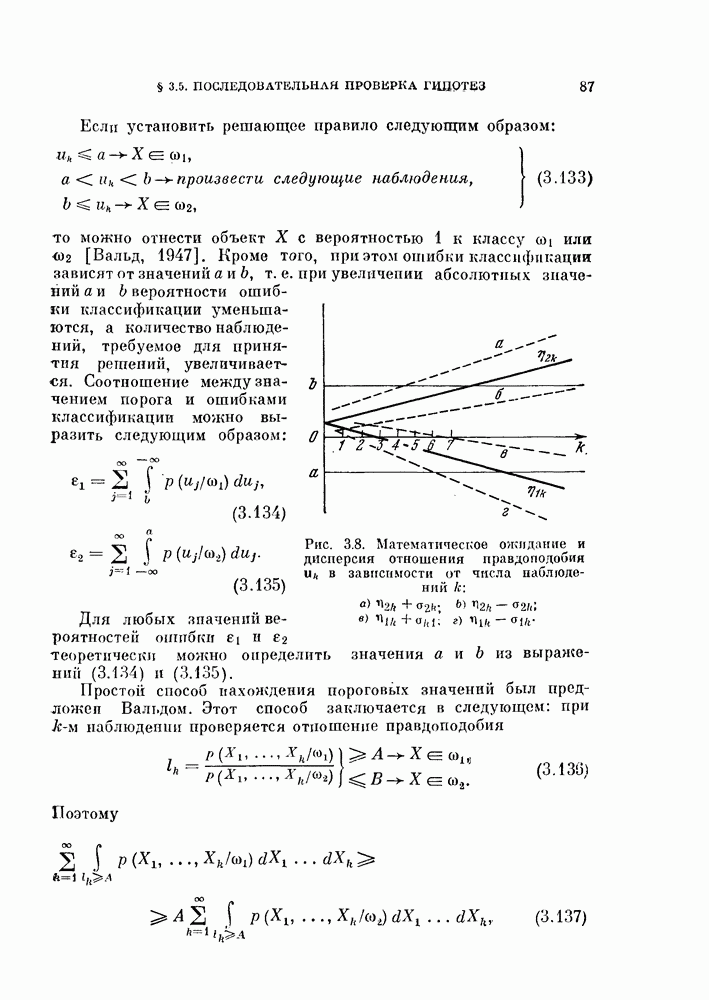
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
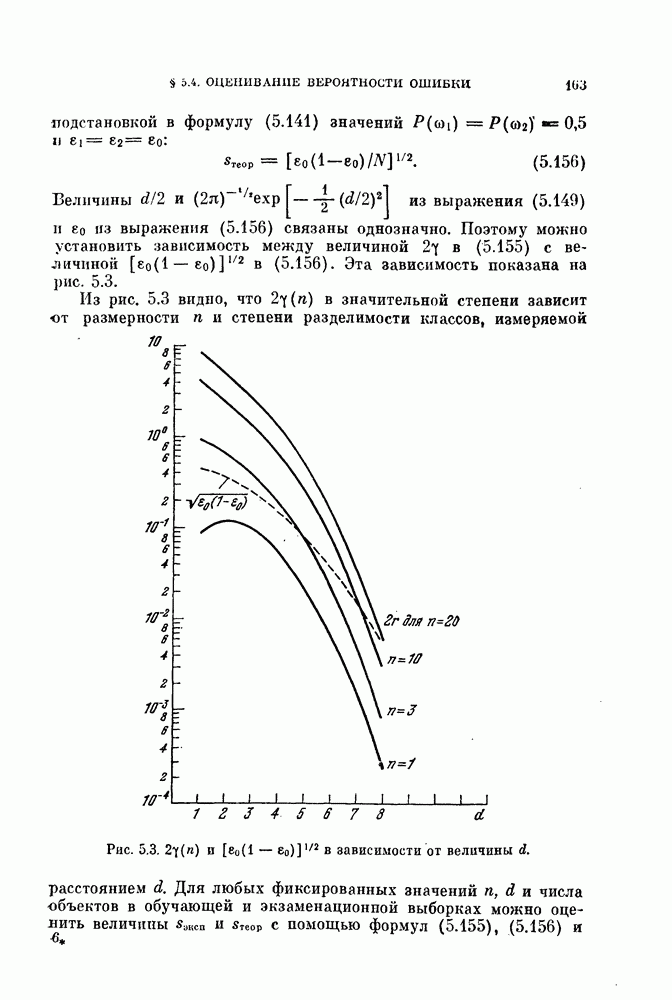
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
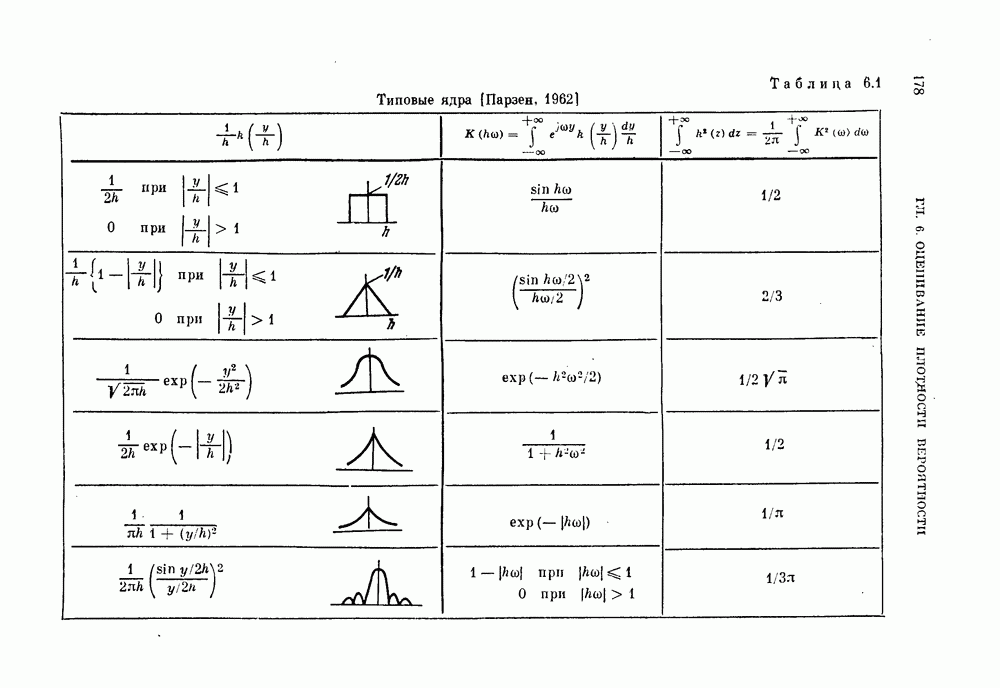
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА