| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ВВЕДЕНИЕ
В данной книге рассмотрены основные математические методы, применяемые для описания статистических процессов принятия решений в задаче распознавания образов. Интуитивно ясно, что до некоторой степени процесс принятия решений человеком имеет отношение к распознаванию образов; например, в шахматной игре следующий ход делается в зависимости от ситуации (образа), сложившейся в данный момент времени на шахматной доске; решение о том, покупать или продавать акции на бирже, также принимается в результате анализа сложного информационного образа. Поэтому целью создания теории распознавания образов являлось выявление сложных механизмов процессов принятия решений, а также автоматизация этих процессов с помощью средств вычислительной техники.
Однако ввиду сложности проблемы распознавания образов основные исследования в этой области были сосредоточены на более реальных задачах, таких как распознавание букв латинского алфавита и классификация кривых. Задачей настоящей книги является рассмотрение математических моделей такого рода практических задач и изложение основных математических методов их решения. Несмотря на то что в литературе предложено много подходов для описания и более сложных процессов принятия решений, анализ этих подходов лежит вне круга вопросов, затронутых в данной книге.
§ 1.1. Формулировка задачи распознавания образов
Многие важные приложения теории распознавания образов относятся к задачам классификации кривых и геометрических фигур. Рассмотрим, например, задачу диагностики неисправности машины (которая может находиться как в исправном, так и в неисправном состояниях) по шуму, издаваемому в процессе ее работы и регистрируемому микрофоном. Форма кривой напряжения, измеренного на выходе микрофона, является
характеристикой того, исправна машина или неисправна, и задача диагностики сводится к классификации кривых, полученных от исправных и неисправных машин. (С другой стороны, распознавание печатных букв английского алфавита соответствует задаче классификации геометрических фигур.)
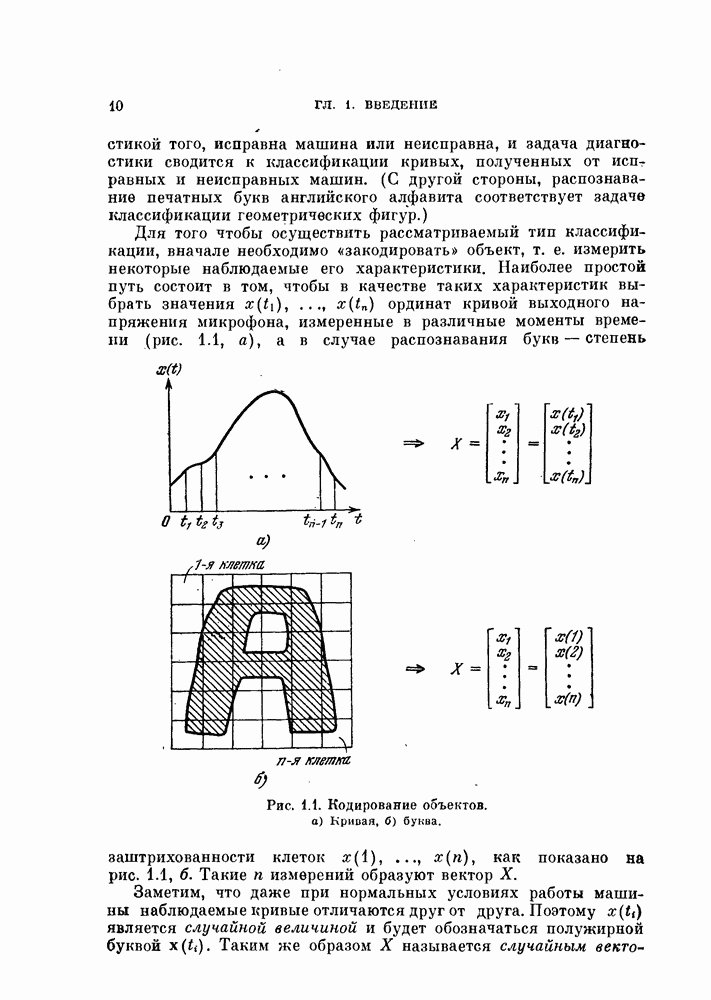
Для того чтобы осуществить рассматриваемый тип классификации, вначале необходимо «закодировать» объект, т. е. измерить некоторые наблюдаемые его характеристики. Наиболее простой путь состоит в том, чтобы в качестве таких характеристик выбрать значения  ординат кривой выходного напряжения микрофона, измеренные в различные моменты времени (рис. 1.1, а), а в случае распознавания букв — степень заштрихованности клеток
ординат кривой выходного напряжения микрофона, измеренные в различные моменты времени (рис. 1.1, а), а в случае распознавания букв — степень заштрихованности клеток  как показано на рис. 1.1, б.
как показано на рис. 1.1, б.
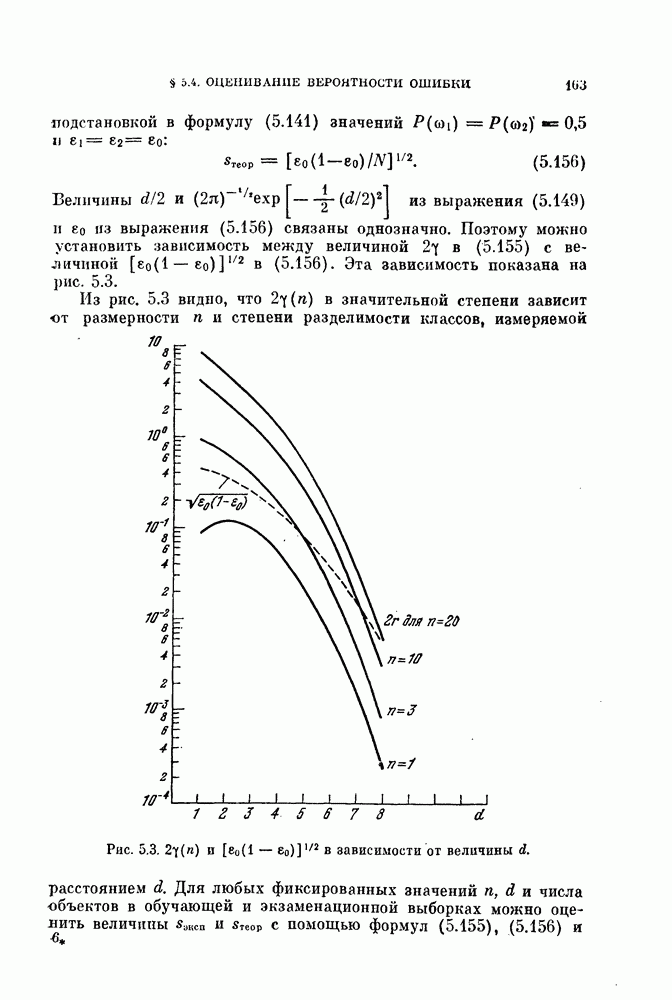
Рис. 1.1. (см. скан) Кодирование объектов, а) Кривая, б) буква.
Такие  измерений образуют вектор X.
измерений образуют вектор X.
Заметим, что даже при нормальных условиях работы машины наблюдаемые кривые отличаются друг от друга. Поэтому  является случайной величиной и будет обозначаться полужирной буквой
является случайной величиной и будет обозначаться полужирной буквой  Таким же образом X называется случайным вектором,
Таким же образом X называется случайным вектором,
если его компоненты являются случайными величинами, и обозначается X.
Подобные же соображения распространяются и на буквы: наблюдение  имеет разные значения для различных написаний одной и той же буквы А, и поэтому
имеет разные значения для различных написаний одной и той же буквы А, и поэтому  также является случайной величиной,
также является случайной величиной,  случайным вектором.
случайным вектором.
Таким образом, каждая кривая или буква выражается вектором в  -мерном пространстве, а множество кривых или букв образуют распределение вектора X в
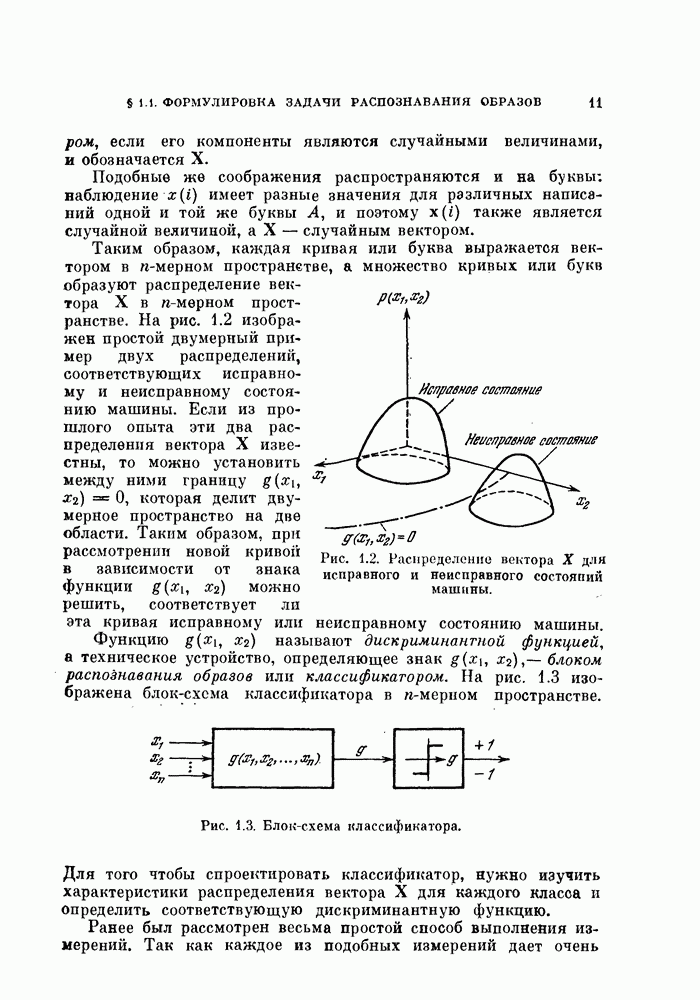
-мерном пространстве, а множество кривых или букв образуют распределение вектора X в  -мерном пространстве. На рис. 1.2 изображен простой двумерный пример двух распределений, соответствующих исправному и неисправному состоянию машины. Если из прошлого опыта эти два распределения вектора X известны, то можно установить между ними границу
-мерном пространстве. На рис. 1.2 изображен простой двумерный пример двух распределений, соответствующих исправному и неисправному состоянию машины. Если из прошлого опыта эти два распределения вектора X известны, то можно установить между ними границу  которая делит двумерное пространство на две области. Таким образом, при рассмотрении новой кривой в зависимости от знака функции
которая делит двумерное пространство на две области. Таким образом, при рассмотрении новой кривой в зависимости от знака функции  можно решить, соответствует ли эта кривая исправному или неисправному состоянию машины.
можно решить, соответствует ли эта кривая исправному или неисправному состоянию машины.
Функцию  называют дискриминантной функцией, а техническое устройство, определяющее знак
называют дискриминантной функцией, а техническое устройство, определяющее знак  -блоком распознавания образов или классификатором. На рис. 1.3 изображена блок-схема классификатора в
-блоком распознавания образов или классификатором. На рис. 1.3 изображена блок-схема классификатора в  -мерном пространстве.
-мерном пространстве.

Рис. 1.2. Распределение вектора X для исправного и неисправного состояний машины.

Рис. 1.3. Блок-схема классификатора.
Для того чтобы спроектировать классификатор, нужно изучить характеристики распределения вектора X для каждого класса и определить соответствующую дискриминантную функцию.
Ранее был рассмотрен весьма простой способ выполнения измерений. Так как каждое из подобных измерений дает очень
мало информации об объекте, то на практике обычно требуется большое число измерений  которое может доходить до нескольких сотен или тысяч. Такая высокая размерность затрудняет решение многих задач распознавания образов. С другой стороны, классификация, производимая человеком, обычно основывается на небольшом числе признаков, как например, максимальная величина, основная частота и т. д. Каждое из этих измерений несет значительную информацию для целей классификации и выбирается в соответствии с физическим смыслом задачи.
которое может доходить до нескольких сотен или тысяч. Такая высокая размерность затрудняет решение многих задач распознавания образов. С другой стороны, классификация, производимая человеком, обычно основывается на небольшом числе признаков, как например, максимальная величина, основная частота и т. д. Каждое из этих измерений несет значительную информацию для целей классификации и выбирается в соответствии с физическим смыслом задачи.
Очевидно, что с уменьшением числа входных величин классификатора его проектирование упрощается. Для того чтобы добиться этого, следует наметить некоторые пути для выбора или извлечения существенных информативных признаков из всей совокупности наблюдаемых. Эту задачу называют задачей выбора информативных признаков, и она составляет другой важный раздел теории распознавания образов. Выбор признаков можно рассматривать как отображение исходного  -мерного пространства в пространство меньшей размерности. При этом необходимо сохранить свойство разделимости распределений, соответствующих разным классам. Следовательно, отображение должно быть выполнено без существенной потери этого свойства.
-мерного пространства в пространство меньшей размерности. При этом необходимо сохранить свойство разделимости распределений, соответствующих разным классам. Следовательно, отображение должно быть выполнено без существенной потери этого свойства.
Таким образом, как показано на рис. 1.4, задача распознавания образов состоит из двух частей: выбор информативных признаков и проектирование классификатора.

Рис. 1.4. Блок-схема системы распознавания образов.
На практике между этими частями нет четкой границы. Действительно, классификатор можно представить как устройство для выбора признаков, которое отображает  признаков в один (дискриминантная функция). Однако в данной книге удобно разделить задачу распознавания на две части и изучать их независимо друг от друга.
признаков в один (дискриминантная функция). Однако в данной книге удобно разделить задачу распознавания на две части и изучать их независимо друг от друга.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
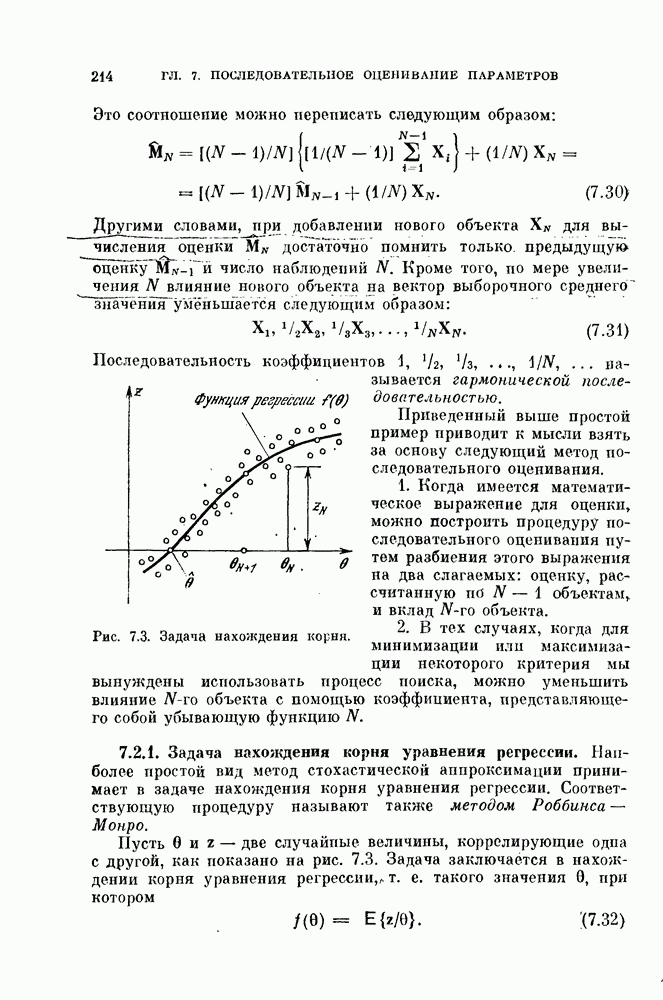
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
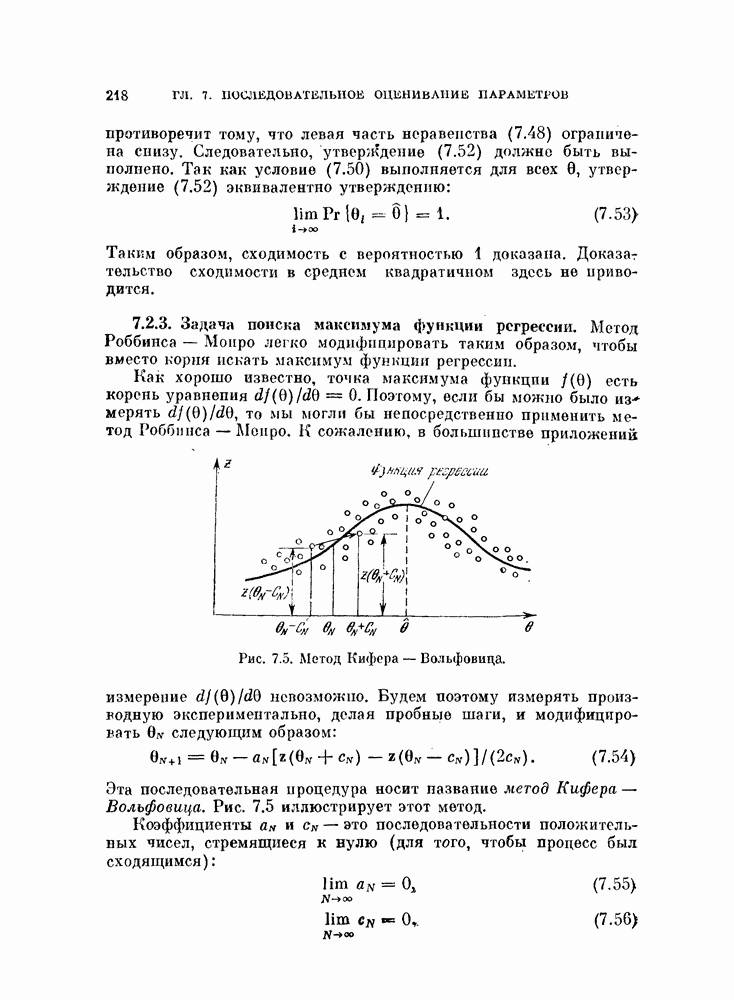
- 7.2.3. Задача поиска максимума функции регрессии.
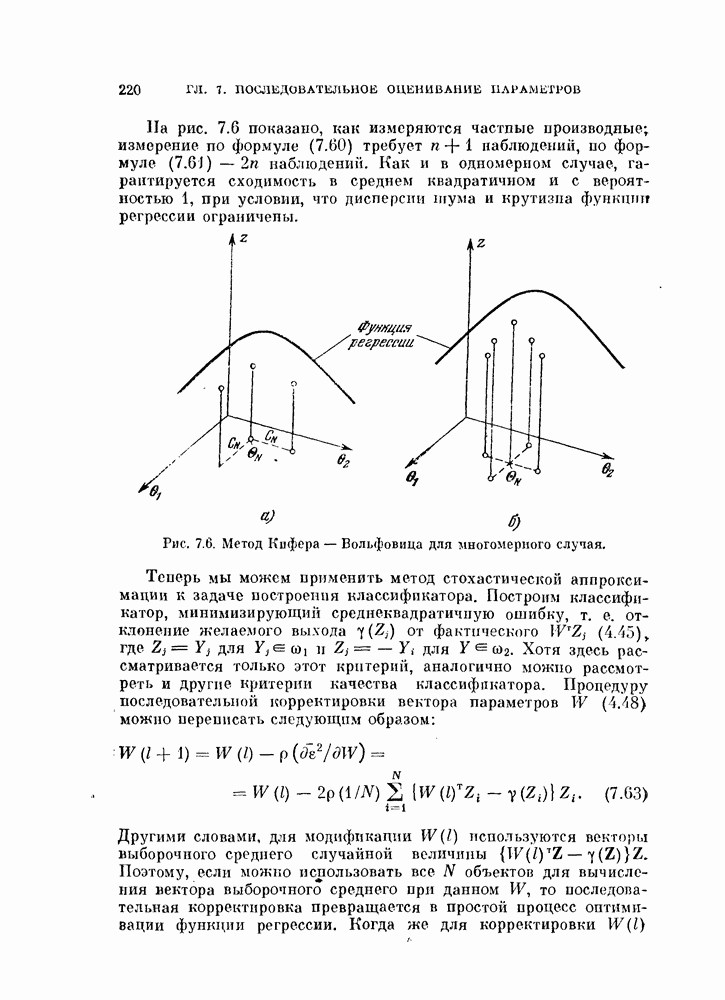
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
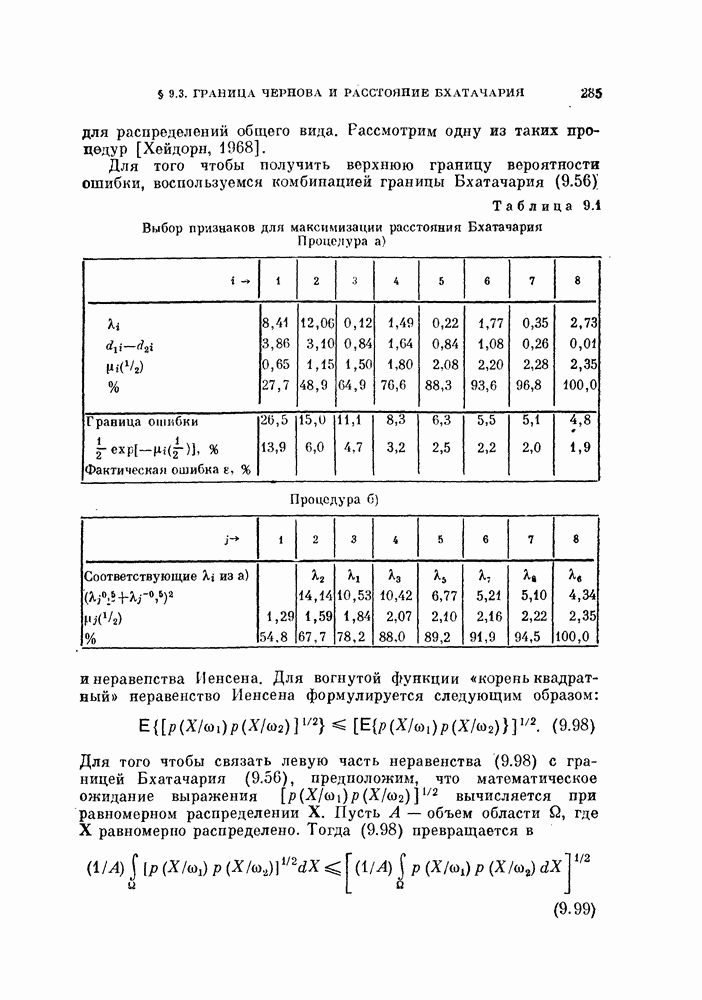
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
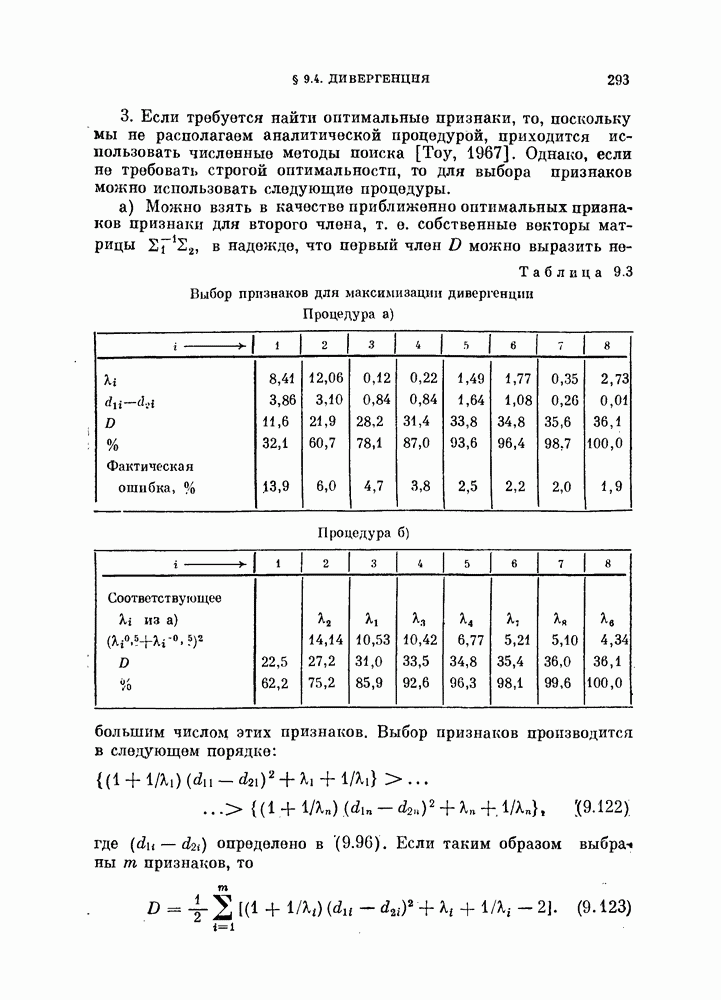
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА