| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
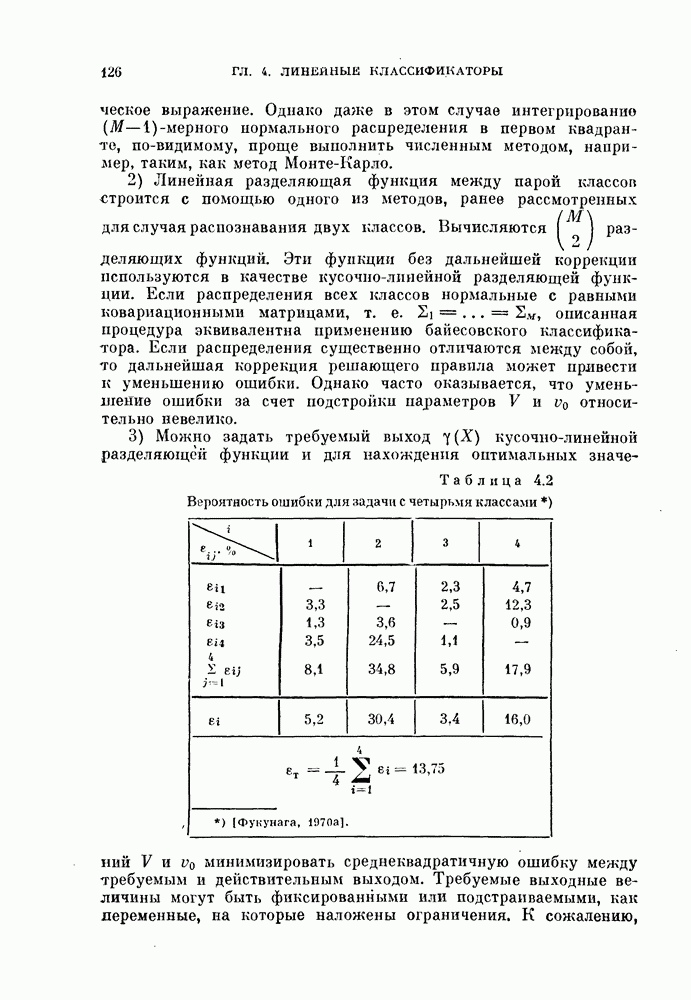
10.1.2. Неитеративный алгоритм.
Так как истинная размерность данных определяется локальными размерностями, то при неограниченном числе наблюдений и отсутствии шума истинная размерность находится уменьшением размера локальных областей до тех пор, пока получаемая размерность не достигнет предельного значения. На практике, однако, имеется несколько факторов, усложняющих эту процедуру: 1) ограниченное число наблюдений; 2) наличие шума; 3) большой расход машинного времени.
Рассмотрим первые два пункта более подробно. Так как максимальная размерность множества выборочных векторов имеет размерность, меньшую, чем число векторов, необходимо обеспечить наличие достаточного числа векторов в каждой локальной области. При ограниченном числе наблюдений может оказаться, что при достаточном числе векторов локальная область будет слишком большой для того, чтобы множество данных вблизи данной точки можно было аппроксимировать поверхностью. В таких локальных областях оценка размерности оказывается выше, чем истинная размерность.
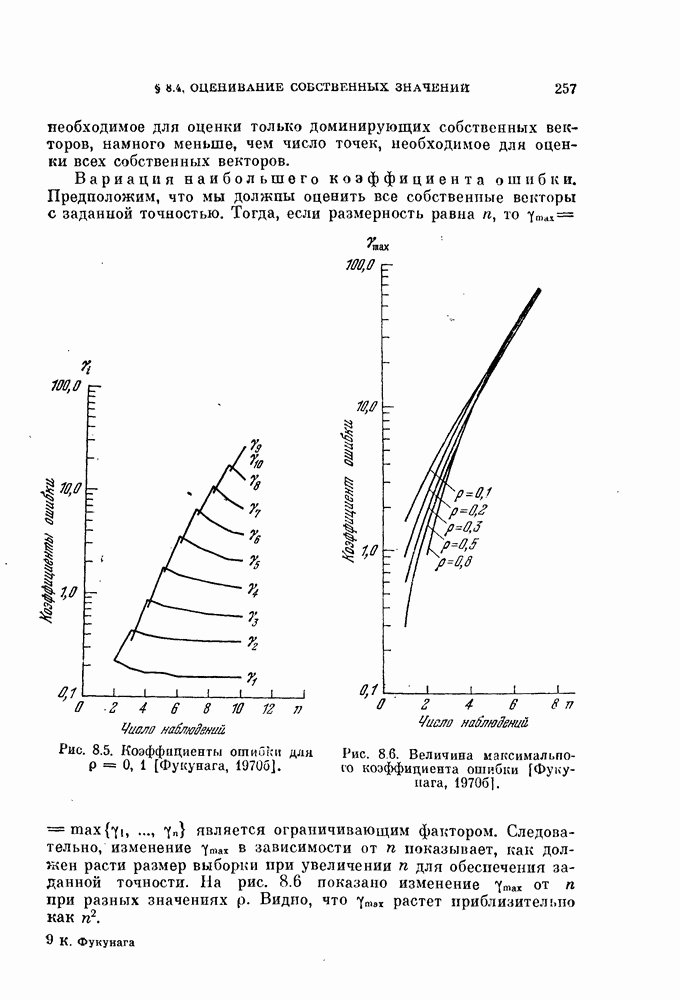
Наиболее простая процедура оценки локальной размерности состоит в вычислении собственных значений выборочной ковариационной матрицы в локальной области и подсчете числа доминирующих собственных значений. Величина порога, выбранного для отделения доминирующих собственных значений, влияет на оценку размерности. Пусть величина порога  составляет
составляет  от величины наибольшего собственного значения. Число объектов, необходимое для оценки числа доминирующих собственных значений, обычно во много раз меньше, чем требуется для оценки самих собственных значений. Опыт показывает, что это число
от величины наибольшего собственного значения. Число объектов, необходимое для оценки числа доминирующих собственных значений, обычно во много раз меньше, чем требуется для оценки самих собственных значений. Опыт показывает, что это число  должно лишь в 2—3 раза прёвышать число доминирующих собственных значений
должно лишь в 2—3 раза прёвышать число доминирующих собственных значений  независимо от числа переменных
независимо от числа переменных  Например при
Например при  достаточно, чтобы
достаточно, чтобы  даже для
даже для  Так как для большинства приложений
Так как для большинства приложений  то для определения собственных значений следует использовать метод, примененный в примере 2.20.
то для определения собственных значений следует использовать метод, примененный в примере 2.20.
Добавление шума приводит к необходимости ограничивать снизу размеры локальных областей. Это показано на рис. 10.3. Как говорилось выше, при большом размере области можно получить завышенную оценку истинной размерности. С другой стороны, уменьшение размера локальной области уменьшает доминирующие собственные значения относительно составляющей шума. Поэтому мы должны выбрать некоторое компромиссное
вначение размера локальных областей. Кроме того, необходимо установить более высокий порог для предотвращения влияния шума на оценку размерности. Так как эти настраиваемые параметры зависят от исходных данных, то желательно иметь гибкую вычислительную систему, такую, чтобы оператор имел возможность целенаправленно менять эти параметры при переходе от задачи к задаче и от одной локальной области к другой.
Рассмотрим один из воможных алгоритмов решения этой задачи [Фукунага, 1971а].
1. Выбор размера локальных областей. Хотя размер локальной области может меняться от области к области, удобнее вначале выбрать его фиксированным. Подходящий размер выбирается после изучения связи между размером и результирующей размерностью в окрестности объекта, ближайшего к выборочному среднему значению всего множества объектов.

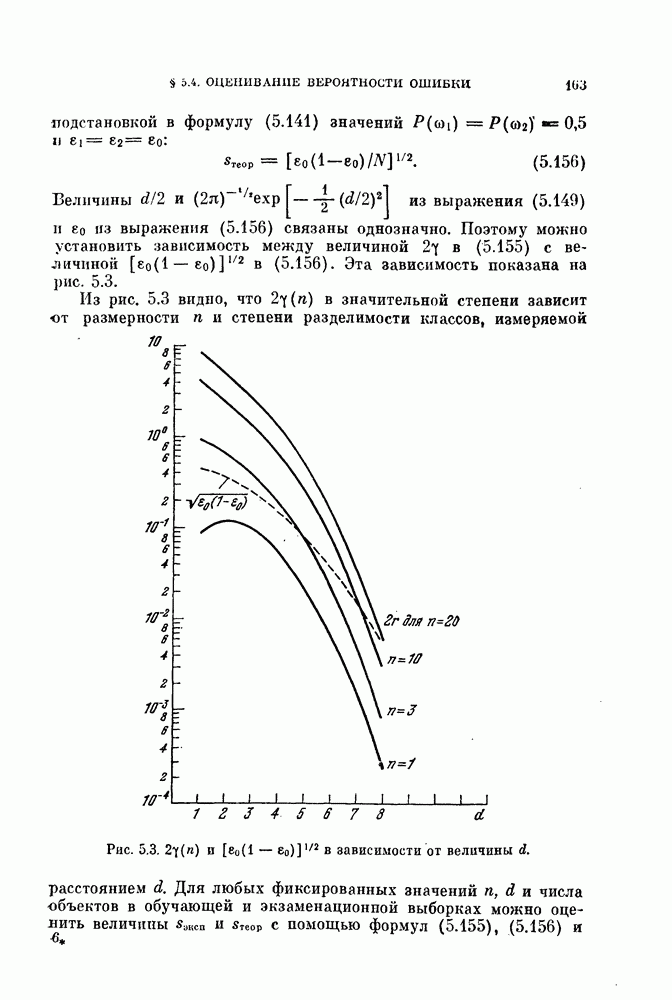
Рис. 10.3. Влияние шума.
Размер задается или радиусом гиперсферы, или числом объектов в локальной области. Оператор должен иметь возможность корректировать размер всякий раз, когда в этом возникнет необходимость.
2. Выбор локальных центров. Решение этой задачи требует поиска в пространстве высокой размерности и включает много компромиссных решений, касающихся, например, выбора размера локальной области, величины перекрытия и метода поиска. Одно из возможных решений состоит в том, чтобы в качестве первого локального центра выбрать первый объект из списка объектов. Объекты локальной области, построенной вокруг этого первого объекта, используются для определения локальной размерности, а затем исключаются из списка. Эта процедура повторяется до тех пор, пока список не станет пустым. Для определения истинной размерности исходных данных вычисляются статистики локальных размерностей.
Пример 10.1. Гауссовская последовательность является распространенной случайной функцией, так как она с приемлемой точностью аппроксимирует многие сигналы, встречающиеся на практике, а для ее описания достаточно трех параметров, как показано в (10.2). В рассматриваемом примере параметры  были равномерно распределены в интервалах
были равномерно распределены в интервалах


(кликните для просмотра скана)
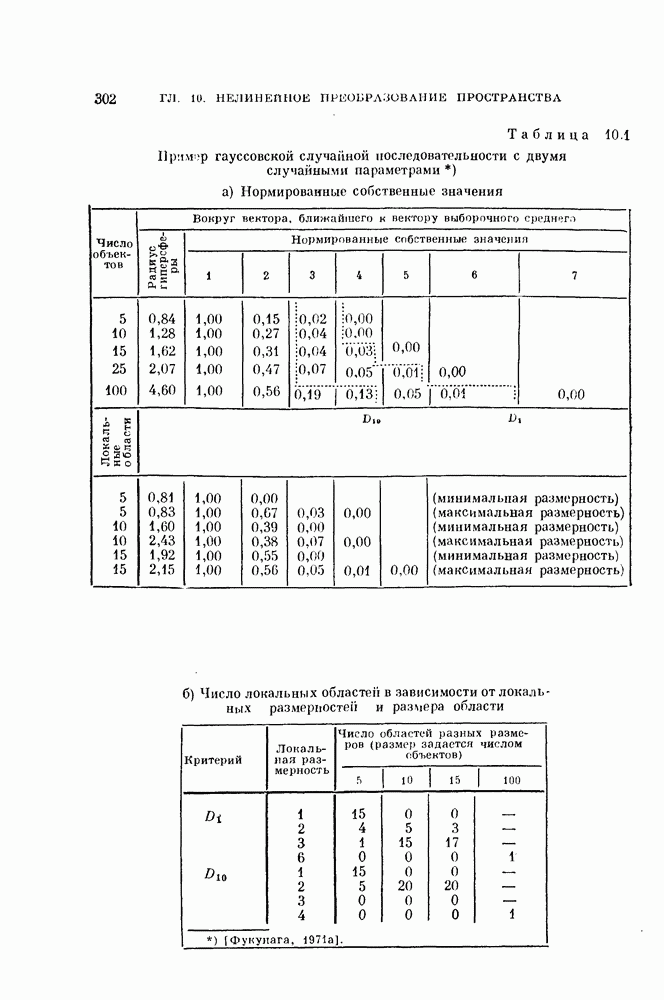
а  При каждом случайно выбранном наборе параметров генерировалось 100 20-мерных объектов. Результаты, относящиеся к этому примеру, приведены в табл. 10.1.
При каждом случайно выбранном наборе параметров генерировалось 100 20-мерных объектов. Результаты, относящиеся к этому примеру, приведены в табл. 10.1.
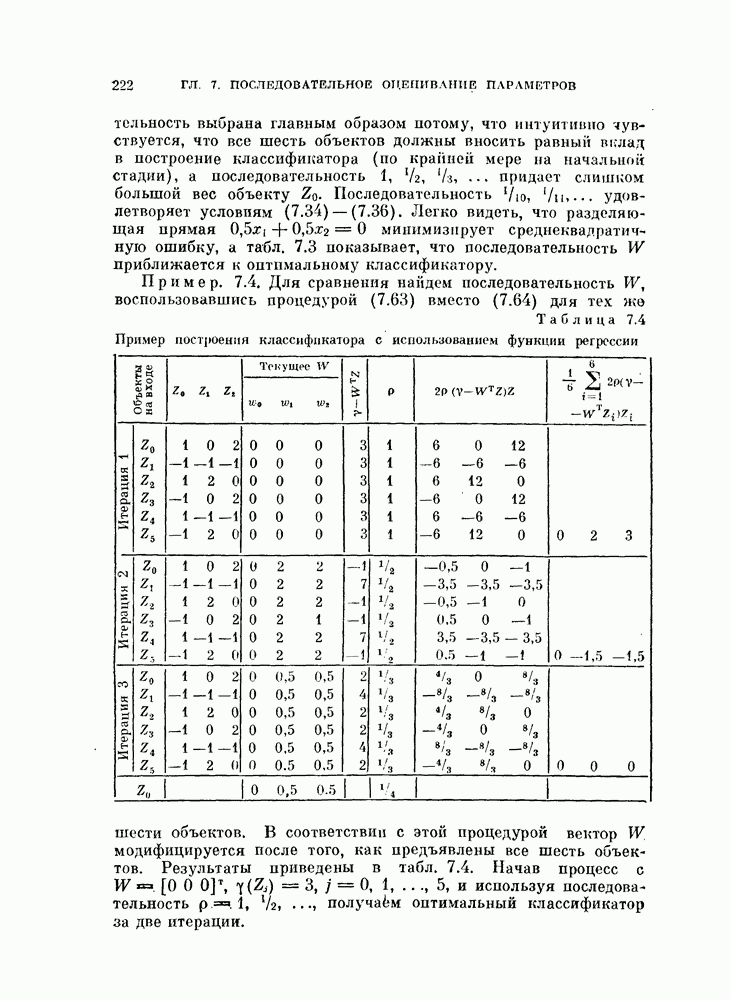
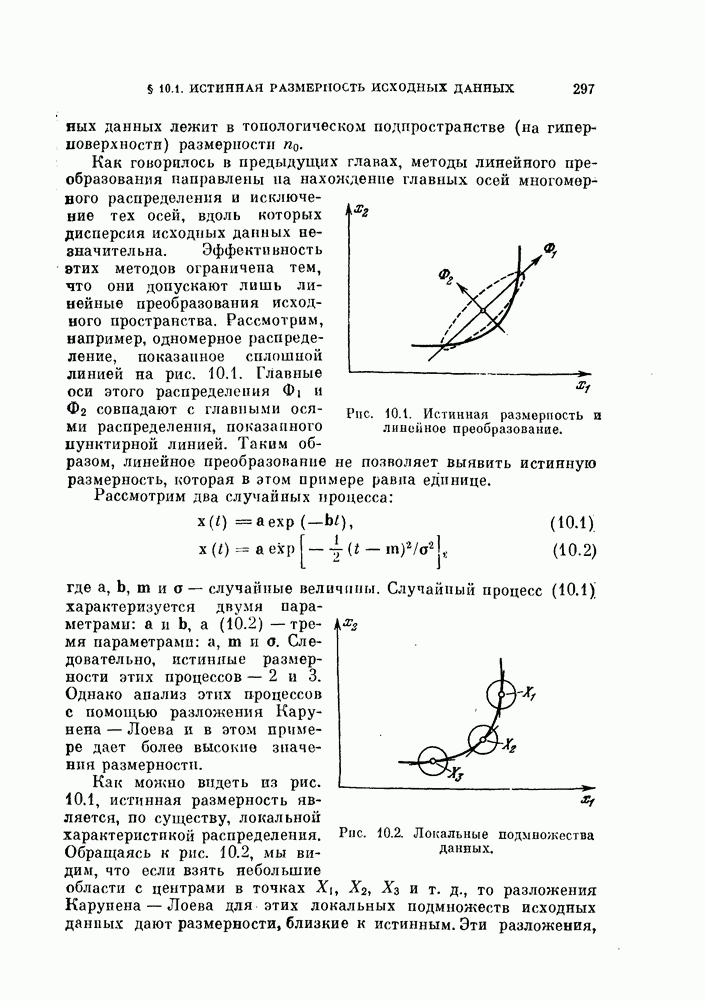
Данные приведены лишь для некоторых типичных локальных областей, так как разница между максимальными и минимальными размерностями невелика. Табл. 10.16 — это одна из итоговых таблиц, построенных в процессе работы алгоритма. Опа показывает, что истинная размерность равна 2. Глобальное разложение Карунена — Лоева дает размерность 4 для критерия  и 6 для критерия
и 6 для критерия 
Пример 10.2. В этом примере для генерирования данных также использовалась гауссовская последовательность с тремя случайными параметрами, равномерно распределенными в интервалах

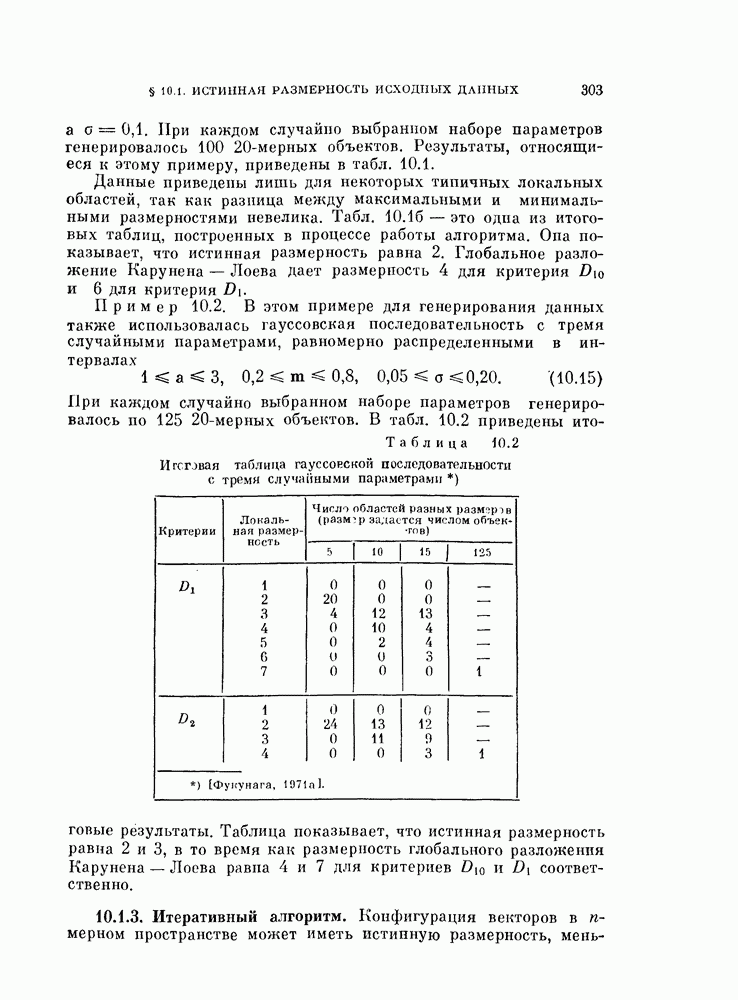
При каждом случайно выбранном наборе параметров генерировалось по 125 20-мерных объектов. В табл. 10.2 приведены итоговые результаты.
Таблица 10.2
Итоговая таблица гауссовской последовательности с тремя случайными параметрами

Таблица показывает, что истинная размерность равна 2 и 3, в то время как размерность глобального разложения Карунена — Лоева равна 4 и 7 для критериев  соответственно.
соответственно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
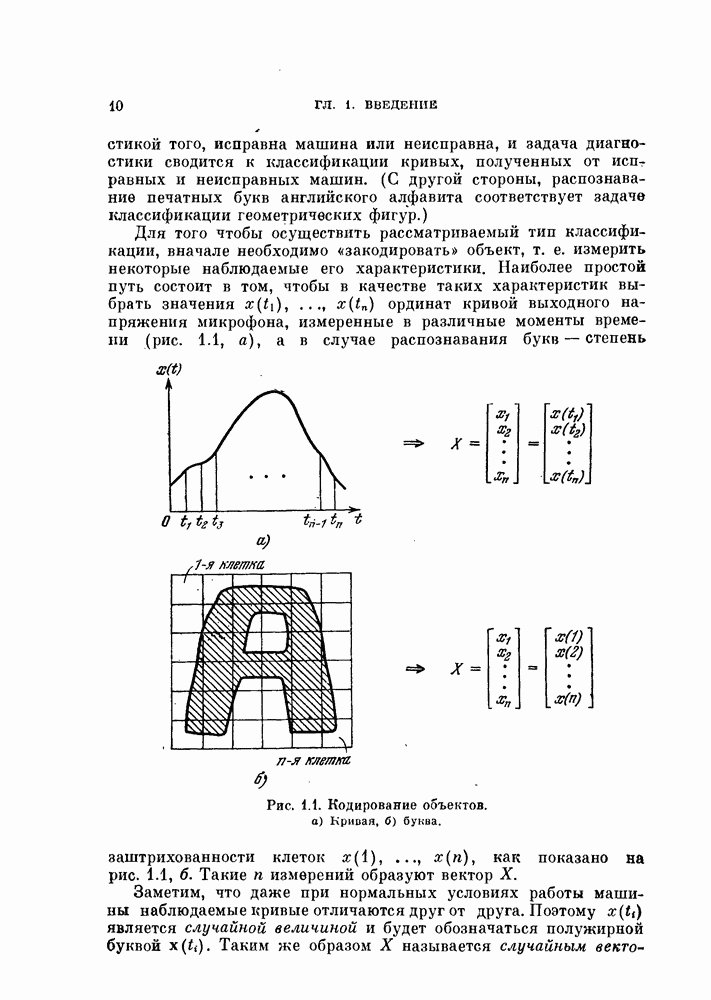
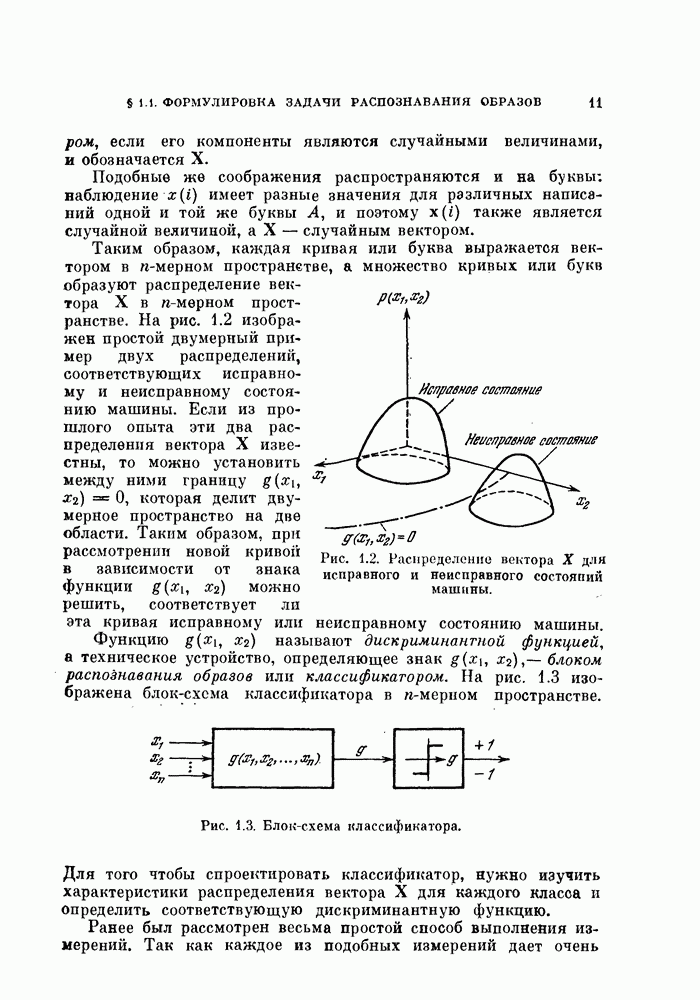
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
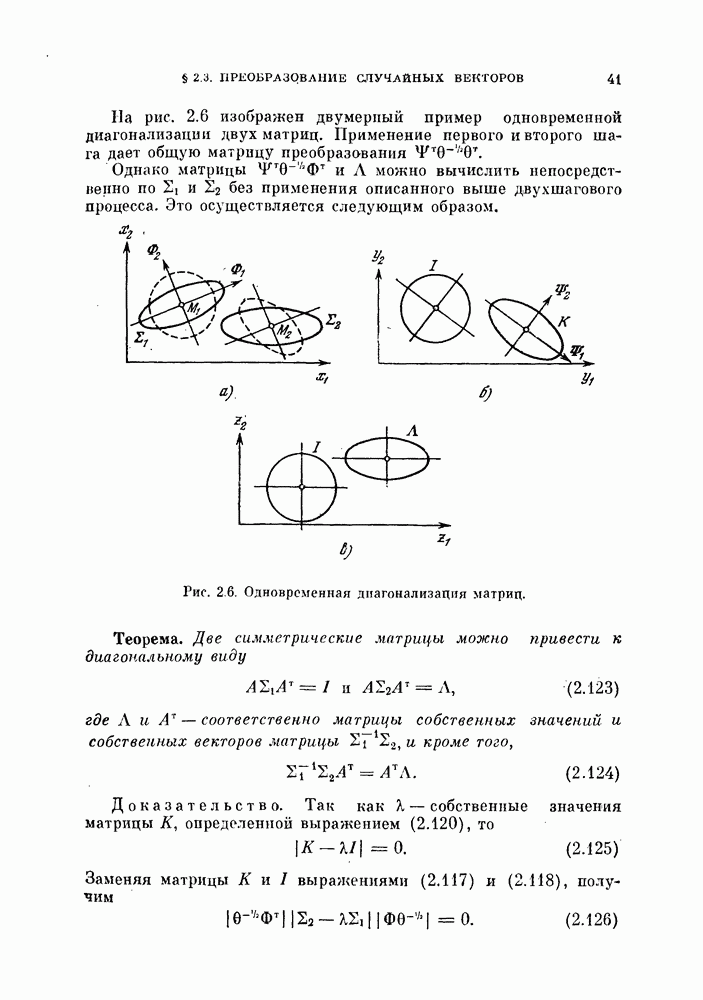
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
- 2.3.5. Одновременная диагонализация двух матриц.
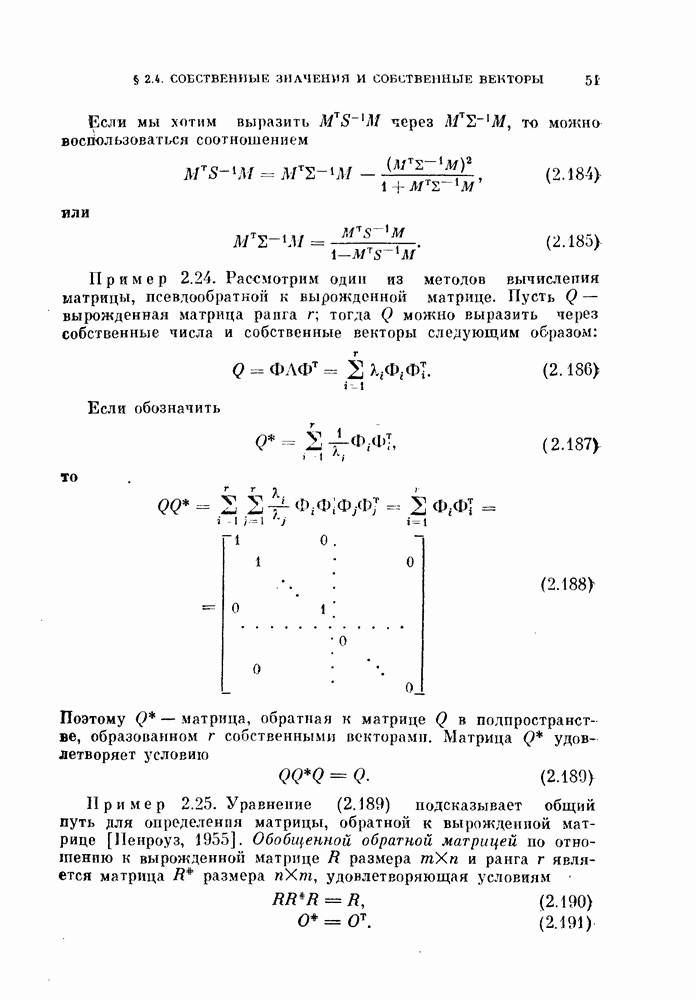
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
- 7.2.3. Задача поиска максимума функции регрессии.
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
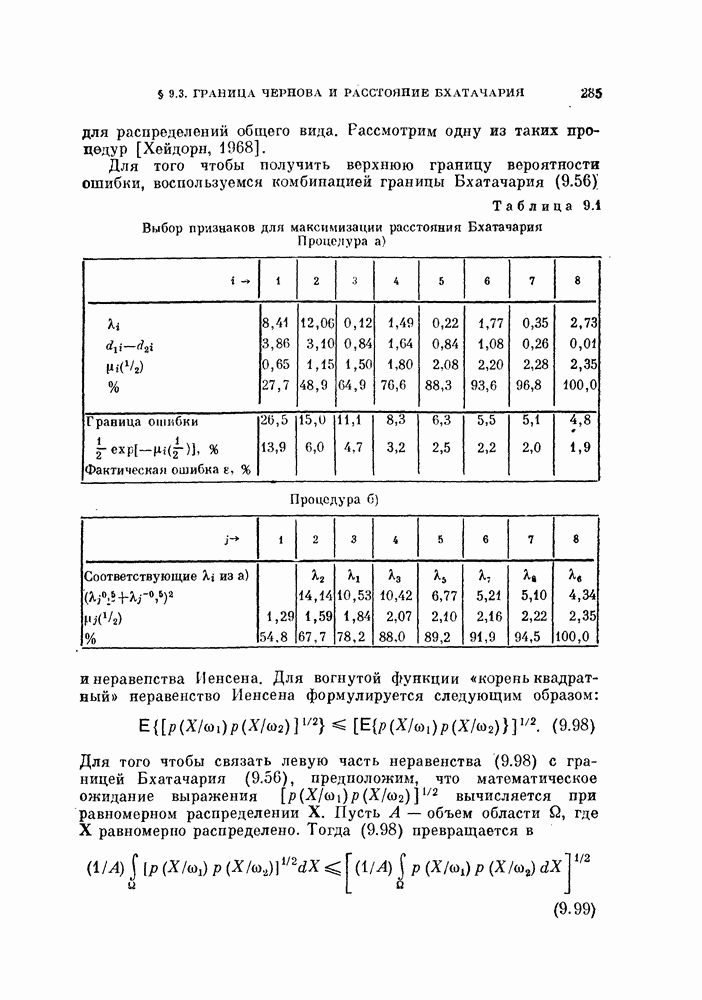
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
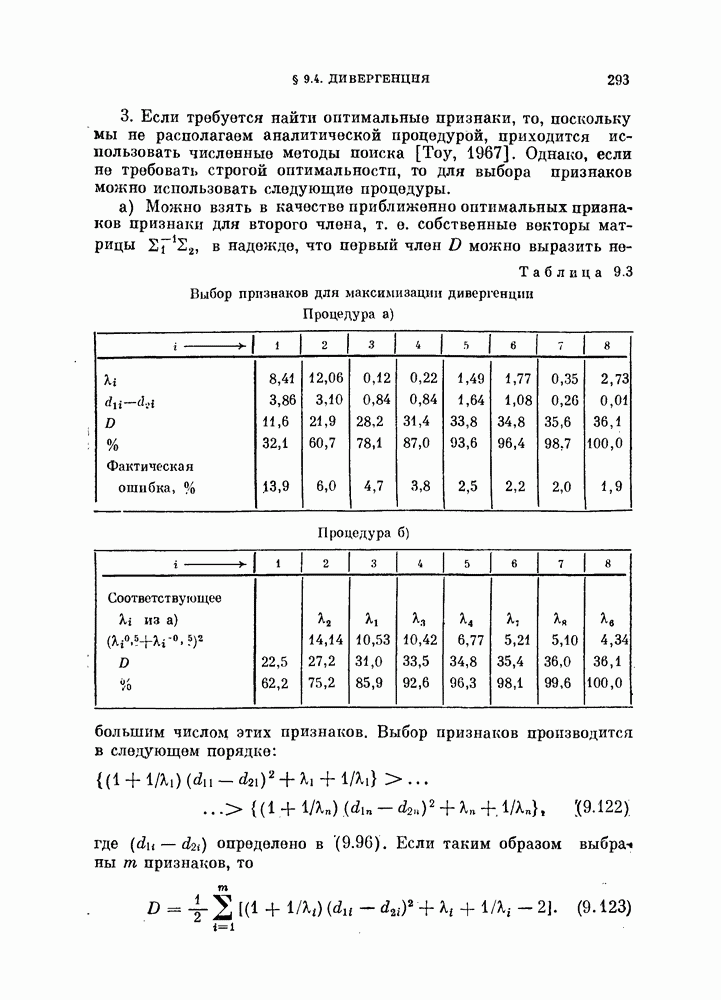
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА