| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4.3. Метод разбиения выборки.
Для того чтобы разбить имеющиеся объекты на обучающую и экзаменационную выборки  изучим, как это разбиение влияет на дисперсию оценки вероятности ошибки.
изучим, как это разбиение влияет на дисперсию оценки вероятности ошибки.
Вначале предположим, что имеется бесконечное число объектов для синтеза классификатора и  объектов для проверки его качества. При бесконечном числе объектов синтезируемый классификатор является классификатором для истинных распределений, и его вклад в дисперсию равен нулю. Для фиксированного классификатора организуем селективную выборку. В этом случае распределение опенки вероятности ошибки подчиняется биномиальному закону с дисперсией
объектов для проверки его качества. При бесконечном числе объектов синтезируемый классификатор является классификатором для истинных распределений, и его вклад в дисперсию равен нулю. Для фиксированного классификатора организуем селективную выборку. В этом случае распределение опенки вероятности ошибки подчиняется биномиальному закону с дисперсией

где  — истинная вероятность ошибки
— истинная вероятность ошибки  класса (см. выражение (5.131)).
класса (см. выражение (5.131)).
С другой стороны, если имеется  объектов для синтеза классификатора и бесконечное число экзаменационных объектов, то оценка вероятности ошибки выражается следующим образом:
объектов для синтеза классификатора и бесконечное число экзаменационных объектов, то оценка вероятности ошибки выражается следующим образом:

где  — область пространства признаков, соответствующая
— область пространства признаков, соответствующая  классу. В этом случае подынтегральные выражения постоянны, но граница этих областей изменяется в зависимости от выборки из
классу. В этом случае подынтегральные выражения постоянны, но граница этих областей изменяется в зависимости от выборки из  объектов.
объектов.
Дисперсию оценки  для плотности вероятности генеральной совокупности вычислить сложно. Однако в случае нормальных распределений объектов в классах с равными ковариационными матрицами интегралы в (5.142) можно преобразовать к одномерным интегралам
для плотности вероятности генеральной совокупности вычислить сложно. Однако в случае нормальных распределений объектов в классах с равными ковариационными матрицами интегралы в (5.142) можно преобразовать к одномерным интегралам

где  определяются условными математическими ожиданиями:
определяются условными математическими ожиданиями:

Это преобразование основано на том, что для нормальных распределений с равными ковариационными матрицами байесовский классификатор — линейный, а распределение отношения правдоподобия также является нормальным распределением. Подобные выражения встречались в формулах (3.35) — (3.38).
Заметим, что даже если две истинные ковариационные матрицы равны, то оценки их различны. Однако для упрощения предположим, что обе эти оценки равиы и имеют вид

где  число объектов класса
число объектов класса  используемых для синтеза классификатора.
используемых для синтеза классификатора.
Математическое ожидание оценки  было определено в работе [Окомото, 1963]. Так как выражение для этого математического ожидания достаточно громоздкое, то здесь приводится
было определено в работе [Окомото, 1963]. Так как выражение для этого математического ожидания достаточно громоздкое, то здесь приводится
наипростейший случай, когда 

где  — расстояние между двумя векторами математических ожиданий, определяемое по формуле
— расстояние между двумя векторами математических ожиданий, определяемое по формуле

Величина  является минимальной вероятностью ошибки байесовского классификатора. Так как
является минимальной вероятностью ошибки байесовского классификатора. Так как  — минимальное значение оценки
— минимальное значение оценки  то распределение для
то распределение для  является причинным. Поэтому можно определить оценку дисперсии величины
является причинным. Поэтому можно определить оценку дисперсии величины  , основанную на ее математическом ожидании. Предположим, что плотность вероятности Де является плотностью вероятности гамма-распределения, которое включает в себя широкий класс причин
, основанную на ее математическом ожидании. Предположим, что плотность вероятности Де является плотностью вероятности гамма-распределения, которое включает в себя широкий класс причин  распределений. Тогда
распределений. Тогда

Математическое ожидание и дисперсия плотности (5.151) равны:

Исключая с, получим верхнюю границу дисперсии  , т. е.
, т. е.

Таким образом, степень влияния числа обучающих объектов на оценку вероятности ошибки  в случае нормальных распределений с равными ковариационными матрицами и равными
в случае нормальных распределений с равными ковариационными матрицами и равными  риорными вероятностями равна
риорными вероятностями равна

Величину  из (5.155) следует сравнить с величиной
из (5.155) следует сравнить с величиной  которая характеризует влияние числа объектов в экзаменациовной выборке на оценку вероятности ошибки. Значение
которая характеризует влияние числа объектов в экзаменациовной выборке на оценку вероятности ошибки. Значение  получается
получается
подстановкой в формулу (5.141) значений 

Величины  из выражения (5.149) и
из выражения (5.149) и  из выражения (5.156) связаны однозначно. Поэтому можно установить зависимость между величиной
из выражения (5.156) связаны однозначно. Поэтому можно установить зависимость между величиной  в (5.155) с величиной
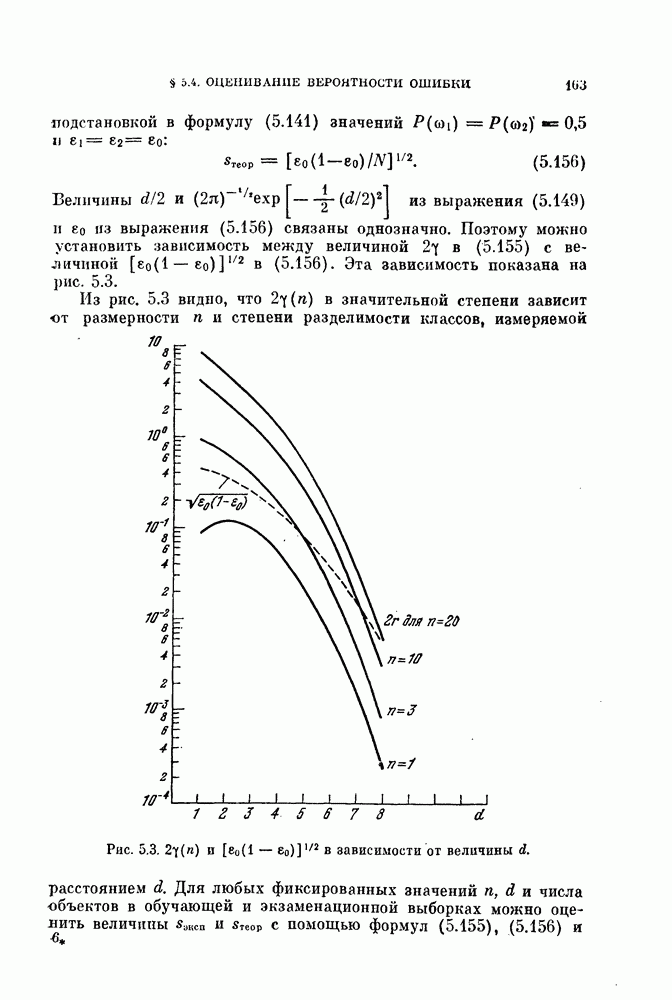
в (5.155) с величиной  в (5.156). Эта зависимость показана на рис. 5.3.
в (5.156). Эта зависимость показана на рис. 5.3.
Из рис. 5.3 видно, что  в значительной степени зависит
в значительной степени зависит  размерности
размерности  и степени разделимости классов, измеряемой расстоянием
и степени разделимости классов, измеряемой расстоянием 
Рис. 5.3. (см. скан)  в зависимости от величины
в зависимости от величины 
Для любых фиксированных значений  и числа объектов в обучающей и экзаменационной выборках можно оценить величины
и числа объектов в обучающей и экзаменационной выборках можно оценить величины  и
и  с помощью формул (5.155), (5.156) и
с помощью формул (5.155), (5.156) и
рис. 5.3, Поскольку с ростом  величина
величина  уменьшается не быстрее чем
уменьшается не быстрее чем  уменьшается не быстрее чем
уменьшается не быстрее чем  то для многих случаев большее число объектов должно быть использовано для экзамена, а не для проектирования классификатора.
то для многих случаев большее число объектов должно быть использовано для экзамена, а не для проектирования классификатора.
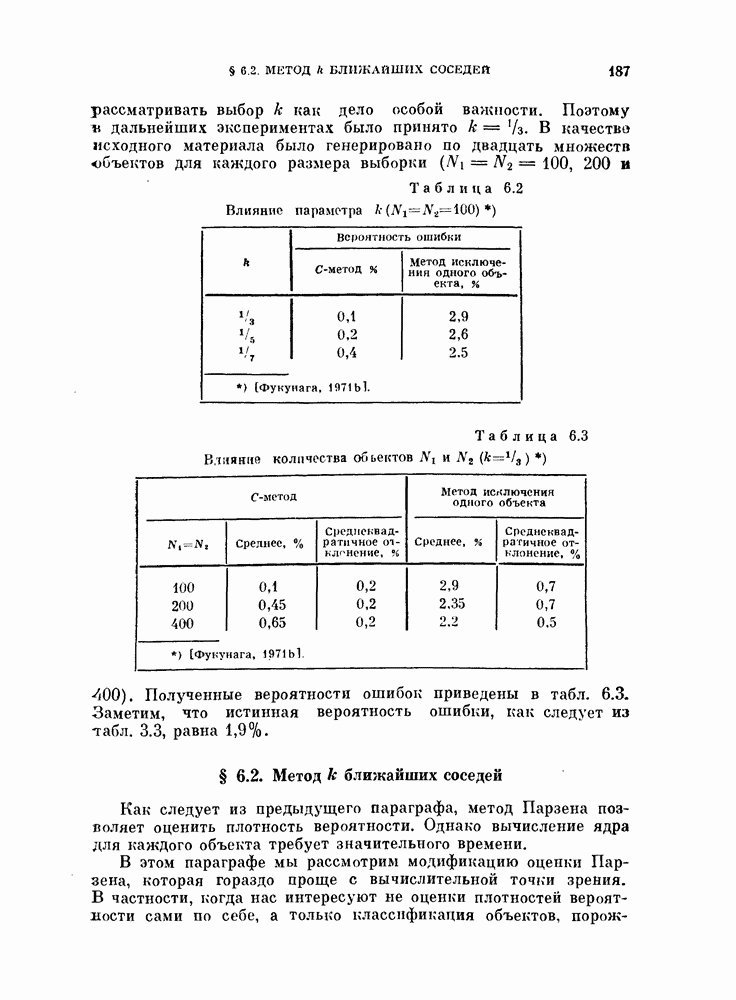
Пример 5.7. Для распространения вышеприведенного результата на случай нормальных распределений с неравными ковариационными матрицами были проведены эксперименты для стандартных данных  Размер обучающей выборки для каждого класса выбирался равным 12, 50, 100, 200 и 400 объектам
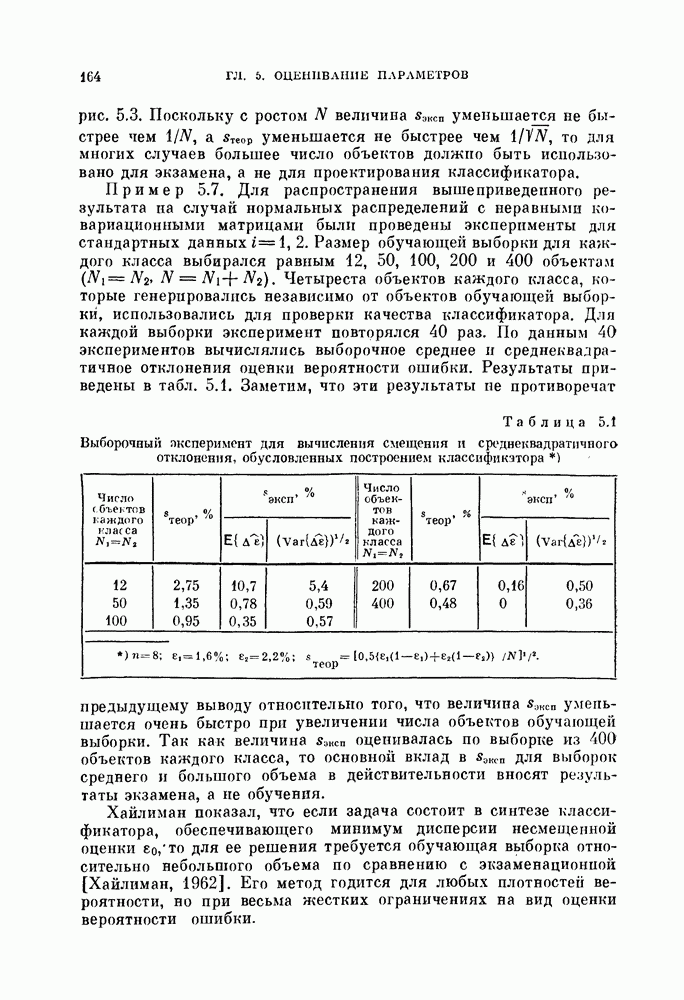
Размер обучающей выборки для каждого класса выбирался равным 12, 50, 100, 200 и 400 объектам  Четыреста объектов каждого класса, которые генерировались независимо от объектов обучающей выборки, использовались для проверки качества классификатора. Для каждой выборки эксперимент повторялся 40 раз. По данным 40 экспериментов вычислялись выборочное среднее и среднеквадратичное отклонения оценки вероятности ошибки. Результаты приведены в табл. 5.1. Заметим, что эти результаты не противоречат
Четыреста объектов каждого класса, которые генерировались независимо от объектов обучающей выборки, использовались для проверки качества классификатора. Для каждой выборки эксперимент повторялся 40 раз. По данным 40 экспериментов вычислялись выборочное среднее и среднеквадратичное отклонения оценки вероятности ошибки. Результаты приведены в табл. 5.1. Заметим, что эти результаты не противоречат
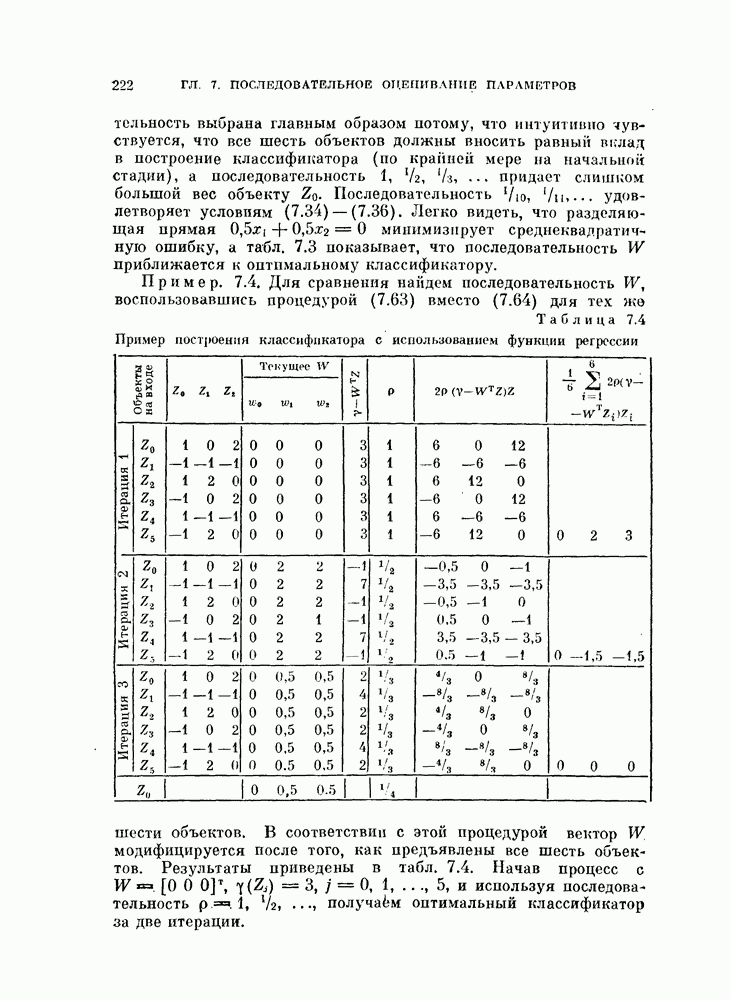
Таблица 5.1. Выборочный эксперимент для вычисления смещения и среднеквадратичного отклонения, обусловленных построением классификатора

предыдущему выводу относительно того, что величина  уменьшается очень быстро при увеличении числа объектов обучающей выборки. Так как величина
уменьшается очень быстро при увеличении числа объектов обучающей выборки. Так как величина  оценивалась по выборке из 400 объектов каждого класса, то основной вклад в
оценивалась по выборке из 400 объектов каждого класса, то основной вклад в  для выборок среднего и большого объема в действительности вносят результаты экзамена, а не обучения.
для выборок среднего и большого объема в действительности вносят результаты экзамена, а не обучения.
Хайлиман показал, что если задача состоит в синтезе классификатора, обеспечивающего минимум дисперсии несмещенной оценки  для ее решения требуется обучающая выборка относительно небольшого объема по сравнению с экзаменационной [Хайлиман, 1962]. Его метод годится для любых плотностей вероятности, но при весьма жестких ограничениях на вид оценки вероятности ошибки.
для ее решения требуется обучающая выборка относительно небольшого объема по сравнению с экзаменационной [Хайлиман, 1962]. Его метод годится для любых плотностей вероятности, но при весьма жестких ограничениях на вид оценки вероятности ошибки.
Исключение задания класса для объектов экзаменационной выборки.
Для того чтобы оценить вероятность ошибки как при обучении, так и на экзамене, требуются выборки объектов, в которых известно, какой объект к какому конкретному классу принадлежит. Однако в некоторых случаях получение такой информации связано с большими затратами.
Рассмотрим метод оценки вероятности ошибки, не требующий информации о принадлежности объектов экзаменационной выборки к конкретному классу [Чоу, 1970]. Применение этого метода наиболее эффективно в случае, когда при оптимальном разбиении выборки на обучающую и экзаменационную, число объектов в экзаменационной выборке больше, чем в обучающей.
Введем критическую область для задач классификации М классов:

где  - плотность вероятности смеси,
- плотность вероятности смеси,  критический у ровень,
критический у ровень,  Условие (5.157) устанавливает, что если для данного объекта X значения
Условие (5.157) устанавливает, что если для данного объекта X значения  вычисленные для каждого класса М, не превышают величины
вычисленные для каждого класса М, не превышают величины  то объект X не классифицируют вообще; в противном случае объект X классифицируют и относят его к
то объект X не классифицируют вообще; в противном случае объект X классифицируют и относят его к  классу. Таким образом, вся область значений X делится на критическую область
классу. Таким образом, вся область значений X делится на критическую область  и допустимую область
и допустимую область  причем размеры обеих областей являются функциями критического уровня
причем размеры обеих областей являются функциями критического уровня 
При таком решающем правиле вероятность ошибки  коэффициент отклонения
коэффициент отклонения  и коэффициент правильного распознавания
и коэффициент правильного распознавания  будут равны
будут равны

и

Предположим, что область отклонения увеличивается на  за счет изменения значения
за счет изменения значения  на
на  Тогда те X, которые раньше распознавались правильно, теперь отклоняются:
Тогда те X, которые раньше распознавались правильно, теперь отклоняются:

Интегрируя (5.161) в пределах области  получим
получим

где  — приращения
— приращения  вызванные изменением
вызванные изменением  формулы (5.160) следует, что неравенство (5.162) можно переписать следующим образом:
формулы (5.160) следует, что неравенство (5.162) можно переписать следующим образом:

Суммируя по всем дискретным значениям  от 0 до
от 0 до  , получим
, получим

Полагая  получаем интеграл Стилтьеса
получаем интеграл Стилтьеса

Уравнение (5.165) показывает, что вероятность ошибки  может быть вычислена после того, как известна зависимость между значениями
может быть вычислена после того, как известна зависимость между значениями  и
и  Из решающего правила (5.157) следует, что при
Из решающего правила (5.157) следует, что при  область отклонения отсутствует, так что байесовская ошибка
область отклонения отсутствует, так что байесовская ошибка  Кроме того, из формулы (5.165) можно установить взаимосвязь между вероятностью ошибки и коэффициентом отклонения, так как изменение вероятности ошибки можно вычислить как функцию от изменения коэффициента отклонения.
Кроме того, из формулы (5.165) можно установить взаимосвязь между вероятностью ошибки и коэффициентом отклонения, так как изменение вероятности ошибки можно вычислить как функцию от изменения коэффициента отклонения.

Рис. 5.4. Приращение областей отклонения. 
Воспользуемся выражением (5.165) для исключения задания класса объектов экзаменационной выборки. Для этого поступим следующим образом.
1. Для определения  при
при  где
где  — дискретный шаг переменной
— дискретный шаг переменной  будем использовать относительно дорогостоящие классифицируемые объекты. Это показано на рис. 5.4.
будем использовать относительно дорогостоящие классифицируемые объекты. Это показано на рис. 5.4.
2. Подсчитаем число неклассифицированных объектов экзаменационной выборки, которые попали в область  разделим это число на общее число объектов и обозначим полученное отношение через
разделим это число на общее число объектов и обозначим полученное отношение через 
3. Тогда из выражения (5.165) следует, что оценка вероятности ошибки

В описанной процедуре использовалось то, что коэффициент отклонения является функцией от плотности вероятности смеси, а не от плотностей вероятности отдельных классов. Поэтому после того, как по классифицированным объектам найдены расширенные области отклонения, в дальнейшем для оценивания  и вероятности ошибки
и вероятности ошибки  нет необходимости использовать классифицированные объекты.
нет необходимости использовать классифицированные объекты.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
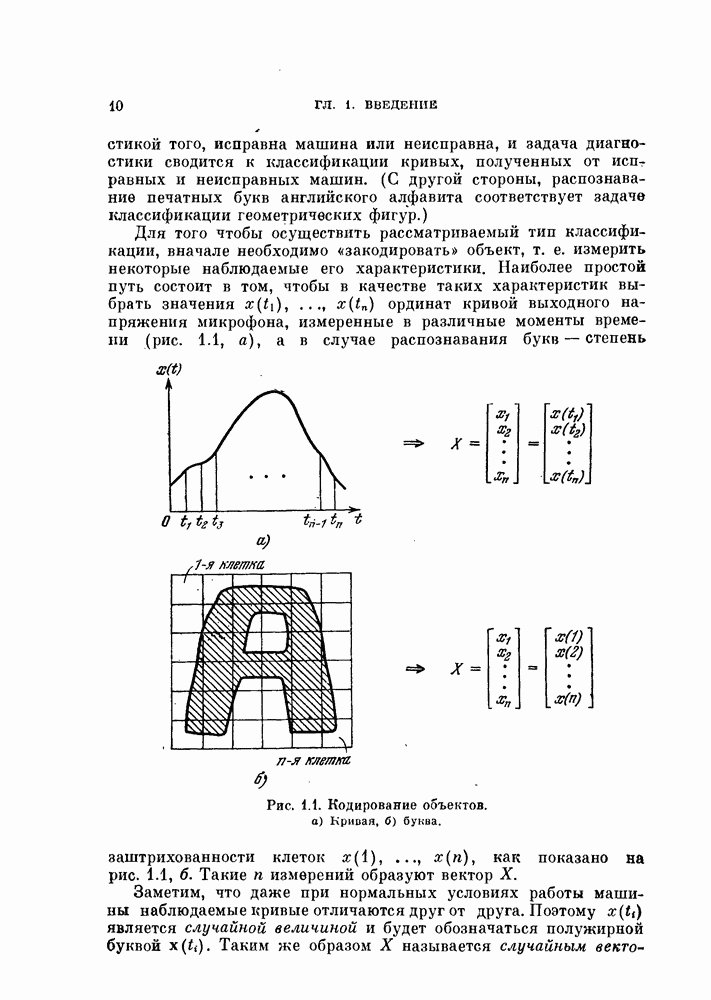
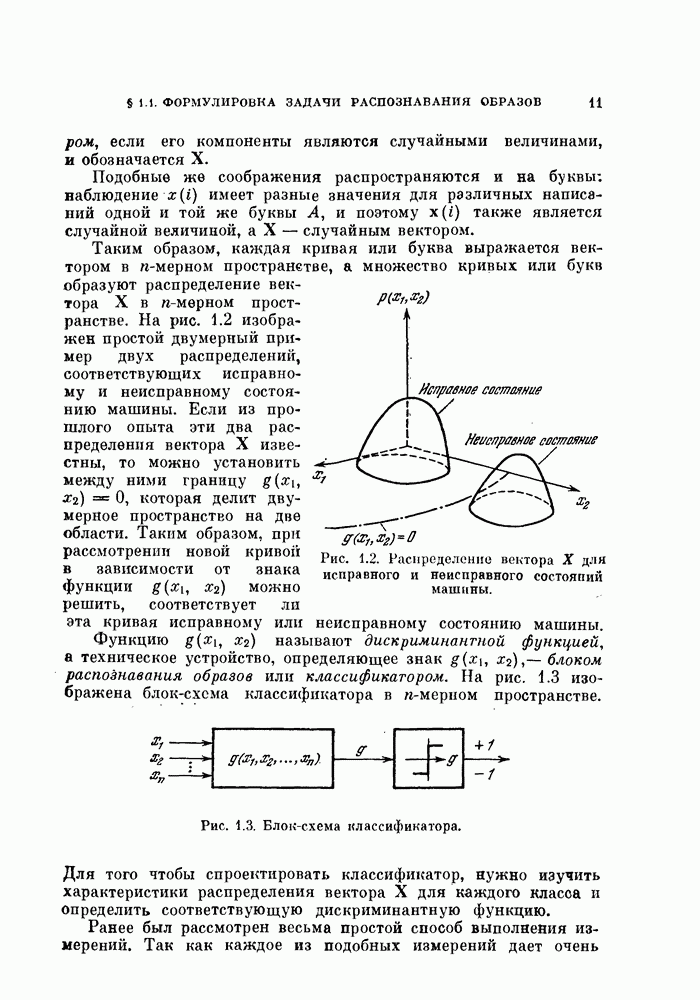
- § 1.1. Формулировка задачи распознавания образов
- § 1.2. Обзор содержания книги по главам
- Глава 2. СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ СВОЙСТВА
- § 2.1. Случайные векторы и их распределение
- 2.1.2. Условные плотности вероятности.
- 2.1.3. Параметры распределения.
- 2.1.4. Некоррелированные, ортогональные, независимые случайные векторы.
- § 2.2. Свойства распределений
- 2.2.1. Характеристические функции.
- 2.2.2. Нормальные распределения.
- 2.2.3. Стохастическая сходимость.
- § 2.3. Преобразование случайных векторов
- 2.3.2. Линейное преобразование.
- 2.3.3. Ортонормированное преобразование.
- 2.3.4. Декоррелирующее преобразование.
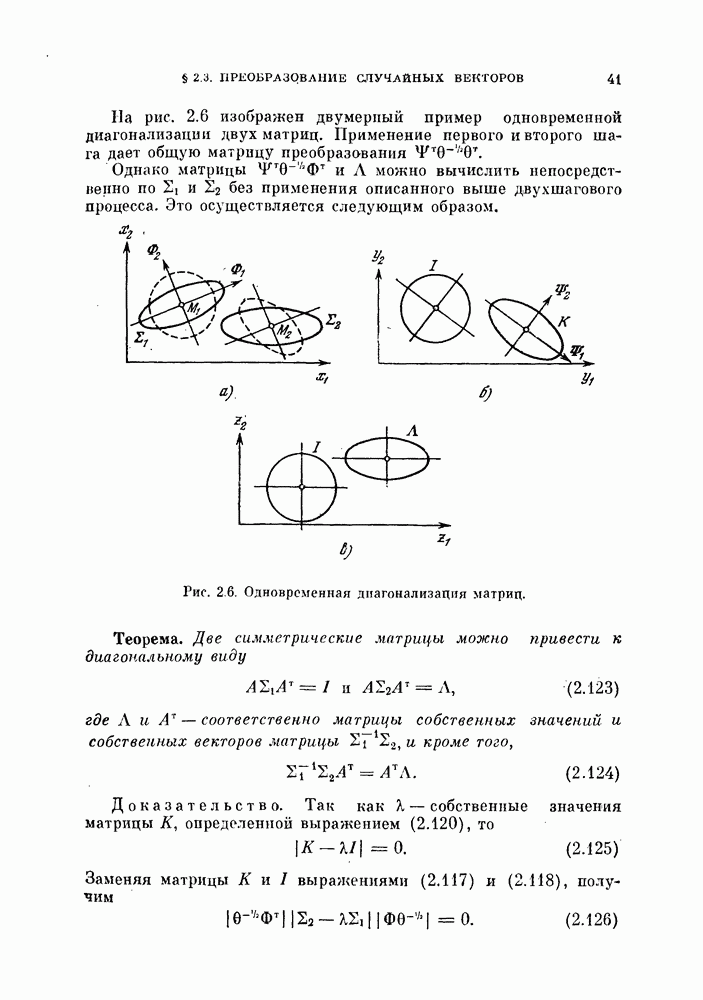
- 2.3.5. Одновременная диагонализация двух матриц.
- § 2.4. Свойства собственных значений и собственных векторов
- 2.4.2. Положительная определенность.
- 2.4.3. След матрицы.
- 2.4.4. Определитель и ранг матрицы.
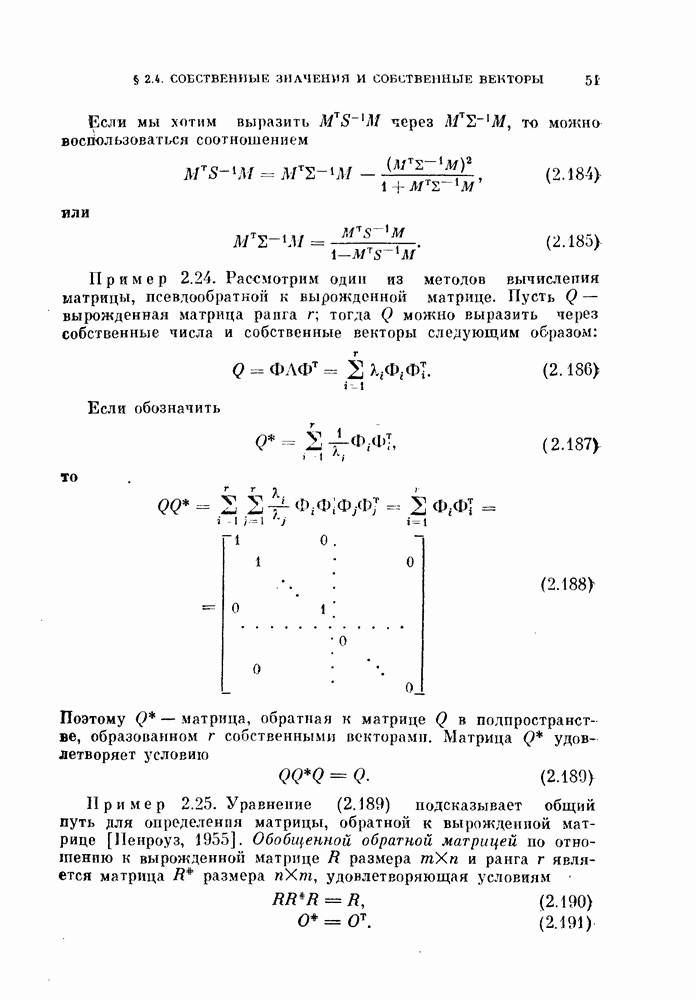
- 2.4.5. Обращение матриц.
- 2.4.6. Теория возмущений.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 3. ПРОВЕРКА ГИПОТЕЗ
- § 3.1. Проверка простых гипотез
- 3.1.2. Байесовское решающее правило, минимизирующее функцию риска.
- 3.1.3. Критерий Неймана — Пирсона.
- 3.1.4. Минимаксный критерий.
- § 3.2. Вероятность ошибки при проверке гипотез
- 3.2.2. Независимые случайные величины.
- 3.2.3. Вероятность ошибки для нормальных случайных векторов X.
- § 3.3. Верхние границы вероятности ошибки
- 3.3.2. Выражения для верхних границ в случае нормальных распределений.
- § 3.4. Другие критерии проверки гипотез
- 3.4.2. Критерий проверки сложных гипотез.
- § 3.5. Последовательная проверка гипотез
- 3.5.1. Последовательный критерий Вальда.
- 3.5.2. Реализация последовательного критерия Вальда.
- 3.5.3. Байесовский последовательный критерий.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 4. ЛИНЕЙНЫЕ КЛАССИФИКАТОРЫ
- § 4.1. Байесовский линейный классификатор
- § 4.2. Линейная разделяющая функция, минимизирующая вероятность ошибки решения
- 4.2.1. Линейная разделяющая функция, минимизирующая вероятность ошибки.
- 4.2.2. Обобщенная формула для различных критериев.
- § 4.3. Линейная разделяющая функция, минимизирующая среднеквадратичную ошибку решения
- 4.3.2. Совместная нормировка смеси в случае нормальных распределений.
- § 4.4. Требуемый выход и среднеквадратичная ошибка решения
- 4.4.2. Доказательство сходимости для случая линейной разделимости классов.
- § 4.5. Другие разделяющие функции
- 4.5.1. Линейные разделяющие функции для бинарных входов.
- 4.5.2. Кусочно-линейные разделяющие функции.
- 4.5.3. Обобщенные линейные разделяющие функции.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 5. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 5.1. Оценивание неслучайных параметров
- 5.1.2. Оценки моментов.
- 5.1.3. Оценка максимального правдоподобия.
- 5.1.4. Достаточная оценка.
- § 5.2. Оценивание случайных параметров
- 5.2.3. Оценка, минимизирующая среднеквадратичную ошибку.
- 5.2.4. Выпуклые и симметричные функции штрафа.
- § 5.3. Интервальное оценивание
- 5.3.2. Порядковые статистики.
- 5.3.3. Толерантные пределы для распределений.
- § 5.4. Оценивание вероятности ошибки
- 5.4.2. Оценка вероятности ошибки, когда классификатор заранее не задан.
- 5.4.3. Метод разбиения выборки.
- 5.4.4. Метод исключения одного объекта в случае нормальных распределений.
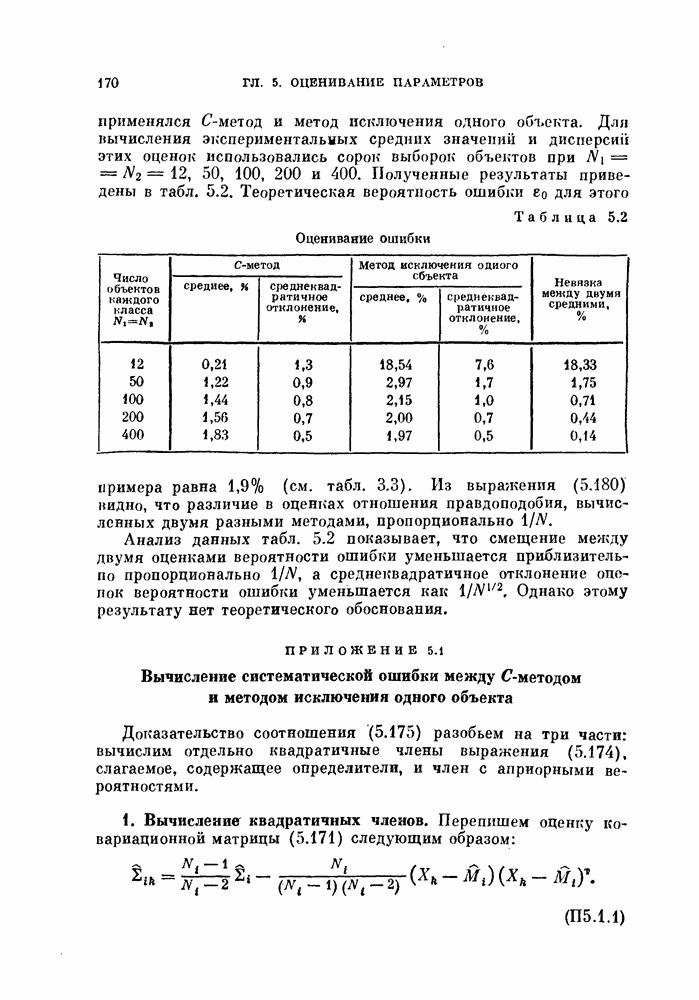
- ПРИЛОЖЕНИЕ 5.1. Вычисление систематической ошибки между С-методом и методом исключения одного объекта
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 6. ОЦЕНИВАНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ
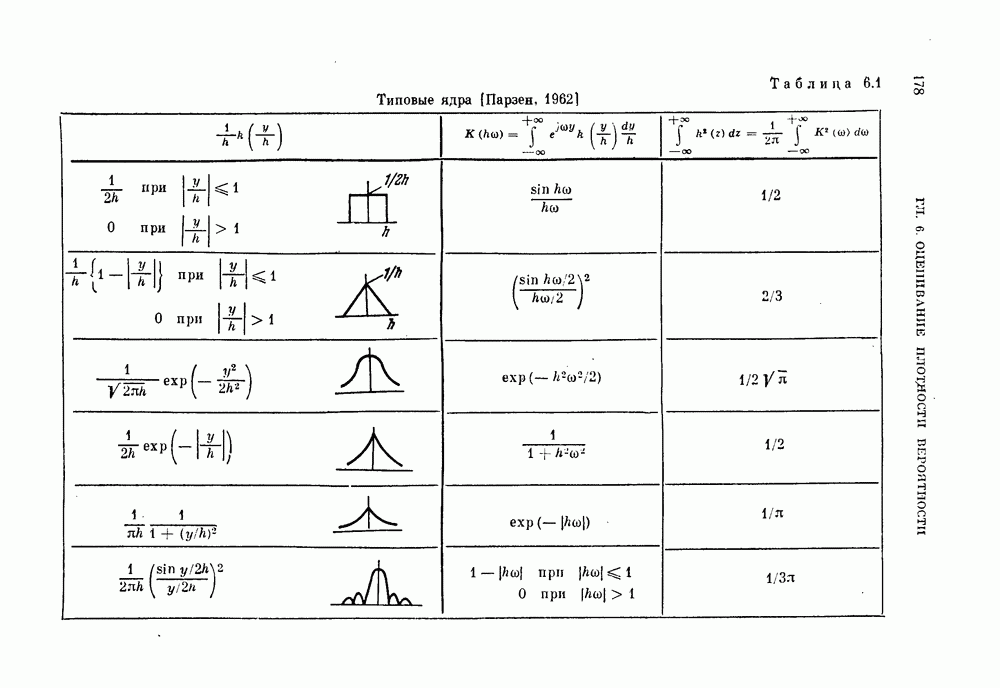
- § 6.1. Оценка Парзена
- 6.1.2. Доказательство асимптотической несмещенности и состоятельности.
- 6.1.3. Равномерная сходимость и оценивание моды.
- 6.1.4. Обобщение на случай многомерной плотности вероятности.
- § 6.2. Метод k ближайших соседей
- 6.2.2. Решающее правило, основанное на методе k ближайших соседей.
- 6.2.3. Обобщение на случай нескольких классов.
- 6.2.4. Модифицированное правило k ближайших соседей.
- § 6.3. Метод гистограмм
- § 6.4. Разложение по базисным функциям
- 6.4.2. Плотность вероятности в случае двоичных переменных.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 7. ПОСЛЕДОВАТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- § 7.1. Последовательная корректировка линейного классификатора
- 7.1.1. Линейный классификатор для задач распознавания двух классов.
- 7.1.2. Доказательство сходимости для случая линейной разделимости классов.
- 7.1.3. Линейный классификатор для задач распознавания со многими классами.
- § 7.2. Стохастическая аппроксимация
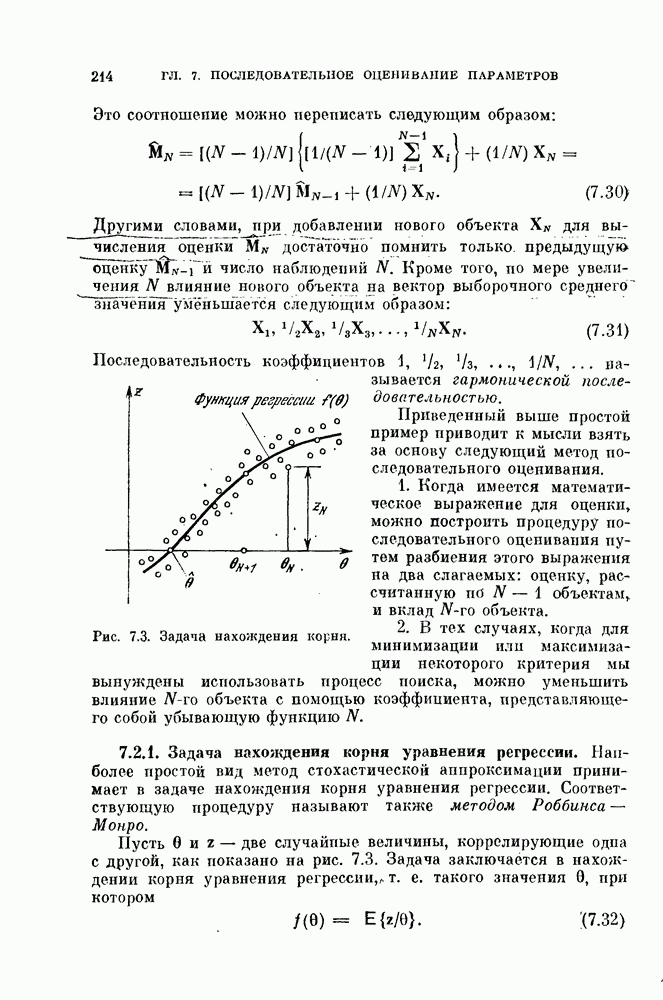
- 7.2.1. Задача нахождения корня уравнения регрессии.
- 7.2.2. Доказательство сходимости метода Роббинса — Монро
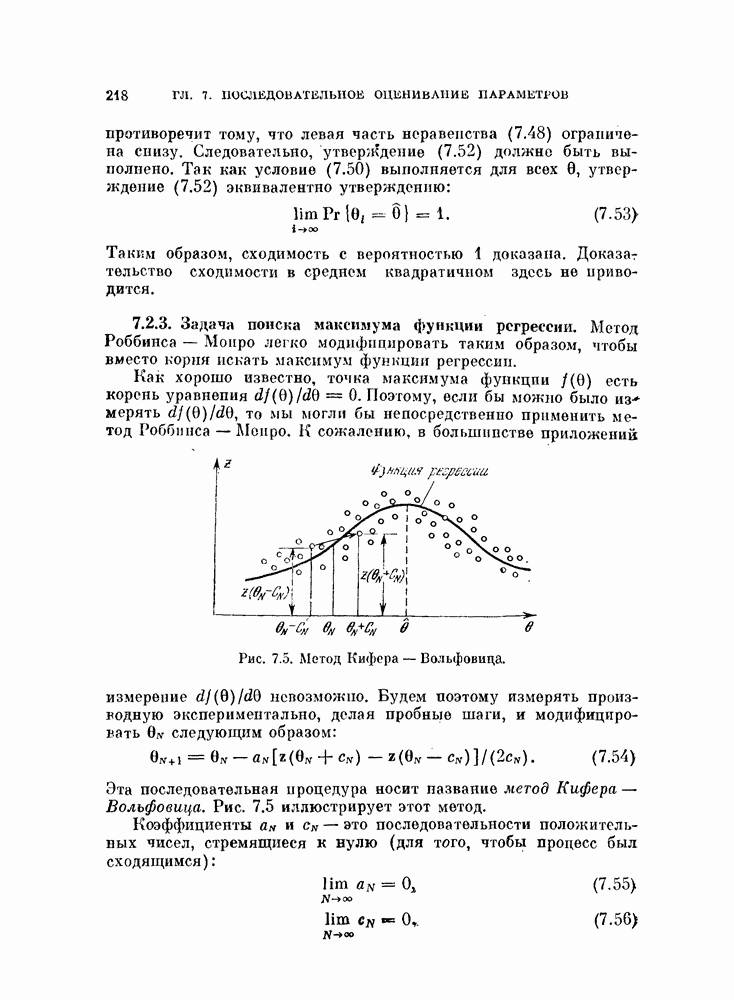
- 7.2.3. Задача поиска максимума функции регрессии.
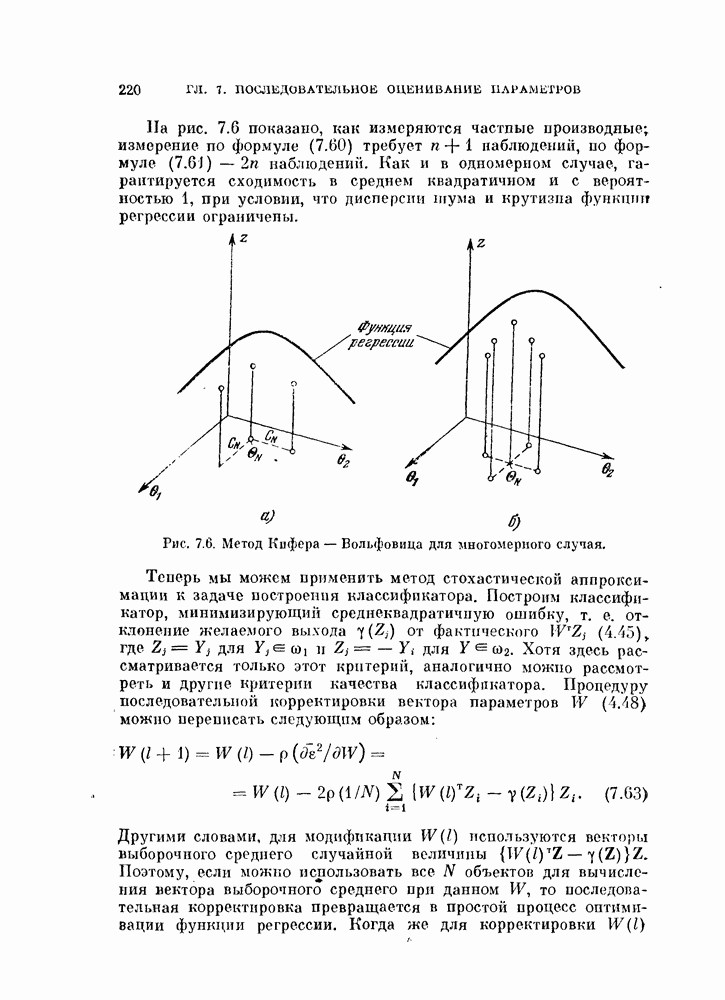
- 7.2.4. Обобщение на многомерный случай.
- 7.2.5. Метед потенциальных функций.
- 7.2.6. Ускорение сходимости.
- § 7.3. Последовательное байесовское оценивание
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 8. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА ДЛЯ СЛУЧАЯ ОДНОГО РАСПРЕДЕЛЕНИЯ
- § 8.1. Дискретное разложение Карунена — Лоева
- 8.1.2. Проблема нормализации.
- § 8.2. Другие критерии для случая одного распределения
- 8.2.2. Энтропия совокупности.
- 8.2.3. Общие замечания, относящиеся к выбору признаков в случае одного распределения.
- § 8.3. Разложение Карунена — Лоева для случайных процессов
- 8.3.2. Стационарный процесс.
- § 8.4. Оценивание собственных значений и собственных векторов
- 8.4.1. Определение размерности.
- 8.4.2. Оценивание собственных значений и собственных векторов.
- 8.4.3. Доминирующие собственные значения.
- ПРИЛОЖЕНИЕ 8.2. Ускоренное вычисление собственных значений и собственных векторов
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 9. ВЫБОР ПРИЗНАКОВ И ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ
- § 9.1. Общие свойства разделимости классов
- § 9.2. Дискриминантный анализ
- 9.2.2. Выбор признаков, максимизирующих критерий J1
- 9.2.3. Выбор признаков, максимизирующих критерий J2
- 9.2.4. Выбор признаков, максимизирующих критерий J3
- 9.2.5. Выбор признаков, максимизирующих критерий J4
- 9.2.6. Обобщение на случай многих классов.
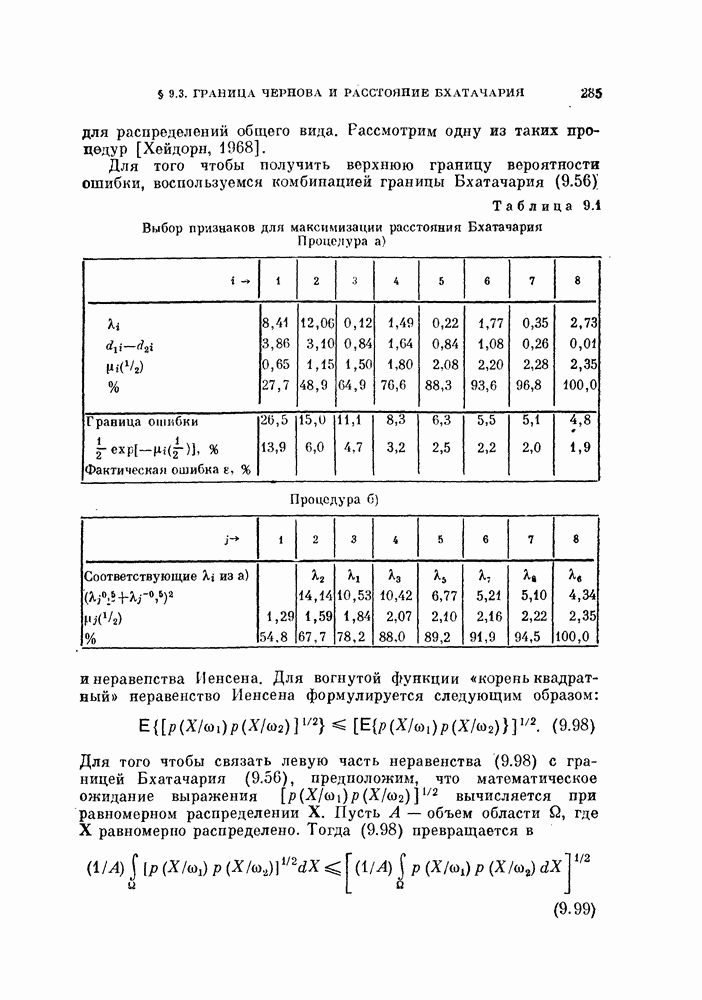
- § 9.3. Граница Чернова и расстояние Бхатачария
- 9.3.2. Выбор признаков для нормальных распределений.
- 9.3.3. Верхняя граница для распределений, отличных от нормального.
- 9.3.4. Случай многих классов.
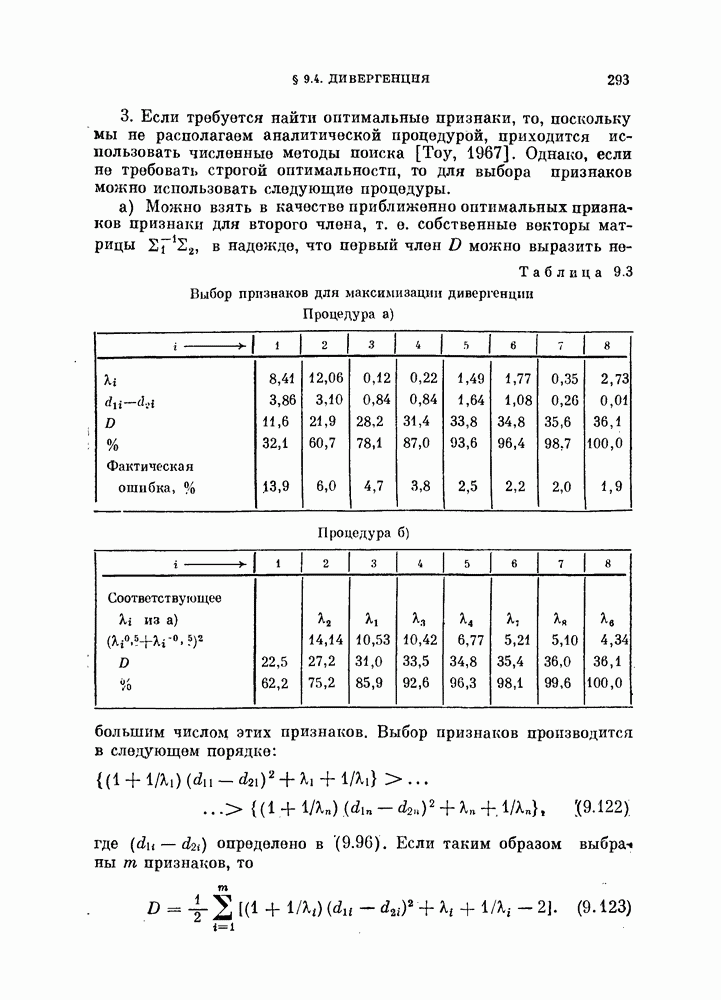
- § 9.4. Дивергенция
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 10. НЕЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ ИСХОДНОГО ПРОСТРАНСТВА
- 10.1.1. Локальные свойства распределения.
- 10.1.2. Неитеративный алгоритм.
- 10.1.3. Итеративный алгоритм.
- § 10.2. Улучшение разделимости с помощью нелинейного преобразования
- 10.2.1. Улучшение разделимости, сохранение структуры, расстояния между объектами выборки.
- 10.2.2. Неитеративный алгоритм.
- § 10.3. Двумерные отображения
- 10.3.2. Расстояние до двух фиксированных точек.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- Глава 11. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
- § 11.1. Алгоритм автоматической классификации
- 11.1.2. Определение числа классов.
- § 11.2. Параметрические критерии качества классификации
- 11.2.2. Сходимость процедуры, основанной на правиле ближайшего среднего.
- § 11.3. Иепараметрические критерии качества классификации
- 11.3.2. Непараметрический алгоритм автоматической классификации.
- 11.3.3. Асимптотические свойства процедуры.
- § 11.4. Другие процедуры автоматической классификации
- 11.4.2. Иерархическая классификация.
- 11.4.3. Классификация в режиме диалога.
- ЗАДАНИЕ НА СОСТАВЛЕНИЕ ПРОГРАММ
- ЛИТЕРАТУРА